| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202243646 | |
| Published online | 10 August 2022 | |
Letter to the Editor
Intervelocity of galaxy pairs in ΛCDM
Observed velocity peak at ∼130 km s−1 not unique to modified Newtonian dynamics
Leibniz-Institute for Astrophysics, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: mpawlowski@aip.de
Received:
26
March
2022
Accepted:
16
July
2022
Context. Observational studies of pairs of galaxies have uncovered that their differential line-of-sight velocities indicate the presence of a peak in their three-dimensional (3D) intervelocity distribution at 130−150 km s−1. It had been argued that galaxy pairs in the standard model of cosmology, ΛCDM, should not exhibit such an intervelocity peak, while modified Newtonian dynamics (MOND) predicts such a preferred intervelocity for paired galaxies. However, no direct comparison with ΛCDM applying the same selection criteria and methodology as the observational studies has been performed at present, placing the comparison on uncertain footing.
Aims. To rectify this situation, we investigate this potential challenge to ΛCDM by determining whether an analog of the observed intervelocity peak is present in galaxy pairs within the IllustrisTNG-300 cosmological simulation.
Methods. We identified galaxy pairs following the observational study’s selection criteria, measured their projected velocity difference, and analyzed both the de-projected and the full velocity difference for this galaxy pair sample in the simulation.
Results. We recovered a deprojected intervelocity peak at ∼130 km s−1 for galaxy pairs selected from the simulation. The full 3D velocity information available for the pairs in the simulation also reveals a clear preference for this intervelocity.
Conclusions. The intervelocity peak among galaxy pairs does not appear to be a feature unique to MOND, as it is also present in ΛCDM. Thus, it cannot be claimed to be a unique success characteristic of either theory over the other. Developing the galaxy pair intervelocity into a test of gravity in the low-acceleration regime will require more detailed studies to identify measurable differences among the models.
Key words: galaxies: groups: general / galaxies: interactions / galaxies: kinematics and dynamics / galaxies: statistics / dark matter
© M. S. Pawlowski et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Nottale & Chamaraux (2018a) obtained one of the largest samples of galaxy pairs (13 114 pairs) based on spectroscopic velocity information, using observed galaxies from the HyperLEDA database (Makarov et al. 2014), allowing for the (statistical) deprojection of the distribution in line-of-sight velocity differences Δv between pair members to obtain the distribution of full three-dimensional (3D) intervelocities, vdeproj (Nottale & Chamaraux 2018b). By applying this deprojection to their pair catalog, Nottale & Chamaraux (2020) identified a robust peak at vdeproj ∼ 150 km s−1. Scarpa et al. (2022a,b) confirmed this intervelocity peak with an expanded input galaxy catalog, reporting its location to be at vdeproj = 132 ± 5 km s−1.
Scarpa et al. (2022a) proposed that galaxy pairs can be used to test gravity in the low acceleration regime, specifically to investigate the dark matter alternative modified Newtonian dynamics (MOND, Milgrom 1983; Famaey & McGaugh 2012). Since the MOND force at low accelerations (a ≪ a0, as realized for galaxy pairs) is proportional to 1/r, the total mutual velocity of a pair of galaxies in circular orbit is set by their mass and independent of separation, r. The absolute magnitude limit of the observed pairs (MB < −18.5) sets a typical galaxy mass scale, which then translates into a typical intervelocity. Scarpa et al. (2022b) demonstrated that a realistic B-band mass-to-light ratio of M/L ∼ 1 reproduces the observed peak position in MOND.
In contrast, Scarpa et al. (2022a) argued that the velocity peak is “hard to justify in the context of numerical simulations of cosmological structure formation”. This assessment appears mostly based on Moreno et al. (2013), who study galaxy pairs in the Millennium simulation (Springel et al. 2005). These authors found a broad distribution in intervelocities of pairs identified by 3D separation. Such a pair-selection is possible in simulations where full phase-space information is available, but not directly comparable to the observational pair-finding algorithm that must rely on only projected positions and redshift velocities. The simulation study also allows much more extreme mass ratios between paired galaxies, while the observational study applies a stricter isolation criterion. Nevertheless, pairs in Moreno et al. (2013) do display an intervelocity peak at ∼200 km s−1 if restricted to a central-satellite subsample. Considering only pairs whose mutual binding energy dominates, as opposed to them being bound to a third object, their intervelocity distribution even reaches a maximum between 100 and 200 km s−1. Therefore, it has not been firmly established that the observed peak is absent in a ΛCDM simulation when galaxy pairs have been selected following the observational study’s approach.
We set out to determine whether an intervelocity peak between paired galaxies is indeed absent in a ΛCDM context. If this were the case, the observed peak would constitute both a serious challenge to ΛCDM and a success for MOND. We approached this task by identifying galaxy pairs in the modern hydrodynamical cosmological simulation IllustrisTNG-300 (Nelson et al. 2018, 2019; Springel et al. 2018; Pillepich et al. 2018). To ensure direct comparability, we mock-observed the simulation to only consider projected positions and line-of-sight velocities when identifying pairs, followed the pair-finding algorithm of the observational studies, and applied the same statistical deprojection algorithm to obtain the 3D intervelocities.
2. Simulation, galaxy, and pair selection
Nottale & Chamaraux (2018a)’s galaxy sample covers those with B-band magnitudes of MB < −18.5 and heliocentric redshifts of 2500 < v < 16 500 km s−1, which (in the absence of peculiar velocities) corresponds to distances of 37 < d < 244 Mpc, adopting a Hubble constant of H0 = 67.74 km s−1 Mpc−1. To make a fair selection of simulated galaxies using the same constraints, we require a hydrodynamic simulation with a box size exceeding 200 Mpc. Here, we elected to use IllustrisTNG-300, a hydrodynamic cosmological simulation spanning a periodic box of length Lbox = 300 Mpc under a Planck Collaboration XIII (2016) cosmology.
Following Nottale & Chamaraux (2018a), we created a catalog of simulated subhalo-based galaxies with MB < −18.5 and we mock-observed along each of the simulation’s three orthonormal axes. For an axis a ∈ {x, y, z}, we placed an observer on the a = 0 plane at the edge of the simulation box and observed along the positive a axis. We note that the parallax is assumed to be negligible due to the large distances involved. We calculated the redshift of each galaxy at distance Da along an axis a as:
where vpec is the peculiar velocity of the galaxy in the simulation’s co-moving frame. By rejecting galaxies with a redshift outside 2500 < v < 16 500 km s−1, we obtained samples between 109 000 and 116 000 individual galaxies depending on the axis1. Limitations of this mock-observational approach are discussed in Appendix A. In the following, we focus on the z-axis projection to avoid cluttered figures, but comparisons between the different projections are shown in Appendix B.
We investigated a “base” sample directly using the positions and velocities of the simulation’s galaxy catalog, without introducing any errors. We also generated a “full” sample with an apparent magnitude cut-off at mB = 19, similar to the observational galaxy catalog and corresponding to an apparent magnitude of MB = −18 observed at the maximum redshift of 16 000 km s−1 (see Fig. 1 in Nottale & Chamaraux 2018a). For each simulated galaxy, velocity errors were drawn with replacement from the errors in the magnitude-limited HyperLEDA galaxy database to ensure that our overall error distribution follows that of the observational catalog. The velocity, v, of the galaxy was then displaced by a random draw from a Gaussian distribution with the error as its standard deviation. We also generated two randomized samples: “shuffled velocities”, for which the galaxy velocities were re-assigned randomly while their positions (and thus spatial clustering) were kept, and “random positions”, with positions randomly selected from a uniform distribution within the simulation volume.
To obtain the list of galaxy pair candidates from our mock galaxy catalogs, we closely followed the successive selection criteria of the observational study (Nottale & Chamaraux 2018a). Specifically, we identified pairs for which the two galaxies: (1) have B-band magnitudes MB < −18.5, (2) have a projected line-of-sight velocity difference of Δv = Δvz < 500 km s−1, (3) have a projected separation of 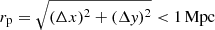 , and (4) fulfill a reciprocity criterion to exclude multiples or hierarchical groups. We then required these candidate pairs to be isolated using the ratio ρ = r3/rp, where r3 is the separation of the next-nearest galaxy (within 500 km s−1 from the pair) from the pair midpoint. If no nearby galaxy with MB < −18.5 was found, the magnitude range was expanded to include galaxies up to 2.5 mag fainter than the fainter pair member. Only galaxies with ρ > 2.5 were retained, resulting in 7840 (8595) pairs for our base (full) galaxy catalog. Stricter limits on ρ can be applied to look at particularly isolated galaxy pair samples.
, and (4) fulfill a reciprocity criterion to exclude multiples or hierarchical groups. We then required these candidate pairs to be isolated using the ratio ρ = r3/rp, where r3 is the separation of the next-nearest galaxy (within 500 km s−1 from the pair) from the pair midpoint. If no nearby galaxy with MB < −18.5 was found, the magnitude range was expanded to include galaxies up to 2.5 mag fainter than the fainter pair member. Only galaxies with ρ > 2.5 were retained, resulting in 7840 (8595) pairs for our base (full) galaxy catalog. Stricter limits on ρ can be applied to look at particularly isolated galaxy pair samples.
3. Comparison to the observed galaxy pair catalog
In Fig. 1, we compare the observed galaxy pairs (Nottale & Chamaraux 2018a) with our base and full galaxy pair samples, as well as the two randomized samples. Observed and simulated galaxy pairs follow comparable distributions in the on-sky separation, with most having rp < 200 kpc. One difference is the much-reduced peak at small rp for the observed sample: very small separations are over-represented in the simulated pairs. This is likely caused by an observational bias. In the simulation, all galaxy positions and velocities are known and included in the input catalogs. In contrast, in the observational galaxy catalog galaxies that are projected on top of each other (or have only very small separations) are likely either not included, are included as one object, or do not both have measured redshift velocities due to fiber positioning constraints in surveys. To address this difference, we confirmed that rejecting galaxy pairs with rp < 20 kpc in our simulation’s pair catalog does not affect our later results. Randomizing only the galaxy velocities retains their spatial clustering and thus distribution in rp, while randomized positions result in a much broader distribution.
 |
Fig. 1. Distributions of galaxy–galaxy pair properties. Left panel shows the projected separation rp, middle panel shows the difference in line-of-sight velocity Δv, and right panel shows the isolation criterion ρ. In all panels, the observed galaxy pairs are highlighted as a grey filled histogram, while the mock-observed simulation data are shown as lines for the base (blue dashed) and full (red solid) sample, as well as the two randomized test samples with shuffled velocities but retained positions (green dotted) and randomized positions (yellow dotted). |
The middle panel of Fig. 1 shows the difference in the line-of-sight velocities Δv of the galaxies in a pair, which is the quantity to be deprojected to obtain the distribution of 3D intervelocities of paired galaxies. The observed and the simulated galaxy pairs again show a similar behavior, with an initially steeply declining distribution that flattens at higher Δv. This is slightly more pronounced even for the simulated full sample including velocity errors than for the observational sample, possibly related to underestimated errors or unaccounted systematics in the spectroscopic velocities, which would result in a bias towards larger velocity differences. Both randomized samples show much flatter distributions in Δv, suggesting that the shape of the distribution has a physical origin.
The right panel of Fig. 1 shows the distribution of the isolation criterion, ρ. A very similar decrease in the relative number of more isolated pairs is present in all samples, although pairs in the simulation show a slight excess at small ρ over the observational sample. This is likely a result of the simulation having a full coverage of all galaxies, compared to some degree of incompleteness in the observational catalog.
Nottale & Chamaraux (2018a) found that about 10% of the galaxies with MB < −18.5 are members of fairly isolated pairs (ρ > 5), and that highly isolated pairs (ρ ≥ 10) contribute 32.5% of the total number of pairs. We find 4439 fairly isolated pairs in the base sample (8.1% of 109 603 galaxies) and 4892 in the full sample (8.9% of 109 609 galaxies), and that 34.0% (34.5%) of the pairs in the base (full) sample have ρ ≥ 10. The similarity between the simulated and observed pairs in these quantities gives us confidence in our mock-observational approach, and the agreement also in the distributions discussed above might already be seen as a success of the simulation in reproducing a galaxy sample comparable to the observational study.
4. Intervelocity distribution of galaxy pairs
For an optimal comparability with the observational studies, we initially focused on the de-projection of the velocity difference of our galaxy pair catalog into the 3D intervelocity distribution. The de-projection is made with the algorithm proposed by Nottale & Chamaraux (2018b):
The formula is based on the fact that a randomly oriented velocity v with a given value is equally projected along a given axis, that is, the probability distribution of vz is constant from 0 to |v|. The deprojected velocity distribution can then be derived by inverting the probability distribution of vz. The derivative in Eq. (2) is calculated using the differences between constant intervals separated by two bins. This method proves more accurate and generates a smoother de-projected distribution (Nottale & Chamaraux 2018b). We binned the probability distribution of Δv with a width of 32 km s−1 to ensure a monotonically decreasing distribution. Other bin widths result in very similar plots, in particular, the peaks at ∼130 km s−1 are reliably recovered.
The similarity in Δv between the observed and simulated galaxy pairs (Fig. 1) suggests that their deprojected intervelocities might also be compatible. This is confirmed in Fig. 2, which shows the results of the velocity deprojection for three choices of isolation. Both the observed and the simulated pair samples display clear intervelocity peaks at vdeproj ∼ 130 km s−1.
 |
Fig. 2. Deprojected velocities for the observed pairs (grey) and mock-observed simulation without (blue), with (red), and with doubled (turquoise) velocity errors. The light-red histogram in the background shows the v3D intervelocity distribution for the full sample, as determined from the peculiar velocity difference of the galaxy pairs using the available full phase-space information of the simulation. Also shown are the two-Gaussian model fits to the histograms used to determine the positions of the velocity peak. The peak position and its 1σ-uncertainty are indicated by solid lines at the bottom of the figure. |
To measure the positions of the prominent intervelocity peaks, we fit them with a double-Gaussian model to account for the peak and a broader background distribution. The peak positions are vdeproj = 88 ± 13, 125 ± 7, and 125 ± 4 km s−1 for the simulated full sample (ρ > 2.5), fairly isolated pairs (ρ > 5), and highly isolated pairs (ρ ≥ 10), respectively. For the observed pair catalog the same cuts in ρ result in peak positions of vdeproj = 113 ± 18, 113 ± 5, and 132 ± 13 km s−1, respectively. In all three cases, the peak positions agree within their 1σ uncertainties between the simulated and the observed galaxy pairs. These intervelocity peaks are approximately the same intervelocity of vdeproj ∼ 150 km s−1 reported by Nottale & Chamaraux (2020) and vdeproj = 132 ± 5 km s−1 reported by Scarpa et al. (2022b).
The peak in our base and full samples are more pronounced than the observed one. The reason might be that the simulation data are, by definition, much cleaner, while observational biases and underestimated or unaccounted-for measurement errors and systematics in the observational data set can wash out correlations, thus reducing the velocity peak strength, and add contamination by spurious pairs at higher intervelocities. We tested this hypothesis with a simulated galaxy catalog for which we doubled velocity errors relative to the full sample (turquoise lines in Fig. 2). The resulting distribution of vdeproj is indeed more consistent with the observed sample and the peak strength is reduced, but its position is not substantially affected.
The simulation data provide access to the full 6D phase-space of the galaxy pairs, such that we can also immediately investigate the pairs’ 3D intervelocity v3D without deprojection. This is shown as the red filled histogram in Fig. 2 for the full sample (and in Fig. 2 for the base sample and various test samples). It confirms the de-projection analysis: for galaxy pairs identified in the simulation a clear intervelocity peak is present at v3D = 132 ± 1 km s−1, with a width of σv3D = 61 ± 2 km s−1.
5. The intervelocity peak as a physical feature
To investigate the origin of the intervelocity peak in the simulation, we performed a number of tests and additional comparisons. These are illustrated in Fig. 3, showing distributions in the 3D separation of the two pair members r3D and their full 3D intervelocity, v3D.
 |
Fig. 3. Full 3D separation r3D (top panels) and 3D intervelocity v3D (bottom panels) for our base (blue shaded histograms) and full (red solid line) simulation galaxy pair catalogs. Left panels show a comparison with the two randomized samples for which either only the galaxy velocities were shuffled among all considered galaxies or their positions were randomly drawn from a uniform distribution. The middle panels show a comparison among galaxy pairs that share a common halo ID in the simulation with those that do not. Right panels show a comparison of the results for different ranges of the pair primary’s absolute magnitude. |
We first compared the simulated samples to the two randomized samples (left panels in Fig. 3). While the shuffled velocities sample preserves the spatial clustering and results in a very similar distribution in r3D as for the mock-observed samples, neither randomized sample reproduces the velocity distribution or its narrow peak. Instead, they display broad maxima at v3D = 426 ± 8 and 491 ± 11 km s−1, respectively. This is close to the velocity limit of the pair selection algorithm and thus likely driven by that constraint. This suggests that the velocity peak identified in the simulation is not merely an emergent feature of the typical galaxy distribution or their typical peculiar velocities, but rather has a physical origin related to galaxies associated with each other.
To investigate such a physical association, we determined which galaxy pairs identified in the mock-observed simulation share the same halo ID. These have been identified as being physically associated by the halo finder. We find that 83.4% (82.5%) of the galaxy pairs in the base (full) sample share a common halo ID, indicating that the galaxy pair finding criteria are very good at identifying truly associated galaxies, with only one sixth being contamination by spurious pairs. We also find that 75.2% (74.4%) of the pairs share a unique halo ID not shared by any other pair, indicating that only a small fraction of pairs is associated with massive halos (likely galaxy clusters) hosting more than one pair.
In the middle panels of Fig. 3, we show distributions in r3D and v3D for pairs with and without a common halo ID. Only galaxy pairs in a common halo have small values for r3D, as expected for physically associated systems. They also drive the bulk of the velocity peak at v3D ∼ 130 km s−1, while the (spurious) pairs belonging to different halos preferentially show lower intervelocities. This appears to be in line with their larger distance, resulting in lower mutual acceleration. Again, fitting a two-Gaussian model, we find that pairs associated to the same halo display a peak position of v3D = 138 ± 1 km s−1 for the full sample, while those belonging to different halos have a peak position at v3D = 88 ± 2 km s−1. The corresponding positions for the base sample do not differ substantially.
Finally, we compare different ranges in the absolute magnitude MB, 1 of the more luminous galaxy of each pair. This is based on an extended galaxy pair catalog where fainter galaxies with MB, 1 ≤ −17 were also considered. As shown in the right panels of Fig. 3, their spatial distributions are comparable, but pairs with more luminous primaries display higher intervelocities. We find peaks at v3D = 86 ± 1, 117 ± 1, and 153 ± 1 km s−1 for the subsequently more luminous samples in Fig. 3. This is in line with a physical origin of the intervelocity peak as being caused by the mutual acceleration of paired galaxies, with more luminous (and thus on average more massive) primary galaxies resulting in higher accelerations, causing larger velocities. The absolute magnitude limit of the observational study then determines which galaxy masses contribute to the identified pairs most, implicitly setting the intervelocity peak of the sample.
We tested the latter in the simulation by calculating the circular velocity 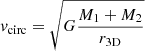 of each galaxy pair, using the total mass of each galaxy, M1, 2, obtained from the galaxy catalog of the simulation. We ignored pairs with separations exceeding 1 Mpc, as these are most likely the result of non-physical contamination. The distribution of vcirc as well as the full 3D velocity difference v3D of the galaxy pairs is plotted in Fig. 4. For pairs with separations of 100 kpc–1 Mpc, vcirc provides an excellent match to v3D with both showing a pronounced peak at ∼130 km s−1, and a median v3D in the simulation of 161.9 km s−1 while vcirc for the median galaxy masses and separation is 157.5 km s−1. However, for pairs with separations closer than 100 kpc, the circular velocity calculation over-estimates their 3D velocity difference. This is expected, as the velocities of interacting galaxies will be decreased due to dynamical friction once the halos overlap, and the overlapping halos invalidate the implicit assumption of point masses, such that the effective masses in the calculation are smaller than the total masses M1 and M2.
of each galaxy pair, using the total mass of each galaxy, M1, 2, obtained from the galaxy catalog of the simulation. We ignored pairs with separations exceeding 1 Mpc, as these are most likely the result of non-physical contamination. The distribution of vcirc as well as the full 3D velocity difference v3D of the galaxy pairs is plotted in Fig. 4. For pairs with separations of 100 kpc–1 Mpc, vcirc provides an excellent match to v3D with both showing a pronounced peak at ∼130 km s−1, and a median v3D in the simulation of 161.9 km s−1 while vcirc for the median galaxy masses and separation is 157.5 km s−1. However, for pairs with separations closer than 100 kpc, the circular velocity calculation over-estimates their 3D velocity difference. This is expected, as the velocities of interacting galaxies will be decreased due to dynamical friction once the halos overlap, and the overlapping halos invalidate the implicit assumption of point masses, such that the effective masses in the calculation are smaller than the total masses M1 and M2.
 |
Fig. 4. 3D intervelocity, v3D and calculated circular velocity vcirc for galaxy pairs identified in the simulation with separations r3D < 100 kpc (blue) and 100 kpc < r3D < 1 Mpc. For sufficiently separated pairs, the circular velocity provides a good estimate of the 3D intervelocity, suggesting a physical origin of the intervelocity peak driven by the typical masses and separations of the selected galaxy pairs. |
6. Discussion and conclusions
Pairs of galaxies identified in the observational galaxy catalog HyperLEDA (Makarov et al. 2014; Nottale & Chamaraux 2018a) have been found to display a peak in their deprojected (3D) intervelocity distribution at vdeproj = 130−150 km s−1 (Nottale & Chamaraux 2020; Scarpa et al. 2022a,b). To determine whether such a feature is expected in a cosmological context within ΛCDM, we carried out a mock-observation of galaxies from the IllustrisTNG-300 simulation (Nelson et al. 2019) and applied the observational approach to identify galaxy pairs. We recovered a pronounced peak in the intervelocity of isolated pairs, both via a deprojection of line-of-sight velocity differences (Nottale & Chamaraux 2018b) at vdeproj = 125 ± 7 km s−1 and via the direct 3D intervelocity of the identified galaxy pairs at v3D = 132 ± 1 km s−1.
The agreement between the position of the intervelocity peak of the observational studies and the peak we identified in the simulation is striking, and can be considered a success of the simulation – and, by extension, ΛCDM – in reproducing this observed feature. It is likely to be of a physical origin since it is not present in randomized galaxy samples, set by the majority of identified pairs for which both galaxies belong to a common dark matter halo; and its position is scaled with the pair primary’s luminosity and thus mass. It appears plausible that the intervelocity peak of galaxy pairs as a probe of the total mass of galaxies is related to abundance matching or the stellar mass-halo mass (SMHM) relation. Via these relations, the considered range of galaxy luminosities translates into a corresponding range in total masses, which, in turn, determine the dynamics leading to a preferred intervelocity. Finding that this intervelocity in ΛCDM is consistent with the one expected in MOND might then result from the fact that the TNG model was devised to reproduce the SMHM relation (Pillepich et al. 2018). Since abundance matching, such as that of Behroozi et al. (2013), is consistent with the observed baryonic Tully–Fisher relation (see Fig. 4 of Li et al. 2022), which, in turn, matches the MOND predictions, this might explain why the considered galaxy luminosities in this cosmological simulation are tied to just the right total halo mass to reproduce the observed feature of the intervelocity distribution.
Recovering the intervelocity peak with a ΛCDM simulation does not reduce the success of MOND in reproducing it, but it shows that (1) MOND is not the only model offering an explanation for this effect and (2) ΛCDM is not immediately challenged by the observed intervelocity peak of galaxy pairs. This does not mean that the dynamics of isolated galaxy pairs cannot be developed into a useful tool to test gravitational dynamics in the low-acceleration regime. However, this will require more dedicated research to determine how the peak comes about in the cosmological context, the ways in which the predictions of the intervelocity distributions between ΛCDM, MOND, and other models differ (e.g., are there environmental effects), and what observational data will be required to discriminate these alternatives.
Acknowledgments
We thank Mordehai Milgrom for interesting discussions, and the anonymous referee for helpful suggestions, that both improved our manuscript. M. S. P. acknowledges funding of a Leibniz-Junior Research Group (project number J94/2020) and a KT Boost Fund by the German Scholars Organization and Klaus Tschira Stiftung. P. L. is supported by the Alexander von Humboldt Foundation.
References
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Relat., 15, 10 [Google Scholar]
- Li, P., McGaugh, S. S., Lelli, F., et al. 2022, ApJ, 927, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [Google Scholar]
- Moreno, J., Bluck, A. F. L., Ellison, S. L., et al. 2013, MNRAS, 436, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, D., Pillepich, A., Springel, V., et al. 2018, MNRAS, 475, 624 [Google Scholar]
- Nelson, D., Springel, V., Pillepich, A., et al. 2019, Comput. Astrophys. Cosmol., 6, 2 [Google Scholar]
- Nottale, L., & Chamaraux, P. 2018a, Astrophys. Bull., 73, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Nottale, L., & Chamaraux, P. 2018b, A&A, 614, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nottale, L., & Chamaraux, P. 2020, A&A, 641, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018, MNRAS, 475, 648 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scarpa, R., Falomo, R., & Treves, A. 2022a, MNRAS, 510, 2167 [Google Scholar]
- Scarpa, R., Falomo, R., & Treves, A. 2022b, MNRAS, 512, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [Google Scholar]
- Springel, V., Pakmor, R., Pillepich, A., et al. 2018, MNRAS, 475, 676 [Google Scholar]
Appendix A: Comparisons of the observed and simulated galaxy catalogs
While our mock-observational approach and our pair finding algorithm closely follow that of the observational study, a number of differences are present: (1) our simplified approach does not cover the same volume in shape as the observational galaxy catalog, (2) the simulation is not affected by spatial biases, obscuration, or crowding issues, and (3) we employ a simplified treatment of velocity measurement errors.
The distribution of galaxy pairs in absolute B-band magnitude MB and redshift velocity v is shown in Fig. A.1. The former shows the similarity in the covered magnitude range, although the observational sample is lacking in galaxies fainter than MB = −20. This is likely due to insufficient completeness of the observational catalog as compared to the complete galaxy catalog available for the simulation. The distributions in velocity highlight the difference in the selection volumes of the observational study and our mock-observational approach using the IllustrisTNG-300 simulations. The observational sample rises with redshift, as a larger volume of spherical shells contributes to the galaxy distribution. Such a volume is not feasible due to the limited simulation box size. Consequently, the apparent magnitude bias resulting in less rejected pairs at higher redshifts discussed in Nottale & Chamaraux (2018a) is not as severe for our mock-observed simulation samples. We can therefore expect the latter to be less contaminated by non-isolated pairs.
 |
Fig. A.1. Properties of galaxy pairs for the observed galaxy pair catalog properties from Nottale & Chamaraux (2018a) (grey shaded histograms) and galaxy data from the IlustrisTNG-300 simulation. For the latter, the blue histogram corresponds to our base model without velocity errors, and the red histograms are from our full model mimicking apparent magnitude biases and errors on the observed line-of-sight velocity. Left panel: Distribution of galaxy pair members in B-band magnitude MB. Right panel: Distribution of galaxy pairs in velocity, v, consisting of redshift and peculiar velocity. |
Figure A.2 compares the error of the pair velocity difference, ϵΔv, for the observational pair catalog and the one obtained for our full sample, for which velocity errors are drawn from the errors of the HyperLEDA galaxy database. This approach typically results in similar errors for pairs: a strong and sharp peak at small 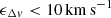 , and another, broader peak at higher ϵΔv. However, there are some differences in the details, such as the relative height of the first peak and the position of the second one. We suspect that some correlation between galaxy errors in the observational data is a possible cause of this.
, and another, broader peak at higher ϵΔv. However, there are some differences in the details, such as the relative height of the first peak and the position of the second one. We suspect that some correlation between galaxy errors in the observational data is a possible cause of this.
 |
Fig. A.2. Comparison of velocity errors for the observed and simulated galaxy pair samples. Left panel: Distribution of errors ϵΔv on the line-of-sight velocity difference Δv of galaxy pairs. Right panel: Errors on individual velocity measurements for the two corresponding partner galaxies (more luminous partner on the horizontal axis). Some error correlation is present for the observed sample, but absent in our mock observed simulation data. |
This appears to be confirmed by the right panel of Fig. A.2, which plots the individual velocity errors for the two members of a pair against each other. Some of the observed pairs indeed show correlation between their velocity errors. This is not unexpected, as galaxies close to each other on the sky might have likely been measured with the same technique, instrument, or survey, resulting in them sharing similar errors. This can result in low-error galaxies as well as high-error galaxies being predominantly associated with each other, compared to a completely random error assignment. Such effects are difficult to accurately reproduce in mock-observing the simulation. However, they are not expected to significantly alter the results, because the velocities are only relevant for the pair finding algorithm, where they are generally smaller than the allowed velocity difference of 500 km s−1, and for the deprojected intervelocity, which however turns out to agree with the error-free, 3D intervelocity peak of galaxy pairs in the simulation. This is confirmed by the absence of substantial differences between the results for our base and full input catalogs, despite the former being entirely devoid of any velocity errors.
Appendix B: Deprojected velocities for projections along other axes
In Fig. B.1m we plot the intervelocities of galaxy pairs obtained from the deprojection approach of Sect. 4 for the mock-observed (full) galaxy samples projected along the three different axes of the simulation box. Overall, the presence of the intervelocity peak is stable and its peak position is consistent with that of the observed galaxy pairs. However, some differences in the deprojected intervelocity distributions along the three axes are present and illustrate the degree of uncertainty in the velocity deprojection approach.
 |
Fig. B.1. Deprojected velocities, similar to Fig. 2 but showing the mock-observed simulation along the three different axes of the simulation box. |
To more accurately determine the position of the deprojected intervelocity peak despite the wide velocity bins required by the deprojection algorithm, Scarpa et al. (2022b) have performed the deprojection with a range of bin width and then averaged the resulting histograms by re-sampling with a bin width of 1 km s−1. For completeness, we follow their approach for our simulation data in Fig. B.2. Specifically, we applied the deprojection algorithm for bin width between 25 and 40 km s−1, re-sampled the resulting de-projected histograms in bins of 1 km s−1 width, and averaged them. This results in a smoother deprojected velocity distribution that helps in identifying the position of the intervelocity peak, although we warn that the choice of bin width and range, as well as numerical noise due to relatively small pair sample sizes, can introduce difficult to quantify biases and inaccuracies in this method. This is illustrated by showing not only the z-axis projection for the simulations, but also those for the x and y directions. The different directions of projection of the simulated galaxy distribution also result in some differences in the re-sampled deprojected intervelocity curves, the amount of which gives an idea of the accuracy levels of such curves.
 |
Fig. B.2. Deprojected intervelocities obtained from averaging deprojections with bin width between 25 and 40 km s−1, following the approach introduced by Scarpa et al. (2022b). |
All Figures
 |
Fig. 1. Distributions of galaxy–galaxy pair properties. Left panel shows the projected separation rp, middle panel shows the difference in line-of-sight velocity Δv, and right panel shows the isolation criterion ρ. In all panels, the observed galaxy pairs are highlighted as a grey filled histogram, while the mock-observed simulation data are shown as lines for the base (blue dashed) and full (red solid) sample, as well as the two randomized test samples with shuffled velocities but retained positions (green dotted) and randomized positions (yellow dotted). |
| In the text | |
 |
Fig. 2. Deprojected velocities for the observed pairs (grey) and mock-observed simulation without (blue), with (red), and with doubled (turquoise) velocity errors. The light-red histogram in the background shows the v3D intervelocity distribution for the full sample, as determined from the peculiar velocity difference of the galaxy pairs using the available full phase-space information of the simulation. Also shown are the two-Gaussian model fits to the histograms used to determine the positions of the velocity peak. The peak position and its 1σ-uncertainty are indicated by solid lines at the bottom of the figure. |
| In the text | |
 |
Fig. 3. Full 3D separation r3D (top panels) and 3D intervelocity v3D (bottom panels) for our base (blue shaded histograms) and full (red solid line) simulation galaxy pair catalogs. Left panels show a comparison with the two randomized samples for which either only the galaxy velocities were shuffled among all considered galaxies or their positions were randomly drawn from a uniform distribution. The middle panels show a comparison among galaxy pairs that share a common halo ID in the simulation with those that do not. Right panels show a comparison of the results for different ranges of the pair primary’s absolute magnitude. |
| In the text | |
 |
Fig. 4. 3D intervelocity, v3D and calculated circular velocity vcirc for galaxy pairs identified in the simulation with separations r3D < 100 kpc (blue) and 100 kpc < r3D < 1 Mpc. For sufficiently separated pairs, the circular velocity provides a good estimate of the 3D intervelocity, suggesting a physical origin of the intervelocity peak driven by the typical masses and separations of the selected galaxy pairs. |
| In the text | |
 |
Fig. A.1. Properties of galaxy pairs for the observed galaxy pair catalog properties from Nottale & Chamaraux (2018a) (grey shaded histograms) and galaxy data from the IlustrisTNG-300 simulation. For the latter, the blue histogram corresponds to our base model without velocity errors, and the red histograms are from our full model mimicking apparent magnitude biases and errors on the observed line-of-sight velocity. Left panel: Distribution of galaxy pair members in B-band magnitude MB. Right panel: Distribution of galaxy pairs in velocity, v, consisting of redshift and peculiar velocity. |
| In the text | |
 |
Fig. A.2. Comparison of velocity errors for the observed and simulated galaxy pair samples. Left panel: Distribution of errors ϵΔv on the line-of-sight velocity difference Δv of galaxy pairs. Right panel: Errors on individual velocity measurements for the two corresponding partner galaxies (more luminous partner on the horizontal axis). Some error correlation is present for the observed sample, but absent in our mock observed simulation data. |
| In the text | |
 |
Fig. B.1. Deprojected velocities, similar to Fig. 2 but showing the mock-observed simulation along the three different axes of the simulation box. |
| In the text | |
 |
Fig. B.2. Deprojected intervelocities obtained from averaging deprojections with bin width between 25 and 40 km s−1, following the approach introduced by Scarpa et al. (2022b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



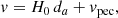
![$$ \begin{aligned} P_{ v}({ v}) = -{ v}\Big [\frac{\mathrm{d}P_{{ v}_z}({ v}_z)}{\mathrm{d}{ v}_z}\Big ]_{ v}. \end{aligned} $$](/articles/aa/full_html/2022/08/aa43646-22/aa43646-22-eq3.gif)