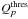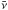| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322169 | |
| Published online | 29 October 2013 | |
Search for muon neutrinos from gamma-ray bursts with the ANTARES neutrino telescope using 2008 to 2011 data⋆,⋆⋆
1 Institut d’Investigació per a la Gestió Integrada de les Zones Costaneres (IGIC) – Universitat Politècnica de València, C/Paranimf 1, 46730 Gandia, Spain
2 GRPHE – Institut universitaire de technologie de Colmar, 34 rue du Grillenbreit, BP 50568, 68008 Colmar, France
3 CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
4 Technical University of Catalonia, Laboratory of Applied Bioacoustics, Rambla Exposició,08800 Vilanova i la Geltrú, Barcelona, Spain
5 INFN – Sezione di Genova, Via Dodecaneso 33, 16146 Genova, Italy
6 Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen Centre for Astroparticle Physics, Erwin-Rommel-Str. 1, 91058 Erlangen, Germany
7 Direction des Sciences de la Matière – Institut de recherche sur les lois fondamentales de l’Univers – Service d’Électronique des Détecteurs et d’Informatique, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
8 Nikhef, Science Park 105, 1098XG Amsterdam, The Netherlands
9 APC, Université Paris Diderot, CNRS/IN2P3, CEA/IRFU, Observatoire de Paris, Sorbonne Paris Cité, 75205 Paris, France
10 IFIC – Instituto de Física Corpuscular, Edificios Investigación de Paterna, CSIC – Universitat de València, Apdo. de Correos 22085, 46071 Valencia, Spain
11 LAM – Laboratoire d’Astrophysique de Marseille, Pôle de l’Étoile Site de Château-Gombert, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
12 INFN – Sezione di Bologna, Viale Berti-Pichat 6/2, 40127 Bologna, Italy
13 Dipartimento di Fisica dell’Università, Viale Berti Pichat 6/2, 40127 Bologna, Italy
14 INFN – Sezione di Roma, P.le Aldo Moro 2, 00185 Roma, Italy
15 Dipartimento di Fisica dell’Università La Sapienza, P.le Aldo Moro 2, 00185 Roma, Italy
16 Institute for Space Sciences, 77125 Bucharest, Măgurele, Romania
17 Clermont Université, Université Blaise Pascal, CNRS/IN2P3, Laboratoire de Physique Corpusculaire, BP 10448, 63000 Clermont-Ferrand, France
18 Géoazur, Université Nice Sophia-Antipolis, CNRS/INSU, IRD, Observatoire de la Côte d’Azur, Sophia Antipolis, France
19 INFN – Sezione di Bari, via E. Orabona 4, 70126 Bari, Italy
20 INFN – Laboratori Nazionali del Sud (LNS), Via S. Sofia 62, 95123 Catania, Italy
21 Mediterranean Institute of Oceanography (MIO), Aix-Marseille University, 13288, Marseille Cedex 9, France
22 Université Paris-Sud, 91405 Orsay Cedex, France
23 Kernfysisch Versneller Instituut (KVI), University of Groningen, Zernikelaan 25, 9747 AA Groningen, The Netherlands
24 INFN – Sezione di Pisa, Largo B. Pontecorvo 3, 56127 Pisa, Italy
25 Dipartimento di Fisica dell’Università, Largo B. Pontecorvo 3, 56127 Pisa, Italy
26 Royal Netherlands Institute for Sea Research (NIOZ), Landsdiep 4, 1797 SZ ’t Horntje (Texel), The Netherlands
27 Institut für Theoretische Physik und Astrophysik, Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
28 Universiteit Utrecht, Faculteit Betawetenschappen, Princetonplein 5, 3584 CC Utrecht, The Netherlands
29 Universiteit van Amsterdam, Instituut voor Hoge-Energie Fysica, Science Park 105, 1098 XG Amsterdam, The Netherlands
30 Dr. Remeis-Sternwarte and ECAP, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
31 Moscow State University, Skobeltsyn Institute ofNuclear Physics, Leninskie gory, 119991 Moscow, Russia
32 INFN – Sezione di Catania, Viale Andrea Doria 6, 95125 Catania, Italy
33 Dipartimento di Fisica ed Astronomia dell’Università, Viale Andrea Doria 6, 95125 Catania, Italy
34 Direction des Sciences de la Matière – Institut de recherche sur les lois fondamentales de l’Univers – Service de Physique des Particules, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
35 Département de Physique Nucléaire et Corpusculaire, Université de Genève, 1211 Geneva, Switzerland
36 IPHC – Institut Pluridisciplinaire Hubert Curien – Université de Strasbourg et CNRS/IN2P3, 23 rue du Loess, BP 28, 67037 Strasbourg Cedex 2, France
37 ITEP – Institute for Theoretical and Experimental Physics, B. Cheremushkinskaya 25, 117218 Moscow, Russia
38 Universiteit Leiden, Leids Instituut voor Onderzoek in Natuurkunde, 2333 CA Leiden, The Netherlands
39 Dipartimento di Fisica dell’Università, Via Dodecaneso 33, 16146 Genova, Italy
40 University Mohammed I, Laboratory of Physics of Matter and Radiations, BP 717, 6000 Oujda, Morocco
41 Université du Sud Toulon-Var, CNRS-INSU/IRD UM 110, Marseille, 83957 La Garde Cedex, France
Received: 28 June 2013
Accepted: 20 August 2013
Aims. We search for muon neutrinos in coincidence with GRBs with the ANTARES neutrino detector using data from the end of 2007 to 2011.
Methods. Expected neutrino fluxes were calculated for each burst individually. The most recent numerical calculations of the spectra using the NeuCosmA code were employed, which include Monte Carlo simulations of the full underlying photohadronic interaction processes. The discovery probability for a selection of 296 GRBs in the given period was optimised using an extended maximum-likelihood strategy.
Results. No significant excess over background is found in the data, and 90% confidence level upper limits are placed on the total expected flux according to the model.
Key words: neutrinos / gamma-ray burst: general / methods: numerical
Appendices are available in electronic form at http://www.aanda.org
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/559/A9
© ESO, 2013
1. Introduction
Gamma-ray bursts (GRBs) are short and very intense flashes of high-energy gamma rays, which occur unpredictably and isotropically over the sky (Meegan et al. 1992). Over timescales of the order of a few seconds, they release as much energy as the Sun in its entire lifetime (see Woosley & Bloom 2006, for a review). The doubly peaked distribution of burst durations measured by the BATSE satellite led Kouveliotou et al. (1993) to the classification of GRBs into two types (see also Paciesas et al. 1999). The sub-class of long bursts (with durations ≳2s) has been shown to be associated with supernovae of type I b/c (see e.g. Galama et al. 1998). For the short bursts (≲2s duration) it is much harder to measure the fast-fading afterglow emission and thereby obtain information about their origin. However, they are now widely accepted to originate from the merging of two compact objects, for example neutron stars and black holes (Eichler et al. 1989; Nakar 2007).
In the fireball model (as proposed by Mészáros & Rees 1993), the observed electromagnetic radiation is explained by highly relativistic outflows of material, most likely collimated in jets pointed towards the Earth. Shock fronts emerge in these outflows in which electrons are accelerated (Rees & Mészáros 1992). The synchrotron emission of these relativistic electrons and subsequent inverse Compton-scattering of the emitted photon field causes the observed gamma-ray radiation (Mészáros 2006). Within the framework of the fireball model, protons can also be shock-accelerated, which yields emission of high-energy neutrinos accompanying the electromagnetic signal of the burst (Waxman 1995a, 2000; Waxman & Bahcall 1997). The detection of neutrinos from GRBs would be unambiguous proof for hadronic acceleration in cosmic sources, and could also serve to explain the origin of the cosmic-ray flux at ultra-high energies (Waxman 1995b).
Several limits over a wide range of energies have been placed on the neutrino emission from GRBs, for instance from experiments such as Super-Kamiokande (Fukuda et al. 2002), AMANDA (Achterberg et al. 2008), Baikal (Avrorin et al. 2011), RICE (Besson et al. 2007), and ANITA (Vieregg et al. 2011). Very-large-volume neutrino telescopes such as ANTARES and IceCube are sensitive to neutrino fluxes above approximately 100GeV; since they simultaneously observe at least half the sky, they are ideal instruments to search for any high-energy neutrino flux from GRBs. The data from ANTARES in its construction phase in 2007 with the first five detection lines deployed (Adrián-Martínez et al. 2013) and from IceCube in its IC 22, IC 40, and IC 59 detector phases from 2007 to 2010 (Abbasi et al. 2010, 2011, 2012) have previously been analysed in searches for this emission, with corresponding limits set in the TeV to PeV energy range. Due to its location at the South Pole, the IceCube detector has sensitivity for Northern Hemisphere sources, whereas the ANTARES detector, being situated at a latitude of 43°, has sensitivity for Southern Hemisphere sources.
In this paper we present a search for prompt GRB neutrino emission in the period from the end of 2007 to 2011 with the ANTARES telescope using 296 bursts, out of which 90% have not been included in the previously mentioned references. In contrast to previous analyses, this search has for the first time been optimised for a fully numerical neutrino-emission model, based on Hümmer et al. (2010, 2012).
This paper is organised as follows: in Sect. 2, the ANTARES neutrino telescope is briefly introduced. A description of how the burst parameters are obtained and how the final sample is selected is given in Sect. 3. Models for the expected neutrino spectra within the fireball paradigm are described in Sect. 4, including the numerical model NeuCosmA, which is used for the optimisation of the analysis. In Sect. 5, we describe Monte Carlo simulations of GRB neutrino events that yield the detector response to the signal. The background distribution is estimated from data, as reported in Sect. 6. From these distributions, pseudo-experiments were generated that, by exploiting an extended maximum-likelihood ratio method, were used to optimise the search to obtain the highest discovery potential for the neutrino flux – this is presented in Sect. 7. In Sect. 8, we investigate whether the discovery potential can be improved by limiting the analysis to an optimised sub-sample of the bursts. Results of the analysis and the derived limits are provided in Sect. 9.
2. ANTARES detector and data taking
The underwater neutrino telescope ANTARES (see Ageron et al. 2011) is primarily designed for detecting relativistic muons from charged-current interactions of cosmic muon neutrinos1 with matter in or close-by to the detector. The passage of these muons through the seawater induces the emission of Cherenkov light that is then detected by an array of photo-multiplier tubes (PMTs). Using the time and position information of the photons, the muon trajectory is reconstructed. The original neutrino direction is then inferred from the measured muon direction – at the energies considered here, the uncertainty introduced by the scattering angle is negligible compared to the detector’s resolution.
The ANTARES telescope is located in the Mediterranean Sea at a depth of 2.4km. The detector consists of twelve vertical “strings” anchored to the seabed, each of which is held upright by a buoy at the top. They are separated from each other by a typical distance of 70m. The twelve strings, each with a length of 450m, are equipped with 25 triplets of PMTs, building a three-dimensional array of 885 PMTs in total2. The triplets have a vertical spacing of 14.5m between them, whereas the first triplet is placed at a height of 100m above the seabed.
Bioluminescence and radioactive decay of 40K produce a random optical background that can vary between 50 and 300kHz per PMT, depending for example on the time of the year or the sea current. A multi-level online triggering procedure is applied to select possible particle signatures – see Aguilar et al. (2007) for a more detailed description.
In addition to the cosmic neutrino signal that the ANTARES experiment is searching for, there are other processes that can produce muon tracks in the detector that are considered as background events. Air showers are generated when high-energy cosmic rays hit the Earth’s atmosphere. Among other particles, muons and neutrinos are produced in these showers. Since only the (weakly interacting) neutrinos are capable of traversing the Earth, it can effectively be used as a “shield” against all particles but neutrinos. By searching only for upgoing particles therefore, the atmospheric downgoing muon background can be rejected. Nevertheless, muons from above can also produce signals in the detector that appear as upgoing events. Using quality cuts on the reconstruction parameters, these falsely reconstructed atmospheric muon tracks can be suppressed to a rate of 0.4 events per day.
Atmospheric neutrinos produced by cosmic rays below the horizon can also traverse the Earth, and represent the main background component (~three events per day after quality cuts, see Adrián-Martínez et al. 2012) to the cosmic neutrinos.
In the analysis presented in the following, the requirement of temporal and spatial coincidence with a recorded GRB reduces the number of expected background events to ~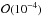 per GRB (see Sect. 6), and an extended likelihood method is furthermore used to distinguish between signal and background events. Data collected between December 6, 2007 and the end of 2011 were analysed. The first six months of this period comprised the last phase of construction of the apparatus, after the deployment of detection lines 6 to 10, with the last two lines installed in May 2008. In that period, the instrumented volume of the detector increased from 0.008 to 0.011km3 at full size. The corresponding average effective area to muon neutrinos as a function of the energy is shown in Fig. 1 for different declination bands. The huge increase of effective area with energy, a common feature of neutrino telescopes, is due not only to the increase of the neutrino cross-section, but also to that of the muon range, which can reach several kilometres at the highest energies. The total integrated livetime of the data in coincidence with the selected 296 GRB search-time windows is 6.6 h.
per GRB (see Sect. 6), and an extended likelihood method is furthermore used to distinguish between signal and background events. Data collected between December 6, 2007 and the end of 2011 were analysed. The first six months of this period comprised the last phase of construction of the apparatus, after the deployment of detection lines 6 to 10, with the last two lines installed in May 2008. In that period, the instrumented volume of the detector increased from 0.008 to 0.011km3 at full size. The corresponding average effective area to muon neutrinos as a function of the energy is shown in Fig. 1 for different declination bands. The huge increase of effective area with energy, a common feature of neutrino telescopes, is due not only to the increase of the neutrino cross-section, but also to that of the muon range, which can reach several kilometres at the highest energies. The total integrated livetime of the data in coincidence with the selected 296 GRB search-time windows is 6.6 h.
 |
Fig. 1 Time-averaged muon-neutrino effective area of the ANTARES neutrino telescope as a function of energy for different declination bands δ for the considered data-taking period. Typical quality cuts as derived in this analysis (Λ > −5.35, β < 1°) are applied. |
3. GRB selection and parameters
The GRB parameters needed for the search and the simulation of expected neutrino fluxes are primarily obtained from different tables provided by the Swift (Gehrels et al. 2004) and Fermi (Atwood et al. 2009; Meegan et al. 2009) collaborations. This information is then supplemented using a table supplied by the IceCube Collaboration (Aguilar 2011), which is created by parsing the Gamma-ray Coordinates Network (GCN) notices3. In Appendix A, we specify how these tables are merged, how often burst parameters are taken from each of them, and how the search-time windows are defined.
Selection of GRBs.
For the final sample, GRBs are required to meet certain criteria as specified in Table 1 – short bursts, for instance, are excluded as this class is much less understood. A total of 296 bursts pass these selection cuts, of which 10% are also included in the most recent gamma-ray-burst search from IceCube (Abbasi et al. 2012). The distribution of the selected bursts in equatorial coordinates is shown in Fig. 2. Out of this selection, GRB 110918 outshines all others by at least half an order of magnitude in the expected neutrino flux (see Sect. 4). It is at the same time one of the most intense bursts ever observed by the Konus-Wind instrument (Aptekar et al. 1995; Golenetskii et al. 2011). Unfortunately, both Swift and Fermi satellites were Earth-occulted at the time of the burst (Krimm et al. 2011), but Swift could still observe the afterglow emission after ~30h. The measured parameters for this exceptional burst are given in Table A.2.
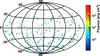 |
Fig. 2 Sky distribution of the selected 296 GRBs in equatorial coordinates. The gamma-ray fluence of each burst is colour-coded. The instantaneous field of view of the ANTARES detector is 2πsr; within a period of 24 h, the sky up to a declination of 47° is visible. |
4. Calculation of neutrino spectra
To calculate the expected neutrino spectra, we focused on the recently developed fully numerical NeuCosmA model (Hümmer et al. 2010, 2012). In addition, we also present the widely used analytical approach of Guetta et al. (2004) in the following.
4.1. Analytic approaches
Waxman & Bahcall (1997) were the first to calculate the expected neutrino flux in coincidence with the electromagnetic GRB in the framework of the standard fireball internal shock model, using averaged burst parameters as measured by the BATSE instrument on board the CGRO satellite (Band et al. 1993). Their calculation was based on the assumption of Fermi-accelerated protons in the relativistic ejecta of the burst interacting with the associated photon field to produce pions via the Δ-resonance. The subsequent decay of charged pions and muons leads to the emission of high-energy neutrinos. The authors derived a doubly broken power-law spectrum for the neutrinos. Their model is referred to as the standard Waxman-Bahcall GRB neutrino flux, and is for instance used to set limits with the BAIKAL (Avrorin et al. 2011) and AMANDA (Achterberg et al. 2008) experiments. Guetta et al. (2004) modified the formulae of Waxman and Bahcall to calculate individual neutrino fluxes for the bursts. Such individual burst predictions are used in recent searches with IceCube (Abbasi et al. 2010, 2011, 2012), RICE (Besson et al. 2007), and ANITA (Vieregg et al. 2011). Note in particular that the most recent IceCube limit was a factor of 3.7 below predictions made using this model. This could either indicate the need for rejection of the model, a modification of the parameters upon which it is based, or for more detailed modelling of the neutrino emission within the fireball paradigm.
To calculate the analytic spectrum as shown in Fig. 3a, blue solid line, the formulae given in Abbasi et al. (2010, Appendix A) were applied.
 |
Fig. 3 a) Expected |
In principle, Guetta et al. (2004) predicted different break energies for νμ and 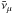 (see Guetta et al. 2004, Eqs. (A.10) and (A.11)), yielding three breaks in the combined
(see Guetta et al. 2004, Eqs. (A.10) and (A.11)), yielding three breaks in the combined 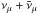 spectrum (or in the single νμ spectrum when taking oscillations into account) as shown in Fig. 3a, blue dashed – in the previous ANTARES analysis (Adrián-Martínez et al. 2013), this effect has been accounted for.
spectrum (or in the single νμ spectrum when taking oscillations into account) as shown in Fig. 3a, blue dashed – in the previous ANTARES analysis (Adrián-Martínez et al. 2013), this effect has been accounted for.
4.2. NeuCosmA model
Monte Carlo algorithms such as SOPHIA (see Mücke et al. 2000) have improved the calculations of photohadronic interactions in astrophysical processes. Hümmer et al. (2012) showed that a more detailed treatment of the particle physics involved in calculating the neutrino spectra greatly changes the resulting neutrino flux predictions compared with those described in Sect. 4.1. Using their neutrinos from cosmic accelerators (NeuCosmA) code, the authors pointed out how the full photohadronic interaction cross-section, individual treatment of secondary particles (including energy losses), and neutrino mixing affect the predicted neutrino flux (Hümmer et al. 2010, 2012; Baerwald et al. 2012). Owing to these effects, the doubly peaked structure of the spectrum from muon and pion decays now features an additional high-energy component from K+ decays. Moreover, the authors discussed several problems with the older neutrino flux estimations, such as using the real average photon energy instead of the peak energy of the photon distribution, taking the full width of the Δ-resonance into account, and simulating the energy losses of secondary particles as well as the energy dependence of the mean free path of protons (see also He et al. 2012). The combination of all these effects gives rise to a prediction for the neutrino yield that is about one order of magnitude below the result of Guetta et al. (2004).
Note that the NeuCosmA model, however, does not introduce any new assumptions on the nature of GRBs in general, but applies known physics in greater detail within the paradigm of the fireball model. Hence, limits on these predictions will first of all constrain parameters governing the fireball model (such as the boost factor Γ of the jet), and might later on probe the fireball paradigm itself.
Predictions made by the NeuCosmA model are used to optimise this analysis. In Fig. 3a, a comparison between the predicted neutrino spectra from Guetta et al. (2004) and from NeuCosmA is shown exemplarily for GRB 110918. Figure 3b shows all individual numerical neutrino spectra and their sum.
5. Simulation and signal probability density function
For each GRB in the selection, neutrino events were generated with high statistics to simulate the predicted NeuCosmA spectrum. They were then reconstructed to compute the acceptance of the detector. Their distribution gives the signal probability density function (PDF) labelled 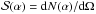 , with α being the space angle between the reconstructed track direction and the gamma-ray-burst’s coordinates.
, with α being the space angle between the reconstructed track direction and the gamma-ray-burst’s coordinates.
Firstly, the passage of neutrinos from the direction of a GRB through the Earth was simulated. If they interacted with matter sufficiently close to or in the detector, the resulting hadronic shower from the break-up of the target nucleon was generated. The secondary particles were then propagated through the medium, inducing the emission of Cherenkov photons on their trajectory. The response of the PMTs to the emitted Cherenkov light was then simulated, taking into account the detector and environmental conditions at the time of the GRB occurrence. For a more detailed description of the simulation scheme, see Adrián-Martínez et al. (2012).
For each GRB, 4 × 109 muon neutrinos were simulated. No background events were generated, as the background rate was estimated using the data themselves (see Sect. 6).
The applied track reconstruction algorithm is the same as used in Adrián-Martínez et al. (2012). It is based on a multi-step algorithm to maximise the likelihood of an assumed track hypothesis. The reconstruction returns two quality parameters, namely the track-fit quality parameter Λ and the estimated angular uncertainty on the muon track direction β. Cuts on these parameters can be used to improve the signal-to-noise ratio. To ensure a good directional reconstruction of the selected neutrino candidates, we required β < 1°. For a sample of track candidates with high reconstruction quality (Λ > −5.2), this cut has been shown to remove most of the remaining atmospheric muons that were falsely reconstructed as upgoing without significantly affecting the neutrino signal: atmospheric muons are reduced by a factor of 1.2 × 10-5, while atmospheric neutrinos are reduced by 0.19. The total background due to atmospheric events is decreased by 10-6 (Adrián-Martínez et al. 2012). In this analysis, the same cut combination would leave ~60...70% of a typical GRB signal. However, the narrow time windows (typically a few tens of seconds, see Table 2 for per-GRB values) yield intrinsically low background in coincidence with each GRB, allowing one to loosen the cuts on the Λ parameter. These were then optimised for each burst individually.
To account for the satellite’s uncertainty on the direction of the GRB, the reconstructed space angle was additionally smeared with a Gaussian of the appropriate width.
The resulting distribution of events relative to the GRB direction for each cut on Λ was then fitted with the function 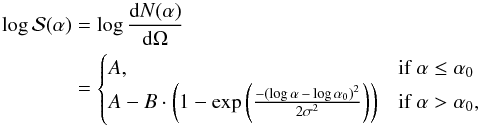 (1)with the free parameters A, B, α0, and σ as shown in Fig. 4. In the final analysis, events with an angular distance of up to 10° from the burst positions were included in the maximum-likelihood search.
(1)with the free parameters A, B, α0, and σ as shown in Fig. 4. In the final analysis, events with an angular distance of up to 10° from the burst positions were included in the maximum-likelihood search.
An investigation of shower-like events (e.g. from neutral current interactions of νμ) revealed that these contribute only negligibly to the signal PDF up to 10°, as the original neutrino direction cannot be adequately reconstructed because of the spherical signatures of these interactions.
Optimisation results for the ten most promising GRBs.
 |
Fig. 4 Simulated and reconstructed signal events per solid angle Ω versus the logarithm of the space angle α in degrees for the burst GRB 110918: muon tracks are plotted in black, shower-like events are drawn in green. The corresponding fit is shown in red (see Eq. (1)). The grey dotted line indicates the median angular spread of events ⟨ α ⟩ = 0.32°. The blue dashed line shows the flat background distribution ℬ(α) as calculated in Sect. 6. Cut values Λ > − 5.5 and β < 1° are applied here. |
6. Background estimation
Upgoing atmospheric neutrinos constitute the main background component for each GRB, with a smaller contribution coming from misreconstructed downgoing atmospheric muons. To estimate the mean number of background events μb for each Λ cut for each burst as realistically as possible, data were used. However, as the number of upgoing events is very low (~four per day, see Adrián-Martínez et al. 2012, Table 1), long time periods are needed to yield sufficient statistics, which in turn requires averaging over different data-taking conditions (in particular because of seasonal variations of the optical background). To compensate for this, we first estimated the average rate of reconstructed events in the GRB’s direction ⟨ n(θ,φ)GRB ⟩ allruns in local coordinates zenith θ and azimuth φ using data from the entire 2007 to 2011 period, then adjusted it for varying data-taking conditions (for a detailed description, see Appendix B).
For the final search, the number of background events in coincidence with each burst and within a search cone of 10° around its position was evaluated to be of the order of 10-4. The background PDF, ℬ(α), was considered to be flat in Ω within this cone, as shown in Fig. 4 for GRB 110918.
7. Pseudo-experiments and extended maximum-likelihood ratio
In the following, we show how pseudo-experiments were generated to compute the significance of a measurement, then how the cut on the reconstruction quality parameter Λ was optimised for each GRB to yield the highest discovery probability for a signal according to the NeuCosmA model.
For the pseudo-experiments, signal and background events i with space angle αi were drawn randomly from the normalised signal 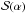 and background ℬ(α) PDFs corresponding to each chosen cut on Λ. For each pseudo-experiment with a total number of events ntot, the test statistic Q was calculated as follows:
and background ℬ(α) PDFs corresponding to each chosen cut on Λ. For each pseudo-experiment with a total number of events ntot, the test statistic Q was calculated as follows: ![\begin{equation} Q = \max_{\mu^{\prime}_\mathrm{s} \in [0,n_\mathrm{tot}]} \left( \sum\limits_{i\,=\,1}^{n_\mathrm{tot}} \log \frac{\mu^\prime_\mathrm{s} \mathcal{S}(\alpha_i) + \mu_\mathrm{b} \mathcal{B}(\alpha_i)}{\mu_\mathrm{b} \mathcal{B}(\alpha_i)} - (\mu^{\prime}_\mathrm{s} +\mu_\mathrm{b}) \right). \label{eq:ex_max_likelihood} \end{equation}](/articles/aa/full_html/2013/11/aa22169-13/aa22169-13-eq114.png) (2)This is the so-called extended maximum-likelihood ratio (Barlow 1990) with an a priori knowledge of the expected number of background events μb (as evaluated in Sect. 6 and Appendix B). Higher values of Q indicate that the measurement is more compatible with the signal hypothesis. The signal contribution
(2)This is the so-called extended maximum-likelihood ratio (Barlow 1990) with an a priori knowledge of the expected number of background events μb (as evaluated in Sect. 6 and Appendix B). Higher values of Q indicate that the measurement is more compatible with the signal hypothesis. The signal contribution 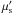 is scanned between 0 and ntot, its value corresponding to the maximum of the sum in Eq. (2) returns the estimated signal
is scanned between 0 and ntot, its value corresponding to the maximum of the sum in Eq. (2) returns the estimated signal 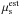 .
.
 |
Fig. 5 Probability distributions of Q-values, hns(Q), for different numbers of injected signal events, ns. Black: background only, h0(Q); red, green, blue ... : ns = 1,2,3... injected signal events. Grey vertical lines indicate the threshold values |
In the following, hns(Q) denotes the distribution of Q-values for ns injected signal events with a Poisson-distributed number of background events with expectation value μb. The significance of a measurement is determined by its p-value4, which is given by the probability to yield Q-values at least as high as that observed if the background-only hypothesis were true. Hence, using the background-only distribution h0(Q), the lowest Q-value 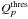 that is necessary to claim a discovery with a certain p-value can be calculated with
that is necessary to claim a discovery with a certain p-value can be calculated with 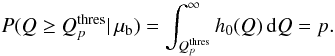 (3)The probability distributions hns(Q) for different ns are shown in Fig. 5, with the threshold Q-values indicated by the grey dashed lines. The probability distribution of Q values for any number of expected signal events μs is calculated via
(3)The probability distributions hns(Q) for different ns are shown in Fig. 5, with the threshold Q-values indicated by the grey dashed lines. The probability distribution of Q values for any number of expected signal events μs is calculated via 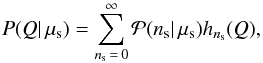 (4)with the Poisson distribution
(4)with the Poisson distribution 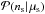 giving the probability of observing ns events from a mean number of expected events μs. The integral of P(Q | μs) gives the model discovery potential
giving the probability of observing ns events from a mean number of expected events μs. The integral of P(Q | μs) gives the model discovery potential 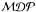 ; it is the probability to make a discovery assuming that the model was correct:
; it is the probability to make a discovery assuming that the model was correct: 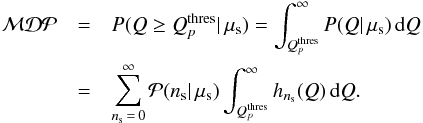 (5)The value of the Λ cut at a given significance level is then chosen as that which maximises the
(5)The value of the Λ cut at a given significance level is then chosen as that which maximises the 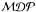 for the value of μs predicted by the NeuCosmA model (see Sect. 4.2). Figure 6 shows
for the value of μs predicted by the NeuCosmA model (see Sect. 4.2). Figure 6 shows 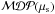 of GRB 110918 for 3σ, 4σ, and 5σ versus an arbitrary number of signal events. The distribution P(Q | μs) from Eq. (4) was also used to set upper limits on the number of signal events when no discovery is made. For example, when the final analysis returns Qmeas, we set a 90% confidence level (C.L.) upper limit
of GRB 110918 for 3σ, 4σ, and 5σ versus an arbitrary number of signal events. The distribution P(Q | μs) from Eq. (4) was also used to set upper limits on the number of signal events when no discovery is made. For example, when the final analysis returns Qmeas, we set a 90% confidence level (C.L.) upper limit 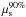 on the signal by rejecting all event expectations μs that would lead to values Q > Qmeas in 90% of all pseudo-experiments:
on the signal by rejecting all event expectations μs that would lead to values Q > Qmeas in 90% of all pseudo-experiments: 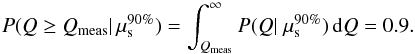 (6)When no event was measured (Qmeas = 0), a 90% C.L. upper limit was set at 2.3, the lowest possible value5.
(6)When no event was measured (Qmeas = 0), a 90% C.L. upper limit was set at 2.3, the lowest possible value5.
 |
Fig. 6 Model discovery potential |
For each number of injected signal events ns, 105 pseudo-experiments were generated6 to derive the signal distributions hns(Q). Using this procedure, the model discovery potential was calculated for any given μs, and the final cut on Λ for each GRB was found.
8. Search optimisation
In the following, the best trade-off between an increased sample and the associated statistical penalty is investigated. In general, a weighting factor, wi, could be assigned to each GRB according to the predicted flux from the model. However, this would result in the search being very sensitive to the combined uncertainty from the NeuCosmA model and especially to the parameters upon which it is based. An alternative approach is to include only the NGRB most promising candidates, where to maintain the same overall probability of making a false discovery, the p-value for each burst must be divided by the total trial factor NGRB. By ordering the bursts from highest to lowest 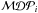 , the most promising NGRB can be chosen to maximise the combined probability of making a significant discovery from any of them. The total model discovery potential is then calculated via
, the most promising NGRB can be chosen to maximise the combined probability of making a significant discovery from any of them. The total model discovery potential is then calculated via 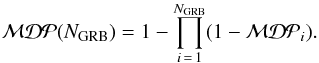 (7)The resulting distributions of
(7)The resulting distributions of 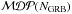 as a function of the size of the considered sub-sample of GRBs are shown in Fig. 7 for 3σ, 4σ and 5σ (thick lines). The 3σ
as a function of the size of the considered sub-sample of GRBs are shown in Fig. 7 for 3σ, 4σ and 5σ (thick lines). The 3σ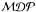 distribution rises to a maximum of 0.059 at a sample size of 106 GRBs, but is relatively flat around its highest value. For a search optimised for 3σ it is therefore reasonable to take the whole set of GRBs, as it does not decrease the
distribution rises to a maximum of 0.059 at a sample size of 106 GRBs, but is relatively flat around its highest value. For a search optimised for 3σ it is therefore reasonable to take the whole set of GRBs, as it does not decrease the 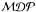 significantly (around 3.4%) and the search remains less model-dependent. The 5σ
significantly (around 3.4%) and the search remains less model-dependent. The 5σ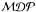 distribution, on the other hand, is prominently peaked at NGRB = 1, with NGRB = 2 being almost equivalent (
distribution, on the other hand, is prominently peaked at NGRB = 1, with NGRB = 2 being almost equivalent (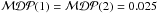 ) – the model discovery potential then decreases for larger samples. Even for NGRB = 2, the second strongest GRB contributes only a small fraction to the discovery potential.
) – the model discovery potential then decreases for larger samples. Even for NGRB = 2, the second strongest GRB contributes only a small fraction to the discovery potential.
For comparison, the distributions for a simple counting search (in which all events passing the cut criteria carry equal weighting) are also shown in Fig. 7 (thin lines). To mimic this search, a radius cut αcut for each GRB was calculated from the known background μb at fixed reasonable quality cuts (Λ > − 5.5,β < 1°) and the given significance level p/NGRB. Applying this search radius cut on the signal PDF 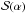 , the expected number of signal events μs can be estimated and consequently the
, the expected number of signal events μs can be estimated and consequently the 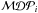 evaluated as the probability of detecting more than zero events.
evaluated as the probability of detecting more than zero events.
As expected, the 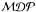 curves for a counting analysis are well below those for the likelihood method, showing the advantage of the search method used in this analysis. The shapes of the curves, on the other hand, are quite similar, and the same conclusions can be drawn from them, namely that using the whole sample gives the best discovery probability at 3σ and using only the individual GRB 110918 at 5σ.
curves for a counting analysis are well below those for the likelihood method, showing the advantage of the search method used in this analysis. The shapes of the curves, on the other hand, are quite similar, and the same conclusions can be drawn from them, namely that using the whole sample gives the best discovery probability at 3σ and using only the individual GRB 110918 at 5σ.
 |
Fig. 7 Model discovery potential |
Based on these results, we decided to optimise the quality cut on Λ for a likelihood search on the whole sample of 296 GRBs at the 3σ significance level. Because 3σ is not enough to claim a discovery, we predefined a cut on Λ that was optimised for a 5σ discovery, which was then used for a separate search for the emission from GRB 110918 only.
Optimised cuts Λcut for the final analysis as well as the accordingly expected number of background and signal events, the median angular resolution, and the search-time window are shown in Table 2 for the ten most promising GRBs. A full list for the 296 selected bursts can be found at the CDS.
9. Results and discussion
Using the strategy outlined above, we analysed ANTARES data from the end of 2007 to 2011 searching for neutrino events in coincidence with the search-time windows and within 10° around each GRB. No data events passed this selection within the accumulated search duration of 6.6 h. Hence, the measured Q-value is zero.
 |
Fig. 8 a) Expected muon neutrino spectra of the most promising burst GRB 110918 (solid lines) from NeuCosmA (Hümmer et al. 2010) (red) and Guetta et al. (2004) (blue). Limits on these predictions are shown in the energy ranges where we expect 90% of the flux (dashed lines). b) Sum of the 296 individual gamma-ray-burst muon neutrino spectra (red and blue solid lines) and limits set by this analysis on the total flux expected from the sample (red and blue dashed lines). The IceCube IC 40+IC 59 limit (Abbasi et al. 2012) on the neutrino emission from 300 GRBs and the first ANTARES limit from 2007 using 40 GRBs (Adrián-Martínez et al. 2013) are also shown in black (dashed) and grey (dash-dotted), respectively. The right-hand axis represents the inferred quasi-diffuse flux limit E2Φν (Eq. (8)). |
In total, 0.06 neutrino events from GRBs are expected from the NeuCosmA model, where only a small contribution of 4.6 × 10-5 events is not due to particle tracks produced by muon neutrinos – the Guetta model predicts 0.5 signals from muon neutrinos. The overall background in the 10° cones is 0.05 events. The 90% C.L. upper limits on the expected number of signal events μs from each model are thus set to 2.3 events, and the corresponding limits on the muon neutrino flux, Fν, from GRB 110918 as well as on the cumulative flux from the whole sample are shown in Fig. 8. The simple treatment of the Guetta model is represented here (see Fig. 3 a, solid line). For the NeuCosmA model, the limit on the total flux lies a factor of 38 above the expected spectrum (4.4 for Guetta). The right-hand axis of Fig. 8b represents the limits translated into limits on the inferred quasi-diffuse neutrino flux: 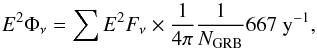 (8)where
(8)where 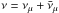 , assuming that each analysed sample represents an average burst distribution and that the annual rate of long bursts is 667 per year.
, assuming that each analysed sample represents an average burst distribution and that the annual rate of long bursts is 667 per year.
The first ANTARES limit (Adrián-Martínez et al. 2013) obtained for 40 GRBs during the construction phase of the detector in the year 2007 is also shown in Fig. 8b. That analysis was based on the Guetta model (accounting for different break energies of νμ and 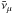 ) and employed a counting method searching for neutrino events in a two-degree cone around each burst. Using the data from the IC 40 and IC 59 detector phases in 2008 to 2010, IceCube recently published a more stringent limit on the neutrino emission as predicted by the “simple” Guetta model (Abbasi et al. 2012), which is also shown in Fig. 8b.
) and employed a counting method searching for neutrino events in a two-degree cone around each burst. Using the data from the IC 40 and IC 59 detector phases in 2008 to 2010, IceCube recently published a more stringent limit on the neutrino emission as predicted by the “simple” Guetta model (Abbasi et al. 2012), which is also shown in Fig. 8b.
Because of the larger effective area of the IceCube detector, the new ANTARES limit presented in this paper does not set additional constraints on the Guetta emission model. Note, however, that both detectors have complementary sky coverage and therefore the analysed sample of GRBs differs significantly. 90% of the analysed bursts have not previously had their neutrino emission constrained. When comparing limits obtained in different analyses, however, one should keep in mind that the precise shapes of the spectra – and thus, of the limits – depend on the actual selected sample, the measured parameters of the individual bursts and their uncertainty, the set of default parameters and on the chosen model.
10. Conclusion
Using data from the ANTARES detector, a search for muon neutrinos in coincidence with 296 GRBs occurring between the end of 2007 and 2011 has been performed. No events passed the selection criteria and limits on the neutrino flux were derived. For the NeuCosmA model, a limit on E2Fν of 0.35 − 5.6GeVcm-2 in the energy range from 7.5 × 104GeV to 1.0 × 107GeV was derived and compared with limits obtained in previous analyses.
This work is the first analysis based on an advanced numerical calculation of GRB neutrinos: the NeuCosmA code includes full photohadronic interaction cross-sections, energy losses of secondary particles, and flavour mixing. The neutrino flux has been shown to be an order of magnitude below that predicted by previous analytic approaches. This helps to resolve the tension between the non-observation of a neutrino signal and the most stringent experimental constraint currently available (Abbasi et al. 2012), which was a factor of 3.7 below the predictions made by the Guetta model.
Hence, existing limits do not yet constrain realistic neutrino emission models based on an internal shock scenario. Nevertheless, the collection of more data with active experiments such as ANTARES and IceCube, as well as with the planned neutrino telescope KM3NeT, will certainly allow the widely established fireball paradigm for GRBs to be probed in the near future.
Online material
Appendix A: GRB selection
Usage of the GRB parameter catalogues.
The table of the Swift satellite7 contains data from the three on-board instruments BAT (gamma rays), XRT (X-rays), and UVOT (ultraviolet), ordered with increasing position-measurement accuracy from arcminutes to sub-arcseconds. The information provides BAT spectral measurements in the energy range from 15 to 150keV. The Swift BAT2 Catalogue (Sakamoto et al. 2011)8 provides re-analysed Swift data, so the spectral information therein is considered to be more accurate. The Fermi GBM Burst Catalogue9 (Goldstein et al. 2012; Paciesas et al. 2012) supplies the best spectral information in the energy range from 10keV to 1MeV: the peak flux spectrum and the spectrum averaged over the burst duration (which is eventually used for the neutrino spectrum calculation) is fitted with four different spectral functions. The angular resolution is of the order of degrees. The IceCube Collaboration also provides a table with GRB parameters10 (Aguilar 2011), which is created by parsing the Gamma-ray Coordinates Network (GCN) notices11. This table is used to fill up missing parameter values for GRBs that have been found in at least one of the other tables.
When merging the information on the GRB parameters, we assigned priorities to the measured values according to their considered accuracy. The priorities of parameters are shown in Table A.1 in square brackets, as well as the percentage of how often information was obtained from each source.
Standard gamma-ray-burst parameters as described in the text.
When a parameter could not be measured, standard values as given in Table A.2 were used to calculate the spectra. The form of the photon spectrum is determined by the spectral indices α and β with the break energy ϵpeak giving their transition. The isotropic luminosity Liso can be calculated from the redshift z and the total measured fluence in gamma rays ℱ (given in the energy range from Emin to Emax) via 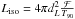 with the luminosity distance dL. In case of unknown redshift z, we took the default value of Liso. T90 is the time in which 90% of the fluence is emitted. The other parameters such as the jet Lorentz boost factor Γ, the fraction of jet energy in electrons ϵe and in the magnetic field ϵB, the ratio of energy in electrons and protons fe, the average fraction of proton energy transferred to a pion ⟨ xp → π ⟩ and the variability of the gamma-ray light curve tvar are not present in the tables and hence were taken as default. The standard values are the same as given in Aguilar (2011), with some differences to the IC 22 (Abbasi et al. 2010) default values: z = 2.0, Γ = 300, Liso = 1051ergs-1. Baerwald et al. (2012) give a very elaborate overview about the NeuCosmA spectra changing with the input parameters.
with the luminosity distance dL. In case of unknown redshift z, we took the default value of Liso. T90 is the time in which 90% of the fluence is emitted. The other parameters such as the jet Lorentz boost factor Γ, the fraction of jet energy in electrons ϵe and in the magnetic field ϵB, the ratio of energy in electrons and protons fe, the average fraction of proton energy transferred to a pion ⟨ xp → π ⟩ and the variability of the gamma-ray light curve tvar are not present in the tables and hence were taken as default. The standard values are the same as given in Aguilar (2011), with some differences to the IC 22 (Abbasi et al. 2010) default values: z = 2.0, Γ = 300, Liso = 1051ergs-1. Baerwald et al. (2012) give a very elaborate overview about the NeuCosmA spectra changing with the input parameters.
The parameters of the extraordinarily strong GRB 110918 are presented in Table A.3.
The time window of the search, Tsearch, for emission from each burst is delineated by the start and stop times as measured by the satellites or, when these are not provided in the catalogues, as T90 ± 30%. Additionally, we accounted for the detector’s data acquisition uncertainty (0.4s), the satellite time given in integer seconds (1s), and the light propagation from a satellite through Earth to the detector (0.5s) by adding another ± 2s to the search-time window.
Gamma-ray-burst parameters of GRB 110918 as described in the text.
Appendix B: Background estimation
We estimated the background event rate for each GRB separately. First, the time-averaged reconstructed event rate in the data from late 2007 to 2011 from the direction of the GRB was estimated. Either the rate averaged over all data-taking runs at the GRB’s position (θ,φ)GRB was used, or – if resulting in a higher rate – the mean of the corresponding time-averaged rates within a 10° cone around this position. This establishes a conservative background estimate, accounting for non-uniformity of the background in the vicinity of the GRB’s position.
To take into account the varying efficiency of the detector with time, this average rate was then scaled by a correction factor ci for each data-taking run i of ~2.5 h. Each ci was calculated by the ratio of the total number of events (in all directions) in the corresponding run ni to the average total number of events for the respective run duration ti (see Eq. (B.1)). As ni may be very small for short runs, the 90% C.L. upper limit was used instead. Additionally, factors for specific run periods cperiod were applied taking into account differences between longer phases of similar run conditions. These values were obtained by fitting the background rate in certain periods separately. This approach assumes that the total number of events – dominated mostly by downgoing atmospheric muons – is proportional to the number of upgoing events. To test this assumption, we determined the measured and estimated rates of upgoing events in longer time periods of a few days, excluding data-taking runs in which GRBs occurred. The measured rate was always found to be μmeas < 1.5 μest, thus we conservatively increased the estimate by 50%. Consequently, the expected number of background events in coincidence with each GRB search-time window Tsearch was calculated via 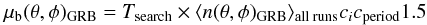 (B.1)with
(B.1)with ![\hbox{$c_i = \frac{\left[ n_i \right]^{90\%}}{t_i \sum n_j / \sum t_j}$}](/articles/aa/full_html/2013/11/aa22169-13/aa22169-13-eq224.png) , where j includes all data-taking runs.
, where j includes all data-taking runs.
IceCube: http:// grbweb.icecube.wisc.edu
Acknowledgments
The authors acknowledge the financial support of the funding agencies: Centre National de la Recherche Scientifique (CNRS), Commissariat à l’énergie atomique et aux énergies alternatives (CEA), Agence National de la Recherche (ANR), Commission Européenne (FEDER fund and Marie Curie Program), Région Alsace (contrat CPER), Région Provence-Alpes-Côte d’Azur, Département du Var and Ville de La Seyne-sur-Mer, France; Bundesministerium für Bildung und Forschung (BMBF), Germany; Istituto Nazionale di Fisica Nucleare (INFN), Italy; Stichting voor Fundamenteel Onderzoek der Materie (FOM), Nederlandse organisatie voor Wetenschappelijk Onderzoek (NWO), the Netherlands; Council of the President of the Russian Federation for young scientists and leading scientific schools supporting grants, Russia; National Authority for Scientific Research (ANCS), Romania; Ministerio de Ciencia e Innovación (MICINN), Prometeo of Generalitat Valenciana and MultiDark, Spain; Agence de l’Oriental and CNRST, Morocco. We also acknowledge the technical support of Ifremer, AIM and Foselev Marine for the sea operation and the CC-IN2P3 for the computing facilities. We would like to thank Walter Winter for helpful discussions and making it possible to use the NeuCosmA model.
References
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2010, ApJ, 710, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2011, Phys. Rev. Lett., 106, 141101 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2012, Nature, 484, 351 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Achterberg, A., Ackermann, M., Adams, J., et al. 2008, ApJ, 674, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Adrián-Martínez, S., Al Samarai, I., Albert, A., et al. 2012, ApJ, 760, 53 [Google Scholar]
- Adrián-Martínez, S., Samarai, I. Al, Albert, A., et al. 2013, J. Cosmology Astropart. Phys., 2013, 006 [Google Scholar]
- Ageron, M., Aguilar, J. A., Al Samarai, I., et al. 2011, Nucl. Instr. Meth. A, 656, 11 [CrossRef] [Google Scholar]
- Aguilar, J. A. 2011, in Proc. of the 32nd International Cosmic Ray Conf., 8, ICRC, ed. IUPAP (Institute of High Energy Physics, Beijing), 232 [Google Scholar]
- Aguilar, J. A., Albert, A., Ameli, F., et al. 2007, Nucl. Instr. Meth. A, 570, 107 [Google Scholar]
- Aptekar, R., Frederiks, D., Golenetskii, S., et al. 1995, Space Sci. Rev., 71, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Avrorin, A., Aynutdinov, V., Belolaptikov, I., et al. 2011, Astron. Lett., 37, 692 [Google Scholar]
- Baerwald, P., Hümmer, S., & Winter, W. 2012, Astropart. Phys., 35, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, R. 1990, Nucl. Instr. Meth. A, 297, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Besson, D., Razzaque, S., Adams, J., & Harris, P. 2007, Astropart. Phys., 26, 367 [NASA ADS] [CrossRef] [Google Scholar]
- de Ugarte Postigo, A., Gorosabel, J., Castro-Tirado, A. J., & Thoene, C. C. 2011, GCN Circ., 12375, 1 [NASA ADS] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Fukuda, S., Fukuda, Y., Ishitsuka, M., et al. 2002, ApJ, 578, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Burgess, J. M., Preece, R. D., et al. 2012, ApJS, 199, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Golenetskii, S., Aptekar, R., Frederiks, D., et al. 2011, GCN Circ., 12362, 1 [NASA ADS] [Google Scholar]
- Guetta, D., Hooper, D., Alvarez-Muñiz, J., Halzen, F., & Reuveni, E. 2004, Astropart. Phys., 20, 429 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-N., Liu, R.-Y., Wang, X.-Y., et al. 2012, ApJ, 752, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hümmer, S., Rüger, M., Spanier, F., & Winter, W. 2010, ApJ, 721, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Hümmer, S., Baerwald, P., & Winter, W. 2012, Phys. Rev. Lett., 108, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, Lett., 413, L101 [Google Scholar]
- Krimm, H. A., Mangano, V., & Siegel, M. H. 2011, GCN Report, 350, 1 [NASA ADS] [Google Scholar]
- Levan, A. J., Tanvir, N. R., Wiersema, K., Berger, E., & Fox, D. 2011, GCN Circ., 12368, 1 [NASA ADS] [Google Scholar]
- Meegan, C. A., Fishman, G. J., Wilson, R. B., et al. 1992, Nature, 355, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P. 2006, Rep. Prog. Phys., 69, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1993, ApJ, 405, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., Engel, R., Rachen, J. P., Protheroe, R. J., & Stanev, T. 2000, Comput. Phys. Comm., 124, 290 [Google Scholar]
- Nakar, E. 2007, Phys. Rep., 442, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Paciesas, W. S., Meegan, C. A., Pendleton, G. N., et al. 1999, ApJS, 122, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Paciesas, W. S., Meegan, C. A., von Kienlin, A., et al. 2012, ApJS, 199, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Mészáros, P. 1992, MNRAS, 258, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Baumgartner, W. H., et al. 2011, ApJS, 195, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Wiersema, K., Levan, A. J., Greiss, S., & Gaensicke, B. 2011, GCN Circ., 12365, 1 [NASA ADS] [Google Scholar]
- Vieregg, A. G., Palladino, K., Allison, P., et al. 2011, ApJ, 736, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E. 1995a, Phys. Rev. Lett., 75, 386 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Waxman, E. 1995b, ApJ, 452, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E. 2000, ApJS, 127, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E., & Bahcall, J. 1997, Phys. Rev. Lett., 78, 2292 [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Time-averaged muon-neutrino effective area of the ANTARES neutrino telescope as a function of energy for different declination bands δ for the considered data-taking period. Typical quality cuts as derived in this analysis (Λ > −5.35, β < 1°) are applied. |
| In the text | |
 |
Fig. 2 Sky distribution of the selected 296 GRBs in equatorial coordinates. The gamma-ray fluence of each burst is colour-coded. The instantaneous field of view of the ANTARES detector is 2πsr; within a period of 24 h, the sky up to a declination of 47° is visible. |
| In the text | |
 |
Fig. 3 a) Expected |
| In the text | |
 |
Fig. 4 Simulated and reconstructed signal events per solid angle Ω versus the logarithm of the space angle α in degrees for the burst GRB 110918: muon tracks are plotted in black, shower-like events are drawn in green. The corresponding fit is shown in red (see Eq. (1)). The grey dotted line indicates the median angular spread of events ⟨ α ⟩ = 0.32°. The blue dashed line shows the flat background distribution ℬ(α) as calculated in Sect. 6. Cut values Λ > − 5.5 and β < 1° are applied here. |
| In the text | |
 |
Fig. 5 Probability distributions of Q-values, hns(Q), for different numbers of injected signal events, ns. Black: background only, h0(Q); red, green, blue ... : ns = 1,2,3... injected signal events. Grey vertical lines indicate the threshold values |
| In the text | |
 |
Fig. 6 Model discovery potential |
| In the text | |
 |
Fig. 7 Model discovery potential |
| In the text | |
 |
Fig. 8 a) Expected muon neutrino spectra of the most promising burst GRB 110918 (solid lines) from NeuCosmA (Hümmer et al. 2010) (red) and Guetta et al. (2004) (blue). Limits on these predictions are shown in the energy ranges where we expect 90% of the flux (dashed lines). b) Sum of the 296 individual gamma-ray-burst muon neutrino spectra (red and blue solid lines) and limits set by this analysis on the total flux expected from the sample (red and blue dashed lines). The IceCube IC 40+IC 59 limit (Abbasi et al. 2012) on the neutrino emission from 300 GRBs and the first ANTARES limit from 2007 using 40 GRBs (Adrián-Martínez et al. 2013) are also shown in black (dashed) and grey (dash-dotted), respectively. The right-hand axis represents the inferred quasi-diffuse flux limit E2Φν (Eq. (8)). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.