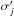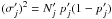| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 32 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424287 | |
| Published online | 24 January 2017 | |
Modelling clumpy photon-dominated regions in 3D
Understanding the Orion Bar stratification
I. Physikalisches Institut, Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
e-mail: sandree@ph1.uni-koeln.de
Received: 27 May 2014
Accepted: 16 September 2016
Context. Models of photon-dominated regions (PDRs) still fail to fully reproduce some of the observed properties. In particular they do not reproduce the combination of the intensities of different PDR cooling lines together with the chemical stratification, as observed for example for the Orion Bar PDR.
Aims. We aim to construct a numerical PDR model, KOSMA-τ 3D, to simulate full spectral cubes of line emission from arbitrary PDRs in three dimensions (3D). The model will reproduce the intensity of the main cooling lines from the Orion Bar PDR and the observed layered structure of the different transitions.
Methods. We built up a 3D compound, made of voxels (3D pixels) that contain a discrete mass distribution of spherical “clumpy” structures, approximating the fractal ISM. To analyse each individual clump the new code was combined with the KOSMA-τ PDR model. Probabilistic algorithms were used to calculate the local FUV flux for each voxel as well as the voxel-averaged line emissivities and optical depths, based on the properties of the individual clumps. Finally, the computation of the radiative transfer through the compound provided full spectral cubes. To test the new model we tried to simulate the structure of the Orion Bar PDR and compared the results to observations from HIFI/Herschel and from the Caltech Submillimetre Observatory (CSO). In this context new Herschel data from the HEXOS guaranteed-time key program is presented.
Results. Our model is able to reproduce the line-integrated intensities within a factor of 2.5 and the observed stratification pattern within 0.016 pc for the [Cii] 158 μm and different 12/13CO and HCO+ transitions, based on the representation of the Orion Bar PDR by a clumpy edge-on cavity wall. In the cavity wall, a large fraction of the total mass needs to be contained in clumps. The mass of the interclump medium is constrained by the FUV penetration. Furthermore, the stratification profile cannot be reproduced by a model that has the same amount of clump and interclump mass in each voxel; dense clumps need to be removed from the PDR surface.
Key words: photon-dominated region / ISM: structure / ISM: clouds / submillimeter: ISM / infrared: ISM / radiative transfer
© ESO, 2017
1. Introduction
Stars form from the interstellar medium (ISM), in its dense and cold regions, inside molecular clouds. Hence, a better understanding of the chemical and physical processes taking place in molecular clouds, their internal structure, and the interaction between molecular clouds and the interstellar radiation field is an important step to constrain our knowledge on star formation processes.
The energy which heats the different components of the ISM can originate from different sources, for instance from cosmic rays, from the dissipation of (magnetised) turbulence, or from the interstellar radiation field (including radiation from nearby stars). In photon-dominated (or photo-dissociation) regions (PDRs) the dominating energy input is provided by the interstellar radiation field. More precisely, a PDR is a region in interstellar space where the photon energies fall below the ionisation energy of hydrogen, but where the interstellar far-UV (FUV) radiation field still dominates the heating processes and the chemistry of the ISM (photon energies: 6 eV < hν < 13.6 eV). Here, the lower threshold of 6 eV is an estimate of the work function of a typical interstellar dust grain. The estimate of the work function varies in literature. 6 eV are stated in de Jong et al. (1980), more recent works discuss examples with work functions of 5 eV and of 7 eV (Hollenbach & Tielens 1999), Weingartner & Draine (2001b) adopt 4.4 eV for graphite grains and 8 eV for silicates. Cooling of the gas is dominated by fine structure line emission by atoms and ions, especially [Oi] 63 μm and 145 μm, [Cii] 158 μm and [Ci] 609 μm and 370 μm, by H2 rovibrational, and by molecular rotational lines (mainly CO) (Tielens & Hollenbach 1985; Hollenbach & Tielens 1997). Far-infrared (far-IR) continuum emission by dust grains and the emission features of polycyclic aromatic hydrocarbons (PAHs) are observed. At high densities gas and dust are tightly coupled via collisions and the IR emission of the dust grains can contribute to the cooling of the gas. As PDR emission dominates the IR and sub-millimetre spectra of star forming regions and galaxies (Röllig et al. 2007) they are the subject of many observations and extensive modelling. Photon-dominated regions can be found in many different astrophysical scenarios, however, here we focus on the transition zone between Hii- and molecular regions illuminated by the strong FUV radiation from young stars.
Many different PDR models have been developed aiming to relate the observed line and continuum emission to the physical parameters of the emitting region and to understand the physical processes taking place in PDRs (e.g. Tielens & Hollenbach 1985; Sternberg & Dalgarno 1989; Koester et al. 1994). The models focus on different key aspects and exploit different geometries. An overview, emphasizing advantages and disadvantages of the different PDR models, can be found in the comparison study by Röllig et al. (2007). Since then, most of the codes have been significantly improved (see e.g. Röllig et al. 2013; Le Bourlot et al. 2012; Ferland et al. 2013). A major new step was provided by the extension to fully three-dimensional configurations, which allows for the modelling of PDRs with arbitrary geometries, by Bisbas et al. (2012).
In the molecular clouds the FUV field is attenuated, mainly due to absorption by dust grains. The decreasing FUV field strength causes a layered structure of different chemical transitions, referred to as chemical stratification. Chemical stratification can be observed in many different PDRs and within different scenarios, for instance in the Hii region and molecular cloud M17 (Stutzki et al. 1988; Pellegrini et al. 2007; Pérez-Beaupuits et al. 2012), the Horsehead Nebula (Pety et al. 2007), planetary nebulae (for example NGC 7027, see Graham et al. 1993) or within protoplanetary disks (see for instance Kamp et al. 2010). Furthermore, it is observed in the Orion Bar PDR as discussed in Sect. 3.
In other PDRs we find a spatial coexistence of different PDR tracers that can be explained by a clumpy or filamentary cloud structure (Stutzki et al. 1988; Stutzki & Guesten 1990; Howe et al. 1991). Actually, most observations of molecular clouds show filamentary, turbulent structures and substructures on all scales observed so far. Such clouds can be described by fractal scaling laws. Fractal structures contain surfaces everywhere throughout the cloud, hence, a large fraction of the molecular material is located close to a surface. Combined with a low volume filling factor (VFF) of the dense condensations this implies that surfaces inside the clouds are exposed to the interstellar radiation field and form PDRs (Burton et al. 1990; Ossenkopf et al. 2007).
Several attempts have been made to model the 3D and inhomogeneous structure of PDR gas. For instance, Stutzki et al. (1998) have proven that the fractal properties can be mimicked by an ensemble of clumps with an appropriate mass spectrum. Based on this approach Cubick et al. (2008) show that an ensemble of such clumps, immersed in a thin inter-clump medium, can be used to simulate the large scale fine structure emission from the Milky Way. More recently, Glover et al. (2010) developed 3D simulations of the turbulent interstellar gas with coupled thermal, chemical and dynamical evolution. Levrier et al. (2012) use the Meudon PDR code to compare the chemical abundances in a homogeneous cloud to the chemical abundances in a cloud with density fluctuations.
However, a distribution of spherical clumps of different sizes that enables modelling of arbitrary 3D geometries has not yet been described. For the Orion Bar PDR, one of the most prominent PDRs in the solar neighbourhood, a match between observations and simulation results of the high-J CO line intensities, combined with the observed stratification profile is still pending. Plane-parallel PDR models fail in this context, because a match of the high-J CO line intensities always requires high densities which imply a very sharp and dense PDR structure that is not consistent with the observed stratification covering, in the case of the Orion Bar PDR, at least 0.03 pc (see for example Pellegrini et al. 2009, or the data presented in this work, Sect. 3.2). For example in Röllig et al. (2007, their Fig. 11) the C+-to-C-to-CO transition has been simulated using many different PDR codes (for a gas density of 105.5 cm-3 and an FUV field strength of 105 times the mean interstellar radiation field Draine 1978). For all models the transition takes place at optical depths AV ≲ 4 and using AV/NH = 6.289 × 10-22 cm-2 (Röllig et al. 2007) we find that the stratified layers do not cover more than 0.0065 pc. More sophisticated models are necessary to reproduce the observed line intensities as well as the observed chemical stratification. To overcome this deficiency we have set up an extension of the KOSMA-τ PDR code, denoted KOSMA-τ 3D, which enables us to model clumpy PDRs in 3D. The code supports a spatial variation of PDR parameters, like the mean density, the clump-size distribution, or the strength of the impinging FUV field. Furthermore, to exploit the copious information contained in observed line profiles, the new code analyses a region at arbitrary velocities and hence the simulations of full line profiles.
In Sect. 2 we discuss the extension of the KOSMA-τ PDR model to a clumpy 3D PDR model. To test the new code we use selected observations of the Orion Bar PDR which are presented in Sect. 3. The 3D model of the Orion Bar PDR is discussed in Sect. 4. In Sect. 5 we present the fitting process: first we discuss the parameters that are varied within our model set-up and define functions of merit that are used for the evaluation of different models. We do then present the simulation outcome for many different models and provide a discussion. The results are summarised in Sect. 6.
2. 3D PDR modelling
In this section we discuss the extension of the KOSMA-τ PDR model to a clumpy 3D PDR model. First the properties of the KOSMA-τ PDR model are summarised and modelling of the inhomogeneous ISM based on fractal structures is discussed. Afterwards, the 3D model set-up is described including all steps which are necessary to simulate maps and spectra, comparable to astronomical observations.
2.1. The KOSMA-τ PDR model
The KOSMA-τ PDR model1 (Röllig et al. 2006) has been developed at the University of Cologne in collaboration with the Tel-Aviv University. Contrary to many other models (see Röllig et al. 2007, and references therein), which are based on plane-parallel geometries, the KOSMA-τ model utilises a spherical geometry, clumps, to model the structure of a PDR.
A single clump is parameterised by its total hydrogen mass Mcl, the surface hydrogen density ns = nH,s + 2 nH2,s and the strength of the incident FUV field. The FUV flux is assumed to be isotropic (see discussion in Sect. 5.4.5) and is measured in units of the Draine field integrated over the FUV range (χ0 = 2.7 × 10-3 erg s-1 cm-2, Draine 1978). In addition, the model accounts for cosmic ray primary ionisations at a constant rate. In this work a rate of 2 × 10-16 s-1 per H2 molecule is used (Hollenbach et al. 2012). In the model the radial density distribution n(r) of the clumps is divided into a core and an outer region: 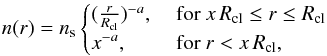 (1)where Rcl is the radius of the clump and xRcl with x ∈ [0,1] is the radius of the clump core. The exponent, a, and the size of the core are input parameters of the KOSMA-τ code, a = 0 and x ≠ 0 for example enforces a constant density sphere. In many studies (Stoerzer et al. 1996; Cubick et al. 2008) and also in this work, a = 1.5 and x = 0.2 are chosen with the aim to generate clumps that approximate Bonnor-Ebert spheres2. Consequently, the averaged density of one clump is given by
(1)where Rcl is the radius of the clump and xRcl with x ∈ [0,1] is the radius of the clump core. The exponent, a, and the size of the core are input parameters of the KOSMA-τ code, a = 0 and x ≠ 0 for example enforces a constant density sphere. In many studies (Stoerzer et al. 1996; Cubick et al. 2008) and also in this work, a = 1.5 and x = 0.2 are chosen with the aim to generate clumps that approximate Bonnor-Ebert spheres2. Consequently, the averaged density of one clump is given by 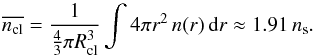 (2)To analyse such a clump the frequency dependent mean (averaged over the full solid angle) FUV intensity is derived at different positions between clump centre and clump surface (for different radii r ∈ [0,Rcl]). This calculation is based on the multi component dust radiative transfer (MCDRT) code (see Yorke 1980; Szczerba et al. 1997; Röllig et al. 2013) and includes isotropic scattering. The same code accounts for the IR continuum radiative transfer inside the clump. The KOSMA-τ PDR code includes H2 self-shielding based on the results from Draine & Bertoldi (1996), furthermore, CO photodissociation is computed based on Visser et al. (2009).
(2)To analyse such a clump the frequency dependent mean (averaged over the full solid angle) FUV intensity is derived at different positions between clump centre and clump surface (for different radii r ∈ [0,Rcl]). This calculation is based on the multi component dust radiative transfer (MCDRT) code (see Yorke 1980; Szczerba et al. 1997; Röllig et al. 2013) and includes isotropic scattering. The same code accounts for the IR continuum radiative transfer inside the clump. The KOSMA-τ PDR code includes H2 self-shielding based on the results from Draine & Bertoldi (1996), furthermore, CO photodissociation is computed based on Visser et al. (2009).
To derive the physical conditions and the chemical composition of the clump, the KOSMA-τ code iteratively solves the following steps: the chemical network, which can be assembled from a modular chemical network (Röllig et al. 2013), is used to derive local abundances, based on the local conditions. Using line-of-sight-integrated escape probabilities for the main cooling lines the local energy balance, that is heating and cooling processes are evaluated in steady state. After sufficient iterations (when a pre-defined convergency criterion is met; here: when the calculated column densities vary less than 1% between subsequent iterations), ray tracing through the clump is solved for lines of sight at different impact parameters p from the centre point of the spherical clump. For details on the ONION radiative transfer model see Gierens et al. (1992). The emission from the spherical clumps is not sensitive to their internal density structure, but fully parametrised by their surface density. A parameter study by Mertens (2013) showed that modifications of the internal density profile hardly change the chemical abundance profiles as long as the surface density is kept constant.
In the first part of the KOSMA-τ 3D PDR code the averaged attenuation of the FUV flux caused by clumps with different masses and densities is needed. The second part of the code uses clump-averaged line intensities and optical depths of atomic and molecular transitions. To derive the averaged FUV attenuation of a clump we calculate the hydrogen column density along a line of sight through the clump, depending on the impact parameter, that is 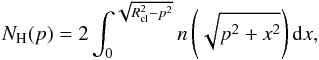 (3)where n(...) is the density profile as given by Eq. (1). NH(p) can be used to calculate the attenuation in the FUV range, τj, FUV(p)3, assuming that both quantities are proportional to each other (see Sect. 2.3.2). Furthermore, the attenuation of line intensities is proportional to the factor exp(−τ(p)) (see for example Eq. (B.3)), where τ(p) denotes the optical depth for a line of sight with impact parameter p. Therefore, the factor exp(−τ(p)) needs to be averaged over the projected surface of the clump, meaning that for each clump we numerically solve the integral
(3)where n(...) is the density profile as given by Eq. (1). NH(p) can be used to calculate the attenuation in the FUV range, τj, FUV(p)3, assuming that both quantities are proportional to each other (see Sect. 2.3.2). Furthermore, the attenuation of line intensities is proportional to the factor exp(−τ(p)) (see for example Eq. (B.3)), where τ(p) denotes the optical depth for a line of sight with impact parameter p. Therefore, the factor exp(−τ(p)) needs to be averaged over the projected surface of the clump, meaning that for each clump we numerically solve the integral ![\begin{equation} \overline{\tau_{j,\, {\rm FUV}}}= -\ln\left[ \frac{2}{R_{{\rm cl}}^2}\int_{0}^{R_{{\rm cl}}}{\rm e}^{-\tau_{j,\, {\rm FUV}}(p)}\, p \,{\rm d}p \right]. \label{Eq:tauClAvFUV} \end{equation}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq44.png) (4)The line intensities Ij, line(p) of different atomic and molecular transitions have been averaged correspondingly, that is
(4)The line intensities Ij, line(p) of different atomic and molecular transitions have been averaged correspondingly, that is 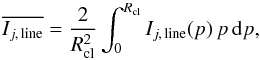 (5)and the optical depths of the different transitions, τj, line(p), are processed analogously to Eq. (4). The
(5)and the optical depths of the different transitions, τj, line(p), are processed analogously to Eq. (4). The 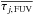 ,
, 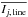 and
and 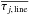 have been derived on a parameter grid of surface densities, clump masses and impinging FUV fluxes. The KOSMA-τ 3D code introduced in this work imports such a model grid and, if necessary, interpolates between gridpoints to derive the intensities and optical depths needed in the simulations. Details on the grid used for the presented Orion Bar simulations are summarised in Table 1.
have been derived on a parameter grid of surface densities, clump masses and impinging FUV fluxes. The KOSMA-τ 3D code introduced in this work imports such a model grid and, if necessary, interpolates between gridpoints to derive the intensities and optical depths needed in the simulations. Details on the grid used for the presented Orion Bar simulations are summarised in Table 1.
Overview of the most important model parameter.
2.2. Modelling the fractal ISM
The fractal structure of molecular clouds can be mimicked by a superposition of spherical clumps following a well-defined clump-mass spectrum, building up a clumpy ensemble (Stutzki et al. 1998; Cubick et al. 2008). The clump-mass spectrum can be described by a power-law 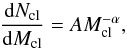 (6)giving the number of clumps dNcl in the mass bin dMcl. In addition the masses of the clumps are related to their radii Rcl by the mass-size relation
(6)giving the number of clumps dNcl in the mass bin dMcl. In addition the masses of the clumps are related to their radii Rcl by the mass-size relation 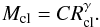 (7)The power-law exponents α and γ have been subject to many studies. Kramer et al. (1998) present clump mass spectra, derived using the square-fitting procedure gaussclump (Stutzki & Guesten 1990), of seven different molecular clouds, covering a wide range of physical properties and cloud sizes. They test and discuss the reliability of the mass spectra by studying the dependence on the control parameter of the decomposition algorithm. For all clouds from their sample they find that α lies between 1.6 and 1.8 implying that small clumps are more numerous. No turnover of the power-law index is observed especially not for small, gravitationally unbound objects.
(7)The power-law exponents α and γ have been subject to many studies. Kramer et al. (1998) present clump mass spectra, derived using the square-fitting procedure gaussclump (Stutzki & Guesten 1990), of seven different molecular clouds, covering a wide range of physical properties and cloud sizes. They test and discuss the reliability of the mass spectra by studying the dependence on the control parameter of the decomposition algorithm. For all clouds from their sample they find that α lies between 1.6 and 1.8 implying that small clumps are more numerous. No turnover of the power-law index is observed especially not for small, gravitationally unbound objects.
The power-law exponent γ has for instance been discussed by Elmegreen & Falgarone (1996). They analysed different cloud surveys from literature (based on different methods of clump identification) and find an exponent γ = 2.4−3.7 for single cloud surveys and an “all-cloud slope” in the range 2.2−2.5. Hence, smaller clumps are expected to be denser. Using a second method they derive a fractal dimension D = 2.3 ± 0.3 for the same surveys which theoretically is expected to be equal to the exponent γ.
Heithausen et al. (1998) combined and analysed large and small scale data of the Polaris Flare to derive the power law slopes over a mass range of at least 5 orders of magnitude, from several ten solar masses, down to masses less than that of Jupiter (about 10-3M⊙). Using the CO 1−0 and 2−1 lines they find α = 1.84 and γ = 2.31, values which are comparable to the ranges stated above and which we adapt for this work.
We note that in some more recent works (see review by Offner et al. 2014, and references therein) a turnover in the core-mass function has been reported for low-mass clumps. Such a deviation from the power-law is not included in the KOSMA-τ 3D PDR code. The influence of the very small clumps on the simulation outcome is investigated in Sect. 5.3.5.
2.2.1. Continuous description
Assuming that the masses of the clumps in an ensemble lie between a lower and an upper cut-off mass, ml and mu, one can derive the number of clumps Nens in the ensemble (see Cubick et al. 2008): 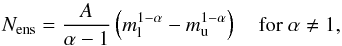 (8)and the total ensemble mass
(8)and the total ensemble mass 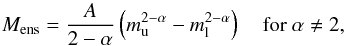 (9)relating the constant A to the ensemble mass. For the observed values of α below two an ensemble contains more low-mass than high-mass clumps, still, the high-mass clumps provide a larger fraction of the ensemble mass. The constant C in Eq. (7) depends on the averaged ensemble density ρens and the cut-off masses:
(9)relating the constant A to the ensemble mass. For the observed values of α below two an ensemble contains more low-mass than high-mass clumps, still, the high-mass clumps provide a larger fraction of the ensemble mass. The constant C in Eq. (7) depends on the averaged ensemble density ρens and the cut-off masses: 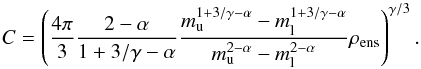 (10)
(10)
2.2.2. Discrete description
We use a discrete description for a simplified numerical treatment of the clumpy ensemble (see Cubick 2005). Here, the mass spectrum of the clumps is not continuous, but represented by clumps at discrete mass points { Mj } j = 1...nM. We use a logarithmic parameter scale, in other words 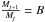 with B = 10. Indices are ordered with increasing masses. For the Orion Bar simulations we used MnM = 1 M⊙ (Lis & Schilke 2003, see Sect. 4) whereas the simulations of the whole Milky Way by Cubick (2005) rather correspond to MnM = 100 M⊙. We assume that the number of clumps Nj with mass Mj is given by the power law
with B = 10. Indices are ordered with increasing masses. For the Orion Bar simulations we used MnM = 1 M⊙ (Lis & Schilke 2003, see Sect. 4) whereas the simulations of the whole Milky Way by Cubick (2005) rather correspond to MnM = 100 M⊙. We assume that the number of clumps Nj with mass Mj is given by the power law 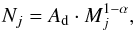 (11)with a constant Ad (d = discrete) similar to Eq. (8). This yields for the total mass MJ of clumps with mass Mj
(11)with a constant Ad (d = discrete) similar to Eq. (8). This yields for the total mass MJ of clumps with mass Mj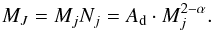 (12)For each ensemble the total mass of the ensemble Mens and the averaged ensemble density ρens are input parameters which can be fixed if the physical parameters of the PDR are known or they can be used as fitting parameters otherwise. The total ensemble mass is given by Mens = ∑ jNjMj. Inserting Nj from Eq. (11) we find
(12)For each ensemble the total mass of the ensemble Mens and the averaged ensemble density ρens are input parameters which can be fixed if the physical parameters of the PDR are known or they can be used as fitting parameters otherwise. The total ensemble mass is given by Mens = ∑ jNjMj. Inserting Nj from Eq. (11) we find 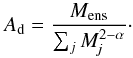 (13)The density of the individual clumps in the ensemble deviates from the ensemble averaged density ρens according to the mass-size relation (Eq. (7)), depending on their specific masses. For given mass points { Mj } j = 1...nM the volumes { Vj } j = 1...nM of individual clumps can be calculated using Eq. (7) which yields
(13)The density of the individual clumps in the ensemble deviates from the ensemble averaged density ρens according to the mass-size relation (Eq. (7)), depending on their specific masses. For given mass points { Mj } j = 1...nM the volumes { Vj } j = 1...nM of individual clumps can be calculated using Eq. (7) which yields 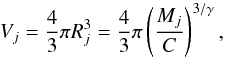 (14)and consequently the averaged density of a clump is found to be
(14)and consequently the averaged density of a clump is found to be 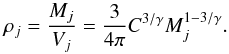 (15)The ensemble averaged density ρens is equal to the total ensemble mass, divided by the total ensemble volume
(15)The ensemble averaged density ρens is equal to the total ensemble mass, divided by the total ensemble volume 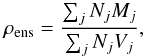 (16)and inserting Eqs. (11) and (14) we derive
(16)and inserting Eqs. (11) and (14) we derive 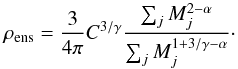 (17)Inserting Eq. (15) yields an expression for the density of clumps with mass Mj as a function of the average ensemble density,
(17)Inserting Eq. (15) yields an expression for the density of clumps with mass Mj as a function of the average ensemble density, 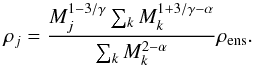 (18)In addition, the number of clumps Nj with mass Mj, as a function of the total ensemble mass, is found by combining Eqs. (11) and (13):
(18)In addition, the number of clumps Nj with mass Mj, as a function of the total ensemble mass, is found by combining Eqs. (11) and (13): 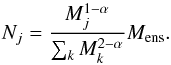 (19)Nj as given by Eq. (19) and ρj given via Eq. (18) uniquely define the parameters of the overall ensemble.
(19)Nj as given by Eq. (19) and ρj given via Eq. (18) uniquely define the parameters of the overall ensemble.
In the 3D model the clumps of an ensemble are randomly distributed in a voxel (3D pixel) with a known volume Δs3 (see Sect. 2.3.3). The VFF, that is the fraction of the volume filled by clumps is given by 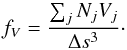 (20)In principle for the discrete description artificial cut-off masses can be chosen in such a way that the parameters of the discrete description match those of the continuous description. However, one should note that it is not possible to conserve the total mass and the number of clumps within a mass interval when switching from the continuous to the discrete description (while using B = 10). Here, we have fixed the total ensemble mass which is assumed to be a known quantity. As the continuous description is not needed for the 3D PDR model, we will stick to the discrete description as an independent model.
(20)In principle for the discrete description artificial cut-off masses can be chosen in such a way that the parameters of the discrete description match those of the continuous description. However, one should note that it is not possible to conserve the total mass and the number of clumps within a mass interval when switching from the continuous to the discrete description (while using B = 10). Here, we have fixed the total ensemble mass which is assumed to be a known quantity. As the continuous description is not needed for the 3D PDR model, we will stick to the discrete description as an independent model.
2.3. Three-dimensional set-up
In irradiated molecular clouds we find position dependent conditions: the FUV field strength will decrease with increasing depth into the clouds due to extinction; furthermore, the average density and composition of the cloud may change. To model PDRs we set up a 3D model which can replicate arbitrary geometries using voxels. Each voxel contains at least one clumpy ensemble. Furthermore, for each mass point and for each voxel a velocity dispersion between the individual clumps is applied. The radiative transfer (Sect. 2.3.4) enables the simulation of line-integrated maps as well as the modelling of full line profiles.
2.3.1. Ensemble statistics: area filling and clumps intersecting one line of sight
In the 3D set-up each ensemble is contained in a 3D voxel having a projected surface area Δs2 perpendicular to the line of sight between the observer and the voxel. The shape of the projected surface is arbitrary, but the volume should be spanned by the product of this surface area with the voxel depth. For the presented algorithm for example a cuboid or a cylinder could be used and give the same results. A different viewing angle to the same geometry, therefore needs a re-sampling of the density structure into new voxels where the z axis is parallel to the line of sight. The clumps, building up the ensemble, are randomly positioned in the voxel resulting in a number surface density Nj/ Δs2 for each mass point j.
If we consider an arbitrary line of sight, perpendicular to the projected area Δs2, through the ensemble, the probability distribution describing with how many randomly positioned clumps of mass Mj the line of sight intersects is given by the binomial distribution 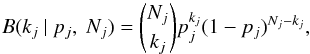 (21)where kj is the number of clumps pierced by the line of sight, pj is the probability that the line of sight intersects with a specific clump of mass Mj and Nj is the total number of clumps with mass Mj. The intersection probability pj is given by
(21)where kj is the number of clumps pierced by the line of sight, pj is the probability that the line of sight intersects with a specific clump of mass Mj and Nj is the total number of clumps with mass Mj. The intersection probability pj is given by 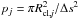 .
.
In the following Sects. 2.3.2 and 2.3.3 binomial distributions (Eq. (21)) are used to calculate ensemble-averaged quantities, namely the ensemble-averaged FUV attenuation as well as ensemble-averaged line intensities and optical depths. As binomial distributions are discrete probability distributions, the numbers of clumps, Nj, need to be integer values. This is not automatically provided by Eq. (19), however, scaling of the surface size Δs2 (projected surface of the voxel = pixel) does not change the results for the ensemble-averaged quantities as long as the number surface density, Nj/ Δs2, is kept constant for each mass point. Therefore, we rather consider a scaled “superpixel” of area (Δs′)2 = Δs2·c with a constant c> 0. Consequently, the numbers of clumps, Nj, need to be scaled accordingly: N′j = Nj·c. The constant c is chosen in a way that the following conditions are met:
-
a)
The projected clump areas of the largestclumps need to be smaller than a superpixel area:
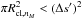 , in other words
, in other words 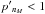 .
. -
b)
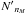 , that is the number of clumps with mass MnM, is always an integer value.
, that is the number of clumps with mass MnM, is always an integer value. -
c)
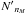 is chosen to be the smallest value possible that does not contradict a) or b) to optimise for computing speed. This typically implies
is chosen to be the smallest value possible that does not contradict a) or b) to optimise for computing speed. This typically implies 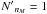 . In this work scaling to
. In this work scaling to 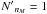 is only performed for the ensemble representing the dense clumps. For the interclump medium, which contains only one type of clumps,
is only performed for the ensemble representing the dense clumps. For the interclump medium, which contains only one type of clumps, 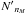 is chosen to be larger (typically
is chosen to be larger (typically 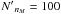 ). For details see Appendix A.
). For details see Appendix A.
After clump numbers and pixel surface area have been scaled the numbers of clumps, N′j ≠ nM, are rounded to integer values. As the numbers of low-mass clumps are significantly higher then the number of high-mass clumps, 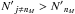 , due to the clump-mass-spectrum (see Eq. (6)) these rounding errors are negligible.
, due to the clump-mass-spectrum (see Eq. (6)) these rounding errors are negligible.
In general, rounding errors can always be decreased by scaling to larger surface areas and consequently larger numbers of clumps. However, we found that the error made by rounding after step c) is already negligible and therefore optimised for computing speed. Furthermore, to increase the computing speed, the binomial distribution can be approximated by a normal distribution if the expected value μj = Njpj ≫ 1 and the number of clumps Nj → ∞. In the code this simplification is implemented for the case μj> 5 and Nj> 1000. However, in the presented Orion Bar set-up we usually find μj< 5 due to the low number surface densities.
2.3.2. Voxel dependent FUV field strength
The line intensities and optical depths of the clumps contained in the voxels at different positions in the 3D model depend on the local FUV field strength. The FUV flux, coming from a known direction, is attenuated inside the PDR.
The FUV attenuation is proportional to the total hydrogen column density along the line of sight between the FUV source and the respective voxel. Röllig et al. (2013) discuss the FUV extinction in terms of the FUV-to-V colour, kFUV = ⟨ A(λ) /A(V) ⟩ λ, where the averaging is performed over an energy range from 6 to 13.6 eV. The FUV-to-V colour kFUV is derived based on different grain-size distributions for the interstellar dust. For the model of the Orion Bar we adapt kFUV ≈ 1.7 based on the grain-size distribution from Weingartner & Draine (2001a) for RV = 5.5 (RV = AV/ (E(B−V)) is the ratio between visual extinction and reddening), the highest carbon abundance (for RV = 5.5) in the small-grain populations and a constant grain volume per hydrogen atom during their fitting process4. RV = 5.5 has been observed towards Θ1 Ori C and is potentially representative for very dense clouds (Draine & Bertoldi 1996). The high carbon abundance in small grains is justified by the observation of strong PAH features in the Orion Bar region (Pilleri et al. 2012). Combining kFUV with the normalisation for the extinction curve AV/NH = 5.3 × 10-22 cm2 from Weingartner & Draine (2001a), hydrogen column densities that have been derived for different lines of sight through individual clumps (see Eq. (3)) can be transformed into the related FUV attenuations.
For a given ensemble, let X be the set of all possible combinations of clumps intersecting one line of sight, that is X = { kj } j = 1,...,nM with 0 ≤ kj ≤ N′j. Consequently, one specific combination of clumps is described by an element x ∈ X, which is a set of nM numbers that provide the number of clumps that intersect at each mass point j. For an element x the FUV attenuation along the line of sight is given by 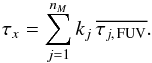 (22)The probability to find this combination of clumps intersecting the line of sight is the product of binomial distributions, Eq. (21),
(22)The probability to find this combination of clumps intersecting the line of sight is the product of binomial distributions, Eq. (21), 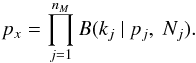 (23)In principle Eq. (23) has to be evaluated for each possible combination, however, some combinations are highly improbable and can be neglected within the algorithm to increase its computing speed. This is done by only accounting for numbers of clumps kj which lie in a
(23)In principle Eq. (23) has to be evaluated for each possible combination, however, some combinations are highly improbable and can be neglected within the algorithm to increase its computing speed. This is done by only accounting for numbers of clumps kj which lie in a 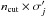 interval5 around the expected value of the respective binomial distribution. Calculations presented in this paper have been performed with ncut = 3. In the presented simulations we found
interval5 around the expected value of the respective binomial distribution. Calculations presented in this paper have been performed with ncut = 3. In the presented simulations we found 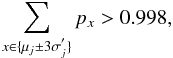 (24)confirming the low error of our approximation. Finally, the ensemble-averaged FUV attenuation can be derived using
(24)confirming the low error of our approximation. Finally, the ensemble-averaged FUV attenuation can be derived using 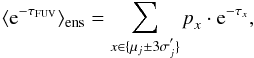 (25)where ⟨ ⟩ ens denotes the ensemble-averaged value. The FUV attenuation in each voxel can then be described by the effective optical depth ⟨ τFUV ⟩ ens = −ln( ⟨ e− τFUV ⟩ ens). If a voxels contains two ensembles to represent interclump medium and dense clumps, the algorithm presented above needs to be run for both ensembles separately. Finally, the ensemble-averaged contributions from clump and interclump medium are summed up, meaning that ⟨ τFUV ⟩ tot = ⟨ τFUV ⟩ ens,cl + ⟨ τFUV ⟩ ens,inter.
(25)where ⟨ ⟩ ens denotes the ensemble-averaged value. The FUV attenuation in each voxel can then be described by the effective optical depth ⟨ τFUV ⟩ ens = −ln( ⟨ e− τFUV ⟩ ens). If a voxels contains two ensembles to represent interclump medium and dense clumps, the algorithm presented above needs to be run for both ensembles separately. Finally, the ensemble-averaged contributions from clump and interclump medium are summed up, meaning that ⟨ τFUV ⟩ tot = ⟨ τFUV ⟩ ens,cl + ⟨ τFUV ⟩ ens,inter.
2.3.3. Ensemble-averaged emissivities and opacities
Similar to the FUV attenuation, we need the ensemble-averaged line intensities and optical depths of each voxel to compute the emission of the PDR. Clump averaged line intensities 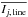 and optical depths
and optical depths 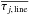 are provided by the KOSMA-τ model (see Sect. 2.1). In principle, the ensemble-averaged emissivities and optical depths can be derived based on the same algorithm as the ensemble-averaged FUV attenuation in Sect. 2.3.2. However, there is one major difference: while FUV absorption is a continuum process, line absorption and emission is velocity dependent and hence we have to account for the intrinsic velocities of single clumps. An algorithm accounting for a velocity distribution between identical cloud fragments has already been discussed by Martin et al. (1984). The algorithm presented here is similar but capable to treat ensembles made of different clumps.
are provided by the KOSMA-τ model (see Sect. 2.1). In principle, the ensemble-averaged emissivities and optical depths can be derived based on the same algorithm as the ensemble-averaged FUV attenuation in Sect. 2.3.2. However, there is one major difference: while FUV absorption is a continuum process, line absorption and emission is velocity dependent and hence we have to account for the intrinsic velocities of single clumps. An algorithm accounting for a velocity distribution between identical cloud fragments has already been discussed by Martin et al. (1984). The algorithm presented here is similar but capable to treat ensembles made of different clumps.
In the KOSMA-τ 3D code the velocity-space is discretised into velocity bins of width Δv around the centre velocities vi (i = 1,...,imax) and the velocity of each clump from a bin vi ± Δv/ 2 is approximated by vi. Furthermore, we assume a Gaussian velocity distribution with standard deviation σens,j for the clumps at mass point j, accounting for random motions of the single clumps. If Nj is the total number of clumps at mass point j then the number of clumps at mass point j whose centre velocity lies inside the bin around centre velocity vi is given by 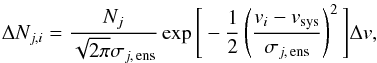 (26)where vsys denotes the systematic velocity of the whole region (or of the voxel). The same discussion as in Sect. 2.3.1 applies here, on other words it is necessary to ensure that the numbers of clumps ΔNj,i are integer values which can be achieved by scaling of the pixel size. To convert the ΔNj,i into integer values
(26)where vsys denotes the systematic velocity of the whole region (or of the voxel). The same discussion as in Sect. 2.3.1 applies here, on other words it is necessary to ensure that the numbers of clumps ΔNj,i are integer values which can be achieved by scaling of the pixel size. To convert the ΔNj,i into integer values 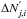 the algorithm presented in Sect. 2.3.1 is used. In general the scaling factor (factor c in Sect. 2.3.1) will be different for each velocity bin.
the algorithm presented in Sect. 2.3.1 is used. In general the scaling factor (factor c in Sect. 2.3.1) will be different for each velocity bin.
If we consider a specific emission line and an observing velocity vobs6 we are interested in the contributions to the line intensity and optical depth provided by the clumps at all centre velocities { vi } around velocity vobs. To derive the contribution from the clumps at a single centre velocity vi, we use (analogously to Sect. 2.3.2) combinations7 of clumps xi ∈ Xi with Xi = { kj,i } j = 1,...,nM and with 0 ≤ kj,i ≤ ΔN′j,i. Furthermore, one can calculate the line intensities and optical depths of each combination xi, which are given by 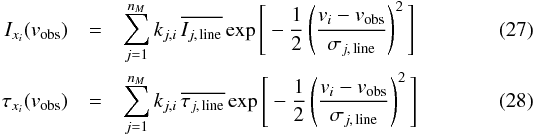 where σj, line is the intrinsic line width (standard deviation) of a single clump at mass point j and
where σj, line is the intrinsic line width (standard deviation) of a single clump at mass point j and 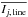 and
and 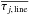 are the clump-averaged (Eqs. (4) and (5)) line-centre (peak) intensities and optical depths computed by the KOSMA-τ PDR code. In Eqs. (27) and (28) is would be more precise to average over the velocity bin, that is replace the exponential function by
are the clump-averaged (Eqs. (4) and (5)) line-centre (peak) intensities and optical depths computed by the KOSMA-τ PDR code. In Eqs. (27) and (28) is would be more precise to average over the velocity bin, that is replace the exponential function by 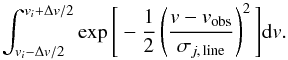 (29)However, we found that the effect of the integral is small. In a test run with 11 velocity bins with vi = 6.3,7.3,...,16.3 we compared the calculated ensemble-averaged quantities with and without integrating over the exponential function for different ensembles (clumps and interclump or only interclump medium), different vobs, and for the different transitions analysed in this paper. The worst case relative deviation is about 3%, for most other constellations the deviation is orders of magnitude smaller. As the integral significantly increases the computing time it is only optional in the code and not included in the presented simulations.
(29)However, we found that the effect of the integral is small. In a test run with 11 velocity bins with vi = 6.3,7.3,...,16.3 we compared the calculated ensemble-averaged quantities with and without integrating over the exponential function for different ensembles (clumps and interclump or only interclump medium), different vobs, and for the different transitions analysed in this paper. The worst case relative deviation is about 3%, for most other constellations the deviation is orders of magnitude smaller. As the integral significantly increases the computing time it is only optional in the code and not included in the presented simulations.
As discussed in Sect. 2.3.1 the probability to find a specific combination of clumps (a specific element xi ∈ Xi) on a line of sight through the voxel is given by 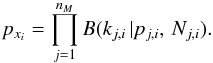 (30)As a next step the effective line intensity and optical depth of each velocity bin is calculated by averaging over all combinations of clumps found in one bin, that is
(30)As a next step the effective line intensity and optical depth of each velocity bin is calculated by averaging over all combinations of clumps found in one bin, that is 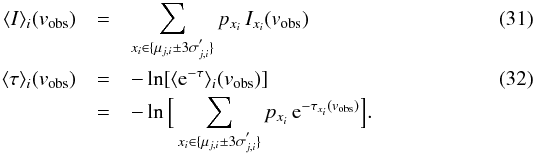 Here, the expected values, μj,i, and the corresponding standard derivations, σj,i, depend on mass point and velocity bin. Finally, the contributions from the different bins are summed up to give the complete ensemble-averaged intensity and optical depth
Here, the expected values, μj,i, and the corresponding standard derivations, σj,i, depend on mass point and velocity bin. Finally, the contributions from the different bins are summed up to give the complete ensemble-averaged intensity and optical depth 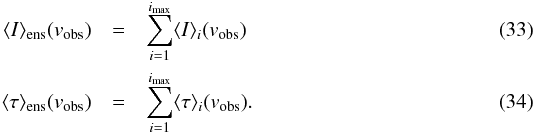 In Eqs. (27) and (33), where we sum up the line intensities from different clumps and velocity bins, we have assumed that the line is locally optically thin. By choosing the voxel size Δs sufficiently small, this condition can always be met. The “probabilistic approach” presented in this section for the calculation of the ensemble-averaged quantities was verified by comparison to a second method (see Appendix A). If a voxel contains two ensembles the line intensities and optical depths of both ensembles are calculated separately and summed up, as described in Sect. 2.3.2.
In Eqs. (27) and (33), where we sum up the line intensities from different clumps and velocity bins, we have assumed that the line is locally optically thin. By choosing the voxel size Δs sufficiently small, this condition can always be met. The “probabilistic approach” presented in this section for the calculation of the ensemble-averaged quantities was verified by comparison to a second method (see Appendix A). If a voxel contains two ensembles the line intensities and optical depths of both ensembles are calculated separately and summed up, as described in Sect. 2.3.2.
2.3.4. Radiative transfer
In the 3D PDR simulations the geometry of the PDR is replicated using voxels having the volume (Δs)3. To derive maps and spectra that are comparable to observations the radiative transfer through the 3D model needs to be calculated. An example for a 3D set-up is shown in Fig. 1 (replicating the Orion Bar PDR, which will be introduced in Sect. 3). Each small cube in Fig. 1 represents one voxel and the colour scale shows the FUV flux at the different voxels within the compound, for an FUV source located at the position [0,22.3,30].
 |
Fig. 1 3D compound replicating a possible geometry (model 1m, see Table 5) of the Orion Bar PDR. Each cube represents one voxel filled with at least one clumpy ensemble. Coordinates are given in voxel sizes, corresponding to 0.01 pc. The colour scale (Green 2011) shows the impinging FUV flux, calculated for each voxel, for a FUV source located at [0,22.3,30]. The direction to Earth corresponds to the positive z direction. |
The attenuation of the FUV photons inside the PDR is given by the sum of the optical depths, ⟨ τFUV ⟩ ens, of all voxels between the FUV source and the voxel of interest. The KOSMA-τ 3D code accounts for the absorption of photons and for isotropic scattering within the individual clumps (see Sect. 2.1). The code uses voxels with the shape of a cuboids, which are oriented in a way that one side of the cuboid is perpendicular to the line of sight between observer and voxel (z-axis). The voxels need to be sufficiently small to trace all relevant changes of different quantities within the compound, but some compromise has to be made to reduce the overall computational effort. Therefore, the KOSMA-τ 3D code can make use of a set-up where the FUV attenuation is calculated for different positions within the voxels, that is to say on a 3D Cartesian grid at sub-voxel scale, and is averaged over the voxel afterwards. For each sub-voxel the code derives the line of sight that connects the centre-point of the sub-voxel and the source of the FUV radiation and evaluates which voxels intersect with this line of sight (i.e. shield FUV radiation). The FUV attenuation is weighted by the distance that is effectively crossed by a FUV photon within each voxel. The simulations presented in this work have been performed using a 3 × 3 × 3 voxel sub-grid. For the calculation of the ensemble-averaged line intensity and line optical depth (see Sect. 2.3.3), and consequently also for the radiative transfer, the sub-voxel grid is not used. This has two reasons: (a) while the lines of sight between the observer and a voxel are oriented perpendicular to the voxel surface, this is in general not the case for the lines of sight between the FUV source and the voxels. If we would calculate the FUV attenuation between FUV source and voxels by just summing up the ⟨ τFUV ⟩ ens between the position of the FUV source and the midpoints of the voxels we would introduce unnecessarily large errors in the case where a voxel is partly shielded by another voxel in the foreground; (b) the sub-voxel treatment is too costly for the calculation of the ensemble-averaged line intensity and optical depth where calculations need to performed at different (here: imax = 21) velocities.
We perform the radiative transfer for the same velocities vobs that have already been used in Sect. 2.3.3. The ensemble-averaged volume emissivity and absorption coefficient, ⟨ ϵ ⟩ ens(vobs) and ⟨ κ ⟩ ens(vobs), are calculated based on the results from the last section, Eqs. (33) and (34), that is 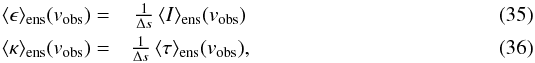 where Δs denotes the depth of the voxel along the line of sight. In the following we will omit the velocity dependence (vobs) and the “ensemble-averaged brackets” ⟨ ... ⟩ ens in our formulae for readability reasons.
where Δs denotes the depth of the voxel along the line of sight. In the following we will omit the velocity dependence (vobs) and the “ensemble-averaged brackets” ⟨ ... ⟩ ens in our formulae for readability reasons.
For radiation travelling a distance ds along a straight path the change in intensity is given by the equation of radiative transfer, which (omitting the dependence on frequency) reads 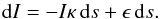 (37)Integration along a straight path length, between 0 and Δs, yields
(37)Integration along a straight path length, between 0 and Δs, yields ![\begin{eqnarray} I = {\rm e}^{-\int_{0}^{\Delta s} \kappa\, {\rm d} x}\left[ \int_0^{\Delta s} \epsilon\, {\rm e}^{\int_{0}^{s'} \kappa\, {\rm d} x}\, {\rm d}s' + I_{\rm bg}\right], \label{Eq:radtrans2} \end{eqnarray}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq219.png) (38)where Ibg = I(0) is the background intensity of radiation travelling along the same path. For radiative transfer from voxel p−1 to the neighbouring voxel p (Ossenkopf et al. 2001) ϵ and κ are linearly interpolated. Therefore, we define ϵ = e0 + e1s′ and κ = k0 + k1s′ with s′ ∈ [0,Δs] and with
(38)where Ibg = I(0) is the background intensity of radiation travelling along the same path. For radiative transfer from voxel p−1 to the neighbouring voxel p (Ossenkopf et al. 2001) ϵ and κ are linearly interpolated. Therefore, we define ϵ = e0 + e1s′ and κ = k0 + k1s′ with s′ ∈ [0,Δs] and with 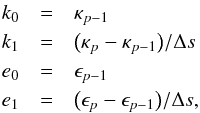 (39)which can be inserted into Eq. (38) yielding
(39)which can be inserted into Eq. (38) yielding ![\begin{equation} I=\frac{1}{{\rm e}^{k_0\Delta s+\frac{1}{2}k_1(\Delta s)^2}}\left[ \int_0^{\Delta s}(e_0+e_1\cdot s'){\rm e}^{k_0 s'+\frac{1}{2}k_1 (s')^2}{\rm d}s' + I_{\rm{bg}}\right]. \label{Eq:linearApproxRadTrans} \end{equation}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq228.png) (40)Equation (40) is solved numerically and tabulated for the simulations (see Appendix B).
(40)Equation (40) is solved numerically and tabulated for the simulations (see Appendix B).
3. The Orion Bar PDR
The Orion Bar PDR is a prominent feature located in the Orion Nebula (M42, NGC 1976). In observations of typical cooling lines from the UV down to radio wavelength and the IR continuum the bar appears as a bright rim. With a distance of 414 ± 7 pc (Menten et al. 2007) the Orion Bar PDR is one of the nearest and hence brightest PDRs to the terrestrial observer. Consequently, a large amount of observations of the Orion Bar PDR has been performed providing us with an excellent test case for PDR models.
Chemical stratification has been observed for the Orion Bar PDR by different groups (Tielens et al. 1993; van der Werf et al. 1996; Simon et al. 1997; Marconi et al. 1998; Walmsley et al. 2000; van der Wiel et al. 2009; Pellegrini et al. 2009; Bernard-Salas et al. 2012). For example van der Wiel et al. (2009) discuss a layered structure with C2H emission peaking close to the ionisation front (IF), followed by H2CO and SO, while other species like C18O, HCN and 13CO peak deeper into the cloud.
Nowadays, it has become clear that a “simple” homogeneous (i.e. non-clumpy) bar is an insufficient description of the Orion Bar PDR. High angular resolution observations show that the bar breaks down into substructure. The commonly accepted picture is that the bar includes an extended gas component of nH = 104−5 cm-3 that causes the chemical stratification and is the dominating origin for low-J molecular line emission. Embedded in this so-called interclump medium, a clumpy high-density (nH = 106−7 cm-3) component is needed to provide the emission of the high-density tracers, among others the lines of high-J CO isotopologues, CO+, and the observed H2 or OH (for a summary and additional references see Goicoechea et al. 2011). The low filling factor of the dense clumps ensures that the FUV field can penetrate deep into the cloud. We cannot list all observations that have dealt with the spatial structure of the Orion Bar. Just to name a few, Young Owl et al. (2000) presented combined single-dish and interferometric data of HCO+ and HCN J = 1−0 which show a clumpy NE and SW bar, Lis & Schilke (2003) showed interferometric data of the Orion Bar PDR in H13CN and H13CO+ and identify at least ten dense condensations in the H13CN image, and individual clumps have also been resolved by van der Werf et al. (1996) who showed that a PDR surface can be found on each clump inside the Orion Bar. More recent studies on the structure of the Orion Bar PDR have been performed by Goicoechea et al. (2011), Cuadrado et al. (2015).
3.1. Geometry
A common explanation for the existence of the bar is the Blister model: the Orion Nebula embeds a cluster of bright and young stars which ionise their surrounding medium creating an Hii-region inside the molecular cloud. At the side of the nebula facing Earth this “Hii-bubble” has broken out of the cloud, enabling observations of the cavity and of the Orion Bar PDR which forms one of the edges of the cavity, illuminated by the strong FUV radiation from the young star cluster (see for example Wen & O’dell 1995, and references therein).
The dominating ionising source and most massive star is Θ1 Ori C which produces ~80% of the H-ionising photons. Θ1 Ori D, the second most massive star of the Trapezium system, accounts for another ~15% (Draine 2011). The IF, as marked for example by the peak position of the [Oii] or [Feii] emission (Walmsley et al. 2000), [Sii] (Pellegrini et al. 2009), or [Nii] (Bernard-Salas et al. 2012) is located at 111′′ (corresponding to 0.223 pc) projected distance from Θ1 Ori C.
The flux at the IF is estimated to correspond to an enhancement over the average interstellar radiation field, χ0, by a factor ≈4.4 × 104 (Hogerheijde et al. 1995; Jansen et al. 1995) (the series of papers by Hogerheijde et al. 1995; and Jansen et al. 1995, is hereafter abbreviated HJ95). We have verified that this value lies in the probable range (see Appendix C).
Different geometries have been proposed to model the Orion Bar, the dominating idea is a slightly inclined face-on/edge-on/face-on geometry first introduced by HJ95. A schematic picture of this geometry is shown in Fig. 2. Many other workgroups use adoptions of this geometry to model observations (see e.g. Pellegrini et al. 2009). Due to the increased column density along the line of sight, this geometry naturally explains the observed intensity peak. The depth of the cavity, the inclination angle of the bar (α′, not to be confused with the power-law exponent α from Eq. (6)) and the z-position (position on the line of sight to the observer) of the illuminating cluster are subject to discussions. Different possibilities are indicated in Fig. 2.
The face-on/edge-on/face-on geometry is consistent with all the far-IR and submm observations, but an indication that this geometry needs at least some modifications stems from optical observations (Alves & McCaughrean 2002) that show some shadowing at the very edge of the Orion Bar. This would be explained by a configuration where the Orion Bar is not the edge of a cavity but rather a filament as proposed by Walmsley et al. (2000), Arab et al. (2012).
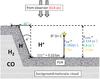 |
Fig. 2 Face-on/edge-on/face-on Orion Bar geometry as proposed by HJ95. Values are taken from: green: HJ95; red: Menten et al. (2007); blue: Pellegrini et al. (2009); and orange: van der Werf et al. (2013). For the inclination angle, α′, values between less than 3° and 15° have been discussed (Jansen et al. 1995; Melnick et al. 2012). |
3.2. Observations
A tremendous amount of data is available for the Orion Bar PDR. Recent observations of the Orion Bar PDR, observed with the Herschel Space Observatory (Pilbratt et al. 2010), can for instance be found in Habart et al. (2010), Goicoechea et al. (2011), Nagy et al. (2013, 2015). Recently, the whole Orion molecular cloud 1 region, which includes the Orion Bar PDR, has been mapped velocity resolved by Goicoechea et al. (2015).
As the aim of this paper focuses on the description and the testing of the KOSMA-τ 3D code, we selected only observations of abundant and simple species: CO isotopologues, HCO+ and the [Cii] cooling line. An expansion including many more species is of course possible.
We used [Cii], CO 10−9, CO 16−15, 13CO 5−4, 13CO 10−9 and HCO+6−5 line observations of the Orion Bar PDR observed with the Heterodyne Instrument for the Far-Infrared (HIFI, de Graauw et al. 2010) on-board the Herschel Space Observatory (Pilbratt et al. 2010)8. The observations were performed as part of the EXtra-Ordinary Sources (HEXOS) guaranteed-time key program (Bergin et al. 2010). Combined with low-J CO and HCO+ rotational lines (see below) these lines are well suited to trace the chemical stratification observed in the Orion Bar PDR.
The [Cii] observations have already been discussed in Ossenkopf et al. (2013). Furthermore, Nagy et al. (2015) show an HCO+ map. All other Herschel data is presented here for the first time. Further analysis of the data will be provided in subsequent papers (Choi et al. 2014; Nagy et al. 2017)9.
All presented HIFI/Herschel observations are strips across the bar with a width of 1′ or more, except for the CO 16−15 observations where a single cut has been observed. The observations were taken in the on-the-fly (OTF) observing mode around the centre position (αJ2000 = 5h35m20.81s, δJ2000 = −5°25′17.1′′) with a position angle perpendicular to the bar, that is 145° east of north, and an OFF position 6 arcmin southeast of the map. The observations used the Wide-Band-Spectrometer (WBS) with a frequency resolution of 1.1 MHz which corresponds to 0.17 km s-1 at the rest frequency of the [Cii] line. Both polarizations were averaged to improve the signal-to-noise ratio. Integration times varied between 4 and 30 s resulting in noise levels between a 0.02 and 0.3 K. The high-frequency HIFI/Herschel data, in other words the maps of [Cii] and CO 16−15 have been reduced in HIPE as described by Ossenkopf et al. (2013). All other lines were analysed using the GILDAS software10 for baseline subtraction and spatial re-sampling. An overlay of our data, [Cii] overplotting 13CO 10−9, is shown in Fig. 3.
 |
Fig. 3 Orion Bar observed with HIFI/Herschel. The green contours show [Cii] line intensities integrated between 7 and 13 km s-1. The contours range between 200 and 800 K km s-1 in steps of 100 K km s-1. The colour scale gives the 13CO 10−9 line intensity, integrated between 9 and 12 km s-1. The reference position is the CSO reference position (5h35m20.122s, −5°25′21.96′′). |
The line intensities (Table 2) are given on a Tmb scale. For the HIFI/Herschel observations Tmb is a factor 1.26 to 1.5 higher than 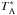 , depending on the respective frequency (Roelfsema et al. 2012). As discussed by Ossenkopf et al. (2013), the scaling from
, depending on the respective frequency (Roelfsema et al. 2012). As discussed by Ossenkopf et al. (2013), the scaling from 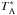 to Tmb is questionable for very extended emission (like [Cii]) where the error beam of the telescope is likely to be filled with emission of approximately the same brightness as the main beam. Hence, for extended emission our intensities are upper limits.
to Tmb is questionable for very extended emission (like [Cii]) where the error beam of the telescope is likely to be filled with emission of approximately the same brightness as the main beam. Hence, for extended emission our intensities are upper limits.
Our data set is combined with ground-based observations of CO 2−1, CO 3−2, CO 6−5, 13CO 3−2, 13CO 6−5 and HCO+3−2 observed with the Caltech Submillimeter Observatory (CSO) (Lis, priv. comm.). The CSO observations are typically more extended but overlap with the HIFI/Herschel maps. To facilitate the comparison between the maps, the reference positions of all maps have been shifted to be equal to the CSO reference position (5h35m20.122s, −5°25′21.96′′).
To simplify the analysis of the stratification profile, the maps have been rotated around the CSO reference position by −145° (−145° clockwise), resulting in an orientation of the Orion Bar parallel to the x-axis (see Figs. 3 and 4). As we focus on the stratification of the chemical and excitation structure across the Orion Bar, the observed spectra have been averaged along rows of pixels11 parallel to the x-axis ensuring that we average over clumps and interclump medium. In the x-range between −11.3″ and −43.5″ the Orion Bar has a very straight appearance in all of our maps and an average over ~30″ guarantees that we are not affected by individual clumps, but consider a clump-ensemble on the observational side as well. Lis & Schilke (2003) observe the size of dense condensations in the Orion Bar and find sizes between 3.81″ and 7.96″ and Young Owl et al. (2000) discuss clumps of 9″ size, supporting our approach.
Gaussian profiles were fitted to the averaged spectra. We have fitted two Gaussian profiles, one profile fixed at a centre velocity of 8 km s-1 to exclude the emission from the Orion Ridge (van der Tak et al. 2013). The other profile fits the main component at about 11 km s-1 originating from the Orion Bar. Integration of this component provided the line-integrated intensity, averaged for the respective row (y-position). The peak position was determined by fitting a parabola to the row-averaged intensities at the different y-positions. As deviations between the fitting points and the fitted parabolas are very small, we assume the pointing error of the telescope as the main uncertainty in the determination of the peak position. The pointing errors are 2.4″ for HIFI/Herschel (Pilbratt et al. 2010) and 3″ for CSO data12. The resulting peak intensities and y-offsets are summarised in Table 2 for the different transitions. Table 2 indicates a peculiarity of the HCO+ 3–2 transition. It seems to peak in front of all the other molecular transitions, including HCO+ 6–5 that should tracer warmer gas, while the profiles of both lines are very similar. We have no evidence for a pointing problem in these data so that we stick to the formal errors, but as there is no physical scenario that would explain this peak offset we rather question the role of the HCO+ 3–2 peak position in the fit of the stratification pattern in the discussion (Sect. 5.4.1).
 |
Fig. 4 [Cii] integrated intensity (same as the contours in Fig. 3, but rotated by −145°). In this orientation Θ1 Ori C in the north-west of the bar is at the bottom of the map. The green line marks the cut with the highest averaged line-integrated intensity, including all pixels with x-offsets between −11.3′ and −43.5′. |
Summary of averaged integrated intensities and spatial offsets of the observations.
4. 3D Model of the Orion Bar PDR
We have composed a 3D model of the Orion Bar PDR from cubic voxels with an edge length of 0.01 pc, corresponding to 5.0″ at the distance of 414 pc. The voxel size is small enough to trace physical changes in the PDR and to analyse stratification effects, but large enough to ensure that the total number of voxels can be treated on a standard PC. Furthermore, for all observations that have been fitted in this work, the resulting pixel size is at least a factor two smaller than the beamsize. Our Cartesian coordinate system was chosen in such a way that the x-direction is parallel to the Orion Bar and the z-direction points towards the observer. As we were mainly interested in the stratification of the Orion Bar here, the current model ignores any variation of the density structure in x-direction. This reduces the number of free parameters, but excludes for the moment the simulation of additional structures like the Orion Ridge.
In this work we focus on geometries for the Orion Bar PDR that are based on the HJ95 series of papers, in other words on geometries that consist of an almost edge-on cavity wall facing the illumination from Θ1 Ori C (see Figs. 1 and 2). Aiming for a fit of the observations presented in Sect. 3.2 different parameters have been varied in this model set-up. An overview over these parameters is provided in Sect. 5.1. In Sect. 5.2 we discuss the measures that are used to evaluate our fits. A second geometry that has been discussed for the Orion Bar is the filament model proposed by Walmsley et al. (2000) and Arab et al. (2012). This model consists of a cylinder in the plane of the sky with the main symmetry axis along the bar (see Fig. D.2). In Appendix D we show preliminary tests of this geometry, which indicate that a simultaneous reproduction of the observed stratification pattern and the line intensities based on the cylindrical model is problematic. For this geometry, the short lines of sight through the compound close to y = 0 enforce that the emission peaks appear deep in the cloud, where the FUV flux is low. This reduces the line-integrated intensities and increases the scatter between the y-offsets calculated for the different transitions.
The main illuminating source Θ1 Ori C is 111″ away from the IF. This corresponds to a separation by 22.3 voxels in y-direction between star and interface. In x-direction, the location of the star defines our zero point, meaning that in voxel units Θ1 Ori C is located at [0,yIF + 22.3,zstar] in the model. The z position of the star (zstar) is not exactly known (see Fig. 2) and has become one of our fitting parameters.
Based on C18O 3−2 observations and assuming a conversion factor of NH2/N(C18O) = 5 × 106, HJ95 derive a total H2 column density of NH2 = 6.5 × 1022 cm-2 along the line of sight (peak) for a path length of 0.6 pc. For a uniform density along the line of sight this translates into nH2 = NH2/ (0.6 pc) = 3.5 × 104 cm-3. Consequently, the total average mass in a voxel with volume (0.01 pc)3 is: 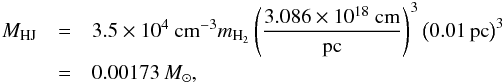 (41)which we used as baseline for our simulations.
(41)which we used as baseline for our simulations.
The clump ensembles in the models contain clumps at the mass points [10-3,10-2,10-1,100]M⊙, implying that one voxel typically only contains fractions of clumps, meaning that Nj< 1. The upper mass limit matches the resolved clump masses in the range 0.5−1.5M⊙ determined for the Orion Bar PDR by Lis & Schilke (2003). The lower limit of 10-3M⊙ is used as the smallest mass contained in the available KOSMA-τ input grid because, to gain a good approximation of a fractal geometry, the inclusion of very small structures is desired. We discuss this choice and show simulation results based on models using different mass points in Sect. 5.3.5. In the KOSMA-τ 3D code the pixels are scaled to superpixels (see Sect. 2.3.1). In the simulations presented here, after the scaling process, each “supervoxel” usually contains one clump at mass point 100M⊙ and consequently { Nj } = [331,48,7,1] for the different mass points (see Eq. (19), results rounded to integer values).
The thin interclump medium is mimicked by a second clump ensemble with an averaged density that is about two orders of magnitude lower than the averaged density of the dense clumps. To approximate a relatively homogeneous interclump medium, we started our simulations using small clumps of 10-2M⊙. Furthermore, the VFF of the interclump medium should be equal to unity or smaller. Therefore, we needed to add the condition 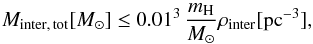 (42)or equivalently
(42)or equivalently 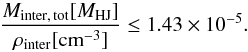 (43)For a discussion of the interclump parameter Minter, tot and ρinter see Sect. 5.1. We started our simulations with a VFF of unity in Sect. 5.3.1. Different choices for the mass point and the VFF of the interclump medium are tested in Sect. 5.3.6.
(43)For a discussion of the interclump parameter Minter, tot and ρinter see Sect. 5.1. We started our simulations with a VFF of unity in Sect. 5.3.1. Different choices for the mass point and the VFF of the interclump medium are tested in Sect. 5.3.6.
In this work we did not fit full line profiles. Therefore, the velocity spread between the clumps in one ensemble (σj, ens, see Eq. (26)) has been fixed. We discuss our choice of the σj, ens and show examples of simulated line profiles in Sect. 5.3.7.
The KOSMA-τ 3D code allows for the simulation of (2D) maps. As an example, Figs. 5 and 6 show simulated maps of line-integrated CO 3−2 intensities, before and after the convolution with a Gaussian beam of 21.9″ FWHM, matching the CSO beam used in the observations. The maps are based on model 1m (see Table 5). We find a combination of the imprint of the sharp edge of the bar and a curvature stemming from the varying distance to the illuminating star. The convolution blurs the edge and the emission peak, but still allows to recover the stratification of the emission.
For our systematic parameter study we have reduced the map size (and the beam convolution) to a cut of only one pixel in x-direction across the Orion Bar. Such a cut enables us to derive the line-integrated intensities and peak offsets within a computing time of about six hours13. For the 2D maps 18 days of computing time are needed. Typical simulated cuts are shown in Fig. 7 based on model 6j (see Sect. 5.3.6 and Table 5).
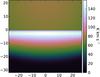 |
Fig. 5 Simulated map of line-integrated CO 3−2 emission of the Orion Bar PDR, based on model 1m (see Table 5). The coordinates are given in units of pixels. One pixel corresponds to 0.01 pc or 5″ on the sky. The illuminating star Θ1 Ori C is located at x = 0 and y = 22.3 on top of the map. |
The maps of the Orion Bar can include radiation from the background molecular cloud (see Fig. 2). Therefore, we should in principle extend our model into the negative z-direction until we have reached a depth were none of the investigated tracers is excited anymore. However, to reduce computing time, the background molecular cloud was cut off at z = −20 in our systematic parameter study. At z = −20 the FUV flux has usually dropped below one Draine field (see Fig. 1). To investigate possible contributions to the final maps/cuts from the background molecular cloud we have re-run the simulation of model 2b (which provides one of the best fits of the line-integrated intensities; see Sect. 5.3.3 and Table 5), but with the compound extended to z = −100.
Figures 8 and 9 show simulated cuts through the Orion Bar model 2b, before the extension. The colour scales in these plots give the line centre intensity emitted by each voxel, in Fig. 8 for CO 2−1 and in Fig. 9 for CO 16−15. The figures show that CO 16−15 is only excited close to the PDR surface, where the FUV flux is relatively high. Hence, the background molecular cloud will not be visible in the final line maps. For CO 2−1 the situation is different: the excitation only depends weakly on the FUV flux and hence, the voxels still emit at z = −20. However, the effect of adding the background cloud to the simulation is still small due to the high optical depth of the CO 2−1 line. Overall, we find that adding the background molecular cloud slightly changes the quality of the fit of the line-integrated intensities (see Table 5), but it does not change the outcome of our systematic parameter study.
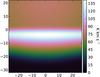 |
Fig. 6 Same as Fig. 5 but after convolution with a Gaussian beam of 21.9″ or 4.4 pixels FWHM (see Table 2). |
 |
Fig. 7 Simulated cuts perpendicular to the Orion Bar, based on model 6j (see Table 5). Each colour scale gives the line-integrated intensity of the transition indicated above the respective cut. |
The total column density of the Orion Bar can be constrained from optically thin tracers that are only weakly sensitive to the PDR conditions. HJ95 provide line-integrated intensities of the C18O 2−1 and 3−2 transitions at the emission peak of the Orion Bar PDR. Due to the low optical depths of these transitions compared to the other CO isotopologues, they provide an upper limit for the total (volume-averaged) column density of the dense clumps, including the background cloud. Table 3 compares the intensities from HJ95 to the simulated line-integrated intensities based on models 2b, 6j, and 2b_ext, having cut-offs at z = −20 and at z = −100. In contrast to all PDR simulations, HJ95 observed a C18O 2−1 line that is significantly weaker than the 3−2 line. This could be explained by a cold foreground layer. However, as we have not included foreground material into our models, a detailed fit of that line is beyond the scope of this work. Therefore, we concentrate on the C18O 3−2 line for the column density estimate like HJ95.
We find that the contribution from the interclump medium to the C18O 2−1 and 3−2 line emission is negligible. Furthermore, the increase of the C18O line-integrated intensities due to the background extension is low. Using the HJ95 column density of NH2 = 6.5 × 1022 cm-2 leads to line intensities that are too low by more than a factor of two. Models 2b and 6j contain a mass per voxel of 2 MHJ combined with a total depth of 0.8 pc (cut-off at z = −20, parameters Mcl, tot, dcavity, see Sect. 5.1). The total (volume-averaged) column of the ensembles of dense clumps is NH2 ≈ 1.7 × 1023 cm2, a factor 2.7 higher than the value that was found by HJ95. The two models provide intensities that are too high by 40% and 25% compared to the observations so that we consider the column density of 1.7 × 1023 cm2 as the upper limit. Consequently, we have excluded models with higher column densities from our simulation runs. Lower columns are always allowed in our models, as they could be compensated by a deeper background cloud that is invisible in all the PDR tracers discussed here.
 |
Fig. 8 Cut through the Orion Bar model 2b. For each voxel the colour scale gives the CO 2−1 line intensity of dense clumps and interclump medium, at the line centre (at 11.3 km s-1). The illuminating star Θ1 Ori C is located at [0,22.3,30]. |
5. Parameter scans
5.1. Parameters
In the following we summarise the parameters that are varied within our simulation runs. If available we also give values taken from HJ95 which will be used as an initial guess for our simulations.
Mcl, tot: the mass contained in dense clumps per voxel. Based on HJ95 we have estimated the total mass per voxel, MHJ, in Eq. (41). Furthermore, HJ95 state that about 10% (i.e. 0.1 MHJ) of the molecular material14 is contained in clumps.
Minter, tot: the mass contained in the interclump medium per voxel. Following HJ95 the interclump medium accounts for 90% of the total molecular column density. Using their values, that is ρinter = 2 nH2 = 2 × 3 × 104 cm-3 and a total interclump mass of 0.9 MHJ in one voxel with a volume of (0.01 pc)3, the VFF is about 1.05 (see Sect. 4; per voxel this corresponds (statistically) to 0.156 clumps with a mass of 10-2M⊙ and a volume of 6.74 × 10-6 pc3). In some of the presented simulations (see Sect. 5.3.1) Minter, tot is no independent parameter, but coupled to ρinter to ensure an interclump-VFF of unity. Therefore, in our first simulation runs where Minter, tot (and ρinter) were varied, ρinter = 6 × 104 cm-3 corresponds to Minter, tot = 0.848MHJ (instead of 0.9 MHJ).
ρcl: the ensemble-averaged hydrogen nucleus density of the dense clumps. HJ95 derive 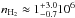 cm-3 (i.e. ρcl ≈ 2 × 106 cm-3) using only one type of dense clumps.
cm-3 (i.e. ρcl ≈ 2 × 106 cm-3) using only one type of dense clumps.
ρinter: the ensemble-averaged hydrogen nucleus density of the interclump medium. HJ95 derive 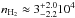 cm-3 (i.e. ρinter ≈ 2 × 3 × 104 cm-3) for a homogeneous interclump medium. In some simulations ρinter is coupled to Minter, tot (see above).
cm-3 (i.e. ρinter ≈ 2 × 3 × 104 cm-3) for a homogeneous interclump medium. In some simulations ρinter is coupled to Minter, tot (see above).
α′: the inclination angle of the bar (see Fig. 2). Jansen et al. (1995) discuss that an inclination angle α′< 3° is probable.
zstar: the z-position of the illuminating source, which is not discussed in HJ95. Here, we started our simulations using zstar = 0.3 pc, on other words with the illuminating source located at half height of the cavity.
IUV: the FUV flux from the illuminating source, Θ1 Ori C, at the position of the IF. HJ95 state 4.4 × 104χ0. We provide an estimate of IUV in Appendix C. The flux I(r) at a position r of a voxel at the cloud surface (i.e. not affected by FUV absorptions) is given by 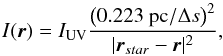 (44)where 0.223 pc is the observed distance in y-direction between Θ1 Ori C and the Orion Bar (see Sect. 3.1), rstar is the position of the illuminating source in our model and Δs is the edge-length of one voxel in pc.
(44)where 0.223 pc is the observed distance in y-direction between Θ1 Ori C and the Orion Bar (see Sect. 3.1), rstar is the position of the illuminating source in our model and Δs is the edge-length of one voxel in pc.
dcavity: the depth of the cavity (see Fig. 2). HJ95 assume 0.6 pc.
dclumps: the depth into the cloud at which dense clumps appear. With this parameter we have tested whether the same amount of clump and interclump mass is contained in each voxel, independent from the depth into the PDR, or if there is there a process that removes dense clumps from the surface. The models discussed in HJ95 do not account for such an effect, but it is proposed in their text.
ml,cl: the lowest mass point of the ensemble of dense clumps. HJ95 find that a single-density model cannot explain the observed line ratios and assume that a range of densities appears in the beam. They construct their model with two density components (clump and interclump medium) as a first order approximation. Here, we started our simulations with dense clumps down to 10-3M⊙.
minter: mass point used for the interclump medium. The interclump medium is represented by identical clumps of mass minter. Here, we used minter = 10-2M⊙ as initial guess.
Overview over fitting parameters.
5.2. Model assessment
To evaluate the goodness of the fit, accounting for the simultaneous reproduction of the integrated line intensities and the Orion Bar stratification structure, we have determined the y-position and the integrated intensity of the pixel with the highest integrated intensity for each transition from our simulated cuts.
The stratification is measured in terms of the y-offset of the intensity peak relative to the [Cii] peak position: Δyi = y[CII]−yi where the index i refers to different transitions (a negative Δyi indicates a shift towards Θ1 Ori C). Simulations and observations have been compared by deriving the difference between the respective offsets, 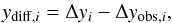 (45)where Δyobs,i refers to the observations (by definition, ydiff,CII = 0 for [Cii], our reference coordinate). The relative differences between simulated and observed peak integrated intensities are given by Irel,i = Ifit,i/Iobs,i. We summarise the ydiff,i and the Irel,i of different models and transitions in scatter plots (see for example Figs. 10 and 11), which yield a clear way to compare the models and to identify systematic behaviour. In addition, we define measures to evaluate the goodness of our fits. For the y-offsets we have used a chi-square test, namely
(45)where Δyobs,i refers to the observations (by definition, ydiff,CII = 0 for [Cii], our reference coordinate). The relative differences between simulated and observed peak integrated intensities are given by Irel,i = Ifit,i/Iobs,i. We summarise the ydiff,i and the Irel,i of different models and transitions in scatter plots (see for example Figs. 10 and 11), which yield a clear way to compare the models and to identify systematic behaviour. In addition, we define measures to evaluate the goodness of our fits. For the y-offsets we have used a chi-square test, namely ![\begin{equation} \chi_{\rm off}^2 = \sum_i \left[ \frac{\Delta y_i - \Delta y_{{\rm obs}, i}}{{\rm Err}(\Delta y_{{\rm obs}, i})}\right]^2, \label{Eq:chi_off} \end{equation}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq351.png) (46)where Err(Δyobs,i) denotes the error of the offsets derived from the observations, as stated in Table 2, and the sum runs over all simulated transitions. A typical chi-square test, as used in Eq. (46), evaluates the model in terms of absolute (squared) differences between the observed and the fitted values. For the line-integrated intensities we aimed for a figure of merit which evaluates our models in terms of factors, for instance a simulation result that deviates from the observations by a factor two has the same quality as a results that is wrong by a factor of one half. Therefore, we define
(46)where Err(Δyobs,i) denotes the error of the offsets derived from the observations, as stated in Table 2, and the sum runs over all simulated transitions. A typical chi-square test, as used in Eq. (46), evaluates the model in terms of absolute (squared) differences between the observed and the fitted values. For the line-integrated intensities we aimed for a figure of merit which evaluates our models in terms of factors, for instance a simulation result that deviates from the observations by a factor two has the same quality as a results that is wrong by a factor of one half. Therefore, we define ![\begin{equation} \chi_{\rm I}^2 = \sum_i \left[ \frac{{\rm Log}_{10}(I_{{\rm fit},i}) - {\rm Log}_{10}(I_{{\rm obs},i})}{0.434\ {\rm Err}(I_{{\rm obs},i})/I_{{\rm obs},i}} \right]^2, \label{Eq:chi_inten} \end{equation}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq353.png) (47)where the errors Err(Iobs,i) are stated in Table 2 and the denominator has been derived by error propagation, that is
(47)where the errors Err(Iobs,i) are stated in Table 2 and the denominator has been derived by error propagation, that is 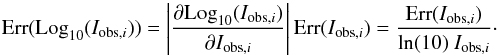 (48)When parameters are varied during the fitting process the line intensities and the y-offsets are usually affected in a very different manner. To make the effects of parameter variations visible we state
(48)When parameters are varied during the fitting process the line intensities and the y-offsets are usually affected in a very different manner. To make the effects of parameter variations visible we state 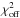 and
and 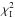 separately for each simulation run. However, to evaluate how well the stratification pattern and the line-integrated intensities are matched by a specific model we use the sum
separately for each simulation run. However, to evaluate how well the stratification pattern and the line-integrated intensities are matched by a specific model we use the sum 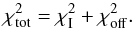 (49)Furthermore, the quality of a fit in the statistical sense is given by the reduced chi-square
(49)Furthermore, the quality of a fit in the statistical sense is given by the reduced chi-square 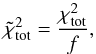 (50)where f = N−M are the degrees of freedom (see Press et al. 1992). Here, N = 23 is the number of quantities that are fitted, namely the line-integrated intensities of 12 different transitions plus the 11 y-offsets relative the [Cii] peak position, and M is the number of parameters that can be adjusted. In this work M varies between different series of simulations.
(50)where f = N−M are the degrees of freedom (see Press et al. 1992). Here, N = 23 is the number of quantities that are fitted, namely the line-integrated intensities of 12 different transitions plus the 11 y-offsets relative the [Cii] peak position, and M is the number of parameters that can be adjusted. In this work M varies between different series of simulations.
The best method to derive a good fit would be to systematically explore the parameter space in all directions. Unfortunately, due to the large number of free parameters, this cannot be done within an acceptable amount of computing time. Hence, we have chosen the following approach: the values taken from HJ95, as summarised in Sect. 5.1, were used as an initial guess for our simulations. Successively “series of models” have been run, where in each series at least two parameters have been varied at a time. Based on the 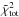 -test the best model from each series was then selected and the parameters have been kept for the next series. In case of interdependences between parameters we tried to vary these parameters at the same time.
-test the best model from each series was then selected and the parameters have been kept for the next series. In case of interdependences between parameters we tried to vary these parameters at the same time.
5.3. Simulation runs
Overview of different model set-ups.
5.3.1. Ensemble-averaged densities and masses per voxel
 |
Fig. 10 Scatter plot of the line-integrated intensities for selected models from Sects. 5.3.1, 5.3.3 and 5.3.4. For each transition the ratio between simulated and observed line-integrated intensity at the respective peak position, Irel,i = Ifit,i/Iobs,i, is plotted on a logarithmic scale. The different transitions are indicated on the abscissa and different symbols mark the different models. |
 |
Fig. 11 Scatter plot of the y-offsets of selected models from Sects. 5.3.1, 5.3.3 and 5.3.4. For each transition the difference between the offset of the simulated and the observed peak position, as defined in Eq. (45), is plotted. All offsets are relative to the [Cii] peak position, hence, for the reference [Cii] transition ydiff is always zero. A negative offset indicates that the simulated emission peak is shifted too far into the direction of Θ1 Ori C, a positive offset indicates that the emission appears too deep in the cloud. The different transitions are indicated on the abscissa and different symbols mark different models. |
Each voxel within a compound is filled by two ensembles, one representing the dense clumps and one representing the interclump medium. We started our simulation runs investigating models where these ensembles are the same within each voxel (i.e. dclumps = 0, see Sect. 5.1) and refer to these models as homogeneous. Examples of inhomogeneous models are given in Sect. 5.3.6.
The total mass of the clump and interclump medium contained in each voxel, as well as the related ensemble-averaged densities, have a strong influence on the simulation outcome. Especially in the homogeneous models, these parameters are interdependent: both components can contribute to the FUV attenuation and hence control the line intensities emitted by both components. (In model 1c the dense clumps do only account for 1.4% of the total FUV attenuation. In model 1m, where the total mass of the ensemble of dense clumps has been increased, 29% of the total FUV attenuation is due to this ensemble.) Therefore, we varied these parameters (Mcl,tot, ρcl, Minter,tot and ρinter) first. For all other parameters we have used our initial guess (Table 4). An overview of different model set-ups is given in Table 5.
In our first series of models (represented by models 1c to 1D in Table 5) we have coupled ρinter to Minter,tot, enforcing a VFF of unity for the interclump medium. In these runs we have tested ensemble-averaged densities of 106, 2 × 106 and 4 × 106 cm-3 for the dense clumps combined with total ensemble masses between 0.1 and 2 MHJ. An ensemble-averaged density of 4 × 106 cm-3 combined with the four mass points implies that the smallest clumps have densities of about 107 cm-3 (see Eq. (18)). Higher densities are not possible with the current input grid (see Table 1). As discussed in Sect. 4 models with Mcl,tot> 2MHJ (combined with dcavity = 0.6 pc) have been excluded. For the interclump medium we have tested densities between 6 × 103 and 105 cm-3, which implies total masses per voxel between 0.0858 and 1.43 MHJ. For these models the degree of freedom (see Sect. 5.2) is f = 23−3 = 20 if a VFF of unity is enforced and f = 19 if Minter,tot and ρinter are treated independently.
In models 1c and 1m or similarly in models 1d, 1i and 1n, the total mass of the dense clumps has been increased from 0.1 to 2 MHJ while all other parameters remain unchanged. From all tested models the parameters of model 1d are closest to the values from HJ95. Figure 10 gives an overview over the ratios between simulated and observed line-integrated intensities for selected transitions. We find that the “HJ95-model” 1d does not reproduce any of the fitted line-integrated intensities, except for [Cii]. However, all other intensities are too low, often by orders of magnitude. Model 1i uses the same parameters, but with Mcl,tot increased to 0.5 MHJ, which increases the line intensities of the species that are (dominantly) emitted by the dense clumps, namely the high-J CO isotopologues and the HCO+ transitions. Still, the resulting line intensities are too low, except for [Cii]. In model 1n, which uses Mcl,tot = 2MHJ, the line intensities of most transitions are still too low, but the fit does significantly improve compared to the models discussed above.
Model 1j uses the same parameters as model 1i except for the density (and therefore also the total mass) of the interclump medium, which has been increased. In Fig. 10 one can see how the line-integrated intensities of the transitions which are (at least partially) emitted by the interclump medium, namely [Cii] and the low-J CO isotopologues, increase. The line intensities of the other transitions decrease due to the stronger FUV attenuation in the cloud.
Overall, we find that increasing Mcl,tot improves the quality of our fit (lower 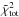 ). Furthermore, from comparing for example model 1m with 1B (or 1n and 1C; see Table 5 or Fig. 10) one can see that a higher ensemble-averaged density of ρcl = 4 × 106 cm-3 provides lower
). Furthermore, from comparing for example model 1m with 1B (or 1n and 1C; see Table 5 or Fig. 10) one can see that a higher ensemble-averaged density of ρcl = 4 × 106 cm-3 provides lower 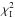 and, although
and, although 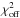 can increase, lower
can increase, lower 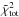 .
.
The spatial offsets of the different peak positions do mainly depend on the FUV attenuation in the cloud and on the peak position of the [Cii] line which is the reference for all other transitions. Figure 11 gives an overview over the ydiff,i (see Eq. (45)) of the models that have already been included in Fig. 10. For models 1d and 1i we find that the emission peaks of the CO 2−1 and 12/13CO 3−2 transitions (for model 1d also of the 13CO 5−4 and 12/13CO 6−5 transitions) are shifted too far into the cloud by about five to nine pixels (0.05 to 0.09 pc). For model 1c (not shown separately but with a high 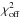 in the table) the CO 2−1 and the 12/13CO 3−2 emission peaks are shifted even further into the cloud, they appear about 20 pixel behind the [Cii] emission peak. Based on these transitions and for the current set-up, we have to conclude that the FUV attenuation in the cloud is significantly too weak. However, for most other transitions, the offsets are found to be too small and hence a deeper FUV penetration would be necessary to increase their y-offsets. Model 1j with Mcl,tot = 0.5 and Minter,tot = 1.43 shows a similar, but less pronounced behaviour compared to models 1d and 1i (see Fig. 11). We conclude that a fit of the stratification pattern based on the set-ups presented in this section and an interclump-VFF = 1 is not possible.
in the table) the CO 2−1 and the 12/13CO 3−2 emission peaks are shifted even further into the cloud, they appear about 20 pixel behind the [Cii] emission peak. Based on these transitions and for the current set-up, we have to conclude that the FUV attenuation in the cloud is significantly too weak. However, for most other transitions, the offsets are found to be too small and hence a deeper FUV penetration would be necessary to increase their y-offsets. Model 1j with Mcl,tot = 0.5 and Minter,tot = 1.43 shows a similar, but less pronounced behaviour compared to models 1d and 1i (see Fig. 11). We conclude that a fit of the stratification pattern based on the set-ups presented in this section and an interclump-VFF = 1 is not possible.
5.3.2. Reduction of the interclump medium
For models 1E to 1aa the constraint that the interclump-VFF needs to be unity has been dropped. Models 1z to 1aa in Table 5 use Mcl,tot = 2 and ρcl = 4 × 106 cm-3. Models 1z to 1D show how the composition of the interclump medium affects the fit in terms of the chi-square tests. We find that the fit improves in terms of 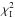 and
and 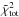 if the amount and VFF of the interclump medium is reduced, allowing for a deeper FUV penetration into the cloud. The
if the amount and VFF of the interclump medium is reduced, allowing for a deeper FUV penetration into the cloud. The 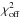 are somewhat more random, which is probably due to changing y-offsets of the [Cii] reference position (see below). The models with a interclump−VFF ≪ 1, in other words models 1E, 1bb and 1P, provide similar
are somewhat more random, which is probably due to changing y-offsets of the [Cii] reference position (see below). The models with a interclump−VFF ≪ 1, in other words models 1E, 1bb and 1P, provide similar 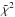 -values and we cannot discriminate between these models based on our set-up. However, as we needed to decide with which model we wanted to continue our simulations in the next section, we computed
-values and we cannot discriminate between these models based on our set-up. However, as we needed to decide with which model we wanted to continue our simulations in the next section, we computed 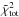 with a higher precision than integer values in Table 5. Based on these results, model 1P with
with a higher precision than integer values in Table 5. Based on these results, model 1P with 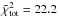 provides the best fit of all models discussed so far. It uses ρinter = 105 cm-3 and Minter,tot = 0.1MHJ, resulting in an VFF of 0.07 for the interclump medium. We note that for our best fitting models the intensities of the CO 16−15 and HCO+6−5 transitions are somewhat too high here compared to the observations (see model 1P in Fig. 10).
provides the best fit of all models discussed so far. It uses ρinter = 105 cm-3 and Minter,tot = 0.1MHJ, resulting in an VFF of 0.07 for the interclump medium. We note that for our best fitting models the intensities of the CO 16−15 and HCO+6−5 transitions are somewhat too high here compared to the observations (see model 1P in Fig. 10).
In all models the simulated y-offsets of the line peak positions of (nearly) all transitions tend to be too low. The best fit in terms of the stratification pattern ( ) is obtained by model 1E (see Table 5). However, for this model the simulated y-offsets relative to the [Cii] emission peak are too small for all simulated tracers (except HCO+3−2, see Fig. 11) and some transitions (12/13CO 6−5 and CO 16−15) appear at the same offset as [Cii]. Furthermore, in model 1E the interclump medium has been completely removed, while the existence of some interclump medium has been deduced from several observations. Overall, model 1P provides the best combined fit of intensity and stratification, but when we actually look at the stratification pattern it becomes clear that the fit of the pattern is not satisfactory. Good fits of the stratification pattern are only found if inhomogeneous models are used (see Sect. 5.3.6).
) is obtained by model 1E (see Table 5). However, for this model the simulated y-offsets relative to the [Cii] emission peak are too small for all simulated tracers (except HCO+3−2, see Fig. 11) and some transitions (12/13CO 6−5 and CO 16−15) appear at the same offset as [Cii]. Furthermore, in model 1E the interclump medium has been completely removed, while the existence of some interclump medium has been deduced from several observations. Overall, model 1P provides the best combined fit of intensity and stratification, but when we actually look at the stratification pattern it becomes clear that the fit of the pattern is not satisfactory. Good fits of the stratification pattern are only found if inhomogeneous models are used (see Sect. 5.3.6).
5.3.3. α′ and IUV
In a second series of simulations the effects of varying the inclination angle α′ and the FUV flux at the cloud surface have been investigated. We have tested inclination angles of α′ = 0°, 3°, 7° and 15°, and have simultaneously increased the FUV flux by 25% and by 50% compared to the original HJ95 value. All other parameters in this second series have been adopted from the best model from the previous section, namely model 1P. As we optimised two additional parameters in this section we have used f = 23−6 = 17 degrees of freedom for the calculation of the 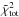 .
.
For all tested α′ and in the tested parameter range, the fit of the line-integrated intensities depends only weakly on IUV (see for example the comparison between models 1P and 2b, where the FUV flux at the PDR surface has been increased by 50%, in Table 5). Based on the 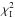 , the best fit of the line-integrated intensities is provided by models 2b, 2e and 2h (
, the best fit of the line-integrated intensities is provided by models 2b, 2e and 2h (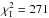 , 273 and 272 respectively), which use IUV = 6.6 × 104χ0 combined with α′ = 3°, 0° or 7°. These models are found to fit the line-integrated intensities of all transition within a factor of about two or better, for model 2h we find Irel,CO 6−5 = 0.49 and Irel,HCO+ 6−5 = 2.04 with the Irel of all other transitions lying between these values. For models 2b and 2e the Irel are slightly higher (see also model 2e in Fig. 10). As increasing IUV mainly increases the line intensities of the “outlier transitions” (see Sect. 5.4.2), we have not tested models with IUV higher than 6.6 × 104χ0.
, 273 and 272 respectively), which use IUV = 6.6 × 104χ0 combined with α′ = 3°, 0° or 7°. These models are found to fit the line-integrated intensities of all transition within a factor of about two or better, for model 2h we find Irel,CO 6−5 = 0.49 and Irel,HCO+ 6−5 = 2.04 with the Irel of all other transitions lying between these values. For models 2b and 2e the Irel are slightly higher (see also model 2e in Fig. 10). As increasing IUV mainly increases the line intensities of the “outlier transitions” (see Sect. 5.4.2), we have not tested models with IUV higher than 6.6 × 104χ0.
Changing the inclination angle has two effects. In general, choosing a small α′ provides more excited column along one line of sight through the compound and hence increases the line-integrated intensities of the optically thin transitions. However, increasing α′ broadens the emission peak, which can also lead to an increase of line-integrated intensities after the beam convolution. Overall, we find that changing α′ from 3° to 0° or 7° has an negligible effect on the line-integrated intensities, however, for α′ = 15° the fit becomes worse (see for example model 2i in Table 5).
A more significant effect is that the fit of the stratification pattern is found to be best for α′ = 0°, independent from the choice of IUV. For larger inclination angles, especially for α′ = 15°, 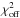 increased. The lowest
increased. The lowest 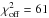 is provided by model 2e, which fits the y-offsets of two transitions (CO 2−1 and HCO+3−2) within the observational uncertainty, however, for all other transitions the simulated y-offsets relative to the [Cii] peak are too small. Model 2e is also included in the scatter plots, Figs. 10 and 11.
is provided by model 2e, which fits the y-offsets of two transitions (CO 2−1 and HCO+3−2) within the observational uncertainty, however, for all other transitions the simulated y-offsets relative to the [Cii] peak are too small. Model 2e is also included in the scatter plots, Figs. 10 and 11.
5.3.4. dcavity and zstar
In a third simulation run two geometrical parameters have been varied, the depth of the cavity that defines the length of the line of sight through the bar (dcavity) and the z-position of the illuminating source (zstar). These parameters are partly interdependent: the column of material that is excited in the bar depends on the position of the star relative to the cavity wall. We have varied both parameters, dcavity and zstar, between 0.1 and 0.6 pc, which includes the range of values found in literature (see Fig. 2). In addition, we have investigated two models where the star is lying outside of the cavity (dcavity = 0.3 pc and zstar = 0.4 pc, and dcavity = 0.6 pc and zstar = 0.7 pc). In Sect. 4 we have derived an upper limit for the total molecular column density along a line of sight through a model compound, which was found to correspond to Mcl,tot = 2 MHJ for dcavity = 0.6 pc. Hence, for the models where dcavity has been reduced, we also tested models where Mcl,tot has been increased to provide the same upper column density limit (see for example models 3r and 3n in Table 5). All other parameters used in this section have been adopted from model 2e. For the degree of freedom we used f = 23−8 = 15 as eight different parameters have been adjusted at this point.
Briefly, the result of this simulation run is that model 2e, which has the deep cavity (dcavity = 0.6 pc) with the star at half-height (zstar = 0.3 pc) is already the best configuration. Model 3a (see Table 5) with the very shallow cavity (dcavity = 0.1 and zstar = 0.1 pc) can be excluded, because in this model the emission of some transitions from the back of the cavity (“below” the illuminating source) is about as strong as the emission from the bar itself. Most extremely for HCO+6−5 the emission at y ≳ 20 of the simulated cut is significantly stronger than the emission from the bar, causing the high 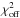 of this model.
of this model.
For all models where the total column density of the ensembles of dense clumps is reduced compared to model 2e, the simulated line intensities decrease for all transitions, increasing the 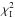 and hence decreasing the quality of the fit (see for example model 3c). On the other side, for models 3n (dcavity = 0.3 pc, zstar = 0.3 pc and Mcl,tot = 4 MHJ) and 3r (dcavity = 0.4 pc, zstar = 0.4 pc and Mcl,tot = 3 MHJ), which have the same column density of the dense clumps as model 2e, the fit of the line-integrated intensities improves slightly compared to model 2e. This improvement stems from two effects. Placing the illuminating source close to the outer edge of the cavity puts the hottest material in the PDR closest to the observer. Therefore, after the radiative transfer, the line-integrated intensities tend to be increased. Second, if the same amount of material is comprised in a shorter bar, the material is – on average – closer to the illuminating source, which increases the line-integrated intensities (see Sect. 5.3.3). Therefore, the
and hence decreasing the quality of the fit (see for example model 3c). On the other side, for models 3n (dcavity = 0.3 pc, zstar = 0.3 pc and Mcl,tot = 4 MHJ) and 3r (dcavity = 0.4 pc, zstar = 0.4 pc and Mcl,tot = 3 MHJ), which have the same column density of the dense clumps as model 2e, the fit of the line-integrated intensities improves slightly compared to model 2e. This improvement stems from two effects. Placing the illuminating source close to the outer edge of the cavity puts the hottest material in the PDR closest to the observer. Therefore, after the radiative transfer, the line-integrated intensities tend to be increased. Second, if the same amount of material is comprised in a shorter bar, the material is – on average – closer to the illuminating source, which increases the line-integrated intensities (see Sect. 5.3.3). Therefore, the 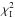 of a model with the same column density as models 3n and 3r, but with dcavity = 0.6 pc and zstar = 0.6, is slightly higher. However, as model 2e provides a better fit of the stratification pattern, is still has the lowest
of a model with the same column density as models 3n and 3r, but with dcavity = 0.6 pc and zstar = 0.6, is slightly higher. However, as model 2e provides a better fit of the stratification pattern, is still has the lowest 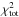 and
and 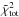 .
.
5.3.5. ml,cl and minter
 |
Fig. 12 Same as Fig. 10, plotted for selected models from Sects. 5.3.5 and 5.3.6. In addition, model 2e from Sect. 5.3.3 is given for comparison. |
 |
Fig. 13 Same as Fig. 11, plotted for selected models from Sects. 5.3.5 and 5.3.6. In addition, model 2e from Sect. 5.3.3 is given for comparison. |
As discussed in Sect. 4, all models presented so far have used an ensemble with four mass points, [10-3,10-2,10-1,100]M⊙ (i.e. ml,cl = 10-3M⊙), for the ensemble of dense clumps. Only the upper limit of one M⊙ can be inferred from observations. Furthermore, the interclump medium was represented by identical clumps of 10-2M⊙. In this section, we show the impact of these choices. For the lower cut-off mass of the ensemble of dense clumps we used ml,cl = 10-2M⊙ and ml,cl = 100M⊙ in addition to the initial value, where the second choice implies that the ensemble only contains clumps with one M⊙. Each of these choices was combined with minter = 10-3, 10-2, 10-1 or 100M⊙ for the clumps representing the interclump medium. For the degrees of freedom we have used f = 23−10 = 13 as ten different parameters have been adjusted so far.
Independent of the choice of minter, we find that the models that use ml,cl = 10-3M⊙ provide the best fits. For example models 2e, 4b and 4d (see Table 5) all use minter = 10-2M⊙, but different ml,cl. The Irel of the different transitions of these models are shown in the scatter plot Fig. 12. We can see how the line – intensities of the different transitions systematically decrease when ml,cl increases, especially CO 16−15 is affected. As the line-integrated intensities of all transitions except for CO 16−15 and HCO+6−5 tend to be too low, 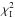 increases with increasing ml,cl.
increases with increasing ml,cl.
Varying the mass of the individual clumps of the interclump medium (while keeping the total mass Minter,tot fixed) changes the FUV attenuation and hence has an impact on the line-integrated intensities and on the stratification pattern. For example for ρinter = 105 cm-3 and Minter = 0.1MHJ used in this series, decreasing minter from 10-2 to 10-3M⊙ increases the FUV attenuation per voxel by a factor 1.7, due to the more even distribution of the ISM. The line emission of the interclump medium also depends on the size of the individual clumps. Model 4f shows that an increase of the clump size in the interclump medium reduces the emission from the interclump gas, shifting the peak of the [Cii] line into the molecular cloud so that the observable stratification is strongly reduced. The optimal choice of minter depends on ml,cl, however, for the models that use ml,cl = 10-3M⊙ and hence provide the best fits, the further result clearly favour minter = 10-2M⊙. Overall, we find that model 2e, with ml,cl = 10-3M⊙ and minter = 10-2M⊙ provides the best fit in terms of stratification and line-intensities.
5.3.6. Inhomogeneous models
Based on the homogeneous models shown so far, the line-integrated intensities can be fitted within a factor of about two for all simulated transitions. However, the homogeneous models fail in reproducing the observed stratification pattern (see discussion of models 2h/2e in Sect. 5.3.3). Furthermore, different authors (Parmar et al. 1991; HJ95; Young Owl et al. 2000) propose that the ISM in the Orion Bar is not uniformly distributed. Instead they present observations and models, which suggest that the inset of dense material, embedded in the thinner interclump medium, is only found at about 10″−20″ into the cloud.
Consequently, we have tested series of models incorporating such a step. We have limited ourselves to the idealised density profile that is produced if the parameter dclumps (see Sect. 5.1) is chosen to be larger than zero. For these inhomogeneous models the FUV attenuation close to the PDR surface (as defined by dclumps) only depends on the composition of the interclump medium. The dense clumps only contribute deep in the cloud, hence the impact of varying ρcl and Mcl,tot becomes smaller.
We have varied the parameter dclumps to be equal to 0.02, 0.03 and 0.04 pc, as suggested by the observations. As the FUV attenuation within the cloud does significantly change compared to the homogeneous models when the dense clumps are removed, we have simultaneously varied the composition of the interclump medium a second time. Therefore, we have tried values of ρinter between 6 × 103 and 105 cm-3 and Minter between 0.05 and 0.5 MHJ. Furthermore, previous simulation runs have shown that for some inhomogeneous models α′ = 3° provides better results than α′ = 0° and hence we have repeated the simulation runs of our most promising models with α′ = 3° instead of α′ = 0°. In Table 5 the names of the inhomogeneous α′ = 0°-models start with a 5 (only model 5h is listed), while the names of the inhomogeneous α′ = 3°-models start with a 6. All other parameters have been adopted from model 2e. As, compared to the models from the previous section, we have fitted one additional parameter (dclumps), we have used f = 23−11 = 12 for the calculation of the related 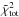 .
.
The best-fitting models of these simulation runs are (sorted for increasing 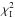 and decreasing
and decreasing 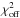 in Table 5) models 6b, 5h, 6a, 6j, 6k and 6l. We find that all of these models use Minter between 0.1 and 0.4 MHJ combined with ρinter = 105 cm-3 and hence have VFFs of the interclump medium between 0.07 and 0.28. For these models and based on our set-up we cannot clearly discriminate between α′ = 0° and α′ = 3°. Models 6a, 6j, 6k and 6l provide lower
in Table 5) models 6b, 5h, 6a, 6j, 6k and 6l. We find that all of these models use Minter between 0.1 and 0.4 MHJ combined with ρinter = 105 cm-3 and hence have VFFs of the interclump medium between 0.07 and 0.28. For these models and based on our set-up we cannot clearly discriminate between α′ = 0° and α′ = 3°. Models 6a, 6j, 6k and 6l provide lower 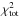 -values than the corresponding α′ = 0°-models (not shown) while model 5h is slightly better than model 6b. Furthermore, dclumps is 0.02 or 0.04 pc for these models. The observed stratification pattern is not sensitive to the exact choice.
-values than the corresponding α′ = 0°-models (not shown) while model 5h is slightly better than model 6b. Furthermore, dclumps is 0.02 or 0.04 pc for these models. The observed stratification pattern is not sensitive to the exact choice.
Models 6b, 5h and 6a provide the best fit of the line-integrated intensities (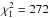 or 273) of all models that have been investigated in this section, but they do not provide any improvements compared to model 2e from Sect. 5.3.3. In terms of the fit of the line intensities, the inhomogeneous model does not provide any improvement, but it also does not deteriorate the fit. The situation is very different when considering the stratification pattern. Model 6l provides
or 273) of all models that have been investigated in this section, but they do not provide any improvements compared to model 2e from Sect. 5.3.3. In terms of the fit of the line intensities, the inhomogeneous model does not provide any improvement, but it also does not deteriorate the fit. The situation is very different when considering the stratification pattern. Model 6l provides 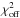 as low as 15, which has not been reached by any other model. In Fig. 13 we can see how for model 6l the relative y-offsets lie in the (0 ± 0.01) pc interval for all transitions, except for the HCO+3−2 transition. The Irel simulated for model 6l lie between 0.33 (13CO 10−9) and 1.04 (CO 16−15; see also Fig. 12).
as low as 15, which has not been reached by any other model. In Fig. 13 we can see how for model 6l the relative y-offsets lie in the (0 ± 0.01) pc interval for all transitions, except for the HCO+3−2 transition. The Irel simulated for model 6l lie between 0.33 (13CO 10−9) and 1.04 (CO 16−15; see also Fig. 12).
Models 6j and 6k (see Table 5 and Figs. 12, 13) are examples for compromises between models 2e/6b/5h/6a and model 6l. Model 6k fits the y-offsets of all transitions within 0.016 pc and has Irel between 0.4 and 1.3. For model 6j the y-offset of 13CO 10−9 is too small (−0.026 pc), for all other transitions the y-offsets are fitted within 0.017 pc. Furthermore, the Irel of model 6j lie between 0.46 and 1.6. Overall, model 6j provides the lowest 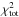 of all models tested in the scope of this work. The simulated cuts of this model are shown in Fig. 7. In terms of a simple best fitting model, 2e is very good (2e provides the lowest
of all models tested in the scope of this work. The simulated cuts of this model are shown in Fig. 7. In terms of a simple best fitting model, 2e is very good (2e provides the lowest 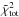 ), but when explicitly asking for a reproduction of the stratification, only inhomogeneous models work. Then models 6j and 6k are much better.
), but when explicitly asking for a reproduction of the stratification, only inhomogeneous models work. Then models 6j and 6k are much better.
5.3.7. Line profiles
 |
Fig. 14 Line profiles of selected transitions of model 6j. The full lines show the simulated profiles, the dashed lines are Gaussian profiles with the same peak intensity as the respective profile, but with linewidths of FWHM = 2 km s-1 and FWHM = 4 km s-1, matching the observed total velocity dispersions. For each transition the y-offset corresponds to the position with the highest line-integrated intensity. |
In addition to the maps and cuts presented in Sect. 4 the KOSMA-τ 3D code is capable of simulating line profiles for each individual pixel of a simulation.The beam convolution is performed by KOSMA-τ 3D as a second step for the line-integrated intensity maps. The simulation of the line profiles is based on the velocity dependent ensemble averaged line intensities and optical depths, which have been discussed in Sect. 2.3.3, and on the velocity dependent radiative transfer as discussed in Sect. 2.3.4. The line width of single clumps (σj, line, which may depend on the mass point j of the individual clump, see Eqs. (27) and (28)) in the KOSMA-τ input grid, is σj, line ≈ 0.71 km s-1 (i.e. FWHM = 1.67 km s-1 or a Doppler broadening parameter of b = 1 km s-1). The ensemble velocity dispersion (σj, ens, see Eq. (26)) is an additional input/fit parameter. Both, σj, line and σj, ens, can be different for clump and interclump medium.
Here, we did not aim for a fit of the line profiles observed in the Orion Bar PDR, and have used a fixed velocity dispersion based on some observed line widths σtot,j. For the total velocity dispersion of the dense clumps we have used σtot,j ≈ 0.85 km s-1 (FWHM = 2 km s-1) and for the interclump medium we applied σtot,j ≈ 1.70 km s-1 (FWHM = 4 km s-1) as typical values for the Orion Bar PDR (see Nagy et al. 2013, and references therein). The clump and interclump ensemble velocity dispersion then follows from 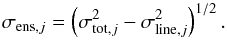 (51)Consequently, our input parameters are σens,j ≈ 0.47 km s-1 for the ensemble of dense clumps and σens,j ≈ 1.54 km s-1 for the ensemble representing the interclump medium. The systematic velocity of all voxel (see parameter vsys in Eq. (26)) has been set to vsys = 11.3 km s-1. Sampling the spectra at 21 different velocities around vsys, with a spacing of 0.5 km s-1 provides resolved profiles (see velocities vi and vobs in Sect. 2.3.3).
(51)Consequently, our input parameters are σens,j ≈ 0.47 km s-1 for the ensemble of dense clumps and σens,j ≈ 1.54 km s-1 for the ensemble representing the interclump medium. The systematic velocity of all voxel (see parameter vsys in Eq. (26)) has been set to vsys = 11.3 km s-1. Sampling the spectra at 21 different velocities around vsys, with a spacing of 0.5 km s-1 provides resolved profiles (see velocities vi and vobs in Sect. 2.3.3).
The full lines in Fig. 14 show selected line profiles from the model with the lowest 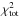 , namely model 6j (see Sect. 5.3.6). The dashed lines in the figure are Gaussian line profiles with the same peak intensity as the respective profile, but with linewidths of FWHM = 2 km s-1 and FWHM = 4 km s-1, corresponding to the input linewidths. By comparing the simulated profiles with the Gaussian profiles we can see that a large fraction of the [Cii] emission is emitted by the interclump medium, while the transitions of the CO isotopologues and of HCO+ are dominantly emitted by the dense clumps. Furthermore, some profiles appear broadened as suggested by observations (Nagy et al. 2017), however, fit and quantitative comparison are left for future work.
, namely model 6j (see Sect. 5.3.6). The dashed lines in the figure are Gaussian line profiles with the same peak intensity as the respective profile, but with linewidths of FWHM = 2 km s-1 and FWHM = 4 km s-1, corresponding to the input linewidths. By comparing the simulated profiles with the Gaussian profiles we can see that a large fraction of the [Cii] emission is emitted by the interclump medium, while the transitions of the CO isotopologues and of HCO+ are dominantly emitted by the dense clumps. Furthermore, some profiles appear broadened as suggested by observations (Nagy et al. 2017), however, fit and quantitative comparison are left for future work.
5.4. Discussion
We find that a geometry of the Orion Bar region similar to the geometry derived in HJ95 is well suited to reproduce the observed stratification and line intensities. Significant conclusions can be drawn, however, from our unsuccessful attempts to simultaneously fit the line intensities and the peak positions measuring the geometrical stratification of the Orion Bar PDR. Initial simulations based on a cylindrical geometry (see Appendix D) are less promising.
5.4.1. The stratification pattern
The definition of 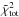 based on the measurement and modelling accuracies leads to a fit that is typically dominated by the contribution of the intensity mismatches. It seems much more difficult to tweak the model towards a fit of all line intensities within the measured accuracy than towards a fit of the observed stratification pattern. Consequently, we have aimed for two goals that are not easily unified: on the one hand we wanted to provide the best fit in the statistical sense, in other words the lowest value of
based on the measurement and modelling accuracies leads to a fit that is typically dominated by the contribution of the intensity mismatches. It seems much more difficult to tweak the model towards a fit of all line intensities within the measured accuracy than towards a fit of the observed stratification pattern. Consequently, we have aimed for two goals that are not easily unified: on the one hand we wanted to provide the best fit in the statistical sense, in other words the lowest value of 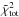 ; on the other hand we wanted to reproduce the observed stratification pattern as good as possible.
; on the other hand we wanted to reproduce the observed stratification pattern as good as possible.
The lowest 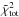 , namely
, namely 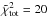 , and hence the best fit in the statistical sense, is provided by models 2d and 2e, which fit the line-integrated intensities of all transitions within a factor 2.2 (the Irel of the different transitions lie between 0.50 and 2.1 for model 2d and between 0.51 and 2.2 for model 2e). However, these models cannot reproduce the stratification pattern observed for the Orion Bar PDR. All models from Sects. 5.3.1 to 5.3.5 indicate that a reproduction of the stratification pattern based on a homogeneous set-up (i.e. models that contain the same ensembles of clumps in each voxel; dclumps = 0) is impossible.
, and hence the best fit in the statistical sense, is provided by models 2d and 2e, which fit the line-integrated intensities of all transitions within a factor 2.2 (the Irel of the different transitions lie between 0.50 and 2.1 for model 2d and between 0.51 and 2.2 for model 2e). However, these models cannot reproduce the stratification pattern observed for the Orion Bar PDR. All models from Sects. 5.3.1 to 5.3.5 indicate that a reproduction of the stratification pattern based on a homogeneous set-up (i.e. models that contain the same ensembles of clumps in each voxel; dclumps = 0) is impossible.
The observable stratification in the line-integrated intensity maps must stem from a combination of spatially varying excitation conditions, column densities, and line widths from clump and interclump medium (see Fig. 14 and also Fig. D.2) along the different lines of sight through the inclined cavity wall, modified by the beam convolution. As the homogeneous models fail to reproduce the stratification, we had to switch to models where dense clumps only exist at some depth into the cloud; dclumps> 0) in Sect. 5.3.6.
This is in agreement with previous models and observations. Van der Werf et al. (1996) identify an elongated clump with a thickness of about 10″ at ~20″ from the IF into the cloud, and deduce a density increase in this region based on CS 5−4 and C34S 3−2 observations and a Large Velocity Gradient (LVG) model. Parmar et al. (1991) proposed already a clumpy picture of the PDR with an increasing size and number of clumps from the IF into the molecular cloud. This was later adopted by HJ95. A detailed investigation was performed by Young Owl et al. (2000). They found that the Orion Bar is best modelled when incorporating a ridge of dense clumps into a thinner interclump medium at a depth of 20″. This is in agreement with our model fit where dense clumps had to be added to the interclump medium at a depth of 10″ to 20″, to reproduce the observed chemical stratification.
The best fit of the stratification pattern is provided by model 6l, which has 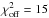 , fitting the relative y-offsets within (0 ± 0.01) pc, that is in about the accuracy of the simulations, except for HCO+3−2. As the HCO+3−2 peak position provides a major outlier in the observational data (see Sect. 3.2), we rather speculate that the unsuccessful fit of this position might be caused by a problem in the observational data. For further improvements in the fit of the stratification pattern, based on our current method, higher resolution observations and smaller voxel sizes are necessary. We have also found models that provide good compromises between the fit of the stratification pattern and the line-integrated intensities, overall, model 6j provides the lowest
, fitting the relative y-offsets within (0 ± 0.01) pc, that is in about the accuracy of the simulations, except for HCO+3−2. As the HCO+3−2 peak position provides a major outlier in the observational data (see Sect. 3.2), we rather speculate that the unsuccessful fit of this position might be caused by a problem in the observational data. For further improvements in the fit of the stratification pattern, based on our current method, higher resolution observations and smaller voxel sizes are necessary. We have also found models that provide good compromises between the fit of the stratification pattern and the line-integrated intensities, overall, model 6j provides the lowest 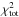 (see Sect. 5.3.6).
(see Sect. 5.3.6).
The parameters of the “best-fitting” models are summarised in Table 4. Our simulations show that these models can reproduce the stratification pattern, however a discrimination between the tested values for the depth at which the inset begins, dclumps = 0.02, 0.03 or 0.04 pc, is not possible. The best fits of the line-integrated intensities come from homogeneous models, or, if these are excluded, from models with dclumps = 0.02 pc. The best fit of the stratification pattern comes from a model with dclumps = 0.04 pc.
5.4.2. Line intensities
When using the original parameters from HJ95 (see Table 4) we find that almost all line intensities are too low compared to the observed line-integrated intensities. Only the [Cii] intensity, which originates predominantly from the interclump medium, can be roughly reproduced by the original HJ95-model. Even when considering the optically thin C18O lines that were used to derive the column densities we need at least a factor 1.5 more mass per voxel than suggested by HJ95 (see Sect. 4). To enable a fit of the other line-integrated intensities within a factor between two or three, the best-fitting models (see Sect. 5.4.1) use Mcl,tot = 2MHJ15 for a depth of the cavity of 0.6 pc. Consequently, our total mass per voxel is a factor 2.1 to 2.4 higher (for Minter,tot = 0.1 to 0.4 MHJ; see Sect. 5.4.4) than the value inferred from HJ95.
The difference can be explained from the nature of the different models. HJ95 use a two component (clump and interclump medium) model with a uniform kinetic temperature of Tkin = (85 ± 30) K (for both components) to fit the observations. In the KOSMA-τ PDR code, the full gas temperature distribution is calculated as a function of the clump radius. For a clump of 1 M⊙ with a hydrogen surface density of ns = 106 cm-3 and an FUV flux at the clump surface of 104χ0, the KOSMA-τ PDR code computes a clump-averaged temperature of 67 K, relatively close to the value by HJ95. However, in the KOSMA-τ simulations there is a significant change in temperature between surface and core. If we compute the average temperature “felt” by a particular molecule, which is obtained when weighing the temperature profile by the abundance of the different species, we obtain very different temperatures. C+, being abundant in a hot surface layer, feels an average temperature of about 1600 K while CO and 13CO feel temperatures of 38 K, and HCO+ of about 32 K.
The emission of all optically thin molecular species is therefore significantly weaker in our model than in the 85 K model from HJ95. As the line intensities are roughly proportional to the source function, which is itself determined by the excitation temperature, we find that a change of the gas temperature from 85 K to 38 K reduces the line intensities by a factor of about 2.5 for the lower-J CO lines. This explains the new upper limit on the molecular column density, deduced from the same C18O observations in Sect. 4, compared to the model of HJ95. By using a 2.7 times higher column density than HJ95, our best fitting model (6j) overestimates the C18O 3–2 line-integrated intensity by about 25% (see Sect. 4). This is better than the deviation that we find between our fit and observations for the other CO isotopologues. Taking the constraints from the C18O observations we cannot further increase the total column densities. However, all our model fits show the tendency that in particular the low- and mid-J lines from CO, 13CO, and HCO+ are somewhat too weak.
The line-integrated intensities of our best-fitting models follow a general trend, which is visible in the scatter plots, for example in Fig. 12. While for many models the fit of the [Cii] line-integrated intensity is satisfactory, it tends to be too low for other transitions, especially for CO 2−1, 3−2 and 6−5 and for 13CO 6−5 and 10−9. Even with model 3n, which provides the best fit of the line-integrated intensities, only a factor 0.54 of the observed CO 2−1 line-integrated intensity is reproduced (see Fig. 10). On the other side, the line-integrated intensities of the CO 16−15 and HCO+6−5 transitions are predicted too high, in our best-fitting models by a factor of about two.
The numerical experiments show that the intensity of the CO 16−15 and HCO+6−5 transitions depend strongly on the FUV flux that is available for the excitation of the gas in the dense clumps. Other transitions (e.g. low-J transitions of the CO isotopologues) are less affected. The FUV flux is governed mainly by the composition of the interclump medium. Due to the numerous low-J line observations used within our fitting process, the models are forced into a parameter range where the interclump gas is strongly reduced, resulting in a high FUV flux within the cloud and therefore overall increased line-integrated intensities. The effect on [Cii], which stems from both dense clumps and interclump gas, is minor, but for the sensitive high-J rotational lines, we obtain the outliers with too high predictions, that have been described above. The pattern becomes even stronger when we add very small and dense clumps, in other words when we reduce ml,cl. In the opposite case, by increasing the amount of interclump medium and hence reducing the FUV flux in the cloud, we can adjust all relative intensities to similar values, in other words remove the characteristic pattern, but then all intensities (except for [Cii]) are too low. This issue asks for a new mechanism, which systematically increases the line-integrated intensities of all, in particular the low-J, molecular transitions.
Adding the background molecular cloud (see Sect. 4 and model 2b_ext in Table 5) increases the line-integrated intensities of the low-J transitions of the CO isotopologues and of HCO+3−2, which can be excited by very low FUV fluxes. Consequently, the extension of the compound improves the fit of line-integrated intensities (while the influence on the stratification pattern is small) and slightly flattens the scatter plot of the Irel. The amount of background material is, however, constrained by the C18O limit as discussed in Sect. 4, so that no significant change to our results is possible from this side.
An enhancement of the CO line intensities on the modelling site might be possible when including non-equilibrium effects due to an advancing IF: Störzer & Hollenbach (1998) find that in such models low-J CO lines can be enhanced by a factor two compared to equilibrium models. The mid-J CO lines can also be affected.
5.4.3. Composition of the dense clumps
The characteristic intensity pattern obtained based on the original model parameters from HJ95 (Model 1d) shows a growing discrepancy between the predicted line intensities and the observed values with the rotational level for our linear molecules. Moreover, it does not reproduce the observed stratification pattern at all. This indicates that in this set-up the molecular material is too cold and too evenly distributed. As a consequence, we had to concentrate more mass in dense clumps and reduce the fraction of interclump mass to explain the observed intensities. Apart from the need for a higher total voxel mass discussed above, a reasonable fit of the integrated intensities is only possible when increasing the fraction of material that is contained in the dense clumps from the 10% in HJ95 to 83–95%.
Clump densities found in the literature cover 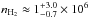 cm-3 (HJ95, corresponding to ρcl = 2 × 106 cm-3), 3 × 106 cm-3 (Young Owl et al. 2000) or between 3 × 106 and 1.2 × 107 cm-3 (assuming that the clumps are virialised, see Lis & Schilke 2003).
cm-3 (HJ95, corresponding to ρcl = 2 × 106 cm-3), 3 × 106 cm-3 (Young Owl et al. 2000) or between 3 × 106 and 1.2 × 107 cm-3 (assuming that the clumps are virialised, see Lis & Schilke 2003).
When comparing ensemble-averaged densities of ρcl = 106 cm-3 and 4 × 106 cm-3 for the dense clumps we find that the higher density slightly improve the fit of the line-integrated intensities. Unfortunately, we could not test higher ensemble-averaged densities than 4 × 106 cm-3 due to the boundaries of the KOSMA-τ parameter grid. It only provided densities up to 107 cm-3, while a full clump spectrum with an average density of 107 cm-3 would contain some clumps with significantly higher density.
In Sect. 5.3.5, we have tested models for which the lower cut-off mass of the ensemble of dense clumps has been increased relative to the initial value of 10-3M⊙. We notice that the small (and dense) clumps contribute to the molecular emission. Removing them, while keeping the ensemble-averaged density and total mass fixed, systematically decreases the line-integrated intensities of all transitions (except [Cii]), especially for the high-J transitions of the CO isotopologues. As the simulated line-integrated intensities tend to be too low in our models, the fit of the line-integrated intensities improves if small and dense clumps are included. Consequently, our simulations do not support the “turn-over” in the clump-mass function that has been suggested by some authors (see Sect. 2.2).
For model 6j the radii of the clumps at the different mass points are { Rj } j = 1...4 = { 0.0008,0.0022,0.0059,0.0159 } pc for the ensemble of dense clumps and 0.010 pc for the interclump medium. At the distance of 414 pc to Earth the size of the largest clumps (2 × 0.0159 pc) correspond to 15.8′′, which is about a factor two lager than the sizes that have been observed/derived by Lis & Schilke (2003) and Young Owl et al. (2000; see Sect. 3.2).
5.4.4. Composition of the interclump medium
The interclump medium has to account for a significant fraction of the [Cii] emission and partly for the emission of the low-J HCO+, CO and 13CO lines. Its main effect is, however, the attenuation of the FUV field, effectively lowering the gas temperature in the dense clumps. Ensembles with a more homogeneous distribution of the ISM within the voxels, which is for example achieved by reducing the ensemble-averaged density while keeping the total mass constant, cause stronger FUV attenuation.
The original HJ95-parameters correspond to a VFF of the interclump medium of (nearly) unity. In a homogeneous set-up the combination of dense clumps (with Mcl,tot = 2MHJ) and interclump medium provides too much FUV attenuation to allow for sufficient excitation of the (especially high-J) transitions that emit at some depth into the cloud. Based on simulations of inhomogeneous models with an interclump-VFF of unity (not shown) we conclude that if we limit ourselves to an interclump-VFF of one, we can fine-tune the composition of the interclump medium to optimise the fit of the stratification pattern or of the line-integrated intensities, but we do not find a set of parameters providing both.
In the homogeneous set-up the fits converges towards models that use a large amount of mass in the dense clumps, but no interclump medium (see models 1z and 1E). However, such models clearly contradict the observed stratification pattern and direct observations of the interclump medium (e.g. Stutzki et al. 1988; Ossenkopf et al. 2013). If we optimise the inhomogeneous models after dropping the constraint of the fixed interclump-VFF we find the best-fitting models with an interclump-VFF between 0.07 and 0.28, discussed in Sect. 5.4.1.
In our initial model we used clumps of 10-2M⊙ to represent the interclump medium. In Sect. 5.3.5, we varied this assumption to use clumps of 10-3M⊙, 10-2M⊙, and 1M⊙ instead. Changing the mass points has two major effects. First, the mass points yield a possibility to fine-tune the FUV attenuation in the cloud. Representing the interclump medium by clumps with 10-3M⊙, which allows for a more homogeneous distribution of the ISM, increases the FUV attenuation in the cloud, degrading the quality of the fit. Second, the small clumps also contribute to the molecular emission. If we increase the size of the clumps in the interclump medium, the reduced emission from the interclump gas leads to stratification offsets that are too small compared to the observed structure. Hence, our initial guess turned out to be a good choice.
For the interclump medium densities in the range 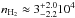 cm-3 (HJ95, corresponding to ρinter = 6 × 104 cm-3), 5 × 104 cm-3 (Young Owl et al. 2000) or 2 × 105 cm-3 (Simon et al. 1997) have been proposed. Our best-fitting models have a hydrogen nucleus density of 105 cm-3. If we correct this number by the VFFs between 0.07 and 0.28 found for our best models, we obtain an average density of the interclump medium over the volume of the voxel of 7 × 103 to 2.8 × 104 cm-3, which is somewhat lower.
cm-3 (HJ95, corresponding to ρinter = 6 × 104 cm-3), 5 × 104 cm-3 (Young Owl et al. 2000) or 2 × 105 cm-3 (Simon et al. 1997) have been proposed. Our best-fitting models have a hydrogen nucleus density of 105 cm-3. If we correct this number by the VFFs between 0.07 and 0.28 found for our best models, we obtain an average density of the interclump medium over the volume of the voxel of 7 × 103 to 2.8 × 104 cm-3, which is somewhat lower.
The Herschel observation (Fig. 3) shows that [C ii] has a rather smooth emission profile across the bar. Figure A.11 shows [C ii] emission of the interclump medium of model 6j. In this figure we have used a number surface density corresponding to 80 voxels along one line of sight, which is typical for the models discussed in this work. The figure shows that although the VFF of the interclumps medium of model 6j is only 0.04, the emission becomes rather smooth, especially if we consider that it is observed with an instrument resolution of about 0.02 pc.
5.4.5. The FUV illumination
In this work we have assumed that the FUV radiation field incident on a clump surface is isotropic. However, we have also applied the KOSMA-τ 3D code to the Orion Bar PDR, where the FUV irradiation comes from one dominating source and consequently from a defined direction. Therefore, one could argue that our (isotropic) approach increases the hot PDR surface area inside the cloud leading to an overestimation of the species originating form the hot gas, for instance the high-J CO lines. However, at some depth into the cloud, the FUV photons are efficiently scattered (Stoerzer et al. 1996) and the assumption of an isotropic radiation field becomes reasonable. For the description of the surface of the Orion Bar a model using beamed illumination would be more precise.
We have started our simulations with an FUV flux at the IF of 4.4 × 104χ0, adopted from HJ95. Furthermore, in Sect. 5.3.3 we have shown how increasing this values by 25% and 50% slightly improves the fit of the line-integrated intensities, but the effect is small compared to variations of other parameters. Changes of the FUV flux due to FUV attenuation inside the cloud, which is governed by the composition of the ensembles, has a significantly stronger impact on the simulation outcome. Hence, our models cannot be used to determine the FUV flux that is incident on the cloud surface.
In Sect. 5.3.4 we have presented models with inclination angels of the bar of 0°, 3°, 7° or 15°. From investigations of the line intensities emitted by the different voxels of the model compound we find that some species emit rather locally (see for example Fig. 9). For these species increasing the inclination angle can reduce the excited column density along a line of sight through the compound, into the direction of the observer. Still, an increase of the line-integrated intensity in the final map is possible, due to the beam convolution. In the simulations we had to compromise between these effects. For other tracers the excitation is less dependent on the FUV flux and the emission comes from a more extended region (see for example Fig. 8). For these transitions the impact of the inclination angle is smaller. The stratification pattern is produced by the rather complicated combination between FUV attenuation, inclined geometry of the bar and beam convolution. It is difficult to disentangle these effects, however, in general the pattern becomes more random, and hence harder to fine-tune, for large inclination angles. Our best-fitting inhomogeneous models use α = 3° or less. Such a small inclination angle was proposed by Melnick et al. (2012).
5.4.6. Further model improvements
As a solution to the overall insufficient fit of the line intensities of the combination of all tracers considered here, it might be useful to play with the isotopic abundances. A lower 18O abundance could potentially fit the observed high intensities of the CO and 13CO lines under the column density constraint from the C18O observations. Non-equilibrium models for the PDR chemistry as proposed by Störzer & Hollenbach (1998) could also lead to an enhancement of the CO line intensities.
To deal with the relatively high mismatch of the modelled line intensities compared to the mismatch of the stratification pattern, it may be useful to create a new chi-square criterion with a higher weight of the y-offsets that allows for a better combined fit of both model aspects. Another possibility to obtain further constraints would be to fit the whole intensity profile along the cuts and not only the pixels that provide the peak intensities. A model with a more complex density structure than our idealised sharp transition might further improve our fit. Furthermore, a systematic fit of the line profiles, as discussed in Sect. 5.3.7, would provide further constraints. Important information could come for example from the fit to more complicated line profiles as, in the context of the Orion Bar, seen for different transitions of CH+ and SH+ (Nagy et al. 2013).
A further improvement of the fit based on the chi-square tests could come from a more deliberate selection of the fitted tracers (if available). For example, with the current selection, only [Cii] is sensitive to the thin and hot interclump gas at the IF. An inclusion of other transitions that are expected to peak at the IF, as for instance CH+ and SH+ (Nagy et al. 2013) or OH+ (van der Tak et al. 2013) could increase the weight of a correct fit of the interclump medium.
In an ideal approach we should have repeated the two-dimensional scans using different sets of initial parameters and different successions for the parameter variations, to guarantee to find the globally best fit. This was, however, practically impossible due to the relatively large computational effort for each model run. In this way our fit may not be the best possible one, but our approach guarantees that we understand the effect of every individual parameter.
6. Summary
The observation of high-density, high temperature tracers combined with a layered structure of the Orion Bar spanning over more than 15″ rules out any description of the PDR in terms of a simple plane-parallel model. Photon-dominated regions, like molecular clouds, are clumpy and filamentary.
We propose a numerical model that is based on the representation of any PDR by an ensemble of clumps (possibly immersed in a thin interclump medium). Our new model KOSMA-τ 3D builds on the KOSMA-τ PDR code. It enables us to simulate the emission of star forming regions with arbitrary 3D geometries. The region is modelled using cubic voxels where each voxel is filled with clumpy structures, following a discrete mass distribution. The ensemble properties can vary between different voxels. Using a probabilistic algorithm for the calculation of the ensemble-averaged FUV extinction the incident FUV flux is derived for each voxel. A velocity dependent version of the probabilistic algorithm is used to calculate ensemble-averaged line intensities and optical depths and allows us to simulate the radiative transfer through the compound. The output of our code includes line-integrated intensity maps and full line profiles.
As a first test of the new model we performed simulations of the Orion Bar PDR. In these simulations we tried to simultaneously reproduce the line-integrated intensities and the spatial offsets of the emission peaks, for different transitions of CO isotopologues, HCO+ and [Cii]. Different geometries and parameter combinations have been tried out.
We find that a line fit is only possible if we invoke a process that removes dense clumps close to the PDR surface. The detailed stratification profile cannot be reproduced by models with a spatially constant ratio of clump to interclump gas.
The composition (i.e. the ensemble-averaged density and the total mass of the ensemble) of the interclump medium as well as the total molecular column density provided by the dense clumps are the most critical parameters for the simultaneous fit of the line intensities and the stratification structure of the Orion Bar. The interclump medium governs the FUV attenuation and hence the spatial layering while the clumps produce most of the emission from the molecular tracers. Our fit requires an ensemble-averaged density of 4 × 106 cm-3 for the ensemble of dense clumps and an ensemble-averaged density of 105 cm-3 for ensemble representing the interclump medium. Furthermore, for our best models we need a VFF of the interclump medium between 0.07 and 0.28, which indicates that also the interclump medium is not homogeneous, but breaks up into sub-structure.
To reproduce the observed line-integrated intensities, a large ratio (between 5 and 20) of total clump to total interclump mass is needed. This contradicts the earlier estimates by HJ95.
The depth of the cavity and the position of the illuminating source are of minor importance, as long as the total molecular column density is fixed. Only positions of the illuminating source close (~0.1 pc) to the background molecular cloud can be excluded. Furthermore, the observations are best reproduced if a small inclination angle of the bar, in the order of 3°, is used in the model.
The focus of this work was on testing the new 3D PDR model and on fitting line-integrated intensity maps of the Orion Bar PDR. A systematic comparison of the simulated line profiles to observations is left for future work.
The index j is related to the mass of the clump (see Sect. 2.2.2).
The grain-size distribution denoted with WD01-25 in Röllig et al. (2013) from line 25 in Table 1 in Weingartner & Draine (2001a) was used.
Atomic hydrogen is only contained in a thin surface layer (AV ≲ 0.1) of a PDR (see for example Röllig et al. 2007). Hence, in the comparison between simulated (column) densities and the results stated in HJ95, we assume that the contribution of atomic hydrogen is negligible, meaning that we use N ≈ 2 NH2 and ρ ≈ 2 nH2 when comparing to the molecular densities from HJ95.
The ratio between the Draine field χ0 and the Habing field G0 (both integrated over the FUV range) is χ0/G0 ≈ 1.71 (Draine & Bertoldi 1996).
Available online: http://www.mpe.mpg.de/~martins/SED.html
Acknowledgments
We thank D. Lis for providing the CSO data and helpful comments. S. Andree-Labsch thanks the Deutsche Telekom Stiftung and the Bonn-Cologne Graduate School of Physics and Astronomy for support by means of stipends. Modelling of irradiated molecular clouds is carried out within the Collaborative Research Center 956, sub-project C1, funded by the Deutsche Forschungsgemeinschaft (DFG). Furthermore, we wish to thank the anonymous referee for his/her suggestive and detailed comments.
References
- Alves, J. F., & McCaughrean, M. J. 2002, in The Origin of Stars and Planets: The VLT View (Springer Verlag) [Google Scholar]
- Arab, H., Abergel, A., Habart, E., et al. 2012, A&A, 541, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard-Salas, J., Habart, E., Arab, H., et al. 2012, A&A, 538, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisbas, T. G., Bell, T. A., Viti, S., Yates, J., & Barlow, M. J. 2012, MNRAS, 427, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Hollenbach, D. J., & Tielens, A. G. G. M. 1990, ApJ, 365, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, Y., van der Tak, F. F. S., Bergin, E. A., & Plume, R. 2014, A&A, 572, L10 [Google Scholar]
- Cuadrado, S., Goicoechea, J. R., Pilleri, P., et al. 2015, A&A, 575, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cubick, M. 2005, Diploma Thesis, Physikalisches Institut, University of Cologne [Google Scholar]
- Cubick, M., Stutzki, J., Ossenkopf, V., Kramer, C., & Röllig, M. 2008, A&A, 488, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, T., Boland, W., & Dalgarno, A. 1980, A&A, 91, 68 [NASA ADS] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, in Physics of the interstellar and intergalactic medium (Princeton University Press), 326 [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G., & Falgarone, E. 1996, ApJ, 471, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mexicana Astron. Astrofis., 49, 137 [Google Scholar]
- Gierens, K. M., Stutzki, J., & Winnewisser, G. 1992, A&A, 259, 271 [NASA ADS] [Google Scholar]
- Glover, S. C. O., Federrath, C., Mac Low, M.-M., & Klessen, R. S. 2010, MNRAS, 404, 2 [NASA ADS] [Google Scholar]
- Goicoechea, J. R., Joblin, C., Contursi, A., et al. 2011, A&A, 530, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Teyssier, D., Etxaluze, M., et al. 2015, ApJ, 812, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, J. R., Herbst, T. M., Matthews, K., et al. 1993, ApJ, 408, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2011, Bull. Astron. Soc. India, 39, 289 [Google Scholar]
- Habart, E., Dartois, E., Abergel, A., et al. 2010, A&A, 518, L116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Heithausen, A., Bensch, F., Stutzki, J., Falgarone, E., & Panis, J. F. 1998, A&A, 331, L65 [NASA ADS] [Google Scholar]
- Hogerheijde, M. R., Jansen, D. J., & van Dishoeck, E. F. 1995, A&A, 294, 792 [NASA ADS] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Hollenbach, D., Kaufman, M. J., Neufeld, D., Wolfire, M., & Goicoechea, J. R. 2012, ApJ, 754, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, J. E., Jaffe, D. T., Genzel, R., & Stacey, G. J. 1991, ApJ, 373, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, D. J., Spaans, M., Hogerheijde, M. R., & van Dishoeck, E. F. 1995, A&A, 303, 541 [NASA ADS] [Google Scholar]
- Kamp, I., Tilling, I., Woitke, P., Thi, W.-F., & Hogerheijde, M. 2010, A&A, 510, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koester, B., Stoerzer, H., Stutzki, J., & Sternberg, A. 1994, A&A, 284, 545 [NASA ADS] [Google Scholar]
- Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
- Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levrier, F., Le Petit, F., Hennebelle, P., et al. 2012, A&A, 544, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., & Schilke, P. 2003, ApJ, 597, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J. G. 1993, PASP, 105, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Testi, L., Natta, A., & Walmsley, C. M. 1998, A&A, 330, 696 [NASA ADS] [Google Scholar]
- Martin, H. M., Hills, R. E., & Sanders, D. B. 1984, MNRAS, 208, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melnick, G. J., Tolls, V., Goldsmith, P. F., et al. 2012, ApJ, 752, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mertens, M. 2013, Bachelor’s Thesis, Universität zu Köln, Physikalisches Institut, Cologne, Germany [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nagy, Z., Van der Tak, F. F. S., Ossenkopf, V., et al. 2013, A&A, 550, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagy, Z., Ossenkopf, V., Van der Tak, F. F. S., et al. 2015, A&A, 578, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagy, Z., Choi, Y., Ossenkopf-Okada, V., et al. 2017, A&A, in press DOI: 10.1051/0004-6361/201628916 [Google Scholar]
- Offner, S. S. R., Clark, P. C., Hennebelle, P., et al. 2014, Protostars and Planets VI, 53 [Google Scholar]
- Ossenkopf, V., Trojan, C., & Stutzki, J. 2001, A&A, 378, 608 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., Rollig, M., Cubick, M., & Stutzki, J. 2007, in Molecules in Space and Laboratory, eds. J. L. Lemaire, & F. Combes, 95 [Google Scholar]
- Ossenkopf, V., Röllig, M., Neufeld, D. A., et al. 2013, A&A, 550, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parmar, P. S., Lacy, J. H., & Achtermann, J. M. 1991, ApJ, 372, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., Brogan, C. L., et al. 2007, ApJ, 658, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., Ferland, G. J., Shaw, G., & Heathcote, S. 2009, ApJ, 693, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Beaupuits, J. P., Wiesemeyer, H., Ossenkopf, V., et al. 2012, A&A, 542, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Goicoechea, J. R., Gerin, M., et al. 2007, in Molecules in Space and Laboratory, eds. J. L. Lemaire, & F. Combes, 13 [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pilleri, P., Montillaud, J., Berné, O., & Joblin, C. 2012, A&A, 542, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flanney, B. P. 1992, Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd edn. (New York: Cambridge University Press) [Google Scholar]
- Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A&A, 451, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Abel, N. P., Bell, T., et al. 2007, A&A, 467, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Szczerba, R., Ossenkopf, V., & Glück, C. 2013, A&A, 549, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, R., Stutzki, J., Sternberg, A., & Winnewisser, G. 1997, A&A, 327, L9 [NASA ADS] [Google Scholar]
- Simón-Díaz, S., & Stasińska, G. 2011, A&A, 526, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stahl, O., Wade, G., Petit, V., Stober, B., & Schanne, L. 2008, A&A, 487, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Stoerzer, H., Stutzki, J., & Sternberg, A. 1996, A&A, 310, 592 [Google Scholar]
- Störzer, H., & Hollenbach, D. 1998, ApJ, 495, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., & Guesten, R. 1990, ApJ, 356, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., Stacey, G. J., Genzel, R., et al. 1988, ApJ, 332, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M. 1998, A&A, 336, 697 [NASA ADS] [Google Scholar]
- Szczerba, R., Omont, A., Volk, K., Cox, P., & Kwok, S. 1997, A&A, 317, 859 [NASA ADS] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., Meixner, M. M., van der Werf, P. P., et al. 1993, Science, 262, 86 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Tak, F. F. S., Nagy, Z., Ossenkopf, V., et al. 2013, A&A, 560, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Werf, P. P., Stutzki, J., Sternberg, A., & Krabbe, A. 1996, A&A, 313, 633 [NASA ADS] [Google Scholar]
- van der Werf, P. P., Goss, W. M., & O’Dell, C. R. 2013, ApJ, 762, 101 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wiel, M. H. D., van der Tak, F. F. S., Ossenkopf, V., et al. 2009, A&A, 498, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walmsley, C. M., Natta, A., Oliva, E., & Testi, L. 2000, A&A, 364, 301 [NASA ADS] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001a, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001b, ApJS, 134, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wen, Z., & O’dell, C. R. 1995, ApJ, 438, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W. 1980, A&A, 86, 286 [NASA ADS] [Google Scholar]
- Young Owl, R. C., Meixner, M. M., Wolfire, M., Tielens, A. G. G. M., & Tauber, J. 2000, ApJ, 540, 886 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Testing the probabilistic approach
In Sect. 2.3.3 ensemble-averaged line intensities and optical depths have been derived based on binomial distributions (referred to as probabilistic approach). This formalism was verified using a direct approach that calculates the ensemble-averaged quantities for a specific realisation of an ensemble. Here, the direct approach is presented for the [Cii], CO 3−2 and CO 16−15 lines. As it requires a relatively large amount of computing time (the calculation of the ensemble-averaged line intensity and optical depth of one “small” map with 1184 × 1184 pixel, for instance Fig. A.5, takes about two hours) it is not used in the simulations of the KOSMA-τ 3D code, where ensemble-averaged quantities need to be calculated for about 105 different ensembles. However, we used it to calculate the ensemble-averaged quantities of selected ensembles with known parameters to be compared to the results of the probabilistic approach. This serves three purposes:
Firstly, to verify that the ensemble-averaged quantities calculated with the probabilistic approach match the averaged quantities of real random realisations (random positions for each clump) of the ensemble.
Secondly, to verify that averaging over the clump projected area (see Sect. 2.1) can be used (the method presented here accounts for the full (non-averaged) profiles Iline(p) and τline(p) with p being the impact parameter, or radial distance from the centre point of the clump).
Thirdly, to understand how much the ensemble-averaged quantities of the same ensemble can vary depending on the random positions of the individual clumps.
As discussed in Sect. 2.3.1 we consider randomly distributed clumps of masses Mj with a fixed number surface density Nj/ (Δs)2. The projected surfaces of the clumps may overlap. We focus on the discussion of one ensemble representing dense clumps and in addition, for the 1.9 THz [Cii] transition, we show results of one typical ensemble representing the interclump medium (see below). The “dense-clump” ensemble tested in this appendix contains clumps with masses { Mj } j = 1...nM = { 10-3,10-2,10-1,100 }M⊙ and a total mass of 0.00346 M⊙ per (0.01 pc)2 projected surface area (which translates into Nj/ (Δs)2 using Eq. (19)). The ensemble averaged density has been fixed to be 4 × 106 cm-3, the averaged densities of individual clumps have been calculated using Eq. (18).
As discussed in Sect. 2.3.1 a clumpy ensemble can be scaled to arbitrary numbers of clumps as long as the number surface density for each mass point, 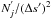 , is kept constant. For the direct approach we have created squared maps of a size (Δs′)2 in which the (centre points of the)
, is kept constant. For the direct approach we have created squared maps of a size (Δs′)2 in which the (centre points of the) 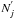 clumps are randomly distributed. Two different map sizes are used in this appendix, small maps contain one and large maps contain two clumps at mass point 1 M⊙. In the maps we ignore an area of the thickness Rcl,max/ 2 around the edges because that region could be affected by clumps with centres outside of the map, that are no taken into account here.
clumps are randomly distributed. Two different map sizes are used in this appendix, small maps contain one and large maps contain two clumps at mass point 1 M⊙. In the maps we ignore an area of the thickness Rcl,max/ 2 around the edges because that region could be affected by clumps with centres outside of the map, that are no taken into account here.
Maps of random representations of the ensemble of dense clumps are shown in Figs. A.1, A.2, A.5 and A.7. For all presented maps an FUV flux of 104χ0 has been used. For instance, the colour scale of Fig. A.1 shows the line centre intensity of the [Cii] line, summed up along lines of sight perpendicular to the printed surface. [Cii] emission is strongest in the outer layers of the clumps. It is affected by limb brightening. The resulting intensity profile Iline(p) (see Eq. (5)), where the [Cii] line intensity is highest at the edge of each (sufficiently large) projected clump, is clearly visible in Fig. A.1. Analogously to Fig. A.1 maps showing the optical depth have been simulated. For example Fig. A.2 shows the same map as Fig. A.1 but with the colour scale giving the optical depth of the [Cii] transition.
 |
Fig. A.1 Large map (see text) showing one representation of the test ensemble, consisting of randomly distributed clumps. The colour scale gives the line centre intensity of the 1.9 THz [Cii] transition where the line intensity is highest in the outer layer of each clump. This maps shows the 22nd representation from Fig. A.3. The ensemble is shown in a superpixel, in other words with the area filling factor of a normal 0.01 pc pixel, but scaled in the lateral directions to contain enough clumps of each size. |
 |
Fig. A.2 Same as Fig. A.1 but with the colour scale giving the optical depth of the 1.9 THz [Cii] transition. |
 |
Fig. A.3 Ensemble-averaged [Cii] line centre intensities for different realisations of the test ensemble. The circles show the ensemble-averaged intensities of 20 different small intensity maps and the squares give the values for ten different large intensity maps as presented in Fig. A.1. The black line gives the mean value of the 30 maps, weighted by the respective number of grid points. For the 20 small maps the average is (2.24 ± 0.50) K and for the ten large maps it is (2.17 ± 0.33) K. The stated error is the standard deviation, which, as expected, is larger for the smaller maps. The red, dashed line gives the value derived using the probabilistic approach for the same ensemble. The difference between the two approaches is about 2.6%. |
 |
Fig. A.4 Same as Fig. A.3 but plotted for the ensemble-averaged optical depths, τ, of the [Cii] line. For the [Cii] line the difference between the probabilistic approach and the average over the 30 results derived with the direct approach is about 2.6% for line intensities and optical depths. |
 |
Fig. A.5 Small map of one representation of the test ensemble. The colour scale gives the optical depth of the CO 3−2 line (line centre), which is highest for lines of sight through the dense cloud cores. This map shows the first realisation from Fig. A.6. The increasing optical depth towards the clump centres provide the visual impression that the clumps are smaller than their actual size. |
 |
Fig. A.6 Ensemble-averaged optical depths of the CO 3−2 line. The circles show the results for ten different realisations of the ensemble as presented in Fig. A.5. The black line gives the mean value of the ten maps, namely (0.038 ± 0.006) where 0.006 is the standard deviation. The red, dashed line gives the value derived with the probabilistic approach for the same ensemble. The difference between the two approaches is about 3.7% (and about 3.5% for the line intensities which are not shown). |
 |
Fig. A.7 Small map showing the line centre intensity of the CO 16–15 line (colour scale). This map corresponds to the 5th representation from Fig. A.8 where the large clump is sitting at the lower edge, causing a small ensemble-averaged intensity and optical depth. |
 |
Fig. A.8 Ensemble-averaged intensities of the CO 16–15 line (line centre). The circles show the results for ten different realisations of the ensemble as presented in Fig. A.7. The black line gives the mean value of the ten maps, namely (7.6 ± 1.0) K where 1.0 is the standard deviation. The red, dashed line gives the value derived by the probabilistic approach for the same ensemble. Here, the two lines are lying on top of each other (the difference between the two approaches is about 0.004% for the line intensities and about 0.8% for the optical depths which are not shown here). |
 |
Fig. A.9 Intensity map showing a representation of the interclump medium with initially 100 identical clumps (a few clumps have been cut away during the removal of the edges of the map). The colour scale gives the line centre intensities of the [Cii] line. |
 |
Fig. A.10 Ensemble-averaged [Cii] line centre intensities of different realisations of the interclump-ensemble. The circles show the ensemble-averaged intensities of ten different maps containing ten clumps and the squares give the values for ten different maps with 100 clumps as presented in Fig. A.9. The black line gives the mean value of the 20 maps, weighted by the respective number of grid points. For the maps with ten clumps the average is (24.4 ± 7.1) K and for the maps with 100 clumps it is (23.6 ± 1.0) K, where the stated error is the standard deviation. The red, dashed line gives the value derived by the probabilistic approach (for NnM = 1 = 100 clumps) for the same ensemble. The two results agree within 0.4% (intensities) and 0.8% (optical depths, not shown). |
 |
Fig. A.11 Map showing the interclump medium of model 6j, with a surface density corresponding to the full line of sight of the model provided by 80 voxels. The colour scale shows 1−Exp(−τCII). |
Each map has been derived on a spatial grid with a grid-spacing dgrid ≪ Δs′ (see Sect. 2.3.1). The large maps, for instance Fig. A.1, contain ngrid = 1741 × 1741 grid points while the small maps (see Figs. A.5 and A.7) contain ngrid = 1184 × 1184 grid points. For each map the ensemble-averaged quantities were calculated using 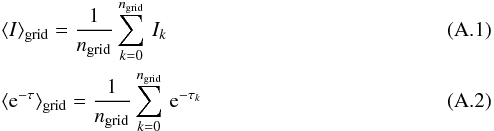 where the index k denotes different gridpoints. The resulting ⟨ I ⟩ grid and ⟨ e− τ ⟩ grid can be compared to the results from the binomial approach (Eqs. (A.4) and (A.5)).
where the index k denotes different gridpoints. The resulting ⟨ I ⟩ grid and ⟨ e− τ ⟩ grid can be compared to the results from the binomial approach (Eqs. (A.4) and (A.5)).
In the presented comparison we account for only one velocity bin with centre-velocity vi = v1 = vsys. This velocity bin contains all clumps of the ensemble and Eq. (26) simplifies to 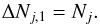 (A.3)Furthermore, due to vi = vobs, Eqs. (27) and (28) simplify to
(A.3)Furthermore, due to vi = vobs, Eqs. (27) and (28) simplify to  giving the line-centre intensity and optical depth for each combination of clumps. As we do not have to sum up contributions from different centre-velocities, the ensemble-averaged quantities are provided by Eqs. (32) and (33), for i = 1. These are compared to the results from the probabilistic approach.
giving the line-centre intensity and optical depth for each combination of clumps. As we do not have to sum up contributions from different centre-velocities, the ensemble-averaged quantities are provided by Eqs. (32) and (33), for i = 1. These are compared to the results from the probabilistic approach.
For the [Cii] line the ensemble-averaged line intensity and optical depth have been derived for 30 different realisations of the ensemble including 20 small and ten large maps. The results are summarised in Figs. A.3 and A.4 for the intensities and optical depths, respectively. As expected, the averaged values calculated for single realisation in Figs. A.3 and A.4 show some scatter, which is larger for the smaller maps (this effect is better visible in Fig. A.10 where the size-difference between the maps is larger). The scatter shows us how much single representations of the ensemble, which might exist in molecular clouds, can differ from the mean value derived with the probabilistic approach. The black lines give the line intensity or optical depth averaged over the 30 results of the individual representations. Within this calculation the maps got different weights, proportional to their respective sizes. The red, dashed lines show the ensemble-averaged quantities for the same ensemble, calculated using the probabilistic approach. For [Cii] the two approaches agree within 2.6% for line intensities and optical depths.
The reliability of the approach presented here depends on the size of the calculated maps and on the number of representations of the ensemble to be averaged over. However, a statistical difference remains between simulating one very large map or several smaller maps with the same total size. This difference can be understood from the different [Cii] maps: while for the large maps with (for example) NnM = 2 a clump at the highest mass point can overlap with a clump of the same kind, this overlap is not possible for the small maps with NnM = 1. However, Fig. A.3 shows that this difference is negligible for the dense ensembles in this work, due to their small area filling factors. For the interclump medium, which has a higher area filling factor, the situation is different (see below).
For each CO line ten small maps have been analysed. Figure A.5 shows such a map with the optical depth of the CO 3−2 transition given on the colour scale. As expected the CO 3−2 optical depth is highest for lines of sight intersecting with the dense cloud cores. The related statistical overview is shown in Fig. A.6. We find that the two approaches agree within 3.7% (3.5%) for the optical depths (line intensities). Possibly, increasing the number of samples could improve this result.
For the CO 16−15 line we present an intensity map in Fig. A.7 and the related statistical overview in Fig. A.8. The map (Fig. A.7) shows the 5th realisation of the ensemble from Fig. A.8. Here, the large clump is sitting at the lower edge of the map and is partly cut away causing the small ensemble-averaged intensity (and optical depth). However, this situation is part of the normal statistics. For CO 16−15 the agreement between the two approaches is excellent (which is coincidental due to the rather low number of sample maps), we find deviations between the two approaches of 0.004% and 0.8% for line intensities and optical depths, respectively.
In addition to the ensemble of dense clumps we have tested one typical “interclump-ensemble”. This ensemble contains clumps at one mass point (10-2M⊙), a total ensemble mass of 0.5 × 0.00173M⊙ per (0.01 pc)2 projected surface area, and an ensemble averaged density of 1.91 × 104 cm-3. It has an area filling factor (N1π(R1)2/ (Δs)2, i.e. not accounting for the fact that clumps do overlap) of about 0.8. The clumps are lying on a gridpoint of the KOSMA-τ model grid, making interpolations unnecessary. One representation of this ensemble is shown in Fig. A.9 where the colour scale gives the [Cii] line (centre) intensity. The map originally contained 100 identical clump, a few clumps have been cut away during the removal of the edges of the map. One should note that for this ensemble the clumps at mass point 10-2M⊙ are about a factor six larger compared to the previous ensemble, due to the reduced density. The [Cii] intensities of different realisations of the ensemble, for maps that contained initially 10 or 100 clumps, are shown in Fig. A.10. The comparison to the probabilistic approach shows that the deviation between the two results lies below 1% for line intensities and optical depths. For the interclump medium the probabilistic approach yields an ensemble-averaged [Cii] line centre intensity of 23.68 K for NnM = 1 = 10 and of 23.57 K for NnM = 1 = 100.
The excellent agreement between the two approaches for the interclump ensemble indicates that averaging over the projected surface (see Sect. 2.1) hardly introduces any error. Furthermore, the interpolation between the line profiles Iline(p) and τline(p), as needed for the ensemble of dense clumps during the analysis with the direct approach, does not cause large deviations. All compared results are found to agree within the statistical scatter, which is quantified by the standard deviations of the scatter of the ensemble-averaged quantities, calculated with the direct approach.
In addition to the ensembles used for the statistical analysis in this section, we have added Fig. A.11, which shows clumps based on the parameters of the interclump medium of model 6j (see Table 5), with a number surface density corresponding to 80 voxels along a line of sight. This figure is further discussed in Sect. 5.4.4.
Appendix B: Numerical handling of the radiative transfer
A solution of the equation of radiative transfer, based on linear approximations of the emission and absorption coefficient, has been presented in Sect. 2.3.4. Here, we discuss the numerical handling of the integral in Eq. (40) in the KOSMA-τ-3D code. The numerical integrations in this section were performed using Wolfram Mathematica16. Before we solve the integral in Eq. (40) we need to distinguish three different cases:
-
Case 1).
If no absorption takes place betweentwo pixels, that is k0 = 0 and k1 = 0, the equation of radia-tive transfer (Eq. (37)) reduces to
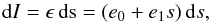 (B.1)and integration between 0 and Δs yields
(B.1)and integration between 0 and Δs yields 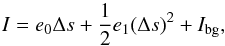 (B.2)where Ibg indicates the incident background emission. This case (i.e. an infinite source function and hence an infinite excitation temperature) cannot occur in any physical source. However, in the code it is needed if there are “holes” in the set-up in other words if voxels on a line of sight are not occupied by an ensemble (at a specific velocity) or for artificial sources which have been constructed in a way that voxels emit at a specific frequency without absorbing it. Practically, in the code, the condition | k0 Δs | < 10-10 and k1 = 0 has been used for this case, avoiding errors due to numerical inaccuracies.
(B.2)where Ibg indicates the incident background emission. This case (i.e. an infinite source function and hence an infinite excitation temperature) cannot occur in any physical source. However, in the code it is needed if there are “holes” in the set-up in other words if voxels on a line of sight are not occupied by an ensemble (at a specific velocity) or for artificial sources which have been constructed in a way that voxels emit at a specific frequency without absorbing it. Practically, in the code, the condition | k0 Δs | < 10-10 and k1 = 0 has been used for this case, avoiding errors due to numerical inaccuracies. -
Case 2).
If the absorption coefficient does not change between two pixels, meaning that k1 = 0 but k0 ≠ 0, Eq. (40) reduces to
![\appendix \setcounter{section}{2} \begin{equation} I={\rm e}^{-k_0\Delta s}\left[ \int_0^{\Delta s}(e_0+e_1\, s'){\rm e}^{k_0 s'}{\rm d}s' + I_{\rm{bg}}\right], \label{Eq:case2} \end{equation}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq517.png) (B.3)and numerical integration yields
(B.3)and numerical integration yields ![\appendix \setcounter{section}{2} \begin{equation} I={\rm e}^{-k_0\Delta s}\left[\left(\frac{e_0k_0 + e_1(k_0\Delta s - 1)}{k_0^2} \right){\rm e}^{k_0\Delta s} - \left(\frac{e_0k_0-e_1}{k_0^2}\right) + I_{\rm{bg}}\right]. \end{equation}](/articles/aa/full_html/2017/02/aa24287-14/aa24287-14-eq518.png) (B.4)Practically, in the code, the condition k0> 103k1Δs has been used for this case.
(B.4)Practically, in the code, the condition k0> 103k1Δs has been used for this case. -
Case 3).
The third case is the general case which is always used if k1 ≠ 0. Numerical integration of Eq. (40) yields
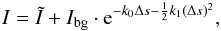 (B.5)with
(B.5)with 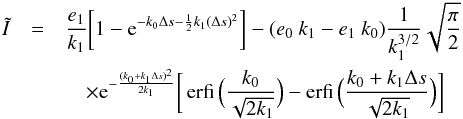 (B.6)where erfi(...) denotes the imaginary Error Function.
(B.6)where erfi(...) denotes the imaginary Error Function.  is further discussed below.
is further discussed below.
Implementation, runtime and precision of the imaginary error functions in Eq. (B.6) are problematic for large function values. In the code this is avoided by the following rearrangements and substitutions:
-
The function
 , Eq. (B.6), can be written as
, Eq. (B.6), can be written as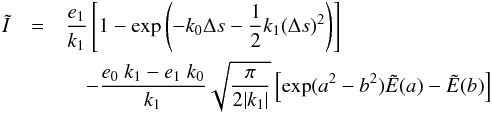 (B.7)with
(B.7)with 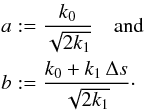 (B.8)
(B.8) -
The function
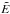 has been constructed in a way that (subtractions between) large numbers are avoided. It is different for k1> 0 and k1< 0. Furthermore, it can be approximated for large and small function values. For k1> 0 it is given by
has been constructed in a way that (subtractions between) large numbers are avoided. It is different for k1> 0 and k1< 0. Furthermore, it can be approximated for large and small function values. For k1> 0 it is given by 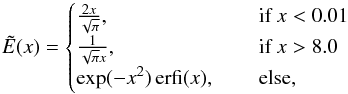 (B.9)for k1< 0 (and consequently imaginary a and b) it is given by
(B.9)for k1< 0 (and consequently imaginary a and b) it is given by 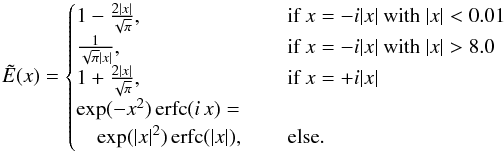 (B.10)
(B.10)
For 0.01 ≤ | x | ≤ 8.0 both functions, Eqs. (B.9) and (B.10), have been tabulated. The code interpolates linearly between the tabulated values. Maser lines (k0 + k1Δs< 0, i.e. x = + i | x |) are treated in linear approximation. Hence, the code should not be used for strong maser lines. For all other x, including weak maser lines (x = + i | x | with | x | < 0.1), the relative error made by interpolation or approximation of 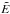 is less than one percent.
is less than one percent.
Appendix C: FUV flux at the ionisation front
Jansen et al. (1995) state that the radiation field incident on the Orion Bar corresponds to an enhancement over the average interstellar radiation field, χ0, of a factor ≈4.4 × 104. Other authors give similar values, Marconi et al. (1998) estimate a flux of 1−3 × 104 times the average interstellar field. Arab et al. (2012), Young Owl et al. (2000), Walmsley et al. (2000) used 1−4 G0 at the IF with G0 being the Habing field (Habing 1968)17.
Here, we have re-estimated the FUV flux at the IF, originating from Θ1 Ori C, based on synthesised stellar spectra provided by Martins et al. (2005)18. Different spectra from their sample have been investigated, for stars having effective temperatures between 35 000 and 39 540 K which covers the spectral classes from O7V to O6V. Different authors (Stahl et al. 2008; Pellegrini et al. 2009; Arab et al. 2012) obtained varying results for the spectral class of Θ1 Ori C, all falling in the range between O6 and O7.
The selected spectra have been integrated in the FUV range, 2066 to 911 Å (6 to 13.6 eV), and the resulting flux at the position of the Orion Bar has been computed. For this calculation, the distance between Θ1 Ori C and the Orion Bar has been assumed to be 0.223 pc, in other words equal to the projected distance (neglecting a possible offset in radial direction which is not precisely known, see Sect. 3.1). The calculated fluxes fall between 17 and 373 erg s-1 cm-2 (0.63 × 104χ0−13.8 × 104χ0), covering the range of values discussed above.
The FUV flux representative for an O6.5 star (Teff = 36 826 K, Martins et al. 2005) is found to be 38 erg s s-1 cm-2 or 1.4 × 104χ0 at the IF. The flux of 4.4 × 104χ0 from HJ95 is best reproduced by the star from the sample with Teff = 37 760 K, which indicates the spectral class O6.5V (Martins et al. 2005). The calculated FUV fluxes make strong FUV absorption inside the Hii region between star and PDR improbable in agreement with the lack of dust observed in the cavity. Dust must have been blown out by the strong stellar winds.
Appendix D: Cylindrical models
 |
Fig. D.1 Simulated cuts perpendicular to the Orion Bar, based on model Cyl. 5 (see Table D.1). Each colour scales gives the line-integrated intensity of the transitions indicated above the respective cut. |
 |
Fig. D.2 Cut through the cylindrical Orion Bar model Cyl. 4. For each voxel the colour scale gives the [Cii] line intensity of dense clumps and interclump medium, at the line centre (at 11.3 km s-1). The illuminating star Θ1 Ori C is located at [0,22.3,30]. |
 |
Fig. D.3 Same as Fig. D.2 but plotted for the outer line wing (at 8.3 km s-1). Effectively, only the interclump medium contributes at this velocity. |
As discussed in Sect. 4 we have also tested models where the Orion Bar has a cylindrical shape (see Figs. D.2 and D.3). The tests of this geometry are based on the assumption that the sets of parameters that provide the best simulation results for the HJ95 geometry are also good initial guesses for the cylindrical model. We have used a cylindrical model with a deep cavity, dcavity = 0.6 pc, and hence a radius for the cylinder of 0.3 pc. The centre point of the cut through the cylinder is [0,−30,30] and the illuminating source is located at [0,22.3,30] (see Fig. D.2). The inclination parameter α′ is not needed for a cylinder. Table D.1 gives an overview over some cylindrical models. The second column of the table refers to the corresponding model from Table 5 for the remaining parameters, in other words to the composition of the clump ensembles, IUV and dclumps.
Overview over cylindrical models.
Figures D.2 and D.3 show cuts through the cylindrical model Cyl. 4, which is an inhomogeneous model with dclumps = 0.02 pc. The colour scales give the [Cii] line intensity emitted by the dense clumps and the interclump medium of the respective voxel at a specific velocity, Fig. D.2 shows the line-centre intensity (at 11.3 km s-1) and Fig. D.3 the emission in the line wing (at 8.3 km s-1). Figure D.2 illustrates that at the line centre velocity the [Cii] emission is dominated by the dense clumps, that only start two voxels below the cloud surface. Due to the higher velocity dispersion of the interclump medium (see Sect. 5.3.7), the 8.3 km s-1 channel in Fig. D.3 is dominated by the [Cii] emission from the interclump medium, providing the highest line intensities in the voxels that are closest to the illuminating source. The observable stratification pattern follows from the radiative transfer and the beam convolution of these pictures.
In general, for cylindrical models the y-offsets where the line-integrated intensity peaks for the different transitions are shifted deeper into the cloud (into the negative y-direction) compared to the corresponding cavity-wall models. For all models listed in Table D.1 the [Cii] line-integrated intensity peak (i.e. the reference positions for the y-offsets) is shifted by one to three pixels deeper into the PDR compared to the cavity-wall model with the same parameters. As an example Fig. D.1 shows the simulated cuts of model Cyl. 5. Here the [Cii] peak lies at y = −0.08 pc, while the peak appears at y = −0.06 pc in model 6j. Hence, to provide a stratification pattern, the y-offsets of all other transitions need to be shifted even deeper into the cloud in the cylindrical models. This is hardly observed. The line intensity is dominated by the column density along the line of sight given by the cylindrical geometry, less by changing composition or excitation conditions. For the cylinder the lines of sight through the compound close to y = 0 are shorter than the lines of sight through the cloud material in the cavity-wall set-up (assuming small α′). Therefore, the intensity peaks are shifted from the edge of the cloud to positions where the lines of sight through the compound and hence the column densities are larger. This leads to the higher y-offsets in the cylindrical model.
Depending on the specific model set-up, the 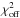 can decrease or increase when we switch from the cavity-wall models to the cylindrical geometry. However, this comparison is ambitious, as the
can decrease or increase when we switch from the cavity-wall models to the cylindrical geometry. However, this comparison is ambitious, as the 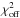 of the HJ95-models also depend on the inclination angle α′. Similar to the HJ95-models we find that the fit of the stratification pattern is better when an inhomogeneous model (i.e. models Cyl. 4 to Cyl. 7) is used, compared to the homogeneous set-ups (models Cyl. 1 to Cyl. 3). None of the homogeneous models can reproduce any stratification for the CO 10−9 transition. Models Cyl. 5, 6 and 8 do provide peak positions Δyi< 0 relative to the [Cii] peak (see Sect. 5.2) for all transitions. However, the Δyi scatter around the observed values, complicating the fine-tuning of the stratification pattern. None of the tested models reaches the
of the HJ95-models also depend on the inclination angle α′. Similar to the HJ95-models we find that the fit of the stratification pattern is better when an inhomogeneous model (i.e. models Cyl. 4 to Cyl. 7) is used, compared to the homogeneous set-ups (models Cyl. 1 to Cyl. 3). None of the homogeneous models can reproduce any stratification for the CO 10−9 transition. Models Cyl. 5, 6 and 8 do provide peak positions Δyi< 0 relative to the [Cii] peak (see Sect. 5.2) for all transitions. However, the Δyi scatter around the observed values, complicating the fine-tuning of the stratification pattern. None of the tested models reaches the 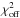 of our best HJ95-models.
of our best HJ95-models.
With the parameters from Table 5 the cylindrical geometry provides always systematically lower line-integrated intensities for all transitions than the cavity-wall model, resulting in a deteriorated fit (in terms of the 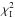 ). This reduction results from a combination of two effects: (a) shorter lines of sight and hence reduced column densities at the front of the cylinder; (b) less FUV flux available for the excitation when the peaks are shifted deeper into the cloud (see above). This already shows the fundamental problem of cylindrical models.
). This reduction results from a combination of two effects: (a) shorter lines of sight and hence reduced column densities at the front of the cylinder; (b) less FUV flux available for the excitation when the peaks are shifted deeper into the cloud (see above). This already shows the fundamental problem of cylindrical models.
Consequently, we find that the fits based on the tested cylindrical model do not reach the quality (in terms of the 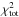 ) of the HJ95- models. Of course these results could be improved if step-by-step fine-tuning of the parameters is performed, however, fine-tuning of the stratification patter is expected to be difficult due to the scattering of the Δyi of the different transitions. An improvement of the fit of the line-integrated intensities might be possible if the mass per voxel in the dense clumps is drastically increased, leading to larger molecular column densities close to y = 0. A cylinder with less curvature might also provide better results.
) of the HJ95- models. Of course these results could be improved if step-by-step fine-tuning of the parameters is performed, however, fine-tuning of the stratification patter is expected to be difficult due to the scattering of the Δyi of the different transitions. An improvement of the fit of the line-integrated intensities might be possible if the mass per voxel in the dense clumps is drastically increased, leading to larger molecular column densities close to y = 0. A cylinder with less curvature might also provide better results.
All Tables
Summary of averaged integrated intensities and spatial offsets of the observations.
All Figures
 |
Fig. 1 3D compound replicating a possible geometry (model 1m, see Table 5) of the Orion Bar PDR. Each cube represents one voxel filled with at least one clumpy ensemble. Coordinates are given in voxel sizes, corresponding to 0.01 pc. The colour scale (Green 2011) shows the impinging FUV flux, calculated for each voxel, for a FUV source located at [0,22.3,30]. The direction to Earth corresponds to the positive z direction. |
| In the text | |
 |
Fig. 2 Face-on/edge-on/face-on Orion Bar geometry as proposed by HJ95. Values are taken from: green: HJ95; red: Menten et al. (2007); blue: Pellegrini et al. (2009); and orange: van der Werf et al. (2013). For the inclination angle, α′, values between less than 3° and 15° have been discussed (Jansen et al. 1995; Melnick et al. 2012). |
| In the text | |
 |
Fig. 3 Orion Bar observed with HIFI/Herschel. The green contours show [Cii] line intensities integrated between 7 and 13 km s-1. The contours range between 200 and 800 K km s-1 in steps of 100 K km s-1. The colour scale gives the 13CO 10−9 line intensity, integrated between 9 and 12 km s-1. The reference position is the CSO reference position (5h35m20.122s, −5°25′21.96′′). |
| In the text | |
 |
Fig. 4 [Cii] integrated intensity (same as the contours in Fig. 3, but rotated by −145°). In this orientation Θ1 Ori C in the north-west of the bar is at the bottom of the map. The green line marks the cut with the highest averaged line-integrated intensity, including all pixels with x-offsets between −11.3′ and −43.5′. |
| In the text | |
 |
Fig. 5 Simulated map of line-integrated CO 3−2 emission of the Orion Bar PDR, based on model 1m (see Table 5). The coordinates are given in units of pixels. One pixel corresponds to 0.01 pc or 5″ on the sky. The illuminating star Θ1 Ori C is located at x = 0 and y = 22.3 on top of the map. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but after convolution with a Gaussian beam of 21.9″ or 4.4 pixels FWHM (see Table 2). |
| In the text | |
 |
Fig. 7 Simulated cuts perpendicular to the Orion Bar, based on model 6j (see Table 5). Each colour scale gives the line-integrated intensity of the transition indicated above the respective cut. |
| In the text | |
 |
Fig. 8 Cut through the Orion Bar model 2b. For each voxel the colour scale gives the CO 2−1 line intensity of dense clumps and interclump medium, at the line centre (at 11.3 km s-1). The illuminating star Θ1 Ori C is located at [0,22.3,30]. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but with the CO 16−15 line intensity given on the colour scale. |
| In the text | |
 |
Fig. 10 Scatter plot of the line-integrated intensities for selected models from Sects. 5.3.1, 5.3.3 and 5.3.4. For each transition the ratio between simulated and observed line-integrated intensity at the respective peak position, Irel,i = Ifit,i/Iobs,i, is plotted on a logarithmic scale. The different transitions are indicated on the abscissa and different symbols mark the different models. |
| In the text | |
 |
Fig. 11 Scatter plot of the y-offsets of selected models from Sects. 5.3.1, 5.3.3 and 5.3.4. For each transition the difference between the offset of the simulated and the observed peak position, as defined in Eq. (45), is plotted. All offsets are relative to the [Cii] peak position, hence, for the reference [Cii] transition ydiff is always zero. A negative offset indicates that the simulated emission peak is shifted too far into the direction of Θ1 Ori C, a positive offset indicates that the emission appears too deep in the cloud. The different transitions are indicated on the abscissa and different symbols mark different models. |
| In the text | |
 |
Fig. 12 Same as Fig. 10, plotted for selected models from Sects. 5.3.5 and 5.3.6. In addition, model 2e from Sect. 5.3.3 is given for comparison. |
| In the text | |
 |
Fig. 13 Same as Fig. 11, plotted for selected models from Sects. 5.3.5 and 5.3.6. In addition, model 2e from Sect. 5.3.3 is given for comparison. |
| In the text | |
 |
Fig. 14 Line profiles of selected transitions of model 6j. The full lines show the simulated profiles, the dashed lines are Gaussian profiles with the same peak intensity as the respective profile, but with linewidths of FWHM = 2 km s-1 and FWHM = 4 km s-1, matching the observed total velocity dispersions. For each transition the y-offset corresponds to the position with the highest line-integrated intensity. |
| In the text | |
 |
Fig. A.1 Large map (see text) showing one representation of the test ensemble, consisting of randomly distributed clumps. The colour scale gives the line centre intensity of the 1.9 THz [Cii] transition where the line intensity is highest in the outer layer of each clump. This maps shows the 22nd representation from Fig. A.3. The ensemble is shown in a superpixel, in other words with the area filling factor of a normal 0.01 pc pixel, but scaled in the lateral directions to contain enough clumps of each size. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but with the colour scale giving the optical depth of the 1.9 THz [Cii] transition. |
| In the text | |
 |
Fig. A.3 Ensemble-averaged [Cii] line centre intensities for different realisations of the test ensemble. The circles show the ensemble-averaged intensities of 20 different small intensity maps and the squares give the values for ten different large intensity maps as presented in Fig. A.1. The black line gives the mean value of the 30 maps, weighted by the respective number of grid points. For the 20 small maps the average is (2.24 ± 0.50) K and for the ten large maps it is (2.17 ± 0.33) K. The stated error is the standard deviation, which, as expected, is larger for the smaller maps. The red, dashed line gives the value derived using the probabilistic approach for the same ensemble. The difference between the two approaches is about 2.6%. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.3 but plotted for the ensemble-averaged optical depths, τ, of the [Cii] line. For the [Cii] line the difference between the probabilistic approach and the average over the 30 results derived with the direct approach is about 2.6% for line intensities and optical depths. |
| In the text | |
 |
Fig. A.5 Small map of one representation of the test ensemble. The colour scale gives the optical depth of the CO 3−2 line (line centre), which is highest for lines of sight through the dense cloud cores. This map shows the first realisation from Fig. A.6. The increasing optical depth towards the clump centres provide the visual impression that the clumps are smaller than their actual size. |
| In the text | |
 |
Fig. A.6 Ensemble-averaged optical depths of the CO 3−2 line. The circles show the results for ten different realisations of the ensemble as presented in Fig. A.5. The black line gives the mean value of the ten maps, namely (0.038 ± 0.006) where 0.006 is the standard deviation. The red, dashed line gives the value derived with the probabilistic approach for the same ensemble. The difference between the two approaches is about 3.7% (and about 3.5% for the line intensities which are not shown). |
| In the text | |
 |
Fig. A.7 Small map showing the line centre intensity of the CO 16–15 line (colour scale). This map corresponds to the 5th representation from Fig. A.8 where the large clump is sitting at the lower edge, causing a small ensemble-averaged intensity and optical depth. |
| In the text | |
 |
Fig. A.8 Ensemble-averaged intensities of the CO 16–15 line (line centre). The circles show the results for ten different realisations of the ensemble as presented in Fig. A.7. The black line gives the mean value of the ten maps, namely (7.6 ± 1.0) K where 1.0 is the standard deviation. The red, dashed line gives the value derived by the probabilistic approach for the same ensemble. Here, the two lines are lying on top of each other (the difference between the two approaches is about 0.004% for the line intensities and about 0.8% for the optical depths which are not shown here). |
| In the text | |
 |
Fig. A.9 Intensity map showing a representation of the interclump medium with initially 100 identical clumps (a few clumps have been cut away during the removal of the edges of the map). The colour scale gives the line centre intensities of the [Cii] line. |
| In the text | |
 |
Fig. A.10 Ensemble-averaged [Cii] line centre intensities of different realisations of the interclump-ensemble. The circles show the ensemble-averaged intensities of ten different maps containing ten clumps and the squares give the values for ten different maps with 100 clumps as presented in Fig. A.9. The black line gives the mean value of the 20 maps, weighted by the respective number of grid points. For the maps with ten clumps the average is (24.4 ± 7.1) K and for the maps with 100 clumps it is (23.6 ± 1.0) K, where the stated error is the standard deviation. The red, dashed line gives the value derived by the probabilistic approach (for NnM = 1 = 100 clumps) for the same ensemble. The two results agree within 0.4% (intensities) and 0.8% (optical depths, not shown). |
| In the text | |
 |
Fig. A.11 Map showing the interclump medium of model 6j, with a surface density corresponding to the full line of sight of the model provided by 80 voxels. The colour scale shows 1−Exp(−τCII). |
| In the text | |
 |
Fig. D.1 Simulated cuts perpendicular to the Orion Bar, based on model Cyl. 5 (see Table D.1). Each colour scales gives the line-integrated intensity of the transitions indicated above the respective cut. |
| In the text | |
 |
Fig. D.2 Cut through the cylindrical Orion Bar model Cyl. 4. For each voxel the colour scale gives the [Cii] line intensity of dense clumps and interclump medium, at the line centre (at 11.3 km s-1). The illuminating star Θ1 Ori C is located at [0,22.3,30]. |
| In the text | |
 |
Fig. D.3 Same as Fig. D.2 but plotted for the outer line wing (at 8.3 km s-1). Effectively, only the interclump medium contributes at this velocity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.