| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 24 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201220040 | |
| Published online | 07 February 2013 | |
Online material
Appendix A: SZ map reconstruction methods
In this Appendix we discuss the different SZ map reconstruction methods applied to the Planck data in Sect. 4.1.
-
1.
MILCA (Hurier et al. 2010):The thermal SZ signal reconstruction is performed on thesix Planck all-sky maps from 100 GHzto 857 GHz. MILCA (Modified InternalLinear Combination Algorithm) is a component separa-tion approach aiming at extracting a chosen component(here the thermal SZ signal) from a multi-channel set ofinput maps. It is mainly based on the well known InternalLinear Combination approach (e.g., Eriksenet al. 2004), that searches for thelinear combination of the input maps that minimises the varianceof the final reconstructed map by imposing spectral constraints.In this paper, we applied MILCA using two constraints: preserva-tion of the thermal SZ signal (knowing the SZ spectral signature);and removal of the CMB contamination in the final SZ map (alsomaking use of the well known spectrum of the CMB). In addition,to compute the weights of the linear combination, we have usedthe extra degrees of freedom to minimise residuals from othercomponents (2 degrees) and from the noise (2 degrees). The noisecovariance matrix was estimated from the frequency error maps(see Sect. 2).
-
2.
NILC: Needlet ILC performs a linear combination of the observed maps which has minimum variance under the constraint of offering unit response to the component of interest (here the thermal SZ, whose frequency scaling is known). The weights of the ILC depend on the covariance between the various observations, and can be computed, for example, on domains of the observed pixels (pixel space) or angular scales (spherical harmonics). In the case of NILC, covariances (and hence weights for component separation) are computed independently in domains of a needlet decomposition (spherical wavelet frame). The needlet decomposition provides localisation of the ILC filters both in pixel and in multipole space, allowing us to deal with local contamination conditions varying both in position and in scale. NILC was developed to extract a CMB map from WMAP data (Delabrouille et al. 2009) and was also tested for SZ effect extraction in Leach et al. (2008). Multi-component extensions have been investigated by Remazeilles et al. (2011).
-
3.
GMCA (Bobin et al. 2008) is a blind source separation method developed for separating sources from instantaneous linear mixtures. The components are assumed to be sparsely represented (i.e., have a few significant samples in a specific basis) in a so-called sparse representation Ψ (typically wavelets). The assumption that the components have a sparse representation in the wavelet domain is equivalent to assuming that most components have a certain spatial regularity. These components and their spectral signatures are then recovered by minimising the number of significant coefficients in Ψ. Recently, L-GMCA has been further introduced to analyse the CMB data in a local and multi-scale manner (Bobin et al. 2008). More precisely, the multi-channel data are analysed in four frequency bands in spherical harmonics (i.e., wavelet bands). In each wavelet band, GMCA is applied locally on small patches with band-dependent sizes. In each band, the observations are analysed at the same band-dependent resolution. In Bobin et al. (2008), it was shown this local analysis approach enhances the separation quality. The spectral signatures of CMB, free-free and SZ are assumed to be known.
 |
Fig. A.1
Comparison between the SZ profile reconstruction from MILCA, NILC and GMCA The comparison is presented in the form of the averaged stacked radial profile from our 62 clusters of the ESZ-XMM sample, individually scaled respectively in the x- and y-axis directions according to R500 and Φ (Eq. (12)). The light-red shaded area marks the dispersion about the average stacked profile for the MILCA method. The points within each individual profile are correlated at about the ~ 20% level (see Sect. 4.2) and the plotted errors correspond to the square root of the diagonal elements of the covariance matrix of the profile. The solid black line (labelled in the legend as “Expected from PA10”) is the average stacked profile obtained from the expected SZ individual profiles drawn from the universal pressure profile by A10, parameterised according R500 and Y500 derived from the XMM-Newton data analysis presented in Planck Collaboration (2011f). The two dotted lines indicate the associated dispersion across the sample. The bottom panel shows the value of χ at each point of the observed profiles with respect to the expectations from the universal profile of A10. |
| Open with DEXTER | |
Appendix B: Validation on simulations
B.1. Profiles
We have validated our reconstruction of the SZ signal and profile computation methods with simulations. We used the Planck sky model (PSM, Delabrouille 2012) to simulate the whole sky as seen by Planck. The PSM includes most astrophysical components acting as foreground or background contamination with respect to the SZ signal (i.e., Galactic dust, free-free and synchrotron emission, extragalactic sources in the infrared and radio parts of the spectrum and CMB). For the instrumental noise we added to the simulation the all-sky error map drawn from the Planck jack-knife maps at each frequency (see Sect. 2), thus mimicking the noise properties of the actual survey (noise and systematic effects). For the SZ component, we built a full sky template for all the 1743 clusters from the MCXC meta-catalogue (Piffaretti et al. 2011), which includes all 62 clusters in our sample. Each cluster was modelled assuming spherical symmetry and a thermal pressure distribution following the universal profile from A10. We recall that the universal pressure profile provided by these authors is the best fit of a generalised NFW profile (Nagai et al. 2007a) to the median profile derived from the REXCESS pressure profile and the predictions from three different sets of numerical simulations (i.e., from Borgani et al. 2004; Nagai et al. 2007a,b; Piffaretti & Valdarnini 2008). In our case, the universal pressure profile is parametrised using the values of R500 and M500 from the MCXC, together with the M–YX scaling relation from Arnaud et al. (2007, 2010) to estimate Y500.
We processed the simulated Planck sky maps through each of our SZ map reconstruction methods. For our sample of 62 clusters, we extracted the patches and computed the individual profiles as described in Sect. 4.2. We stacked the simulated profiles for the three methods after renormalisation, making use of the aforementioned R500 and Y500 values from the MCXC prescription.
The resulting stacked profiles are displayed in Fig. A.1. All three tested methods agree remarkably well over the whole radial range. Taking into account the correlated errors of each profile, the χ2 over the radial range (0–10) × R500 for NILC and GMCA with respect to MILCA are 0.78 and 1.54, respectively. The reconstructed profiles are also in good agreement with the reconstructed stacked model. Accounting for the errors on the model and the correlated errors between points on the reconstructed profiles, the reduced χ2 for MILCA, NILC and GMCA with respect to the stacked model profile are 0.80, 0.66 and 1.03 within 3 × R500. This excellent agreement also translates into a small relative error below 15% in the same range of radii. Beyond R ~ 2 R500, the three reconstructed profiles drop slightly below the input model, even though they still agree within their dispersions and errors. This drop is caused by an intrinsic over-prescription of point sources in the PSM simulations with respect to real data. Despite our careful masking, the unidentified or unresolved extra sources in the PSM affect the power spectrum of the noise, increasing the background level and making it more difficult to detect the SZ signal further out in the simulations than in real data. We stress that this is an effect limited to our test simulations, and not relevant for the real data.
B.2. Consistency between Y500 measurements
 |
Fig. B.1
Comparison of Y500 values from the Planck cluster detection method (MMF3) against our best fit for each of our 62 clusters (from NILC in this case). In both cases the distribution of thermal pressure is assumed to follow a universal pressure profile (A10) for which the scaled radius R500 is fixed to the XMM-Newton best fit value. See Sect. 6.3 for details. |
| Open with DEXTER | |
To further validate the above, and as a consistency check with previous Planck results, we fitted each individual SZ profile with a projected, PSF-convolved universal pressure profile. We fixed R500 to the best fitting X-ray value from Planck Collaboration (2011f) and only fitted the normalisation, Y500. For a given profile, P, with an associated covariance matrix, C, and a model M, the χ2 statistic can be expressed as 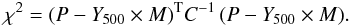 (B.1)The solution that minimises χ2, Y500, and its associated uncertainty, σY500, are analytic:
(B.1)The solution that minimises χ2, Y500, and its associated uncertainty, σY500, are analytic: 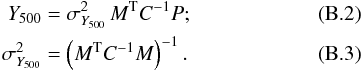 We compared the resulting value of Y500 to those obtained from the detection algorithms PwS and MMF3. Both detection algorithms were run under the same assumptions, i.e., universal pressure profile with the “non-standard” parameterisation and a fixed size (R500). The fluxes were derived from the Planck nominal mission survey maps. These fluxes are in agreement with those extracted from the Planck first year survey (Planck Collaboration 2011f). For instance, for MMF3, the average ratio is 1.04 ± 0.09, compatible within the average relative errors with the fluxes extracted from the nominal mission.
We compared the resulting value of Y500 to those obtained from the detection algorithms PwS and MMF3. Both detection algorithms were run under the same assumptions, i.e., universal pressure profile with the “non-standard” parameterisation and a fixed size (R500). The fluxes were derived from the Planck nominal mission survey maps. These fluxes are in agreement with those extracted from the Planck first year survey (Planck Collaboration 2011f). For instance, for MMF3, the average ratio is 1.04 ± 0.09, compatible within the average relative errors with the fluxes extracted from the nominal mission.
The relation between the integrated Comptonisation parameters derived from the SZ profiles and from the detection methods is displayed for MMF3 vs NILC fuxes in Fig. B.1. A BCES linear fit accounting for the errors in both x- and y-axis directions (Akritas & Bershady 1996) yields a best fitting slope and normalisation of 1.00 ± 0.02 and 0.01 ± 0.01 (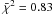 ), respectively. There is 4% dispersion about this relation. Furthermore, the median and associated deviation for the one-to-one ratios of PwS and MMF3 fluxes compared to the fitted NILC profile values are 1.03 ± 0.11 and 0.98 ± 0.08, respectively. The median ratios for the errors are 1.10 ± 0.36 are 1.64 ± 0.34. The errors associated with our best fit values are in very good agreement with those from PwS; however, they are smaller than those derived from the MMF3 method. This difference with MMF3 might be explained by the different treatment of the noise. Whilst we estimated the noise from the surroundings of the clusters, defined according to the scaled radius of each target, and PwS also used a local computation of the noise, the MMF3 algorithm used a larger area to characterise the noise properties. Our tests against the PwS and MMF3 fluxes emphasise our grasp on the characterisation of the local noise for each target, and further assess the reliability of our estimates of the statistical errors in our stacked profiles.
), respectively. There is 4% dispersion about this relation. Furthermore, the median and associated deviation for the one-to-one ratios of PwS and MMF3 fluxes compared to the fitted NILC profile values are 1.03 ± 0.11 and 0.98 ± 0.08, respectively. The median ratios for the errors are 1.10 ± 0.36 are 1.64 ± 0.34. The errors associated with our best fit values are in very good agreement with those from PwS; however, they are smaller than those derived from the MMF3 method. This difference with MMF3 might be explained by the different treatment of the noise. Whilst we estimated the noise from the surroundings of the clusters, defined according to the scaled radius of each target, and PwS also used a local computation of the noise, the MMF3 algorithm used a larger area to characterise the noise properties. Our tests against the PwS and MMF3 fluxes emphasise our grasp on the characterisation of the local noise for each target, and further assess the reliability of our estimates of the statistical errors in our stacked profiles.
Such agreement between the fluxes derived from our fit over the cluster profiles and those from the detection algorithm, strongly confirms the reliability of our SZ flux estimate and further strengthen the overall result stated in the Planck collaboration early papers that the SZ and the X-ray fluxes within R500 are fully consistent (Planck Collaboration 2011c,d,e,f).
Appendix C: Pressure profiles of individual clusters
In this appendix we present the individual pressure profiles obtained from Planck and XMM-Newton data for each of the 62 clusters in our sample (see Fig. C.1). We show the agreement with the universal pressure profile (A10) and provide the best fitting model for each cluster to the GNFW profile in Table C.1. The following hard limit priors were adopted during the fitting procedure: 0 < P0 < 100; 0 < c500 < 10; 0 < α < 10; and 0 < β < 15.
 |
Fig. C.1
Measured individual pressure profiles for the ESZ-XMM sample using the Planck and XMM-Newton data. As for the stacked pressure profile, the maximum difference point-to-point between the three SZ reconstruction methods have been taken into account in the Planck measurement error budget (Sect. 6.3). The best fit model on each individual profile is shown as a blue solid line. The black and green solid curves mark the best fit model to the stacked SZ+X-ray pressure profile (Sect. 6.2) and the A10 best fit model, respectively. |
| Open with DEXTER | |
 |
Fig. C.1
continued. |
| Open with DEXTER | |
 |
Fig. C.1
continued. |
| Open with DEXTER | |
 |
Fig. C.1
continued. |
| Open with DEXTER | |
Best fit parameters for a generalised NFW pressure profile for individual clusters.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


