© The Authors 2025

1 Introduction

Hydrogen, the most abundant element in the universe, forms the fundamental building blocks of countless astrophysical environments. Among hydrogen-related molecular systems, the hydrogen molecular ion 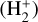$\left({\text{H}}_2^{+}\right)$, as the simplest ionic molecule comprising two protons and a single electron, is ubiquitously present within interstellar clouds and planetary atmospheres (Coppola et al. 2013). In these environments, the pervasive presence of intense radiation, particularly ultraviolet photons, frequently induces dissociation of 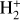${\text{H}}_2^{+}$ ions. Consequently, an accurate and comprehensive understanding of the photodissociation mechanisms of 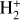${\text{H}}_2^{+}$ is essential to astrophysics, significantly influencing theoretical modeling of interstellar chemistry and planetary atmospheric dynamics.

Historically, the photodissociation of 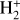${\text{H}}_2^{+}$ was first systematically investigated by Bates et al. (Bates 1952) in 1952 using a semiempirical approach aimed at elucidating stellar atmospheric opacity. Driven by advancements in both experimental nuclear fusion techniques and observational astrophysics, sub-stantial research interest subsequently emerged regarding hydrogenic molecular ions (Dehmelt & Jefferts 1962; Dunn 1968; Sharp 1970; Von Busch & Dunn 1972). Moreover, contemporary experimental capabilities employing strong laser fields or ultrashort laser pulses have revealed novel photodissociation phenomena, extending beyond traditional resonant dissociation pathways (Charron et al. 1993; Paul et al. 2010; Pan 2023). Collectively, these developments have considerably broadened our understanding of molecular dissociation dynamics, underlining the necessity for accurate theoretical frameworks.

Although structurally simplistic, 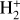${\text{H}}_2^{+}$ exhibits a remarkably complex spectrum of electronic states and dissociation channels. Consequently, accurate theoretical calculations and precise experimental determination of its photodissociation cross sections remain active and critical research domains. Notably, earlier investigations have frequently neglected the role of shape resonances, transient quasi-bound states that markedly amplify cross-section magnitudes and profoundly modulate dissociation dynamics (Stancil 1994; Heays et al. 2017). However, accumulating evidence suggests that these resonances substantially modify the resulting photodissociation cross sections, thereby impacting local astrophysical chemical evolution and material distributions (Beyer 2016; McCurdy & Mowrey 1982). Given this context, it is paramount to incorporate shape resonances explicitly and precisely in photodissociation studies.

Addressing this critical gap, the current study investigates the photodissociation process of 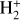${\text{H}}_2^{+}$ while explicitly considering the influence of shape resonances. Through a comprehensive comparison with prior theoretical frameworks presented by Stancil and Heays, we refine and update existing cross-sectional data, and we elucidate the role and magnitude of shape resonance effects. Ultimately, this work provides enhanced theoretical predictions, which facilitate more accurate astrophysical interpretations and significantly advance the fidelity of spectral modeling and astronomical observations.

Section 2 briefly outlines the theoretical framework that underpins photodissociation processes. Section 3 presents and discusses the computational results for electronic structure calculations and LTE photodissociation cross sections. Finally, Section 4 summarizes the key findings and discusses implications for future research. Atomic units are consistently employed throughout this paper unless otherwise noted.

2 Theory and calculations

2.1 Photodissociation cross section

In this section, we provide an in-depth theoretical treatment of partial photodissociation cross sections, and integrate insights from previous foundational studies (Miyake et al. 2011; Pattillo et al. 2018; Barinovs & Van Hemert 2004; McMillan et al. 2016; Yang et al. 2020; Bai et al. 2021). The transition cross section from an initial bound state, i, to a continuum final state, f, is formulated as $${\sigma }^{fi}\left(E_{\text{ph}}\right)=2{\pi }^2\alpha \frac{\text{d}{ℱ}^{fi}}{\text{d}{E}_{\text{ph}}},$$(1) where α = e²/(ℏc) is the fine-structure constant, and E_ph denotes photon energy. The generalized oscillator strength density, explicitly incorporating rotational state degeneracies, is represented by $$\frac{\text{d}{ℱ}^{fi}}{\text{d}{E}_{\text{ph}}}=\frac{2}{3}{E}_{\text{ph}}\left(\frac{2-{\delta }_{0,{\text{Λ}}^{\prime }+{\text{Λ}}^{\prime \prime }}}{2-{\delta }_{0,{\text{Λ}}^{\prime \prime }}}\right)\underset{J^{\prime }}{{{\displaystyle \sum }}^{\text{}}}\frac{S_{J^{\prime }}\left(J^{\prime \prime }\right)}{\mathcal{W}\left(J^{\prime \prime }\right)}{\left|D^{fi}\left(J^{\prime },J^{\prime \prime }\right)\right|}^2,$$(2) with Λ′ and Λ″ representing electronic orbital angular momentum projections along the internuclear axis for final and initial electronic states, respectively. The transition dipole moment (TDM) matrix element, $$D^{fi}\left(J^{\prime },J^{\prime \prime }\right)=\langle {\chi }_{k^{\prime }{J}^{\prime }}^f(R)|D^{fi}(R)|{\chi }_{{\nu }^{\prime \prime }{J}^{\prime \prime }}^i(R)\rangle ,$$(3) characterizes the rovibrational transition between initial bound state, ν″J″, and final continuum state, k′J′, involving integration over internuclear distance, R. Here, D^fi(R) denotes the electronic TDM, and the rovibrational wavefunctions ${\chi }_{{\nu }^{\prime \prime }{J}^{\prime \prime }}^i(R)$ and ${\chi }_{k^{\prime }{J}^{\prime }}^f(R)$ describe initial and continuum states, respectively. The rotational line strengths were computed using Hönl-London factors S _J′ (J″) appropriate for doublet-doublet transitions, following the formalism of Kovács (Kovacs 1969). The ²Σ ← ²Σ electronic transition is $$S_{J^{\prime }}\left(J^{\prime \prime }\right)=\{\begin{array}{cc}2J^{\prime \prime }-\frac{1}{2J^{\prime \prime }}& \text{for P}-\text{branch},\\ 2\left(J^{\prime \prime }+1\right)-\frac{1}{2\left(J^{\prime \prime }+1\right)}& \text{for R}-\text{branch},\end{array}$$(4) and the corresponding total Hönl-London weight is given by $$\mathcal{W}\left(J^{\prime \prime }\right)=2\left(2J^{\prime \prime }+1\right)-\frac{2J^{\prime \prime }+1}{2J^{\prime \prime }\left(J^{\prime \prime }+1\right)}.$$(5)

For the ²Π ← ²Σ electronic transition, the Hönl-London factors are $$S_{J^{\prime }}\left(J^{\prime \prime }\right)=\{\begin{array}{cc}{J}^{\prime \prime }-1-\frac{1}{4J^{\prime \prime }}& \text{for P}-\text{branch,}\\ \begin{array}{l}2J^{\prime \prime }+1-\frac{J^{\prime \prime }+1/2}{J^{\prime \prime }\left(J^{\prime \prime }+1\right)}\\ J^{\prime \prime }+2-\frac{1}{4\left(J^{\prime \prime }+1\right)}\end{array}& \begin{array}{l}\text{for Q}-\text{branch,}\\ \text{for R}-\text{branch}\end{array}\end{array}$$(6) with a corresponding total Hönl-London weight of $$\mathcal{W}\left(J^{\prime \prime }\right)=2\left(2J^{\prime \prime }+1\right)-\frac{3\left(2J^{\prime \prime }+1\right)}{4J^{\prime \prime }\left(J^{\prime \prime }+1\right)}.$$(7)

These expressions properly incorporate spin-orbit coupling and allow for labeling of transitions by P₁/P₂, Q₁/Q₂, and R₁/R₂ branches. At the limit of unresolved spin components, the line strengths were summed accordingly. Compared to the simplified singlet-based expressions used in earlier work (Stancil 1994; Weck et al. 2003), the corrected Hönl-London factors lead to only slight modifications in the cross-section amplitudes, while the overall resonance structure remains virtually indistinguishable by visual inspection.

Notably, cross sections computed in atomic units retain the unit centimeter² when the factor $\frac{4{\pi }^2\alpha }{3}$ is substituted by 2.689 × 10⁻¹⁸. Therefore, the partial photodissociation cross section for transitions from a specific initial rovibrational state ν″J″ is succinctly expressed as (McMillan et al. 2016; Miyake et al. 2011; Pattillo et al. 2018; Bates & Bederson 1988) $$\begin{array}{c}{\sigma }_{{\nu }^{\prime \prime }{J}^{\prime \prime }}\left(E_{\text{ph}}\right)=2.689\times {10}^{-18}{E}_{\text{ph}}\left(\frac{2-{\delta }_{0,{\text{Λ}}^{\prime }+{\text{Λ}}^{\prime \prime }}}{2-{\delta }_{0,{\text{Λ}}^{\prime \prime }}}\right)\\ \times \underset{J^{\prime }}{{{\displaystyle \sum }}^{\text{}}}\frac{S_{J^{\prime }}\left(J^{\prime \prime }\right)}{\mathcal{W}\left(J^{\prime \prime }\right)}{\left|D^{fi}\left(J^{\prime },J^{\prime \prime }\right)\right|}^2{\text{cm}}^2.\end{array}$$(8)

2.2 LTE cross section

Under the assumption of LTE, the rovibrational level populations within the electronic ground state follow the Boltzmann distribution, which results in a temperature-dependent weighting of each state’s contribution to the total photodissociation cross section. Consequently, the aggregate cross section for photodissociation at a given wavelength, λ, and temperature, T, is expressed as a sum over all populated rovibrational states ν″J″, explicitly incorporating their relative thermal populations (Argyros 1974): $$\sigma (\lambda ,\text{T})=\underset{{\nu }^{\prime \prime }{J}^{\prime \prime }}{{{\displaystyle \sum }}^{\text{}}}{\omega }_{{\nu }^{\prime \prime }{J}^{\prime \prime }}{\sigma }_{{\nu }^{\prime \prime }{J}^{\prime \prime }}(\lambda ),$$(9) where the thermal weighting factor ω_{ν″ J″} quantifies the equilibrium fractional population of each rovibrational state and is given by $${\omega }_{{\nu }^{\prime \prime }{J}^{\prime \prime }}=\frac{\left(2J^{\prime \prime }+1\right)\exp \left(-\frac{E_{{\nu }^{\prime \prime }{J}^{\prime \prime }}}{k_{\text{B}}\text{T}}\right)}{Q(\text{T})}.$$(10)

The normalization factor in Eq. (10), known as the rovibrational partition function Q(T), ensures the proper normalization of the distribution across all states and is defined as $$Q(\text{T})=\underset{{\nu }^{\prime \prime }{J}^{\prime \prime }}{{{\displaystyle \sum }}^{\text{}}}\left(2J^{\prime \prime }+1\right)\exp \left(-\frac{E_{{\nu }^{\prime \prime }{J}^{\prime \prime }}}{k_{\text{B}}\text{T}}\right).$$(11)

In these equations, E_{ν″ J″} denotes the rovibrational energy of the bound state ν″J″ relative to the dissociation limit, k_B represents the Boltzmann constant, and the summation spans all energetically accessible rovibrational levels. Therefore, a precise evaluation of σ(λ, T) critically depends upon accurate determination of both the energy levels and the individual partial cross sections σ_{ν″ J″} (λ), enabling reliable astrophysical modeling of photodissociation processes under thermalized astrophysical conditions.

Fig. 1 PECs and TDMs for ${\text{H}}_2^{+}$. Panels a and b depict the PECs for the ${\text{H}}_2^{+}$. Specifically, panel a illustrates the ground state $1^2{\text{Σg}}_{+}^{}$ along with the ten energetically lowest excited states of ${}^2{\text{Σu}}_{+}^{}$ symmetry, represented by solid lines. In panel b, the PECs for the ground state $1^2{\text{Σg}}_{+}^{}$ and six lowest excited states of 2Πu symmetry are illustrated by dashed lines. Panels c and d present the corresponding TDMs describing transitions from the ground state $1^2{\text{Σg}}_{+}^{}$ to the excited electronic states with ${}^2{\text{Σu}}_{+}^{}$ and 2Πu symmetries, respectively, again indicated by solid and dashed lines.

3 Results and discussion

3.1 Potential energy curves and transition dipole moments

Figures 1a–b illustrate the potential energy curves (PECs) computed for the ${\text{H}}_2^{+}$ system. Correspondingly, Figs. 1c–d display the TDMs, which characterize transitions from the electronic ground state $1^2{\text{Σg}}_{+}^{}$ to the excited electronic states ${}^2{\text{Σu}}_{+}^{}$ and ²Π_u, plotted as functions of the internuclear distance R. The PECs utilized in this work stem from high-level quantum-chemical calculations reported in our earlier study (Wang et al. 2024). Building on that foundation, the present investigation contributes the TDM matrix elements as a critical component of the extended analysis. These calculations employed the multireference single- and double-excitation configuration interaction (MRDCI) methodology (Buenker & Phillips 1985), a sophisticated theoretical framework developed by Buenker and collaborators that robustly captures electron correlation effects that are essential for accurately describing electronic state properties.

Examination of the calculated PECs reveals that most excited electronic states of the ${\text{H}}_2^{+}$ ion exhibit purely repulsive characteristics, however, such as 1²Π_u, possess notably shallow potential wells. This structural peculiarity strongly influences the dissociative dynamics initiated upon photoexcitation. Furthermore, as indicated by Eq. (8), the photodissociation cross sections are dominantly governed by the squared magnitude of the TDMs. Given the doublet nature of the ground electronic state, the present investigation is accordingly constrained to transitions exclusively between electronic states of doublet multiplicity, thereby ensuring theoretical consistency and precision in modeling the photodissociation processes.

Fig. 2 Partial photodissociation cross sections of ${\text{H}}_2^{+}$. Panels a and c show cross sections for the transitions $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ and $1^2{\text{Σu}}_{+}^{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ from initial rovibrational levels with rotational quantum number J″ = 0. Panels b and d correspond to transitions from vibrational ground state levels with quantum number ν″ = 0.

3.2 Partial photodissociation cross sections

Considering the transitions $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ and $1^2{\text{Σu}}_{+}^{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ as illustrative examples, Fig. 2 presents detailed partial photodissociation cross sections originating from selected initial rovibrational levels of the ground electronic state to the specified excited states. The notation (ν″, J″, J′) precisely denotes a transition from an initial rovibrational state characterized by vibrational quantum number ν″ and rotational quantum number J″ to a final continuum state distinguished by rotational quantum number J′. Correspondingly, (ν″, J″) represents the aggregate photodissociation cross section, summing over all allowed final rotational states J′ and explicitly incorporating the appropriate Hönl-London factors. Specifically, panels a and c of Fig. 2 illustrate transitions that originate from initial rovibrational states with rotational quantum number J″ = 0, whereas panels b and d illustrate transitions that originate from initial vibrational states with vibrational quantum number ν″ = 0. These photodissociation cross sections were computed using a modified version of the PyDiatomic computational package (Gibson 2024), which is available for download on GitHub at https://github.com/stggh/PyDiatomic. Fig. 2a reveals distinct resonance structures proximate to the Lyman α wavelength within the cross sections that correspond to the $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ electronic transitions. To explore these resonance features in detail, a detailed depiction of shape resonance, exemplified by the $1^2{\text{Πu}}_{}(J^{\prime }=26)\leftarrow 1^2{\text{Σg}}_{+}^{}\left(J^{\prime \prime }=25\right)$ photodissociation cross section, is illustrated in Fig. 3.

Figure 3a displays the PECs for both the ground and the excited 1²Π_u states, including the rotational modification depicted by dashed lines. The potential well associated with the 1²Π_u excited state is notably shallow, with a depth typically not exceeding approximately 0.13 eV. Incorporation of rotational effects introduces a pronounced centrifugal potential barrier, which emerges predominantly at larger internuclear distances due to the centrifugal term $\frac{ħ{\hslash }^{2}J(J+1)}{2\mu R^2}.$. This term causes a significant enhancement in the effective potential V_eff(R, J), thereby forming a barrier conducive to shape resonance phenomena. Fig. 3b illustrates the photodissociation cross section for the $1^2{\text{Πu}}_{}\left(J^{\prime }=26\right)\leftarrow 1^2{\text{Σg}}_{+}^{}\left(J^{\prime \prime }=25\right)$ transition. It is evident that the presence of a potential barrier results in three distinct shape resonance peaks for this transition. These resonances underscore the significant influence of rotational excitation on the photodissociation dynamics and spectral characteristics. Note that shape resonances were identified by analyzing the energy-dependent phase shifts extracted from the continuum wave functions. Rapid variations in the phase shift indicate the presence of resonant states, which manifest as sharp peaks in the photodissociation cross sections. These features are especially prominent for high rotational quantum number levels of the 1²Π_u state near the Lyman α region. The use of a fine energy grid (0.0001 eV) and accurate MRDCI PECs allows these resonance structures to be fully resolved. The photodissociation cross sections for the majority of rovibrational states (with vibrational quantum numbers ν″≤ 18 and rotational quantum numbers J″≤ 30) have been systematically computed over photon wavelengths ranging from 25 nm up to the photodissociation threshold.

Fig. 3 PECs and photodissociation cross sections of ${\text{H}}_2^{+}$ involving $1^2{\text{Σg}}_{+}^{}$ and 12Πu states. Panel a: PECs of the ground state $1^2{\text{Σg}}_{+}^{}$ and excited state 12Πu, shown as solid gray and red lines, respectively. The corresponding rotationally excited states are indicated by dashed lines in matching colors. Panel b: photodissociation cross sections from the rotationally excited states, represented by the solid green line, which clearly exhibit three pronounced shape resonance peaks.

3.3 LTE cross sections

For the ${\text{H}}_2^{+}$ molecular ion, Figs. 4a–p illustrate the comprehensive photodissociation cross sections that correspond to electronic transitions from the ground state $1^2{\text{Σg}}_{+}^{}$ to the six energetically lowest excited states of ²Π_u symmetry and the ten lowest excited states of ${}^2{\text{Σu}}_{+}^{}$ symmetry under LTE conditions. These cross sections are systematically presented as functions of photon wavelength at various thermodynamic temperatures, explicitly including 0, 1000, 2000, 3150, 5040, and 12 600 K. Such extensive temperature coverage facilitates a detailed exploration of thermal effects on the photodissociation dynamics. Notably, as the temperature rises, significant deviations from the cross sections at absolute zero become evident, which underscores the pronounced role of thermally populated rovibrational states in modulating photodissociation behavior.

A detailed inspection of the computed photodissociation cross sections across distinct excited electronic states highlights the dominant role of the partial cross section corresponding to the $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ transition, particularly at longer wavelengths near the Lyman α spectral region. Additionally, resonance structures are also observed in the transition from the ground state to the excited state 5²Π_u. These resonance peaks reflect the existence of a shallow potential well in the 5²Π_u state, which, although present, is notably weaker than the well observed in the 1²Π_u state. The spectral resolution employed in the current computations is precisely set at 0.0001 eV, a choice that determines the accuracy and clarity with which these resonant phenomena and subtle spectral features are represented.

To elucidate the origin of prominent spectral features, Fig. 5a provides the total cross sections partitioned by final excited states. Notably, this allows intuitive visualization, and highlights that the resonance peaks adjacent to the Lyman α line predominantly arise from the $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ transition. Conversely, at longer photon wavelengths, the primary contributions to the total photodissociation cross section originate from the $1^2{\text{Σu}}_{+}^{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ transition. Fig. 5b illustrates the total photodissociation cross sections for the ${\text{H}}_2^{+}$ molecular ion, which are derived by summing contributions across all permissible rovibrational transitions from the ground electronic state to the excited electronic states. These cross sections are systematically presented at various thermodynamic temperatures, explicitly including 0, 1000, 2000, 3150, 5040, and 12 600 K. Comprehensive datasets that correspond to the LTE cross sections depicted in Fig. 5b are provided in the supplementary material accompanying this work.

Additionally, this study includes a comparative analysis of the total photodissociation cross sections obtained here with previously published results. In particular, Fig. 6a presents a direct comparison at 0 K between our calculated cross sections and those reported by Heays (Heays et al. 2017), which demonstrate excellent agreement and thereby confirm the computational accuracy of our methodology. Similarly, comparison with the data provided by Stancil (Stancil 1994) in Figs. 6b and 6c further underscores the pronounced impact of shape resonances near the Lyman α region on the overall cross-sectional profile. Differences observed in the photodissociation cross sections at shorter wavelengths at elevated thermodynamic temperatures (specifically, 3150 and 12 600 K) arise primarily from the incorporation of additional excited electronic states in our computations compared to earlier studies. Notably, weak shape resonance features become discernible near the Lyman α line around 3150 K and become increasingly prominent at higher temperatures up to 12 600 K, which reflects the substantial influence of thermal population redistribution on photodissociation dynamics.

Fig. 4 LTE photodissociation cross sections of ${\text{H}}_2^{+}$ at selected temperatures. Panels a–p display the LTE cross sections that correspond to transitions from the ground electronic state $1^2{\text{Σg}}_{+}^{}$ to the six lowest 2Πu states and the ten lowest ${}^2{\text{Σu}}_{+}^{}$ states of the ${\text{H}}_2^{+}$ molecular ion at selected thermodynamic temperatures: 0, 1000, 2000, 3150, 5040, and 12 600 K. These temperatures have been purposefully chosen to enable direct comparisons with previous theoretical and experimental studies. The cross sections presented here are calculated with a spectral resolution of 0.0001 eV; consequently, resonance features narrower than this resolution are not explicitly resolved.

Fig. 5 Photodissociation cross sections of ${\text{H}}_2^{+}$ at different temperatures. Panel a illustrates the photodissociation cross sections of ${\text{H}}_2^{+}$ from its ground state to various electronically excited states, along with their cumulative sum at a thermodynamic temperature of 12 600 K. Transitions to the 2Πu and ${}^2{\text{Σu}}_{+}^{}$ electronic states are distinctly represented by solid and dashed lines, respectively. Panel b presents the total photodissociation cross sections of the ${\text{H}}_2^{+}$ system computed at selected thermodynamic temperatures. An inset is included to magnify the spectral region surrounding the Lyman α line, clearly highlighting shape resonance features indicated by shaded light gray areas. The full dataset of LTE cross sections is available in the supplementary material.

Fig. 6 Comparison of present and previous photodissociation cross sections. Panels a–c present a comparative analysis between the present computational results (solid lines) and previously published calculations of Heays et al. (2017) and Stancil (1994) (dashed lines).

4 Conclusions

In this study, we investigated partial photodissociation cross sections for transitions that originate from the electronic ground state $1^2{\text{Σg}}_{+}^{}$ to six excited states of ²Π_u symmetry and ten excited states of ${}^2{\text{Σu}}_{+}^{}$ symmetry. By examining thermodynamic temperatures of 0, 1000, 2000, 3150, 5040, and 12 600 K, and assuming a Boltzmann distribution for initial rovibrational populations, we observed pronounced shape resonances near the Lyman α line, notably in the photodissociation cross sections that correspond to the $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ transitions. By employing precise theoretical calculations, the current work significantly enriches existing datasets related to shape resonance-mediated photodissociation processes in the ${\text{H}}_2^{+}$ molecular ion. These refined crosssectional data provide essential theoretical benchmarks for astronomical spectroscopic observations and laboratory photodissociation experiments, while simultaneously offering deeper insight into the molecular photodissociation mechanisms operative in the early universe and ultraviolet-irradiated interstellar environments.

Data availability

All the LTE cross sections depicted in Fig. 5b are published in https://doi.org/10.5281/zenodo.15679287

Acknowledgements

This work was supported by grants from the National Natural Science Foundation of China (Grant No. 12304279, No. 12374238 and No. 12204288) and Doctoral scientific research foundation of Henan Normal University (Grant No. 2023066).

References

All Figures

Fig. 1 PECs and TDMs for ${\text{H}}_2^{+}$. Panels a and b depict the PECs for the ${\text{H}}_2^{+}$. Specifically, panel a illustrates the ground state $1^2{\text{Σg}}_{+}^{}$ along with the ten energetically lowest excited states of ${}^2{\text{Σu}}_{+}^{}$ symmetry, represented by solid lines. In panel b, the PECs for the ground state $1^2{\text{Σg}}_{+}^{}$ and six lowest excited states of 2Πu symmetry are illustrated by dashed lines. Panels c and d present the corresponding TDMs describing transitions from the ground state $1^2{\text{Σg}}_{+}^{}$ to the excited electronic states with ${}^2{\text{Σu}}_{+}^{}$ and 2Πu symmetries, respectively, again indicated by solid and dashed lines.

In the text

Fig. 2 Partial photodissociation cross sections of ${\text{H}}_2^{+}$. Panels a and c show cross sections for the transitions $1^2{\text{Πu}}_{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ and $1^2{\text{Σu}}_{+}^{}\leftarrow 1^2{\text{Σg}}_{+}^{}$ from initial rovibrational levels with rotational quantum number J″ = 0. Panels b and d correspond to transitions from vibrational ground state levels with quantum number ν″ = 0.

In the text

Fig. 3 PECs and photodissociation cross sections of ${\text{H}}_2^{+}$ involving $1^2{\text{Σg}}_{+}^{}$ and 12Πu states. Panel a: PECs of the ground state $1^2{\text{Σg}}_{+}^{}$ and excited state 12Πu, shown as solid gray and red lines, respectively. The corresponding rotationally excited states are indicated by dashed lines in matching colors. Panel b: photodissociation cross sections from the rotationally excited states, represented by the solid green line, which clearly exhibit three pronounced shape resonance peaks.

In the text

Fig. 4 LTE photodissociation cross sections of ${\text{H}}_2^{+}$ at selected temperatures. Panels a–p display the LTE cross sections that correspond to transitions from the ground electronic state $1^2{\text{Σg}}_{+}^{}$ to the six lowest 2Πu states and the ten lowest ${}^2{\text{Σu}}_{+}^{}$ states of the ${\text{H}}_2^{+}$ molecular ion at selected thermodynamic temperatures: 0, 1000, 2000, 3150, 5040, and 12 600 K. These temperatures have been purposefully chosen to enable direct comparisons with previous theoretical and experimental studies. The cross sections presented here are calculated with a spectral resolution of 0.0001 eV; consequently, resonance features narrower than this resolution are not explicitly resolved.

In the text

Fig. 5 Photodissociation cross sections of ${\text{H}}_2^{+}$ at different temperatures. Panel a illustrates the photodissociation cross sections of ${\text{H}}_2^{+}$ from its ground state to various electronically excited states, along with their cumulative sum at a thermodynamic temperature of 12 600 K. Transitions to the 2Πu and ${}^2{\text{Σu}}_{+}^{}$ electronic states are distinctly represented by solid and dashed lines, respectively. Panel b presents the total photodissociation cross sections of the ${\text{H}}_2^{+}$ system computed at selected thermodynamic temperatures. An inset is included to magnify the spectral region surrounding the Lyman α line, clearly highlighting shape resonance features indicated by shaded light gray areas. The full dataset of LTE cross sections is available in the supplementary material.

In the text

	Fig. 6 Comparison of present and previous photodissociation cross sections. Panels a–c present a comparative analysis between the present computational results (solid lines) and previously published calculations of Heays et al. (2017) and Stancil (1994) (dashed lines).
In the text