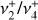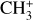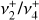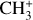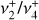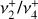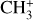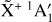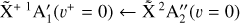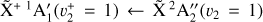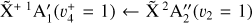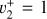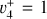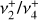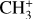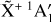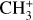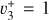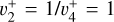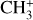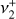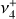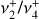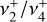EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 680 (December 2023) A&A, 680 (2023) A19 Full HTML
Open Access
Issue
A&A
Volume 680, December 2023
Article Number A19
Number of page(s) 14
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202347765
Published online 05 December 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The methyl cation 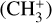has long been considered a pivotal astrochemical species. Because this simple carbocation reacts very slowly with molecular hydrogen, it forms an important intermediate reservoir through which atoms and small diatomic and triatomic species (e.g., H, H2, 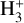, CH+, and 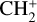) evolve into many other complex organic molecules (Dalgarno 1985; Smith 1992; Wakelam et al. 2010; Gerin et al. 2016; Cernuto et al. 2017; Chabot et al. 2020). Despite its molecular simplicity, 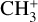has long remained elusive in the interstellar medium. The molecule has a trigonal planar geometry, so the centro-symmetric parent isotopologue lacks a permanent dipole moment and cannot be observed by radio astronomy. A low temperature component (~50 K) was searched for toward Orion IRc2 through the singly deuterated isotopologue, which possesses a small dipole moment (0.3 D), but its detection was tentative, with a maximum abundance relative to molecular hydrogen of 1.0 × 10−10 (Roueff et al. 2013).

Using the Mid-InfraRed Instrument (MIRI) on board the James Webb Space Telescope (JWST), Berné et al. (2023b) very recently achieved the first conclusive detection of 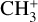in the interstellar medium. The species was observed in emission toward the protoplanetary disk d203-506 in the Orion bar at wavelengths around 7 μm (~1400 cm−1), which correspond to the out-of-plane 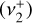and degenerate in-plane 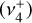bending modes of the cation1. Interestingly, in this strongly UV-irradiated medium (Berné et al. 2023a), 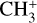shows high-temperature components with resolved rotational structure whose individual quantum number assignments defied analysis at the time of publication owing to strong Coriolis interactions between 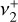and 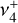(Crofton et al. 1988; Kraemer & Špirko 1991). While the detection of 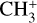is itself robust, accurate knowledge of its rovibrational energy levels is mandatory for deriving a precise excitation temperature and column density from the astronomical data. A deeper theoretical and experimental investigation of the Coriolis interactions between the 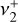and 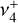bands is thus called for to address this problem and spectroscopically assign the observed transitions.

The vibrational structure of 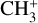and its deuterated isotopologues has been the subject of a number of prior theoretical studies (Botschwina et al. 1983; Kraemer & Špirko 1991; Yu & Sears 2002; Dopfer & Luckhaus 2002; Keçeli et al. 2009; Cunha de Miranda et al. 2010; Thomas et al. 2012; Ragni et al. 2016; Asvany et al. 2018; Nyman & Yu 2019; Meisner et al. 2019; Simmons et al. 2019). Potential energy surfaces (PESs) based on coupled-cluster calculations including single, double, and perturbative triple excitations (CCSD(T)) with large one-electron basis sets have reproduced experimental vibrational frequencies to within a few cm−1 (Meisner et al. 2019; Asvany et al. 2018), demonstrating that its simple closed-shell electronic structure is sufficiently well described by single-reference coupled-cluster theory. While the pure vibrational structure is theoretically well understood, the rovibrational structure of the 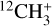parent isotopologue, particularly that of the Coriolis-coupled 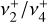band system (Crofton et al. 1988; Jagod et al. 1994), has received less attention. The 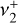and 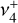normal modes have vibrational energies that differ by only ~ 10 cm−1. Because this energy difference is comparable to the rotational constants (B ≈ 2C ≈ 9.4 cm−1), the rotational fine structure of the dyad is severely perturbed by Coriolis interactions and is highly sensitive to the vibrational energy splitting. Kraemer & Špirko (1991) calculated deperturbed rotational constants and interaction parameters for these states, and Pracna et al. (1993) showed that their infrared (IR) line strengths are highly sensitive to Coriolis interaction-mediated intensity borrowing effects, but this problem appears not to have been revisited with modern electronic structure and nuclear motion methods. In addition to a high-quality PES, it is essential to account for both pure vibrational and rovibrational Coriolis couplings (Cunha de Miranda et al. 2010) to accurately describe these perturbations.

The IR spectrum of 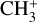has also received experimental attention. A low-temperature vibrational spectrum of the 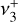band (degenerate asymmetric C–H stretch, around 3 μm) and the 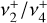dyad was recorded by infrared photodissociation of the He-tagged 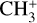ion in a cryogenic ion trap (Asvany et al. 2018). High-resolution IR investigations of the rovibrational structure of the 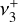band and several hot bands (Crofton et al. 1985, 1988; Jagod et al. 1994) confirmed the planar D3h structure that was first assessed experimentally by Herzberg (1961, 1966). The 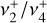rovibrational dyad was also recorded at high resolution, although no spectroscopic assignments were reported (Joo 1996).

Photoionization of the methyl radical has previously been studied experimentally using absorption spectroscopy (Herzberg 1961), mass spectrometry (Elder et al. 1962; Chupka & Lifshitz 1968; Litorja & Ruscic 1997; Aguirre & Pratt 2005; Taatjes et al. 2008; Gans et al. 2010; Loison 2010), and various kinds of photoelectron spectroscopies (Golob et al. 1972; Koenig et al. 1975, 1976; Dyke et al. 1976; Blush et al. 1993; Wiedmann et al. 1994; Bacon & Pratt 1999; Liu et al. 2001; Schulenburg et al. 2006; Cunha de Miranda et al. 2010). Among these works, the only rotationally resolved measurements were the photoelectron spectra of the 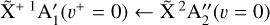origin band by Blush et al. (1993), Wiedmann et al. (1994), and Schulenburg et al. (2006). Liu et al. (2001) recorded an ion pair imaging spectrum that exhibited partially resolved rotational structure from which tentative spectroscopic assignments were proposed for the 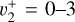, , 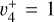and 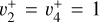overtones and combination levels. To our knowledge, no further experimental data concerning the rotational structure of the 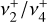dyad of the 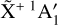electronic ground state of 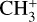– beyond those cited in this introduction – are available in the literature, and no reliable spectroscopic assignments for transitions involving these states have been proposed.

In the following, we present a joint theoretical and experimental investigation of the rovibrational structure of 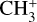. The ab initio calculations carried out in this work combine accurate potential energy and dipole moment surfaces built from highly correlated electronic structure calculations with numerically exact solutions to the nuclear motion Schrödinger equation. As we show below, this approach provides quantitative predictions of the rovibrational parameters needed to assign and fit the unusual quasi-spherical-top rotational structure observed in the high-resolution IR and photoelectron spectra of the 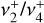dyad. Indeed, these calculations have enabled the full spectroscopic assignments of the astronomical 7 μm bands and the analysis of two experimental spectra recorded in the frame of this study: (1) a leak-out infrared vibrational spectrum of the 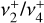dyad of 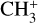and (2) a rotationally resolved photoelectron spectrum of the 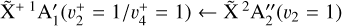band of CH3. This spectroscopic analysis has enabled an accurate derivation of the rotational excitation temperature of in d203-506, as well as an estimate of the beam-averaged column density in this object.

2 Methods

2.1 Quantum chemical calculations

The potential energy surface (PES) of the 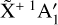electronic ground state of 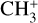was generated from a set of 232 geometries sampled uniformly from an approximate harmonic zero-point vibrational wavefunction. At each geometry, the electronic energies and analytic gradients were computed with the CFOUR package (Matthews et al. 2020; Stanton et al. 2020) using all-electron coupled cluster theory with single, double, and perturbative triple excitations (ae-CCSD(T); Raghavachari et al. 1989; Scuseria 1991; Lee & Rendell 1991) and the correlation-consistent core-valence pentuple-ζ basis set (cc-pCV5Z; Dunning 1989; Woon & Dunning 1995). High-order valence electron correlation effects were estimated by the difference between the frozen-core CCSDT(Q) (Bomble et al. 2005; Matthews 2020) and CCSD(T) energies and gradients evaluated with the cc-pVQZ basis set. The composite “CCSD(T) + ∆[T(Q)]” energies and gradients were used to fit a sixth-order permutationally invariant polynomial (PIP) in the Morse-scaled internuclear distances yij = exp(−rij/a), with a = 2.0 Å (containing 196 independent terms, Braams & Bowman 2009). The relative least-squares fitting weight of the energy versus gradient data was constrained by scaling the gradients with a characteristic length parameter of 0.1 Å, which resulted in similar root-mean-square (rms) residuals for the energies (0.52 cm−1) and scaled gradients (0.54 cm−1). A test surface fit to only the ae-CCSD(T)/cc-pCV5Z component of the data set verified that the fitted surface reproduces the reference equilibrium CH bond length (rCH = 1.087322 Å) to within 10−5 Å. The corresponding harmonic wavenumbers are reproduced within 0.02–0.15 cm−1 of the ab initio values calculated with analytic second derivatives (Gauss & Stanton 1997).

Quasi-variational discrete-variable representation (DVR) nuclear motion calculations were performed on the fitted PES with the NITROGEN software package (Changala 2021). The exact curvilinear kinetic energy operator was evaluated for an internal coordinate system defined by the three CH bond lengths, symmetrized linear combinations of the HCH angles, and the out-of-plane bending angle. Potential-optimized DVR (PO-DVR) basis sets (Light & Carrington 2000; Echave & Clary 1992) were constructed by contracting large, converged one-dimensional sinc-DVRs to a set of 10 PO-DVR points for each vibrational coordinate, which resulted in a final rovibrational basis size of (2J + 1) × 106 for each value of the total angular momentum quantum number J. The rovibrational energies and wavefunctions for J = 0–3 were calculated with an iterative thick-restart, symmetry-projected Lanczos eigensolver (Wu & Simon 2000; Wang & Carrington 2001), utilizing the C2v subgroup of the full D3h molecular symmetry group. This symmetry projection enables the separate diagonalization of the degenerate components of E′ and E″ symmetries, which was found to be essential to reliably converge their respective eigenfunctions. The calculated energies were then used to fit effective Hamiltonians for the v+ = 0 ground state, the 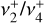bending dyad, and the 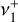and 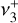CH stretch fundamentals.

Infrared band strengths were calculated using a dipole moment surface (DMS) constructed from the same set of geometries and composite level of theory as the PES. The DMS was represented with a PIP bond-vector expansion, similar to that used by Nyman & Yu (2019),

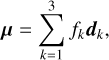
where dk = X(Hk) − X(C) are the vectors connecting the C atom to each of the three H atoms. The fk coefficients are expanded as third-order polynomials in the same yij internuclear coordinates as above (50 independent invariant terms), with an rms fit residual of 2 × 10−3 Debye. Additional anharmonic IR band intensities were calculated via second-order vibrational perturbation theory (Mills 1972) in CFOUR at the ae-CCSD(T)/cc-pCV5Z level of theory, as well as with smaller basis sets (cc-pCV(D,T,Q)Z) and additional diffuse functions (aug-cc-pCV(D,T,Q)Z basis sets).

2.2 Vibrational spectroscopy in a cryogenic ion trap

The 7 μm band system of 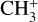was recorded using the FELion cryogenic ion trap beamline at the Free Electron Lasers for Infrared eXperiments (FELIX) Laboratory (Oepts et al. 1995)2. The FELion instrument has been described in detail previously (Jusko et al. 2019) and has been used earlier to record the infrared-predissociation (IRPD) action spectrum of the 7 μm band of 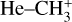(Asvany et al. 2018). To record the vibrational spectrum of the bare (untagged) 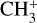, we used the novel leak-out spectroscopy (LOS) method described in Schmid et al. (2022).

For the experiments presented here, 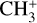ions were produced in an ion storage source by electron impact dissociative ionization of methane (CH4 5.5, Linde AG) using electrons with 40 ± 3 eV energy. The 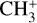ions (with m/z 15) were mass-selected in a quadrupole mass filter, and around 7000 ions were injected into the 22-pole ion trap (Asvany et al. 2010), which was kept at 20 K. The ions were cooled close to the ambient temperature by a short 20–50 ms pulse of helium gas (He 6.0, Linde AG) at the beginning of the trapping cycle. Neon gas was continuously admitted to the trap at an approximate number density of 5 × 1011 cm−3. The temperature and number density were adjusted to maximize the leak-out signal and to avoid the formation of 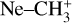complexes (typically below 5% Ne-tagging during the experiments). During the storage period of typically 1.6 s, the ions were irradiated with several pulses of IR radiation from FELIX (FEL2), and then the remaining ions were extracted from the ion trap, mass-selected again for m/z 15, and counted with a Daly-type single-ion counting detector. This cycle was repeated 3–4 times at each laser wavelength to improve the signal-to-noise ratio (S/N). For LOS measurements, the trap electrodes were adjusted so that the ions were just confined, resulting in an off-resonant loss of around 2000 ions from the trap over the trapping period. Upon resonant excitation of the 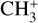ions, collisions with the Ne gas transferred internal energy to kinetic energy, resulting in an additional loss of ions from the trap. Measurements were performed counting either the ions that remained in the trap (depletion mode) or those that left it during the trapping period (leak-out mode). The two modes produced the same vibrational spectrum, but the S/N was improved in the depletion mode. Thus, only this mode was used for measuring the final averaged spectrum.

FEL2 was operated at a repetition rate of 10 Hz with typical macropulse energy inside the ion trap between 8 and 15 mJ. The Fourier-transform limited linewidth of the laser varied between 0.7% and 1% (full-width-at-half-maximum, FWHM) of the central frequency, corresponding to 10–15 cm−1 for the 7μm band (1400 cm−1). The laser was stepped in 0.5 or 1 cm−1 increments. The wavenumber calibration for each individual spectrum was done with a grating spectrometer and was reproducible over the two-day measurement campaign to within 1–2 cm−1, with a systematic uncertainty of a few wavenumbers. The relative depletion signal as a function of wavenumber, D(ṽ) = 1 − NON(ṽ)/NOFF, in the number of ions NON(ṽ) from the baseline value NOFF was normalized to varying laser pulse energy E and pulse number n using I = − In [NON(ṽ)/NOFF]/(nE) (with E in J), giving the intensity I in units of relative cross-section per Joule. The final spectrum is then obtained by averaging (in this case over five individual scans) using statistical binning with a bin size of 1 cm−1.

2.3 Photoelectron spectroscopy

The rotationally resolved photoelectron spectra presented in this paper have been recorded using the VULCAIM setup, which has been described in detail elsewhere (Harper et al. 2022). Briefly, tunable vacuum ultraviolet (VUV) laser radiation in the 79 200–80 250 cm−1 range was generated by difference-frequency mixing (2v1 − v2) in a pulsed jet of atomic krypton using its (4p)6 1S0 → (4p)55p[1/2]0 two-photon transition. The resulting VUV radiation had a linewidth of about ~0.1 cm−1 and an absolute wavenumber accuracy ≪ 0.1 cm−1. All the details about the laser system and its calibration can be found in Harper et al. (2022). The VUV laser was then coupled with a pulsed-field-ionization zero-kinetic-energy (PFI-ZEKE) photoelectron spectrometer (Lamarre et al. 2015; Cunha de Miranda 2011) and a pulsed molecular beam formed from the skimmed output of a pyrolysis reactor source. This source is well known in the literature for efficiently producing the neutral methyl radical from various precursors (Blush et al. 1993; Cunha de Miranda et al. 2010). It consisted of a pulsed valve nozzle (General valve, Parker) coupled to a silicon carbide tube (Saint Gobain Advanced Ceramics), which was resistively heated with a current of a few amperes passed through molybdenum electrodes attached to the tube. The valve was protected from overheating by water cooling and a MACOR (Sceram Ceramics) shield placed between the tube and the valve, which maintained a temperature of ~30 °C.

Nitromethane (CH3NO2, Sigma Aldrich, ReagentPlus, ≥ 99%) diluted in He (1–2%) was used as a precursor to produce CH3. A current of 2 A was found to efficiently produce the CH3 radical while avoiding the production of NO (which has photoelectron transitions in the vicinity of the adiabatic ioniza-tion energy of CH3) and limiting that of cations (such as 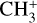). The residual ions produced by the pyrolysis were fully removed from the molecular beam using deflection plates placed between the pyrolysis source and the skimmer.

The photoelectron measurements were performed in the vicinity of two photoionizing transitions: the 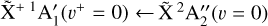origin band (between 79 200 and 79 500 cm−1) and the 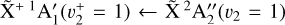sequence band (between 80 000 and 80 250 cm−1). The wavenumber search range for the sequence band was guided by the spectral assignment of the threshold photoelectron spectrum of CH3 recorded by Cunha de Miranda et al. (2010) using a synchrotron facility. Their assignments were based on ab initio calculations and Franck-Condon factor computations. To record these CH3 PFI-ZEKE spectra, we used a two-pulse electric-field sequence, as in Schulenburg et al. (2006), 2 µs after the VUV laser excitation. A pre-pulse of + 166 mV cm−1 (1 µs duration) was used to extract the prompt electrons directly produced by the laser and to pulse ionize the highest Rydberg states. For both the origin and sequence bands, a second pulse (a few µs duration) of −1.329 V cm−1 was used to ionize part of the remaining Rydberg states and propel the ejected electrons toward the microchannel plate detector. The origin band was also recorded using a different pulse sequence, with a second pulse of −0.332 V cm−1, to investigate the evolution of the spectral resolution and the Stark shift with the second pulse amplitude.

In a single measurement, an acceptable S/N was obtained for the experimental spectrum of the origin band with a spectral resolution of 1 cm−1. The measurement was reproduced several times, but the spectrum shown in this article is the result of a single measurement. The measurement of the sequence band was far more challenging. Indeed, radical production is inherently difficult, and the population of the excited v2 = 1 vibrational level of neutral CH3 remained quite small in the supersonic expansion despite the heating in the pyrolysis source. To reach an acceptable S/N, 10 different measurements were summed, and a running average over 20 points was applied on the final spectrum (which slightly degrades the spectral resolution from 1 to 1.5 cm−1).

3 Results and discussion

3.1 JWST spectrum assignment

As discussed above, the 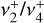rotational fine structure is highly perturbed due to the near-coincidence of the vibrational energy difference (~10 cm−1) and the rotational constants (B ≈ 2C ≈ 9.4 cm−1, Crofton et al. 1988; Jagod et al. 1994). Nonetheless, the rovibrational structure is well described by a relatively compact multistate effective Hamiltonian (Kraemer & Špirko 1991). The spectroscopic parameters derived from the calculated rovibrational energies are summarized in Table 1 for the vibrational ground state and 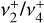dyad. These parameters, together with the anharmonic vibrational band strengths (I2 = 12.58 km mol−1, I4 = 2 × 18.54 km mol−1; see Appendix A), were used to simulate the IR emission spectrum using the PGOPHER program (Western 2018). This simulation is shown in Fig. 1 together with the observed astronomical IR emission spectrum from the protoplanetary disk d203-506 recorded by the MIRI instrument on board JWST (Berné et al. 2023b). In the present work, the spectrum initially reported in Berné et al. (2023b) has been blueshifted to account for the local standard of rest (LSR) velocity, which shifts the line frequencies by about 0.1 cm−1. Details about the procedure can be found in Appendix B.

The close agreement between the calculated and observed spectra enabled the rotational assignment of the 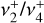dyad. We ultimately assigned 167 IR transitions, confirmed using the LLWP software to generate Loomis-Wood type plots (i.e., following series of transitions of given selection rules, Bonah et al. 2022). A combined fit was performed using both the present astronomical assignments and the laboratory measurements of the 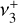band (Jagod et al. 1994). The best-fit experimental parameters for the ground state and 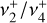are shown in the last column of Table 1, and the corresponding simulated spectrum is plotted in Fig. 2. The excellent agreement between the astronomical spectrum and the final simulation is highlighted in the zoom around the Q-branches presented in Fig. 3. The PGOPHER files used for the assignments and fit log file (containing the assigned line list) are available as electronic supplementary materials on Zenodo3. Further details on the spectroscopic assignments and fit are presented in Appendix C.

The high degree of symmetry of 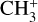leads to extensive sum rules constraining the values of the Coriolis and centrifugal distortion parameters. From these relations, we can estimate the expected values of the lowest-order Coriolis parameters, ζ4 and Fαb, using the previously determined value of ζ3 = 0.11 (Crofton et al. 1988):

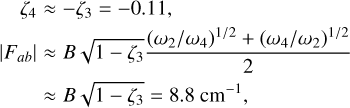
which are in good agreement with the theoretical and experimental values. (Deviations from these relations are expected due to perturbative rovibrational and anharmonic corrections.) The Coriolis parameters of 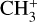are very similar in magnitude as those of the v2/v4 dyad of the isoelectronic molecule BH3 measured by Kawaguchi (1994), who determined ζ4 = −0.08(1) and |Fab| = 7.803(5) cm−1.

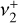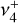It should be noted that the simulated IR line strengths are sensitive to the relative sign of the vibrational dipole matrix elements and the Coriolis interaction parameters because of the complete mixing of and (Pracna et al. 1993). Our phase convention is defined by the matrix elements

where k and l are the projections of the total and vibrational angular momentum, respectively, along the molecular symmetry axis. The transition frequencies alone determine only the relative signs of the four interaction parameters. If we constrain the phase of the normal modes such that the vibrational dipole matrix elements have the same sign, then inspection of the simulations with the observed spectrum shows that the Coriolis parameters must have the signs given in Table 1.

Although the strong Coriolis interactions completely mix the zeroth-order 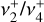character and spoil the k and l quantum numbers, the ∆k = ∆l = ±1 selection rule implied by Eq. (1) ensures that k − l remains a good quantum number, which organizes an emergent quasi-spherical-top rovibrational energy level pattern. In Appendix D, we show that this unusual Coriolis coupling-dominated regime leads to a new, surprisingly simple branch structure with straightforward IR selection rules.

Table 1

Spectroscopic constants of 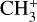in the ground vibronic state and the 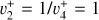dyad.

thumbnail Fig. 1

Astronomical spectrum recorded by the JWST (top trace) and comparison with simulation of the dyad of performed using the unadjusted ab initio parameters (bottom trace). The simulation has been performed at 700 K using the parameters shown in Table 1 and convolved with a Gaussian line shape (FWHM = 0.4 cm−1). The intensity scale is in arbitrary units.

3.2 Vibrational spectrum

The vibrational spectrum of the 7 µm band system of 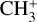recorded by LOS is presented in Fig. 4. Using the best-fit constants reported in Table 1, it is possible to reproduce this spectrum, hence validating the spectroscopic assignments experimentally. We find that a temperature of 75 K and a Gaussian lineshape of 10 cm−1 FWHM nicely reproduces the experimental spectrum (Fig. 4). To obtain the best agreement with the simulated spectrum, the wavenumber scale of the LOS spectrum has been corrected by +4 cm−1, a value within an acceptable range for the systematic uncertainty of the measurements. The band profile is dominated by the Q-branch of the dyad while some rotational substructure is distinguished in the P- and R-branches, with bumps in the regions of the stronger transitions corresponding to the P(1)–P(3) and R(1)–R(3) lines. The stick spectrum of the underlying rovibrational lines seen in Fig. 4 will guide future high-resolution investigations using the LOS method.

thumbnail Fig. 2

Astronomical emission spectrum recorded by JWST and comparison with simulations of the dyad of performed using the best-fit parameters (top panel). The simulation has been performed using the same profile parameters as in Fig. 1 (T = 700 K, FWHM = 0.4 cm−1). The wavenumber residuals of the line-by-line fits are plotted in the lower panel of the figure.

3.3 Photoelectron spectra

Further validation of the spectroscopic parameters derived for the 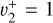and 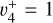states is brought by high-resolution measurements. The two photoionizing transitions recorded in this work, the 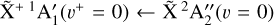origin band and the 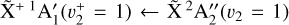sequence band are depicted in Figs. 5 and 6a, respectively. The best-fit constants reported in Table 1 are used to interpret these photoelectron spectra of CH3.

A peculiar feature of the CH3 photoelectron spectrum originates from the frequency of the v2 out-of-plane vibrational mode increasing by about a factor of 2 upon ionization (Cunha de Miranda et al. 2010). This shift moves the 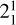sequence band away from the more intense origin band, with which it would usually overlap, making high-resolution photoelectron spectroscopy a method of choice to investigate the rotational structure of the 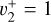state of .

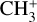The photoionization selection rules for the methyl radical have been discussed in detail by Schulenburg et al. (2006). The photoelectron is ejected from a 2pz orbital, which implies that the photoelectron partial wave has an orbital angular momentum quantum number ℓ = 0 or 2, leading to similar symmetry selection rules as for a single-photon electric dipole transition. This is demonstrated in Eqs. (5) and (7) of Signorell & Merkt (1997). In addition, using the orbital ionization model (Willitsch & Merkt 2005), Schulenburg et al. (2006) derived that the rotational structure of the photoelectron spectrum of CH3 follows the same selection rules as for a (parallel) single-photon electric dipole transition (Herzberg 1966): ∆N = 0, ±1 and ∆K = 0 (where N is the total angular momentum excluding spin, and K is its projection along the symmetry axis). Given the equivalence of the selection rules for standard single-photon electric dipole moment and single-photon ionization, and neglecting the electron spin, one can use the PGOPHER program (Western 2018) to simulate the rotationally resolved photoelectron spectra and thus keep the same formalism as that used in the previous section.

The spectrum of the origin band measured in this work is in excellent agreement with the spectra previously recorded using the PFI-ZEKE technique (Blush et al. 1993; Wiedmann et al. 1994; Schulenburg et al. 2006). To simulate this origin band, we used the rotational constants obtained by Yamada et al. (1981) and this work (Table 1) for the vibronic ground states of CH3 and 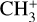, respectively. The resulting simulation is depicted in Fig. 5. The positions of the rotational lines are perfectly reproduced. The disagreements concerning the relative line intensities in the P- and R-branches are due to rovibronic interactions between the different ionization channels. These intensity alterations have been already observed experimentally (Blush et al. 1993; Schulenburg et al. 2006) and have been discussed in detail by Schulenburg et al. (2006).

From the simulation depicted in Fig. 5, one can extract an adiabatic ionization energy of 79 355.3(2) cm−1, which corresponds to the energy difference between the 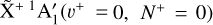and the 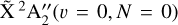rovibronic levels, a value that is not corrected for the Stark shift. Using the procedure described by Hollenstein et al. (2001), the Stark shift correction is estimated here to be about +2 cm−1. The field-free adiabatic ionization energy is thus 79 357.3(12) cm−1, in good agreement with the value of 79 356.2(15) cm−1 obtained by Schulenburg et al. (2006). Our final error bar is increased by 1 cm−1 to account for the potential overestimation of the Stark shift correction. Indeed, the resolution and Stark shift obtained for the origin band with the two different pulse sequences are similar. This suggests that some of the Rydberg states may be predissociated as observed in the PFI-ZEKE spectrum of the propargyl radical (Jacovella et al. 2013).

The spectrum obtained for the 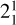sequence band is displayed in panel a of Fig. 6. To simulate the spectrum, we used the molecular constants derived by Yamada et al. (1981) for the neutral v2 = 1 rovibronic levels and the fitted spectroscopic constants derived in Sect. 3.1 shifted by the ionization energy value derived for the origin band without its Stark shift correction. Initially, we thought that the simulation of the 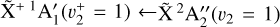transition alone would suffice to reproduce the experimental spectrum. This simulation can be found in panel c of Fig. 6 (blue trace). However, although the Q-branch around 80 135 cm−1 was well reproduced (and at the correct position), many lines were missing in the P- and R-branch sides. This was a hint that the strength of the Coriolis effect between 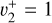and 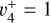rovibrational levels described in Sect. 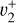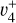3.1 is so strong that the resulting eigenstates have mixed and character. In this case, it is conceivable to observe the 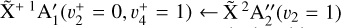vibronic transition. The corresponding spectrum, depicted in panel d of Fig. 6, helps explain the remaining unassigned lines. The complete simulation is displayed in panel b of the same figure, providing an excellent agreement with the experimental spectrum depicted in panel a. It should be pointed out that the only parameters that had to be adjusted manually in our simulation to best reproduce the experimental spectrum are the relative intensity weighting factors. The best agreement was found to be 1:0.4 for 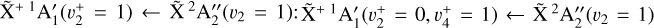. The intensities of a few lines remain overestimated (e.g., at 80 168 and 80 182 cm−1) but most of the observed line positions are well reproduced. The slight intensity discrepancies most likely originate from rovibronic channel interactions which are not taken into account in our model but were already suspected of playing a role in the photoelectron spectrum of the origin band by Schulenburg et al. (2006).

The rotationally resolved PFI-ZEKE spectrum of the 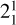sequence band and its analysis provide unambiguous experimental confirmation that the fitted parameters given in Sect. 3.1 are indeed the molecular constants of the 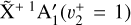and 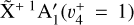states of the methyl cation and thus in turn confirm its detection in a protoplanetary disk in Orion using the JWST.

thumbnail Fig. 3

Zoom around the band centers showing the agreement between the astronomical spectrum and the simulation obtained with the best-fit parameters. All simulations parameters are the same as those of Fig. 2.
thumbnail Fig. 4

LOS spectrum of the dyad of ( electronic state, top trace) and comparison with a PGOPHER simulation performed using the best-fit parameters (bottom trace). The simulations has been performed at T = 75 K, and convolved with a Gaussian line shape (FWHM = 10 cm−1).
thumbnail Fig. 5

Rotationally resolved photoelectron spectrum of the methyl radical in the vicinity of the photoionizing transition. The black curve is the experimental spectrum and the red one a simulation performed at 250 K and convolved with a Gaussian line shape (FWHM = 1 cm−1), see text for details. The R and P branches are labeled by the N quantum number of the neutral species (total angular momentum excluding nuclear and electron spins).
thumbnail Fig. 6

Rotationally resolved photoelectron spectrum of the methyl radical in the vicinity of the and photoionizing transitions. The black curve (panel a) is the experimental spectrum, the red one (panel b) the complete simulation and the blue and green ones (panels c and d) the separated simulations of the ionizing transitions to and , respectively. All simulations have been performed at 250 K and convolved with a Gaussian line shape (FWHM = 1.5 cm−1).
thumbnail Fig. 7

Comparison of the astronomical spectrum (panel a) and simulations of the dyad (other panels) of ( electronic state) for different rotational temperatures (500 K, 700 K, and 900 K in panels b, c, and d, respectively). A zoom into the Q-branch is presented on the right-hand side of the figure. All simulations have been performed using the best-fit parameters (Table 1) and convolved with a Gaussian line shape (FWHM = 0.4 cm−1).
thumbnail Fig. 8

Rotational diagram obtained for a selection of 60 isolated transitions of . The points are the values derived from integration of the astronomical peaks (green diamonds for levels of A2 rovibrational symmetry, blue dots for those of E symmetry), and the black bars are the errors on these values. The solid line is the linear regression within these points and the 2σ range of confidence is represented by the filled region.

3.4 Astronomical implications

Visual inspection of the P-, Q-, and R-contours of the dyad enables a qualitative estimate of the rotational excitation temperature of 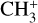in d203-506. Assuming thermal equilibrium, we estimate T = 700 ± 200 K (Fig. 7). A more rigorous approach consists of integrating the area of isolated transitions on the spectrum to extract both the temperature and column density. This procedure is detailed in Appendix E, and the resulting rotational diagram is shown in Fig. 8. The derived level populations are adequately fitted by a single-temperature linear regression, from which we derive a beam-averaged column density for 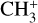of Ntot = (5.4 ± 3.2) × 1011 cm−2 and a rotational temperature of T = 660 ± 80 K (2σ uncertainties). The latter is consistent with the crude estimate based on inspection of the band profile. The rotational temperature of 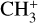is close to but slightly lower than that of H2 (923 ± 48 K, Berné et al. 2023b). This difference is in agreement with the 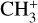emission being deeper inside the photodissociation region (PDR) than H2 rotational emission, which is what is expected from PDR models.

The derived column density may be significantly impacted by multiple systematic effects, including non-equilibrated vibrational and rotational temperatures, and the underlying source geometry, which determines the beam dilution. The reported value of Ntot here assumes total vibrational, rotational, and spin-isomer equilibrium and a completely filled beam. A straight-forward approach to address the beam dilution would be to determine the area of the 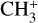emitting layer from the best available H2 models and from this derive a beam filling factor to compare with column density with the same models. A more detailed investigation of the source temperature and geometry will be carried out in an upcoming paper, which will also consider other molecules detected in d203-506.

4 Conclusions

The 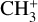rovibrational bands detected in emission around 7 µm by the JWST toward the protoplanetary disk d203-506 have been fully spectroscopically assigned based on complementary theoretical and experimental works:

  • the analysis of the 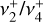dyad (out-of-plane 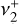and degenerate in-plane 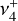bending) was enabled by high-level quantum-chemical calculations that accurately account for the strong Coriolis interactions.

  • the derived spectroscopic constants were validated experimentally by both direct vibrational spectroscopy of these bands using IR leak-out spectroscopy and high-resolution photoelectron spectroscopy of the 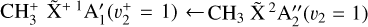band.

These results were used to determine a rotational excitation temperature T = 660 ± 80 K, not far from the derived local H2 rotational temperature T = 923 ± 48 K (Berné et al. 2023b). A beam-averaged column density of 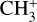in d203-506 was estimated while awaiting refinement from future modeling of the chemical formation, excitation, and radiative transfer processes.

This work motivates a number of follow-up investigations. Detection of the 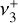band near 3 µm in d203-506 would provide critically needed constraints on the vibrational excitation of 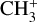in this source. The presently derived spectroscopic constants of the 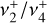dyad may shed light on other high-resolution investigations involving these states that have thus far defied spectroscopic analysis (Joo 1996; Liu et al. 2001) and will motivate both the search for and additional new high-resolution measurements of carbocations and small radicals of astrophysical interest in the laboratory. These results may also stimulate renewed efforts toward the radio astronomical detection of deuterated versions of 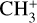(Roueff et al. 2013), the precise millimeter-wave transition frequencies of which are known from highly accurate laboratory measurements (Amano 2010; Töpfer et al. 2016; Jusko et al. 2017).

Acknowledgements

P.B.C. acknowledges support from the US National Science Foundation (Award Nos. PHY-2110489 and AST-2307137). The photoelectron spectroscopy experiment has received financial support from the French “Agence Nationale de la Recherche” (ANR) under Grant No. ANR-17-CE30-0031-01 (Project PRIMA) and ANR-21-CE29-0017 (Project ZEPHIRS), from the “Institut de Physique” (INP) of CNRS, from Paris Ile-de-France Region (DIM ACAV and DIM ACAV+), from the University of Paris-Saclay (Labex PALM), and from the University Paris-Sud (RTRA Triangle de la Physique). This work was also supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI), the “Programme National de Planétologie” (PNP) and the “Commission Spécialisée Astronomie-Astrophysique” (CSAA) of CNRS/INSU with INC/INP cofunded by CEA and CNES. We gratefully acknowledge Radboud University and the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) for support of the FELIX Laboratory. K.S. is supported by the research program “HFML-FELIX: a Dutch Centre of Excellence for Science under Extreme Conditions” (with project number 184.035.011) of the research program “Nationale Roadmap Grootschalige Wetenschappelijke Infastructuur”, which is financed by NWO. The Cologne team is supported by an ERC advanced grant (MissIons: 101020583) and the Deutsche Forschungsgemeinschaft (DFG) via SFB 1601 (project ID 500700252), subprojects B8 and C4. J.R.G. thanks the Spanish MCINN for funding support under grant PID2019-106110GB-I00. This work is based in part on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program #1288. The authors acknowledge the PDRs4All team for developing their observing program with a zero-exclusive-access period. Support for program #1288 was provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127.

Appendix A Infrared band strengths

The variational vibrational wavefunctions were used to compute transition dipole matrix elements,

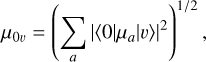
where |0〉 is the vibrational ground state, |υ〉 is an excited state, and µa the projection of the dipole moment along one of the molecule-fixed Eckart-frame axes. The matrix elements computed with the composite CCSD(T)/cc-pCV5Z + Δ[T(Q)]/cc-pVQZ vibrational wavefunctions and DMS are summarized in Table A.1.

Table A.1

IR band strengths of the fundamental vibrational transitions of .

The vibrational band strengths computed with the CCSD(T)/cc-pCV5Z-only PES/DMS either variationally or with vibrational perturbation theory (VPT2) differed from the high-level composite results by less than 1%. The incomplete one-electron basis set is likely a larger source of error. Based on additional CCSD(T) VPT2 calculations with cc-pCV (D,T,Q)Z and aug-cc-pCV(D,T,Q)Z basis sets, we conservatively estimate an error of less than 10% for the band strengths.

Appendix B Calibration of the astronomical spectrum

Because the LSR velocity of HCO+ rotational lines in the Orion Bar and d203-506 is ~10.5 km s−1 (Goicoechea et al. 2016, 2019; Berné et al. 2023a), transitions of are expected to be slightly redshifted, and a small radial velocity correction is required. We calibrated the spectrum wavenumber axis by interpolating between observed, well known H2 lines appearing in the spectrum, which were fitted with a Gaussian profile to extract their precise central position. The lines S(3) (υ = 0, J = 5 → υ = 0, J = 3) to S(7) (υ = 0, J = 9 → υ = 0, J = 7) of H2 were used. (For clarity, these lines have been subtracted from the observed spectra in Figs. 1–3 and 7.) Their precise wavelengths (Roueff et al. 2019) are provided in an extended line list as part of the science enabling products from the “Radiative Feedback from Massive Stars as Traced by Multiband Imaging and Spec-troscopic Mosaics” (PDRs4All, ID 1288) Early Release Science program (Berné et al. 2022).4 The calibrated spectrum recorded with JWST is provided as an electronic supplementary material. Line position accuracy is expected to be better than 0.05 cm−1.

Appendix C Fit details

The final spectroscopic fit minimized the sum-of-squares residuals between the observed and calculated IR transition frequencies of both the 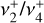dyad from this work and the 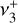band from Jagod et al. (1994). The measurements from Jagod et al. (1994) were weighted according to their expected experimental accuracy, that is, 0.0035 cm−1, while those from the astronomical data were assigned a 0.05 cm−1 uncertainty. A few transitions from Jagod et al. (1994) were excluded from the final fit as we could not reproduce them at their experimental accuracy using the Hamiltonian implemented in PGOPHER. The best-fit parameters of the 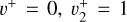and 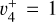states are reported in Table 1 while those of 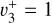are reported in Table C.1.

Table C.1

Spectroscopic constants of 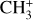in . All values are in cm−1 except that of ζ3, which is dimensionless.

The residuals from the fit are displayed in Fig. C.1. All measurements from Jagod et al. (1994) and assignments from this work are reproduced within 5σ. The reduced standard deviation of the fit is 1.87. We think that to reach a reduced standard deviation closer to unity, higher-order Coriolis interactions than those accounted for in the present model should be taken into account. Attempts to include such parameters in the present fit have proven unsuccessful. Higher-resolution measurements should help constrain the line position assignment and thus eventually enable an improved reproduction of the 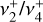dyad.

Note that the Fab,c interaction parameter, defined in Eq. 1, can be transformed by a similarity transformation to the conventional l-doubling parameter (q4) of the degenerate 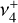mode, such that both cannot be separately determined (Lobodenko et al. 1987). The fits in Table 1 choose q4 = 0. Constraining the interaction parameter Fab,c = 0 instead and optimizing q4 leads to similar fit residuals for both the calculated and experimental effective Hamiltonians.

Appendix 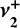D and 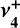contributions to the dyad and its quasi-spherical-top structure

Because the Coriolis perturbations in 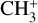are so strong, assessing the 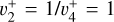character of the energy levels, and hence of the rovibrational transitions, is not straightforward. Individual simulations of the 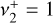and 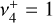bands computed by setting the other transition moment to 0 permit a visual representation of the contribution of each zeroth-order state to a given upper-state, as shown in Fig. D.1. An alternative description of these separate simulations is that they isolate the respective parallel (Δℓ = 0) and perpendicular (Δℓ = +1) character. We note that the sum of the two individual bands does not equal the simulation of both bands simultaneously because of interference of the parallel 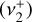and perpendicular 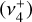transition dipole matrix elements. 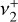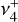Most transitions possess both significant and character. The Q-branch, however, is mainly on its red-end side and 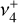on its blue-end side, while the lowest-frequency part of the P-branch exhibits mainly 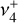character.

thumbnail Fig. C.1

Fit residuals (PGOPHER plot): in black, (data from Jagod et al. 1994); in red, dyad (JWST assignments). The vertical axis equals the dimensionless value of (observed – calculated) /uncertainty.
thumbnail Fig. D.1

Comparison of the astronomical spectrum of (panel a) and simulations of its (panel b) and (panel c) contributions (see text for details). All simulations have been performed using the best-fit parameters (Table 1) at 700 K and convolved with a Gaussian line shape (FWHM = 0.4 cm−1).

The seemingly complex structure of the 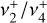band system in reality maintains a regular, ordered pattern based on the value of k − ℓ, which remains a good quantum number even though k and ℓ individually are not (Eq. 1). The rovibrational energies of 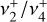are plotted in Fig. D.2. Each trace corresponds to a set of energy levels with a common value of |k − ℓ|. These sets come in groups of 3 branches, whose energies split approximately linearly in J. In the absence of Coriolis perturbations and vibrational energy splittings, these 3 branches would be degenerate with a conventional symmetric-top rotational energy depending only on the k quantum number and independent of ℓ = 0, ± 1. For the true energy levels with J ~ |k − ℓ|, this three-fold degeneracy is approximately preserved because the projection of J perpendicular to the symmetry axis (i.e., the component that mediates the 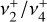interaction) remains small. As J increases, the dominant Fab Coriolis term breaks this degeneracy into three branches with relative energies approximately equal tor 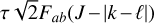, where τ = −1, 0, + 1. In 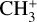, Fab is negative, so the energies of these three types of branches increase with J, stay approximately constant, or decrease with J, respectively.

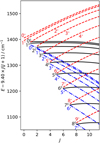thumbnail Fig. D.2

Energy levels of the dyad. An overall J -dependence of 9.4 cm−1 × J(J + 1) has been subtracted for clarity. Each branch is labeled with the value of |k − ℓ|τ. The τ = −1, 0, and + 1 curves are shown by red dashed lines, black solid lines, and blue dotted-dashed lines, respectively.

These rovibrational energy level patterns are qualitatively similar to a triply degenerate vibration of a spherical top (Herzberg 1966), and one might characterize the 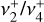dyad as an anisotropic or “quasi-spherical” top with an effective Coriolis parameter of 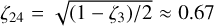. Indeed, in each case the splitting patterns arise when Coriolis interactions amongst three vibrational degrees of freedom are the dominant energy-sorting mechanism. This analogy further extends to the IR transition selection rules. Each P-, Q-, or R-subbranch from a given lower-state K″ -stack has strong transitions only to distinct upper-state manifolds. In addition to a Δ|k − ℓ| = 0 selection rule, there is a Δτ = ΔJ selection rule, where the ground vibrational state has τ″ = 0. This reduces the number of possible subbranches in the IR spectrum, as illustrated in Fig. D.3. Given these selection rules, one expects a rotational spacing of neighboring transitions in each P- or R-subbranch to be 2B(1 − ζ24) ≈ 6.3 cm−1, in good agreement with the typical observed range (5–7 cm−1) and much less than the value for an unperturbed symmetric-top vibrational state (2B ≈ 18 cm−1). As with the spherical-top ΔR = 0 selection rule (where R = J − ℓ is the “pure rotational” angular momentum, di Lauro 2013), the Δτ = ΔJ condition precludes the observation of ground-state IR combination differences, which has likely contributed to the difficulty faced in prior attempts at assigning the 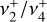dyad.

thumbnail Fig. D.3

Quasi-spherical-top branch assignments of the dyad. Each P-, Q-, and R-subbranch is labeled by the lower state K″ value. The tie-line colors match those used for τ = −1, 0, and + 1 in Fig. D.2. The K″ = 0 branches are missing even-J″ transitions owing to fermionic nuclear spin statistics.

Appendix E Determination of the temperature and column density

By integrating the area of 60 transitions of 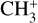, selected because they were isolated from overlapping lines, the population in the upper level, Nu, has been determined using the formula

where Jtot is the integrated intensity of the transition in W m−2 sr−1 and A is its Einstein coefficient (calculated in PGOPHER, using the vibrational dipole matrix elements in Table A.1). The selected transitions and line profile fits are shown in Fig. E.1.

The column density and temperature, Ntot and T, were then calculated using the formula

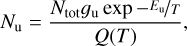
where gu is the degeneracy of the upper level (0 for A1 levels, 4 × (2J + 1) for A2 levels, and 2 × (2J + 1) for E levels; see Berné et al. (2023b) for a detailed spectroscopic description), v is the frequency of the transition, Eu is the energy of the upper level (in units of equivalent temperature), and Q(T) = Σgu exp (−Eu/T) is the total nuclear spin-rovibrational partition function. At 660 K, the partition function of 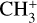is 1345 assuming thermal equilibrium. Fig. 8 in the main text shows the corresponding plot from which a linear regression gave the reported temperature and column density values. Separate fits to rovibrational levels of only A2 symmetry or only E symmetry yielded equivalent temperature and column densities to within small fractions of their respective uncertainties.

thumbnail Fig. E.1

Selected transitions used to determine the temperature and column density of in d203-506. The black trace is the astronomical spectrum; the red trace is a fitted profile consisting of a Gaussian peak, a constant offset, and a linear slope; and the blue trace is the Gaussian peak component only.

References

  1. Aguirre, F., & Pratt, S. T. 2005, J. Chem. Phys., 122, 234303 [NASA ADS] [CrossRef] [Google Scholar]
  2. Amano, T. 2010, A&A, 516, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Asvany, O., Bielau, F., Moratschke, D., Krause, J., & Schlemmer, S. 2010, Rev. Sci. Instrum., 81, 076102 [NASA ADS] [CrossRef] [Google Scholar]
  4. Asvany, O., Thorwirth, S., Redlich, B., & Schlemmer, S. 2018, J. Mol. Spectrosc., 347, 1 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bacon, J., & Pratt, S. 1999, Chem. Phys. Lett., 311, 346 [NASA ADS] [CrossRef] [Google Scholar]
  6. Berné, O., Habart, É., Peeters, E., et al. 2022, PASP, 134, 054301 [CrossRef] [Google Scholar]
  7. Berné, O., Habart, E., Peeters, E., et al. 2023a, Science, submitted [Google Scholar]
  8. Berné, O., Martin-Drumel, M.-A., Schroetter, I., et al. 2023b, Nature, 621, 56 [CrossRef] [Google Scholar]
  9. Blush, J. A., Chen, P., Wiedmann, R. T., & White, M. G. 1993, J. Chem. Phys., 98, 3557 [CrossRef] [Google Scholar]
  10. Bomble, Y. J., Stanton, J. F., Kállay, M., & Gauss, J. 2005, J. Chem. Phys., 123, 054101 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bonah, L., Zingsheim, O., Müller, H. S., et al. 2022, J. Mol. Spectrosc., 388, 111674 [NASA ADS] [CrossRef] [Google Scholar]
  12. Botschwina, P., Flesch, J., & Meyer, W. 1983, Chem. Phys., 74, 321 [NASA ADS] [CrossRef] [Google Scholar]
  13. Braams, B. J., & Bowman, J. M. 2009, Int. Rev. Phys. Chem., 28, 577 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cernuto, A., Lopes, A., Romanzin, C., et al. 2017, J. Chem. Phys., 147, 154302 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chabot, M., IdBarkach, T., Beroff, K., Le Petit, F., & Wakelam, V. 2020, A&A, 640, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Changala, P. B. 2021, NITROGEN, version 2.1.2, https://github.com/bchangala/nitrogen [Google Scholar]
  17. Chupka, W. A., & Lifshitz, C. 1968, J. Chem. Phys., 48, 1109 [NASA ADS] [CrossRef] [Google Scholar]
  18. Crofton, M. W., Kreiner, W. A., Jagod, M.-F., Rehfuss, B. D., & Oka, T. 1985, J. Chem. Phys., 83, 3702 [NASA ADS] [CrossRef] [Google Scholar]
  19. Crofton, M. W., Jagod, M., Rehfuss, B. D., Kreiner, W. A., & Oka, T. 1988, J. Chem. Phys., 88, 666 [CrossRef] [Google Scholar]
  20. Cunha de Miranda, B. K. 2011, Etudes de la photoionisation de radicaux et de réactions ion-molécule d’intérêt planétaire avec du rayonnement VUV synchrotron et laser, PhD Thesis, Université Paris-Sud 11 (Orsay) and Universidade Federal Fluminense (Niterói), France, Brazil [Google Scholar]
  21. Cunha de Miranda, B. K., Alcaraz, C., Elhanine, M., et al. 2010, J. Phys. Chem. A, 114, 4818 [CrossRef] [Google Scholar]
  22. Dalgarno, A. 1985, Molecular Astrophysics, eds. G. H. F. Diercksen, W. F. Huebner, & P. W. Langhoff (Dordrecht: Springer Netherlands), 3 [CrossRef] [Google Scholar]
  23. di Lauro, C. 2013, in Rotational Structure in Molecular Infrared Spectra (Elsevier), 225 [CrossRef] [Google Scholar]
  24. Dopfer, O., & Luckhaus, D. 2002, J. Chem. Phys., 116, 1012 [NASA ADS] [CrossRef] [Google Scholar]
  25. Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [Google Scholar]
  26. Dyke, J., Jonathan, N., Lee, E., & Morris, A. 1976, J. Chem. Soc., Faraday Trans., 2, 72, 1385 [Google Scholar]
  27. Echave, J., & Clary, D. C. 1992, Chem. Phys. Lett., 190, 225 [NASA ADS] [CrossRef] [Google Scholar]
  28. Elder, F. A., Giese, C., Steiner, B., & Inghram, M. 1962, J. Chem. Phys., 36, 3292 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gans, B., Mendes, L. V., Boyé-Péronne, S., et al. 2010, J. Phys. Chem. A, 114, 3237 [CrossRef] [Google Scholar]
  30. Gauss, J., & Stanton, J. F. 1997, Chem. Phys. Lett., 276, 70 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gerin, M., Neufeld, D. A., & Goicoechea, J. R. 2016, ARA&A, 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
  32. Goicoechea, J. R., Pety, J., Cuadrado, S., et al. 2016, Nature, 537, 207 [Google Scholar]
  33. Goicoechea, J. R., Santa-Maria, M. G., Bron, E., et al. 2019, A&A, 622, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Golob, L., Jonathan, N., Morris, A., Okuda, M., & Ross, K. 1972, J. Electron Spectrosc. Relat. Phenom., 1, 506 [CrossRef] [Google Scholar]
  35. Harper, O. J., Chen, N. L., Boyé-Péronne, S., & Gans, B. 2022, Phys. Chem. Chem. Phys., 24, 2777 [NASA ADS] [CrossRef] [Google Scholar]
  36. Herzberg, G. 1961, Proc. Roy. Soc. Lond. A Math. Phys. Sci., 262, 291 [NASA ADS] [Google Scholar]
  37. Herzberg, G. 1966, Molecular Spectra and Molecular Structure III. Electronic Spectra and Electronic Structure of Polyatomic Molecules (Van Nostrand Reinhold) [Google Scholar]
  38. Hollenstein, U., Seiler, R., Schmutz, H., Andrist, M., & Merkt, F. 2001, J. Chem. Phys., 115, 5461 [CrossRef] [Google Scholar]
  39. Jacovella, U., Gans, B., & Merkt, F. 2013, J. Chem. Phys., 139, 084308 [NASA ADS] [CrossRef] [Google Scholar]
  40. Jagod, M.-F., Gabrys, C. M., Rösslein, M., Uy, D., & Oka, T. 1994, Can. J. Phys., 72, 1192 [NASA ADS] [CrossRef] [Google Scholar]
  41. Joo, S. 1996, PhD thesis, The University of Chicago, USA [Google Scholar]
  42. Jusko, P., Stoffels, A., Thorwirth, S., et al. 2017, J. Mol. Spectrosc., 332, 59 [NASA ADS] [CrossRef] [Google Scholar]
  43. Jusko, P., Brünken, S., Asvany, O., et al. 2019, Faraday Discuss., 217, 172 [Google Scholar]
  44. Kawaguchi, K. 1994, Can. J. Phys., 72, 925 [NASA ADS] [CrossRef] [Google Scholar]
  45. Keçeli, M., Shiozaki, T., Yagi, K., & Hirata, S. 2009, Mol. Phys., 107, 1283 [CrossRef] [Google Scholar]
  46. Koenig, T., Balle, T., & Snell, W. 1975, J. Am. Chem. Soc., 97, 662 [CrossRef] [Google Scholar]
  47. Koenig, T., Balle, T., & Chang, J. C. 1976, Spectrosc. Lett., 9, 755 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kraemer, W., & Špirko, V. 1991, J. Mol. Spectrosc., 149, 235 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lamarre, N., Gans, B., Alcaraz, C., et al. 2015, Mol. Phys., 113, 3946 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lee, T. J., & Rendell, A. P. 1991, J. Chem. Phys., 94, 6229 [NASA ADS] [CrossRef] [Google Scholar]
  51. Light, J. C., & Carrington, T. 2000, Adv. Chem. Phys., 114, 263 [Google Scholar]
  52. Litorja, M., & Ruscic, B. 1997, J. Chem. Phys., 107, 9852 [CrossRef] [Google Scholar]
  53. Liu, X., Gross, R., & Suits, A. 2001, Science, 294, 2527 [NASA ADS] [CrossRef] [Google Scholar]
  54. Lobodenko, E., Sulakshina, O., Perevalov, V., & Tyuterev, V. 1987, J. Mol. Spectrosc., 126, 159 [NASA ADS] [CrossRef] [Google Scholar]
  55. Loison, J.-C. 2010, J. Phys. Chem. A, 114, 6515 [CrossRef] [Google Scholar]
  56. Matthews, D. A. 2020, J. Chem. Theory Comput., 16, 6195 [CrossRef] [Google Scholar]
  57. Matthews, D. A., Cheng, L., Harding, M. E., et al. 2020, J. Chem. Phys., 152, 214108 [NASA ADS] [CrossRef] [Google Scholar]
  58. Meisner, J., Hallmen, P. P., Kästner, J., & Rauhut, G. 2019, J. Chem. Phys., 150, 084306 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mills, I. M. 1972, in Molecular Spectroscopy: Modern Research, eds. K. N. Rao, & C. W. Mathews (New York: Academic Press), 115 [CrossRef] [Google Scholar]
  60. Nyman, G., & Yu, H.-G. 2019, AIP Adv., 9, 095017 [Google Scholar]
  61. Oepts, D., van der Meer, A. F. G., & van Amersfoort, P. W. 1995, Infrared Phys. Techn., 36, 297 [NASA ADS] [CrossRef] [Google Scholar]
  62. Pracna, P., Špirko, V., & Kraemer, W. 1993, J. Mol. Spectrosc., 158, 433 [NASA ADS] [CrossRef] [Google Scholar]
  63. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [Google Scholar]
  64. Ragni, M., Bitencourt, A. C. P., Prudente, F. V., Barreto, P. R. P., & Posati, T. 2016, Eur. Phys. J. D, 70, 60 [NASA ADS] [CrossRef] [Google Scholar]
  65. Roueff, E., Gerin, M., Lis, D. C., et al. 2013, J. Phys. Chem. A, 117, 9959 [Google Scholar]
  66. Roueff, E., Abgrall, H., Czachorowski, P., et al. 2019, A&A, 630, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Schmid, P. C., Asvany, O., Salomon, T., Thorwirth, S., & Schlemmer, S. 2022, J. Phys. Chem. A, 2022, 8117 [Google Scholar]
  68. Schulenburg, A. M., Alcaraz, C., Grassi, G., & Merkt, F. 2006, J. Chem. Phys., 125, 104310 [NASA ADS] [CrossRef] [Google Scholar]
  69. Scuseria, G. E. 1991, J. Chem. Phys., 94, 442 [NASA ADS] [CrossRef] [Google Scholar]
  70. Signorell, R., & Merkt, F. 1997, Mol. Phys., 92, 793 [NASA ADS] [CrossRef] [Google Scholar]
  71. Simmons, J., Wang, X.-G., & Carrington, T. 2019, J. Phys. Chem. A, 123, 10281 [CrossRef] [Google Scholar]
  72. Smith, D. 1992, Chem. Rev., 92, 1473 [Google Scholar]
  73. Stanton, J. F., Gauss, J., Cheng, L., et al. 2020, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package [Google Scholar]
  74. Taatjes, C. A., Osborn, D. L., Selby, T. M., et al. 2008, J. Phys. Chem. A, 112, 9336 [CrossRef] [Google Scholar]
  75. Thomas, R. D., Kashperka, I., Vigren, E., et al. 2012, ApJ, 758, 55 [NASA ADS] [CrossRef] [Google Scholar]
  76. Töpfer, M., Jusko, P., Schlemmer, S., & Asvany, O. 2016, A&A, 593, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [CrossRef] [Google Scholar]
  78. Wang, X.-G., & Carrington, T. 2001, J. Chem. Phys., 114, 1473 [NASA ADS] [CrossRef] [Google Scholar]
  79. Western, C. M. 2018, PGOPHER version 10.1, University of Bristol Research Data Repository, https://doi.org/10.5523/bris.3mqfb4glgkr8a2rev7f73t300c [Google Scholar]
  80. Wiedmann, R. T., White, M. G., Wang, K., & McKoy, V. 1994, J. Chem. Phys., 100, 4738 [CrossRef] [Google Scholar]
  81. Willitsch, S., & Merkt, F. 2005, Int. J. Mass Spectrom., 245, 14 [NASA ADS] [CrossRef] [Google Scholar]
  82. Woon, D. E., & Dunning, T. H. 1995, J. Chem. Phys, 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
  83. Wu, K., & Simon, H. 2000, SIAM J. Matrix Anal. Appl., 22, 602 [CrossRef] [Google Scholar]
  84. Yamada, C., Hirota, E., & Kawaguchi, K. 1981, J. Chem. Phys., 75, 5256 [NASA ADS] [CrossRef] [Google Scholar]
  85. Yu, H.-G., & Sears, T. J. 2002, J. Chem. Phys., 117, 666 [NASA ADS] [CrossRef] [Google Scholar]
1

In the following, a plus sign (+) is used when referring to a vibrational mode of the cation.

All Tables

Table 1

Spectroscopic constants of 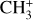in the ground vibronic state and the dyad.

In the text
Table A.1

IR band strengths of the fundamental vibrational transitions of .

In the text
Table C.1

Spectroscopic constants of in . All values are in cm−1 except that of ζ3, which is dimensionless.

In the text

All Figures

thumbnail Fig. 1

Astronomical spectrum recorded by the JWST (top trace) and comparison with simulation of the dyad of performed using the unadjusted ab initio parameters (bottom trace). The simulation has been performed at 700 K using the parameters shown in Table 1 and convolved with a Gaussian line shape (FWHM = 0.4 cm−1). The intensity scale is in arbitrary units.
In the text
thumbnail Fig. 2

Astronomical emission spectrum recorded by JWST and comparison with simulations of the dyad of performed using the best-fit parameters (top panel). The simulation has been performed using the same profile parameters as in Fig. 1 (T = 700 K, FWHM = 0.4 cm−1). The wavenumber residuals of the line-by-line fits are plotted in the lower panel of the figure.
In the text
thumbnail Fig. 3

Zoom around the band centers showing the agreement between the astronomical spectrum and the simulation obtained with the best-fit parameters. All simulations parameters are the same as those of Fig. 2.
In the text
thumbnail Fig. 4

LOS spectrum of the dyad of ( electronic state, top trace) and comparison with a PGOPHER simulation performed using the best-fit parameters (bottom trace). The simulations has been performed at T = 75 K, and convolved with a Gaussian line shape (FWHM = 10 cm−1).
In the text
thumbnail Fig. 5

Rotationally resolved photoelectron spectrum of the methyl radical in the vicinity of the photoionizing transition. The black curve is the experimental spectrum and the red one a simulation performed at 250 K and convolved with a Gaussian line shape (FWHM = 1 cm−1), see text for details. The R and P branches are labeled by the N quantum number of the neutral species (total angular momentum excluding nuclear and electron spins).
In the text
thumbnail Fig. 6

Rotationally resolved photoelectron spectrum of the methyl radical in the vicinity of the and photoionizing transitions. The black curve (panel a) is the experimental spectrum, the red one (panel b) the complete simulation and the blue and green ones (panels c and d) the separated simulations of the ionizing transitions to and , respectively. All simulations have been performed at 250 K and convolved with a Gaussian line shape (FWHM = 1.5 cm−1).
In the text
thumbnail Fig. 7

Comparison of the astronomical spectrum (panel a) and simulations of the dyad (other panels) of ( electronic state) for different rotational temperatures (500 K, 700 K, and 900 K in panels b, c, and d, respectively). A zoom into the Q-branch is presented on the right-hand side of the figure. All simulations have been performed using the best-fit parameters (Table 1) and convolved with a Gaussian line shape (FWHM = 0.4 cm−1).
In the text
thumbnail Fig. 8

Rotational diagram obtained for a selection of 60 isolated transitions of . The points are the values derived from integration of the astronomical peaks (green diamonds for levels of A2 rovibrational symmetry, blue dots for those of E symmetry), and the black bars are the errors on these values. The solid line is the linear regression within these points and the 2σ range of confidence is represented by the filled region.
In the text
thumbnail Fig. C.1

Fit residuals (PGOPHER plot): in black, (data from Jagod et al. 1994); in red, dyad (JWST assignments). The vertical axis equals the dimensionless value of (observed – calculated) /uncertainty.
In the text
thumbnail Fig. D.1

Comparison of the astronomical spectrum of (panel a) and simulations of its (panel b) and (panel c) contributions (see text for details). All simulations have been performed using the best-fit parameters (Table 1) at 700 K and convolved with a Gaussian line shape (FWHM = 0.4 cm−1).
In the text
thumbnail Fig. D.2

Energy levels of the dyad. An overall J -dependence of 9.4 cm−1 × J(J + 1) has been subtracted for clarity. Each branch is labeled with the value of |k − ℓ|τ. The τ = −1, 0, and + 1 curves are shown by red dashed lines, black solid lines, and blue dotted-dashed lines, respectively.
In the text
thumbnail Fig. D.3

Quasi-spherical-top branch assignments of the dyad. Each P-, Q-, and R-subbranch is labeled by the lower state K″ value. The tie-line colors match those used for τ = −1, 0, and + 1 in Fig. D.2. The K″ = 0 branches are missing even-J″ transitions owing to fermionic nuclear spin statistics.
In the text
thumbnail Fig. E.1

Selected transitions used to determine the temperature and column density of in d203-506. The black trace is the astronomical spectrum; the red trace is a fitted profile consisting of a Gaussian peak, a constant offset, and a linear slope; and the blue trace is the Gaussian peak component only.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.