| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | A181 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202453555 | |
| Published online | 04 July 2025 | |
NVSS J151002+570243: Accretion and spin of a z > 4 Fermi-detected blazar
1
Dipartimento di Fisica “Aldo Pontremoli”, Università degli Studi di Milano, Via Celoria 16, 20133
Milano, Italy
2
Dipartimento di Fisica, Sapienza Università di Roma, Piazzale Aldo Moro 5, 00185
Roma, Italy
3
INAF – Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807
Merate, (LC), Italy
⋆ Corresponding author: alzati.2200689@studenti.uniroma1.it
Received:
20
December
2024
Accepted:
13
May
2025
Active galactic nuclei (AGN) at high redshifts feature two of the most peculiar characteristics related to key open questions in AGN physics: they are overly massive, which is not explainable via sub-Eddington accretion, and most of their population hosts relativistic jets that are commonly connected to spinning black holes and are hence less effective in accreting mass onto the black hole. The formation and evolution of such massive objects is currently an open puzzle. Being the most distant blazar consistently detected by Fermi/LATNVSS, J151002+570243 is part of this population, thereby hosting a powerful jet. We tested the hypothesis of a super-Eddington accretion process for this source by modeling its big blue bump with a set of accretion disk emission models. We first tested a standard, geometrically thin, optically thick α-disk, obtaining a mass of Log M/M⊙ = 8.65 ± 0.19 consistent with virial-based results and a significantly sub-Eddington accretion rate of λ = 0.02 ± 0.01. We then focused on the analytic approximations of two numerical models (KERBB and SLIMBH) that take into account the general relativity effects of a spinning black hole (reasonably due to the presence of a jet) and a close-to- or super-Eddington accretion rate . Despite the focus on super-critical accretion, these models confirm a surprisingly low Eddington ratio on the order of 3%. The hypothesis of a continuous accretion at this measured rate is unrealistic, since it would imply a seed black hole mass of ∼106 − 108 M⊙ at redshift z = 20. Hence, we explore the possibility of a continuous super-critical accretion starting from a ∼102 M⊙ seed that would spin up the black hole and eventually contribute to launching the relativistic jet. The measured low accretion rate would thus only occur once the jet is active. This idea would reconcile the existence at z > 4 of extremely massive black holes accreting at somewhat slow rates, with the need for an extremely fast evolution by allowing the formation of stellar-sized black hole seeds even as late as at z ∼ 8.
Key words: methods: analytical / galaxies: active / galaxies: high-redshift / galaxies: jets / quasars: supermassive black holes
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The search of supermassive black holes (SMBHs) in the early Universe has led to the discovery of more than 400 quasars at z > 5.7 in the last 10 years (see for a review Fan et al. 2023, and references therein), and it seems far from being complete. During this time, an always increasing fraction of jetted sources has been discovered at z ≥ 4, leading to the conclusion that relativistic jets are significantly more numerous among the observed quasar population at high redshifts, compared to their analogous lower redshift counterparts (see Sbarrato 2021, for a review). The SMBH masses of this ever-growing sample of sources are at the highest end of the active galactic nuclei (AGN) mass distribution: on average they show M ∼ 109 M⊙ or more. The evolution of such massive black holes requires time, and the age of the Universe at which they are observed does not provide enough time for continuous accretion following standard assumptions (z ∼ 6 corresponds to a Universe age of 900 Myr, while z ∼ 4 is about 1.5 Gyr). This has been dubbed the “mass problem” and currently represents one of the most intriguing open questions of AGN physics. Jets worsen the scenario, since they are typically associated with spinning black holes that are thought to have larger radiative dissipation and thus slower effective mass accretion compared to non-spinning systems.
The excess of jetted sources has been studied by tracing their population via blazar discovery and characterization. As a matter of fact, following simple geometrical assumption, the number of jetted sources with specific features in a well-defined redshift range can be estimated by counting their aligned counterparts. This approach is particularly effective if a blazar is strictly defined as a source observed under a viewing angle, θv, smaller than its beaming angle, θb. The jet-emitting region is strongly relativistic, and we can assume that θb ≃ sin θb and, thus, θb ∼ 1/Γ. Assuming that self-similar AGN jets in a given volume are homogeneously distributed in their orientation, for each detected blazar with θv < 1/Γ, one can assume the presence of ∼2Γ2 analogous sources with their jets oriented randomly in the sky. We know from the literature that the bulk Lorentz factors of jet-emitting regions in blazars are typically in the range of Γ ∼ 8 − 15, when derived from a broad-band spectral energy distribution (SED) modeling that includes the high-energy component1. Such values imply that for each observed blazar, ∼130 − 450 AGNs with the same intrinsic features (e.g., SMBH mass and accretion rate, jet power, and nuclear features) must exist at the same redshifts, making blazars the most efficient tracers of the overall jetted population at high redshifts. At low redshifts the jetted AGN population is easily traced with minor loss in completeness thanks to its extreme radio brightness, which allows jetted sources to be easily included in all-sky radio surveys. The intensified cosmic microwave background (CMB) energy density (scaling as (1 + z)4) is instead responsible for quenching the extended radio emission at roughly z > 3.5 (Ghisellini et al. 2013), preventing an equivalently complete mapping of the jetted AGN population in the radio frequencies. Blazars and their high-energy observation and classification are crucial to trace relativistic jets in the early Universe.
The systematic search for blazars at z > 4 leads to an interesting suggestion: the jetted AGN population traced with this approach is significantly more numerous than the jetted fraction observed in the lower redshift Universe (see e.g., Sbarrato 2021), which is commonly thought to be around 10%, and the fraction derived at high-z from radio observations (9.4 ± 5.7%, Liu et al. 2021). The current z > 4 blazar (and thus overall jetted AGN) population is dominated by M > 109 M⊙, due to limiting sensitivities of all-sky surveys. Therefore, it has been concluded that at least the most massive active SMBHs in the early Universe have a much larger jetted fraction, and likely prefer to form and evolve in jetted AGNs. This was already suggested by Volonteri et al. (2011), who highlighted a slight excess of jetted sources at z > 3 by comparing their comoving number density extracted from the blazar luminosity function of the three-year Burst Alert Telescope (BAT) all-sky survey (Ajello et al. 2009) with the Sloan Digital Sky Survey (SDSS) quasar luminosity function (Shen et al. 2011). Further confirmation was obtained in the following years, culminating in the discovery of the highest-redshift blazar currently known (VLASS J041009.05−013919.88; Bañados et al. 2025), which, at z = 7 extends the issue of finding a significant excess of jetted sources.
The main issue with an extended search of high-z blazars is that the most commonly used evidence of blazars nature, i.e., a γ-ray detection, is not as efficient at z > 3: the all-sky catalogs of γ-ray sources provided by the Large Area Telescope (LAT) on board the Fermi satellite (Atwood et al. 2009) do not reach sensitivities deep enough to detect the steeply falling γ-ray spectra of blazars at such high redshifts. A careful selection of blazar candidates with secure redshift estimates and possibly radio emission is necessary, followed by X-ray observations to confirm the presence of the intense, relativistically beamed inverse Compton emission typical of jets aligned close to our line-of-sight. Motivated by the abundance of jetted sources at high-z, the Fermi/LAT collaboration focused their search for the most powerful known blazars on data, spanning about 10 years of observations. Following a dedicated data analysis, Ackermann et al. (2017) managed to confirm the detection of five blazars at z > 3.1 in ∼92 months of Fermi Pass 8 source class photons in the 60 MeV to 300 GeV energy range. Among these, NVSS J151002+570243 (z = 4.31) was, at the time, the highest-redshift γ-ray source detected by Fermi/LAT. The five Fermi sources obtained with this approach are among the most extreme blazars in terms of jet power, due to their extreme Compton dominance, and also host extremely massive accreting SMBHs (M ∼ 109 − 1010 M⊙). They clearly contribute to tracing a significant excess of jetted sources in the high-zUniverse.
This first systematic search of z > 3.1 γ-ray blazars demonstrated the capability of Fermi/LAT to detect such faint and distant sources, opening the way to further detections in the first 2 billion years of the Universe. To obtain significant detections, targeted searches in binned light curves were performed, to increase the Fermi/LAT data test statistics and catch possible blazar flaring events at high-z. Following this approach, Liao et al. (2018) and Kreter et al. (2020) enlarged the sample of Fermi-detected high-z blazars, extending it to z = 4.72 with the discovery of B3 1428+422.
In this work we focus on the continuously Fermi-detected z > 4 blazar in order to characterize its jet (Sect. 2) andaccretion emission (Sect. 3). We aim at finding signs of fast accretion that could help in justifying its presence in the first 1.5 Gyr of the Universe and ultimately discuss how its jet might be involved in its fast evolution (Sect. 4). In the following we adopt a flat cosmology with a Hubble parameter H0 = 70 km s−1 Mpc−1, and cosmological density parameters ΩM = 0.3 and ΩΛ = 0.7.
2. 1508+5714: A powerful jet 1.5 Gyr after the Big Bang
In order to test the hypothesis of a SMBH accreting at super-Eddington ratio, we studied the SED of NVSS J151002+570243 (also known as SDSS J151002.92+570243.3 and referred to as 1508+5714 here), a high redshift blazar (z = 4.31). Our goal was to estimate the physical parameters of its central black hole by comparing photometric data with three different accretion disk models, each based on different physical assumptions. To this aim, we collected archival data from the Space Science Data Center (SSDC2) and the SDSS3 (Shen et al. 2011).
We first focused on 1508+5714 broadband SED, in order to characterize its relativistic jet emission. To do so, we adopted a phenomenological model presented in Ghisellini et al. (2017) that approximates the SED produced by a relativistic jet aligned close to our line-of-sight with a set of smoothly broken power-laws (for a realistic, physical motivated SED modeling refer to e.g., Gokus et al. 2024). The typical blazar SED is characterized by two humps, generally associated with synchrotron and inverse Compton emission, peaking respectively in the radio-IR and X-γ-rays. The overall emission profile can thus be described by the following set of equations:
which connects at νt with
LS and LC respectively denote the luminosities of the emission produced by the synchrotron radiation and the inverse Compton scattering. These are computed as
The values A, B, and C are constants, obtained by imposing and solving the following conditions:
-
LS + C(νt) = LR(νt),
-
LS + C(νS) = LS(νS) with νS synchrotron peak frequency, and
-
LS + C(νC) = LC(νC) with νC inverse Compton peak frequency.
High-z blazars are among the most powerful blazars known, but they show some differences in their SEDs with respect to the brightest sources in 2FGL (from which the phenomenological model is compiled).
Generally, they show a less prominent synchrotron emission with respect to their optical luminosity (always accretion dominated, see e.g., Sbarrato et al. 2015). A partial quenching of their radio emission by the large CMB energy density (that scales as ∝(1 + z)4) is likely the main reason behind the radio faintness of z > 3 blazars (Ghisellini et al. 2015). This leads to a stronger Compton dominance (CD), which does not necessarily translate into a different radiation field involved in the inverse Compton emission, when compared to lower-z blazars.
Therefore, we adapted the parameters describing the highest luminosity bin in Ghisellini et al. (2017), obtaining the values shown in Table 1. The parameters describe an extremely powerful flat spectrum radio quasar (FSRQ), with more extreme features (higher CD and smaller synchrotron peak frequency) than the highest luminosity bin defined by Ghisellini. This is consistent with what was observed at z > 4 (Sbarrato et al. 2012, 2013), i.e., sources among the most powerful blazars known. Note that this is likely a selection effect, since we are still observing only the brightest fraction of the blazar population, particularly in their high-energy emission.
Parameters used in the phenomenological SED to describe the broadband photometry dataset.
Aside from classification purposes, characterizing the relativistic jet allowed us to evaluate its contribution to the optical and UV emission and thus perform a more precise analysis of the accretion disk.
3. Accretion and black hole mass
High-z blazars clearly show “big blue bumps” in their rest-frame optical-UV emission, similarly to bright quasars. This feature is generally associated with a radiatively efficient, geometrically thin, optically thick accretion disk. We thus modeled this emission with three reasonable accretion disk emission models: the simplest, standard α-disk model (Shakura & Sunyaev 1973), and two models that take into account general relativity effects on the disk emission, as well as the influence of the SMBH spin and possibly close-to- or super-Eddington accretion. We took advantage of the analytic approximations of the numerical models KERRBB (Li et al. 2005) and SLIMBH (Sądowski 2009) developed by Campitiello et al. (2018, 2019), in order to extend their applications to SMBHs and AGNs, in particular. The analytic approximations are particularly convenient, because they explicitly depend on the main physical parameters of the central SMBH, i.e., mass, accretion rate and spin, without being only linked to X-ray data analysis, as is the case for stellar black holes. We thus used three different accretion disk emission models to derive independent estimates of 1508+5714 mass M, spin a, and, most importantly, its accretion rate Ṁ.
As an independent measure and comparison tool, we considered the virial black hole mass, Log Mvir/M⊙ = 8.52 ± 0.39, derived from the optical spectroscopic analysis by Shen et al. (2011). This is the value obtained from the CIV broad emission line. While the three disk emission models are intertwined (see below for details), this is a completely independent mass measure method, and provides crucial information for studying 1508+5714 accretion features.
3.1. A standard α-disk
The first step of our accretion disk analysis focused on characterizing its emission using the standard α-disk model by Shakura & Sunyaev (1973), referred to below as SS73. This model considers the accretion of matter onto a nonrotating black hole in Newtonian approximation; therefore, its emission profile depends only on the mass (M) of the central SMBH and its accretion rate (Ṁ). We also considered anisotropy due to the disk shape and the viewing angle, which is described by a factor 2 cos θ (Calderone et al. 2013). Blazars are observed face on, and thereby we can assume θ ∼ 0 in
Note that the optical spectrum suffers from absorption due to intervening Lyα clouds at wavelengths shorter than λLyα = 1216 Å. We first tried to correct the extended absorption due to the Gunn-Peterson effect via the Meiksin (2006) algorithm, but as this source appears significantly less absorbed than the overall z > 4 population, the corrected flux showed an uncommon and extreme slope, suggesting that we were overcorrecting for absorption. For a safer approach, we thus excluded the absorbed section of the spectrum from our analysis, even if this meant a loss of rest-frame UV information.
Photometric and spectroscopic data were then compared with the SS73 emission profile to obtain estimates of mass and accretion rate (see Fig. 2):
 |
Fig. 1. Broadband SED of 1508+5714. The blue line indicates the total SED that best model the data. The SED includes the jet component (dominated by the two prominent humps in radio and at high-energies) and the accretion disk emission, shown with a red line and yellow band to show its confidence range. Photometric data are shown with purple dots and orange upper limits, while the green line shows the SDSS spectroscopic data. The dataset and related best modeled SED clearly show the typical behavior of a high-z blazar, with a flat radio spectrum, strong Compton dominance, and prominent big blue bump. |
 |
Fig. 2. Zoomed-in visual of the most reliable model for 1508+5714, focused on the accretion disk emission. As in Fig. 1, photometric and spectroscopic data are indicated by purple points and a green line, respectively, while the red solid line indicates the SS73 model obtained with a mass of 4 × 108 M⊙ and an accretion rate of about 2%. The vertical black line highlights the Lyα line frequency, above which we suspect that the Meiksin (2006) algorithm over-corrects the intervening absorption. Therefore, we exclude that section of the spectrum in our modeling. |
The confidence intervals reported here are defined as those values outside which the SED does not properly describe the dataset reliably. Specifically, we explored the M and Ṁ parameter spaces to identify the limits for which the SED emission profile begin to deviate significantly from both photometric and spectroscopic data. These limits define our confidence interval. Noticeably, the confidence interval on the black hole mass derived with this approach is smaller than the intrinsic uncertainty on the virial-based M estimation method (∼0.4 dex). This first analysis suggests a sub-Eddington regime, with Ṁ/ṀEdd = 0.02 ± 0.01.
The analytic approximations we use in Sects. 3.2 and 3.3 require disk emission peak frequency and luminosity as input parameters. We hence derived these values for the best fitting SS73 model:
The confidence intervals on the peak position in frequency and luminosity are calculated as the peak values of the SED emission profiles obtained by assuming the confidence interval extremes of M and Ṁ as inputs (see Fig. 2).
3.2. Considering a spinning black hole
SS73 has been widely used to model AGN emission, including jetted sources and, in particular, blazars, but it has a strong limitation: it does not include any effects related to the black hole spin. Since jets in AGNs are generally associated with a spinning SMBH, we tested a model, which includes this parameter. The KERRBB (Li et al. 2005) model describes the emission from a geometrically thin and optically thick accretion disk, including the effects of general relativity on the dynamics and emission associated with a spinning black hole. The KERRBB does not have a significantly different emission profile, compared to SS73, particularly in the peak region. Hence, the former can reproduce the latter, and vice versa, with the right set of physical parameters. Additionally, we can use the peak position derived in Sect. 3.1 to apply the KERRBB analytic approximation developed by Campitiello et al. (2019, Eqs. A.1, A.2, and A.3):
where λ = Ld/LEdd is the luminosity-defined Eddington ratio, η(a) is the radiative efficiency that depends on the SMBH spin (see e.g., Madau et al. 2014), and gi(a, θ) is defined as
The parameters used in Eq. (11) are taken from Table 2 of Campitiello et al. (2018) and are listed in Table A.1, while a denotes the spin of the black hole. As for the anisotropy of the emission, we assumed that the disk was face on, and hence θ ∼ 0. This analytical approximation provides a family of sets of physical parameters – M, Ṁ, and a – that reproduce the SS73 emission profile fixed at specific peak coordinates, νp and νpL(νp). We derived this family of results for a set of spin values:
thus calculating the corresponding mass M and Eddington ratio λ. We followed a tighter sampling for the values corresponding to a corotating accretion disk, since this set up is most likely associated with jet launching. The set of M and λ estimates are shown in Fig. 3 (orange line) and reported in Table 2. These results outline a large black hole mass of Log M/M⊙ ∼ 8.2 − 8.5, compatible with the virial mass measured in Shen et al. (2011), and again point to a sub-Eddington accretion regime (∼0.03 − 0.06). We also estimated the values of the Eddington ratio, 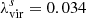 , and the spin, a = 0.627, corresponding to the virial mass value.
, and the spin, a = 0.627, corresponding to the virial mass value.
 |
Fig. 3. KERRBB (solid orange line) and SLIMBH (solid blue line) sets of M and λ values consistent with 1508+5714 data. The two sets of results are compared with the virial mass (vertical red line), in order to estimate the respective values of the Eddington ratio |
Physical parameters derived by accretion disk modeling with SS73, KERRBB, and SLIMBH.
Our analysis with the KERRBB analytical approximation highlights the need for a model designed specifically for super-Eddington accretion rates, in order to further test the sub-Eddington behavior suggested up to now.
3.3. Can it be super-Eddington?
In the context of a black hole accreting at rates Ṁ ∼ ṀEdd, a more accurate depiction of the accretion disk and its radiative emission is given by the SLIMBH model (Abramowicz et al. 1988; Sądowski 2009). In this model some of the initial assumptions of the α-disk are relaxed to obtain a more suitable description of the accretion disk. In particular:
-
The accreting matter follows a sub-Keplerian rotation in most of the disk and a super-Keplerian rotation in the inner part of the disk, instead of following a Keplerian motion as in SS73.
-
The inner edge of the disk is closer to the black hole than the corresponding rin = RISCO for high accretion rates.
-
The energy dissipation in SLIMBH depends strongly on advection processes, rather than radiative emission. This phenomenon changes the geometry from a thin to a slim disk and results in a lower radiative efficiency, with a consequently different emitted flux F(ν).
As for the case of KERRBB, the emission profile of SLIMBH is a multi-temperature blackbody with a peak profile consistent with SS73. Hence, we adopted the same approach as in Sect. 3.2 that focuses on an analytical approximation of the model developed by Campitiello et al. (2019):
These two equations yield
with the assumption that θ ∼ 0, g1 and g2 can be expressed as
Unlike in the KERRBB case, for this approximation the parameters α, β, γ, δ, ϵ depend on the Eddington ratio, and can be generalized as
The parameters 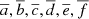 are listed in Table A.2, which is derived from Table A.2 of Campitiello et al. (2019) for the case with viewing angle θν = 0.
are listed in Table A.2, which is derived from Table A.2 of Campitiello et al. (2019) for the case with viewing angle θν = 0.
Similarly to the analytical approximation of KERRBB, sets of three parameters a, M, λ replicate the SS73 emission profile of the given peak coordinates. We hence followed a procedure analogous to that shown in Sect. 3.2 at the same fixed spin values (Eq. 12). Then, we numerically solved Eq. (15) to find the Eddington ratios and masses. The resulting family of solutions is available in Fig. 3 (in blue), which shows a large mass of 8.18 < Log M/M⊙ < 8.83 and a sub-Eddington accretion rate of 0.0320 < λ < 0.0624 (see Table 2). These values are consistent with those found using the KERRBB approximation. This is not surprising, given that SLIMBH at low accretion rates is consistent with the general relativistic assumptions included in KERRBB (see Table 2).
The range of results obtained from our analysis indeed help us draw a strong conclusion: 1508+5714 shows a sub-Eddington accretion regime even when a model specifically developed for close-to- or super-Eddington accretion is implemented.
4. A mature jetted black hole in a young Universe
According to all models tested, 1508+5714 accretes at a significantly sub-Eddington rate and hosts a massive black hole; however, these are not the most extreme values found for high-z quasars. This result has important implications for the evolutionary history of this source. If 1508+5714 had accreted at the same estimated Eddington ratio since its seed formation, its seed black hole mass would not be compatible with the current theoretical expectations for black hole formation in the early Universe (i.e., ∼100 M⊙).
Assuming a Salpeter timescale (Salpeter 1964) for its continuous accretion since z ∼ 20, we can estimate the black hole mass from which 1508+5714 began its evolution, as shown in Fig. 4. Depending on the assumed accretion disk model, the seed mass estimates slightly vary, but they are generally within the range of MS ∼ 2.5 × 106 − 5 × 108 M⊙, with a most likely value of ∼1.3 × 108 M⊙. The detailed values are reported in Table 3. These results are clearly problematic according to seed formation theories (see e.g., Volonteri 2012). In fact, even the hypothesis of the direct collapse of a massive gas cloud into a black hole would not lead to such massive compact objects.
 |
Fig. 4. Black hole mass evolution as a function of time (or redshift, upper axis), for the results obtained with the SLIMBH-based approach (consistent with KERRBB-based results). The data point shows 1508+5714 virial mass and the relative mass range obtained, as seen in Sect. 3.3. The solid blue line and light blue shaded area show how the mass would evolve if it followed the same accretion regime as derived with SLIMBH, starting from z = 20. The derived seed black hole masses, Ms, are labeled. The green shaded area, instead, follows an Eddington-limited evolution in the case of a radiative efficiency ranging between 5 and 10% (dotted and dashed lines, respectively). Following this accretion regime, seed black holes in the range 50−200 M⊙ are inferred between z = 5.5 and z = 8, respectively, as labeled. |
Seed black hole mass values.
Clearly, the assumption of continuous accretion with a fixed (small) Eddington ratio is not realistic. Simulations and theoretical models have recently suggested that high-z quasars may have undergone super-Eddington accretion episodes during their evolution, in order to account for such high masses assembled in a short lifetime. The excess of jetted AGNs observed at z > 4, combined with the necessity of super-Eddington phases, suggests a link between the two factors: the jet might facilitate faster accretion by exploiting part of the gravitational energy released during the accretion (Jolley & Kuncic 2008; Ghisellini et al. 2013), or it might be associated with faster accretion episodes through different channels.
Since fast-spinning black holes are expected to play a significant role in launching relativistic jets, it is plausible that a merger or a continuous accretion episode could efficiently spin up a black hole, ultimately triggering jet formation. Subsequently, the accretion flow can slow down and stabilize at a more moderate accretion rate, while the black hole partially spins down. In a simplified scenario, we assume that 1508+5714 has been accreting at the measured rate throughout its jet lifetime, following an earlier super-Eddington phase. Below, we estimate the possible seed black hole values in this framework: a continuous super-Eddington accretion episode followed by continuous accretion at the rate measured at z = 4.31 for as long as the relativistic jet has been active.
1508+5714 shows an extended jet in LOFAR images (Kappes et al. 2022). The authors estimate the age of this jetted structure by following various assumptions on its inclination and velocity. They derive an extension of 135 kpc with a hotspot speed of 0.06c, estimating an extended jet age of ∼7.3 Myr. The jet appears to be relatively young, which does not allow for a significantly extended evolution with a standard accretion. If we assume that 1508+5714 has maintained the observed accretion rate throughout the entire lifetime of its jet, its central black hole must have already acquired 97−99% of the mass measured at z = 4.31. We thus need to investigate how this mass range can be reached from a reasonable black hole seed (5 − 200 M⊙) before z = 4.329 (i.e., 7.3 Myr earlier than the measured redshift value for our source). To this end, we explore an accretion regime limited to the Eddington luminosity, considering two different assumptions for the radiative efficiency.
Assuming accretion with λ ∼ 1 implies a tight link between the matter accretion rate Ṁ/ṀEdd and the radiative efficiency, since η Ṁ/ṀEdd ∼ 1. We assume (i) a “standard” radiative efficiency of η = 0.1, which implies an accretion rate of Ṁ/ṀEdd = 10; and (ii) a lower radiative efficiency of η = 0.05, corresponding to Ṁ/ṀEdd = 20, which approximates a much lower optical depth or a stronger photon trapping effect, as typically found in highly accreting sources and/or rapidly spinning black holes. The choice of low radiative efficiencies is well supported by the literature, even when accretion occurs in a slim disk during the super-Eddington phase. The SMBH can be spun up by continuous, coherent accretion to near-maximal spin values, a ∼ 1, yet still exhibit lower radiative efficiencies compared to the expected value ∼0.3, due to photon trapping effects (Thorne 1974). If instead chaotic accretion dominates the Eddington or super-Eddington phases, the SMBH spin can be as low as a ∼ 0 (Dotti et al. 2013). Note that these values are in agreement with the results presented by Sądowski (2009) regarding super-Eddington accretion through a slim disk.
Following these assumptions, critical or super-critical accretion could have begun from a reasonable seed of ∼50 − 200 M⊙ as early as redshift z ∼ 8 − 5.5. This is an extremely conservative result in terms of black hole seed formation: by z ∼ 8, massive PopIII stars would have had enough time to evolve and collapse into a massive stellar black hole. We followed an approach that is oversimplified but can be easily applied to many massive jetted AGNs in the early Universe, in order to place more reasonable constraints on their evolution and provide better-informed observational limits to specific theoretical frameworks and simulations.
Another approach that allows for PopIII or massive stellar seed black holes at z ∼ 20 is the exploitation, by jet launching or accelerating mechanisms, of part of the gravitational energy released during accretion (Jolley & Kuncic 2008). Ghisellini et al. (2013) first suggested that the fraction of gravitational energy released, ηtot, can be divided into the radiative efficiency, η, which generates the observed accretion disk emission, and an equivalent “jet efficiency”, ηj, which indicates the fraction of accretion energy involved in launching and/or accelerating the relativistic jet. They suggested this toy model in order to account for the presence of z > 4, M > 109 M⊙ blazars. This simple assumption would reconcile an effective energy release of ηtot ∼ 0.3 from the disk around a maximally spinning black hole with a standard radiative efficiency of η ∼ 0.1, leading to much faster mass accretion onto the SMBH for a fixed observed luminosity. This toy model could be applied in our case too and would certainly help in deriving a ∼102 M⊙ seed black hole at z ∼ 20 for 1508+5714, if the jet were active during the entire process. Nevertheless, the ∼7 Myr old extended radio emission observed by LOFAR is not consistent with the jet age of about 1.3 Gyr required for the hypothesis by Ghisellini et al. (2013). This is why, in this work, we explored a super-critical approach leading to jet triggering, rather than this elegant solution, which has proven valid in the case of other z > 4 blazars.
5. Conclusions
In this paper we studied the broadband emission of the z = 4.31 Fermi-detected blazar 1508+5714, by mainly focusing on its accretion regime and the nature of its seed black hole.
-
We first modeled the overall broadband SED with an analytic approximation of a standard blazar profile. The broadband SED is well constrained in its high-energy part, thanks to the γ-ray detection. The strong Compton dominance is consistent with that observed in high-z blazars, i.e. typically more extreme than that derived for most Fermi-detected blazars.
-
We analyzed the IR-optical-UV emission of 1508+5714 using a standard α-disk model, varying its parameters to produce an emission profile that accurately describes the photometric and spectroscopic data. We derive a large black hole mass of Log M/M⊙ = 8.65 ± 0.19 and a sub-Eddington accretion rate of λ = 0.02 ± 0.01. These results are consistent with the virial-based values obtained in the literature.
-
We then modeled the big blue bump with an analytic approximation of KERRBB developed by Campitiello et al. (2018), which describes the emission from an accretion disk surrounding a spinning black hole and takes into account general relativistic effects. Even with this approach, 1508+5714 accretes significantly below the Eddington limit (Log M/M⊙ ∼ 8.2 − 8.5 and λ ∼ 0.03 − 0.6).
-
Lastly, we tested the analytic approximation of SLIMBH developed by Campitiello et al. (2019), which is similar to KERRBB but is extended to accretion rates higher than the Eddington limit. Despite the possibility of exploring faster accretion regimes, 1508+5714 once again accretes at a sub-Eddington rate, consistent with the KERRBB-based results.
The somewhat slow accretion rates obtained in this work are surprising in the context of such very high redshifts. Active SMBHs at z > 4 are always found to be very massive, and the age of the Universe in this redshift range (< 1.5 Gyr) is not enough for continuous, sub-critical, standard accretion to build them from even massive stellar seed black holes (∼102 M⊙). We thus explored the possibility that 1508+5714 had an early history of super-Eddington accretion, spinning up its black hole to the point of launching a relativistic jet, and only afterward accreted at the observed rates. With an estimate of the ∼7.3 Myr young jet age from LOFAR data (Kappes et al. 2022), we could reconcile the evolution of 1508+5714 with black hole seeds of stellar mass.
Once again, the extreme accretion regimes expected to assemble the observed mass distribution of quasars and blazars at very high redshifts are not caught in the act. Nonetheless, every z > 4 blazar detection or study suggests that relativistic jets might be involved in a fast accretion process, or at least be an effective tracer of a past super-critical event.
The highest values are derived for γ-ray detected sources included in the Swift/BAT and Fermi/LAT all-sky catalogs, while at z > 4 the Lorentz factors appear to be slightly smaller. This might be due to an intrinsic difference, or even to a lack of γ-ray detection, that does not allow for a proper modeling of the high-energy SED component.
Acknowledgments
We would like to thank the referee, Markus Boettcher, for the useful suggestions that helped to clarify and improve the paper. Part of this work is based on archival data and online services provided by the Space Science Data Center – ASI.
References
- Abramowicz, M. A., Czerny, B., Lasota, J. P., & Szuszkiewicz, E. 1988, ApJ, 332, 646 [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2017, ApJ, 837, L5 [CrossRef] [Google Scholar]
- Ajello, M., Costamante, L., Sambruna, R. M., et al. 2009, ApJ, 699, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Bañados, E., Momjian, E., Connor, T., et al. 2025, Nat. Astron., 9, 293 [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., & Dotti, M. 2013, MNRAS, 431, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Campitiello, S., Ghisellini, G., Sbarrato, T., & Calderone, G. 2018, A&A, 612, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campitiello, S., Celotti, A., Ghisellini, G., & Sbarrato, T. 2019, A&A, 625, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotti, M., Colpi, M., Pallini, S., Perego, A., & Volonteri, M. 2013, ApJ, 762, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Bañados, E., & Simcoe, R. A. 2023, ARA&A, 61, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Haardt, F., Della Ceca, R., Volonteri, M., & Sbarrato, T. 2013, MNRAS, 432, 2818 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Haardt, F., Ciardi, B., et al. 2015, MNRAS, 452, 3457 [Google Scholar]
- Ghisellini, G., Righi, C., Costamante, L., & Tavecchio, F. 2017, MNRAS, 469, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Gokus, A., Böttcher, M., Errando, M., et al. 2024, ApJ, 974, 38 [Google Scholar]
- Jolley, E. J. D., & Kuncic, Z. 2008, MNRAS, 386, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Kappes, A., Burd, P. R., Kadler, M., et al. 2022, A&A, 663, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreter, M., Gokus, A., Krauss, F., et al. 2020, ApJ, 903, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., Zimmerman, E. R., Narayan, R., & McClintock, J. E. 2005, ApJS, 157, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Liao, N.-H., Li, S., & Fan, Y.-Z. 2018, ApJ, 865, L17 [Google Scholar]
- Liu, Y., Wang, R., Momjian, E., et al. 2021, ApJ, 908, 124 [Google Scholar]
- Madau, P., Haardt, F., & Dotti, M. 2014, ApJ, 784, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A. 2006, MNRAS, 365, 807 [Google Scholar]
- Sądowski, A. 2009, ApJS, 183, 171 [CrossRef] [Google Scholar]
- Salpeter, E. E. 1964, ApJ, 140, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T. 2021, Galaxies, 9, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Nardini, M., et al. 2012, MNRAS, 426, L91 [Google Scholar]
- Sbarrato, T., Tagliaferri, G., Ghisellini, G., et al. 2013, ApJ, 777, 147 [Google Scholar]
- Sbarrato, T., Ghisellini, G., Tagliaferri, G., et al. 2015, MNRAS, 446, 2483 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [Google Scholar]
- Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
- Volonteri, M. 2012, Science, 337, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Haardt, F., Ghisellini, G., & Della Ceca, R. 2011, MNRAS, 416, 216 [Google Scholar]
Appendix A: KERRBB and SLIMBH parameters
In order to derive realistic estimates of mass, accretion rate and spin of 1508+5714, we applied two analytic approximations of numerical accretion models, i.e., KERRBB and SLIMBH as analyzed by (Campitiello et al. 2018, 2019). Tables A.1 and A.2 report in detail the parameters used to build the SED emission profiles of face-on accretion disks according to the two models.
Parameters used in Eq. 11 to define g1 and g2 in the KERRBB analytic approximation, as derived by Campitiello et al. (2018) for a viewing angle of θ = 0, and reported in their Table 2.
Parameters used in Eq. 17 to define the SLIMBH analytic approximation, as derived by Campitiello et al. (2019) for a viewing angle θ = 0.
All Tables
Parameters used in the phenomenological SED to describe the broadband photometry dataset.
Physical parameters derived by accretion disk modeling with SS73, KERRBB, and SLIMBH.
Parameters used in Eq. 11 to define g1 and g2 in the KERRBB analytic approximation, as derived by Campitiello et al. (2018) for a viewing angle of θ = 0, and reported in their Table 2.
Parameters used in Eq. 17 to define the SLIMBH analytic approximation, as derived by Campitiello et al. (2019) for a viewing angle θ = 0.
All Figures
 |
Fig. 1. Broadband SED of 1508+5714. The blue line indicates the total SED that best model the data. The SED includes the jet component (dominated by the two prominent humps in radio and at high-energies) and the accretion disk emission, shown with a red line and yellow band to show its confidence range. Photometric data are shown with purple dots and orange upper limits, while the green line shows the SDSS spectroscopic data. The dataset and related best modeled SED clearly show the typical behavior of a high-z blazar, with a flat radio spectrum, strong Compton dominance, and prominent big blue bump. |
| In the text | |
 |
Fig. 2. Zoomed-in visual of the most reliable model for 1508+5714, focused on the accretion disk emission. As in Fig. 1, photometric and spectroscopic data are indicated by purple points and a green line, respectively, while the red solid line indicates the SS73 model obtained with a mass of 4 × 108 M⊙ and an accretion rate of about 2%. The vertical black line highlights the Lyα line frequency, above which we suspect that the Meiksin (2006) algorithm over-corrects the intervening absorption. Therefore, we exclude that section of the spectrum in our modeling. |
| In the text | |
 |
Fig. 3. KERRBB (solid orange line) and SLIMBH (solid blue line) sets of M and λ values consistent with 1508+5714 data. The two sets of results are compared with the virial mass (vertical red line), in order to estimate the respective values of the Eddington ratio |
| In the text | |
 |
Fig. 4. Black hole mass evolution as a function of time (or redshift, upper axis), for the results obtained with the SLIMBH-based approach (consistent with KERRBB-based results). The data point shows 1508+5714 virial mass and the relative mass range obtained, as seen in Sect. 3.3. The solid blue line and light blue shaded area show how the mass would evolve if it followed the same accretion regime as derived with SLIMBH, starting from z = 20. The derived seed black hole masses, Ms, are labeled. The green shaded area, instead, follows an Eddington-limited evolution in the case of a radiative efficiency ranging between 5 and 10% (dotted and dashed lines, respectively). Following this accretion regime, seed black holes in the range 50−200 M⊙ are inferred between z = 5.5 and z = 8, respectively, as labeled. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



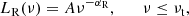
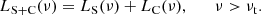
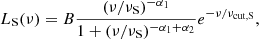
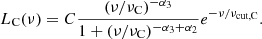
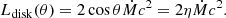
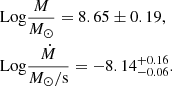
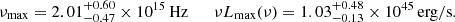
![$$ \begin{aligned}&\frac{M}{10^9\,M_\odot }=\left[\frac{g_1(a,\theta _\nu )\mathcal{A} }{\nu _p}\right]^2\sqrt{\frac{\nu _pL_p}{\mathcal{B} \cos \theta _\nu \, g_2(a,\theta _nu)}}, \end{aligned} $$](/articles/aa/full_html/2025/07/aa53555-24/aa53555-24-eq8.gif)
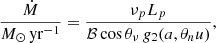
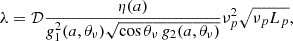
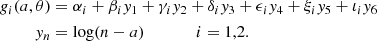
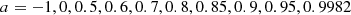
![$$ \begin{aligned}&\frac{\nu _p}{\mathrm{[Hz]}} = 1.22\mathcal{A} \lambda ^{1/4} \left[\frac{M}{10^9\,M_\odot }\right]^{-1/4}g_{1,s} (a,\theta _\nu ,\lambda ), \end{aligned} $$](/articles/aa/full_html/2025/07/aa53555-24/aa53555-24-eq15.gif)
![$$ \begin{aligned}&\frac{\nu _pL(\nu _p)}{\mathrm{[erg/s]}} = 2.21\mathcal{B} \lambda \left[\frac{M}{10^9\,M_\odot }\right]\cos (\theta _\nu )g_{2,s} (a,\theta _\nu ,\lambda ). \end{aligned} $$](/articles/aa/full_html/2025/07/aa53555-24/aa53555-24-eq16.gif)
![$$ \begin{aligned}{[\nu _pL(\nu _p)]^{1/4}\nu _p=\mathcal{E} [g_{2,s}(a,\theta _\nu , \lambda )\cos (\theta _\nu )]}^{1/4}[g_{1,s}(a,\theta _\nu , \lambda )]\sqrt{\lambda }, \end{aligned} $$](/articles/aa/full_html/2025/07/aa53555-24/aa53555-24-eq17.gif)