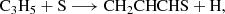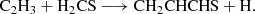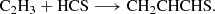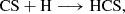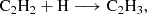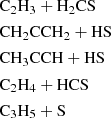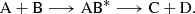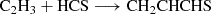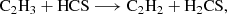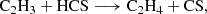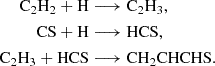EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (May 2025) A&A, 698 (2025) L24 Full HTML
Open Access
Issue
A&A
Volume 698, May 2025
Article Number L24
Number of page(s) 8
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202554670
Published online 16 June 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Sulphur is one of the most abundant elements in the Universe (S/H ∼ 1.35 × 10−5, Yamamoto 2017) but surprisingly, sulphur-bearing molecules are not as abundant as expected in the interstellar medium (ISM). The study of the sulphur chemistry in the ISM is an active research area (Vidal et al. 2017; Navarro-Almaida et al. 2020) due to several open questions regarding the processes that drive the production of sulphur-bearing species in the interstellar environments, as well as the considerable increase in the number of interstellar sulphurated molecules in the last four years, when almost 20% of all known sulphur species in space have been discovered. These detections include small neutral and charged species like NCS, HCCS, H2CCS, H2CCCS, C4S (Cernicharo et al. 2021a), HSO (Marcelino et al. 2023), HNSO (Sanz-Novo et al. 2024a), HC3S+ (Cernicharo et al. 2021b), HCCS+ (Cabezas et al. 2022), and HOCS+ (Sanz-Novo et al. 2024b). However, discoveries of sulphurated molecules meeting the definition of complex organic molecules (COMs, Herbst & van Dishoeck 2009) have also been reported: HCSCCH (Cernicharo et al. 2021c), HC4S (Fuentetaja et al. 2022), NCCHCS (Cabezas et al. 2024), CH3CHS (Agúndez et al. 2025), CH3SCH3 (Sanz-Novo et al. 2025), and c-C3H2S (Remijan et al. 2025). Nevertheless, none of the aforementioned molecules have been found to be a major reservoir of sulphur in the ISM. The numbers from TMC-1 can serve as an example of this fact. In this source, the inventory of detected sulphur molecules accounts for only 0.15% (Agúndez et al. 2025) of the cosmic abundance of sulphur (Asplund et al. 2009). This means that 99.85% of sulphur is missing in cold dense clouds. Potential reservoirs are gaseous atoms (Vidal et al. 2017), gaseous undetected molecules, and compounds such as hydrides or allotropes deposited onto dust grains (Jiménez-Escobar & Muñoz Caro 2011; Shingledecker et al. 2020).

While detections of new sulphur species in the ISM do not help explain the problem of sulphur depletion, they do provide valuable information from a chemical perspective. Sulphur belongs to the chalcogens, along with oxygen. However, these two elements have completely different chemistry in the ISM, even though they share similar electron configurations that enable them to form two covalent bonds in neutral molecules. Most of the interstellar sulphur-bearing molecules have their oxygenated counterpart detected as well, but not the other way round. There are many oxygen-bearing molecules for which the sulphur counterpart remains elusive. In addition, there is not a clear tendency regarding the abundances of the sulphur and oxygenated counterparts. All this has been discussed by Agúndez et al. (2025). Two groups of molecules exemplify these unpredictable behaviours: molecules with aldehyde (R–CHO) or thioaldehyde (R–CHS) moieties. Both aldehyde and thioaldehyde molecules with R = CH3, CCH, and CN have been detected in the ISM (Gottlieb 1973; Irvine et al. 1988; Remijan et al. 2008; Agúndez et al. 2025; Cernicharo et al. 2021c). However, the abundance ratios between the aldehyde and thioaldehyde do not follow any pattern, being 35, 46, and 0.27 for CH3CHO/CH3CHS, HCCCHO/HCCCHS, and NCCHO/NCCHS, respectively. The next aldehyde in complexity detected in space is propenal (CH2CHCHO), also known as acrolein. This species has been detected in several sources (Hollis et al. 2004; Requena-Torres et al. 2008; Manigand et al. 2021; Agúndez et al. 2021), but its sulphur cousin with the chemical formula CH2CHCHS (see Fig. 1), known as thioacrolein, prop-2-enethial, and propenethial (hereafter we use propenethial), has so far eluded detection in interstellar space. In this work, we present the astronomical detection using the QUIJOTE line survey of the thioaldehyde propenethial. The detection of the rotational lines for propenethial in TMC-1 has been achieved thanks to frequency predictions achieved from previous laboratory experiments and new data gathered from millimetre wave spectroscopy measurements of this molecule, which are also presented in this work.

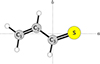thumbnail Fig. 1.

Molecular geometry of the trans conformation of propenethial depicted in the ab inertial plane.

2. Observations

The astronomical observations presented in this work are from the ongoing Yebes 40m Q-band line survey of TMC-1 from the QUIJOTE line survey. A detailed description of the line survey and the data-analysis procedure are provided in Cernicharo et al. (2021d); Cernicharo et al. (2022). Briefly, QUIJOTE consists of a line survey in the Q band (31.0–50.3 GHz) at the position of the cyanopolyyne peak of TMC-1 (αJ2000 = 4h41m41.9s and δJ2000 = +25 ° 41′27.0″). This survey is being carried out using a receiver built within the Nanocosmos project1 consisting of two cooled high-electron-mobility transistor (HEMT) amplifiers covering the Q band with horizontal and vertical polarisation. Fast Fourier transform spectrometers (FFTSs) with 8 × 2.5 GHz and a spectral resolution of 38.15 kHz provide the whole coverage of the Q band in both polarisations. Receiver temperatures are 16 K at 32 GHz, and 30 K at 50 GHz. The experimental setup is described in detail by Tercero et al. (2021).

All observations were performed using the frequency-switching observing mode with a frequency throw of 10 and 8 MHz. The total observing time on the source for data taken with frequency throws of 10 MHz and 8 MHz is 772.6 and 736.6 hours, respectively. Hence, the total observing time on source is 1509.2 hours. The QUIJOTE sensitivity varies between 0.06 mK at 32 GHz and 0.18 mK at 49.5 GHz. The main beam efficiency can be given across the Q band as Beff = 0.797 exp[−(ν(GHz)/71.1)2]. The forward telescope efficiency is 0.97. The telescope beam size at half power intensity is 54.4″ at 32.4 GHz, and 36.4″ at 48.4 GHz. The absolute calibration uncertainty is 10 %. The data were analysed with the GILDAS package2.

3. Results

3.1. Laboratory spectroscopy of CH2CHCHS

Table 1.

Spectroscopic constants of trans-propenethial (A-reduction, Ir-representation) in its ground vibrational state.

thumbnail Fig. 2.

Observed lines of CH2CHCHS in TMC-1. Frequencies and line parameters are given in Table 2. Quantum numbers for the observed transitions are indicated in each panel. The red line shows the synthetic spectrum computed for a rotational temperature of 9 K and a column density of 4.4 × 1010 cm−2 (see text). The blanked channels correspond to negative features created in the folding of the frequency-switching data. The 1σ noise level derived for the nominal spectral resolution of 38.15 kHz is indicated by a horizontal grey band. The observed intensity of the 61, 6-51, 5 and 60, 6-50, 5 lines is probably reduced by partial overlap with negative frequency-switching artefacts. The label U corresponds to unidentified features.

Table 2.

Observed line parameters for CH2CHCHS in TMC-1.

The most stable isomer of propenethial is the trans conformation (Ha et al. 1982). It is a planar near-prolate asymmetric rotor that belongs to Cs symmetry with C1–C2–C3–S dihedral angle of 180° (see Fig. 1). Stark modulation technique was used by Georgiou & Kroto (1980) to investigate its rotational spectrum from 26.5 to 40 GHz. Here, we extend the measurements to 144–179 and 293–321 GHz frequency regions using the Prague semiconductor millimetre wave spectrometer (Kania et al. 2006) employing frequency modulation with the second harmonic lock-in detection. More details are provided in Appendix A. As shown in Table 1, the number of ground state lines measured experimentally has now increased by more than a factor of ten, and the accessed quantum numbers have been significantly extended. The rotational and quartic centrifugal distortion constants have improved significantly over the previous study. Purely K-dependent sextic centrifugal distortion constants, ΦK and ϕK, could not be determined, and their values were fixed to those from quantum-chemical calculations at CCSD/cc-pVTZ level of theory. Table 1 further demonstrates that our calculations are in harmony with the rotational and centrifugal distortion constants obtained. This suggests that ΦJK and ϕJK from Georgiou & Kroto (1980) may have artificial values. The discrepancy in the sextic centrifugal distortion constants from Georgiou & Kroto (1980) and our constants can be explained by their determination primarily from two pairs of near degenerate Ka = 3 transitions, which emerged from reanalysing the previous data. When these transitions are combined with our data, they appeared as outliers and were excluded from the final fit. The molecule features strong a-type R-branch transitions given the dipole moment components μa = 2.58 ± 0.02 D and μb = 0.36 ± 0.04 D (Georgiou & Kroto 1980). These transitions represent the most relevant target from the observational point of view, and their precise predictions are generated on the basis of this work over a wide frequency range.

In addition to the ground state, we also analysed rotational transitions in the lowest-lying excited vibrational state, v18 = 1, and the ground state of the 34S isotopic species. The obtained results are discussed in Appendix A. The complete lists of measured and analysed rotational transitions are available in Zenodo.

3.2. Astronomical detection of CH2CHCHS in TMC-1

Using the frequencies predicted from the laboratory data (see Sect. 3.1 and Table 1), we searched for the Ka = 0 and 1 lines in our QUIJOTE line survey. Twelve lines, with J = 6 up to 9, lie within the coverage of our Q-band data. Of these, seven are confidently detected, centred at the systemic velocity of TMC-1 (5.83 km s−1; Cernicharo et al. 2020) with peak antenna temperatures around 0.5 mK (see Fig. 2). Two lines at the low frequency edge, the 61, 6–51, 5 and 60, 6–50, 5 at 32101.116 and 32571.104 MHz, respectively, are only marginally detected, as seen in the top left and middle panels of Fig. 2. Their intensities are very probably reduced by partial overlap with the negative frequency-switching artefact of weak (< 1 mK) lines lying at ±8 MHz. The remaining three lines covered by our survey are not detected. The transition 81, 7–71, 6, predicted at 44 082.705 MHz, is fully blended with a strong signal arising from the hyperfine component 55–45 of H13CCCN. The other two non-detected lines correspond to the 90, 9–80, 8 and 91, 8–81, 7 transitions, at 48825.731 and 49589.877 MHz, respectively. These two lines are predicted with similar intensities to that of the 91, 9–81, 8 transition, which is detected at 48143.659 MHz. However, they are not observed because the noise is significantly higher in that region of the spectrum. Once we were fully confident in the presence of CH2CHCHS in TMC-1, we searched for the Ka = 2 lines; however, their predicted intensities are below the sensitivity of our data. The derived line parameters for all the observed transitions are given in Table 2.

In order to determine the column density of CH2CHCHS in TMC-1, we assumed local thermodynamic equilibrium (LTE). The sizeable errors in the velocity integrated intensities do not allow us to constrain the rotational temperature precisely. We thus adopted a rotational temperature of 9 K, the gas kinetic temperature in TMC-1 (Agúndez et al. 2023), which is consistent with the observed relative intensities. In addition, we adopted an intrinsic linewidth of 0.6 km s−1 and an emission distribution consisting of a circle with a diameter of 80″, which is compatible with the emission size of most of the molecules mapped in TMC-1 (Cernicharo et al. 2023). Using the derived molecular constants from Table 1 and adopting the dipole moment components of μa = 2.58 D and μb = 0.36 D (Georgiou & Kroto 1980), we derived a column density for CH2CHCHS in TMC-1 of 4.4 × 1010 cm−2.

4. Discussion

The column density value determined in TMC-1 for CH2CHCHS is the smallest one found to date for a thioaldehyde derivative in this source. The more abundant substituted thioaldehyde in TMC-1 is NCCHS with a column density value of 1.3 × 1012 cm−2 (Cernicharo et al. 2021c), followed by HCCCHS and CH3CHS, with abundances of 3.2 × 1011 and 9.8 × 1010 cm−2, respectively (Cernicharo et al. 2021c; Agúndez et al. 2025). CH2CHCHS is 27 and 6.8 times less abundant than NCCHS and HCCCHS, respectively, but just 2 times less abundant than CH3CHS. As recently shown in Agúndez et al. (2025), many of the sulphur-bearing species with a detected oxygen counterpart show significant differences in their abundance ratio behaviour, and as mentioned in the introduction, the thioaldehyde derivatives are examples of this. Adopting the column density derived for CH2CHCHO of 2.2 × 1011 cm−2 (Agúndez et al. 2021), the CH2CHCHO/CH2CHCHS abundance ratio is 4.7. This value is completely different for the ratios found for CH3CHO/CH3CHS, HCCCHO/HCCCHS and NCCHO/NCCHS, which are 35, 46, and 0.27 respectively.

With regard to the chemistry of CH2CHCHS, there is insufficient data in the literature to conclusively determine a dominant formation pathway. Therefore, we conducted quantum chemical calculations to at least rule out non-viable reactive pathways. Our simulations include both gas-phase and surface-phase chemical routes. Further details on the computational methods and results are provided in Appendix B, while we summarise the main findings here. We investigated the feasibility of forming CH2CHCHS in both the gas phase and on dust grains through exploratory calculations. Among all the possible gas-phase reactions, we identified the following neutral-neutral reactions as potential contributors:

C 3 H 5 + S ⟶ CH 2 CHCHS + H , $$ \begin{aligned} \mathrm{C}_3\mathrm{H}_5 + \mathrm{S}&\longrightarrow \mathrm{CH}_2\mathrm{CHCHS + H}, \end{aligned} $$(1)

C 2 H 3 + H 2 CS ⟶ CH 2 CHCHS + H . $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_3 + \mathrm{H}_2\mathrm{CS}&\longrightarrow \mathrm{CH}_2\mathrm{CHCHS + H}. \end{aligned} $$(2)

The first reaction is likely barrierless, although a full determination of branching ratios and competing pathways is postponed to a future study. The second reaction exhibits a small activation barrier of ≥0.7 kcal mol−1 at the level of theory used in our calculations. However, as discussed in Appendix B, this value is within the uncertainty range of our computational method, and the reaction may be barrierless when investigated with higher-level quantum chemistry techniques. A more comprehensive study of these gas-phase reactions is thus warranted. We also investigated the neutral-neutral gas-phase reactions C2H4 + HCS, CH3CCH + HS, and CH2CCH2 + HS as potential sources of CH2CHCHS. However, we find that all of them have sizeable barriers at the entrance channel for the addition. The two latter reactions also theoretically show barriers for the H abstraction channel (Zeng et al. 2016).

We also considered a grain-surface synthesis pathway for CH2CHCHS through the reaction

C 2 H 3 + HCS ⟶ CH 2 CHCHS . $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_3 + \mathrm{HCS} \longrightarrow \mathrm{CH}_2\mathrm{CHCHS}. \end{aligned} $$(3)

Our preliminary calculations, based on an isolated model, suggest that this reaction is barrierless. However, the relatively high binding energies of C2H3 and HCS on water ice (Wakelam et al. 2017; Perrero et al. 2022) significantly hinder its occurrence via conventional diffusive chemistry. Given the substantial exothermicity of the precursor formation reactions (Lamberts 2018; Molpeceres & Rivilla 2022):

CS + H ⟶ HCS , $$ \begin{aligned} \mathrm{CS + H}&\longrightarrow \mathrm{HCS}, \end{aligned} $$(4)

C 2 H 2 + H ⟶ C 2 H 3 , $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_2 + \mathrm{H}&\longrightarrow \mathrm{C}_2\mathrm{H}_3, \end{aligned} $$(5)

along with the high abundance of CS and C2H2 in the ISM, we propose that a non-thermal mechanism could play a crucial role in the grain-surface synthesis of CH2CHCHS.

In addition to neutral-neutral reactions in both the gas phase and on grains, other potential formation mechanisms include ion-molecule reactions in the gas (followed by dissociative recombination), radiative association, or alternative non-thermal grain-mantle processes such as radiolysis. Future studies, combining high-level quantum chemical calculations and astrochemical modelling, will be necessary to comprehensively assess the viability and significance of these formation pathways.

The anomalous ratios observed for acrolein (CH2CHCHO) and propenethial (CH2CHCHS) compared to other thioaldehydes detected in TMC-1 are puzzling. If CH2CHCHS were predominantly formed via grain-surface or mantle reactions, these ratios would be difficult to justify, as CO, and consequently HCO, the oxygen analogue of HCS, is a major constituent of ISM ices. This suggests that gas-phase chemistry plays a dominant role in the formation of CH2CHCHS, as it provides a natural explanation for the observed S-bearing/O-bearing ratios. The literature on acrolein formation pathways is limited but still more extensive than that for sulphur analogues. It is known that reactions such as HCO + C2H4, CH3CCH + OH, and CH2CCH2 + OH do not produce CH2CHCHO in significant amounts (Xie et al. 2005a; Taylor et al. 2008; Daranlot et al. 2012; Zádor & Miller 2015). Additionally, H2CO + C2H3 has been shown to be unfeasible (Xie et al. 2005b), whereas our results suggest that the analogous reaction with thioformaldehyde may still be a viable pathway. The significant differences in sulphur versus oxygen atom addition observed in the C2H5 + S/O → C2H4S/O + H reaction (Agúndez et al. 2025) further support the idea that a similar mechanism could be at play in the formation of CH2CHCHS/O, favouring the sulphur-bearing molecule in this case. Moreover, destruction reactions in both the gas phase and on grains could also influence the relative abundances of CH2CHCHS/O, especially considering the higher dipole moment of CH2CHCHO (3.11 D, Wagner et al. 1957), which may enhance its depletion through gas-phase processes.

5. Conclusions

In the present work, we report the detection of a new sulphur-bearing molecule, propenethial, in TMC-1. The discovery of this sulphur analogue of acrolein is based on previous microwave work and new measurements between 144 and 321 GHz, which confirm the accuracy of the previous data and have led to considerable progress in determining the spectroscopic parameters. Accurate predictions of rotational transition frequencies are now available up to the millimetre wave region and can be further used in the future for the analysis of other line surveys. The investigation of possible chemical pathways to explain our observations suggests that, in the absence of a detailed study on the chemistry of CH2CHCHS, its formation likely results from a combination of gas- and surface-phase reactions. Particularly striking and key to identifying the dominant formation mechanism is the low CH2CHCHO/CH2CHCHS ratio, which points to a gas-phase pathway that is efficient for the S-bearing molecule, but not for its O-bearing counterpart. Propenethial emerges as one of the most complex sulphur-bearing molecules ever detected in the ISM and the most complex identified in TMC-1. Its unsaturated backbone, however, provides a reactive scaffold that could further increase its chemical complexity through interactions with reactive radicals.

6. Data availability

Laboratory data underlying this article are available through the Zenodo repository: https://doi.org/10.5281/zenodo.15395849. The data comprise experimentally measured frequencies of the trans-propenethial in the ground state and the lowest-lying excited vibrational state of the parent species, as well as the ground state of the 34S isotopic species.

Acknowledgments

This work was based on observations carried out with the Yebes 40m telescope (projects 19A003, 20A014, 20D023, 21A011, 21D005, and 23A024). The 40m radiotelescope at Yebes Observatory is operated by the Spanish Geographic Institute (IGN, Ministerio de Transportes y Movilidad Sostenible). We acknowledge funding support from Spanish Ministerio de Ciencia e Innovación through grants PID2022-137980NB-I00, PID2022-136525NA-I00 and PID2023-147545NB-I00. Laboratory spectroscopic work was funded by the Czech Science Foundation (GACR, grant No. 24-12586S). Prague authors gratefully acknowledge this financial support. Computational resources were provided by the e-INFRA CZ project (ID:90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic. G. M. acknowledges the support of the grant RYC2022-035442-I funded by MCIN/AEI/10.13039/501100011033 and ESF+. G.M. also received support from project 20245AT016 (Proyectos Intramurales CSIC). We acknowledge the computational resources provided by the DRAGO computer cluster managed by SGAI-CSIC, and the Galician Supercomputing Center (CESGA). The supercomputer FinisTerrae III and its permanent data storage system have been funded by the Spanish Ministry of Science and Innovation, the Galician Government and the European Regional Development Fund (ERDF).

References

  1. Agúndez, M., Marcelino, N., Tercero, B., et al. 2021, A&A, 649, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Agúndez, M., Marcelino, N., Tercero, B., Jiménez-Serra, I., & Cernicharo, J. 2023, A&A, 677, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Agúndez, M., Molpeceres, G., Cabezas, C., et al. 2025, A&A, 693, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cabezas, C., Agúndez, M., Marcelino, N., et al. 2022, A&A, 657, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Cabezas, C., Agúndez, M., Endo, Y., et al. 2024, A&A, 686, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020, A&A, 642, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021a, A&A, 648, L3 [EDP Sciences] [Google Scholar]
  9. Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021b, A&A, 646, L3 [EDP Sciences] [Google Scholar]
  10. Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021c, A&A, 650, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021d, A&A, 652, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cernicharo, J., Fuentetaja, R., Agúndez, M., et al. 2022, A&A, 663, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cernicharo, J., Tercero, B., Marcelino, N., Agúndez, M., & de Vicente, P. 2023, A&A, 674, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Daly, A. M., Bermúdez, C., Kolesniková, L., & Alonso, J. L. 2015, ApJS, 218, 30 [Google Scholar]
  15. Daranlot, J., Hickson, K. M., Loison, J.-C., et al. 2012, J. Phys. Chem. A, 116, 10871 [Google Scholar]
  16. Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [Google Scholar]
  17. Fuentetaja, R., Agúndez, M., Cabezas, C., et al. 2022, A&A, 667, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Garrod, R. T., Jin, M., Matis, K. A., et al. 2022, ApJS, 259, 1 [NASA ADS] [CrossRef] [Google Scholar]
  19. Georgiou, K., & Kroto, H. 1980, J. Mol. Spectrosc., 83, 94 [Google Scholar]
  20. Gottlieb, C. A. 1973, Molecules in the Galactic Environment, (Wiley-Interscience), 181. [Google Scholar]
  21. Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [Google Scholar]
  22. Ha, T.-K., Nguyen, M. T., & Vanquickenborne, L. 1982, Z. Naturforsch. A, 37, 125 [Google Scholar]
  23. Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Møllendal, H. 2004, ApJ, 610, L21 [Google Scholar]
  25. Irvine, W. M., Brown, R. D., Cragg, D. M., et al. 1988, ApJ, 335, L89 [Google Scholar]
  26. Jiménez-Escobar, A., & Muñoz Caro, G. M. 2011, A&A, 536, A91 [Google Scholar]
  27. Jin, M., & Garrod, R. T. 2020, ApJS, 249, 26 [Google Scholar]
  28. Kania, P., Stříteská, L., Šimečková, M., & Urban, Š. 2006, J. Mol. Struct., 795, 209 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kisiel, Z., Pszczółkowski, L., Medvedev, I. R., et al. 2005, J. Mol. Spectrosc., 233, 231 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kisiel, Z., Pszczółkowski, L., Drouin, B. J., et al. 2012, J. Mol. Spectrosc., 280, 134 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kobayashi, H., Hidaka, H., Lamberts, T., et al. 2017, ApJ, 837, 155 [Google Scholar]
  32. Koucký, J., Kolesniková, L., Uhlíková, T., et al. 2012, J. Chem. Phys., 136, 094309 [Google Scholar]
  33. Lamberts, T. 2018, A&A, 615, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Maeda, S., & Harabuchi, Y. 2021, WIREs Comput. Mol. Sci., 11 [CrossRef] [Google Scholar]
  35. Maeda, S., & Morokuma, K. 2010, J. Chem. Phys., 132, 241102 [Google Scholar]
  36. Maeda, S., Ohno, K., & Morokuma, K. 2013, Phys. Chem. Chem. Phys., 15, 3683 [NASA ADS] [CrossRef] [Google Scholar]
  37. Manigand, S., Coutens, A., Loison, J.-C., et al. 2021, A&A, 645, A53 [EDP Sciences] [Google Scholar]
  38. Marcelino, N., Puzzarini, C., Agúndez, M., et al. 2023, A&A, 674, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Matthews, D. A., Cheng, L., Harding, M. E., et al. 2020, J. Chem. Phys, 152, 214108 [NASA ADS] [CrossRef] [Google Scholar]
  40. McKellar, A., & Appadoo, D. 2008, J. Mol. Spectrosc., 250, 106 [Google Scholar]
  41. Molpeceres, G., & Rivilla, V. M. 2022, A&A, 665, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Navarro-Almaida, D., Le Gal, R., Fuente, A., et al. 2020, A&A, 637, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Neese, F., Wennmohs, F., Becker, U., & Riplinger, C. 2020, J. Chem. Phys., 152, 224108 [NASA ADS] [CrossRef] [Google Scholar]
  44. Perrero, J., Enrique-Romero, J., Ferrero, S., et al. 2022, ApJ, 938, 158 [NASA ADS] [CrossRef] [Google Scholar]
  45. Purvis, G. D., III, & Bartlett, R. J. 1982, J. Chem. Phys., 76, 1910 [NASA ADS] [CrossRef] [Google Scholar]
  46. Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [Google Scholar]
  47. Remijan, A. J., Changala, P. B., Xue, C., et al. 2025, ApJ, 982, 191 [Google Scholar]
  48. Requena-Torres, M. A., Martín-Pintado, J., Martín, S., & Morris, M. R. 2008, ApJ, 672, 352 [Google Scholar]
  49. Sanz-Novo, M., Rivilla, V. M., Müller, H. S. P., et al. 2024a, ApJ, 965, L26 [Google Scholar]
  50. Sanz-Novo, M., Rivilla, V. M., Jiménez-Serra, I., et al. 2024b, ApJ, 965, 149 [Google Scholar]
  51. Sanz-Novo, M., Rivilla, V. M., Endres, C. P., et al. 2025, ApJ, 980, L37 [Google Scholar]
  52. Shingledecker, C. N., Lamberts, T., Laas, J. C., et al. 2020, ApJ, 888, 52 [Google Scholar]
  53. Taylor, S. E., Goddard, A., Blitz, M. A., et al. 2008, PCCP, 10, 422 [CrossRef] [Google Scholar]
  54. Tercero, F., López-Pérez, J. A., Gallego, J. D., et al. 2021, A&A, 645, A37 [EDP Sciences] [Google Scholar]
  55. Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [Google Scholar]
  56. Wagner, R., Fine, J., Simmons, J. W., & Goldstein, J. H. 1957, J. Chem. Phys., 26, 634 [Google Scholar]
  57. Wakelam, V., Loison, J. C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [Google Scholar]
  58. Watson, J. K. G. 1977, in Vibrational Spectra and Structure, ed. J. R. Durig (Amsterdam: Elsevier), 6, 1 [NASA ADS] [Google Scholar]
  59. Werner, H.-J., Knowles, P. J., Manby, F. R., et al. 2020, J. Chem. Phys., 152, 144107 [NASA ADS] [CrossRef] [Google Scholar]
  60. Xie, H.-B., Ding, Y.-H., & Sun, C.-C. 2005a, J. Theor. Comput. Chem., 04, 1029 [Google Scholar]
  61. Xie, H.-B., Ding, Y.-H., & Sun, C.-C. 2005b, J. Phys. Chem A., 109, 8419 [Google Scholar]
  62. Yamamoto, S. 2017, Introduction to Astrochemistry: Chemical Evolution from Interstellar Clouds to Star and Planet Formation (Springer) [Google Scholar]
  63. Zádor, J., & Miller, J. A. 2015, Proc. Comb. Inst., 35, 181 [Google Scholar]
  64. Zeng, Z., Altarawneh, M., Oluwoye, I., Glarborg, P., & Dlugogorski, B. Z. 2016, J. Phys. Chem A, 120, 8941 [Google Scholar]
  65. Zhao, Y., & Truhlar, D. G. 2008, Theo. Chem. Acc., 120, 215 [Google Scholar]
  66. Zheng, J., Xu, X., & Truhlar, D. G. 2011, Theo. Chem. Acc., 128, 295 [Google Scholar]

Appendix A: Details on the laboratory spectroscopy

Following the work of Georgiou & Kroto (1980), the sample of propenethial was prepared by pyrolysis of diallyl sulphide in a quartz tube situated in a cylindrical furnace, with the temperature set to 500 °C. The produced mixture containing also a by-product propene (CH2CHCH3) was introduced into a 2.8 metre long glass cell of the spectrometer without further purification. The optical path was doubled using a polarization grid and a rooftop mirror. The millimetre wave radiation was modulated at the frequency of 28 kHz and the detection system was completed by a demodulation procedure achieved by a lock-in amplifier working at twice the modulation frequency. The measurements were performed under the gas flow conditions at a total pressure between 20 and 30 μbar. A portion of the spectrum is shown in Fig. A.1. The second derivative shape of the lines was fitted to the Gaussian profile function using the Assignment and Analysis of Broadband Spectra (AABS) programme package (Kisiel et al. 2005, 2012).

Quantum-chemical calculations were performed in parallel with the experimental procedure. In particular, we were interested in obtaining reliable estimations of sextic centrifugal distortion constants of the trans conformer. We used coupled cluster theory with single and double substitutions (CCSD, Purvis & Bartlett 1982) with Dunning’s correlation-consistent triple-ζ (cc-pVTZ) basis set (Dunning 1989). The calculations were carried out using the CFOUR programme package (Matthews et al. 2020) and converged to 10−11 atomic units in energy, coupled-cluster amplitude equations, and Hartree–Fock self-consistent field equations. The results are listed in Table 1. The same calculations were undertaken also for the 34S isotopic species (see Table A.1). For completeness, we geometrically optimised also the less stable cis form of propenethial and its spectroscopic constants are provided in Table A.2. However, the obtained zero-point corrected relative energy of 901 cm−1 indicates that its population under the conditions of the present experiment is negligible.

Regularly spaced groups of the ground state a-type R-branch transitions of trans-propenethial were easily identified in the spectrum. Predictions based on molecular parameters from Georgiou & Kroto (1980) allowed smooth and iterative line assignments up to Ka = 16. At this stage, the fit required quartic and sextic centrifugal distortion constants. However, transitions with Ka ≥ 17 were significantly better fitted when a single octic term, LKKJ, was introduced among the adjusted parameters. Finally, several b-type Q- and R-branch transitions were identified in the spectrum. These transitions were more than fifty times weaker than a-type transitions, which is in good agreement with the measured dipole moment components μa = 2.58 ± 0.02 D and μb = 0.36 ± 0.04 D from Georgiou & Kroto (1980). The measured transitions were merged with those from Georgiou & Kroto (1980) and analysed globally employing the A-reduced rotational Hamiltonian in Ir representation (Watson et al. 1977) as implemented in our own programme. S-reduced Hamiltonian was also tested and led to results of very similar quality. As already mentioned in Sect. 3.1, the obtained set of parameters in Table 1 is extended and improved with respect to previous study and, in addition, it matches well our quantum-chemical calculations. As far as the octic constant is concerned, its value might be affected by starting interactions with the lowest-lying excited vibrational state v18 = 1, which lies 140 ± 30 cm−1 above the ground state (Georgiou & Kroto 1980). In fact, we observed signs of perturbations for Ka ≥ 20 transitions especially in the higher-frequency region of our records. Therefore, these transitions were not included in the analysis. The observation of perturbations in the ground state spectra of propenethial is not surprising because the same situation was found for acrolein, the oxygen analogue of propenethial (Daly et al. 2015).

Table A.1 shows that we made progress also in the analysis of v18 = 1 excited vibrational state in terms of the assigned quantum numbers, the number of distinct frequency lines and the parameters determined. However, significant differences in parameter values are evident in comparison to the ground state. This behaviour can be attributed to vibrational-rotational interactions, which were a major complication also in the analysis of the oxygen analogue acrolein (Daly et al. 2015; McKellar & Appadoo 2008). It was shown that in acrolein, v18 = 1 state cannot be properly analysed without considering v13 = 1 state, which in turn requires a simultaneous analysis of v18 = 2 state, and so on. It is highly probable that a similar network of interacting states exists in propenethial. Neglecting these interactions inevitably leads to, for instance, the opposite signs of ΔK and δK parameters compared to the ground state values.

thumbnail Fig. A.1.

Section of the rotational spectrum of propenethial with the assignments of groups of lines belonging to J = 27 ← 26 rotational transitions in the ground state and v18 = 1 excited vibrational state.

Final remarks concern singly substituted isotopic species. Very good signal-to-noise ratio observed in our spectra permitted the identification of rotational transitions of 34S isotopologue in natural abundance. Some transitions were observed also for 13C isotopic species. However, due to frequent blends with strong lines belonging to vibrational satellites of the parent species, we did not proceeded with their analyses. The assignments for 34S isotopologue undertaken by Georgiou & Kroto (1980) were used as the starting point for the present work. Only a-type R-branch transitions were observed and their analysis led to the spectroscopic constants presented in Table A.1. Note, that the rotational constant A is now experimentally determined; in the work of Georgiou & Kroto (1980) it was only estimated from the ground state inertial defect of the parent species. Due to the smaller data set and diversity in transition types in comparison with the parent species, some constants were fixed to their most reliable estimates. Since the experimental ratios of parameters 32X/34X of the 32S and 34S isotopologues are typically well reproduced by quantum-chemical calculations (Koucký et al. 2012), we constrained several constants to scaled values 34Xsc obtained using the simple equation: 34Xsc≅ 32Xexp × (34Xcalc/32Xcalc). Almost identical results are also obtained by fixing their values to those of the parent species, which is another common practice in rotational spectroscopy.

Table A.1.

Spectroscopic constants of trans-propenethial (A-reduction, Ir-representation) in the ground state and lowest-lying excited vibrational state of the parent species 32S, and the ground state of the 34S isotopic species.a

Table A.2.

Spectroscopic constants of cis-propenethial (A-reduction, Ir-representation) calculated at CCSD/cc-pVTZ level of theory.

Appendix B: Details on the quantum chemical calculations of reactivity

B.1. Simulation of gas-phase reactivity

We first explored the following neutral-neutral gas-phase reactions as the most straightforward pathways for the formation of CH2CHCHS:

C 2 H 3 + H 2 CS CH 2 CCH 2 + HS CH 3 CCH + HS C 2 H 4 + HCS C 3 H 5 + S $$ \begin{aligned}&\mathrm{C}_2\mathrm{H}_3 + \mathrm{H}_2\mathrm{CS} \\&\mathrm{CH}_2\mathrm{CCH}_2 + \mathrm{HS} \\&\mathrm{CH}_3\mathrm{CCH + HS} \\&\mathrm{C}_2\mathrm{H}_4 + \mathrm{HCS} \\&\mathrm{C}_3\mathrm{H}_5 + \mathrm{S} \end{aligned} $$(B.1)

Rather than simulating the entire reaction pathway, we determined the entrance barriers, if any, for the formation of the association complex in the gas phase. Specifically, we examined the formation of AB* in the reaction scheme:

A + B ⟶ AB ∗ ⟶ C + D . $$ \begin{aligned} \mathrm{A} + \mathrm{B} \longrightarrow \mathrm{AB}^{*} \longrightarrow \mathrm{C + D}. \end{aligned} $$(B.2)

This approach provides a lower bound for the reaction barrier, which, in several cases, corresponds to the actual barrier height. We focused solely on addition reactions that lead to the formation of reactive adducts, deferring the study of hydrogen abstraction reactions to future work.

The systematic investigation was performed using the MC-AFIR algorithm implemented in the GRRM23 code (Maeda & Morokuma 2010; Maeda et al. 2013; Maeda & Harabuchi 2021), interfaced with the ORCA (v.6.0.0) code (Neese et al. 2020). The RCCSD(T)/aug-cc-pVTZ//M06-2X(D3)/ma-def2-SVP model chemistry (Purvis & Bartlett 1982; Dunning 1989; Zhao & Truhlar 2008; Zheng et al. 2011; Grimme et al. 2010) was employed, with CCSD(T) calculations carried out using MOLPRO (Werner et al. 2020).

Table B.1.

Reaction energies and activation barriers with energies for gas phase reactions in kcal mol−1.

The results for the sampled processes leading to an association complex are collated in Table B.1. Among all the considered reactions, and as indicated in the main text, the reaction between the propyl radical (C3H5) and atomic sulphur (Reaction B.5) emerges as a promising candidate for the formation of the title molecule, owing to the barrierless nature of the complex formation. We identify two possible complexes from this reaction, namely CH2CHCSH2 and c-CH2SCH-CH2. The latter would require extensive molecular reorganization to yield CH2CHCHS, whereas the former could lead to the molecule via direct hydrogen elimination. Interestingly, the possibility of forming a complex at every position of C3H5 arises from the electronic structure of the radical, where the spin density is delocalised over the entire molecule. Further investigations into the reactivity of this radical and its associated reactions are warranted. Nevertheless, it is important to highlight that complex formation via S-atom radical coupling does not always proceed through hydrogen elimination. This is evident in the case of the reaction S + C2H5, where the elimination of HS was found to be the preferred pathway (Agúndez et al. 2025).

All the other reactions (Reactions B.1-B.4) exhibit activation energies that limit their plausibility in forming CH2CHCSH2. However, we found that Reaction B.1 presents an activation barrier of 0.7 kcal mol−1, a value within the uncertainty of the theoretical method used in our calculations. This suggests a more in-depth investigation of this pathway, although, as mentioned above, the formation of a favourable complex alone is not a sufficient condition to ensure the production of a given product.

In summary, our initial exploration suggests Reaction B.5, and potentially Reaction B.1, as possible sources for the formation of CH2CHCSH2.

B.2. Testing potential reactivity atop surfaces

We also considered the radical coupling reaction on ices:

C 2 H 3 + HCS ⟶ CH 2 CHCHS $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_3 + \mathrm{HCS} \longrightarrow \mathrm{CH}_2\mathrm{CHCHS} \end{aligned} $$(B.3)

which could take place on dust grains due to the third-body effect exerted by the ice matrix. To assess the viability of this reaction, we investigated its minimum energy path (MEP) in the absence of an explicit water matrix (e.g. assuming a minor role of the ice in the emergence of kinetic barriers), serving as a preliminary step towards a more in-depth study. Alternative grain-surface reactions, such as:

C 2 H 3 + HCS ⟶ C 2 H 2 + H 2 CS , $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_3 + \mathrm{HCS} \longrightarrow \mathrm{C}_2\mathrm{H}_2 + \mathrm{H}_2\mathrm{CS}, \end{aligned} $$(B.4)

or

C 2 H 3 + HCS ⟶ C 2 H 4 + CS , $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_3 + \mathrm{HCS} \longrightarrow \mathrm{C}_2\mathrm{H}_4 + \mathrm{CS}, \end{aligned} $$(B.5)

could also be relevant. However, their occurrence would only modulate the formation efficiency of CH2CHCHS rather than preclude its formation. The MEP for Reaction B.7, computed at the M06-2X(D3)/ma-def2-TZVP level of theory, is depicted in Fig. B.1, demonstrating a clear barrierless pathway for the formation of the title molecule.

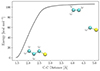thumbnail Fig. B.1.

Minimum energy path for reaction B.7 on dust grains obtained from a potential energy scan. The initial (reactant) and final (product) states are shown as insets.

However, in the context of grain-surface chemistry at the low temperatures of TMC-1, the presence of a barrierless reaction pathway alone does not guarantee its viability. This limitation arises primarily due to the need for reactants to diffuse and encounter each other on dust grains. The diffusion probability of a species depends on its binding energy. Reported binding energies for HCS and C2H3 are 2300 K (Perrero et al. 2022) and ∼2800 K (Wakelam et al. 2017), respectively, suggesting that both species are essentially immobile on a water-ice-coated dust particle at 10 K. Consequently, the formation of CH2CHCHS via Reaction B.7 cannot be explained by conventional diffusive chemistry.

As a first approach to address this limitation, we propose a non-thermal mechanism (Jin & Garrod 2020; Garrod et al. 2022) for CH2CHCHS formation, following the reaction sequence:

C 2 H 2 + H ⟶ C 2 H 3 , CS + H ⟶ HCS , C 2 H 3 + HCS ⟶ CH 2 CHCHS . $$ \begin{aligned} \mathrm{C}_2\mathrm{H}_2 + \mathrm{H}&\longrightarrow \mathrm{C}_2\mathrm{H}_3, \\ \mathrm{CS} + \mathrm{H}&\longrightarrow \mathrm{HCS}, \\ \mathrm{C}_2\mathrm{H}_3 + \mathrm{HCS}&\longrightarrow \mathrm{CH}_2\mathrm{CHCHS}. \end{aligned} $$(B.6)

In the first two reactions, a fraction of the released reaction energy can be transferred to the products, enabling them to transiently roam the surface and enhance their encounter probability. This process mitigates the diffusive constraints imposed by the extremely low temperatures. The feasibility of Reactions B.10 and B.11 has been confirmed both theoretically and experimentally (Kobayashi et al. 2017; Lamberts 2018; Molpeceres & Rivilla 2022), supporting this non-thermal pathway as a viable route for CH2CHCHS synthesis under cold interstellar conditions.

All Tables

Table 1.

Spectroscopic constants of trans-propenethial (A-reduction, Ir-representation) in its ground vibrational state.

In the text
Table 2.

Observed line parameters for CH2CHCHS in TMC-1.

In the text
Table A.1.

Spectroscopic constants of trans-propenethial (A-reduction, Ir-representation) in the ground state and lowest-lying excited vibrational state of the parent species 32S, and the ground state of the 34S isotopic species.a

In the text
Table A.2.

Spectroscopic constants of cis-propenethial (A-reduction, Ir-representation) calculated at CCSD/cc-pVTZ level of theory.

In the text
Table B.1.

Reaction energies and activation barriers with energies for gas phase reactions in kcal mol−1.

In the text

All Figures

thumbnail Fig. 1.

Molecular geometry of the trans conformation of propenethial depicted in the ab inertial plane.
In the text
thumbnail Fig. 2.

Observed lines of CH2CHCHS in TMC-1. Frequencies and line parameters are given in Table 2. Quantum numbers for the observed transitions are indicated in each panel. The red line shows the synthetic spectrum computed for a rotational temperature of 9 K and a column density of 4.4 × 1010 cm−2 (see text). The blanked channels correspond to negative features created in the folding of the frequency-switching data. The 1σ noise level derived for the nominal spectral resolution of 38.15 kHz is indicated by a horizontal grey band. The observed intensity of the 61, 6-51, 5 and 60, 6-50, 5 lines is probably reduced by partial overlap with negative frequency-switching artefacts. The label U corresponds to unidentified features.
In the text
thumbnail Fig. A.1.

Section of the rotational spectrum of propenethial with the assignments of groups of lines belonging to J = 27 ← 26 rotational transitions in the ground state and v18 = 1 excited vibrational state.
In the text
thumbnail Fig. B.1.

Minimum energy path for reaction B.7 on dust grains obtained from a potential energy scan. The initial (reactant) and final (product) states are shown as insets.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.