Table A.1.
Priors adopted on the hyperparameters used in our analyses.
| Hyperparameter | Prior |
|---|---|
| log(ℛref·Gpc3 yr) | 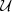 (-2, 1) (-2, 1) |
| α | 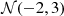 |
| log(fp) | 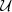 (-6, 0) (-6, 0) |
| βq | 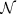 (0, 3) (0, 3) |
| αz | 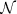 (0, 4) (0, 4) |
| β | 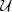 (0, 10) (0, 10) |
| zp | 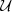 (0.2, 4) (0.2, 4) |
| Mmin | 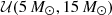 |
| Mmax | 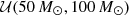 |
| μm | 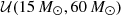 |
| σm | 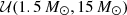 |
| log(δmmin/ M⊙) | 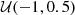 |
| log(δmmax/ M⊙) | 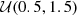 |
| Λhigh & Λlow | Identical prior to p(Λ) above |
| log(ΔzΛ) | 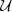 (-1, 1) (-1, 1) |
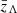 |
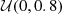 |
| log(ΔmΛ/M⊙) | 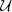 (-1, 3) (-1, 3) |
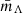 |
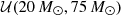 |
Notes: 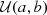 indicates a uniform prior normalized between a and b, and
indicates a uniform prior normalized between a and b, and 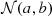 a Gaussian prior with mean a and standard deviation b. When varying a given hyperparameter as a function of mass or redshift, priors on the asymptotic values are identical to the priors listed in the upper portion of the table. When varying the mean of the Gaussian peak in the black hole mass spectrum, for example, we adopt
a Gaussian prior with mean a and standard deviation b. When varying a given hyperparameter as a function of mass or redshift, priors on the asymptotic values are identical to the priors listed in the upper portion of the table. When varying the mean of the Gaussian peak in the black hole mass spectrum, for example, we adopt 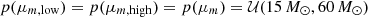 .
.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


