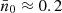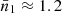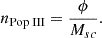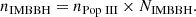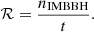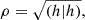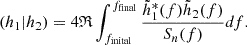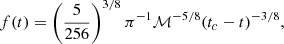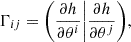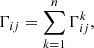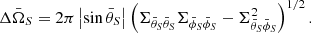EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 697 (May 2025) A&A, 697 (2025) A49 Full HTML
Open Access
Issue
A&A
Volume 697, May 2025
Article Number A49
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202453615
Published online 06 May 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Intermediate-mass black holes (IMBHs), which possess masses ranging from 102 M⊙ to 105 M⊙ (Miller & Colbert 2004), are considered to be the link between supermassive black holes (SMBHs) and stellar mass black holes (SBHs). The search for them is a prominent topic, and the detailed study of the IMBH demographics can help answer key questions such as the seeding mechanisms of SMBHs (Greene et al. 2020), and the co-evolution of galaxies and their central black holes (Volonteri 2010; Kormendy & Ho 2013; King 2023).

The efforts to detect IMBHs through EM observations have not produced the definitive evidence of their existence, (e.g., Rees 1978; Colbert & Miller 2006; Miller & Colbert 2004; Koliopanos 2017; Greene 2012; Mezcua 2017), although several candidates have been proposed within globular clusters, such as 47 Tucanae (Kızıltan et al. 2017) and Omega Centauri (Baumgardt 2017), as well as in certain dwarf galaxies, exemplified by 3XMM J215022.4-055108 (Lin et al. 2018, 2020; Wen et al. 2021). Furthermore, some ultraluminous X-ray sources (ULXs), including M82 X-1 and HLX-1, are also regarded to host potential IMBHs (Ebisuzaki et al. 2001; Kaaret et al. 2001; Matsumoto et al. 2001; Miller 2002; Hopman et al. 2004; Portegies Zwart et al. 2004; King & Dehnen 2005; Patruno et al. 2006; Pasham & Strohmayer 2013). However, EM observations cannot confirm whether a signal originates from an IMBH or multiple black holes (Pooley et al. 2007). On the other hand, the gravitational wave (GW) observation from ground-based detectors such as LIGO and Virgo result in several convincing detections of IMBHs, including the merger event GW190426_190642, GW190521, and GW200220_061928 (Abbott et al. 2024, 2023, 2020). The deduced masses of the remnant black holes all excee 100 M⊙.

On the theoretical side, there are also challenges in understanding the formation channels and sites of IMBHs. Several formation mechanisms have been proposed in addition to the binary black hole mergers, which can be categorized into three principal approaches (Greene et al. 2020): the collapse of population III (Pop III) stars (Madau & Rees 2001; Fryer et al. 2001; Bromm et al. 2002; Bromm & Larson 2004; Lodato & Natarajan 2006; Begelman et al. 2006; Ryu et al. 2016), the direct collapse of gas (Loeb & Rasio 1994; Bromm & Loeb 2003; Latif et al. 2013; Shi et al. 2024), and gravitational runaway mergers involving stars and black holes (BHs) within dense star clusters (González et al. 2021; Rizzuto et al. 2021; Kritos et al. 2023, 2024a,b, 2024c; Sharma & Rodriguez 2024; Fujii et al. 2024). In the early universe, the Pop III stars are expected to have been very massive because molecular hydrogen cooling was inefficient (Bromm & Larson 2004; Karlsson et al. 2013). These stars likely produce black hole remnants of about 100 M⊙, except for those in the 140 − 260 M⊙ range, which instead explode as pair-instability supernovae and left no remnant (Fryer et al. 2001; Heger et al. 2003). IMBHs ranging from 103 − 104 M⊙ can be formed through gravitational runaway mergers(Miller 2002; Portegies Zwart et al. 2004). Additionally, direct collapse can result in IMBHs of 104 − 106 M⊙, avoiding gas fragmentation due to the suppression of cooling (Visbal et al. 2014; Habouzit et al. 2016) and collapses directly into a black hole. For the formation time, Pop III star collapse and direct collapse predominantly occur at high redshifts, while gravitational runaway mergers can occur at all redshifts, depending on the age and dynamics of the star clusters.

To date, there have been no direct GW detections of IMBHs mergers. This is not surprising as the current ground-based GW facilities are not optimized for detecting binary black holes (BBHs) including IMBHs (IMBH-BH) (Han et al. 2017). Compared with LIGO/Virgo/KAGRA (LVK), the upcoming space-borne GW observatories such as TianQin (Luo et al. 2016) and LISA (Danzmann & LISA Study Team 1996), and the next generation ground-based GW detectors such as Einstein Telescope (ET) (Punturo et al. 2010) and Cosmic Explorer (CE) (Reitze et al. 2019), are more sensitive at the lower frequency ranges, thus can detect binaries with IMBHs more efficiently. Theoretical investigations have further underscored the potential of future GW detectors in exploring IMBHs. For instance, Arca Sedda et al. (2021) examined intermediate-mass ratio inspirals (IMRIs) involving IMBHs and compact stellar objects, offering valuable insights into their detection capabilities. Rasskazov et al. (2020) conducted simulations regarding the formation of IMBHs within globular clusters, predicting that LISA could detect at least one merger event during a four-year mission. Moreover, Fragione et al. (2018a,b, 2020) developed cluster models that incorporated IMBHs, demonstrating that observatories such as ET, CE and LISA could potentially identify IMBH-BH mergers across a broad mass spectrum. Furthermore, other observational techniques have also shown promise in detecting IMBHs. For instance, Strokov et al. (2022, 2023) investigated LISA’s ability to detect and constrain IMBHs indirectly via the Doppler effect. Torres-Orjuela (2023) studied the capability of atom interferometers such as DECIGO (Kawamura et al. 2011) to detect IMBHs. Gravitational lensing has also been proposed as a viable method for detecting IMBHs (Kains et al. 2016), while pulsar timing arrays (PTAs) has been identified as another promising tool for detecting IMBHs through prolonged GW observations (Kocsis et al. 2012; Sesana 2015; Dror et al. 2019; Barausse et al. 2023; Steinle et al. 2023).

TianQin is an mHz space-borne GW observatory proposed by China, which would be launched in the 2030s (Luo et al. 2016; Hu et al. 2018; Mei et al. 2021). TianQin has an equilateral triangular configuration composed of three satellites orbiting the Earth at an approximate distance of 105 km. Compared with LISA, TianQin has shorter arms, which makes it more sensitive to the lighter end of the IMBH mass spectrum (Hu 2024; Li et al. 2024). Wang et al. (2022) and Liu et al. (2024) explored the IMBH formation processes and their population properties in Pop III clusters, but the TianQin detection potential for these systems have not been studied in detail. In this work, we aim to quantitatively explore TianQin’s detection ability for intermediate-mass binary black holes (IMBBHs) formed within Pop III clusters. As Fig. 1 shows, we first derived the evolution history of IMBBHs formed in the Pop III clusters based on direct N-body simulations. Combining the merger history and parameter distributions with the spatial distribution of Pop III clusters, we then obtained a mock catalog of IMBBH mergers. By calculating the signal-to-noise ratio (S/N) with TianQin and applying the Fisher information matrix (FIM), we then deduced the expected detection number and Fisher uncertainty.

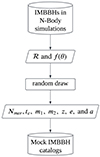thumbnail Fig. 1.

Process of generating mock IMBBH catalogs. ℛ denotes the merger rate, while θ represents IMBBH parameters, including component masses m1 and m2, redshift z, eccentricity e, and semi-major axis a. The distribution function is denoted as f(θ).

The rest of this paper is organized as follows. We investigate the population properties of IMBBHs and introduce the methods used in Sect. 2. In Sect. 3, we estimate the detection capacity of TianQin for IMBBHs. Finally, we draw the conclusion in Sect. 4. Throughout the paper, we adopt the geometrical unit, i.e., G = c = 1, and the standard ΛCDM cosmological model (Planck Collaboration XIII 2016).

2. Method

In this section, we introduce the N-body simulation approach and the initial conditions we use to trace the evolution of Pop III clusters embedded in mini dark matter halos. Furthermore, we analyze the population features of IMBBHs from N-body simulation and introduce the methods utilized to estimate the detection capacity of TianQin for IMBBHs, including GW response signal, S/N, and FIM.

2.1. N-body simulation

In previous studies, Sakurai et al. (2017) investigated IMBH formation without performing long-term simulations, while Reinoso et al. (2018) examined low-mass star-cluster models with minimum Z = 0.0001. In addition, Wang et al. (2022) studied the long-term evolution of Pop III clusters and their IMBHs but did not include primordial binaries.

In this work, we simulated the evolution of Pop III star clusters using the N-body code PETAR (Wang et al. 2020) coupled with the single and binary population-synthesis code BSEEMP (Tanikawa et al. 2020). The initial conditions for the clusters in this study are derived from the long-term model NFWden_long_w9_noms_imf1, which excludes primordial binaries (Wang et al. 2020). This model was chosen because it predicts the formation of very massive stars (VMSs) that evolve into IMBHs with masses up to 103 M⊙. Additionally, new models were introduced to include primordial binaries, where the initial periods, mass ratios, and eccentricities follow the distributions from Sana et al. (2012).

Key parameters for the simulation of Pop III clusters are as follows. The initial mass of the star clusters Mclu = 105 M⊙ (Sakurai et al. 2017), with a half-mass radius rh = 1 pc, which is a typical value for observed star clusters. The central density profile of the clusters is described using the Michie-King model (Michie 1963; King 1966), where the cluster compactness is determined by the ratio of the core radius rc to the tidal radius rt, denoted as W = rc/rt. For our study, we set the initial value of W0 = 9. Furthermore, the initial mass function (IMF) for the stars in these Pop III clusters follows a top-heavy distribution, based on the results from hydrodynamic simulations (Stacy et al. 2016; Chon et al. 2021; Latif et al. 2022). Specifically, the IMF is described by a single power-law profile

p ( m ) ∝ m − 1 , 1 M ⊙ < m < 150 M ⊙ , $$ \begin{aligned} p(m) \propto m^{-1}, \quad 1\,\mathrm{M}_\odot < m < 150\,\mathrm{M}_\odot , \end{aligned} $$

which favors the formation of VMSs and BHs, in contrast to the canonical IMF characterized with a power index of −2.35 (Kroupa 2001; Chabrier 2003). Moreover, for the dark matter halo surrounding the Pop III clusters, we assume that its potential follows the Navarro-Frenk-White (NFW) profile (Navarro et al. 1996), given by

Φ = − G M vir r [ log ( 1 + C ) − C / ( 1 + C ) ] log ( 1 + r / r vir ) , $$ \begin{aligned} \Phi = -\frac{G M_{\text{vir}}}{r \left[ \log (1 + C) - C/(1 + C)\right] }\log \left( 1 + r/r_{\text{vir}}\right), \end{aligned} $$

where Mvir = 4 × 107 M⊙ is the virial mass, rvir = 280 pc is the virial radius, and the concentration C(z) evolves as C(z) = C(0)/(1 + z), where C(0) = 15.3 is the concentration value for the Milky Way halo (Bovy 2015).

2.2. Population of IMBBH

We adopted the N-body simulation results of Pop III cluster model ‘NFWden_long_w9_noms_imf1’ conducted by Liu et al. (2024), where 168 Pop III clusters with primordial binary fraction fb = 0 and 1 were evolved for up to 12Gyr, respectively. We selected the IMBBH mergers formed in these simulations and explored their population properties as below. The distribution of IMBBH merger numbers is shown in Fig. 2.

thumbnail Fig. 2.

Distribution of the merger numbers of IMBBHs from 168 N-body simulations. Solid lines represent fb = 0 (orange) and fb = 1 (blue), respectively. n ¯ 0 ≈ 0.2 $ \bar{n}_0 \approx 0.2 $ and n ¯ 1 ≈ 1.2 $ \bar{n}_1 \approx 1.2 $ are average numbers of IMBBH mergers for the two scenarios.

When fb = 0, in most simulations no IMBBH would merge, while for the remaining cases, one pair of IMBBH could merge. As fb increases to 1, most simulations have at least one IMBBH merger, with a maximum of five IMBBH mergers. This indicates that clusters with a higher primordial binary fraction (fb = 1) can produce more IMBBH events than their lower primordial binary fraction counterparts (fb = 0).

The distributions of IMBBHs mass parameters are presented in Fig. 3. In both cases, the primary masses m1 peaks around 200 M⊙, with a decreasing tail extends to ∼1000 M⊙, and the fb = 1 case exhibits a narrower peak. The distribution of mass ratio q = m2/m1 peaks at about 1, indicating that the component masses of most IMBBHs are comparable.

thumbnail Fig. 3.

Distributions of primary mass m1 (left panel) and mass ratio q = m2/m1 (right panel) of IMBBHs from the Pop III cluster models with fb = 0 (orange) and fb = 1 (blue).

We present the distribution of eccentricities in Fig. 4. In both cases, the simulations predict relatively small natal eccentricities, with approximately 70–80% of the eccentricities in the range e ∈ [0, 0.25]. Only a small fraction of IMBBHs have a very large eccentricity of 0.8 < e < 1. Orbital decay can be accelerated through the binary-single encounter where a binary encounters a third body, the third body can replace a component in the binary. Such binary-single encounters are often associated with a shrunk orbital separation and a large orbital eccentricity for the new binary. Due to the higher portion of primordial binaries, the case with fb = 1 is expected to experience more frequent binary-single encounters, resulting in a higher proportion of larger orbital eccentricity sources.

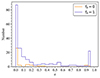thumbnail Fig. 4.

Orbital eccentricity distribution of IMBBHs from the Pop III cluster models with fb = 0 (orange) and fb = 1 (blue) at their formation time.

The redshift distributions of IMBBHs mergers in the simulations are shown in Fig. 5. In both cases of fb = 0 and 1, approximately 40–60% of the mergers occur at high redshifts with z > 6, and the minimum redshift zmin > 0.1.

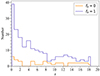thumbnail Fig. 5.

Redshift distribution of IMBBHs from the Pop III cluster models with fb = 0 (orange) and fb = 1 (blue) corresponding to their merger time.

The average number of IMBBHs per cluster is 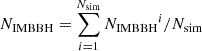N IMBBH = ∑ i = 1 N sim N IMBBH i / N sim $ N_{\text{IMBBH}}=\sum_{i = 1}^{N_{\mathrm{sim}}}{{N_\text{IMBBH}}^i}/N_{\mathrm{sim}} $, where Nsim = 168 is the total number of simulation and NIMBBHi denotes the IMBBHs merger number of each simulation. The result is 0.2 and 1.2 per simulation for fb = 0 and fb = 1 respectively, with the distribution of IMBBHs merger numbers shown in Fig. 2.

In order to extrapolate the merger number within a cluster to the cosmic merger rate, one needs to also derive the number density of Pop III clusters. The typical mass of a Pop III cluster is Msc = 105 M⊙(Wang et al. 2022). Meanwhile, it is derived that the average stellar mass density that originates from Pop III clusters ϕ ranges from 3.2 ×104 M⊙ Mpc−3 (Skinner & Wise 2020) to 2 ×105 M⊙ Mpc−3 (Inayoshi et al. 2021). We can then calculate the number density of Pop III clusters, nPop III, as

n Pop III = ϕ M sc . $$ \begin{aligned} n_{\text{Pop} \text{ III}} = \frac{\phi }{M_{sc}}. \end{aligned} $$

Substituting the values of ϕ and Msc, we obtained the following range for the number density of Pop III clusters, from 0.32 Mpc−3 to 2 Mpc−3. Multiplying this number density by the average number of IMBBH mergers per cluster, NIMBBH, gives the number density of IMBBHs mergers, nIMBBH

n IMBBH = n Pop III × N IMBBH . $$ \begin{aligned} n_{\text{IMBBH}} = n_{\text{Pop} \text{ III}} \times N_{\text{IMBBH}}. \end{aligned} $$

The merger rate ℛ of IMBBHs averaged over redshift can be estimated (see Liu et al. 2024, Eq. (7)) as follows, given by the merger number density divided by the simulation time t

R = n IMBBH t . $$ \begin{aligned} \mathcal{R} = \frac{n_{\text{IMBBH}}}{t}. \end{aligned} $$

With a simulation time span of t = 12 Gyr, the merger rate is shown in Table 1.

Table 1.

Lower and upper limits of average IMBBH merger rate for fb = 0 and fb = 1, denoted as ℛlower and ℛupper.

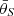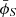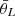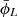Based on the averaged merger rate and the distributions of masses and redshift yielded by kernel density estimation, assuming a uniform distribution in source location as well as orbital orientation, described by parameters θ ¯ S $ \bar{\theta}_{S} $, ϕ ¯ S $ \bar{\phi}_{S} $, θ ¯ L $ \bar{\theta}_{L} $ and ϕ ¯ L $ \bar{\phi}_{L} $, we obtained a simulated IMBBH samples through the Monte Carlo method.

2.3. Gravitational wave signal

According to the different calculation methods, the GW waveform of a BBH can be roughly categorized into three stages: the inspiral, the merger, and the ringdown (IMR). The GWs from circular BBHs only contain the n = 2 harmonic, and more harmonics are included in the case where BBHs are eccentric. For BBHs with small or moderate e, the n = 2 harmonic is always dominant, whereas it no longer dominates in the case where BBHs are highly eccentric (Liu et al. 2022; Chen & Amaro-Seoane 2017). Correctly describing the effect of orbital eccentricities can be challenging when the eccentricities are very large, especially when trying to include the whole IMR stages in the waveform. However, the majority of simulated IMBBHs have e < 0.3 at formation, as illustrated in Fig. 4. With circularization caused by gravitational radiation, the eccentricities shrink significantly. Therefore, for the sake of convenience, we use the widely adopted IMRPhenomD waveform (Husa et al. 2016; Khan et al. 2016) to perform the following calculation. It is a frequency domain waveform that can describe the IMR evolution of a non-precessing non-eccentric BBH.

When GWs from BBHs reach detectors, their waveforms are modulated by the antenna response functions of detectors. By combining the GW waveform with the antenna response function of TianQin, we can derive the corresponding GW signals that include the response in the frequency domain, as presented in the analytical formulas in Liu et al. (2020). In Fig. 6, we plot the sky-polarization-averaged GW signals for IMBBHs formed in the simulations. This indicates that only inspiral GW signals would be observed by space detectors such as TianQin and LISA.

thumbnail Fig. 6.

Sky-polarization-averaged GW signals of IMBBHs modeled with IMRPhenomD (thin lines), overlaid with TianQin (red), LISA (green), and LIGO A+ (blue) sensitivity curves. The merger time is set to 5 years. Dots size scale with total IMBBH mass. Left and right panels correspond to fb = 0 and fb = 1, respectively. The black solid line represents a reference IMBBH (m1 = m2 = 200,  M⊙, z = 2, tc = 5 yr), with red, blue, and black dashed lines marking 1 year, 1 month, and 1 day before merger.

2.4. Signal-to-noise ratio

The strength of signals in the data recorded by detectors can be characterized by S/N. The optimal S/N of signal h accumulated in observation time in one detector can be calculated by

ρ = ( h | h ) , $$ \begin{aligned} \rho =\sqrt{(h|h)}, \end{aligned} $$(1)

where the inner product between two signals h1 and h2 is defined as

( h 1 | h 2 ) = 4 R ∫ f inital f final h ∼ 1 ∗ ( f ) h ∼ 2 ( f ) S n ( f ) d f . $$ \begin{aligned} (h_{1}|h_{2}) = 4\mathfrak{R} \int _{f_{\rm inital}}^{f_{\rm final}}\frac{\tilde{h}_{1}^{*}(f)\tilde{h}_{2}(f)}{S_{n}(f)}df. \end{aligned} $$(2)

The symbols h1(f) and h2(f) are the signals in frequency domain, and * represents their complex conjugate. The one-sided power spectral density (PSD) of detector noise is denoted by Sn(f) in the frequency domain. The initial and final frequencies of inspiral GWs, finitial and ffinal, can be derived by

f ( t ) = ( 5 256 ) 3 / 8 π − 1 M − 5 / 8 ( t c − t ) − 3 / 8 , $$ \begin{aligned} f(t)=\left(\frac{5}{256}\right)^{3/8}\pi ^{-1}\mathcal{M} ^{-5/8}(t_{c}-t)^{-3/8}, \end{aligned} $$(3)

where the chirp mass ℳ = (m1m2)3/5/(m1 + m2)1/5. The observation time of detectors and merger time of BBHs are represented by t and tc, respectively. Note that for IMBBHs merging within the 5-year observation period, we applied a cutoff for the final frequency as 1Hz. For the case where one signal is observed by multiple detectors, the total S/N is

ρ = ∑ j = 1 n ρ j 2 , $$ \begin{aligned} \rho =\sqrt{\sum _{j = 1}^{n} \rho _j^2}, \end{aligned} $$(4)

where ρj is the S/N of signal in the jth detector. We adopt the noise PSD model of TianQin and LISA from Liu et al. (2020) and Robson et al. (2019), respectively. It is worth mentioning that the cosmic redshift z and the mass parameters are totally degenerate. Therefore, in practice, we used the redshifted chirp mass ℳz = (1 + z)ℳ.

2.5. Fisher information matrix

Assuming the noise of detectors is Gaussian and stationary, the measurement precision of physical parameters can be approximated by the Fisher information matrix (FIM) method

Γ ij = ( ∂ h ∂ θ i | ∂ h ∂ θ j ) , $$ \begin{aligned} \Gamma _{ij}=\bigg (\dfrac{\partial h}{\partial \theta ^i}\bigg |\dfrac{\partial h}{\partial \theta ^j}\bigg ), \end{aligned} $$(5)

where θ is the physical parameter set which determines the GW response signals. For multiple detectors, their total FIM is simply the summation of the FIMs of individual detectors

Γ ij = ∑ k = 1 n Γ ij k , $$ \begin{aligned} \Gamma _{ij} = \sum _{k = 1}^{n}\Gamma _{ij}^k, \end{aligned} $$(6)

where Γijk is the FIM of kth detectors. As the Cramér-Rao Lower Bound (CRLB) states, the covariance matrix Σ of any unbiased estimator is lower-bounded by the inverse of the Γ, i.e., Σ = Γ−1. The measurement precision of θi is the square root of ii component of covariance matrix Σ.

3. Result

In this section, we estimate the detection capacity of TianQin for IMBBHs in Pop III clusters, including detection horizon, detection number, and parameter measurement precision, under the assumption that TianQin will operate for 5 years with “3 months on + 3 months off” observation scenario.

3.1. Detection horizon distance

The maximum distance that TianQin could observe, i.e., horizon distance, can be obtained by solving Eq. (1) with a given S/N, as shown in Fig. 7. When S/N = 5, TianQin would detect IMBBHs across a broad mass range, extending up to z = 20. As the S/N increases, the mass range of detectable IMBBHs shifts toward higher masses. This is because only the stronger GW signals from heavier IMBBHs could accumulate enough to reach the given S/N. However, when S/N reaches a very high value, e.g., S/N = 300, TianQin could not detect IMBBHs at very high redshift, because GW signals from distant IMBBHs are too weak to accumulate enough S/N. For IMBBHs formed in Pop III clusters falling in the mass range between 𝒪(102) M⊙ and 𝒪(103) M⊙, as shown in Fig. 3, TianQin could detect sources up to z = 20 when S/N = 5, even as S/N increases to 12, TianQin would still detect sources up to z = 15. This indicates that TianQin has the excellent capability of observing IMBBH mergers throughout the majority of the observable universe.

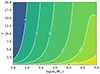thumbnail Fig. 7.

Horizon distances for face-on, equal-mass IMBBHs merging within 5 years, located along TianQin’s normal vector ( θ ¯ S = 94.7 ° $ \bar{\theta}_{S} = 94.7\circ $, ϕ ¯ S = 120.44 ° $ \bar{\phi}_{S} = 120.44\circ $). Masses are given in the source frame.

3.2. Detection number

For each scenario of fb, 200 IMBBH source catalogs were generated based on the underlying IMBBH population. TianQin’s detection performance was then analyzed for these catalogs, with the results presented in Fig. 8 and Table 2.

thumbnail Fig. 8.

Box plots of IMBBH detection numbers from 200 catalogs for fb = 0 and fb = 1, under lower and upper merger rates. Medians are shown as horizontal lines within the boxes.

Table 2.

The average detection number for 5 year observation.

The resulting average number of detections reveals significant variations depending on the S/N threshold, fb, and merger rate assumptions over a 5-year operation time. The upper and lower correspond to the upper and lower limit of merger rate of IMBBHs listed in Table 1. The average detection numbers range from 1(lower) for the fb = 0 scenario with applying an S/N threshold of 12, as the most pessimistic result, to 253(upper) under the fb = 1 scenario for an S/N threshold of 5, as the most optimistic result. Readers are reminded that the accumulation of S/N is non-linear over time, so the detection number does not scale with observation time linearly.

Approximately 10% of IMBBHs exhibit eccentricities above 0.8. To investigate the effect of eccentricity, we computed the dominant harmonic and frequency, following approaches from Wen (2003) and Hamers (2021), for IMBBHs from 168 N-body simulations. Among 39 IMBBHs from the fb = 0 samples and 199 IMBBHs from the fb = 1 samples, only one system has an initial dominant frequency exceeding 1Hz, while nearly 74% of the fb = 0 systems and 62% of the fb = 1 systems have an initial dominant frequency above 0.01Hz. These results indicate that although eccentricity increases the dominant frequency, most systems remain within the TianQin band.

Furthermore, we calculated the S/N for IMBBHs with different eccentricities and component masses from 100 M⊙ to 1000 M⊙ based on methods from Peters (1964) and Kremer et al. (2019). Figure 9 illustrates how eccentricity reduces the S/N: for e = 0.6(0.8, 0.9) the reduction is approximately 0–20% (20–60%, 70–90%). For instance, a detectable IMBBH with parameters m1 = 244 M⊙,  m2 = 230 M⊙, a = 0.005AU, e = 0.9, z = 0.64 experiences an S/N reduction of about 6% (40%, 70%) when e = 0.6(0.8, 0.9).

thumbnail Fig. 9.

S/N variation with eccentricity for IMBBHs of equal-mass components and fixed semi-major axis (0.005 AU). Gray levels indicate masses from 100 M⊙ to 1000 M⊙.

Therefore, for sources with high eccentricity (e > 0.6), our S/N estimates are likely overestimated, and the total number of detectable sources should be lower than those listed in Table 2. Nevertheless, even with an eccentricity of e = 0.8, systems originally detectable with S/N > 12 would still likely exhibit S/N > 5. Therefore, future TianQin detections could serve as an important channel to reveal the formation and evolution of IMBHs as well as Pop III clusters.

3.3. Fisher uncertainty

For those detectable sources with S/N > 12, we further calculated the Fisher uncertainty for four scenarios with varying primordial binary fractions and merger rates. We present the results in Fig. 10, shown with the probability density distributions of relative error for the chirp mass Δℳc/ℳc, symmetric mass ratio Δη/η, and luminosity distance ΔDL/DL, as well as absolute error for coalescence time Δtc, inclination angle Δι, and sky localization 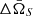Δ Ω ¯ S $ \Delta \bar{\Omega}_S $, which is calculated by

Δ Ω ¯ S = 2 π | sin θ ¯ S | ( Σ θ ¯ S θ ¯ S Σ ϕ ¯ S ϕ ¯ S − Σ θ ¯ S ϕ ¯ S 2 ) 1 / 2 . $$ \begin{aligned} \Delta \bar{\Omega }_S = 2 \pi \left|\sin \bar{\theta }_S\right|\left(\Sigma _{\bar{\theta }_S \bar{\theta }_S} \Sigma _{\bar{\phi }_S \bar{\phi }_S}-\Sigma _{\bar{\theta }_S \bar{\phi }_S}^2\right)^{1 / 2}. \end{aligned} $$

thumbnail Fig. 10.

Fisher uncertainties for IMBBHs in Pop III clusters with S/N ≥ 12. Blue (orange) lines represent fb = 0 (1); solid (dashed) lines indicate upper (lower) merger rates. Smoothed distributions are shown for ℳc, η, DL, tc, ι, and Ω ¯ S $ \bar{\Omega}_S $.

We can first observe that the distribution of different rates (indicated by solid and dashed lines) shows no significant difference. This is expected as the rate should only affect the sample size. Meanwhile, the primordial binary fraction does change the overall precision distributions, although the difference is not significant and can go both directions. For the mass parameters, higher fb corresponds to a more precise constraint. This can be explained by the fact that the fb = 1 case has a narrower peak at the lower end of the IMBBH mass spectrum, as can be observed in Fig. 3. Roughly speaking, the precision of mass parameters is inversely proportional to the number of cycles that a source spends in the band. With a fixed observation time, the lighter sources are associated with higher frequencies, thus a higher number of cycles and better constraints. This behavior is also consistent with previous studies of on stellar-mass binary black holes (Liu et al. 2020) and massive binary black holes (Wang et al. 2019). The precision on merger time is much less sensitive to the fb parameter. This is also reflected in the relevant studies. The constraints on the luminosity distance are poor, with the relative error in DL exceeding 100% in nearly half of the cases. This behavior is also observed in previous studies of GW190521-like events (Liu et al. 2022). We conclude that the same logic applies to this study: the DL − ι degeneracy makes it challenging to pinpoint either parameter. This can also explain the spread of the ι distribution extending to the physical limit of π. The difference in sky localization is less obvious and shows a different tendency, that fb = 0 case instead shows a more precise constraint, which is also consistent with previous studies.

Even a more pessimistic result with fb = 0 shows, that TianQin can constrain the chirp mass ℳc with a relative uncertainty of 10−6, and determine the symmetric mass ratio within 10−2 relative error. Meanwhile, TianQin can constrain the error of coalescence time tc within 1s and for the sky localization 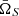Ω ¯ S $ \bar{\Omega}_S $ within 1 deg2. The result indicates TianQin’s ability to constrain the mass and location of IMBBHs with high precision. On the other hand, TianQin could not determine the distance accurately with a high uncertainty for luminosity distance DL with ΔDL/DL around 1. Also for the inclination angle Δι, the relative error is higher than 0.1.

Overall, it is shown that for IMBBH events, TianQin can estimate the mass, sky location, and merger time well while it is less capable of estimating the distance and inclination angle.

4. Conclusion

IMBHs have been a key target for both theoretical and observational astrophysics. The successful identification and reliable measurement of their parameters can provide pivotal insight into the formation history and their co-evolution of the environment. Pop III star clusters, theorized to exist in the metal-poor dark matter halos, could be an important site for producing IMBHs. Recent studies reveal that IMBHs can form binaries and later merge (Wang et al. 2022). In this work, we extend the direct N-body simulation of Pop III clusters to the whole universe, and by investigating the simulated IMBBH mergers, we present the expected gravitational wave detection ability with the TianQin observatory. We further calculated the expected Fisher uncertainties. We find that even in the most pessimistic scenario, and with an S/N threshold of 12, TianQin is still capable of observing IMBBH mergers. The intrinsic parameters that determine the phase evolution can usually be very precisely determined, and the relative uncertainty of chirp mass can be determined to the level of 10−6. Meanwhile, due to the degeneracy between luminosity distance and inclination angle, neither of these parameters can be precisely determined. The overall behavior of the parameter precisions is consistent with previous studies.

As indicated by Fig. 6, the IMR signal of IMBBH can cover both the mHz and the hundred Hz range, making them important potential sources for multi-band GW observations. Therefore, it is interesting to compare the detection abilities among different GW detectors. Ground-based detectors can detect IMBBHs with masses ranging from 100 − 103 M⊙, while spaceborne detectors are more sensitive to the mass ranges of 103 − 105 M⊙. LISA can possibly detect IMBBHs up to redshift z = 20 with S/N up to 100 (Amaro-Seoane et al. 2017). Combinations of next-generation ground-based detectors such as CE and ET could probe IMBBHs with component masses around 1000 M⊙, a 3-detector network can achieve mass measurement errors of ≲0.1% at z = 0.5 and ≲1% at z = 2 with high accuracy of redshift measurement, localized within 1 deg2 with z ≲ 0.5. For binaries with m1, 2 ≲ 300 M⊙, the redshift can be measured with 𝒪(10)% accuracy up to z = 10, which is precise enough for potential electromagnetic counterpart searches (Reali et al. 2024). The atom interferometers such as AION, ZAIGA, and AEDGE would also be capable of detecting IMBBHs (Torres-Orjuela 2023). DECIGO could constrain the masses and spins of the IMBHs within 10% and issue alerts 102 − 103 s before the coalescence, so that the ground-based detectors can be prepared for the observation of the ringdown (Yagi 2012).

Our analysis has a number of caveats. To start with, we extrapolated the evolution of IMBBHs in Pop III clusters from 168 direct simulations. The extrapolation relies on several assumptions, such as the mass of a typical Pop III cluster, the discrete value of the primordial binary fraction, etc. So even though the predicted detection number can cover two orders of magnitude, in reality, the scatter could be larger. Also, the adopted waveform is only reliable for close mass ratio, quasi-circular, aligned-spin binary black holes, while some of the discussed sources can have large mass ratios, non-negligible eccentricities, and randomly oriented spins. Although we expect that the Fisher uncertainty should be correct in terms of order-of-magnitude, and the S/N estimation should be less severely affected, more accurate estimation would need a more accurate waveform model that is reliable in a larger parameter space.

In the future, we plan to extend the analysis to a wider range. In this study, we only consider the IMBBHs in Pop III star clusters, while IMBBHs can form in a variety of astrophysical environments. Possible alternative locations include globular clusters, where the high stellar density can lead to frequent dynamical interactions, promoting the formation and merger of IMBBHs. In addition, active galactic nuclei (AGNs) disks can serve as a fertile ground for IMBBH formation and mergers. The presence of massive gas inflows and interactions with the disk environment could drive the pairing and eventual coalescence of IMBBHs. Dwarf galaxies also provide potential hosts for IMBBHs, particularly due to their lower stellar mass and the possibility that they retain relic IMBHs from earlier cosmic epochs. These smaller galactic systems may hold clues to the early formation pathways of black holes and their role in hierarchical galaxy formation. The extension to a wider array of formation venues can reveal a more comprehensive view of the formation and evolution of IMBHs. The future detailed studies could also provide distinctive features for IMBBHs from different channels, better preparing us for using TianQin observations to probe the underlying environment as well as their formation track.

The other possible extension is to further explore the potential of multi-band GW observations. TianQin can observe the IMBBH inspiral for years in the milli-Hertz band, before finally merge and become detectable for ground-based high-frequency GW detectors. The coordination of detectors operating in different bands at different times has the potential to provide stringent constraint on gravity theory, or enable us to examine the immediate environment of IMBBHs in details. To unleash the full potential of this multi-band collaboration, a more detailed studies is warranted.

Acknowledgments

This work has been supported by the National Key Research and Development Program of China (No. 2023YFC2206701) and the Natural Science Foundation of China (Grants No. 12173104, No. 12261131504). Shuai Liu thanks the support from Zhaoqing City Science and Technology Innovation Guidance Project (No. 241216104168995) and the Young Faculty Research Funding Project of Zhaoqing University (No. qn202518). L.W. thanks the support from the National Natural Science Foundation of China through grant 21BAA00619 and 12233013, the High-level Youth Talent Project (Provincial Financial Allocation) through the grant 2023HYSPT0706, the one-hundred-talent project of Sun Yat-sen University, the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (22hytd09). We also thank Jian-dong Zhang, En-kun Li, Xiang-Yu Lyu, Lu Wang and and Jian-Wei Mei for their usefulcomments. The authors acknowledge the uses of calculating utilitiesof Numpy (Van der Walt et al. 2011), Pandas (McKinney 2011), and Matplotlib (Hunter 2007) for data analysis and plotting.

References

  1. Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102 [Google Scholar]
  2. Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 041039 [Google Scholar]
  3. Abbott, R., Abbott, T. D., Acernese, F., et al. 2024, Phys. Rev. D, 109, 022001 [NASA ADS] [CrossRef] [Google Scholar]
  4. Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, arXiv e-prints [arXiv:1702.00786] [Google Scholar]
  5. Arca Sedda, M., Amaro Seoane, P., & Chen, X. 2021, A&A, 652, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barausse, E., Dey, K., Crisostomi, M., et al. 2023, Phys. Rev. D, 108, 103034 [NASA ADS] [CrossRef] [Google Scholar]
  7. Baumgardt, H. 2017, MNRAS, 464, 2174 [Google Scholar]
  8. Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [Google Scholar]
  12. Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [Google Scholar]
  13. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  14. Chen, X., & Amaro-Seoane, P. 2017, ApJ, 842, L2 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chon, S., Omukai, K., & Schneider, R. 2021, MNRAS, 508, 4175 [NASA ADS] [CrossRef] [Google Scholar]
  16. Colbert, E. J. M., & Miller, M. C. 2006, in The Tenth Marcel Grossmann Meeting. On recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories, eds. M. Novello, S. Perez Bergliaffa, & R. Ruffini, 530 [CrossRef] [Google Scholar]
  17. Danzmann, K., & LISA Study Team 1996, Class. Quant. Grav., 13, A247 [Google Scholar]
  18. Dror, J. A., Ramani, H., Trickle, T., & Zurek, K. M. 2019, Phys. Rev. D, 100, 023003 [Google Scholar]
  19. Ebisuzaki, T., Makino, J., Tsuru, T. G., et al. 2001, ApJ, 562, L19 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fragione, G., Ginsburg, I., & Kocsis, B. 2018a, ApJ, 856, 92 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fragione, G., Leigh, N. W. C., Ginsburg, I., & Kocsis, B. 2018b, ApJ, 867, 119 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fragione, G., Loeb, A., Kremer, K., & Rasio, F. A. 2020, ApJ, 897, 46 [Google Scholar]
  23. Fryer, C. L., Woosley, S. E., & Heger, A. 2001, ApJ, 550, 372 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fujii, M. S., Wang, L., Tanikawa, A., Hirai, Y., & Saitoh, T. R. 2024, Science, 384, 1488 [NASA ADS] [CrossRef] [Google Scholar]
  25. González, E., Kremer, K., Chatterjee, S., et al. 2021, ApJ, 908, L29 [CrossRef] [Google Scholar]
  26. Greene, J. E. 2012, Nat. Commun., 3, 1304 [NASA ADS] [CrossRef] [Google Scholar]
  27. Greene, J. E., Strader, J., & Ho, L. C. 2020, ARA&A, 58, 257 [Google Scholar]
  28. Habouzit, M., Volonteri, M., Latif, M., Dubois, Y., & Peirani, S. 2016, MNRAS, 463, 529 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hamers, A. S. 2021, RNAAS, 5, 275 [Google Scholar]
  30. Han, W.-B., Cao, Z., & Hu, Y.-M. 2017, Class. Quant. Grav., 34, 225010 [Google Scholar]
  31. Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [CrossRef] [Google Scholar]
  32. Hopman, C., Portegies Zwart, S. F., & Alexander, T. 2004, ApJ, 604, L101 [Google Scholar]
  33. Hu, Y. M. 2024, ArXiv e-prints [arXiv:2409.19664] [Google Scholar]
  34. Hu, X.-C., Li, X.-H., Wang, Y., et al. 2018, Class. Quant. Grav., 35, 095008 [Google Scholar]
  35. Hunter, J. D. 2007, CiSE, 9, 90 [Google Scholar]
  36. Husa, S., Khan, S., Hannam, M., et al. 2016, Phys. Rev. D, 93, 044006 [NASA ADS] [CrossRef] [Google Scholar]
  37. Inayoshi, K., Kashiyama, K., Visbal, E., & Haiman, Z. 2021, ApJ, 919, 41 [Google Scholar]
  38. Kaaret, P., Prestwich, A. H., Zezas, A., et al. 2001, MNRAS, 321, L29 [Google Scholar]
  39. Kains, N., Bramich, D. M., Sahu, K. C., & Calamida, A. 2016, MNRAS, 460, 2025 [Google Scholar]
  40. Karlsson, T., Bromm, V., & Bland-Hawthorn, J. 2013, Rev. Mod. Phys., 85, 809 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kawamura, S., Ando, M., Seto, N., et al. 2011, Class. Quant. Grav., 28, 094011 [CrossRef] [Google Scholar]
  42. Khan, S., Husa, S., Hannam, M., et al. 2016, Phys. Rev. D, 93, 044007 [Google Scholar]
  43. King, I. R. 1966, AJ, 71, 64 [Google Scholar]
  44. King, A. 2023, Supermassive Black Holes (Cambridge University Press) [CrossRef] [Google Scholar]
  45. King, A. R., & Dehnen, W. 2005, MNRAS, 357, 275 [Google Scholar]
  46. Kızıltan, B., Baumgardt, H., & Loeb, A. 2017, Nature, 542, 203 [Google Scholar]
  47. Kocsis, B., Ray, A., & Portegies Zwart, S. 2012, ApJ, 752, 67 [Google Scholar]
  48. Koliopanos, F. 2017, in XII Multifrequency Behaviour of High Energy Cosmic Sources Workshop (MULTIF2017), 51 [Google Scholar]
  49. Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
  50. Kremer, K., Rodriguez, C. L., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 99, 063003 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kritos, K., Berti, E., & Silk, J. 2023, Phys. Rev. D, 108, 083012 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kritos, K., Beckmann, R. S., Silk, J., et al. 2024a, arXiv e-prints [arXiv:2412.15334] [Google Scholar]
  53. Kritos, K., Berti, E., & Silk, J. 2024b, MNRAS, 531, 133 [Google Scholar]
  54. Kritos, K., Strokov, V., Baibhav, V., & Berti, E. 2024c, Phys. Rev. D, 110, 043023 [Google Scholar]
  55. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  56. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  57. Latif, M. A., Whalen, D., & Khochfar, S. 2022, ApJ, 925, 28 [NASA ADS] [CrossRef] [Google Scholar]
  58. Li, E. K., Liu, S., Torres-Orjuela, A., et al. 2024, arXiv e-prints [arXiv:2409.19665] [Google Scholar]
  59. Lin, D., Strader, J., Carrasco, E. R., et al. 2018, Nat. Astron., 2, 656 [Google Scholar]
  60. Lin, D., Strader, J., Romanowsky, A. J., et al. 2020, ApJ, 892, L25 [Google Scholar]
  61. Liu, S., Hu, Y.-M., Zhang, J.-D., & Mei, J. 2020, Phys. Rev. D, 101, 103027 [Google Scholar]
  62. Liu, S., Zhu, L.-G., Hu, Y.-M., Zhang, J.-D., & Ji, M.-J. 2022, Phys. Rev. D, 105, 023019 [Google Scholar]
  63. Liu, S., Wang, L., Hu, Y.-M., Tanikawa, A., & Trani, A. A. 2024, MNRAS, 533, 2262 [NASA ADS] [CrossRef] [Google Scholar]
  64. Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
  65. Loeb, A., & Rasio, F. A. 1994, ApJ, 432, 52 [Google Scholar]
  66. Luo, J., Chen, L.-S., Duan, H.-Z., et al. 2016, Class. Quant. Grav., 33, 035010 [NASA ADS] [CrossRef] [Google Scholar]
  67. Madau, P., & Rees, M. J. 2001, ApJ, 551, L27 [Google Scholar]
  68. Matsumoto, H., Tsuru, T. G., Koyama, K., et al. 2001, ApJ, 547, L25 [NASA ADS] [CrossRef] [Google Scholar]
  69. McKinney, W., 2011, Python for High Performance and Scientific Computing, 14, 1 [Google Scholar]
  70. Mei, J., Bai, Y.-Z., Bao, J., et al. 2021, PTEP, 2021, 05A107 [Google Scholar]
  71. Mezcua, M. 2017, Int. J. Mod. Phys. D, 26, 1730021 [Google Scholar]
  72. Michie, R. W. 1963, MNRAS, 125, 127 [Google Scholar]
  73. Miller, M. C. 2002, ApJ, 581, 438 [Google Scholar]
  74. Miller, M. C., & Colbert, E. J. M. 2004, Int. J. Mod. Phys. D, 13, 1 [NASA ADS] [CrossRef] [Google Scholar]
  75. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
  76. Pasham, D. R., & Strohmayer, T. E. 2013, ApJ, 774, L16 [NASA ADS] [CrossRef] [Google Scholar]
  77. Patruno, A., Portegies Zwart, S., Dewi, J., & Hopman, C. 2006, MNRAS, 370, L6 [NASA ADS] [Google Scholar]
  78. Peters, P. C. 1964, Phys. Rev., 136, B1224 [NASA ADS] [CrossRef] [Google Scholar]
  79. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Pooley, D., Blackburne, J. A., Rappaport, S., & Schechter, P. L. 2007, ApJ, 661, 19 [NASA ADS] [CrossRef] [Google Scholar]
  81. Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [Google Scholar]
  82. Punturo, M., Abernathy, M., Acernese, F., et al. 2010, Class. Quant. Grav., 27, 194002 [Google Scholar]
  83. Rasskazov, A., Fragione, G., & Kocsis, B. 2020, ApJ, 899, 149 [NASA ADS] [CrossRef] [Google Scholar]
  84. Reali, L., Cotesta, R., Antonelli, A., et al. 2024, Phys. Rev. D, 110, 103002 [Google Scholar]
  85. Rees, M. 1978, New Sci., 80, 188 [Google Scholar]
  86. Reinoso, B., Schleicher, D. R. G., Fellhauer, M., Klessen, R. S., & Boekholt, T. C. N. 2018, A&A, 614, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Reitze, D., Adhikari, R. X., Ballmer, S., et al. 2019, BAAS, 51, 35 [NASA ADS] [Google Scholar]
  88. Rizzuto, F. P., Naab, T., Spurzem, R., et al. 2021, MNRAS, 501, 5257 [NASA ADS] [CrossRef] [Google Scholar]
  89. Robson, T., Cornish, N. J., & Liu, C. 2019, Class. Quant. Grav., 36, 105011 [NASA ADS] [CrossRef] [Google Scholar]
  90. Ryu, T., Tanaka, T. L., Perna, R., & Haiman, Z. 2016, MNRAS, 460, 4122 [NASA ADS] [CrossRef] [Google Scholar]
  91. Sakurai, Y., Yoshida, N., Fujii, M. S., & Hirano, S. 2017, MNRAS, 472, 1677 [NASA ADS] [CrossRef] [Google Scholar]
  92. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  93. Sesana, A. 2015, in Gravitational Wave Astrophysics, ed. C. F. Sopuerta, ApSSP, 40, 147 [Google Scholar]
  94. Sharma, K., & Rodriguez, C. L. 2024, arXiv e-prints [arXiv:2405.05397] [Google Scholar]
  95. Shi, Y., Kremer, K., & Hopkins, P. F. 2024, A&A, 691, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Skinner, D., & Wise, J. H. 2020, MNRAS, 492, 4386 [NASA ADS] [CrossRef] [Google Scholar]
  97. Stacy, A., Bromm, V., & Lee, A. T. 2016, MNRAS, 462, 1307 [NASA ADS] [CrossRef] [Google Scholar]
  98. Steinle, N., Middleton, H., Moore, C. J., et al. 2023, MNRAS, 525, 2851 [NASA ADS] [CrossRef] [Google Scholar]
  99. Strokov, V., Fragione, G., Wong, K. W. K., Helfer, T., & Berti, E. 2022, Phys. Rev. D, 105, 124048 [Google Scholar]
  100. Strokov, V., Fragione, G., & Berti, E. 2023, MNRAS, 524, 2033 [Google Scholar]
  101. Tanikawa, A., Yoshida, T., Kinugawa, T., Takahashi, K., & Umeda, H. 2020, MNRAS, 495, 4170 [NASA ADS] [CrossRef] [Google Scholar]
  102. Torres-Orjuela, A. 2023, AVS Quantum. Sci., 5, 045002 [Google Scholar]
  103. Van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, CiSE, 13, 22 [Google Scholar]
  104. Visbal, E., Haiman, Z., & Bryan, G. L. 2014, MNRAS, 445, 1056 [NASA ADS] [CrossRef] [Google Scholar]
  105. Volonteri, M. 2010, A&A Rev., 18, 279 [NASA ADS] [CrossRef] [Google Scholar]
  106. Wang, H.-T., Jiang, Z., Sesana, A., et al. 2019, Phys. Rev. D, 100, 043003 [NASA ADS] [CrossRef] [Google Scholar]
  107. Wang, L., Iwasawa, M., Nitadori, K., & Makino, J. 2020, MNRAS, 497, 536 [NASA ADS] [CrossRef] [Google Scholar]
  108. Wang, L., Tanikawa, A., & Fujii, M. 2022, MNRAS, 515, 5106 [NASA ADS] [CrossRef] [Google Scholar]
  109. Wen, L. 2003, ApJ, 598, 419 [NASA ADS] [CrossRef] [Google Scholar]
  110. Wen, S., Jonker, P. G., Stone, N. C., & Zabludoff, A. I. 2021, ApJ, 918, 46 [NASA ADS] [CrossRef] [Google Scholar]
  111. Yagi, K. 2012, Class. Quant. Grav., 29, 075005 [Google Scholar]

All Tables

Table 1.

Lower and upper limits of average IMBBH merger rate for fb = 0 and fb = 1, denoted as ℛlower and ℛupper.

In the text
Table 2.

The average detection number for 5 year observation.

In the text

All Figures

thumbnail Fig. 1.

Process of generating mock IMBBH catalogs. ℛ denotes the merger rate, while θ represents IMBBH parameters, including component masses m1 and m2, redshift z, eccentricity e, and semi-major axis a. The distribution function is denoted as f(θ).
In the text
thumbnail Fig. 2.

Distribution of the merger numbers of IMBBHs from 168 N-body simulations. Solid lines represent fb = 0 (orange) and fb = 1 (blue), respectively. n ¯ 0 ≈ 0.2 $ \bar{n}_0 \approx 0.2 $ and n ¯ 1 ≈ 1.2 $ \bar{n}_1 \approx 1.2 $ are average numbers of IMBBH mergers for the two scenarios.
In the text
thumbnail Fig. 3.

Distributions of primary mass m1 (left panel) and mass ratio q = m2/m1 (right panel) of IMBBHs from the Pop III cluster models with fb = 0 (orange) and fb = 1 (blue).
In the text
thumbnail Fig. 4.

Orbital eccentricity distribution of IMBBHs from the Pop III cluster models with fb = 0 (orange) and fb = 1 (blue) at their formation time.
In the text
thumbnail Fig. 5.

Redshift distribution of IMBBHs from the Pop III cluster models with fb = 0 (orange) and fb = 1 (blue) corresponding to their merger time.
In the text
thumbnail Fig. 6.

Sky-polarization-averaged GW signals of IMBBHs modeled with IMRPhenomD (thin lines), overlaid with TianQin (red), LISA (green), and LIGO A+ (blue) sensitivity curves. The merger time is set to 5 years. Dots size scale with total IMBBH mass. Left and right panels correspond to fb = 0 and fb = 1, respectively. The black solid line represents a reference IMBBH (m1 = m2 = 200,  M⊙, z = 2, tc = 5 yr), with red, blue, and black dashed lines marking 1 year, 1 month, and 1 day before merger.
In the text
thumbnail Fig. 7.

Horizon distances for face-on, equal-mass IMBBHs merging within 5 years, located along TianQin’s normal vector ( θ ¯ S = 94.7 ° $ \bar{\theta}_{S} = 94.7\circ $, ϕ ¯ S = 120.44 ° $ \bar{\phi}_{S} = 120.44\circ $). Masses are given in the source frame.
In the text
thumbnail Fig. 8.

Box plots of IMBBH detection numbers from 200 catalogs for fb = 0 and fb = 1, under lower and upper merger rates. Medians are shown as horizontal lines within the boxes.
In the text
thumbnail Fig. 9.

S/N variation with eccentricity for IMBBHs of equal-mass components and fixed semi-major axis (0.005 AU). Gray levels indicate masses from 100 M⊙ to 1000 M⊙.
In the text
thumbnail Fig. 10.

Fisher uncertainties for IMBBHs in Pop III clusters with S/N ≥ 12. Blue (orange) lines represent fb = 0 (1); solid (dashed) lines indicate upper (lower) merger rates. Smoothed distributions are shown for ℳc, η, DL, tc, ι, and Ω ¯ S $ \bar{\Omega}_S $.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.