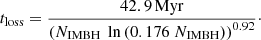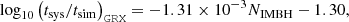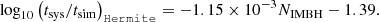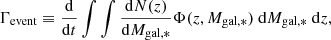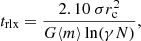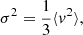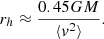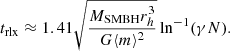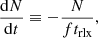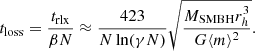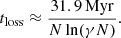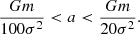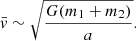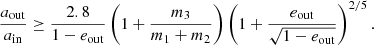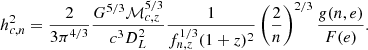| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202348322 | |
| Published online | 16 May 2024 | |
The steady state of intermediate-mass black holes near a supermassive black hole
Leiden Observatory, University of Leiden, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
e-mail: hochart@mail.strw.leidenuniv.nl
Received:
19
October
2023
Accepted:
25
February
2024
Aims. Our aim is to investigate the properties of a cluster of intermediate-mass black holes (IMBHs) surrounding a supermassive black hole (SMBH).
Methods. We simulated clusters of equal-mass IMBHs (mIMBH = 103 M⊙) initialised in a shell between 0.15 ≤ r [pc] ≤ 0.25 centred about a SMBH. We explored the influence of the cluster population and SMBH on the merger rate, the ejection rate, and the escape velocity. For MSMBH = 4 × 106 M⊙, we used both a Newtonian and post-Newtonian formalism, going up to the 2.5th order and including cross terms. We ran 40 and 60 simulations per cluster population for either formalism, respectively. For the other two SMBH masses (MSMBH = 4 × 105 M⊙ and MSMBH = 4 × 107 M⊙), we modelled the system only taking into account relativistic effects. In the case of MSMBH = 4 × 105 M⊙, 30 simulations were run per population. For MSMBH = 4 × 107 M⊙ we ran ten simulations per population. The simulations ended once a black hole escaped the cluster, a merger occured, or the system evolved until 100 Myr.
Results. The post-Newtonian formalism accelerates the loss rate of IMBHs compared to the Newtonian formalism. Ejections occur more often for lighter SMBHs while more massive ones increase the rate of mergers. Although relativistic effects allow for circularisation, all merging binaries have e ≳ 0.97 when measured 1 − 2 kyr before the merging event. The strongest gravitational wave signals are often sourced by IMBH-SMBH binaries that eventually merge. Strong signals were suppressed during our Newtonian calculations since, here, the IMBH typically stalls in the vicinity of the SMBH, before being generally ejected via the slingshot mechanism or experiencing a head-on collision. Weaker and more frequent signals are expected from gravitational wave radiation emitted in a flyby. In our post-Newtonian calculations, 30/406 (7.4%) of the gravitational wave events capable of being observed with LISA and μAres were detected as gravitational wave capture binaries with the remaining being in-cluster mergers. Throughout our investigation, no IMBH-IMBH binaries were detected.
Key words: black hole physics / gravitation / gravitational waves / stars: black holes / stars: kinematics and dynamics / galaxies: nuclei
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
For decades, the idea that supermassive black holes (SMBHs), black holes (BHs) with masses MSMBH ≳ 105 M⊙, reside in galactic centres has been well established (Eckart & Genzel 1997; Ghez et al. 1998, 2000). Since then, the Event Horizon Telescope Collaboration (2019, 2022) has published images of M 87 and the Milky Way’s SMBH (Sgr A*).
By being present in the core of galaxies, SMBHs play a pivotal role in galactic evolution. Two commonly proposed pathways for SMBH formation is via gas accretion (e.g. Volonteri et al. 2003; Begelman et al. 2006) or binary SMBH-SMBH mergers. However, the Eddington limit constrains the accretion rate while dynamical effects stall SMBH binaries once they reach separations of the order of a parsec, suppressing their merging (Begelman et al. 1980).
These mathematical limits placed on the growth rate of SMBHs contradict their observations in the early Universe, for instance that of J1342+0928, an 8 × 108 M⊙ quasar at redshift z = 7.54 (Bañados et al. 2018) or, the recent finding of a 107 ∼ 108 M⊙ BH at redshift z ≈ 10.3 with the James Webb Space Telescope (Bogdán et al. 2023). Observations of these massive objects so early into the life of the Universe tell us that, as of yet, there is unknown physics to uncover, instigating much research in the field (see e.g. Kauffmann & Haehnelt 2000; Madau & Rees 2001; Lodato & Natarajan 2006; Khan et al. 2013; Smith et al. 2018; Regan et al. 2019; Boekholt et al. 2021). In this paper, we investigate the possible role of intermediate-mass black holes (IMBH) in the formation of SMBHs.
As of now, IMBHs have remained elusive with only one detection (a merger remnant with m = 142 M⊙, Abbott et al. 2020). With masses between 102 ≲ M [M⊙]≲105, IMBHs bridge the gap between stellar-mass black holes and SMBHs, and they could be pivotal to understanding SMBH formation. The onset of gravitational wave (GW) astronomy and the development of next-generation gravitational interferometers, such as the Laser Interferometer Space Antenna (LISA; Amaro-Seoane et al. 2017), can allow us to observe the influence of merging events on the growth of SMBHs across cosmic times and give insights on the role of IMBHs during SMBH formation.
More specifically, this paper analyses the scenario proposed by Portegies Zwart & McMillan (2002), who argued that dozens of IMBHs reside in galactic centres. Such a cluster of IMBHs emerges in the following fashion: An IMBH could form through runaway mergers occurring in the core of dense globular clusters (GCs; Miller & Hamilton 2002; Portegies Zwart & McMillan 2002; Giersz et al. 2015). During this time, dynamical friction sinks the GC and IMBH towards the galactic centre (Chandrasekhar 1943). Tidal forces cause the cluster to disintegrate (Gerhard 2001; Portegies Zwart & McMillan 2002; Portegies Zwart et al. 2006; Antonini 2013), leaving only its core and the IMBH getting deposited into the galactic centre. With IMBH arrivals accumulating over time, a steady-state population settles once the IMBH loss rate equals its infall rate.
As initially proposed in Ebisuzaki et al. (2001), the collision component of the steady loss rate then drives the growth of the SMBH. Here, we performed and analysed a series of N-body simulations to derive the characteristics of such a steady-state population and discuss the consequences for GW observatories.
2. Numerical implementation
2.1. N-body integrators
We use the Astronomical Multipurpose Software Environment (AMUSE; Portegies Zwart et al. 2009; Pelupessy et al. 2013; Portegies Zwart & McMillan 2018). This software offers a user-friendly way of tackling complex astronomical questions thanks to its ability to couple various physical regimes together. Focusing purely on gravity, we use two 4th-order Hermite implicit predictor-evaluator-corrector integrators; the Newtonian Hermite (Makino 1991) and its post-Newtonian counter-part HermiteGRX (GRX; Portegies Zwart et al. 2022).
GRX uses the Einstein-Infeld-Hoffman equation (Einstein et al. 1938), which describes the motion of N Schwarzschild BHs (Schwarzschild 1916) in the weak field limit to first order in the post-Newtonian (PN) approximation. GRX expands on the equations by also including the 1 PN cross terms and 2.5 PN term, the latter introducing GW radiation.
Although GRX adopts the simplification derived in Will (2014) to reduce the computational resources needed, it conserves the second-to-highest-ordered pair summations (the cross terms). Doing so forces its wall-clock time to scale with the number of particles as 𝒪(N3), making it more computationally taxing than Hermite and its 𝒪(N2) scaling. Nevertheless, preserving the cross terms is essential to minimise energy errors and introduces a gradual shift in a binary’s semi-major axis, suppressing artificial resonant effects (Rauch & Tremaine 1996; Will 2014).
To suppress numerical errors and better capture close encounters, Hermite and GRX employ regularisation and adaptive time-step techniques (Kustaanheimo et al. 1965; Makino & Aarseth 1992; Mikkola & Tanikawa 1999; Portegies Zwart et al. 2022). The adaptive time-step is dependent on the system’s minimum inter-particle collisional timescale and the free-fall timescale. The near-identical methods adopted by the two integrators allow for a straightforward comparison of their results.
2.2. Initial conditions
We explore how clusters of different IMBH populations, NIMBH, evolve under three SMBH masses; MSMBH = 4 × 105 M⊙, 4 × 106 M⊙ and 4 × 107 M⊙. The second mass is chosen to mimic that of Sgr A* (the Sgr A* model; GRAVITY Collaboration 2019).
Our IMBHs have no intrinsic spin and are of equal mass, with mIMBH = 103 M⊙. This choice follows from Portegies Zwart et al. (2006) who found this to be the average IMBH mass deposited within ten parsecs of the centre of Milky Way (MW)-like galaxies when formed through the runaway scenario described in the introduction. We virialise the system at initialisation to ensure its stability.
The IMBH positions are sampled from a Plummer distribution, and placed on a shell with radius spanning between 0.15 ≤ r [pc] ≤ 0.25 away from the SMBH such that they lie well within Sgr A*’s sphere of influence (≈3 pc). Although theory dictates that density profiles near SMBH follow the Bahcall-Wolf distribution (Bahcall & Wolf 1976), a Plummer distribution is used due to being commonly used to represent relaxed clusters, and the lack of observed Bahcall-Wolf cusp distributions in galactic centres.
Figure D.2 of GRAVITY Collaboration (2020) shows an overview of the available parameter space of the possible IMBH mass orbiting Sgr A* for a given semi-major axis, including previous observations (Yu & Tremaine 2003; Hansen & Milosavljević 2003; Reid & Brunthaler 2004, 2020; Gillessen et al. 2009; Gualandris et al. 2010; Naoz et al. 2020). Although the initialised positions of our IMBH relative to the SMBH tether on the limits of the available parameter space for the MW, the cluster environment tends to settle with half-mass radius rh ≈ 0.45 pc and the IMBHs orbit the SMBH with semi-major axis a ≈ 0.35 pc. Referencing back to GRAVITY Collaboration (2020), the MW centre would be capable of hosting up to NIMBH = 60, assuming they have the same properties as the IMBHs initialised here (mIMBH = 103 M⊙ and a ≈ 0.35 pc).
IMBH velocities are taken from a Maxwellian velocity distribution, with three-dimensional velocity dispersion σ = 50 km s−1. This follows from the observed one-dimensional stellar velocity dispersion at a projected distance of r ≈ 0.1 pc from Sgr A* (Ghez et al. 1998; Schödel et al. 2009) assuming isotropic orbits.
For our relativistic calculations, we investigate clusters populated with 10 ≤ NIMBH ≤ 40. In our Sgr A* model, we separate the populations by intervals of five and run 60 simulations per cluster population. For the other two SMBH masses, we increase this interval to ten and run 30 and 10 simulations per cluster population for the MSMBH = 4 × 105 M⊙ and MSMBH = 4 × 107 M⊙ masses respectively. We also run 40 simulations per cluster population in our Sgr A* model with the Newtonian formalism Hermite, investigating the range 10 ≤ NIMBH ≤ 100 separated by intervals of ten. The Sgr A* model forms the basis of most of our results.
Several reasons motivate our reduced population range with GRX. For one, we want to limit the computational resources expended (recall the 𝒪(N3) scaling). Secondly, observations of the MW centre restrict IMBH populations orbiting Sgr A* with a ≈ 0.3 pc to NIMBH ≲ 60, so there is little physical motivation to analyse larger NIMBH if we assume the MW to be a typical galaxy. Finally, our results show that beyond NIMBH = 40, the median time before a cluster loses an IMBH falls below even the most optimistic MW IMBH infall rate.
The limited number of simulations for our MSMBH = 4 × 107 M⊙ runs is due to it being computationally taxing. Since our sole purpose in exploring this configuration is to assess the impact of SMBH mass on the steady-state population, the ten simulations provide us with an adequate understanding of its influence.
2.3. Stopping conditions
Our code evolves until one of the following is satisfied:
-
tend ≡ tsim = 100 Myr.
-
An IMBH gets ejected from the cluster.
-
A merging event (SMBH-IMBH or IMBH-IMBH) occurs.
The chosen cap on tend is configured for MSMBH = 4 × 106 M⊙. A value chosen based on (Portegies Zwart et al. 2006), who found that in a MW-like galaxy, an IMBH sinks into the inner parsec every tinfall ∼ 7 Myr. With the main goal of the paper being to predict the steady-state population of IMBH, and with tinfall ≪ tend, placing this cap does not influence our inferred steady-state population since the few runs reaching this limit correspond to a population underestimating the steady-state population. The other two conditions allow us to extract when an IMBH is lost from the system, tloss.
2.3.1. Ejections
There are two distinct ways in which ejections occur. The first classification of ejections happens when an IMBH is found to be spatially separated from the cluster centre with rij ≥ 6.00 pc (roughly twice the sphere of influence for Sgr A*). We refer to this set of ejected IMBHs as “drifters”.
The other method detects ejections if an IMBH satisfies all of the following:
-
1.
Its kinetic energy, KE, exceeds the absolute value of its potential energy, |PE|.
-
2.
The IMBH is ≥2.00 pc away from the cluster’s centre of mass (com).
-
3.
An IMBH (subscript i) is moving away from the cluster such that ri, com ⋅ vi, com > 0, where ri, com is the positional separation and vi, com the IMBHs velocity in the cluster centre-of-mass frame of reference. We use AMUSE’s center_of_mass() and center_of_mass_velocity() function to compute either properties for the centre of mass frame respectively. These functions account for all particles present within the simulation.
Generally, drifters satisfy the latter two conditions, but have KE < |PE|.
Figure 1 shows the final 500 kyr in the xy-plane of a GRX simulation ending due to an ejected IMBH. In the figure, although the bottom IMBH follows an eccentric orbit and reaches large separations from the cluster centre, it remains bound. Conditions 1 and 3 ensure that it is not flagged as ejected. Contrariwise, the IMBH in the upper right-hand corner of the figure exhibits a distinct radial trajectory moving away from the cluster.
 |
Fig. 1. Final 500 kyr of an NIMBH = 15 simulation using GRX ending in an ejection. Coloured are the IMBHs, and at the origin lies the SMBH. The panel shows the IMBH trajectory (small dots) and final position (outlined dots) along the xy-plane. |
2.3.2. Mergers
Mergers are detected using AMUSE’s collisional detection function, which gets triggered when two IMBHs are within a distance smaller than the sum of their collisional radii (|rij|≤Rcoll = Ri, coll + Rj, coll). This function is integrated into the algorithm of the N-body integrators, forcing a check for collisions after each internal time step.
The collisional radius of particle i is defined by its innermost stable circular orbit in the Schwarzschild metric, Ri, coll ≡ RISCO = 6GM/c2. For our IMBH and Sgr A* masses, this gives Rcoll, IMBH = 10−2 R⊙ and Rcoll, SMBH = 51 R⊙. Figure 2 shows the final 1.5 Myr of a GRX simulation ending with a merger.
 |
Fig. 2. Final 1.5 Myr of an NIMBH = 15 simulation ending in a merger in the xy-plane using GRX. The dots represent the same information as Fig. 1. The merging IMBH, shown in red, has a larger dot size as its final position relative to the other IMBHs. |
3. Results
3.1. Newtonian vs. post-Newtonian
Table 1 summarises the outcomes of our simulations, emphasising the need for PN terms when simulating clusters of BHs. More explicitly, 90.7% of our Sgr A* simulations end with mergers when including relativistic effects. This reduces to 52.5% in our Newtonian calculations. Tables 2 and 3 show the distribution of outcomes relative to the cluster population.
Simulation outcomes for the various masses.
Simulation outcomes relative to the cluster population for MSMBH = 4 × 106 M⊙ runs.
Simulation outcomes relative to the cluster population for MSMBH = 4 × 105 M⊙ and MSMBH = 4 × 107 M⊙ runs.
Changing the SMBH mass gives different cluster histories. From Table 1 we observe that for the lowest SMBH mass, simulations tend to end with ejections. This reflects the lower escape speed of the cluster and smaller collisional radius of the SMBH. Contrariwise, no ejections occur for the higher SMBH mass.
Figure 3 shows the semi-major axis and eccentricity space occupied by IMBH orbiting around the SMBH during our Sgr A* runs. We restrict our analysis to NIMBH ≤ 40 simulations. To minimise sampling bias, we collect data from individual simulations at a time step equal to the smaller of two values: either the final time step (tsim) of the sampled simulation, or the median time for clusters with equivalent populations and to experience IMBH-loss (med(tloss)) when simulated with relativistic effects. Applying the Kolmogorov-Smirnov test, we find the distributions of the semi-major axis and eccentricities between formalisms to be statistically distinguishable with p-values 6.5 × 10−3 and 1.8 × 10−23 for the semi-major axis and eccentricity distribution respectively. This indicates that although the evolution of individual particles present within the simulation differ which subsequently influences the final outcome, the general macroscopic properties of the cluster are essentially identical no matter the gravitational formalism.
 |
Fig. 3. KDE (top panels) and CDF plots (bottom panels) of the eccentricity (left) and semi-major axis (right) for all IMBHs with respect to the central SMBH evolved in simulations with NIMBH ≤ 40. Parameters are taken at time tsim = min{tsim, med(tGRX4e6)}. |
We note the order-of-magnitude differences in the dynamic range of both the eccentricity, e, and the semi-major axis, a. PN calculations achieve a wider range in eccentricities, with (1 − emin) being roughly an order of magnitude lower, while the semi-major axis can be approximately three orders of magnitude smaller.
The emission of orbital energy from the binary system in the form of GW allows IMBHs to sink near the SMBH. For the Newtonian calculations, stalling occurs at a ≈ 0.1 pc. This tendency explains the higher proportion of simulations ending with mergers when incorporating relativistic effects.
3.2. Ejection events
Table 4 summarises the ejection events for our Sgr A* model. Although results suggest that relativity tends to quicken ejections, it is hard to identify to what extent the PN terms play a role. Namely, since loss-events during Sgr A* runs are dominated by merging events (90.7% of simulations ending with SMBH-IMBH mergers for GRX compared to 52.5% for Hermite) and with GRX being more efficient in inducing SMBH-IMBH mergers, GRX results only look at the (few) ejection outliers who occur quickest, reducing the median ejection time.
Summary of ejection outcomes when MSMBH = 4 × 106 M⊙.
As seen in Fig. 4, there is a weak dependence of NIMBH on both the ejection velocity, vejec, and the time at which the event occurs (smaller tejec). The former is due to a larger cluster population having larger potential energy, resulting in the requirement of larger velocities for the ejection of a particle. The latter is a result of the fact that, with a larger population, the tail end of the Maxwell distribution will be more quickly replenished. This tail end represents the regime in which particles are characterised by velocities larger than the escape velocity. This dependence of time on the cluster population is also seen through the inverse N dependence in the typical cluster loss time (Eq. (A.7)).
 |
Fig. 4. Various ejection properties for Hermite (MSMBH = 4 × 106 M⊙). The upper and lower bars represent the interquartile range. |
Figure 5 shows the ejected velocity distribution found with our Newtonian results. On occasion, the ejection velocity exceeds the MW escape velocity (based on a distance of r = 0.2 pc), with the maximum being vejec, max = 1050 km s−1 (when restricting samples to NIMBH ≤ 40).
 |
Fig. 5. Histogram of Hermite-ejected velocities. Samples are taken from clusters with 10 ≤ NIMBH ≤ 100 and MSMBH = 4 × 106 M⊙. |
Due to the low number of ejection events occurring during the Sgr A* GRX simulations, we focus our analysis on ejection events occurring during MSMBH = 4 × 105 M⊙ runs. In this configuration, the maximum ejected velocity is vejec = 198 km s−1 with Fig. 6 showing the distribution of ejection velocities. The decrease in vejec, max reflects the reduced escape velocity and reduced strength for which the Hills mechanism can slingshot a tertiary particle (Hills 1988, see Appendix A.2).
 |
Fig. 6. Histogram of GRX-ejected velocities where MSMBH = 4 × 105 M⊙. |
The change in binning resolution between Figs. 5 and 6 scales with the range of values spanned. Specifically, we go from Δv ≈ 50 km s−1 for Fig. 5 to Δv ≈ 10 km s−1 for Fig. 6. The different shapes exhibited are thus partly due to differences in binning resolution with enhanced resolution leading to a more disjointed distribution. Nevertheless, differences also have a physical basis attributed to them.
Namely, the GRX histogram has a pronounced right skew. This is due to the different proportions of drifters present. Since drifters tend to have KE < |PE|, they exhibit lower ejection velocities. Overall we find that 27/55 (49.1%) of ejection events occurring in our Newtonian calculations are drifters. During MSMBH = 4 × 106 M⊙ PN runs, a similar proportion was found with 16/32 (50.0%) of ejections being drifters. Comparatively, 48/119 (40.3%) of ejections are drifters when we decrease the SMBH mass. It is therefore likely that the drifter rate is due to SMBH mass rather than the gravitational formalism.
In both cases, the ejected velocity exhibits a Maxwellian distribution, with the most probable outcome corresponding to the ejection velocity of the cluster at r ≈ 0.2 pc.
3.3. Steady-state
Figure 7 shows the dependence of tloss on NIMBH when MSMBH = 4 × 106 M⊙. In all cases, when simulating with Newtonian gravity, it takes substantially longer for the cluster to lose an IMBH.
 |
Fig. 7. Cluster IMBH-loss time as a function of NIMBH where MSMBH = 4 × 106 M⊙. Filled circles signify the median IMBH loss time for a cluster of a given population. The upper bar shows where 75% of the data lies below while the lower one where 25% of the data lies below. The dashed curve represents the line of best fit (see Eq. (1)) and for the classical results. Arrows represent the fact that the upper error is 100 Myr, a value limited by the tend = 100 Myr simulation time. |
We note that the median IMBH-loss time for the Newtonian case with NIMBH = 10 equals the maximum simulation time, with 21/40 (52.5%) simulations evolving to this time. Contrastingly, for NIMBH = 10, the PN formalism reached this cap 6/60 (10.0%) times. The larger proportion of simulations reaching tsim = 100 Myr when using Newtonian gravity suppresses the perceived differences between gravitational frameworks for identical populations.
The dashed curve for the PN results in the figure follows,
The standard errors in our best-fit values are ±36.9 Myr, δα = ±0.175 and δγ = ±0.0571. Here, α and γ denote the denominator’s power law and the term inside the logarithm, respectively. Comparatively, the classical best-fit curve is found to have a slope of 210 ± 148 Myr, α = −1.02 ± 0.15. The Coulomb parameter, γ, is fixed to γ = 0.11 in this case due to its large errors suggesting that the optimal values for this parameter is ambiguous (Virtanen et al. 2020).
Our fitting function contains an additional power-law in the denominator compared to the analytical expression derived in Appendix A. Nevertheless, the fact that the best-fit value for the exponent α is nearly 1, and considering the large spread in tloss, our results support our analytical derivation, which stems from the relaxation time expressed in Spitzer (1987) and Binney & Tremaine (1987).
Although our system is not a purely equal-mass system, when accounting for error bars, our lower-limit extracted γ value lies just outside the literature value of γ = 0.11 (Spitzer 1987; Giersz & Heggie 1994; Spinnato et al. 2003) for equal-mass systems. It is also several factors larger than the corresponding γ value for unequal-mass systems (0.016 ≲ y ≲ 0.026 Giersz & Heggie 1996). This suggests that environments whose potential are dominated by a single object are more akin to single-mass systems than a multi-mass one. Indeed, the relaxation time is driven by weak two-body interactions. Since this is dominated by equal-mass IMBH-IMBH encounters, γ tends towards this value.
The large relative errors show the limitation of our best fit and the sensitivity of results in N-body systems to initial conditions as pointed out by Poincaré (1900). Moreover, the form of Eq. (1) is found by deriving the typical particle ejection time from the cluster, and thus neglects the presence of merging events. Events which dominate our PN runs.
The fact that the PN runs overwhelmingly end in mergers, whereas the classical ones experience merger ≈50% of the time, influences the behaviour of tloss. Indeed, although ejection events and the time taken to merge a two-body system through GW are both characterised by the eccentricity (the former being characterised with e > 1 and the latter having timescales going as tGW ∝ (1 − e2)7/2 Peters 1964), the onset of GW radiation with the inclusion of the 2.5 PN term induces a runaway effect. Namely, as the IMBH sinks into the SMBH’s potential, an increasing amount of orbital energy is removed from the system in the form of GW radiation, which then accelerates the sinking rate of the IMBH.
Another reason behind the different trends observed, and namely the plateauing of tloss at large NIMBH results from the dynamical origin of the merging binary. We can classify merging events into two families; GW capture events in which an eccentric, hard SMBH-IMBH binary evolves until inspiral, and in-cluster mergers, mergers induced when a tertiary particle interacts with some SMBH-IMBH system, nudging one of its constituents, leading the binary to a grazing trajectory. Although the latter scenario forms the bulk of merging events across all cluster populations, GW capture events occur more often for low NIMBH (see Table 6). Since GW capture events take longer and become rarer for large NIMBH, at these larger cluster populations they play a smaller role in enhancing tloss. Overall, the inclusion of the 2.5 PN term introduces the diverging behaviours in the graph.
Figure 8 motivates our decision to reduce the number of simulations run for our MSMBH = 4 × 105 M⊙ configuration to Nsim = 30 per cluster population. In this figure, all points are derived using results from our PN Sgr A* model, differences arise due to values being computed using a different number of simulations. Since the values computed when incorporating Nsim = 30 runs are statistically indistinguishable from values derived with a larger number of runs we restrict ourselves to 30 simulations per configuration.
 |
Fig. 8. Median, upper, and lower percentile range computed when considering a different number of datasets, Nsims. Datum correspond to GRX runs where MSMBH = 4 × 106 M⊙. |
Figure 9 shows how the IMBH-loss rate changes with SMBH mass. The dash curve is the same as that shown in Fig. 7, providing a reference to compare with our Sgr A* model. The lowest SMBH mass shows similar results to our Sgr A* system, although the differences are smaller than what we expect (log10(M1/M2)= − 0.5). This discrepancy between theory and simulations could result from ejection events typically taking longer to happen than mergers. Since the lower SMBH mass experiences no mergers, tloss shifts to higher values approaching a classical-like behaviour. The loss-time during NIMBH = 40 runs diverges away from the general trend since at this population, and with the low cluster mass weakly binding the IMBH, any slight nudge on a particle lying in the outskirts of the cluster can cause it to be ejected.
 |
Fig. 9. Outlined circles denote the median time for a cluster of a given population to experience population loss. The bars denote the interquartile range of the data. Different colours correspond to different SMBH masses. In all cases, relativistic effects are considered. The dashed curve corresponds to the line of best fit for the PN results in the Sgr A* model. Arrows represent the fact that the upper error is 100 Myr, a value limited by the tend = 100 Myr simulation time. |
At the other extreme, the cluster seems to diverge from a system evolving primarily through two-body encounters. This is observed with the average rate of change of the half-mass radius.
Restricting our analysis to NIMBH = 10 runs, Fig. 10 indicates an average half-mass rate-of-change equal to zero for MSMBH = 4 × 107 M⊙ configuration. With such small NIMBH present, the IMBHs form 0.1% of the cluster mass. This means their dynamics are dominated by the SMBH potential and mutual IMBH-IMBH encounters induce only minute changes in orbital parameters as they essentially follow Keplerian orbits. This makes it more difficult for an IMBH to orbit the SMBH with extreme eccentricities e ≈ 1, a parameter essential to reducing the merging timescale if we recall that for a two-body system tGW ∝ (1 − e2)7/2.
 |
Fig. 10. Evolution of the 25% Lagrangian radii (solid lines), 50% Lagrangian radii (rh, dash-dotted lines) and the 75% Lagrangian radii (dotted lines) for NIMBH = 10 PN simulations averaged over all runs. |
3.4. Binary and hierarchical systems
Table 5 shows the statistics on binary and hierarchical systems formed during our simulations. The former satisfy condition (A.8) and (A.9), while the latter condition (A.11). Results incorporate data from complete simulations, meaning binaries emerging in the Newtonian simulations are given more time to evolve.
Summary of results when MSMBH = 4 × 106 M⊙.
Very few binaries evolve to be hard, with similar percentages between the relativistic and Newtonian integrators. We note that the similarities found between formalism are exaggerated since the smaller times simulated during our PN runs mean binaries have less time to evolve. Over time, the 2.5 PN term would cause the binary system to emit radiation through GWs, hardening it. The emission of GW also allows more interactions since the loss of energy from the cluster environment would allow for more frequent close encounters between IMBH as the core becomes denser, potentially allowing soft binaries to form through complex interactions.
Indeed, although subtle, the larger percentage of hard binaries and lower median binary formation times, tbf, indicate that the PN formalism encourages the formation of binaries, a conclusion agreeing with Rodriguez et al. (2018).
Interestingly, the distribution of tbf for both our relativistic and Newtonian formalism suggest an optimal population for binary formation between 15 ≲ NIMBH ≲ 30. This results from the compensating effect of increasing number density allowing for larger amounts of prospective IMBHs to form such systems, but also not having an over-abundance of IMBHs present whose encounters would efficiently disrupt the formation of binaries.
We also note that the relativistic simulations rarely have hierarchical systems emerging ((SMBH, IMBH), IMBH), with only two such systems detected throughout our PN Sgr A* runs. Their rarity is due to their formation taking a considerable amount of time. Taking the median hierarchical formation time, med(thf), for our Newtonian calculations from Table 5 as a reference point, and comparing it to the median time taken for clusters evolved with PN effects to disrupt (Fig. 9), we see that med(thf)> med(tloss).
Figure 11 shows the average fraction of time in which at least one binary exists within the cluster. The colours represent the average number of systems formed for the specific population. The lack of lower error bar for population NIMBH = 20, 35 and 40 for GRX are due to the lower limits being zero.
 |
Fig. 11. Influence of NIMBH on the average percentage of time binary systems are present in MSMBH = 4 × 106 M⊙ simulations. Colours correspond to the average number of systems formed, Nsys (see Table 5). The blue and red dotted line is the line-of-best fit for GRX and Hermite respectively. |
We note the similarities in the results between integrators, exemplified by their similar line of best fits:
For both the Newtonian and PN integrator, no IMBH-IMBH binaries formed. This is due to the cluster’s proximity to the SMBH, whose gravitational influence efficiently disrupts any prospective IMBH-IMBH system. As reference, assuming a 1D velocity dispersion σ = 150 km s−1 and applying condition Eq. (A.9), an SMBH-IMBH system needs a ≤ 0.346 pc to be identified as a binary, whereas an IMBH-IMBH system needs to satisfy a ≤ 8.65 × 10−5 pc (roughly 18 AU).
Figure 12 shows the GWs sourced by hard binaries during our relativistic simulations assuming they are sourced a luminosity distance of DL = 1 Gpc away. Appendix A.3 summarises the calculation procedure with the redshift being found using the relevant cosmological parameters in the Planck Collaboration VI (2020).
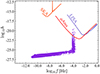 |
Fig. 12. Distribution of GRX GWs emitted in (f, h)-space where MSMBH = 4 × 106 M⊙. Each dot represents an event at a given snapshot emerging from a hard binary. The detectable regions for the Square Kilometer Array (SKA; Smits et al. 2009), μAres (Sesana et al. 2021) and LISA (Amaro-Seoane et al. 2017) are shown on the plot using code developed by Campeti et al. (2021). Calculations assume a luminosity distance of DL = 1 Gpc. |
The key feature is the vertical ascent emerging at frequency f ≈ 10−4 Hz and reaching large strains, h. This is the GW capture branch, characterised by hard binaries of large eccentricities. The GW capture branch has been observed in several papers adopting PN formalisms (e.g. Gültekin et al. 2006; Samsing et al. 2014; Haster et al. 2016; Samsing & Ilan 2018; Rodriguez et al. 2018; Banerjee 2018). Even at DL = 1 Gpc, the GW interferometer μAres will be able to capture binaries emitting radiation during the early phases as they follow the GW capture branch. Nevertheless, the early phases will remain undetectable for both LISA and LIGO, with their observations only achievable during the later stages.
The streaks emerging in Fig. 12 are a natural byproduct of our sampling method whereby we calculate GW signals every 103 years. This discrete sampling method causes persistent GW sources to jump in their GW emission in (f, h) space depending on the systems energy evolution within these 103 years rather than exhibit a continuous evolution. Figure 13 illustrates the emergence of this artificial feature by following the evolution of an SMBH-IMBH binary system from our relativistic calculations identified as being hard.
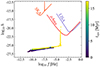 |
Fig. 13. Streak-like feature emerging in (f, h) space from a persistent GRX binary. The colour denotes the age of the binary, tsys. |
3.5. Gravitational waves
This section focuses on GW events occurring in our Sgr A* model assuming the source is DL = 1 Gpc away and satisfies fn, z ≥ 10−12 Hz. We resort to a qualitative analysis since our sampling method prohibits any quantitative analysis. More explicitly, in addition to the limitations introduced by only calculating events occurring at snapshots with intervals of 103 years, many encounters are hyperbolic, making it impossible to solve Eq. (A.14).
Overall, 90.1% and 86.4% of IMBH-IMBH interactions have e ≥ 1 for the relativistic and Newtonian formalism respectively. The minority with e < 1 form transient events, gravitational Bremsstrahlung’s. Even though these events have their components orbit one another with e < 1, these systems are not classified as binary’s since their semi-major axis are typically of the order a ∼ 10−1 pc, several orders of magnitude larger than the a ≲ 8.65 × 10−5 pc threshold needed to form IMBH-IMBH binaries.
Figure 14 shows all the GW sources detected in NIMBH ≤ 40 simulations. The top panel corresponds to PN results, while the bottom one, Newtonian ones. Overall, there are 1.10 GW events occurring per year during our Newtonian simulations for every GW event occurring within the same time frame in our PN simulations. When considering only events observable with μAres (and assuming dL = 10 kpc), there are 2.38 events in favour of the relativistic formalism for every event in our Newtonian calculations.
 |
Fig. 14. f vs. h diagram for all GW events in NIMBH ≤ 40 runs. Events assume DL = 1 Gpc. Top: GRX simulations. Bottom: Hermite simulations. |
No IMBH-IMBH binaries are observed although IMBH-IMBH events are detected. This is due to them being extremely soft transient systems which randomly encounter one another as they orbit the SMBH. Given the softness of these binaries, one can estimate their lifetime to be of the order of their crossing time, τ ∼ rij/vij with rij and vij being their relative separation and velocities respectively. To first-order, the typical IMBH-IMBH distance is ∼0.15 pc with a three-dimensional velocity dispersion ∼150 km s−1 following our initial conditions. This corresponds to a system lifetime of τ ≈ 980 years, a value just below the snapshot resolutions.
When adopting the Newtonian framework, we note the disappearance of the GW capture branch. The need for relativistic effects to reproduce this branch was analytically predicted in Hansen (1972) and Quinlan & Shapiro (1989). Indeed, without the 2.5 PN term, and hence no GW emission, IMBHs have difficulty sinking near the SMBH. This has repercussions on our understanding of GWs emanating from dense environments since these events make a prominent GW demographic observable at Gpc scales with future interferometers.
Both classical and relativistic formalisms are able to capture in-cluster mergers. This branch lying at the upper-frequency regime is sourced by highly eccentric binaries who merge in-between binary-single encounters (Samsing & Ramirez-Ruiz 2017; Rodriguez et al. 2018; Kremer et al. 2019). Characterised by a weaker strain, its early phases will remain observable with future GW interferometers if sources are within our local neighbourhood (DL ∼ 10 Mpc) with the final stages (unresolved here) being observed up to Gpc scales.
Although Newtonian gravity can reproduce the in-cluster merger branch, they occur more often under relativistic calculations, since, as observed in Fig. 3, incorporating relativistic effects allows for more extreme orbital eccentricities and tighter orbits. Table 6 highlights this by showing the increase in the average rate of in-cluster events per simulation, ⟨Nic⟩. The calculations done for the average, ⟨…⟩, count events emanating from the same system multiple times. Contrariwise, Ncap. and Nic only take into account one event per binary system.
Average rate for simulations of a given population to emit GWs within two of the prominent branches.
The dynamical nature of in-cluster mergers is made apparent by the dependence of Nic on NIMBH when evolved under either gravitational framework. The summation of Nic and Ncap. for all cluster populations exceeds the number of mergers found in both cases since at any given simulation, numerous binaries may satisfy the conditions. Moreover, it could be that at times although a SMBH-IMBH binary attains one of the two branches, an ejection or other merging event has already occured, or that the simulation has reached 100 Myr. For our relativistic calculations we find Ncap./Nic = 0.129.
Figure 15 shows the eccentricity of the merger product. The results represent the eccentricity up to < 2 kyr before the merger since information can only be extracted on the binary one time-step before the event occurs. Neglecting the final ∼2 kyr, the eccentricities shown here are skewed towards higher values. As an example, taking into account the tightest binary shown in Fig. 3 (a ≈ 10−3.7 pc and e ≈ 0.975), using Eq. (A.12), this binary system should take ≈1500 years to merge, meaning we did not observe the final 1.5 kyr of its evolution in which the gradual loss of angular momentum would circularise the binary.
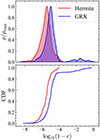 |
Fig. 15. KDE (top) and CDF (bottom) distribution of the eccentricity of merging IMBHs at the final time step. In both cases, the data is restricted to NIMBH ≤ 40 simulations. |
This systematic error has more influence on the GRX curve, since the final stages of coalescence is when the 2.5 PN term becomes most efficient and would allow for evolution of the binary’s orbital parameters. Nevertheless, we remark that given the rapidity of their inspiral, binary systems undergoing GW capture will not be able to completely circularise and still exhibit residual eccentricity. Not only will their residual eccentricities be detectable during the final inspiral, but as seen in Fig. 14, future GW interferometers will be able to identify their extreme eccentricities thousands of years before the final merger.
Figure 16 examines these same events in (a, (1 − e))-space. The solid black line marks the regions where, if unperturbed, a binary will merge within a Hubble time using Eq. (A.12). The grey and black zones correspond to the observable LISA and μAres regime, disregarding their sensitivity limitations. We keep in mind that these events will be unobserved assuming the distances calculated here, and only at the final inspiral phase should we expect to detect them. As noted in Fig. 3, most events tracked here are those sourced by encounters with 0 ≲ e ≲ 0.9 and semi-major axis 0.1 ≲ a [pc]≲1.
 |
Fig. 16. Scatter plot denoting where Hermite and GRX GW events lie in the a vs. log10(1 − e) parameter space. The panels above and on the right show the kernel density estimate. The greyed-out regions denote the frequency range probed by LISA and μAres. The dashed-dotted lines show where the sensitivity of the interferometers is at a maximum, while the dotted ones the frequency range probed (Sesana et al. 2021; Samsing et al. 2014), with the upper bounds for μAres and LISA being the same (f = 1 Hz). The data here is from runs simulated with NIMBH ≤ 40. Top: SMBH-IMBH GW events. Bottom: IMBH-IMBH GW events. |
While a vast majority of SMBH-IMBH events are similar regardless of our choice of solving the system under Newtonian laws of gravity or relativistic ones, the nature of IMBH-IMBH events differ. Namely, in addition to the larger proportion of IMBH-IMBH encounters being hyperbolic for GRX, when calculating with relativistic effects, we find events characterised with smaller eccentricities and semi-major axis’ (with a non-negligible fraction achieving a ≲ 3 Mpc, 620 AU).
Finally, we note the distinct streak exhibited by GRX in the top left of the upper panel of Fig. 16. This shows the evolution of the binaries in the GW capture branch. These SMBH-IMBH systems tend to orbit one another with a ≈ 10−1 pc, and thus are typically identified as soft binaries. These systems however have large eccentricities such that at periastron, a vast amount of orbital energy is emitted from the system, tightening the binary in the process. This removal of angular momentum from the system results in its circularisation explaining their climb to small log10(1 − e) values. In-cluster mergers occupy the region defined with larger semi-major axis and more extreme eccentricities of log10(1 − e)≈10−6.
4. Discussion
4.1. Cluster evolution
In general, although the global trends show similar values whether they evolve under Newtonian or PN gravity, outliers bring forth a different set of outcomes.
Most notably, the 2.5 PN term in GRX allows SMBH-IMBH binaries to emit GWs, tightening their orbits in the process and forming a denser core where interactions between IMBHs are frequent. This not only explains the more extreme a and e values attained in the relativistic case, but also: the enhanced merger rate, the quicker rate for the cluster to lose an IMBH and the appearance of the GW capture branch. From Fig. 3 we also see that in the Newtonian formalism, stalling occurs, with IMBHs struggling to orbit the SMBH with semi-major axis a ≲ 0.1 pc.
Our results show the tendency for the relativistic formalism to suppress ejection events compared to the Newtonian formalism. This result is biased considering that more time is typically needed to eject an IMBH for either gravitational framework (Table 4). For our relativistic calculations, these typical ejection times exceed the median IMBH-loss time tloss. As a result, we keep in mind that some IMBHs present in individual GRX simulations may be evolving towards an ejection pathway only for a merger to occur before.
The tendency for the Newtonian formalism to experience more ejections also has a physical origin. During the close encounters needed to push an IMBH to energies KE > |PE|, the GW energy emitted dampens the IMBHs’ orbital energy and the strength of the gravitational slingshot. Consequentially, when modelling PN terms, ejection events are harder to come by since they require a more substantial interaction to compensate for this energy depletion and push the IMBHs orbit above the e = 1 threshold. Contrariwise, the lack of GW emission in the Newtonian calculations allows interactions to be adiabatic, allowing for its IMBHs to more easily grow their energies and exceed the e = 1 threshold. In both cases, the ejection rate is amplified by our choice of neglecting tidal effects.
We note that drifters are omnipresent in the simulations, occurring most often during our Sgr A* model. When incorporating relativistic effects in our Sgr A* model, 16/32 ejection events were classified as drifters. For MSMBH = 4 × 105 M⊙ this amounted to 48/119. We keep in mind that since we simulate an isolated environment, the fractions are exaggerated as the IMBH is unable to settle elsewhere within the 2.00 ≤ r ≤ 6.00 pc regime.
Investigating drifters and ejection events would provide insights into the nuclear star cluster (NSC), and help constrain locations of interest when searching for IMBHs. If IMBH clusters exist in galactic cores (much in the same way as runaway stars inform us about the cluster history Fujii & Portegies Zwart 2011), a mass and distance-dependent escape velocity imply a surplus of IMBHs lying in a shell depending on the properties of the SMBH and cluster. This would result in a bimodality of the IMBH population distributed in the core of galaxies. The population peak nearest to the SMBH would correspond to the cluster as simulated here, while the outer region would correspond to IMBHs ejected from the cluster with velocities corresponding to the most probable escape velocity.
Finally, our results show the possibility for IMBH to completely unbind from the galaxy, giving rise to the idea of a population of intergalactic IMBHs, possibly accompanied by a few close orbiting stars. Moreover, for our lowest mass configuration, IMBHs are often ejected from the cluster, thus reducing the possibility for such objects to form merging binaries and reducing our chances of observing them through GW emission.
4.2. Steady-state population
In general, increasing the SMBH mass increases tloss. For the lowest mass configuration, most of the simulations ended with ejections. This is mostly due to the lower escape velocities needed, although the reduced amount of GW radiation emitted during close approaches and reduced collisional radii also play a role. For the largest mass, no ejections were observed.
A larger SMBH mass implies an increase in orbital energies. As a result, IMBH-IMBH interactions have a diminished influence on how their orbital parameters evolve, making it challenging for them to enhance their eccentricities. As such, the cluster evolves on much longer time-scales allowing for a larger steady-state population of IMBH in the galactic core.
We note that these outcomes are dependent on our initial conditions. Our choices are motivated through observations of the MW and its generalisation to other galaxies, although allowing for more straightforward comparisons, should be interpreted with some scrutiny. One clear example in the context here, is the identical initialised distances used for our cluster regardless of the SMBH mass. For the lowest mass configuration this encourages ejections as random walk processes can easily diffuse particles initially on the outskirt outwards from the cluster, subsequently unbinding from the environment, while for the larger SMBH mass this encourages mergers. Using the same distance contradicts with theory since binary stalling distances, dependent on the loss cone boundary 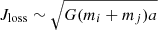 , reduces with binary mass. Moreover, infalling IMBH will not have identical masses. In all cases, modifying these parameters would influence the outcomes and qualitative results found here and could be worth further investigation. Nevertheless, our choices are motivated by the lack of observations of extra-galactic nuclei and the paper being the first of its kind to analyse a cluster of IMBH, providing a foundation for future papers to build from.
, reduces with binary mass. Moreover, infalling IMBH will not have identical masses. In all cases, modifying these parameters would influence the outcomes and qualitative results found here and could be worth further investigation. Nevertheless, our choices are motivated by the lack of observations of extra-galactic nuclei and the paper being the first of its kind to analyse a cluster of IMBH, providing a foundation for future papers to build from.
Looking at our relativistic Sgr A* runs, deviations between theory (Eq. (A.6)) and the best-fit parameters of Eq. (1) are due to a multitude of reasons. The tsim ≤ 100 Myr cap reduces the perceived impact of NIMBH on tloss and consequently overestimates the power-law. This also explains to some extent the larger γ value found compared to the literature. Furthermore, our derivation consists of several approximations, namely; ⟨m⟩≈105 M⊙, 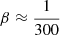 and our choice of the half-mass radius, rh. Each of these influence the constant coefficient. All these discrepancies are amplified with our Newtonian-centric derivation ignoring the PN feature of introducing GW radiation, and for which our extracted parameters are based off. Additionally, we keep in mind that the large fluctuations in tloss, signified by the interquartile range, reduce our confidence on the extracted parameters even though, when accounting for errors, the parameters coincide with theoretical predictions.
and our choice of the half-mass radius, rh. Each of these influence the constant coefficient. All these discrepancies are amplified with our Newtonian-centric derivation ignoring the PN feature of introducing GW radiation, and for which our extracted parameters are based off. Additionally, we keep in mind that the large fluctuations in tloss, signified by the interquartile range, reduce our confidence on the extracted parameters even though, when accounting for errors, the parameters coincide with theoretical predictions.
Taking the inferred MW IMBH infall rate of one every 7 Myr (Portegies Zwart et al. 2006), the relativistic-based results suggest a steady-state population of NIMBH ≈ 10 − 15, a similar result to that predicted in Portegies Zwart et al. (2004). Inferring this population using results derived with the Newtonian integrator, the steady-state population increases to NIMBH ≈ 30. We note that both of these satisfy the available parameter space shown in Fig. D.2 of GRAVITY Collaboration (2019). From our results and those found in Portegies Zwart et al. (2006) we thus expect NIMBH ∼ 10 to lie within the inner half parsec of the MW. This is a value which could drop to NIMBH ∼ 1 if we consider a 1 Gyr infall rate (see Antonini 2013; Arca-Sedda & Gualandris 2018; Askar et al. 2021; Fragione 2022). In both instances, the infall rate is taken as an average over the galactic history, a value which will naturally fluctuate in time and depend on the current stage of the galaxies life.
The large discrepancies between papers in the inferred infall rate stem from the extent tidal forces dissolve the inspiraling GCs. Conservative estimates assume that these GCs capable of hosting IMBH resist the tidal forces and deposit most of their mass to the NSC, whereas the quicker infall rate estimates are due to tidal forces dissolving even the densest GCs before they can deposit their material into the galactic centre.
We now forecast the SMBH-IMBH merging event rate up to redshift z ≤ 3.5, which corresponds to the upper limit with which the EAGLES simulation extracts the best-fit values for the Press-Schechter parameters (see Table A.1 of Furlong et al. 2015). We assume a constant Universal galactic average IMBH infall rate, Γinfall.
Following Fragione (2022), the SMBH-IMBH merging event rate is
where dN(z)/dMgal, * is the number of SMBH-IMBH merging events per galactic stellar mass and Φ(z, Mgal, *) the Press-Schechter function. We assume a constant dN(z)/dMgal, *, normalising the value to the MW stellar mass, MMW, * = 6 × 1010 M⊙ (Licquia & Newman 2015).
For a steady-state population, the number of events per galactic stellar mass per unit time is equivalent to the product between the infall rate and the merging fraction, ζ. Here we adopt ζ = 0.9 following our results in our Sgr A* model.
Using this and integrating Eq. (4) over the galactic mass range capable of hosting an SMBH and the upper bound probed by the EAGLES simulation (Mgal, * ∈ [108, 1012] M⊙), Fig. 17 shows the influence of Γinfall on the cumulative number of events up to z = 3. If the average IMBH infall rate is Γinfall = 0.1 Myr−1, then we expect 590 yr−1 SMBH-IMBH mergers. Contrariwise, using more conservative estimates with Γinfall ∼ Gyr−1, this decreases to 5.90 yr−1.
 |
Fig. 17. Influence of the infall rate, Γinfall, on the cumulative number of SMBH-IMBH merging events up to redshift z ≤ 3.5. |
Fragione (2022) found a 0.1 − 1 yr−1 event rate assuming an infall of Γinfall ∼ Gyr−1. The upper limit corresponds to models where, if a globular cluster is dense enough, it will always form an IMBH. Differences found here with these values are due to us not restricting our results to galaxies capable of hosting both an SMBH and a nuclear star cluster allowing us to omit the ϵ = 0.3 scaling coefficient used in the paper and extending to a larger range of galactic masses.
Accounting for the reduced mass range and incorporating the 0.3 coefficient reduces our forecasting estimates from 5.89 yr−1 to 0.96 yr−1 when assuming a 1 Gyr−1 IMBH infall rate. This falls within the most optimistic predictions in Fragione (2022). Indeed, we stress that this represents the upper limit of expectations as we have neglected the time needed to accumulate a population of IMBH within the galactic centre, and assumed that the host SMBH has the mass of Sgr A* already at birth.
Moreover, our calculation neglects the time needed for IMBHs to form, the distance at which the steady-state IMBH population lie from the SMBH, generalise results based on our Sgr A* model and assume a Universal average of ζ = 0.9, a value that we have observed to depend on the SMBH mass. The latter assumption remains reasonable since a majority of SMBH have mass MSMBH ≥ 106 M⊙ (Hopkins et al. 2008; Kelly & Merloni 2012; Davis et al. 2014).
Reverting back to our own calculations and assuming the same S/N fraction found by Fragione (2022) in similar environments, then 90%, 80%, and 50% of these SMBH-IMBH mergers would have a S/N larger than 10, 30, and 100 respectively with the LISA interferometer. This means anywhere between 5.31 and 531 SMBH-IMBH events with S/N = 10 will be observed per year. Given this wide range depending on the infall rate, the LISA interferometer will play a pivotal role in constraining the existence and steady-state population of IMBH clusters present in galactic centres.
4.3. Binaries and gravitational waves
Theory and numerical results suggest that including the 2.5 PN term encourages binary formation thanks to its capability of emitting binary orbital energy. Results here indirectly suggest this to be the case as well. The PN formalism exhibits a quicker binary formation time and similar values of the number of binaries with the Newtonian formalism, even though they have less time to form them due to the accelerated IMBH-loss rate.
The influence of the shorter simulation time is most apparent with hierarchical systems (stable triples). These systems rarely form in GRX runs since they need millions of years to emerge, exceeding the median time before a cluster evolved under PN gravity experiences an IMBH-loss. The lack of IMBH-IMBH merging events is due to two main factors: the small collisional radii of IMBHs (Rcoll, IMBH = 10−2 R⊙) and the presence of the SMBH, preventing IMBH-IMBH binary formation.
Constraining the simulation time also suppresses the number of highly energetic GW events since PN effects will have less time to dissipate energy from the system, giving rise to a dense core where nearby interactions become ubiquitous. Indeed, it could be the case that by evolving the simulation to longer times a significant amount of IMBH-IMBH events reach regimes where we can begin observing their GW signal.
Indeed, in any given simulation, several IMBH may be on a path towards ejection and/or merger, and thus would have occured soon after the first loss-event has happened. Stopping runs at the onset of a population loss removes the possibility of analysing these secondary population loss events. Although interesting, as it provides further information on the evolution of such clusters, analysing these secondary events remains outside the scope of the paper as our main aim was to estimate the steady-state population of IMBH.
Restricting to NIMBH ≤ 40 runs, although GW events more common with the Newtonian formalism, our PN runs had the tendency to yield stronger signals, exhibiting an enhanced rate at which events lie within the observable regime of LISA and μAres. Indeed, although both relativistic and Newtonian integrators are able to capture the in-cluster merger branch, relativistic gravity more efficiently populates this region with an average rate of 4.48 events lying here per Myr (compared to the 3.10 Myr−1 found with our Newtonian results). The branch’s dynamical origin rather than binary evolution is seen with its disappearance from Fig. 12 and the tendency for its rate to increase for larger NIMBH.
Additionally, Newtonian gravity removes the GW capture branch since the IMBH simulated under this formalism cannot efficiently sink into the SMBH’s potential well where GW radiation will then enables a rapid inspiral. This family of GWs is especially prominent in dense environments, including the galactic nuclei (Samsing & D’Orazio 2018; Tagawa et al. 2021; Samsing et al. 2022).
All mergers have large eccentricities, with values e > 0.97. Nevertheless, with the way our simulation is ran, we are unable to resolve up to 2 kyr before the actual merger. This is a crucial time, especially when taking into account the 2.5 PN term, as vast amounts of GW will allow evolution of the orbital parameters. Even so, these systems will still have observable residual eccentricity at merger (Nishizawa et al. 2016).
Interestingly, although the SMBH-IMBH interactions are restricted to a specific region in parameter space, a bimodality arises for IMBH-IMBH interactions. Its presence could be due to the combination of our sampling method used and the dynamics present in the cluster. Namely, GW events here only consider interactions between the individual with the SMBH and its next two nearest neighbours. At the denser core, interactions occur at close range, often sampling events emitting at larger strains forming the peak at larger strains. The lower peak emerges from weak interactions between IMBHs. This region is heavily sampled as individual IMBHs will most often be found at their apoapsis, where the environment is sparse and only distant interactions occur.
5. Conclusions
We numerically investigate the evolution of a cluster of IMBHs centred on an SMBH. We test out different combinations of cluster populations (10 ≤ NIMBH ≤ 40) and SMBH masses (MSMBH = 4 × 105 M⊙, 4 × 106 M⊙, 4 × 107 M⊙). For each configuration, we calculate the system taking into account relativistic effects up to 2.5 PN.
For MSMBH = 4 × 106 M⊙ we also evolve the system with the Newtonian formalism of gravity, enabling us to compare results between gravitational frameworks. The comparison is made more straightforward since both integrators adopt an implicit predictor-evaluator-corrector scheme to fourth-order.
Overall, we find the following results:
-
1.
Systems evolved with PN terms lose their IMBHs more quickly than its classical counterpart, with the median IMBH-loss time, tloss, being roughly an order-of-magnitude smaller for likewise populations. The time before an IMBH is lost increases for smaller SMBH masses.
-
2.
The lower the SMBH mass, the more ejection events dominate the outcomes. For our Sgr A* configuration (MSMBH = 4 × 106 M⊙), we observe a non-negligible fraction of ejected IMBH having velocities exceed the MW escape velocity.
-
3.
Drifters make a significant portion of the ejection events (48/119 of all ejections for MSMBH = 4 × 105 M⊙ and 16/32 for MSMBH = 4 × 106 M⊙). Their presence may indicate a bimodal IMBH population distribution around galactic cores as they settle around an orbit with the distance being dependent on the most probable escape speed.
-
4.
IMBH-IMBH binary and hierarchical systems struggle to form due to the SMBH disrupting their formation. We observe a slight increase in hard binary’s when incorporating PN terms. Additionally, considering its reduced simulation time yet similar values in number of binaries, we conclude that the PN terms encourage the formation of binary systems.
-
5.
For the Sgr A* model (MSMBH = 4 × 106 M⊙), 90.7% and 52.5% of simulations end with mergers when evolving the system with the relativistic and Newtonian formalism respectively. A result consistent with Portegies Zwart et al. (2022).
-
6.
Mergers are always found to be eccentric (e > 0.97). Mergers in the PN calculations achieve lower eccentricities.
-
7.
In the frequency range probed by future interferometers such as LISA and μAres, two prominent GW branches emerge under the relativistic framework; in-cluster mergers and GW captures. Both PN and Newtonian calculations find in-cluster mergers. Contrastingly, the GW capture branch is unique to the PN formalism.
-
8.
Our PN results find a fraction of Ncap./Nic = 54/420 (12.9%) where Ncap. denotes binaries lying in the GW capture branch, and Nic those in the in-cluster branch.
-
9.
SMBH-IMBH mergers will be observed throughout the Universe with next-generation interferometers. Depending on the infall rate (Myr–Gyr) and computing up to redshift z ≤ 3.5, we predict LISA will detect 531 − 5.31 SMBH-IMBH events yr−1. These values correspond to the upper limit for the given infall rate, neglecting galactic evolution, globular cluster formation and sinking time and the accumulation of IMBH to form a steady-state population.
The investigation provides preliminary results of such an environment with many paths future papers can take to elaborate and further generalise our results. To name a few, one can; include the potential well of an NSC, use a mass distribution for IMBHs, include tidal effects, remove the artificial cap on simulation time, and change initial conditions such as the initial cluster distance, distribution or initial velocity. Manipulating any of these parameters will influence the dynamics and can bring about a more generalised discussion on the possibility of IMBH clusters within galactic cores.
More schematically, one may envisage adopting an adaptable simulation snapshot time whose dependent on the proximity of SMBH-IMBH binaries. Doing so would allow us to better understand the nature of the final stages of SMBH-IMBH merging events.
6. Energy consumption
The 820 simulations conducted during this investigation had a total wall-clock time of 432 days. For the MSMBH = 4 × 105 M⊙ runs, each run used 6 cores, for the other two configurations 18 cores were used per run. In total, the CPU time for all simulations was 7680 days. Assuming a CPU consumption rate of 12 Watt h−1 (Portegies Zwart 2020), the total energy consumption is roughly 2210 kWh. For an emission intensity of 0.283 kWh kg−1 (Wittmann et al. 2013), our calculations emitted 7.8 tonnes of CO2, roughly equivalent to two round trips by plane New York – Beijing.
Acknowledgments
Simulations are conducted on the Academic Leiden Interdisciplinary Cluster Environment (ALICE) computing resources provided by Leiden University. Additionally, we would like to thank Gijs Vermariën, Manuel Arca Sedda and Giacomo Fragione for insightful discussions. Lastly, thank you to the anonymous referee for their invaluable feedback, which significantly improved the quality of this work.
References
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102 [Google Scholar]
- Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, ArXiv e-prints [arXiv:1702.00786] [Google Scholar]
- Antonini, F. 2013, ApJ, 763, 62 [Google Scholar]
- Arca-Sedda, M., & Gualandris, A. 2018, MNRAS, 477, 4423 [Google Scholar]
- Askar, A., Davies, M. B., & Church, R. P. 2021, MNRAS, 502, 2682 [NASA ADS] [CrossRef] [Google Scholar]
- Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1976, ApJ, 209, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S. 2018, MNRAS, 481, 5123 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [Google Scholar]
- Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton University Press) [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Boekholt, T. C. N., Moerman, A., & Portegies Zwart, S. F. 2021, Phys. Rev. D, 104, 083020 [CrossRef] [Google Scholar]
- Bogdán, Á., Goulding, A. D., Natarajan, P., et al. 2023, Nat. Astron., 8, 126 [Google Scholar]
- Campeti, P., Komatsu, E., Poletti, D., & Baccigalupi, C. 2021, JCAP, 2021, 012 [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [Google Scholar]
- Davis, B. L., Berrier, J. C., Johns, L., et al. 2014, ApJ, 789, 124 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazio, D. J., & Samsing, J. 2018, MNRAS, 481, 4775 [CrossRef] [Google Scholar]
- Ebisuzaki, T., Makino, J., Tsuru, T. G., et al. 2001, ApJ, 562, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Eckart, A., & Genzel, R. 1997, MNRAS, 284, 576 [NASA ADS] [Google Scholar]
- Einstein, A., Infeld, L., & Hoffmann, B. 1938, Ann. Math., 39, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Fragione, G. 2022, ApJ, 939, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., & Portegies Zwart, S. 2011, Science, 334, 1380 [Google Scholar]
- Furlong, M., Bower, R. G., Theuns, T., et al. 2015, MNRAS, 450, 4486 [Google Scholar]
- Gerhard, O. 2001, ApJ, 546, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Klein, B. L., Morris, M., & Becklin, E. E. 1998, ApJ, 509, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Morris, M., Becklin, E. E., Tanner, A., & Kremenek, T. 2000, Nature, 407, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Giersz, M., & Heggie, D. C. 1994, MNRAS, 268, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Giersz, M., & Heggie, D. C. 1996, MNRAS, 279, 1037 [NASA ADS] [Google Scholar]
- Giersz, M., Leigh, N., Hypki, A., Lützgendorf, N., & Askar, A. 2015, MNRAS, 454, 3150 [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2019, A&A, 625, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2020, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gualandris, A., Gillessen, S., & Merritt, D. 2010, MNRAS, 409, 1146 [CrossRef] [Google Scholar]
- Gültekin, K., Miller, M. C., & Hamilton, D. P. 2006, ApJ, 640, 156 [CrossRef] [Google Scholar]
- Hansen, R. O. 1972, Phys. Rev. D, 5, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Milosavljević, M. 2003, ApJ, 593, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Haster, C.-J., Antonini, F., Kalogera, V., & Mandel, I. 2016, ApJ, 832, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš, D. 2008, ApJS, 175, 356 [Google Scholar]
- Hut, P. 1983, ApJ, 268, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., & Haehnelt, M. 2000, MNRAS, 311, 576 [Google Scholar]
- Kelly, B. C., & Merloni, A. 2012, Adv. Astron., 2012, 970858 [CrossRef] [Google Scholar]
- Khan, F. M., Holley-Bockelmann, K., Berczik, P., & Just, A. 2013, ApJ, 773, 100 [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kremer, K., Rodriguez, C. L., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 99, 063003 [NASA ADS] [CrossRef] [Google Scholar]
- Kustaanheimo, P., Schinzel, A., Davenport, H., & Stiefel, E. 1965, Journal für die reine und angewandte Mathematik, 1965, 204 [CrossRef] [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [Google Scholar]
- Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Rees, M. J. 2001, ApJ, 551, L27 [Google Scholar]
- Makino, J. 1991, ApJ, 369, 200 [Google Scholar]
- Makino, J., & Aarseth, S. J. 1992, PASJ, 44, 141 [NASA ADS] [Google Scholar]
- Mardling, R. A., & Aarseth, S. J. 2001, MNRAS, 321, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S., & Tanikawa, K. 1999, MNRAS, 310, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., & Hamilton, D. P. 2002, ApJ, 576, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Will, C. M., Ramirez-Ruiz, E., et al. 2020, ApJ, 888, L8 [Google Scholar]
- Nishizawa, A., Berti, E., Klein, A., & Sesana, A. 2016, Phys. Rev. D, 94, 064020 [NASA ADS] [CrossRef] [Google Scholar]
- Pelupessy, F. I., van Elteren, A., de Vries, N., et al. 2013, A&A, 557, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, B1224 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, P. C., & Mathews, J. 1963, Phys. Rev., 131, 435 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poincaré, H. 1900, Acta Math., 13, 5 [Google Scholar]
- Portegies Zwart, S. 2020, Nat. Astron., 4, 819 [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2002, ApJ, 576, 899 [Google Scholar]
- Portegies Zwart, S., & McMillan, S. 2018, Astrophysical Recipes; The Art of AMUSE (Bristol: IOP Publishing) [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., McMillan, S. L. W., et al. 2006, ApJ, 641, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S., McMillan, S., Harfst, S., et al. 2009, New Astron., 14, 369 [Google Scholar]
- Portegies Zwart, S. F., Boekholt, T. C. N., Por, E. H., Hamers, A. S., & McMillan, S. L. W. 2022, A&A, 659, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinlan, G. D., & Shapiro, S. L. 1989, ApJ, 343, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, K. P., & Tremaine, S. 1996, New Astron., 1, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Downes, T. P., Volonteri, M., et al. 2019, MNRAS, 486, 3892 [CrossRef] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2020, ApJ, 892, 39 [Google Scholar]
- Rodriguez, C. L., Amaro-Seoane, P., Chatterjee, S., et al. 2018, Phys. Rev. D, 98, 123005 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., & D’Orazio, D. J. 2018, MNRAS, 481, 5445 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., & Ilan, T. 2018, MNRAS, 476, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., & Ramirez-Ruiz, E. 2017, ApJ, 840, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., MacLeod, M., & Ramirez-Ruiz, E. 2014, ApJ, 784, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., Bartos, I., D’Orazio, D. J., et al. 2022, Nature, 603, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Merritt, D., & Eckart, A. 2009, A&A, 502, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild, K. 1916, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math. Klasse, 1916, 189 [Google Scholar]
- Sesana, A., Korsakova, N., Arca Sedda, M., et al. 2021, Exp. Astron., 51, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. D., Regan, J. A., Downes, T. P., et al. 2018, MNRAS, 480, 3762 [NASA ADS] [CrossRef] [Google Scholar]
- Smits, R., Kramer, M., Stappers, B., et al. 2009, A&A, 493, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spinnato, P. F., Fellhauer, M., & Portegies Zwart, S. F. 2003, MNRAS, 344, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1987, Dynamical Evolution of Globular Clusters (Princeton: Princeton University Press) [Google Scholar]
- Tagawa, H., Kocsis, B., Haiman, Z., et al. 2021, ApJ, 907, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Volonteri, M., Haardt, F., & Madau, P. 2003, ApJ, 582, 559 [Google Scholar]
- Wen, L. 2003, ApJ, 598, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Will, C. M. 2014, Phys. Rev. D, 89, 044043 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B., Kalogera, V., Vecchio, A., et al. 2007, ApJ, 665, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Wittmann, M., Hager, G., Zeiser, T., Treibig, J., & Wellein, G. 2013, Concurrency and Computation: Practice and Experience, 28, 2295 [Google Scholar]
- Yu, Q., & Tremaine, S. 2003, ApJ, 599, 1129 [Google Scholar]
Appendix A: Theoretical background
A.1. Cluster dynamics: two-body relaxation
Once a galaxy’s IMBH in-fall rate, Γinfall, equals its IMBH loss-rate (sourced by ejection or merging events), a steady-state population of IMBH emerges.
Here, we ignore stellar evolution to simplify our analysis of the influence of cluster properties with its particle-loss rate. Doing so means relaxation processes dominate and drives the cluster towards a Maxwellian velocity distribution. The particles experiencing more encounters will generally have large eccentricities and occupy the tail end of the velocity distribution, thereby getting ejected from the system (Binney & Tremaine 1987). Moreover, the eccentricity, e, plays a significant role in mergers through GW emission, exemplified with the merging timescale for a two-body system going as tGW ∝ (1 − e2)7/2.
With ejections and mergers both being driven by relaxation and representing population-loss scenarios within clusters, we estimate the influence of the cluster population, N, on the cluster’s particle-loss time, tloss.
We first assume that our equal-mass system is a singular isothermal sphere (see Appendix B), allowing us to express the relaxation time-scale as (Spitzer 1987)
where σ is the 3D velocity dispersion, rc the cluster radius, ⟨m⟩ the average mass of the cluster constituents, ln(γN) the Coulomb parameter.
Focusing our derivation on the half-mass relaxation, we rewrite σ to the mean-square speed of the stars in the environment,
where at the half-mass radius, rh,
The SMBH dominates the cluster mass, allowing us to rewrite M ≈ MSMBH. Using this simplification and re-arranging Eqn. A.3 for ⟨v2⟩ before substituting it into Eqn. A.2, the relaxation time becomes,
Using the definition of Spitzer (1987), a cluster’s particle-loss-rate is
where β is the reciprocal of the evaporation rate constant, attributed to the rate at which weak encounters eject particles from the system, and found to be 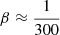 for an isolated cluster (Spitzer 1987; Binney & Tremaine 2008). Inverting Eqn. A.5, the time for a cluster to lose a particle is:
for an isolated cluster (Spitzer 1987; Binney & Tremaine 2008). Inverting Eqn. A.5, the time for a cluster to lose a particle is:
We note that tloss is inversely proportional to Nln(γN). For typical values encountered in our investigation; rh ≈ 0.4 pc and MSMBH = 4 × 106 M⊙, mIMBH = 103 M⊙ which together imply that ⟨m⟩=(mIMBHN + MSMBH)/(N + 1)≈105 M⊙ as long as N ≲ 50, the dissolution time scale becomes
A.2. Binary and hierarchical systems
Binary systems typically require the presence of a third particle to form as this will carry away any excess kinetic energy. Binaries may be categorised as ‘hard’ or ‘soft’ (Heggie 1975; Hut 1983; Spitzer 1987).
Hard binaries are systems whose orbital binding energy exceeds the average kinetic energy of neighbouring stars and thus tend to tighten upon interactions. Mathematically, their semi-major axis satisfies (Binney & Tremaine 1987):
where a denotes the binary’s semi-major axis and m is the mass of the more massive constituent. In this paper, hard binaries satisfy a ≤ Gm/100σ2, while we restrict soft binaries to those satisfying the arbitrarily chosen relaxed condition,
Kinematic arguments show that when a tertiary interacts with a binary system composed of masses m1 and m2, the ejected particle will convert the potential energy released by the binary into its kinetic energy and escape from the system with a velocity
In our context, if interacting with an SMBH-IMBH binary, the ejected IMBH can escape from the cluster at speeds over 1000 km s−1 (see also Hills 1988).
Besides binary systems, hierarchical (three-body systems) can also exist in cluster environments. Hierarchical systems contain an inner binary of masses m1, m2 and semi-major axis ain along with a third particle of mass m3 orbiting the inner binary with semi-major axis aout ≫ ain. Such systems are stable if the ratio of their semi-major axis satisfy (Mardling & Aarseth 2001)
These systems bring forth unique imprints of GWs and can drive the eccentricity of the inner-binary to extreme values through the Lidov-Kozai mechanism (Lidov 1962; Kozai 1962), promoting mergers.
A.3. Gravitational waves
Compact objects such as IMBHs and SMBHs emit GW radiation when they interact. The energy emitted allows their orbits to tighten. For a two-body system, this emission makes them merge on a timescale (Peters 1964)
with μ, the reduced mass
Here we emphasise the extent to which the semi-major axis and eccentricity impact the merging time.
GWs emitted by interacting BHs a redshift z away are observable at frequencies (Wen 2003)
The subscript n denotes the nth harmonic of the GW radiation, relating to the orbital frequency, forb, as fn = nforb.
The corresponding GW strain is (Kremer et al. 2019)
Here, DL is the luminosity distance, g(n, e) a harmonic and frequency-dependent function provided in the appendix of Peters & Mathews (1963), ℳc, z the redshifted chirp mass, expressed as
To account for the limited mission lifetimes (here taken as tobs = 5 yrs), we scale Eqn. A.15 by 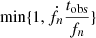 (Willems et al. 2007; D’Orazio & Samsing 2018), where (Kremer et al. 2019)
(Willems et al. 2007; D’Orazio & Samsing 2018), where (Kremer et al. 2019)
Appendix B: Evolving towards an isothermal cluster
Although the system is initialised following a Plummer distribution, the line of best fit in figure 7 assumes an isothermal sphere (see Appendix A). To motivate this, figure B.1 shows the IMBH velocity distribution at 1 Myr in 5 randomly chosen simulations composed of NIMBH = 40 for both GRX and Hermite runs.
The dashed lines represent a fit assuming a Maxwell-Boltzmann (MB) distribution since this represents the velocity distribution in an isothermal sphere. The data appears to globally follow the MB distribution well, although the tails and skewness are poorly represented. The excessive broadening of the fit is due to the outliers with vSMBH ≥ 500 km s−1. These are found to be IMBH within ≲0.1 pc of the SMBH. Their close proximity to the SMBH makes them less prone to weak two-body interactions.
Overall, the fit is found to have a velocity dispersion of 156 and 160 km s−1 for GRX and Hermite respectively.
 |
Fig. B.1. Velocity distribution of the IMBH in the SMBH reference frame for both the classical (Hermite) and PN integrator (GRX) during a single Sgr A* run. Dashed lines show a fitting function when assuming a Maxwell-Boltzmann form. |
All Tables
Simulation outcomes relative to the cluster population for MSMBH = 4 × 106 M⊙ runs.
Simulation outcomes relative to the cluster population for MSMBH = 4 × 105 M⊙ and MSMBH = 4 × 107 M⊙ runs.
Average rate for simulations of a given population to emit GWs within two of the prominent branches.
All Figures
 |
Fig. 1. Final 500 kyr of an NIMBH = 15 simulation using GRX ending in an ejection. Coloured are the IMBHs, and at the origin lies the SMBH. The panel shows the IMBH trajectory (small dots) and final position (outlined dots) along the xy-plane. |
| In the text | |
 |
Fig. 2. Final 1.5 Myr of an NIMBH = 15 simulation ending in a merger in the xy-plane using GRX. The dots represent the same information as Fig. 1. The merging IMBH, shown in red, has a larger dot size as its final position relative to the other IMBHs. |
| In the text | |
 |
Fig. 3. KDE (top panels) and CDF plots (bottom panels) of the eccentricity (left) and semi-major axis (right) for all IMBHs with respect to the central SMBH evolved in simulations with NIMBH ≤ 40. Parameters are taken at time tsim = min{tsim, med(tGRX4e6)}. |
| In the text | |
 |
Fig. 4. Various ejection properties for Hermite (MSMBH = 4 × 106 M⊙). The upper and lower bars represent the interquartile range. |
| In the text | |
 |
Fig. 5. Histogram of Hermite-ejected velocities. Samples are taken from clusters with 10 ≤ NIMBH ≤ 100 and MSMBH = 4 × 106 M⊙. |
| In the text | |
 |
Fig. 6. Histogram of GRX-ejected velocities where MSMBH = 4 × 105 M⊙. |
| In the text | |
 |
Fig. 7. Cluster IMBH-loss time as a function of NIMBH where MSMBH = 4 × 106 M⊙. Filled circles signify the median IMBH loss time for a cluster of a given population. The upper bar shows where 75% of the data lies below while the lower one where 25% of the data lies below. The dashed curve represents the line of best fit (see Eq. (1)) and for the classical results. Arrows represent the fact that the upper error is 100 Myr, a value limited by the tend = 100 Myr simulation time. |
| In the text | |
 |
Fig. 8. Median, upper, and lower percentile range computed when considering a different number of datasets, Nsims. Datum correspond to GRX runs where MSMBH = 4 × 106 M⊙. |
| In the text | |
 |
Fig. 9. Outlined circles denote the median time for a cluster of a given population to experience population loss. The bars denote the interquartile range of the data. Different colours correspond to different SMBH masses. In all cases, relativistic effects are considered. The dashed curve corresponds to the line of best fit for the PN results in the Sgr A* model. Arrows represent the fact that the upper error is 100 Myr, a value limited by the tend = 100 Myr simulation time. |
| In the text | |
 |
Fig. 10. Evolution of the 25% Lagrangian radii (solid lines), 50% Lagrangian radii (rh, dash-dotted lines) and the 75% Lagrangian radii (dotted lines) for NIMBH = 10 PN simulations averaged over all runs. |
| In the text | |
 |
Fig. 11. Influence of NIMBH on the average percentage of time binary systems are present in MSMBH = 4 × 106 M⊙ simulations. Colours correspond to the average number of systems formed, Nsys (see Table 5). The blue and red dotted line is the line-of-best fit for GRX and Hermite respectively. |
| In the text | |
 |
Fig. 12. Distribution of GRX GWs emitted in (f, h)-space where MSMBH = 4 × 106 M⊙. Each dot represents an event at a given snapshot emerging from a hard binary. The detectable regions for the Square Kilometer Array (SKA; Smits et al. 2009), μAres (Sesana et al. 2021) and LISA (Amaro-Seoane et al. 2017) are shown on the plot using code developed by Campeti et al. (2021). Calculations assume a luminosity distance of DL = 1 Gpc. |
| In the text | |
 |
Fig. 13. Streak-like feature emerging in (f, h) space from a persistent GRX binary. The colour denotes the age of the binary, tsys. |
| In the text | |
 |
Fig. 14. f vs. h diagram for all GW events in NIMBH ≤ 40 runs. Events assume DL = 1 Gpc. Top: GRX simulations. Bottom: Hermite simulations. |
| In the text | |
 |
Fig. 15. KDE (top) and CDF (bottom) distribution of the eccentricity of merging IMBHs at the final time step. In both cases, the data is restricted to NIMBH ≤ 40 simulations. |
| In the text | |
 |
Fig. 16. Scatter plot denoting where Hermite and GRX GW events lie in the a vs. log10(1 − e) parameter space. The panels above and on the right show the kernel density estimate. The greyed-out regions denote the frequency range probed by LISA and μAres. The dashed-dotted lines show where the sensitivity of the interferometers is at a maximum, while the dotted ones the frequency range probed (Sesana et al. 2021; Samsing et al. 2014), with the upper bounds for μAres and LISA being the same (f = 1 Hz). The data here is from runs simulated with NIMBH ≤ 40. Top: SMBH-IMBH GW events. Bottom: IMBH-IMBH GW events. |
| In the text | |
 |
Fig. 17. Influence of the infall rate, Γinfall, on the cumulative number of SMBH-IMBH merging events up to redshift z ≤ 3.5. |
| In the text | |
 |
Fig. B.1. Velocity distribution of the IMBH in the SMBH reference frame for both the classical (Hermite) and PN integrator (GRX) during a single Sgr A* run. Dashed lines show a fitting function when assuming a Maxwell-Boltzmann form. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.