EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 692 (December 2024) A&A, 692 (2024) A104 Full HTML
Open Access
Issue
A&A
Volume 692, December 2024
Article Number A104
Number of page(s) 8
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202452050
Published online 16 December 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The formation and growth of intermediate-mass black holes (IMBHs) have been studied intensively over the recent decade (recently, e.g. Ziosi et al. 2014; Hong et al. 2020; Maliszewski et al. 2022; Aros et al. 2021, and citations therein). However, the existence of IMBHs still poses a challenge to astrophysical observations, with no candidate being decisively confirmed thus far. In addition to massive globular clusters and the cores of dwarf galaxies, the presence of IMBHs has also been hypothesised in the Galactic centre, specifically, inside IRS13 (Maillard et al. 2004), which is reportedly a remnant core of a tidally disrupted star cluster (SC). Using the proper motions of stars inside the IRS13 region, several authors have constrained the mass of this possible IMBH (originating within the infalling SC) to some thousands of solar masses (Maillard et al. 2004; Schödel et al. 2005; Fritz et al. 2010) to explain the relatively high stellar velocity dispersions. This estimate has recently been updated by Peißker et al. (2023) to (3.9 ± 0.1) × 104 M⊙, based on the 2D stellar velocity dispersion of (128.86 ± 0.14) km s−1.

Numerical models by Fujii et al. (2009) showed that an IMBH (mass from 3 × 103 M⊙ to 1.6 × 104 M⊙) may form close to the central Sgr A* supermassive black hole (SMBH) via collisions of stars that were initially in a cluster surrounding the SMBH. Furthermore, such an IMBH may help bring other massive stars to the vicinity of the central SMBH and form disks similar to those observed near Sgr A*. However, using a more accurate stellar evolution prescription, Petts & Gualandris (2017) found that an IMBH would not likely grow past a few hundred M⊙. Consequently, it would not be massive enough to experience significant enough dynamical friction to drag stars close to Sgr A*.

The presence of an IMBH in this region would also explain the X-ray emission that coincides with the source IRS13 E3 and the Atacama Large Millimeter/submillimeter Array (ALMA) observations that reveal an ionised ring of gas at that position (Tsuboi et al. 2017; Peißker et al. 2024). Assuming that the gas is virialised, the mass yields 3×104 M⊙. A massive body should also ensure the dynamical stability of its surrounding stellar association since IRS13, containing ~50 confirmed sources (Peißker et al. 2023), is only ≈0.13 pc (projected) or ≈0.4 pc (3D distance) from Sgr A* (see Tsuboi et al. 2020). Although studies that solely focus on this cluster’s dynamical development and lifetime are sparse, broader implications originating from the tidal dissolution of SCs near Sgr A* have been discussed (see, e.g. Fujii et al. 2008; Arca-Sedda & Gualandris 2018; Wang & Lin 2023). Some SCs modelled by these authors end up in the Galactic centre reasonably fast (within a few million years), with masses comparable to the physical properties of IRS13 (see also Bonnell & Rice 2008, who estimated a shorter infall time).

On the other hand, forming an IMBH of tens of thousands of solar masses typically takes an order of magnitude longer than the reported age of the IRS13 members (~4 Myr for the first generation, see Peißker et al. 2023). Among several possible pathways, the two main scenarios for forming IMBHs have been envisaged: runaway mergers of main sequence stars, or accretion of residual gas onto stellar-mass black holes originating from first-generation stars. Even in the best-case scenario based on the formation of very massive stars, runaway mergers produce IMBHs of only ~103 M⊙ within the first 10 Myr (Portegies Zwart et al. 2004; González Prieto et al. 2024; Hypki 2023). The specific values are shown in Fig. 11. The stellar densities required to build up an IMBH of mass ≳ 104 M⊙ are very high (>108 M⊙ pc−3), as shown in the ‘FAST’ scenario described by Giersz et al. (2015), and they are more common in nuclear clusters of small galaxies than in SCs (including globular clusters). In the gas accretion scenario, the IMBH mass has been shown to grow up to 104 M⊙; however, even with an accretion rate close to the Eddington rate, the timescale is of the order of 20–40 Myr (Vesperini et al. 2010).

Furthermore, Gualandris & Merritt (2009) analysed the constraints on the mass and semi-major axis of a potential IMBH orbiting Sgr A* with N-body models (based on the stability of the inner S cluster) and an extensive review of the literature. They revealed that the existence of a massive object with MIMBH ≳ 2 × 104 M⊙ at a distance of 0.4 pc from Sgr A* is inconsistent with observations (see also Reid & Brunthaler 2004). The recent research by Zheng et al. (2024) also notes that an IMBH companion of Sgr A* with a mass of 104 M⊙ is enough to explain the stellar kinematics in the inner parsec.

These works raise three main questions: (1) whether the hypothetical IMBH needs to follow the same evolutionary path as IRS13, or whether its position in this stellar association can be coincidental; (2) what role does an IMBH play against the continuous gravitational tides of an SMBH; (3) whether we need an IMBH to explain the stellar motions within a tidally dissolved cluster. We address these questions in this paper by investigating the dynamical interplay between tidally disrupted stellar systems and an IMBH orbiting close to an SMBH.

thumbnail Fig. 1

Timescales for the growth of IMBH masses by runaway mergers in star cluster models described in Portegies Zwart et al. (2004), Hypki (2023), and González Prieto et al. (2024) are shown with triangle, circle, and cross symbols, respectively.

2 Orbiting clusters

2.1 Models

We first analysed a set of models of IRS13-like SCs (with 44 stars) to assess their stability while orbiting in the extreme tidal field of the central SMBH (MSgrA* = 4.297 × 106 M⊙; see GRAVITY Collaboration 2022). The stellar positions were randomly drawn from the Plummer (1911) distribution with an exponential cutoff, so that the SC would have a maximal radius of ≈0.07 pc (i.e. the approximate size of IRS13 at the assumed galactocentric distance of 8.5 kpc; see Peißker et al. 2023)2. For simplicity, the SCs were generated with equal-mass stars (1 or 10 M⊙) and an isotropic stellar velocity distribution. The SCs were initialised with an IMBH in the centre. We first considered three values for its mass, 103 M⊙ (Maillard et al. 2004), 104 M⊙ (Schödel et al. 2005), and 4 × 104 M⊙ (Peißker et al. 2023, 2024), to represent the proposed values for IRS13. Then we extended our analysis to a wider range of IMBHs. We also varied the initial trajectory of the SC around the SMBH – either circular with a radius of 0.4 pc, or elliptical with the pericentre at this same distance and 0.5 eccentricity. For comparison, we also ran a set of models with isolated clusters, without an SMBH.

Numerically, the initial conditions were created using the AGAMA package (Vasiliev 2019) and ensuring that the whole SC was bound and in virial equilibrium. Because of the large range of masses, we chose to integrate the models with the symplectic Wisdom–Holman integrator WHFAST (Wisdom & Holman 1991; Rein & Tamayo 2015), which is part of the REBOUND N-body code (Rein & Liu 2012). All objects (i.e. stars, the IMBH, and the SMBH) were treated as point masses; general-relativistic effects, gas, and dust were not implemented in these simulations, but are planned for our follow-up research.

2.2 Results

We find that all orbiting SCs expand and dissolve within a fraction of a million years, i.e. comparable to their orbital period (this is consistent with Peißker et al. 2024). This result is similar regardless of the stellar masses or the mass of the IMBH. However, we notice a slightly slower rate of dissolution in the models on initially eccentric orbits (compare the same lines between the bottom two panels in Figs. 2 and 3). Although the IRS13-sized SC was initially bound, and, in the case of the most massive IMBH, also fully embedded within its Hill radius3, even such a massive point-mass object cannot hold the stars together. In fact, the opposite effect is seen: the main reason for the stellar escape is the interaction between the stars and the IMBH. Shortly after the start of the simulations (≲10−4 Myr), we noted the formation of a hard star–IMBH binary in all models, which then started dynamically heating the SC and enhanced the dissolution. Therefore, another, more extended massive component would perhaps be necessary to bind such an SC (see von Fellenberg et al. 2022; Jia et al. 2023; Singhal 2024).

We further illustrate the rates of dissolution of the SCs in Fig. 4, where we plot the evolutionary times when the number of stars bound to the IMBH decreased by half. Regardless of the IMBH mass (here we show a wider range of MIMBH), the trend remains, that is, the dissolution of isolated SCs containing 1 M⊙ stars is an order of magnitude slower than when the same SCs orbit the SMBH. This is visible in the comparison between the black crosses in the figure and the other black points4.

In the isolated case, this dynamical heating is more efficient in the SCs containing the 10 M⊙ stars, where the central binary can become harder (see the top panel of Figs. 2 and 3), and also for the lower-mass IMBHs, where the required escape velocity is lower (see the top panel of Fig. 2 and the low-mass part in Fig. 4). Since the orbiting SCs are tidally limited, even stars that do not reach the escape velocity are unbound from the IMBH when they travel beyond the Hill radius. Consequently, the dissolution is mainly driven by the SMBH–IMBH interaction, and the difference in stellar escapes is not as pronounced between the models with 1 M⊙ and 10 M⊙. We show further evidence of this in Fig. 4, where the SCs with an IMBH below a few hundred M⊙ are destroyed almost immediately and, regardless of stellar mass, even an IMBH of thousands of solar masses cannot hold the SC together for more than a fraction of a million years (see the circles and triangles forming a plateau above 103 M⊙).

As expected, at a distance of 0.4 pc from the SMBH, the long-term survival of such a small cluster is not plausible. Thus our orbital models lead us to conclude that rather than a self-gravitating, relaxed, and bound system, the object we identify as IRS13 is more likely a random present-day clumping of stars, potentially deposited in the vicinity of Sgr A* from farther away (see also the remarks in Maillard et al. 2004; Fujii et al. 2008). Consequently, estimating the mass of its hypothetical central IMBH purely based on the stellar velocity dispersions of its members may lead to higher uncertainties, and can only give its upper mass limit.

To support this result further, we plot the 3D velocity dispersion of the bound stars in Fig. 5. We emphasise that these modelled SCs suffered dissolution despite having initial stellar velocity dispersions five to ten times lower than that of the real IRS13 cluster.

thumbnail Fig. 2

Time evolution of the number of stars bound to the IMBH (colour-coded based on its mass) in the SC models containing 44 stars initially and an IRS13-like IMBH. Each panel shows a different set of models, either isolated or on a specified orbit. The line style (dashed or solid) corresponds to the stellar masses in the SC. The average from ten realisations is shown.
thumbnail Fig. 3

Similar to Fig. 2, but for the time evolution of the half-mass radii. The Hill radius of each IMBH is drawn with a pale-coloured line of the corresponding model. The average from ten realisations of each model is shown.
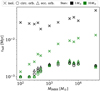thumbnail Fig. 4

Time when the number of stars bound to the IMBH dropped by half (i.e. from 44 to 22). Different SCs are represented by the mass of their IMBHs on the horizontal axis. Different symbols indicate whether the SC is isolated, on a circular orbit, or on an eccentric orbit around the SMBH. The stellar masses are represented by colours.

3 Infalling clusters

We tested several scenarios of what could plausibly happen with more populous SCs infalling into the central parsec from distances orders of magnitude larger.

thumbnail Fig. 5

Similar to Fig. 2, but for the time evolution of the velocity dispersion. The average from ten realisations of each model is shown.

3.1 Models

We performed a series of N-body simulations of SCs of different sizes and numbers of stars falling into the central regions of the Milky Way Galaxy (MW) from the initial distance of about 10–100 pc on various trajectories. We followed their evolution numerically using PETAR (Wang et al. 2020), with GALPY (Bovy 2015) to set the external potential. In the computations, we combined the bulge, the disk, and the halo (as implemented in GALPY’s MWPotential2014) with a Keplerian central SMBH (mass of MSgrA*). We also used GALPY to include a timeevolving Keplerian potential representing an IMBH on a circular orbit around the SMBH (MIMBH = 4 × 104 M⊙, r = 0.4 pc, orbiting in the same plane as the SC) such that the IMBH feels the gravitational force of the other external potentials and the SC. We note that we did not consider the scenario in which the IMBH is in the SC initially because of the formation time constraints presented above (see also Fig. 1).

All stars were treated as point masses, and primordial binary stars were not included. However, the dynamical formation of binaries was permitted in the simulations. To minimise the number of free parameters, we did not include star formation, stellar evolution, or the gas component; those are planned for our follow-up research. Considering the stellar composition of IRS13, we restricted the maximum mass of the initial mass function by 10 M⊙; we kept the lower limit at 0.08 M⊙ and used the slopes from Kroupa (2001). The stellar distribution for all SCs followed King (1966) with W0 = 6 (numerically created with MCLUSTER; Küpper et al. 2011). Table 1 lists the initial conditions selected for each SC run.

3.2 Results

3.2.1 Tidal disruption of the SCs

All infalling SCs show a similar evolution (see the visualisations in Fig. 6). As they perform one or more orbits around the SMBH, they are being stripped of stars and dissolved, forming disks and prominent spiral structures. The specific scenario and its timescale depend on several factors.

The first one is the trajectory. The farther the SC orbits from the SMBH, the longer its core survives. We can compare, for instance, the models 100k-100-v10 and 100k-100-v5 in Fig. 6: both SCs are the same, except the former has a higher initial velocity and thus lower eccentricity. The SC’s core is visible as the thinner arching line in each plot. The core of the model 100k-100-v5 becomes almost fully dissolved during its third visit to the SMBH, whereas the core of 100k-100-v10 seems intact. We note that since the SC loses stars, which carry away angular momentum, the core does not follow a closed ellipse, but instead a Rosetta orbit, forming several spiral-like structures depending on the number of passages through the pericentre.

The second factor is the compactness of the SC (i.e. its initial half-mass radius); however, the concrete scenario here also depends on the orbit. For the SCs with pericentres farther from the SMBH (compare 100k-100-v5 and 100k-100-v10 with their wider ‘-w’ counterparts in Fig. 6), the cores of the initially wider models become even more tidally extended as early as during their second passage near the SMBH. The high-density line becomes very fuzzy, and in the case of 100k-100-v10-w, the split into two fainter cores is also visible. For the SCs that fall much closer to the SMBH, the opposite trend is observed: the initially compact models suffer total disruption during the first passage near the SMBH, whereas the wider SCs expand but do not dissolve completely. We can compare 100k-50-v5 and 100k-100-v1 with their -w counterparts in Fig. 6: the plots of the wide SCs display several orbits, but the initially compact SCs show a smooth colour gradient.

The formation of the disk-like structures is also linked with SC dissolution. If the SC dissolves completely, a stronger circular (or semi-circular) overdensity forms and slowly expands away from the SMBH. This can be seen very clearly in Fig. 6, in the models 50k-20-v10, 100k-50-v5, and 100k-100-v1 as the sharp, dark bows at higher radii. As the system relaxes, these expanding concentric structures mix with other stars and merge into a singular denser circle with a radius similar to the initial position of the SC. The timescale for this process is shorter when the number of stars in the system is smaller (compare, e.g. 20k-10-v20, 50k-20-v10, and 100k-50-v5). The strength of this final disk depends on the initial orbit and the dissolution rate – readers can compare, for example, 20k-10-v5 (with the smallest density), 20k-10-v10, and 20k-10-v20 (with the highest density), or similarly the models 50k-10-v5, 50k-10-v10, and 50k-20-v10.

Table 1

Initial conditions of the SC models.

thumbnail Fig. 6

Time evolution of the infalling SCs and the emergence of temporary disk-like structures (see Sect. 3 and Table 1 for the naming convention and model parameters). The vertical axis shows the galactocentric distance, and the colour gradient corresponds to the number of stars in each pixel. The horizontal dotted black line is the galactocentric distance of the IMBH. We emphasise that the size of the SC or its core is to be measured in the vertical direction. Downward pointing spikes are formed by stars that are brought close to the SMBH. At larger distances, the inclined overdensities constitute emerging ring-like features that originate from a gradually dissolving SC.
thumbnail Fig. 7

Time evolution of the number of stars in a specified region (left-hand plots) and their velocity dispersion (right-hand plots), as seen in xy projection. For each model (columns), the values in four regions are shown: around the IMBH (top row), on the opposite side of the SMBH from the IMBH (labelled 180°), and in two regions perpendicular to the SMBH–IMBH vector (labelled ±90°). The dashed lines show the known population and velocity dispersion of IRS13, respectively.
thumbnail Fig. 8

Same as Fig. 7, but for the xz projection. Only two regions are shown: around the IMBH (top row) and the region on the opposite side of the SMBH from the IMBH (labelled 180°).

3.2.2 Influence of the IMBH

The SCs must have favourable initial conditions in order to deposit enough stars in the central regions of the MW. They either have to be sufficiently close (tens of parsecs) or, if they are farther away, experience more radial orbits – we can compare the stellar densities at the IMBH’s orbit in Fig. 6. This is consistent with Kim & Morris (2003), who studied the inspiral of SCs due to dynamical friction from <30 pc and found that only the densest (≳106 M⊙ pc−3) and most massive SCs can contribute to the stellar population in the central parsec. Similar results were also reported by Fujii et al. (2008) and Petts & Gualandris (2017). We mark the models that managed to fall inside the inner half parsec around the SMBH in Table 1. We henceforth only focus on those models.

To mimic observations, we analysed our data in 2 D projections – either perpendicular to the Galactic plane (model coordinates xy, see Fig. 7) or from within the Galactic plane (coordinates xz, see Fig. 8). We evaluated the impact of the IMBH on the stellar motions of a tidally disrupted SC by focusing on four regions along the IMBH’s orbit. They are circular areas of radii 0.1 pc, located (1) around the instantaneous position of the IMBH (i.e. x=x•, y=y•, and z=z•); (2) on the opposite side of the SMBH from the IMBH (i.e. x=−x•, y=−y•, and z=−z•); and (3 and 4) in the directions perpendicular to the SMBH – these last two are only shown in the xy projection (i.e. x=±y• and y=∓x•). Hence, all regions are the same distance from the SMBH but should experience different influences from the IMBH.

Due to the higher level of foreground and background contamination, the number of stars in each area is higher in the xz projection than in the xy projection (compare the left-hand panels of Figs. 7 and 8). In the 50k-10-v5 and 50k-10-v10 models, the number of stars is comparable to the population of IRS13; in the other two models, the values are lower, especially in the xy projection.

The right-hand panels of Figs. 7 and 8 also show that regardless of the position of the IMBH, stars in all regions have the same velocity dispersion in a given projection. Moreover, except for the σxy value during the initial passage of the SC through the MW core, the velocity dispersion is always in the range 100–300 km s−1, hence similar to or higher than the measured value in IRS13. This reveals that at a distance of 0.4 pc from the SMBH, the stellar velocity dispersion of a tidally dissolved cluster is mainly driven by the SMBH, not an IMBH.

Our models also indicate a high level of star mixing in the central half parsec. Therefore, the stellar associations observed in one time-snapshot usually do not survive together for more than a few thousand years.

4 Conclusions

We have modelled the stability of stellar clusters and associations in the gravitational field of the SMBH in the MW, taking into account the influence of the extreme tidal field in the neighbourhood of the central SMBH. We have shown that an IRS13-like association is likely not a self-gravitating cluster, and even the presence of an IMBH of 4×104 M⊙ cannot ensure its long-term stability and does not prevent its gradual dissolution in the time frame of a few thousand years (as is also seen in the observations, see Peißker et al. 2023, 2024).

We have revisited arguments from the literature against the existence of such a massive IMBH so close to Sgr A*. Based on numerical modelling of the growth of IMBHs, we also emphasise that the origin of an IMBH of this mass is probably not the same as that of IRS13. For more information, readers can also refer to Takekawa et al. (2017), who found two gaseous clouds in the central region of our Galaxy that likely contain black holes that have plunged into them.

We have further shown that if IRS13 is a remnant of a tidally disrupted SC, the velocity dispersion of its members is mainly determined by the infall event and the SMBH. The effect of the IMBH is only secondary, or even negligible. Consequently, we question whether the estimates of a potential IMBH in IRS13 based on stellar kinematics are reliable.

Although we have gained new insights into the dynamical interplay between SCs, IMBHs, and SMBHs, we are aware that our current results are only based on simulations performed within the N-body approach with an external tidal field. Since the timescale for the dynamical stability of IRS13 is so short, this conclusion would likely remain unchanged even with the background gas, but the infall of SCs could play out differently. Therefore, we also aim to include the hydrodynamical treatment of gas and star formation to assess the potential limitations of the present approach, but this is currently a work in progress which remains beyond the scope of the current paper.

We also note that arguments similar to those we put forward in this paper may apply to the IRS1W dense stellar association, which is located on the side of Sgr A* opposite IRS13 and at a comparable distance from the SMBH (Hosseini 2022, 2023; Hosseini et al. 2024). This confirms that the Galactic centre is a promising location for exploring the tentative formation mechanisms of IMBHs and setting further constraints on their presence.

Acknowledgements

We thank Richard Wünsch and Michal Zajaček for valuable discussions, Long Wang for help with PETAR, and Eugene Vasiliev for help with AGAMA. V.P. has received funding from the European Union’s Horizon Europe and the Central Bohemian Region under the Marie Skłodowska-Curie Actions – COFUND, Grant agreement ID 101081195 (“MERIT”). V.P. is also grateful for the access to the computational resources provided by the e-INFRA CZ project (ID:90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic; and the computational cluster VIRGO at the Astronomical Institute of the Czech Academy of Sciences; V.K. thanks the Czech Science Foundation grant GM24-10599M. V.P. and V.K. also acknowledge the support from the project RVO:67985815 at the Czech Academy of Sciences. F.P. gratefully acknowledges the Collaborative Research Center 1601 funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1601 [sub-project A3] – 500700252. The Python programming language with NumPy (Harris et al. 2020) and Matplotlib (Hunter 2007) were used in this project. The REBOUND’s SimulationArchive format was used to store fully reproducible simulation data (Rein & Tamayo 2017). This research has made use of NASA’s Astrophysics Data System Bibliographic Services.

References

  1. Arca-Sedda, M., & Gualandris, A. 2018, MNRAS, 477, 4423 [Google Scholar]
  2. Aros, F. I., Sippel, A. C., Mastrobuono-Battisti, A., et al. 2021, MNRAS, 508, 4385 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bonnell, I. A., & Rice, W. K. M. 2008, Science, 321, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
  5. Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2010, ApJ, 721, 395 [Google Scholar]
  6. Fujii, M., Iwasawa, M., Funato, Y., & Makino, J. 2008, ApJ, 686, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  7. Fujii, M., Iwasawa, M., Funato, Y., & Makino, J. 2009, ApJ, 695, 1421 [NASA ADS] [CrossRef] [Google Scholar]
  8. Giersz, M., Leigh, N., Hypki, A., Lützgendorf, N., & Askar, A. 2015, MNRAS, 454, 3150 [Google Scholar]
  9. González Prieto, E., Weatherford, N. C., Fragione, G., Kremer, K., & Rasio, F. A. 2024, ApJ, 969, 29 [CrossRef] [Google Scholar]
  10. GRAVITY Collaboration (Abuter, R., et al.) 2022, A&A, 657, L12 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gualandris, A., & Merritt, D. 2009, ApJ, 705, 361 [NASA ADS] [CrossRef] [Google Scholar]
  12. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
  13. Hong, J., Askar, A., Giersz, M., Hypki, A., & Yoon, S.-J. 2020, MNRAS, 498, 4287 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hosseini, S. E. 2022, in Black-hole activity feedback from Bondi-radius to galaxy-cluster scales, 4 (Cologne-Prague-Brno meeting, Masaryk Univ., Brno), 4 [Google Scholar]
  15. Hosseini, S. E. 2023, PhD thesis, Universität zu Köln (Cologne), Germany [Google Scholar]
  16. Hosseini, S. E., Eckart, A., Zajaček, M., et al. 2024, ApJ, 975, 261 [CrossRef] [Google Scholar]
  17. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hypki, A. 2023, IAU Symp., 8, 11 [Google Scholar]
  19. Jia, S., Xu, N., Lu, J. R., et al. 2023, ApJ, 949, 18 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kim, S. S., & Morris, M. 2003, ApJ, 597, 312 [NASA ADS] [CrossRef] [Google Scholar]
  21. King, I. R. 1966, AJ, 71, 64 [Google Scholar]
  22. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  23. Küpper, A. H. W., Maschberger, T., Kroupa, P., & Baumgardt, H. 2011, MNRAS, 417, 2300 [Google Scholar]
  24. Maillard, J. P., Paumard, T., Stolovy, S. R., & Rigaut, F. 2004, A&A, 423, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Maliszewski, K., Giersz, M., Gondek-Rosinska, D., Askar, A., & Hypki, A. 2022, MNRAS, 514, 5879 [NASA ADS] [CrossRef] [Google Scholar]
  26. Peißker, F., Zajaček, M., Thomkins, L., et al. 2023, ApJ, 956, 70 [CrossRef] [Google Scholar]
  27. Peißker, F., Zajaček, M., Labaj, M., et al. 2024, ApJ, 970, 74 [CrossRef] [Google Scholar]
  28. Petts, J. A., & Gualandris, A. 2017, MNRAS, 467, 3775 [NASA ADS] [Google Scholar]
  29. Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
  30. Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [Google Scholar]
  31. Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [Google Scholar]
  32. Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [Google Scholar]
  34. Rein, H., & Tamayo, D. 2017, MNRAS, 467, 2377 [NASA ADS] [Google Scholar]
  35. Schödel, R., Eckart, A., Iserlohe, C., Genzel, R., & Ott, T. 2005, ApJ, 625, L111 [CrossRef] [Google Scholar]
  36. Singhal, M. 2024, in Galactic Nuclei in the Cosmological Context, id. 6 [Google Scholar]
  37. Takekawa, S., Oka, T., Iwata, Y., Tokuyama, S., & Nomura, M. 2017, ApJ, 843, L11 [NASA ADS] [CrossRef] [Google Scholar]
  38. Tsuboi, M., Kitamura, Y., Uehara, K., Miyawaki, R., & Miyazaki, A. 2017, IAU Symp., 322, 115 [NASA ADS] [Google Scholar]
  39. Tsuboi, M., Kitamura, Y., Tsutsumi, T., et al. 2020, PASJ, 72, L5 [NASA ADS] [CrossRef] [Google Scholar]
  40. Vasiliev, E. 2019, MNRAS, 482, 1525 [Google Scholar]
  41. Vesperini, E., McMillan, S. L. W., D’Ercole, A., & D’Antona, F. 2010, ApJ, 713, L41 [NASA ADS] [CrossRef] [Google Scholar]
  42. von Fellenberg, S. D., Gillessen, S., Stadler, J., et al. 2022, ApJ, 932, L6 [NASA ADS] [CrossRef] [Google Scholar]
  43. Wang, L., & Lin, D. N. C. 2023, ApJ, 944, 140 [NASA ADS] [CrossRef] [Google Scholar]
  44. Wang, L., Iwasawa, M., Nitadori, K., & Makino, J. 2020, MNRAS, 497, 536 [NASA ADS] [CrossRef] [Google Scholar]
  45. Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [Google Scholar]
  46. Zheng, X. Wang, L., Lin, D., Burkert, A., & Mao, S. 2024, https://doi.org/10.21203/rs.3.rs-4845404/v1 [Google Scholar]
  47. Ziosi, B. M., Mapelli, M., Branchesi, M., & Tormen, G. 2014, MNRAS, 441, 3703 [Google Scholar]
1

We note that several factors may influence the timescales plotted in Fig. 1. First, the number of models analysed by Portegies Zwart et al. (2004) was limited, since the work focused on two particular young SCs (MGG-9 and MGG-11) that may not represent the variety of possible conditions for IMBH formation. Second, although González Prieto et al. (2024) explored many SC models with an IMBH, they only report its mass growth for some. In contrast, Hypki (2023) explored a wider set of models and reports the formation times of all IMBHs.

2

We also tested other models where the initial distribution function was either uniform or based on King (1966) with W0 = 3, 6 and 9. However, due to the small number of stars, the results are comparable with the Plummer models we show.

3

The Hill radius at time t is given by rHill (t)=dS-I (t)MIMBH1/3(3MIMBH+3MSgrA* )−1/3$\[r_{\text {Hill }}(t)=d_{\text {S-I }}(t) M_{\mathrm{IMBH}}^{1 / 3}(3 M_{\mathrm{IMBH}}+3 M_{\text {SgrA* }})^{-1 / 3}\]$, where dS–I is the separation of the SMBH and IMBH.

4

Our models also show that for the isolated SCs, the more massive IMBHs can retain about a dozen bound stars for ~2 Myr, whereas the orbiting SCs dissolve completely and much sooner (see, e.g. Fig. 2).

All Tables

Table 1

Initial conditions of the SC models.

In the text

All Figures

thumbnail Fig. 1

Timescales for the growth of IMBH masses by runaway mergers in star cluster models described in Portegies Zwart et al. (2004), Hypki (2023), and González Prieto et al. (2024) are shown with triangle, circle, and cross symbols, respectively.
In the text
thumbnail Fig. 2

Time evolution of the number of stars bound to the IMBH (colour-coded based on its mass) in the SC models containing 44 stars initially and an IRS13-like IMBH. Each panel shows a different set of models, either isolated or on a specified orbit. The line style (dashed or solid) corresponds to the stellar masses in the SC. The average from ten realisations is shown.
In the text
thumbnail Fig. 3

Similar to Fig. 2, but for the time evolution of the half-mass radii. The Hill radius of each IMBH is drawn with a pale-coloured line of the corresponding model. The average from ten realisations of each model is shown.
In the text
thumbnail Fig. 4

Time when the number of stars bound to the IMBH dropped by half (i.e. from 44 to 22). Different SCs are represented by the mass of their IMBHs on the horizontal axis. Different symbols indicate whether the SC is isolated, on a circular orbit, or on an eccentric orbit around the SMBH. The stellar masses are represented by colours.
In the text
thumbnail Fig. 5

Similar to Fig. 2, but for the time evolution of the velocity dispersion. The average from ten realisations of each model is shown.
In the text
thumbnail Fig. 6

Time evolution of the infalling SCs and the emergence of temporary disk-like structures (see Sect. 3 and Table 1 for the naming convention and model parameters). The vertical axis shows the galactocentric distance, and the colour gradient corresponds to the number of stars in each pixel. The horizontal dotted black line is the galactocentric distance of the IMBH. We emphasise that the size of the SC or its core is to be measured in the vertical direction. Downward pointing spikes are formed by stars that are brought close to the SMBH. At larger distances, the inclined overdensities constitute emerging ring-like features that originate from a gradually dissolving SC.
In the text
thumbnail Fig. 7

Time evolution of the number of stars in a specified region (left-hand plots) and their velocity dispersion (right-hand plots), as seen in xy projection. For each model (columns), the values in four regions are shown: around the IMBH (top row), on the opposite side of the SMBH from the IMBH (labelled 180°), and in two regions perpendicular to the SMBH–IMBH vector (labelled ±90°). The dashed lines show the known population and velocity dispersion of IRS13, respectively.
In the text
thumbnail Fig. 8

Same as Fig. 7, but for the xz projection. Only two regions are shown: around the IMBH (top row) and the region on the opposite side of the SMBH from the IMBH (labelled 180°).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.