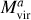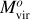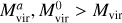EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 692 (December 2024) A&A, 692 (2024) A32 Full HTML
Open Access
Issue
A&A
Volume 692, December 2024
Article Number A32
Number of page(s) 9
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202451484
Published online 29 November 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Mock catalogs of galaxies and galaxy clusters are essential tools for the statistical analysis of galaxy redshift surveys (such as EUCLID, Amendola et al. 2016, DESI, Levi et al. 2013, J-PAS, Benitez et al. 2014, and the Nancy Grace Roman space telescope, Spergel et al. 2015). Their usefulness lies in their ability to capture not only the main statistical properties of the spatial distribution of dark matter tracers in the Universe (n– point statistics), but also the behavior of such properties as a function of a number of intrinsic properties (e.g., luminosity, stellar mass, color, and star formation rate), which are key to understanding the processes of galaxy cluster assembly and galaxy formation and evolution (see e.g., Euclid Collaboration 2024b).

Intrinsic galaxy and galaxy cluster properties in mock catalogs can be robustly derived from high-resolution hydro-simulations (e.g., Nelson et al. 2019; Dubois et al. 2021; Feldmann et al. 2023). However, as the cost of this method typically scales with the size of the sample and with the degree of details of the baryonic process involved, it remains challenging to use it for the vast cosmological volumes currently surveyed. While this obstacle is rapidly being overcome (see e.g. Schaye et al. 2023), the true difficulty arises when thousands of realizations of this type of simulation are needed for covariance matrix analysis. Dark-matter-only simulations (see e.g., Angulo & Hahn 2022, and references therein) can replicate large cosmological volumes with samples of halos and sub-halos, on top of which galaxies can be placed using a number of techniques, such as halo occupation distribution techniques (see e.g., Cooray 2002; Cooray & Sheth 2002; Berlind & Weinberg 2002; Kravtsov et al. 2004) or sub-halo abundance matching (see e.g., Vale & Ostriker 2004; Kravtsov et al. 2004; Conroy et al. 2006; Favole et al. 2016). In this scenario, halo properties are robustly derived from the distribution of dark matter particles (see e.g., Mansfield & Avestruz 2021, and references therein) and used as proxies for the generation of galaxy positions and intrinsic properties. However, dark-matter-only simulations can be also expensive in terms of computing time, due to the large volumes and the high-mass resolution needed to accurately resolve the halos and sub-halos containing the types of observed galaxies (e.g., luminous red galaxies and emission-line galaxies), and again, due to the number of realizations required for robust estimates of covariance matrices.

Approximated methods (see e.g. Bond & Myers 1996; Scoccimarro & Sheth 2002; Manera et al. 2013; Sousbie et al. 2008; Monaco et al. 2002, 2013; Munari et al. 2017; Berner et al. 2022; Tassev et al. 2013; Koda et al. 2016; Izard et al. 2018; White et al. 2014; Howlett et al. 2015; Feng et al. 2016; Kitaura et al. 2014; Avila et al. 2015; Balaguera-Antolínez et al. 2019; Balaguera-Antolínez et al. 2020, 2023; Baratta et al. 2020, 2023, and references therein) and learning approaches (see e.g., Zhang et al. 2019; He et al. 2019; Villaescusa-Navarro et al. 2021; Piras et al. 2023; Ding et al. 2024) have been shown to provide fast and relatively accurate (on the scales of interest) realizations of dark matter halos with phase-space coordinates. Nevertheless, for these methods to be applicable in building galaxy mock catalogs, they need to surmount one difficulty, namely, accomplishing the precise assignment of halo intrinsic properties (e.g., virial mass, velocity dispersion, concentration, and spin). This task is key because the abundance and clustering probes of dark matter tracers, when explored as a function of intrinsic properties (e.g., stellar masses and X-ray luminosities), is very sensitive to the underlying scaling relations adopted to assign these properties (see e.g Balaguera-Antolínez et al. 2012, for an example on the construction of mock catalaogs for galaxy clusters). The assignment of halo properties constrained to reproduce the large-scale clustering signal is the scientific target of this paper, which represents the second in a number of papers dedicated to the connection between halo properties and large-scale structure (Balaguera-Antolínez et al. 2024).

Keeping in mind that N-body simulations can be considered to provide, to our knowledge, the most realistic representation of the distribution of dark matter halos and its statistical properties in a cosmological volume, the precision of an assignment procedure can be captured in the comparison of a number of statistics, such as the halo abundance, scaling relations among the halo properties, and two (and higher) order statistics, with respect to the corresponding N–body estimates. In particular, the signature of large-scale effective bias (see e.g., Kaiser 1984; Fry & Gaztanaga 1993; Kauffmann et al. 1997; Sheth & Tormen 2004; Gao et al. 2005; Wechsler et al. 2006; Gao & White 2007; Croton et al. 2007; Angulo et al. 2008; Dalal et al. 2008; Faltenbacher & White 2010; Lee et al. 2017; Lazeyras et al. 2017; Montero-Dorta et al. 2017, 2020, 2021; Mao et al. 2018; Musso et al. 2018; Sato-Polito et al. 2019; Contreras et al. 2019; Xu et al. 2021; Lee & Moon 2024; Montero-Dorta & Rodriguez 2024) is key to connecting models of galaxy and/or halo populations with the measurements of abundance and clustering as a function of a given property. Retrieving this signal with accuracy is particularly difficult in the context of calibrated or learning oriented methods (where only phase-space coordinates are available), and the assignment of properties can only be done through the mining of the correlation between those halo properties and the underlying dark matter density field. Different approaches (e.g., Zhao et al. 2015; Balaguera-Antolínez et al. 2023; Fang et al. 2024) have been proposed to perform this task, using local and non-local properties on the underlying dark matter density field. Although this information helps to reproduce the clustering signal as a function of halo number counts (see e.g., Balaguera-Antolínez et al. 2019), it is not sufficient to fully replicate the signal of primary (i.e, clustering as a function of a primary halo property) and secondary (i.e, dependency of halo clustering on a secondary halo property at fixed values of primary property) large-scale bias, especially for massive halos (see e.g., Wong & Taylor 2012; Balaguera-Antolínez et al. 2023). It is key to emphasize, in this context, that methods designed to assign galaxy properties to sub-halos based on the properties of parent halos (as e.g. machine learning approaches, see e.g., Ramakrishnan et al. 2021; Forero-Sánchez et al. 2022; de Santi et al. 2022; Rodrigues et al. 2023) can reproduce the large-scale bias, mainly due to the fact that the signature is already encoded in the parent halo properties used as the basis for learning.

In this work, we present the multi-scale halo property assignment (MSHA) algorithm, designed to assign intrinsic properties to dark matter halos through the assessment of the scaling relation between halo properties and the statistical properties of dark matter and dark matter halos. As a novelty, the algorithm uses the assignment of individual large-scale effective halo bias (see e.g., Paranjape et al. 2018), which provides a novel window for the analysis of primary and secondary halo bias (see e.g., Contreras et al. 2021; Balaguera-Antolínez et al. 2024), along with a multi-scale (MS) strategy to account for halo exclusion.

To assess the performance of the strategy proposed in the MSHA algorithm, we use the UNITSim1 (Chuang et al. 2019), which consists in a set of paired-fixed amplitude (Angulo & Pontzen 2016) cosmological N–body simulations, evolved from redshift ɀ = 99 until ɀ = 0 in a cosmological volume of 1(Gpch−1)3 (see e.g., Angulo & Pontzen 2016; Garrison et al. 2018; Villaescusa-Navarro et al. 2018; Chuang et al. 2019; Zhai et al. 2019; Klypin et al. 2020; Maksimova et al. 2021, for more details in this type of simulations). The dark matter field (constructed from 40963 dark matter particles) is represented by a mesh of ***(eq1)***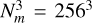Nm3=2563$N_m^3 = {256^3}$, and the halo catalogs are built using the ROCKSTAR algorithm (Behroozi et al. 2013), with a minimum halo mass of 2 × 1011 M⊙h−1 (see Balaguera-Antolínez et al. 2024, for more details on the halo properties in this simulation). In forthcoming publications, we shall describe ongoing developments on the assignment algorithm, as well as applications to light cones.

The structure of this paper is as follows. In Sect. 2, we present the halo and dark matter field properties used in the MSHA algorithm. In Sect. 3, we describe its main features, followed by an example of the performance in Sect. 4. We end with discussions in Sect. 5 and finally our conclusions.

2 Dark matter and dark matter halo properties

2.1 Properties of the dark matter density field

Statistical properties of the dark matter distribution δdm(r), such as the local density or tidal field2, are key to reproducing halo number counts with precise two- and three-point statistics (see e.g., Balaguera-Antolínez et al. 2019; Pellejero-Ibañez et al. 2020; Balaguera-Antolínez et al. 2020, 2023; Bartlett et al. 2024). The information of the tidal field can be used in the form of a cosmic web classification (i.e., knots, filaments, sheets, voids; see e.g., Hahn et al. 2007; van de Weygaert et al. 2009; Forero-Romero et al. 2009; Aragon-Calvo 2016; Yang et al. 2017; Paranjape et al. 2018) or through the construction of combinations of its eigenvalues such as its invariants (see e.g., Paranjape et al. 2018; Kitaura et al. 2022), the prolateness, the ellipticity (see e.g., Mo et al. 2010), the tidal anisotropy parameter, (see e.g., Paranjape et al. 2018) or the mass of collapsing regions (see e.g., Zhao et al. 2015; Balaguera-Antolínez et al. 2019). In this work, we take the local density and the cosmic web classification as the main dark matter properties (hereafter, {Θ}dm) and thus as the input to the MSHA algorithm. The details on these properties, computed for the reference simulation, can be found at Balaguera-Antolínez et al. (2024).

2.2 Halo environment properties

Following Balaguera-Antolínez et al. (2024), we computed a number of properties {Θ}H for each tracer by collecting information on the surrounding tracers within a sphere of radius R, namely, i) the so-called relative local mach number ℳR and ii) the local overdensity δR. The relative local mach number is the measure of the local kinematic temperature of the tracer distribution (see e.g., Nagamine et al. 2001; Agarwal & Feldman 2013; Meriot et al. 2022), while the local overdensity δR is defined as the excess of tracers with respect to the mean number density around each tracer. The scale R used in the computation of these quantities is in principle a free parameter. We have chosen R = 3 Mpc/h, a scale in which both cosmic web environment and local overdensity help to shape the halo number clustering (see e.g., Wu et al. 2024). The analysis by Balaguera-Antolínez et al. (2024) demonstrates that these environment properties display the largest correlations with the large-scale effective bias.

2.3 Individual large-scale effective bias

Following Paranjape et al. (2018); Ramakrishnan et al. (2019); Han et al. (2019); Paranjape & Alam (2020); Contreras et al. (2021); Balaguera-Antolínez et al. (2024), we assigned an effective large-scale halo bias to each tracer (with position ri) as: 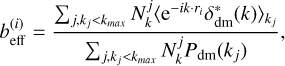beff(i)=∑j,kj<kmaxNkj〈 e−ik⋅riδdm*(k) 〉kj∑j,kj<kmaxNkjPdm(kj),$b_{{\rm{eff}}}^{(i)} = {{\sum\nolimits_{j,{k_j} < {k_{max}}} {N_k^j} {{\left\langle {{{\rm{e}}^{ - ik \cdot {r_i}}}\delta _{{\rm{dm}}}^*(k)} \right\rangle }_{{k_j}}}} \over {\sum\nolimits_{j,{k_j} < {k_{max}}} {N_k^j} \sum\limits_{j,{k_j} < {k_{\max }}} {N_k^j} {P_{{\rm{dm}}}}\left( {{k_j}} \right)}},$(1)

where δdm(k) is the Fourier transform of the dark matter density field, Pdm(kj) its power spectrum, and ***(eq3)***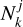Nkj$N_k^j$ is the number of Fourier modes in the j-the spherical bin in Fourier space. The sum is carried over the range of wavenumbers, kj < kmax, in which the ratio between the halo and the dark matter power spectra is constant3. Balaguera-Antolínez et al. (2024) shows that the effective bias as a function of multiple halo properties, as obtained from standard approaches (for example, measurements of auto and cross-power halo power spectrum in bins of that halo property, see e.g., Balaguera-Antolínez 2014; Pollack et al. 2014), is consistent with the results obtained from Eq. (1) and with known calibrations in the literature, such as the bias-halo mass relation (Tinker et al. 2010, see also Paranjape et al. 2018). Assigning a bias to each object allowed us to include the clustering signal (up to a given scale kmax) in the halo property assignment machinery. We note that we can also compute secondary bias (see e.g., Smith et al. 2009), which can help improve the signal of higher-order statistics in terms of halo properties. For the purpose of this work, we used only the effective bias and have left quadratic bias for a forthcoming study.

Compared with previous attempts to assign halo properties, the inclusion of the large-scale effective bias is key to retrieving properties that replicate the large-scale pattern drawn by such tracers. As we will show in the following sections, not including this bias yields halo properties that, even if they depict the correct abundance, fail at reproducing primary and secondary bias, particularly at the high-mass end of the halo mass function, even if non-local properties of the dark matter field are included.

2.4 Target halo properties

Here we briefly describe the halo properties we aimed to reconstruct. In general, the properties of dark matter halos can be separated into a primary ηp and a secondary ηs set. These sets can be defined in a number of ways, such as correlation with the underlying dark matter density field (see e.g., Balaguera-Antolínez et al. 2023) or by a principal component analysis of the halo properties (Skibba & Macciò 2011; Zhou et al. 2023; Balaguera-Antolínez et al. 2024). We label as”primary” properties those directly probing the depth of the potential wells of dark matter halos, such as virial mass, velocity dispersion, or maximum circular velocity Vmax (see e.g., Zehavi et al. 2019). In this work, we used the latter as the main property, followed by the virial mass Mvir. As the secondary properties, we used the halo spin (Bullock et al. 2001) and halo concentration Cvir ≡ Rvir/Rs, where Rvir is the virial radius and Rs the scale radius, obtained based on fits to a NFW profile (Navarro et al. 1996) within the ROCKSTAR algorithm (see e.g., Knebe et al. 2011; Mansfield & Kravtsov 2020).

3 The algorithm

The MSHA algorithm4 is aimed at assigning halo intrinsic properties (such as those discussed in Sect. 2.4), constrained to provide the correct large-scale clustering signal as a function of those properties. The input to the algorithm is made up of two components, namely:

  • A reference simulation, which is ideally one (or a number of) realization(s) of a tracer distribution in an N-body simulation, from which we can access to the dark matter density field and a halo catalog (with intrinsic properties).

  • A target or mock realization of dark matter halos (with phase-space coordinates), and its corresponding dark matter density field.

Two main features characterize this algorithm. First, we explicitly implement the assignment of individual halo bias using Eq. (1) in order to mine its correlations with halo properties (Balaguera-Antolínez et al. 2024). This is a key ingredient, as it directs the distribution of halo properties toward the correct large-scale signal, where the two-point statistics of the tracers is assessed as a function of their intrinsic properties. Second, theMSHA algorithm accounts for halo exclusion (see e.g., Porciani & Giavalisco 2002; Balaguera-Antolínez 2014; García & Rozo 2019) by implementing a so-called MS algorithm, described by Balaguera-Antolínez et al. (2023).

The main idea behind the MS approach is that the tracers with the largest values on primary properties ηp (e.g., virial mass, maximum circular velocity, or velocity dispersion) are those delineating the statistical properties on large scales. Accordingly, high values on these properties should be prevented from being assigned to close pairs. To achieve this, the MSHA algorithm divides the range of available values of the reference primary property ηp into a number of intervals or levels. Each level is in turn characterized by a spatial mesh covering the simulation volume, whose resolution is given by the number of reference tracers with values ηp in that level, such that on average, each spatial cell within each level is populated by one tracer5. The exclusion effect, being linked to the size of dark matter halos, can be more pronounced toward low redshift, with the increment in the abundance of high-mass halos (see e.g. Balaguera-Antolínez 2014).

The assignment of halo properties is performed in a hierarchical order, in which a main property is assigned first (in our case, Vmax), and subsequent assignment campaigns follow using the information of the properties already assigned (see e.g., Sinigaglia et al. 2021, for applications to hydro-simulations). The first assignment is done explicitly using the MS technique, reading the values of the main property from the reference catalog, and assigning these to mock tracers in a top-bottom order: that is, starting from the highest level (containing the highest values of ηp), it sorts the values of the properties ηp and assigns them from highest values in each level, simultaneously preventing the assignment of two consecutive values of ηp to tracers living in the same spatial cell. Values below the minimum of ηp defined by the last level are assigned from the (unsorted) remaining set of reference properties, which is indeed the approach followed for all mock tracers when MS is not applied. In both cases, the process takes into account the dependencies with local and non-local properties {Θ} presented in Sect. 2.

The MSHA algorithm contains a number of options to prevent failed attempts to assign the main property. The main source of failure is linked to the so-called cosmic variance, which is embodied in this scenario as the difference between the actual number of tracers in the reference and the number of tracers in the mock in a given bin of {Θ}. To mitigate this, the MS approach uses tolerance percentages ƒℓ ≤ 1 to reduce the number of tracers to be assigned in a given level, assigning the remaining fraction as in a non-MS scenario. In that case, if the number of requested properties is larger than the number of available properties in the reference (in a given bin of {Θ}), the property is assigned following the conditional probability distribution 𝒫ℓ(ηp|{Θ}) assessed for every level ℓ. Finally, if the set of properties {Θ}mock find no representation in the set {Θ}ref, the value of ηp assigned to the tracers is drawn from the global distribution.

The flow chart in Fig. 1 depicts the main steps followed in the assignment of halo properties. This procedure can be generalized to any number of reference simulations (strictly speaking, an ensemble of independent realizations built from the same initial power spectrum) from which the conditional probability distributions 𝒫(ηp|{Θ}) can be obtained (as shown by Balaguera-Antolínez et al. 2023).

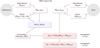thumbnail Fig. 1

Flow chart representing the algorithm designed to assign halo properties. The reference simulation provides a dark matter density field and its corresponding halo catalogs, with phase-space coordinates and intrinsic properties.

4 Application

We have used a set of paired and fixed-amplitude N-body simulations (at redshift ɀ = 0, ɀ = 0.5, and ɀ = 1) to show the performance of the method. This represents the set reference mock. With this type of simulation, even if the initial conditions display the same amplitude of power spectrum, differences in the occupancy of the bins designed to build the scaling relations can arise through gravitational evolution coupling of initially randomly distributed phases (see e.g., Angulo & Pontzen 2016; Villaescusa-Navarro et al. 2018).

Following the procedure described in Sect. 3, we assigned maximum circular velocities to the halos in the mock simulation, on top of which we assigned virial mass6 through the assessment of the probability distribution ***(eq4)***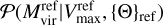P(Mvirref∣Vmaxref,{Θ}ref)${\cal P}\left( {M_{{\rm{vir}}}^{{\rm{ref}}}\mid V_{{\rm{max}}}^{{\rm{ref}}},{{\left\{ \Theta \right\}}_{{\rm{ref}}}}} \right)$, sampling as: 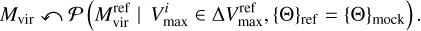Mvir↶P(Mvirref∣Vmaxi∈ΔVmaxref,{ Θ }ref={ Θ }mock).${M_{{\rm{vir}}}}{\cal P}\left( {M_{{\rm{vir}}}^{{\rm{ref}}}\mid V_{\max }^i \in \Delta V_{\max }^{{\rm{ref}}},{{\left\{ \Theta \right\}}_{{\rm{ref}}}} = {{\left\{ \Theta \right\}}_{{\rm{mock}}}}} \right).$(2)

In Fig. 2, we present the impact of the property assignment in the large-scale effective bias as a function of virial mass7. In particular, we show three different scenarios, namely, assignment i) using only dark matter properties, ii) adding the effective bias, iii) using dark matter and halo environment properties, and iv) adding the effective bias along with the previous set, for three cosmological redshifts (ɀ = 0, ɀ = 0.5, and ɀ = 1). In each of these cases, we present the results with and without the MS approach applied in the assignment of Vmax.

In general, as shown in Fig. 2, implementing the information of the halo environment properties and the large-scale bias yields a clustering signal in agreement, on large scales, with the clustering signal measured from the mock catalog using the original properties, especially on the high-mass halo population (where the impact of the MS approach is noticeable, given that exclusion effects are more dominant as long as ɀ → 0 and at large scales). It also is observed that as long as we approach ɀ = 0, the presence for properties beyond those of the dark matter is more evident (we have verified this trend performing the same analysis at ɀ = 0.5 and ɀ = 3).

Next, we used halo concentration Cvir and halo dimension-less spin λB as examples of the assignment of secondary properties. To establish the hierarchical approach to the assignment of properties, we referred to Balaguera-Antolínez et al. (2024), where it is shown that the correlation between halo concentration and mass is larger than that between mass and halo spin. Accordingly, we started by assigning halo concentration by measuring from the reference the scaling relation ***(eq6)***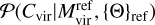P(Cvir∣Mvirref,{ Θ }ref)${\cal P}\left( {{C_{{\rm{vir}}}}\mid M_{{\rm{vir}}}^{{\rm{ref}}},{{\left\{ \Theta \right\}}_{{\rm{ref}}}}} \right)$ and sampling from it as 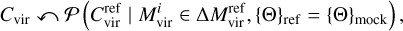Cvir↶P(CvirRef∣Mviri∈ΔMvirref,{ Θ }ref={ Θ }mock),${C_{{\rm{vir}}}}{\cal P}\left( {C_{{\rm{vir}}}^{{\rm{Ref}}}\mid M_{{\rm{vir}}}^i \in \Delta M_{{\rm{vir}}}^{{\rm{ref}}},{{\left\{ \Theta \right\}}_{{\rm{ref}}}} = {{\left\{ \Theta \right\}}_{{\rm{mock}}}}} \right),$(3)

where the masses ***(eq8)***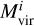Mviri$M_{{\rm{vir}}}^i$ correspond to the values assigned with Eq. (2). Similarly, for the assignment of halo spin, we measured the scaling relation ***(eq9)***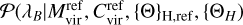P(λB∣MvirTef ,Cvirref,{ Θ }H,ref,{ΘH)${\cal P}({\lambda _B}\mid M_{{\rm{vir}}}^{{\rm{Tef}}},C_{{\rm{vir}}}^{{\rm{ref}}},{\left\{ \Theta \right\}_{{\rm{H}},{\rm{ref}}}},\{ {\Theta _H})$ and sample values as 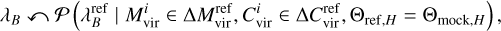λB↶P(λBref∣Mviri∈ΔMvirref,Cviri∈ΔCvirref,Θref,H=Θmock,H),${\lambda _B}{\cal P}\left( {\lambda _B^{{\rm{ref}}}\mid M_{{\rm{vir}}}^i \in \Delta M_{{\rm{vir}}}^{{\rm{ref}}},C_{{\rm{vir}}}^i \in \Delta C_{{\rm{vir}}}^{{\rm{ref}}},{\Theta _{{\rm{ref}},H}} = {\Theta _{{\rm{mock}},H}}} \right),$(4)

where we did not include the dark matter properties and solely relied on the halo intrinsic and environment properties.

To assess the precision of the the signal of secondary bias, we divided the sample into quartiles of the secondary property and measured the mean effective bias in bins of a primary property. In Fig. 3, we display the ratios of effective bias in these two quar-tiles of the secondary properties with respect to the same signal measured from the reference simulations, and for three different snapshots of the UNITSim. In general, all tests displayed ~10% discrepancy with respect to the reference. The largest difference was obtained when only dark matter properties were used, in agreement with previous results in the literature. The inclusion of halo environment properties ΘH and/or effective bias contributes to assigning halo properties with a secondary bias signature within ~10% difference with respect to the reference. The results of Fig. 3 were obtained using MS, and we have verified that this choice produces better results than the case without MS at the redshifts shown in that figure.

thumbnail Fig. 2

Large-scale effective bias as a function of virial mass, assigned as described in Sect. 3. The main panels (a,b,c,d) show the effective bias measured from the reference and the results from the property assignment at ɀ = 0 (left), ɀ = 0.5 (center), and ɀ = 1 (right column), with (labeled Assignment+MS) and without (labeled Assignment) the MS approach. Panel a shows the results of using only dark matter properties Θdm in the assignment of maximum circular velocity and virial mass. Panel b shows the results of adding the information from the individual bias. Panel c shows the results after including halo environment properties ΘH, and panel d shows the result of including both bias and environment properties. The bottom panels show, in each case, the ratio to the primary bias obtained from the mock catalog using its original properties (the latter shown as black points in all main panels). The gray region in these bottom panels depicts 10% deviation with respect to unity. The error bars denote the error on the mean bias-property relation.
thumbnail Fig. 3

Secondary effective bias as a function of halo virial mass. This plot compares (with ratios) the effective bias measured reference and the mock after assignment, at two different cosmological redshifts (shown in different columns) and using different combinations of halo vs. dark matter properties, as shown in the legends. Panels a and b show the secondary bias using halo concentration, for the lower and upper quartiles computed in each mass bin, respectively. Similarly, panels c and d show the secondary bias as a function of halo spin. In all plots, the shaded region denotes a 10% deviation from unity. In all cases, MS is employed. The error bars are computed by adding in quadrature the corresponding uncertainties in each bias estimate.

5 Discussion

Our results show that the use of individual effective bias (Eq. (1)) can be relevant in the process of reconstructing and/or assigning halo properties to generate reliable halo mock catalogs that follow the expected large-scale clustering signal. While the absence of the information on effective bias or halo environment properties in the assignment can still generate robust scaling relations between halo properties (especially toward high redshifts, as seen in panels (a) of Fig. 2), using this information can improve the resulting clustering signal. The signal of mean large-scale primary bias (i.e, as shown in Fig. 2) is one of the key probes in the clustering analysis of current galaxy redshift surveys (see e.g., Tutusaus et al. 2020), as it can provide insights on the galaxy and cluster scaling relations (see e.g., Cooray & Sheth 2002; Balaguera-Antolínez 2014; Shi & Sheth 2018) and physics of the early Universe (i.e, primordial non-Gaussianities, see e.g., Giannantonio et al. 2012; Euclid Collaboration 2024a). As such, it is important to minimize deviations in the mean primary bias (with respect to the results of N-body simulations) when constructing mock catalogs, as it can propagate from the covariance matrix to the likelihood and lead to biased results (Artis et al. 2021; Euclid Collaboration 2023).

The inclusion of halo environment properties and effective bias is also key if secondary bias (key to assessing the impact of, for example, HOD assumptions on the galaxy population, see e.g., Hearin et al. 2016; Lehmann et al. 2017) is expected to be present in the mock catalog. It can be shown that effective bias as a function of, for example, virial mass, in quartiles ∆ηs = ∆ηs(Mvir) of a secondary property ηs can be mathematically decomposed as 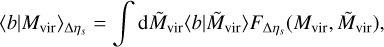〈 b∣Mvir 〉Δηs=∫dM˜vir〈 b∣M˜vir 〉FΔηs(Mvir,M˜vir),${\left\langle {b\mid {M_{{\rm{vir}}}}} \right\rangle _{\Delta {\eta _s}}} = \int {\rm{d}} {{\tilde M}_{{\rm{vir}}}}\left\langle {b\mid {{\tilde M}_{{\rm{vir}}}}} \right\rangle {F_{\Delta {\eta _s}}}\left( {{M_{{\rm{vir}}}},{{\tilde M}_{{\rm{vir}}}}} \right),$(5)

where ***(eq12)***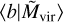〈 b∣M˜vir 〉$\left\langle {b\mid {{\tilde M}_{{\rm{vir}}}}} \right\rangle $ is the primary bias, 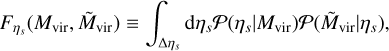Fηs(Mvir,M˜vir)≡∫Δηs dηsP(ηs∣Mvir)P(M˜vir∣ηs),${F_{{\eta _s}}}\left( {{M_{{\rm{vir}}}},{{\tilde M}_{{\rm{vir}}}}} \right) \equiv \int_{\Delta {\eta _s}} {{\rm{d}}} {\eta _s}{\cal P}\left( {{\eta _s}\mid {M_{{\rm{vir}}}}} \right){\cal P}\left( {{{\tilde M}_{{\rm{vir}}}}\mid {\eta _s}} \right),$(6)

and 𝒫(ηs|Mvir) denotes the scaling relation between ηp and Mvir. Thus, the signal of secondary bias (e.g., as shown in Fig. 3) is sensitive to the full scaling relation (i.e, all the moments of the conditional probability distribution 𝒫(ηs|Mvir) In Fig. 4, we show the 2D and 1D distribution of halo properties and effective bias from the reference simulation, as well as from the different experiments performed in this paper. While there are sizable differences (e.g., in the Vmax − Cvir relation), in general, the reconstruction of the halo properties provides not only a robust set of halo-scaling relations but also reconstructs the large-scale halo connection through primary (≤ 5%) and secondary (≤ 15% differences) bias, as can be read from Figs. 3 and 4.

The performance of the MSHA algorithm can depend on how detailed the different scaling relations (assessed from the reference and to be sampled onto the mock catalog) are determined. However, the level of refinement is not arbitrary as we can eventually enter an overfitting regime. This can eventually precipitate a failed attempt to assign properties when a new set of density field (or another realization of the reference fields) and its halo distribution is used as a target mock, and, as such, a limit in the number of bins (or tolerance thresholds) is imposed.

In Fig. 5, we present an example of the scaling relation between the assigned halo mass and the true value of that property as read from the reference simulation used as the mock catalog (at ɀ = 0). In general, there is a large scatter between the true and assigned property, which varies little among the different setups shown. In Fig. 6, we display the correlation coefficient between the properties shown in Fig. 5 for halos with true and assigned masses above the values in the x-axis, indicating that in general, the reconstruction improves toward large halo masses. The large scatter seen at the low halo mass region likely arises from the degeneracies between the different dark matter properties (e.g., cosmic web types) and the mass of the halos hosted therein, which cannot be broken by the inclusion of large-scale bias (as it also shows large scatter with respect to halo mass, see e.g., Balaguera-Antolínez et al. 2024). While the impact of such degeneracy is small when measuring the signal of large-scale effective bias, it can be crucial when populating intermediate and low-mass halos with galaxies. In forthcoming work, we will add learning algorithms to reduce this scatter and provide a more accurate reconstruction of halo properties.

thumbnail Fig. 4

2D scaling relations between halo properties and large-scale halo effective bias in the UNITSim at ɀ = 0. The different lines in the contours (denoting surfaces of equal number of tracers) and the 1D distributions show the result from different setups in the assignment algorithm, as shown in the legend.
thumbnail Fig. 5

Scaling relation between the logarithm of the assigned virial mass ***(eq14)***Mvira$M_{{\rm{vir}}}^a$ and the logarithm of the true virial mass ***(eq15)***Mviro$M_{{\rm{vir}}}^o$, for four different setups in the assignment algorithm (at ɀ = 0). The color coding and contours indicate the constant number of tracers from high (blue) to low (red).
thumbnail Fig. 6

Correlation coefficient between the assigned mass and the original mass at ɀ = 0 for different setups used in the assignment algorithm, for cuts in the true and assigned masses ***(eq16)***Mvira,Mvir0>Mvir$M_{{\rm{vir}}}^a,M_{{\rm{vir}}}^0 > {M_{{\rm{vir}}}}$.

6 Conclusions

In this paper, we have described a strategy to assign intrinsic halo properties in halo mock catalogs generated with the so-called calibrated methods (see e.g., Balaguera-Antolínez et al. 2019). These methods can provide sets of independent halo realizations with phase-space coordinates and their underlying dark matter density field, although they will lack intrinsic halo properties. Such properties are key in order to generate mock galaxy catalogs using a number of techniques (see e.g., Monaco et al. 2013; Alam et al. 2020; Euclid Collaboration 2024b).

While the assignment of halo properties can be accurately performed based on the abundance or conditional probability distributions, the resulting two-point statistics on large-scales, expressed as a function of that particular property, is not fully captured (see for example Zhao et al. 2015; Balaguera-Antolínez et al. 2023). A higher precision in the clustering signal (with respect to N–body estimates) can be achieved when conditional mass (or any other property) functions are implemented, using local (for example, dark matter density) and non-local (for example the properties of dark matter tidal field) information of the underlying dark matter density field. Nevertheless, these ingredients cannot induce the correct signal of large-scale effective bias, especially for massive tracers.

With the possibility of individually computing large-scale bias for dark matter tracers (see e.g., Paranjape et al. 2018; Contreras et al. 2021; Balaguera-Antolínez et al. 2024), it is feasible to assign intrinsic halo properties ensuring that the two-point statistics, in particular, the signal of primary and secondary halo bias measured on large-scales, are closer to what is measured from, for example, a N–body simulation. The algorithm described in this paper makes use of this fact, complementing it with with the MS approach, designed to account for the phenomena of halo exclusion. It can implement other dark matter properties, such as tidal anisotropy, peak statistics (see e.g., Peacock & Heavens 1985), or shear velocity field (see e.g., Libeskind et al. 2018). Similarly, other non-local halo properties such as the neighbor statistics can be included.

We can summarize the main results of this paper as follows:

  • Using the information of the halo individual large-scale bias, halo environment, and dark matter properties, plus the MS approach, the MSHA algorithm can assign intrinsic properties to dark matter halos with a resulting large-scale primary bias (i.e., expressed as a function of primary properties such as virial mass and maximum circular velocity) within ~5% precision with respect to the signal obtained using the properties in the the reference simulation (see Fig. 2);

  • The reconstruction of the secondary bias is also favored by the inclusion of the large-scale individual bias, although the differences among the different setups shown in Fig. 3 are rather small;

  • As a byproduct of the reconstruction of halo bias, halo properties, such as virial mas, are also recovered. This yields correlations between assigned and original halo properties of ~0.5 for high masses, as shown in Fig. 5. We note that the algorithm in its current state is not specifically designed to recover halo properties with high precision, but rather to replicate the property-bias relation;

  • Our results motivate further developments of this algorithm using, for example, learning techniques. This would help to improve the precision in the reconstruction of intrinsic properties, especially for low mass halos, which is key to the assignment of galaxies to dark matter halos in catalogs generated with approximated methods.

Acknowledgements

We would like to thank the referee for his/her commnets to the draft, which helped to improve the presentation of our results. We also thank J.Garcia-Farieta for comments on the early version of the manuscript. We also acknowledge Chia-Hsun Chuang, Gustavo Yépez and F.-S. Kitaura for granting access to the UNITSim. ABA acknowledges the Spanish Ministry of Economy and Competitiveness (MINECO) under the Severo Ochoa program SEV-2015-0548 grants. The UNITSim has been run at the MareNostrum Supercomputer hosted by the Barcelona Supercomputing Center, Spain, with computing time granted by PRICE under grant number 2016163937. ADMD thanks the IAC facilities and Fondecyt for financial support through the Fondecyt Regular 2021 grant 1210612. No AI application has been used to generate neither text, figures data, nor code for this article.

References

  1. Agarwal, S., & Feldman, H. A. 2013, MNRAS, 432, 307 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alam, S., Peacock, J. A., Kraljic, K., Ross, A. J., & Comparât, J. 2020, MNRAS, 497, 581 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amendola, L., Appleby, S., Avgoustidis, A., et al. 2016, arXiv e-prints [arXiv: 1606.00180] [Google Scholar]
  4. Angulo, R. E., & Hahn, O. 2022, Liv. Rev. Computat. Astrophys., 8, 1 [CrossRef] [Google Scholar]
  5. Angulo, R. E., & Pontzen, A. 2016, MNRAS, 462, Ll [Google Scholar]
  6. Angulo, R. E., Baugh, C. M., & Lacey, C. G. 2008, MNRAS, 387, 921 [NASA ADS] [CrossRef] [Google Scholar]
  7. Aragon-Calvo, M. A. 2016, MNRAS, 455, 438 [CrossRef] [Google Scholar]
  8. Artis, E., Melin, J.-B., Bartlett, J. G., & Murray, C. 2021, A&A, 649, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Avila, S., Murray, S. G., Knebe, A., et al. 2015, MNRAS, 450, 1856 [NASA ADS] [CrossRef] [Google Scholar]
  10. Balaguera-Antolínez, A. 2014, A&A, 563, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Balaguera-Antolínez, A., Sánchez, A. G., Böhringer, H., & Collins, C. 2012, MNRAS, 425, 2244 [NASA ADS] [CrossRef] [Google Scholar]
  12. Balaguera-Antolínez, A., Kitaura, F.-S., Pellejero-Ibáñez, M., Zhao, C., & Abel, T. 2019, MNRAS, 483, L58 [CrossRef] [Google Scholar]
  13. Balaguera-Antolínez, A., Kitaura, F.-S., Pellejero-Ibáñez, M., et al. 2020, MNRAS, 491, 2565 [Google Scholar]
  14. Balaguera-Antolínez, A., Kitaura, F.-S., Alam, S., et al. 2023, A&A, 673, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Balaguera-Antolínez, A., Montero-Dorta, A. D., & Favole, G. 2024, A&A, 685, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Baratta, P., Bel, J., Plaszczynski, S., & Ealet, A. 2020, A&A, 633, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Baratta, P., Bel, J., Gouyou Beauchamps, S., & Carbone, C. 2023, A&A, 673, Al [Google Scholar]
  18. Bartlett, D. J., Ho, M., & Wandelt, B. D. 2024, arXiv e-prints [arXiv:2405.00635] [Google Scholar]
  19. Behroozi, P. S., Wechsler, R. H., & Wu, H.-Y. 2013, ApJ, 762, 109 [NASA ADS] [CrossRef] [Google Scholar]
  20. Benitez, N., Dupke, R., Moles, M., et al. 2014, arXiv e-prints [arXiv: 1403.5237] [Google Scholar]
  21. Berlind, A. A., & Weinberg, D. H. 2002, ApJ, 575, 587 [Google Scholar]
  22. Berner, P., Refregier, A., Sgier, R., et al. 2022, J. Cosmology Astropart. Phys., 2022, 002 [CrossRef] [Google Scholar]
  23. Bond, J. R., & Myers, S. T. 1996, ApJS, 103, 1 [NASA ADS] [CrossRef] [Google Scholar]
  24. Bullock, J. S., Dekel, A., Kolatt, T. S., et al. 2001, ApJ, 555, 240 [NASA ADS] [CrossRef] [Google Scholar]
  25. Chuang, C.-H., Yepes, G., Kitaura, F.-S., et al. 2019, MNRAS, 487, 48 [NASA ADS] [CrossRef] [Google Scholar]
  26. Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2006, ApJ, 647, 201 [Google Scholar]
  27. Contreras, S., Zehavi, I., Padilla, N., et al. 2019, MNRAS, 484, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  28. Contreras, S., Angulo, R. E., & Zennaro, M. 2021, MNRAS, 504, 5205 [CrossRef] [Google Scholar]
  29. Cooray, A. 2002, ApJ, 576, L105 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [Google Scholar]
  31. Croton, D. J., Gao, L., & White, S. D. M. 2007, MNRAS, 374, 1303 [Google Scholar]
  32. Dalal, N., White, M., Bond, J. R., & Shirokov, A. 2008, ApJ, 687, 12 [NASA ADS] [CrossRef] [Google Scholar]
  33. de Santi, N. S. M., Rodrigues, N. V. N., Montero-Dorta, A. D., et al. 2022, MNRAS, 514, 2463 [CrossRef] [Google Scholar]
  34. Ding, S., Lavaux, G., & Jasche, J. 2024, A&A, 690, A236 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Dubois, Y., Beckmann, R., Bournaud, F., et al. 2021, A&A, 651, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Euclid Collaboration (Castro, T., et al.) 2023, A&A, 671, A100 [CrossRef] [EDP Sciences] [Google Scholar]
  37. Euclid Collaboration (Sciotti, D., et al.) 2024a, A&A, 691, A318 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Euclid Collaboration (Castander, F. J., et al.) 2024b, A&A, submitted [Google Scholar]
  39. Faltenbacher, A., & White, S. D. M. 2010, ApJ, 708, 469 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fang, F., Cai, Y.-C., Li, Z., et al. 2024, MNRAS, 530, 2355 [NASA ADS] [CrossRef] [Google Scholar]
  41. Favole, G., Comparat, J., Prada, F., et al. 2016, MNRAS, 461, 3421 [NASA ADS] [CrossRef] [Google Scholar]
  42. Feldmann, R., Quataert, E., Faucher-Giguère, C.-A., et al. 2023, MNRAS, 522, 3831 [NASA ADS] [CrossRef] [Google Scholar]
  43. Feng, Y., Chu, M.-Y., Seljak, U., & McDonald, P. 2016, MNRAS, 463, 2273 [NASA ADS] [CrossRef] [Google Scholar]
  44. Forero-Romero, J. E., Hoffman, Y., Gottlöber, S., Klypin, A., & Yepes, G. 2009, MNRAS, 396, 1815 [Google Scholar]
  45. Forero-Sánchez, D., Chuang, C.-H., Rodriguez-Torres, S., et al. 2022, MNRAS, 513 [Google Scholar]
  46. Fry, J. N., & Gaztanaga, E. 1993, ApJ, 413, 447 [NASA ADS] [CrossRef] [Google Scholar]
  47. Gao, L., & White, S. D. M. 2007, MNRAS, 377, L5 [NASA ADS] [CrossRef] [Google Scholar]
  48. Gao, L., Springel, V., & White, S. D. M. 2005, MNRAS, 363, L66 [NASA ADS] [CrossRef] [Google Scholar]
  49. García, R., & Rozo, E. 2019, MNRAS, 489, 4170 [NASA ADS] [CrossRef] [Google Scholar]
  50. Garrison, L. H., Eisenstein, D. J., Ferrer, D., et al. 2018, ApJS, 236, 43 [NASA ADS] [CrossRef] [Google Scholar]
  51. Giannantonio, T., Porciani, C., Carron, J., Amara, A., & Pillepich, A. 2012, MNRAS, 422, 2854 [Google Scholar]
  52. Hahn, O., Porciani, C., Carollo, C. M., & Dekel, A. 2007, MNRAS, 375, 489 [NASA ADS] [CrossRef] [Google Scholar]
  53. Han, J., Li, Y., Jing, Y., et al. 2019, MNRAS, 482, 1900 [NASA ADS] [CrossRef] [Google Scholar]
  54. He, S., Li, Y., Feng, Y., et al. 2019, PNAS, 116, 13825 [NASA ADS] [CrossRef] [Google Scholar]
  55. Hearin, A. P., Zentner, A. R., van den Bosch, F. C., Campbell, D., & Tollerud, E. 2016, MNRAS, 460, 2552 [NASA ADS] [CrossRef] [Google Scholar]
  56. Howlett, C., Manera, M., & Percival, W. J. 2015, Astron. Comput., 12, 109 [NASA ADS] [CrossRef] [Google Scholar]
  57. Izard, A., Fosalba, P., & Crocce, M. 2018, MNRAS, 473, 3051 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kauffmann, G., Nusser, A., & Steinmetz, M. 1997, MNRAS, 286, 795 [NASA ADS] [CrossRef] [Google Scholar]
  60. Kitaura, F.-S., Yepes, G., & Prada, F. 2014, MNRAS, 439, L21 [NASA ADS] [CrossRef] [Google Scholar]
  61. Kitaura, F.-S., Balaguera-Antolínez, A., Sinigaglia, F., & Pellejero-Ibáñez, M. 2022, MNRAS, 512, 2245 [NASA ADS] [CrossRef] [Google Scholar]
  62. Klypin, A., Prada, F., & Byun, J. 2020, MNRAS, 496, 3862 [NASA ADS] [CrossRef] [Google Scholar]
  63. Knebe, A., Knollmann, S. R., Muldrew, S. I., et al. 2011, MNRAS, 415, 2293 [Google Scholar]
  64. Koda, J., Blake, C., Beutler, F., Kazin, E., & Marin, F. 2016, MNRAS, 459, 2118 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kravtsov, A. V., Berlind, A. A., Wechsler, R. H., et al. 2004, ApJ, 609, 35 [Google Scholar]
  66. Lazeyras, T., Musso, M., & Schmidt, F. 2017, J. Cosmol. Astro-Part. Phys., 2017, 059 [CrossRef] [Google Scholar]
  67. Lee, J., & Moon, J.-S. 2024, arXiv e-prints [arXiv:2406.11182] [Google Scholar]
  68. Lee, C. T., Primack, J. R., Behroozi, P., et al. 2017, MNRAS, 4, 3834 [NASA ADS] [CrossRef] [Google Scholar]
  69. Lehmann, B. V., Mao, Y.-Y., Becker, M. R., Skillman, S. W., & Wechsler, R. H. 2017, ApJ, 834, 37 [NASA ADS] [CrossRef] [Google Scholar]
  70. Levi, M., Bebek, C., Beers, T., et al. 2013, arXiv e-prints [arXiv: 1308.0847] [Google Scholar]
  71. Libeskind, N. I., van de Weygaert, R., Cautun, M., et al. 2018, MNRAS, 473, 1195 [NASA ADS] [CrossRef] [Google Scholar]
  72. Maksimova, N. A., Garrison, L. H., Eisenstein, D. J., et al. 2021, MNRAS, 508, 4017 [NASA ADS] [CrossRef] [Google Scholar]
  73. Manera, M., Scoccimarro, R., Percival, W. J., et al. 2013, MNRAS, 428, 1036 [Google Scholar]
  74. Mansfield, P., & Avestruz, C. 2021, MNRAS, 500, 3309 [Google Scholar]
  75. Mansfield, P., & Kravtsov, A. V. 2020, MNRAS, 493, 4763 [NASA ADS] [CrossRef] [Google Scholar]
  76. Mao, Y.-Y., Zentner, A. R., & Wechsler, R. H. 2018, MNRAS, 474, 5143 [NASA ADS] [CrossRef] [Google Scholar]
  77. Meriot, R., Khochfar, S., Oñorbe, J., & Smith, B. 2022, MNRAS, 512, 27 [NASA ADS] [CrossRef] [Google Scholar]
  78. Mo, H., van den Bosch, F. C., & White, S. 2010, Galaxy Formation and Evolution (UK: Cambridge University Press) [Google Scholar]
  79. Monaco, P., Theuns, T., & Taffoni, G. 2002, MNRAS, 331, 587 [Google Scholar]
  80. Monaco, P., Sefusatti, E., Borgani, S., et al. 2013, MNRAS, 433, 2389 [NASA ADS] [CrossRef] [Google Scholar]
  81. Montero-Dorta, A. D., & Rodriguez, F. 2024, MNRAS, 531, 290 [NASA ADS] [CrossRef] [Google Scholar]
  82. Montero-Dorta, A. D., Pérez, E., Prada, F., et al. 2017, ApJ, 848, L2 [NASA ADS] [CrossRef] [Google Scholar]
  83. Montero-Dorta, A. D., Artale, M. C., Abramo, L. R., et al. 2020, MNRAS, 496, 1182 [NASA ADS] [CrossRef] [Google Scholar]
  84. Montero-Dorta, A. D., Chaves-Montero, J., Artale, M. C., & Favole, G. 2021, MNRAS, 508, 940 [NASA ADS] [CrossRef] [Google Scholar]
  85. Munari, E., Monaco, P., Koda, J., et al. 2017, J. Cosmol. Astro-Part. Phys., 2017, 050 [CrossRef] [Google Scholar]
  86. Musso, M., Cadiou, C., Pichon, C., et al. 2018, MNRAS, 476, 4877 [Google Scholar]
  87. Nagamine, K., Ostriker, J. P., & Cen, R. 2001, ApJ, 553, 513 [NASA ADS] [CrossRef] [Google Scholar]
  88. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
  89. Nelson, D., Springel, V., Pillepich, A., et al. 2019, Computat. Astrophys. Cosmol., 6, 2 [NASA ADS] [CrossRef] [Google Scholar]
  90. Paranjape, A., & Alam, S. 2020, MNRAS, 495, 3233 [NASA ADS] [CrossRef] [Google Scholar]
  91. Paranjape, A., Hahn, O., & Sheth, R. K. 2018, MNRAS, 476, 3631 [NASA ADS] [CrossRef] [Google Scholar]
  92. Peacock, J. A., & Heavens, A. F. 1985, MNRAS, 217, 805 [NASA ADS] [CrossRef] [Google Scholar]
  93. Pellejero-Ibañez, M., Balaguera-Antolínez, A., Kitaura, F.-S., et al. 2020, MNRAS, 493, 586 [CrossRef] [Google Scholar]
  94. Piras, D., Joachimi, B., & Villaescusa-Navarro, F. 2023, MNRAS, 520, 668 [Google Scholar]
  95. Pollack, J. E., Smith, R. E., & Porciani, C. 2014, MNRAS, 440, 555 [CrossRef] [Google Scholar]
  96. Porciani, C., & Giavalisco, M. 2002, ApJ, 565, 24 [NASA ADS] [CrossRef] [Google Scholar]
  97. Ramakrishnan, S., Paranjape, A., Hahn, O., & Sheth, R. K. 2019, MNRAS, 489, 2977 [NASA ADS] [CrossRef] [Google Scholar]
  98. Ramakrishnan, S., Paranjape, A., & Sheth, R. K. 2021, MNRAS, 503, 2053 [NASA ADS] [CrossRef] [Google Scholar]
  99. Rodrigues, N. V. N., de Santi, N. S. M., Montero-Dorta, A. D., & Abramo, L. R. 2023, MNRAS, 522, 3236 [NASA ADS] [CrossRef] [Google Scholar]
  100. Sato-Polito, G., Montero-Dorta, A. D., Abramo, L. R., Prada, F., & Klypin, A. 2019, MNRAS, 487, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  101. Schaye, J., Kugel, R., Schaller, M., et al. 2023, MNRAS, 526, 4978 [NASA ADS] [CrossRef] [Google Scholar]
  102. Scoccimarro, R., & Sheth, R. K. 2002, MNRAS, 329, 629 [NASA ADS] [CrossRef] [Google Scholar]
  103. Sheth, R. K., & Tormen, G. 2004, MNRAS, 350, 1385 [NASA ADS] [CrossRef] [Google Scholar]
  104. Shi, J., & Sheth, R. K. 2018, MNRAS, 473, 2486 [NASA ADS] [CrossRef] [Google Scholar]
  105. Sinigaglia, F., Kitaura, F.-S., Balaguera-Antolínez, A., et al. 2021, ApJ, 921, 66 [NASA ADS] [CrossRef] [Google Scholar]
  106. Skibba, R. A., & Macciò, A. V. 2011, MNRAS, 416, 2388 [NASA ADS] [CrossRef] [Google Scholar]
  107. Smith, R. E., Hernández-Monteagudo, C., & Seljak, U. 2009, Phys. Rev. D, 80, 063528 [NASA ADS] [CrossRef] [Google Scholar]
  108. Sousbie, T., Courtois, H., Bryan, G., & Devriendt, J. 2008, ApJ, 678, 569 [NASA ADS] [CrossRef] [Google Scholar]
  109. Spergel, D., Gehrels, N., Baltay, C., et al. 2015, arXiv e-prints [arXiv: 1503.03757] [Google Scholar]
  110. Tassev, S., Zaldarriaga, M., & Eisenstein, D. J. 2013, J. Cosmology Astropart. Phys., 6, 036 [CrossRef] [Google Scholar]
  111. Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
  112. Tutusaus, I., Martinelli, M., Cardone, V. F., et al. 2020, A&A, 643, A70 [EDP Sciences] [Google Scholar]
  113. Vale, A., & Ostriker, J. P. 2004, MNRAS, 353, 189 [Google Scholar]
  114. van de Weygaert, R., Aragon-Calvo, M. A., Jones, B. J. T., & Platen, E. 2009, arXiv e-prints [arXiv: 0912.3448] [Google Scholar]
  115. Villaescusa-Navarro, F., Naess, S., Genel, S., et al. 2018, ApJ, 867, 137 [NASA ADS] [CrossRef] [Google Scholar]
  116. Villaescusa-Navarro, F., Anglés-Alcázar, D., Genel, S., et al. 2021, ApJ, 915, 71 [NASA ADS] [CrossRef] [Google Scholar]
  117. Wechsler, R. H., Zentner, A. R., Bullock, J. S., Kravtsov, A. V., & Allgood, B. 2006, ApJ, 652, 71 [NASA ADS] [CrossRef] [Google Scholar]
  118. White, M., Tinker, J. L., & McBride, C. K. 2014, MNRAS, 437, 2594 [NASA ADS] [CrossRef] [Google Scholar]
  119. Wong, A. W. C., & Taylor, J. E. 2012, ApJ, 757, 102 [NASA ADS] [CrossRef] [Google Scholar]
  120. Wu, J. F., Kragh Jespersen, C., & Wechsler, R. H. 2024, arXiv e-prints [arXiv:2402.07995] [Google Scholar]
  121. Xu, X., Zehavi, I., & Contreras, S. 2021, MNRAS, 502, 3242 [NASA ADS] [CrossRef] [Google Scholar]
  122. Yang, X., Zhang, Y., Lu, T., et al. 2017, ApJ, 848, 60 [NASA ADS] [CrossRef] [Google Scholar]
  123. Zehavi, I., Kerby, S. E., Contreras, S., et al. 2019, ApJ, 887, 17 [NASA ADS] [CrossRef] [Google Scholar]
  124. Zhai, Z., Benson, A., Wang, Y., Yepes, G., & Chuang, C.-H. 2019, MNRAS, 490, 3667 [NASA ADS] [CrossRef] [Google Scholar]
  125. Zhang, X., Wang, Y., Zhang, W., et al. 2019, arXiv e-prints [arXiv: 1902.05965] [Google Scholar]
  126. Zhao, C., Kitaura, F.-S., Chuang, C.-H., et al. 2015, MNRAS, 451, 4266 [NASA ADS] [CrossRef] [Google Scholar]
  127. Zhou, S., Zhang, P., & Chen, Z. 2023, MNRAS, 523, 5789 [NASA ADS] [CrossRef] [Google Scholar]
2

With components 𝒯ij = ∂i∂jϕ, where ϕ satisfies Poisson equation ∇2ϕ = δdm.

3

We have used a maximum wavenumber kmax = 0.08 hMpc−1, up to which, at the redshifts explored in this work, the ratio Ph(k)/Pdm(k) is compatible with a constant value.

4

The MSHA algorithm is part of the C++ library CosmiCodes found at https://github.com/balaguera/CosmicCodes

5

The algorithm uses as input parameter the number of levels and the size of the mesh of each level, from which the range of the intervals in the property ηp are computed. That is, the number of tracers in each interval equals the size of the mesh given as input parameter.

6

For the assignment of Vmax using MS, we have used three levels with sizes 163, 643, and 1283, with 100 bins in local density, four cosmic web types, 10 bins in local overdensity, 10 bins in Mach number and 15 bins in large-scale bias. The tolerance factors are chosen to be 0.9 for all levels. At ɀ = 0, the fraction of Vmax assigned in each level is ~0.01, 1.2 and ~10% of the total number of available tracers, for levels ℓ = 1 (most massive halos), ℓ = 2 and ℓ = 3 respectively. Below the last level, no MS is applied; in this case, ~70% of tracers are assigned a property from the reference, while the remaining fraction are assigned a property using the global distribution. For the assignment of virial mass and secondary properties, 100 bins in Vmax and Mvir are used, respectively. This setup leads to ~3,7,8, and 12% global differences in abundance with respect to the reference, when measured as a function of Vmax, Mvir, Cvir, and λB respectively.

7

Even if the first assignment corresponds to Vmax, we show the results in terms of Mvir as it is more familiar within the large-scale structure community.

All Figures

thumbnail Fig. 1

Flow chart representing the algorithm designed to assign halo properties. The reference simulation provides a dark matter density field and its corresponding halo catalogs, with phase-space coordinates and intrinsic properties.
In the text
thumbnail Fig. 2

Large-scale effective bias as a function of virial mass, assigned as described in Sect. 3. The main panels (a,b,c,d) show the effective bias measured from the reference and the results from the property assignment at ɀ = 0 (left), ɀ = 0.5 (center), and ɀ = 1 (right column), with (labeled Assignment+MS) and without (labeled Assignment) the MS approach. Panel a shows the results of using only dark matter properties Θdm in the assignment of maximum circular velocity and virial mass. Panel b shows the results of adding the information from the individual bias. Panel c shows the results after including halo environment properties ΘH, and panel d shows the result of including both bias and environment properties. The bottom panels show, in each case, the ratio to the primary bias obtained from the mock catalog using its original properties (the latter shown as black points in all main panels). The gray region in these bottom panels depicts 10% deviation with respect to unity. The error bars denote the error on the mean bias-property relation.
In the text
thumbnail Fig. 3

Secondary effective bias as a function of halo virial mass. This plot compares (with ratios) the effective bias measured reference and the mock after assignment, at two different cosmological redshifts (shown in different columns) and using different combinations of halo vs. dark matter properties, as shown in the legends. Panels a and b show the secondary bias using halo concentration, for the lower and upper quartiles computed in each mass bin, respectively. Similarly, panels c and d show the secondary bias as a function of halo spin. In all plots, the shaded region denotes a 10% deviation from unity. In all cases, MS is employed. The error bars are computed by adding in quadrature the corresponding uncertainties in each bias estimate.
In the text
thumbnail Fig. 4

2D scaling relations between halo properties and large-scale halo effective bias in the UNITSim at ɀ = 0. The different lines in the contours (denoting surfaces of equal number of tracers) and the 1D distributions show the result from different setups in the assignment algorithm, as shown in the legend.
In the text
thumbnail Fig. 5

Scaling relation between the logarithm of the assigned virial mass ***(eq14)***Mvira$M_{{\rm{vir}}}^a$ and the logarithm of the true virial mass ***(eq15)***Mviro$M_{{\rm{vir}}}^o$, for four different setups in the assignment algorithm (at ɀ = 0). The color coding and contours indicate the constant number of tracers from high (blue) to low (red).
In the text
thumbnail Fig. 6

Correlation coefficient between the assigned mass and the original mass at ɀ = 0 for different setups used in the assignment algorithm, for cuts in the true and assigned masses ***(eq16)***Mvira,Mvir0>Mvir$M_{{\rm{vir}}}^a,M_{{\rm{vir}}}^0 > {M_{{\rm{vir}}}}$.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.