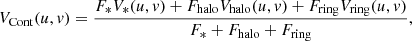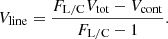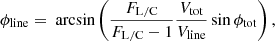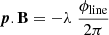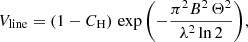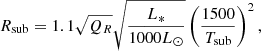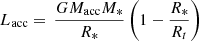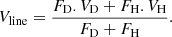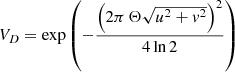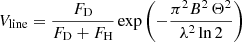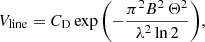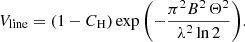| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202451254 | |
| Published online | 03 October 2024 | |
The GRAVITY young stellar object survey
XIV. Investigating the magnetospheric accretion-ejection processes in S CrA N⋆⋆
1
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
2
I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
3
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, 06300 Nice, France
4
Max-Planck-Institute for Radio Astronomy, Auf dem Hügel 69, 53121 Bonn, Germany
5
Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
6
INAF-Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
7
School of Physics, University College Dublin, Dublin 4, Belfield, Ireland
8
Instituto de Astronomia, Universidad Nacional Autonoma de Mexico, Apdo. Postal 70264 Ciudad de Mexico 04510, Mexico
9
Max Planck Institute for Extraterrestrial Physics, Giessenbachstrasse, 85741 Garching bei München, Germany
10
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, France
11
CENTRA, Centro de Astrofísica e Gravitação, Instituto Superior Técnico, Avenida Rovisco Pais 1, 1049 Lisboa, Portugal
12
Universidade do Porto, Faculdade de Engenharia, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal
Received:
25
June 2024
Accepted:
1
August 2024
Context. The dust- and gas-rich protoplanetary disks around young stellar systems play a key role in star and planet formation. While considerable progress has recently been made in probing these disks on large scales of a few tens of astronomical units (au), the central au requires further investigation.
Aims.We aim to unveil the physical processes at play in the innermost regions of the strongly accreting T Tauri Star S CrA N by means of near-infrared interferometric observations. As recent spectropolarimetric observations suggest that S CrA N might undergo intense ejection processes, we focus on the accretion–ejection phenomena and on the star–disk interaction region.
Methods. We obtained interferometric observations with VLTI/GRAVITY in the K-band during two consecutive nights in August 2022. The analysis of the continuum emission, coupled with the differential analysis across the Brγ line, allows us to constrain the morphology of the dust and the gas distribution in the innermost regions of S CrA N and to investigate their temporal variability. These observations are compared to magnetospheric accretion–ejection models of T Tauri stars and to previous observations in order to elucidate the physical processes operating in these regions.
Results. The K-band continuum emission is well reproduced with an azimuthally modulated dusty ring with a half-light radius of 0.24 au (∼20 R*), an inclination of ∼30°, and a position angle of ∼150°. As the star alone cannot explain such a large sublimation front, we propose that magnetospheric accretion is an important dust-heating mechanism leading to this continuum emission. The Brγ-emitting region (0.05–0.06 au; 5–7 R*) is found to be more compact than the continuum, to be similar in size or larger than the magnetospheric truncation radius. The on-sky displacements across the Brγ spectral channels are aligned along a position angle offset by 45° from the disk, and extend up to 2 R*. This is in agreement with radiative transfer models combining magnetospheric accretion and disk winds. These on-sky displacements remain unchanged from one night to another, while the line flux decreases by 13%, suggesting a dominant contribution of wind to the origin of the Brγ line.
Conclusions. Our observations support the scenario where the Brγ line originates from a combination of (variable) accretion–ejection processes in the inner disk region.
Key words: accretion / accretion disks / techniques: interferometric / stars: individual: S CrA N
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The young solar-mass stars, the so-called classical T Tauri stars (CTTSs), are still accreting matter from their circumstellar disks and are the site of intense magnetospheric accretion–ejection processes. Notably, within the framework of the magnetospheric accretion scenario, the stellar magnetic field truncates the inner disk close to the central star (i.e., at a few hundredths of an astronomical unit (au) away) and forces matter to be funneled onto the star along the magnetic field lines, creating accretion shocks at the stellar surface (Bouvier et al. 2007; Hartmann et al. 2016). These events are responsible for the emission-rich spectra of CTTSs, which in some cases display exceptionally intense and variable lines (White & Basri 2003). Temporal variability of photometry is very frequently observed in CTTSs on different timescales, ranging from subdaily to monthly periods, regardless of whether accretion is strong (e.g., Siwak et al. 2016 for RU Lup) or not (e.g., Rucinski et al. 2008; Siwak et al. 2011 for TW Hya). The variations in shape and intensity of emission lines can be stochastic, episodic or periodic (see Fischer et al. 2023, for a review of accretion variabilities). The origin of this variability is still poorly constrained and multitechnique and/or multiwavelength campaigns are required to understand it. Such a simultaneous multitechnique approach has recently proven effective in providing unique constraints for the CTTS DoAr 44: while spectropolarimetry (with ESPaDOnS and SPIRou at CFHT) allowed kinematics studies across many (variable) spectral lines and monitoring of the magnetic field topology (Bouvier et al. 2020a), near-infrared spectro-interferometry across the Brγ line with GRAVITY at VLTI (GRAVITY Collaboration 2017a) allowed resolution of the hydrogen-emitting region at a scale of a few stellar radii (Bouvier et al. 2020b). Combining the different techniques is helpful for disentangling the contribution of accretion and ejection flows to the Brγ line (GRAVITY Collaboration 2020, 2023a,b).
We apply this multitechnique approach to the strongly accreting T Tauri star S CrA North (hereafter, S CrA N). The strong accretors generally exhibit more intense and more variable emission lines (e.g., Venuti et al. 2014 for the objects of the NGC 2264 cluster). As they are often deeply embedded in a complex environment, they are difficult to observe, notably in the visible/near-infrared range. Due to their high accretion luminosity, the central objects are highly veiled. As such, they have been poorly studied, and it is still unclear as to whether the strong accretor status corresponds to a specific evolutionary stage or a specific geometrical configuration of CTTSs.
S CrA N is the Northern component of the S CrA binary system, located near the most extincted region of the Corona Australis cloud at a distance of ∼150 pc (Dobashi et al. 2005). The two components are observed close to each other (1.3 arcsec, see Zhang et al. 2023). They are similar in mass and are coeval, with spectral type K6 (Gahm et al. 2018, and references therein). S CrA was first identified as a variable T Tauri binary by Joy (1945), and as a bright member of the YY Ori class by Walker (1972). The two components present broad redshifted absorptions in various emission lines (e.g. Fe II λ4924,λ5018,λ5169, He I D3, higher Balmer lines, see Gahm et al. 2018; Nowacki et al. 2023), which is indicative of material falling onto the central objects at free-fall velocities (Krautter et al. 1990), thus offering preliminary evidence of the strong accretor nature of this binary system (Petrov et al. 2014). Many studies later confirmed this status in a variety of manners: the spectral features observed in its spectrum have never been fully reproduced, but the most promising results were obtained using strong accretion models (Gahm et al. 2018) in combination with intense chromospheric emission models (Petrov et al. 2011; Dodin & Lamzin 2012). Evidence has been found of a highly dust- and gas-rich environment indicative of a remnant envelope at large scales (Sicilia-Aguilar et al. 2013) and a massive dusty disk (∼102 M⊕ and ∼100 au in radius) is observed around S CrA N (Cazzoletti et al. 2019; Zhang et al. 2023). Combined with a flat spectral energy distribution (e.g. Sullivan et al. 2019), these elements indicate a very young age as discussed in Nowacki et al. (2023) (henceforth N23), who led an observing campaign in optical spectropolarimetry with CFHT/ESPaDOnS to derive the star’s fundamental parameters (Table 1) and magnetic field topology. This system was also studied by near-infrared interferometry and the previous observations showed the presence of a bright sublimation front at the inner rim of the disk (0.13–0.15 au, when considering a distance of 152.4 pc; Vural et al. 2012; GRAVITY Collaboration 2017b).
Parameters of S CrA N relevant for this work.
In this paper, we present a study of the inner rim of the disk surrounding S CrA N and its inward regions, based on a richer and higher-quality GRAVITY data set. We find significant differential signals across the Brγ line during two consecutive nights. Section 2 details the GRAVITY observations and the data reduction we applied. Section 3 presents our results on the K-band continuum and Brγ line-emitting regions, which are then discussed in Section 4. In Section 5 we provide an interpretation of the presented results in the context of S CrA N and strong accretors in general and outline our conclusions.
2. Observations and data reduction
S CrA N was observed during two nights (August 19 and 20, 2022) as part of Guaranteed Time Observations with GRAVITY (GRAVITY Collaboration 2017a) combining the four Unit Telescopes (UTs, 8.2 m in diameter each) of the ESO/VLTI. With interferometric baselines B ranging between 40 and 130 m, we reached an angular resolution of λ/2Bmax = 1.7 mas at a wavelength of λ = 2.2 μm, corresponding to 0.26 au at 152 pc. The instrument was used in dual field mode (see GRAVITY Collaboration 2017a) with S CrA S feeding the fringe tracker (FT) working at ∼ 1 kHz speed (Lacour et al. 2019) to freeze the atmospheric effects and lock the interferometric signals for the science channel (SC). Once the fringes were locked, we recorded N six-minute sequences (each made up of 12 exposures of 30 s) every ∼10 minutes on S CrA N with the SC at high spectral resolution (R∼4000; Δv = 74 km/s). We recorded 9 files on August 19, and 12 on August 20. To calibrate the instrumental transfer function, we observed two different calibrators. One before, and one after the exposures on the scientific target. These were chosen to be single stars, close in angular distance and magnitude to the target, and with very small and known diameters according to the SearchCal software (Bonneau et al. 2011) of the JMMC1. For both nights, the atmospheric conditions were good with a seeing ranging from 0.6″to 1.1″, and a coherence time τ0 longer than 6 ms. We provide a detailed log of the observations in Table 2.
Log of the GRAVITY observations of S CrA.
We processed all the data with the standard GRAVITY pipeline (Lapeyrere et al. 2014). Each file contains the complex visibilities and closure phases of S CrA S in the FT, and of S CrA N in the SC. For S CrA N, the differential visibilities and phases as a function of the spectral channels can be retrieved, notably across the Brγ line. When comparing the observations of the calibrator common to the two nights, HD 186419, we detected a chromatic effect in the SC data of the second night, as displayed in Fig. A.1. We therefore calibrated all the SC data of the second night with the first calibrator, HD 176047, which does not show this effect. When looking at the S CrA N data, these chromatic effects are observed for most of the observations of the first night, and for a few files of the second night. Because such an effect might affect the absolute calibration of the visibility, we only used the data from the second night to constrain the dusty inner ring. This effect does not impact the differential observables across the Brγ line.
3. Results
The data were analysed in two steps. First, a fitting of the whole K-band continuum emission was performed to constrain the dust distribution. Then, the hydrogen-emitting region was studied, as differential visibilities and differential phases were observed across the Brγ line.
3.1. The K-band continuum-emitting region
We used the visibilities squared and the closure phases over the K-band of the second night to constrain the geometry of the corresponding emitting region. We binned the SC data to obtain five spectral channels over the whole band. The emitting region appears to be well resolved with visibilities squared of as low as 0.25 at the longest baselines and to exhibit a slight departure from centro-symmetry with closure phases of 1–2° (Fig. 1). We followed the same approach as Lazareff et al. (2017) and GRAVITY Collaboration (2019, 2021) to fit the visibility curve as a function of the baseline and the closure phase signals with a geometrical model. To consider conservative error bars, we fixed floor values on the error estimates provided by the data reduction pipeline, amounting to 2% on the visibilities squared and to 0.35° on the closure phases as estimated from the root mean square (rms) variations at the center of the K-band. We fitted our data with a composite model including a point-like source for the star, a halo contribution from the extended environment, and a first-order azimuthally modulated Gaussian ring component accounting for the emission of the inner dusty disk. At the spatial frequencies (u, v), the complex visibility is thus described by the linear combination:
 |
Fig. 1. GRAVITY observations of S CrA N on 2022 August 20: K-band continuum visibilities squared (left) and closure phases (center) as a function of baseline (gray symbols) superimposed with the best-fit ring model (right). The modeled quantities are depicted in colors matching the (u-v) plane coverage shown in the inset on the right. The lower panels show the residuals of the model in units of σ. Shaded bands highlight 1-, 3-, and 5σ levels. |
where V* = 1 is the visibility of the star that is unresolved at our angular resolution; Vhalo = 0 is the visibility of the component that is supposed to be much more extended than the GRAVITY field of view and fully resolved, even by the shortest baselines; Vring is the visibility of the ring model; F*, Fhalo, and Fring are the flux contributions of the star, the halo, and the ring, respectively, with F* + Fhalo + Fring = 1.
We refer to Lazareff et al. (2017) for a detailed description of the modeling approach; more specifically, see their Table 5 for the analytical expression of Vring(u, v), their Table 7 for the parametrizations of the ring model, their Equations (4) and (8) for the spectral dependence and the parametrization of the azimuthally modulated ring (c1 and s1 coefficients), and their Sect. 3.3 for the fitting procedure. As the spectral index of the star is fixed from its effective temperature, the nine free parameters of our geometrical ring model are the flux contributions of the halo and of the ring, the half-light radius of the Gaussian ring, its inclination and position angle, its width relative to its half-light radius, its spectral index, and the two coefficients c1 and s1 of the azimuthal modulation. As the dusty environment is not fully resolved, its flux contribution and its size are partially degenerate, as emphasized in Lazareff et al. (2017). We used a starting value of Fring between 0.35 and 0.45 estimated from the spectral energy distribution of Varga et al. (2018) but kept this parameter free in the whole fitting process.
The parameters of the best-fit ring model are given in Table 3 and shown in Fig. 1 along with their corresponding residuals when comparing to the SC data. The best model corresponds to a Gaussian ring contributing to about 40% of the total flux, with a half-flux radius of 1.55 mas (i.e., 0.24 au at 152.4 pc), an inclination of 30°, a position angle (PA) of about 150°, a spectral index range corresponding to a black-body emission at about 1800–2100 K, and an intensity enhancement located on the northeast side (see the right panel of Fig. 1).
Best-fit parameters for the azimuthally modulated ring model.
3.2. The Brγ line spectrum
As GRAVITY is equipped with a spectrograph, we were able to retrieve the Brγ line spectrum for each observing date. To this end, we first performed Local Standard of Rest (LSR) correction for all the observations, and so the kinematics of the line are expressed in the frame of the star. We then used the PMOIRED Python library (Mérand 2022) to correct the GRAVITY wavelength calibration, based on a telluric model, and obtained a normalized spectrum corrected from this telluric spectrum (see Appendix B for the detailed process). No additional contribution of the photosphere to the Brγ line was considered, because the veiling of S CrA N is sufficiently strong in the near-infrared (∼4 in H-band; Sullivan et al. 2019) to consider the photospheric component negligible with respect to the line emission. The above procedure provides the Brγ line-to-continuum flux ratios FL/C for both dates, which are shown in the bottom-right panel of Fig. 2. This quantity shows very little dispersion during a single night over the whole line (≤ 7%). It also shows a 13% variability between the two epochs, indicating a definite clear variation in the accretion–ejection processes on a daily timescale, which is expected for T Tauri stars (e.g. Hartmann et al. 2016). The line also shows a remarkable asymmetry in the profile, with a milder blue wing, and a steeper red wing with a peak slightly centered in the red (+30 km/s). We used FL/C to define the velocity domain where we consider the interferometric differential quantities across the Brγ line as relevant: we took all the spectral channels for which FL/C exceeds 10% of the peak value observed, which corresponds to a threshold of FL/C > 1.04 (or ∼ 40 for the S/N). The relevant spectral channels are illustrated with a blue-to-red color, and the threshold limit is delimited by a dotted horizontal gray line in Fig. 2.
 |
Fig. 2. Brγ differential interferometric observables of S CrA N: Squared differential visibilities (left); differential phases (middle); u-v plane coverage (upper-right); line-to-continuum flux ratio in the reference frame of the star, LSR- and tellurics-corrected (lower-right). Each color used in the u-v coverage plot corresponds to an interferometric baseline and is consistent over all panels. For the interferometric observables, the plots include the quantities for each frame (solid lines) and the median for August 19 (circles) and for August 20 (squares). Uncertainties are given in all plots (vertical bars), and are smaller than the symbol if not visible. Gray shaded regions correspond to the velocities that are not considered for our Brγ line analysis (see text for details). |
3.3. Morphology of the Brγ line-emitting region
We analyzed the differential interferometric observables to constrain the geometry of the regions responsible for the emission of the Brγ line in S CrA N. The remarkable S/N observed both in differential visibility (up to 40) and phase (up to 10) allow relative sizes and astrometric displacements to be measured with an accuracy of 20 μas and 5 μas, respectively.
3.3.1. The differential interferometric data
We forced the visibilities squared in the continuum adjacent to the Brγ line to match the absolute visibility values predicted by our K-band continuum best-fit model. As depicted in the left panel of Fig. 2, the differential visibilities are clearly higher across the emission line than in the continuum, indicating a more compact line-emitting region than the ∼0.24 au inner dusty disk ring model presented earlier. Over both nights, the scatter of the differential visibilities for the different frames is significant, notably for the longest baselines (in blue and green in the left panel of Fig. 2) due to the change of the projected baselines during the night. Regarding the differential phases, a clear signal is detected for all baselines in the Brγ line individual frames, revealing an asymmetric emitting region. The higher amplitudes of a few degrees for peak to peak are detected for the longest baselines, when the region is more resolved. The S-shape of the differential phases appears asymmetric for all the baselines, with a stronger amplitude in the blue part of the line.
3.3.2. The pure-line quantities
To constrain the morphology of the Brγ line-emitting region, we disentangled the contributions from the continuum and the line using the line-to-continuum flux ratio FL/C. In the regime of marginally resolved sources, we extracted the so-called pure-line visibility Vline (see Appendix B of GRAVITY Collaboration 2023b, for the developments leading to this formula):
The pure line visibility was used to derive the pure-line differential phases across the Brγ line ϕline, which was obtained from the total phase ϕtot thanks to the total visibility Vtot, and the line-to-continuum flux ratio FL/C as follows (see GRAVITY Collaboration 2023b, for the details):
where ϕtot is the total differential phase (which is shown for each baseline in Fig 2). This quantity was computed for each observation and at each baseline, before the values were combined in order to get a single pure-line differential phase per night and per channel. Each value was taken as the median over all observations, and the associated uncertainties were computed following the Student’s t-distribution. The benefit of such a merger is a significant decrease in the uncertainties, resulting in a much more precise estimate of the photocenter displacements of the line. The resulting pure-line phases are shown for each baseline in the left panel of Fig. 3, superimposed on the total phases of the individual frames.
 |
Fig. 3. Asymmetry of the Brγ-emitting region of S CrA N. Left : Pure-line differential phases. The pure line differential phases are depicted by blue-to-red color coded symbols for August 19 (circles) and August 20 (squares), while the observed phases for each individual observation (similar to Fig. 2) are depicted in solid lines, with their color corresponding to their baseline. Right : On-sky photocenter shifts with respect to the continuum photocenter (in (0, 0) as a function of velocity (coded from blue to red colors). The light-yellow cones correspond to the uncertainties on the major axis orientation of the inner dusty disk. The background symbols are the displacements obtained from individual files. |
3.3.3. Asymmetry of the Brγ-emitting region
To measure the on-sky photocenter shift across Brγ, we used the linear relationship of marginally resolved sources between the photometric displacement’s coordinate vector p along a given projected baseline matrix B and the associated pure-line differential phase matrix ϕline at a given wavelength λ (Lachaume 2003):
In the present case, B and ϕline are a (2 × 6) and a (1 × 6) matrix, respectively. By inverting B, one recovers the coordinates of the photocenter shift p relative to the photocenter of the continuum. We performed this inversion for all velocity channels of the Brγ line. This way, we obtained the astrometric displacement of Brγ for each spectral channel (right panel of Fig. 3), which is completely independent of the model used. These photocenter shifts form a rather simple pattern, with a preferential orientation misaligned by ∼45° with respect to the major axis PA of the inner dusty disk; they lie in a very compact configuration (within ∼150 μas, i.e., ∼0.023 au, which corresponds to one-tenth of the half-flux radius of the K-band continuum emission). The blue velocity channels (material moving toward the observer) centered around the null velocity (white circles/squares), and the red velocity channels (material moving away from the observer) clearly depart from the null velocity in the northeast direction for ∼150 μas until v ∼ 100 km/s. Beyond this velocity, the shifts remain centered around the same position. The position of the star relative to the continuum’s photocenter is consistent with the null velocity shifts, when propagating the uncertainties of the continuum model : its coordinates in the reference frame attached to the photocenter of the continuum are −102 ± 95 μas toward the east and −164 ± 95 μas toward north. It is worth noting that, despite the fact that they are affected by larger error bars, the individual file displacements (visible as light-colored background symbols in Fig. 3) seem to form a more complex pattern with departures of the higher velocities from the straight line mentioned here.
3.3.4. Size of the Brγ-emitting region
A way to disentangle the different processes at play, and further our understanding of the morphology of the emitting region is to use a geometrical model to reproduce the spatial distribution of the emitting region at each velocity channel of the Brγ line. In the case of S CrA N, the pure-line visibilities (especially at low frequencies) are not satisfactorily reproduced by a Gaussian disk alone (as it is usually done for CTTS, see e.g. GRAVITY Collaboration 2023a,b), and so a composite model combining a Gaussian disk model and a fully resolved halo was adjusted to the data. The expression of the pure-line visibility is then (see Appendix C for the justifications and developments leading to the formula):
CH is the relative contribution of the halo to the total flux, Θ is the half-width at half-maximum (HWHM) of the Gaussian disk, B and λ are a given projected baseline and wavelength of observation. This projected baseline takes into account an inclination of the disk (α) along a PA measured from north to east. This model is adjusted independently to the nine observations of August 19 and to the 12 observations of August 20, taking full advantage of the high quality of the single-frame data to provide strong constraints on the χ2 minimization procedure. Because a degeneracy is expected between the halo and the size of the emitting region (in a marginally resolved regime), the data were fitted first with a contribution of the halo fixed to the value of the continuum (10%). Then, the contribution of the halo was adjusted, while the other parameters were set to the values that minimize χ2 in the previous procedure. The best model corresponds to a disk whose HWHM is equal to 0.43 ± 0.06 mas (0.06 ± 0.01 au), inclined by 51° ± 13° around a PA of 141° ±10°. The contribution of the halo is within 8.9 ± 0.3%. These models yield a χr2 of 0.83 on average, with residuals contained within 1σ for most of the points. The best-fit models for all velocity channels are illustrated in Fig. 4, detailed in Table 4, and six of them are compared against the measured pure-line visibilities in Fig. 5.
 |
Fig. 4. Characteristic sizes of the Brγ-emitting region of S CrA N as a function of velocity (coded from blue to red colors) for August 19 (circles) and August 20 (squares). The red, green and blue areas correspond to the stellar, truncation, and corotation radii, respectively. The dashed gold line marks one-quarter of the half-light radius derived for the inner dusty ring model for the sake of comparison. Colored symbols with gray error bars in the background correspond to the sizes derived from individual files. The distance used is 154.2 pc. |
Best-fit parameters with 1σ error bars for the Halo + Gaussian disk model of the Brγ pure-line visibilities.
 |
Fig. 5. Pure-line visibility fits for August 19th (left column) and 20th (right column). Each row consists of two subplots : The top one includes the pure-line visibilities squared and their 1σ uncertainty observed at a given velocity (mentioned in the panel) superimposed with the corresponding model including a Gaussian disk and a halo. The bottom one illustrates the residuals of the model in units of σ. Three shades of gray mark the 1-,3-, and 5σ levels. The color of the data points corresponds to the baseline. |
4. Discussion
From our VLTI/GRAVITY observations obtained on S CrA N on two successive nights in August 2022, we derived the characteristic sizes of the near-infrared-emitting regions and traced their on-sky displacement. The outstanding quality of the data sets provides new insights into the innermost regions of this strong accretor. In this section, we discuss how these results constrain the accretion–ejection processes in a global view of this young system.
4.1. The star–disk interaction region
It is generally accepted that the star–disk interaction for T Tauri stars is dominated by magnetospheric accretion: the ∼1 kG stellar magnetic field truncates the inner gaseous disk at the truncation radius Rt; the matter is accreted onto the central star along the magnetic funnels and falls on an accretion spot. Combined with a heated inner disk in Keplerian rotation, this scenario offers several origins for the Brγ-emission line. Our clear astrometric offset of the Brγ emitting region of about ∼150 μas (i.e., 0.023 au), which is misaligned by ∼45° with respect to the major axis of the inner dusty disk (Fig. 3), does not favor a pure disk in Keplerian rotation, for which the photocenter shift would trace a line parallel to the disk’s major axis, with the photocenters of the fastest velocities closer to the null velocity than the photocenters of the slowest velocities (see Mendigutía et al. 2015, for a typical example). Instead, our astrometric displacements are more in agreement with polar phenomena, such as accretion flows and/or outflows. The visibilities recorded with GRAVITY in the Brγ line correspond to an emitting region of ∼0.05–0.06 au at the zero-velocity channel, which is located well within the inner dusty disk for which we derived a half-flux radius of 0.24 au. This characteristic size of the Brγ line region corresponds to ∼5 R*, which is close to the truncation radius Rt = 4.4 ± 0.9 R* (∼0.05 au) we obtain when applying the scaling of Pantolmos et al. (in prep.) with the S CrA N parameters given in Table 1. As depicted in Fig. 4, some blueshifted channels do extend further than the truncation radius, but all are included within the corotation radius of Rcor = 6.4 ± 1.7 R* (∼0.07 au). Noting that the Gaussian model we used to model the Brγ line-emitting region might underestimate the size of the magnetosphere by up to a factor two depending on the phase of observation (see Fig. 6 of Tessore et al. 2023), the distribution of sizes we derive is definitely larger than Rt in most of the spectral channels. This suggests that the Brγ is the result of a combination of magnetospheric accretion and outflow processes. Previous observations of blueshifted forbidden emission lines and P Cygni profiles in S CrA N support the presence of outflows in the vicinity of the star (e.g. Carmona et al. 2007; Gahm et al. 2018, N23). This is also supported by the comparison of our findings with magneto-hydrodynamic (MHD) simulations. Wojtczak et al. (in revision) computed synthetic interferometric observables for the strongly accreting T Tauri star RU Lup, with stellar parameters and inclination similar to those of S CrA N (M* = 0.8 M⊙; R* = 2.5 R⊙; Teff = 4300 K; Prot = 7 days; ̇Macc = 2 × 10−7M⊙.yr−1; d = 157.5 pc; i ∼ 20°, see Tables 1 and 3). The hybrid model used by these authors includes an axisymmetric magnetosphere and a biconical magneto-centrifugal disk wind, and exhibits a constant size of about 0.06 au at the center of the Brγ line, a larger size in the blue wing (up to ∼0.1 au), and astrometric displacements at the core of the line along a line of about 0.03 au misaligned with the inner disk major axis. All these characteristics are remarkably similar to our observations (see their Fig. 7-left). When comparing to the other targets of the GRAVITY sample (GRAVITY Collaboration 2021, 2023b), S CrA N appears to be similar to the strongly accreting ones (e.g. RU Lup, AS 205 N), with a sublimation radius located at 0.1–0.2 au, and a Brγ emission more extended than the corotation radius, suggesting it originates from a combination of magnetospheric accretion and disk winds.
4.2. Evidence for sustained disk winds
Beyond the truncation radius, the open magnetic field lines of the star are expected to produce transient magnetospheric ejections as well as disk winds (see, e.g. Romanova et al. 2009; Zanni & Ferreira 2013; Pantolmos et al. 2020). In their spectroscopic study of S CrA N, N23 detected outflow signatures (namely Balmer lines blueshifted absorptions, and [OI] and [SII] forbidden emissions) that might be reproduced by a hot (∼9000 K), dense (∼5 × 10−11 g.cm−3) wind launched from a region extending up to ∼20 R* (i.e., 0.24 au), with a mass-loss rate of ̇Mwind ∼ 10−8M⊙.yr−1. This size is comparable to the range of the location of the inner rim (0.13–0.24 au) determined for the dusty disk in the K-band (see Vural et al. 2012; GRAVITY Collaboration 2017b, and this work). A good tracer of the kinematics and structure of the inner gaseous disk is the 12CO gas emission (Pontoppidan et al. 2011). Using CRIRES(+) observations of S CrA N, Banzatti et al. (2022) and Grant et al. (2024) detected triangular CO lines in emission and two distinct velocity components of the CO emission: the broad (BC) and the narrow (NC) components. When scaling their values to our stellar parameters (Table 1), we derive a half-width at half maximum for the BC, 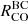 , of 0.4 ± 0.1 au for Banzatti et al. (2022) and of 0.14 ± 0.05 au for Grant et al. (2024), respectively; for the NC,
, of 0.4 ± 0.1 au for Banzatti et al. (2022) and of 0.14 ± 0.05 au for Grant et al. (2024), respectively; for the NC, 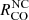 of 8 ± 3 au and 4 ± 1, respectively. When comparing with the half-flux radius of the inner dusty disk (0.24 au), the CO broad component seems to originate from a region inside or close to the dust sublimation radius, while the NC definitely arises from a region beyond the dust sublimation radius in the disk. To reproduce these CO features (shapes and radii of the emission), Pontoppidan et al. (2011) and Banzatti et al. (2022) developed different models that support the presence of sustained disk winds with ̇Mwind ∼ 10−8M⊙.yr−1, which is typically one-tenth of the ̇Macc.
of 8 ± 3 au and 4 ± 1, respectively. When comparing with the half-flux radius of the inner dusty disk (0.24 au), the CO broad component seems to originate from a region inside or close to the dust sublimation radius, while the NC definitely arises from a region beyond the dust sublimation radius in the disk. To reproduce these CO features (shapes and radii of the emission), Pontoppidan et al. (2011) and Banzatti et al. (2022) developed different models that support the presence of sustained disk winds with ̇Mwind ∼ 10−8M⊙.yr−1, which is typically one-tenth of the ̇Macc.
4.3. Magnetospheric accretion as a dust-heating mechanism
The near-infrared excess observed in the spectral energy distribution of CTTSs is generally interpreted as the hot dust emission located at the inner edge of the disk where the dust grains sublimate. This sublimation radius (in au) can be computed by (Monnier & Millan-Gabet 2002):
where QR is the absorption efficiencies of the dust, L* is the luminosity of the star, and Tsub is the temperature of dust sublimation.
Considering Teff = 4300 K for S CrA N and grain sizes ranging from 0.01 μm to 1 μm, QR spreads between 1 and 4 (see their Fig. 2). With a typical sublimation temperature Tsub ranging between 1300 K and 1700 K and L* = 1.7 L⊙, Rsub ranges between 0.04 and 0.15 au, which is twice less than the half-light radius of the dusty disk we derived (0.24 au). Our geometrical model is likely too simple to capture the complex radial and vertical structure of the inner rim but this might not explain the size difference. As pointed out by Pinte et al. (2008), the stellar scattered light has a non-negligible contribution in the interferometric measurements for T Tauri stars (see their Fig. 3), and so we a halo to our model in order to account for this contribution, at least partly, and derived a halo contribution of ∼10% in the K-band continuum and in the Brγ line. As this scattering is very unlikely to account for the large continuum K-band half-flux radius, additional dust heating sources and/or properties should be invoked. Indeed, the sublimation rim position strongly depends on the dust composition (pure silicate, here), cooling efficiency, and backwarming effects. More constraints are needed for a better description of the disk mineralogy (e.g., in the mid-infrared with MATISSE).
As S CrA N is a strongly accreting T Tauri Star, we tested the heating by the stellar accretion spot(s). The spot(s) created by magnetospheric accretion at the surface of the star could be modeled as a ∼9000 K blackbody (using Eq. (9) from Hartmann et al. 2016, assuming a filling factor of 0.05 for the spot) which makes it a good candidate, especially since the previous spectropolarimetric study of N23 revealed the presence of such a feature. Although the complete calculations of the intricate chemicophysical reactions of the dust in this context go beyond the scope of this paper, we can estimate the magnitude of change in Rsub provoked by the accretion shock heating. In Eq. 6, the stellar luminosity could be replaced by the sum of the stellar and accretion luminosities, the latter being computed assuming a complete conversion of kinetic energy into radiation, as :
Using the parameters from Table 1 and a truncation radius Rt = 4.4 ± 0.9 R*, we get Lacc = 0.9 ± 0.3 L⊙. In this situation, an equivalent effective temperature can be obtained as Teq4 = (1 − f)Teff4 + fTacc4, where f is the filling factor of the accretion spot. Keeping the assumption of f = 0.05, Teq ∼ 5000 K. Then, QR ranges between 1 and 6 and consequently Rsub increases up to 0.19 au, assuming the same kind of dust as previously.
As expected, the heating contribution from an accretion spot increases the sublimation radius. The remaining difference still requires that we consider different contributions beyond this simple model. For example, an extended magnetosphere composed of one or more accretion column could contribute to the heating of the dust. A gaseous disk undergoing the strong accretion rates measured in S CrA N(10−7M⊙.yr−1) and therefore producing viscous heating could also be contemplated. Although the former could be modeled (as in, e.g. Pittman et al. 2022), the latter is more difficult to constrain a priori. As no evidence of protoplanets has been found in the inner regions of this system so far, the presence of a cavity carved by a nascent planet appears more unlikely.
4.4. Hints of variable accretion and/or ejection ?
Temporal variability in photometry and/or spectroscopy is frequently observed on different timescales for CTTSs (Fischer et al. 2023). For S CrA N, previous CO observations (Banzatti et al. 2022; Grant et al. 2024) suggest a variable emission, and potentially a variable disk wind (see Sect. 4.2). Regarding the magnetospheric accretion process, the ratio of the truncation to the corotation radius Rt/Rcor = 0.7 ± 0.2 we obtained is close to the transition between stable and unstable accretion regimes of 0.8 stated by Pantolmos et al. (in prep.). This suggests a variable accretion process and supports the presence of two opposite accretion columns with different densities proposed by N23, as a consequence of the dipolar magnetic field and its non-null (≥5°) magnetic obliquity they derived. Thanks to the high quality of our GRAVITY data, we can investigate the variations across the Brγ line between the two nights of observation. Notably, we observed a flux decrease by 13% between the two nights (bottom-right panel of Fig. 2). Following the methodology of Prato et al. (2003) we measured the equivalent width (EW) of the Brγ-line of our GRAVITY median spectra to probe the accretion rate between −500 and +500 km/s. We obtained −91 ± 2 km/s and −82 ± 1 km/s for August 19 and August 20, respectively, which corresponds to an average value of EW encountered in S CrA N for Brγ (between −30 km/s and −120 km/s, see Prato et al. 2003; Sullivan et al. 2019; GRAVITY Collaboration 2023b). The EW determined from GRAVITY decreases between the two nights, suggesting that the star may exhibit variable accretion and/or variable ejection. Between the two nights, the interferometric signatures remain similar within our uncertainties (see Fig. 4 for the size of the Brγ line-emitting region, and Fig. 3 for the on-sky displacement across the emission line). Based on the simulations of interferometric signatures for nonaxisymmetrically accreting magnetospheres as a function of rotation phase (see Fig. 5 in Tessore et al. 2023), we would have expected to detect an orientation change of the on-sky displacement across the Brγ line in an interval of 1 day as the star (and the accretion funnel with it) rotated by 2 π/7.3 rad. As the orientation of the photocenter shift remains clearly the same between the two nights, we favor a significant contribution from a more extended, axisymmetric component; likely a variable disk wind, which could be the dominating origin of the Brγ line. Such a wind can be relatively axisymmetric, preserving the photocenters and size of the region, and varies on the scale of a few days in terms of flux, if indeed it is driven by gas dynamics at the magnetosphere–disk boundary where the Keplerian period is similar to the rotation period of the star (see e.g. the models of Knigge et al. 1995; Lima et al. 2010; Zanni & Ferreira 2013).
4.5. The larger-scale environment of S CrA N
Previous large-scale observations of the S CrA system indicate the presence of structures at spatial scales ranging from 10 au to 10 000 au, which we can attempt to link to those detected in the innermost regions of S CrA N as depicted in Fig. 6. Regarding the dust distribution, SPHERE images in polarized light obtained by Zhang et al. (2023) reveal a complex environment around the S CrA system with fragmented structures, such as spirals in the disk surrounding S CrA N at a few tens of au, and streamers around the secondary component (see top pannel of Fig. 6). Due to the high complexity of the environment, the precise morphology of the disk around S CrA N is hard to constrain from these observations, and dust continuum emission is unresolved with ALMA Cazzoletti et al. (2019), which would have been helpful in order to bridge the inner and outer scales. While the polarized intensity images suggest the near side of the outer disk is towards east (Zhang et al. 2023), our continuum best-fit model leads to a brighter and thus a far side in the east direction. Should the outer disk’s orientation from SPHERE be confirmed, this would indicate a misalignment between the inner and the outer parts, which could lead to shadows in the disk that have not been detected so far. In the SPHERE images, bright emission can be distinguished as a polar departure from S CrA N in the east direction (see dotted cone in the top panel of Fig. 6). If real, this structure is remarkably well aligned toward HH 82, and could be interpreted as an outflow from the large-scale disk; similarly, the streamer from S CrA S in the southeast direction could be connected to HH 729, both Herbig-Haro objects being located at ∼20 000 au (Reipurth & Graham 1988; Kumar et al. 2011; Peterson et al. 2011). Nevertheless, the PAs of these Herbig-Haro objects (∼95° and ∼115°) do not allow us to connect them to any of the phenomena discussed in our work so far. In the same respect, regarding the gas distribution, ALMA observations exhibit a complex 12CO emission at a scale of a few thousand au with different kinematic features (see Fig. 6-bottom; Gupta et al. 2023), and a blueshifted (by a few km/s) structure oriented toward HH 82, which do not seem to be connected with our observations. However the complex environment of the S CrA system makes the existence of all these structures highly speculative, and new observations at higher resolution and/or intermediate scales (e.g. with VLTI/MATISSE) are required to better constrain the morphology of this complex system.
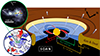 |
Fig. 6. S CrA N at different scales. Right: Representation of the star–disk interaction region (not to scale), with the characteristic sizes derived in this work. The obliquity of the magnetosphere is simply illustrative as no consolidated value exists. Top-left: SPHERE polarized intensity image from Zhang et al. (2023), and the directions toward the HH objects associated to S CrA. We also reported the PA of the dusty disk measured from the K-band continuum and the orientation of photocenter shifts as yellow, red and blue cones, respectively. Dashed cones highlight the suggested outflow emission (see text). Bottom-left: ALMA 12CO(2–1) first moment map from Gupta et al. (2023). The cone is reported from the SPHERE observations, and the HH82 direction is indicated. Both images have been rotated to have the same orientation as the sketch, where the north and east directions are shown. |
5. Conclusions
In the present work, we used two successive VLTI/GRAVITY near-infrared interferometric observations with the UTs to constrain the innermost regions of the strong accretor S CrA N. For the first time, we managed to detect accurate interferometric differential signals in the Brγ-emitting line with a cadence of about 10 minutes. We summarize our findings as follows:
-
The K band continuum emission is reproduced with a first-order azimuthally modulated ring with a half-light radius of 0.24 au (20 R*), an inclination of ∼30°, a position angle of ∼150°. The location of the modulation of the brightness suggests the near side of the inner disk in the southwest direction. The half-flux radius appears to be variable over a few years, with previous determinations of 0.13–0.15 au in the K band.
-
We find that the sublimation radius should be at least twice closer than the half-light radius of the continuum we measure. This suggests that magnetospheric accretion might be an important mechanism responsible for dust sublimation on top of stellar luminosity. Beyond our simple approach of a single spot, the contribution of an extended magnetosphere and a hot inner viscous disk can also be envisioned, particularly for such a strong accretion rate (̇Macc ∼ 10−7 M⊙.yr−1).
-
A compact region is found to be responsible for the Brγ emission (∼0.06 au or 5–6 R*). This emission presumably comes from both magnetospheric accretion and disk winds, based on the comparison of its size to the magnetic truncation radius. The on-sky displacements across the spectral channels of the Brγ line appear to be misaligned with respect to the dusty disk by ∼45° and extend up to 0.023 au. This misalignement suggests that these photocenter shifts trace polar processes as magnetospheric accretion funnels and/or outflows. This is in line with the multitude of evidence for disk winds in this source, notably spectroscopic signatures, and with the tilted dipolar magnetic field topology reconstructed in a previous work.
-
We find this object to be in line with other strong accretors from the GRAVITY sample with an average sublimation radius (0.1–0.2 au), and a Brγ-emitting region larger than the corotation radius, suggesting that this emission originates from a combination of magnetospheric accretion and disk winds.
-
While the flux of the Brγ line moderately decreases from one night to the next by 13%, the interferometric quantities remain almost unchanged, which favors a dominant contribution from an axisymmetric component like a disk wind.
-
We were not able to find any clear connection between the inner scales we probed with GRAVITY and the speculative complex dust and gas structures detected with SPHERE and ALMA.
These results demonstrate the power of near-infrared optical long-baseline interferometry in providing unique inputs for advanced modeling of acretion–ejection models and for probing the innermost regions of the young stellar systems by combining spatial, spectral, and temporal resolutions.
Available at www.jmmc.fr/searchcal
The code in its original version, along with tutorials and full license can be found at https://github.com/amerand/PMOIRED
Acknowledgments
This work was supported by CNRS/INSU, by the ”Programme National de Physique Stellaire” (PNPS) of CNRS/INSU co-funded by CEA and CNES, and by Action Spécifique ASHRA of CNRS/INSU co-funded by CNES. This work has been supported by the French National Research Agency (ANR) in the framework of the “Investissements d’Avenir” program (ANR-15-IDEX-02) and in the framework of the “ANR-23-EDIR-0001-01” project. M.B. received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (PROTOPLANETS, grant agreement No. 101002188). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agree ment No742095;SPIDI: Star-Planets-Inner Disk-Interactions, http://www.spidi-eu.org). A.C.G. acknowledges support from PRIN-MUR 2022 20228JPA3A “The path to star and planet formation in the JWST era (PATH)” funded by NextGeneration EU and by INAF-GoG 2022 “NIR-dark Accretion Outbursts in Massive Young stellar objects (NAOMY)” and Large Grant INAF 2022 “YSOs Outflows, Disks and Accretion: towards a global framework for the evolution of planet forming systems (YODA)”. J.S.-B. acknowledges the support received from the UNAM PAPIIT project IA 105023 This research has made use of the Jean-Marie Mariotti Center Aspro (http://www.jmmc.fr/aspro) and SearchCal (http://www.jmmc.fr/searchcal) services co-developped by LAGRANGE and IPAG, and of CDS Astronomical Databases SIMBAD and VIZIER (http://cdsweb.u-strasbg.fr/). Finally, we thank an anonymous referee for fruitful exchanges leading to the present article.
References
- Banzatti, A., Abernathy, K. M., Brittain, S., et al. 2022, AJ, 163, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, J. P., & Segransan, D. 2007, New Astron. Rev., 51, 576 [CrossRef] [Google Scholar]
- Bonneau, D., Delfosse, X., Mourard, D., et al. 2011, A&A, 535, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 479 [Google Scholar]
- Bouvier, J., Alecian, E., Alencar, S. H. P., et al. 2020a, A&A, 643, A99 [EDP Sciences] [Google Scholar]
- Bouvier, J., Perraut, K., Le Bouquin, J. B., et al. 2020b, A&A, 636, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carmona, A., van den Ancker, M. E., & Henning, T. 2007, A&A, 464, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoletti, P., Manara, C. F., Liu, H. B., et al. 2019, A&A, 626, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, S1 [Google Scholar]
- Dodin, A. V., & Lamzin, S. A. 2012, Astron. Lett., 38, 649 [Google Scholar]
- Fischer, W. J., Hillenbrand, L. A., Herczeg, G. J., et al. 2023, ASP Conf. Ser., 534, 355 [NASA ADS] [Google Scholar]
- Gahm, G. F., Petrov, P. P., Tambovsteva, L. V., et al. 2018, A&A, 614, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grant, S. L., Bettoni, G., Banzatti, A., et al. 2024, A&A, 684, A213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2017a, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Garcia Lopez, R., et al.) 2017b, A&A, 608, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Perraut, K., et al.) 2019, A&A, 632, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Garcia Lopez, R., et al.) 2020, Nature, 584, 547 [Google Scholar]
- GRAVITY Collaboration (Perraut, K., et al.) 2021, A&A, 655, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Soulain, A., et al.) 2023a, A&A, 674, A203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Wojtczak, J. A., et al.) 2023b, A&A, 669, A59 [Google Scholar]
- Gupta, A., Miotello, A., Manara, C. F., et al. 2023, A&A, 670, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [Google Scholar]
- Joy, A. H. 1945, ApJ, 102, 168 [Google Scholar]
- Knigge, C., Woods, J. A., & Drew, J. E. 1995, MNRAS, 273, 225 [NASA ADS] [Google Scholar]
- Krautter, J., Appenzeller, I., & Jankovics, I. 1990, A&A, 236, 416 [NASA ADS] [Google Scholar]
- Kumar, M. S. N., Sharma, S., Davis, C. J., Borissova, J., & Grave, J. M. C. 2011, A&A, 533, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lachaume, R. 2003, A&A, 400, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Dembet, R., Abuter, R., et al. 2019, A&A, 624, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lapeyrere, V., Kervella, P., Lacour, S., et al. 2014, Proc. SPIE, 9146, 91462D [Google Scholar]
- Lazareff, B., Berger, J. P., Kluska, J., et al. 2017, A&A, 599, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lima, G. H. R. A., Alencar, S. H. P., Calvet, N., Hartmann, L., & Muzerolle, J. 2010, A&A, 522, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., de Wit, W. J., Oudmaijer, R. D., et al. 2015, MNRAS, 453, 2126 [CrossRef] [Google Scholar]
- Mérand, A. 2022, SPIE Conf. Ser., 12183, 121831N [Google Scholar]
- Monnier, J. D., & Millan-Gabet, R. 2002, ApJ, 579, 694 [Google Scholar]
- Nowacki, H., Alecian, E., Perraut, K., et al. 2023, A&A, 678, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pantolmos, G., Zanni, C., & Bouvier, J. 2020, A&A, 643, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, D. E., Caratti o Garatti, A., Bourke, T. L., et al. 2011, ApJS, 194, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Petrov, P. P., Gahm, G. F., Stempels, H. C., Walter, F. M., & Artemenko, S. A. 2011, A&A, 535, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, P. P., Gahm, G. F., Herczeg, G. J., Stempels, H. C., & Walter, F. M. 2014, A&A, 568, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Ménard, F., Berger, J. P., Benisty, M., & Malbet, F. 2008, ApJ, 673, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Pittman, C. V., Espaillat, C. C., Robinson, C. E., et al. 2022, AJ, 164, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., & Smette, A. 2011, ApJ, 733, 84 [Google Scholar]
- Prato, L., Greene, T. P., & Simon, M. 2003, ApJ, 584, 853 [Google Scholar]
- Reipurth, B., & Graham, J. A. 1988, A&A, 202, 219 [NASA ADS] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [Google Scholar]
- Rucinski, S. M., Matthews, J. M., Kuschnig, R., et al. 2008, MNRAS, 391, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Henning, T., Linz, H., et al. 2013, A&A, 551, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siwak, M., Rucinski, S. M., Matthews, J. M., et al. 2011, MNRAS, 410, 2725 [NASA ADS] [CrossRef] [Google Scholar]
- Siwak, M., Ogloza, W., Rucinski, S. M., et al. 2016, MNRAS, 456, 3972 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, K., Prato, L., Edwards, S., Avilez, I., & Schaefer, G. H. 2019, ApJ, 884, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Tessore, B., Soulain, A., Pantolmos, G., et al. 2023, A&A, 671, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varga, J., Ábrahám, P., Chen, L., et al. 2018, A&A, 617, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Bouvier, J., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vural, J., Kreplin, A., Kraus, S., et al. 2012, A&A, 543, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, M. F. 1972, ApJ, 175, 89 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. J., & Basri, G. 2003, ApJ, 582, 1109 [Google Scholar]
- Zanni, C., & Ferreira, J. 2013, A&A, 550, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y., Ginski, C., Huang, J., et al. 2023, A&A, 672, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Chromatic effects
The calibrator HD 186419 was observed on both nights at similar observing slots (i.e., at UT04:41 and UT04:45). As expected, the FT visibilities squared are identical for both nights. HD 186419 appears to be almost unresolved (with visibilities squared V2 around 0.90-0.98) and could be used to estimate the instrumental transfer function. Strikingly, while the FT tracked and locked the fringes during the whole observing sequences, the SC data appear different between the two nights (see the relative variation of visibility squared between the two epochs V2(20)/V2(19)−1) in Fig. A.1). Except for the longest baseline U1-U4, the visibility squared of August, 20 exhibits more pronounced curvatures with wavelength, and smaller values notably at the edges of the spectral range. The data also show an offset in visibility squared for the shortest baselines. Such behaviours could be explained by fringe jumps that affect more the wavelengths that are further away from the center of the spectral band because the spectral slope of the fringes is larger at the edges. The discrepancies appear also to be larger when UT2 and UT3 are involved, suggesting a worse performance of the adaptive optics and/or higher vibration effects on these telescopes specifically. Because such an effect might affect the absolute calibration of the visibility, we only used the data from the second night to constrain the dusty inner ring. This effect does not impact the differential observables across the Brγ line.
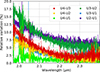 |
Fig. A.1. Variation of squared visibility of the calibrator HD 186419 between our two epochs, as a function of wavelength, while colors code for the baseline. |
Appendix B: Flux normalization with PMOIRED
 |
Fig. B.1. An example of S CrA N spectrum normalization with the PMOIRED tools (see text for details) on August, 20th. |
PMOIRED is a modeling tool particularly suited for GRAVITY data. Here, we highlight the use we made of the tellcorr Python3 library for flux normalization and wavelength calibration in the case of S CrA N. This process has been shown in one of the very handful examples of PMOIRED available online2.
The library includes a 1D grid of atmospheric models. Its only parameter is the precipitable water vapour (PWV). The code performs a fit of the continuum spectrum over the whole K band. A telluric transmission function is inferred, along with a continuum model which is obtained thanks to a spline model of 35 nodes (for the high resolution mode of GRAVITY) fitted to the observed spectrum. Thanks to the telluric model obtained, a refined spectral dispersion of the instrument can be estimated, which we used for the present work. The normalized spectrum is finally obtained by dividing the observed spectrum by the continuum and the telluric model. This operation has been performed on all the spectra of each night. We illustrate the different aforementioned quantities in Fig. B.1, and give the derived PWV in Table B.1.
Precipitable water vapor (PWV) of the atmospheric models that best reproduce the GRAVITY K band continuum for all spectra.
Appendix C: A fully resolved halo in Brγ
Best-fit parameters with 1σ error bars for the Halo + Gaussian disk model of the Brγ pure-line visibilities. The PAs are from north to east.
Prior to any fitting procedure, a cautious analysis of the pure-line visibility curves reveals that a simple Gaussian disk model is not suited to reproduce these data. The low frequency values are too low, and the high frequency values decrease too slowly with frequency. Both effects can be addressed with the addition of a fully resolved halo to the model. to illustrate the lacks of the simple Gaussian model, we show in Table and Fig. C.1 the results obtained when fitting the Brγ pure line visibilities with such a model. We can see that the residuals are much more dispersed (up to 5σ) than with a halo (see Fig. 5). We also see systematic deviations of the model from the data. These deviations follow a clear trend for each baseline, regardless of the exact parameters obtained, suggesting that the inclined Gaussian disk model is not completely representative of the inner regions flux distribution. This claim is strengthened by the reduced χ2, which are a factor 2 to 12 higher than when considering a halo in the model (see Table C.1).
The implementation of a fully resolved halo requires to express the Brγ pure line visibilities Vline as composite (just like for the continuum analysis) with two contributors : a disk and a halo. When considering FD and FH, the disk and halo individual fluxes and VD and VH their respective visibility :
By definition, VH = 0, while the visibility of the disk VD is given in, e.g., Berger & Segransan (2007) :
With Θ the Gaussian HWHM. And since 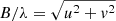 :
:
We identify the contribution of the disk with respect to the total flux 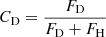 which can be expressed as a function of the contribution of the halo relative to the total flux
which can be expressed as a function of the contribution of the halo relative to the total flux 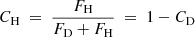 , for the sake of discussion. Hence the expression used in our modeling of the Brγ differential data (see main text) :
, for the sake of discussion. Hence the expression used in our modeling of the Brγ differential data (see main text) :
The main effect we observe from this modeling is a decrease by a factor ∼1.5 of the size of the disk when putting ∼9% of the total flux into an unresolved halo.
All Tables
Best-fit parameters with 1σ error bars for the Halo + Gaussian disk model of the Brγ pure-line visibilities.
Precipitable water vapor (PWV) of the atmospheric models that best reproduce the GRAVITY K band continuum for all spectra.
Best-fit parameters with 1σ error bars for the Halo + Gaussian disk model of the Brγ pure-line visibilities. The PAs are from north to east.
All Figures
 |
Fig. 1. GRAVITY observations of S CrA N on 2022 August 20: K-band continuum visibilities squared (left) and closure phases (center) as a function of baseline (gray symbols) superimposed with the best-fit ring model (right). The modeled quantities are depicted in colors matching the (u-v) plane coverage shown in the inset on the right. The lower panels show the residuals of the model in units of σ. Shaded bands highlight 1-, 3-, and 5σ levels. |
| In the text | |
 |
Fig. 2. Brγ differential interferometric observables of S CrA N: Squared differential visibilities (left); differential phases (middle); u-v plane coverage (upper-right); line-to-continuum flux ratio in the reference frame of the star, LSR- and tellurics-corrected (lower-right). Each color used in the u-v coverage plot corresponds to an interferometric baseline and is consistent over all panels. For the interferometric observables, the plots include the quantities for each frame (solid lines) and the median for August 19 (circles) and for August 20 (squares). Uncertainties are given in all plots (vertical bars), and are smaller than the symbol if not visible. Gray shaded regions correspond to the velocities that are not considered for our Brγ line analysis (see text for details). |
| In the text | |
 |
Fig. 3. Asymmetry of the Brγ-emitting region of S CrA N. Left : Pure-line differential phases. The pure line differential phases are depicted by blue-to-red color coded symbols for August 19 (circles) and August 20 (squares), while the observed phases for each individual observation (similar to Fig. 2) are depicted in solid lines, with their color corresponding to their baseline. Right : On-sky photocenter shifts with respect to the continuum photocenter (in (0, 0) as a function of velocity (coded from blue to red colors). The light-yellow cones correspond to the uncertainties on the major axis orientation of the inner dusty disk. The background symbols are the displacements obtained from individual files. |
| In the text | |
 |
Fig. 4. Characteristic sizes of the Brγ-emitting region of S CrA N as a function of velocity (coded from blue to red colors) for August 19 (circles) and August 20 (squares). The red, green and blue areas correspond to the stellar, truncation, and corotation radii, respectively. The dashed gold line marks one-quarter of the half-light radius derived for the inner dusty ring model for the sake of comparison. Colored symbols with gray error bars in the background correspond to the sizes derived from individual files. The distance used is 154.2 pc. |
| In the text | |
 |
Fig. 5. Pure-line visibility fits for August 19th (left column) and 20th (right column). Each row consists of two subplots : The top one includes the pure-line visibilities squared and their 1σ uncertainty observed at a given velocity (mentioned in the panel) superimposed with the corresponding model including a Gaussian disk and a halo. The bottom one illustrates the residuals of the model in units of σ. Three shades of gray mark the 1-,3-, and 5σ levels. The color of the data points corresponds to the baseline. |
| In the text | |
 |
Fig. 6. S CrA N at different scales. Right: Representation of the star–disk interaction region (not to scale), with the characteristic sizes derived in this work. The obliquity of the magnetosphere is simply illustrative as no consolidated value exists. Top-left: SPHERE polarized intensity image from Zhang et al. (2023), and the directions toward the HH objects associated to S CrA. We also reported the PA of the dusty disk measured from the K-band continuum and the orientation of photocenter shifts as yellow, red and blue cones, respectively. Dashed cones highlight the suggested outflow emission (see text). Bottom-left: ALMA 12CO(2–1) first moment map from Gupta et al. (2023). The cone is reported from the SPHERE observations, and the HH82 direction is indicated. Both images have been rotated to have the same orientation as the sketch, where the north and east directions are shown. |
| In the text | |
 |
Fig. A.1. Variation of squared visibility of the calibrator HD 186419 between our two epochs, as a function of wavelength, while colors code for the baseline. |
| In the text | |
 |
Fig. B.1. An example of S CrA N spectrum normalization with the PMOIRED tools (see text for details) on August, 20th. |
| In the text | |
 |
Fig. C.1. Same as Fig 5, but with the halo’s contribution forced to 0%. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.