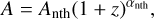| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A188 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202451055 | |
| Published online | 08 October 2024 | |
Baryonification extended to thermal Sunyaev Zel’dovich
1
Institut für Astrophysik (DAP), Universität Zürich,
Winterthurerstrasse 190,
8057
Zurich,
Switzerland
2
Donostia International Physics Center (DIPC),
Paseo Manuel de Lardizabal, 4,
20018,
Donostia-San Sebastián,
Gipuzkoa,
Spain
3
IKERBASQUE, Basque Foundation for Science,
48013,
Bilbao,
Spain
★ Corresponding author; giovanni.arico@uzh.ch
Received:
10
June
2024
Accepted:
2
September
2024
Baryonification algorithms model the impact of galaxy formation and feedback on the matter field in gravity-only simulations by adopting physically motivated parametric prescriptions. In this paper, we extend these models to describe gas temperature and pressure, allowing for a self-consistent modelling of the thermal Sunyaev-Zel’dovich effect, weak gravitational lensing, and their cross-correlation, down to small scales. We validate our approach by showing that it can simultaneously reproduce the electron pressure, gas, stellar, and dark matter power spectra as measured in all BAHAMAS hydrodynamical simulations. Specifically, with only two additional free parameters, we can fit the electron pressure auto- and cross-power spectra at 10% while reproducing the suppression in the matter power spectrum induced by baryons at the per cent level, for different active galactic nuclei (AGN) feedback strengths in BAHAMAS. Furthermore, we reproduce BAHAMAS convergence and thermal Sunyaev Zel’dovich angular power spectra within 1% and 10% accuracy, respectively, down to ℓ = 5000. When used jointly with cosmological rescaling algorithms, the baryonification presented here allows for a fast and accurate exploration of cosmological and astrophysical scenarios. Therefore, it can be employed to create mock catalogues, lightcones, and large training sets for emulators aimed at interpreting forthcoming multi-wavelength observations of the large-scale structure of the Universe.
Key words: galaxies: clusters: intracluster medium / cosmic background radiation / cosmological parameters / large-scale structure of Universe
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The increasing precision of modern large-scale structure (LSS) surveys has pushed the statistical errors of the measurements below the level of uncertainties of our theoretical models. To fully exploit the potential of current and future surveys, an overall improvement in the accuracy of our models as well as an understanding of systematic errors is required.
For instance, in the analysis of weak lensing (WL) data, a large fraction of data cannot be used because of a dominant systematic theoretical error: the unknown effects of baryonic processes on small scales (e.g. Krause et al. 2021; Secco et al. 2022; Amon et al. 2022). Recently, baryonification algorithms (Schneider & Teyssier 2015; Schneider et al. 2019; Aricò et al. 2020, 2021a) have been used to flexibly model the relevant baryonic processes and to robustly infer the cosmological parameters (Schneider et al. 2022; Aricò et al. 2023; García-García et al. 2024). However, the marginalisation over several unconstrained free baryonic parameters degrades the cosmological information that can be extracted, and it might introduce prior volume effects in the analyses. In this regard, the simultaneous analysis of multiple observables and their cross-correlation is particularly interesting because it allows the removal of uncorrelated systematics and the breaking of parameter degeneracies.
By informing the baryonification with external data sets, we can better constrain the baryonic parameter space and break degeneracies with cosmology. This approach was pursued, for example by Schneider et al. (2022) and Bigwood et al. (2024), where the authors combined cosmic shear and kinematic Sunyaev-Zel’dovich (kSZ) data, plus the gas fraction from X-ray data in the case of Schneider et al. (2022). Grandis et al. (2024), instead, used a combination of X-ray gas fractions and X-ray gas profiles to predict the suppression in the matter power spectrum caused by baryons.
Another possible avenue is the exploitation of weak-lensing cross-correlations with thermal Sunyaev-Zel’dovich (tSZ). These two probes are highly complementary; the first one provides the integral along the line of sight of matter, and the second one provides the electron pressure. Baryonic physics impacts the two observables with different angular and redshift dependencies. Various analyses of the cross-correlation between WL and tSZ were carried out in the last decade (Van Waerbeke et al. 2014; Hojjati et al. 2017; Osato et al. 2020; Gatti et al. 2022; Pandey et al. 2022; Tröster et al. 2022). Despite the improvements in theoretical modelling, the limiting factors are the lack of tight priors on the nuisance parameters and the difficulties in modelling the non-linearities and baryonic physics.
Currently, the most self-consistent predictions of the (nonlinear) WL × tSZ cross-correlations come from cosmological hydrodynamical simulations. These simulations simultaneously follow the gravitational collapse of structure and the evolution of gas thermodynamics, using numerical prescription to implement galaxy formation and astrophysical feedback. However, given their computational costs, reaching the required volumes and resolutions is difficult. Another complication is that we need predictions covering a large parameter space in cosmology and astrophysics. Modern supercomputers and codes are filling up this gap, increasingly larger simulations can be run, and the calibration of the so-called subgrid parameters is improving as well (Schaye et al. 2010; Le Brun et al. 2014; McCarthy et al. 2017; van Daalen et al. 2020; Salcido et al. 2023; Hernández-Aguayo et al. 2023; Ferlito et al. 2023; Schaye et al. 2023; Kugel et al. 2023), but it is still not sufficient for full Bayesian analyses. Moreover, it is not guaranteed that the physical models implemented in these simulations are correct. Alternatively to hydrodynamical simulations, one can extend the halo model to model baryonic components empirically (e.g. Mead et al. 2020; Pandey et al. 2024), or paste baryons into N-body simulations, either with machine learning (e.g. Tröster et al. 2019) or with analytical profiles (e.g. Osato & Nagai 2023).
For this study, we took a different approach, building on the baryon correction model (BCM, also known as baryonifi-cation, Schneider & Teyssier 2015; Schneider et al. 2019; Aricò et al. 2020, 2021b). This algorithm perturbs the mass field of N-body simulations taking into account the effect of several baryonic components. Taking advantage of the baryonification framework, which provides the gas density profiles of haloes in the N-body simulation, we computed the expected temperature and pressure profiles analytically, under the assumptions of a polytropic equation of state for the gas. As a result, we can provide accurate modelling of both dark matter and baryonic fields up to small scales, and allow for joint predictions of WL and tSZ. We validated our approach by comparing it against a state-of-the-art hydrodynamical simulation, BAHAMAS (McCarthy et al. 2017, 2018).
Our baryonification approach inherits the benefits of the models presented in Mead et al. (2020); Pandey et al. (2024), and Osato & Nagai (2023), and addresses some of their shortcomings. For example, it does not lack accuracy in the transition between one-halo and two-halo terms as the halo model, and does not rely on the assumption of linear bias. It also ensures a better consistency between mass and pressure profiles than the baryon pasting algorithm. Additionally, our method does not require hydrodynamical simulations for calibration and is self-consistent at the field level, and thus it can be used for predicting higher-order statistics.
This paper is structured as follows: in Sect. 2 we summarise the baryon correction model and show how to extend it to thermodynamical properties; in Sect. 3 we explain how to predict the tSZ from a baryonified simulation; in Sect. 4 we compare our results against the BAHAMAS hydrodynamical simulation; in Sect. 5 we draw our conclusions.
2 Modelling
In this section, we briefly recap the baryonification, and explain the steps needed to extend the algorithm to predict thermodynamical properties.
2.1 Baryonification
Baryonification algorithms displace the particles in N-body simulations to account for the effects of stars and gas on dark matter (Schneider & Teyssier 2015). For each halo of an N-body simulation snapshot, the density profiles of several baryonic and dark matter components are analytically calculated, and then summed to obtain a total ‘baryonified’ density profile. From the difference between this and the original ‘gravity-only’ halo profile, one can work out the displacement field that, when applied to the halo particles, corrects for baryonic effects.
With slightly different flavours, the baryonification has been proven to be accurate in modelling the two-point (Schneider & Teyssier 2015; Schneider et al. 2019, 2020; Aricò et al. 2020, 2021a; Giri & Schneider 2021) and three-point (Aricò et al. 2021a) statistics of the cosmic matter field, WL peaks (Weiss et al. 2019; Lu & Haiman 2021; Lee et al. 2023), galaxy-galaxy lensing (Contreras et al. 2023; Chaves-Montero et al. 2023), X-ray gas fraction, and density profiles (Grandis et al. 2024), and it was applied to cosmic shear data (Schneider et al. 2022; Chen et al. 2023; Aricò et al. 2023; García-García et al. 2024; Bigwood et al. 2024), lensing maps (Lu et al. 2022; Fluri et al. 2022; Kacprzak et al. 2023; Lu et al. 2023; Gatti et al. 2024), and cross-correlations of dark matter haloes with cosmic dispersion measures (Shirasaki et al. 2022).
The model we employed for this study is based on Aricò et al. (2020, 2021b), and features up to seven free parameters:
Mc is defined as the characteristic halo mass at which half of the gas is expelled by baryonic feedback;
β regulates the slope of the retained gas fraction as a function of its host halo mass;
η determines the maximum distance reached by the ejected gas as a function of the halo escape radius;
M1,z0,cen is the characteristic halo mass hosting a central galaxy with a mass fraction of 0.023 at ɀ = 0; and
θinn, θout, and Minn parameterise the gas density profiles, as expressed in Eqs. (2) and (3).
2.2 Multiple cosmic fields
A standard baryonification only predicts the overall cosmic density field, without specifying the individual distributions of gas and stars.
In Appendix B of Aricò et al. (2020), it was proposed to subsample the matter field, by tagging each particle as part of a given baryonic component and reassigning its mass. In this way, it is possible to end up with separate cosmic density fields for dark matter, gas, and stars.
We took a similar approach with minor modifications. The methodology proposed in Aricò et al. (2020) has a relatively high level of discreteness noise, caused by the subsampling of the initial number of particles. In particular, the more baryonic components that are used, the fewer particles available for sampling. We avoided this problem by splitting each particle in the baryonified simulation into Nc particles, where Nc is the number of BCM components considered. These Nc particles have the same positions as the parent particle, and their masses sum up to the parent particle’s original mass.
To do this, we took the differential cumulative halo mass profiles of the BCM components 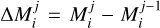 , and the cumulative final mass profile
, and the cumulative final mass profile 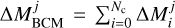 , where the index i runs over the baryonic components and the index over the halo radial bins. The mass of each particle inside r200 (prior to the BCM displacement), for a given component and radial bin, is the following:
, where the index i runs over the baryonic components and the index over the halo radial bins. The mass of each particle inside r200 (prior to the BCM displacement), for a given component and radial bin, is the following:
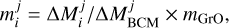 (1)
(1)
where mGrO is the original mass of particles in a gravity-only simulation. One can decide to create a different cosmic field for each individual BCM, or to group some components together (e.g. a component summing bound and ejected gas, or one summing central and satellite galaxies). For the particles outside r200 (prior to the BCM displacement), we simply fixed the mass of dark matter particles as mDM = (1 – Ωb/Ωm) × mGrO, and the one of the gas as mgas = Ωb/Ωm × mGrO
In Fig. 1, we show a visualisation of the cosmic density field for dark matter, galaxies, as well as bound and ejected gas, as generated by baryonifying one of the simulations described in Aricò et al. (2020) with the algorithm presented here. Since, in this case, we have opted for strong active galactic nuclei (AGN) feedback, only the most massive haloes in the simulation have retained a gas reservoir, while small haloes have their gas ejected into the intracluster medium, tracing the LSS fairly well. Galaxies have been placed at the centres of their host haloes, and their size and mass depend on the masses of the respective host haloes, according to the relations detailed in Aricò et al. (2020).
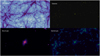 |
Fig. 1 Cosmic density fields obtained by applying our baryonification to an N-body simulation. Specifically, the total matter density field is decomposed into dark matter (top left), galaxies (top right), bound gas in hydrostatic equilibrium (bottom left), and gas ejected by feedback processes (bottom right). The BCM parameters have been set to values that generate strong AGN feedback. |
2.3 Thermodynamical profiles
To model the thermodynamical state of the gas, we first parameterised pressure and temperature profiles in haloes, and then assigned a given pressure and temperature to each particle, according to its radial distance from the halo centres.
We started from the analytical gas density profile employed in Aricò et al. (2021b),
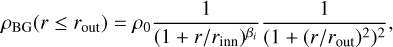 (2)
(2)
where ρ0 is a normalisation factor, and rinn and rout define where the slope changes at small and large radii, respectively. We define the inner radius rinn = θinn × r200 and outer radius rout = θout × r200, beyond which the gas profile perfectly traces the dark matter, that is to say, it is described by a Navarro–Frenk–White (NFW) profile (Navarro et al. 1997). The gas inner slope depends on the halo mass as
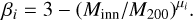 (3)
(3)
We set θinn, θ0ut, Minn, and µi as free parameters.
Then, we assumed a polytropic equation of state of the gas, that is, that the total gas pressure follows 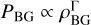 , where Γ is the polytropic index. Specifically, we set
, where Γ is the polytropic index. Specifically, we set
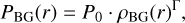 (4)
(4)
with G being the gravitational constant and ρs the dark matter density at the NFW scale radius rs. For this work, we modelled the polytropic index as
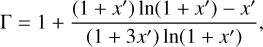 (6)
(6)
where x′ = c × θ0ut and c is the halo concentration. This parametrisation follows the works of Komatsu & Seljak (2001); Bulbul et al. (2010); Martizzi et al. (2013); Schneider & Teyssier (2015), and Aricò et al. (2020), which assume a gas in hydrostatic equilibrium and polytropic equation of state. By additionally matching the slope of the gas with that of dark matter on large scales, one can avoid having free parameters. We allowed for more freedom in the profiles to reproduce the results from hydrodynamical simulations more closely across a wide range of halo masses (see e.g. Aricò et al. 2021b).
2.4 Non-thermal pressure
Gas within haloes is not solely supported by thermal pressure. Hydrodynamical simulations and (indirect) observations have shown that a considerable amount of non-thermal pressure is expected (see e.g. Shaw et al. 2010; Hurier & Angulo 2018; Akino et al. 2022). Taking the so-called hydrostatic mass bias into account, it is possible to reconcile the total mass of the clusters estimated with ‘direct’ measurements (i.e. weak lensing) with those inferred assuming hydrostatic equilibrium from X-ray or microwave observations, for example. The hydrostatic mass bias is related to the non-thermal pressure support not accounted for, arguably produced by turbulence, cosmic rays, and magnetic fields (Green et al. 2020; Ettori & Eckert 2022). The non-thermal contribution can be as high as 50% of the total pressure in the outskirts of the haloes, and therefore impacts tSZ predictions significantly, which are only sensitive to thermal pressure.
Shaw et al. (2010) showed with simulated clusters that the total pressure profiles are expected to follow a polytropic equation of state better than the thermal pressure profiles (however, see e.g. Ghirardini et al. 2019, for observational thermal profiles well described by a polytrope). In particular, Green et al. (2020) studied the non-thermal contribution using analytical total pressure profiles (Komatsu & Seljak 2001), a non-thermal contribution driven by halo mass assembly (Shi & Komatsu 2014), and models for the mass assembly histories (Parkinson et al. 2008; van den Bosch et al. 2014). They find that the non-thermal term is roughly universal when expressed as a function of peak height, and they compare their results against hydrodynamical simulations finding a good agreement.
For this study, we employed Eq. (4) to model the total pressure and then applied the fitting function by Green et al. (2020) to remove the non-thermal contribution. Thus, the thermal pressure profile is
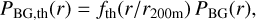 (7)
(7)
with the radii x = r/r200 m and peak height v = v200 m being referred to spheres where the mean density is 200 times larger than the mean matter density of the universe. The best-fitting values found in Green et al. (2020) are A = 0.495, B = 0.719, C = 1.417, D = -0.166, E = 0.265, and F = −2.116.
with Anth and αnth being free parameters to model possible residual dependences on the amplitude and redshift of the nonthermal contribution, as well as possible departures from the normalisation of the mass-pressure relation assumed in Eq. (5).
2.5 Temperature
By imposing the ideal gas law, the temperature profile is
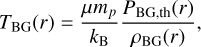 (10)
(10)
where mp is the proton mass and kB is the Boltzmann constant. For simplicity, we assumed a fully ionised gas composed of X = 76% hydrogen and Y = 24% helium. Thus, in our case, the mean molecular weight is µ = 4/(5X + 3) ≈ 0.59.
In Fig. 2, we show an example of the density, pressure, and temperature profiles in haloes with a mass comprised between 1013 h−1M⊙ and 1015 h−1 M⊙. In this case, we set the best-fitting parameters to the matter power spectrum of the BAHAMAS simulation (McCarthy et al. 2017). For reference, we over-plotted the virial temperature and the ‘universal’ pressure profiles from Arnaud et al. (2010), which have been fitted to massive galaxy clusters of M ≥ 1014 h−1 M⊙. We observed that, in this specific case, the virial temperature and universal profiles are fairly close to our BCM profiles, especially for massive haloes. We stress that the free parameters of our model impact both the shape and normalisation of the thermodynamical profiles, and can be, in principle, fit to profiles from either simulations or observations.
 |
Fig. 2 Density (upper panel), pressure (central panel), and temperature (lower panel) profiles of the bound gas for haloes in the mass range 1013–1015 h−1 M⊙, according to the legend. We show both total and thermal pressure, with solid and dotted lines, respectively. For visual comparison, we show the ‘universal’ pressure profiles from Arnaud et al. (2010) and the virial temperature with dashed liens. We stress that the BCM parameters allow for changes in the shape and normalisation of the profiles, and, in this case, we did not tune them to reproduce any specific profile. |
2.6 Particle assignment
Once the profiles were computed, we assigned a given temperature and pressure to each particle belonging to the halo as a function of its distance from the host halo centre, and iterated for all the haloes in a simulation. Operationally, we stored only the temperature of particles to save memory since the thermal pressure was trivially obtained through the ideal gas law (Eq. (10)).
For simplicity, we assumed that the gas ejected from haloes by feedback has the same temperature profile as the bound gas, that is, it thermalises instantaneously. Alternatively, one could assign the background temperature Tfleld to the ejected component, or attempt more complex parametrisations that link the ejected gas temperature to proxies of the AGN feedback, for example the total amount of ejected gas or the central galaxy mass (via its relation to the supermassive black hole mass). However, we note that the ejected gas component in massive haloes typically has small mass fractions and a low density, and thus we expect its contribution to tSZ to be typically subdominant.
We subsequently assigned a temperature to particles that do not belong to any halo. The mass of these gas particles was obtained by weighting the gravity-only particle mass with the cosmic baryon fraction, mg = Ωb/Ωm × mGrO. We assumed its temperature to be constant and a free parameter of the model, with a fiducial value of Tfleld = 106 K. From hydrodynamical simulations and observations, we expect this to be the so-called warm-hot intergalactic medium (WHIM), which has low densities and temperatures between 105 and 107 K (Cen & Ostriker 1999; Roncarelli et al. 2007; de Graaff et al. 2019).
We note that, in previous works, Mead et al. (2020) fixed the temperature of the gas outside haloes (both the ejected and field components) to T ≈ 106.5 K, whereas Osato & Nagai (2023) set Tfleld = 0 K. Assuming Tfleld = 0 K means to ignore the contribution of the gas around haloes and in filaments, which is subdominant but has been detected nonetheless (Van Waerbeke et al. 2014; de Graaff et al. 2019), and can be particularly important in the large-scale cross-correlation between total matter and electron pressure. In Mead et al. (2020), the ejected gas was added as a linear background in the two-halo term, because of the technical difficulties of having a gas shell around haloes, since the truncation of dark matter would introduce an anti-correlation with the gas. This procedure, however, likely underestimates the correlation of the ejected gas with their respective haloes, in the transition between one-halo and two-halo terms. In our approach, this problem is naturally solved.
Finally, we could obtain a total gas mass and temperature fields by summing over ‘gas’ particles: mgas = ∑imi and Tgas = Σi miTi. We note that, in doing so, the particles have a smooth and spherically symmetric radial temperature and pressure. On the contrary, the density is neither smooth nor spherical symmetric, due to the perturbative nature of the baryonification algorithm (the displacement field is spherical symmetric, but the initial and final particle distribution is not). We expect the gas clumpiness to impact the tSZ signal weakly, contrary to the X-ray emissivity, see for example Khedekar et al. (2013); Battaglia et al. (2015); Ettori (2015), and Lyskova et al. (2023). We note that the density clumpiness is by construction inherited in the BCM, and we ignore the effects of pressure clumping for now, leaving its modelling for future works.
In Fig. 3, we show a visualisation of the density field in a baryonified simulation, weighted by gas mass and temperature. We can notice how the temperature-weighted map is more diffuse than the mass, because of the shallower slope of the gas temperature profiles with respect to the density.
 |
Fig. 3 Density field in a baryonified simulation, weighted by the gas mass (left panel) and temperature (right panel). The BCM parameters have been tuned to generate relatively strong AGN feedback. |
3 Thermal Sunyaev-Zel’dovich and convergence
The tSZ effect is a spectral distortion in the cosmic microwave background (CMB) caused by the inverse Compton scattering of CMB photons with hot electrons. The relative difference in temperature of the photons can be computed as
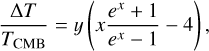 (11)
(11)
where TCMB = 2.726 K and x = hv/(kBTCMB) is the dimen-sionless frequency, h the Planck constant, kB the Boltzmann constant, and v the photon frequency. The parameter y is known as Compton-y parameter,
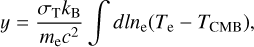 (12)
(12)
with me, ne, and Te being the electron rest mass, number density, and temperature, respectively, and σT is the Thomson cross-section. Thus, the Compton-y parameter is the integral of the electron thermal pressure along the line of sight.
In the previous section, we have shown how to produce a gas mass and temperature field with baryonification. We can use the mass and temperature to compute a ‘Compton weight’ associated with each gas particle. We followed Roncarelli et al. (2007) and McCarthy et al. (2014), and write the weight of the i-particle as
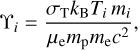 (13)
(13)
with mp being the rest proton mass and c the speed of light. The mean molecular weight per electron was assumed to be µe ≈ 2/(1 + X) ≈ 1.14.
To predict the angular power spectrum of our Compton-y maps, 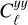 , we could proceed in two different ways:
, we could proceed in two different ways:
(i) baryonify the snapshots of a simulation, measure the 3D y power spectrum, PΥΥ (k, ð), and compute 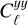 by integrating the 3D spectra numerically;
by integrating the 3D spectra numerically;
(ii) build a lightcone with the baryonified snapshots, create a Compton-y map by integrating particles along the line of sight weighted by ϒ producing, and measure its angular power spectrum.
The first approach has the flexibility to be applied independently from the specifics of a lightcone, and it could be easily accelerated by emulating the Compton 3D power spectra as a function of redshift. On the other hand, producing lightcones can be useful, for example, to compute higher-order statistics or apply angular masks. Analogously, we can study the WL cosmic convergence, that is, the apparent distortion of background galaxies caused by the gravitational potential of the LSS, either by integrating the 3D matter power spectrum, or by projecting particles onto a lightcone.
Either of the two approaches can be combined with a ‘cosmology rescaling’, which modifies the cosmology of an N-body simulation by perturbing the position and velocity of its particles (Angulo & White 2010; Zennaro et al. 2019; Contreras et al. 2020; Angulo et al. 2021). Explicitly, we can apply the cosmology rescaling and baryonification to a set of snapshots before computing Pϒϒ(k, ɀ) or building the lightcone. This combined approach would allow for a fast exploration of both cosmologica and baryonic parameters, while maintaining very accurate predictions.
 |
Fig. 4 Convergence (left panel) and Compton-y maps (right panel) generated by integrating up to ɀ = 1, a lightcone with a field of view of 10° × 10° built using a baryonified N-body simulation. |
3.1 Sky projections
The angular power spectrum of Compton y can be written as a function of the 3D Compton power spectrum:
 (14)
(14)
where χ is the comoving distance and χH is the comoving distance of the Hubble sphere.
Analogously, we projected the 3D matter power spectrum, Pmm(k, ɀ), to get the WL convergence angular power spectrum
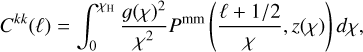 (15)
(15)
where the lensing kernel ɡ(χ) reads as
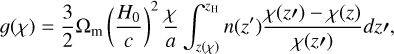 (16)
(16)
with n(ɀ′) being the normalised redshift distribution of the sources. We note that this is the convergence power spectrum expected exclusively from the gravitational potential of the LSS, ignoring other contributions for simplicity, such as the intrinsic alignment of galaxies.
3.2 Lightcones: Convergence and compton maps
We employed a scheme similar to the onion universe of Fosalba et al. (2008) to create lightcones, where the observer was placed at the centre of the simulation box. We built the lightcone by adding shells of particles at increasingly larger comoving distances from the observer, slicing the simulation snapshots at the correspondent redshift.
We replicated the box, randomly rotating and mirroring it to avoid the repetition of the same structure along the line of sight. In this way, it was possible to build full-sky maps, as well as maps with a smaller field of view.
To create the Compton-y maps, we simply integrated the particles weighted by ϒ/Ap along the line of sight, where Ap is the physical area subtended by the pixel at the particle distance from the observer.
Analogously, within the Born and thin lens approximations (see e.g. Petri et al. 2017), we could create convergence maps, k(θ), by integrating along the line of sight of the excess surface mass density,
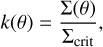 (17)
(17)
where the critical surface density is
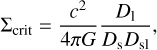 (18)
(18)
with Ds, D1, and Dsl being the angular diameter distances of the source, lens, and source-lens planes, respectively. In particular, we built 100 equispaced lens planes where we computed Σ(θ) and Σcrit, assigning particles with a nearest-grid-point scheme to meshes of 20482 pixels. We then summed up the contribution to the convergence for each pixel (see e.g. Fosalba et al. 2008; Giocoli et al. 2015; Castro et al. 2018; Hilbert et al. 2020).
In Fig. 4, we show as an example the convergence and Compton-y maps generated by creating a lightcone with a field of view of 10° × 10° up to ɀ = 1. We produced them starting from an N-body simulation of L = 512 h−1Mpc of box side and N = 15363 particles, scaling cosmology from TheOne (see e.g. Table 1 of Pellejero Ibañez et al. 2023) to the nine-year Wilkinson Microwave Anisotropy Probe (WMAP9) (Hinshaw et al. 2013) and setting the astrophysics to BAHAMAS-like feedback (McCarthy et al. 2017).
The Compton-y map appears clumpier than the convergence because the tSZ is more sensitive to massive haloes,  . Furthermore, the projected tSZ signal is sensitive to a wide range of redshifts, its power scaling as (1 + ɀ)2, whereas the convergence has a narrower redshift kernel. Since our lensing sources have been placed at ɀ = 1, the lensing kernel peaks around z ≈ 0.5, and goes to zero at ɀ = 0 and ɀ = 1. Thus, even if some correlation between the convergence and the tSZ map can be visually found, not all the features of the tSZ map have a counterpart in the convergence map. Most of the structures visible in the tSZ map with no counterpart in convergence are thus massive haloes at low and high redshifts, the former having larger angular sizes in the map. Conversely, predominant structures in the convergence map without a clear counterpart in tSZ are likely to be overdensities around ɀ ≈ 0.5.
. Furthermore, the projected tSZ signal is sensitive to a wide range of redshifts, its power scaling as (1 + ɀ)2, whereas the convergence has a narrower redshift kernel. Since our lensing sources have been placed at ɀ = 1, the lensing kernel peaks around z ≈ 0.5, and goes to zero at ɀ = 0 and ɀ = 1. Thus, even if some correlation between the convergence and the tSZ map can be visually found, not all the features of the tSZ map have a counterpart in the convergence map. Most of the structures visible in the tSZ map with no counterpart in convergence are thus massive haloes at low and high redshifts, the former having larger angular sizes in the map. Conversely, predominant structures in the convergence map without a clear counterpart in tSZ are likely to be overdensities around ɀ ≈ 0.5.
For this reason, we employed two different strategies to smooth the maps. For the convergence map, we simply applied a Gaussian smoothing of ≈0.6′. For the Compton-y map, we instead adopted a redshift-dependent smoothing. Specifically, we split the lightcone into slices of 50 comoving megaparsecs along the line of sight, and applied, to each slice, a Gaussian smoothing proportional to the angular diameter distance of the mean intra-particle distance at the average redshift. In so doing, we have a ≈10′ smoothing for the closest objects, and increasingly smaller smoothing angles until reaching ≈0.1′ for objects at ≈3300 Mpc (ɀ = 1 ). Thus we avoided the strong particle discreteness noise in the Compton-y map coming from clusters close to the observer.
4 Comparison with hydrodynamical simulations
In this section, we explain how we tested if our baryonification approach can reproduce the predictions of hydrodynamical simulations. Against BAHAMAS (McCarthy et al. 2017, 2018), we compare a suite of simulations specifically calibrated with observations with a gas fraction in haloes, and, therefore, particularly well suited to study baryonic effects on LSS.
Our comparison has some intrinsic limitations since i) doing a fit using large simulations directly is computationally demanding, even when using a highly optimised baryonification algorithm; and ii) the BAHAMAS simulation has a box of 400 h−1Mpc, and it is affected by cosmic variance at around a 10% level at k ≈ 0.1 h Mpc−1. Focusing on the ratio with respect to the gravity-only matter power spectrum would suppress the cosmic variance of the total matter power spectrum, but this is not trivially true for the electron pressure. In particular, Mead et al. (2020) found that cosmic variance impacts the BAHAMAS electron pressure power spectrum at the same order of magnitude as the AGN feedback calibration. Therefore, we performed a simple parameter optimisation, leaving, to future work, the making of emulators of the 3D Compton power spectrum, which are to be added to the BACCOemu framework (Angulo et al. 2021; Aricò et al. 2021a, 2022; Zennaro et al. 2023; Pellejero Ibañez et al. 2023). The emulated Compton power spectrum can be integrated to give the tSZ power spectrum analogously to the matter power spectrum with WL convergence. Moreover, the use of recent large hydrodynamical simulations, such as the FLAMINGO suite (Schaye et al. 2023; Kugel et al. 2023), would be a valid option to suppress cosmic variance in future tests.
We note that Mead et al. (2020) conducted a comparable analysis, using the halo-model-based HMx (Mead et al. 2020; Tröster et al. 2022) to fit the BAHAMAS total matter auto power spectrum within a few per cent accuracy. However, the fitting accuracy for the total matter-electron pressure cross-power spectrum was limited to 15%. These authors also highlight the challenges in fitting the electron pressure auto power spectrum, as well as the simultaneous fitting of the gas power spectrum and the matter-electron pressure cross power spectrum. They emphasise that difficulties might arise due to either cosmic variance or model limitations, such as the adoption of a simple non-thermal prescription.
For this work, we adopted a more complex non-thermal contribution prescription (Green et al. 2020), embedded in the fully non-linear framework given by the baryonification. We measured the power spectra in two interlaced Fourier grids of 5123 cells (folded twice; see e.g. Aricò et al. 2021b), and a triangular-shaped clouds mass assignment scheme.
We simultaneously fit the suppression S (k), electron pressure, and mass-electron pressure cross power spectra, considering a 1, 5, and 10% error in the measurements, respectively, within the scales k ∈ [0.3, 5 h Mpc−1] and at ɀ = 0. We employed a particle swarm algorithm1 for the optimisation, employing five particles and 50 steps, varying a total of six free parameters in logarithmic space: four from the baryonification model by Aricò et al. (2021b), log10M(Mc/(h−1 M⊙)), log10 η, log10 θinn, and log10(M1,z0,cen/(h−1 M⊙)), plus one to control the temperature of the background gas, log10 Tfleld, and one to modulate the amplitude of non-thermal pressure, log10 Anth. We fixed log10 β = −0.45, log10 θout = 0, and log10(Minn/(h−1 M⊙)) = 13.5 to ease the multidimensional optimisation, and, as a further speed-up, we initialised the swarm with the best-fitting parameters to the BAHAMAS total matter power spectrum found in Aricò et al. (2021a). After inspecting the BAHAMAS electron pressure at different redshifts, we also set the non-thermal redshift scaling to αnth = 1.5.
4.1 3D power spectra
We show the BAHAMAS suppression in the matter power spectrum, S (k), in the top-left panel of Fig. 5, considering three different AGN feedback scenarios, namely the one with the AGN temperature TAGN = 107.6,107.8, and 108.0 K. Even when fitting them along with the electron pressure auto- and cross-power spectra S(k), we could reproduce them at the per cent level. In the bottom-left panel of Fig. 5, we report the ratio of the power spectra measured in our simulations to that measured in BAHAMAS. First, we note that the matter power spectrum of our gravity-only simulation run with TheOne cosmology is ≈30% off with respect to the WMAP9-like BAHAMAS. Remarkably, after applying the cosmology scaling (a process without any free parameters involved), the discrepancy was reduced to ≈2%. Both the electron pressure and matter-electron pressure power spectra are fitted to better than a 10% accuracy. We report in Table 1 our BCM best-fitting parameters.
In the right panel of Fig. 5, we show with dash lines our predictions for dark matter, gas, stars, electron pressure, and total-electron pressure power spectra at ɀ = 0, compared to BAHAMAS TAGN = 107.8K. We see that the BCM overestimates the BAHAMAS power spectra of stars at all scales and gas on small scales, which were not explicitly fitted. To check if the model is flexible enough to reproduce them, we refit all the spectra simultaneously, varying the aforementioned free parameters plus the αsat described in Aricò et al. (2021b), which regulates the mass fraction in satellite galaxies. This parameter has a very weak impact on matter and electron pressure power spectra, but it is important to reproduce the stellar power spectrum on large scales. We show in Fig. 5 this new fit with solid lines. We find that the gas and stellar power spectra fit have indeed been improved significantly.
 |
Fig. 5 Comparison between BAHAMAS and BCM power spectra. Left panel, top: Matter power spectrum suppression S (k) measured at ɀ = 0 in three BAHAMAS simulations, with an AGN temperature of TAGN = 107.6, 107.8, and 108.0 K (red, green, and blue circles, respectively). As solid lines, we show the respective predictions of baryoniflcation when simultaneously fitting the S (k), the electron pressure, and the matter-electron pressure power spectra of each simulation. Left panel, bottom: Ratio of power spectra measured in our baryonified simulations to the BAHAMAS ones, for matter (solid lines), electron pressure (dashed lines), and the matter–electron pressure cross (dotted lines). Right panel: Power spectra of matter, dark matter, gas, galaxy, electron pressure (in units of eV cm−3), and matter-electron pressure, measured in BAHAMAS AGN tuned at ɀ = 0 (circles; colours are as described in the legend). We show the baryoniflcation fits to the total matter and electron pressure auto- and cross-correlation with dashed lines, and a simultaneous fit to all the power spectra with solid lines. |
Baryoniflcation best-fitting parameters to the matter and electron pressure auto- and cross-power spectra measured in BAHAMAS at ɀ = 0, with the AGN feedback strengths specified in the first row.
4.2 Angular power spectra
We employed the best-fitting parameters to the TAGN = 107.8 K simulation, and built 30 lightcones with a field of view of 10° × 10° up to ɀ = 1, following the procedure detailed in Sect. 3.2. Each lightcone takes approximately 2.5 hours in 32 cores, including the application of cosmology scaling and baryoniflcation to each of the 24 snapshots used.
As described in Sect. 3.2, we projected the light-cones into Compton-y and convergence-smoothed maps of 2048 × 2048 pixels (e.g. Fig. 4). We show their power spectra in Fig. 6, and display the angular power spectra as a comparison, which were obtained by numerically integrating the 3D power spectra of both our baryonified simulation and BAHAMAS, as described in Sect. 3.1. We measured the power spectra of the convergence and tSZ maps using the routine provided in LENST00LS2 (Petri et al. 2017). For comparison, we also display BAHAMAS as dotted lines.
We find that the mean angular power spectrum measured with our 30 lightcone realisations is in excellent agreement with the convergence power spectra integrals, and in good agreement with the tSZ, which is well within 1σ. As expected and discussed in the previous sections, the cosmic variance affects the Compton power spectrum more severely than the convergence. The limited size of our maps, as well as their relatively low number, may cause the differences that we observe. We also note that the binning strategy mildly affects the largest scales shown.
When comparing our results to BAHAMAS, we find that the convergence is reproduced at 1%, whereas the tSZ power spectrum is at ≈10%. This is consistent with the accuracy we found for the 3D matter and electron pressure power spectra at ɀ = 0, and thus validates our assumptions of the redshift dependence of baryonic effects. We note that various hydrodynamical simulations might present different redshift dependence, and, eventually, this should be tested with observations in a wide range of redshifts.
As a reference, we overplotted the tSZ power spectra obtained from Planck data release 4 by Tanimura et al. (2022). The models reproduce the CMB data well, although we remind the reader that we were integrating the tSZ only up to ɀ = 1, and thus missing the contribution of higher redshifts. In particular, higher redshifts contribute more to smaller scales. To quantify this, we computed the ratio of the tSZ signal in BAHAMAS when integrating until ɀ = 2 and ɀ = 1: at ℓ ≈ 100 the difference is ≈3%, and increases to ≈6% at ℓ ≈ 1000.
Using the BAHAMAS simulations, McCarthy et al. (2014, 2018) have shown the sensitivity of tSZ to cosmology, and in particular to neutrino masses, as well as to the strength of AGN feedback. The methodology proposed here enables us to explore a much larger parameter space in both cosmology and astrophysics. The BCM is designed to be a rather simple model that can accurately reproduce some statistics of cosmological interest with a few physically motivated free parameters. However, as we constrain it with an increasing number of multi-wavelength observations and cross-correlations, we should carry out consistency checks and make mock parameter inferences, to test for a possible bias introduced by our theoretical assumptions. To this end, we plan to build emulators of the 3D power spectra presented here and perform a more in-depth exploration of the parameter space. Moreover, we warrant further tests of the BCM thermodynamical profiles against both observations and simulations.
 |
Fig. 6 Angular power spectra of convergence (left panel) and tSZ (right panel) using the mean of 30 independent baryonifled lightcones (thick black line) and integrating the power spectra of the snapshots of our baryonifled simulation numerically (dotted blue line). The field of view of each lightcone is 10° × 10°, up to ɀ = 1 (all the sources for convergence are considered to be at ɀ = 1). The shaded area marks the standard deviation of the 30 lightcone realisations. For comparison, we plot the integrals of the 3D power spectra of BAHAMAS TAGN = 107.8 K with dotted blue lines, and the tSZ power spectrum extracted from Plack data release 4 with black circles. |
5 Conclusions
In this paper, we have presented an extension of the baryonification method allowing us to model the gas mass, temperature, and pressure in cosmological gravity-only N-body simulations.
After applying the traditional baryonification, we resampled the matter field with dark matter, gas, and stellar particles. Assuming a polytropic equation of state for the gas inside haloes, we then assigned a temperature, a pressure, and a Compton weight to each gas particle.
We added only two extra free parameters, one to regulate the temperature of the gas particles outside haloes and one for the amplitude of the non-thermal pressure contribution. Our novel algorithm enables fast and accurate predictions of the tSZ effect and its cross-correlation with the weak lensing convergence. We have shown that our baryonification, along with the cosmology scaling, can be used to produce lightcones in a wide variety of cosmological and astrophysical scenarios, with a small computational cost (a few CPU hours).
We have discussed the advantages of our approach with respect to previous works (Mead et al. 2020; Osato & Nagai 2023), and in particular its self-consistent modelling of the gas mass and pressure within and outside haloes.
We tested our model against the hydrodynamical simulations BAHAMAS (McCarthy et al. 2017, 2018), finding that it can simultaneously reproduce the total, dark matter, gas, stellar, and electron pressure 3D power spectra, as well as the Compton-y and convergence angular power spectra. In particular, we find that we can fit the matter power spectrum suppression at a 1% level and the electron pressure auto- and cross-correlation at better than 10%, down to k = 5 h Mpc−1 for different AGN strengths in BAHAMAS. Similarly, we can reproduce the convergence and tSZ power spectra at 1% and 10%, respectively, by fixing the redshift dependence of the non-thermal pressure contribution.
In the future, we plan to build emulators of the 3D power spectra of the electron pressure and its cross-correlation with the matter density contrast. The same framework can be extended to model fields such as kSZ, X-ray, and cosmic infrared background (see e.g. Stein et al. 2020, and references therein).
We anticipate that this will pave the way for joint analyses of multi-wavelength surveys and cross-correlation of different fields down to non-linear scales, paramount to optimally extracting cosmological and astrophysical information from the planned LSS surveys.
Acknowledgements
We thank Alexander Mead, Tillman Tröster, and Ian McCarthy, for providing the BAHAMAS power spectra data with the related Python functions to read them. We thank Sergio Contreras for the help with the cosmology scaling algorithm, Jens Stücker for the visualisation code used to display the simulations, and Matteo Zennaro, Aurel Schneider, and Daisuke Nagai for useful discussions. We acknowledge the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) for providing the avenue where some of these discussions have been carried out. REA acknowledges support from project PID2021-128338NB-I00 from the Spanish Mnistry of Science and support from the European Research Executive Agency HORIZON-MSCA-2021-SE-01 Research and Innovation programme under the Marie Sklodowska-Curie grant agreement number 101086388 (LACEGAL). We acknowledge the use of the following software: BACCO & pso BACCO (Aricò et al. 2021b), LENSTOOLS (Petri et al. 2017), NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), Matplotlib (Hunter 2007).
References
- Akino, D., Eckert, D., Okabe, N., et al. 2022, PASJ, 74, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Amon, A., Gruen, D., Troxel, M. A., et al. 2022, Phys. Rev. D, 105, 023514 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, R. E., & White, S. D. M. 2010, MNRAS, 405, 143 [NASA ADS] [Google Scholar]
- Angulo, R. E., Zennaro, M., Contreras, S., et al. 2021, MNRAS, 507, 5869 [NASA ADS] [CrossRef] [Google Scholar]
- Aricò, G., Angulo, R. E., Hernández-Monteagudo, C., et al. 2020, MNRAS, 495, 4800 [Google Scholar]
- Aricò, G., Angulo, R. E., Contreras, S., et al. 2021a, MNRAS, 506, 4070 [CrossRef] [Google Scholar]
- Aricò, G., Angulo, R. E., Hernández-Monteagudo, C., Contreras, S., & Zennaro, M. 2021b, MNRAS, 503, 3596 [Google Scholar]
- Aricò, G., Angulo, R. E., & Zennaro, M. 2022, arXiv e-prints [arXiv:2104.14568] [Google Scholar]
- Aricò, G., Angulo, R. E., Zennaro, M., et al. 2023, A&A, 678, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2015, ApJ, 806, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Bigwood, L., Amon, A., Schneider, A., et al. 2024, arXiv e-prints [arXiv:2404.06098] [Google Scholar]
- Bulbul, G. E., Hasler, N., Bonamente, M., & Joy, M. 2010, ApJ, 720, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, T., Quartin, M., Giocoli, C., Borgani, S., & Dolag, K. 2018, MNRAS, 478, 1305 [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chaves-Montero, J., Angulo, R. E., & Contreras, S. 2023, MNRAS, 521, 937 [Google Scholar]
- Chen, A., Aricò, G., Huterer, D., et al. 2023, MNRAS, 518, 5340 [Google Scholar]
- Contreras, S., Angulo, R. E., Zennaro, M., Aricò, G., & Pellejero-Ibañez, M. 2020, MNRAS, 499, 4905 [Google Scholar]
- Contreras, S., Angulo, R. E., Chaves-Montero, J., White, S. D. M., & Aricò, G. 2023, MNRAS, 520, 489 [Google Scholar]
- de Graaff, A., Cai, Y.-C., Heymans, C., & Peacock, J. A. 2019, A&A, 624, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S. 2015, MNRAS, 446, 2629 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., & Eckert, D. 2022, A&A, 657, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferlito, F., Springel, V., Davies, C. T., et al. 2023, MNRAS, 524, 5591 [CrossRef] [Google Scholar]
- Fluri, J., Kacprzak, T., Lucchi, A., et al. 2022, Phys. Rev. D, 105, 083518 [NASA ADS] [CrossRef] [Google Scholar]
- Fosalba, P., Gaztañaga, E., Castander, F. J., & Manera, M. 2008, MNRAS, 391, 435 [NASA ADS] [CrossRef] [Google Scholar]
- García-García, C., Zennaro, M., Aricò, G., Alonso, D., & Angulo, R. E. 2024, J. Cosmology Astropart. Phys., 2024, 024 [CrossRef] [Google Scholar]
- Gatti, M., Pandey, S., Baxter, E., et al. 2022, Phys. Rev. D, 105, 123525 [NASA ADS] [CrossRef] [Google Scholar]
- Gatti, M., Campailla, G., Jeffrey, N., et al. 2024, arXiv e-prints [arXiv:2405.10881] [Google Scholar]
- Ghirardini, V., Ettori, S., Eckert, D., & Molendi, S. 2019, A&A, 627, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giocoli, C., Metcalf, R. B., Baldi, M., et al. 2015, MNRAS, 452, 2757 [Google Scholar]
- Giri, S. K., & Schneider, A. 2021, J. Cosmology Astropart. Phys., 2021, 046 [CrossRef] [Google Scholar]
- Grandis, S., Aricò, G., Schneider, A., & Linke, L. 2024, MNRAS, 528, 4379 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S. B., Aung, H., Nagai, D., & van den Bosch, F. C. 2020, MNRAS, 496, 2743 [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Aguayo, C., Springel, V., Pakmor, R., et al. 2023, MNRAS, 524, 2556 [CrossRef] [Google Scholar]
- Hilbert, S., Barreira, A., Fabbian, G., et al. 2020, MNRAS, 493, 305 [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [Google Scholar]
- Hojjati, A., Tröster, T., Harnois-Déraps, J., et al. 2017, MNRAS, 471, 1565 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G., & Angulo, R. E. 2018, A&A, 610, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kacprzak, T., Fluri, J., Schneider, A., Refregier, A., & Stadel, J. 2023, J. Cosmology Astropart. Phys., 2023, 050 [CrossRef] [Google Scholar]
- Khedekar, S., Churazov, E., Kravtsov, A., et al. 2013, MNRAS, 431, 954 [Google Scholar]
- Komatsu, E., & Seljak, U. 2001, MNRAS, 327, 1353 [Google Scholar]
- Krause, E., Fang, X., Pandey, S., et al. 2021, arXiv e-prints [arXiv:2105.13548] [Google Scholar]
- Kugel, R., Schaye, J., Schaller, M., et al. 2023, MNRAS, 526, 6103 [NASA ADS] [CrossRef] [Google Scholar]
- Le Brun, A. M. C., McCarthy, I. G., Schaye, J., & Ponman, T. J. 2014, MNRAS, 441, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. E., Lu, T., Haiman, Z., Liu, J., & Osato, K. 2023, MNRAS, 519, 573 [Google Scholar]
- Lu, T., & Haiman, Z. 2021, MNRAS, 506, 3406 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, T., Haiman, Z., & Zorrilla Matilla, J. M. 2022, MNRAS, 511, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, T., Haiman, Z., & Li, X. 2023, MNRAS, 521, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Lyskova, N., Churazov, E., Khabibullin, I.I., et al. 2023, MNRAS, 525, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Martizzi, D., Teyssier, R., & Moore, B. 2013, MNRAS, 432, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Le Brun, A. M. C., Schaye, J., & Holder, G. P. 2014, MNRAS, 440, 3645 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2017, MNRAS, 465, 2936 [Google Scholar]
- McCarthy, I. G., Bird, S., Schaye, J., et al. 2018, MNRAS, 476, 2999 [NASA ADS] [CrossRef] [Google Scholar]
- Mead, A. J., Tröster, T., Heymans, C., Van Waerbeke, L., & McCarthy, I. G. 2020, A&A, 641, A130 [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Osato, K., & Nagai, D. 2023, MNRAS, 519, 2069 [Google Scholar]
- Osato, K., Shirasaki, M., Miyatake, H., et al. 2020, MNRAS, 492, 4780 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, S., Gatti, M., Baxter, E., et al. 2022, Phys. Rev. D, 105, 123526 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, S., Salcido, J., To, C.-H., et al. 2024, arXiv e-prints [arXiv:2401.18072] [Google Scholar]
- Parkinson, H., Cole, S., & Helly, J. 2008, MNRAS, 383, 557 [Google Scholar]
- Pellejero Ibañez, M., Angulo, R. E., Zennaro, M., et al. 2023, MNRAS, 520, 3725 [Google Scholar]
- Petri, A., Haiman, Z., & May, M. 2017, Phys. Rev. D, 95, 123503 [NASA ADS] [CrossRef] [Google Scholar]
- Roncarelli, M., Moscardini, L., Borgani, S., & Dolag, K. 2007, MNRAS, 378, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Salcido, J., McCarthy, I. G., Kwan, J., Upadhye, A., & Font, A. S. 2023, MNRAS, 523, 2247 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Dalla Vecchia, C., Booth, C. M., et al. 2010, MNRAS, 402, 1536 [Google Scholar]
- Schaye, J., Kugel, R., Schaller, M., et al. 2023, MNRAS, 526, 4978 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, A., & Teyssier, R. 2015, J. Cosmology Astropart. Phys., 12, 049 [CrossRef] [Google Scholar]
- Schneider, A., Teyssier, R., Stadel, J., et al. 2019, J. Cosmology Astropart. Phys., 2019, 020 [CrossRef] [Google Scholar]
- Schneider, A., Stoira, N., Refregier, A., et al. 2020, J. Cosmology Astropart. Phys., 2020, 019 [CrossRef] [Google Scholar]
- Schneider, A., Giri, S. K., Amodeo, S., & Refregier, A. 2022, MNRAS, 514, 3802 [NASA ADS] [CrossRef] [Google Scholar]
- Secco, L. F., Samuroff, S., Krause, E., et al. 2022, Phys. Rev. D, 105, 023515 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, L. D., Nagai, D., Bhattacharya, S., & Lau, E. T. 2010, ApJ, 725, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., & Komatsu, E. 2014, MNRAS, 442, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Shirasaki, M., Takahashi, R., Osato, K., & Ioka, K. 2022, MNRAS, 512, 1730 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, G., Alvarez, M. A., Bond, J. R., van Engelen, A., & Battaglia, N. 2020, J. Cosmology Astropart. Phys., 2020, 012 [CrossRef] [Google Scholar]
- Tanimura, H., Douspis, M., Aghanim, N., & Salvati, L. 2022, MNRAS, 509, 300 [Google Scholar]
- Tröster, T., Ferguson, C., Harnois-Déraps, J., & McCarthy, I. G. 2019, MNRAS, 487, L24 [Google Scholar]
- Tröster, T., Mead, A. J., Heymans, C., et al. 2022, A&A, 660, A27 [CrossRef] [EDP Sciences] [Google Scholar]
- van Daalen, M. P., McCarthy, I. G., & Schaye, J. 2020, MNRAS, 491, 2424 [Google Scholar]
- van den Bosch, F. C., Jiang, F., Hearin, A., et al. 2014, MNRAS, 445, 1713 [NASA ADS] [CrossRef] [Google Scholar]
- Van Waerbeke, L., Hinshaw, G., & Murray, N. 2014, Phys. Rev. D, 89, 023508 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261 [CrossRef] [Google Scholar]
- Weiss, A. J., Schneider, A., Sgier, R., et al. 2019, J. Cosmology Astropart. Phys., 2019, 011 [Google Scholar]
- Zennaro, M., Angulo, R. E., Aricò, G., Contreras, S., & Pellejero-Ibáñez, M. 2019, MNRAS, 489, 5938 [NASA ADS] [CrossRef] [Google Scholar]
- Zennaro, M., Angulo, R. E., Pellejero-Ibáñez, M., et al. 2023, MNRAS, 524, 2407 [Google Scholar]
All Tables
Baryoniflcation best-fitting parameters to the matter and electron pressure auto- and cross-power spectra measured in BAHAMAS at ɀ = 0, with the AGN feedback strengths specified in the first row.
All Figures
 |
Fig. 1 Cosmic density fields obtained by applying our baryonification to an N-body simulation. Specifically, the total matter density field is decomposed into dark matter (top left), galaxies (top right), bound gas in hydrostatic equilibrium (bottom left), and gas ejected by feedback processes (bottom right). The BCM parameters have been set to values that generate strong AGN feedback. |
| In the text | |
 |
Fig. 2 Density (upper panel), pressure (central panel), and temperature (lower panel) profiles of the bound gas for haloes in the mass range 1013–1015 h−1 M⊙, according to the legend. We show both total and thermal pressure, with solid and dotted lines, respectively. For visual comparison, we show the ‘universal’ pressure profiles from Arnaud et al. (2010) and the virial temperature with dashed liens. We stress that the BCM parameters allow for changes in the shape and normalisation of the profiles, and, in this case, we did not tune them to reproduce any specific profile. |
| In the text | |
 |
Fig. 3 Density field in a baryonified simulation, weighted by the gas mass (left panel) and temperature (right panel). The BCM parameters have been tuned to generate relatively strong AGN feedback. |
| In the text | |
 |
Fig. 4 Convergence (left panel) and Compton-y maps (right panel) generated by integrating up to ɀ = 1, a lightcone with a field of view of 10° × 10° built using a baryonified N-body simulation. |
| In the text | |
 |
Fig. 5 Comparison between BAHAMAS and BCM power spectra. Left panel, top: Matter power spectrum suppression S (k) measured at ɀ = 0 in three BAHAMAS simulations, with an AGN temperature of TAGN = 107.6, 107.8, and 108.0 K (red, green, and blue circles, respectively). As solid lines, we show the respective predictions of baryoniflcation when simultaneously fitting the S (k), the electron pressure, and the matter-electron pressure power spectra of each simulation. Left panel, bottom: Ratio of power spectra measured in our baryonified simulations to the BAHAMAS ones, for matter (solid lines), electron pressure (dashed lines), and the matter–electron pressure cross (dotted lines). Right panel: Power spectra of matter, dark matter, gas, galaxy, electron pressure (in units of eV cm−3), and matter-electron pressure, measured in BAHAMAS AGN tuned at ɀ = 0 (circles; colours are as described in the legend). We show the baryoniflcation fits to the total matter and electron pressure auto- and cross-correlation with dashed lines, and a simultaneous fit to all the power spectra with solid lines. |
| In the text | |
 |
Fig. 6 Angular power spectra of convergence (left panel) and tSZ (right panel) using the mean of 30 independent baryonifled lightcones (thick black line) and integrating the power spectra of the snapshots of our baryonifled simulation numerically (dotted blue line). The field of view of each lightcone is 10° × 10°, up to ɀ = 1 (all the sources for convergence are considered to be at ɀ = 1). The shaded area marks the standard deviation of the 30 lightcone realisations. For comparison, we plot the integrals of the 3D power spectra of BAHAMAS TAGN = 107.8 K with dotted blue lines, and the tSZ power spectrum extracted from Plack data release 4 with black circles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



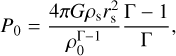
![${f_{{\rm{th}}}}(x) = A\left( {1 + {e^{ - {{(x/B)}^C}}}} \right){(v/4.1)^{D/\left( {1 + {{[x/E]}^F}} \right)}},$](/articles/aa/full_html/2024/10/aa51055-24/aa51055-24-eq11.png)