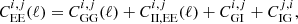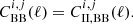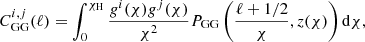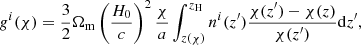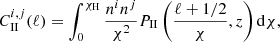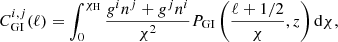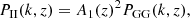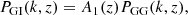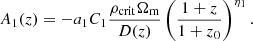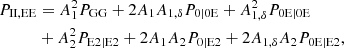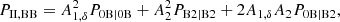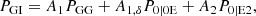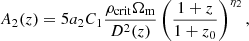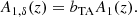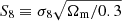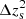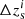| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202346539 | |
| Published online | 12 October 2023 | |
DES Y3 cosmic shear down to small scales: Constraints on cosmology and baryons
1
Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland
e-mail: giovanni.arico@uzh.ch
2
Donostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia-San Sebastián, Guipuzkoa, Spain
e-mail: reangulo@dipc.org
3
IKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Spain
4
Department of Physics (Astrophysics), University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
5
Kavli Institute for the Physics and Mathematics of the Universe (WPI), UTIAS, The University of Tokyo, Kashiwa, Chiba 277-8583, Japan
6
Department of Astrophysics Research, Instituto de Astrofísica de Canarias, C.Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
7
Departamento de Astrofísica, Universidad de La Laguna, Avenida Francisco Sánchez s/n, 38205 La Laguna, Tenerife, Spain
Received:
30
March
2023
Accepted:
2
August
2023
We present the first analysis of cosmic shear measured in DES Y3 that employs the entire range of angular scales in the data. To achieve this, we built upon recent advances in the theoretical modelling of weak lensing provided by a combination of N-body simulations, physical models of baryonic processes, and neural networks. Specifically, we used BACCOemu to model the linear and non-linear matter power spectrum including baryonic physics, allowing us to robustly exploit scales smaller than those used by the DES Collaboration. We show that the additional data produce cosmological parameters that are tighter but consistent with those obtained from larger scales, while also constraining the distribution of baryons. In particular, we measured the mass scale at which haloes have lost half of their gas, log Mc = 14.38−0.56+0.60 log(h−1 M⊙), and a parameter that quantifies the weighted amplitudes of the present-day matter inhomogeneities, S8 = 0.799−0.015+0.023. Our constraint on S8 is statistically compatible with that inferred from the Planck satellite data at the 0.9σ level. We find instead a 1.4σ shift in comparison to that from the official DES Y3 cosmic shear, because of different choices in the modelling of intrinsic alignment, non-linearities, baryons, and lensing shear ratios. We conclude that small scales in cosmic shear data contain valuable astrophysical and cosmological information and thus should be included in standard analyses.
Key words: gravitational lensing: weak / surveys / cosmological parameters / large-scale structure of Universe
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The standard cosmological model, ΛCDM, has been heavily stress-tested in the past decade. The increasingly precise measurements of the cosmic microwave background (CMB), and the recently achieved ability of large-scale-structure (LSS) missions to compete with other current methods, have highlighted some tensions on cosmological parameters as estimated by different probes. In particular, a significant tension (> 4σ) is found in the value of the expansion rate of the Universe today, as estimated using the inverse ladder or the CMB data from the Planck satellite (the so-called H0 tension; see e.g., Verde et al. 2019; Riess et al. 2022). A milder tension (2–3σ) is found when constraining the growth of structure with CMB data and low-redshift probes such as weak gravitational lensing (WL) and galaxy clustering (the so-called σ8 or S8 tension; see e.g., Heymans et al. 2021; Abbott et al. 2022; García-García et al. 2021).
Many ideas have been proposed to solve or at least reduce these tensions: exotic models of dark energy (e.g., Pourtsidou & Tram 2016; Marra & Perivolaropoulos 2021; Heisenberg et al. 2023) and dark matter (e.g., decaying dark matter, see Chen et al. 2021; Bucko et al. 2023), an interacting dark sector (e.g., Lucca 2021), modified gravity (see e.g., Nguyen et al. 2023), a non-linear suppression of the matter power spectrum, possibly given by baryonic physics (Schneider et al. 2022; Amon & Efstathiou 2022), and modifications to the halo mass function (Gu et al. 2023). However, no definitive consensus has been reached so far (Verde et al. 2019; Wong et al. 2020). Although these tensions could be caused by a fundamental shortcoming of ΛCDM, they could also originate from physical processes absent from the theory modelling or from unknown systematic errors in the observations.
In the spirit of advancing the current state of cosmological analyses by adopting a more complete description of cosmic probes, we present a reanalysis of the cosmic shear measured by the Dark Energy Survey (DES, The Dark Energy Survey Collaboration 2005; Dark Energy Survey Collaboration 2016; Secco et al. 2022; Amon et al. 2022). We include several improvements in the theoretical modelling of the data, most notably, an explicit model for the role of baryons in WL, which allows us to include small scales that were usually neglected in previous analyses. With these, we study to which degree the current S8 tension might be caused by baryonic physics.
Cosmic shear is the correlation in the apparent shape of galaxies that is induced by the gravitational potential of the intervening matter between these galaxies and us. Shear is particularly interesting because it directly probes the cosmic density field (dark matter and baryons) and bypasses the need for modelling galaxy bias. Thus, it offers a complementary probe to galaxy survey analyses.
The cosmic shear signal is very weak. Therefore, only large photometric surveys have had enough statistical power so far to constrain the cosmological parameters in a competitive way with respect to other probes. The analysis is quite complex and relies on a robust modelling of galaxy shapes, photometric redshifts, non-linearities in the growth of structures, intrinsic alignment of galaxies, and so on. Nonetheless, in the past years, several Collaborations, such as DES (Abbott et al. 2022), the Kilo-Degree Survey (KiDS, Heymans et al. 2021), and the Hyper Supreme-Cam (HSC Hikage et al. 2019), have successfully carried out these types of analyses. In the next years, stage IV surveys such as Euclid (Laureijs et al. 2011), DESI (DESI Collaboration 2016), and LSST (Ivezić et al. 2019), are expected to dramatically improve on the current cosmological constraints.
To fully exploit current and future WL data, we need to model all the physical processes that shape the distribution of matter in the universe. In particular, astrophysical feedback, such as supermassive black hole accretion and supernovae feedback, pushes gas outside the dark matter haloes, modifying the cosmic matter density fields on small scales (Schaye et al. 2010; Schneider & Teyssier 2015; van Daalen et al. 2020). This causes a non-trivial suppression of the expected cosmic shear signal, depending on the strength of the feedback and also on the cosmology, mainly via the relative quantity of baryons available (Ωb/Ωm; Schneider et al. 2019; van Daalen et al. 2020; Aricò et al. 2021b). When the role of baryonic processes is ignored, cosmological inferences become biased, and it has been identified as one of the main WL systematics, especially when considering the WL signal on small scales (see e.g., Semboloni et al. 2011; Chisari et al. 2018; Schneider et al. 2020).
Several approaches have been proposed to mitigate the effects of baryons on cosmic shear, including analytical parametrisations (e.g., Harnois-Déraps et al. 2015), principal component analysis (PCA; Eifler et al. 2015; Huang et al. 2019), the halo model (e.g., Semboloni et al. 2011; Mohammed et al. 2014; Fedeli 2014; Mead et al. 2015, 2021, 2020; Debackere et al. 2020), and baryonification (Schneider & Teyssier 2015; Schneider et al. 2019; Aricò et al. 2020).
The official DES analysis does not attempt to model baryons, but instead relies on angular scale cuts informed by hydrodynamical simulations, where data points at scales thought to be potentially affected by baryons are discarded. In this way, only 227 out of the total 400 data points are used for the analysis, which means that not all the available information is used. Secco et al. (2022) and Amon et al. (2022) also employed another angular scale cut, referred to as “ΛCDM optimised”, with 273 data points. For simplicity, we refer only to the standard DES scale cuts. We take a different approach in this work by directly modelling the relevant baryonic processes. This has the advantage of fully exploiting the DES data, and is also expected to provide more conservative cosmological estimates because the estimates i) are obtained after marginalisation over the uncertainty associated with baryons, and ii) do not make any a priori assumption about the range of scales affected by baryons.
In our analysis, we account for the effects of galaxy formation and gas physic using a baryonification algorithm (Aricò et al. 2020, 2021a) applied to the outputs of cosmological N-body simulations. Baryonification displaces the particles in gravity-only simulations according to analytical prescriptions based on physically motivated assumptions. This approach is flexible enough to match the modifications induced by baryons in two- and three-point statistics at the percent level, as measured in dozens of different current hydrodynamical simulations. Operationally, we use the neural-network emulators collected in BACCOemu (Angulo et al. 2021; Aricò et al. 2021b, 2022), which deliver accurate and fast predictions of the linear, non-linear, and baryonic contribution to the matter power spectrum. We simultaneously vary the parameters of the cosmological and baryonic model, thus capturing possible degeneracies. We find that in this way, we are able to further extract cosmological information and separate it from the astrophysical content.
This paper is structured as follows: in Sect. 2 we briefly summarise our dataset, the DES Y3 cosmic shear catalogue. In Sect. 3 we describe the details of our model and pipeline. In Sect. 4 we report our choices for the Bayesian inference. In Sect. 5 we compare our results with previous works and external datasets in light of the S8 tension. In Sect. 6 we discuss our results and conclude.
2. Data
We employed the public cosmic shear dataset released by the DES Collaboration after three years of data collection1. This includes the cosmic shear correlation functions measured using the GOLD catalogue, which includes more than 100 million galaxy shapes, and the corresponding covariance matrix. The sky coverage is 4143 deg2, the mean redshift of the source galaxies is z = 0.63, and the galaxy weighted number density is neff = 5.59 arcmin−2. We refer to the DES papers for more details (Flaugher et al. 2015; Morganson et al. 2018; Sevilla-Noarbe et al. 2021; Gatti et al. 2021; Myles et al. 2021; Krause et al. 2021; Amon et al. 2022; Secco et al. 2022).
The catalogue of source galaxies was split into four broad redshift bins, roughly equipopulated between z = [0, 1.5] (the maximum nominal redshift is at z = 3, although the number density is very low after z = 1.5 ). The two shear correlation functions, ξ±, are measured in 20 logarithmic angular bins between 2.5 and 250 arcminutes. Joining auto- and cross-correlations for both ξ+ and ξ−, we have a total of 400 data points that are reduced to 227 when the DES scale cuts are considered. The covariance was obtained analytically by summing the Gaussian contribution, the four-point connected part, the super-sample contribution, the survey geometrical effects, and the shape noise (Friedrich et al. 2021). We show our data vector in Fig. 1, where we highlight the data points that were removed by the DES scale cuts with grey bands.
 |
Fig. 1. Cosmic shear correlation functions, ξ±, measured by DES Y3 in four redshift bins, for a total of 400 data points. In the lower left corner we display ξ+, and in the upper right corner, we show ξ−, both multiplied by 104θ for clarity. The corresponding redshift bins are indicated in each subplot. The grey bands show the scales that were discarded in the analysis carried out by the DES Collaboration. We display the best-fitting models that we obtained using the full data vector when considering only gravity (solid blue line), and additionally considering baryonic processes (dashed red line). |
3. Model
3.1. Cosmic shear
We obtained the shear correlation functions in the redshift bins i, j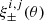 by decomposing the shear field into E and B modes and combining the angular power spectra as
by decomposing the shear field into E and B modes and combining the angular power spectra as
(Crittenden et al. 2002; Schneider et al. 2002; Krause et al. 2021). The 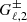 functions were defined from the Legendre polynomials following Stebbins (1996). We efficiently computed Eq. (1) by using the fast Fourier transforms FFTLog (Talman 1978). We used the Limber approximation (Limber 1953), which was shown to be accurate enough for DES Y3 data (Krause et al. 2021). We explicitly verified that the post-Limber correction proposed by Kitching et al. (2017) does not significantly affect our results (≤0.1σ in the cosmology inference).
functions were defined from the Legendre polynomials following Stebbins (1996). We efficiently computed Eq. (1) by using the fast Fourier transforms FFTLog (Talman 1978). We used the Limber approximation (Limber 1953), which was shown to be accurate enough for DES Y3 data (Krause et al. 2021). We explicitly verified that the post-Limber correction proposed by Kitching et al. (2017) does not significantly affect our results (≤0.1σ in the cosmology inference).
The angular power spectra 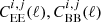 were computed summing the relevant contributions,
were computed summing the relevant contributions,
The purely gravitational signal is given by the term CGG(ℓ), which only contributes to E modes. Within a flat ΛCDM model, we can compute this term as
where PGG(k, z) is the matter power spectrum, χ is the comoving distance, and z is the corresponding redshift. The lensing kernel gi(χ) reads
where ni(z) is the normalised galaxy redshift distribution in each i bin (see Myles et al. 2021, for details of how these are obtained in the DES case), and zH is the redshift of the Hubble sphere. The other terms, CII, EE(ℓ) and CGI, are given by the intrinsic alignment of galaxies, and we recapitulate them in the next section.
3.2. Intrinsic alignment
The measured shear signal includes the physical correlation of galaxy shapes in the sky, which is often referred to as the intrinsic alignment of galaxies. Within a flat ΛCDM framework and using the Limber approximation, the auto-correlation of the intrinsic alignment is given by
and the cross correlation between gravitational shear and intrinsic alignment reads
where for brevity, we omitted the dependence of g, n, and z on χ.
We implemented two models of the intrinsic alignment of galaxies: the non-linear model (NLA; Bridle & King 2007), and the more complex tidal alignment and tidal torque model (TATT; Blazek et al. 2019). The NLA model, with two free parameters, can be considered a specific case of the more general TATT (five free parameters).
Within NLA, the intrinsic alignment auto-correlation and the cross correlation with cosmic shear are
respectively, with
Here, C1 is a normalization constant that is typically set to C1 = 5 × 10−14 (h2 M⊙ Mpc3)−2 (Hirata & Seljak 2004; Bridle & King 2007), z0 = 0.62 is typically assumed in a DES analysis (Secco et al. 2022; Amon et al. 2022), and a1, η1 are free parameters.
In the TATT model, we instead have
and
where for the sake of brevity, we omitted scale and redshift dependences. The power spectra P0|0E, P0E|0E, P0B|0B, and so on were computed within the perturbation theory of Blazek et al. (2019), to which we refer for the details. We evaluated these power spectra using the public code FAST-PT (McEwen et al. 2016; Fang et al. 2017).
Following the convention of Secco et al. (2022) and Amon et al. (2022), we defined
We therefore have the additional free parameters a2, η2, and bTA. When a2 = 0 and bTA = 0 are fixed, TATT is reduced to NLA. There is no consensus on the regime in which NLA and TATT are valid (see e.g., Samuroff et al. 2023). Previous works on DES data have constrained the amplitude parameters of the intrinsic alignment, a1, a2, of the GOLD catalogue to be consistent with zero (Secco et al. 2022; Amon et al. 2022; Abbott et al. 2022; Samuroff et al. 2023). Bayesian evidence indeed prefers a model without any intrinsic alignment, followed by the NLA model. TATT is disfavoured because of its relatively high number of parameters, combined with a low signal compared to the cosmological signal. This can be seen as a preference towards simpler intrinsic alignment models for DES data. Therefore, we employed NLA as our fiducial model. Nonetheless, because we employed angular scales that were previously discarded, we repeated the full analysis with TATT to confirm the robustness of our inference.
3.3. Matter power spectrum
We evaluated the matter power spectrum PGG(k, z) by employing a series of neural network emulators from the BACCO simulation project (Angulo et al. 2021). Specifically, the matter power spectrum was decomposed into three different components: a linear part given by perturbation theory, a non-linear boost function given by N-body simulations, and a baryonic correction given by a baryonification algorithm.
The linear component is a direct emulation of the Boltzmann solver CLASS (Lesgourgues 2011), which speeds up the calculations by several orders of magnitude (Aricò et al. 2022) while introducing a negligible error. The non-linear boost function is built by interpolating results at more than 800 different cosmologies, obtained from five high-resolution N-body simulations of ≈2 Gpc and 43203 particles, together with the method developed by Angulo & White (2010), Angulo & Hilbert (2015), Zennaro et al. (2019), Contreras et al. (2020), and Angulo et al. (2021). This algorithm manipulates the output of a simulation to mimic the expected particle distribution in a very wide cosmological space, with an accuracy of 3% in the power spectrum at k ≈ 5h Mpc−1 in ΛCDM, including massive neutrinos (Contreras et al. 2020; Angulo et al. 2021). Finally, the baryonic correction was computed by applying a baryonification algorithm (Schneider & Teyssier 2015; Aricò et al. 2020) to the N-body simulations.
These emulators were collected in the public repository BACCOemu (Angulo et al. 2021; Aricò et al. 2021b, 2022). We used an updated version of the public emulators that extends the non-linear boost functions from scales k ≤ 5 h Mpc−1 to k ≤ 10 h Mpc−1 and from redshifts z ≤ 1.5 to z ≤ 3 by employing a suite of five higher-resolution N-body simulations (L ≈ 750 Mpc and 22883 particles). The new emulator also features an updated version of the cosmology rescaling algorithm, including a new halo mass function and concentration-mass relation (Ondaro-Mallea et al. 2022; López-Cano et al. 2022), which improves its accuracy. Moreover, the cosmological parameter space was expanded by the addition of a suite of 35 new simulations that encapsulate the priors used here. The only exception is the cold matter cosmic density, Ωc, which nonetheless was extended from [0.23, 0.4] to [0.15, 0.47] (we extrapolated with HALOFIT outside of these boundaries). Typically, more than 99% of the posterior evaluations are within the BACCOemu priors. We show a comparison between HALOFIT and BACCOemu in Appendix A, and we refer to Zennaro et al. (in prep.) for further details and validation.
3.4. Baryonic effects
We modelled the baryonic processes that impact the cosmic density field with a baryonification scheme (Schneider & Teyssier 2015; Aricò et al. 2020). The baryonification, or Baryon correction model (BCM), displaces the particles of a gravity-only simulation according to analytical corrections to take the effects of different baryonic processes on the density field into account. In this framework, haloes are assumed to be constituted by galaxies, gas in hydrostatic equilibrium, and dark matter. A given fraction of the gas is expelled from the haloes by accreting supermassive black holes, and the dark matter back-reacts on the baryon gravitational potential with a quasi-adiabatic relaxation. The BCM has been proven flexible enough to reproduce the two- and three-point statistics of several hydrodynamical simulations (Aricò et al. 2021a; Giri & Schneider 2021), and it has been used to analyse cosmic shear data (Schneider et al. 2022; Chen et al. 2023).
We employed the emulator of the BCM suppression in the matter power spectrum described in Aricò et al. (2020). The emulator fully captures the degeneracies between astrophysical processes and cosmology, and is accurate at the percent level (Aricò et al. 2021b). It has a total of 15 free parameters, 7 to describe the baryonic processes, and 8 for cosmology. We further test the accuracy of the BCM emulator in the modelling of DES Y3 cosmic shear analysis in Appendix B, where we compare the BCM with the hydrodynamical simulation BAHAMAS (McCarthy et al. 2017, 2018).
The cosmological parameter space in which the BCM emulator was trained is smaller than the DES priors. Thus, when sampling a cosmological model that lies outside the emulator space, we set the cosmological parameters of the baryonic response to the closest cosmology available. Additionally, we explicitly set the (cold) cosmic baryon fraction, Ωb/Ωcdm + b, to the closest available value. We expect this to be a good approximation because i) the 1σ region obtained by analysing only the large scales of DES broadly fits into the emulator priors, and ii) the baryonic feedback is mainly dependent on the (cold) cosmic baryon fraction, which is reasonably well covered by our emulator (Ωb/Ωcdm + b ∈ [0.1, 0.26], more than 98% of the posterior samples in our fiducial run fall within this interval).
Our BCM emulator was previously applied to DES Y3 data in Chen et al. (2023) to constrain the impact of astrophysical feedback. They used small-scale DES Y3 shear measurements to constrain Mc, which is the baryonic parameter to which the data are most sensitive. That is, the characteristic halo mass (M200,crit expressed in h−1 M⊙) in which half of the cosmic gas fraction is expelled from the halo by astrophysical processes. Chen et al. (2023) reported that 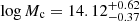 . In the analysis, the cosmology was varied within a prior given by the posterior provided by the 3x2pt analysis of DES Y3, which is the combination of cosmic shear with galaxy clustering and galaxy-galaxy lensing (Abbott et al. 2022).
. In the analysis, the cosmology was varied within a prior given by the posterior provided by the 3x2pt analysis of DES Y3, which is the combination of cosmic shear with galaxy clustering and galaxy-galaxy lensing (Abbott et al. 2022).
The other free parameters of the BCM describe the shape of the density profile of the hot gas (θinn,θout,Minn), the galaxy-halo mass ratio (Mz0,cen), the AGN feedback range η, and the gas fraction - halo mass slope (β). We refer to Aricò et al. (2021a,b) for further details.
We set all the BCM parameters free to avoid relying on a specific hydrodynamical simulation. We also explicitly tested the impact of fixing all the BCM parameters except for Mc, as was done in Chen et al. (2023).
3.5. Nuisance parameters
Following the DES Collaboration, we modelled the uncertainties on the photometric redshift estimate of source galaxies as the shift in the redshift distributions in each redshift bin 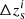 . Furthermore, we modelled the unaccounted-for effects of the shape calibration and blending of the galaxy shapes with a multiplicative bias independently for each redshift bin, mi. For the photometric errors and shear bias, we employed the informative priors used in Secco et al. (2022) and Amon et al. (2022).
. Furthermore, we modelled the unaccounted-for effects of the shape calibration and blending of the galaxy shapes with a multiplicative bias independently for each redshift bin, mi. For the photometric errors and shear bias, we employed the informative priors used in Secco et al. (2022) and Amon et al. (2022).
3.6. Pipeline
We implemented a WL analysis pipeline from scratch. The pipeline was interfaced with the cosmology library BACCO (Angulo et al., in prep.) and the BACCOemu emulators. It is written in python, with a multi-threaded C core for the most computationally demanding functions. As input, the pipeline takes a series of parameters (including cosmological, astrophysical, intrinsic alignment, photometric errors, and shear bias parameters), and it outputs the predicted shear correlation functions.
We performed the Bayesian analysis with a nested sampling algorithm, the public code POLYCHORD (Handley et al. 2015). We followed the guidelines of Lemos et al. (2022; Table 3) and used their publication-quality setting, which features 500 live points and a tolerance of 0.01. We assumed a Gaussian likelihood with a covariance matrix provided by the DES collaboration.
In contrast to the official DES analysis, we chose not to include the so-called shear ratios (Sánchez et al. 2022; Amon et al. 2022). Defined in Sánchez et al. (2022), shear ratios measure the galaxy-galaxy lensing produced by the same lenses with different source galaxy samples. The authors found that even at the smallest angular scales measured by DES Y3, these ratios are robust to changes in cosmology, baryonic processes, and galaxy bias, but are highly sensitive to the source galaxy redshift distribution and intrinsic alignment. Despite the potential benefits, we opted to focus on shear data alone for two reasons: i) we avoid complications such as modelling of the galaxy bias, which we should coherently include in our current framework, and ii) we can better isolate the information on intrinsic alignment and redshift distributions coming from the small scales of cosmic shear.
We generally used the same priors as the official DES analyses (Secco et al. 2022; Amon et al. 2022; Abbott et al. 2022), except for the upper boundary of Ωm, which was 0.7 in our analysis instead of 0.9, the boundary of h, which was 0.9 instead of 0.91, and instead of the sum of neutrino masses Mν, which was 0.4 instead of 0.6, to fit in the parameter space of our emulator. We verified with HALOFIT that these new priors did not significantly affect our final results. Specifically, we only detect a small bias of less than 0.1σ on the cosmological constraints, given by the different prior on Mν. This broadly agrees with what was found in Secco et al. (2022) and Amon et al. (2022) when fixing the sum of neutrino masses. The priors on baryonic parameters were those discussed in Aricò et al. (2021b), which were chosen to be wide enough to encompass X-ray observations and hydrodynamical simulations.
We summarise the priors we used in Table 1. In our fiducial run, we used the NLA intrinsic alignment model, that is, a2 = η2 = bta = 0. We also included an additional flat prior Ωbh2 ≤ 0.04 given by Big Bang nucleosynthesis (Beringer et al. 2012), analogously to that adopted in CosmoSIS and by the DES Collaboration (Zuntz et al. 2015; Abbott et al. 2022).
Priors on the free parameters employed in our Bayesian analyses.
We validated our pipeline by performing a model comparison with the public codes implemented in CosmoSIS (Zuntz et al. 2015) and in the core cosmology library (CCL;Chisari et al. 2019), finding an excellent agreement between the three. We also performed a test run employing HALOFIT (Takahashi et al. 2012) and NLA and using the official DES scale cuts. We compare these results with the chains run with the DES pipeline and CosmoSIS in Fig. 2, where we show only the Ωm − S8 plane for convenience. The chains against which we compared were from private communications because the public chains include shear ratios. Throughout the paper, we use the definition 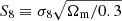 . We find a difference between the two pipelines of about 0.1σ, which agrees very well when we consider all the different details of the implementation (e.g., binning, numerical accuracy, interpolation, and emulators). Although not shown here, we verified that the agreement holds true for all the free parameters of the model.
. We find a difference between the two pipelines of about 0.1σ, which agrees very well when we consider all the different details of the implementation (e.g., binning, numerical accuracy, interpolation, and emulators). Although not shown here, we verified that the agreement holds true for all the free parameters of the model.
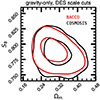 |
Fig. 2. Comparison between the posterior distribution on |
As a further validation of our pipeline and in order to check for possible biases introduced when analysing the smallest scales used in this work, we computed the χ2 values obtained using an independent advanced model, and compared them with ours. We used a model composed of i) EuclidEmulator2 (Euclid Collaboration 2021) for the non-linear matter power spectrum, ii) the baryonic suppression measured in the BAHAMAS suite of hydrodynamical simulations (McCarthy et al. 2017), and iii) the TATT intrinsic alignment of galaxies (Blazek et al. 2019).
Comparing this model with our fiducial one for different cosmological and baryonic parameters (Planck and DES Y3 best-fitting cosmologies (Planck Collaboration VI 2020; Amon et al. 2022; Secco et al. 2022), and the BAHAMAS low, reference, and high AGN suppressions), we find fractional differences in χ2 below 1%. By contrast, the difference in χ2 between baryonic modelling and gravity-only is about 5–15%. The difference in χ2 between NLA and TATT is highly dependent on the value of the TATT parameters (a2, bTA), and can be lower than 1% and higher than 20%. We do not know the amplitudes of TATT for a survey such as DES a priori, although previous studies point toward low amplitudes (and thus smaller χ2 differences). Therefore, we compared the results obtained with NLA and TATT a posteriori in Appendix E.
Finally, we note that we evaluated a likelihood in less than 0.5 seconds on a common laptop with our pipeline, whereas it takes about 8 seconds to run a standard DES Y3 cosmic shear likelihood evaluation with CosmoSIS.
4. Analysis
In this section, we employ the pipeline described and validated in Sect. 3 to obtain constraints on the cosmology, baryonic physics, and intrinsic alignment of galaxies. We explore different levels of complexity in our model and study their impact on cosmology inference. We focus on the derived cosmological parameter S8, and on Ωm. When showing the credible levels in the S8 − Ωm plane, we display the 1σ and 2σ levels (i.e. 39% and 86% in 2D), as opposed to the 68% and 95% normally shown in DES papers, to visually help the assessment of the tensions between different models and datasets. Unless stated otherwise, we quote all our constraints as the mode of the 1D marginalised posterior, plus and minus the respective 34th percentiles. We caution against directly comparing with the official DES constraints, which typically report the mean of the marginalised posterior. To facilitate the comparison, we reanalysed the DES Collaboration chains with the same routine as we used for our chains (ChainConsumer; Hinton 2016). We report in Table 2 the constraints obtained with the mode and in Table C.1 those with the median of the posteriors, and their respective 34th percentiles.
Constraints (mode of the 1D marginalised posteriors and the respective 34th percentiles) on S8 and Ωm obtained applying DES scale cuts and using all the angular scales.
4.1. Constraints on cosmology and goodness of fit
In Fig. 3 we show the posterior distribution functions of the cosmological parameters S8 and Ωm assuming only gravitational interactions (left panel) and including our fiducial seven-parameter baryonic model (right panel). In each case, we display our results when applying DES scale cuts (black lines) and when employing all scales (red). When using our fiducial model and analysing all the angular scales available, we obtain 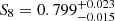 and
and 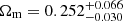 . In Table 2 we report the constraints on S8 and Ωm obtained with different modelling choices, and in Appendix C we show the posteriors of all the free cosmological parameters in our fiducial run.
. In Table 2 we report the constraints on S8 and Ωm obtained with different modelling choices, and in Appendix C we show the posteriors of all the free cosmological parameters in our fiducial run.
 |
Fig. 3. 1σ and 2σ credible levels on S8 and Ωm obtained using BACCO, considering only gravity in structure formation (left panel) and including baryonic effects (right panel). The solid black lines refer to runs to which scale cuts were applied, and the solid red lines show runs in which all scales are used. The dotted black line in the right panel shows the results of the gravity-only model with scale cuts for reference. |
The models with and without baryons both provide a statistically good fit of the data, as shown in Fig. 1 (solid red and dashed blue lines, respectively). More quantitatively, we report the goodness of fit for all our models in Table 3, defined with the reduced χ2,
Goodness of fit of our models given the DES Y3 data vector.
where 𝒟 is our data vector, ℳ is our model, 𝒞 is the covariance, and the degrees of freedom (d.o.f.) are found by subtracting the number of parameters Nθ from the number of data points (N𝒟). We used as Nθ either the number of free parameters Nfree or the number of effective parameters Neff as defined in Raveri & Hu (2019). When using Nfree, we find a slightly higher  in the case with baryons with respect to the gravity-only run (
in the case with baryons with respect to the gravity-only run (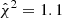 and
and 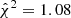 , respectively), due to the seven additional free parameters. When using Neff, we instead find
, respectively), due to the seven additional free parameters. When using Neff, we instead find 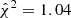 with baryons and
with baryons and 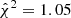 in the gravity-only case, which corresponds to p-values of 0.27 and 0.24, respectively. Nonetheless, the posteriors in the S8-Ωm plane are quite different, the gravity-only posterior is tighter and shifted towards lower values of S8.
in the gravity-only case, which corresponds to p-values of 0.27 and 0.24, respectively. Nonetheless, the posteriors in the S8-Ωm plane are quite different, the gravity-only posterior is tighter and shifted towards lower values of S8.
4.2. Cosmological information at small scales
Although the DES measurements of the shear correlation functions reach angles as small as 2.5 arcminutes, the DES Collaboration has so far refrained from modelling these small scales because of possible biases in the cosmology inference due to the effects of baryons. In particular, they set different angular scale cuts for ξ+ and ξ− and each redshift bin.
The DES scale cuts were chosen such that the difference in χ2 between analyses carried on with a given synthetic data vector and the same data vector contaminated with the baryonic effects predicted by the hydrodynamical simulation OWLS-AGN (Schaye et al. 2010) is lower than a given threshold (for more details, see e.g., Krause et al. 2021). This results in retaining 227 data points over 400 (166 in ξ+, 61 in ξ−).
To quantify the amount of cosmological information loss when discarding the small angular separations from the analysis, we ran our pipeline with and without these scale cuts. First, we neglected the effects of baryonic physics to obtain a sense of the improvement in the cosmological constraints in an ideal scenario, even though the constraints are likely biased. We show the 1σ and 2σ credible levels of S8 and Ωm in the left panel of Fig. 3. Adopting the DES scale cuts, we obtain 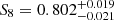 , whereas including smaller scales, we find
, whereas including smaller scales, we find 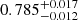 . This constraint is tighter by 30%. This can be seen as the upper limit on the cosmological information that we can potentially gain when modelling the small scales. We note, however, that this figure is specific to DES Y3 data because it depends on the statistical accuracy with which small scales are measured. For surveys with a higher number density of background galaxies, better photometry and angular resolution, we expect the gains to be more substantial.
. This constraint is tighter by 30%. This can be seen as the upper limit on the cosmological information that we can potentially gain when modelling the small scales. We note, however, that this figure is specific to DES Y3 data because it depends on the statistical accuracy with which small scales are measured. For surveys with a higher number density of background galaxies, better photometry and angular resolution, we expect the gains to be more substantial.
When small scales are included, the S8 posterior shifts by about 0.5σ towards lower values. This is likely caused by baryonic processes: the lack of modelling of the suppression in the matter power spectrum caused by baryons could be compensated for by a lower inferred value of σ8 and Ωm. Hence, to be able to exploit the data on small scales, it is necessary to explicitly model the role of baryonic physics.
4.3. Impact of baryons
Baryonic processes such as gas cooling, galaxy formation, and active galactic nuclei (AGN) modify the cosmic matter power spectrum in a nontrivial way. The scales and amplitudes of their effects are currently debated and might affect the cosmology inference if they are not properly taken into account.
We modelled the impact of baryonic processes on the cosmic shear via the baryonification emulator described in Sect. 3.4. We show the constraints on S8 and Ωm that we obtained with and without scale cuts in the right panel of Fig. 3. We obtain 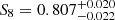 with the DES scale cuts and
with the DES scale cuts and 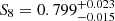 without scale cuts. Interestingly, when we applied the scale cuts, the marginalisation over baryons did not broaden the S8 constraints significantly, although it slightly shifted the posterior towards high S8, by 0.2σ. This might be caused by a residual signal of baryonic effects in the data vector even after imposing the scale cuts, or it might also be a projection effect given by the unconstrained baryonic parameters.
without scale cuts. Interestingly, when we applied the scale cuts, the marginalisation over baryons did not broaden the S8 constraints significantly, although it slightly shifted the posterior towards high S8, by 0.2σ. This might be caused by a residual signal of baryonic effects in the data vector even after imposing the scale cuts, or it might also be a projection effect given by the unconstrained baryonic parameters.
The marginalisation over seven free baryonic parameters has significantly more impact when all the angular scales are analysed: we find the constraint on S8 ≈ 24% weaker than in the gravity-only case, degrading part of the additional cosmological information contained in the small scales. However, we find no bias in the S8-Ωm introduced by the addition of the small scales in the analysis. Moreover, we gain cosmological information when marginalising over baryons and extending to smaller scales. When comparing the constraints we obtain with and without the angular scale cuts, we find S8 and Ωm that are 10% and 22% tighter, respectively.
This finding validates the robustness of the modelling of baryonic processes at all the scales employed in this work. We note that the marginalisation over seven free baryonic parameters is a conservative choice, because as shown in Appendix D, only one of these parameters is strongly constrained by our data.
Therefore, information added on baryonic processes, either with constraints from external datasets or educated guesses from hydrodynamical simulations, could help recover the cosmological information lost in the marginalisation, at least partially. For instance, we could fix the unconstrained baryonic parameters to a value inferred with hydrodynamical simulations, analogously to Chen et al. (2023). By setting all the parameters except for Mc to the best-fitting parameters of the matter power spectrum of the hydrodynamical simulations BAHAMAS at z = 0, we obtained 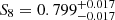 , which agrees perfectly with our fiducial case, but is 15% tighter and with a better
, which agrees perfectly with our fiducial case, but is 15% tighter and with a better 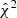 .
.
4.4. Constraints on baryons
By including all available angular scales in our analysis, we were able to constrain the astrophysical processes that modify the gravitational evolution of the cosmic density field. In particular, it has been shown that the suppression in the matter power spectrum is proportional to the gas fraction expelled from haloes by baryonic feedback processes (Schneider & Teyssier 2015; van Daalen et al. 2020). We parametrised this fraction with Mc, which is the characteristic halo mass for which half of the gas is depleted.
In Fig. 4 we show our constraints on log Mc when including or excluding the small scales that were removed in the official DES analysis. When we applied the DES scale cuts, log Mc was unconstrained, as expected, even though the data might have a residual sensitivity to baryonic effects, with higher values of Mc slightly preferred (blue line). When we analysed all the angular scales, we obtained a tight constraint ![$ \log M_{\mathrm{c}} = 14.38^{+0.60}_{-0.56} \, [\log ({h^{-1}{M}_{ \odot}})] $](/articles/aa/full_html/2023/10/aa46539-23/aa46539-23-eq83.gif) (red line).
(red line).
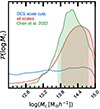 |
Fig. 4. Posterior distribution functions of log Mc obtained in our fiducial run using all angular scales (red) and applying scale cuts (blue). We compare this with the posterior obtained by Chen et al. (2023) using only small scales, fixing six baryonic parameters, and applying a prior on cosmology given by the 3x2pt analysis of DES Y3 (Abbott et al. 2022). |
We find an excellent agreement between our estimate of Mc and that obtained by Chen et al. (2023; green line), who employed the same model as we did. However, our constraints are slightly weaker due to the different assumptions in the two analyses: first, Chen et al. (2023) employed an informative prior on cosmology, with all cosmological parameters fixed except for σ8 and Ωm, given by the 3x2pt analysis of DES Y3. Second, Chen et al. (2023) used only the data points with angles smaller than the DES scale cuts and a TATT intrinsic alignment model, and they fixed all the baryonic parameters except for Mc to the best-fitting values of the hydrodynamical simulation OWLS-AGN (Schaye et al. 2010). The different priors in cosmology (i.e. the additional information on cosmology retrieved by galaxy clustering, galaxy-galaxy lensing, and shear ratios) likely have the largest impact.
The posterior of log Mc hits the boundary of its prior at log Mc = 15 [log(h−1 M⊙)]. This prior was chosen to broadly encompass the current measurement of gas fractions in galaxy clusters measured in X-rays (Vikhlinin et al. 2006; Arnaud et al. 2007; Sun et al. 2009; Giodini et al. 2009; Gonzalez et al. 2013), as well as the prediction of hydrodynamical simulations McCarthy et al. (2017, 2018). Therefore, we note that we explicitly added to our analysis prior information on the quantity of gas inside haloes, which cannot be lower than half the cosmic baryon fraction for haloes with mass M200, c = 1015h−1 M⊙. Even when we argue that the prior on Mc is broad enough given the X-ray data, we plan to build the next version of the baryonic emulator by extending the prior Mc to higher values to better cover the parameter space allowed by WL-only data.
The remaining six free baryonic parameters were unconstrained, and we show their posteriors in Appendix D.
Finally, in Fig. 5 we show the estimated suppression in the matter power spectrum at z = 0. Specifically, we show the 1σ credible interval that we obtained by taking into account the full posterior of the free cosmological and baryonic parameters in our analysis. We compare it to the BCM best-fitting models to several current hydrodynamical simulations, obtained in Aricò et al. (2021b): EAGLE (Schaye et al. 2015; Crain et al. 2015; McAlpine et al. 2016), Illustris (Vogelsberger et al. 2014), Illustris TNG (Pillepich et al. 2018; Springel et al. 2018), OWLS-AGN (Schaye et al. 2010), and BAHAMAS (McCarthy et al. 2017, 2018). We infer a suppression of about 10% at k = 2h Mpc−1, which broadly agrees with the BAHAMAS suite and OWLS-AGN, but it is stronger than EAGLE and Illustris TNG and milder than Illustris. This finding agrees perfectly with Chen et al. (2023), although because we let all the baryonic parameters free, our model is more flexible at large scales, for example (which are dominated by η, i.e. the distance range of the AGN feedback), and small scales (modulated by 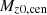 and θinn, which regulate the galaxy-halo mass relation and inner shape of the gas, respectively).
and θinn, which regulate the galaxy-halo mass relation and inner shape of the gas, respectively).
 |
Fig. 5. 1σ credibility region of the suppression in the matter power spectrum at z = 0 caused by baryons, inferred by the BCM model with DES Y3 data (shaded grey area). We display the ratio of the matter power spectrum affected by baryonic processes to the spectrum calculated considering only gravity. For comparison, we show the BCM models obtained in Aricò et al. (2021b), fitting several current hydrodynamical simulations referenced in the main text, according to the legend. |
4.5. Correlation between cosmological and baryonic parameters
Constraints on cosmology and baryonic physics are not independent. For instance, the impact of AGN on the matter field depends on the amount of gas that is affected by feedback from supermassive black holes, and therefore on the cosmic baryon fraction Ωb/Ωm. Moreover, the amplitude of the linear density fluctuations, σ8, affects the baryonic feedback in a minor and less trivial way (Schneider et al. 2020; Aricò et al. 2021b). We can thus expect to find a correlation between S8 and Mc. We show the 1σ and 2σ credible levels of these two parameters in Fig. 6. The degeneracy is weak but clear, so that at high values of Mc correspond high values of S8. For comparison, we display as bands the Planck TT+TE+EE+lowE 1σ intervals on S8 obtained by the DES Collaboration (Planck Collaboration VI 2020; Secco et al. 2022) and our gravity-only analysis with all the angular scales. Following the degeneracy direction in S8 − Mc, the lower values of Mc agree with the S8 values obtained by our DES gravity-only analysis, whereas at high values of Mc, the value of S8 becomes more compatible with Planck. We study the implications in the context of the so-called S8 tension in Sect. 5, but before, we discuss the constraints on intrinsic alignments from our small-scale analysis.
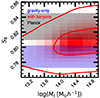 |
Fig. 6. Degeneracy between S8 and log Mc, displaying the 1σ and 2σ credible levels (red), and using all angular scales. For comparison, we show as a horizontal band the 1σ constraints on S8 obtained by analysing all angular scales without modelling baryons (blue), and using the Planck TT+TE+EE+lowE posterior obtained by the DES Collaboration (black; Planck Collaboration VI 2020; Secco et al. 2022). |
4.6. Constraints on intrinsic alignment
Our model allows us to constrain the intrinsic alignment of galaxies taking advantage of all the angular scales of DES Y3. With the NLA model and using DES angular scale cuts, we find 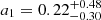 and
and 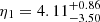 . Interestingly, when small scales are included, a tighter constraint on η1 but not on a1 is obtained: removing the scale cuts, we infer
. Interestingly, when small scales are included, a tighter constraint on η1 but not on a1 is obtained: removing the scale cuts, we infer 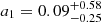 and
and 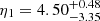 .
.
The NLA model seems to be sufficient to describe the full range of angular scales in DES. The NLA is statistically preferred over TATT: the ratio of the Bayesian evidence ℛ = 𝒵NLA/𝒵TATT = 3.0 ± 1.2. This value indicates a moderate or substantial preference for NLA over TATT, according to the commonly used (and somewhat arbitrary) Jeffreys scale (Jeffreys 1935). For comparison, the baryonic model with seven free parameters is preferred to the gravity-only model with a ℛ = 1.5 ± 1.2, and freeing only the baryonic parameter Mc, ℛ = 5.14 ± 1.2. Despite this, the goodness of fit is marginally better with TATT, 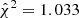 , with respect to NLA
, with respect to NLA 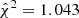 .
.
Our inferred amplitudes of TATT in the DES galaxy sample are very low and consistent with zero, in agreement with Secco et al. (2022) and Amon et al. (2022). This means that the intrinsic alignment contribution is subdominant with respect to the cosmological signal, and that simpler models are statistically preferred. We also find internal degeneracies in TATT that produce a multi-modal posterior of the tidal torque amplitude. We further analyse and discuss the results obtained with TATT in Appendix E.
5. The S8 tension
In this section, we compare the cosmological constraints that we obtained by analysing the cosmic shear of DES Y3 with external datasets in light of the so-called S8 difference. We also compare our results with the official results obtained by the DES Collaboration, and discuss the main differences in the analyses.
Throughout this section, we quantify the difference among datasets or analyses by approximating the marginalised posteriors as Gaussian-distributed functions, and considering the mean and standard deviation following Heymans et al. (2021) for instance (for a method that takes non-Gassianity into account, see e.g., Raveri & Doux 2021).
5.1. Effect of different model assumptions on the S8 tension
In Fig. 7 we compare our results with the results from the analysis of Planck satellite data including temperature and polarisation measurements (TT+TE+EE+lowE power spectra). Specifically, we used the chains made available by the DES Collaboration2, where the Planck likelihood is sampled over the same prior-space used in the DES analysis (and therefore almost identical to ours). We also show our fiducial analysis (no scale cuts, explicit model for baryons, NLA for intrinsic alignments, and emulators for the matter power spectrum) as red lines, and the gravity-only case as blue lines.
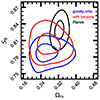 |
Fig. 7. 1σ and 2σ credible levels on S8 and Ωm using the Planck TT+TE+EE+lowE posteriors of the DES Collaboration (black; Planck Collaboration VI 2020; Secco et al. 2022) and DES Y3 cosmic shear data, analysing all the angular scales either with our fiducial model (red) or without modelling baryons (blue) obtained in this work. |
Our marginalised posteriors on S8 are in tension by 1.9σ in the gravity-only case compared to Planck. However, the difference reduces to 0.9σ when marginalising over baryonic effects. Therefore, our data suggest that at present, Planck and DES Y3 are not statistically in tension. Additionally, the agreement between the data might increase further if, for instance, external datasets (e.g., X-ray gas fraction) constrain the baryonic parameters to relatively strong feedback.
Combining these datasets is a non-trivial task because of different systematics, such as hydrostatic mass bias and data covariances, and it is beyond the scope of this work. However, this could be an interesting avenue to investigate in the future.
To explore further how the S8 posterior is affected by the modelling of baryons, we considered two different scenarios. First, we fixed all the baryonic parameters except for Mc to the best-fitting values of the matter power spectrum measured in the hydrodynamical simulation BAHAMAS at z = 0. These values, obtained by Aricò et al. (2021b), are log ηb = −0.33, log βb = −0.28, log Mz0,cen = 10.21[log(h−1 M⊙)], log θinn = −0.62, log θout = 0.12, log Minn = 9.95[log(h−1 M⊙)]. Second, to gain a sense of the most extreme shift in S8 that can be caused by baryonic processes, we set the baryonic parameters to the values that maximise the feedback allowed by our emulator. We thus set log Mc = 15[log(h−1 M⊙)], log ηb = −0.7, log βb = 0.7, log Mz0,cen = 9[log(h−1 M⊙)], log θinn = −0.53, log θout = 0, log Minn = 9[log(h−1 M⊙)]. We note that these parameters are already ruled out by X-ray data, even though we find that they still provide a good fit to the DES Y3 cosmic shear data. We dubbed this model BCM-extreme.
We summarise all our S8 constraints in Fig. 8 and in Table 2. We note that the S8 values inferred with and without scale cuts generally agree well, except for the gravity-only models, where they present 0.5σ (with NLA) and 0.9σ (with TATT) shifts. In particular, our gravity-only analysis with DES scale cuts differs by less than 1σ from Planck when using either NLA or TATT. We can conclude that the DES angular scale cuts reliably remove the baryonic effects, which must be accounted for only when analysing the full DES data vector. This is not true for scenarios with very high baryonic feedback. For example, in our BCM-extreme case, the DES Y3 cosmic shear and Planck agree well (0.1σ), both with and without scale cuts. However, we stress that this a very unlikely baryonic scenario, in which all the gas within haloes up to M = 1015h−1 M⊙ has been pushed for tens of megaparsec, and it must simply be taken as an extreme upper limit of the impact of baryonic processes.
 |
Fig. 8. S8 constraints obtained in this work with different analysis strategies for the DES Y3 data, either applying the scale cuts (grey data points) or employing all the angular scales (red data points). We highlight our fiducial model by displaying a red band that corresponds to its 1σ credible interval. We employed our baryonification (BCM) with one or seven free parameters or fixed all the parameters to extreme baryonic feedback. This last model, dubbed BCM-extreme, differs from X-ray observations, and should be considered as an upper limit for baryonic effects. We also varied the intrinsic alignment model choosing either NLA or TATT. For comparison, in the lower part of the panel we display the constraints obtained from the DES Collaboration chains with scale cuts, adding or removing the shear ratios (black data points; Secco et al. 2022; Amon et al. 2022; Abbott et al. 2022). Moreover, we include the external datasets specified in the legend (blue data points; Planck Collaboration VI 2020; Asgari et al. 2021; Li et al. 2023; Philcox & Ivanov 2022; Nunes & Vagnozzi 2021; Madhavacheril et al. 2023), which we describe in more detail in the main text. We highlight the 1σ region preferred by Planck with a blue band. |
Finally, by comparing the S8 values obtained by varying intrinsic alignment models, we observe in Fig. 8 that the S8 posteriors are generally broader and shifted towards lower values when using TATT. This trend could be caused by internal degeneracies and projection effects of the TATT parameters, which are allowed to vary over a broad parameter space that is not physically motivated, as speculated also by Secco et al. (2022). We explore this in more detail in Appendix E.
5.2. Comparison with the official DES Y3 analysis
Our constraint on S8 is systematically higher than that obtained with the same dataset by the DES Collaboration (Secco et al. 2022; Amon et al. 2022). Even when applying the DES scale cuts, our gravity-only results are 1.4σ away from those of the DES Collaboration. This is a significant discrepancy because both analyses used exactly the same shear correlation functions. We now explore the origin of this discrepancy.
In Fig. 9 we illustrate the impact of various modelling ingredients and choices in the S8 − Ωm constraints. We now discuss specific differences in the analyses.
 |
Fig. 9. Impact of the different modelling choices on explaining the different fiducial cosmological constraints obtained by the DES Collaboration (DES TATT + SR; Secco et al. 2022; Amon et al. 2022) and this work (BACCOemu NLA BCM). We show the 1σ credible level of S8 and Ωm (solid lines) and maximum posteriors (stars) obtained by the DES Collaboration with the CosmoSIS pipeline and different choices regarding the intrinsic alignment model and the use of shear ratios (black, brown, and red, according to the legend). Analogously, we also show our results, obtained with the BACCO pipeline using HALOFIT (orange), or BACCOemu without and with baryons (green and blue, respectively). |
Intrinsic alignments. The fiducial intrinsic alignment model is an important choice. We estimate a shift toward high S8 between 0.4σ and 0.7σ when using NLA instead of TATT, depending on modelling choices such as scale cuts, baryonic modelling, and shear ratios. As we have argued before (Sect. 4.6), although TATT is a more complete description of intrinsic alignments in principle, the additional complexity is not justified by the current data. This is the case for the DES analysis and scale cuts as well as for our approach including small scales.
Shear ratios. Another difference is that we did not employ the lensing shear ratios. In the DES analysis, excluding the shear ratios increases S8 by ≈0.1 and 0.3σ when employing NLA and TATT, respectively. The shift is arguably caused by stronger constraints on the photo-z uncertainties and intrinsic alignment parameters. In agreement with our finding, Secco et al. (2022) and Amon et al. (2022) reported that the inclusion of shear ratios shifts the intrinsic alignment amplitude towards slightly negative values (although still compatible with zero). This is not expected physically in the absence of systematic errors in the data. On the other hand, with a physically motivated prior a1 ∈ [0, 5], these authors find that their posteriors on S8 did not shift significantly. However, the impact is dependent on the intrinsic alignment model used and the addition or subtraction of shear ratios.
5.2.1. Photo-z distributions
An advantage of using shear ratios is that they provide information on the redshift distribution of background galaxies. Notably, we find that small scales provide a similar level of information on photometric redshifts. It is thus interesting to compare their constraints because including shear ratios or not does affect the inferred S8 value. We show as an example the posterior of 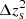 in Fig. 10 (see Appendix F for other redshift bins). This photo-z parameter differs most between our analysis and that of DES with shear ratios.
in Fig. 10 (see Appendix F for other redshift bins). This photo-z parameter differs most between our analysis and that of DES with shear ratios.
 |
Fig. 10. Prior (black) and posteriors of the photo-z shift in the second tomographic bin |
Firstly, when the small scales are included, a constraining power on 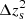 is provided, which is similar to that of shear ratios, even after marginalisation over baryons. Specifically, in our fiducial analysis, we obtain
is provided, which is similar to that of shear ratios, even after marginalisation over baryons. Specifically, in our fiducial analysis, we obtain ![$ \sigma[\Delta z_{\rm s}^2]\approx0.012 $](/articles/aa/full_html/2023/10/aa46539-23/aa46539-23-eq94.gif) when applying DES scale cuts, and ≈0.01 when including small scales. This precision is comparable to the precision that is obtained when shear ratios are included, ≈0.009. Our approach has the advantage of not relying on the modelling of the galaxy-galaxy lensing, and thus galaxy bias, lenses redshift distributions, and so on.
when applying DES scale cuts, and ≈0.01 when including small scales. This precision is comparable to the precision that is obtained when shear ratios are included, ≈0.009. Our approach has the advantage of not relying on the modelling of the galaxy-galaxy lensing, and thus galaxy bias, lenses redshift distributions, and so on.
Moreover, we note that our posterior on 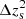 agrees well with the Gaussian prior and with the analysis with DES scale cuts. Instead, when using shear ratios, the data prefer a shift in the mean photo-z of ≈0.0025. Given the sensitivity of the shear signal to the redshift distributions of the sources, these might cause part of the small shift in the cosmological constraints observed when comparing results with and without shear ratios. The information extracted from the small scales of the cosmic shear is not alarmingly different from the information contained in the small scales of shear ratios. However, as the precision of WL surveys increases, this comparison can provide a good sanity check to highlight possible shortcomings in the modelling of cosmic shear and galaxy-galaxy lensing.
agrees well with the Gaussian prior and with the analysis with DES scale cuts. Instead, when using shear ratios, the data prefer a shift in the mean photo-z of ≈0.0025. Given the sensitivity of the shear signal to the redshift distributions of the sources, these might cause part of the small shift in the cosmological constraints observed when comparing results with and without shear ratios. The information extracted from the small scales of the cosmic shear is not alarmingly different from the information contained in the small scales of shear ratios. However, as the precision of WL surveys increases, this comparison can provide a good sanity check to highlight possible shortcomings in the modelling of cosmic shear and galaxy-galaxy lensing.
5.2.2. Non-linear modelling
Another difference is that we employed a more precise model for the non-linear matter power spectrum, especially in the case of massive neutrinos. We show in Appendix A the difference in our cosmology constraints that is obtained when using our non-linear emulator or HALOFIT, which was used by the DES Collaboration. By using BACCOemu, the S8 constraints are shifted by 0.4σ toward high values when applying DES scale cuts, and up to 0.5 when considering all angular scales. The slightly different choice for the Mν prior has a comparatively small effect of 0.1σ.
Baryonic modelling and pipeline. Finally, we note an additional 0.2σ shift caused by the marginalisation over baryons when applying DES scale cuts. We should also consider a 0.1σ shift given by the pipeline implementations in BACCO and CosmoSIS.
To summarise, we find that the fiducial modelling of intrinsic alignment and non-linearities cause the largest shift in S8. Notably, most of the effects listed here shift the S8 posterior towards higher values. Thus, as shown in Fig. 9, smaller effects (with DES scale cuts) such as the baryon marginalisation and the addition of shear ratios, other than the difference in Mν prior, also accumulate to cause the final 1.4σ discrepancy that we report.
5.3. Comparison with other datasets
When assuming ΛCDM, several authors have claimed that LSS observations prefer statistically lower values of S8 compared to temperature and polarisation fluctuations measured by Planck (Planck Collaboration VI 2020). For instance, by using only BOSS data and exploiting the full shape of the galaxy power spectrum and bispectrum, Philcox & Ivanov (2022) inferred S8 = 0.751 ± 0.039. This figure agrees with lensing measurements and is lower than Planck. Nunes & Vagnozzi (2021) used a compilation of growth rates from the redshift space distortions (RSD) measured in different surveys, combined with baryonic acoustic oscillations (BAO) and type Ia supernovae, and found 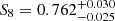 .
.
For weak-lensing data, Secco et al. (2022) and Amon et al. (2022) found that the DES Y3 cosmic shear is different by 2.3σ from Planck, according to the so-called Bayesian suspiciousness (Handley & Lemos 2019), where the prior volume effects are removed from the Bayes ratios. When projected to the S8 parameters, they found 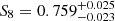 , while Planck data suggest
, while Planck data suggest 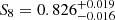 . When galaxy-galaxy lensing and galaxy clustering are added (3x2pt analysis), the suspiciousness decreases to 0.7σ.
. When galaxy-galaxy lensing and galaxy clustering are added (3x2pt analysis), the suspiciousness decreases to 0.7σ.
Similarly, with the cosmic shear analysis of the Kilo Degree Survey (KiDS), Asgari et al. (2021) measured 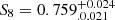 and reported a 3σ tension in the S8 posterior. Combining the KiDS cosmic shear analysis with the redshift-space galaxy clustering from the Baryon Oscillation Spectroscopic Survey (BOSS; Alam et al. 2015) and the 2-degree Field Lensing Survey (2dFLenS, Blake et al. 2016), Heymans et al. (2021) obtained
and reported a 3σ tension in the S8 posterior. Combining the KiDS cosmic shear analysis with the redshift-space galaxy clustering from the Baryon Oscillation Spectroscopic Survey (BOSS; Alam et al. 2015) and the 2-degree Field Lensing Survey (2dFLenS, Blake et al. 2016), Heymans et al. (2021) obtained 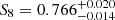 , and claimed a tension with Planck between 2σ and 3σ.
, and claimed a tension with Planck between 2σ and 3σ.
Recently, the Subaru Hyper Supreme-Cam (HSC) Collaboration published the cosmic shear analysis after the third year of data collection, reporting 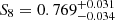 with correlation functions (Li et al. 2023), and
with correlation functions (Li et al. 2023), and 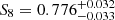 with power spectra (Dalal et al. 2023).
with power spectra (Dalal et al. 2023).
Our fiducial constraint on S8 is systematically higher but broadly agrees with results from the shear-only analyses of these surveys. Our preferred value is approximately 1.5σ higher than that of KIDS-1000, 1.4σ higher than in DES Y3, and 0.8σ above HSC Y3 (analysis with correlation functions). It is unclear, however, how much of this tension would be reduced by homogenising analysis choices and the improvements we adopted in our pipeline, given the different scales and redshifts probed in the analyses. At the small scales, KiDS-1000 stops at 0.5 arcmins in xi+ and 4 arcmins in xi−, whereas HSC Y3 stops at 7.1 arcmins in ξ+ and 31.2 arcmins in ξ−. The two surveys model the baryonic suppression with HMcode (Mead et al. 2015).
Using more refined baryonic modelling, the BCM emulator described in Giri & Schneider (2021), Schneider et al. (2022) analysed the cosmic shear measured by KiDS-1000 using external data from X-ray and kinetic Sunyaev-Zel’dovich (kSZ). In agreement with our results, they found that baryons reduce the tension with Planck, from 3.8σ to 2.6σ in KiDS. They noted that KiDS-1000 data alone are not enough to constrain baryonic physics (whereas we find that DES Y3, arguably due to the larger sky area, can constrain the most important parameter, Mc). By adding X-ray and kinetic Sunyaev-Zel’dovich (SZ) data, they were able to constrain three out of seven baryonic parameters, and measured a mild-to-strong feedback that broadly agreed with that measured with DES Y3. Overall, they reported a similar impact of baryons on cosmology as what we found by analysing all the angular scales of DES Y3, a shift in S8 of about 1σ towards higher S8.
Using HMcode (Mead et al. 2020) as a model for baryons, Tröster et al. (2022) combined the cosmic shear from KiDS-1000 with the cross correlation between shear and thermal SZ (tSZ), measured by Planck and the Atacama Cosmology Telescope (ACT; Mallaby-Kay et al. 2021). They reported an improvement on the S8 constraint of 40% in the joint analysis, but did not reduce the S8 tension: they inferred 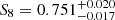 , at 3.4σ from Planck (see also a similar analysis by Robertson et al. (2021) cross-correlating KiDS with Planck/ACT CMB lensing). However, because HMcode has explicitly been calibrated to reproduce the BAHAMAS hydrodynamical simulations, it is not clear whether these results would hold with more flexible baryonic modelling such as that we propose here.
, at 3.4σ from Planck (see also a similar analysis by Robertson et al. (2021) cross-correlating KiDS with Planck/ACT CMB lensing). However, because HMcode has explicitly been calibrated to reproduce the BAHAMAS hydrodynamical simulations, it is not clear whether these results would hold with more flexible baryonic modelling such as that we propose here.
Interestingly, a very recent analysis of the CMB lensing from ACT DR6, in combination with BAO data, reported S8 = 0.849 ± 0.028 (Madhavacheril et al. 2023; Qu et al. 2023), which agrees perfectly with the inference from Planck CMB anisotropies.
A different way to improve the accuracy of current constraints is to take advantage of the fact that at the moment, LSS surveys are largely independent of each other. Combining six different cosmic shear, galaxy clustering, and CMB lensing surveys, García-García et al. (2021) placed a tight constraint of 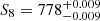 , 3.4σ in tension with Planck. Unfortunately, precise non-linearities and baryons were not included in this analysis. Additionally, the modelling inevitably requires several assumptions regarding the way in which galaxies trace the underlying matter field.
, 3.4σ in tension with Planck. Unfortunately, precise non-linearities and baryons were not included in this analysis. Additionally, the modelling inevitably requires several assumptions regarding the way in which galaxies trace the underlying matter field.
Finally, as we have discussed in the previous section, our analysis pipeline and choices deliver constraints that differ somewhat from those of the official DES Collaboration. Thus, it would be interesting in the future to reanalyse the data from KiDS and HSC jointly, including small-scale information and the advances we have described in this paper. Furthermore, as these WL surveys provide measurements that are at different redshifts, they could be combined to further constrain the time evolution of baryonic processes.
Similarly, it is important to study the role of the intrinsic alignment models and photo-z systematic errors in greater detail. Finally, to robustly combine WL with clustering data, it will be essential to consider the accuracy of current models for galaxy biasing. For instance, correlations between galaxy number and halo properties, baryons, and assembly bias all affect galaxy clustering and galaxy-galaxy lensing in different manners (see e.g., Chaves-Montero et al. 2023; Contreras et al. 2023), but they are commonly neglected in mock catalogues that are used to validate lensing pipelines. We plan to address all these issues in the future.
6. Conclusions
We have analysed the cosmic shear correlation functions measured in DES Y3, exploiting all the angular scales measured for the first time. We implemented a new fast pipeline to predict the cosmic shear correlation functions, and employed the neural network emulators of BACCOemu to accurately predict the matter power spectrum with non-linearities and baryonic effects. Our main findings are the following:
We find additional information at small scales. Constraints on S8 are tighter by 30% when astrophysical processes are ignored, and still 10% (15%) tighter when marginalising over seven (1) baryonic parameters. These numbers are specific to DES, and we expect the gains to be larger in upcoming surveys.
The S8 posterior shifts by ≈0.5σ towards lower values when removing DES scale cuts and not modelling baryonic effects. The cosmological inference is instead robust against scale cuts when modelling baryons with a baryonification algorithm (Fig. 3).
We constrained baryonic feedback via the BCM parameter Mc. We obtained ![$ \log M_{\mathrm{c}} [{h^{-1}{M}_{ \odot}}] = 14.38^{+0.60}_{-0.56} $](/articles/aa/full_html/2023/10/aa46539-23/aa46539-23-eq105.gif) , which means that haloes with mass M200, c = 1014h−1 M⊙ have lost half of their gas reservoir (Fig. 4).
, which means that haloes with mass M200, c = 1014h−1 M⊙ have lost half of their gas reservoir (Fig. 4).
We find a correlation between S8 and Mc, so that stronger baryonic effects correspond to higher S8. In light of the “S8” tension, this means that stronger baryonic feedback increases the agreement between DES Y3 and Planck (Fig. 6).
We inferred 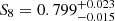 and
and 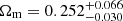 when including the entire range of scales in DES and conservatively marginalising over seven free baryonic parameters. This value S8 is 0.9σ lower than that preferred by Planck TT+TE+EE+lowE data (Fig. 7).
when including the entire range of scales in DES and conservatively marginalising over seven free baryonic parameters. This value S8 is 0.9σ lower than that preferred by Planck TT+TE+EE+lowE data (Fig. 7).
Our inferred value of S8 differs from that inferred in the official DES analysis by 1.4σ (Fig. 9). This is a significant difference because both analyses employed very similar datasets. We attribute the discrepancy to five factors: i) the modelling of intrinsic alignments, ii) the computation of the non-linear power spectrum, iii) the modelling of baryons, iv) the employment of shear ratios by the DES Collaboration, and v) a minor difference between the pipeline and priors used.
We can conclude that with the current data, the modelling details significantly affect the parameter inference and therefore the assessment of the tensions between different datasets. Improving the modelling, as well as explicitly taking into account the theoretical uncertainties in the analysis, appears to be a key step to delivering robust cosmological constraints.
We showed that we can accurately model the cosmic shear of DES Y3, down to the smallest scales available. At these scales, cosmology and astrophysical processes are tightly intertwined, and disentangling them is not an easy task.
In the future, we plan to do this by consistently joining different datasets. Specifically, we will perform a 3x2pt analysis and also model galaxy-galaxy lensing and galaxy clustering to very small scales, by exploiting non-linear bias emulators included in BACCOemu (Zennaro et al. 2023; Pellejero-Ibañez et al. 2022, 2023). To inform the baryonic model, we plan to use X-ray, thermal and kinetic Sunyaev-Zel’dovich datasets, and their cross correlations when possible. This analysis will be of particular importance in the light of the upcoming surveys, such as Euclid and LSST, where the solidity of our modelling framework will be stress-tested in an unprecedented way.
Acknowledgments
We thank David Alonso, Dragan Huterer, Marco Gatti, Francisco Maion, Aurel Schneider, Lucas Secco, and the anonymous referee, for carefully reading the manuscript and providing valuable feedback. We additionally thank Aurel Schneider and Lucas Secco for sharing the chains and results of their analyses, and Marco Gatti for inspiring Fig. 9. We thank all the members of the cosmology group at DIPC for stimulating discussions and help in running N-body simulations. The authors acknowledge the support of the E.R.C. grant 716151 (BACCO). R.E.A. acknowledges the support of the Project of Excellence Prometeo/2020/085 from the Conselleria d’Innovació, Universitats, Ciéncia i Societat Digital de la Generalitat Valenciana, and of the project PID2021-128338NB-I00 from the Spanish Ministry of Science. S.C. acknowledges the support of the “Juan de la Cierva Incorporacíon” fellowship (IJC2020-045705-I). C.H.-M. acknowledges the support of project PID2021-126616NB-I00 from the Spanish Ministry of Science. The authors also acknowledge the computer resources at MareNostrum and the technical support provided by Barcelona Supercomputing Center (RES-AECT-2019-2-0012 and RES-AECT-2020-3-0014). We acknowledge the use of the following software: BACCO & BACCOemu (Angulo et al. 2021; Aricò et al. 2021b, 2022), Fast-PT (McEwen et al. 2016; Fang et al. 2017), POLYCHORD (Handley et al. 2015), CosmoSIS (Zuntz et al. 2015), Core Cosmology Library (CCL, Chisari et al. 2019), NumPy (Harris et al. 2020), mcfit (https://github.com/eelregit/mcfit), SciPy (Virtanen et al. 2020), Matplotlib (Hunter 2007), ChainConsumer (Hinton 2016), corner (Foreman-Mackey 2016), anesthetic (Handley 2019). The data underlying this article will be shared on reasonable request to the corresponding author. This project used public archival data from the Dark Energy Survey (DES). Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology FacilitiesCouncil of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft, and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, The Ohio State University, the OzDES Membership Consortium, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. Based in part on observations at Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.
References
- Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2022, Phys. Rev. D, 105, 023520 [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
- Amon, A., & Efstathiou, G. 2022, MNRAS, 516, 5355 [CrossRef] [Google Scholar]
- Amon, A., Gruen, D., Troxel, M. A., et al. 2022, Phys. Rev. D, 105, 023514 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, R. E., & Hilbert, S. 2015, MNRAS, 448, 364 [CrossRef] [Google Scholar]
- Angulo, R. E., & White, S. D. M. 2010, MNRAS, 405, 143 [NASA ADS] [Google Scholar]
- Angulo, R. E., Zennaro, M., Contreras, S., et al. 2021, MNRAS, 507, 5869 [NASA ADS] [CrossRef] [Google Scholar]
- Aricò, G., Angulo, R. E., Hernández-Monteagudo, C., et al. 2020, MNRAS, 495, 4800 [Google Scholar]
- Aricò, G., Angulo, R. E., Contreras, S., et al. 2021a, MNRAS, 506, 4070 [CrossRef] [Google Scholar]
- Aricò, G., Angulo, R. E., Hernández-Monteagudo, C., Contreras, S., & Zennaro, M. 2021b, MNRAS, 503, 3596 [Google Scholar]
- Aricò, G., Angulo, R. E., & Zennaro, M. 2022, Open Res. Eur., 499, 152 [CrossRef] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2007, A&A, 474, L37 [CrossRef] [EDP Sciences] [Google Scholar]
- Asgari, M., Lin, C.-A., Joachimi, B., et al. 2021, A&A, 645, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beringer, J., Arguin, J.-F., Barnett, R. M., et al. 2012, Phys. Rev. D, 86, 010001 [CrossRef] [Google Scholar]
- Blake, C., Amon, A., Childress, M., et al. 2016, MNRAS, 462, 4240 [NASA ADS] [CrossRef] [Google Scholar]
- Blazek, J. A., MacCrann, N., Troxel, M. A., & Fang, X. 2019, Phys. Rev. D, 100, 103506 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, S., & King, L. 2007, New J. Phys., 9, 444 [Google Scholar]
- Bucko, J., Giri, S. K., & Schneider, A. 2023, A&A, 672, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaves-Montero, J., Angulo, R. E., & Contreras, S. 2023, MNRAS, 521, 937 [Google Scholar]
- Chen, A., Huterer, D., Lee, S., et al. 2021, Phys. Rev. D, 103, 123528 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, A., Aricò, G., Huterer, D., et al. 2023, MNRAS, 518, 5340 [Google Scholar]
- Chisari, N. E., Richardson, M. L. A., Devriendt, J., et al. 2018, MNRAS, 480, 3962 [Google Scholar]
- Chisari, N. E., Alonso, D., Krause, E., et al. 2019, ApJS, 242, 2 [Google Scholar]
- Contreras, S., Angulo, R. E., Zennaro, M., Aricò, G., & Pellejero-Ibañez, M. 2020, MNRAS, 499, 4905 [Google Scholar]
- Contreras, S., Angulo, R. E., Chaves-Montero, J., White, S. D. M., & Aricò, G. 2023, MNRAS, 520, 489 [Google Scholar]
- Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Crittenden, R. G., Natarajan, P., Pen, U.-L., & Theuns, T. 2002, ApJ, 568, 20 [NASA ADS] [CrossRef] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Dalal, R., Li, X., Nicola, A., et al. 2023, ArXiv e-prints [arXiv:2304.00701] [Google Scholar]
- Dark Energy Survey Collaboration (Abbott, T., et al.) 2016, MNRAS, 460, 1270 [Google Scholar]
- Debackere, S. N. B., Schaye, J., & Hoekstra, H. 2020, MNRAS, 492, 2285 [Google Scholar]
- Eifler, T., Krause, E., Dodelson, S., et al. 2015, MNRAS, 454, 2451 [Google Scholar]
- Euclid Collaboration (Knabenhans, M., et al.) 2021, MNRAS, 505, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., Blazek, J. A., McEwen, J. E., & Hirata, C. M. 2017, JCAP, 2017, 030 [Google Scholar]
- Fedeli, C. 2014, JCAP, 4, 028 [NASA ADS] [Google Scholar]
- Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Software, 1, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Friedrich, O., Andrade-Oliveira, F., Camacho, H., et al. 2021, MNRAS, 508, 3125 [NASA ADS] [CrossRef] [Google Scholar]
- García-García, C., Ruiz-Zapatero, J., Alonso, D., et al. 2021, JCAP, 2021, 030 [CrossRef] [Google Scholar]
- Gatti, M., Sheldon, E., Amon, A., et al. 2021, MNRAS, 504, 4312 [NASA ADS] [CrossRef] [Google Scholar]
- Giodini, S., Pierini, D., Finoguenov, A., et al. 2009, ApJ, 703, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Giri, S. K., & Schneider, A. 2021, JCAP, 2021, 046 [Google Scholar]
- Gonzalez, A. H., Sivanandam, S., Zabludoff, A. I., & Zaritsky, D. 2013, ApJ, 778, 14 [Google Scholar]
- Gu, S., Dor, M.-A., van Waerbeke, L., et al. 2023, MNRAS, 525, 4871 [Google Scholar]
- Handley, W. 2019, J. Open Source Software, 4, 1414 [Google Scholar]
- Handley, W., & Lemos, P. 2019, Phys. Rev. D, 100, 043504 [NASA ADS] [CrossRef] [Google Scholar]
- Handley, W. J., Hobson, M. P., & Lasenby, A. N. 2015, MNRAS, 450, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Harnois-Déraps, J., van Waerbeke, L., Viola, M., & Heymans, C. 2015, MNRAS, 450, 1212 [Google Scholar]
- Harris, C. R., Jarrod Millman, K., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Heisenberg, L., Villarrubia-Rojo, H., & Zosso, J. 2023, Phys. Dark Universe, 39, 101163 [NASA ADS] [CrossRef] [Google Scholar]
- Heitmann, K., Lawrence, E., Kwan, J., Habib, S., & Higdon, D. 2014, ApJ, 780, 111 [Google Scholar]
- Heymans, C., Tröster, T., Asgari, M., et al. 2021, A&A, 646, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hikage, C., Oguri, M., Hamana, T., et al. 2019, PASJ, 71, 43 [Google Scholar]
- Hinton, S. R. 2016, J. Open Source Software, 1, 00045 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., & Seljak, U. 2004, Phys. Rev. D, 70, 063526 [Google Scholar]
- Huang, H.-J., Eifler, T., Mandelbaum, R., & Dodelson, S. 2019, MNRAS, 488, 1652 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
- Jeffreys, H. 1935, Math. Proc. Cambridge Philos. Soc., 31, 203 [Google Scholar]
- Kitching, T. D., Alsing, J., Heavens, A. F., et al. 2017, MNRAS, 469, 2737 [Google Scholar]
- Krause, E., Fang, X., Pandey, S., et al. 2021, ArXiv e-prints [arXiv:2105.13548] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lemos, P., Weaverdyck, N., Rollins, R. P., et al. 2022, MNRAS, 521, 1184 [Google Scholar]
- Lesgourgues, J. 2011, ArXiv e-prints [arXiv:1104.2932] [Google Scholar]
- Li, X., Zhang, T., Sugiyama, S., et al. 2023, ArXiv e-prints [arXiv:2304.00702] [Google Scholar]
- Limber, D. N. 1953, ApJ, 117, 134 [NASA ADS] [CrossRef] [Google Scholar]
- López-Cano, D., Angulo, R. E., Ludlow, A. D., et al. 2022, MNRAS, 517, 2000 [CrossRef] [Google Scholar]
- Lucca, M. 2021, Phys. Dark Universe, 34, 100899 [NASA ADS] [CrossRef] [Google Scholar]
- Madhavacheril, M. S., Qu, F. J., Sherwin, B. D., et al. 2023, ArXiv e-prints [arXiv:2304.05203] [Google Scholar]
- Mallaby-Kay, M., Atkins, Z., Aiola, S., et al. 2021, ApJS, 255, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Marra, V., & Perivolaropoulos, L. 2021, Phys. Rev. D, 104, L021303 [NASA ADS] [CrossRef] [Google Scholar]
- McAlpine, S., Helly, J. C., Schaller, M., et al. 2016, Astron. Comput., 15, 72 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2017, MNRAS, 465, 2936 [Google Scholar]
- McCarthy, I. G., Bird, S., Schaye, J., et al. 2018, MNRAS, 476, 2999 [NASA ADS] [CrossRef] [Google Scholar]
- McEwen, J. E., Fang, X., Hirata, C. M., & Blazek, J. A. 2016, JCAP, 2016, 015 [CrossRef] [Google Scholar]
- Mead, A. J., Peacock, J. A., Heymans, C., Joudaki, S., & Heavens, A. F. 2015, MNRAS, 454, 1958 [NASA ADS] [CrossRef] [Google Scholar]
- Mead, A. J., Tröster, T., Heymans, C., Van Waerbeke, L., & McCarthy, I. G. 2020, A&A, 641, A130 [EDP Sciences] [Google Scholar]
- Mead, A., Brieden, S., Tröster, T., & Heymans, C. 2021, MNRAS, 502, 1401 [Google Scholar]
- Mohammed, I., Martizzi, D., Teyssier, R., & Amara, A. 2014, ArXiv e-prints [arXiv:1410.6826] [Google Scholar]
- Morganson, E., Gruendl, R. A., Menanteau, F., et al. 2018, PASP, 130, 074501 [NASA ADS] [CrossRef] [Google Scholar]
- Myles, J., Alarcon, A., Amon, A., et al. 2021, MNRAS, 505, 4249 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, N. M., Huterer, D., & Wen, Y. 2023, Phys. Rev. Lett., 131, 111001 [CrossRef] [Google Scholar]
- Nunes, R. C., & Vagnozzi, S. 2021, MNRAS, 505, 5427 [NASA ADS] [CrossRef] [Google Scholar]
- Ondaro-Mallea, L., Angulo, R. E., Zennaro, M., Contreras, S., & Aricò, G. 2022, MNRAS, 509, 6077 [Google Scholar]
- Pellejero-Ibañez, M., Stücker, J., Angulo, R. E., et al. 2022, MNRAS, 514, 3993 [Google Scholar]
- Pellejero-Ibañez, M., Angulo, R. E., Zennaro, M., et al. 2023, MNRAS, 520, 3725 [Google Scholar]
- Philcox, O. H. E., & Ivanov, M. M. 2022, Phys. Rev. D, 105, 043517 [CrossRef] [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018, MNRAS, 475, 648 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourtsidou, A., & Tram, T. 2016, Phys. Rev. D, 94, 043518 [CrossRef] [Google Scholar]
- Qu, F. J., Sherwin, B. D., Madhavacheril, M. S., et al. 2023, ArXiv e-prints [arXiv:2304.05202] [Google Scholar]
- Raveri, M., & Doux, C. 2021, Phys. Rev. D, 104, 043504 [NASA ADS] [CrossRef] [Google Scholar]
- Raveri, M., & Hu, W. 2019, Phys. Rev. D, 99, 043506 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, N. C., Alonso, D., Harnois-Déraps, J., et al. 2021, A&A, 649, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samuroff, S., Blazek, J., Troxel, M. A., et al. 2019, MNRAS, 489, 5453 [NASA ADS] [CrossRef] [Google Scholar]
- Samuroff, S., Mandelbaum, R., Blazek, J., et al. 2023, MNRAS, 524, 2195 [Google Scholar]
- Sánchez, C., Prat, J., Zacharegkas, G., et al. 2022, Phys. Rev. D, 105, 083529 [CrossRef] [Google Scholar]
- Schaye, J., Dalla Vecchia, C., Booth, C. M., et al. 2010, MNRAS, 402, 1536 [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schneider, A., & Teyssier, R. 2015, JCAP, 12, 049 [Google Scholar]
- Schneider, A., Teyssier, R., Stadel, J., et al. 2019, JCAP, 2019, 020 [Google Scholar]
- Schneider, P., van Waerbeke, L., Kilbinger, M., & Mellier, Y. 2002, A&A, 396, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, A., Stoira, N., Refregier, A., Weiss, A. J., et al. 2020, JCAP, 2020, 019 [CrossRef] [Google Scholar]
- Schneider, A., Giri, S. K., Amodeo, S., & Refregier, A. 2022, MNRAS, 514, 3802 [NASA ADS] [CrossRef] [Google Scholar]
- Secco, L. F., Samuroff, S., Krause, E., et al. 2022, Phys. Rev. D, 105, 023515 [NASA ADS] [CrossRef] [Google Scholar]
- Semboloni, E., Hoekstra, H., Schaye, J., van Daalen, M. P., & McCarthy, I. G. 2011, MNRAS, 417, 2020 [Google Scholar]
- Sevilla-Noarbe, I., Bechtol, K., Carrasco Kind, M., et al. 2021, ApJS, 254, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Pakmor, R., Pillepich, A., et al. 2018, MNRAS, 475, 676 [Google Scholar]
- Stebbins, A. 1996, ArXiv e-prints [arXiv:astro-ph/9609149] [Google Scholar]
- Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, R., Sato, M., Nishimichi, T., Taruya, A., & Oguri, M. 2012, ApJ, 761, 152 [Google Scholar]
- Talman, J. D. 1978, J. Comput. Phys., 29, 35 [NASA ADS] [CrossRef] [Google Scholar]
- The Dark Energy Survey Collaboration 2005, ArXiv e-prints [arXiv:astro-ph/0510346] [Google Scholar]
- Tröster, T., Mead, A. J., Heymans, C., et al. 2022, A&A, 660, A27 [CrossRef] [EDP Sciences] [Google Scholar]
- van Daalen, M. P., McCarthy, I. G., & Schaye, J. 2020, MNRAS, 491, 2424 [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nature Astron., 3, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, Nature, 509, 177 [Google Scholar]
- Wong, K. C., Suyu, S. H., Chen, G. C.-F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
- Zennaro, M., Angulo, R. E., Aricò, G., Contreras, S., & Pellejero-Ibáñez, M. 2019, MNRAS, 489, 5938 [NASA ADS] [CrossRef] [Google Scholar]
- Zennaro, M., Angulo, R. E., Pellejero-Ibáñez, M., et al. 2023, MNRAS, 524, 2407 [Google Scholar]
- Zuntz, J., Paterno, M., Jennings, E., et al. 2015, Astron. Comput., 12, 45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Modelling of non-linearities
The DES Collaboration employs HALOFIT (Takahashi et al. 2012) to predict the non-linear matter power spectrum (e.g. Secco et al. 2022; Amon et al. 2022). HALOFIT has a nominal accuracy of 10% at k = 10 h Mpc−1 (Takahashi et al. 2012). Krause et al. (2021) showed that accuracy is enough to model the shear signal over the scales relevant for DES Y3, that is, it causes a shift < 0.3σ compared to the EuclidEmulator and CosmoEmu emulators (Euclid Collaboration 2021; Heitmann et al. 2014).
Generally, the accuracy of HALOFIT, as well as HMcode, BACCOemu, and other emulators, has been tested only over a relatively small cosmological space with respect to the prior used in DES analysis or even compared to the ≈2 − 3σ regions of the posteriors. This could cause bias in cosmological parameters as the error could be significantly larger in some regions of the parameter space, for instance, for very massive neutrinos.
To test the performance of HALOFIT in a larger cosmological space, we carried out a suite of 20 N−body simulations in which the cosmological parameters were randomly distributed over the prior space. These simulations had a mass resolution so that the power spectrum converged at a few percent level at z = 0 and k = 10h Mpc−1. HALOFIT performed remarkably well, considering that it was fitted to only 16 N−body simulations, and achieved a precision of around 20%. This could still introduce significant biases in our cosmological constraints, however.
Building emulators over large cosmological space volumes is very challenging. This would require a large number of high-resolution simulations in principle. Alternatively, here we exploited the cosmology scaling of Angulo & White (2010) and Angulo et al. (2021). Therefore, we built an updated version of BACCOemu by employing a suite of 35 N−body simulations run with various cosmologies. These simulations were then scaled to more than 1000 cosmological parameter sets and ten redshifts. We then trained a neural network that quickly predicted the non-linear power spectrum. We estimate that our emulator reached a precision of about 5 − 10% to k = 10 h Mpc−1. We refer to Zennaro et al. (in prep.) for all the details.
We now determined the differences in the cosmology inference using either HALOFIT or BACCOemu when modelling the DES Y3 shear correlation functions down to angles θ = 2.5 arcmins. For this test, we used an NLA model and did not include baryonic processes to isolate the effects of the non-linear matter power spectrum. Fig. A.1 shows that the 1σ and 2σ credible levels of S8 obtained with BACCOemu are systematically higher than in HALOFIT by almost 0.5σ. When DES scale cuts are applied, the difference is slightly smaller, about 0.4σ, due to a smaller amount of non-linearities in the data vector. Thus, we find a larger bias given by non-linearities with respect to Krause et al. (2021), arguably because of the larger cosmological parameters space used here, where the accuracy of HALOFIT is lower.
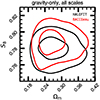 |
Fig. A.1. 1σ and 2σ credible interval on S8 and Ωm when modelling the matter power spectrum with HALOFIT (black) or BACCOemu (red). All the angular scales are used, not considering baryonic processes. |
Appendix B: Comparison with hydrodynamical simulations
The baryonification emulator in BACCOemu has been extensively tested against several hydrodynamical simulations (Aricò et al. 2021b; Chen et al. 2023). Here, we further tested the ability of the emulator to mimic the impact of the baryonic processes as predicted by a complex hydrodynamical simulation. To do this, we took the suppression in the matter power spectrum measured in BAHAMAS (McCarthy et al. 2017, 2018), at z ∈ [0.,3.] and k ∈ [10−2, 5 × 102]h Mpc−1, and used it as a fiducial baryonic suppression for the cosmology inference in the analysis of the cosmic shear measured by DES Y3. We compared it to the results that we obtained when employing the BCM, fixing the free parameters to the best-fitting values to the matter power spectrum of BAHAMAS at z = 0. The best-fitting parameters, obtained by Aricò et al. (2021b), are log Mc = 13.62[log(h−1 M⊙)], log ηb = −0.33, log βb = −0.28, log Mz0,cen = 10.21[log(h−1 M⊙)], log θinn = −0.62, log θout = 0.12, log Minn = 9.95[log(h−1 M⊙)].
We show the comparison between the two posteriors in the S8-Ωm plane in Fig. B.1. The cosmological constraints agree very well, highlighting the remarkable flexibility and accuracy of the BCM emulator, and assessing its adequacy to study DES Y3 data. In particular, this shows the negligible impact of the relatively restricted regime of validity of the emulator (z ∈ [0.,2.5] and k ∈ [10−2, 10 h Mpc−1]), and of the assumption of no redshift evolution of the baryonification parameters. The parameters do not change with redshift, but their effects on the power spectrum vary with redshift due to the halo mass function evolution, for example.
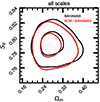 |
Fig. B.1. 1σ and 2σ credible levels on S8 and Ωm obtained by assuming the baryonic feedback measured in BAHAMAS (black) and using the BCM with the best-fitting parameters to the matter power spectrum at z = 0 of BAHAMAS (red). |
Appendix C: Cosmological parameters
We present in Fig. C.1 the posteriors of all the free cosmological parameters in our analyses when applying DES scale cuts and when analysing all the scales. The main gain in constraining power when analysing the small scales is in Ωm, and S8 or alternatively σ8. We also obtain somewhat better constraints in the Hubble parameter. Specifically, when analysing the full data vector, we constrained the normalisation of the primordial linear matter power spectrum 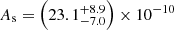 and the amplitude of the linear matter density fluctuations
and the amplitude of the linear matter density fluctuations 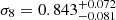 . We also weakly constrained the dimensionless Hubble constant
. We also weakly constrained the dimensionless Hubble constant 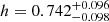 , and the tilt of the primordial matter power spectrum,
, and the tilt of the primordial matter power spectrum, 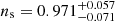 . The baryonic density remained unconstrained (although high values of Ωb are slightly disfavoured), as was the sum of neutrino masses Mν.
. The baryonic density remained unconstrained (although high values of Ωb are slightly disfavoured), as was the sum of neutrino masses Mν.
 |
Fig. C.1. Posteriors of the cosmological parameters, obtained by analysing all the angular scales of DES Y3 cosmic shear with our fiducial model (black). For comparison, we overplot the 1σ and 2σ credible levels obtained with DES scale cuts (red). |
We also report here Tab. C.1, where we quote the median of the 1D marginalised posteriors on S8 and Ωm and their respective 34th percentiles (as opposed to the maximum posterior of Tab. 2). We report for comparison the values we obtained when analysing the DES Collaboration chains (Secco et al. 2022; Amon et al. 2022), as in the official DES papers they typically report the mean values instead.
Constraints (median of the 1D marginalised posteriors and respective 34th percentiles) on S8 and Ωm obtained applying DES scale cuts and using all the angular scales. We explored different models, with NLA or TATT intrinsic alignment, gravity-only, or applying a baryonification with one or seven free parameters (BCM1 and BCM7, respectively). We also included a model with an extreme implementation of AGN feedback. We report for comparison the constraints we obtained by analysing the DES Collaboration chains, with and without shear ratios (SR).
Appendix D: Baryonic parameters
In the main text, we reported the posterior of Mc, the only baryonic parameter that is strongly constrained by the cosmic shear of DES Y3. Here we report for completeness the posteriors of all the seven baryonic parameters available in BACCOemu. All the baryonic parameters are sampled in log-space.
The parameters are η, which regulates the baryonic feedback range; β, the slope of the gas fraction - halo mass; the gas density shape (θinn,θout,Minn); and Mz0,cen, the galaxy-halo mass relation. We show their posteriors in Fig. D.1. Mc is the only significantly constrained parameter: We obtained ![$ \log M_{\mathrm{c}}=14.38^{+0.60}_{-0.56} \, [\log ({h^{-1}{M}_{ \odot}})] $](/articles/aa/full_html/2023/10/aa46539-23/aa46539-23-eq152.gif) . The constraints are robust to the intrinsic alignment model assumed.
. The constraints are robust to the intrinsic alignment model assumed.
 |
Fig. D.1. Posteriors of the baryonic parameters obtained by analysing all the angular scales of DES Y3 cosmic shear with our fiducial model. |
Appendix E: Tidal alignment and tidal torque
The tidal alignment and tidal torque (TATT) model is inspired by perturbation theory and aims to predict the intrinsic alignment of galaxies by considering a perturbative expansion of the cosmic density and tidal fields (Blazek et al. 2019). Three terms are considered: a linear term (tidal alignment), a quadratic term (tidal torque), and a cross term, with a total of five free parameters a1, η1, a2, η2, and bTA. We have reported the respective equations in §3.2.
It is not clear on which scales the NLA and TATT are valid because the theoretical limits given by linear and perturbation theory are practically overcome by using a full non-linear power spectrum. This is generally dependent on the galaxy sample analysed because red galaxies are expected to have higher tidal alignment amplitudes (a1 ∈ [3,5]) than blue galaxies (a1 ∈ [0,1]) (Samuroff et al. 2019, 2023).
The cosmic shear analysis made by the DES Collaboration on year 3 data has highlighted a low amplitude of intrinsic alignment 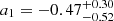 and
and 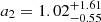 , much lower than the cosmological signal (Secco et al. 2022; Amon et al. 2022). A model without an intrinsic alignment is marginally preferred with respect to NLA and TATT by Bayesian evidence. Therefore, Secco et al. (2022) and Amon et al. (2022) concluded a posteriori that both NLA and TATT are suited for the analysis of DES Y3 data.
, much lower than the cosmological signal (Secco et al. 2022; Amon et al. 2022). A model without an intrinsic alignment is marginally preferred with respect to NLA and TATT by Bayesian evidence. Therefore, Secco et al. (2022) and Amon et al. (2022) concluded a posteriori that both NLA and TATT are suited for the analysis of DES Y3 data.
We employed smaller scales than in the analysis of Secco et al. (2022) and Amon et al. (2022), thus we reassessed the impact of scale cuts on the intrinsic alignment parameters after marginalising over seven baryonic parameters. We verified that the marginalisation only slightly degrades the TATT parameters constraints, without shifting them in any particular direction.
We show the posteriors of the TATT parameters in Fig. E.2, with and without DES scale cuts (black and red lines, respectively). With scale cuts, we obtain 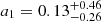 and
and 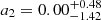 , whereas we obtain
, whereas we obtain 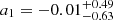 and a fully bimodal a2 when using all the scales. The amplitudes we find are consistent with zero in both cases. As noted in Secco et al. (2022) and Amon et al. (2022), a2 presents a multi-modal posterior. In contrast to Secco et al. (2022) and Amon et al. (2022), who reported that adding more data points at small scales (their ΛCDM-optimised case) the multimodality was alleviated, we find that the multi-modality is exacerbated when small scales are added. According to Amon et al. (2022), this multi-modality is given by internal degeneracies in the TATT model and it can degrade and shift the posterior on S8.
and a fully bimodal a2 when using all the scales. The amplitudes we find are consistent with zero in both cases. As noted in Secco et al. (2022) and Amon et al. (2022), a2 presents a multi-modal posterior. In contrast to Secco et al. (2022) and Amon et al. (2022), who reported that adding more data points at small scales (their ΛCDM-optimised case) the multimodality was alleviated, we find that the multi-modality is exacerbated when small scales are added. According to Amon et al. (2022), this multi-modality is given by internal degeneracies in the TATT model and it can degrade and shift the posterior on S8.
In Fig. E.1 we show the posterior projected onto the S8 - Ωm plane when assuming NLA and TATT, and compare it to Planck. Employing TATT, we obtain 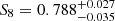 , a looser constraint than NLA. The posterior also shifts to lower S8 and Ωm, at ≈2σ from Planck. This could be an effect of the degeneracy between a1 and a2, as discussed above. As noted by Secco et al. (2022) and Amon et al. (2022), the intrinsic alignment amplitude would be expected to be a1 ≥ 0 in absence of systematics. Therefore, we imposed a1 ≥ 0 as a prior and obtained the dotted contours in Fig. E.1. With NLA, this new prior slightly shifts (0.1σ) the S8 contours towards Planck, whereas with TATT, the largest effect is a shift of 0.4% in Ωm.
, a looser constraint than NLA. The posterior also shifts to lower S8 and Ωm, at ≈2σ from Planck. This could be an effect of the degeneracy between a1 and a2, as discussed above. As noted by Secco et al. (2022) and Amon et al. (2022), the intrinsic alignment amplitude would be expected to be a1 ≥ 0 in absence of systematics. Therefore, we imposed a1 ≥ 0 as a prior and obtained the dotted contours in Fig. E.1. With NLA, this new prior slightly shifts (0.1σ) the S8 contours towards Planck, whereas with TATT, the largest effect is a shift of 0.4% in Ωm.
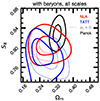 |
Fig. E.1. Posteriors of S8 of DES Y3 cosmic shear when employing as intrinsic alignment model NLA (red) or TATT (blue), compared to Planck TT+TE+EE+lowE. To model DES Y3 cosmic shear, we considered a baryonification with seven free parameters. We show with dotted lines the posteriors that we obtained when imposing a physically motivated prior on the intrinsic alignment amplitude a1 ∈ [0, 5]. |
 |
Fig. E.2. Posteriors of TATT parameters when analysing all the angular scales of DES Y3 cosmic shear with our fiducial model (black). For comparison, we overplot the 1σ and 2σ credible levels obtained with DES scale cuts (red). |
Appendix F: Shear bias and photo-z uncertainties
We display in Fig. F.1 the parameter posteriors of the shear biases mi that take galaxy shape miscalibration and blending into account, and the photo-z uncertainties  , that is, the shift of the source redshift distribution in the i bin. We show the posteriors obtained with and without scale cuts, using NLA and marginalising over seven free baryonic parameters. We compare them with the respective informative Gaussian priors, and additionally, with the posteriors obtained by the DES Collaboration adding the likelihood of the lensing shear ratios. These ratios were shown to be particularly sensitive to the redshift distribution of the source galaxies (Sánchez et al. 2022; Amon et al. 2022).
, that is, the shift of the source redshift distribution in the i bin. We show the posteriors obtained with and without scale cuts, using NLA and marginalising over seven free baryonic parameters. We compare them with the respective informative Gaussian priors, and additionally, with the posteriors obtained by the DES Collaboration adding the likelihood of the lensing shear ratios. These ratios were shown to be particularly sensitive to the redshift distribution of the source galaxies (Sánchez et al. 2022; Amon et al. 2022).
 |
Fig. F.1. Priors (dotted grey lines) and posteriors of the shear biases mi and photo-z uncertainties |
The posteriors of the shear biases all agree well. In some cases, for instance m4, analysing the small scales improves the constraints similarly to the addition of the shear ratios.
The  posteriors also agree well with the priors. We note that the constraints obtained with shear ratios are generally tighter than those with scale cuts, and they agree with our full-scale analysis. In some cases, notably
posteriors also agree well with the priors. We note that the constraints obtained with shear ratios are generally tighter than those with scale cuts, and they agree with our full-scale analysis. In some cases, notably 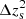 and
and 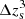 , the results we obtained from analysing the full data vector and the results obtained by the DES Collaboration using large scales and shear ratios are slightly different. Our constraints agree better with the priors.
, the results we obtained from analysing the full data vector and the results obtained by the DES Collaboration using large scales and shear ratios are slightly different. Our constraints agree better with the priors.
All Tables
Constraints (mode of the 1D marginalised posteriors and the respective 34th percentiles) on S8 and Ωm obtained applying DES scale cuts and using all the angular scales.
Constraints (median of the 1D marginalised posteriors and respective 34th percentiles) on S8 and Ωm obtained applying DES scale cuts and using all the angular scales. We explored different models, with NLA or TATT intrinsic alignment, gravity-only, or applying a baryonification with one or seven free parameters (BCM1 and BCM7, respectively). We also included a model with an extreme implementation of AGN feedback. We report for comparison the constraints we obtained by analysing the DES Collaboration chains, with and without shear ratios (SR).
All Figures
 |
Fig. 1. Cosmic shear correlation functions, ξ±, measured by DES Y3 in four redshift bins, for a total of 400 data points. In the lower left corner we display ξ+, and in the upper right corner, we show ξ−, both multiplied by 104θ for clarity. The corresponding redshift bins are indicated in each subplot. The grey bands show the scales that were discarded in the analysis carried out by the DES Collaboration. We display the best-fitting models that we obtained using the full data vector when considering only gravity (solid blue line), and additionally considering baryonic processes (dashed red line). |
| In the text | |
 |
Fig. 2. Comparison between the posterior distribution on |
| In the text | |
 |
Fig. 3. 1σ and 2σ credible levels on S8 and Ωm obtained using BACCO, considering only gravity in structure formation (left panel) and including baryonic effects (right panel). The solid black lines refer to runs to which scale cuts were applied, and the solid red lines show runs in which all scales are used. The dotted black line in the right panel shows the results of the gravity-only model with scale cuts for reference. |
| In the text | |
 |
Fig. 4. Posterior distribution functions of log Mc obtained in our fiducial run using all angular scales (red) and applying scale cuts (blue). We compare this with the posterior obtained by Chen et al. (2023) using only small scales, fixing six baryonic parameters, and applying a prior on cosmology given by the 3x2pt analysis of DES Y3 (Abbott et al. 2022). |
| In the text | |
 |
Fig. 5. 1σ credibility region of the suppression in the matter power spectrum at z = 0 caused by baryons, inferred by the BCM model with DES Y3 data (shaded grey area). We display the ratio of the matter power spectrum affected by baryonic processes to the spectrum calculated considering only gravity. For comparison, we show the BCM models obtained in Aricò et al. (2021b), fitting several current hydrodynamical simulations referenced in the main text, according to the legend. |
| In the text | |
 |
Fig. 6. Degeneracy between S8 and log Mc, displaying the 1σ and 2σ credible levels (red), and using all angular scales. For comparison, we show as a horizontal band the 1σ constraints on S8 obtained by analysing all angular scales without modelling baryons (blue), and using the Planck TT+TE+EE+lowE posterior obtained by the DES Collaboration (black; Planck Collaboration VI 2020; Secco et al. 2022). |
| In the text | |
 |
Fig. 7. 1σ and 2σ credible levels on S8 and Ωm using the Planck TT+TE+EE+lowE posteriors of the DES Collaboration (black; Planck Collaboration VI 2020; Secco et al. 2022) and DES Y3 cosmic shear data, analysing all the angular scales either with our fiducial model (red) or without modelling baryons (blue) obtained in this work. |
| In the text | |
 |
Fig. 8. S8 constraints obtained in this work with different analysis strategies for the DES Y3 data, either applying the scale cuts (grey data points) or employing all the angular scales (red data points). We highlight our fiducial model by displaying a red band that corresponds to its 1σ credible interval. We employed our baryonification (BCM) with one or seven free parameters or fixed all the parameters to extreme baryonic feedback. This last model, dubbed BCM-extreme, differs from X-ray observations, and should be considered as an upper limit for baryonic effects. We also varied the intrinsic alignment model choosing either NLA or TATT. For comparison, in the lower part of the panel we display the constraints obtained from the DES Collaboration chains with scale cuts, adding or removing the shear ratios (black data points; Secco et al. 2022; Amon et al. 2022; Abbott et al. 2022). Moreover, we include the external datasets specified in the legend (blue data points; Planck Collaboration VI 2020; Asgari et al. 2021; Li et al. 2023; Philcox & Ivanov 2022; Nunes & Vagnozzi 2021; Madhavacheril et al. 2023), which we describe in more detail in the main text. We highlight the 1σ region preferred by Planck with a blue band. |
| In the text | |
 |
Fig. 9. Impact of the different modelling choices on explaining the different fiducial cosmological constraints obtained by the DES Collaboration (DES TATT + SR; Secco et al. 2022; Amon et al. 2022) and this work (BACCOemu NLA BCM). We show the 1σ credible level of S8 and Ωm (solid lines) and maximum posteriors (stars) obtained by the DES Collaboration with the CosmoSIS pipeline and different choices regarding the intrinsic alignment model and the use of shear ratios (black, brown, and red, according to the legend). Analogously, we also show our results, obtained with the BACCO pipeline using HALOFIT (orange), or BACCOemu without and with baryons (green and blue, respectively). |
| In the text | |
 |
Fig. 10. Prior (black) and posteriors of the photo-z shift in the second tomographic bin |
| In the text | |
 |
Fig. A.1. 1σ and 2σ credible interval on S8 and Ωm when modelling the matter power spectrum with HALOFIT (black) or BACCOemu (red). All the angular scales are used, not considering baryonic processes. |
| In the text | |
 |
Fig. B.1. 1σ and 2σ credible levels on S8 and Ωm obtained by assuming the baryonic feedback measured in BAHAMAS (black) and using the BCM with the best-fitting parameters to the matter power spectrum at z = 0 of BAHAMAS (red). |
| In the text | |
 |
Fig. C.1. Posteriors of the cosmological parameters, obtained by analysing all the angular scales of DES Y3 cosmic shear with our fiducial model (black). For comparison, we overplot the 1σ and 2σ credible levels obtained with DES scale cuts (red). |
| In the text | |
 |
Fig. D.1. Posteriors of the baryonic parameters obtained by analysing all the angular scales of DES Y3 cosmic shear with our fiducial model. |
| In the text | |
 |
Fig. E.1. Posteriors of S8 of DES Y3 cosmic shear when employing as intrinsic alignment model NLA (red) or TATT (blue), compared to Planck TT+TE+EE+lowE. To model DES Y3 cosmic shear, we considered a baryonification with seven free parameters. We show with dotted lines the posteriors that we obtained when imposing a physically motivated prior on the intrinsic alignment amplitude a1 ∈ [0, 5]. |
| In the text | |
 |
Fig. E.2. Posteriors of TATT parameters when analysing all the angular scales of DES Y3 cosmic shear with our fiducial model (black). For comparison, we overplot the 1σ and 2σ credible levels obtained with DES scale cuts (red). |
| In the text | |
 |
Fig. F.1. Priors (dotted grey lines) and posteriors of the shear biases mi and photo-z uncertainties |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\xi ^{i,j}_{\rm \pm }(\theta ) = \sum \limits _{\ell } \frac{2\ell +1}{2 \pi \ell ^2 \, (\ell +1)^2} \left[ G^{+}_{\ell ,2} (\cos \theta ) \pm G^{-}_{\ell ,2}(\cos \theta ) \right] \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \times \left[ C^{i,j}_{\rm EE}(\ell ) \pm C^{i,j}_{\rm BB}(\ell ) \right] \end{aligned} $$](/articles/aa/full_html/2023/10/aa46539-23/aa46539-23-eq4.gif)