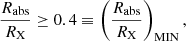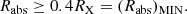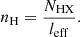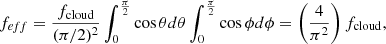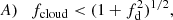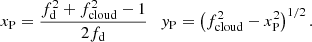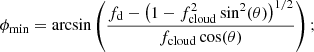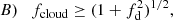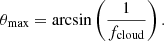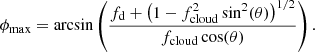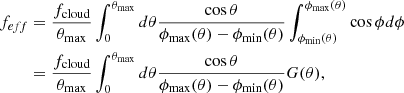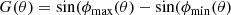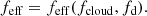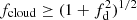| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A175 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202449686 | |
| Published online | 07 October 2024 | |
X-ray occultations in active galactic nuclei: Physical properties of eclipsing clouds as part of the broad-line region cloud ensemble
1
Dipartimento di Fisica e Astronomia, Università di Firenze, Via G. Sansone 1, I-50019 Sesto Fiorentino, Firenze, Italy
2
INAF – Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, Firenze, Italy
Received:
21
February
2024
Accepted:
23
July
2024
Context. Short-term X-ray variability in active galactic nuclei (AGNs) can be explained as being due to varying X-ray absorption induced by the temporary occultation of the primary X-ray source, when moving absorbing clouds cross the line of sight to the X-ray source itself. Earlier work suggests that these absorbing clouds have physical properties similar to those of broad-line region (BLR) emitting clouds and are located in the same spatial region.
Aims. We intend to extract physical information on each individual absorber associated with any given occultation event detected in our sample and to analyse general properties of the cloud ensemble whose components can produce X-ray eclipses.
Methods. From the analysis of previously detected occultation events, two ‘observables’ characterising each single occultation event can be derived: the peak fractional hardness ratio variation (ΔHR/HR) and the duration of the event normalised by a characteristic eclipse timescale evaluated for each AGN source. To determine the eclipsing cloud properties, we devised a procedure a) based on simplifying assumptions on the geometry of both the X-ray source and the cloud-like gas condensations, and on the cloud X-ray absorbing properties in the energy range of interest (2–10 keV), and b) relying on a set of simulated instrumental responses from both XMM and Suzaku relevant instruments to different incoming X-ray spectra, absorbed with varying absorber column density and maximum covering factor during the occultation. Thus, we derived information on the individual cloud producing any given occultation event, determining the cloud radius normalised to that of the X-ray source, the spatial location of the cloud, and an estimate of the cloud gas number density for reasonable values of the equivalent absorber column density.
Results. The physical properties of eclipsing clouds that we obtained are consistent with those of BLR clouds. We can exclude the dominance, in the ensemble cloud size distribution, of clouds larger than about 10–12 times the Schwarzschild radius characterising each AGN, and we do not find any significant dependence of the cloud physical size on the distance from the central black hole, in agreement with the results of our previous work. As for the number density of these gas condensations, with our procedure we obtained values within a range of ∼109 − 1011 cm−3, which is consistent with the estimates derived from broad emission line analysis.
Key words: galaxies: active / galaxies: Seyfert / X-rays: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Significant X-ray variability is a common property of active galactic nuclei (AGNs). It is generally accepted that AGN emission from the innermost regions is processed and selectively absorbed by intervening material in the nuclear and circumnuclear region. The multi-wavelength analysis of the observed radiation allows one to picture a general structure of AGNs in which the inner region is surrounded by somewhat toroidal absorbers of a clumpy nature, whose specific physical and geometrical properties are still a matter of study and debate. These absorbers particularly affect X-ray radiation and the analysis of X-ray variability can be turned into an analysis of the absorber properties and their possible variations.
In the past, the detailed investigation of a small number of individual sources led to the idea that short-time X-ray variability can be interpreted in terms of varying absorption due to the passage of an absorbing clump-like (or cloud-like) structure of gaseous material intersecting the line of sight to the central primary X-ray source, resulting in a temporary ‘occultation’ of the primary X-ray source itself. From these investigations (Risaliti et al. 2007, 2009, 2011; Maiolino et al. 2010; Nardini & Risaliti 2011; Bianchi et al. 2009; Sanfrutos et al. 2013), a general scenario in which the clumpy absorbers re identified with broad-line region (BLR)-like clouds crossing the line of sight to the X-ray source, and thus temporarily ‘eclipsing’ the X-ray source itself, has been proposed. In this framework, these occultations are the origin of the observed changes in the X-ray spectrum, causing its short-term variability. Following this general interpretation, in Torricelli-Ciamponi et al. (2014, hereafter referred to as Paper I) we started developing a method of analysing observed X-ray hardness-ratio light curves that allows one to detect reliable and statistically significant candidate occultations, and we applied it to a representative sample of about 40 AGNs, selected as the brightest sources with ‘long’ XMM-Newton and/or Suzaku observations. With this method, we identified a total of 65 reliable occultation events in 14 of the AGN sources in the sample.
In a second piece of work (Pietrini et al. 2019, from now on Paper II), we analysed the consequences of coupling the constraints on properties of the broad-line emitting gas, inferred from spectroscopic observations in the framework of a BLR consisting of an ensemble of cloud-like components, with the constraints defined by the global analysis of the X-ray source occultations detected in Paper I. The purposes of the Paper II analysis were to define the viability of the proposed scenario and to assess global properties of an orbiting cloud ensemble satisfying both types of constraints mentioned above.
In the present paper, we intend to fully exploit the capabilities of the method and the amount of information gained from Paper I analysis and from the results of Paper II regarding the properties of the distribution in size for clouds belonging to the ensemble orbiting in the inner region of the AGN. In fact, we want to find a relation between the measured observable quantities for each detected eclipse event and the eclipsing cloud properties, in order to obtain a better and more detailed description of clouds in the central region.
A huge amount of work has been devoted to the study of the broad emission lines observed in AGN spectra. These characteristic spectral features arise from photoionised gas moving in the inner region of the AGN, subject to the gravitational potential of the central black hole (Wang et al. 2017). However, the physical and dynamical conditions as well as the spatial distribution of the gas contributing to the line emission are still not fully understood (Ruff et al. 2012; Raimundo et al. 2020). Different theoretical models of the BLR have been proposed, mainly divided into two different general families: models based on a continuous distribution of emitting gas (outflows, winds or outer regions of the accretion disc) on the one hand and models based on the distribution of individual cloud-like gas condensations orbiting the black hole potential on the other. Both types of models give positive answers to some of the open questions about the BLR, but at the same time fail to meet other requirements (see, for instance, Czerny 2019).
However, a BLR composed of an ensemble of individual gas clumps can give an explanation to the short-time variability of AGN X-ray emission in terms of temporary occultation of the X-ray source produced by a rather small cloud crossing the line of sight to the source itself.
In the framework of a BLR composed of a large number of small gas condensations (‘clouds’) orbiting around the central black hole, a successful approach to the explanation of broad-line observations is that of the ‘LOC’ (Locally Optimally emitting Clouds) model, introduced by Baldwin et al. (1995) (see Ruff et al. 2012; Schnorr-Müller et al. 2016) and subsequently used by several authors (see, for instance, Bottorff et al. 2002; Korista & Goad 2000, 2004). Within the LOC model approach, the typical range of gas number density for the gas in clouds can be inferred as 108 cm−3 < nH < 1012 cm−3 (see also Schnorr-Müller et al. 2016; Netzer 2008, 2013). More recent analyses and simulations of line emission (especially based on 2017 CLOUDY version, Ferland et al. 2017) confirm a range of gas number density, nH, with values in any case between 109 and 1012 cm−3 (Panda 2020; Marziani et al. 2010), and a maximum range for the total column density of BLR individual clouds of around 1022 − 1024 cm−2.
As a matter of fact, it seems very difficult to further improve information on cloud physical properties using these types of line analysis, because any inference about physical quantities’ values is sort of averaged over a very large number of individual gas condensations. On the contrary, within the interpretative framework of short-term X-ray variability that we adopt, in our present approach it is indeed possible to analyse the physical properties of an individual gas condensation, even though this is of course feasible only for a limited number of cases, corresponding to the eclipse events detected and identified. Therefore, assuming that it is correct to interpret AGN short-term X-ray variability in terms of temporary occultations by clouds crossing the line of sight to the X-ray source, while moving in the gravitational potential of the central black hole, our present method of analysis, coupled with our previous work (Paper I and Paper II), may give interesting and significant information on individual gas condensations. Also, we can show that indeed gas condensations responsible for X-ray absorption are consistent with the typical conditions inferred for BLR clouds for the vast majority of our sample of detected short-time X-ray absorption events.
To this purpose, our work is presented as follows. In Sect. 2, we recall the main features of the sample of X-ray light curves we examined in Paper I. We also identify the two main ‘observables’ that can be extracted from each eclipse event analysis; namely, the fractional peak hardness ratio variation, ΔHR/HR, and the event duration, τ0. In Paper I no attention had been devoted to the eclipse duration, but in Sect. 3 we analyse in detail its relevance, by introducing a simple representative geometry for the occultation event, together with a few simplifying but descriptive assumptions about the clouds in the hypothesis that they do belong to a population including BLR clouds as well. Section 3 also includes a brief discussion of the fractional hardness ratio variation as a function of the eclipse covering factor and of the X-ray absorbing column density, as it stems from our analysis of synthetic light curves (simulated observations) with XMM and Suzaku. The relations determined in Sect. 3 represent useful tools for the interpretation of each detected event. The procedure adopted for obtaining information on the cloud occulting the X-ray source in each of our observed eclipse events is then described in Sect. 4. In Sect. 5, we discuss the ranges of cloud physical parameters derived from the analysis of all the events detected in our sample, taking also the information on cloud physical size inferred from Paper II analysis into account. In the final part of this section, we also compare the results obtained with our procedure for two of Mrk 766 light-curves with the outcome of a spectral analysis of the same light-curves performed by Risaliti et al. (2011), obtaining good agreement. Our conclusions are presented in Sect. 6.
2. The sample and its analysis
We refer to Paper I (Sect. 3) for the details of the source sample definition, of the choice of the energy bands for the hardness ratio (HR), and, especially, of our method of analysis. Here, we just give a summary of the main points that are specific to our method (see also Appendix A).
In Paper I, for a sample of type-1 to Compton-thin type-2 AGNs consisting of about 40 of the brightest X-ray sources with long archival XMM-Newton and Suzaku observations, we analysed the hardness ratio (HR) light curves, where HR ≡ F(5 − 10 keV)/F(2 − 4 keV) (see Sect. 2 of Paper I for details).
It is important to remark that, as it is discussed in Sect. 2 of Paper I, we chose to restrict our analysis in the 2 − 10 keV energy range, and therefore our search is sensitive only to occultations by clouds with a column density in the range of ∼1023 − 1024 cm−2. Also, we have limitations on the temporal range of the detectable occultations and our search is sensitive to durations between ∼10 ks, in order to have enough statistics, and ∼1 day, to be able to isolate and properly identify an HR variation event within a single observation. Thus, these conditions are limiting our analysis to a subsample of possible absorbers producing a temporary occultation of the X-ray source. Of course, this does not exclude the existence of temporarily obscuring absorbers characterised by larger column densities and/or longer timescales; our search is just not sensitive to them, and thus we cannot discuss them properly on the basis of our observed occultation events.
The events considered here are those for which a) the HR variations were found to be statistically significant (with a probability of random variability < 0.001) and b) the peak fractional hardness ratio variation (ΔHR/HR) of the event is ΔHR/HR > 0.1, since a statistically significant event can be unambiguously interpreted as an eclipse event only if this latter condition is satisfied, as we discussed in Paper I (Sect. 4).
Our analysis will be based on two observational quantities: the fractional HR variation, ΔHR/HR, of a given eclipse, and the duration of the eclipse, τ0. The fractional HR variation, ΔHR/HR, is straightforwardly defined (see Paper I and Appendix A). The eclipse duration, τ0, is the total duration of the observed event from its start to the end; since each event is modelled with a Gaussian function, τ0 is related to the Gaussian width parameter, w, and we chose to define τ0 as the full width of the Gaussian at one twentieth of the Gaussian peak, so that τ0 = 4.9w (see Appendix A).
We note that our choice of a Gaussian function is arbitrary but quite effective. The shape of the HR variations in light curves is not predictable and our aim was to reproduce the most significant variations with simple functions, defined just by some measure of height and width: a Gaussian function is therefore a suitable and valid representation. However, the choice of the exact shape of the function does not affect our analysis and our results (see Paper I).
In Paper I we have defined for each observed source a characteristic timescale for the eclipse, Δtecl, as Δtecl ≃ 3RX/vcloud, where RX is the X-ray source radius, which we assume to be 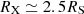 , where RS is the Schwarzschild radius and vcloud = (GMBH/RBLR)0.5 is the Keplerian velocity of clouds at the characteristic BLR distance, RBLR, from the AGN centre. As it is described in Paper II, for the sources of our sample we derived the value of RBLR from Bentz et al. (2013) radius luminosity correlation, RBLR ≃ 33.65[L5100/1044]0.533 light days (where L5100 ≡ λlλ(erg s−1) at λ = 5100 Å). We adopted, when available, the values of L5100 reported in the literature and, instead, derived L5100 as an extrapolation from the monochromatic 2 keV flux when the value of L5100 was not available in the literature (see also Paper I for details). The adopted values of MBH are those reported in Table 1 of the present paper, as gathered, together with their uncertainties from the references mentioned in Table 1. It is interesting to compare the actual ‘measured’ durations, τ0, of significant events that can be unambiguously classified as occultation candidates with such a characteristic eclipse timescale for the corresponding source. For the vast majority of our detected candidate eclipse events, the obtained value of τ0 falls in a range within an order of magnitude difference with respect to our generically estimated eclipse timescale for their corresponding source. Thus, it appears that the non-dimensional parameter, τ0/Δtecl, obtained by accounting for the estimated eclipse timescale of the source of the given event, can be a meaningful representation of our observable ‘duration of an eclipse event’. Also, normalising the duration, τ0, of each eclipse event with a timescale (Δtecl) representative of the phenomenon for the source of our sample in whose light curves we detected the event itself, we can gather our observational data, {Δ(HR)/HR, τ0/Δtecl}, all together in a plot that gives their visual representation. Therefore, we have chosen to plot in Fig. 1 the two observables of our analysis, showing the derived values of Δ(HR)/HR versus the corresponding τ0/Δtecl for the statistically significant and reliable candidate eclipse events that we have revealed with our procedure. The values of Δ(HR)/HR and τ0/Δtecl, which we have obtained for all the observed reliable occultation events and which are shown in Fig. 1, are also reported in Table A.1 in Appendix A.
, where RS is the Schwarzschild radius and vcloud = (GMBH/RBLR)0.5 is the Keplerian velocity of clouds at the characteristic BLR distance, RBLR, from the AGN centre. As it is described in Paper II, for the sources of our sample we derived the value of RBLR from Bentz et al. (2013) radius luminosity correlation, RBLR ≃ 33.65[L5100/1044]0.533 light days (where L5100 ≡ λlλ(erg s−1) at λ = 5100 Å). We adopted, when available, the values of L5100 reported in the literature and, instead, derived L5100 as an extrapolation from the monochromatic 2 keV flux when the value of L5100 was not available in the literature (see also Paper I for details). The adopted values of MBH are those reported in Table 1 of the present paper, as gathered, together with their uncertainties from the references mentioned in Table 1. It is interesting to compare the actual ‘measured’ durations, τ0, of significant events that can be unambiguously classified as occultation candidates with such a characteristic eclipse timescale for the corresponding source. For the vast majority of our detected candidate eclipse events, the obtained value of τ0 falls in a range within an order of magnitude difference with respect to our generically estimated eclipse timescale for their corresponding source. Thus, it appears that the non-dimensional parameter, τ0/Δtecl, obtained by accounting for the estimated eclipse timescale of the source of the given event, can be a meaningful representation of our observable ‘duration of an eclipse event’. Also, normalising the duration, τ0, of each eclipse event with a timescale (Δtecl) representative of the phenomenon for the source of our sample in whose light curves we detected the event itself, we can gather our observational data, {Δ(HR)/HR, τ0/Δtecl}, all together in a plot that gives their visual representation. Therefore, we have chosen to plot in Fig. 1 the two observables of our analysis, showing the derived values of Δ(HR)/HR versus the corresponding τ0/Δtecl for the statistically significant and reliable candidate eclipse events that we have revealed with our procedure. The values of Δ(HR)/HR and τ0/Δtecl, which we have obtained for all the observed reliable occultation events and which are shown in Fig. 1, are also reported in Table A.1 in Appendix A.
Parameters and quantities, derived within the newly calculated Paper II model described in the text, for sources with detected reliable occultations.
 |
Fig. 1. Observables plot: Fractional hardness ratio variability, Δ(HR)/HR, versus the normalised eclipse duration, τecl = τ0/Δtecl, for each reliable eclipse event detected in Paper I. |
3. Interpreting the observables in the broad-line-region-like eclipsing clouds scenario
To address the interpretation of the two observables identified in the previous section and characterising each detected event, we present in the following subsections a geometrical and kinematical representation of the occultation event and the results of our analysis of the function HR = HR(CF, nH) derived from the simulation of ‘synthetic’ observations performed with XMM-Newton-EPIC/PN and Suzaku-XIS instruments, where CF is the maximum covering factor of the X-ray source produced by the absorber and nH is the X-ray absorption column density (see also Appendix B.1); in the following we shall define NHX = nH.
3.1. The geometry of eclipsing clouds and of the occultation event: Our assumptions and eclipse duration
In order to obtain a relation between eclipsing times and cloud geometrical properties, we make the following simplifying assumptions.
(a) The X-ray source is spherically symmetric.
(b) The eclipsing clouds, which we suppose to be components of the BLR cloud ensemble, are spherical as well, with the radius Rcloud, and are characterised by a constant gas number density, nH.
(c) Since the range of ionisation states in the BLR does not affect the X-ray absorption in the 2–10 keV energy range of our interest, we consider the whole cloud to be an X-ray absorber, so that we set
and in the following we shall use both notations with the same meaning.
(d) The absorber velocity on the plane of the sky is a constant vector; that is, it is both constant in value (here denoted by vc) and in direction, for the whole duration of the eclipse. There may of course be a velocity component along the line of sight as well, but it does not influence the occultation duration.
With these assumptions, we can depict a general geometry of an occultation event, as is delineated in Fig. 2. In the figure, both the spherical X-ray source and the X-ray absorber are projected on the plane of the sky, which is that of the page. With the adopted choice of Cartesian axes, the line of sight to the X-ray source coincides with the z axis coming out of the page (to the observer). The absorber is moving on the plane of the sky with a constant velocity, vc, in (a direction that we have identified as) the y direction. At time t1, the absorber projection starts to touch and overlap the X-ray source disc (of radius RX), and this instant marks the beginning of the eclipse; symmetrically, when the rear border of the projected X-ray absorber disc (of radius Rabs = Rcloud) leaves the source projection, at time t2, the eclipse comes to its end. In principle, we identify the time lapse t2 − t1 ≡ τ0 with the duration of the occultation.
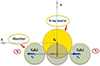 |
Fig. 2. Schematic illustration of an eclipse event as seen on the sky plane from the observer line of sight (z-direction, normal to the page). The distance, HCX ≡ d, between the source centre, CX, and the straight line trajectory of the absorber projection centre, C0, during the eclipse, represents a sort of ‘impact parameter’, d, for the occultation and is depicted in red. |
We define the impact parameter, d, as the distance between the centre (CX) of the projection on the plane of the sky of the X-ray source and the straight line trajectory of the centre (C0) of the eclipsing cloud projection on the sky (see Fig. 2).
We also introduced the non-dimensional parameters
From our simplified geometry, it is easy to write
where Y0 = [(1+fabs)2−fd2]1/2 and 2Y0RX is the distance between the positions of the eclipsing cloud centre at the beginning and at the end of the eclipse (C0(t1) and C0(t2) in Fig. 2.
Equation (2) can be rewritten to obtain the duration of the event normalised by the eclipse timescale for the source to which the event refers, Δtecl (defined in Paper I and here reminded in Sect. 2). We assume that the velocity of the cloud is Keplerian – that is, vc = (GMBH/rc)1/2, where rc is the distance of the eclipsing cloud from the central black hole – and we obtain
This last form of the geometrical and kinematical relationship is one of the tools that we use in the following to get some insight in the physics of the absorbers and, in particular, to derive the distance, rc, in units of the characteristic BLR radius, RBLR, as
We note that from Eq. (3), given the choice of Δtecl as a representative occultation timescale for each given AGN source and Δtecl dependence on the characteristic BLR radius (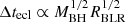 , from its definition), normalising the radial distance of the cloud, rc, with RBLR comes as a natural choice. It is also important to remark that the dimensional radial cloud distance, rc, bears no dependence on the value of RBLR, as it can be seen from Eq. (4), just expressing Δtecl and RX explicitly, so that
, from its definition), normalising the radial distance of the cloud, rc, with RBLR comes as a natural choice. It is also important to remark that the dimensional radial cloud distance, rc, bears no dependence on the value of RBLR, as it can be seen from Eq. (4), just expressing Δtecl and RX explicitly, so that
therefore, the only role of RBLR is that of a scaling characteristic length parameter. Thus, the normalised distance, 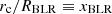 , can be derived as a function of the observable τ0/Δtecl (or, equivalently, the dimensional distance, rc, can be derived from τ0 using the same equation multiplied by RBLR, that is Eq. (5)), once the impact parameter, fd, is chosen and the normalised absorber radius, fabs = fcloud, is determined: xBLR = xBLR(τ0/Δtecl, fd, fabs).
, can be derived as a function of the observable τ0/Δtecl (or, equivalently, the dimensional distance, rc, can be derived from τ0 using the same equation multiplied by RBLR, that is Eq. (5)), once the impact parameter, fd, is chosen and the normalised absorber radius, fabs = fcloud, is determined: xBLR = xBLR(τ0/Δtecl, fd, fabs).
Equation (2), or equivalently Eq. (3) above, can also be formally solved for the expected radius of the absorber normalised to the source radius, fabs ≡ Rabs/RX, obtaining a general form
where, similarly to what illustrated for rc, the apparent dependence on RBLR cancels in the ratio RBLR/Δtecl2. From Eq. (6), it is clear that for a fixed normalised distance, rc/RBLR, the minimum value of the normalised radius of the absorber that produces an occultation with the given duration, τ0/Δtecl, is attained for d = 0 (fd = 0), which is when the trajectory of the cloud centre crosses the centre of the source circular projection on the plane of the sky, a configuration that we can define as a ‘central’ geometry for the occultation (CXH = d = 0 in Fig. 2).
3.2. Fractional hardness ratio variation, Δ(HR)/HR, as an indicator of the eclipse covering factor
In Paper I we analysed the ‘synthetic’ hardness ratio, HR, expected from ‘simulated’ observations performed with XMM-Newton-EPIC/PN and Suzaku-XIS instruments changing the values of NHX (equivalent column density of the X-ray absorbing BLR cloud) and CF, covering factor of the eclipsing absorber in the model spectrum (see also Appendix B.1). The predicted hardness ratio, HR, can thus be evaluated as a function of the values of NHX and CF: 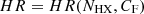 . Based on these results, we find a rather well-established relation between the peak fractional variation of hardness ratio, Δ(HR)/HR, and the corresponding maximum covering factor attained during an occultation due to the passage of a ‘typical’ BLR-like cloud, characterised by a given value of NHX (see Appendix B for more detail). Provided the absorber equivalent column density falls in a relatively narrow range around ∼1023 cm−2, the relation between Δ(HR)/HR and CF turns out to be rather tight and we can therefore somewhat ‘translate’ the ‘observed’ value of Δ(HR)/HR for a given event into an estimate of the maximum covering factor
. Based on these results, we find a rather well-established relation between the peak fractional variation of hardness ratio, Δ(HR)/HR, and the corresponding maximum covering factor attained during an occultation due to the passage of a ‘typical’ BLR-like cloud, characterised by a given value of NHX (see Appendix B for more detail). Provided the absorber equivalent column density falls in a relatively narrow range around ∼1023 cm−2, the relation between Δ(HR)/HR and CF turns out to be rather tight and we can therefore somewhat ‘translate’ the ‘observed’ value of Δ(HR)/HR for a given event into an estimate of the maximum covering factor 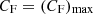 characterising that occultation event (or vice versa).
characterising that occultation event (or vice versa).
We remind here that information on the X-ray absorber column density, NHX, which clearly is a central quantity in the interpretation of the observed fractional variation of hardness ratio in an occultation, can be obtained as a result of X-ray spectroscopical analyses performed on a number of different AGNs and available in literature (see Bianchi et al. 2012 and Paper II, Sect. 9): from these, values of NHX are inferred and turn out to fall in a relatively narrow range of values around 10−23 cm−2, so that a representative range of values for the X-ray absorber equivalent column density, NHX, can be taken approximately between 5 × 1022 and 2 × 1023 cm−2.
Within the geometrical framework described in Sect. 3.1, the maximum covering factor attained during an occultation event can be geometrically computed (see Appendix B.2), depending on the parameters {fabs, fd} (defined in Eq. (1)). As is illustrated in Appendix B.2, extensive calculations for wide ranges of the parameters {fabs, fd} allowed us to derive the relation among 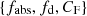 ; in particular, fabs can be thus determined for given {fd, CF} values. Conversely, any given value of CF can be obtained in occultations due to absorbers with different values of the normalised projected radius fabs = Rabs/RX, depending on the specific value of the impact parameter, fd, characterising the occultation event.
; in particular, fabs can be thus determined for given {fd, CF} values. Conversely, any given value of CF can be obtained in occultations due to absorbers with different values of the normalised projected radius fabs = Rabs/RX, depending on the specific value of the impact parameter, fd, characterising the occultation event.
The inferred relationship between Δ(HR)/HR and the corresponding (CF)max, combined with the dependence of the covering factor on the geometrical parameters of the occultation, has a couple of immediate consequences, that we mention here and discuss in Appendix B.3.
First, the minimum value of 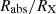 for any given event corresponds to null ‘impact parameter’ for the occultation – that is, fd = 0, (see also Eq. (6)) – and it is given by
for any given event corresponds to null ‘impact parameter’ for the occultation – that is, fd = 0, (see also Eq. (6)) – and it is given by 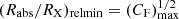 . Second, from our constraints for ‘bona fide’ candidate eclipse events, we derived (see Appendix B.3) a limiting condition on the size of any absorber responsible for our observed eclipse events, defined as
. Second, from our constraints for ‘bona fide’ candidate eclipse events, we derived (see Appendix B.3) a limiting condition on the size of any absorber responsible for our observed eclipse events, defined as
Clouds with smaller size, normalised by the X-ray source radius, cannot produce detectable temporary X-ray absorption events that can reliably be interpreted as occultations. Thus, all the clouds corresponding to eclipse events shown in the plot of Fig. 1 must have a radius that satisfies the condition
The limiting condition expressed by relation (7) shows that within our framework for the eclipse scenario there certainly is a selection effect related to the central black hole mass of the AGN, MBH, and the minimum physical size of an absorber capable of producing a reliable and detectable eclipse increases linearly with increasing black hole mass of the AGN (see Appendix C).
4. Extracting physical information information on the occulting clouds
In addition to the assumptions discussed in Sect. 3.1, we also assume NHX to be a parameter of our analysis, so that we can choose its value in the inferred representative range mentioned in Sect. 3.2. The other fundamental physical parameter is the mass of the central black hole, MBH, which also sets the natural length-scale through the assumption
In the following, we illustrate and discuss our procedure to extract physical information on the specific cloud producing the occultation for each detected eclipse event.
Given the value of MBH referring to the AGN in whose observed light curves we have detected any specific event, we chose the values of the two other relevant parameters,
that is, we chose the X-ray absorbing equivalent column density and the geometrical impact parameter for the occultation.
We could then derive, for the given event, the physical parameters of the occulting cloud,
that is, the normalised radius of the cloud (remembering that, with our assumptions, fcloud = fabs), its normalised distance from the AGN central black hole, and its (constant) gas number density, starting from the specific values of the two observables, Δ(HR)/HR and τ0/Δtecl, and making appropriate use of the relation between the X-ray absorption equivalent column density, NHX, and the cloud gas number density, nH (involving a representative estimate of the ‘effective’ absorption depth of the spherical cloud, which we must define; see Sect. 4.3). It is apparent that changing the value of the physical parameter NHX and/or that of the geometrical one, fd, we obtain different solutions for the occulting cloud properties {fcloud, xBLR, nH} for any given detected eclipse event, so that there is a degeneracy in the eclipse explanation. Since the equivalent absorption column density, NHX, is rather well constrained, as was discussed above, the unknown impact parameter of any given occultation is mostly responsible for such a degeneracy.
4.1. Deriving the eclipsing cloud radius for each event
In our scenario for any given event, the central black hole mass parameter, MBH, is identified by the corresponding AGN. Once the values of the parameters {NHX, fd} are also chosen, the observed value of Δ(HR)/HR defines the corresponding value of the normalised cloud radius 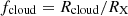 . In fact, using our results of the analysis of the expected hardness ratio and its variations with varying absorbing column density, NHX, and absorber covering factor, CF, from ‘simulated’ observations of XMM-Newton and Suzaku instruments (see Sect. 3.2 and Appendix B), we have determined a relation between Δ(HR)/HR and CF for any given NHX of interest; namely, Δ(HR)/HR = Δ(HR)/HR(NHX, CF). Also, the geometrically calculated maximum covering factor, CF, is a function of the impact parameter, fd, and of the absorbing cloud radius, fabs = fcloud; that is, CF = CF(fd, fcloud). Therefore, for each given event, once the parameters, {NHX, fd}, have been chosen, the observed value of Δ(HR)/HR, with the given NHX, determines that of CF (see Fig. B.2) and the latter, depending on the chosen value of fd, defines the corresponding normalised cloud radius, fcloud (see Fig. B.3, black lines). In other words, the normalised cloud radius, fcloud, required to explain the eclipse event, is indeed the one that allows the cloud to carry out an occultation with impact parameter, fd, causing a maximum covering factor, CF(fcloud, fd), which, in turn, with the chosen value of the parameter, NHX, produces just the observed value of the peak relative hardness ratio variation,
. In fact, using our results of the analysis of the expected hardness ratio and its variations with varying absorbing column density, NHX, and absorber covering factor, CF, from ‘simulated’ observations of XMM-Newton and Suzaku instruments (see Sect. 3.2 and Appendix B), we have determined a relation between Δ(HR)/HR and CF for any given NHX of interest; namely, Δ(HR)/HR = Δ(HR)/HR(NHX, CF). Also, the geometrically calculated maximum covering factor, CF, is a function of the impact parameter, fd, and of the absorbing cloud radius, fabs = fcloud; that is, CF = CF(fd, fcloud). Therefore, for each given event, once the parameters, {NHX, fd}, have been chosen, the observed value of Δ(HR)/HR, with the given NHX, determines that of CF (see Fig. B.2) and the latter, depending on the chosen value of fd, defines the corresponding normalised cloud radius, fcloud (see Fig. B.3, black lines). In other words, the normalised cloud radius, fcloud, required to explain the eclipse event, is indeed the one that allows the cloud to carry out an occultation with impact parameter, fd, causing a maximum covering factor, CF(fcloud, fd), which, in turn, with the chosen value of the parameter, NHX, produces just the observed value of the peak relative hardness ratio variation, 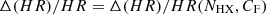 , for the given event.
, for the given event.
4.2. Deriving the eclipsing cloud spatial location for each event
Again, for any given occultation event in our sample (defining the AGN parameter MBH), once we have determined the appropriate fcloud for a specific choice of the occultation parameters 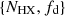 as discussed above, we can immediately derive the distance of the occulting cloud from the central black hole, rc, from Eq. (4), using the other observable of the eclipse event; namely, the normalised occultation duration, τ0/Δtecl. In fact, Eq. (4) gives the distance normalised with the characteristic BLR size, RBLR, xBLR ≡ rc/RBLR, as a function of
as discussed above, we can immediately derive the distance of the occulting cloud from the central black hole, rc, from Eq. (4), using the other observable of the eclipse event; namely, the normalised occultation duration, τ0/Δtecl. In fact, Eq. (4) gives the distance normalised with the characteristic BLR size, RBLR, xBLR ≡ rc/RBLR, as a function of 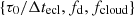 .
.
4.3. Deriving the occulting cloud gas number density for each event
More elaboration is needed to infer a representative and reliable estimate of the cloud gas number density, nH, which we have assumed as constant throughout the spherical cloud. To do this, we need to properly express the equivalent X-ray absorbing column density, NHX, in terms of the gas number density and of an appropriately ‘averaged’ effective depth of the cloud as an absorber, which we indicate as leff. We thus need to devise a procedure to evaluate this effective depth, leff, depending of course on the cloud normalised radius, fcloud, and also on the specific geometry of the occultation, through the parameter fd; in fact, fcloud and fd together define the portion of the spherical occulting cloud that happens to intercept the X-ray source projection on the sky plane. We show in Appendix C our approach to a simplified but representative derivation of the normalised effective depth, 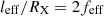 , where we have introduced a normalised ‘effective radius’, feff, for an immediate comparison with fcloud. In this derivation, the normalised effective depth turns out to be a function of both fcloud and fd, since, as is shown in Appendix C, it is
, where we have introduced a normalised ‘effective radius’, feff, for an immediate comparison with fcloud. In this derivation, the normalised effective depth turns out to be a function of both fcloud and fd, since, as is shown in Appendix C, it is
This is the length scale that most representatively connects the parameter NHX with our estimate of the gas number density, nH, of the cloud of normalised radius determined in Sect. 4.1 that is occulting the X-ray source with the chosen geometric impact parameter, fd, through the relation
so that we obtain the gas number density of the cloud as
5. Matching solutions to detected events: Results for physical parameters of occulting clouds
Each one of the actual detected events (shown in Fig. 1) corresponds to an AGN with a central black hole mass, MBH; for each of the detected events, we thus identified the physical properties, {fcloud, xBLR, nH}, of a cloud with equivalent X-ray absorbing column density equal to the chosen value, NHX, and obscuring the given X-ray source with the chosen value of the impact parameter, fd, that determines the specific geometry of the eclipse.
We define this as a ‘best match’ solution for a given event, meaning that it is the one obtained by identifying the fcloud value that, once given the parameters MBH and {NHX, fd}, corresponds to the best reproduction of the Δ(HR)/HR value derived for that event from our analysis of Paper I. Figure 3 represents the best matches obtained for the detected events assuming a value of 1023 cm−2 for the absorbing column density parameter, NHX, and central geometry occultations (fd = 0).
 |
Fig. 3. Best match solutions obtained for our detected events in the case of central geometry. Yellow dots represent best matches for NGC 3783 detected eclipse events, cyan dots show best matches for those of MCG 06-30-15, green dots show matches obtained for events referring to all other sources with MBH < 6.5, red dots are for all other sources with MBH > 7, and finally blue dots are best match events referring to intermediate mass sources with 6.5 < MBH < 7, where MBH ≡ log(MBH/M⊙). |
The results shown in Fig. 3 are representative, but merely exemplifying; in fact, the properties of a cloud that can explain any given observed occultation event depend on the specific choice of the two parameters {NHX, fd} and for different values of these parameters we obtain different ‘solutions’ describing the specific observed event, whose interpretation is thus degenerate (see Sect. 4). Increasing the impact parameter, fd – that is, choosing more and more off-centre occultation configurations – leads to an increase in the normalised absorber size, fabs(=fcloud), in order to maintain the maximum covering factor at the value corresponding to the measured Δ(HR)/HR for the given detected event (see Appendix B).
We can somewhat reduce the degeneracy of possible solutions explaining each event and extract information on the physical parameters of the occulting clouds, by taking also into consideration our results of Paper II on the global properties of the ensemble of clouds orbiting in the central region of the AGN.
From Fig. 3 it is clear that, taking only central geometry occultations into account, a number of events are explained with an eclipsing cloud that is located farther than the external boundary (set at 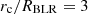 ) of the region that in Paper II we considered as the one in which our cloud ensemble was spatially distributed. Allowing for non-central geometries, we can find solutions corresponding to clouds closer to the central black hole (see Eq. (4) and Appendix B.2). However, even choosing an impact parameter of the occultation fd = 4, for the majority of those events the only solutions that we obtain still correspond to clouds ‘external’ to the region occupied by the cloud ensemble with the specific choice of spatial boundary parameters adopted in Paper II. Clearly this would imply an inconsistency, if we want to directly take the outcome of Paper II into account with the aim to analyse and discuss our best matching solutions for eclipse events.
) of the region that in Paper II we considered as the one in which our cloud ensemble was spatially distributed. Allowing for non-central geometries, we can find solutions corresponding to clouds closer to the central black hole (see Eq. (4) and Appendix B.2). However, even choosing an impact parameter of the occultation fd = 4, for the majority of those events the only solutions that we obtain still correspond to clouds ‘external’ to the region occupied by the cloud ensemble with the specific choice of spatial boundary parameters adopted in Paper II. Clearly this would imply an inconsistency, if we want to directly take the outcome of Paper II into account with the aim to analyse and discuss our best matching solutions for eclipse events.
Thus, still following the prescriptions and procedure of Paper II, we have worked out again the properties of the global model of the cloud ensemble, by appropriately modifying the values of two quantities upon which the model depends, namely the external boundary of the region over which the clouds belonging to the model ensemble are spatially distributed and the number of detected occultation events taken into account, so as to guarantee full consistency in our use of the resulting relevant properties of the cloud ensemble model in the present analysis.
Our first step was to enlarge the spatial region for our cloud ensemble, with respect to the case presented explicitly in Paper II, pushing the outer boundary approximately to the sublimation radius. For our sample of sources showing eclipse events, typically this turns out to be Rsubl ∼ 6RBLR (using the relation Rsubl ∼ 0.5(Lbol/1046)0.5pc with Lbol ∼ 9L5100, see Netzer 2013, 2015); as a consequence, we can reasonably assume a new outer boundary, ROUT = gexRBLR, for the spatial region where the clouds of our global model of Paper II are distributed as ROUT = 6RBLR, thus choosing a new value for the non-dimensional parameter, gex, introduced in Paper II; namely, gex = 6.
Furthermore, we decided to discard from our sample analysis those occultation events that, even considering extremely off-centre (fd ≥ 4) geometries, are still explained in our scenario by eclipsing clouds located farther than the new outer boundary of the cloud ensemble model region, being xBLR > gex = 6. This choice changes the number of detected eclipse events, Necl, for a few sources and therefore also changes the total number of events of our sample that we take into account from 65 to 59, excluding a total of 6 events, of which 2 for NGC 4395, 1 for NGC 4051, 2 for MCG 06-30-15 and 1 for NGC 1365. These four sources are those whose value of Necl is modified with respect to its original value in the sample. Also, the above-mentioned ‘rejected’ events still are the same and only ones that would correspond to occulting clouds farther than 6RBLR for even more extreme geometries; that is, fd > 4.
Hence, we recalculated a global model for the cloud ensemble producing both contributions to broad lines and X-ray occultations (see Paper II), assuming its external boundary at around the sublimation radius (i.e. choosing gex = 6) and excluding from the total number of events taken into account those that can only be explained with solutions that correspond to clouds located outside the region occupied by our model ensemble. This is an elementary but reasonable choice, and the few ‘eliminated’ events could of course be explained by gas condensations located farther away than the region occupied by broad-line emitting clouds, and as such not belonging to the cloud ensemble we have modelled, or by some more complex description that cannot be provided within the limits of our present simple geometrical and dynamical assumptions. Numerical values for physical quantities derived for the cloud ensemble may be changed with respect to those referring to the published model of Paper II, but the ‘newly’ calculated model for the cloud ensemble does maintain the same features and properties derived and discussed in Paper II.
The specific results of this ‘new’ global model for the ensemble of clouds can be now taken into account in order to explore the possibility of defining quantitative constraints on cloud size, thus investigating the actual viability of each one of our best-matching solutions. Of course from now on we discuss results referring only to the 59 events that we considered for the building of the global model of the cloud ensemble mentioned above (see Appendix A and Table A.1 therein) and all the figures illustrating our outcome in the next subsections only show solutions matching those same events.
5.1. Physical size of clouds and degeneracy of solutions
It is worth reminding ourselves here of the results of Paper II on the shape of the number density distribution in size characterising the ensemble of clouds orbiting the black hole in the central region of an AGN, comprising clouds that contribute to broad-line formation and potentially produce occultations of the X-ray source; such results in fact still maintain their validity within the modified version of the global model of the cloud ensemble that we are now dealing with. This distribution turns out to be a decreasing function of the cloud physical size (see Paper II), with a power law of exponent equal to −2, so that in general it is much less likely that an eclipse event is due to a ‘large’ (fcloud > 4) cloud with respect to the case for the same event being explained by a ‘small’ (fcloud ≲ 1) cloud occultation, because ‘large’ clouds are by far less numerous than ‘small’ ones.
Defining a limitation in physical normalised size of the occulting clouds would lead to a more stringent identification of the range of gas number density for the ensemble of clouds.
Adopting the new parameters discussed above for the model introduced in Paper II, from our recalculation of the global model for the cloud ensemble we can derive an estimate of the maximum physical size of clouds for each of the AGN sources showing X-ray eclipse events; this estimate thus takes into account both the constraints from observationally inferred properties of clouds contributing to the broad-line formation and those obtained from our analysis of X-ray occultations (see Paper II) into account. The notation for such an estimate of the maximum cloud physical radius used in Paper II is r2, but here we identify this same estimate with the symbol R2, so that (fcloud)max = (Rcloud)max/RX = R2/RX. In Table 1 we report the values of R2/RX derived for each of the sources showing reliable occultations. These values for R2/RX are clearly larger than the ones reported in Paper II because of the change of parameters (gex = 6 mainly, and for some AGN sources also the number of detected events considered) that we adopted for full consistency of our present discussion. Nevertheless, for 6 sources (mostly those with a central black hole mass about or larger than 107 M⊙) it turns out that (fcloud)max is in the range 4 − 7. Thus, for these sources, we have a significant limitation to occulting cloud size and, as a consequence, a constrain on degeneracy of eclipse event interpretation, since for eclipse events detected for these same sources we can exclude explanations that would require a cloud with fcloud > (fcloud)max. This limitation only pertains to those AGN sources for which (fcloud)max ∼ 4 − 7, and therefore we cannot obtain a general strong constraint on the cloud size directly from our definition of (fcloud)max. In fact, for the other AGN sources, we find an estimate of the cloud radius upper limit that is typically larger ((fcloud)max ∼ {12 − 27}) or significantly larger for the most extreme cases of NGC 4395 and NGC 4051, corresponding to the smallest black hole masses in our AGN sample. Thus, in the following we discuss the issue of cloud size along a more general line of reasoning.
We can now take into consideration
(a) the number of reliable eclipse events, Necl, that we have effectively considered for each AGN source according to the discussion presented above (for each source Necl is shown in Table 1) as well as
(b) the properties of the number density distribution in cloud size for our model cloud ensemble, dN/dR, which was derived with Paper II procedure under the assumption that such a distribution does not depend on the distance from the central black hole. Thus, using the value of Necl together with dN/dR, for each AGN source in our sample we can determine the expected number of eclipses, among the Necl detected, that can be due to clouds with radius in the interval between a given value of the cloud radius, Ri, and the maximum radius R2 obtained (see Table 1) for that source. To obtain this result, we start using the number density distribution in radius for the clouds, dN/dR (see Sects. 4 and 7 of Paper II), to derive, for each of our AGN sources, the fraction of potentially occulting clouds in a given range of radii ![$ [R_\mathrm{i}, R_2] $](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq34.gif) , as
, as
where R1x ≡ 0.4RX is the minimum value of cloud radius for a cloud whose possible eclipsing effects could be detected with our method of analysis (see Sects. 4 and 5). Because of its derivation, the quantity Frac[Ri, R2] defined above also bears no dependence on the distance from the central black hole, so that for each source we can use Frac[Ri, R2] to evaluate the expected number of eclipses, among the Necl detected, that can be due to clouds with radius in the interval [Ri, R2]. We define this number as
For each of the AGN sources in our sample, Table 1 shows the values of necl determined for different intervals of cloud radius.
The range of fcloud values explaining the events in our sample depends on the eclipse impact parameter value fd, as it is apparent from Fig. 4, with fcloud typically increasing with increasing fd. Taking again the properties of the number density distribution in cloud size for our model cloud ensemble into account, for any of the sources in our sample the expected fraction of potentially eclipsing clouds with fcloud > 5 − 6 turns out to be < 6 − 7% at most: smaller clouds are always strongly dominant in number. For fcloud in the range [6, R2/RX] we obtain necl(6, R2/RX)∼0.5 only for MGC 063015, whereas for most of the other sources in that range of normalised cloud radii the estimated necl is significantly lower or inexistent.
 |
Fig. 4. Best match solutions for cloud physical size obtained for our detected events in different geometries: circles again refer to central geometry (fd = 0), but we also show matches for fd = 1 (filled hexagons), fd = 2 (filled triangles) and fd = 4 (large filled triangles). Colour code is the same as in Fig. 3. In each panel hollow circles or triangles represent event descriptions that, for the specific fd value, must be discarded, since the occulting clouds are located farther than the chosen outer border of the cloud ensemble; the corresponding events are only explainable with fd = 4 or larger. |
Therefore, we can reasonably conclude that, except for MGC 063015 (and possibly, NGC 1365), even for those sources for which the distribution in size is characterised by (fcloud)max > 6 (see the fourth column of Table 1), it is highly unlikely that one occultation event is explained with clouds with size larger than ∼6RX. Hence, the analysis of our sample of detected occultation events, consistently taking into account also the outcome of our study of a global model for the cloud ensemble performed following the method presented in Paper II, indicates that in any case very large (fcloud > 6) clouds do not give a significant contribution to explaining occultations in our sample and we can rather safely exclude that such clouds are responsible for our detected events. This somewhat poses some limitations on degeneracy in the interpretation of any given occultation event, due to the unknown impact parameter of the eclipse.
Figure 4 shows the values of the normalised cloud radius Rcloud/RX plotted as a function of the resulting cloud distance from the central ionising source rc/RBLR (in units of the AGN BLR radius) for the best match solutions describing our detected events obtained assuming NHX = 1023 cm−2 for four representative choices of the geometrical configuration of the occultation, i.e four different values of the impact parameter fd. Each of the four panels of Fig. 4 presents the best matching solutions obtained for our detected eclipse events, assuming the specific value of fd labeling the panel. It is apparent that the events for which we find a solution in central geometry (fd = 0, upper left panel) are also explained with an off-centre geometry occultation produced by a larger cloud (see, for instance, upper right panel, for the case fd = 2). Inspecting Fig. 4, the lower right panel, showing solutions with impact parameter of the occultation fd = 4, of course presents only event explanations corresponding to clouds located within the chosen external boundary ROUT/RBLR = 6 for the cloud spatial distribution (see beginning of Sect. 5); on the contrary, in the other panels, pertaining to smaller values of the occultation impact parameter, solutions with eclipsing clouds located at larger distances still appear (as hollow circles or triangles, instead of coloured filled ones), since they refer to events that, when choosing fd = 4 can be explained by clouds belonging to our ensemble, redefined at the beginning of Sect. 5, that is, clouds located at rc < 6RBLR. We have chosen to keep these latter solutions in the plots, as an exemplification of another way to remove degeneracy of solutions for a given event: in these cases, even though we can find an explanation of the event with fd < 4, for consistency with our global model for the cloud ensemble only strongly off-centre solutions, that is those for fd = 4, which involve clouds placed within the ensemble spatial region, are going to be regarded as representative solutions for the given event.
From Fig. 4 it is also apparent that all the solutions shown (independently of the value of the impact parameter fd characterising the occultation geometry) correspond to Rcloud/RX within a range ∼0.4 − 5; this result contributes to strengthen the idea of a robust preponderance of clouds of limited size in the ensemble orbiting in the AGN central region. Moreover, this same figure also shows that the normalised cloud size of occulting clouds bears no significant dependence on the distance of the cloud from the central black hole, normalised with the characteristic length scale of the BLR, rc/RBLR, consistently with our previous assumptions of Paper II.
5.2. Gas number density for X-ray eclipsing clouds
In Fig. 5, we show the corresponding values of the gas number density nH, as derived from Eq. (8), for clouds explaining the detected occultations according to our model solutions, again plotted with respect to the resulting cloud distance from the central ionising source; each panel refers to one of the different geometrical configurations chosen to illustrate our search for model solutions matching the observed events. The gas number density is a physical parameter that has been extensively studied for the gas contributing to broad-line formation and whose range of values has been inferred from detailed analysis and modelling of the emitted broad lines, even though each observed broad line is the product of the integrated contribution of the whole ensemble of emitting cloud-like gas structures. Thus, it is worth examining more closely our results regarding nH for the individual clouds that can explain each of our detected eclipse events.
 |
Fig. 5. Gas number density from best match solutions obtained for our detected events in different geometries. Here we impose the constraints on maximum normalised physical size of the cloud described for Fig. 4 and colour codes are the same as in Fig. 4. |
1) Even taking possible different geometries of the occultation into account, Fig. 5 shows that the range of resulting possible values of gas number density is in agreement with the one inferred from analysis of broad emission lines (typically ∼109 − a few1011 cm−3 or, considering the most extended interval, 108 − 1012 cm−3 ; see, for instance, Elvis 2017; Korista & Goad 2000) thus confirming our interpretation of the temporary X-ray absorption as due to X-ray source occultation by a cloud belonging to the same ensemble of BLR clouds and crossing the line of sight to the X-ray source itself.
2) Reminding that the colour code refers to ranges or specific values of the AGN central black hole mass, Fig. 5 illustrates that for a fixed value of the X-ray absorbing column density, namely NHX = 1023 cm−2, and taking into account a given geometry of the occultation into account, the range of gas number density depends on MBH, again as a consequence of the different cloud physical size range detectable depending on MBH. We have no definite information on whether the most representative value of NHX bears some dependence on the central black hole value MBH. We have thus explored the solutions for the extreme values of our interval of interest for the X-ray absorbing column density, that is NHX = 5 × 1022 cm−2 and 2 × 1023 cm−2, and in Fig. 6 we show the corresponding results for the gas number density of occulting clouds explaining the events detected in our sample for two different values of the impact parameter (fd = 0, 2). An inspection of Fig. 6, as compared to the two upper panels of Fig. 5 confirms the agreement of our derived values of nH with the typical range inferred from broad-line analysis, mentioned above, independently of the specific value of NHX considered in the relevant interval. We just mention that, in order to explore NHX values close to our sensitivity interval upper limit (see Sect. 2), we have also analysed possible descriptions of our occultation events with occulting clouds characterised by NHX = 5 × 1023 cm−2, still obtaining results compatible with BLR-like cloud properties.
 |
Fig. 6. Gas number density from best match solutions obtained for our detected events and for two different values of the absorbing column density NHX, as shown by the labels in each panel. Here we impose the constraints on maximum normalised physical size of the cloud described for Fig. 4 and colour codes are the same as in Fig. 4. |
3) As noted above, the gas number density of the cloud depends on the AGN black hole mass MBH; from Eq. (8) it is apparent that this dependence enters through 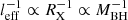 . Considering the statistical errors as reported in Table 1, their effect on nH would be substantially negligible in most cases. Even allowing for a more conservative average factor of 2 uncertainty on black hole mass estimates, the resulting gas number densities would in any case remain within the typical interval for BLR-like clouds.
. Considering the statistical errors as reported in Table 1, their effect on nH would be substantially negligible in most cases. Even allowing for a more conservative average factor of 2 uncertainty on black hole mass estimates, the resulting gas number densities would in any case remain within the typical interval for BLR-like clouds.
We note in passing that a similar line of reasoning could be applied to the effects of such a factor of 2 uncertainty on MBH on the cloud linear size that scales linearly with MBH (Rabs = Rcloud = fabsRX ∝ MBH; see also Appendix C).
4) For each of our AGNs, imposing the upper limit for Rcloud/RX, reported in Table 1 as R2/RX (see Sect. 5.1) allows us to evaluate a lower limitation on the gas number density for clouds in the ensemble orbiting around the central black hole. This is a general result for clouds of the ensemble orbiting on a range of distances approximately between ∼0.1RBLR and ∼6RBLR (see Sect. 5.1), independently of the phenomenology through which clouds manifest themselves (contributing to broad-line formation or occulting the X-ray source). In fact, we estimate (nH)min by using Eq. (8) with fd = 0, so that the ratio feff/fcloud is independent on fcloud (see Sect. 4.3 and Appendix C) as well as properly representative to our present purposes, and with fcloud = (fcloud)max = R2/RX for each of the AGN sources in our sample; thus we obtain minimum values for nH ranging from ∼2 × 108 cm−3 to ∼5 × 109 cm−3, a range that is consistent with the lower limit constraints derived from broad-line analysis.
5.3. Spatial location of absorbing clouds
Going back to Fig. 3, it is clear that the original distribution in distance (normalised to RBLR) of the matching solutions for eclipsing clouds would span a rather large range, with 0.05 ≲ rc/RBLR ≲ 102. As for the upper limit of normalised cloud distance xBLR = rc/RBLR, we have explained our choice (based on consistency reasons as illustrated at the beginning of Sect. 5) to keep the discussion of results centred on a range of distances whose upper limit is the external boundary, (xBLR)max = gex = 6, of the model here adopted for the spatial region occupied by the cloud ensemble that was introduced in Paper II. Turning our attention to Fig. 4, for the off-centre occultation solution panels (fd > 0) the range in rc/RBLR is more limited than for central occultation solutions (fd = 0) on the small values side, because of the coupling of our restriction on the normalised cloud size (see Table 1 and Sect. 5.1) with the fact that for any event increasing the impact parameter fd implies a solution with a larger normalised cloud size. A closer inspection anyway shows that the majority of the possible event matching solutions corresponds to clouds located between rc/RBLR ∼ 0.1 and rc/RBLR ∼ 6.
The results shown in Fig. 4 are fully consistent with the assumption of no significant dependence of the distribution in size of clouds on spatial distance from the central black hole. From Eq. (4), it is clear that the occultation duration has a crucial role in defining the spatial position of the occulting cloud: the shorter the duration of the eclipse event (requiring in our scenario a larger transverse velocity component), the closer to the central black hole is the occulting cloud located. This is of course true independently of the chosen distance normalisation: the same conclusion holds for dimensional distance rc and distance normalised to the gravitational radius of each source, i.e xg = rc/Rg with Rg = GMBH/c2); to this respect, the exemplifying Fig. 7 shows the best-matching solutions with cloud size plotted against xg = rc/Rg for two different choices of eclipse impact parameter.
 |
Fig. 7. Cloud physical size for occultation matching solutions plotted versus cloud distance normalised to the gravitational radius of the AGN source specific to the eclipse event. Symbols and colour codes are the same as in Fig. 4. |
Events that in our simple framework are only matched by solutions corresponding to clouds located very close to the central black hole (xg ∼ 102 or even xg < 102) are most probably not correctly explained by our elementary model: keplerian velocities would be around or larger than c/10 and this would make the description through our very simple model unreliable and incorrect. This may be the case for the inner red dot, corresponding to an event of PG 1501+106, only appearing in the left panel of Fig. 7 and the two events of NGC 3783 explained by the solutions appearing as the two innermost yellow dots in Figs. 3 to 7. Figure 7 better shows that the same can be true for the NGC 4151 event whose solution is represented by the second innermost red dot in the fd = 0 panel.
Plotting solutions with respect to 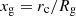 also facilitates a discussion and a comparison with the outcome of Markowitz et al. (2014) work, searching for and analysing ‘discrete X-ray absorption events’ in a sample of Seyfert AGNs from the archive of RXTE.
also facilitates a discussion and a comparison with the outcome of Markowitz et al. (2014) work, searching for and analysing ‘discrete X-ray absorption events’ in a sample of Seyfert AGNs from the archive of RXTE.
Among the sources of the sample of Markowitz et al. (2014) there are 9 of the 14 AGN sources for which we do find significant and reliable X-ray absorption events (see Table 1 and Papers I and II). However, Markowitz et al. (2014) detected secure events for only 4 of these nine sources we have in common. Also, typically Markowitz et al. (2014) absorption events are characterised by a duration that is significantly longer than those characterising the majority of our events; this is both due to the nature of RXTE observations analysed and to the authors’ method of analysis, thus probing essentially a different and admittedly somewhat ‘complementary’ portion of the parameter space of absorbers (pag. 6 Markowitz et al. 2014) with respect to the portion that can be studied analysing XMM-Newton and Suzaku observations, like we did.
The four sources showing secure X-ray absorption events in both works (Markowitz et al. 2014 and the present one) are NGC 5506, NGC 3227, NGC 3783 and Mrk 79. We find some sort of agreement with the results for NGC 5506 and NGC 3227: for these sources the range of spatial location of BLR emitting clouds does overlap the region of estimated locations of eclipsing clouds. For Mrk 79 the single detected event in our work can be explained with eclipsing cloud solutions such that xBLR > 1 (actually ∼2.75 for central geometry), but decreasing towards unity with increasingly off-centre geometries: again a qualitative agreement with Markowitz et al. (2014) results can be claimed for this source as well. As for NGC 3783, we have detected several (8) reliable events in this source light curves and they can be all explained with occultations due to clouds located in a rather large interval straddling the nominal BLR radius, thus supporting our scenario with an ensemble of clouds spatially distributed around this position, that can both contribute to broad-line emission and potentially produce X-ray eclipses. In Markowitz et al. (2014) work, the two secure detected events for NGC 3783 are both characterised by significantly longer durations and thus the corresponding absorbing clouds derived location turns out to be much farther away from the central black hole with respect to our work deductions; hence, we deal with different conditions and cannot find an agreement. In any case, it is interesting that, even though with different methods of analysis, these studies show a spatial distribution of cloud-like gas structures on a rather extended range of distances around the nominal estimate of the BLR radius, RBLR.
In fact, we remind that (as exemplified in Fig. 3) we do find solutions explaining our detected eclipse events on a large interval of distances (between ∼0.05RBLR and ∼102RBLR). Nevertheless, for consistency with our global model of cloud ensemble built following Paper II ‘recipe’, we restrict our attention to solutions with rc/RBLR ≲ 6 when we want to apply and combine the properties of such a model cloud ensemble to our present results. This is a physically reasonable choice, given that our selection of the external boundary of the spatial region where our model system of clouds is distributed roughly represents the sublimation radius for the AGNs in our sample, that is a distance beyond which physical conditions of gas condensations can be expected to change, thus requiring a different and more composite description with respect to our simple model.
5.4. A comparison with spectral analysis results in the case of Mrk 766
Risaliti et al. (2011) analysed in detail 4 observations of XMM-Newton-EPIC/PN (4 orbits), performing a spectral fitting of the portions of light curves showing a significant temporal variation of hardness ratio. Among the various observations of Mrk 766 that we have studied, both of Suzaku and of XMM-Newton, we have analysed three of those discussed in Risaliti et al. (2011) (R11 from now on). We can thus compare our results for the expected physical parameters of clouds producing the occultations (that we suppose are at the origin of the temporary variation of hardness ratio in the light curves examined), with those of R11, obtained through the analysis of the X-ray spectrum extracted on the time intervals corresponding to the same occultation events.
For a better comparison, we chose to perform a new fit (with respect to the one of Paper I) of the two light curves obtained from XMM-Newton-EPIC/PN observations of may 23 2005 and may 25 2005 respectively, namely the first and second orbit studied by R11. In fact, still using our method of Paper I, we fitted the temporal variations of hardness ratio analysing the two light curves altogether, thus obtaining a better and more reliable definition of the ‘constant’ hardness ratio level underlying the temporal variations of HR representing significant X-ray variability events that can be safely interpreted as occultations by a cloud like structure crossing the line of sight to the X-ray source. We thus obtained, for the three events detected in those two light curves, observable values that can be different from those reported in Paper I for those same events, especially for what regards the fractional hardness ratio ΔHR/HR. Using these new values for the event observables, we determined the best matching solutions for the occulting cloud responsible for each event in our simple model scenario. First, from the ΔHR/HR value for each event we derived (see also Fig. B.2) the CF values for the ranges of NHX (in the interval ∼1023 − 2 × 1023 cm−2) inferred from the spectral analysis performed by R11 for the various subintervals (see Table 2 of R11). The obtained values of CF (around 0.62–0.73, see third panel of Fig. 8) are in accordance with those derived from spectral analysis of R11. Then, among the possible solutions (degenerate because of possible different geometries of the eclipse event), we selected our ‘best’ solutions for the other physical parameters of the three events; these solutions are shown in Fig. 8.
 |
Fig. 8. Best matching solutions for the three events that we have detected and were also spectrally analysed by Risaliti et al. (2011), chosen so as to maximise the agreement with R11 results for NHX and CF values as reported in their paper. Blue points indicate a solution with NHX = 1023 cm−2, whereas red ones refer to cases in which NHX = 2 × 1023 cm−2; circular dots show central geometry solutions (fd = 0) and triangles indicate a case with impact parameter of the occultation fd = 2. |
The good agreement obtained for the cloud gas number density, that R11 estimate in the range ∼1010 − 1011 cm−3, supports our method of analysis and substantiates its possible use on large samples of sources for which a complete spectral analysis is not possible.
As for the range of cloud spatial positions, R11 mention an interval of 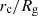 values around 103 − 104, which the authors actually recognise to be not very strongly constrained; again, the lower right panel of Fig. 8 shows a rather good agreement.
values around 103 − 104, which the authors actually recognise to be not very strongly constrained; again, the lower right panel of Fig. 8 shows a rather good agreement.
6. Summary and conclusions
Our analysis of a composite sample of bright X-ray AGN sources, performed in Paper I, shows that X-ray variability events that are explainable as temporary occultations of the X-ray source itself are quite widespread and frequent. The amount of data analysed deserves a more thorough and deeper analysis, with the aim of extracting physical information on the occulting absorbers.
As was brought up in Sect. 2 and discussed in detail in Paper I, the sample is composed of type-1 to Compton-thin type-2 AGNs, thus excluding Compton-thick sources, and the energy interval analysed is the 2–10 keV range, so our Paper I search for eclipses is sensitive only to occultations by clouds with a column density in the range of ∼1023 − 1024 cm−2 at most. Also, our analysis of Paper I is sensitive to occultation durations no longer than about 1 day. These conditions are of course confining our study to a subsample of all possibile temporary absorbers of the AGN X-ray source. In fact, cases of long-term variability and/or Compton-thick eclipses are already known (Ricci et al. 2016; Marchesi et al. 2022). Indeed, our method has limitations on the range of eclipse duration and cloud column density. This point has been discussed in more detail in Paper I; however, it is worth remembering that the detection of the possible eclipse in a light curve requires a measurable change in hardness ratio within a timescale shorter than the typical duration of an observation. This excludes long-term variability due to, for example, more distant clouds. It also excludes cases like NGC 1068 (Zaino et al. 2020), where even the low-absorption state is almost Compton-thick, implying that the hardness ratio in the 2–10 keV range is nearly constant during an eclipse. Instead, it doesn’t exclude extreme cases where a Compton-thick cloud obscures an otherwise Compton thin source. Based on the observations of NGC 1365 (Risaliti et al. 2005), we know that these cases may occur, but they are very rare.
The important point here is that these limitations do not affect our main conclusion: eclipses by Compton-thin BLR clouds are common in local AGNs, and allow us to investigate the physical properties of the absorbing BLR clouds. These conclusions hold even if there are additional sources of absorption by far away circumnuclear gas and or by thicker clouds.
In Paper II we started our study with a global approach, restricting our interest to the assessment of overall properties of a system of orbiting ‘clouds’ (gas condensations) that can both contribute to the emission of broad lines and produce temporary X-ray source absorption, through occultation; thus, we concluded that such a system can exist (in the inner region of AGNs), being consistent with both BLR observational constraints and the conditions derived from the investigation of the sample of detected eclipse events described in Paper I from a general point of view.
In the present work, we adopted a different approach, by also taking into account and analysing the specific characteristics of each single eclipse event detected in our sample and devising a procedure that enables us to derive physical information on individual gas condensations (‘clouds’) producing the occultation, even though based on strongly simplifying assumptions. Our aim is to extract more knowledge on the properties of clouds that are part of the system orbiting in the central region of AGNs and defining the BLR and, thus, to strengthen and confirm our proposed scenario. To pursue this goal, we have examined the duration, τ0, of each detected eclipse event, that was derived in our light curve analysis of Paper I, but not yet investigated in our previous papers.
We have devised (and described in detail, see Sects. 3 and 4) a procedure through which we can analyse each single detected eclipse event with the aim of defining ranges of physical parameters for the specific cloud-like structure producing the occultation, thus attempting at gaining insight into the physical conditions of the single unit of gas condensation of the ensemble. In fact, we analysed our detected events, trying to match them with possible theoretical conditions (physical properties) for eclipsing clouds. To this aim, we considered the results of X-ray spectroscopical analysis present in literature and performed for several single sources, indicating an absorbing column density, NHX, in a rather narrow range around 1023 cm−2 (see, for instance, Bianchi et al. 2012). Thus, we have discussed results referring to a fixed value NHX = 1023 cm−2 that we assumed as representative of the X-ray eclipse phenomenon (even though we explored a range in column density =[0.5 × 1023, 2 × 1023] cm−2) to determine possible occulting cloud properties. Because the selected value of NHX is right in the narrow range inferred from X-ray absorption analysis, our results on clouds producing such absorption through X-ray source occultation can be taken as representative and reliable.
The main aspects and results of the present work are the following.
-
From this analysis of our sample of eclipse events, except for very few cases, the properties (distance from the central BH, physical size, gas number density) of each individual cloud producing temporary X-ray absorption, by means of a transitory occultation of the central X-ray source, are indeed consistent with those of gas condensations in the BLR (see Fig. 3). Thus, we can safely conclude that BLR clouds do produce temporary absorption as observed in AGN X-ray spectrum and significantly contribute to this observed absorption phenomenon. Very few cases are in fact explainable with occulting clouds located at distances from the AGN centre that are (even significantly) larger than the representative BLR size, RBLR, and we may consider those as not belonging to the BLR itself. In our work, we consider as representative of the external boundary of the BLR ensemble of clouds a distance ∼6RBLR, roughly corresponding to (comparable with) the sublimation radius for our AGN sources (see Sect. 5 and references therein). According to this choice, we have discussed in detail results pertaining to occultation events explainable with gas condensations that we regard as being part of the BLR (Sects. 5.1 and following). Thus, this sample of temporary X-ray absorption events, whose detection we have discussed in Paper I, is indeed valuable, since the present analysis in terms of occultation events gives the opportunity to ‘see’ the individual gas condensation producing each occultation event, through its effect as an X-ray absorber.
-
From Figs. 3 and 4 it is clear that, for any given geometry of the occultation, no significant trend of increase for Rcloud/RX (=fcloud) appears with increasing rc/RBLR. For example, in the case of central geometry it is Rcloud/RX ∈ [0.4, 1] and this range is basically unchanged independently of the distance. It is just the degeneracy of explanations of each single event (due to unknown geometry of the occultation) that allows the possibility of clouds with normalised physical size Rcloud/RX > 1 to be involved. Our present conclusion on the substantial lack of dependence of cloud size range on the distance from the central black hole is in agreement with the assumption of Paper II that the number density distribution in size of clouds is independent of distance.
-
Availing ourselves of this outcome, we have consistently used the results of Paper II to verify that indeed the analysis of our sample of occultations indicates that in general the size of occulting clouds turns out to be ‘limited’ to at most a few times the size of the X-ray source, excluding the dominance of ‘very large’ clouds. In fact, for any eclipse event, the size of the occulting cloud depends of course on the geometry of the occultation, but in our analysis we identified the following two main points supporting our present conclusion. a) For a few of our sources (6 out of 14) the cloud size is certainly strongly limited by the estimate of cloud maximum size R2, deriving from our results for the global model of the cloud ensemble devised following Paper II procedure with the adapted parameters for the cloud location outer boundary and for the number of eclipse events taken into account for the AGN sources in our sample (see Sect. 5 and 5.1). Indeed, for these six AGNs we obtain R2/RX in the range ∼4 − 7, that is a maximum size ‘small’ enough to define a significant limitation to the radius of an occulting cloud: for those sources it certainly must be Rcloud/RX ≤ R2/RX ∼ 4 − 7. b) More in general, using the properties of the number density distribution in size of clouds, derived in Paper II, we showed (see Sect. 5.1) that in any case (i.e. for any of our AGN sources), it is highly improbable that an eclipse in our sample is produced by a cloud with Rcloud/RX ≥ 5 − 6. Very large clouds may of course be present in the cloud ensemble, but their numbers are negligible with respect to those of clouds with characteristic size comparable with (or at most a few times) that of the X-ray source and their presence is very unlikely to be revealed directly by short-time X-ray absorption events, like those we are studying.
-
From the analysis of solutions matching our detected events observables, we conclude that the inferred values for gas number density nH turn out to be within the range of values derived from broad emission lines analysis, typically 109 − 1011 cm−3, and this outcome is independent of the geometry of the eclipse. Clearly, the specific value of the X-ray absorber column density NHX influences the resulting values of the gas number density; however, within the rather narrow range NHX ∼ 5 × 1022 − 2 × 1023 cm−2, identified by X-ray spectroscopical analysis (see Bianchi et al. 2012), such an effect does not change our conclusions about the derived cloud gas number density, which is consistent anyway with the range of values implied by broad emission lines investigation.
Our results are also confirmed by the following considerations.
We have discussed a comparison of our results with those of Markowitz et al. (2014) work, finding no significant elements of contrast, especially since M14 work investigates discrete X-ray absorption events whose parameters are expected to be in a range somewhat complementary to our case because of the RXTE data set the authors deal with (typically significantly longer events detectable and detected).
Also, we have exploited the results of the spectral analysis of Mrk 766 discussed in R11 by comparing them with those obtained with our present procedure for the 3 eclipse events that R11 and the present work have in common. We find substantial agreement on physical parameters derived using the two different approaches in our present work and in R11. In fact, even if the initial (first step) method used by R11, based on the analysis of the hardness ratio light curve is analogous to the one we used, the relevant difference is that in the case of R11 this method is used only to find the time intervals of the possible eclipses. All the subsequent analysis is done through a complete spectroscopic analysis of the data. Therefore, the parameters derived by R11 can be considered a ‘gold standard’ to calibrate our analysis of the light curves, which does not include the analysis of the spectral data. This certainly gives support to our method of search for and analysis of the eclipse events in the sample examined, despite the simple modelling adopted, and it is particularly relevant since our present procedure of analysis has the quality of being widely usable for many more sources than those for which spectral analysis can be performed. Overall, the consistency of most of our results again indicates the reliability of our proposed scenario for explaining X-ray short-term variations as due to temporary absorption by a cloud-like gas condensation eclipsing the X-ray source while moving under the gravitational influence of the AGN central black hole. Also, it supports the validity of the procedure we devised to interpret the combination of observables that characterise each single detected eclipse event in order to extract physical information on the individual gas condensation crossing the line of sight to the X-ray source and temporarily occulting it. The resulting physical properties of these gas condensations indeed confirm the plausibility of their being part of the same ensemble of cloud-like gas structures that contribute to the formation of the observed broad emission lines.
Acknowledgments
GTC thanks INAF-Osservatorio Astrofisico di Arcetri for support. We also thank the anonymous referee for interesting and useful comments for improvement of the paper.
References
- Baldwin, J., Ferland, G., Korista, K., & Verner, D. 1995, ApJ, 455, L119 [NASA ADS] [Google Scholar]
- Bentz, M. C., & Katz, S. 2015, PASP, 127, 67 [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [Google Scholar]
- Bentz, M. C., Cackett, E. M., Crenshaw, D. M., et al. 2016, ApJ, 830, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Piconcelli, E., Chiaberge, M., et al. 2009, ApJ, 695, 781 [Google Scholar]
- Bianchi, S., Maiolino, R., & Risaliti, G. 2012, Adv. Astron., 2012, 782030 [CrossRef] [Google Scholar]
- Bottorff, M. C., Baldwin, J. A., Ferland, G. J., Ferguson, J. W., & Korista, K. T. 2002, ApJ, 581, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B. 2019, Open Astron., 28, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2017, ApJ, 847, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [Google Scholar]
- Korista, K. T., & Goad, M. R. 2000, ApJ, 536, 284 [Google Scholar]
- Korista, K. T., & Goad, M. R. 2004, ApJ, 606, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Risaliti, G., Salvati, M., et al. 2010, A&A, 517, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malizia, A., Bassani, L., Bird, A. J., et al. 2008, MNRAS, 389, 1360 [CrossRef] [Google Scholar]
- Marchesi, S., Zhao, X., Torres-AlbÃ, N., et al. 2022, ApJ, 935, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A. G., Krumpe, M., & Nikutta, R. 2014, MNRAS, 439, 1403 [Google Scholar]
- Marziani, P., Sulentic, J. W., Negrete, C. A., et al. 2010, MNRAS, 409, 1033 [Google Scholar]
- Nardini, E., & Risaliti, G. 2011, MNRAS, 417, 2571 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 2008, New Astron. Rev., 52, 257 [CrossRef] [Google Scholar]
- Netzer, H. 2013, The Physics and Evolution of Active Galactic Nuclei (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [Google Scholar]
- Panda, S., et al. 2020, in XXXIX Polish Astronomical Society Meeting, eds. K. Małek, M. Polińska, A. Majczyna, et al., 10, 261 [NASA ADS] [Google Scholar]
- Pietrini, P., Torricelli-Ciamponi, G., & Risaliti, G. 2019, A&A, 628, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raimundo, S. I., Vestergaard, M., Goad, M. R., et al. 2020, MNRAS, 493, 1227 [Google Scholar]
- Ricci, C., Bauer, F. E., Arevalo, P., et al. 2016, ApJ, 820, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, F., La Franca, F., Marconi, A., et al. 2017, MNRAS, 471, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., Fabbiano, G., Baldi, A., & Zezas, A. 2005, ApJ, 623, L93 [Google Scholar]
- Risaliti, G., Elvis, M., Fabbiano, G., et al. 2007, ApJ, 659, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Miniutti, G., Elvis, M., et al. 2009, ApJ, 696, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Nardini, E., Salvati, M., et al. 2011, MNRAS, 410, 1027 [Google Scholar]
- Ruff, A. J., Floyd, D. J. E., Webster, R. L., Korista, K. T., & Landt, H. 2012, ApJ, 754, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Sanfrutos, M., Miniutti, G., AgÃs-González, B., et al. 2013, MNRAS, 436, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Schnorr-Müller, A., Davies, R. I., Korista, K. T., et al. 2016, MNRAS, 462, 3570 [CrossRef] [Google Scholar]
- Torricelli-Ciamponi, G., Pietrini, P., Risaliti, G., & Salvati, M. 2014, MNRAS, 442, 2116 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-M., Du, P., Brotherton, M. S., et al. 2017, Nat. Astron., 1, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, L. M., Lewis, K. T., Koss, M., et al. 2010, ApJ, 710, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Zaino, A., Bianchi, S., Marinucci, A., et al. 2020, MNRAS, 492, 3872 [Google Scholar]
Appendix A: Investigation method for reliable eclipse event detection: Light curve analysis
Referring to Paper I for a full description of our method of analysis, here we summarise its main features. For the sources in our sample, we extracted the light curves for each observation with the required duration available in XMM-Newton and Suzaku archives. The choice the energy bands [soft and hard: (2-4) keV and (5-10) keV respectively] stems from our analysis of Paper I aiming to maximise the hardness ratio variations expected as a result of absorption variability induced by the temporary occultation of the source by a gaseous structure with X-ray absorption equivalent column density nH in the range [5 × 1022 − 2 × 1023] cm−2; this range of column density excludes absorbers typical of ‘Compton-thick’ sources, consistently with our sample choice, as explained in Sect. 2 of Paper I, and, conversely, is representative of physical conditions expected for typical ‘clouds’ of the BLR.
In Paper I we have fully analysed the hardness ratio light curves in our sample by fitting them with a constant plus a number of variation components modelled with Gaussian curves superimposed to the constant level. In general, we started from the simplest possible model, the ‘zero-step’, defined by just a constant in time (HR = const.=K0 for the whole duration of the observation), and then adding further components, thus generating a progressively more complex model. Each one of the events identified in the fitting procedure of a light curve has been evaluated in terms of its significance by applying the F-test to the comparison of the two models fitting with and without that particular event component. Thus, the n-th variation component in a given light curve is characterised by a null probability value Fn, representing the significance of the specific component (as it is explained in Paper I and reported explicitly in Table 2 of that same paper): the lower the value of Fn is, the higher is the significance of the corresponding event. At the end of the fitting process, each one of the analysed light curves is characterised by the parameters of the final fit (N-th step) defined by a constant, Kn, that represents the constant level of hardness ratio underlying the variation events, plus N Gaussian shaped variation components. Thus, the ensemble of the parameters defining the final fit comprises the constant Kn, the parameters defining each of the various Gaussian components (peak value of the n-th component, An, width parameter wn and location in time along the light curve, tn, with index n = 1...N) and the respective significance, represented by the null probability value Fn associated with the n-th component according to an F-test analysis (see Paper I). Table 2 of Paper I includes the parameters relevant to the present analysis for all the light curves in our sample, but it does not report the width parameter of the single events detected.
From the ratio of the peak value, An, of each event to the underlying constant level of the final fit of a light curve, Kn, we evaluated the peak fractional hardness ratio variation, which is then ΔHR/HR ≡ An/Kn for the n-th event of a light curve in which we detected a total of N distinguishable HR Gaussian shaped variation components. The width parameter wn was not discussed in Paper I, but in the present work it is used to determine the duration of the eclipse event, that we define as τ0 (see Sect. 2). Within our interpretative framework, we measure the total observed duration of the eclipse, from its start (when the occulting absorber begins to intercept the source projection on the sky) to its end (when the rear brim of the moving absorber leaves the source projection) as the total time interval, τ0, over which the HR variation event extends in the light curve. To evaluate τ0 from our fits we have chosen to define it operatively as the width of the Gaussian component, describing the HR variation event, at a reference fractional height of its peak value close enough to its base to be representative of the total time extension of the variation. Specifically, we define τ0 as the full width (FW) of the Gaussian at 1/20 of its peak value (An for the n-th component in a given light curve), that is, τ0 = FW(An/20). In terms of the full width half maximum (FWHM ≡ 2.3548wn) of the Gaussian component, we have τ0 ≃ 4.9wn ≃ 2.08FWHM. With the definition above, we consider this estimate of τ0 as our measure of the actual duration of each occultation candidate event we have revealed in our analysis.
In Table A.1, for all the 59 detected events that fulfil the conditions discussed in Sect. 5 and are subsequently analysed in that same section, we show the relevant quantities as derived from the final fit parameters, including the event duration τ0 and the null probability value F, that defines the event significance.
Specifics of each event among the 57 under examination: AGN source, observing instrument (S for Suzaku, X for XMM-Newton), date of the observation, order number of the event for any given source, ‘significance’ log F (as determined in Paper I), the derived observable quantity ΔHR/HR, normalised event duration and duration τ0 (in ks) of the event.
Appendix B: Event ‘observables’ and cloud parameters
B.1. Relation between CF and Δ(HR)/HR
One of our observed quantities is the fractional hardness ratio variation Δ(HR)/HR of the detected eclipse event in the examined light curve. As we have shown in Paper I and mentioned in Sect. 2, it must be Δ(HR)/HR > 0.1 in order to guarantee an unambiguous interpretation of the corresponding event as an eclipse candidate.
In Paper I, convolving theoretical spectral models (absorbed power-law models) with the response matrices of both XMM-Newton-EPIC/PN and Suzaku-XIS instruments and using the XSPEC package, we have chosen the energy bands defining the most appropriate hardness ratio for our analysis, namely HR = F(5 − 10 keV)/F(2 − 4 keV) (where F represents the resulting photon flux in the specified energy range). We have then analysed the dependence of this hardness ratio HR on parameters γ, nH, CF (respectively, photon spectral index, hydrogen column density of the intervening absorber and covering factor of the absorber itself) and defined a ‘synthetic’ HR = HR(γ, nH, CF, R), where R is the ratio between the normalisation of the reflected to the direct power law components of the spectrum, for the case of no reflected component (R = 0). The result is (see Sect. 4.3 of Paper I) that the behaviour of the fractional variation in hardness ratio Δ(HR)/HR with changing column density of the eclipsing absorber, NH = NHX, for any fixed value of the covering factor CF, is essentially independent of the specific value of γ within a reasonable range representative of AGN X-ray sources (see in particular Fig. 6 of Paper I, where we exemplify the results of our analysis by showing explicitly how the value of Δ(HR)/HR for any given NHX and CF of interest for our event sample remains unchanged when assuming γ = 2 or 2.3).
We thus discuss the results pertaining to ‘simulations’ effected with synthetic spectra characterised by γ = 2 as a representative value and we consider the predicted hardness ratio HR as a function of of the values of NHX and CF, 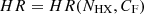 .
.
In Fig. B.1, we show the expected fractional variation in hardness ratio from synthetic spectra with γ = 2, for occultations by absorbers with different column density NHX, here indicated with nH, and with different covering factor conditions in the case of type 1 sources and of Compton-thin type 2 sources as well (the latter are represented by the dotted lines below each of the type 1 curves, corresponding to a given CF value). This figure suggests the possibility of relating the observed value of the fractional variation of hardness ratio Δ(HR)/HR with the corresponding maximum covering factor for reasonable values of the eclipsing cloud column density. The inferred relationship between Δ(HR)/HR and CF for the range of interest of nH values, NH = 5 × 1022 − 2 × 1023cm−2, is shown in Fig. B.2. Based on these results, we find a rather well established relation between the peak fractional variation of hardness ratio, Δ(HR)/HR, and the corresponding maximum covering factor attained during an occultation due to the passage of a ‘typical’ BLR-like cloud characterised by a given X-ray absorbing column density NHX.
 |
Fig. B.1. Fractional variation of hardness ratio as a function of NHX for fixed values of the covering factor, CF. Blue labels specify the value of CF for which each group of curves is obtained. For each CF value chosen, solid black curves represent the results of Suzaku-XIS simulations for type-1 sources, whereas the long-dashed red ones show those derived for type-1 with XMM-Newton-EPIC/PN. When present, the third short-dashed red line of each CF-value group of curves represents the case for type-2 XMM simulations. |
The results discussed above are important to our purposes in a twofold way.
i) Provided the absorber column density falls in a relatively narrow range around ∼1023cm−2, the relation between Δ(HR)/HR and CF turns out to be rather tight and we can therefore somewhat translate the observed value of Δ(HR)/HR for a given event into an estimate of the maximum covering factor 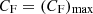 characterising that occultation event.
characterising that occultation event.
ii) Since from a model occultation, characterised by a given geometry (normalised impact parameter fd) and a value of the normalised projected size of the absorber (fabs), the corresponding maximum covering factor CF can be analytically calculated (see following Appendix B2), we can conversely evaluate the value of relative variation of the hardness ratio Δ(HR)/HR expected for that specific model occultation, when observed by XMM or Suzaku instruments.
B.2. Covering factor and geometry of occultation
In our simple hypothesis of spherical symmetry for both the X-ray source and the cloud (see Sect. 3.1), the value of the maximum covering factor attained during an occultation event can be geometrically computed from the evaluation of the maximum intersection area of the circles that represent the projections on the sky of the eclipsing cloud and of the source during the occultation itself. The value of CF is obtained by normalising this intersection area by the area ( ) of the circular projection of the X-ray source on the sky plane and it is a function of the two quantities
) of the circular projection of the X-ray source on the sky plane and it is a function of the two quantities 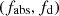 , that is, of the absorber radius and of the impact parameter, both normalised by the source radius RX (see Eq. (1)).
, that is, of the absorber radius and of the impact parameter, both normalised by the source radius RX (see Eq. (1)).
Extensive calculations of the value of CF for wide ranges of the parameters 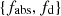 allowed us to derive the relation among {fabs,fd,CF}, defining a matrix that enables us to obtain the couples {fabs,fd} that produce any given value of the maximum covering factor CF. From this matrix we obtained the dependence of fabs on fd and CF values, namely
allowed us to derive the relation among {fabs,fd,CF}, defining a matrix that enables us to obtain the couples {fabs,fd} that produce any given value of the maximum covering factor CF. From this matrix we obtained the dependence of fabs on fd and CF values, namely 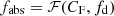 , defining, for each given value of the maximum covering factor CF, the corresponding function
, defining, for each given value of the maximum covering factor CF, the corresponding function 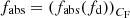 , and, as a consequence, the value of
, and, as a consequence, the value of ![$ Y_0= \left[(1+f_\mathrm{{abs}})^2- f_\mathrm{d}^2\right]^{1/2} $](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq47.gif) as
as 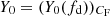 .
.
 |
Fig. B.2. Δ(HR)/HR as a function of CF for different values of the column density. The dotted line curve corresponds to NH = 5 × 1022cm−2, the solid curve to NH = 1 × 1023cm−2, the short-dashed curve to NH = 2 × 1023cm−2, the long-dashed curve to NH = 3 × 1023cm−2, and the dash-dotted curve refers to NH = 5 × 1023cm−2 |
 |
Fig. B.3. Black curves represent fabs as a function of the normalised impact parameter, fd, for a given value of CF. Red curves show Y0 (see Eq. 2) again as a function of fd and constant CF. Red curves are labelled with CF values; in the same order, increasing upwards, the same labels also apply to the black curves. |
This is illustrated in Fig. B.3, where we represent the results for the intervals fabs = 0 − 6 and fd = 0 − 5. Referring to that exemplifying figure, once we have derived an estimate for the value of CF from the observed Δ(HR)/HR and chosen the value for fd (normalised impact parameter), we can determine the value of the parameter fabs (normalised size of the absorber projected on the plane of the sky) from the black curve 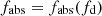 identified by the specific value of CF estimated, and, in turn, the value of Y0 must be on the corresponding curve
identified by the specific value of CF estimated, and, in turn, the value of Y0 must be on the corresponding curve 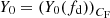 . Thus, in Fig. B.3 each of the plotted black curves represents the locus of points defined by the couples of values
. Thus, in Fig. B.3 each of the plotted black curves represents the locus of points defined by the couples of values 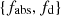 that produce a given value of the maximum covering factor CF, labelling the curve, and those couples identify the corresponding values of Y0 associated with that same CF. Again referring to Fig. B.3, it is interesting to point out that :
that produce a given value of the maximum covering factor CF, labelling the curve, and those couples identify the corresponding values of Y0 associated with that same CF. Again referring to Fig. B.3, it is interesting to point out that :
(1) for any given value of the impact parameter fd an increase in the value of the maximum covering factor CF requires an increase in the absorber normalised projected radius fabs and of the corresponding Y0;
(2) the value of CF estimated from Δ(HR)/HR determines the range of possible values of Y0, plotted in Fig. B.3 as a function of the impact parameter fd; reasonably assuming eclipsing clouds such that the absorber radius Rabs is at most ∼ a few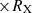 , for
, for 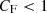 , this range of Y0 turns out to be rather limited, decreasing its extent with decreasing CF value.
, this range of Y0 turns out to be rather limited, decreasing its extent with decreasing CF value.
B.3. Determining the condition on minimum value of normalised size of X-ray absorber 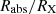
Based on the results discussed in the previous subsections of the present Appendix B, we can derive the absolute minimum value for 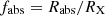 for absorbers that can be detected with our procedure of analysis [see Eq. (7) in Sect. 3].
for absorbers that can be detected with our procedure of analysis [see Eq. (7) in Sect. 3].
Under the conditions discussed in Appendix B.1, for a given event the observed value of Δ(HR)/HR can be translated into an estimate of the maximum covering factor 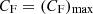 characterising that occultation event. Therefore, once for any given event we have translated the observed value of Δ(HR)/HR into a representative value of CF, we can also exploit our results on the dependence of the maximum covering factor CF on the values of the geometrical parameters of the occultation
characterising that occultation event. Therefore, once for any given event we have translated the observed value of Δ(HR)/HR into a representative value of CF, we can also exploit our results on the dependence of the maximum covering factor CF on the values of the geometrical parameters of the occultation 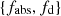 , discussed in the previous Appendix B.2, and immediately derive the corresponding minimum value of
, discussed in the previous Appendix B.2, and immediately derive the corresponding minimum value of 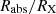 (i.e. fabs) for the given event. In fact, Eq. (6) immediately shows that for a given eclipse event the minimum value of
(i.e. fabs) for the given event. In fact, Eq. (6) immediately shows that for a given eclipse event the minimum value of 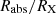 is attained for
is attained for 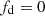 and this is also clear from the curves
and this is also clear from the curves 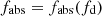 for each given value of CF in Fig. B.3.
for each given value of CF in Fig. B.3.
For a ‘central’ occultation geometry, that is for fd = 0, the maximum covering factor value is geometrically given by the simple relation 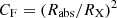 , so that, once determined the CF characterising the given event from Δ(HR)/HR, the minimum value of the non-dimensional size of the absorber is derived as
, so that, once determined the CF characterising the given event from Δ(HR)/HR, the minimum value of the non-dimensional size of the absorber is derived as  ; the subscript ‘relmin’ indicates that this is a minimum value referring to the specific eclipse event considered.
; the subscript ‘relmin’ indicates that this is a minimum value referring to the specific eclipse event considered.
A second significant consequence derives from the fact that for ‘bona fide’ candidate eclipse events it must be Δ(HR)/HR > 0.1 (see Sect. 2). On the basis of the inferred relationship between Δ(HR)/HR and CF and taking into account that the values of interest for NHX are between 5 × 1022 and 2 × 1023 cm−2, the condition Δ(HR)/HR > 0.1 implies 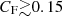 (see Figs. B.1 and B.2). From this we conclude that for all the events plotted in Fig. 1 the ‘absorbers’ responsible for such eclipse events must have a radius Rabs such that the corresponding non-dimensional value
(see Figs. B.1 and B.2). From this we conclude that for all the events plotted in Fig. 1 the ‘absorbers’ responsible for such eclipse events must have a radius Rabs such that the corresponding non-dimensional value 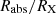 is ≥0.151/2 ∼ 0.4, that is
is ≥0.151/2 ∼ 0.4, that is
corresponding to Eq. (7) of Sect. 3. The above condition [Eq. (7)] thus defines the absolute minimum value of the normalised X-ray absorber radius consistent with the lower limit value for CF required to have reliable eclipse candidates defined above. Hence, all the clouds corresponding to eclipse events shown in the plot of Fig. 1 must have a radius Rabs that satisfies the condition
The limiting condition expressed by relation (7) shows that within our framework for the eclipse scenario there certainly is a selection effect related to the central black hole mass of the AGN, MBH. This selection effect comes from our analysing procedure: absorbers that are ‘very small’ with respect to the X-ray source size RX (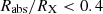 ) cannot induce any detectable and reliable eclipsing effect on the X-ray source, because of the very small maximum covering factor they can produce, with a resulting non-significant fractional hardness ratio variation (i.e. below 0.1, see Sect. 2); this, in turn, implies that the minimum physical size of an absorber capable of producing a reliable and detectable eclipse increases linearly with increasing black hole mass of the AGN, since we have assumed
) cannot induce any detectable and reliable eclipsing effect on the X-ray source, because of the very small maximum covering factor they can produce, with a resulting non-significant fractional hardness ratio variation (i.e. below 0.1, see Sect. 2); this, in turn, implies that the minimum physical size of an absorber capable of producing a reliable and detectable eclipse increases linearly with increasing black hole mass of the AGN, since we have assumed 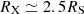 , with RS Schwarzschild radius (see Sect. 2) and thus it is
, with RS Schwarzschild radius (see Sect. 2) and thus it is 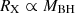 .
.
Appendix C: Derivation of a normalised effective depth to X-ray absorption for a spherical cloud
In Sect. 4.3 we discuss the estimate of the occulting cloud gas number density nH, that for a chosen value of the parameter NHX, equivalent X-ray absorption column density, depends on the size of the occulting cloud normalised by that of the X-ray source, fcloud, and on the geometry parameter of the eclipse, fd. Indeed, since our clouds are supposedly spherical, we have to derive an evaluation of the representative ‘effective’ depth of the cloud as an X-ray absorber, 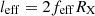 , through which we can reliably estimate the gas number density as
, through which we can reliably estimate the gas number density as
In the definition of leff, we have introduced the quantity feff as a sort of normalised effective ‘radius’, for immediate comparison with fcloud. Considering the condition of maximum coverage, that is, when (referring to Fig. 2) 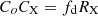 , a spherical gas condensation offers to the incoming X-ray photons a different physical depth depending on the position {x, y} on the sky plane of any given point of the portion of the absorber projection superimposing on that of the X-ray source, that is the occultation region on the sky plane. We can thus derive the effective depth leff by appropriately ‘averaging’ on the actual depths parallel to the line of sight (along the z-direction, as shown in panel (b) of Fig. C.1) in the region of superposition of the cloud projection on the sky plane onto that of of the X-ray source. Here we illustrate our approach to a simplified but representative derivation of feff = leff/2.
, a spherical gas condensation offers to the incoming X-ray photons a different physical depth depending on the position {x, y} on the sky plane of any given point of the portion of the absorber projection superimposing on that of the X-ray source, that is the occultation region on the sky plane. We can thus derive the effective depth leff by appropriately ‘averaging’ on the actual depths parallel to the line of sight (along the z-direction, as shown in panel (b) of Fig. C.1) in the region of superposition of the cloud projection on the sky plane onto that of of the X-ray source. Here we illustrate our approach to a simplified but representative derivation of feff = leff/2.
Referring to Fig. C.1 for the coordinate system and using all lengths normalised to the source size RX, we can introduce an angle θ on the sky plane {x, y}; each θ value identifies in the spherical eclipsing cloud a circular section parallel to the plane {x, z} by defining its distance, y(θ), from the maximum cross section of the cloud, lying on the plane {x, z} itself, as y(θ) = fcloudsin(θ) and its radius r(θ) as r(θ) = fcloudcos(θ). The maximum cross section of the cloud, lying on the plane {x, z} and whose centre is the cloud centre C0, is defined by θ = 0 rad. On each of these circular sections of the cloud we can identify the height x of any of its chords parallel to the line of sight direction to the observer (i.e. the z-axis direction) from the plane {y, z} (on which the circular section centre lies), by introducing the angle ϕ from the circular section diameter parallel to the z-axis. On the circular section identified by a given value of θ, the height on the plane {y, z} of a given chord along the line of sight direction is x(θ, ϕ) = r(θ)sin(ϕ) = fcloudcos(θ)sin(ϕ) and, most importantly, its length (again normalised to RX) is lch(θ, ϕ) = 2r(θ)cos(ϕ) = 2fcloudcos(θ)cos(ϕ). In order to properly average on all the lengths effectively representing a depth the X-ray photons encounter along the line of sight, it is necessary to appropriately define the interval of values of θ and, for each given θ value, the interval of values of ϕ; these intervals depend on the specific occultation, namely on the parameters 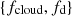 , that define the shape of the intersection region of the two circles representing respectively the projection on the sky plane of the source and of that of the eclipsing cloud; this region is the occultation region.
, that define the shape of the intersection region of the two circles representing respectively the projection on the sky plane of the source and of that of the eclipsing cloud; this region is the occultation region.
For a central geometry of the occultation, that is fd = 0, (and provided fcloud ≤ 1, which is always the case for our detected eclipse events when fd = 0 is chosen) this averaging is very simply obtained as
In the present Appendix, we devote our attention to the exemplifying cases of non-central geometry that we have shown in the main text, that is occultations with an impact parameter 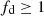 . In these cases, for a realistic and reliable estimate of nH it is more appropriate to determine the maximum value of the angle θ (see exemplifying Fig. C.1), and then derive the minimum value of ϕ as well as its maximum value for each of the cloud cross sections parallel to the plane {x, z} and characterised by a value of θ ∈ [0, θmax], that is ϕmin(θ) and ϕmax(θ). These limiting values depend on the geometry of the occultation, that is on the specific values of fcloud and fd. Two different regimes can be identified (see also Fig. C.2a and C.2b). The first one pertains to the cases in which
. In these cases, for a realistic and reliable estimate of nH it is more appropriate to determine the maximum value of the angle θ (see exemplifying Fig. C.1), and then derive the minimum value of ϕ as well as its maximum value for each of the cloud cross sections parallel to the plane {x, z} and characterised by a value of θ ∈ [0, θmax], that is ϕmin(θ) and ϕmax(θ). These limiting values depend on the geometry of the occultation, that is on the specific values of fcloud and fd. Two different regimes can be identified (see also Fig. C.2a and C.2b). The first one pertains to the cases in which
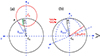 |
Fig. C.1. Schematic representation of the maximum coverage condition for an exemplifying case of non-central occultation geometry; here |
that is those geometrical conditions in which the intersection points between the two circumferences centred in C0 and CX respectively are located at a distance from the y-axis (along which the cloud centre is supposed to move) smaller than the one between C0 and CX, that is, fd (see Fig. C.2a). In this case, θmax is defined as the angle subtended by the arc from the point of intersection of the cloud projection circumference with the x-axis (θ = 0) to the point (identified as P in Fig. C.2a) of intersection of the two circumferences delimiting the source and cloud projections on the sky plane {x, y}. Therefore, we have
where 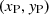 are the coordinates of point P on the sky plane and are defined as
are the coordinates of point P on the sky plane and are defined as
When condition (C.2) is satisfied, the maximum value for the angle ϕ is ϕmax(θ) = π/2 independently of the specific θ value (i.e. of the circular section parallel to the plane {x, z} considered and whose portion of interest, projected on the sky plane, {x, y}, is identified as the green line parallel to x-axis in Fig. C.2a); on the other hand the corresponding minimum value of ϕ does indeed depend on the value of θ, as well as on those of fcloud and fd, following the relation
the angle ϕ thus varies in the interval [ϕmin(θ),π/2]. In the second case we deal with
implying that the distance from the y-axis of the intersection points between the two circumferences centred in C0 and CX is now larger than, or equal to, fd (see Fig. C.2b). In the present case, the maximum value of the angle θ is the one defined by the x-axis and the radius C0K, where point K is on the cloud projection circumference and at a distance from the x-axis equal to the source unit radius, as shown in Fig. C.2b, so that 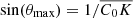 and thus
and thus
From Fig. C.2b it is apparent that ϕmax on a given circular section of the spherical occulting cloud and parallel to plane (x, z) depends on the value of θ characterising the specific circular section. Defining θp as the value of θ formed by the x-axis and the radius from C0 to the point P of intersection between the two circumferences, it is
where 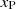 and
and 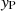 are again given by Eq. (C4); for
are again given by Eq. (C4); for ![$ \theta\in[0, \theta_\mathrm{p}] $](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq90.gif) we have ϕmax = π/2, whereas for
we have ϕmax = π/2, whereas for ![$ \theta\in(\theta_\mathrm{p}, \theta_{\mathrm{max}}] $](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq91.gif) simple geometrical calculations give
simple geometrical calculations give
As for ϕmin, its dependence on θ and on the parameters 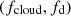 is correctly defined by Eq. (C.5) also in the present case of
is correctly defined by Eq. (C.5) also in the present case of 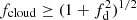 .
.
With these evaluations of the new limits of integration, we can apply the same averaging method shown in Eq. (C.1), that in the general case for 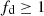 gives
gives
where
and θmax, ϕmax, ϕmin depend on the specific case, as illustrated above. In each of the cases discussed, at least ϕmin always depends on fcloud and fd, so that in general it is
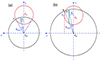 |
Fig. C.2. Panels (a) and (b) illustrate the maximum coverage condition with X-ray source and occulting cloud seen projected on the sky plane {x, y} respectively for case A), in which |
All Tables
Parameters and quantities, derived within the newly calculated Paper II model described in the text, for sources with detected reliable occultations.
Specifics of each event among the 57 under examination: AGN source, observing instrument (S for Suzaku, X for XMM-Newton), date of the observation, order number of the event for any given source, ‘significance’ log F (as determined in Paper I), the derived observable quantity ΔHR/HR, normalised event duration and duration τ0 (in ks) of the event.
All Figures
 |
Fig. 1. Observables plot: Fractional hardness ratio variability, Δ(HR)/HR, versus the normalised eclipse duration, τecl = τ0/Δtecl, for each reliable eclipse event detected in Paper I. |
| In the text | |
 |
Fig. 2. Schematic illustration of an eclipse event as seen on the sky plane from the observer line of sight (z-direction, normal to the page). The distance, HCX ≡ d, between the source centre, CX, and the straight line trajectory of the absorber projection centre, C0, during the eclipse, represents a sort of ‘impact parameter’, d, for the occultation and is depicted in red. |
| In the text | |
 |
Fig. 3. Best match solutions obtained for our detected events in the case of central geometry. Yellow dots represent best matches for NGC 3783 detected eclipse events, cyan dots show best matches for those of MCG 06-30-15, green dots show matches obtained for events referring to all other sources with MBH < 6.5, red dots are for all other sources with MBH > 7, and finally blue dots are best match events referring to intermediate mass sources with 6.5 < MBH < 7, where MBH ≡ log(MBH/M⊙). |
| In the text | |
 |
Fig. 4. Best match solutions for cloud physical size obtained for our detected events in different geometries: circles again refer to central geometry (fd = 0), but we also show matches for fd = 1 (filled hexagons), fd = 2 (filled triangles) and fd = 4 (large filled triangles). Colour code is the same as in Fig. 3. In each panel hollow circles or triangles represent event descriptions that, for the specific fd value, must be discarded, since the occulting clouds are located farther than the chosen outer border of the cloud ensemble; the corresponding events are only explainable with fd = 4 or larger. |
| In the text | |
 |
Fig. 5. Gas number density from best match solutions obtained for our detected events in different geometries. Here we impose the constraints on maximum normalised physical size of the cloud described for Fig. 4 and colour codes are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6. Gas number density from best match solutions obtained for our detected events and for two different values of the absorbing column density NHX, as shown by the labels in each panel. Here we impose the constraints on maximum normalised physical size of the cloud described for Fig. 4 and colour codes are the same as in Fig. 4. |
| In the text | |
 |
Fig. 7. Cloud physical size for occultation matching solutions plotted versus cloud distance normalised to the gravitational radius of the AGN source specific to the eclipse event. Symbols and colour codes are the same as in Fig. 4. |
| In the text | |
 |
Fig. 8. Best matching solutions for the three events that we have detected and were also spectrally analysed by Risaliti et al. (2011), chosen so as to maximise the agreement with R11 results for NHX and CF values as reported in their paper. Blue points indicate a solution with NHX = 1023 cm−2, whereas red ones refer to cases in which NHX = 2 × 1023 cm−2; circular dots show central geometry solutions (fd = 0) and triangles indicate a case with impact parameter of the occultation fd = 2. |
| In the text | |
 |
Fig. B.1. Fractional variation of hardness ratio as a function of NHX for fixed values of the covering factor, CF. Blue labels specify the value of CF for which each group of curves is obtained. For each CF value chosen, solid black curves represent the results of Suzaku-XIS simulations for type-1 sources, whereas the long-dashed red ones show those derived for type-1 with XMM-Newton-EPIC/PN. When present, the third short-dashed red line of each CF-value group of curves represents the case for type-2 XMM simulations. |
| In the text | |
 |
Fig. B.2. Δ(HR)/HR as a function of CF for different values of the column density. The dotted line curve corresponds to NH = 5 × 1022cm−2, the solid curve to NH = 1 × 1023cm−2, the short-dashed curve to NH = 2 × 1023cm−2, the long-dashed curve to NH = 3 × 1023cm−2, and the dash-dotted curve refers to NH = 5 × 1023cm−2 |
| In the text | |
 |
Fig. B.3. Black curves represent fabs as a function of the normalised impact parameter, fd, for a given value of CF. Red curves show Y0 (see Eq. 2) again as a function of fd and constant CF. Red curves are labelled with CF values; in the same order, increasing upwards, the same labels also apply to the black curves. |
| In the text | |
 |
Fig. C.1. Schematic representation of the maximum coverage condition for an exemplifying case of non-central occultation geometry; here |
| In the text | |
 |
Fig. C.2. Panels (a) and (b) illustrate the maximum coverage condition with X-ray source and occulting cloud seen projected on the sky plane {x, y} respectively for case A), in which |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



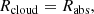
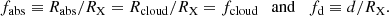
![$$ \begin{aligned} \tau _0 = {2 R_{\rm X}\over v_{\rm {c}}} \left[ (1+f_{\rm {abs}})^2-f_{\rm d}^2\right]^{1/2}={2 R_{\rm X}\over v_{\rm {c}}}Y_0 , \end{aligned} $$](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq8.gif)
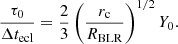
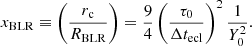
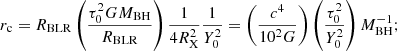
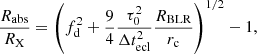
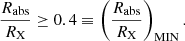
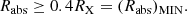
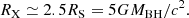
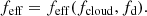
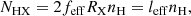
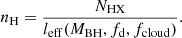
![$$ \begin{aligned} Frac_{\rm {[R_{i}, R_{2}]}} = {\int ^{R_2}_{R_{\rm i}} (\mathrm{d}N/ \mathrm{d}R) \mathrm{d}R\over \int ^{R_2}_{R_{\rm {1x}}} (\mathrm{d}N/ \mathrm{d}R) \mathrm{d}R}, \end{aligned} $$](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq35.gif)
![$$ \begin{aligned}n_{\rm {ecl}} [R_{\rm i}/R_{\rm X},R_2/R_{\rm X}] = Frac_{\rm {[R_{i}, R_2]}} N_{\rm {ecl}}.\end{aligned} $$](/articles/aa/full_html/2024/10/aa49686-24/aa49686-24-eq36.gif)