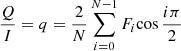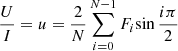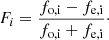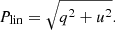| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A216 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202348572 | |
| Published online | 10 October 2024 | |
Varying linear polarisation in the dust-free gamma-ray burst 210610B
1
Instituto de Astrofísica de Andalucía, Glorieta de la Astronomía s/n, 18008 Granada, Spain
2
Observatoire de la Côte d’Azur, Université Côte d’Azur, Boulevard de l’Observatoire, 06304 Nice, France
3
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
4
Astronomical Institute of the Czech Academy of Sciences (ASU-CAS), Fričova 298, 251 65 Ondřejov, Czech Republic
5
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
6
INAF – Osservatorio di Astrofisica e Scienza dello Spazio, Via Piero Gobetti 93/3, 40129 Bologna, Italy
7
Frontier Research Institute for Interdisciplinary Sciences, Tohoku University, Sendai 980-8578, Japan
8
Astronomical Institute, Graduate School of Science, Tohoku University, Sendai 980-8578, Japan
9
Hessian Research Cluster ELEMENTS, Giersch Science Center, Max-von-Laue-Strasse 12, Goethe University Frankfurt, Campus Riedberg, 60438 Frankfurt am Main, Germany
10
INAF – Brera Astronomical Observatory, Merate, Italy
11
Centre for Astrophysics Research, University of Hertfordshire, Hatfield AL10 9AB, UK
12
Clemson University, Department of Physics and Astronomy, Clemson, SC 29634, USA
13
Centre for Astrophysics and Cosmology, Science Institute, University of Iceland, Dunhagi 5, 107 Reykjavík, Iceland
14
School of Physics and Centre for Space Research, O’Brien Centre for Science North, University College Dublin, Belfield, Dublin 4, Ireland
15
INAF – Rome Astronomical Observatory, Via Frascati 33, I-00078 Monte Porzio Catone, Italy
16
University of Messina, MIFT Department, Via F. S. D’Alcontres 31, 98166 Messina, Italy
17
Astronomical Institute Anton Pannekoek, University of Amsterdam, PO Box 94249 1090 GE Amsterdam, The Netherlands
18
Physics Department, University of Calabria, Via P. Bucci, 87036 Arcavacata di Rende, CS, Italy
19
INFN-Laboratori Nazionali di Frascati, Via Enrico Fermi 54, 00044 Frascati, RM, Italy
20
School of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK
21
Capodimonte Astronomical Observatory, INAF-Napoli, Salita Moiariello 16, 80131 Napoli, Italy
22
Inter-University Institute for Data Intensive Astronomy & Department of Astronomy, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
23
School of Mathematical and Physical Sciences, Macquarie University, Macquarie, NSW 2109, Australia
24
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO-3D), Australia
Received:
12
November
2023
Accepted:
23
February
2024
Context. Long gamma-ray bursts (GRBs) are produced by the collapse of some very massive stars, that emit ultra-relativistic jets. When the jets collide with the interstellar medium they decelerate and generate the so-called afterglow emission, which has been observed to be polarised.
Aims. We study the polarimetric evolution of the GRB 210610B afterglow, at z = 1.1341. This allows us to evaluate the role of geometric and/or magnetic mechanisms in the GRB afterglow polarisation.
Methods. We observed GRB 210610B using imaging polarimetry with CAFOS on the 2.2 m Calar Alto Telescope and FORS2 on the 4 × 8.1 m Very Large Telescope. Complementary optical spectroscopy was obtained with OSIRIS on the 10.4 m Gran Telescopio Canarias. We studied the GRB light-curve from X-rays to the optical bands and the Spectral Energy Distribution (SED). This allowed us to strongly constrain the line-of-sight extinction. Finally, we studied the GRB host galaxy using optical to NIR data to fit the SED and derive its integrated properties.
Results. GRB 210610B had a bright afterglow with a negligible line-of-sight extinction. Polarimetry was obtained at three epochs: during an early plateau phase, at the time when the light curve breaks, and after the light curve steepened. We observe an initial polarisation of ∼4% that goes to zero at the time of the break, and it then again increases to ∼2%, with a change in the position angle of 54 ± 9 deg. The spectrum shows features with very low equivalent widths. This indicate a small amount of material in the line of sight within the host.
Conclusions. The lack of dust and the low amount of material in the line of sight to GRB 210610B allowed us to study the intrinsic polarisation of the GRB optical afterglow. The GRB polarisation signals are consistent with ordered magnetic fields in refreshed shock or/and hydrodynamics-scale turbulent fields in the forward shock.
Key words: polarization / techniques: polarimetric / gamma-ray burst: individual: GRB 210610B
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Gamma-ray bursts (GRBs) are among the most energetic electromagnetic explosions that have been observed in the Universe. These events have two main emission episodes: the prompt-emission and the afterglow-emission phases. The prompt emission represents the first observable electromagnetic emission and is dominated by gamma-ray photons lasting seconds to minutes after the onset of the burst. The afterglow has a synchrotron spectrum ranging from radio to gamma-rays and evolves in time during much longer time spans.
GRBs are typically classified as short or long according to their measured T901 duration in gamma-rays (Kouveliotou et al. 1993). Short GRBs (sGRB) are associated with the coalescence of two compact objects, their T90 duration is typically shorter than 2 seconds, and their X-ray spectrum is hard. The discovery of a sGRB associated with the gravitational wave (GW) detection GW 170817 definitively linked a sGRB with the merger of two neutron stars (Abbott et al. 2017). On the other hand, long GRBs (lGRB) that show T90 longer than 2 seconds and have a softer spectra in the prompt emission phase. These are cataclysmic events associated with the collapse of massive stars. They are also associated with the detection of broad-line (BL) type Ic supernovae (SNe) (see e.g. Galama et al. 1998; Hjorth et al. 2003). Lately, several events detecting a kilonova (KN) emission in a burst with a duration of dozen seconds have cast doubts on the 2-seconds division as the unique criterion to distinguish between sGRBs and lGRBs (Rastinejad et al. 2022; Troja et al. 2022; Yang et al. 2022; Gompertz et al. 2023; Levan et al. 2023, 2024).
The prompt emission in a GRB is powered by a newly formed compact object that is fed by the surrounding material. Accretion onto this compact object launches ultra-relativistic jets, in which the prompt emission is generated through internal dissipation processes including internal shocks (see e.g. Rees & Meszaros 1994; Sari & Piran 1997; Kobayashi et al. 1997). This prompt high-energy emission releases isotropic-equivalent energies that can reach up to 1055 erg (see e.g. Burns et al. 2023), although the real released energy can be several orders of magnitude lower due to the jet collimation.
Polarimetry is an essential tool for explaining GRB physics. Using this technique, we can test models that include magnetic fields and the geometrical characteristics that are at play, and we can determine how they evolve throughout the different phases of the GRB. The study of the prompt emission polarisation and its temporal evolution can help us to understand how the jet is powered by the central engine. The long and extremely bright GRB 221009A was observed during the prompt- and afterglow-emission phase by the Imaging X-ray Polarimetry Explorer (IXPE) and only upper limits were obtained (Negro et al. 2023). Studies of the prompt-emission polarisation with instrument calibrated to perform polarimetry are rare so far. The Astrosat mission with the on-board Cadmium-Zinc-Telluride Imager (CZTI) instrument shows the prompt emission as highly polarised, while for POLAR, GRBs are lowly polarised or not polarised at all (see e.g. Gill et al. 2021).
The material ejected through the jets eventually collides with the circumburst material, decelerating as interacts with it. These forward shocks generate a broadband synchrotron emission that is known as the afterglow. This bright shock can be observed during days or even months in the case of radio frequencies. In certain cases, a reverse shock that propagates backwards within the relativistic jet can be observed at early times (see e.g. Mészáros & Rees 1997; Piran 1999). Different models predict this emission to be polarised. Gruzinov & Waxman (1999) proposed a model in which the afterglow would show patches with locally ordered magnetic fields randomly oriented but with many of them sharing a common direction leading to a global low level of polarisation in the GRB afterglow.
The number of studies using optical linear imaging polarimetry and spectropolarimetry techniques is still very small (see e.g. Covino & Gotz 2016). The first GRB with a polarisation detection in the afterglow was GRB 990510. Its polarisation degree (PD) was 1.7%, 0.7 days after detection (Covino et al. 1999; Wijers et al. 1999). Many efforts have been made to increase the sample of polarimetric measurements, but the faintness of these objects, their fast evolution, and the long observing times required for a good signal-to-noise ratio (S/N) leave us with less than 20 GRBs with a measurement above 3σ. Fast reaction is crucial for observing the first GRB phases in which a higher PD might be expected. The highest measured value was for GRB 120308A with a PD of 28% 5 minutes after the burst, which rapidly decreased to 16% as the afterglow evolved (Mundell et al. 2013). A high PD of ∼10% was also measured for GRB 020405, GRB 090102 and GRB 091208B (Bersier et al. 2003; Steele et al. 2009; Uehara et al. 2012). All of them were observed earlier than 0.01 days after the GRB detection. Observations at later stages shows this sources as lowly-polarised with some degree of variability throughout their light-curve evolution. The most detailed example is GRB 030329 (Greiner et al. 2003) whose PD evolves somewhat randomly from 0.91% at 0.5 days to 1.4% 37.5 days after the burst.
Afterglow polarisation must be understood together with the surrounding environment. Dust in the line of sight can change the observed PD and prevent the measurement of the intrinsic polarisation (Lazzati et al. 2003). This measurement by itself is also incomplete when it is not followed by the study of the light-curve evolution. It is crucial for distinguishing between the models that have been proposed to explain the GRB jet physics to understand whether there is a break in the light curve and how the polarisation behaves before, during and after this break (see e.g. Covino & Gotz 2016).
We present a comprehensive study of GRB 210610B, its afterglow emission and its environment using different techniques. Polarimetric, spectral and photometric observations were secured for this bright long GRB. We also observed the putative host galaxy in order to characterise it and place the GRB into context. This work is structured as follows: In Section 2 we present the observations of both, the afterglow and the underlying galaxy. In Section 3 we present the results of the analysis of the linear polarimetry of the afterglow, the light curve and its spectrum, as well as the analysis of the galaxy. In Section 4 we discuss the results by setting the framework into which GRB 210610B is embedded. We also place the results of the GRB afterglow polarimetry measurements into context. Finally, in Section 5 we present the conclusions.
Throughout this study, we describe the spectral and temporal evolution of the data using the convention by which Fν ∝ t−αν−β. We adopt a cosmological model with H0 = 67.3 km s−1 Mpc−1, ΩM = 0.315 and ΩΛ = 0.685 (Planck Collaboration XVI 2014).
2. Observations
2.1. High-energy data
GRB 210610B was first detected by the Gamma-ray Burst Monitor (GBM) on board the Fermi observatory at 19:51:05.05 UT of 10 June 2021 with a T90 = 55.04 ± 0.72 s and a fluence of (1104.2 ± 0.5)×10−5 erg cm−2 in the 10 keV to 10 MeV band (Malacaria et al. 2021; von Kienlin et al. 2020). At the redshift of the GRB (see Sect. 3.3), the computed isotropic energy is 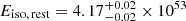 erg in the 0.1 keV to 10 MeV band. This value is fully consistent with the so-called Amati relation (Amati et al. 2002; Amati 2006) for long GRBs. The burst was detected ∼22 s later by the Burst Alert Telescope (BAT; Barthelmy et al. 2005) on board the Neil Gehrels Swift Observatory with coordinates RA = 16h15m45s, Dec = +14° 23′29″ and an uncertainty of 3′. The X-Ray Telescope (XRT; Burrows et al. 2005) started observing the source 89.9 s after BAT and quasi-simultaneously, the Ultraviolet/Optical Telescope (UVOT; Roming et al. 2005) observed the field in the White band. The image showed a new bright source within the XRT position with a magnitude in the Swift/UVOT native system of 13.70 ± 0.14, uncorrected for galactic extinction (Page et al. 2021). The later analysis, presented in Siegel et al. (2021), updated this value to 13.63 ± 1.10 and the source location to RA = 16h15m40.40s, Dec = +14° 23′56.9″ with an uncertainty of
erg in the 0.1 keV to 10 MeV band. This value is fully consistent with the so-called Amati relation (Amati et al. 2002; Amati 2006) for long GRBs. The burst was detected ∼22 s later by the Burst Alert Telescope (BAT; Barthelmy et al. 2005) on board the Neil Gehrels Swift Observatory with coordinates RA = 16h15m45s, Dec = +14° 23′29″ and an uncertainty of 3′. The X-Ray Telescope (XRT; Burrows et al. 2005) started observing the source 89.9 s after BAT and quasi-simultaneously, the Ultraviolet/Optical Telescope (UVOT; Roming et al. 2005) observed the field in the White band. The image showed a new bright source within the XRT position with a magnitude in the Swift/UVOT native system of 13.70 ± 0.14, uncorrected for galactic extinction (Page et al. 2021). The later analysis, presented in Siegel et al. (2021), updated this value to 13.63 ± 1.10 and the source location to RA = 16h15m40.40s, Dec = +14° 23′56.9″ with an uncertainty of 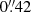 .
.
In the refined analysis from the BAT data, the burst had a T90 duration of T90 = 69.38 ± 2.53 s in the 15 to 350 keV band with an Epeak = 339.3 ± 218.6 keV(Krimm et al. 2021). The burst showed a hardness ratio (HR)2 of 1.78 ± 0.04. This falls in the upper part of the bulk of the HR distribution for long GRBs (see e.g. Lien et al. 2016). The burst was also detected by Konus-Wind observatory with a duration ∼100 s (Frederiks et al. 2021). The HR of the burst, its T90, and its isotropic energy release classify GRB 210610B as a long GRB.
2.2. Linear polarimetry imaging
We observed the GRB 210610B following the Swift/BAT alert with two different instruments in linear polarimetry mode. We first observed it with the Calar Alto Faint Object Spectrograph (CAFOS) mounted on the 2.2 meter telescope at Calar Alto Observatory3. The observations started 0.08 days after the Swift/BAT detection with an exposure per half-wave plate (HWP) position angle (see below) of 900 s in R band. A second observation was obtained with the FOcal Reducer and low dispersion Spectrograph (FORS2) mounted on the Unit Telescope 1 of the Very Large Telescope (VLT) of the European Southern Observatory (ESO)4. The VLT/FORS2 observations started 0.24 days after the GRB alert in RSpecial, bHigh, and zSpecial bands with 180 s exposure time per image and with two cycles with the same configuration.
For both instruments, observations were obtained using the HWP in four different rotation angles of 0.0°, 22.5°, 45.0°, and 67.5° and with a Wollaston prism to split the light into the ordinary (o) and extraordinary (e) beams. A mask was set to avoid overlapping of the light from the two beams.
To calibrate the CAHA/CAFOS observations, one high- and one zero-polarised standard star were observed following the same procedure as for the GRB. The flat-fields in the corresponding band were obtained with the full optical setup in the light path. For the VLT/FORS2 data, calibration and standard observations were performed as specified in the FORS2 User Manual (Anderson 2015).
We obtained a second epoch with VLT/FORS2 in RSpecial ∼ 1 day. We increased the exposure time per image up to 300 s to account for the fading of the source by performing two cycle for this observations.
2.3. Photometry
Photometric observations were performed using several instruments at different observatories and in multiple bands. In this section, we describe the details of each of the observations. The measured photometry is compiled in Table A.1.
2.3.1. Small Binocular Telescope
The Small Binocular Telescope (SBT), located at the Ondřejov Observatory, observed GRB 210610B at dusk with the two 20 cm Newtonian astrographs mounted on a common mount. The main detectors have 4096 × 4096 pixel CCDs that provide a field of view of 3.5° × 3.5° with a 3.14″ sampling. Operations are designed such that the readout time of one camera equals the exposure time of the other camera to avoid any blind time during the observation.
The SBT observations started ∼860 s after the burst. During the early follow-up phase, 12 s exposures were taken without a filter. Afterwards, the observations consisted of up to 34 exposures of 120 s each in SDSS-r′ band (see Table A.1 for further details). Observations were interrupted at 23:47 UT, almost 4 h after the GRB detection.
The afterglow was not detected in single exposures, and we therefore stacked the images to obtain an acceptable (S/N). We used montage to obtain a weighted image co-addition similarly to Morgan et al. (2008), which optimises for the variable background caused by dusk and thick cirrus.
As for the images in r′ band, photometric calibration was performed against the Atlas catalogue, which uses the Pan-STARRS catalogue for faint targets. Images in the clear band were calibrated against the r′ band and a polynomial correction involving photometric colours g′−r′, r′−i′, and i′−z′ was performed. Photometric measurements obtained this way are shifted compared to the original standard r′ band by a correction that depends on the object colour. This correction can be computed from the fitted relation when the photometric colours of the afterglow are known. By fitting the complete photometric set with an empirical broken power law we, determined this correction to be kc − r = −0.0045 mag. Therefore, under the assumption that the afterglow shows no colour evolution, we are able to convert the unfiltered values from SBT into r′ by simply subtracting kc − r.
2.3.2. FRAM-ORM telescope
The 25 cm telescope FRAM-ORM, is operated as part of CTA-N at Roque de los Muchachos at La Palma, Spain. The telescope is equipped with a 1024 × 1024 pixel CCD detector and a Bessel filter set, which provides a field of view of 26′×26′ with a pixel scale of 1.5″.
FRAM-ORM observed the GRB starting at 20:49 UT (1 h after trigger) and obtained a total of 83 × 60 s images in R band using a total of 1.5 h of observing time. Images were reduced using standard procedures and combined into groups in order to provide a good (S/N). Photometry was performed in a similar way as for the SBT unfiltered images, using r′ band and r′−i′ band catalogue values. The derived correction factor is kR − r = −0.036 mag.
2.3.3. Telescope D50
The D50 Telescope is a 0.5 m Newtonian robotic telescope located at Ondřejov Observatory. It has a 1024 × 1024 EMCCD camera with a field of view 20′×20′, scaled at 1.18″ per pixel. The telescope is equipped with an SDSS filter set.
D50 started observing 0.06 days after the burst detection, starting with SDSS-r′ band and followed by a set of observations in SDSS-g′, r′, i′, and z′ bands using different exposure times (see Table A.1 for further details). During the first night, the telescope spent 3.2 h on target and stopped at 01:05 UT. There were additional observations in night 2, 4, 5, and 7, collecting 16.75 h of further follow-up data.
All images were processed in a standard manner performing dark subtraction, flat-field correction, and fringe removal for i′ and z′, and the images were co-added when necessary. Photometry was performed using the SDSS catalogue in the corresponding band. The GRB afterglow emission is detected even at the latest epoch.
2.3.4. CAHA/CAFOS
In addition to the polarimetric observation, we performed further imaging of the afterglow in the second night with CAFOS on the 2.2 m telescope of the Calar Alto Observatory. The images were corrected using bias and flat fields using standard procedures in IRAF. The observations were performed with the RC filter and calibrated with respect to PanSTARRS field stars, for which a filter correction was used to derive AB magnitudes in the RC band. These magnitudes were then transformed into the r′ band using the colour information that we have from the afterglow. The final values are shown in Table A.1.
2.3.5. GTC/HiPERCAM
The field of GRB 210610B was observed in four epochs using the HiPERCAM multi-band imager (Dhillon et al. 2021) mounted on the 10.4 m Gran Telescopio de Canarias (GTC) at Roque de los Muchachos Observatory (La Palma, Spain) using programme GTCMULTIPLE2C-21A (PI: de Ugarte Postigo). HiPERCAM simultaneously obtains observations in the five SDSS filters (u′, g′, r′, i′, z′) using efficient dichroic beam-splitters and multiple cameras. The last of our observations was obtained almost two months after the burst when the emission was dominated by the host galaxy (see Fig. 1).
 |
Fig. 1. Colour images of the field using the g′, r′ and i′ bands of HiPERCAM at 1 day and 58 days after the burst, respectively. In the first image the afterglow is strongly detected, in the second image, it has faded and the host galaxy dominates the emission. 2.7 arcsec north-west of the host galaxy lies a companion galaxy at the same photometric redshift of the host (see Sect. 3.4). |
The data reduction was performed using an automatic shell script that finds and organises the files, calls commands from the HiPERCAM pipeline to perform bias and flat corrections and converts the HiPERCAM one-dimension fits files into classical two-dimension fits images. Further IRAF procedures allow us to obtain an even background from the different quadrants of each detector. Finally, the images are registered and combined using SWARP (Bertin 2010). Photometry was performed with aperture photometry using reference field stars from the PanSTARRS catalogue. For the last epoch, we used the same aperture to compare the results to the rest of the data. Additionally, we performed photometry of the complete host galaxy adapting the aperture to its light, and in a similar way, we obtained photometry of a nearby object north-west of the host, which we identified as a companion galaxy at the same redshift (see Sect. 3.4).
2.3.6. Perek 2 m telescope
The Perek 2.0 m telescope at the Ondřejov Observatory observed GRB 210610B afterglow 6 days after the burst in SDSS-g′ band. The photometric camera of this telescope has a 1092 × 736 pixel CCD with a field of view of 5′×7′ scaled at 0.4″/pixel. After standard imaging data reduction and after imaging co-addition, photometry was performed as for the D50 telescope. The GRB afterglow is well detected.
2.3.7. GTC/EMIR
Late-time near-infrared (NIR) observations were performed on 19 February 2022 in search for the host galaxy of GRB 210610B with the EMIR instrument (Garzón et al. 2022) mounted on the 10.4m GTC telescope with programme GTCMULTIPLE2H-21B (PI: de Ugarte Postigo). The observation consisted of a total exposure of 349 × 3 s in H band. The data reduction was performed using a self-made pipeline that corrects flat fields, does background subtraction, bad-pixel masking, alignment and combination of the frames. The host galaxy was not detected in the final frame down to a 3-σ limiting magnitude of 22.9 mag.
2.4. Spectroscopy
We observed GRB 210610B using the long-slit mode of the Optical System for Imaging and low Resolution Integrated Spectroscopy (OSIRIS) (Cepa et al. 2000) mounted on the 10.4 m GTC. The observation consisted of 3 × 900 s exposures with grism R1000B and a slit width of 1″ oriented at the parallactic angle5. The mean epoch of the observation was 11 June 2021 at 01:59:14 UT (6.12972 h after the Swift trigger) at a mean airmass of 1.13.
Flux calibration was performed relative to an observation of the Ross 640 (Oke 1974) spectrophotometric standard, observed at the beginning of the same night and using the same grism. The afterglow spectrum shows a very strong continuum, with a median (S/N) of ∼100 per dispersion element and weak absorption features.
3. Results
3.1. Linear polarimetric analysis
For all linear polarimetry data, we performed regular imaging-reduction processes. Images were bias subtracted and flat-field corrected using PyRAF tasks (Science Software Branch at STScI 2012). The flat field correction for VLT/FORS2 was performed as specified in González-Gaitán et al. (2020). For CAHA/CAFOS, we combined the flat fields using PyRAF, and we used a customized Python script to separate the o and e beams into two separate images. We normalised each beam to the corresponding median value and created the o and e beam combined flat. We followed the same procedure for each image. We performed this correction since flat fields were obtained with the full optics on the light pathway. This led to a rather different count rate in each beam what would have led to an inaccurate normalisation. Finally, we split all the reduced images into an o and e image and applied the L.A. Cosmic algorithm (van Dokkum 2001) to remove cosmic rays.
We used PyRAF to measure the on-frame full width at half maximum (FWHM) in each image including the high- and zero-polarised standard stars. The FWHM was measured independently for the o and e beam since the shape of the point spread function (PSF) can vary, especially for sources with a high degree of polarisation.
To obtain reference field stars we used a source detection algorithm based on DAOStarFinder in Photutils and applied it to the background-subtracted o and e images separately. The selected sources were those with a threshold above the median plus three times the standard deviation of the background. The statistics were calculated per beam and per angle position of the HWP using a sigma clipping of the masked image. From these sources, we discarded those that were clearly extended and those that lay too close or partially within the instrumental mask edges. We also checked whether the source was saturated in any of the beams. We ended up with five sources, including GRB 210610B, in the FORS2 images and five sources in the CAFOS images. The sources from FORS2 and CAFOS images are different due to saturation or because sources fall at the mask edges.
We performed aperture photometry using circular apertures with a radius equal to the FWHM and applied infinite-aperture corrections using a custom Python script to the FORS2 data. In order to avoid contamination by a nearby spurious source, we measured the flux for the CAHA/CAFOS data using a fixed aperture of three times the FWHM per image and per beam and subtracted the sky of an annulus around the source with an inner and outer radius of four and five times the FWHM, respectively. In the FORS2 images, this spurious source was outside the measured region. The errors for the aperture photometry were obtained considering each beam as an unique image, that is, we separated the ordinary stripes from the extraordinary stripes.
With the measured flux values per source and per beam, fo and fe, we obtained the Stokes parameters Q and U describing the linear polarisation (see e.g. Patat & Romaniello 2006; Bagnulo et al. 2009) for each of our images. We used the normalised Stokes parameter for the linear polarisation.
where N is the number of positions of the half-wave plate, I is the intensity, and Fi is the normalised flux difference per HWP position angle,
Following the equations above, we can obtain the polarisation degree Plin,
For the position angle, we followed the formalism as used in Bagnulo et al. (2009).
We then corrected for the effects of optics and detector in the polarisation images. To do this, zero-polarised standard stars were observed in the corresponding bands with VLT/FORS2 following the procedures detailed in Anderson (2015). For CAHA/CAFOS, observations of standard stars were carried out in the same night. In the case of VLT/FORS2, b- and z-band standards were completely saturated, and no subsequent standards were found in the ESO archive around the time of the observation. For the R band, the standards were also saturated. We then used WD1620−391 for the zero-polarised standard star, observed 18 days after the GRB, for VLT/FORS2, and BD+33 2642 (Turnshek et al. 1990) for CAHA/CAFOS observed in the same night as GRB 210610B.
We finally removed the effect on the polarisation induced by the dust in the Milky Way (MW). To do this, we measured the q and u parameters for the field stars in our images. However, FORS2 is known to have a radial profile in which the polarisation varies across the field from the optical axis towards the edges of the detectors (see e.g. González-Gaitán et al. 2020). To account for this effect, we applied the corresponding correction by using the q, u background correction and the instrumental polarisation maps presented in González-Gaitán et al. (2020). We then measured the Galactic interstellar polarisation (Galactic ISP, or GISP) using three methods, following Wiersema et al. (2012): First, we measured the mean values for the q, u parameters from the field stars. Then we performed a one-dimensional Gaussian fit to the q, u values of the field stars by generating a normal distribution of values for the q, u within their corresponding errors, and we then fitted a Gaussian to each Stokes parameter. Finally, we performed a two-dimensional Gaussian fit to the q, u, adapting the procedure from the one-dimensional Gaussian fit (see Fig. 2 for an example of the two-dimensional Gaussian fit). All the q, u fitted parameters are consistent within the errors, and we therefore vectorially subtracted the mean value from the q, u values for the GRB. The mean sky values are listed in Table 1, which are all consistent with or close to zero. Both q and u show some variation from one epoch to the next, which we assumed is due to different sky background light between the epochs6.
 |
Fig. 2. Two-dimensional Gaussian fit to the field stars q, u parameters. Left: Normal distribution of randomly generated data around the q, u values. The amplitude to generate the data is the Stokes parameter errors. Central panel: two-dimensional Gaussian model fitted to the data points. Right: Residuals. |
Measured values for the linear polarisation and PA of GRB 210610B.
For the CAFOS images, the same analysis was performed, although we were unable to correct for background polarisation and instrumental polarisation across the images because we lack a characterisation as we have for FORS2. However, lunar illumination was close to 0%, and we do not expect a high instrumental polarisation (Patat & Taubenberger 2011) for CAFOS. Indeed, the two-dimensional Gaussian fit to the field stars (see Fig. 2) shows it to be consistent with no polarisation from the ISM and implicitly, no polarisation from the CAFOS instrument.
After the polarisation induced by the MW dust was removed we calculated the final polarisation from both instruments in all the filters. Next, we needed to consider the contribution to the polarisation from the dust in the host galaxy itself. Since the information is more limited than for the dust in the MW we assumed a Serkowski law (Serkowski et al. 1975) for the host galaxy. From the spectral energy distribution (SED) fit of the GRB light curve, we obtained the colour excess on the line of sight (see Sect. 3.2). Assuming this value as the extinction of the afterglow at the host galaxy, using PISP(%)≤9.0 × E(B − V), we find that the contribution from the host galaxy could be as high as PHost ISP ≤ 0.09%. We note that in extragalactic sight lines, this may not be applicable because the dust properties may differ from those of the MW (Nagao et al. 2022). This value is well below the PD measured for the afterglow, and we therefore considered the host contribution to be negligible. Finally, we corrected for the polarisation definition bias with the modified asymptotic estimator (MAS) Plaszczynski et al. (2014). The corrected values for the polarisation degree are shown in Table 1 before and after the bias correction.
We also determined the polarisation position angle (PA) for the GRB afterglow. The FORS2-measured raw PA was corrected for chromaticity using the tabulated values per bandpass presented in Anderson (2015). We then corrected for it using the standard star Hiltner 652, observed on the 19, July 2021, although the PA correction is very small with Δθ = 0.5 ± 0.9. The high polarisation standard in RSpecial band closest in time to the GRB was also saturated in at least one beam. We corrected the derived PA value of the standard to the value presented in Cikota et al. (2017). As the measured b-band value for the PA in Hiltner 652 is very close to the B band value in Cikota et al. (2017) we use B band to correct for the b-band value. For the z band, no observations were found so far for this standard, and we therefore used the PA for the I band in Cikota et al. (2017). The high polarisation standard observed for CAFOS, Hiltner 960, was corrected to the “theoretical” value following Schmidt et al. (1992).
We detect polarisation at ≳3σ significance for the first and last epochs, while the second epoch is consistent with zero polarisation. We detect 1σ polarisation in the R band on the second epoch. We consider this measurement, together with the R band observation at ∼0.26 days for the b and z band as limit, however. Since the MAS correction is not completely applicable when PD/σP < 3.0, we did not apply this correction to the mentioned limits. In this PD regime, the PA would behave erratically and, we therefore cannot treat it as a limit.
3.2. Light-curve analysis
We first modelled the optical and X-ray light curves simultaneously with a smoothly broken power law (Beuermann et al. 1999), F = (F1κ + F2κ)−1/κ, where FX = fbreak(t/tbreak)−αX, fbreak being the flux density at the break time tbreak, κ is the break smoothness parameter, and the subscripts 1, 2 indicate pre- and post-break, respectively. We did not consider data before 0.06 days (∼5 ks) because they are still dominated by the initial rapid decay. Even before any modelling was performed, it is clear that the optical light curve is initially flat at least until ∼0.25 days (∼20 ks; see Fig. 3), while at the same time the X-ray behaviour is difficult to discern, though the two groups of observations at 4 ks and 7 ks show possible fading, in contrast to the optical. Not knowing the precise evolution of the early X-ray data, we allowed the initial X-ray decay to be different from the optical. Note that a different decay implies a colour evolution between X-rays and the optical. We find a shallow break with tbreak, opt = 0.326 ± 0.011 d (27.7 ± 1.2 ks), a flat optical decay with α1, opt = 0.00 ± 0.01, and an optical to X-ray decay index α2, break = 1.85 ± 0.04, with a break smoothness κ = 1.4 ± 0.1, with χ2/d.o.f. = 2.6.
 |
Fig. 3. GRB optical to X-ray light curve fit to available photometry (see Table A.1) and Swift X-ray data. The grey shaded region is not taken into account for the fit as it may be contaminated by the prompt emission. The clear cyan regions mark the times we chose to derive the SED of the light curve. The data are shown with an offset in flux for better visibility. |
After the break, we analysed the full optical to X-ray SED when we the coverage in both frequency regimes was best. To build this SED, we first created the XRT spectra using the time-slice tool in the XRT repository (Evans et al. 2007, 2009) in the range 30 ks−50 ks at a mid-time of 1.2 days. We then shifted the optical GTC/HIPERCAM ugriz data at 1.097 days closer to these times using the decay indices found above.
We modelled the afterglow SED from optical to X-ray frequencies using Xspec v12.13.0 (Arnaud 1996). The redshift was fixed to z = 1.1341, and we fixed the Galactic hydrogen column density to NH = 3.94 × 1020 cm−2 (Willingale et al. 2013). The data are best modelled by a single power-law (χ2/d.o.f. = 264.5/298) with 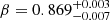 , intrinsic absorption
, intrinsic absorption 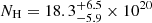 cm−2 (using the Tübingen-Boulder ISM absorption model; Wilms et al. 2000) and E(B − V) < 0.01 mag, using the Small Magellanic Cloud (SMC) extinction law (Pei 1992).
cm−2 (using the Tübingen-Boulder ISM absorption model; Wilms et al. 2000) and E(B − V) < 0.01 mag, using the Small Magellanic Cloud (SMC) extinction law (Pei 1992).
We also obtained an optical to X-ray SED at 0.079 days (6871 s) taking the X-ray data between 6000 and 8000 s and using the optical light curve above to shift the corresponding griz photometry. After fixing the redshift, extinction, and absorption as for the late epoch and following the same fitting procedure, we find that the data are best modelled by a broken power law (χ2/d.o.f. = 143.3/197) with 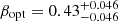 , and βX = βopt + 0.5, which indicates the presence of a spectral break, like the cooling break for synchrotron emission. We note that the spectral index of the high-frequency branch is consistent with the value found at late time, suggesting that the break shifted to lower frequencies with time, which is expected for an ISM environment within the fireball model and before the jet-break occurs (Sari et al. 1998). However, the shallow decay of the early light curve cannot be explained within the standard fireball model, unless we consider a more complex scenario such as an energy injection (e.g., Zhang et al. 2006).
, and βX = βopt + 0.5, which indicates the presence of a spectral break, like the cooling break for synchrotron emission. We note that the spectral index of the high-frequency branch is consistent with the value found at late time, suggesting that the break shifted to lower frequencies with time, which is expected for an ISM environment within the fireball model and before the jet-break occurs (Sari et al. 1998). However, the shallow decay of the early light curve cannot be explained within the standard fireball model, unless we consider a more complex scenario such as an energy injection (e.g., Zhang et al. 2006).
3.3. Optical afterglow spectrum
The afterglow spectrum observed by OSIRIS ∼0.25 days after the burst shows several transitions of Fe II, Mg II, and Mg I (see Table 2), all of them at a common redshift of z = 1.1341 ± 0.0004 (see Fig. 4 and Table 2). This value is a lower limit for the burst redshift due to the non-detection of fine-structure lines excited by the GRB itself. The detection of the afterglow in the bluest band from Swift/UVOT sets an upper limit of z = 1.7, using the so-called Lyman drop-out technique, following (Jakobsson et al. 2012). Considering this limit and the lack of absorption lines common to GRBs (Christensen et al. 2011) at higher redshift, we hence adopted z = 1.1341 as the redshift of GRB 210610B. We also detected two absorption features that correspond to the Mg II doublet in an intervening system at z = 0.5572 ± 0.0002.
Equivalent widths in the observer frame measured in the afterglow spectrum.
 |
Fig. 4. Absorption spectroscopy and line properties for GRB 210610B. Top: Spectral features detected at the redshift of the GRB, plotted in red, and the features from the intervening system are shown in blue. The dashed blue line shows the error spectrum. Bottom: Line-strength diagram for the spectral features in the host galaxy. The diagram compares the features measured in our spectrum (red) with the average values of a larger sample (black) (see Sect. 3.3). |
The equivalent widths (EWs) of the detected absorption lines were measured using the http://grbspec.iaa.es/ database tools (de Ugarte Postigo et al. 2014; Blažek et al. 2020) (see Table 2). We followed de Ugarte Postigo et al. (2012) to compare these values with the common trend for long GRB sight-line environments. The line strength parameter (LSP) measured for GRB 210610B is extremely low, LSP = −2.17 ± 1.13, implying that this line of sight has weaker features than 99.85% of the GRBs in the aforementioned sample. The line-strength diagram in Fig. 4 shows that the Fe II lines are particularly weak and are only detected through the very high signal-to-noise ratio of the spectrum. The magnesium features are stronger, but still among the weakest in the sample. The low EW values imply a low column density and hence a low amount of gas and possibly dust in the line of sight consistent with a negligible dust-induced polarisation.
3.4. Host galaxy
We observed the location of GRB 210610B ∼58 days after the burst using GTC/HiPERCAM and ∼253 days after with GTC/EMIR. In the HiPERCAM images, we detect an underlying object at the GRB position and we consider this object to be the host. We also find a putative companion galaxy towards north-west of the host candidate (see Fig. 1) at a distance of 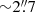 , which would correspond to a distance of 22 kpc at the redshift of the system. The photometry of the host galaxy is shown in Table A.1, together with the values for the companion.
, which would correspond to a distance of 22 kpc at the redshift of the system. The photometry of the host galaxy is shown in Table A.1, together with the values for the companion.
We performed a SED analysis for the two galaxies assuming that both of them are at the GRB redshift. For this analysis, we used the SED fitting code CIGALE7 (Burgarella et al. 2005; Noll et al. 2009; Boquien et al. 2019) in its latest version. To fit the star formation history (SFH), we chose a delayed star formation history with an age for the main stellar population ranging from 0.1 to 13 Gyr and a late burst with an age varying from 20−500 Myr. We allowed the code to vary the corresponding mass fraction from the total galaxy mass for the late burst from 0, which implies a single decaying exponential for the SFH modelling, up to 0.6, that is, 60% of the total galaxy mass. We use the initial mass function (IMF) as described in Chabrier (2003) with a Bruzual & Charlot (2003) stellar population model, assuming a stellar sub-solar metallicity (Z*) for the galaxy (see Sects. 3.3 and 4) that was set to vary from 0.004 to 0.008, according to the scheme used in Bruzual & Charlot (2003). The nebular emission was modelled considering the same metallicity values for the gas.
For the attenuation law, we considered the modified Calzetti et al. (2000) law implemented in CIGALE, assuming a Small Magellanic Cloud (SMC) extinction law for the attenuation of the emission lines. We did not observe a colour evolution for the Galactic-dust-corrected (Schlafly & Finkbeiner 2011) magnitudes, and we do not detect the host galaxy in the H band down to 22.9 magnitudes. This might indicate a low level of dust emission due to low dust heating from UV massive star photons, indicating a low number of massive stars or an intrinsic lack of dust in this system. Since the amount of detected Mg, typically formed in the explosion of massive stars, is large compared to the amount of Fe in the traced system, although still low for common lGRBs sight-lines (see Fig. 4), this favours the scenario of low intrinsic extinction rather than the absence of massive stars (see Sect. 4 for an extended explanation). Therefore, we chose the colour excess of the nebular lines to be lower than 0.1. The slope of the attenuation curve (Boquien et al. 2019) was allowed to vary between −0.6 and 0.6. For the dust emission, we selected the Dale et al. (2014) models and allowed the exponent that controls the radiation field distribution of the re-emitted energy by dust heating to vary between 1.0 and 3.0.
We applied the same SED fit to both galaxies. However, the companion galaxy shows colour excess in the HiPERCAM observations, and we therefore allowed the colour excess for the nebular lines to range up to 0.4. The results for the computed physical properties from the SED fit can be found in Table 3 and the best fit is shown in Fig. 5. The SED of the companion galaxy allowed us to determine a photometric redshift that is consistent with the redshift for GRB 210610B. The companion is at a distance of 2.67 arcsec, corresponding to a physical distance of 22.6 kpc at a redshift of z = 1.1341. We therefore assumed that these two galaxies are part of a group.
Fitted physical properties of the putative host galaxy of GRB 210610B and its putative companion.
 |
Fig. 5. GRB host SED with the corresponding residuals modelled using the CIGALE fitting code (Burgarella et al. 2005; Noll et al. 2009; Boquien et al. 2019) for the putative host galaxy of GRB 210610B. The vertical blue arrow indicates the H band upper limit. |
4. Discussion
A broad study of the GRB prompt and afterglow emission together with its host galaxy is crucial for better constraints of the characteristics of GRB 210610B. The burst prompt emission presents the GRB as a hard burst, as observed by Swift, positioning it in the top part of the long GRB region of the hardness ratio versus T90 relation (see e.g. Lien et al. 2016). The isotropic equivalent energy, together with the observed peak energy, shows that GRB 210610B is fully consistent with the Amati relation (Amati et al. 2002; Amati 2006) for long GRBs. The prompt, high-energy emission of GRB 210610B has been analysed with Fermi data by Chen et al. (2022). They reported that the prompt emission is best fit by a hybrid jet model (Gao & Zhang 2015) in which a hot fireball component dominates the emission in the beginning, while a Poynting flux component supersedes at later times. Chen et al. (2022) described these results as consistent with the magnetar model as a plausible central engine (Metzger et al. 2011).
4.1. Host galaxy
The SED analysis of the GRB 210610B host reveals a galaxy with a low stellar mass, consistent with a dwarf galaxy that is actively forming stars and has low extinction. At the same redshift, the companion is more massive than the GRB host, with a higher stellar mass but lower SFR. The extinction for this galaxy is also higher than that of the GRB host assuming the same extinction law.
From the afterglow spectrum, we find that GRB 210610B is embedded in an environment with low amounts of Fe II and somewhat higher values for Mg II and Mg I. The low amount of Fe could be indicative of a low number of SN Ia in the host, since these explosions are the main sources of Fe (Pagel 2009). This could mean that either there is an intrinsic lack of this type of stellar explosions near the absorber site or that the system itself is too young to have been Fe-enriched via SN Ia. However, the absence of fine-structure lines in the spectrum does not allow us to determine the distance of the absorbing clouds to the explosion site and, therefore, the afterglow spectrum could be tracing gas in the external parts of the host galaxy, where we would expect it to be less enriched. Nevertheless, we find a higher relative value for the EWs of Mg, although it is still low compared to the mean value found for GRB sites (de Ugarte Postigo et al. 2012). Mg is released into the ISM through the explosion of massive stars (Pagel 2009). Together with the low amount of Fe, this might suggest that the host galaxy is a very young system. This is also supported by the extinction we measure from the SED fit. The AV value may indicate that the host galaxy has a low amount of dust, which is expected for a low metallicity and, therefore, for a young system.
4.2. Afterglow
The GRB afterglow follows a decay-plateau-decay behaviour with an initial decay that is well fitted by a broken power law with an optical spectral slope at ∼0.08 days of 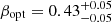 and a βXR ∼ 0.83. Afterwards, the light curve enters a plateau phase that lasts ∼0.247 days to finally change to the final decay at ∼0.326 days after burst. This final decay is better fitted by a power law with
and a βXR ∼ 0.83. Afterwards, the light curve enters a plateau phase that lasts ∼0.247 days to finally change to the final decay at ∼0.326 days after burst. This final decay is better fitted by a power law with 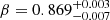 , consistent within errors with βXR at ∼0.08 days after GRB. The change in the spectral slope at ∼0.08 days might be indicating a spectral break at the beginning of the plateau phase. The SED fit shows negligible extinction on the line of sight towards the GRB and a low X-ray hydrogen column density, as compared to NH values for relatively low redshift GRBs (Campana et al. 2010). This low NH together with the low E(B − V), contradicts what would be expected for low-redshift bursts, where a higher dust-to-gas ratio is expected for lowly NH X-ray absorbed bursts (Campana et al. 2010).
, consistent within errors with βXR at ∼0.08 days after GRB. The change in the spectral slope at ∼0.08 days might be indicating a spectral break at the beginning of the plateau phase. The SED fit shows negligible extinction on the line of sight towards the GRB and a low X-ray hydrogen column density, as compared to NH values for relatively low redshift GRBs (Campana et al. 2010). This low NH together with the low E(B − V), contradicts what would be expected for low-redshift bursts, where a higher dust-to-gas ratio is expected for lowly NH X-ray absorbed bursts (Campana et al. 2010).
4.3. Polarisation
Our polarisation observations match three very important stages of the GRB 210610B afterglow light-curve. The first polarimetry measurements were performed 0.1205 days after burst, right after the light curve entered the plateau. The second epoch at ∼0.26 days is close to the end of this plateau phase, almost consistent with the break of the optical light curve at 0.326 days after the GRB. After this, the light curve undergoes its final decay, where a final polarimetry epoch was observed. The afterglow is polarised at the beginning and towards the end of the light-curve evolution, but not around the optical break at 0.326 days after burst, where the polarisation drops to zero with a small rise to 0.61% in the next observation, which is slightly above the PHost ISP limit, but only at a 2.5-σ level. In the final decay, the polarisation increases to 2.27% and then decreases to 1.69% as the afterglow fades away. We find that b and z bands show polarisation values consistent with zero at a close epoch to the 2.5-σR-band measurement. Therefore, the multi-band observations do not allow us to asses chromaticity/achromaticity in the afterglow polarisation. The PA varies by ∼54° between the 3σ detections. The measured polarisation is well consistent with prior measurements for linear polarimetry of GRB afterglows, as shown in Fig. 6.
 |
Fig. 6. Comparison of GRB 210610B polarisation evolution to previous detections of GRB afterglow positive polarisation. Top: Measured GRB linear polarisation degree on the optical afterglow emission. The white and green stars mark the polarisation degree measured for GRB 210610B in all bands. As for all the data points, we did not make a distinction on the photometric band in which the polarisation was measured. We only selected the measured values that show a P/σP > 3 for all bursts, including GRB 210610B. The filled circles indicate the bursts for which a light curve is shown in bottom panel, and empty squares represent the bursts that are not represented in this last panel. The data and references can be found in Table B.1. Middle panel: PA measured for each corresponding burst and epoch in the same fashion as in the top panel. Note that as for GRB 021004 there is no measured PA. To better distinguish the PA changes, we subtracted the first PA value to all values and calculated the absolute value for those with a mean value below zero. We do not find significant PA changes except for GRB 121024A, GRB 091018, GRB 030329, and GRB 210610B. We note that the measures were carried out with different instruments, and the data reduction and analysis can be different from the one we followed in this work. Bottom panel: Light curve for some exemplary burst with data available in the literature GRB 020405 (Masetti et al. 2003), GRB 020813 (Gorosabel et al. 2004), GRB 021004 (de Ugarte Postigo et al. 2005), GRB 030329 (Lipkin et al. 2004), GRB 091018 (Wiersema et al. 2012), GRB 121024A (Wiersema et al. 2014), and GRB 210610B. |
One important aspect when determining the intrinsic polarisation is to constrain any contribution from the dust in the host galaxy. A possible polarisation from the MW was removed during the analysis (see Sect. 3.1). The SED fit to the GRB light curve results in a negligible value for the afterglow extinction on the line of sight and the inferred upper limit for the GRB host ISP is rather small compared to errors of the measured 3-σ polarisation detections (see Sect. 3.1). This means that either the polarisation contribution of the host galaxy along the line of sight is well below the PHost ISP limit or that this contribution would cancel the afterglow polarisation out. The relatively high values we measured for the 3σ detections and the very low limit for the host galaxy polarisation led us to assume that the host contribution is negligible. This low extinction also supports the scenario in which the polarisation is interpreted as intrinsic to the GRB afterglow. This is further confirmed by the polarisation non-detection in the second epoch, which is an indirect measurement of the host ISP.
4.4. Theoretical Interpretations of the polarisation signals
The first polarimetry observations show a rather high linear polarisation degree of ∼4% at t ∼ 0.1205 day. Considering that the observations were carried out during a shallow decay/plateau phase, a non-negligible fraction of optical photons might originate from refreshed shocks in the original ejecta from the central engine. As previous polarimetry studies of the early afterglow indicate that ejecta from the central engine contain large-scale ordered magnetic fields, at least for a subgroup of GRBs if not for all (e.g. Mundell et al. 2013), the refreshed shock emission can be polarised due to the ordered magnetic fields in the ejecta. The combination of the polarised refreshed shock emission and unpolarised forward shock emission is likely to give low-/intermediate-polarisation signals. For GRB 191016A, Shrestha et al. (2022) reported the detection of polarisation signals with P ∼ 5 − 15% which are coincident with the start of the plateau phase. An energy injection model was discussed to explain the coincidence.
The optical light curve starts to decline at t ∼ 0.2 days (see the top panel of Fig. 7). This indicates that the energy injection stops around that time and that the optical band is dominated by the forward-shock emission well before the second polarisation epoch is conducted at t ∼ 0.24 day. The magnetic fields in the forward-shock region (the shocked ambient medium) are conventionally assumed to be generated locally by microscopic instabilities in shocks (see e.g. Medvedev & Loeb 1999), and they are expected to be highly tangled. The PD of the forward-shock emission is expected to be zero when the line of sight does not run along the jet edge. The low polarisation at t ∼ 0.24 − 0.28 days can be explained naturally when the optical emission is dominated by the forward-shock emission.
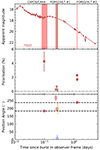 |
Fig. 7. Afterglow, PD and PA evolution of GRB 210610B. Top panel: GRB 210610B light curve for the r band (see Table A.1). We converted the SBT Clear band and R band into r band as indicated in Sects. 2.3.1 and 2.3.2. The vertical stripes from left to right denote the first polarimetry epoch (CAHA/CAFOS) and the second and third epochs (both with VLT/FORS2). The host observations in r band are marked with a dashed red line. Middle panel: Evolution of the linear polarisation of GRB 210610B. The red dots shows the measured polarisation for R band, and blue and orange triangles denote the lower limits in the b and z bands. Bottom panel: Linear polarisation measured PA for GRB 210610B. The detections are marked with filled circles, and the corresponding PAs for the PD limits are marked with empty squares as these values are neither lower nor upper limits. The dashed black lines denote the PA for the first (bottom) and the third (top) epoch. |
Due to the relativistic beaming effect, the observer can see only a small visible region (a small patch with an angular size of 1/Γ, located around the point at which the line of sight intersects the jet) instead of the entire surface of a shock front. The visible region appears as a ring due to a relativistic limb-brightening effect (Granot et al. 1999). Synchrotron emission from each small segment of the ring can be polarised when the random magnetic fields parallel and perpendicular to the shock normal have different averaged strengths. However, the net PD is zero because of the symmetry of the visible region.
As the forward shock slows down, the angular size of the visible region grows as 1/Γ ∝ t3/8 (ISM) or t1/4 (wind medium). Eventually, a part of the ring is located outside the jet edge and the emission region becomes asymmetric. This might have occurred by the third polarisation epoch at t ∼ 1.27 day. Between the second and third epochs, the angular size of the visible region can grow by a factor of ∼1.7 (ISM) or 1.4 (wind medium). Optical linear polarisation measurements have been carried out for many late GRB afterglows typically several hours to a few days after the prompt gamma-ray emission (e.g. Covino & Gotz 2016). In this period, a jet break is expected to occur. The detection or upper limits of the linear PD are generally low (less than a few percent), which might indicate that the shock-generated random magnetic fields parallel and perpendicular to the shock normal have similar averaged strengths. The polarisation signals P ∼ 2% at t ∼ 1.27 days might be explained in this geometrical model. If the large-scale magnetic fields in the ejecta are toroidal, the PA change between t ∼ 0.24 days and t ∼ 1.27 days is expected to be 0 or 90°. However, the large-scale magnetic fields in the ejecta can be largely distorted before they inject energy into the forward shock (or the original magnetic structure can be very different from the toroidal configuration). The position angle change can be any value. However, this model predicts a steeper decline at late times. Even in the non-spreading jet model, the expected decay index is α = 3(p − 1)/4 + 3/4 ∼ 2.05 (ISM) or (3p − 1)/4 + 1/2 ∼ 2.30 (wind medium) for p = 2.74, which is steeper than the observed value α = 1.85 ± 0.04. If we rely on the rather high value of p obtained from the SED modelling, we can rule this geometrical model out.
The nature of magnetic fields that are generated in shock instabilities is not yet fully understood. The microscopic-scale tangled magnetic fields may decay so rapidly in the downstream of the shock that they could not account for the observed synchrotron flux (e.g. Sironi et al. 2015). Alternatively, the forward-shock region could have magnetic field turbulence on large scales, comparable to the width of shocked region ∼R/16Γ (e.g. Sironi & Goodman 2007). In this case, the PD and PA temporally change in a random manner, and PD 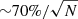 , where N is the number of patches with a coherent magnetic field within the angular scale 1/ΓGruzinov & Waxman (1999). Kuwata et al. (2023) constructed a semi-analytic model with a varying large-scale turbulent field in the forward-shock region, for which they performed numerical calculations in the case of isotropic turbulence and zero viewing angle. They obtained a randomly varying PD on a timescale of hours at a level of ∼1 − 3% and PA with changes that were not limited to 90°. These properties appear to be consistent with our data of GRB 210610B. When hydrodynamic-scale turbulent magnetic fields are assumed, we have two possible scenarios: (1) the ∼4%, ∼0.2%, and ∼2% polarisation signals are all due to turbulent magnetic fields, or (2) the ∼4% polarisation signal is due to polarised refreshed shock emission, and the other two signals are due to turbulent magnetic fields.
, where N is the number of patches with a coherent magnetic field within the angular scale 1/ΓGruzinov & Waxman (1999). Kuwata et al. (2023) constructed a semi-analytic model with a varying large-scale turbulent field in the forward-shock region, for which they performed numerical calculations in the case of isotropic turbulence and zero viewing angle. They obtained a randomly varying PD on a timescale of hours at a level of ∼1 − 3% and PA with changes that were not limited to 90°. These properties appear to be consistent with our data of GRB 210610B. When hydrodynamic-scale turbulent magnetic fields are assumed, we have two possible scenarios: (1) the ∼4%, ∼0.2%, and ∼2% polarisation signals are all due to turbulent magnetic fields, or (2) the ∼4% polarisation signal is due to polarised refreshed shock emission, and the other two signals are due to turbulent magnetic fields.
For non-spreading top-hat jets with microscopic-scale tangled fields, the PD light curve would have two maxima around a jet break, with the polarisation PA changing by 90° between the first and second maximum (Ghisellini & Lazzati 1999; Sari 1999). A possible jet break associated with the PA change of 90° has been detected for GRB 121024A (Wiersema et al. 2014). We studied a non-axisymmetric top-hat jet model (homogeneous jets with elliptic jet edge) to determine whether the main features can be explained in this model. Jets like this might be produced due to the interaction between jets and stellar envelope/neutron star wind ejecta (see Fig. 1 in Lamb et al. 2022) or jet precession (Huang et al. 2019). For non-axisymmetric jets, the PA change can be different from 90°. Following Sari (1999), we estimated the polarisation light curve and the PA change around a jet break. However, we find that this model does not work for this event. The main reasons are that (a) this model also predicts the steep decay at late times, as discussed in the geometrical model. (b) We needed to fine-tune the timing of the second polarisation measurement (we need to place the observation precisely in the “valley” of the polarisation curve), or equivalently, we needed to fine-tune a combination of parameters that provide the jet break time. (c) In the “valley”, the polarisation needs to be very low (0.18−0.6%), compared to the earlier observation of ∼4%. To achieve this, Stokes u also needs to be almost zero when q flips sign. According to our rough parameter search (the geometrical parameters were ellipse eccentricity, ellipse orientation, and viewing angle), the eccentricity of the jet edge needs to be lower than roughly about 0.3. The low eccentricity does not allow the PA change to be significantly different from 90° (in our example case to fit the polarisation light curve, the PA change is about 80°).
5. Conclusions
GRB 210610B presents an exceptional scenario for performing polarimetry on the optical afterglow of a GRB. The light curve follows a decay-plateau-decay trend with a break after the plateau phase to a steep decay of the light curve. The SED modelling of the afterglow from X-rays to the optical indicates a dust free line of sight towards the GRB as well as a low NH. This negligible amount of dust is confirmed by the low AV value we derive for the host galaxy and is further confirmed for the polarisation non-detection on the second polarimetry epoch. We also find that the GRB is embedded in a low-mass galaxy that seems to have a low amount of metals, which is indicative of a very young system.
The low amount of dust we find for GRB 210610B allowed us to study the intrinsic polarisation of the GRB afterglow. The optical afterglow is polarised at the beginning of the plateau phase of the light curve, disappears around the break achromatically, and reappears in the final decay of the light curve. In this complex behaviour, the first epoch seems to be dominated by the refreshed shock, which could explain the high polarisation value, while in the following epoch, the polarisation degree drops to zero as the forward shock would be dominating the optical emission. In the final decay of the light curve, the polarisation increases to ∼2% which could be explained assuming a geometrical model or hydrodinamics-scale turbulent magnetic fields.
Some models predict that GRB afterglow polarisation evolves from high polarisation at early stages, while the prompt emission or the refreshed shocks dominate, followed by a fast decay of the polarisation often reaching a zero polarisation. Afterwards, the polarisation again increases to moderate/low values, including changes in the polarisation position angle (see Covino & Gotz 2016 for a review). To better understand the polarisation evolution of GRBs, we should pursue two approaches: On one hand, we need to study polarisation throughout different GRB light curve phases, and on the other hand we need to obtain larger samples of GRBs.
Data availability
The CAFOS data are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/690/A216
The hardness ratio or spectral hardness (Kouveliotou et al. 1993) for a GRB is the ratio between the fluence emitted during the prompt emission in the 50–100 keV band over the 25–50 keV band.
Acknowledgments
JFAF acknowledges support from the Spanish Ministerio de Ciencia, Innovación y Universidades through the grant PRE2018-086507. JFAF acknowledges financial support from the Severo Ochoa grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033. AR acknowledge support from PRIN-MIUR 2017 (grant 20179ZF5KS). This work is partly based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma. Partly based on observations collected at the Centro Astronómico Hispano en Andalucía (CAHA) at Calar Alto, operated jointly by Junta de Andalucía and Consejo Superior de Investigaciones Científicas (IAA-CSIC). This work made use of the GRBspec database https://grbspec.eu. This work has made extensive use of IRAF and Python, particularly with astropy (Astropy Collaboration 2013, http://www.astropy.org), matplotlib (Caswell et al. 2020), photutils (Bradley et al. 2019), numpy (Harris et al. 2020), and Scipy (Virtanen et al. 2020).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, ApJ, 848, L13 [CrossRef] [Google Scholar]
- Amati, L. 2006, MNRAS, 372, 233 [Google Scholar]
- Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, J. 2015, FORS2 User Manual (European Southern Observatory), 96.0 [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landolfi, M., Landstreet, J. D., et al. 2009, PASP, 121, 993 [Google Scholar]
- Barth, A. J., Sari, R., Cohen, M. H., et al. 2003, ApJ, 584, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [Google Scholar]
- Bersier, D., McLeod, B., Garnavich, P. M., et al. 2003, ApJ, 583, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2010, Astrophysics Source Code Library [record ascl:1010.068] [Google Scholar]
- Beuermann, K., Hessman, F. V., Reinsch, K., et al. 1999, A&A, 352, L26 [NASA ADS] [Google Scholar]
- Blažek, M., de Ugarte Postigo, A., Kann, D. A., et al. 2020, SPIE Conf. Ser., 11452, 1145218 [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, L., Sipőcz, B., Robitaille, T., et al. 2019, https://doi.org/10.5281/zenodo.3568287 [Google Scholar]
- Brivio, R., Covino, S., D’Avanzo, P., et al. 2022, A&A, 666, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., & Iglesias-Páramo, J. 2005, MNRAS, 360, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, E., Svinkin, D., Fenimore, E., et al. 2023, ApJ, 946, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Thöne, C. C., de Ugarte Postigo, A., et al. 2010, MNRAS, 402, 2429 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, T. A., Droettboom, M., Lee, A., et al. 2020, https://doi.org/10.5281/zenodo.3898017 [Google Scholar]
- Cepa, J., Aguiar, M., Escalera, V. G., et al. 2000, SPIE Conf. Ser., 4008, 623 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chen, J.-M., Peng, Z.-Y., Du, T.-T., & Yin, Y. 2022, ApJ, 932, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., Fynbo, J. P. U., Prochaska, J. X., et al. 2011, ApJ, 727, 73 [CrossRef] [Google Scholar]
- Cikota, A., Patat, F., Cikota, S., & Faran, T. 2017, MNRAS, 464, 4146 [Google Scholar]
- Covino, S., & Gotz, D. 2016, Astron. Astrophys. Trans., 29, 205 [NASA ADS] [Google Scholar]
- Covino, S., Lazzati, D., Ghisellini, G., et al. 1999, A&A, 348, L1 [NASA ADS] [Google Scholar]
- Covino, S., Malesani, D., Ghisellini, G., et al. 2003, A&A, 400, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dale, D. A., Helou, G., Magdis, G. E., et al. 2014, ApJ, 784, 83 [Google Scholar]
- de Ugarte Postigo, A., Castro-Tirado, A. J., Gorosabel, J., et al. 2005, A&A, 443, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Fynbo, J. P. U., Thöne, C. C., et al. 2012, A&A, 548, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Blazek, M., Janout, P., et al. 2014, SPIE Conf. Ser., 9152, 91520B [NASA ADS] [Google Scholar]
- Dhillon, V. S., Bezawada, N., Black, M., et al. 2021, MNRAS, 507, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [Google Scholar]
- Frederiks, D., Golenetskii, S., Lysenko, A., et al. 2021, GRB Coordinates Network, 30196, 1 [NASA ADS] [Google Scholar]
- Fynbo, J. P. U., Izzo, L., de Ugarte Postigo, A., Malesani, D. B., & Pursimo, T. 2021, GRB Coordinates Network, 30182, 1 [NASA ADS] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [Google Scholar]
- Gao, H., & Zhang, B. 2015, ApJ, 801, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Garzón, F., Balcells, M., Gallego, J., et al. 2022, A&A, 667, A107 [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., & Lazzati, D. 1999, MNRAS, 309, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, R., Kole, M., & Granot, J. 2021, Galaxies, 9, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Gompertz, B. P., Ravasio, M. E., Nicholl, M., et al. 2023, Nat. Astron., 7, 67 [Google Scholar]
- González-Gaitán, S., Mourão, A. M., Patat, F., et al. 2020, A&A, 634, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorosabel, J., Rol, E., Covino, S., et al. 2004, A&A, 422, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorosabel, J., de Ugarte Postigo, A., Castro-Tirado, A. J., et al. 2010, A&A, 522, A14 [CrossRef] [EDP Sciences] [Google Scholar]
- Granot, J., Piran, T., & Sari, R. 1999, ApJ, 513, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Klose, S., Reinsch, K., et al. 2003, Nature, 426, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Gruzinov, A., & Waxman, E. 1999, ApJ, 511, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Sollerman, J., Møller, P., et al. 2003, Nature, 423, 847 [Google Scholar]
- Ho, A. Y. Q., Perley, D. A., Yao, Y., et al. 2022, ApJ, 938, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, B.-Q., Lin, D.-B., Liu, T., et al. 2019, MNRAS, 487, 3214 [CrossRef] [Google Scholar]
- Jakobsson, P., Hjorth, J., Malesani, D., et al. 2012, ApJ, 752, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Krimm, H. A., Barthelmy, S. D., Cummings, J. R., et al. 2021, GRB Coordinates Network, 30207, 1 [NASA ADS] [Google Scholar]
- Kuwata, A., Toma, K., Kimura, S. S., Tomita, S., & Shimoda, J. 2023, ApJ, 943, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, G. P., Nativi, L., Rosswog, S., et al. 2022, Universe, 8, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Covino, S., di Serego Alighieri, S., et al. 2003, A&A, 410, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levan, A. J., Malesani, D. B., Gompertz, B. P., et al. 2023, Nat. Astron., 7, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Levan, A. J., Gompertz, B. P., Salafia, O. S., et al. 2024, Nature, 626, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Lien, A., Sakamoto, T., Barthelmy, S. D., et al. 2016, ApJ, 829, 7 [Google Scholar]
- Lipkin, Y. M., Ofek, E. O., Gal-Yam, A., et al. 2004, ApJ, 606, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Magalhaes, A. M., Pereyra, A., Dominici, T., & Abraham, Z. 2003, GRB Coordinates Network, 2163, 1 [NASA ADS] [Google Scholar]
- Malacaria, C., Hristov, B., & Fermi GBM Team 2021, GRB Coordinates Network, 30199, 1 [NASA ADS] [Google Scholar]
- Mandarakas, N., Blinov, D., Aguilera-Dena, D. R., et al. 2023, A&A, 670, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masetti, N., Palazzi, E., Pian, E., et al. 2003, A&A, 404, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Medvedev, M. V., & Loeb, A. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1997, ApJ, 476, 232 [CrossRef] [Google Scholar]
- Metzger, B. D., Giannios, D., Thompson, T. A., Bucciantini, N., & Quataert, E. 2011, MNRAS, 413, 2031 [Google Scholar]
- Morgan, A. N., Vanden Berk, D. E., Roming, P. W. A., et al. 2008, ApJ, 683, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Mundell, C. G., Kopač, D., Arnold, D. M., et al. 2013, Nature, 504, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Patat, F., Maeda, K., et al. 2022, ApJ, 941, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Negro, M., Di Lalla, N., Omodei, N., et al. 2023, ApJ, 946, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oke, J. B. 1974, ApJS, 27, 21 [Google Scholar]
- Page, K. L., Gropp, J. D., Kennea, J. A., et al. 2021, GRB Coordinates Network, 30170, 1 [NASA ADS] [Google Scholar]
- Pagel, B. E. J. 2009, Nucleosynthesis and Chemical Evolution of Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
- Patat, F., & Romaniello, M. 2006, PASP, 118, 146 [Google Scholar]
- Patat, F., & Taubenberger, S. 2011, A&A, 529, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [Google Scholar]
- Perley, D. A. 2021, GRB Coordinates Network, 30216, 1 [NASA ADS] [Google Scholar]
- Piran, T. 1999, Phys. Rep., 314, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plaszczynski, S., Montier, L., Levrier, F., & Tristram, M. 2014, MNRAS, 439, 4048 [NASA ADS] [CrossRef] [Google Scholar]
- Rastinejad, J. C., Gompertz, B. P., Levan, A. J., et al. 2022, Nature, 612, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Meszaros, P. 1994, ApJ, 430, L93 [Google Scholar]
- Rol, E., Wijers, R. A. M. J., Vreeswijk, P. M., et al. 2000, ApJ, 544, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Rol, E., Wijers, R. A. M. J., Fynbo, J. P. U., et al. 2003, A&A, 405, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
- Sari, R. 1999, ApJ, 524, L43 [CrossRef] [Google Scholar]
- Sari, R., & Piran, T. 1997, MNRAS, 287, 110 [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schmidt, G. D., Elston, R., & Lupie, O. L. 1992, AJ, 104, 1563 [Google Scholar]
- Science Software Branch at STScI 2012, Astrophysics Source Code Library [record ascl:1207.011] [Google Scholar]
- Serkowski, K., Mathewson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Shrestha, M., Steele, I. A., Kobayashi, S., et al. 2022, MNRAS, 509, 5964 [Google Scholar]
- Siegel, M. H., Baer, M., Page, K. L., & Swift/UVOT Team 2021, GRB Coordinates Network, 30247, 1 [NASA ADS] [Google Scholar]
- Sironi, L., & Goodman, J. 2007, ApJ, 671, 1858 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., Keshet, U., & Lemoine, M. 2015, Space Sci. Rev., 191, 519 [CrossRef] [Google Scholar]
- Steele, I. A., Mundell, C. G., Smith, R. J., Kobayashi, S., & Guidorzi, C. 2009, Nature, 462, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Fryer, C. L., O’Connor, B., et al. 2022, Nature, 612, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Turnshek, D. A., Bohlin, R. C., Williamson, R. L., et al. 1990, AJ, 99, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Uehara, T., Toma, K., Kawabata, K. S., et al. 2012, ApJ, 752, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Urata, Y., Toma, K., Covino, S., et al. 2023, Nat. Astron., 7, 80 [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- von Kienlin, A., Meegan, C. A., Paciesas, W. S., et al. 2020, ApJ, 893, 46 [Google Scholar]
- Wiersema, K., Curran, P. A., Krühler, T., et al. 2012, MNRAS, 426, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersema, K., Covino, S., Toma, K., et al. 2014, Nature, 509, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, R. A. M. J., Vreeswijk, P. M., Galama, T. J., et al. 1999, ApJ, 523, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Yang, J., Ai, S., Zhang, B.-B., et al. 2022, Nature, 612, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [Google Scholar]
Appendix A: Afterglow and host galaxy photometry
Photometry of the afterglow of GRB 210610B.
Appendix B: Linear polarisation measurements on GRBs afterglow emission.
Measured values for the linear polarisation and PA of GRB afterglows from the literature.
All Tables
Fitted physical properties of the putative host galaxy of GRB 210610B and its putative companion.
Measured values for the linear polarisation and PA of GRB afterglows from the literature.
All Figures
 |
Fig. 1. Colour images of the field using the g′, r′ and i′ bands of HiPERCAM at 1 day and 58 days after the burst, respectively. In the first image the afterglow is strongly detected, in the second image, it has faded and the host galaxy dominates the emission. 2.7 arcsec north-west of the host galaxy lies a companion galaxy at the same photometric redshift of the host (see Sect. 3.4). |
| In the text | |
 |
Fig. 2. Two-dimensional Gaussian fit to the field stars q, u parameters. Left: Normal distribution of randomly generated data around the q, u values. The amplitude to generate the data is the Stokes parameter errors. Central panel: two-dimensional Gaussian model fitted to the data points. Right: Residuals. |
| In the text | |
 |
Fig. 3. GRB optical to X-ray light curve fit to available photometry (see Table A.1) and Swift X-ray data. The grey shaded region is not taken into account for the fit as it may be contaminated by the prompt emission. The clear cyan regions mark the times we chose to derive the SED of the light curve. The data are shown with an offset in flux for better visibility. |
| In the text | |
 |
Fig. 4. Absorption spectroscopy and line properties for GRB 210610B. Top: Spectral features detected at the redshift of the GRB, plotted in red, and the features from the intervening system are shown in blue. The dashed blue line shows the error spectrum. Bottom: Line-strength diagram for the spectral features in the host galaxy. The diagram compares the features measured in our spectrum (red) with the average values of a larger sample (black) (see Sect. 3.3). |
| In the text | |
 |
Fig. 5. GRB host SED with the corresponding residuals modelled using the CIGALE fitting code (Burgarella et al. 2005; Noll et al. 2009; Boquien et al. 2019) for the putative host galaxy of GRB 210610B. The vertical blue arrow indicates the H band upper limit. |
| In the text | |
 |
Fig. 6. Comparison of GRB 210610B polarisation evolution to previous detections of GRB afterglow positive polarisation. Top: Measured GRB linear polarisation degree on the optical afterglow emission. The white and green stars mark the polarisation degree measured for GRB 210610B in all bands. As for all the data points, we did not make a distinction on the photometric band in which the polarisation was measured. We only selected the measured values that show a P/σP > 3 for all bursts, including GRB 210610B. The filled circles indicate the bursts for which a light curve is shown in bottom panel, and empty squares represent the bursts that are not represented in this last panel. The data and references can be found in Table B.1. Middle panel: PA measured for each corresponding burst and epoch in the same fashion as in the top panel. Note that as for GRB 021004 there is no measured PA. To better distinguish the PA changes, we subtracted the first PA value to all values and calculated the absolute value for those with a mean value below zero. We do not find significant PA changes except for GRB 121024A, GRB 091018, GRB 030329, and GRB 210610B. We note that the measures were carried out with different instruments, and the data reduction and analysis can be different from the one we followed in this work. Bottom panel: Light curve for some exemplary burst with data available in the literature GRB 020405 (Masetti et al. 2003), GRB 020813 (Gorosabel et al. 2004), GRB 021004 (de Ugarte Postigo et al. 2005), GRB 030329 (Lipkin et al. 2004), GRB 091018 (Wiersema et al. 2012), GRB 121024A (Wiersema et al. 2014), and GRB 210610B. |
| In the text | |
 |
Fig. 7. Afterglow, PD and PA evolution of GRB 210610B. Top panel: GRB 210610B light curve for the r band (see Table A.1). We converted the SBT Clear band and R band into r band as indicated in Sects. 2.3.1 and 2.3.2. The vertical stripes from left to right denote the first polarimetry epoch (CAHA/CAFOS) and the second and third epochs (both with VLT/FORS2). The host observations in r band are marked with a dashed red line. Middle panel: Evolution of the linear polarisation of GRB 210610B. The red dots shows the measured polarisation for R band, and blue and orange triangles denote the lower limits in the b and z bands. Bottom panel: Linear polarisation measured PA for GRB 210610B. The detections are marked with filled circles, and the corresponding PAs for the PD limits are marked with empty squares as these values are neither lower nor upper limits. The dashed black lines denote the PA for the first (bottom) and the third (top) epoch. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.