EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 689 (September 2024) A&A, 689 (2024) L5 Full HTML
Open Access
Issue
A&A
Volume 689, September 2024
Article Number L5
Number of page(s) 11
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202451166
Published online 30 August 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open access funding provided by Max Planck Society.

1. Introduction

Recent observations support that the planet formation process is already underway in Class II disks of ≳1 Myr old (Andrews et al. 2018; Manara et al. 2018; Benisty et al. 2021; Izquierdo et al. 2022; Testi et al. 2022), with one critical evidence being the ubiquitous annular substructures (rings, gaps, and cavities) found in these disks at millimeter (mm) wavelengths, (Huang et al. 2018; Long et al. 2018). This is because the annular substructures are either due to the presence of planets or they are places where dust grains can accumulate, a necessary step for grain growth that can lead to the formation of planetary cores (Bae et al. 2023).

High-resolution observations resolving the dust emission in younger disks (Class 0/I with ages ≲0.5 Myr, Dunham et al. 2014) have been conducted to determine the emergence of annular substructures. Only a small number of these younger disks exhibit such substructures, and all of them are Class I (Sheehan & Eisner 2018; Segura-Cox et al. 2020; Nakatani et al. 2020; Ohashi et al. 2023; Yamato et al. 2023; Shoshi et al. 2024; Hsieh et al. 2024). This limited number of detections could imply that the planet formation process starts primarily during the later stages of protostellar evolution. Alternatively, the lack of substructures in most Class 0/I disks surveyed so far might be due to the observed emission being optically thick, particularly at 1.3 mm, which is the most common choice of wavelength. This is supported by multiwavelength studies at a resolution of between 70 and a few 100 au, which already suggested high optical depths at disk scales for embedded sources (Jørgensen et al. 2007; Li et al. 2017; Ko et al. 2020). Recent multiwavelength studies at higher resolution (≲15 au) also support high optical depths at 1.3 mm in young protostellar disks (Galván-Madrid et al. 2018; Liu 2021; Zamponi et al. 2021; Maureira et al. 2022; Xu et al. 2023; Guerra-Alvarado et al. 2024a).

In this Letter, we use ALMA observations at a longer wavelength (3 mm) to resolve the disk continuum emission towards the deeply embedded Class 0 protostar Oph A SM1. Oph A SM1 (hereafter SM1) is located in the Oph A region in the Ophiuchus molecular cloud at a distance of 137 pc (Ortiz-León et al. 2018). The spectral energy distribution (SED) is consistent with a cold ∼17 K core with a mass of 1.3 M⊙ (Pattle et al. 2015). The protostellar source is not detected at wavelengths of ≤70 μm by Spitzer or Herschel/PACS (Friesen et al. 2018; Kawabe et al. 2018). Based on the upper limit to the flux at 70 μm, Friesen et al. (2018) derived a maximum internal luminosity of ∼1 L⊙1. No large-scale outflow has been detected either. Friesen et al. (2018) detected CO (2-1) emission consistent with a low-velocity outflow (< 6 km s−1) with a length of ≲2000 au, implying a dynamical time of 1.6 × 103 yr or less (Kawabe et al. 2018). SM1 also shows variable hard X-ray emission, which is expected from young, actively accreting protostars (Gagné et al. 2004; Kawabe et al. 2018). Towards the compact source, a mass-infall rate of 3 × 10−5 M⊙ yr−1 was derived from an inverse P Cygni profile detected in CO (Friesen et al. 2018). Based on these observations, SM1 has been proposed as possibly the youngest protostar in Ophiuchus (Friesen et al. 2014, 2018; Kawabe et al. 2018).

2. Data

The ALMA band 3 observations using the C-10 configuration were obtained in September 2021. The observations were part of the Cycle 7 project ID:2019.1.01074.S (PI: M. Maureira). The spectral setup consisted of four spectral windows with central frequencies of between 93 and 105 GHz. The spectral setup was maximized for continuum observations, and thus the maximum bandwidth of 1.875 GHz for each spectral window was used. These observations were planned to be combined with the C-6 configuration of the FAUST2 ALMA Large program (Codella et al. 2021), which covers the same frequency range (project ID:2018.1.01205.L, PI: S. Yamamoto). We used CASA (CASA Team et al. 2022) to calibrate and image the data. We performed self-calibration separately for the observations in the extended and compact configuration, which were then combined and self-calibrated together. The cleaning in the self-calibration iterations was done first with the “multiscale” and later with the “mtmfs” deconvolver, with nterms = 2 for the final phase and amplitude steps. A robust parameter of zero was set with four scales for cleaning in all steps. A manual mask was set and adjusted during the process when necessary. The details of the self-calibration iterations can be found in Appendix A. The self-calibration process improved the overall image fidelity and resulted in signal-to-noise ratio (S/N) improvements of ∼40% and ∼10% for the extended configuration only, and combined dataset, respectively. The final synthesized beam and rms considering the region around SM1 are 0.060″ × 0.042″ (at PA –79.5°) and 25 μJy beam−1, respectively.

3. Analysis

The left panel of Figure 1 shows the 3 mm continuum observations towards SM1. The observations reveal a disk structure with a nearly face-on orientation, with a brightness temperature peak of 57 K and a 3σ contour extending up to ∼40 au from the center. Using CASA imfit, we fit a 2D Gaussian to the emission resulting in center coordinates right ascension (RA): 16:26:27.852, declination (Dec): –24:23:59.723, an inclination (assuming circular geometry) of 15.6°, and position angle (PA) of 147 ± 35°. We used these values to deproject the emission, and produce an azimuthally averaged radial intensity profile3. The right panel in Figure 1 shows the resultant intensity profile expressed in brightness temperature, calculated using the full Planck function. The error is calculated as 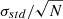, where σstd and N are the standard deviation and number of beams in each bin.

thumbnail Fig. 1.

ALMA observations towards SM1. Left: 3 mm continuum observations of the SM1 disk. Right: Azimuthally averaged brightness temperature profile calculated using the full Planck function displayed in logarithmic scale. The corresponding 1σ uncertainties are shown in gray. Green dashed and solid vertical curves mark the same radial distance from the center in both panels, corresponding to the location of the deviation in the radial intensity profile and the location of the 3σ emission contour in the map, respectively.

Radial intensity profiles of disks are usually well described by a power law in radius for the inner part, which is then truncated in the outer disk (Hartmann et al. 1998; Isella et al. 2009; Tripathi et al. 2017; Tazzari et al. 2021). For SM1, while the inner (< 20 au) and the outermost (> 40 au) regions show such smoothly declining behavior there is a clear intensity deviation near 30 au. This type of feature is similarly observed in several intensity profiles from the DSHARP and ODISEA samples of Class II and Class I/II disks, respectively (Huang et al. 2018; Cieza et al. 2021).

3.1. Modeling the disk intensity profile

We fit the full intensity profile with three different models: a smooth disk, a disk with a gap, and a disk with a ring. We first considered the intensity profile of a smooth disk. For this, we used a modified version of the self-similar profile (Lynden-Bell & Pringle 1974) with distinct power-law indices constraining the inner and outer cutoff behaviors (Long et al. 2019; Manara et al. 2019; Tazzari et al. 2021). The intensity profile has the form:

(1)

where r is the radius, rc is the characteristic radius, γ1 the inner disk power-law index, and γ2 the power-law index describing the slope of the exponential cutoff. Together with rc, γ1, and γ2, the fourth free parameter is taken as the total flux of the model, Ftot. The structured disk models considering either a gap or a ring are visually similar as both exhibit a dip in the profile. The difference comes from how these features are modeled. Following Long et al. (2019), we modeled these by considering either a smooth disk with a single carved gap or a smooth disk with a single ring exterior to the disk. Both the gap and ring are modeled as a Gaussian. The profile of the gap or ring is added to the smooth disk model as , where ra, Ia, and σa, corresponding to the radius, intensity peak, and width of the ring or gap, respectively, are additional free parameters. Each model was convolved with the synthesized beam and values for each of the parameters were obtained using the Python module emcee (Foreman-Mackey et al. 2013). Details of the fit setup and resultant values for the parameters as well as corner plots are in Appendix B.

Figure 2 shows, for all three models, the resultant fit and residuals. The smooth disk profile systematically overestimates and then underestimates the intensity near ∼30 au where the deviation in intensity is observed. The middle and right panels show the results when considering a disk with an inner gap and an outer ring, respectively. Both models can reproduce the feature near ∼30 au and thus both lead to an improvement in the residuals. The models with gap and ring locate the annular substructure at a radius of 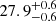au and 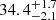au, respectively. The resultant σa are 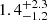au and 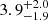au for the gap and the ring, respectively. Table B.1 summarizes the resultant values for the parameters in each model.

thumbnail Fig. 2.

Fits to the disk intensity profile and residuals for three different models. The orange curves in the top panels show 100 profiles drawn randomly from the posterior distributions. The observed profile is shown with a black solid line. The resultant median residual is shown in the bottom panels (solid black line) as well as 1σ dispersion around the median residual (orange shaded area). The gray shaded area corresponds to the 1σ uncertainty of the intensity profile in all panels. Left: Smooth disk profile. Middle: Disk profile with a gap at ∼28 au. The black horizontal segment shows the range of values for the gap radius enclosing 68% of the posterior distribution around the median. Right: Disk profile with a ring at ∼34 au. The black horizontal segment shows the range of values for the ring radius enclosing 68% of the posterior distribution around the median.

To compare the three models, we use the Akaike information criterion (AIC)4, which is widely applied for model evaluation and selection (Cavanaugh & Neath 2019; Choudhury et al. 2021; Valdivia-Mena et al. 2022). The AIC takes into account the goodness of the fit but also the possible over fitting when the number of free parameters increases, as in the case of the nonsmooth models considered here. The model with the lowest AIC is favored over the others. The AIC values are 37.8, 21.2, and 19.8 for the smooth disk, disk with a gap, and disk with a ring, respectively. The smooth disk model can be excluded based on the significant difference5 (≳10) in AIC values compared with those including an annular substructure. On the other hand, although the AIC value is lower for the model with a ring, the difference is not sufficient to favor one of the two nonsmooth models. In summary, nonsmooth disk models are statistically preferred over smooth disk models and the observed disk profile can be well reproduced by considering either a gap carved at 28 au within a disk with a radius6 of 40 au or a ring at 34 au outside a disk with a radius of 27 au.

3.2. Optical depth, temperature, and mass

Following Segura-Cox et al. (2020) and Cieza et al. (2016), we calculated the intraband spectral index α by imaging the lower-sideband and upper-sideband spectral windows separately using the parameters for imaging described in Sect. 2. We calculated the intensity profile for each image similar to Figure 1 and calculated alpha as α = ln(Iν1/Iν2)/ln(ν1/ν2), where ν1 and ν2 correspond to 106.05 GHz and 94.05, respectively. Due to the limited sensitivity, the profile for α is limited to the inner ∼30 au. Beyond this radius, α values are smaller than the 3σ statistical uncertainty, leaving α unconstrained. We note that besides the statistical uncertainties considered here, there is a systematic uncertainty at all radii of 0.1 due to a 0.8% flux-calibration error between spectral windows (Francis et al. 2020).

Figure 3 shows the resultant spectral index profile overlaid with the intensity profile. At about 15 au, the spectral index reaches the optically thick limit value of 2 and remains slightly below at small radii; outside this radius, it increases, reaching values of between 3 and 4, consistent with a reduction in the optical depth. To estimate the optical depth and dust temperature, we followed Segura-Cox et al. (2020) and fit the emission of the profiles at 106 GHz and 94 GHz with a modified blackbody. In the inner region with the low spectral index values, the derived temperature converges to the brightness temperature. This is the expected behavior in the optically thick limit and thus it is also independent of the adopted value for the power-law index of the dust opacity β. At larger radii, temperature and optical depth are degenerate due to the emission becoming optically thinner. Following Segura-Cox et al. (2020), we computed the temperature therein by extrapolating the temperature obtained in the optically thick regime (r ≲ 15 au) assuming a radial profile with a power-law exponent of –0.5 (passive heating). The resultant temperature and 3 mm optical depth profiles are overlaid in Figure 3. The temperature in the region with the gap and ring is about 15 and 13 K, respectively, while the optical depth at 3 mm is below 1 therein. We note that we obtained a power-law exponent value of γ1 ∼ −0.7 from the intensity profile fit in the inner region of the disk (Table B.1). This is steeper than that expected from passive heating and suggests the presence of accretion or viscous heating. The presence of this type of nonradiative heating has also been suggested in other young disks (e.g., Liu et al. 2019; Zamponi et al. 2021; Maureira et al. 2022; Takakuwa et al. 2024). Accretion or viscous heating is expected to dominate in the inner parts of disks, while irradiation is expected to still dominate the outer regions (Mordasini et al. 2015). Nevertheless, extrapolating the temperature profile outwards assuming such a steeper power-law exponent would further lower the temperature and therefore increase the optical depth at a given radius by up to 20% and 30%, respectively. This would still result in a τ3mm of below one at the location of the gap or ring feature.

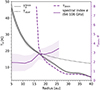thumbnail Fig. 3.

Radial profiles of the in-band spectral index, optical depth, and temperature towards SM1. The solid purple line shows the in-band spectral index. The shaded area shows the 1σ uncertainty. The estimated 3 mm optical depth and temperature profiles are shown with dashed purple and dotted black lines, respectively. The temperature profile is extrapolated beyond r ∼ 15 au following a r−0.5 power law. The observed brightness temperature profile is overlaid in solid gray, similar to Figure 1.

The derived temperature is a factor of ∼2 lower than those derived at similar radii toward other disks surrounding embedded sources (hereafter embedded disks) with bolometric luminosities of ∼1 L⊙ and showing ring or gap structures (Segura-Cox et al. 2020; Sai et al. 2023). The upper limit to the SM1 protostar luminosity is ∼1 L⊙ (Friesen et al. 2018). We can therefore estimate a lower limit to the source luminosity by assuming the difference in disk temperature between these sources is only due to luminosity (i.e., flaring is similar for these embedded disks and temperature in this region is set by irradiation only). In a passive disk, the temperature and central source luminosity are related by Tmid(r)∝(φL*)1/4/r1/2, where φ is the flaring angle (Chiang & Goldreich 1997). The factor 2 difference in temperature implies a factor 16 lower luminosity for SM1 of ∼0.08 L⊙. Thus, it is possible that SM1 is a very low luminosity Class 0 protostar or VeLLO (Dunham et al. 2008), in agreement with the very cold SED observed for this source. This would suggest that SM1 is either an extremely young protostar with very little mass accreted so far or is a more evolved Class 0 protostar observed in a quiescent period of accretion (Pineda et al. 2011; Maureira et al. 2020). The former is favored by the observed outflow properties, such as its short length and dynamical time (Friesen et al. 2018).

We also used the derived optical depth profile τ3mm in Figure 3 to estimate the mass of the disk as 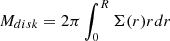, where Σ(r) = τ3mm(r)/κ3mm and κ3mm is the dust opacity. We used a constant value for τ3mm of 8 for the inner ∼15 au region (see Figure 3) and R = 40 au to obtain a conservative estimation. Using an opacity at 3 mm of ∼1 cm2 gr−1 (Beckwith et al. 1990; Birnstiel et al. 2018) and a gas-to-dust ratio of 100, we estimate a total gas mass of 0.13 M⊙ (or ∼430 M⊕ dust mass). About half of this mass corresponds to the outer region with τ3mm < 8. The estimated mass in solids for this disk is in agreement with the range derived for a sample of Class 0 disks also using long-wavelength observations (9 mm), resulting in masses that are 50 times higher than those of Class II disks (Tychoniec et al. 2020). Nevertheless, we note that the derived mass could be higher or lower by a factor of 2–5 due to uncertainties on the dust opacities, which can show large variations depending on the considered grain properties (e.g., Ricci et al. 2010; Birnstiel et al. 2018).

4. Discussion

In this work, we show that both a disk with a gap and a disk with an outer ring can explain the observed deviation in the intensity profile of this young Class 0 disk. This type of deviation or inflection point in the intensity profile has also been interpreted as unresolved gaps or rings for several Class II disks, and interestingly, in those cases it also appears to be located near the edge of the disk structure (e.g., WSB 52, Sz 129, and RU Lup in Huang et al. 2018). Similarly, the Class I disk IRS 63 was revealed to have a ring and a gap near the location of two inflection points in its intensity profile (Segura-Cox et al. 2020; Cieza et al. 2021). The lifetime of Class 0 protostars, such as SM1, is estimated to be ∼0.15 Myr (Dunham et al. 2014); therefore the evidence for a gap or a ring in SM1 suggests a fast emergence of dust substructures in disks. This is in agreement with several observational studies showing that the amount of solid material in Class II disks of only about 1 Myr old is insufficient to explain the observed exoplanet systems (Manara et al. 2018; Tychoniec et al. 2020; Testi et al. 2022). In addition, the evolution of the dust mass for Class II disks can be explained by internal regeneration of dust due to early (≲0.5 Myr) planet formation (Testi et al. 2022; Bernabò et al. 2022). Thus, substructures at stages as early as the one found here could indeed indicate the presence of a planet, or could suggest the fast subsequent formation of a planetary core. Theoretically, the possibility of a planet at such early times depends on whether or not the conditions for the streaming instability (dust-to-gas ratio near unity and dust grains only moderately coupled to the gas) could be present in such a young disk (Youdin & Goodman 2005). In recent years, theoretical studies have started to investigate this question. Cridland et al. (2022) find that the conditions for streaming instability are met on timescales of 0.1–0.2 Myr for regions in the disk at a distance of a few tens of astronomical units (au), with masses from a few M⊕ to tens of M⊕ available to form planetesimals. The favorable conditions are aided by the early decoupling of grains with sizes of ≳10 μm in the infalling envelope and disk (Bate & Lorén-Aguilar 2017; Lebreuilly et al. 2020; Cridland et al. 2022). Such masses agree with the possible range of planetary masses derived from the gap properties in this work, although there are large uncertainties (see Appendix D). On the other hand, alternative studies find that the conditions are not met in young Class 0/I disks, as their high turbulence and density would prevent the growth, decoupling, and settling of dust (e.g., Drążkowska & Dullemond 2018; Xu & Armitage 2023). In the more conservative scenario in which an early substructure – such as that in SM1 – precedes the formation of planetesimals, numerical simulations find that in young embedded disks, infalling dust can accumulate at the outer disk’s edge, resulting in a ring structure (Kuznetsova et al. 2022). This scenario therefore aligns with the disk plus ring model found in Sect. 3 as a plausible explanation for the observed deviations in the SM1 disk intensity profile. Moreover, recent numerical simulations show that such dust accumulation could start even before the formation of the protostar (Bhandare et al. 2024). In summary, the discussion above suggests that although several independent observations – including those presented here – support the early formation of planets during the embedded Class 0/I stages, theoretical studies are yet to form a consensus as to whether or not planetesimal formation mechanisms can be effective in these disks.

In addition to the possibilities discussed above, other scenarios that could potentially lead to the observed deviation in the intensity profile of SM1 are: changes in the dust opacity at the location of ice lines (Cieza et al. 2016), variation of grain sizes, and dust accumulation at pressure bumps caused by planets (Cieza et al. 2021; Pinilla et al. 2019). The derived temperature at the gap or ring location (∼13 − 15 K) is close to the freeze-out temperature range of N2 (17–21 K, Fayolle et al. 2016; Huang et al. 2018), while the CO and CO2 ice lines fall in the optically thick part of the disk. Thus, it is possible that the deviation is due to the location of the N2 ice line, which can lead to changes in the dust properties. Multiwavelength and high-resolution observations are needed to better constrain the temperature and grain properties at this location (e.g., Macías et al. 2021; Guerra-Alvarado et al. 2024b).

Finally, when the emission from the disk becomes optically thick, the intensity starts to trace the temperature profile instead of a combination of the temperature and optical depth (Guerra-Alvarado et al. 2024b). This makes the detection of substructures more difficult, and can therefore result in underestimation of the frequency of substructure in the younger (≲0.5 Myr) embedded disks (Ohashi et al. 2023; Hsieh et al. 2024). The problem is exacerbated if the disk is observed at higher inclinations, adding uncertainty as to the origin of features in the profile (e.g., Sai et al. 2023). This may help explain the low frequency of substructure found thus far in embedded disks, and will be discussed in more detail in a forthcoming paper. We predict that the optical depth at 1.3 mm for SM1 would indeed be above one within 40 au of the central source, which, depending on the assumed dust properties, can indeed reduce the contrast of the observed deviation in the profile (see Figure C.1), making its detection more challenging. Our observations at longer wavelengths, combined with the low inclination of the source, have resulted in optically thin emission beyond 20 au (Figure 3), making SM1 a more robust case for the detection of substructure in a deeply embedded Class 0 source.

5. Summary and conclusions

We use ALMA observations at 3 mm with a resolution of 6.9 au to probe substructures in the deeply embedded Class 0 disk surrounding Oph A SM1. The observations reveal a nearly face-on disk with a radius of ∼40 au. The radial intensity profile shows deviation near 30 au that can be reproduced either by considering a gap at radius of 28 au or an outer ring at a radius of 30 au. A smooth profile is statistically excluded. The 3 mm emission at the location of the substructure is optically thin, which is a critical condition to reveal such features. The evidence from SM1 suggests that we should be cautious of the possibility that annular substructures could emerge early, during the Class 0 stage (≲0.2 Myr), but remain difficult to identify in current observations. More observations using longer wavelengths or targeting disks in which the optical depth can be mitigated are needed to more robustly constrain the onset and frequency of substructures during the embedded stages.

1

The relatively high upper limit is due to bright extended 70 μm emission near the location of SM1; see Friesen et al. (2018) for details.

2

Fifty AU Study of the chemistry in the disk/envelope system of Solar-like protostars.

6

Radius containing 95% of the flux.

Acknowledgments

The authors thank Masayuki Yamaguchi and Munan Gong for insightful discussions on imaging techniques and disk theory, respectively. The authors also kindly thank the anonymous referee for the comments that helped improve the manuscript. Part of this work was supported by the Max-Planck Society. D.M.S. is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-2102405. ClCo, LP, EB and GS acknowledge the PRIN-MUR 2020 BEYOND-2p (“Astrochemistry beyond the second period elements”, Prot. 2020AFB3FX), the project ASI-Astrobiologia 2023 MIGLIORA (Modeling Chemical Complexity, F83C23000800005), the INAF-GO 2023 fundings PROTO-SKA (Exploiting ALMA data to study planet forming disks: preparing the advent of SKA, C13C23000770005), the INAF Mini-Grant 2022 “Chemical Origins” (PI: L. Podio), INAF-Minigrant 2023 TRIESTE (“TRacing the chemIcal hEritage of our originS: from proTostars to planEts”; PI: G. Sabatini), and the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 2.2.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenerationEU– Project Title 2022JC2Y93 Chemical Origins: linking the fossil composition of the Solar System with the chemistry of protoplanetary disks – CUP J53D23001600006 - Grant Assignment Decree No. 962 adopted on 30.06.2023 by the Italian Ministry of Ministry of University and Research (MUR). L.L. acknowledges the support of DGAPA PAPIIT grants IN108324 and IN112820 and CONACyT-CF grant 263356. This project has received funding from the European Research Council (ERC) under the European Union Horizon Europe programme (grant agreement No. 101042275, project Stellar-MADE). Y.A. acknowledges support by NAOJ ALMA Scientific Research Grant code 2019-13B. EB knowledge support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2094 – 390783311.

References

  1. Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bae, J., Isella, A., Zhu, Z., et al. 2023, ASP Conf. Ser., 534, 423 [NASA ADS] [Google Scholar]
  3. Bate, M. R., & Lorén-Aguilar, P. 2017, MNRAS, 465, 1089 [Google Scholar]
  4. Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [Google Scholar]
  5. Benisty, M., Bae, J., Facchini, S., et al. 2021, ApJ, 916, L2 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bernabò, L. M., Turrini, D., Testi, L., Marzari, F., & Polychroni, D. 2022, ApJ, 927, L22 [CrossRef] [Google Scholar]
  7. Bhandare, A., Commerçon, B., Laibe, G., et al. 2024, A&A, 687, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Birnstiel, T., Dullemond, C. P., Zhu, Z., et al. 2018, ApJ, 869, L45 [CrossRef] [Google Scholar]
  9. CASA Team, Bean, B., Bhatnagar, S., et al. 2022, PASP, 134, 114501 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cavanaugh, J. E., & Neath, A. A. 2019, WIREs Comp. Stats., 11, e1460 [CrossRef] [Google Scholar]
  11. Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [Google Scholar]
  12. Choudhury, S., Pineda, J. E., Caselli, P., et al. 2021, A&A, 648, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cieza, L. A., Casassus, S., Tobin, J., et al. 2016, Nature, 535, 258 [Google Scholar]
  14. Cieza, L. A., González-Ruilova, C., Hales, A. S., et al. 2021, MNRAS, 501, 2934 [Google Scholar]
  15. Codella, C., Ceccarelli, C., Chandler, C., et al. 2021, Front. Astron. Space Sci., 8, 227 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cridland, A. J., Rosotti, G. P., Tabone, B., et al. 2022, A&A, 662, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Drążkowska, J., & Dullemond, C. P. 2018, A&A, 614, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dunham, M. M., Crapsi, A., Evans, N. J., II, et al. 2008, ApJS, 179, 249 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 195 [Google Scholar]
  20. Fayolle, E. C., Balfe, J., Loomis, R., et al. 2016, ApJ, 816, L28 [Google Scholar]
  21. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  22. Francis, L., Johnstone, D., Herczeg, G., Hunter, T. R., & Harsono, D. 2020, AJ, 160, 270 [NASA ADS] [CrossRef] [Google Scholar]
  23. Friesen, R. K., Di Francesco, J., Bourke, T. L., et al. 2014, ApJ, 797, 27 [NASA ADS] [CrossRef] [Google Scholar]
  24. Friesen, R. K., Pon, A., Bourke, T. L., et al. 2018, ApJ, 869, 158 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gagné, M., Skinner, S. L., & Daniel, K. J. 2004, ApJ, 613, 393 [CrossRef] [Google Scholar]
  26. Galván-Madrid, R., Liu, H. B., Izquierdo, A. F., et al. 2018, ApJ, 868, 39 [CrossRef] [Google Scholar]
  27. Guerra-Alvarado, O. M., van der Marel, N., Di Francesco, J., et al. 2024a, A&A, 681, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Guerra-Alvarado, O. M., Carrasco-González, C., Macías, E., et al. 2024b, A&A, 686, A298 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [Google Scholar]
  30. Hsieh, C. H., Arce, H. G., Maureira, M. J., et al. 2024, ApJ, submitted [arXiv:2404.02809] [Google Scholar]
  31. Huang, J., Andrews, S. M., Dullemond, C. P., et al. 2018, ApJ, 869, L42 [NASA ADS] [CrossRef] [Google Scholar]
  32. Isella, A., Carpenter, J. M., & Sargent, A. I. 2009, ApJ, 701, 260 [Google Scholar]
  33. Izquierdo, A. F., Facchini, S., Rosotti, G. P., van Dishoeck, E. F., & Testi, L. 2022, ApJ, 928, 2 [NASA ADS] [CrossRef] [Google Scholar]
  34. Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2007, ApJ, 659, 479 [Google Scholar]
  35. Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2016, PASJ, 68, 43 [NASA ADS] [Google Scholar]
  36. Kawabe, R., Hara, C., Nakamura, F., et al. 2018, ApJ, 866, 141 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ko, C.-L., Liu, H. B., Lai, S.-P., et al. 2020, ApJ, 889, 172 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kuznetsova, A., Bae, J., Hartmann, L., & Mac Low, M.-M. 2022, ApJ, 928, 92 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lebreuilly, U., Commerçon, B., & Laibe, G. 2020, A&A, 641, A112 [EDP Sciences] [Google Scholar]
  40. Li, J. I.-H., Liu, H. B., Hasegawa, Y., & Hirano, N. 2017, ApJ, 840, 72 [NASA ADS] [CrossRef] [Google Scholar]
  41. Liu, H. B. 2021, ApJ, 914, 25 [NASA ADS] [CrossRef] [Google Scholar]
  42. Liu, H. B., Mérand, A., Green, J. D., et al. 2019, ApJ, 884, 97 [NASA ADS] [CrossRef] [Google Scholar]
  43. Long, F., Pinilla, P., Herczeg, G. J., et al. 2018, ApJ, 869, 17 [Google Scholar]
  44. Long, F., Herczeg, G. J., Harsono, D., et al. 2019, ApJ, 882, 49 [Google Scholar]
  45. Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
  46. Macías, E., Guerra-Alvarado, O., Carrasco-González, C., et al. 2021, A&A, 648, A33 [EDP Sciences] [Google Scholar]
  47. Manara, C. F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Manara, C. F., Tazzari, M., Long, F., et al. 2019, A&A, 628, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Maureira, M. J., Arce, H. G., Dunham, M. M., et al. 2020, MNRAS, 499, 4394 [NASA ADS] [CrossRef] [Google Scholar]
  50. Maureira, M. J., Gong, M., Pineda, J. E., et al. 2022, ApJ, 941, L23 [NASA ADS] [CrossRef] [Google Scholar]
  51. Mordasini, C., Mollière, P., Dittkrist, K. M., Jin, S., & Alibert, Y. 2015, IJAsB, 14, 201 [NASA ADS] [Google Scholar]
  52. Nakatani, R., Liu, H. B., Ohashi, S., et al. 2020, ApJ, 895, L2 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ohashi, N., Tobin, J. J., Jørgensen, J. K., et al. 2023, ApJ, 951, 8 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 869, L33 [Google Scholar]
  55. Pattle, K., Ward-Thompson, D., Kirk, J. M., et al. 2015, MNRAS, 450, 1094 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pineda, J. E., Arce, H. G., Schnee, S., et al. 2011, ApJ, 743, 201 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pinilla, P., Benisty, M., Cazzoletti, P., et al. 2019, ApJ, 878, 16 [Google Scholar]
  58. Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [CrossRef] [EDP Sciences] [Google Scholar]
  59. Rosotti, G. P., Juhasz, A., Booth, R. A., & Clarke, C. J. 2016, MNRAS, 459, 2790 [Google Scholar]
  60. Sai, J., Yen, H.-W., Ohashi, N., et al. 2023, ApJ, 954, 67 [NASA ADS] [CrossRef] [Google Scholar]
  61. Segura-Cox, D. M., Schmiedeke, A., Pineda, J. E., et al. 2020, Nature, 586, 228 [NASA ADS] [CrossRef] [Google Scholar]
  62. Sheehan, P. D., & Eisner, J. A. 2018, ApJ, 857, 18 [NASA ADS] [CrossRef] [Google Scholar]
  63. Shoshi, A., Harada, N., Tokuda, K., et al. 2024, ApJ, 961, 228 [NASA ADS] [CrossRef] [Google Scholar]
  64. Takakuwa, S., Saigo, K., Kido, M., et al. 2024, ApJ, 964, 24 [NASA ADS] [CrossRef] [Google Scholar]
  65. Tazzari, M., Clarke, C. J., Testi, L., et al. 2021, MNRAS, 506, 2804 [NASA ADS] [CrossRef] [Google Scholar]
  66. Testi, L., Natta, A., Manara, C. F., et al. 2022, A&A, 663, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Tripathi, A., Andrews, S. M., Birnstiel, T., & Wilner, D. J. 2017, ApJ, 845, 44 [Google Scholar]
  68. Tychoniec, Ł., Manara, C. F., Rosotti, G. P., et al. 2020, A&A, 640, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Valdivia-Mena, M. T., Pineda, J. E., Segura-Cox, D. M., et al. 2022, A&A, 667, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  71. Xu, W., & Armitage, P. J. 2023, ApJ, 946, 94 [NASA ADS] [CrossRef] [Google Scholar]
  72. Xu, W., Ohashi, S., Aso, Y., & Liu, H. B. 2023, ApJ, 954, 190 [NASA ADS] [CrossRef] [Google Scholar]
  73. Yamato, Y., Aikawa, Y., Ohashi, N., et al. 2023, ApJ, 951, 11 [NASA ADS] [CrossRef] [Google Scholar]
  74. Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
  75. Zamponi, J., Maureira, M. J., Zhao, B., et al. 2021, MNRAS, 508, 2583 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Data self-calibration

For the extended configuration observations (C-10) we performed phase self-calibration only. We performed several iterations reducing the solint interval from ’inf’ down to ’10s’, combininig all the spectral windows for the final step. This phase-only self-calibration process improved the S/N of the image by about 40%. For the more compact (C-6) configuration, there were seven spectral windows, two of which contained spectral line emission. Line-free channels were used to obtain a continuum model that was then used for self-calibration using solint=’int’ (per 6s integration), while per-scan (8-10 minutes) solutions were used for amplitude and phase self-calibration once the model was sufficiently complete. For the combined self-calibration, we averaged both datasets in time and frequency. We averaged in time in bins of 9 seconds. We averaged in frequency up to the maximum that would not result in a reduction of the intensity larger than ∼1% for sources away from the phase center due to bandwidth smearing7. The primary beam response at the location of SM1 is 0.35 because the target of this field was the Class 0 source VLA 1623-2417. The final channel width used was 30 MHz. We performed four successive steps of phase-only self-calibration in the combined dataset. In the first one, we use solint=’inf’, gaintype=’G’ and combined all spectral windows. For this first round, we used the final image after self-calibration of the extended configuration as the model. This aligns the two datasets to the peak position of the extended configuration and thus corrects for differences in the peak positions across datasets arising from proper motion or astrometric errors of the observations. The resultant model was then used for the next steps all with gaintype=’T’. The solint values for the next iterations were ’inf’, ’30s’, ’int’. For the last two iterations all spectral windows were combined. Finally, we performed three steps of amplitude self-calibration with solint=’inf’. In the first one we combined all spectral windows and used solnorm=T, then we switched to solnorm=T and finally we allowed solutions to be calculated per spectral window. For the combined self-calibration the improvement in S/N was about 10%.

Appendix B: Fit of the intensity profiles

We used emcee (Foreman-Mackey et al. 2013) to fit the beam convolved models to the data. The logarithms of the convolved model and the data were used in the likelihood function in order to consider the fractional errors instead of the absolute errors. This is to avoid a higher weight on the brighter parts of the disk with respect to the weaker extended outer parts. The convolution of the model was done using the function fftconvolve from the Python module scipy.fftconvolve (Virtanen et al. 2020). We used uniform priors for each parameter which are summarized for the individual models in Table B.2. We use 50 walkers and run it up to a maximum of 300,000 steps stopping the run when the number of steps was larger than 100× the autocorrelation time (which is the effective number of independent steps) and the autocorrelation time estimation varied by less than 1%. The burn-in was computed as twice the autocorrelation time and the chains were thinned using a thinning parameter of half the autocorrelation time. The resulting chains showed no large-scale variations. Figures B.1 to B.3 show the resultant corner plots. Table B.1 summarized the resultant median for the free parameters in each model with their respective lower and upper range enclosing 68% of the distribution around the median. The last row shows the radius of the disk enclosing the 95% of the total flux R95. We note that for the gap model there is a degeneracy between models with a deep and narrow gap or a shallow broad one as both lead to a similar profile once convolved with the beam. Given that the posteriors of the intensity peak and width for the gap models show significant tension, extreme values for the width (small or large) seem less likely. Higher resolution observations are required to improve the constrains on the gap morphology.

thumbnail Fig. B.1.

Corner plot results for the smooth disk profile. The dashed lines marked the median value and the lower and upper range enclosing the 68% of the distribution around the median.

thumbnail Fig. B.2.

Same as Figure B.1 but for the model of a disk with a gap.

thumbnail Fig. B.3.

Same as Figure B.1 but for the model of a disk with a ring.

Table B.1.

Resultant parameters for each model.

Table B.2.

Priors for each parameter and model.

Appendix C: Intensity and optical depth predictions at 1.3 mm

Figure C.1 shows the predicted 1.3 mm intensity profiles and optical depth for SM1 by extrapolating τ3mm, using constant β values between 1 and 1.7, and the temperature profile derived in Section 3.2. At 1.3 mm the optical depth increases reaching values greater than 1 throughout the profile. The increase in optical depth also reduces the contrast of the gap/ring feature as the intensity approaches the temperature profile. Similarly, the increased optical depth leads to a flattening or ‘bump’ in the profile from 15 to 25 au. This feature in the profile, which is interior to the observed 3 mm intensity feature, and therefore not due to the presence of dust substructure but due to the optically thick emission. Figure C.1 also shows the predictions for SM1 if it were inclined by 60°. This inclination corresponds to an increase in optical depth by a factor of about 2. The predictions show that in such situations the profile could appear featureless (upper edge dark blue shaded region).

thumbnail Fig. C.1.

Predictions for the brightness temperature and optical depth profiles at 1.3 mm based on the observed 3 mm profile for SM1 (solid gray line). The widths of the shaded areas correspond to the resultant range of the profiles, considering β between 1 and 1.7. The darker blue corresponds to the predicted profile if the disk had been observed at a higher inclination (i = 60°). The black dotted line corresponds to the derived temperature for SM1 as in Figure 3.

Appendix D: Estimation of planetary mass from gap properties

Numerical simulations show that when a gap is opened due to the presence of a planet, the width of the gap normalized by its distance to the star is correlated with the ratio between the star and the planet masses. The exact relation also depends on the thickness of the disk (H/R) at the location of the planet and on the viscosity parameter αvis (Kanagawa et al. 2016; Rosotti et al. 2016). In the case of SM1, several of these parameters are unknown, including the protostar mass. Following Equation 4 in Kanagawa et al. (2016) and assuming αvis = 10−3, an aspect ratio H/R∼0.1-0.3 (following the Segura-Cox et al. 2020 derivation for the Class I disk IRS 63) and a 1 M⊙ protostar, we obtain possible planet masses in the range from few tens to 200 M⊕. The planet’s mass scales linearly with the protostar mass. A comparable range is found when compared with the numerical simulations by Rosotti et al. (2016). We should be cautious not to overinterpret these values given the number of unknown parameters. Nonetheless, the potential upper range agrees with the estimated planet masses for the gaps in the Class I disk IRS 63, and the possible range agrees with numerical estimates of the mass budget for planetary core formation through the streaming stability in young disks (Cridland et al. 2022). Molecular line observations are required to obtain the protostar mass for SM1, which would allow us to set tighter constraints on both the disk’s dynamical state and the possible planetary masses.

All Tables

Table B.1.

Resultant parameters for each model.

In the text
Table B.2.

Priors for each parameter and model.

In the text

All Figures

thumbnail Fig. 1.

ALMA observations towards SM1. Left: 3 mm continuum observations of the SM1 disk. Right: Azimuthally averaged brightness temperature profile calculated using the full Planck function displayed in logarithmic scale. The corresponding 1σ uncertainties are shown in gray. Green dashed and solid vertical curves mark the same radial distance from the center in both panels, corresponding to the location of the deviation in the radial intensity profile and the location of the 3σ emission contour in the map, respectively.
In the text
thumbnail Fig. 2.

Fits to the disk intensity profile and residuals for three different models. The orange curves in the top panels show 100 profiles drawn randomly from the posterior distributions. The observed profile is shown with a black solid line. The resultant median residual is shown in the bottom panels (solid black line) as well as 1σ dispersion around the median residual (orange shaded area). The gray shaded area corresponds to the 1σ uncertainty of the intensity profile in all panels. Left: Smooth disk profile. Middle: Disk profile with a gap at ∼28 au. The black horizontal segment shows the range of values for the gap radius enclosing 68% of the posterior distribution around the median. Right: Disk profile with a ring at ∼34 au. The black horizontal segment shows the range of values for the ring radius enclosing 68% of the posterior distribution around the median.
In the text
thumbnail Fig. 3.

Radial profiles of the in-band spectral index, optical depth, and temperature towards SM1. The solid purple line shows the in-band spectral index. The shaded area shows the 1σ uncertainty. The estimated 3 mm optical depth and temperature profiles are shown with dashed purple and dotted black lines, respectively. The temperature profile is extrapolated beyond r ∼ 15 au following a r−0.5 power law. The observed brightness temperature profile is overlaid in solid gray, similar to Figure 1.
In the text
thumbnail Fig. B.1.

Corner plot results for the smooth disk profile. The dashed lines marked the median value and the lower and upper range enclosing the 68% of the distribution around the median.
In the text
thumbnail Fig. B.2.

Same as Figure B.1 but for the model of a disk with a gap.
In the text
thumbnail Fig. B.3.

Same as Figure B.1 but for the model of a disk with a ring.
In the text
thumbnail Fig. C.1.

Predictions for the brightness temperature and optical depth profiles at 1.3 mm based on the observed 3 mm profile for SM1 (solid gray line). The widths of the shaded areas correspond to the resultant range of the profiles, considering β between 1 and 1.7. The darker blue corresponds to the predicted profile if the disk had been observed at a higher inclination (i = 60°). The black dotted line corresponds to the derived temperature for SM1 as in Figure 3.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.