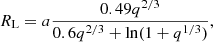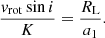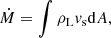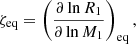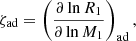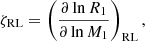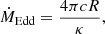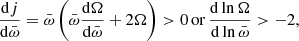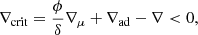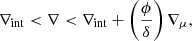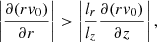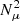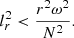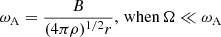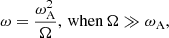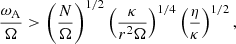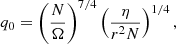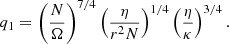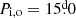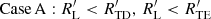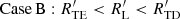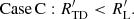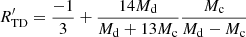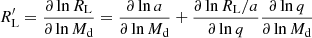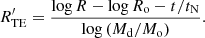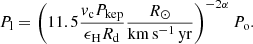| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A154 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348290 | |
| Published online | 09 September 2024 | |
Double periodic variable V4142 Sgr: A key to approaching the stellar dynamo
1
Departamento de Astronomía, Universidad de Concepción, Casilla 160-C, Concepción, Chile
2
Astronomical Observatory, Volgina 7, 11060 Belgrade 38, Serbia
3
Isaac Newton Institute of Chile, Yugoslavia Branch, 11060 Belgrade, Serbia
4
Department of Astrophysics, American Museum of Natural History, Central Park West and 79th Street, New York, NY 10024, USA
Received:
16
October
2023
Accepted:
24
May
2024
Aims. In this work we focus on the double periodic variable (DPV) star V4142 Sgr, aiming to provide a deeper understanding of its evolution, the formation of its accretion disk, and the operation of magnetic dynamos within the donor star. We analyze its characteristics in detail as well as the phenomena associated with DPV stars more generally.
Methods. The model was implemented using the stellar evolution code MESA r22.11.1. The modeling process starts from the zero age main sequence and incorporates differential rotation to facilitate the creation of a stellar dynamo in the donor star. We adjusted the model by employing a chi-square algorithm, minimizing the deviation between theoretical and observed values based on previously published fundamental parameters for this system. Our analysis includes an evaluation of various parameters, such as initial masses, orbital periods, mixing parameters, the thermohaline parameter, and metallicities. We assessed the algorithm convergence and set the stopping criterion at 20% helium core depletion in the donor star. A comprehensive analysis was conducted at each evolutionary stage, utilizing the Tayler–Spruit formalism to understand the mechanism of magnetic dynamos.
Results. The model begins by adjusting fundamental parameters published for this system through a chi-squared optimization algorithm, adopting an initial orbital period of 15.0 days and initial masses for the donor and gainer star of Mi, d = 3.50 M⊙ and Mi, g = 1.50 M⊙, with a metallicity associated with this type of DPV of Z = 0.02. It successfully converges with six degrees of freedom and 5% confidence, resulting in a chi-squared value of 0.007. In addition, the best-fit model for V4142 Sgr shows it is in thermal-timescale mass transfer. Our analysis provides insights into the role of differential rotation in facilitating the formation of a stellar dynamo. Additionally, we have determined that our type-B gainer star is located in a region similar to other type-B DPVs that have undergone rejuvenation due to the transfer of matter. The size of the gainer star shrinks considerably, but it rejuvenates thanks to the material acquired from its donor companion. As for the donor star, the creation and amplification of magnetic fields are influenced by the mixing diffusivity, DST, which is activated by advection outside the overshooting zone.
Key words: dynamo / instabilities / binaries: general / circumstellar matter / stars: early-type / stars: mass-loss
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Current double periodic variable (DPV) star models assume a semidetached binary system of intermediate masses with a hot B-type star dubbed the gainer, which is surrounded by an optically thick accretion disk accumulating matter from a less massive and more evolved star, dubbed the donor. The donor star is typically an A/F/G-type giant (Mennickent 2017; Rosales Guzmán et al. 2018). However, some new studies consider the possibility of the existence of dynamos in some Algol-type variables; following this line of reasoning, Schleicher & Mennickent (2017) proposed an explanation for the long cycles of DPV stars based on magnetic cycles of the most evolved star, considering that the Applegate mechanism should induce cyclic changes in the donor star’s equatorial radius and therefore the mass transfer rate (Applegate & Patterson 1987). This is not something new: Sarna et al. (1997) examined the possibility of tracking the existence of dynamos in Algol-type stars that show mass loss, while Peterson et al. (2010) reported magnetic activity based on the fact that since the rotation periods of the two stars are tidally locked to the orbital period, the rapid rotation drives a magnetic dynamo. Indirect evidence for such a dynamo was also reported in the DPV star V393 Sco by Mennickent et al. (2018), and explored for first time in the evolutionary tracks of V495 Centauri through numerical simulations by Rosales et al. (2019). Through 3D magnetohydrodynamic simulations, Navarrete et al. (2020) demonstrated the importance of the magnetohydrodynamic dynamo on stellar structure.
To constrain the extreme ends of the DPV population regarding the distribution of the long cycle, we have studied the DPV star V4142 Sgr, which belongs to the group of DPVs with the longest orbital periods. The system is composed of a B-type gainer star hidden by a large optically and geometrically thick accretion disk, which shows Balmer line emissions with a spatial horseshoe shape distribution; this emission forms its proper atmosphere, which has a radial extension Rd = 22.8 ± 0.3 R⊙; there is also evidence of gas emission with a persistent V < R asymmetry of the Hα emission line, potentially located at the hotspot caused by the shock in the accretion stream. Its companion is an evolved K1 III-type star with clear evidence of chromospheric activity (Rosales et al. 2023). The system was found to have a long cycle of 1206 days (i.e., approximately 39 times the orbital period).
We conducted a complementary analysis of the DPV V4142 Sgr, which is classified as an eclipsing Algol detached binary and has been given the ID 180745-2824.1, with equatorial coordinates α2000 = 18 : 07 : 45, δ2000 = −28 : 24 : 06 (see Fig. 1); it has an apparent magnitude of V = 10.94 ± 0.04 mag and a magnitude variation of Vamp = 2.019 ± 0.05 mag (Pojmanski 1997). It was reported as a DPV by Mennickent & Rosales (2014) and studied by Rosales et al. (2023), who, based on photometric and spectroscopic analyses, concluded that the system comprises DPVs.
 |
Fig. 1. Aitoff projection of well-studied Galactic DPV stars (orange triangles) from the Variable Star Index (VSX)1. Semidetached Algol primaries from Dervişoǧlu et al. (2010) are also shown as black points, and other DPVs yet to be studied and reported in VSX are shown as green dots. V4142 Sgr is represented by a blue star with an orange border. |
We applied the Modules for Experiments in Stellar Astrophysics (MESA2; Eggleton 1971; Paxton 2004; Paxton et al. 2011, 2013), which was developed to calculate the evolution of stars in a wide range of parameters, with independent modules for experiments in stellar astrophysics of close binary systems (Paxton et al. 2015, 2018). Our goal was to enhance our understanding of the evolution of V4142 Sgr and its connection with stellar dynamos. However, it is important to emphasize that MESA is a 1D stellar evolution code, and the 1D approach may not adequately address certain problems that require more sophisticated multidimensional approaches. To achieve this, we utilized the reported fundamental physical parameters and applied the statistical chi-square method to model a system that fits the observed data.
2. The model
When a star in a binary system evolves and expands enough to reach its Roche lobe (RL), it is referred to as Roche lobe overflow (RLOF). This occurs when the star that is about to fill its RL expands as it evolves, approaching its Roche limit more and more closely. As it approaches that limit, material from the star can begin to flow toward the companion star through an accretion disk or via a bridge of matter. This process can lead to significant changes in the structure and evolution of the stars. Mass transfer can influence the rotation rate, nuclear stability, and future evolution of the stars in the binary system. Thus, interactions in nearby binary stars are generally discussed in terms of the Roche potential. This term is defined as a vector or scalar magnitude, which represents the distorted shape of a star in a binary system (Kopal 1959, 1978) in which there is a region around of the star where the orbiting material is gravitationally bound, commonly known as the RL. The modules for experiments in stellar astrophysics of MESA were developed to evolves an interacting pair of differentially rotating stars undergoing mass transfer, loss of mass and angular momentum. These find an analytic approximation of the RL around the primary star (Eggleton 1983, 2006), computing the size of this volume through numerical integration, according to
where RL represents the effective radius for the critical equipotential of the RL, a is the orbital separation between the two stars, and q = M2/M1 = K1/K2 is the mass ratio between the secondary and primary masses or the ratio in term of the radial velocities (RVs). Conventionally, it is considered that the more massive star begins to evolve faster and becomes equal to the radius of a sphere with a volume equal to that of the RL. Unfortunately, in several semidetached systems the mass ratio q cannot be determined directly from the RVs; this may be due to the gainer star being surrounded by a gas stream that distorts its spectrum but is hidden by the accretion disk. Despite this, it is possible to study these systems by combining the previously mentioned Eqs. (3.5) and (3.9) from Eggleton (2006), resulting in Eq. (2):
This synchronism, observed in most DPVs, involves the compatibility of a synchronously rotating donor star that fills the RL. This situation can be analyzed using a composite equation derived from the aforementioned equations by Eggleton (2006). The primary objective of this analysis is to comprehend synchronism in interacting binaries. Here a1 is the radius of the orbit of the donor star about the center of gravity, vrot is the rotational velocity, and K is half-amplitude of the RV.
To determine the stellar evolution of close binary stars, it is necessary to know some fundamental parameters. These parameters include the masses during the zero-age main sequence (ZAMS), orbital period (P), mass ratio (q), orbital separation (a), spectral types (providing information about temperature and intrinsic luminosity), eccentricity (e), initial metallicity (Z), and Roche limits. These parameters provide crucial information about the evolutionary stages and allow us to understand how the system will change over time. Additionally, the alpha mixing length parameter (αml) is another important parameter in the context of stellar evolution. It describes convection within a star and provides valuable information about the degree of material mixing within convective regions. This parameter ensures accuracy and realistic results during numerical simulations. In general, it is assumed that the evolution of close binaries follows the mass exchange defined by Kippenhahn & Weigert (1967), Kippenhahn et al. (1967), and Lauterborn (1970). Therefore, these models, along with the aforementioned fundamental parameters, contribute to a comprehensive understanding of the stellar evolution of close binary systems by considering the interplay between mass transfer, convective mixing, and other relevant physical processes. From now on, we will refer to the primary and secondary components as the donor and gainer, respectively. It is important to exercise caution with these designations to avoid confusion. When the more massive star evolves and fills its RL during core hydrogen burning, we have what is known as Case A. At this stage, the evolution of the donor star is slow and primarily governed by the nuclear timescale. During the mass transfer process, its evolution remains stable along the main sequence. As the donor star gradually fills its RL, it eventually departs from the main sequence before helium ignition. At this point, the donor star crosses the Hertzsprung gap while undergoing hydrogen-shell burning. The mass transfer is driven by the rapid expansion of the starś envelope, causing the gas to accelerate from subsonic to supersonic velocities through the Lagrangian point L1. This scenario is referred to as Case B (thermal timescale). Subsequently, the mass transfer continues due to envelope expansion at the helium-shell burning stage. The donor star fills its RL after core helium ignition, leading to further interactions between both stars before the donor star reaches the end of its life. Mass transfer in this phase occurs on a dynamic timescale and is often unstable. These systems often evolve into a common envelope phase, known as Case C (Hilditch 2001).
2.1. Mass transfer
Mass transfer can have several significant effects on the stellar evolution and properties of DPV systems. It can alter the internal structure of the donor and gainer star, resulting in changes to their chemical composition, temperature, and density. The availability of material for nuclear fusion can also be affected, leading to variations in the stellar luminosity and temperature during the process. The stellar evolution itself can be influenced, potentially accelerating or delaying certain evolutionary processes such as the main sequence exit, ignition of fusion layers, gravitational collapse, or eventually contributing to the generation of stellar dynamos, as shown by Rosales et al. (2019).
Additionally, changes in the orbit can have a significant impact on the binary system. The transfer of angular momentum during mass transfer can cause the orbit to expand or contract, leading to changes in the orbital period and eccentricity. However, an interesting and remarkable property of DPVs is the constancy of their orbital periods, which usually does not occur in Algols undergoing RLOF mass transfer, as indicated by Garrido et al. (2013). Material flowing from one star to another during mass transfer can form an accretion disk around the gainer star, adopting unusual structures as observed in the case reported by Rosales et al. (2023). Furthermore, mass transfer can induce tidal effects in stars, resulting in luminosity changes or changes in the shape or structure of the accretion disk, as observed by Garcés et al. (2018). In addition, this process can be accompanied by stellar winds from the mass-losing star or the ejection of matter from the accretor (Soberman et al. 1997). It was suspected that some interacting binary systems show variations in the wind generated in the stream-disk impact region (van Rensbergen et al. 2008; Mennickent et al. 2016b). For example, the interacting binary V393 Scorpii, studied by Mennickent et al. (2012), shows evidence of a cyclically variable bipolar wind. For mass transfer, we employed an approach in the region where stellar gravity and tidal forces balance. When the star fills its RL, it triggers mass transfer to its companion or recipient. The entire process is governed by several parameters provided by MESA that allow the transfer of matter to be controlled and adjusted in various scenarios. All these parameters represent the fraction of accreted material related to the transferred material. Some of the parameters used to govern the distribution are as follows:
-
(α): the alpha mass fraction represents the fast wind mode associated with a spherically symmetrical outflow from the donor star, known as the Jeans mode, in the form of a fast wind.
-
(β): this mass fraction is associated with the isotropic re-emission mode. In this mode, the mass flux is transported from the donor star to the vicinity of the accretor, where it is ejected as an isotropic fast jet from the recipient.
-
(δ): this transfer mode is considered an intermediate mode or mass loss to a ring. It represents a more complex transfer mode that can have different interpretations. In some cases, it can be associated with a constant and stable mass transfer rate. The ejected mass carries the characteristic angular momentum of a circumbinary system.
-
(ϵ): this parameter is used to describe unstable or discontinuous mass transfer phases. It can represent episodic mass transfer events or interruptions in mass transfer due to specific phenomena in the binary system. This mass fraction is accreted by the primary, as the donor star has filled its RL. Here, matter is lost from the vicinity of the donor, through the inner Lagrange point, to the vicinity of the accretor, arriving with a high angular momentum.
Once the donor star expands, the flow from its outermost layers accelerates and converges toward the Lagrange point L1, reaching speeds of sound close to this location. The material rushes onto the gainer star, becoming so dense that it becomes opaque, preventing light from easily escaping. This phenomenon is known as the optically thick overflow, and the rate of mass transfer is determined as (Kolb & Ritter 1990)
where ρL and vs are respectively the density and the sound speed of the flow at the L1 point. However, the stability criterion for the mass transfer is normally understood in terms of the mass–radius relationship according to (Soberman et al. 1997; Tout et al. 1997)
where ζeq corresponds to the radial response of the donor to mass loss when it happens slowly enough for the star to remain in thermal equilibrium, the radial response, ζad, will occur when the timescale is much shorter than the thermal timescale, but still slow enough for the star to retain hydrostatic equilibrium, while the ζRL will determine the value of ṀRLOF if the overflowing star satisfies the equation ζeq > ζRL, then it will remain within its RL by transferring mass and maintaining thermal equilibrium. However, if ζad < ζeq < ζRL, the star will deviate from hydrostatic equilibrium and the process will become dynamic. However, during this process the donor star loses material through its atmosphere or outer shell, and this material accumulates on the companion. In this context, the Eddington accretion is defined by the mass transfer from the companion star to the gainer star. The gravitational pull of the accreting star pulls in material that is ejected from the companion star, creating an accretion disk around the star. As the material falls toward the accreting star, it heats up and emits radiation that is eventually strong enough to prevent the accretion (Burger & Katz 1983):
where R represents the radius of the accretor star and κ is a parameter that describes the opacity of a star, which refers to the ability of a material to absorb and scatter radiation that passes through a specific region. MESA controls the stability of the mass of the donor star during the transfer, taking into account the stability of mass in binary systems. Criteria such as the von Zeipel stability criterion (von Zeipel 1924) and the thermal stability criterion are used to determine if a star is losing or gaining mass based on its structure and properties. In addition, MESA also ensures the consistency between mass loss and mass transfer by employing self-consistent calculations. It provides both explicit and implicit methods for computing mass transfer rates. In the explicit computation, the value of ṀRLOF is set at the beginning of a step, while the implicit method involves an iterative process until the desired tolerance is achieved. Additionally, MESA considers the composition of the accreted material, which is set to match that of the donor surface. Furthermore, the specific entropy of the accreted material is made consistent with the surface of the accretor (Paxton et al. 2015). These robust procedures enhance the accuracy and reliability of the mass loss and transfer calculations within MESA.
2.2. Mass loss
The mass loss through stellar winds is an inherent phenomenon in the evolutionary process of stars, where the interaction of centrifugal forces with matter causes deviations in their symmetry. Many of the predictions of models of stellar rotation are now compared with observations of surface abundances and velocities, with interferometric studies of main sequence stars that are confirmed through observational data (Johnstone et al. 2015). To estimate the most appropriate mass-loss rate by winds in our simulation, we considered the Reimers model or scheme. The choice between the Reimers and Jager formalisms for modeling the wind phenomenon in the red giant branch (RGB) scheme is primarily based on inherent differences in the cause of mass loss. In the case of the Jager scheme, mass loss through wind is linked to a combination of factors such as convection, radiation, and thermal pulses in the outer layers of the star. This set of processes can lead to mass loss in the form of stellar wind. However, observations do not support the occurrence of this phenomenon in DPV systems, let alone in the donor star. On the other hand, the formalism proposed by Reimers is grounded in the premise that mass loss in a giant star is due to a combination of convection processes in the outer layers of the star. This perspective aligns more realistically with the systems we observe where the donor is filling its RL, providing a more accurate representation of the underlying mechanisms of stellar mass loss in these contexts. When the evolved star has depleted its nuclear fuel in the core and is in an advanced stage of its evolution on the asymptotic giant branch (AGB), it experiences intense mass loss and expels its outer layers of material in the form of stellar winds. In this case, we considered the cool wind scheme proposed by Bloecker (1995). Regarding the hot winds that occur during the transition from the RGB phase to the AGB, we incorporated the Dutch scheme for mass loss, using a predetermined scaling factor proposed by de Jager et al. (1988). This scheme provides a simplified way to estimate stellar mass loss, but we must consider that other factors can influence stellar mass loss, such as stellar metallicity, rotation, the presence of magnetic fields, and binary interactions. Finally, to ensure an accurate representation of the mass-loss process in intermediate-mass stars during the helium core burning phase, we must consider small enough time steps to allow the convergence of results.
2.3. Internal structure and rotation
Considering that at least one of the stars, in this case, the donor star, is composed of highly conductive plasma, allowing for the presence and evolution of magnetic fields within it, and incorporating differential rotation, it is expected that different layers or regions will exhibit varying rotational speeds. This is due to the conservation of angular momentum during mass transfer. The differential rotation within the donor star can give rise to magnetic and fluid instabilities, where the movement and interaction of the plasma lead to the formation of shear structures, such as the dynamical shear instability (Zahn 1992), and turbulence in the stellar plasma. These shear structures play a role in amplifying preexisting magnetic fields through stretching and deformation processes, thus creating a self-sustaining magnetic dynamo. Thus, the rotation plays a crucial role in stars as it introduces deviations from spherical symmetry due to the interaction between centrifugal forces and matter. It is well established that early-type stars often exhibit high average rotational velocities, which significantly decrease during the F-star stage, from around 150 km s−1 to less than 10 km s−1 according to Tassoul (2000).
Furthermore, if density gradients are present in the different layers, oscillations and disturbances in the fluid can occur, facilitating the amplification of magnetic fields. This instability is known as the Solberg–Hoiland (SH) instability. A phenomenon that can occur in systems like these with accretion disks, where there is a gradual difference in rotational velocity along a density gradient, is the secular shear instability. This instability arises from the presence of shear forces in the medium, resulting from the difference in rotational velocities between different regions. As material moves across the density gradient, a shearing effect can destabilize the system.
During the mass transfer from the donor star to its companion can trigger instabilities in the structure and give rise to events such as the SH instability (Wasiutynski 1946). This instability is related to the hydrostatic stability of the accreting star. Additionally, the mass transfer transfer process increases the pressure in the outer layers of the gainer star, but if this pressure increases too rapidly, it can exceed the gravity’s support capacity and lead to instability. This can result in violent stellar pulsations, where the star experiences periodic fluctuations in its luminosity and size. However, in rotating stars, and in the case of the donor star, the distribution of angular velocity can play an important role in convective stability. The SH instability occurs when the decrease in angular velocity toward the outer regions of the star is moderate according to the Rayleigh criterion, which states that the stability of a convective layer requires that the rate of change of angular velocity with distance be greater than a certain critical threshold. In this instability, stellar rotation creates a gradient of angular velocity within the star. If this gradient is sufficiently moderate according to the Rayleigh criterion –
where 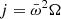 is the angular momentum, Ω corresponds to the angular velocity, and
is the angular momentum, Ω corresponds to the angular velocity, and 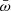 represents the distance from the rotational axis to the element fluid (Maeder 2009) – then it can generate convective instabilities within the star. This means that the gas layers inside the star can undergo unstable convective motions. Additionally, considering the mixing processes in the donor star, whose chemical composition varies with depth, semi-convection can influence the generation and evolution of magnetic fields by promoting the interaction between the plasma and magnetic fields through material mixing. Furthermore, it is important to consider the Goldreich-Schubert-Fricke (GSF) instability, which arises due to differential rotation in the stellar core. This instability generates gravity waves and disturbances in the fluid, favoring the generation and amplification of magnetic fields. Finally, the rapid rotation in stars, particularly the spin-up effect that occurs in the donor star during mass transfer, leads to flow parallelism with the magnetic field lines. This aspect also impacts the structure and transport of magnetic fields within the stellar interior.
represents the distance from the rotational axis to the element fluid (Maeder 2009) – then it can generate convective instabilities within the star. This means that the gas layers inside the star can undergo unstable convective motions. Additionally, considering the mixing processes in the donor star, whose chemical composition varies with depth, semi-convection can influence the generation and evolution of magnetic fields by promoting the interaction between the plasma and magnetic fields through material mixing. Furthermore, it is important to consider the Goldreich-Schubert-Fricke (GSF) instability, which arises due to differential rotation in the stellar core. This instability generates gravity waves and disturbances in the fluid, favoring the generation and amplification of magnetic fields. Finally, the rapid rotation in stars, particularly the spin-up effect that occurs in the donor star during mass transfer, leads to flow parallelism with the magnetic field lines. This aspect also impacts the structure and transport of magnetic fields within the stellar interior.
Stars have a complex internal structure with different layers and regions of varying temperatures and chemical compositions, where both can vary rapidly with depth. This means that heavier and colder material can be found above lighter and hotter material, which is unstable and leads to convective motions in the affected layer. However, in some stars, the convective layers can extend beyond the predicted theoretical limits. This is due to various factors, such as stellar rotation, chemical composition, or energy flow in the stellar core. As the convective layers extend beyond what is predicted, the phenomenon of overshooting occurs. It can affect the internal structure of a star, mixing material and changing the chemical composition in regions where it should not normally occur. It can also influence the duration and characteristics of certain evolutionary stages, such as the main sequence phase or the combustion phases of heavier elements in the stellar core. Thermohaline instability occurs in radiative zones due to the presence of the inverse molecular weight gradient, μ. The gradient of the molecular weight ∇μ = (dlnμ/dlnP) plays a crucial role along with the local gradient ∇ad − ∇. It represents the variation in the stellar chemical composition with respect to pressure and is induced by the reaction 3He + 3He → 4He + 21H occurring in the outer zone of the hydrogen burning layer (Vauclair 2008), converting two particles into three as predicted by Ulrich (1972). The medium can become dynamically unstable if
where 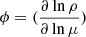 and
and 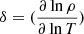 , known as the Ledoux criterion. It is a condition used to determine convective stability in the context of thermohaline instability, based on the comparison between the adiabatic gradient ∇ad and the temperature gradient ∇. On the other hand, when the process of mass and energy transport in the interior of the star occurs in regions where the composition gradient, ∇μ, exceeds the temperature gradient, ∇, convective motions are less efficient and the mixing of chemical substances is slower, as predicted by Schwarzschild (1906). This is referred to as semi-convection and is considered an intermediate phenomenon between complete convection and pure conduction:
, known as the Ledoux criterion. It is a condition used to determine convective stability in the context of thermohaline instability, based on the comparison between the adiabatic gradient ∇ad and the temperature gradient ∇. On the other hand, when the process of mass and energy transport in the interior of the star occurs in regions where the composition gradient, ∇μ, exceeds the temperature gradient, ∇, convective motions are less efficient and the mixing of chemical substances is slower, as predicted by Schwarzschild (1906). This is referred to as semi-convection and is considered an intermediate phenomenon between complete convection and pure conduction:
where ∇int ≈ ∇ad and ∇ ≈ ∇rad (Maeder 2009). In the inner layers where there are significant differences in temperature and chemical composition. These differences can be caused by the nuclear fusion process in the core of the star, and as the material heats up and becomes enriched with heavier elements in the core, a gradient of temperature and composition is established. Under these conditions, Eddington-Sweet circulation is initiated when the hotter and enriched material rises toward the outer layers of the star, while the colder and less enriched material descends toward the inner layers. This circulation pattern forms upward and downward currents that transport heat and material throughout the star (Baker & Kippenhahn 1959), which considers that a rotating star cannot be in thermal, hydrostatic, and radiative equilibrium at the same time. This is due to the differences between surfaces of constant temperature and constant pressure, leading to the development of large-scale circulations, and horizontal turbulence tends to rapidly smooth out non-homogeneities in the isobars. In the Eddington-Sweet circulation approach, the perpendicular component of the circulation velocity is primarily considered, as horizontal turbulence is responsible for smoothing out the inhomogeneities. The circulation process is approximated through diffusion along the radial coordinate.
When the material moving upward in a convective region is chemically denser than the surrounding material (i.e., it contains more atoms or molecules per unit volume compared to another material), its density increases even further as it rises. This can lead to instability and mixing of the material in the convective region, which is when the GSF instability (Goldreich & Schubert 1967; Fricke 1968) plays a fundamental role in the instability in rotating stars with profiles showing gradients along radial and vertical coordinates. It consists of two criteria, the first related to stabilization by the temperature gradient, which is eliminated due to thermal conduction. The second criterion is an analog to Taylor–Proudman (Kippenhahn 1974; Tassoul 1978). The criterion for the GSF instability condition in the limit of non-viscosity and non-stratification is governed by the following relationship:
where lr and lz are the radial and vertical length scales of the system. This tells us that if the vertical gradient of the turbulent flow is weak, instability is expected only for very short radial wavelength perturbations, for a clear understanding, we recommend taking a look at Figure 2, where a schematic illustration of the convection, semi-convection, thermohaline convection, and radiative stability regions is presented in terms of the Brunt-Väisälä frequencies 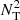 for the horizontal axis and Nμ for the vertical axis, respectively. In this context,
for the horizontal axis and Nμ for the vertical axis, respectively. In this context, 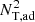 represents the variation in oscillation frequency due to gradients in potential temperature. The subscript “ad” indicates that this specification is commonly used in stellar interiors because convection is adiabatic. Meanwhile,
represents the variation in oscillation frequency due to gradients in potential temperature. The subscript “ad” indicates that this specification is commonly used in stellar interiors because convection is adiabatic. Meanwhile, 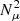 represents the variation in oscillation frequency due to gradients in the molar fraction μ in the stratified medium.
represents the variation in oscillation frequency due to gradients in the molar fraction μ in the stratified medium.
 |
Fig. 2. Schematic illustration of instability regions of Brunt-Väisälä frequency, convection, semi-convection, thermohaline convection, and radiative stability in the plane. We show the thermal and compositions terms |
2.4. The stellar dynamo
The physical mechanism responsible for the generation and maintenance of magnetic fields in stars plays a crucial role in many aspects of stellar physics, such as stability, chromospheric activity, and radiation emission. Differential rotation, convection, and other instabilities generate plasma currents and velocity gradients within the star. These processes lead to the generation of magnetic fields through the dynamo effect. MESA implemented a stellar dynamo proposed by Spruit (2002) called the Spruit-Tayler (ST) dynamo to explain the generated magnetic fields. The ST dynamo takes into account the angular velocity, Ω, the magnetic diffusivity, η, the Brunt-Väisäla frequency, N, the instability growth rate, ω, and the gradient q = ∂lnΩ/∂lnr, where q corresponds to the dimensionless differential rotation rate when the thermal diffusion can be neglected (q0) and when the thermal diffusion is considered (q1). The latter occurs when the stratification effects are dominated by the composition gradient. Here, the vertical displacement, lr, of the perturbed fluid has an upper limit:
Therefore, the displacement is restricted by its kinetic energy. This upper limit assumes that magnetic energy can be converted into vertical motion. However, the idea that movements perpendicular to the axis of rotation do not work against the rotational force is only valid near the axis of rotation. But this limit is determined by the length scale at which magnetic diffusion dissolves any new poloidal field faster than it is produced by instability, according to Pitts & Tayler (1985). Thus, the instability growth rate is as follows:
and
where ωA corresponds to the Alfvén frequency, ρ and r are the local densities and radius. This limit is most relevant for the processes considered in the ST dynamo. This model assumes that the rotational velocity is a function of the radial coordinate and that the initial magnetic field must be weak enough to neglect inertial magnetic forces, allowing the radial component Br to be affected by differential rotation. After a few rotations, this would become predominantly azimuthal, meaning Bϕ > Br, and it would increase linearly until it becomes unstable. Then, if the differential rotation is strong enough to create and sustain a dynamo process, the generated azimuthal field must be large enough to trigger the Tayler instability. However, thermal diffusion can influence the generation of magnetic fields due to its effect on the stability of the plasma and electric currents. The temperature distribution inside the stellar interior can affect the efficiency of magnetic field generation and its subsequent amplification through the dynamo process. When thermal diffusion occurs, temperature variations can induce density and pressure gradients in the plasma, which in turn can affect the flow of electric current and the dynamics of the magnetic field. These changes in the plasma structure can influence the efficiency of magnetic field generation and maintenance. This process can be affected by stratification, as temperature and density differences can influence the efficiency of heat transfer. In the presence of entropy stratification, heat transfer can be affected, resulting in variations in physical properties such as temperature and density. These variations can be caused by different physical processes, such as nuclear fusion in the stellar core, convection, and thermal diffusion; in other words, the stabilizing effect of stratification due to the entropy gradient is reduced by thermal diffusion, and instabilities can appear more easily. Irrespective of the strength of the azimuthal field, the condition formulated by Spruit is
the microscopic magnetic diffusivity, given by η = 7 × 1011lnΛT−3/2 cm2 s−1 (where lnΛ ≈ 5 − 10 is the Coulomb logarithm), is considered small compared to the thermal diffusivity κ = 16σT3/(3κRρ2cp), where cp is the specific heat at constant pressure. This implies that heat transfer is more dominant than magnetic diffusion in the dynamo process. However, the conditions necessary to validate the above equation are ωa ≪ N ≪ Ω and η ≪ κ, where N represents the buoyancy frequency, and r is the radial length scale (Spruit 2002). Nevertheless, the ST model establishes a minimum threshold of shear rate required to generate the critical magnetic field strengths that trigger Tayler instability. This parameter depends on the characteristics of the stellar system and the properties of the plasma, and its determination requires specific theoretical analyses and numerical simulations for each particular case. Therefore, its equations are as follows:
The parameters q0 and q1 are associated with the generation of magnetic fields and the Tayler instability. These parameters describe the behavior of the dynamo and the evolution of the magnetic field inside the star. In this context, q0 represents the minimum critical shear rate required to trigger the Tayler instability, assuming no thermal diffusion is considered. On the other hand, q1 represents the shear rate necessary to generate the critical magnetic field intensities that drive convective currents and the Tayler instability, taking into account thermal diffusion.
2.5. The fitting procedure
In this study, we present an evolutionary model developed using MESA for the DPV V4142 Sgr. This enhanced version of the model was based on the initial approach proposed by Rosales et al. (2019) for the DPV V495 Cen system. We implemented specific guidelines to ensure the appropriate handling of mass transfer from the donor star to its companion. Additionally, we imposed a limitation on the companion’s ability to accumulate mass at a high rate, as constrained by the Eddington accretion rate. This simulation has resulted in the formation of an accretion disk on the gainer star. This model for DPV considers binary interaction from the ZAMS with a nearly conservative mass transfer process, where the accretor or gainer star may lose a certain fraction of mass through winds until the depletion of 20% of 4He (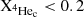 ) in the donor star. We used the physical and orbital parameters for this system published by Mennickent & Rosales (2014) and Mennickent et al. (2003) as a verification criterion. These parameters provide a solid foundation for our analysis and ensure the accuracy of our results. To achieve this, we carried out a series of simulations varying different parameters to understand their influence on the evolution of stars. We adjusted the masses of the donor star and the gainer star in a range from 2.50 ≤ Mi, dg ≤ 4.0 solar masses, with increments of 0.1 M⊙. Additionally, we explored the orbital period in a range from 2.0 ≤ Pi, o ≤ 20 days, using steps of 0.1 d to observe how the proximity between the stars affects their joint evolution. In addition, we investigated the value of the alpha mixing length 0.1 ≤ αml ≤ 2.0 with increments of 0.1, and the alpha semi-convection varying it from 0.01 to 1.0 with increments of a factor of 10 (0.01, 0.1, and 1.0), both in the donor and accreting companion stars (Langer et al. 1985). Likewise, we analyzed the value of the thermohaline parameter in a range from 0.1 ≤ Th ≤ 2.0 with increments of 0.1. Regarding the α and β mass fractions, we also took them into consideration. We varied the alpha mass fraction from 0.0005 ≤ α ≤ 0.5, with increments of 0.001, and explored the range of the β mass fraction from 0.0001 ≤ β ≤ 0.1 with a step of 0.0001. In this way, we were able to evaluate a wide range of parameters that allowed us to obtain a detailed overview of the evolution of the DPV V4142 Sgr. The system has a total mass of MT = 4.97 ± 0.5 M⊙, the current radius of the donor star is Rd = 19.4 ± 0.2 R⊙, while the accretor or gainer star has a radius of Rg = 6.35 ± 0.2 R⊙, and an orbital period of
) in the donor star. We used the physical and orbital parameters for this system published by Mennickent & Rosales (2014) and Mennickent et al. (2003) as a verification criterion. These parameters provide a solid foundation for our analysis and ensure the accuracy of our results. To achieve this, we carried out a series of simulations varying different parameters to understand their influence on the evolution of stars. We adjusted the masses of the donor star and the gainer star in a range from 2.50 ≤ Mi, dg ≤ 4.0 solar masses, with increments of 0.1 M⊙. Additionally, we explored the orbital period in a range from 2.0 ≤ Pi, o ≤ 20 days, using steps of 0.1 d to observe how the proximity between the stars affects their joint evolution. In addition, we investigated the value of the alpha mixing length 0.1 ≤ αml ≤ 2.0 with increments of 0.1, and the alpha semi-convection varying it from 0.01 to 1.0 with increments of a factor of 10 (0.01, 0.1, and 1.0), both in the donor and accreting companion stars (Langer et al. 1985). Likewise, we analyzed the value of the thermohaline parameter in a range from 0.1 ≤ Th ≤ 2.0 with increments of 0.1. Regarding the α and β mass fractions, we also took them into consideration. We varied the alpha mass fraction from 0.0005 ≤ α ≤ 0.5, with increments of 0.001, and explored the range of the β mass fraction from 0.0001 ≤ β ≤ 0.1 with a step of 0.0001. In this way, we were able to evaluate a wide range of parameters that allowed us to obtain a detailed overview of the evolution of the DPV V4142 Sgr. The system has a total mass of MT = 4.97 ± 0.5 M⊙, the current radius of the donor star is Rd = 19.4 ± 0.2 R⊙, while the accretor or gainer star has a radius of Rg = 6.35 ± 0.2 R⊙, and an orbital period of 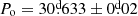 . The orbital velocity of the donor is Vo, d = 89.2 ± 0.5 (km s−1), and of the gainer is Vo,g = 25.56 ± 1.20 (km s−1). The initial parameters used to run the model include an initial metallicity of Z = 0.02.
. The orbital velocity of the donor is Vo, d = 89.2 ± 0.5 (km s−1), and of the gainer is Vo,g = 25.56 ± 1.20 (km s−1). The initial parameters used to run the model include an initial metallicity of Z = 0.02.
To generate the dynamo within the donor star, we incorporated a surface rotation velocity Vrot.,sup. = 26 km s−1. Additionally, in order to control the rate at which angular momentum is transported within the star, we set the angular diffusion coefficient to DL = 0.1, the diffusion coefficient for material mixing to Dm = 0.01, and included the dynamical shear instability with DSI = 0.1. We turned off the SH instability parameter DSH = 0.0, which occurs when a differentially rotating fluid experiences a perturbation that induces variations in fluid density and pressure. This instability is more relevant in the accretion disk around the gainer star. Since the system is synchronized, tidal effects, changes in orbital period, and changes in the mass transfer rate require the inclusion of the Secular Shear Instability, which was set to DSSI = 0.1. For the role of angular momentum redistribution and heat transport, it was also necessary to set the value for Eddington-Sweet circulation to DES = 0.0. Now, to generate the interaction between the convection flow and the magnetic field within the star, we set the GSF parameter to DGSF = 0.1. Finally, we incorporated the ST magnetic dynamo model with a value of DST = 0.1, which is not very high as we are interested in understanding this dynamo generation and its effect on photometric variability, considering that the spectral type of the donor star is of K spectral type. We used a more recent version of the MESA code unlike the first model presented for the DPV V495 Cen, proposed by Rosales et al. (2019), where the de Jager cold wind scheme was employed, to the Reimers cold wind scheme for low to intermediate mass stars after the main sequence but before entering the AGB phase. In addition, it has been set with a scale factor wc, R = 1.0, where the subscript c corresponds to cold winds and R represents the Reimers scheme. During the depletion of nuclear fuel and the entry into the AGB stage, we considered the Blocker cold wind scheme with a fixed scale factor, wc, B = 1.0, where the subscript B stands for the Blocker scheme. However, for the hot winds that occur during the transition from the RGB phase to the AGB, we considered the Dutch scheme with a scale factor wh, D = 1 × 10−4 and its subscript D represents the scheme Dutch. These schemes provide a simplified way to estimate the mass loss rate and explain the evolutionary process that stars undergo.
Furthermore, we have identified areas in the evolutionary tracks that exhibit minimal and practically negligible deviations compared to other reference models. Although the change is not significant, as it involves only a very low-scale mass loss due to the wind, we consider it necessary to make adjustments and highlight it. These areas are identified and span from the depletion of central hydrogen in the donor star to shortly after the star increases the size of its RL but before the onset of mass transfer. However, we have observed inconsistencies in the trajectory when the donor star reaches its minimum RL. Here, we note that the de Jager scheme shows alterations during the evolution of the trajectory and is not continuous or smooth. These findings led us to assume that the deviations are minimal and negligible, especially considering the more significant uncertainties in other parameters. An important conclusion from these calculations is that the models do not appear to be very sensitive to the choice between the de Jager or Reimers formalisms (see Fig. 3).
 |
Fig. 3. Comparison of two wind schemes used to model the wind phenomenon in the RGB scheme. The evolutionary track of the donor star in blue corresponds to the de Jager formalism; its companion gainer is represented by the black line. In red, it represents the Reimers formalism, with its companion represented by the green line. Areas with differences between formalisms are labeled z1, z2, and z3. |
To ensure the convergence of results using the model for V4142 Sgr, we implemented a chi-square optimization algorithm, which involves minimizing the deviation between theoretical and observed values. The algorithm was developed by varying the mass, radius, orbital period (see Fig. 4), mixing length parameter, αml, and thermohaline parameter, Th, for both stars. The model exhibits significant consistency with the current observed values of the system, suggesting a mass for the donor star of Mf, d = 1.05 M⊙, which falls within our range of Md = 1.11 ± 0.20 M⊙, and a radius of Rf, d = 19.20 R⊙ compared to the observed value of Rd = 19.4 ± 0.2 R⊙. Here, the subscript “f” corresponds to the initial of “final” word. As for the gainer star, an estimated mass of Mf, g = 3.93 M⊙ is obtained, while the observed value is Mg = 3.86 ± 0.3 M⊙, and a calculated radius of Rf, g = 6.39 R⊙, which fits within the expected range for a star with a radius of Rg = 6.35 ± 0.20 R⊙. Additionally, the final orbital period of the system is 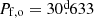 compared to the observed value of
compared to the observed value of 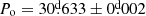 , presenting a difference of ΔPo = 0.005 d with an age system of Age = 280.1676 Myr. This discrepancy is entirely expected in a numerical modeling of such complexity (see Table 1). Thus, the implementation of the method successfully converged with these initial parameters, yielding a chi-square value of χ20.95, 6 = 0.007 (see Fig. 5).
, presenting a difference of ΔPo = 0.005 d with an age system of Age = 280.1676 Myr. This discrepancy is entirely expected in a numerical modeling of such complexity (see Table 1). Thus, the implementation of the method successfully converged with these initial parameters, yielding a chi-square value of χ20.95, 6 = 0.007 (see Fig. 5).
 |
Fig. 4. Evolution of orbital and stellar parameters of V4142 Sgr. Left: schematic behavior of radius and mass for both stars. While the two stars evolve separately, the donor star (black line) expands to fill the RL, and the initial radius of the gainer star (dashed red line) increases and later decreases during the rejuvenation. Center: evolution of the orbital period as a function of the mass of the primary star (donor) for V4142 Sgr. Right: theoretical orbital velocity curve for both components as a function of their masses. The orbital velocity of the primary component (black line) increases during the mass-loss process, known as spin-up, and later decreases, reaching the current value. The RV of the companion (i.e., gainer) star (dashed red line) decreases, and its mass increases. |
 |
Fig. 5. Best model for V4142 Sgr with 16 freedom degrees and all optimized parameter values for both stars, with a Δχ20.95, 6 = 0.007. |
Evolutionary stages of DPV V4142 Sgr.
3. The evolution of V4142 Sgr
The formation of DPV V4142 Sgr began approximately 280.1676 million years ago. During the main sequence stage, the donor star and the gainer begin to fuse hydrogen through nuclear reactions, generating a tremendous amount of energy that increases the temperature and luminosity of the donor star (A stage; see Fig. 6). As the donor star starts to age, it evolves off the main sequence (B stage) into a stage known as the terminal age main sequence (TAMS), which takes only 0.89 million years. Subsequently, the central hydrogen of the donor star depletes, leading to a material supply or material ratio inversion (see Fig. 7) of 1H/4He after 137.11 million years (X1 stage). This process is relatively slow but crucial during the evolution. However, the gainer star does not undergo significant changes in its core’s central supply (a stage) during this time. Throughout the hydrogen depletion stage, the star expands and increases its temperature, resulting in it becoming larger and brighter (C stage). However, due to this depletion, the star begins to exceed the RL limits; its temperature increases by 0.06 dex, and it experiences a slight increase in luminosity of 0.08 dex (D stage). Up to this point, its companion, the gainer, remains relatively unchanged, staying on the main sequence in the same location for the first 279.725 million years. However, at this moment, the donor star tends to restore equilibrium, and as it cools down, mass transfer starts toward its companion (E stage). During this brief time span of only 0.33 million years, the gainer star ascends the main sequence while slowly depleting its central hydrogen (b stage) and eventually evolves off the sequence as it begins to accrete material from its donor companion. When mass transfer begins (E stage) from the donor star to its companion, the luminosity of this star starts to decrease by about 0.8 dex. At this moment, the system is in its shortest orbital period, 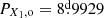 . The central hydrogen is depleted while the 4Hec concentration reaches its maximum and will subsequently drop rapidly in a very short period of time (see Fig. 8). Simultaneously, the well-known mass inversion (U1 stage) occurs, causing the donor star to become the less massive one and age much faster, while having the opposite effect on its companion, which rejuvenates with all the hydrogen it has received (c stage). As the mass transfer reaches its peak values, the donor star reaches its minimum luminosity (F stage), resulting in a slight decrease of 0.06 dex. It initiates with logL/L⊙ = 2.179 and drops to a minimum of logL/L⊙ = 1.610. At the same time as the mass transfer begins, the donor star’s volume decreases, and its radius decreases by 40%, thus reaching the minimum RL.
. The central hydrogen is depleted while the 4Hec concentration reaches its maximum and will subsequently drop rapidly in a very short period of time (see Fig. 8). Simultaneously, the well-known mass inversion (U1 stage) occurs, causing the donor star to become the less massive one and age much faster, while having the opposite effect on its companion, which rejuvenates with all the hydrogen it has received (c stage). As the mass transfer reaches its peak values, the donor star reaches its minimum luminosity (F stage), resulting in a slight decrease of 0.06 dex. It initiates with logL/L⊙ = 2.179 and drops to a minimum of logL/L⊙ = 1.610. At the same time as the mass transfer begins, the donor star’s volume decreases, and its radius decreases by 40%, thus reaching the minimum RL.
 |
Fig. 6. Evolutionary track of the DPV V4142 Sgr with a secondary star (black line) of initial mass Mi, d = 3.50 M⊙ and its companion (red line) of Mi, g = 1.50 M⊙. The dashed blue line represents the evolutionary track of a single star, identical to the initial mass of the gainer star, using the same initial parameters that were used to model the gainer, until central helium depletion (XHec < 0.2). The green line represents the evolutionary track for a single star, using the same donor initial parameters. The most important points during the evolution are labeled together with the initial and final theoretical masses. The blue zone represents the threshold of rejuvenated B-type stars. The uppercase black letters mark each stage of the donor star, while the lowercase red letters represent the stages of the gainer star (see Table 1). |
 |
Fig. 7. Central abundance of 1H and 4He for V4142 Sgr. The mass-fraction inversion (X1 stage) of the donor star (black line) is shown before the mass transfer (E stage) and mass inversion (U1 stage). The gainer star evolves over a more extended timescale, during which it fails to achieve the mass-fraction inversion, and its 1H increases slightly, by 0.04 M⊙, during the accretion phase (E stage), allowing it to rejuvenate before the mass transfer concludes (H stage), as indicated by the green arrow. |
 |
Fig. 8. Hertzsprung-Russell diagrams of the binary evolution. The color bar shows the central hydrogen and helium mass fraction for both components until the hydrogen depletion, 1H. This shows that the gainer star rejuvenates before losing most of its size slowly over its lifetime, whereas the donor star suffers a rapid exhaustion of helium during the mass transfer phase. |
In the context of mass transfer, it is observed that once this process (E stage) begins, approximately 280.055 million years (Myr) pass before the donor star experiences a first minimum in the mass transfer rate, reaching approximately a rate of 2 × 10−5 M⊙ yr−1. At this point, the transfer tends to decrease for a brief period until it reaches a rate of 1.775 × 10−5 M⊙ yr−1, and then resumes before mass inversion occurs. During this process, the maximum mass transfer rate is achieved when the donor star reaches its minimum RL value (F stage). At this point, the orbital velocity of the donor star is within its maximum possible values (see Fig. 4), and the donor star enters the final stage of optically thick mass transfer (G stage; see Fig. 9).
 |
Fig. 9. Theoretical variation in the mass transfer and Ṁd curve of the donor star. Left: theoretical variation in mass transfer until helium depletion is reached for initial masses Mi, d = 3.50 M⊙ and Mi, g = 1.50 M⊙, for an initial orbital period |
In the realm of binary interaction and conservative processes, a distinction can be made between modes 1, 2, and 3, also known as cases A, B, and C. As widely acknowledged, these modes are governed by specific timescales. The nuclear corresponds to Case A, the thermal to Case B, and the hydrodynamic to Case C (Eggleton 2006). For these processes to occur, certain fundamental conditions related to the rate at which the RL radius responds to the mass of the star within the lobe, Md, must be satisfied:
Here 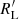 denotes the rate at which the RL radius responds to the mass Md of the star within the lobe, defined as a logarithmic derivative. The subscript TD refers to the same rate under thermal disequilibrium. The condition is that the response rate under thermal equilibrium (TE) is less than the rate of change in the RL and this is less than the rate under thermal disequilibrium (TD). the rate of response in thermal disequilibrium must be less than the rate of response of the RL. These conditions establish critical limits governing the dynamics of binary stars in each mode, providing a clear conceptual framework for understanding the evolution of these systems. Therefore, we evaluated our system and determined to which mode it currently corresponds using the following equations (Eggleton 2006; Woods et al. 2012):
denotes the rate at which the RL radius responds to the mass Md of the star within the lobe, defined as a logarithmic derivative. The subscript TD refers to the same rate under thermal disequilibrium. The condition is that the response rate under thermal equilibrium (TE) is less than the rate of change in the RL and this is less than the rate under thermal disequilibrium (TD). the rate of response in thermal disequilibrium must be less than the rate of response of the RL. These conditions establish critical limits governing the dynamics of binary stars in each mode, providing a clear conceptual framework for understanding the evolution of these systems. Therefore, we evaluated our system and determined to which mode it currently corresponds using the following equations (Eggleton 2006; Woods et al. 2012):
Leveraging the spectroscopic results of Rosales et al. (2023) and the modeling values for the current stage of the system, we replaced parameters in Eqs. (21), (22), and (23). This indicated that the radius of the donor star during the transfer fulfilled the condition RTE < RL < RTD (Case B). Subsequently, an analysis of the donor star’s temperature throughout its evolution showed that, after crossing the Hertzsprung gap at the beginning of the blue loop (C stage; Fig. 6), the evolutionary process can only be dominated by a thermal timescale. The model developed with MESA, by achieving the best fit, suggests that the system is in Case B, providing two independent confirmations (see Fig. 10). Therefore, once the system exits the blue loop (D stage), it is dominated by a thermal timescale, in a Case B mass transfer.
 |
Fig. 10. Evolution of the donor star size and effective temperature in V4142 Sgr. Left: evolution of the donor star size with an initial mass of 3.5 M⊙ in the binary system DPV V4142 Sgr, with a companion that has an initial mass of 1.5 M⊙. We show the phases in which cases A, B, and C of RLOF can occur, depending on the age of the system. The inversion of the 1H/4He ratio (X1 stage) is represented by a brown dot, the mass transfer (E stage) by a blue dot, and the current stage of the system (X2 stage) by a red dot. Right: effective temperature, Teff, as a function of age (in years) for V4142 Sgr. We shown that the donor star, after crossing the Hertzsprung gap during the onset of the blue loop (stages C and D), follows an evolutionary track until reaching its current stage (X2 stage) on a thermal timescale. This continues until it reaches the final stage of non-optically thick mass transfer (H stage), stopping shortly before helium depletion. |
Impact and disk systems can be analyzed on a fractional radius diagram (the radius relative to the orbital separation) and the mass ratio. We observe that the fractional radius of the accreting star, Rg/aorb. = 0.091, along with the mass ratio q = 0.266, places V4142 Sgr in the stream circularization region. This implies that if mass transfer occurs due to RL overflow, the gas stream would efficiently surround the receiving star. On the other hand, the disk of V4142 Sgr has a fractional radius of Rdisk/aorb. = 0.325 ± 0.004 (Rosales et al. 2023) and is located in the material circularization region, forming an accretion disk around the receiving star (see Fig. 11). In the case of the gainer star during this stage, the mass of the convective core (Mcc) tends to increase by 0.25 M⊙, but the density of the star has decreased from 0.178 (g cm−3), and the rate of change of angular momentum indicates that the gaining star’s angular momentum has decreased over time by more than 1.45E38 (g cm2 s−1), in contrast to previous moments before mass transfer when the variation was positive, increasing by more than 0.7 (g cm2 s−1) (see Fig. 12). Returning to the context of its decrease, this could be due to stellar winds or other mechanisms of angular momentum loss, such as torque on the accretion disk and tidal forces, which would explain the persistent V < R relationship in the Hα profile observed in V495 Cen and V4142 Sgr by Rosales Guzmán et al. (2018), Rosales et al. (2023). This relationship is defined as the ratio between the relative intensity peaks and the normalized continuum, V/R = (Iv − 1)/(Ir − 1).
 |
Fig. 11. Fractional radius, relative to the orbital separation, for primaries in Algols with and without disks. Red dots represents to the DPV stars. Below the circularization radius (shown by the solid bottom line), a disk should be formed, and below the top line, a disk might be formed. Semidetached Algol primaries from Dervişoǧlu et al. (2010) are also shown, as gray points. This figure is adapted from Mennickent et al. (2016a). |
 |
Fig. 12. Rate of change of the angular momentum of the gainer star versus the central density logarithm. Most important stages are labeled. |
After traversing the stage of the minimum RL value, a mere 24 100 years later, optically thick mass transfer comes to a halt. Nevertheless, the transfer process persists. At this juncture, the orbital period begins to increase, accompanied by an expansion in the radius of the donor star, as well as a simultaneous rise in luminosity and temperature. Meanwhile, the gainer star embarks on its return to the main sequence and initiates a process of rejuvenation (d stage), characterized by a reduction in radius and a progressive accretion of mass. For the first time, we have identified a zone where accreting B-type stars are located in well-studied systems, such as AU Mon, DQ Velorum, HD 170582, HD 50526, V495 Cen, and V4142 Sgr, following mass transfer and hydrogen capture from their donor companions. We refer to this region as the rejuvenation zone of the winning stars. In the case of V4142 Sgr, this rejuvenation begins at 280.090 million years during hydrogen rejuvenation 1H (stage c), as shown in Fig. 6 and Table 1. Here, their size significantly decreases, and they are rejuvenated by all the accreted material from their donor companions. Simultaneously, the mass of the convective core increases by 82%. We observed that the central abundance of hydrogen in the gainer star is 1Hi = 0.671, while at the end of the accretion process, at 280.9710 Myr, this fraction slightly increases to 1Hi = 0.682. This goes against the notion of aging in an accreting star. In comparison, a single star with the same initial mass has a hydrogen abundance of 1Hi = 0.699. However, when considering a single star with the same age as the gainer star, within the category of rejuvenated stars, the comparison of hydrogen abundances is no longer similar, meaning the single star has already consumed a significantly high portion of its hydrogen. This suggests that during the accretion process, the receiving star was able to retain part of its previous chemical composition Fig. 7. As for its radius, we note that the initial radius was Ri = 1.49 R⊙, reaching a maximum of Rmax = 19.28 R⊙ before returning to a final size of Rf = 6.39 R⊙. This aligns with the idea that the star would not retain memory of its less massive past (Braun & Langer 1995).
The donor star, on the other hand, has aged significantly due to the mass transfer process. Subsequent to the current evolutionary stage of V4142 Sgr, the donor star’s mass transfer reaches its culmination (H stage). During this phase, the companion star rapidly crosses the threshold of rejuvenation and relocates within the main sequence, assuming a higher mass compared to its initial value. The accretion disk dutifully contributes a portion of its mass to the accreting star, prompting it to evolve as a single star of greater mass, Mg = 4.27 M⊙ (f and g stages), as opposed to its initial 1.5 M⊙. This remarkably swift process, spanning from the current stage to the cessation of mass transfer and the gainer star’s crossing of the rejuvenation threshold, within a mere 0.8 Myr. In contrast, while the donor progresses toward the depletion of its central helium (4He) and reaches the 20% threshold, it will take an additional 25 Myr (I stage).
4. The long cycle
The nature of the second photometric variation cycle is currently unknown. These photometric variations, dubbed “long period” (Pl), are closely linked to the orbital period, with the long period being approximately 33 times longer than the orbital period (Po; Mennickent et al. 2003, 2016b; Poleski et al. 2010; Mennickent 2017) and Pl = 30.82 ± 1.33 (Rosales et al. 2023). However, Schleicher & Mennickent (2017) proposed an explanation for the long cycles of DPVs based on magnetic cycles of the more evolved star. They suggest that the Applegate mechanism should induce cyclic changes in the equatorial radius of the donor and, consequently, in the mass transfer rate (Applegate & Patterson 1987):
The model successfully replicates the observed physical parameters for V4142 Sgr. To predict the long period, which critically depends on the convective velocity of the donor star (νc), we have chosen to employ Eq. (15) from Schleicher & Mennickent (2017). This decision is based on the potential variability of the zone size, which could impact our estimation of various parameters. Since MESA already provides the convective velocity value, this equation proves to be more useful and straightforward in this context.
To achieve this, we selected the maximum value of convective velocity as a function of the star’s radius, assuming that this maximum value would activate the dynamo. Additionally, we used the current values of mass (M) and radius (R) of the donor star at each analyzed stage. This allowed us to obtain the Rossby number and Dynamo value. Finally, to estimate the power-law index (alpha), we fixed the ratio between the long and orbital periods at 39.367 and calculated the value of alpha (α) to satisfy this fixed ratio. Moreover, we ensured that the calculated value met the condition specified by Schleicher & Mennickent (2017), where alpha varies between 1/3 and 5/6.
By applying the dynamo equation, we successfully calculated a dynamo number for the current stage of V4142 Sgr, obtaining a value of D = 293.9296 (dimensionless). With a power-law index α = 0.6462 (dimensionless), the relationship between the long period and the orbital period (Pl/Po = 39.369 ± 0.326, d) of this system remains valid. Consequently, we successfully reproduced the existence of this second period in our findings. Additionally, we have successfully identified the regions where the long period is found, ranging from the minimum RL (F stage) to the current stage of this system (X2 stage). Nevertheless, we do not yet understand if this phenomenon can be influenced by mass transfer (E stage) or activated through mass inversion (U1 stage). Therefore, through our model, we confirm the possible presence of a dynamo in the donor star (see Table 2).
Conditions for long period occurrence in DPV V4142 Sgr.
The basic concept behind the alpha mixing model was to consider stellar convection as one of the key factors in rejuvenating the accreting star. This refers to the transport of energy due to the upward movement of hot material and the downward movement of cold material within a star. The mixing length, denoted as αml, represents the average distance that a parcel of hot or cold gas travels before mixing with its surrounding environment. In other words, it measures the extent to which different materials mix due to convection. We independently modified this value regardless of the specific physical conditions inside the star. Furthermore, we employed a mixing length theory scheme by Henyey et al. (1965). Typically, a value of αml between 1 and 2 is assumed for Sun-like stars (Canuto 1990). In this case, we assumed values between 0.6 ≤ αml ≤ 1.9 for both stars simultaneously, while the remaining parameters were held constant. We were able to identify regions where this parameter played a fundamental role in the gainer star. It can be observed that for lower values of αml, the gainer star remains attached to the main sequence for a longer period compared to higher values of the same parameter (see Fig. 13). The rejuvenation process is much more abrupt for these higher values, indicating that for high αml values, the rejuvenation process is transient until it reaches a threshold where other accreting B-type stars rejuvenated by transfer from their companion are located. For the donor star, the values demonstrate that mass transfer is significantly prolonged until it reaches the minimum RL limit. This decline is notably steeper compared to other periods of mass transfer. Additionally, we did not notice any significant effect or change in the stellar dynamo, leading us to dismiss the possibility of this parameter having an influence on its production. With the same model, we analyzed how the alpha mixing length (αml) and alpha semi-convection (αsc) parameters behave in a system modeled by van Rensbergen et al. (2008) with initial masses M1 = 15.0 M⊙, M2 = 13.50 M⊙, and an initial orbital period Po, i = 5.0 d. For this case, we observed that in massive stars, the parameter αml has no influence on the evolutionary track of the massive stars. This is considered a relevant aspect to emphasize when working with intermediate masses (Fig. 14).
 |
Fig. 13. Schematic behavior of the αml and thermohaline parameters for V4142 Sgr. Left: schematic behavior of the mixed length parameter (αml) for different values. This parameter regulates the so-called rejuvenation process in the gainer star. Although it has no influence on the evolution of the mass transfer, stellar masses, or binary period, it significantly affects the evolutionary path of the secondary star during mass transfer until the end of optically thick mass transfer, aging it for lower values of αml (opposite to the behavior of the gainer star). Right: schematic behavior for different values of the thermohaline parameter, where no significant changes are observed during the evolution of both stars. |
 |
Fig. 14. Schematic representation of the alpha mixing length parameter (αml) for various values in a massive binary system with a total mass of 28.5 M⊙. |
Later, we fixed the parameter αml at 1.0 and started varying the thermohaline coefficient in the range 1.5 ≤ Thl ≤ 2.5, using a Kippenhahn scheme (Kippenhahn et al. 1980). In this case, we did not detect significant changes in the evolutionary path of the DPV V4142 Sgr for the donor or the gainer star. Therefore, in our model, this parameter does not have a major influence on the evolution of binary systems. However, we noticed that the system’s evolution is much faster with a higher alpha mixing length parameter, completing the evolutionary process in much less time. This can be useful for adjusting the rate at which both stars, either together or individually, evolve and and thus achieve a higher accuracy of the models. In the case of αml = 0.6, the donor star reaches the minimum RL in approximately 280.085 Myr, while for αml = 1.9, this process takes around 274.438 Myr. The difference between both scenarios is approximately 5.647 Myr.
5. Stellar dynamo in the donor star
The stellar dynamo is a physical process that should occur within the donor star, generating magnetic fields through the action of movement and rotation of ionized gases in its core. These magnetic fields can play a crucial role in the stellar activity of the donor star through mass transfer onto the accretion disk and its companion. When the star rotates, the plasma within it can move at different speeds in different layers. This velocity difference creates a shear effect. In the presence of shear, magnetic instabilities can arise and amplify the existing magnetic fields, generating a dynamo. According to Spruit (2002), the generation of magnetic fields through differential rotation has been considered as a process operating in the convective zone. However, magnetic fields can also be generated in stratified layers in the presence of differential rotation. This means that convection is not necessarily the primary factor for the dynamo’s operation if we are in the presence of a toroidal magnetic field, which could replace the role that convection plays as an instability mechanism. Therefore, differential rotation is an azimuthal amplification mechanism that stretches field lines and forms a toroidal field (Spruit 2002).
From the ZAMS to the point of inversion of the 1H/4He ratio, we have observed that the Eulerian diffusion coefficient for mixing (cm2 s−1; see Fig. 15) near the core is much more intense in the convective zone of the star between 0 < Md (M⊙) < 0.65, which shows a slight decrease in the overshooting zone until Md = 0.98 M⊙. However, this diffusion coefficient stops outside of this zone, and elements that exhibit higher diffusivity will be transported by advection, causing the diffusion coefficient to gradually increase until it reaches almost the original values in the outermost layer of the star starting from Md = 1.0 M⊙ onward, during the first 138 Myr. However, it is noteworthy that after exiting the overshooting zone, this coefficient undergoes a sharp decrease, then increases, and ultimately becomes, on average, 4 times lower than that observed near the core; when it reaches the surface, it is 2.6 times lower compared to in the core. It is possible that this event called advection has been able to mechanically capture a retention of electric charges and force the flow of currents, leading to the generation of a seed magnetic field as proposed by Biermann (1950) and the presence of magnetic fields outside the convective mixing and overshooting zones.
 |
Fig. 15. Profiles of the poloidal magnetic field, Br, and the toroidal magnetic field, Bϕ, generated by the ST dynamo in the donor star at different evolutive stages. The profiles represents the stages of inversion of the 1H/4He ratio (X1 stage), the initiation of mass transfer (E stage), the mass inversion (U1 stage), and the current stage (X2 stage). The Eulerian diffusion coefficient for mixing is shown in orange, the ST diffusion coefficient as a brown line, the poloidal magnetic field in black, the toroidal magnetic field in green, the angular momentum in blue, and the angular velocity in red. |
Additionally, the presence of the toroidal magnetic field, Bϕ, appears in the overshooting zone shortly after the decay of the diffusion coefficient “D,” becoming predominant once outside of this overshooting zone. Following this, the radial magnetic field Br appears immediately with significantly lower values than the toroidal field, possibly caused by the same differential rotation. It is also possible that the convective transport process has affected the distribution and intensity of this field, including interaction to a lesser extent with its companion (gainer), altering the distribution and intensity of this field as well.
The mixing diffusivity associated with the generation of the magnetic field through the ST dynamo (DST) describes the efficiency with which turbulence and convective currents mix, including the transport and distribution of the magnetic field, as well as the generation and amplification of the magnetic field itself. Within the convective and overshooting zone, this efficiency is zero and appears immediately when the diffusion coefficient starts to be activated due to advection outside the overshooting zone (Md = 1 M⊙), surpassing it and leading to the diffusion coefficient D. However, the creation and amplification of these magnetic fields suggest that there is a connection or indirect influence between the mixing diffusivity DST and the generation of the magnetic fields in that region, as this and the toroidal field seem to be generated in the outermost parts of the overshooting zone. Once mass transfer (E stage) begins, we observe that the mixing diffusivity associated with the ST dynamo (DST) describes the behavior of the Eulerian diffusion coefficient and the poloidal magnetic field. Both occur in the convective zone, extending from the core center to the first 0.5 M⊙, where the overshooting zone becomes diffuse and challenging to identify. Additionally, we note that the magnetic fields during this process are stronger near the core and decay as they approach the stellar surface. This pattern remains nearly unchanged until the mass inversion (U1 stage). However, the toroidal magnetic field appears to maintain an indirect connection with this mixing diffusivity DST and continues to dominate over the poloidal field.
In the current stage (X2 stage) of the V4142 Sgr system, the model suggests the presence of a dominant toroidal magnetic field, which is nearly twice as strong as the poloidal field within the convective region of the star. However, the mixing diffusivity coefficients DST no longer describe the behavior of these fields, suggesting that they have been activated, linked from the convective zones of the donor star to its surface (see Table 3).
ST dynamo parameters in DPV V4142 Sgr.
The relationship between the Brunt-Väisälä frequency and entropy tells us that there are regions where entropy decreases toward the exterior due to a decrease in convection. Both radiative transport and convection evacuate any excess entropy that may exist within a star. We know that the following gradients; ∇ext, which represents the external gradient, ∇int, corresponding to the internal gradient in a fluid element, and ∇ad, which represents the internal gradient of a moving cell without temperature exchange with the surroundings, are positive quantities that vary with temperature (T) and pressure (P), since both parameters increase simultaneously within the star. With this, we can understand that the adiabatic gradient ∇ad is flatter than the internal gradient ∇int because the temperature in an upward-moving cell decreases more rapidly due to heat loss. In a convective zone, the relationship between the gradients is as follows: ∇rad > ∇ext > ∇int > ∇ad, where we see the relationship that the radiative gradient maintains with the other three temperature gradients. The second gradient refers to the stability criterion for convection, while the last relationship indicates that the adiabatic gradient is flatter. However, convection in the stellar interior tells us that adiabatic convection inside the star implies that the temperature gradient is equal to the adiabatic gradient (i.e., ∇int = ∇ad), which in turn tells us that ∇rad > ∇ad, known as the Schwarzschild criterion, which is similar to the Ledoux criterion for convective instabilities.
In the context of convection, we analyze the internal structure of both the donor and the gainer stars using Kippenhahn diagrams. For the case of the donor, which starts from the ZAMS until helium depletion XHe, c < 0.2, we were able to identify that the convective zone of the donor star is below 0.75 M⊙ (see Fig. 16), and all nuclear production occurs below 2 M⊙, with only 50% of this production taking place below 1 M⊙, far from the surface, which reaches 3.5 M⊙. Additionally, both convection and nuclear production gradually decrease as the system evolves and approaches mass transfer (E stage). Furthermore, we have identified a zone of thermohaline instability activation after previous mass transfer and post inversion of the 1H/4He ratio toward the central 1H exhaustion transition (D stage) from overshooting zone until the upper limit of star, which reappears once the star increases the size of the RL due to the exhaustion of 1H, intermittently appearing at different stages of evolution after the mass transfer stage. In addition, the overshooting zone coexists from 0.75 to 1.2 M⊙ and decreases over time before disappearing once mass transfer has begun. Another interesting structural change in the donor star is that the helium abundance concentrated mostly between 0.2 and 0.7 M⊙ after mass transfer. However, before the mass transfer stage, the mass of the central helium was 0.6 M⊙, leaving a star predominantly composed of helium exposed up to its upper limits. After mass transfer, the nuclear production rate εnuc is generated in two regions of the star, one near the surface (0.65–0.7 M⊙) and the other in the innermost core (≤0.05 M⊙). Additionally, we have noticed that the convective core of the donor has decreased by almost 74% from 0.75 M⊙ to 0.2 M⊙, and a small semi-convection layer appears immediately after the end of mass transfer (U2) post convective zone.
 |
Fig. 16. Kippenhahn diagrams showing the internal structure of the donor star, accompanied by a zoomed-in view with some principal events labeled. The donor star has an initial mass of Mi, d = 3.50 M⊙. The evolution stops when the donor star reaches core helium depletion, XHe, c < 0.2. The x-axis gives the age after ignition of hydrogen in units of Myr. The different layers are characterized by their values of M/M⊙. Shown are the convection mixing (hatched green), semi-convection mixing (red), overshooting mixing (crosshatched purple), the He core mass (red dot), thermohaline mixing (hatched yellow), and the surface of the star (solid black line). |
In the case of the gainer star (see Fig. 17), its interior seems to remain much more stable than expected. For the gainer star case, we identified a convective zone from its center to 0.18 M⊙, with a relatively low nuclear production rate that remains largely unchanged for most of its lifetime from the ZAMS to moments prior to mass transfer (E stage). In addition, we identified an overshooting zone from 0.18 to 0.38 M⊙ relatively constant during all evolution track previous to the mass transfer stage. However, after mass transfer, its convective core immediately grew by 82%, reaching a mass of 1.0 M⊙. Following this, a overshooting zone appears 1.0 M⊙ to 1.5 M⊙. Additionally, the nuclear production rate εnuc increased significantly, occurring within a central mass of 0.75 M⊙ before mass transfer and distributing within a central mass of 1.5 M⊙.
 |
Fig. 17. Kippenhahn diagrams showing the internal structure of the gainer star with an initial mass of Mi, g = 1.50 M⊙. The evolution stops when the donor star reaches core helium depletion, XHe, c < 0.2. The x-axis gives the age after ignition of hydrogen in units of Myr. The different layers are characterized by their M/M⊙ values. Shown are the convection mixing (hatched green), semi-convection mixing (red), overshooting mixing (crosshatched purple), thermohaline mixing (hatched gold), and the surface of the star (solid black line). |
However, after the mass transfer most of the nuclear production (60%) occurs within 1.2 M⊙ and the remaining 40% within 2.18 M⊙. These results suggest that the rejuvenation of the accreting star is linked to a larger convective core and other minors instabilities near its surface. This phenomenon persists from the onset of mass transfer until the model stops, at which point the accreting star has moved to the main sequence with a new mass. At this stage (f stage), mass transfer from its donor companion has ceased.
6. Discussion
In our study, we delve into the implications of the MESA code’s reliance on the ST dynamo model, a model that, on a general scale, remains relatively untested and not thoroughly understood. The ongoing efforts in conducting simulations to systematically validate this model suggest potential uncertainties that should be carefully considered.
A notable challenge arises from the fact that the ST dynamo model might not be the exclusive or definitive mechanism at play. Convective stars could potentially exhibit other dynamo models, such as the regular alpha-omega or alpha square dynamos. The complexity of stellar interiors may introduce additional mechanisms that contribute to the dynamo process, thus complicating our overall understanding.
An inherent limitation lies in our treatment of dynamo models within the 1D framework of MESA. This approach, while providing valuable insights, represents an extreme simplification. Consequently, the results obtained from such models carry a degree of uncertainty. It is crucial to acknowledge this limitation and interpret the findings in light of this inherent uncertainty.
Assuming the correctness of the ST dynamo in principle, our attention shifts to the specific parameterization in Section 2.5. We observe that numerous parameters are set with high precision, yet the potential impact of variations in these parameters on the outcomes remains unclear and undiscussed. This raises the question of how the results would evolve if certain parameters were varied to some extent.
Of particular importance in this context is the value of the dM/dt parameter. The best fit model is found at dM/dt = 7.76E − 6 M⊙ yr−1 (Table 1). In the conservative case, this should imply a change of the orbital period of (dP/dt)/P of 1.5E − 5 yr−1. This rate of change is not detected, which could imply that we have probably found the object toward the wings of the mass transfer event curve, or that the process is not conservative. This also points to possible uncertainties in our models.
This uncertainty underscores the importance of a more comprehensive exploration of the parameter space. Specifically, understanding the sensitivity of the results to variations in key parameters could provide valuable insights into the robustness of our findings. This consideration becomes particularly relevant for future work, emphasizing the necessity of a systematic examination of potential uncertainties in the context of dynamo models within the MESA framework.
7. Conclusions
In this comprehensive study, we have delved into the intricate evolutionary stages of the close interacting binary V4142 Sgr, meticulously tracing its development using the sophisticated MESA code. By comparing our findings with the published parameters of the binary, we identified the most optimal representative model: χ20.95, 6 = 0.007. Our research yields significant insights into this intriguing celestial system. We can summarize our key results as follows:
-
We confirm that the DPV V4142 Sgr is successfully represented by a model that includes conservative mass transfer, providing valuable information about its initial parameters. It started with a donor star mass of Mi, d = 3.50 M⊙ and radius of Ri, d = 2.22 R⊙; for the gainer star, the initial mass was Mi, g = 1.50 M⊙, the initial radius was Ri, g = 1.49 R⊙, and the initial orbital period was
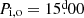 , for a fixed metallicity system of Z = 0.02.
, for a fixed metallicity system of Z = 0.02. -
The model indicates that the age of the DPV V4141 Sgr system is 280.1676 Myr. The calculated final mass for the donor star is Mf, d = 1.05 M⊙, with a radius of R = 19.20 R⊙ and a temperature of Tf, d = 4229 K. Its companion has a final mass of Mf, d = 3.93 M⊙, a radius of R = 6.39 R⊙, and a temperature of Tf, d = 14 798 K.
-
The inversion of the 1H/4He material ratio in the donor star occurred at 138.000 Myr (i.e., almost halfway through its current life), while its companion (the gainer star) remains almost unchanged.
-
The inversion of the mass ratio (280.1115 Myr) of the two stars occurred in a rather rapid time span of 0.0565 Myr, and the orbital period decreased abruptly by 40%, reaching
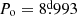 .
. -
During this stage, the mass of the convective core (Mcc) of the gainer star increased by 0.25 M⊙, while the stellar density decreased to 0.178 g cm−3. The rate of change in angular momentum reveals a significant decrease, exceeding 1.45E38 g cm2 s−1 over time. This decline contrasts with moments prior to mass transfer when the variation was positive, with an increase exceeding 0.7 g cm2 s−1. This change could be attributed to various factors, such as stellar winds or mechanisms of angular momentum loss (e.g., torque on the accretion disk and tidal forces). Furthermore, these factors could explain the persistent V < R relationship in the Hα profile observed in V495 Cen and V4142 Sgr, as reported in Rosales Guzmán et al. (2018) and Rosales et al. (2023).
-
Within a group of five carefully examined DPV systems, we have identified a zone where most of the DPVs’ gainer stars are located. These gainers, along with the gainer of DPV V4142 Sgr, are expected to have undergone rejuvenation due to hydrogen (stage c), as shown in Figure 6 and Table 1, during its accretion phase. During this process, V4142 Sgr decreased significantly in size and the mass of its convective core increased by 82%.
-
In addition, the alpha mixing length parameter, αml, affected the evolutionary paths of the trial models of V4142 Sgr, either accelerating or delaying their evolution. This is not observed in our models of more massive binaries. On the other hand, varying the thermohaline parameter had no practical effect on the evolutive routes in our attempts to reproduce the V4142 Sgr system.
-
The successful reproduction of the second period for V4142 Sgr was achieved using a dynamo number D = 293.9296 and a power-law index α = 0.6462 (dimensionless). Additionally, three stages in the evolutionary track were identified, confirming the presence of the dynamo and suggesting the possibility of its initiation from the minimum RL (F stage).
-
In the donor star, the mixing coefficient for the mixture is very intense within the convective zone and overshooting region from the ZAMS until the inversion of the 1H/4He material ratio, and there is no apparent presence of magnetic fields within them. The mixing diffusivity associated with the generation of magnetic fields through the ST dynamo within these zones is negligible. However, once the mixing coefficient D decays, the poloidal and toroidal magnetic fields, along with the mixing coefficient DST caused by advection outside the overshooting zone, are immediately activated. This suggests that the creation and amplification of these magnetic fields are influenced by the mixing diffusivity DST, which will shape them during the rest of their evolution.
-
Regarding the internal structure of the two stellar components, the mass-transfer rate in the convective core of the donor star decreased from 0.75 M⊙ Myr−1 to 0.2 M⊙ Myr−1, a 73% decrease. Meanwhile, the gainer star mass increased by 82%. Additionally, the nuclear production rate in the donor star dramatically dropped to a value below the 0.2 M⊙ Myr−1 limit, in complete contrast to the gainer star, whose total nuclear production is concentrated within the 2.18 M⊙ Myr−1 range.
-
Our numerical model suggests that the rejuvenation of the gainer star is associated with a larger convective core and other types of instabilities that can occur near its surface such as semi-convection, which is present throughout the evolutionary process. In other words, a larger convective core reduces mass loss through winds in the outer regions, as commonly observed in B-type stars. This leads to a continuous mixing of hydrogen with the helium received from its companion, increasing its lifespan and allowing it to remain as a B-type star for a significant portion of its evolutionary process.
Acknowledgments
R.E.M., D.S., and J.A.R. acknowledge support by the ANID BASAL project FB210003, FONDECYT Regular 1190621. R.E.M. and D.S. gratefully acknowledges support by FONDECYT Regular 1201280. J.A.R. gratefully acknowledges support by financial support from Nucleo Milenio TITANS ICN-ANID NCN19-058, and to the grant Vicerrectoría de Investigación y Desarrollo (VRID) Postdoctoral DICA N181/23. NWCL gratefully acknowledges the generous support of a Fondecyt General grant 1230082, as well as support from Millenium Nucleus NCN19_058 (TITANs) and funding via the BASAL Centro de Excelencia en Astrofisica y Tecnologias Afines (CATA) grant PFB-06/2007. NWCL also thanks support from ANID BASAL project ACE210002 and ANID BASAL projects ACE210002 and FB210003.
References
- Applegate, J. H., & Patterson, J. 1987, ApJ, 322, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, N., & Kippenhahn, R. 1959, Z. Astrophys., 48, 140 [NASA ADS] [Google Scholar]
- Biermann, L. 1950, Z. Naturforsch. Teil A, 5, 65 [CrossRef] [Google Scholar]
- Bloecker, T. 1995, A&A, 297, 727 [Google Scholar]
- Braun, H., & Langer, N. 1995, A&A, 297, 483 [NASA ADS] [Google Scholar]
- Burger, H. L., & Katz, J. I. 1983, ApJ, 265, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1990, A&A, 227, 282 [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- Dervişoǧlu, A., Tout, C. A., & Ibanoǧlu, C. 2010, MNRAS, 406, 1071 [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Eggleton, P. 2006, Evolutionary Processes in Binary and Multiple Stars (Cambridge: Cambridge University Press) [Google Scholar]
- Fricke, K. 1968, Z. Astrophys., 68, 317 [NASA ADS] [Google Scholar]
- Garcés, L. J., Mennickent, R. E., Djurašević, G., Poleski, R., & Soszyński, I. 2018, MNRAS, 477, L11 [CrossRef] [Google Scholar]
- Garrido, H. E., Mennickent, R. E., Djurašević, G., et al. 2013, MNRAS, 428, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Schubert, G. 1967, ApJ, 150, 571 [Google Scholar]
- Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [Google Scholar]
- Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge: Cambridge University Press) [Google Scholar]
- Johnstone, C. P., Güdel, M., Brott, I., & Lüftinger, T. 2015, A&A, 577, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kippenhahn, R. 1974, IAU Symp., 66, 20 [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1967, Z. Astrophys., 65, 251 [NASA ADS] [Google Scholar]
- Kippenhahn, R., Kohl, K., & Weigert, A. 1967, Z. Astrophys., 66, 58 [NASA ADS] [Google Scholar]
- Kippenhahn, R., Ruschenplatt, G., & Thomas, H.-C. 1980, A&A, 91, 175 [NASA ADS] [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Kopal, Z. 1978, Dynamics of Close Binary Systems (Dordrecht: Springer) [Google Scholar]
- Kopal, Z. 1959, ASPL, 8, 81 [NASA ADS] [Google Scholar]
- Langer, N., El Eid, M. F., & Fricke, K. J. 1985, A&A, 145, 179 [NASA ADS] [Google Scholar]
- Lauterborn, D. 1970, A&A, 7, 150 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin Heidelberg: Springer) [Google Scholar]
- Mennickent, R. E. 2017, Serb. Astron. J., 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., & Rosales, J. 2014, IBVS, 6116, 1 [NASA ADS] [Google Scholar]
- Mennickent, R. E., Pietrzyński, G., Diaz, M., & Gieren, W. 2003, A&A, 399, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennickent, R. E., Kołaczkowski, Z., Djurasevic, G., et al. 2012, MNRAS, 427, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., Otero, S., & Kołaczkowski, Z. 2016a, MNRAS, 455, 1728 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., Zharikov, S., Cabezas, M., & Djurašević, G. 2016b, MNRAS, 461, 1674 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., Schleicher, D. R. G., & San Martin-Perez, R. 2018, PASP, 130, 094203 [CrossRef] [Google Scholar]
- Navarrete, F. H., Schleicher, D. R. G., Käpylä, P. J., et al. 2020, MNRAS, 491, 1043 [Google Scholar]
- Paxton, B. 2004, PASP, 116, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, W. M., Mutel, R. L., Güdel, M., & Goss, W. M. 2010, Nature, 463, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Pitts, E., & Tayler, R. J. 1985, MNRAS, 216, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [Google Scholar]
- Poleski, R., Soszyński, I., Udalski, A., et al. 2010, Acta Astron., 60, 179 [NASA ADS] [Google Scholar]
- Reimers, D. 1975, Mémoires of the Société Royale des Sciences de Liège, 8, 369 [Google Scholar]
- Rosales, J. A., Mennickent, R. E., Schleicher, D. R. G., & Senhadji, A. A. 2019, MNRAS, 483, 862 [Google Scholar]
- Rosales, J. A., Mennickent, R. E., Djurašević, G., et al. 2023, A&A, 670, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosales Guzmán, J. A., Mennickent R. E., Djurašević G., Araya I., Curé M., 2018, MNRAS, 476, 3039 [NASA ADS] [CrossRef] [Google Scholar]
- Sarna, M. J., Muslimov, A., & Yerli, S. K. 1997, MNRAS, 286, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., & Mennickent, R. E. 2017, A&A, 602, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild, K. 1906, WisGo, 195, 41 [NASA ADS] [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, J.-L. 1978, Princeton Series in Astrophysics (Princeton: University Press) [Google Scholar]
- Tassoul, J.-L. 2000, Stellar Rotation / Jean-Louis Tassoul (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Tout, C. A., Aarseth, S. J., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 291, 732 [NASA ADS] [Google Scholar]
- Ulrich, R. K. 1972, ApJ, 172, 165 [NASA ADS] [CrossRef] [Google Scholar]
- van Rensbergen, W., De Greve, J. P., De Loore, C., & Mennekens, N. 2008, A&A, 487, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vauclair, S. 2008, IAU Symp., 252, 97 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wasiutynski, J. 1946, Astrophys. Norvegica, 4, 1 [NASA ADS] [Google Scholar]
- Woods, T. E., Ivanova, N., van der Sluys, M. V., & Chaichenets, S. 2012, ApJ, 744, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Aitoff projection of well-studied Galactic DPV stars (orange triangles) from the Variable Star Index (VSX)1. Semidetached Algol primaries from Dervişoǧlu et al. (2010) are also shown as black points, and other DPVs yet to be studied and reported in VSX are shown as green dots. V4142 Sgr is represented by a blue star with an orange border. |
| In the text | |
 |
Fig. 2. Schematic illustration of instability regions of Brunt-Väisälä frequency, convection, semi-convection, thermohaline convection, and radiative stability in the plane. We show the thermal and compositions terms |
| In the text | |
 |
Fig. 3. Comparison of two wind schemes used to model the wind phenomenon in the RGB scheme. The evolutionary track of the donor star in blue corresponds to the de Jager formalism; its companion gainer is represented by the black line. In red, it represents the Reimers formalism, with its companion represented by the green line. Areas with differences between formalisms are labeled z1, z2, and z3. |
| In the text | |
 |
Fig. 4. Evolution of orbital and stellar parameters of V4142 Sgr. Left: schematic behavior of radius and mass for both stars. While the two stars evolve separately, the donor star (black line) expands to fill the RL, and the initial radius of the gainer star (dashed red line) increases and later decreases during the rejuvenation. Center: evolution of the orbital period as a function of the mass of the primary star (donor) for V4142 Sgr. Right: theoretical orbital velocity curve for both components as a function of their masses. The orbital velocity of the primary component (black line) increases during the mass-loss process, known as spin-up, and later decreases, reaching the current value. The RV of the companion (i.e., gainer) star (dashed red line) decreases, and its mass increases. |
| In the text | |
 |
Fig. 5. Best model for V4142 Sgr with 16 freedom degrees and all optimized parameter values for both stars, with a Δχ20.95, 6 = 0.007. |
| In the text | |
 |
Fig. 6. Evolutionary track of the DPV V4142 Sgr with a secondary star (black line) of initial mass Mi, d = 3.50 M⊙ and its companion (red line) of Mi, g = 1.50 M⊙. The dashed blue line represents the evolutionary track of a single star, identical to the initial mass of the gainer star, using the same initial parameters that were used to model the gainer, until central helium depletion (XHec < 0.2). The green line represents the evolutionary track for a single star, using the same donor initial parameters. The most important points during the evolution are labeled together with the initial and final theoretical masses. The blue zone represents the threshold of rejuvenated B-type stars. The uppercase black letters mark each stage of the donor star, while the lowercase red letters represent the stages of the gainer star (see Table 1). |
| In the text | |
 |
Fig. 7. Central abundance of 1H and 4He for V4142 Sgr. The mass-fraction inversion (X1 stage) of the donor star (black line) is shown before the mass transfer (E stage) and mass inversion (U1 stage). The gainer star evolves over a more extended timescale, during which it fails to achieve the mass-fraction inversion, and its 1H increases slightly, by 0.04 M⊙, during the accretion phase (E stage), allowing it to rejuvenate before the mass transfer concludes (H stage), as indicated by the green arrow. |
| In the text | |
 |
Fig. 8. Hertzsprung-Russell diagrams of the binary evolution. The color bar shows the central hydrogen and helium mass fraction for both components until the hydrogen depletion, 1H. This shows that the gainer star rejuvenates before losing most of its size slowly over its lifetime, whereas the donor star suffers a rapid exhaustion of helium during the mass transfer phase. |
| In the text | |
 |
Fig. 9. Theoretical variation in the mass transfer and Ṁd curve of the donor star. Left: theoretical variation in mass transfer until helium depletion is reached for initial masses Mi, d = 3.50 M⊙ and Mi, g = 1.50 M⊙, for an initial orbital period |
| In the text | |
 |
Fig. 10. Evolution of the donor star size and effective temperature in V4142 Sgr. Left: evolution of the donor star size with an initial mass of 3.5 M⊙ in the binary system DPV V4142 Sgr, with a companion that has an initial mass of 1.5 M⊙. We show the phases in which cases A, B, and C of RLOF can occur, depending on the age of the system. The inversion of the 1H/4He ratio (X1 stage) is represented by a brown dot, the mass transfer (E stage) by a blue dot, and the current stage of the system (X2 stage) by a red dot. Right: effective temperature, Teff, as a function of age (in years) for V4142 Sgr. We shown that the donor star, after crossing the Hertzsprung gap during the onset of the blue loop (stages C and D), follows an evolutionary track until reaching its current stage (X2 stage) on a thermal timescale. This continues until it reaches the final stage of non-optically thick mass transfer (H stage), stopping shortly before helium depletion. |
| In the text | |
 |
Fig. 11. Fractional radius, relative to the orbital separation, for primaries in Algols with and without disks. Red dots represents to the DPV stars. Below the circularization radius (shown by the solid bottom line), a disk should be formed, and below the top line, a disk might be formed. Semidetached Algol primaries from Dervişoǧlu et al. (2010) are also shown, as gray points. This figure is adapted from Mennickent et al. (2016a). |
| In the text | |
 |
Fig. 12. Rate of change of the angular momentum of the gainer star versus the central density logarithm. Most important stages are labeled. |
| In the text | |
 |
Fig. 13. Schematic behavior of the αml and thermohaline parameters for V4142 Sgr. Left: schematic behavior of the mixed length parameter (αml) for different values. This parameter regulates the so-called rejuvenation process in the gainer star. Although it has no influence on the evolution of the mass transfer, stellar masses, or binary period, it significantly affects the evolutionary path of the secondary star during mass transfer until the end of optically thick mass transfer, aging it for lower values of αml (opposite to the behavior of the gainer star). Right: schematic behavior for different values of the thermohaline parameter, where no significant changes are observed during the evolution of both stars. |
| In the text | |
 |
Fig. 14. Schematic representation of the alpha mixing length parameter (αml) for various values in a massive binary system with a total mass of 28.5 M⊙. |
| In the text | |
 |
Fig. 15. Profiles of the poloidal magnetic field, Br, and the toroidal magnetic field, Bϕ, generated by the ST dynamo in the donor star at different evolutive stages. The profiles represents the stages of inversion of the 1H/4He ratio (X1 stage), the initiation of mass transfer (E stage), the mass inversion (U1 stage), and the current stage (X2 stage). The Eulerian diffusion coefficient for mixing is shown in orange, the ST diffusion coefficient as a brown line, the poloidal magnetic field in black, the toroidal magnetic field in green, the angular momentum in blue, and the angular velocity in red. |
| In the text | |
 |
Fig. 16. Kippenhahn diagrams showing the internal structure of the donor star, accompanied by a zoomed-in view with some principal events labeled. The donor star has an initial mass of Mi, d = 3.50 M⊙. The evolution stops when the donor star reaches core helium depletion, XHe, c < 0.2. The x-axis gives the age after ignition of hydrogen in units of Myr. The different layers are characterized by their values of M/M⊙. Shown are the convection mixing (hatched green), semi-convection mixing (red), overshooting mixing (crosshatched purple), the He core mass (red dot), thermohaline mixing (hatched yellow), and the surface of the star (solid black line). |
| In the text | |
 |
Fig. 17. Kippenhahn diagrams showing the internal structure of the gainer star with an initial mass of Mi, g = 1.50 M⊙. The evolution stops when the donor star reaches core helium depletion, XHe, c < 0.2. The x-axis gives the age after ignition of hydrogen in units of Myr. The different layers are characterized by their M/M⊙ values. Shown are the convection mixing (hatched green), semi-convection mixing (red), overshooting mixing (crosshatched purple), thermohaline mixing (hatched gold), and the surface of the star (solid black line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.