| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A282 | |
| Number of page(s) | 16 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202449630 | |
| Published online | 19 July 2024 | |
Extreme magnetic field modulus variability of the Bp star HD 57372
1
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail: shubrig@aip.de
2
NASA Ames Research Center,
Moffett Field,
CA
94035,
USA
3
Apache Point Observatory and New Mexico State University,
P. O. Box 59,
Sunspot,
NM,
88349-0059,
USA
Received:
16
February
2024
Accepted:
14
May
2024
Context. In chemically peculiar Ap/Bp stars with large-scale organised magnetic fields of simple centred dipole configuration, the ratio between the maximum and the minimum of the mean magnetic field modulus is on the order of 1.25. Values of two or more are observed only for very few Ap/Bp stars and are indicative of a very unusual magnetic field geometry.
Aims. Determining the magnetic field structure of Ap/Bp stars is bound to provide a different insight into the physics and the origin of the magnetic fields in early-type stars. In this respect, the Bp star HD 57372 is of particular interest because strongly variable magnetically split lines have been observed in HARPS and APOGEE spectra.
Methods. We obtained and analysed measurements of the mean magnetic field modulus and of the mean longitudinal magnetic field using near-infrared spectra and optical polarimetric spectra distributed over the stellar rotation period.
Results. The mean magnetic field modulus 〈B〉 of HD 57372, as estimated from absorption lines that are split via the Zeeman effect and resolved in both optical and near-infrared spectra, is found to vary by an extraordinary amount: about 10 kG. The exceptional value of three for the ratio between the maximum and the minimum of the field modulus is indicative of a very unusual geometry for HD 57372’s magnetic field. All observable quantities were found to vary in phase with the photometric period of 7.889 days. This includes the longitudinal magnetic field 〈Bz〉, which varies from −6 kG up to 1.7 kG in FORS2 spectra, as well as the metal line strengths, whose equivalent widths change by up to 50% of their mean values over the course of the rotation period. The B8 temperature class of HD 57372 also places it among the hottest stars known to exhibit resolved, magnetically split lines.
Key words: stars: chemically peculiar / stars: early-type / stars: magnetic field / stars: individual: HD 57372 / stars: variables: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
For well over 50 yr, it has been known that a significant fraction of late B-type and A-type stars host strong, large-scale magnetic fields that lead to peculiar surface abundances and hence also to their classification as chemically peculiar (CP) Ap/Bp stars (Babcock 1958). These stars are slow rotators as a rule when compared to their non-magnetic analogues. In the most extreme cases of slow rotation, strong magnetic fields, and the presence of magnetically sensitive spectral lines, it is possible to resolve the individual magnetically split components in unpolarised light. Measurement of the wavelength separations of the split components combined with knowledge of the associated quantum numbers gives a very simple yet extremely valuable measure of the intrinsic surface magnetic field strength as averaged over the visible hemisphere, a quantity known as the magnetic field modulus (〈B〉; see Mathys 1990a; Mathys & Lanz 1992; Mathys et al. 1997; Mathys 2017). For all other magnetic stars, diagnosis of the intrinsic magnetic field strength usually relies on spectropolari-metric observations of circular polarisation over the full rotation period.
The first example of resolved magnetically split lines (RMSL) in an Ap/Bp star was HD 215441 (more commonly known as Babcock’s star; Babcock 1960), and despite more than a hundred additional examples having subsequently been found, Babcock’s star remains unique to this day. Not only is it the most magnetic main-sequence star known (〈B〉 ~ 34 kG), it is a relatively rapid rotator (compared to most RMSL stars) and also the hottest star for which RMSL have been observed. In particular, Preston (1969) used a time series 〈B〉 measurement to confirm that the 9.49-day photometric period found by Jarzębowski (1960) was in fact the rotational period (Prot) of Babcock’s star, and based on the strength of temperature sensitive features in the spectra, he concluded that the temperature class could be as hot as B3 or B4.
In contrast to Babcock’s star, the majority of Ap/Bp stars known to exhibit RMSL have far longer rotation periods. For example, the 29-yr rotation of HD 50169 could only be determined after a few decades of observation (Mathys et al. 2019), and the rotation period of HD 101065 (also known as Przybyl-ski’s Star; Przybylski 1961) could be constrained to ~188 yr by Hubrig et al. (2018) despite the rather short observational baseline. With early-to-mid A spectral types, typical RMSL stars are also cooler than Babcock’s star, and with 〈B〉 usually less than 10 kG, they are also considerably less magnetic (Mathys 2017).
The most comprehensive study of RMSL stars to date is by Mathys (2017), who has essentially provided an encyclopaedia on the magnetic properties of what at the time was an 84-star sample. Among the key findings of this work was confirmation of an already-suspected dearth of short-period binaries among the RMSL stars, leading to the suspicion that the peculiarities of these stars may stem from binary mergers. In lieu of a theory for generating a magnetic field in a purely radiative atmosphere, the binary merger hypothesis is a promising one that has only recently gained traction to the point where a theoretical basis is now being developed (e.g. Schneider et al. 2020).
For numerous RMSL stars, both the 〈B〉 and the brightness of the stars vary as a function of rotation phase due to the changing viewing angle of the magnetic poles such that rotation periods can be determined from either photometry or spectroscopy. These variations can often be successfully reproduced under the assumption of a simple dipole using the framework developed by Preston (1969) in his study of Babcock’s star, whereby the ratio of q = 〈B〉max/〈B〉min should be on the order of 1.25 in the case of a pure dipole. For some of the RMSL stars, however, the magnetic field geometry is clearly more complicated. Out of a subset of 28 RMSL stars with known rotation periods over which 〈B〉 has been measured, Mathys (2017) found eight stars with q > 1.25, six of which had q > 1.3. Among these six stars, the A3p star HD 65339 stood out as exceptionally remarkable, considering Prot = 8.03 days, q ~ 2.27, and Δ〈B〉 = 〈B〉max − 〈B〉min ~ 9.7 kG (see also Mathys et al. 1997). In terms of Δ〈B〉, the only fair comparison currently known is the A2p star HD 126515, for which Δ〈B〉 ~ 6 kG, albeit over a much longer timescale of Prot ~ 130 days.
In the context of q, it is worth mentioning HR 465, which has long been known as one of the most extreme Bp stars with respect to its exotic atomic line content (e.g. Cowley et al. 1975), complicated variability over its long ~21 -year rotation period (Scholz 1978), and an unprecedentedly large q ~ 3.8 (Mathys et al. 1997; Giarrusso et al. 2022). As with Babcock’s star, HR 465 is thus a severe outlier among the RMSL stars, but in this case it represents the extreme low end of all measured magnetic field moduli, with 〈B〉 < 3 kG on average.
Here, we present a new example of an RMSL Bp star whose magnetic properties are every bit as exceptional as those of Ap stars such as HD 65339 and HR465. Prior to this work, HD 57372 had not been specifically mentioned in any papers beyond inclusion in the Bernhard et al. (2015) search for photometric variability in CP stars. These authors reported a V-band magnitude that varies between 7.90 and 7.93 over the course of a 7.888-day period. The B8p Si spectral type, indicating enhanced Si features in the optical, was reported in the catalogue of CP stars by Renson & Manfroid (2009).
Four medium-resolution H-band spectra of HD 57372 have been obtained by the northern Apache Point Observatory Galactic Evolution Experiment (APOGEE; Majewski et al. 2017; Wilson et al. 2019) spectrograph, which operates as a subcomponent of the fifth instalment of the Sloan Digital Sky Survey (SDSS-V; e.g. Ahumada et al. 2020, and Kollmeier, J.A., in prep.). Intriguingly, our inspection of these spectra showed extreme short-term variability of RMSL. To investigate HD 57372 in more detail, we acquired eight high-resolution polarimetric spectra from the High Accuracy Radial Velocity Planet Searcher (HARPS; Pepe et al. 2000; Mayor et al. 2003) instrument attached to the European Southern Observatory (ESO) 3.6-m telescope and twelve low-resolution polari-metric spectra from the FOcal Reducer/low dispersion Spectro-graph 2 (FORS2) mounted on the 8.2-m Antu unit of the Very Large Telescope (VLT). In addition, numerous observations of HD 57372 by the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) are also available, and we made use of them in order to refine the rotation period.
The paper is laid out as follows: Sect. 2 describes the spec-troscopic and photometric data, including the TESS light curve and associated refinement of Prot. In Sect. 3, we discuss the Gaia DR3 parameters, and in Sect. 4, the magnetic field variability of HD 57372 in both the optical and the near-infrared (NIR) H-band is presented. In Sect. 5, we explore stellar parameters assessed based on the Banner line Hδ and surface abundances of HD 57372 in comparison to other magnetic Ap/Bp stars. Finally, in Sect. 6, we compare HD 57372 with Ap/Bp stars known to exhibit magnetically resolved lines and discuss its magnetic field structure.
2 Spectroscopy and photometry
2.1 SDSS 2.5 m/APOGEE
HD 57372 was observed by the APOGEE spectrograph on the Sloan 2.5-m telescope (Gunn et al. 2006) at the Apache Point Observatory (APO) four times over the course of a week between 2020 December 29 and 2021 January 6. The spectra have a resolution of about 22 500 and cover most of the H-band (15 145–16 960 Å; vacuum wavelengths used throughout this paper when referring to the H-band) onto three detectors, with gaps between 15 800 and 15 860 Å and 16 430 and 16 480 Å due to non-overlapping wavelength coverage of the detectors. Total exposure times ranged from 49 to 82 minutes, and the associated signal-to-noise ratios range from 230 to 264. The reduction was carried out using the standard APOGEE data reduction pipeline described in Nidever et al. (2015), with the only post-reduction steps being continuum normalisation via fitting low-order polynomials to line-free regions, correction of the wavelengths to the rest frame based on Gaussian fitting of narrow absorption lines, and manual removal of otherwise distracting airglow emission residuals. When analysing individual absorption lines, we also re-normalised the local continuum in small regions enclosing the lines.
2.2 ESO 3.6 m/HARPSpol
HD 57372 was observed with HARPS in the spectropolarimetric mode eight times between 2022 April 23 and 2022 May 1. In the spectropolarimetric mode, HARPS has a resolving power of about 115 000 and a wavelength coverage from 3780 to 6910 Å, with a small gap between 5259 and 5337 Å. The data was reduced on La Silla using the HARPS data reduction pipeline. The normalisation of the spectra to the continuum level is described in detail by Hubrig et al. (2013).
2.3 VLT 8 m/FORS2
Twelve spectropolarimetric observations of HD 57372 were obtained in service mode using FORS2 at the spectral resolution of about 2000 between 2021 November 24 and 2022 April 1. The data reduction and analysis methods used for 〈Bz〉 measurement have been described in detail in numerous previous papers (e.g. Schöller et al. 2017; Chojnowski et al. 2022) and are not repeated here. As in those papers, the FORS2 data yielded two 〈Bz〉 datasets for the magnetic field measurements: one using only the hydrogen Balmer series lines (〈Bz〉hyd) and another using the entire spectrum from each observation (〈Bz〉aIJ).
2.4 TESS light curve and rotation period
HD 57372 was observed 1086 times in TESS Sector 7 (120 s cadence) between 2019 January 8 and 2019 February 1, 3485 times in TESS Sector 33 (600 s cadence) between 2020 December 18 and 2021 January 13, 3474 times in TESS Sector 34 (600 s cadence) between 2021 January 14 and 2021 February 8, and 10654 times in TESS Sector 61 (200 s cadence) between 2023 January 18 and 2023 February 12, bringing the grand total to just over 100 days of TESS exposure time spread out over 18 699 individual observations. We used the LIGHTKURVE (Lightkurve Collaboration 2018) code to download the simple aperture photometry, to which was applied a pixel mask accounting for blending with neighbour stars. After removing systematic trends and outliers via the TESSCUT code (Brasseur et al. 2019), we were left with a total of 18 064 TESS data points. The light curves from each sector are shown in the upper panels of Fig. 1.
Analysis of the TESS data with the time series software package PERIOD04 (Lenz & Breger 2005) indicates a primary frequency of f = 0.12675795 ± 2.1 × 10−7, which corresponds to a rotation period of Prot = 7.889148 ± 1.3 × 10−5. This result agrees well, albeit with far greater precision, with what has been found in past studies. In the bottom panel of Fig. 1, all of the TESS data has been phase folded by Prot using 2458 492.07 as a JD of maximum brightness. As is common for Ap/Bp stars (e.g. Jagelka et al. 2019), due to inhomogeneous elemental abundances and magnetic field strengths across their surfaces, the light curve of HD 57372 is quite irregular. Each rotation of HD 57372 witnesses two local brightness minima at ϕ ~ 0.32 and ~0.72 that enclose a local brightness maximum roughly halfway between at ϕ ~ 0.52. With rotation phases (ϕrot) in hand, Table 1 summarises the spectroscopic observations of HD 57372, providing Universal Times (UT) at mid-exposure, Julian dates (JD) at mid-exposure minus 2 400 000, instruments used, exposure times, signal-to-noise ratios, and ϕrot.
Summary of the spectroscopic observations of HD 57372.
 |
Fig. 1 TESS light curve of HD 57372. The upper panels show the observed data from each of the four TESS sectors. The grey points in the lower panel are all of the data phased by the 7.889148 d rotation period and with 2458 492.07 as a reference epoch of maximum brightness. Magenta points show the data binned in increments of ϕrot = 0.005. |
3 Gaia DR3 parameters and radial velocity measurements
Although HD 57372 appears to be a single star in the 2MASS and DSS images provided on the HD 57372 SIMBAD page, the star has been identified as a visual double star in past studies. For example, the Tycho Double Star Catalogue (Fabricius et al. 2002) reported a component separation of ~2″, with the brighter component having magnitudes of BT = 8.15 and VT = 8.30 and the fainter component having BT = 9.05 and VT = 9.11. The third data release of the Gaia mission (Gaia DR3; Gaia Collaboration 2016; Gaia Collaboration 2023) also reported two sources within 2″ of HD 57372, one with G = 8.289 and one with G = 9.121. The Gaia DR3 parallaxes and proper motions of the brighter star (π = 2.412 mas, µα = −7.928 mas yr−1, µδ = 4.130 mas yr−1) are quite similar to those of the fainter star (π = 2.378 mas, µα = −8.592 mas yr−1, µδ = 4.263 mas yr−1) such that it is possible the two stars are physically associated. In this case, the orbital period will be on the order of several thousand years. Spectroscopic parameters were only given for the fainter star. These included a radial velocity of υr = 24.63 km s−1 as well as an effective temperature of Teff = 13963 K, which is in good agreement with the B8 temperature class quoted for HD 57372 in the Renson & Manfroid (2009) catalogue of CP stars.
The radial velocity reported by Gaia for the fainter component of HD 57372 is quite close to the values we find from the APOGEE and HARPS spectra of the brighter, magnetic component. For the radial velocity measurements using the APOGEE H-band spectra of HD 57372, we relied on the Mg II 16765 Å, Ca II 16654 Å, Ce III 15961 Å, and Ce III 16133 Å lines. These are among the strongest identified lines covered, and their entire profiles could be satisfactorily fit with single Gaussians during epochs when the magnetic field strength was relatively low such that the magnetic splitting was not resolved. In the spectra where magnetic splitting was resolved, we fit Gaussians to the central components of the quasi-triplet features of the Ca II and Ce III, discarding the Mg II line due to its distorted, non-triplet morphology. Barycentric velocity corrections were applied to the resulting averages of each spectrum, and the standard deviations of the line-by-line measurements were adopted as error estimates. This yielded an overall average of υr = 21.88 ± 2.80 km s−1 across the four APOGEE spectra, with individual υr ranging from 21.30–22.87 km s−1. From this, we had no reason to suspect that HD 57372 is a member of a binary system, or at least not of a short-period binary.
In the HARPS optical spectra, υr was measured similarly using Cr II and Fe II lines. The lines were selected on the basis of relatively short wavelengths (<4800 Å) and relatively low effective Landé factors (geff < 0.7) in order to minimise the effects of magnetic splitting. This yielded an overall average of υr = 22.45 ± 0.86 km s−1 across the eight HARPS spectra, with individual υr ranging from 21.63 to 23.51 km s−1. The surprisingly large υr scatter here seems to be caused by an inhomogeneous chemical element distribution on the stellar surface that is typically observed in Ap/Bp stars and a complicated magnetic field geometry rather than being due to binarity. However, our attempts to phase the individual υr values with the rotation period did not show any conclusive correlation.
Although the Gaia data do not indicate the fainter component of HD 57372 as being variable, the brighter component is classified as a photometric variable with a 7.888 d period. Considering that this is in good agreement with the rotation period of the magnetic component of HD 57372 indicated by our data while also accounting for the aforementioned radial velocity agreement, we proceeded under the assumption that the aforementioned Gaia DR3 spectroscopic parameters (including the surface gravity of log g = 4.399 and the stellar radius of R* = 1.88 R⊙) in fact pertain to the Bp star HD 57372 that is the focus of this paper. Assuming that the TESS 7.889 d period is in fact the rotation period of HD 57372, the R* = 1.88 R⊙ would then imply a rotational velocity at the equator υeq = 12 km s−1.
The relatively small angular separation of the two objects may lead to contamination of the primary spectrum by the secondary. The APOGEE fibres subtend 2″ on the sky, whereas the HARPS fibres have a diameter of 1″, and the used FORS2 slit was 0.4″. Therefore, for the APOGEE observations, we expected that some light of the secondary was captured. For HARPS and FORS2, we assumed contamination to be rather small. However, we did not see any evidence for a second star in our data. Further, as we show in the following sections, all observables vary according to a rotation period that can be independently measured from photometry, Zeeman splitting variability, line strength variability, and longitudinal field variability, confirming that they are tied to one single star. All results presented in our paper are typical for a single magnetic star, albeit an extreme one.
4 Magnetic field measurements
4.1 H-band variability of the magnetic field modulus
We present in the upper panel of Fig. 2 line identifications in the H-band spectra of HD 57372. As is typical for late-Bp stars, the hydrogen Brackett series are the strongest features in the spectra, while the metal line content is dominated by the rare-earth ion Ce III along with singly ionised elements, such as Mg II, Si II, and Ca II. We also show in the spectrum of HD 57372 most of the unidentified lines that were previously discussed by Chojnowski et al. (2019, 2020, 2023). These features have no likely counterparts in the existing atomic data.
The lower panel of Fig. 2 highlights the remarkable variability of spectral lines over the course of one week. Whereas the ϕrot = 0.361 and 0.375 spectra show hardly any evidence of magnetic splitting, most of the lines are clearly split by a strong magnetic field during the ϕrot = 0.121 and 0.993 spectra. The best examples of this are Ca II 16654 Å and Ce III 16133 Å, both of which have quasi-triplet Zeeman patterns.
Atomic transitions where the upper and lower energy levels both have total angular momentum quantum numbers equal to 0.5 (i.e. J1 = J2 = 0.5) but only one of the levels is split (i.e. with a non-zero Landé factor, g1 = 0, g2 > 0 or g1 > 0, g2 = 0) are known as Zeeman doublets. In absence of the partial Paschen-Back effect, which should not have too strong an impact at the modest field strengths in question, this combination of J and g values leads to a Zeeman pattern consisting of two π components, each of which overlaps in wavelength or velocity space with a corresponding σ component. In these cases, the mean magnetic field modulus can be estimated via 〈B〉 (G)= 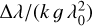 (Mathys et al. 1997), where g is the Landé factor of the split level, k is a constant equal to 4.671 × 10−13 kG−1 Å−1, λ0 is the rest wavelength of the transition in units of Å, and Δλ is the separation of the Zeeman doublet components in units of Å. For a pure Zeeman triplet, g is either the Landé factor of the split level of the transition, if the other level is unsplit, or if the transition is between two split levels that have the same Landé factor, the value of the latter.
(Mathys et al. 1997), where g is the Landé factor of the split level, k is a constant equal to 4.671 × 10−13 kG−1 Å−1, λ0 is the rest wavelength of the transition in units of Å, and Δλ is the separation of the Zeeman doublet components in units of Å. For a pure Zeeman triplet, g is either the Landé factor of the split level of the transition, if the other level is unsplit, or if the transition is between two split levels that have the same Landé factor, the value of the latter.
No such transitions are present in the H-band spectra of HD 57372, so in order to estimate 〈B〉 from the Zeeman quasi-triplet features that are present, we replaced g with the effective Landé factors (geff; see equation 4 of Mathys 1990b) of the transitions and Δλ with half of the separation of the outer triplet components. This makes it straightforward to estimate 〈B〉 from the ϕrot = 0.121 and 0.993 APOGEE spectra of HD 57372. The most cleanly split lines in these spectra are Ca II 16654 Å and Ce III 16133 Å, and from them we found 〈B〉 ~ 14.5 kG at ϕrot = 0.121 and ~15.3 kG at ϕrot = 0.993.
The question to then investigate was how low 〈B〉 is during the ϕrot = 0.361 and ϕrot = 0.375 spectra. Figure 3 represents our attempt to answer this question. We have yet to see resolved magnetic splitting in the unknown line at 15 335 Å in the APOGEE spectra of any star, meaning that it has quite a low geff and thus is relatively insensitive to the magnetic field. The 15 335 Å line is by far the narrowest line in the APOGEE spectra of HD 57372, and it has an observed minimum full width at half maximum (FWHM) of ~21 km s−1 in the ϕrot = 0.361 spectrum. To demonstrate this, a Gaussian of this FWHM has been plotted over the 15 335 Å line profiles.
In the Ca II 16654 Å and Ce III 16133 Å panels of Fig. 3, we have assumed that ~21 km s−1 is roughly the intrinsic FWHM in the absence of a magnetic field, and we have also approximated the Zeeman patterns as simple ensembles of three Gaussians with fixed FWHM = 21 km s−1. The positions and depths of the individual Gaussians have been adjusted manually in order to arrive at the displayed results. Although the quoted 〈B〉 values are highly uncertain during the ϕrot = 0.361 and 0.365 spectra, the implication is that 〈B〉 has dropped below 6 kG and hence that 〈B〉 changes by nearly 10 kG over the course of each rotation cycle.
It is worth noting the high degree of asymmetry of the line profiles in the ϕrot = 0.121 spectrum. This is atypical of the APOGEE-observed Ap/Bp stars that exhibit RMSL and is likely due to the rotational Doppler shifts of the contributions to the observed disc-integrated lines coming from different parts of the stellar disc.
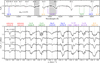 |
Fig. 2 Line identifications in the H-band spectra of HD 57372. Upper panel: line identifications in the APOGEE spectrum of HD 57372 at the rotational phase ϕrot = 0.375. The hydrogen Brackett series lines are labelled along the top, while metal lines are labelled along the bottom. Unidentified lines are indicated by small red ticks below the spectrum. Lower panel: variability of individual lines as a function of ϕrot. |
 |
Fig. 3 Mean magnetic field modulus estimates from the Ce III 16133 Å and Ca II 16654 Å lines in the APOGEE H-band spectra. The relatively magnetically insensitive unknown line at 15 335 Å is shown in order to demonstrate that it is well fit by a single Gaussian with FWHM = 21 km s−1 during the low-〈B〉 epochs. For Ce III 16133 Å and Ca II 16654 Å, the triple Gaussians each have the same FWHM = 21 km s−1. The associated 〈B〉 estimates are given below each line profile, but it is important to note that the low-〈B〉 values are highly uncertain due to the magnetic splitting being unresolved at APOGEE’s resolution . |
4.2 Optical variability of the magnetic field modulus
Before analysing the rich line content of the optical HARPS spectra of HD 57372, we repeated with the HARPS spectra the exercise detailed in the previous subsection for estimating 〈B〉, though in this case making use of Zeeman doublet features. Similar to the APOGEE spectra, RMSL are observed in numerous lines in half of the HARPS spectra, while 〈B〉 was too weak for any RMSL to be observed in the other half. The middle and right-hand panels of Fig. 4 show the two best available Zeeman doublet features: Fe II 6149 Å (g = 2.70) and Si II 6699 Å (g = 2.67). Several other doublets, such as Ti II 4315 Å (g = 2.63) and Fe II 4385 Å (g = 2.68), are also covered by the HARPS spectra, but we focus on the longer wavelength lines since blending is far more of a concern in the 4300 Å region and because the Zeeman splitting is larger for a fixed g or geff as wavelength increases.
Also shown in Fig. 4 is Fe II 4491 Å, which is the best available of a magnetically insensitive (geff = 0.43) line that shows no resolved splitting in any of the HD 57372 spectra. Whereas lines with geff = 0 (e.g. Fe I 5434 Å) are often present in the optical spectra of Ap stars, HD 57372 is sufficiently hot that Fe I lines are very weak or not present. During the low-〈B〉 HARPS spectra, the Fe II 4491 Å has an observed FWHM of roughly 16 km s−1. Taking into account unresolved splitting that will slightly broaden the line, the Gaussian used to fit this line shown in Fig. 4 has a fixed FWHM = 14 km s−1.
As can be seen in this figure, the Si II 6699 Å line, provides a satisfactory fit to the magnetically split doublet components during the low- and high-ϕrot phases, where the splitting is resolved. However, in the case of Fe II 6149 Å, which is the most frequently used 〈B〉 diagnostic since it is present and relatively strong for the majority of Ap stars (Mathys 2017), the splitting is during all epochs contaminated by one or more unknown features such that a simple double Gaussian composite is insufficient for a satisfactory fit. The presence of the Si II 6699 Å line, on the other hand, requires quite severe Si enhancement, and not only is this the case for HD 57372, the line is quite isolated, with no likely contaminants in the vicinity. Our placement of the Fe II 6149 Å double Gaussians in Fig. 4 was therefore guided by what is shown for Si II 6699 Å, which we regard as the ground truth in this case.
It is important to note that no algorithmic fitting occurred in the creation of Figs. 3 and 4. Rather, the positions and depths of the Gaussians were all adjusted manually in order to achieve qualitative best fits. These plots are useful for guiding the eye, but they do not provide formal errors. The level of uncertainty is clearly quite high between ϕrot = 0.2 and 0.7 given that magnetic splitting was unresolved in the associated spectra.
Even in the spectra where the splitting was resolved, the behaviour of the splitting is quite different with respect to most RMSL stars for three reasons. First, in all of the HARPS spectra of HD 57372 that exhibit RMSL, there is a high degree of asymmetry in the depths of the low- and high-velocity Zeeman components. At low ϕrot, the high-velocity components are shallower than the low velocity components, and the depths of the shallower components diminish as ϕrot increases. Second, the positions of the components appear to drift towards higher velocity as ϕrot increases from ϕrot = 0. These behaviours then appear to reverse at some intermediate ϕrot value such that the mirror image occurs as ϕrot approaches unity. Third, the observed line profiles of the unblended, pure Zeeman doublet Si II 6699 Å line cannot be accounted for with a simple two-Gaussian composite during any of the ϕrot extrema spectra. On the other hand, there is no reason to expect the shapes of the split components to be Gaussian, as even for very slowly rotating stars, they depend on the distribution of the magnetic field strength over the visible stellar disc. Given the non-negligible value of the projected equatorial velocity, the shape difference between the blue and red components of the Fe II and Si II doublets in HD 57372 reflects the different combinations of Zeeman and Doppler effects on different parts of the stellar surface. The similar behaviour of the Fe II and Si II doublet lines considered here strengthens this interpretation, even though part of the component difference in Fe II must also result from a partial Paschen-Back effect.
 |
Fig. 4 Similar to Fig. 3 but for the HARPS optical spectra. As in that figure, the best available magnetically insensitive line (Fe II 4491 Å) is also shown, and the displayed Gaussians for the lines Fe II 6149 Å and Si II 6699 Å have fixed FWHM = 16 km s−1. This value is based on the Si II 6699 Å, where it gives the best fit to the magnetically split doublet components at such rotation phases as 0.046, 0.793, and 0.923. The Gaussian used to fit the line Fe II 4491 Å has a fixed FWHM = 14 km s−1. Its depth has been fixed to match the observed depth in the ϕrot = 0.540 spectrum. |
 |
Fig. 5 LSD Stokes I (bottom), and Stokes V (top) calculated using HARPS spectropolarimetric observations of HD 57372 recorded on different rotation phases. The employed line mask includes all identified spectral lines that appear to be unblended or minimally blended in. The rotational phases and the measured longitudinal magnetic field strengths are presented on the top. The dashed lines in the Stokes V panels indicate the mean uncertainties, which for the presented line mask are of the order of the thickness of these lines. |
4.3 Longitudinal magnetic field
4.3.1 HARPS observations
As we have done in our previous studies using HARPSpol data (see, e.g. Järvinen et al. 2020), we employed the least-squares deconvolution (LSD) technique following the description given by Donati et al. (1997) in order to increase the accuracy of the mean longitudinal magnetic field (〈Bz〉) determination on different rotation phases. The parameters of the lines used to calculate the LSD profiles were taken from the Vienna Atomic Line Database (VALD3; Kupka et al. 2011). Only lines that appear to be unblended or minimally blended in the Stokes I spectra were included in the line mask. The resulting profiles were scaled according to the line strength and sensitivity to the magnetic field. The final line mask contains 87 lines and includes Si, Ti, Cr, Fe, and Sr lines as well as lines belonging to the rare-earth element (REE) group, namely Nd, Dy, and Er. The LSD profiles calculated with this line mask are shown in Fig. 5. Since the diagnostic null polarisation spectrum calculated according to the definition of Donati et al. (1997) is featureless and perfectly flat, it is not presented in this figure. The mean longitudinal magnetic field is usually determined by computing the first-order moment of the LSD Stokes V profile according to Mathys (1989).
Further, as numerous studies of Ap/Bp stars in the past have revealed that different elements typically show different abundance distributions across the stellar surface, we carried out LSD magnetic field measurements using line masks for each element separately. These previous studies also indicated a kind of symmetry between the topology of the magnetic field and the element distribution. Thus, the magnetic field’s structure can potentially be studied through measurements that use spectral lines of each element separately. In Fig. A.1, we present the measurements of the longitudinal magnetic field using line masks containing Ti II, Cr II, Fe II, and Sr II lines, whereas Fig. A.2 shows the results for twice-ionised REE elements Dy III, Er III, and Nd III. Additionally, we present in Fig. A.3 magnetic field measurements carried out separately for the Si II and Si III lines in order to check for the presence of anomalies related to the vertical abundance stratification frequently observed in Ap/Bp stars (e.g. Hubrig et al. 2018). The measured mean longitudinal magnetic field strengths for all line masks are presented in Table A.1.
The presence of a magnetic field in the LSD profile is evaluated according to Donati et al. (1992), who defined a Zeeman profile with a false alarm probability of (FAP) ≤ 10−5 as a definite detection, whereas 10−5 < FAP ≤ 10−3 is a marginal detection, and FAP > 10−3 is a non-detection. All the line masks used for the eight epochs give definite detections.
The general behaviour of the mean longitudinal magnetic field strength calculated for all masks is rather similar: The field is positive throughout observed rotation phases 0.288–0.540 and negative in the phases 0.793–0.179. For the field calculated using the line mask with all 87 spectral lines, the strongest negative field (-3.32 ± 0.09 kG) was measured around the phase 0, whereas the strongest positive field (1.43 ± 0.04 kG) was detected around the phase 0.5. The observed single change of the field polarity hints at a prevailing dipolar field structure. The LSD Stokes I profiles presented in Fig. 5 appear asymmetric when the field has negative polarity, indicating the presence of an inhomo-geneous element surface distribution and are almost symmetric when the field shows positive polarity.
The longitudinal magnetic field strengths measured using Sr II and the iron-peak elements Ti II, Cr II, and Fe II show very similar behaviour. The strongest field of negative polarity is measured around the phase 0. The Ti II lines give the strongest field of −3.68 ± 0.18 kG followed by Cr II and Fe II, whereas when using the Sr II lines, the field is clearly weaker, with a strength of −2.51 ± 0.43 kG. The Ti II lines show the strongest positive field of 1.82 ± 0.08 kG at the phase 0.540. The positive magnetic longitudinal magnetic field measured using the Sr II LSD profiles shows a maximum field strength at the phase 0.288. The presence of asymmetric Stokes I profiles in the phases with the negative field indicate surface inhomogeneous abundance distribution of these elements.
Interestingly, the longitudinal magnetic fields of negative polarity measured using different REE line masks (Fig. A.2) appear to be much stronger than fields measured using other elements. Similar to several previous studies of Ap/Bp stars, this can be explained by the fact that these elements are distributed on the stellar surface closer to the location of the magnetic pole of negative polarity (e.g. Hubrig et al. 2018; Järvinen et al. 2020). The measurements using Dy III lines account for −5.56 ± 0.40 kG, and those for Nd III and Er III are around −4 kG. On the other hand, the positive longitudinal magnetic field strengths for REEs are comparable with those obtained for iron-peak elements. The Stokes I profiles exhibit a distinct structure in all rotation phases, indicating a surface inhomogeneous abundance distribution.
We did not find any indication for the presence of a vertical stratification of Si; the line profiles using both the Si II and Si III lines are very similar. Also, the measured longitudinal fields do not differ much apart from the negative field extrema, with 〈Bz〉 = −3.25 ± 0.15 kG measured for the Si II lines and 〈Bz〉 = −2.28 ± 0.09 kG for the Si III lines. Otherwise, the magnetic fields measured using both line lists follow the common pattern, being most negative around the phase 0 and most positive around phase 0.5.
Radial velocity and magnetic field measurements.
4.3.2 FORS2 observations
Twelve FORS2 spectropolarimetric observations of HD 57372 were obtained in service mode over a few months from 2021 to 2022. Unfortunately, some observations covered similar rotation phases, for example, around the phases 0.1, 0.25, and 0.37, implying larger gaps in the rotation phase coverage between 0.38 and 0.81 and between 0.81 and 0.99. The measurements of the mean longitudinal magnetic field were carried out using procedures presented in prior work (e.g. Hubrig et al. 2004a,b; Schöller et al. 2017). The obtained longitudinal magnetic field strengths, using for the measurements only the hydrogen Balmer series lines (〈Bz〉hyd) and using the entire spectrum (〈Bz〉all), present clear rotational modulation, which is expected for a large-scale organised dipole field structure, and show a change of polarity, with the strongest mean longitudinal magnetic field of negative polarity 〈Bz〉all = −6.05±0.09 kG in the rotation phase 0.990 and the strongest field of positive polarity 〈Bz〉all = 1.72±0.09 kG in the rotation phase 0.367.
In Table 2, we present, along with the radial velocity measurements reported in Sect. 3, our magnetic field measurements using all NIR and optical observations at our disposal, acquired with different instruments. Photometric, spectroscopic, and mag-netic variability of HD 57372 as a function of rotation phase is presented in Fig. 6. All measurements show a good correlation with the TESS light curve, exhibiting stronger (in absolute values) mean magnetic field moduli, mean longitudinal magnetic fields, and line profile intensities of the studied elements in rotational phases around the light curve maximum. Remarkably, equivalent widths change by up to 50% of their mean values over the course of a rotation period.
5 Atmospheric parameters and abundances
Our visual inspection of the available high-resolution spectra of HD 57372 suggests that this star, similar to other magnetic Ap/Bp stars, is extreme in its abundances of several elements. In order to estimate the stellar parameters and surface abundances of HD 57372, we created a small grid of synthetic spectra using the SYNTHE programme with ATLAS9 model atmospheres (Kurucz 2005) and the VALD atomic line list. To minimise the impact of magnetic broadening, we focused our analysis on the average of the four HARPS spectra taken during intermediate rotational phases when no magnetic splitting was observed (ϕrot = 0.288, 0.305, 0.415, 0.540). The rotational velocity was fixed to υsini = 14 km s−1 based on the width of Fe II 4491 Å, which (as previously noted) is one of the least magnetically sensitive lines present in the spectra. The microturbulent velocity was fixed to 2 km s−1.
The effective temperature (Teff) and surface gravity (log g) were assessed based on the Balmer series lines with some consideration given to the behaviour of metal lines, for example, the weakness of the Fe I lines and the strength of the Fe III lines. Whereas neutral helium is a good Teff diagnostic for normal late-B stars, it is usually found to be depleted on the surfaces of late-Bp stars, such as HD 57372. A total of 78 synthetic spectra were created, with Teff ranging from 11 500 to 15 000 K in steps of 500 K and with log g ranging from 3.7 to 4.5 in steps of 0.1 dex. The left panel of Fig. 7 shows some of the synthetic spectra that provide a reasonable match to the Hδ line of HD 57372.
Although the model spectrum with Teff = 12 500 K and log g = 3.8 provides a good fit to the cores of the Balmer series lines, we find it is important to note the following aspects. First, the optical spectra of HD 57372 contain a plethora of lines with no reasonable counterparts in the available atomic data. It is therefore reasonable to expect the depths of the hydrogen lines to be blanketed to some extent. Second, while Si I and Fe I are all but absent from the observed spectra, lines from Si II, Si III, Fe II, and Fe III are plentiful. Adoption of Teff = 12 500 K results not only in neutral Si and Fe lines that are far too strong but also in large discrepancies between the singly ionised versus doubly ionised abundances of Si and Fe.
As for the hotter model spectra, those with Teff ≥ 14 000 K are disfavoured due to the poor fits to the cores of the Balmer lines. We thus conclude that the Teff of HD 57372 is likely in the range 12 500–14 500 K and that the log g is likely in the range 3.8–4.2, and we proceeded to estimate abundances for the case of Teff = 13500 K and log g = 4.0. Due to the aforementioned prevalence of unknown lines in the spectra of HD 57372 as well as the inevitable effects of magnetic broadening, even during the low-〈B〉 epochs, we used the equivalent width (Wλ) matching technique to derive the abundances.
The vast majority of identifiable lines in the observed spectra can be attributed to Fe II, so we began by estimating the iron abundance based on 78 lines that appeared to be minimally blended. For each line, the continuum normalisation was adjusted in 300 km s−1 windows centred on the rest wavelengths, and Wλ was then measured via direct flux integration in fixed 20 km s−1 windows centred on the rest wavelengths. The same procedure was then applied to synthetic spectra, with [Fe/H] being adjusted until the synthetic Wλ matched the observed Wλ. Obvious outliers (mostly due to blending with unknown lines) were then rejected, and the line-by-line abundances were averaged. A total of 64 lines yielded [Fe+/H] = 1.610 ± 0.182. From visual inspection it was clear that the doubly ionised iron abundance did not agree with that of the singly ionised iron, so the Fe III abundance was estimated independently in the same manner using an initial list of nine lines that appeared to be free of blending with Fe II. This yielded [Fe++ /H] = 2.089 ± 0.222 from a total of nine lines. All subsequent abundance estimates were carried with fixed [Fe/H] = 1.610.
The next strongest and most numerous contributions to the observed spectra beyond iron include Ti II, Si II, S II, and Cr II. We proceeded with these elements iteratively by first estimating the Ti II abundance and keeping it constant for subsequent abundance estimates. We then estimated the Si II abundance and kept it constant for subsequent abundance estimates. This approach was repeated for a total of 31 ions that we are confident contribute to the observed spectra. The only exceptions to this general process were oxygen, silicon, and aluminium, for which both singly ionised and doubly ionised lines are present. Similar to the case of iron, the abundances of different ionisation stages were estimated independently for these elements. In the right panel of Fig. 7, we show a good fit of the observed Hδ line by the atmosphere model with abundances adjusted as quoted in Table 3.
With some noteworthy exceptions, the trend in the abundance results presented in Table 3 is generally similar to those of the majority of Ap/Bp stars whose abundances have been estimated previously (e.g. Ghazaryan et al. 2018). As is demonstrated in Fig. 8, helium is clearly depleted with respect to solar. This is a common feature of Ap/Bp star photospheres, as is the strong enhancement of silicon, iron-peak elements, and strontium and the very strong enhancement of rare-earth elements. However, one element certainly sticks out due to its remarkable overabundance: we detected a strong chlorine enhancement of 3.14 dex above solar. It appears to be stronger than ever reported for any Ap/Bp star in the past, albeit there are just six stars in the literature for which chlorine abundances have been reported. Our estimate of the ionised chlorine abundance using three different synthetic spectra is presented in Fig. 9.
 |
Fig. 6 Variability of HD 57372 as a function of rotation phase. The phase-binned TESS light curve (magenta points in Fig. 1) is shown as grey points in each panel. The ordinate scaling of the light curve is similar to that of the bottom panel of Fig. 1, but the associated y-axis tick labels have been omitted to emphasise the units of the scatter points. Panel 1 shows the 〈B〉 estimates from the Si II 6699 Å line in the HARPS spectra and from the Ce III 16133 Å and Ca II 16654 Å lines in the APOGEE spectra. Panel 2 shows the HARPS 〈Bz〉 measurements, including those obtained from numerous metal lines, from three Si III lines, from 11 Dy III lines, and from 22 Fe II lines. These ions were selected simply to demonstrate the larger degree of scatter in 〈Bz〉 when 〈B〉 is high. Panel 3 shows the 〈Bz〉 measurements from the FORS2 data, including those from the full spectra and those from the hydrogen lines. Panel 4 shows the equivalent width variations for four example ions, with the numbers of lines averaged for each ion given in parentheses. |
 |
Fig. 7 Synthetic spectra compared to our observations. Left: comparison of the observed Hδ line (black dots) from the mean low-〈B〉 spectrum of HD 57372 to solar abundance synthetic spectra (coloured curves) covering a range of Teff and log g. Right: similar to the left panel but with the blue curve showing the solar abundance synthetic spectrum with the adopted Teff = 13 500 K and log g = 4.0 and the red curve being the same but with abundances adjusted as quoted in Table 3. |
Abundance estimates from the mean low-〈B〉 HARPS spectrum of HD 57372.
 |
Fig. 8 Estimate of the helium abundance from the He I 5875 Å line for the case of Teff = 13 500 K and log g = 4.0. The dotted line is a synthetic spectrum with solar helium abundance, while the solid red line has a decreased helium abundance. Observed minus synthetic residuals are shown in the bottom panel. |
6 Discussion
HD 57372 possesses a very strong magnetic field with an exceptionally large amplitude of variation regarding the magnetic field modulus of about 10 kG over the rotation period of 7.889 d. The maximal strength of 〈B〉 = 15.66 kG was measured using the Zeeman triplet Ce III 16133 Å, and the lowest 〈B〉 = 5.23 kG was estimated using the Zeeman doublet Si II 6699 Å. All observable quantities were found to vary in phase. This includes the longitudinal magnetic field 〈Bz〉, which varies in FORS2 spectra from roughly −6 kG up to +1.7 kG, as well as the metal line strengths, whose equivalent widths change by up to 50% of their mean values over the course of a rotation period. In the high-resolution spectra recorded in visual and NIR spectra, we detected significant variability in the line profiles over the rotation cycle. We also observed in Stokes I spectra significant distortion of the resolved components of the Zeeman doublets Si II 6699 Å and Fe II 6149 Å. Such distortions are most likely due to a combination of different amounts of Doppler and Zeeman effects on different parts of the stellar surface covered by chemical spots.
The exceptional value of three for the ratio between the maximum and the minimum of the mean magnetic field modulus that is observed in this Bp star is indicative of a very unusual geometry for its magnetic field. In Fig. 10, we compare HD 57372 to other Ap/Bp stars known to exhibit RMSL in the optical. Most of the measurements were provided by Mathys et al. (1997), Elkin et al. (2012), Mathys (2017, and references therein), and Giarrusso et al. (2022). In the top panel of this figure, we present the maximum or only available 〈B〉 estimates as a function of Prot. Only a handful of other stars show a stronger 〈B〉 than HD 57372. The distribution of the ratio q of the maximum to the minimum of the mean magnetic field modulus measured in HD 57372 is presented in the bottom panel of Fig. 10 along with the ratio of 〈B〉max over 〈B〉min for other Ap/Bp stars as a function of Prot. Among the presented stars, only HR 465 shows a stronger value for the ratio q, on the order of 3.8 (Mathys et al. 1997; Giarrusso et al. 2022), with the second strongest ratio of about 2.3 being determined for HD 65339 (Mathys et al. 1997). It is notable that the magnetic field of the Ap star HD 65339, with a rotation period of 8.03 d (Mathys 2017, and references therein), shows a complex structure with the best fit of the 〈B〉 variation curve using the superposition of a cosine wave and its first harmonic (e.g. Mathys 2017, and references therein). As for the Bp star HR 465, which has a very long rotation period of about 22.7 yr (Mathys 2017, and references therein), Giarrusso et al. (2022) have concluded that its magnetic field structure should show some significant departure from a centred dipole. When inspecting figure 4 in Giarrusso et al. (2022), we noted that the shapes of the 〈B〉 phase curves of both stars, HR 465 and HD 57372, show similarly broad, fairly flat minima and sharper-peaked maxima.
For Ap/Bp stars, it is quite common to see variations in the strength of their magnetic field. These variations can easily be described by the oblique rotator model, which was introduced by Stibbs (1950). The stellar magnetic field is rotating with the star, and one can see different aspects of it. The oblique rotator assumes a dipolar magnetic field tilted with the obliquity angle β with respect to the rotation axis, which itself is inclined with respect to the line of sight by the angle i. In the cases that i is zero, one is looking at the rotation pole, and no modulation of the magnetic field with rotation can be seen. The same is true in cases of β = 0, that is, the magnetic field axis is aligned with the rotation axis.
Our longitudinal magnetic field measurements show just one change of polarity, suggesting that the field topology of HD 57372 is predominantly dipolar. Using the oblique rotator model, the inclination angle i between the rotation axis of the star and the line of sight is usually constrained if the rotation period and the stellar radius R are known and from the measurements of υsini. In Sect. 3, we reported υeq = 12 km s−1 using Gaia DR3 determinations log g = 4.399 and the stellar radius of R* = 1.88 R⊙ and assuming the TESS photometric period of 7.889 d. On the other hand, we adopted somewhat different stellar parameters, Teff = 13 500 K and log g = 4.0, in Sect. 5 to achieve a better match to the Hδ line of HD 57372. The lower values for log g and Teff imply a slightly larger stellar radius and therefore a larger equator velocity υeq, although it cannot be greater than 14 km s−1, as estimated in Sect. 4.2 using the magnetically weakly sensitive Fe II 4491 Å line with the relatively low effective Landé factor geff = 0.43. The implication of the finding that the values for equator velocity and the projected rotation velocity υsini are nearly the same is that the inclination angle i between the rotation axis of the star and the line of sight is close to 90°. However, with this angle, we would expect equal field strengths for both negative and positive poles, whereas our magnetic field measurements show a much stronger field of negative polarity.
In the following, we assume the inclination angle i = 85 ± 5° to test whether it is still possible to describe the magnetic field structure of HD 57372 by a simple dipolar field geometry. The general description for the strength of the observed longitudinal magnetic field for a simple centred dipole was presented by Preston (1967):
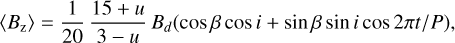 (1)
(1)
with 〈Bz〉 as the effective magnetic field, β as the angle between the rotation axis and the magnetic axis, i as the angle between the rotation axis and the line of sight, P as the rotation period of the star, u as the limb-darkening coefficient, and Bd as the strength of the dipolar magnetic field.
The relative amplitude of variation of the longitudinal field is usually characterised by the parameter r representing the ratio between Bɀ,min and Bɀ,max. In our case with Bɀ,max = −6.0 ± 0.1 kG and Bɀ,min = 1.7 ± 0.1 kG measured in FORS2 spectra using the entire spectra, we calculated r = −3.53 ± 0.22. Using the formula
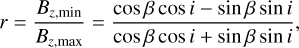 (2)
(2)
we calculated a very small obliquity angle: β = 8.90 ± 8.81°. With the limb-darkening coefficient of 0.4 (Claret 2019), we obtained an incredibly strong and implausible polar magnetic field strength of Bd = −84 ± 52 kG. It is not clear whether the exceptional structure of the magnetic field in HD 57372 is related to the unusually high field strength or to the presence of significant departures of its magnetic field from the simple centred dipole magnetic field geometry.
On the other hand, given the poor phase coverage, particularly between the rotation phases 0.2 and 0.8 (where the field modulus becomes smaller and the longitudinal field measurements indicate positive polarity), our assumption of sinusoidal field variability may be wrong. Obviously, additional high-resolution spectroscopic and polarimetric observations with a denser coverage of the rotation cycle are necessary to better constrain the phase curves for the mean field modulus and the mean longitudinal field that can be in fact anharmonical, with noticeable deviations from a sinusoid. In our observations, the 〈B〉 maximum coincides with the negative longitudinal magnetic field 〈Bz〉all extrema measured in HARPS and FORS2 spectra, while the 〈B〉 minimum is found close in phase with positive longitudinal magnetic fields. However, in case of a centred dipole where both poles come alternatively into view as the star rotates, we should also expect the modulus variation curve to appear as a perfect double wave, that is, we would see a sinusoid with twice the rotation frequency of the star. From the simultaneous consideration of the phase curves of variation of the longitudinal field and of the mean field modulus based on a more complete observational dataset, it will become possible to better constrain the magnetic field structure while taking into account a dipole offset along its axis or the superposition of dipole, quadrupole, and octupole components.
 |
Fig. 9 Estimate of the ionised chlorine abundance. The observed spectrum is shown as black dots. As indicated in the legend, three synthetic spectra are shown. The dotted grey curve has solar abundances across the board, and the dashed blue curve has nearly all abundances except for Cl adjusted to the values given in Table 3. The solid red curve is similar to the blue curve except that [Cl+ /H] has been increased by 3.14 dex. |
 |
Fig. 10 Comparison of HD 57372 to other stars known to exhibit RMSL in the optical. Upper panel: maximum or only available 〈B〉 estimate as a function of Prot. Lower panel: ratio of 〈B〉max over 〈B〉min as a function of Prot. In both panels, some of the more exceptional stars are indicated with their own symbol and colour. |
Acknowledgements
We thank the referee G. Mathys for constructive comments that helped us to improve the paper. Funding for the Sloan Digital Sky Survey V has been provided by the Alfred P. Sloan Foundation, the Heising-Simons Foundation, the National Science Foundation, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. SDSS telescopes are located at Apache Point Observatory, funded by the Astrophysical Research Consortium and operated by New Mexico State University, and at Las Campanas Observatory, operated by the Carnegie Institution for Science. The SDSS web site is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration, including Caltech, The Carnegie Institution for Science, Chilean National Time Allocation Committee (CNTAC) ratified researchers, The Flatiron Institute, the Gotham Participation Group, Harvard University, Heidelberg University, The Johns Hopkins University, L’Ecole polytechnique fédérale de Lausanne (EPFL), Leibniz-Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Extraterrestrische Physik (MPE), Nanjing University, National Astronomical Observatories of China (NAOC), New Mexico State University, The Ohio State University, Pennsylvania State University, Smithsonian Astrophysical Observatory, Space Telescope Science Institute (STScI), the Stellar Astrophysics Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Illinois at Urbana-Champaign, University of Toronto, University of Utah, University of Virginia, Yale University, and Yunnan University. Based on observations made with ESO Telescope at the La Silla Observatory under programme IDs 0108.D-0205〈B〉 and 0109.C-0265(A). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work has made use of the VALD, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
Appendix A Longitudinal magnetic field measurements using HARPS spectropolarimetric observations
The measured mean longitudinal magnetic field strengths for all line masks are presented in Table A.1. The LSD Stokes I and V profiles calculated for the separate masks with Ti II, Cr II, Fe II, and Sr II are presented in Fig. A.1. The results of the LSD technique applied to the line masks constructed for rare-earth elements Nd III, Dy III, and Er III are presented in Fig. A.2. The comparison between Stokes I and V profiles calculated for once and twice-ionised Si lines is shown in Fig. A.3. As diagnostic null spectra for all measurements appeared flat and featureless, they are not presented in these figures. The dashed lines in the Stokes V panels indicate the mean uncertainty, which in numerous cases is not larger than the thickness of these lines.
LSD mean longitudinal magnetic field measurements for different line masks.
 |
Fig. A.1 Four panels present HARPS LSD Stokes I and Stokes V spectra of HD 57372 employing line masks with Sr II, Ti II, Cr II, Fe II lines, and ionSrii lines. The dashed lines in the Stokes V panels indicate the mean uncertainties, which for the presented line masks are of the order of the thickness of these lines. |
References
- Ahumada, R., Prieto, C. A., Almeida, A., et al. 2020, ApJS, 249, 3 [Google Scholar]
- Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babcock, H. W. 1958, ApJ, 128, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Babcock, H. W. 1960, ApJ, 132, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Bernhard, K., Hummerich, S., Otero, S., & Paunzen, E. 2015, A&A, 581, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasseur, C. E., Phillip, C., Fleming, S. W., et al. 2019, Astrocut: Tools for creating cutouts of TESS images, Astrophysics Source Code Library [record ascl:1905.007] [Google Scholar]
- Chojnowski, S. D., Hubrig, S., Hasselquist, S., et al. 2019, ApJ, 873, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Chojnowski, S. D., Hubrig, S., Hasselquist, S., et al. 2020, MNRAS, 496, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Chojnowski, S. D., Hubrig, S., Labadie-Bartz, J., et al. 2022, MNRAS, 516, 2812 [NASA ADS] [CrossRef] [Google Scholar]
- Chojnowski, S. D., Hubrig, S., Nidever, D. L., et al. 2023, MNRAS, 522, 5931 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2019, Res. Notes Am. Astron. Soc., 3, 17 [Google Scholar]
- Cowley, C. R., Allen, M. S., & Aikman, G. C. L. 1975, Nature, 258, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Semel, M., & Rees, D. E. 1992, A&A, 265, 669 [Google Scholar]
- Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [Google Scholar]
- Elkin, V. G., Kurtz, D. W., & Nitschelm, C. 2012, MNRAS, 420, 2727 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, C., Høg, E., Makarov, V. V., et al. 2002, A&A, 384, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghazaryan, S., Alecian, G., & Hakobyan, A. A. 2018, MNRAS, 480, 2953 [NASA ADS] [CrossRef] [Google Scholar]
- Giarrusso, M., Cecconi, M., Cosentino, R., et al. 2022, MNRAS, 514, 3485 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Ilyin, I., Schöller, M., & Lo Curto, G. 2013, Astron. Nachr., 334, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Kurtz, D. W., Bagnulo, S., et al. 2004a, A&A, 415, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Szeifert, T., Schöller, M., Mathys, G., & Kurtz, D. W. 2004b, A&A, 415, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Järvinen, S. P., Madej, J., et al. 2018, MNRAS, 477, 3791 [NASA ADS] [Google Scholar]
- Jagelka, M., Mikulášek, Z., Hümmerich, S., & Paunzen, E. 2019, A&A, 622, A199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Järvinen, S. P., Hubrig, S., Mathys, G., et al. 2020, MNRAS, 499, 2734 [CrossRef] [Google Scholar]
- Jarzębowski, T. 1960, Acta Astron., 10, 119 [Google Scholar]
- Kupka, F., Dubernet, M. L., & VAMDC Collaboration 2011, Balt. Astron., 20, 503 [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 14 [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [Google Scholar]
- Lightkurve Collaboration (Cardoso, J. V. d. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mathys, G. 1989, Fund. Cosmic Phys., 13, 143 [Google Scholar]
- Mathys, G. 1990a, A&A, 232, 151 [NASA ADS] [Google Scholar]
- Mathys, G. 1990b, A&A, 236, 527 [NASA ADS] [Google Scholar]
- Mathys, G. 2017, A&A, 601, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G., & Lanz, T. 1992, A&A, 256, 169 [NASA ADS] [Google Scholar]
- Mathys, G., Hubrig, S., Landstreet, J. D., Lanz, T., & Manfroid, J. 1997, A&AS, 123, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G., Romanyuk, I.I., Hubrig, S., et al. 2019, A&A, 624, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Nidever, D. L., Holtzman, J. A., Allende Prieto, C., et al. 2015, AJ, 150, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Delabre, B., et al. 2000, SPIE Conf. Ser., 4008, 582 [NASA ADS] [Google Scholar]
- Preston, G. W. 1967, ApJ, 150, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Preston, G. W. 1969, ApJ, 156, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Przybylski, A. 1961, Nature, 189, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Renson, P., & Manfroid, J. 2009, A&A, 498, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., et al. 2020, MNRAS, 495, 2796 [NASA ADS] [CrossRef] [Google Scholar]
- Schöller, M., Hubrig, S., Fossati, L., et al. 2017, A&A, 599, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, G. 1978, Astron. Nachr., 299, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Stibbs, D. W. N. 1950, MNRAS, 110, 395 [Google Scholar]
- Wilson, J. C., Hearty, F. R., Skrutskie, M. F., et al. 2019, PASP, 131, 055001 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 TESS light curve of HD 57372. The upper panels show the observed data from each of the four TESS sectors. The grey points in the lower panel are all of the data phased by the 7.889148 d rotation period and with 2458 492.07 as a reference epoch of maximum brightness. Magenta points show the data binned in increments of ϕrot = 0.005. |
| In the text | |
 |
Fig. 2 Line identifications in the H-band spectra of HD 57372. Upper panel: line identifications in the APOGEE spectrum of HD 57372 at the rotational phase ϕrot = 0.375. The hydrogen Brackett series lines are labelled along the top, while metal lines are labelled along the bottom. Unidentified lines are indicated by small red ticks below the spectrum. Lower panel: variability of individual lines as a function of ϕrot. |
| In the text | |
 |
Fig. 3 Mean magnetic field modulus estimates from the Ce III 16133 Å and Ca II 16654 Å lines in the APOGEE H-band spectra. The relatively magnetically insensitive unknown line at 15 335 Å is shown in order to demonstrate that it is well fit by a single Gaussian with FWHM = 21 km s−1 during the low-〈B〉 epochs. For Ce III 16133 Å and Ca II 16654 Å, the triple Gaussians each have the same FWHM = 21 km s−1. The associated 〈B〉 estimates are given below each line profile, but it is important to note that the low-〈B〉 values are highly uncertain due to the magnetic splitting being unresolved at APOGEE’s resolution . |
| In the text | |
 |
Fig. 4 Similar to Fig. 3 but for the HARPS optical spectra. As in that figure, the best available magnetically insensitive line (Fe II 4491 Å) is also shown, and the displayed Gaussians for the lines Fe II 6149 Å and Si II 6699 Å have fixed FWHM = 16 km s−1. This value is based on the Si II 6699 Å, where it gives the best fit to the magnetically split doublet components at such rotation phases as 0.046, 0.793, and 0.923. The Gaussian used to fit the line Fe II 4491 Å has a fixed FWHM = 14 km s−1. Its depth has been fixed to match the observed depth in the ϕrot = 0.540 spectrum. |
| In the text | |
 |
Fig. 5 LSD Stokes I (bottom), and Stokes V (top) calculated using HARPS spectropolarimetric observations of HD 57372 recorded on different rotation phases. The employed line mask includes all identified spectral lines that appear to be unblended or minimally blended in. The rotational phases and the measured longitudinal magnetic field strengths are presented on the top. The dashed lines in the Stokes V panels indicate the mean uncertainties, which for the presented line mask are of the order of the thickness of these lines. |
| In the text | |
 |
Fig. 6 Variability of HD 57372 as a function of rotation phase. The phase-binned TESS light curve (magenta points in Fig. 1) is shown as grey points in each panel. The ordinate scaling of the light curve is similar to that of the bottom panel of Fig. 1, but the associated y-axis tick labels have been omitted to emphasise the units of the scatter points. Panel 1 shows the 〈B〉 estimates from the Si II 6699 Å line in the HARPS spectra and from the Ce III 16133 Å and Ca II 16654 Å lines in the APOGEE spectra. Panel 2 shows the HARPS 〈Bz〉 measurements, including those obtained from numerous metal lines, from three Si III lines, from 11 Dy III lines, and from 22 Fe II lines. These ions were selected simply to demonstrate the larger degree of scatter in 〈Bz〉 when 〈B〉 is high. Panel 3 shows the 〈Bz〉 measurements from the FORS2 data, including those from the full spectra and those from the hydrogen lines. Panel 4 shows the equivalent width variations for four example ions, with the numbers of lines averaged for each ion given in parentheses. |
| In the text | |
 |
Fig. 7 Synthetic spectra compared to our observations. Left: comparison of the observed Hδ line (black dots) from the mean low-〈B〉 spectrum of HD 57372 to solar abundance synthetic spectra (coloured curves) covering a range of Teff and log g. Right: similar to the left panel but with the blue curve showing the solar abundance synthetic spectrum with the adopted Teff = 13 500 K and log g = 4.0 and the red curve being the same but with abundances adjusted as quoted in Table 3. |
| In the text | |
 |
Fig. 8 Estimate of the helium abundance from the He I 5875 Å line for the case of Teff = 13 500 K and log g = 4.0. The dotted line is a synthetic spectrum with solar helium abundance, while the solid red line has a decreased helium abundance. Observed minus synthetic residuals are shown in the bottom panel. |
| In the text | |
 |
Fig. 9 Estimate of the ionised chlorine abundance. The observed spectrum is shown as black dots. As indicated in the legend, three synthetic spectra are shown. The dotted grey curve has solar abundances across the board, and the dashed blue curve has nearly all abundances except for Cl adjusted to the values given in Table 3. The solid red curve is similar to the blue curve except that [Cl+ /H] has been increased by 3.14 dex. |
| In the text | |
 |
Fig. 10 Comparison of HD 57372 to other stars known to exhibit RMSL in the optical. Upper panel: maximum or only available 〈B〉 estimate as a function of Prot. Lower panel: ratio of 〈B〉max over 〈B〉min as a function of Prot. In both panels, some of the more exceptional stars are indicated with their own symbol and colour. |
| In the text | |
 |
Fig. A.1 Four panels present HARPS LSD Stokes I and Stokes V spectra of HD 57372 employing line masks with Sr II, Ti II, Cr II, Fe II lines, and ionSrii lines. The dashed lines in the Stokes V panels indicate the mean uncertainties, which for the presented line masks are of the order of the thickness of these lines. |
| In the text | |
 |
Fig. A.2 Same as in Fig. A.1 but for REEs Nd III, Dy III, and Er III. |
| In the text | |
 |
Fig. A.3 Same as in Fig. A.1 but for Si II and Si III. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


