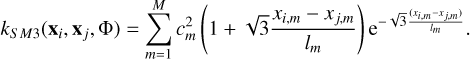| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348960 | |
| Published online | 08 July 2024 | |
An improved correction of radial velocity systematics for the SOPHIE spectrograph★
1
Aix-Marseille Univ, CNRS, CNES, Institut Origines, LAM,
Marseille,
France
e-mail: salome.grouffal@lam.fr
2
ENS Paris-Saclay,
Gif-sur-Yvette,
France
3
Institut d’astrophysique de Paris, UMR 7095 CNRS université pierre et marie curie,
98 bis, boulevard Arago,
75014
Paris,
France
4
Observatoire Astronomique de l’Université de Genève,
51 Chemin de Pegasi b,
1290
Versoix,
Switzerland
Received:
14
December
2023
Accepted:
24
April
2024
High-precision spectrographs can on occasion exhibit temporal variations in their reference velocity or nightly zero point (NZP). One way to monitor the NZP is to measure bright stars, whose intrinsic radial velocity variation is assumed to be much smaller than the instrument precision. The variations of these bright stars, which is primarily assumed to be instrumental, are then smoothed into a reference radial velocity time series (master constant) that is subtracted from the observed targets. While this method is effective in most cases, it does not fully propagate the uncertainty arising from NZP variations. We present a new method for correcting for NZP variations in radial velocity time series. This method uses Gaussian processes based on ancillary information to model these systematic effects. Moreover, it enables us to propagate the uncertainties of this correction into the overall error budget. Another advantage of this approach is that it relies on ancillary data that are collected simultaneously with the spectra and does not solely depend on dedicated observations of constant stars. We applied this method to the SOPHIE spectrograph at the Haute-Provence Observatory using a few instrument housekeeping data, such as the internal pressure and temperature variations. Our results demonstrate that this method effectively models the red noise of constant stars, even with a limited number of housekeeping data, while preserving the signals of exoplanets. Using simulations with mock planets and real data, we found that this method significantly improves the false-alarm probability of detections. It improves the probability by several orders of magnitude. Additionally, by simulating numerous planetary signals, we were able to detect up to 10% more planets with small-amplitude radial velocity signals. We used this new correction to reanalyse the planetary system around HD158259 and to improve the detection of the outermost planets. We propose this technique as a complementary approach to the classical master-constant correction of the instrumental red noise. We also suggest to decrease the observing cadence of the constant stars to optimise the telescope time for scientific targets.
Key words: instrumentation: spectrographs / methods: data analysis / techniques: radial velocities / planetary systems / stars: individual: HD 158259
Full Tables D.1 and F.1 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/687/A148
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The radial velocity (RV) technique is one of the most prolific techniques for detecting and characterising exoplanets. Since the discovery of 51 Peg b (Mayor & Queloz 1995), a total of 1079 planets1 have been discovered using the RV technique. This technique remains the most efficient technique for measuring the mass of exoplanets, which is essential for understanding their composition.
However, instruments suffer from systematics. These sys-tematics mainly concern instruments that are not in vacuum chambers, such as the SOPHIE spectrograph (Perruchot et al. 2008; Bouchy et al. 2009), which is mounted on the 1.93 m telescope of the Haute-Provence Observatory2. Despite being stabilised in pressure and temperature, the SOPHIE spectro-graph is still sensitive to small environmental variations that are not perfectly monitored by calibrations. This leads to a long-term variation in the nightly zero point (hereafter, NZP) of the spectrograph, as presented by Courcol et al. (2015).
To correct for these instrumental variations, a sliding median is used to build an estimate of the NZP based on the RV variations of a few bright stars that are assumed to be constant. This NZP model, known as the master constant, is subtracted from the RV time series measured with SOPHIE (Courcol et al. 2015; Heidari et al. 2024). This method has been shown to significantly decrease the RV root mean square (RMS) of the star HD 185144 from 5.4 m s−1 to 1.6 m s−1 (Courcol et al. 2015), enabling the detection of low-mass planets (Hobson et al. 2018, 2019; Díaz et al. 2019; Hara et al. 2020). However, by subtracting the master constant from the RV time series before their analysis, the error budget is not fully propagated. This can potentially affect the false-alarm probability (FAP) of detections and might introduce uncertainties in the estimation of planetary parameters.
Gaussian processes (hereafter GPs) are now increasingly used in many domains of astrophysics, especially to model stochastic processes in both photometry and RV time series (e.g., see review by Aigrain & Foreman-Mackey 2023). GPs provide a flexible and mathematically simple approach to modelling stochastic processes. GPs could be an interesting alternative for correcting NZP variations in RV spectrographs such as SOPHIE.
In this work, we propose a method that uses GPs based on ancillary information to improve the correction for NZP variations in RV time series. This method is inspired by the method that is commonly used to correct for space-based photometry in transit detection (Gibson et al. 2012; Aigrain et al. 2016) and transmission spectroscopy (Evans et al. 2015, 2017). Using GPs, we can handle the correlation between the RVs and ancillary information without choosing any deterministic functional form. We applied this method to SOPHIE data using the housekeeping data as ancillary information, such as pressure and temperature, which is measured by the spectrograph every 6 minutes.
This paper is organised as follows. Section 2 presents the different housekeeping data and their potential impact on the RV time series. Section 3 describes the GP model and the proposed method. In Sect. 4, we apply the method on SOPHIE constant stars and test it on mock planets, highlighting its improvement in detecting low-mass planets. Section 5 demonstrates the application of the method on the system HD 158259. Finally, in Sect. 6, we present our conclusions, discuss the impact on observing strategies and planet detection with SOPHIE, and consider possible avenues for further improvement.
 |
Fig. 1 Variations in housekeeping data monitored at different locations of the SOPHIE instrument with a cadence of 6 min. The pressure corresponds to the internal pressure inside the nitrogen-filled tank where the dispersal elements are located. The temperature is monitored in the air of the container, the air in the spectrograph, the shutter, the east and west granite benches, the grating, the cryostat cover, the ferrule, and the Coudé tube (path of the fibres from the telescope to the spectrograph; see Perruchot et al. (2008) and the Haute-Provence Observatory website for more details). Near BJD = 2 457 700, the SOPHIE thermal regulation was upgraded, improving the temperature stability inside the spectrograph. |
2 Systematic effects in radial velocity spectrographs
The RV time series of a star is the addition of the astrophysical signal, some correlated noise from systematics, and uncorrelated white noise. These systematics might result from variations in the spectral indices of the air inside the spectrograph, especially if it is not a vacuum tank. Fluctuations in temperature and pressure cause the change in the spectral indices. For instance, a small variation of 1 mbar in pressure might induce a spectral shift up to 300 m s−1, and a temperature variation of 1 K might cause a shift of up to 90 m s−1 (Eggenberger & Udry 2010). To limit these variations, the SOPHIE spectrograph is located in a pressure- and temperature-controlled chamber. Great efforts have already been made by the observatory staff to limit these variations. However, some fluctuations of the internal pressure and temperature measured in the spectrograph environment are still observed (see Fig. 1 and Table F.1) and are expected to cause RV systematics.
Figure 1 shows that several of these housekeeping data exhibit similar patterns, suggesting that they are correlated. To evaluate this correlation, the heat map in Fig. 2 shows the Pearson coefficient between all the housekeeping variables presented in Fig. 1. The containers, the ferrule, the east and west bench, and the grating are correlated with each other with a Pearson coefficient above 0.5 and up to 0.98. Only the temperature at the Coudé tube is not correlated with the other parameters. The cryostat also shows a different behaviour with a strong negative linear correlation with the other parameters. As a consequence, we only considered as housekeeping data (i) the internal pressure and the temperatures of the (ii) air in the container, (iii) the Coudé tube, and (iv) the cryostat.
 |
Fig. 2 Heat map of the Pearson coefficients to evaluate the linear correlation between the 10 housekeeping variables available for the SOPHIE instrument. |
3 Gaussian processes to correct for nightly zero-point variations
3.1 Gaussian process model
A GP is a type of stochastic process y(x) such that for any finite collection of input x1,…,xN, the distribution of vector 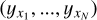 is a multivariate Gaussian distribution (Rasmussen & Williams 2006). We can write the joint probability distribution p(y) over the finite sample (of dimension N) of data y = {yi}i=1,…,N from the GP as
is a multivariate Gaussian distribution (Rasmussen & Williams 2006). We can write the joint probability distribution p(y) over the finite sample (of dimension N) of data y = {yi}i=1,…,N from the GP as
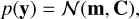 (1)
(1)
where m is the mean vector and represents the other deterministic effects, such as the proper motion of the star or constant offset of the instrument, and C is the covariance matrix, such as Cij = k(|ti − tj|), with k(|ti − tj|) commonly called the kernel.
We assume the RV time series of a star y0(t0) sampled at times 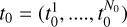 , such that at each time, housekeeping data
, such that at each time, housekeeping data 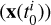 such as pressure and temperature are available. We search for exoplanets around this star. We also have time series of p constant stars yi(ti), i = 1,…, p. For each i, yi(ti) is the time series of the RV of the constant star i, sampled at times
such as pressure and temperature are available. We search for exoplanets around this star. We also have time series of p constant stars yi(ti), i = 1,…, p. For each i, yi(ti) is the time series of the RV of the constant star i, sampled at times 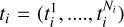 . We assumed that all the stars are affected by the same nightly zero point shift, ɀ(t). This was modelled as a GP whose mean was assumed to be zero and whose kernel k was defined over variables x and depended on hyperparameters Φ. We ignored the uncertainties on the input variables such as pressure and temperature. The covariance between ɀ sampled at time ti and tj is k(xi(ti), xj(tj); Φ). The covariance of ɀ sampled at times ti and tj is denoted by Vij(Φ).
. We assumed that all the stars are affected by the same nightly zero point shift, ɀ(t). This was modelled as a GP whose mean was assumed to be zero and whose kernel k was defined over variables x and depended on hyperparameters Φ. We ignored the uncertainties on the input variables such as pressure and temperature. The covariance between ɀ sampled at time ti and tj is k(xi(ti), xj(tj); Φ). The covariance of ɀ sampled at times ti and tj is denoted by Vij(Φ).
We further assumed that their measurements are affected by photon noise. The photon noise affecting star i measured at time 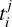 is denoted by
is denoted by 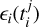 . The vectors ϵi were assumed to be Gaussian, with a vanishing mean and a covariance Σi. Finally, each star was assumed to have a deterministic mean function depending on the variables θi, mi(t; θi),
. The vectors ϵi were assumed to be Gaussian, with a vanishing mean and a covariance Σi. Finally, each star was assumed to have a deterministic mean function depending on the variables θi, mi(t; θi),
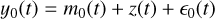 (2)
(2)
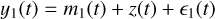 (3)
(3)
 (4)
(4)
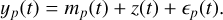 (5)
(5)
When we concatenate the column vectors (yi(ti)) with i = 0,…, p into a single column vector of size 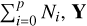 , the model of the data is fully described by the mean and covariance of Y. Its mean µ(θ0, …θp) is the concatenation of vectors (mi(ti)) i = 0..p, and its covariance C is a block matrix such that its i, jth element is an Ni × Nj matrix,
, the model of the data is fully described by the mean and covariance of Y. Its mean µ(θ0, …θp) is the concatenation of vectors (mi(ti)) i = 0..p, and its covariance C is a block matrix such that its i, jth element is an Ni × Nj matrix,
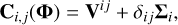 (6)
(6)
where δij is the Kronecker symbol. Equivalently,
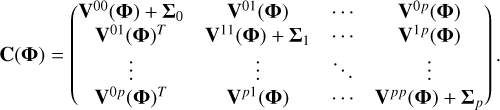 (7)
(7)
where Σ1: is a block diagonal matrix with matrices Σi on the diagonal. V0,1:(Φ) is a matrix of size 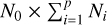 that can be described as N blocks each of size N0 × Ni made of V0i(Φ). Finally, V1:,1:(Φ) is an
that can be described as N blocks each of size N0 × Ni made of V0i(Φ). Finally, V1:,1:(Φ) is an 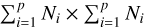 matrix.
matrix.
The variables µ(θ0,…, θp), which are denoted µ(θ) for simplicity, and C(ϕ) fully describe the likelihood of the concatenated vector of all available data Y, p(Y | θ, Φ),
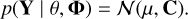 (9)
(9)
In principle, this likelihood can directly be used to infer the parameters θ and Φ. However, this requires the inversion of the full matrix C, which might be costly.
To infer the GP hyperparameters of the kernel, we proceeded as follows: We first linearly interpolated the values of each housekeeping variable at the times of the observation after removing outliers at more than 3σ from the median. The housekeeping variables were measured every 6 minutes, and we chose the closest value to the observation time of the star. Each variable was normalised at a zero mean and divided by its standard deviation. Finally, we computed the posterior distribution of the parameters of our model, Θ and Φ, based on the data of the constant stars.
Using the Bayes theorem, we write the posterior distribution as
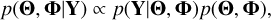 (10)
(10)
with p(Y |Θ, Φ) the likelihood defined in Eq. (9), and p(Θ, Φ) the prior on the parameters.
We derived the posterior distribution for each hyperparame-ter and planetary parameter using a Bayesian method. We used the Markov chain Monte Carlo (MCMC) method as implemented in the emcee package (Foreman-Mackey et al. 2013) to explore the joint posterior distribution of the parameters. The convergence of the MCMC was tested using the integrated autocorrelation time that quantifies the Monte Carlo error and the efficiency of the MCMC (Goodman & Weare 2010). We checked that all the chains were longer than 50 times the integrated autocorrelation time.
3.2 Choice of the kernel
The covariance kernel k(xi,xj; Φ), quantifies the self-similarity of the GP. In classical least-square regression, a simple and diagonal covariance matrix is assumed, and the variance associated with each observation is known. However, this assumption does not hold in general, especially when considering instrumental systematics. The covariance kernel addresses this issue and allows for more complex and flexible covariance models. The choice of the kernel is a fundamental part of GP regressions as it encodes the structure of the random variations of the process. In our study, we tested two different kernels: the square-exponential kernel, and the Matérn 3/2 kernel (Rasmussen & Williams 2006). Additionally, following the approach of Gibson (2014), we tested two methods for combining the kernels of each housekeeping variable. The first method involves using a kernel with the product of each individual kernel, which captures the dependences between dependent housekeeping variables as follows:
According to the strong linear correlations shown in Fig. 2, this seems to be the preferred approach as the housekeeping parameters are likely caused by the same physical process and hence depend on each other. The other solution we tested is a sum of the various kernels representative of a set of independent variables as follows:
Here, c is the height-scale hyperparameter, and l is the inverse length-scale hyperparameter controlling the correlation length. Kernels with a few hyperparameters such as the square-exponential or Matérn 3/2 are preferred over other kernels such as the rational quadratic (Eq. (4.19) in Rasmussen & Williams 2006) to avoid that the GPs are too flexible. As the impact of each variation on the RV time series is unknown, we tested the two approaches.
Time-dependent kernels were also initially considered, but were too flexible and significantly affected the planetary signals. In the worst cases, the planetary signal completely vanished regardless of the functional forms of the kernel.
3.3 Two NZP corrections: GP master constant, and noise model
We suggest two approaches to correct for NZP variations based on GPs. Following Eqs. (2.23) and (2.24) from Rasmussen & Williams (2006), the mean and covariance of the distribution of yi(t0) conditioned on yi(ti), i = 1,..p, denoted by 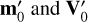 are
are
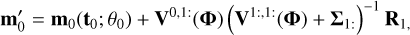 (15)
(15)
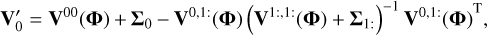 (16)
(16)
where R1: is the column vector of dimension 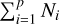 concatenating y1(t1) − m1(t1; θ1),…, yp(tp) − mp(tp; θp). To simplify the analysis, two choices can be made.
concatenating y1(t1) − m1(t1; θ1),…, yp(tp) − mp(tp; θp). To simplify the analysis, two choices can be made.
- 1.
The values of Φ can be instantiated as maximising the likelihood describing constant star RV datasets y1(t1),…, yp(tp), and Φ can be considered as a constant in Eqs. (15) and (16). In this case, we computed a new master constant based on the GP prediction.
- 2.
The posterior distribution of Φ can be computed conditioned on y1(t1),…, yp(tp) and be used as a prior in the analysis of the RV time series of interest, y0, with the covariance
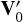 and the mean
and the mean 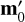 . This approach gives more conservative uncertainties.
. This approach gives more conservative uncertainties.
This second approach might also be directly implemented in the periodogram analyses of the ℓ1 (Hara et al. 2017) to search for periodic signals in the data. We modelled the red noise in the ℓ1 as the covariance instantiated with the kernel whose parameters were adjusted on constant stars.
4 Application to SOPHIE constant stars
To correct for NZP variations, the classical master constant was initially developed by Courcol et al. (2015) based on four constant stars that were assumed to have no planets: HD 185144 (Howard et al. 2010), HD 9407, HD 221354, and HD 89269A (Howard et al. 2011), along with 51 other targets that are monitored by SOPHIE. Recently, Heidari et al. (2024) updated the master constant using a larger sample of constant stars, including the initial four and all the SOPHIE sub-programme 1 (SP1) targets (Bouchy et al. 2009) with low RV jitter and no detected periodic signal in their periodogram. We adopted the same sample of constant stars to train our GP-based NZP correction.
4.1 Kernel selection
The first step was to select which housekeeping variable were used for the NZP correction. As explained in Sect. 2, some housekeeping variables show the same pattern and are likely different proxies of the same effect. Thus, we initially tested the air temperature in the container and the spectrograph, the Coudé tube, and the cryostat. Since changes in pressure inside the spectrograph might cause an RV variation at a level of several hundred m s−1 (Eggenberger & Udry 2010), we also tested the internal pressure in our initial list of housekeeping variables.
We fitted the sample of constant stars from Heidari et al. (2024) using the MCMC method described in Sect. 3. We used the five aforementioned housekeeping variables and both the additive (Eq. (13)) and multiplicative (Eq. (11)) SE kernels. Uniform priors were used for all hyperparameters. In both cases, the MCMC was able to constrain the hyperparameters for all housekeeping variables, except for the cryostat. For the hyper-parameter of the latter, the posterior distribution was similar to that of the prior. Since its hyperparameter is unconstrained, we concluded that the cryostat has no significant impact on the NZP variations. Therefore, we excluded it from the following analysis, but kept the other four housekeeping variables: the internal pressure, the temperatures of the air in the container and spectrographs, and the Coudé tube.
The second step was to select the best kernel from the list presented in Sect. 3.2 using the cross-validation method (see Chap. 5 of Rasmussen & Williams 2006). We divided the RV data of the constant star sample into two sets: a training set with 67% of the data, selected randomly, and a test set with the remaining 33%. The hyperparameters of the four kernels using the MCMC algorithm were estimated on the training set. We then computed the likelihood of the test set at each step of the MCMC. The upper panel of Fig. 3 displays the posterior distributions of the log-likelihood of the test set for each kernel. The multiplicative kernels (Eqs. (11) and (12)) give a higher log-likelihood and are therefore preferred over the additives ones, especially for the SE kernel. This corroborates our hypothesis that all the housekeeping variables depend on each other. In this analysis, the multiplicative M3 kernel exhibits the highest log-likelihood, and we therefore adopted it. The Matérn class kernel offers a degree of variability of the process in between exponential kernels (non-derivable realisations) and SE kernels (smooth realisations) (Rasmussen & Williams 2006).
The third step involved evaluating whether considering multiple housekeeping variables improved the analysis. We performed the same cross-validation as for the choice of the kernel, but with different housekeeping variables. The lower panel of Fig. 3 presents the results. The full model, selected with a multiplicative M3 kernel, is shown in blue. We also tested a model with only the temperature of the Coudé tube (green), only the temperature of the air in the container (yellow), and with the three temperatures combined in a multiplicative M3 kernel (purple). Considering only one temperature yields a significantly lower log-likelihood than considering all three temperatures. The pressure alone (red histogram) performs better than using the temperature alone, confirming that pressure has a greater impact on the NZP variations. This analysis demonstrates that the highest log-likelihood is achieved with the full model. We also attempted to add a time-based SE kernel to the multiplicative M3 kernel based on the housekeeping variables. This resulted in an equivalent log-likelihood.
As discussed in Sect. 2, the amplitude of the temperature and pressure variations decreases significantly near BJD = 2 457 700 due to an upgrade of the thermal regulation in the spectrograph (Hobson et al. 2018). This upgrade improved the instrumental stability and consequently decreased the NZP variations. The covariance matrix between the RV time series and the housekeeping data should therefore be affected as well.
Thus, we decided to split the analysis into two parts to consider this upgrade. The first fit with an MCMC of the constant star time series was therefore made only with an M3 multiplicative kernel on the three temperatures and pressure to avoid the over-flexibility of a time-based SE kernel.
The posterior distributions for each parameter are reported in the corner plots in Figs. A.1 and A.2 as blue histograms before and after the upgrade (respectively). The median and 68.3% credible intervals are specified for each parameter. The temperature variations in the container strongly influence the RVs before the upgrade on the spectrograph, but they no longer affect them after the upgrade. This is consistent with the upgrade, which focuses on the thermal regulation of the air inside the spectro-graph (as shown in Fig. 1) to better isolate the instrument from the air inside the container.
The final result of the MCMC for this GP noise model (Eq. (12)) is shown in Fig. 4, where its prediction is compared with the master constant developed by Heidari et al. (2024). The RMS of the residuals for the classical master constant correction is about 2.27 m s−1, slightly larger than the RMS of the residual from our GP prediction with a value of 2.15 m s−1. We were able to reproduce the main variations in the constant stars using only the pressure and three temperature variations. The difference between the classical master constant and the work presented here is shown in the lower panel of Fig. 4. At BJD ≈ 2 456 710, all the constant stars show a significant drop in the RV that is not reproduced by the GPs. This drop is contemporaneous with a change in the wavelength calibration of the spectrograph (Hobson et al. 2018) and is thus independent of the temperature or pressure inside the instrument.
Figure 5 shows the quantile–quantile analysis of the residuals of the classical master constant correction and the GP master constant from this work. The cumulative distribution function of the residuals is compared to the theoretical quantiles from a normal distribution. The analysis demonstrates that the GP master constant yields more Gaussian residuals, especially in the tail of the distribution. This supports the use of this method.
Figure 6 compares the periodograms of the residues from the new GP master constant and the master constant correction (Heidari et al. 2024). No signal at a specific period is identified in the residuals from the method developed in this work. The peak at ≈360 days and the peak around 3000 days are significant in the classical method correction. As discussed in Heidari (2023), these signals are likely due to instrumental variations and a potential long-period signal in one of the constant stars. Even though they are still present in the master constant correction, they have already been much improved since the last master constant developed in Courcol et al. (2015). The absence of these signals in the GP methods highlights that the latter probably corrects the annual temperature and pressure variations better. As no peak is identified in the periodogram of the residuals, we decided to include no other parameters in the MCMC.
As the GPs are based on housekeeping variables, they should not model the Keplerian variation of a planet if it is present in the constant star. Even when constant stars show no significant variations over several years, the presence of a planet with a very small amplitude cannot be ruled out. This ensures that the GP does not consider such a planet important. To investigate this, we chose the constant star HD 185144 and injected a Keplerian signal with an amplitude of 1 m s−1 and an orbital period of 11 days or 200 days. We then performed the same GP analysis on the time series of all constant stars, including the star with the injected planet. Figure 7 illustrates the results with two periodograms of the residuals. In both cases, the signal of the injected planet is detected, demonstrating that the GP does not model a signal that is unrelated to pressure and temperature variations. These signals are also absent in the periodogram of the GP master constant and are not injected during the correction of the NZP of a star.
 |
Fig. 3 Results of the cross-validation method for selecting the best kernel. Upper panel: we compared four kernels with multiplicative and additive kernels with a Matérn 3/2 (M3) or a square-exponential (SE) kernels with the temperature of the air in the container, and the spectro-graph, temperature of the Coudé tube, and pressure. The model that obtained the highest log-likelihood was preferred. This is the multiplicative M3 kernel (MM3) in hashed blue. Lower panel: comparison of the M3 or MM3 kernel with the difference number of housekeeping variables. We compared models with only one temperature (yellow and green), with pressure alone (red), with only three temperatures (purple), the multiplicative M3 kernel with three temperatures and pressure (blue), and the multiplicative M3 kernel with the addition of an SE kernel on time (pink). |
 |
Fig. 4 Result of the fit of the NZP with GPs. Upper panel: SOPHIE RVs for the constant stars are represented as black dots with error bars. The master constant time series developed by Heidari et al. (2024) is represented as orange dots. The new GP master constant developed in this work and trained on the constant stars is represented with blue dots, and the blue shaded area represents the corresponding uncertainties. Lower panel: difference between the master constant method (MC) and the GP master constant method (GP MC). |
 |
Fig. 5 Quantile–quantile analysis comparing the quantile of the residuals for the master constant correction (orange dots) and the GP master constant correction (blue dots) with the corresponding theoretical quantile of a normal distribution. When the cumulative distribution of the residuals follows a normal distribution, the residuals should be aligned along a 45° line (red line). |
4.2 Test on simulated planets
To test the method for detecting and characterising exoplanets, we simulated mock planets in the RV data of the constant star HD 89269A. We injected planets with periods ranging from 2 to 3000 days and with a semi-amplitude ranging from 0.5 to 10 m s−1, both with a logarithmic scale. For each simulation, the eccentricity of the orbit was randomly chosen in a beta distribution following Kipping (2013) for multi-planetary systems and with a random argument of periastron between 0 and 2π. We evaluated the number of planets detected in a grid of cells in Fig. 8. We generated 40 planets within each cell with random periods and semi-amplitudes within a given range. A planet was considered detected when its orbital period was valid with an error of 2% and its FAP (FAPs, determined following the method described in Delisle et al. 2020) was logıo(FAP) ≤ −1.3. For each mock planet, we generated an 11-periodogram and considered only the most significant peak. We then counted the number of detected planets within each cell. We tested both the GP correction and the classical NZP correction for each simulated planet (first and second panels of Fig. 8). This analysis aimed to identify the more efficient method given a region of parameters. The last panel of Fig. 8 shows the difference between the two methods regarding the number of detected planets. A red cell is characterised by more detections by the GP method, and a blue cell has more detections by the classical methods.
Throughout the entire parameter space, the GP method detected more planets with 2% more planets using this method. Although this number is small because many planets were detected in both cases, the GP method is more efficient for small amplitudes. Within the range 0.5–1.2 m s−1, the GP method detected 7.4% more planets and even 10% more planets in the range 0.5–0.7 m s−1. For long periods, the classical method remains slightly better in some cases, primarily because GPs tend to lower the detection level of long-period signals. Therefore, the new GP instrumental correction could be used to detect small planetary signals.
This study was performed with a single-planet system for simplicity alone, and we did not use the GP noise model directly in the periodogram because it tends to lower the FAP of the signal.
When a planet is detected after the NZP correction, its orbital parameters should also be correct. We injected a three-planet system in the constant star HD 89269A. The first planet had a semi-amplitude of 4 m s−1, an orbital period of 35 days, and a circular orbit. The second planet had a semi-amplitude of 3 m s−1, an orbital period of 90 days, and an eccentric orbit with e = 0.3. The last planet had a semi-amplitude of 2.5 m s−1 and an orbital period of 264 days. All parameters are indicated in Table B.1. All planets were clearly detected with a log10(FAP) ≤ −1.3. We then modelled these simulated data with an MCMC using the three methods for correcting the NZP variations. For all orbital parameters, we adopted large uniform priors, and we used an MCMC with 40 walkers with 3 × 104 iterations and 4 × 104 steps of burn-in.
The results of the fits are provided in Table B.1. For the three methods, the parameters are recovered within 1σ. The classical master constant and the GP master constant show similar median and 68.3% credible intervals. The third method is different as it models the covariance matrix directly within the MCMC, although the hyperparameters are constrained within the posterior of the constant star training. As discussed in Evans et al. (2015), this approach is much faster than using large and uniform priors for the hyperparameters because GPs are computationally expensive. The derived uncertainties are therefore lower limits of the true uncertainties, but are more accurate than those obtained with the master constant method, where the uncertainties are not propagated. As reported in Table B.1, the uncertainties for all the periods and amplitude parameters are larger by between 1.5 and 2 times with the GP noise model. For the eccentricities and argument of periastron, the uncertainties are equivalent. The GPs reflect our ignorance of instrumental systematics and produce more consistent uncertainties on the planetary parameters.
 |
Fig. 6 Generalised Lomb–Scargle (GLS) periodogram (Zechmeister & Kürster 2009) of the residuals. The residuals of the NZP correction with the classical method are shown in orange, and the correction with the GP done in this work is shown in blue. The FAP at 1% is represented as a dotted purple line. |
 |
Fig. 7 GLS periodograms of the residuals after the GP correction of the NZPs. Two planets were injected in one of the constant stars of the total constant stars time series with an orbital period of 11 days (upper panel) and 200 days (lower panel). The FAP at 1% is represented as a dotted purple line. The period of the injected planet is highlighted with a vertical red line. |
4.3 Gaussian process predictions
Four constant stars are monitored with SOPHIE every possible night. This monitoring decreases the time allocated to the search for exoplanets. We have developed a new method that can predict the variations in the NZP using only a few housekeeping variables. As a result, it may be possible to decrease the observations of constant stars.
To test this, we produced three different datasets. One dataset with the complete time series of constant stars introduced in Sect. 4.1, one dataset from which 20% of the data were randomly removed from the complete time series, and a last dataset from which 40% of the data were randomly removed. We decreased the number of observations but kept the number of constant stars observed so that observations were available throughout all years. We then applied exactly the same method as described in Sect. 3.1 to these new datasets. As before, we divided the constant star dataset into two to account for the thermal regulation upgrade (at BJD ~ 2 457 700). To compare the probability distribution of each hyperparameter, we produced two corner plots that show the posterior distributions of the hyperparameters for all three datasets. The two correlation diagrams are presented in Appendices A.1 and A.2. The posterior distributions before and after the instrumental upgrade are consistent. The set in which 40% of the time stamps of all constant stars are removed shows some divergences, in particular for the temperature of the container length-scale hyperparameter (lcontainer). This result is promising because it indicates that even with fewer constant star observations, we can still produce a noise model that explains most of the NZP variations. Monitoring constant stars is still necessary to train the GP accurately, but it can be done at a lower cadence.
To test whether the cadence decrease impacts planetary signal detection, we tested these two GP master constants with fewer data points with our mock planetary system injected into HD 89269A. In all three cases, the RMS of the residuals are at the level of 3.6 m s−1. Concerning the detection level, we also used the ℓ1 and computed the FAPs of each signal. Even with 40% fewer observations of the constant star data, the three mock planets are fully recovered, and their FAPs are only marginally lower than those found in Sect. 4.2.
5 Application to planetary systems
In this section, we test our new method for correcting for NZP variations on a known planetary system: HD 158259, which hosts six exoplanets in a 3:2 mean-motion resonance (Hara et al. 2020). This detection was sensitive to the noise model, and we wished to compare it with other instrumental systematical corrections. Five planets were detected in RVs at 3.4, 5.2, 7.9, and 12 days and another planet was detected at 1.84 or 2.17 days, which are aliases of each other. Another candidate planet was detected at 17.4 days. The internal planet at 2.17 days has been confirmed in transit with TESS observations. Hara et al. (2020) used the master constant developed at that time and tested new noise models. They selected the best noise model based on a cross-validation. We compared the published FAPs with three other corrections: first, using the same noise model as in Hara et al. (2020), but with the master constant by Heidari et al. (2024), then using the new GP master constant developed in this work, and finally, using the raw data without any master constant correction, and directly applying our noise model in the ℓ1.
The results for each planet are shown in Fig. 9. The log10 (FAP) are reported for each method, and the results are quite different for the planets. Planet b alone is confirmed by transit, and a significant improvement is visible in the detection for the three methods compared to the published one. The master constant developed by Heidari et al. (2024) and the GP master constant show similar results, but the noise model show a higher FAP. The situation is similar for planet c at 3.4 days. However, for the other planets (d, e, f, and g), the GP noise model significantly improved the detection, with planet g now significantly detected.
The application of the GP noise model on this system shows that we recovered all the planets with an equal or better FAP, without using the red-noise model used in Hara et al. (2020). The period of planet b found with the GP correction is equal to the period detected with TESS and not to its alias of 1.84 days as in Hara et al. (2020).
We performed an MCMC to model the six planets of this system. In Table E.1, we compared the posteriors obtained with a GP noise model with the posteriors from Hara et al. (2020). We used the same priors and stellar mass as in Hara et al. (2020). With a noise model only based on pressure and temperatures and the addition of a jitter, we found compatible orbital parameters for all the planets. In this case, the noise model was based on instrumental conditions. To confirm the signals of the planets, we evaluated whether the six planetary signals were coherent over time. We considered a window of 60 RV data points that we shifted point by point until the end of the time series. We evaluated the amplitude of the signal and the phase of each planet, considering a circular orbit, in each window. The result is shown in Fig. 10 and follows the method in Hara et al. (2022). For the six planets, the semi-amplitude and phase are constant over the observations, which reinforces the hypothesis that these signals are constant in time and have a planetary origin. With this study, the hypothesis that HD 158259g is a planet is strengthened and will be fully confirmed with more observations in a follow-up paper.
 |
Fig. 8 Number of planets detected as a function of the period and semi-amplitude of the RV signal. The upper panel depicts the number of planets detected using the new GP master constant correction, and the second panel shows the classical master constant correction. The grid cell colours indicate the number of planets detected with the colour scale at the right. The darkest colour means that more planets were detected. White cells contain no detected planets. The last panel shows the difference between the two methods regarding detected planets. Red means that more planets are detected with the GP method, and blue means that more planets are detected with the classical method. White cells mean that both methods detected the same number of planets. A planet is detected if log10(FAP) ≤ −1.3 and the orbital period is close to the injected period. |
 |
Fig. 9 log10(FAP) for each instrumental variation correction of HD 158259 RVs. On the y-axis, we show the four different corrections: the published correction, the master constant developed by Heidari et al. (2024), the new GP master constant, and raw data with the GP noise model. Coloured stars represent the FAPs, and each planet has a colour: yellow stars show planet b, pink stars show planet c, blue stars show planet d, green stars show planet e, orange stars show planet f, and purple stars show planet g. |
 |
Fig. 10 Evaluation of the stability of the signal over time for the six planets in HD 158259. The orbital period of each planet was fixed to the period found with the MCMC that is written above each panel. The semi-amplitude (orange) and phase (blue) are estimated in a window of 60 RV data points that we shifted point by point. The shaded area shows the uncertainties. |
6 Discussion and conclusion
High-precision spectrographs are crucial for detecting and characterising exoplanets. This paper introduced an improved method for understanding and correcting the NZP variations in the SOPHIE spectrograph. While the SOPHIE spectrograph is stabilised in pressure and temperature, it is not placed in a vacuum chamber. By studying the NZP pattern using constant stars monitored with SOPHIE, we aimed to overcome instrumental instabilities. Additionally, we used ancillary information from the instrument, namely pressure and temperature variations, which are measured every 6 minutes. Previously, these parameters were not used to correct NZP variations. GPs are employed to analyse the impact of pressure and temperature variations on the RV time series. GPs allow the modelling of correlated noise and to accurately propagate uncertainties in planetary parameters. The product of multivariate Matérn-3/2 kernels is suitable for modelling these NZP variations. This study allowed us to understand the influence of environmental conditions on SOPHIE RV measurements. The flexibility of the GPs allowed us to handle complex correlations when no a priori knowledge of the impact of external variations on the data is available.
We used the same set of constant stars as for the classical master constant correction. These stars were monitored for over a decade since 2012. To correct for the NZP variations, we propose two approaches based on the housekeeping data: (1) the classical master constant is replaced by a GP master constant from the prediction of the best kernel fitted on the constant stars, and (2) a noise model that can be self-consistently implemented within MCMC or the ℓ1 with the hyperparameters trained on the constant stars. The GP master constant with associated uncertainties is provided in the appendices (Table D.1). One main limitation of this method is that GPs are computationally expensive.
Using GPs to correct NZP leads to the detection of more planets with small amplitudes. We showed that up to 10% more planets could be detected with an amplitude below 1 m s−1. Therefore, the GP method has the potential to unveil lower-mass planets across a wide range of orbital periods. For larger amplitudes, both the GP master constant and the classical master constant developed by Heidari et al. (2024) have a similar efficiency in correcting for NZP variations.
As already discussed in Sect. 5 and in Hara et al. (2020), it is important to compare different noise models to assess the validity of a planet detection. We applied the method on the complex planetary system HD 158259 with small amplitude signals. The new correction of the NZP variations helped us to confirm planets b to f of the system and reinforced the hypothesis that the signal at 17.44 days might be a planet. We discuss in Sect. 4.3 that the observational cadence of the constant stars might be reduced without affecting the results. However, completely discontinuing their monitoring and relying solely on housekeeping data might be too risky. The temperature and pressure variations cannot explain all the NZP variations, as we already mentioned with the update of the wavelength calibration (end of Sect. 4.1).
An RV analysis is a complex process, and various external factors and steps in the reduction pipeline can introduce instrumental systematics. Factors such as seeing variations, observational conditions, Barycentic Earth RV, opto-mechanical variations of the instrument, and other effects must be considered to fully understand the instrumental variability. While additional ancillary information could be incorporated into our GP-based method, computational cost and parameter degeneracy remain the primary limitations. Nonetheless, using pressure and temperature variations alone, we successfully captured the main variations of NZP. This method will be applied to other planetary systems discovered with SOPHIE.
Acknowledgements
The project leading to this publication has received funding from the Excellence Initiative of Aix-Marseille University – A*Midex, a French “Investissements d’Avenir programme” AMX-19-IET-013. This work was supported by the “Programme National de Planétologie” (PNP) of CNRS/INSU. The authors would like to thank the team at OHP and in particular Francois Moreau for the pressure and temperature measurements.
Appendix A Results of the GP analysis
 |
Fig. A.1 Correlation diagram for the posterior density functions of all parameters for the GP analysis of the constant stars with BJD<2457700 days. The blue histogram corresponds to the complete dataset with all constant stars available. The orange histograms are the results for 80% of this dataset, and the green histogram shows this for 60% of this dataset. The dotted blue lines show the median values for the complete dataset and limit the 68.3% highest density intervals. The corresponding values are written above each parameter. |
 |
Fig. A.2 Correlation diagram for the posterior density functions of all parameters for the GP analysis of the constant stars with BJD>2457700 days. The blue histogram corresponds to the complete dataset with all constant stars available. The orange histograms are the results for 80% of this dataset, and the green histogram shows this for 60% of the dataset. The dotted blue lines show the median values for the complete dataset and limit the 68.3% highest-density intervals. The corresponding values are written above each parameter. |
Appendix B Parameters of the injected planets in HD 89269A
List of implemented and fitted parameters for planets injected in HD 89269A.
Appendix C Priors and posteriors GP analysis
GP hyperparameters used in the analysis.
Appendix D Result GP master constant
GP master constant values
Appendix E HD 158259’s analysis
Estimate and credible interval of the orbital parameters for the six planets of HD 158259 and a GP noise model compared with the published values in (Hara et al. 2020)
Appendix F Temperature and pressure measurements on SOPHIE
Temperatures and pressure measurements on the SOPHIE spectrograph since 2012
References
- Aigrain, S., & Foreman-Mackey, D. 2023, ARA&A, 61, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Aigrain, S., Parviainen, H., & Pope, B. J. S. 2016, MNRAS, 459, 2408 [NASA ADS] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courcol, B., Bouchy, F., Pepe, F., et al. 2015, A&A, 581, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J. B., Hara, N., & Ségransan, D. 2020, A&A, 638, A95 [EDP Sciences] [Google Scholar]
- Díaz, R. F., Delfosse, X., Hobson, M. J., et al. 2019, A&A, 625, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, A., & Udry, S. 2010, in EAS Publications Series, eds. T. Montmerle, D. Ehrenreich, & A. M. Lagrange, 41, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, T. M., Aigrain, S., Gibson, N., et al. 2015, MNRAS, 451, 680 [Google Scholar]
- Evans, T. M., Sing, D. K., Kataria, T., et al. 2017, Nature, 548, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gibson, N. P. 2014, MNRAS, 445, 3401 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Roberts, S., et al. 2012, MNRAS, 419, 2683 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Computat. Sci., 5, 65 [Google Scholar]
- Hara, N. C., Boué, G., Laskar, J., & Correia, A. C. M. 2017, MNRAS, 464, 1220 [Google Scholar]
- Hara, N. C., Bouchy, F., Stalport, M., et al. 2020, A&A, 636, A6 [Google Scholar]
- Hara, N. C., Delisle, J.-B., Unger, N., & Dumusque, X. 2022, A&A, 658, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heidari, N. 2023, PhD thesis, Aix-Marseille Université, France [Google Scholar]
- Heidari, N., Boisse, I., Hara, N. C., et al. 2024, A&A, 681, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobson, M. J., Díaz, R. F., Delfosse, X., et al. 2018, A&A, 618, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobson, M. J., Delfosse, X., Astudillo-Defru, N., et al. 2019, A&A, 625, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [Google Scholar]
- Howard, A. W., Johnson, J. A., Marcy, G. W., et al. 2011, ApJ, 730, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- Perruchot, S., Kohler, D., Bouchy, F., et al. 2008, SPIE Conf. Ser., 7014, 70140J [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning, (Cambridge: MIT, Press), 266 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
As listed on The Exoplanet Encyclopedia (http://exoplanet.eu/) accessed on November 23, 2023.
All Tables
Estimate and credible interval of the orbital parameters for the six planets of HD 158259 and a GP noise model compared with the published values in (Hara et al. 2020)
All Figures
 |
Fig. 1 Variations in housekeeping data monitored at different locations of the SOPHIE instrument with a cadence of 6 min. The pressure corresponds to the internal pressure inside the nitrogen-filled tank where the dispersal elements are located. The temperature is monitored in the air of the container, the air in the spectrograph, the shutter, the east and west granite benches, the grating, the cryostat cover, the ferrule, and the Coudé tube (path of the fibres from the telescope to the spectrograph; see Perruchot et al. (2008) and the Haute-Provence Observatory website for more details). Near BJD = 2 457 700, the SOPHIE thermal regulation was upgraded, improving the temperature stability inside the spectrograph. |
| In the text | |
 |
Fig. 2 Heat map of the Pearson coefficients to evaluate the linear correlation between the 10 housekeeping variables available for the SOPHIE instrument. |
| In the text | |
 |
Fig. 3 Results of the cross-validation method for selecting the best kernel. Upper panel: we compared four kernels with multiplicative and additive kernels with a Matérn 3/2 (M3) or a square-exponential (SE) kernels with the temperature of the air in the container, and the spectro-graph, temperature of the Coudé tube, and pressure. The model that obtained the highest log-likelihood was preferred. This is the multiplicative M3 kernel (MM3) in hashed blue. Lower panel: comparison of the M3 or MM3 kernel with the difference number of housekeeping variables. We compared models with only one temperature (yellow and green), with pressure alone (red), with only three temperatures (purple), the multiplicative M3 kernel with three temperatures and pressure (blue), and the multiplicative M3 kernel with the addition of an SE kernel on time (pink). |
| In the text | |
 |
Fig. 4 Result of the fit of the NZP with GPs. Upper panel: SOPHIE RVs for the constant stars are represented as black dots with error bars. The master constant time series developed by Heidari et al. (2024) is represented as orange dots. The new GP master constant developed in this work and trained on the constant stars is represented with blue dots, and the blue shaded area represents the corresponding uncertainties. Lower panel: difference between the master constant method (MC) and the GP master constant method (GP MC). |
| In the text | |
 |
Fig. 5 Quantile–quantile analysis comparing the quantile of the residuals for the master constant correction (orange dots) and the GP master constant correction (blue dots) with the corresponding theoretical quantile of a normal distribution. When the cumulative distribution of the residuals follows a normal distribution, the residuals should be aligned along a 45° line (red line). |
| In the text | |
 |
Fig. 6 Generalised Lomb–Scargle (GLS) periodogram (Zechmeister & Kürster 2009) of the residuals. The residuals of the NZP correction with the classical method are shown in orange, and the correction with the GP done in this work is shown in blue. The FAP at 1% is represented as a dotted purple line. |
| In the text | |
 |
Fig. 7 GLS periodograms of the residuals after the GP correction of the NZPs. Two planets were injected in one of the constant stars of the total constant stars time series with an orbital period of 11 days (upper panel) and 200 days (lower panel). The FAP at 1% is represented as a dotted purple line. The period of the injected planet is highlighted with a vertical red line. |
| In the text | |
 |
Fig. 8 Number of planets detected as a function of the period and semi-amplitude of the RV signal. The upper panel depicts the number of planets detected using the new GP master constant correction, and the second panel shows the classical master constant correction. The grid cell colours indicate the number of planets detected with the colour scale at the right. The darkest colour means that more planets were detected. White cells contain no detected planets. The last panel shows the difference between the two methods regarding detected planets. Red means that more planets are detected with the GP method, and blue means that more planets are detected with the classical method. White cells mean that both methods detected the same number of planets. A planet is detected if log10(FAP) ≤ −1.3 and the orbital period is close to the injected period. |
| In the text | |
 |
Fig. 9 log10(FAP) for each instrumental variation correction of HD 158259 RVs. On the y-axis, we show the four different corrections: the published correction, the master constant developed by Heidari et al. (2024), the new GP master constant, and raw data with the GP noise model. Coloured stars represent the FAPs, and each planet has a colour: yellow stars show planet b, pink stars show planet c, blue stars show planet d, green stars show planet e, orange stars show planet f, and purple stars show planet g. |
| In the text | |
 |
Fig. 10 Evaluation of the stability of the signal over time for the six planets in HD 158259. The orbital period of each planet was fixed to the period found with the MCMC that is written above each panel. The semi-amplitude (orange) and phase (blue) are estimated in a window of 60 RV data points that we shifted point by point. The shaded area shows the uncertainties. |
| In the text | |
 |
Fig. A.1 Correlation diagram for the posterior density functions of all parameters for the GP analysis of the constant stars with BJD<2457700 days. The blue histogram corresponds to the complete dataset with all constant stars available. The orange histograms are the results for 80% of this dataset, and the green histogram shows this for 60% of this dataset. The dotted blue lines show the median values for the complete dataset and limit the 68.3% highest density intervals. The corresponding values are written above each parameter. |
| In the text | |
 |
Fig. A.2 Correlation diagram for the posterior density functions of all parameters for the GP analysis of the constant stars with BJD>2457700 days. The blue histogram corresponds to the complete dataset with all constant stars available. The orange histograms are the results for 80% of this dataset, and the green histogram shows this for 60% of the dataset. The dotted blue lines show the median values for the complete dataset and limit the 68.3% highest-density intervals. The corresponding values are written above each parameter. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



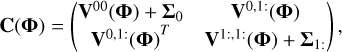
![${k_{{\rm{PSE}}}}\left( {{{\bf{x}}_i},{{\bf{x}}_j},\Phi } \right) = {c^2}\prod\limits_{m = 1}^M {\exp } \left[ { - {{{{\left( {{x_{i,m}} - {x_{j,m}}} \right)}^2}} \over {l_m^2}}} \right].$](/articles/aa/full_html/2024/07/aa48960-23/aa48960-23-eq20.png)
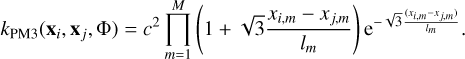
![${k_{SSE}}\left( {{{\bf{x}}_i},{{\bf{x}}_j},\Phi } \right) = \sum\limits_{m = 1}^M {c_m^2} \exp \left[ { - {{{{\left( {{x_{i,m}} - {x_{j,m}}} \right)}^2}} \over {l_m^2}}} \right].$](/articles/aa/full_html/2024/07/aa48960-23/aa48960-23-eq22.png)