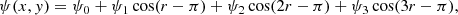| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 15 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202348700 | |
| Published online | 04 June 2024 | |
Turbulence and particle energization in twisted flux ropes under solar-wind conditions
1
Istituto per la Scienza e Tecnologia dei Plasmi (ISTP), Consiglio Nazionale delle Ricerche, Via Amendola 122/D, 70126 Bari, Italy
e-mail: oreste.pezzi@istp.cnr.it
2
The Blackett Laboratory, Department of Physics, Imperial College London, London SW7 2AZ, UK
3
Istituto di Astrofisica e Planetologia Spaziali, Istituto Nazionale di Astrofisica, Via del Fosso del Cavaliere 100, 00133 Rome, Italy
4
Space and Plasma Physics, School of Electrical Engineering and Computer Science, KTH Royal Institute of Technology, Teknikringen 31, 11428 Stockholm, Sweden
5
Dipartimento di Fisica, Università della Calabria, Ponte P. Bucci, Cubo 31C, 87036 Arcavacata di Rende, CS, Italy
6
Istituto Nazionale di Astrofisica – INAF, Direzione Scientifica, Roma, Italy
7
Bartol Research Institute and Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA
Received:
22
November
2023
Accepted:
1
March
2024
Context. The mechanisms regulating the transport and energization of charged particles in space and astrophysical plasmas are still debated. Plasma turbulence is known to be a powerful particle accelerator. Large-scale structures, including flux ropes and plasmoids, may contribute to confining particles and lead to fast particle energization. These structures may also modify the properties of the turbulent, nonlinear transfer across scales.
Aims. We aim to investigate how large-scale flux ropes are perturbed and, simultaneously, how they influence the nonlinear transfer of turbulent energy toward smaller scales. We then intend to address how these structures affect particle transport and energization.
Methods. We adopted magnetohydrodynamic simulations perturbing a large-scale flux rope in solar-wind conditions and possibly triggering turbulence. Then, we employed test-particle methods to investigate particle transport and energization in the perturbed flux rope.
Results. The large-scale helical flux rope inhibits the turbulent cascade toward smaller scales, especially if the amplitude of the initial perturbations is not large (∼5%). In this case, particle transport is inhibited inside the structure. Fast particle acceleration occurs in association with phases of trapped motion within the large-scale flux rope.
Key words: acceleration of particles / magnetohydrodynamics (MHD) / plasmas / turbulence / methods: numerical / solar wind
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Charged particles energized to extremely high energies are ubiquitous in the Universe, as shown by direct observations in the heliosphere (Reames 1999; Dresing et al. 2023) and inferred from remote observations of far astrophysical systems (Lazarian et al. 2012; Amato & Casanova 2021; Cristofari 2021). Despite decades of research on the topic, starting from the seminal works by Fermi (1949, 1954), the mechanisms responsible for particle acceleration in nearly collisionless plasmas are still elusive.
Among different fundamental processes leading to efficient particle energization (Fisk & Gloeckler 2012; Retinò et al. 2022), large-scale plasma turbulence has been central in different recent theoretical and numerical efforts (e.g., Lazarian et al. 2020, and references therein). In particular, intermittency gives rise to inhomogeneous patches of coherent structures, such as vortices, current sheets, plasmoids, and flux ropes, across a vast range of spatial scales (Matthaeus et al. 2015; Marino & Sorriso-Valvo 2023). In the solar wind, these locally generated plasma structures, whose origin is possibly associated with magnetic reconnection, are often complemented by structures of solar origin traveling in the heliosphere (e.g., Malandraki et al. 2019). As a matter of fact, flux-rope-like structures are routinely observed in the heliosphere at different distances from the Sun (Hu et al. 2014, 2018; Khabarova et al. 2021; Réville et al. 2022, and references therein).
A first interesting aspect concerns the dynamical evolution of “meso-scale” structures observed at both large (fluid) and small (kinetic) scales (Viall et al. 2021). How meso-scale structures are affected by the turbulent background in which they travel and, at the same time, mediate the cascade of turbulence toward smaller scales is still a puzzle. Different studies, performed in the context of solar coronal loops, investigated the propagation of magnetohydrodynamics (MHD) waves and the onset of instabilities in magnetic flux tubes. Emonet & Moreno-Insertis (1998) explored the dynamics of twisted flux ropes in a stratified medium, mimicking their emergence from the solar convection zone, while Srivastava et al. (2010) reported the evidence of kink instability in the context of a solar flare. The propagation of kink and torsional Alfvén waves, relevant for coronal heating through, for example, the resonant absorption or the generation of the Kelvin-Helmholtz instability at the boundary of coronal loops, has been extensively investigated (Terradas et al. 2008; Antolin & Shibata 2010; Antolin et al. 2014, 2017; Magyar et al. 2015; Karampelas et al. 2017; Howson et al. 2017). Within the context of coronal heating, a complementary and widely investigated approach considers the evolution of perturbed coronal flux tubes leading to energy dissipation through magnetic reconnection events, eventually enhanced by fluid-scale instabilities (Einaudi & Velli 1994; Georgoulis et al. 1998; Einaudi et al. 1996, 2021; Galsgaard & Nordlund 1996, 1997; Gerrard & Hood 2003; Archontis & Hood 2013; Threlfall et al. 2021; Cozzo et al. 2023). More recently, Díaz-Suárez & Soler (2021, 2022) described the transition from linear phase-mixing to turbulence – mediated by Kelvin-Helmholtz instability – in a coronal loop perturbed by torsional Alfvén waves. Díaz-Suárez & Soler (2022) also examined the role of the twist in the magnetic field structure of the coronal loops, finding that the twist has a stabilizing effect on the Kelvin-Helmholtz instability, thus preventing the transition to turbulent behavior.
A second challenging issue regards understanding how these structures mediate the transport and energization of particles. In the solar corona, flux ropes – often associated with solar flares – are known to produce intense X-ray emission (Pinto et al. 2015, 2016), thus being potential sites of intense particle acceleration (Turkmani et al. 2005, 2006; Gordovskyy & Browning 2011). A different perspective highlights the role of large-scale structures, of which flux ropes are a sub-ensemble, in trapping particles. Trapped particles may be quickly energized, as shown in numerous numerical and theoretical efforts that investigated the role of magnetic reconnection in generating islands and plasmoids whose merging or contraction leads to efficient particle energization (Drake et al. 2006; Oka et al. 2010; Kowal et al. 2011, 2012; le Roux et al. 2015, 2018, 2019; Pezzi et al. 2021). The role of particle trapping has also been explored in the context of magnetic discontinuities (Malara et al. 2021) and switchbacks (Malara et al. 2023). More generally, plasma turbulence produces coherent structures possibly trapping particles and leading to fast particle acceleration (Dmitruk et al. 2003, 2004; Drake et al. 2006; Servidio et al. 2016; Pecora et al. 2018; Pisokas et al. 2018; Trotta et al. 2020; Sioulas et al. 2020; Pezzi et al. 2022; Lemoine 2022). In this case, the acceleration process is quite complex and characterized by the interplay between stochastic acceleration due to turbulent MHD fluctuations and experienced by all the particles and, possibly, fast and intense energization associated with trapping and perceived by a relatively small number of particles (Ambrosiano et al. 1988; Sioulas et al. 2020; Pezzi et al. 2022). These extensive works have been complemented by observational analyses studying particle acceleration in small-scale flux ropes (Khabarova et al. 2015, 2016) as well as large-scale flux-tube structures (Pecora et al. 2021; McComas et al. 2023). In particular, Pecora et al. (2021) confirmed that twisted flux tubes are a transport barrier for energetic particles, which, as a result, are confined within or at the boundary of the flux tube itself (Tooprakai et al. 2007, 2016; Krittinatham & Ruffolo 2009). In the context of particle acceleration at shocks, turbulent structures have been found to be responsible for additional energization due to their ability to trap particles and, more generally, influence their transport properties (Zank et al. 2015). This complex picture about the interplay between shocks and turbulent structures has been emerging in recent theoretical (Zank et al. 2021), numerical (Nakanotani et al. 2021; Trotta et al. 2022, 2023), and observational (Kilpua et al. 2023) studies.
This work furthers the present understanding of the two above discussions. In particular, we address (a) how plasma turbulence is influenced and perturbs a large-scale flux rope and (b) how the perturbed flux rope affects particle transport and energization, using a combination of MHD and test-particle simulations. The MHD approach is adopted to investigate the development of plasma turbulence in the presence of a large-scale flux rope, generated as a Grad–Shafranov equilibrium with parameters in qualitative accordance with those observed in the solar wind (Hu et al. 2018). Test-particle simulations are then employed to study particle transport and energization in the perturbed flux rope.
By performing different runs in which the flux rope is perturbed with large-scale fluctuations whose initial energy is varied within two orders of magnitude, we show that the turbulent cascade within the flux rope is generally inhibited. As the amplitude of initial perturbations increases, this effect vanishes as turbulence dominates on the effect of the large-scale magnetic structure. Then, we investigate how the turbulent flux rope influences particle transport and energization by performing test-particle simulations under a stationary assumption. Our main findings are that, in cases of small perturbation amplitude, particle transport is inhibited within the structure that can entrap particles. While trapped, particles can experience an efficient acceleration due to intense electric fields.
The structure of the paper is the following. Section 2 describes the adopted numerical models and the setup of numerical simulations. Section 3 discusses how turbulence affects the flux rope and what differences arise in the turbulent cascade inside or outside the structure. Section 4 analyzes how particle transport and acceleration is influenced by the presence of the flux rope. In Sect. 5, we conclude by summarizing our findings.
2. Numerical model and simulation setup
The numerical method adopted in the current work combines a compressible MHD algorithm and a test-particle code. The MHD code is exploited to perturb the initial equilibrium, which is characterized by a flux rope built through the Grad–Shafranov technique. Test-particle methods allow us to analyze particle transport and acceleration in the perturbed turbulent flux rope. We provide details about the numerical model and simulations setup here.
2.1. Compressible MHD solver
The MHD code numerically integrates the three-dimensional equations of the compressible magnetohydrodynamics that, in normalized units, can be written as
where (ρ, v, T, B)(x, t) are, respectively, the magnetofluid density, velocity, temperature, and the magnetic field, while γ = 5/3 is the adiabatic index. Equations (1)–(4) are normalized as follows. Lengths, times, and velocities are, respectively, scaled to the energy-containing scale LA, Alfvén crossing time tA = LA/vA, and Alfvén speed 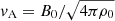 , evaluated with the normalizing magnetic field B0 and density ρ0. The algorithm also includes the Hall and electron pressure terms in the induction equation for the magnetic field, which were turned off for this study.
, evaluated with the normalizing magnetic field B0 and density ρ0. The algorithm also includes the Hall and electron pressure terms in the induction equation for the magnetic field, which were turned off for this study.
The normalized pressure is P = β0ρT/2, where β0 is the kinetic-to-magnetic pressure ratio evaluated with the normalizing quantities n0, B0, and T0, that is, in cgs units 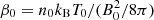 . This ensures that normalized density and temperature are on the order of ∼1, and, in normalized units, β = P/(B2/2) = β0 ⋅ (ρT/B2). Hence, the effective plasma β can actually change in the computational domain due to either nonhomogeneous equilibrium quantities or possible perturbations. We here set B0 = 5 nT, n0 = 10 cm−3, LA = 5 × 103 km, and T0 ≃ 1.4 × 105 K, thus providing vA ≃ 35 km s−1 and β0 = 2.
. This ensures that normalized density and temperature are on the order of ∼1, and, in normalized units, β = P/(B2/2) = β0 ⋅ (ρT/B2). Hence, the effective plasma β can actually change in the computational domain due to either nonhomogeneous equilibrium quantities or possible perturbations. We here set B0 = 5 nT, n0 = 10 cm−3, LA = 5 × 103 km, and T0 ≃ 1.4 × 105 K, thus providing vA ≃ 35 km s−1 and β0 = 2.
Equations (1)–(4) are integrated prescribing a logarithmic regularization to the density ρ ≡ eg and solving the equivalent equation for g with the purpose of better describing possible discontinuities and shocks. Moreover, we integrate the MHD equations for the magnetic potential a in place of the magnetic field B = ∇ × a to guarantee ∇ ⋅ B = 0.
Magnetohydrodynamics equations are integrated on a tri-periodic cube of size Lx = Ly = Lz = L = 2πLA, discretized with Nx = Ny = Nz = N = 512 grid points in each direction. The algorithm adopts a pseudo-spectral method (Canuto et al. 2006) based on fast Fourier transform (FFTW) routines (Frigo 1999) to compute the right-hand side of MHD equations. Hence, spatial derivatives are computed in the Fourier space, while products between variables are calculated in physical space. Then, the time evolution is performed through a second-order Runge-Kutta scheme. In order to ensure numerical stability, we adopted the standard dealiasing procedure at kalias = 2/3kmax (kmax = N/2) and implemented hyper-viscous terms (∝∇4) in Eqs. (2)–(4), with the hyper-viscous coefficients ν ≃ 10−8. Here, we exploited the “COmpressible Hall Magnetohydrodynamics simulations for Plasma Astrophysics” (COHMPA) code (Vásconez et al. 2015; Perri et al. 2017; Pezzi et al. 2017), which employs a domain-parallelization strategy based on the MPI paradigm.
Magnetohydrodynamics simulations are initialized by perturbing a two-dimensional Grad–Shafranov equilibrium, which produces a flux rope. The details of the Grad–Shafranov technique are reported in Appendix A. The initial condition is characterized by a decrease of kinetic pressure P, and an increase of the out-of-plane magnetic vector potential az inside the structure with respect to the surrounding environment, as shown in Fig. 1. The flux-rope width is LFR ≃ 2 LA, while the scale associated with flux-rope gradients is LΔ ≃ LA. As described in Appendix A, the magnetic field associated with the magnetic vector potential az has a dipolar structure in the plane, while its z-component increases in the flux rope with respect to the external region. Owing to the presence of a parallel component in the equilibrium magnetic field, magnetic field lines twist along the flux-rope axis. Such a behavior can be appreciated in Fig. 2, which displays the magnetic field lines colored with the intensity of the current density, j = ∇ × B.
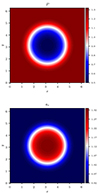 |
Fig. 1. Overview of initial two-dimensional equilibrium, showing the maps of the kinetic pressure P (top) and the out-of-plane potential vector az (bottom). |
 |
Fig. 2. Three-dimensional magnetic field lines of equilibrium flux-rope structure. Lines are colored with the magnitude of the magnetic field vorticity; i.e., the current density. |
This configuration is often observed in the solar wind, although the solar wind exhibits a large variability in terms of flux-rope parameters and overall configuration (Hu et al. 2018). The plasma β changes from the external value of ∼1.5 to the internal value of ∼0.3 (red line in Fig. 3), while the local density of magnetic helicity hm = a ⋅ B increases in the structure (blue line in Fig. 3).
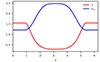 |
Fig. 3. One-dimensional profile of β (red) and density of magnetic helicity hm (blue) along x, evaluated at y = Ly/2. |
The initial equilibrium is perturbed with large-scale fluctuations of magnetic field δb and bulk speed δv such that Hc = ⟨δv ⋅ δb⟩≃0 and Hm = ⟨δa ⋅ δb⟩≃0, with δb = ∇ × δa. These fluctuations have a fully three-dimensional polarization: 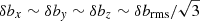 . In the Fourier space, the energy is injected in the 2k0 ≤ k ≤ 7k0 shells, where k0 = 2π/LA = 1 and
. In the Fourier space, the energy is injected in the 2k0 ≤ k ≤ 7k0 shells, where k0 = 2π/LA = 1 and 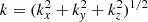 , with a flat energy spectrum. Table 1 summarizes the most relevant numerical parameters of MHD simulations.
, with a flat energy spectrum. Table 1 summarizes the most relevant numerical parameters of MHD simulations.
Parameters of perturbations used in the MHD simulations.
2.2. Test-particle solver
The normalized motion equations of Np = 103 test protons of mass mp and charge e, namely,
are here integrated numerically. In Eqs. (5) and (6) rp, vp, and pp = γpvp are the particle position, velocity, and momentum, while E and B are the electric and magnetic fields generated through the MHD simulations. We assume stationary electromagnetic fields and consider a static snapshot of these fields when the turbulence is most developed (t* in Table 1; see below). Periodic boundary conditions are also imposed on particle trajectories in each direction. Equations (5) and (6) are scaled analogously to the MHD simulations. In particular, the Lorentz factor is 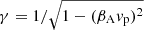 , where βA = vA/c ≃ 10−4. Equations (5) and (6) are integrated by adopting the relativistic Boris method (Ripperda et al. 2018; Dundovic et al. 2020; Pezzi et al. 2022). The electric and magnetic fields are interpolated at the particle position through a trilinear interpolation method (Birdsall & Langdon 2004). The electric field in Eq. (6) is the inductive one derived through Ohm’s law: E = −v × B. We neglect the resistive electric field for two reasons. First, hyper-viscous terms in MHD simulations, including hyper-resistivity, are not intended to describe any physical effects, but only to complement the dealiasing procedure in stabilizing numerical simulations. Second, their characteristic scale is much smaller than the minimum particle gyroradius adopted in test-particle simulations, as discussed in the following.
, where βA = vA/c ≃ 10−4. Equations (5) and (6) are integrated by adopting the relativistic Boris method (Ripperda et al. 2018; Dundovic et al. 2020; Pezzi et al. 2022). The electric and magnetic fields are interpolated at the particle position through a trilinear interpolation method (Birdsall & Langdon 2004). The electric field in Eq. (6) is the inductive one derived through Ohm’s law: E = −v × B. We neglect the resistive electric field for two reasons. First, hyper-viscous terms in MHD simulations, including hyper-resistivity, are not intended to describe any physical effects, but only to complement the dealiasing procedure in stabilizing numerical simulations. Second, their characteristic scale is much smaller than the minimum particle gyroradius adopted in test-particle simulations, as discussed in the following.
The parameter α = tAΩ0, where Ω0 = eB0/mpc is the proton cyclotron frequency, is related to the extension of the turbulent inertial range, since it can be rewritten as α = LA/dp, where dp is the proton skin depth of the background plasma (Dmitruk et al. 2004; González et al. 2016). At variance with Pezzi et al. (2022), we here consider nonrelativistic particles, with an initial speed of ∼vA in a β ∼ 1 plasma. In this case, 1/α roughly corresponds to the initial particle gyroradius in normalized units. To require that the particle gyroradius is larger than the grid size – thus avoiding spurious numerical effects – we are forced to artificially reduce α. Considering the above normalizing parameters, α ≃ 50; that is, rg ≃ 0.02 LA ≃ 2Δx and speed vp ≃ vA. We anticipate that the resonant wave number associated with the particle gyroradius kLA = LA/rg = 50 is close to the end of the inertial-like range of turbulence and larger than either dealiasing scale and dissipative scales at which the resistive electric field is expected to become significant. To double-check, we verified that our results in terms of acceleration and transport do not change by including the resistive electric field. We note that the value of the particle gyroradius is limited by setting it to be larger than the grid size. Other methods, for example those based on the stochastic differential equations (Wijsen et al. 2022), allow to consider much smaller Larmor radii with respect to the ones considered here through the parametrization of the transport processes, that is, by prescribing the particle diffusion coefficient a priori.
When decreasing α to feasible yet unrealistic values such that rg, 0 > Δx, we kept fixed small scales (the ones related to particle motion) and we implicitly decreased LA and the turbulence correlation length lc. From this perspective, the initial particle energy is about a few eV, compatible with the thermal plasma population at temperature T0. Moreover, all other parameters are similar to solar-wind observations. Such a procedure has already been adopted in the literature (see, e.g., González et al. 2016). An alternative, not implemented here, would be to set LA to realistic values such that lc ≃ 5 × 106 km and then increase the initial particle gyroradius to values that can be afforded with simulations (i.e., α ≃ 50). In this case, one may reach relativistic energies, thus relaxing the constrain on α since for relativistic particles rg = 1/α is no longer valid (Pezzi et al. 2022). Another alternative would consider relativistic electrons (see, e.g., Trotta et al. 2020). In this case, the α factor should include the mass ratio mp/me since MHD is normalized essentially to protons, while test particles would be electrons. This issue is not crucial for our study since particle transport and energization are regulated by the relative values of the particle gyroradius rg, the turbulent correlation length lc, and the flux-rope characteristic scales LFR and LΔ. The variability of these parameters, as well as the different options for setting particle energy and species, will be explored in a future work.
We performed test-particle simulations by considering different kinds of spatial injections for better understanding the role of the flux rope in particle transport and acceleration. In particular, protons are injected: (i) homogeneously throughout the entire three-dimensional computational box; (ii) inside the large-scale flux rope, namely, on the vertical line at (x, y) = (π, π); and (iii) outside the large-scale flux rope, which is on the surface of the open cylinder centered at (π, π) of radius r = π. The first injection is useful to understand global transport properties, while the second and third injections allow us to distinguish regions inside and outside the structure, respectively. For all these different cases, initial particle velocities are distributed uniformly on the surface of a sphere of constant energy. The numerical time step is always set to 1/20 of the initial gyroperiod.
3. Turbulence and intermittency in twisted flux ropes
In this section, we discuss how turbulence shapes the flux rope and the peculiarities in the energy transfer process directly caused by this large scale structure. As a result of the underlying nonlinearities, the energy of perturbations, initially confined at small wave numbers, transfers toward higher wave numbers. A standard proxy of this nonlinear transfer is the time evolution of ⟨j2⟩(t), with ⟨…⟩ being the average over the computational box, which is displayed in Fig. 4. In all our numerical experiments, ⟨j2⟩(t) increases to reach a peak, corresponding to the time instant at which turbulent activity is most intense, here denoted with t*. With the exception of Run B, where the peak was not fully reached at the end of the run, the peak is then followed by a decreasing phase related to numerical dissipation in these MHD simulations. Hereafter, we focus on the analysis of turbulence at the peak time instant t*.
 |
Fig. 4. Time evolution of ⟨j2⟩(t) for different runs in Table 1. Vertical dashed lines indicate the time instant t* at which, for each run, we perform the subsequent analyses on turbulence and particle transport. |
The distribution of current structures in the plane perpendicular to the flux rope axis, (x, y, z = Lz/2), is depicted in Fig. 5 for the different runs in Table 1. As expected, the different color bar in each panel indicates that stronger initial perturbations are associated with more intense current structures.
 |
Fig. 5. Two-dimensional overviews of current density |j| in the plane (x, y, z = Lz/2) perpendicular to flux-rope axis, for the different runs in Table 1 computed at t = t*. |
For small initial perturbation (top left panel), the most intense current structures are localized along the shear of the flux rope. Erratic current sheets are also observed in the region outside of the flux-rope structure. At the shear location, current structures are circular arcs in the plane perpendicular to the flux-rope axis. These structures, which may be due to phase-mixing along the shear (Valentini et al. 2017; Maiorano et al. 2020), are elongated in the direction of the flux rope axis. This behavior, which is expected from fundamental MHD anisotropy arguments (Shebalin et al. 1983), can be appreciated from Fig. 6, where the current density maps in the plane parallel to the flux-rope axis, (x, y = Ly/2, z), are displayed for RUN A (top) and RUN D (bottom). Multiple anisotropies, induced by both the mean large scale field and the radial magnetic shear, may also arise.
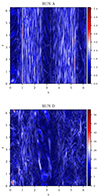 |
Fig. 6. Two-dimensional overviews of current density |j| in the plane (x, y = Ly/2, z) parallel to flux rope axis, for RUN A (top) and RUN D (bottom) computed at t = t*. |
As the level of fluctuations increases, the current structures distribute randomly in the plane perpendicular to the flux rope, resembling the patch of current structures in fully developed homogeneous turbulence simulations (e.g., Servidio et al. 2011). This feature is confirmed by inspecting the current density maps in the plane parallel to the flux rope axis (Fig. 6, bottom panel). Indeed, in RUN D, current sheets are not localized within the flux-rope boundary and tend to permeate the entire computational plane, diffusing particularly outside the flux rope. This suggests that the coupling with the flux-rope shear is less relevant in the presence of strong fluctuations, which can self-couple to generate homogeneous-like turbulence.
It is worth noticing that the core of the flux rope is a region of relatively weak current structures. Such a feature is particularly clear in the case of small initial perturbations. This suggests that, far from the shear region, the flux rope inhibits the development of turbulence, and remains – at least in its inner part – a quasi-equilibrium structure. This behavior can be expected since the flux rope is an MHD equilibrium characterized by a net magnetic helicity, and nonlinear couplings are formally depleted inside it (Servidio et al. 2008).
Being a quasi-equilibrium structure, the flux rope is not completely destroyed by fluctuations, even for the strongest perturbation level analyzed here, and despite the presence of small-scale current structures flowing into the entire computational domain. As it can be easily appreciated in Fig. 7, which displays, for RUN D, the two-dimensional contour plots of the temperature in the plane perpendicular to the flux-rope axis, the flux rope is still present with its cold core. The temperature pattern is highly structured outside the flux rope, where warm blobs of plasma on large scales are surrounded by regions with temperature variations at smaller scales, co-located with intense small-scale current sheets (bottom right panel of Fig. 5). These regions also show blobs of cold plasma, possibly transported by turbulent fluctuations from the central part of the flux rope. Such transport is suppressed in cases of weak perturbations (not shown here).
 |
Fig. 7. Two-dimensional overview of temperature T at vertical position z = Lz/2 for RUN D t = t*. |
In order to obtain further insights about the nonlinear couplings occurring in the system, Fig. 8 shows the magnetic energy spectra as a function of the wave numbers perpendicular (top) and parallel (bottom) to the flux-rope axis. Perpendicular spectra, Eb(k⊥), are computed by averaging along the parallel direction and assuming isotropy in the perpendicular plane (i.e., summing the energy over circular shells in the k⊥ plane). Similarly, parallel spectra Eb(k∥) are calculated by averaging along the two perpendicular directions in the spectral space. Before computing the magnetic energy spectra, we removed the initial equilibrium magnetic field, whose gradients are nevertheless confined to low wave numbers.
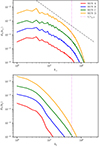 |
Fig. 8. Magnetic energy spectra for different runs in Table 1 computed at t = t*. Top and bottom plots show the perpendicular and parallel spectra, i.e., Eb(k⊥) and Eb(k∥), respectively. The dashed gray line shows the Kolmogorov prediction, |
As a result of nonlinear couplings, the energy of fluctuations, initially confined at large scales, spreads toward higher wave numbers. The energy-containing scale of fluctuations, visually estimated as the location of the spectral peak in Fig. 8, is roughly lc ∼ 1 − 1.5 LA. Velocity spectra are similar to magnetic ones, while compressive effects remain, on average, weak. The transfer of turbulent fluctuations is anisotropic, and parallel spectra are generally steeper than perpendicular ones. In the perpendicular directions, a power-law spectrum, with a slope compatible with the Kolmogorov prediction, is generated and extends for about a decade (6 ≲ k⊥ ≲ 50). At higher wave numbers, numerical dissipative effects steepen the spectrum. Interestingly, such a Kolmogorov-like spectrum also forms when initial fluctuations are weak and the nonlinear coupling is also affected by the coupling of the perturbations and the flux-rope shears via, for instance, phase-mixing.
We complement the above-discussed global spectral analysis with a local analysis, based on the increments of the magnetic field B and the flow speed v and aimed at highlighting differences occurring in turbulent transfer inside and outside the flux rope. Given the 2.5D configuration of the equilibrium flux rope (i.e., three-dimensional vectors depending only on two independent variables), and considering that the most intense nonlinear couplings occur in the directions transverse to the flux-rope axis, the following analysis has been carried out in the (x, y) plane. In order to improve the statistics, we performed an ensemble average over all the Nz = 512 planes perpendicular to the flux-rope axis. For consistency with the magnetic energy spectra, we removed the initial equilibrium structure. Starting from the entire plane (x, y), we extracted four straight cuts of length L/2 = πLA along the x and y directions. Two of them are centered in the equilibrium structure and are representative of the inner part of the flux rope. Another two are instead placed at the boundaries of the simulation domain and probe the fields outside the flux rope. On each of these cuts, we separately computed the longitudinal increments of the magnetic field, flow speed, and Elsasser variables. Finally, the two sets of increments have been combined in the analysis to improve the statistics.
We first calculated the structure functions of order q as 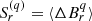 , where ΔB indicates the generic longitudinal increment of the magnetic field at the spatial scale r. The structure functions are expected to grow as power laws of the increments’ scale separation (Frisch 1995). Due to the intermittent nature of turbulence, which is characterized by intense inhomogeneities in both space and time at different scales, the scaling exponents ζq of the structure functions,
, where ΔB indicates the generic longitudinal increment of the magnetic field at the spatial scale r. The structure functions are expected to grow as power laws of the increments’ scale separation (Frisch 1995). Due to the intermittent nature of turbulence, which is characterized by intense inhomogeneities in both space and time at different scales, the scaling exponents ζq of the structure functions, 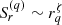 , exhibit an anomalous scaling as a function of the order q, which deviates from the linear trend predicted by globally self-similar theories of turbulence (Kolmogorov 1941; Kraichnan 1965). Consequently, the flatness of magnetic field increments, defined as
, exhibit an anomalous scaling as a function of the order q, which deviates from the linear trend predicted by globally self-similar theories of turbulence (Kolmogorov 1941; Kraichnan 1965). Consequently, the flatness of magnetic field increments, defined as ![$ F(r)\equiv {S\!}_{r}^{(4)}/[{S\!}_{r}^{(2)}]^2 $](/articles/aa/full_html/2024/06/aa48700-23/aa48700-23-eq15.gif) , exhibits an increasing power-law trend from large to small scales (Frisch 1995; Carbone & Sorriso-Valvo 2014).
, exhibits an increasing power-law trend from large to small scales (Frisch 1995; Carbone & Sorriso-Valvo 2014).
The top panels of Fig. 9 display the flatness F(r) of the magnetic field increments as a function of the scale separation r, obtained inside (red) and outside (blue) the flux rope for RUN A (left) and RUN D (right). Outside the flux rope, F(r) exhibits a similar power-law increase in the inertial range (r ≳ 0.2 − 0.3 LA) in both RUN A and RUN D. Inside the flux rope, the profile of F(r) is similar to what was found outside the flux rope for RUN D. In contrast, the flatness F(r) does not exhibit the typical power-law range in the inertial scales for RUN A. These features suggest that the fluctuations are intermittent outside the flux rope, with properties that are qualitatively independent of the initial perturbation’s amplitude. On the other hand, similar intermittency is only observed inside the flux rope for large amplitude perturbations.
 |
Fig. 9. Local analysis of turbulent properties inside and outside the flux rope for RUN A and RUN D. Top: flatness F(r) of magnetic field increments as a function of separation scale r for RUN A (left) and RUN D (right) and for data sampled inside (red) and outside (blue) the flux rope. Dotted line is the reference Gaussian flatness value. Middle: scaling exponents ζq as function of order q for RUN A (left) and RUN D (right) evaluated inside (red) and outside (blue) the flux rope for the magnetic field. Dotted lines represent the linear scaling, while solid lines indicate the p-model best fit for each data sample. The Hurst exponents h = ζ2/2 are 0.42 (inside) and 0.35 (outside) for RUN A and 0.40 (inside) and 0.42 (outside) for RUN D. Bottom: Politano-Pouquet’s term Y(r) as function of separation scale r, computed inside (red) and outside (blue) the flux rope for RUN A (left) and RUN D (right). The dotted lines indicate the linear scaling. Filled circles correspond to −Y(r) and empty circles to Y(r). |
To further investigate this aspect, in the middle panels of Fig. 9 we show the scaling exponents ζq as a function of the order q, obtained inside (red) and outside (blue) the flux rope for RUN A (left) and RUN D (right). Given the limited range of scales of the simulation, we adopted the extended self-similarity method (Benzi et al. 1993) for estimating scaling exponents more reliably. In both RUN A and RUN D, the magnetic field scaling exponents computed outside the flux rope (circles) deviate from the linear scaling ζq ∼ hq, where h = ζ2/2 indicates the Hurst exponent, predicted by assuming the global self-similarity (dotted lines in middle panels of Fig. 9). To reproduce the observed anomalous scaling trend, we performed the best fit of ζq(q) adopting the following expression obtained from the p-model (Meneveau & Sreenivasan 1987) (solid lines in middle panels of Fig. 9):
The parameter p of the model, which represents the weight of the energy repartition in the multiplicative process used to mimic the turbulent energy cascade, is p ≃ 0.82 in RUN A outside the flux rope and p ≃ 0.78 in RUN D both outside and inside. Such values indicate strong intermittency, larger than typically observed in neutral flows (Meneveau & Sreenivasan 1987) and roughly compatible with estimates in the solar wind (Carbone 1993; Sorriso-Valvo et al. 2018) and in the terrestrial magnetosheath (Yordanova et al. 2008; Quijia et al. 2021). Conversely, for small initial perturbations (RUN A) the magnetic field’s scaling exponents exhibit a quasi-linear scaling inside the flux rope. A quasi-linear trend of this kind can be associated with the interaction between turbulence and large-scale gradients of the flux rope, which in turn tend to inhibit the complete development of turbulence for low amplitudes of perturbations. As the level of initial perturbations increases (RUN D), the values obtained for ζq inside the flux rope indeed reconcile with the one observed outside in the case of strong initial perturbations.
Finally, we complemented the above framework focusing on the properties of intermittency by assessing how the nonlinear energy transfer typical of the inertial range of scales is influenced by the presence of the large-scale flux rope. To this end, we use the ensemble of cuts defined above to estimate the Politano-Pouquet law for homogeneous, locally isotropic, incompressible MHD turbulence (Politano & Pouquet 1998; Carbone et al. 2009). Defining 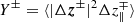 as the mixed third-order structure functions of the Elsasser variables z± = v ± (4πρ)−1/2b, the Politano-Pouquet law predicts
as the mixed third-order structure functions of the Elsasser variables z± = v ± (4πρ)−1/2b, the Politano-Pouquet law predicts
where ϵ indicates the total energy transfer rate of the turbulent cascade.
The bottom panels of Fig. 9 show the terms −Y(r) (filled circles) obtained for RUN A (left) and RUN D (right) and computed inside (red) and outside (blue) the flux rope. When −Y(r) exhibits a linear scaling, an energy transfer toward smaller scales occurs. Figure 9 also presents the values obtained for Y(r) (empty circles), which, conversely, can be associated with an inverse energy cascade (Sorriso-Valvo et al. 2007; Marino & Sorriso-Valvo 2023). As illustrated in the bottom panels of Fig. 9, outside the flux rope for RUN A and both outside and inside the flux rope for RUN D, a rather pronounced linear regime tends to emerge in the inertial range, which is indicative of the occurrence of a direct turbulent energy transfer. In contrast, inside the flux rope for RUN A, Y(r) is always positive, thus suggesting the absence of energy transfer toward smaller scales. Moreover, no linear trends are observed in the range of scales corresponding to the inertial range outside the flux rope. Interestingly, when computing the Politano-Pouquet law inside the flux rope, a characteristic scale emerges (r* ∼ LA), at which the scaling law breaks down for both RUN A and RUN D. This could highlight both the energy-containing scale of turbulence, lc ≃ 1 − 1.5 LA, or the coupling of the fluctuations with the gradients of the background equilibrium, whose typical size is again LΔ ≃ LA. The inhomogeneous equilibrium flux rope may indeed dynamically influence the properties of the nonlinear energy transfer (Wan et al. 2009), and the simple removal of the equilibrium structures before the statistical analysis does not exclude its possible dynamical effects on the cascade. By extensively testing different regions outside the flux rope, we finally observed that subtle variations in the emergence of a stable linear scaling in the Politano-Pouquet law may occur (not shown). These issues may be related to both the limited scale separation between the large-scale equilibrium flux rope and the turbulent fluctuations, and the limited box size, which influences the length of the cut (here, on the order of some correlation lengths).
To summarize this section, the analysis of intermittency and energy transfer rate confirms that the flux rope generally inhibits the nonlinear transfer of turbulent energy across scales when turbulence is relatively weak. In this case, other processes, including linear phase-mixing, are responsible for transferring energy toward smaller scales in the shear region of the flux rope. Otherwise, in regions outside the flux rope, as well as inside of it for large amplitude perturbations, the turbulence exhibits consistent statistical features in terms of scaling laws and energy transfer rate.
4. Particle transport and energization in twisted flux ropes
In this section, we explore how the presence of the turbulent flux rope influences particle transport and acceleration. We focus on test-particle simulations where the static electromagnetic fields are selected from the MHD simulations at t = t*. Assuming static fields implies that the characteristic times of particle transport and acceleration are smaller compared to the times responsible for the formation and possible dissipation of the underlying flux rope. However, as discussed in the following, our results indicate that the diffusive and slowest acceleration times are actually ∼103 tA, while the perturbed flux rope has been generated within a shorter time, that is, t* ∼ 50 − 100 tA. Such a finding would suggest performing test-particle simulations in non-static fields (González et al. 2017; Trotta & Burgess 2019). We leave this aspect for future works and justify the static assumption as follows.
First of all, as they are quasi-equilibrium structures, it is not unreasonable to assume that flux ropes are long-lived structures, capable of traveling in the solar wind over times much longer than the standard energy transfer time of fully developed turbulence, the latter being a rough estimate of the dynamical time associated with the turbulent flux rope. Moreover, our simulations are in decay, while in the solar wind one could imagine a continuous injection of energy at large scales responsible for generating perturbed flux ropes statistically similar to the one adopted in our test-particle simulations. In such a case, even if dissipated, these perturbed flux ropes may be quickly generated again by plasma turbulence on short time scales; thus, they are available to efficiently contribute to particle transport and acceleration. Finally, acceleration processes occur with different characteristic timescales and the fast energization process, which is relevant for efficiently energizing trapped particles, has a characteristic time shorter than or comparable to the dynamical time associated with the turbulent flux rope.
Our analysis begins by exploring the properties of particle transport in physical space. For each type of particle injection as described in Sect. 2, we calculated the running time diffusion coefficients along each direction as 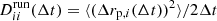 , with Δrp, i(Δt) being the particle displacement along the ith direction (i = x, y, z) during a time interval of Δt = t − t0 (t0 = 0), and ⟨…⟩ the average on the particle ensemble. Figure 10 shows the time evolution of the running time diffusion coefficients perpendicular and parallel to the background magnetic field (i.e., to the flux-rope axis), which are, respectively,
, with Δrp, i(Δt) being the particle displacement along the ith direction (i = x, y, z) during a time interval of Δt = t − t0 (t0 = 0), and ⟨…⟩ the average on the particle ensemble. Figure 10 shows the time evolution of the running time diffusion coefficients perpendicular and parallel to the background magnetic field (i.e., to the flux-rope axis), which are, respectively, 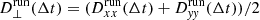 and
and 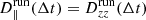 . For simplicity, we focus on the two extreme perturbations levels, RUN A (top) and RUN D (bottom).
. For simplicity, we focus on the two extreme perturbations levels, RUN A (top) and RUN D (bottom).
 |
Fig. 10. Time evolution of parallel |
On short time lags, Δt, interesting differences arise in 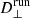 for small amplitudes of the initial perturbations (RUN A). When injecting particles inside the flux rope (red lines in Fig. 10), the perpendicular diffusion coefficient is significantly smaller than the corresponding values achieved by injecting particles throughout the entire box or outside the flux rope (blue and green lines in Fig. 10). We interpret this behavior as a trapping effect of the flux rope, hindering perpendicular diffusion. The particle escape from the flux rope, where perpendicular diffusion is restored, is probably due to the underlying acceleration process occurring within the flux rope, which prevents trapping after reaching sufficiently large particle gyroradii. As the time lag Δt increases, these differences disappear, and running diffusion coefficients, which do not depend on the kind of particle injection, tend to reach a diffusive plateau in all cases. Since particles also continue to be stochastically accelerated on long times, the running diffusion coefficients do not formally achieve the diffusive plateau.
for small amplitudes of the initial perturbations (RUN A). When injecting particles inside the flux rope (red lines in Fig. 10), the perpendicular diffusion coefficient is significantly smaller than the corresponding values achieved by injecting particles throughout the entire box or outside the flux rope (blue and green lines in Fig. 10). We interpret this behavior as a trapping effect of the flux rope, hindering perpendicular diffusion. The particle escape from the flux rope, where perpendicular diffusion is restored, is probably due to the underlying acceleration process occurring within the flux rope, which prevents trapping after reaching sufficiently large particle gyroradii. As the time lag Δt increases, these differences disappear, and running diffusion coefficients, which do not depend on the kind of particle injection, tend to reach a diffusive plateau in all cases. Since particles also continue to be stochastically accelerated on long times, the running diffusion coefficients do not formally achieve the diffusive plateau.
To highlight that particles are actually trapped within the large-scale flux rope in the case of weak initial perturbations (RUN A), Fig. 11 shows the particle density in the plane perpendicular to the flux rope axis for the injection inside (top) and outside (center) the flux rope and throughout the entire box (bottom). We selected the time instant t ≃ 1200 tA, which corresponds to the phase in which the perpendicular running diffusion coefficient is weaker when injecting particles inside the flux rope. Figure 11 shows that, in the case of injection inside the structure, particles condensate inside the flux rope, thus limiting the perpendicular transport. Conversely, when injecting particles outside the flux rope, particles preferentially stay outside the structure, though some particles enter it. Finally, when injected throughout the entire box, a combination of the two effects is observed with a roughly ergodic particle arrangement in space and a region of higher density in the flux rope.
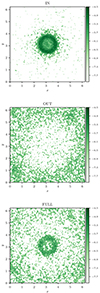 |
Fig. 11. Particle density in perpendicular plane (x, y) averaged along the z direction for RUN A and at the time t ≃ 1200 tA. Top, center, and bottom plots refer to injecting particles inside and outside the flux rope and randomly in the entire box, respectively. |
We now explore the properties of particle acceleration in the perturbed flux rope. In particular, Fig. 12 displays the time evolution of the average kinetic energy for the different injections considered in this work for RUN A. We focus here on this low-amplitude run, where the influence of the flux rope on particle dynamics is the most significant.
 |
Fig. 12. Average kinetic energy as function of time for RUN A. The inset shows, for the case of uniform injection, the time evolution of the average perpendicular (dot-dashed) and parallel (dashed) energies. For reference, we also report the average kinetic energy with a solid line. |
When injecting particles outside the flux rope (blue line) or in the entire computational domain (green line), the average particle energization displays a linear growth, possibly characterized by two distinct regimes: the first one, which occurs for t ≲ 3000 tA, being faster than the second. Conversely, when particles are released inside the flux rope, the average energization is exponential in the first time window (t ≲ 3000 tA), while later it shows a linear trend with a slope similar to the one achieved with the other kinds of particle injections in this late time range.
The energy corresponding to the change from the (fast) exponential growth to the linear one in the case of particles injected in the flux rope roughly corresponds to a particle gyroradius rg ∼ LΔ. Indeed, since rg, 0 = 0.02 LA and vp, 0 ≃ vA, the condition rg ≃ LΔ ≃ LA yields v ≃ 50 vA or 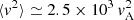 . This suggests that the mechanisms responsible for the fast acceleration preferentially observed when injecting particles inside the flux rope are, on average, no longer efficient when rg > LΔ. These mechanisms could presumably be active at the flux-rope boundary, (and, thus, they are maximized when injecting particles in the flux rope) and associated with particles trapped in the magnetic structures and experiencing an intense electric field therein, essentially due to gradients in the plasma bulk speed (Pezzi et al. 2022). To support this interpretation, we verified that RUN B is still characterized by a double regime of acceleration. Similarly to RUN A, the first phase of energization is exponential and breaks at a value of the average particle energy compatible with rg ≃ LΔ. However, the acceleration is faster in RUN B compared to RUN A. Hence, the characteristic acceleration timescale decreases as the intensity of turbulence increases. Given the presence of the equilibrium magnetic structure with no bulk speed counterparts, the first-order electric field is E ∝ δvB0, where δv is the bulk speed perturbation and B0 is the equilibrium, inhomogeneous magnetic field. This rough estimate of the inductive electric field indicates that stronger turbulence is associated with more intense electric fields that accelerate particles, thus implying a faster (on average) process of energization.
. This suggests that the mechanisms responsible for the fast acceleration preferentially observed when injecting particles inside the flux rope are, on average, no longer efficient when rg > LΔ. These mechanisms could presumably be active at the flux-rope boundary, (and, thus, they are maximized when injecting particles in the flux rope) and associated with particles trapped in the magnetic structures and experiencing an intense electric field therein, essentially due to gradients in the plasma bulk speed (Pezzi et al. 2022). To support this interpretation, we verified that RUN B is still characterized by a double regime of acceleration. Similarly to RUN A, the first phase of energization is exponential and breaks at a value of the average particle energy compatible with rg ≃ LΔ. However, the acceleration is faster in RUN B compared to RUN A. Hence, the characteristic acceleration timescale decreases as the intensity of turbulence increases. Given the presence of the equilibrium magnetic structure with no bulk speed counterparts, the first-order electric field is E ∝ δvB0, where δv is the bulk speed perturbation and B0 is the equilibrium, inhomogeneous magnetic field. This rough estimate of the inductive electric field indicates that stronger turbulence is associated with more intense electric fields that accelerate particles, thus implying a faster (on average) process of energization.
When injecting particles outside the flux rope or throughout the entire box, the average particle acceleration still exhibits a double phase, which is characterized by a fast yet linear initial acceleration. This indicates that fewer particles still experience the electric field responsible for fast acceleration compared to the case of injection inside the flux rope, thus implying the steepening of the average energization process. In other words, a particle injected outside the flux rope has a finite yet low probability of entering the flux rope. We note that for stronger initial perturbations (RUN C and RUN D, not shown) the energization is similar for all the different injections. This confirms that the intense turbulent fluctuations mask the effect of the large-scale flux rope in accelerating particles.
Therefore, turbulent fluctuations have a threefold impact on particle energization. They generally allow for particle acceleration since the background flux rope is purely magnetic (no electric field). Below a certain threshold, turbulence tends to decrease the characteristic times associated with fast exponential acceleration of trapped particles. Above the threshold, turbulent fluctuations mask the effect of the underlying flux rope, thus producing a detrapping effect on particles possibly confined in the flux rope.
We further elucidate how particles are accelerated in the simulations by looking at their perpendicular and parallel energies. In the inset of Fig. 12, it is shown that the mean perpendicular energy (dot-dashed line) is systematically larger than the parallel one (dashed line). In this analysis, performed for the case of uniform injection in the simulation domain, parallel and perpendicular velocities for each particle are computed with respect to the local magnetic field, which has been interpolated along the particle trajectory. Other injections are in qualitative agreement with what is reported in the inset of Fig. 12. At the beginning of the simulation, 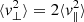 as a result of the isotropic injection in velocity space. Suddenly, and up to times of t ≃ 100 tA, the average perpendicular energy increases much faster than the parallel one as a result of fast acceleration processes related to particle trapping in the large-scale flux rope. This leads to a preferentially perpendicular energization. For longer times, the average parallel energy also increases for the underlying second-order process still energizing particles. Finally, for times of t > 1000 tA the isotropy of the velocity distribution is restored as
as a result of the isotropic injection in velocity space. Suddenly, and up to times of t ≃ 100 tA, the average perpendicular energy increases much faster than the parallel one as a result of fast acceleration processes related to particle trapping in the large-scale flux rope. This leads to a preferentially perpendicular energization. For longer times, the average parallel energy also increases for the underlying second-order process still energizing particles. Finally, for times of t > 1000 tA the isotropy of the velocity distribution is restored as 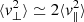 . We anticipate that trapping and fast perpendicular energization are recovered in all the different regimes we identified in the averaged energization process. However, at the beginning of the simulation, fast acceleration occurs in an environment weakly accelerated by slower processes, such as second-order energization, which eventually isotropize the velocity distribution. Hence, the effect of trapping and consequent fast perpendicular energization is much more visible in the initial phase of the time history of the average kinetic energy. Such a result, in agreement with previous studies elucidating the role of particle trapping in turbulent structures in their subsequent acceleration (e.g., Dmitruk et al. 2004; Dalena et al. 2014; Kowal et al. 2012; Sioulas et al. 2020; Trotta et al. 2020; Li et al. 2021; Pezzi et al. 2022), was here tested in a simulation dominated by a single, large-scale structure immersed in a turbulent background. It is therefore extremely interesting to address the interplay between particle trapping and energization in such a setting.
. We anticipate that trapping and fast perpendicular energization are recovered in all the different regimes we identified in the averaged energization process. However, at the beginning of the simulation, fast acceleration occurs in an environment weakly accelerated by slower processes, such as second-order energization, which eventually isotropize the velocity distribution. Hence, the effect of trapping and consequent fast perpendicular energization is much more visible in the initial phase of the time history of the average kinetic energy. Such a result, in agreement with previous studies elucidating the role of particle trapping in turbulent structures in their subsequent acceleration (e.g., Dmitruk et al. 2004; Dalena et al. 2014; Kowal et al. 2012; Sioulas et al. 2020; Trotta et al. 2020; Li et al. 2021; Pezzi et al. 2022), was here tested in a simulation dominated by a single, large-scale structure immersed in a turbulent background. It is therefore extremely interesting to address the interplay between particle trapping and energization in such a setting.
An important insight about the complexity of the energization mechanism is revealed in Fig. 13, where for the case of uniform injection we show the perpendicular and parallel energy history for the average sample (solid lines) and the same quantities for some individual particles (shaded lines) randomly selected from the entire sample. A rather complex picture emerges, characterized by intense burst of acceleration occurring at different times for different particles.
 |
Fig. 13. Perpendicular (top) and parallel (bottom) kinetic energy as function of time averaged over the whole particle set (solid line) and for individual particles (shaded lines) for the case of uniform injection. |
To clarify such a behavior, particles showing the most intense energization were selected, and their dynamics were studied in detail. Episodes of rapid acceleration have been found to be related to trapping in the turbulent flux rope. This is shown in Fig. 14, where the energy time-history of a single particle undergoing strong acceleration is shown together with its parallel and perpendicular energies (black, blue, and red lines, respectively). It is interesting to note that this particle was trapped and then escaped the structure to be trapped later in another event of fast acceleration. This behavior, made possible here by the periodicity of the simulation, elucidates the possible behavior whereby particles undergo multiple trapping events at different structures. Such a scenario, successfully invoked previously for multi-stage particle acceleration in localized networks of acceleration centers (Arzner & Vlahos 2004; Vlahos et al. 2004; Dalena et al. 2014), will be investigated in future works involving more than one flux rope with different sizes. Rapid acceleration is driven by strong increases in perpendicular energy. Furthermore, trajectory analysis shows that such strong energization happens when trapping in the flux rope is active (Figs. 14b–d). Contrarily, when the particle is not trapped, no strong energization is observed.
 |
Fig. 14. Energy time-history and position of one of the most accelerated particles in the simulations. (a): total (black), perpendicular (red), and parallel (blue) energy for one of the most accelerated particles in the simulations. (b)–(d): particle position during the shaded times in (a) colored by particle energy. In the background, the magnetic field magnitude is shown in gray scale for the z = Lbox/2 plane. |
To conclude, we remark that trapping is a local-in-time process with a rather fast timescale that is experienced by few particles and leads, preferentially, to a perpendicular energization (Fig. 14). This effect tends to anisotropize the velocity distribution function of particles (see Dalena et al. 2014). In contrast, both the diffusive (in space) transport due to the magnetic turbulence and the diffusive (in energy) transport due to the underlying second-order energization mechanism – these occurring on much longer timescales compared to trapping-related phenomena – make the distribution function isotropic, as we observe, at later times, in Fig. 12.
5. Conclusions
Turbulence in space plasmas is known to be structured and characterized by a cross-scale path of structures, which include magnetic islands, plasmoids, and turbulent eddies (Servidio et al. 2009). In addition to the presence of these structures dynamically generated by turbulence, meso-scale structures such as flux ropes can also be of solar origin due to their association with coronal mass ejections (see, e.g., Hu et al. 2018; Pecora et al. 2021; Long et al. 2023). Although with different parameters, magnetic flux ropes are observed in the solar corona and are expected to be crucial for energizing particles (see, e.g., Antolin & Shibata 2010; Pinto et al. 2015; Díaz-Suárez & Soler 2021). More generally, the presence of magnetic islands and plasmoids allows for fast particle energization, as shown by several authors in rather different contexts (Drake et al. 2006; Kowal et al. 2012; Trotta et al. 2020; Pezzi et al. 2022).
There are a number of antecedents of the present work that introduce some of the concepts advanced in the present study; examples include: effects of trapping and escape on transport (Tooprakai et al. 2007, 2016); particle exclusion (Seripienlert et al. 2010; Pecora et al. 2021); multi-stage acceleration (Dalena et al. 2014); and the importance of trapping in particle acceleration (Ambrosiano et al. 1988). In this work, we further elaborated these concepts by addressing (i) how turbulence perturbs – and is influenced by – a large-scale flux rope; and (ii) how a large-scale flux rope impacts particle transport and energization.
To this aim, by means of three-dimensional compressible MHD simulations performed with the COmpressible Hall Magnetohydrodynamics simulations for Plasma Astrophysics (COHMPA) algorithm, we built a twisted flux rope with the Grad–Shafranov technique, and we perturbed it with large-scale fluctuations. Distinctive behaviors are observed in the cases of small or large amplitudes of the initial perturbations. Indeed, as fluctuations are small, the turbulent transfer toward small scales is generally inhibited by the presence of the large-scale structure, as evidenced by the scaling exponents ζq of the structure functions. On the other hand, in the case of intense perturbations, these mask the effect of the flux rope and scalings exponents reconcile with intermittent turbulence expectations. Our results complement the recent works by Díaz-Suárez & Soler (2021, 2022), obtained within the context of coronal loops, since we characterize the properties of turbulent transfer inside and outside the large-scale flux rope in detail. Such a characterization may drive further analyses aimed at characterizing the turbulent transfer in flux ropes observed in situ.
Similarly, the flux rope is of key importance in regulating particle transport and acceleration in the case in which it is weakly affected by turbulence. In this case, particles can be trapped by the large-scale structure that inhibits their transport in the directions perpendicular to the flux-rope axis. Particles injected inside the flux rope generally have a higher probability of being trapped within the structure. There, they can undergo episodes of intense and fast acceleration due to gradients in the electric field, mainly resulting from the presence of gradients in the plasma bulk speed. This finding supports the recent observations by Pezzi et al. (2022), where a few particles, trapped in large-scale coherent structures, were experiencing fast and exponential energization, while the bulk of the particles were undergoing the standard second-order energization leading to diffusion in energy space. Owing to the presence of the large-scale flux rope, the setup adopted here maximizes the probability that particles are trapped and then energized during this peculiar stage of their motion.
We note that by focusing on the idealized case in which particles move in a fractal set of scattering centers and undergo purely stochastic energization when they collide with these scattering centers, Sioulas et al. (2020) also showed that particles – trapped within regions where scattering centers concentrate – can then be efficiently energized through a pile-up of several stochastic energization events. Our results do not contradict observations by Sioulas et al. (2020), and further studies should be performed to compare these different methods, thus also contributing to elucidating (i) the basic mechanisms leading to fast particle acceleration in turbulent plasmas and (ii) the regimes of applicability of idealized energization models to turbulent environments.
This first study focused on a flux rope in solar-wind conditions, though in this system flux ropes exhibit a large variability of their fundamental parameters (Hu et al. 2018). However, the above questions are rather general, and other scenarios, characterized by different parameters, deserve careful treatment. As an example, we mention the interesting cases of coronal loops or flux ropes observed at different distances from the Sun. Again under the guise of understanding the interaction of Alfvénic wave packets (Moffatt 1969; Parker 1965; Pezzi et al. 2017), further studies will focus on the collisions of magnetic flux ropes, possibly orientated along different axes, as well as the dynamical evolution of multiple flux tubes.
To conclude, in future works we will explore a broader set of parameters by changing (i) the ratio of the turbulent correlation length with respect to the flux-rope size, (ii) the ratio of the flux-rope size and the particle gyroradius, and (iii) the typical scale of the large-scale flux-rope gradients. We also assumed that the turbulent flux rope achieves a stationary state in which we performed test-particle simulations. As discussed at length, it can be expected that flux ropes are long-lived structures that survive for several dynamical times. However, in the future, we intend to perform simulations with non-static field. Finally, future work may exploit a different numerical model in which we do not impose periodic boundary conditions for the direction parallel to the flux-rope axis (Galsgaard & Nordlund 1996, 1997; Gerrard & Hood 2003), as considering a tri-periodic computational box influences both the dynamical evolution of the flux tube and the properties of particle transport and energization.
Acknowledgments
The authors are grateful to the reviewer for the comments which improved the manuscript. O.P. thanks R. Vainio and A. Verdini for productive discussions on this topic. O.P., L.S.V., and F.P. acknowledge the project “2022KL38BK – The ULtimate fate of TuRbulence from space to laboratory plAsmas (ULTRA)” (Master CUP B53D23004850006) by the Italian Ministry of University and Research, funded under the National Recovery and Resilience Plan (NRRP), Mission 4 – Component C2 – Investment 1.1, “Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN 2022)” (PE9) by the European Union – NextGenerationEU. This work has received funding from the European Unions Horizon 2020 research and innovation programme under grant agreement No. 101004159 (https://www.serpentine-h2020.eu). L.S.-V. is supported by the Swedish Research Council (VR) Research Grant N. 2022-03352. W.H.M. is partially supported at the University of Delaware by US National Science Foundation grant AGS/PHYS-2108834 (NSFDOE), by NASA Heliophysics GI grant (PSP) 80 NSSC21K1765, and by the PSP ISOIS Theory and modeling project on subcontract SUB0000165 from Princeton University. The simulations have been performed at the Newton cluster at University of Calabria and the work is supported by “Progetto STAR 2-PIR01 00008” (Italian Ministry of University and Research). S.S. acknowledges supercomputing resources and support from ICSC-Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing-and hosting entity, funded by European Union-NextGenerationEU. This work was partially supported by the Royal Society (UK) and the Consiglio Nazionale delle Ricerche (Italy) through the International Exchanges Cost Share scheme/Joint Bilateral Agreement project “Multi-scale electrostatic energisation of plasmas: comparison of collective processes in laboratory and space” (award numbers IEC/R2/222050 and SAC.AD002.043.021).
References
- Amato, E., & Casanova, S. 2021, J. Plasma Phys., 87, 845870101 [NASA ADS] [CrossRef] [Google Scholar]
- Ambrosiano, J., Matthaeus, W. H., Goldstein, M. L., & Plante, D. 1988, J. Geophys. Res., 93, 14383 [Google Scholar]
- Antolin, P., & Shibata, K. 2010, ApJ, 712, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P., Yokoyama, T., & Van Doorsselaere, T. 2014, ApJ, 787, L22 [Google Scholar]
- Antolin, P., De Moortel, I., Van Doorsselaere, T., & Yokoyama, T. 2017, ApJ, 836, 219 [Google Scholar]
- Archontis, V., & Hood, A. W. 2013, ApJ, 769, L21 [Google Scholar]
- Arzner, K., & Vlahos, L. 2004, ApJ, 605, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Benzi, R., Ciliberto, S., Tripiccione, R., et al. 1993, Phys. Rev. E, 48, R29 [CrossRef] [Google Scholar]
- Birdsall, C. K., & Langdon, A. B. 2004, Plasma Physics via Computer Simulation (CRC Press) [Google Scholar]
- Canuto, C., Hussaini, M. Y., Quarteroni, A., & Zang, T. A. 2006, Spectral Methods (Springer-Verlag) [CrossRef] [Google Scholar]
- Carbone, V. 1993, Phys. Rev. Lett., 71, 1546 [NASA ADS] [CrossRef] [Google Scholar]
- Carbone, F., & Sorriso-Valvo, L. 2014, Eur. Phys. J. E, 37, 61 [CrossRef] [Google Scholar]
- Carbone, V., Sorriso-Valvo, L., & Marino, R. 2009, EPL (Europhys. Lett.), 88, 25001 [NASA ADS] [CrossRef] [Google Scholar]
- Cozzo, G., Reid, J., Pagano, P., Reale, F., & Hood, A. W. 2023, A&A, 678, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cristofari, P. 2021, Universe, 7, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Dalena, S., Rappazzo, A. F., Dmitruk, P., Greco, A., & Matthaeus, W. H. 2014, ApJ, 783, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Suárez, S., & Soler, R. 2021, A&A, 648, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Suárez, S., & Soler, R. 2022, A&A, 665, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dmitruk, P., Matthaeus, W. H., Seenu, N., & Brown, M. R. 2003, ApJ, 597, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Dmitruk, P., Matthaeus, W. H., & Seenu, N. 2004, ApJ, 617, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. F., Swisdak, M., Che, H., & Shay, M. A. 2006, Nature, 443, 553 [Google Scholar]
- Dresing, N., Rodríguez-García, L., Jebaraj, I. C., et al. 2023, A&A, 674, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dundovic, A., Pezzi, O., Blasi, P., Evoli, C., & Matthaeus, W. H. 2020, Phys. Rev. D, 102, 103016 [NASA ADS] [CrossRef] [Google Scholar]
- Einaudi, G., & Velli, M. 1994, Space Sci. Rev., 68, 97 [CrossRef] [Google Scholar]
- Einaudi, G., Velli, M., Politano, H., & Pouquet, A. 1996, ApJ, 457, L113 [NASA ADS] [Google Scholar]
- Einaudi, G., Dahlburg, R. B., Ugarte-Urra, I., et al. 2021, ApJ, 910, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Emonet, T., & Moreno-Insertis, F. 1998, ApJ, 492, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi, E. 1949, Phys. Rev., 75, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi, E. 1954, ApJ, 119, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2012, Space Sci. Rev., 173, 433 [Google Scholar]
- Frigo, M. 1999, Proceedings of the ACM SIGPLAN 1999 Conference on Programming Language Design and Implementation, 169 [CrossRef] [Google Scholar]
- Frisch, U. 1995, Turbulence: The Legacy of AN Kolmogorov (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Galsgaard, K., & Nordlund, Å. 1996, J. Geophys. Res., 101, 13445 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., & Nordlund, Å. 1997, J. Geophys. Res., 102, 219 [CrossRef] [Google Scholar]
- Georgoulis, M. K., Velli, M., & Einaudi, G. 1998, ApJ, 497, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Gerrard, C. L., & Hood, A. W. 2003, Sol. Phys., 214, 151 [CrossRef] [Google Scholar]
- González, C. A., Dmitruk, P., Mininni, P. D., & Matthaeus, W. H. 2016, Phys. Plasmas, 23, 082305 [CrossRef] [Google Scholar]
- González, C. A., Dmitruk, P., Mininni, P. D., & Matthaeus, W. H. 2017, ApJ, 850, 19 [CrossRef] [Google Scholar]
- Gordovskyy, M., & Browning, P. K. 2011, ApJ, 729, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Howson, T. A., De Moortel, I., & Antolin, P. 2017, A&A, 607, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, Q., Qiu, J., Dasgupta, B., Khare, A., & Webb, G. M. 2014, ApJ, 793, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Q., Zheng, J., Chen, Y., le Roux, J., & Zhao, L. 2018, ApJS, 239, 12 [Google Scholar]
- Karampelas, K., Van Doorsselaere, T., & Antolin, P. 2017, A&A, 604, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khabarova, O., Zank, G. P., Li, G., et al. 2015, ApJ, 808, 181 [Google Scholar]
- Khabarova, O. V., Zank, G. P., Li, G., et al. 2016, ApJ, 827, 122 [Google Scholar]
- Khabarova, O., Malandraki, O., Malova, H., et al. 2021, Space Sci. Rev., 217, 38 [CrossRef] [Google Scholar]
- Kilpua, E., Vainio, R., Cohen, C., et al. 2023, Ap&SS, 368, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Kowal, G., de Gouveia Dal Pino, E. M., & Lazarian, A. 2011, ApJ, 735, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., de Gouveia Dal Pino, E. M., & Lazarian, A. 2012, Phys. Rev. Lett., 108, 241102 [NASA ADS] [CrossRef] [Google Scholar]
- Kraichnan, R. 1965, Phys. Fluids, 8, 1385 [NASA ADS] [CrossRef] [Google Scholar]
- Krittinatham, W., & Ruffolo, D. 2009, ApJ, 704, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., Vlahos, L., Kowal, G., et al. 2012, Space Sci. Rev., 173, 557 [Google Scholar]
- Lazarian, A., Eyink, G. L., Jafari, A., et al. 2020, Phys. Plasmas, 27, 012305 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine, M. 2022, Phys. Rev. Lett., 129, 215101 [NASA ADS] [CrossRef] [Google Scholar]
- le Roux, J. A., Zank, G. P., Webb, G. M., & Khabarova, O. 2015, ApJ, 801, 112 [Google Scholar]
- le Roux, J. A., Zank, G. P., & Khabarova, O. V. 2018, ApJ, 864, 158 [Google Scholar]
- le Roux, J. A., Webb, G. M., Khabarova, O. V., Zhao, L.-L., & Adhikari, L. 2019, ApJ, 887, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Li, X., Guo, F., & Liu, Y.-H. 2021, Phys. Plasmas, 28, 052905 [NASA ADS] [CrossRef] [Google Scholar]
- Long, D. M., Green, L. M., Pecora, F., et al. 2023, ApJ, 955, 152 [CrossRef] [Google Scholar]
- Magyar, N., Van Doorsselaere, T., & Marcu, A. 2015, A&A, 582, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiorano, T., Settino, A., Malara, F., et al. 2020, J. Plasma Phys., 86, 825860202 [NASA ADS] [CrossRef] [Google Scholar]
- Malandraki, O., Khabarova, O., Bruno, R., et al. 2019, ApJ, 881, 116 [Google Scholar]
- Malara, F., Perri, S., & Zimbardo, G. 2021, Phys. Rev. E, 104, 025208 [CrossRef] [Google Scholar]
- Malara, F., Perri, S., Giacalone, J., & Zimbardo, G. 2023, A&A, 677, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, R., & Sorriso-Valvo, L. 2023, Phys. Rep., 1006, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Matthaeus, W. H., Wan, M., Servidio, S., et al. 2015, Philos. Trans. R. Soc. London Ser. A, 373, 20140154 [Google Scholar]
- McComas, D. J., Sharma, T., Christian, E. R., et al. 2023, ApJ, 943, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Meneveau, C., & Sreenivasan, K. 1987, Phys. Rev. Lett., 59, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K. 1969, J. Fluid Mech., 35, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Nakanotani, M., Zank, G. P., & Zhao, L.-L. 2021, ApJ, 922, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, M., Phan, T. D., Krucker, S., Fujimoto, M., & Shinohara, I. 2010, ApJ, 714, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1965, Space Sci. Rev., 4, 666 [Google Scholar]
- Pecora, F., Servidio, S., Greco, A., et al. 2018, J. Plasma Phys., 84, 725840601 [Google Scholar]
- Pecora, F., Servidio, S., Greco, A., et al. 2021, MNRAS, 508, 2114 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., Servidio, S., Vaivads, A., & Valentini, F. 2017, ApJS, 231, 4 [Google Scholar]
- Pezzi, O., Parashar, T. N., Servidio, S., et al. 2017, ApJ, 834, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzi, O., Pecora, F., Le Roux, J., et al. 2021, Space Sci. Rev., 217, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzi, O., Blasi, P., & Matthaeus, W. H. 2022, ApJ, 928, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, R. F., Vilmer, N., & Brun, A. S. 2015, A&A, 576, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, R. F., Gordovskyy, M., Browning, P. K., & Vilmer, N. 2016, A&A, 585, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pisokas, T., Vlahos, L., & Isliker, H. 2018, ApJ, 852, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, H., & Pouquet, A. 1998, Phys. Rev. E, 57, R21 [CrossRef] [Google Scholar]
- Quijia, P., Fraternale, F., Stawarz, J. E., et al. 2021, MNRAS, 503, 4815 [NASA ADS] [CrossRef] [Google Scholar]
- Reames, D. V. 1999, Space Sci. Rev., 90, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Retinò, A., Khotyaintsev, Y., Le Contel, O., et al. 2022, Exp. Astron., 54, 427 [CrossRef] [Google Scholar]
- Réville, V., Fargette, N., Rouillard, A. P., et al. 2022, A&A, 659, A110 [CrossRef] [EDP Sciences] [Google Scholar]
- Ripperda, B., Bacchini, F., Teunissen, J., et al. 2018, ApJS, 235, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Seripienlert, A., Ruffolo, D., Matthaeus, W. H., & Chuychai, P. 2010, ApJ, 711, 980 [Google Scholar]
- Servidio, S., Matthaeus, W. H., & Dmitruk, P. 2008, Phys. Rev. Lett., 100, 095005 [NASA ADS] [CrossRef] [Google Scholar]
- Servidio, S., Matthaeus, W. H., Shay, M. A., Cassak, P. A., & Dmitruk, P. 2009, Phys. Rev. Lett., 102, 115003 [Google Scholar]
- Servidio, S., Dmitruk, P., Greco, A., et al. 2011, Nonlinear Process. Geophys., 18, 675 [CrossRef] [Google Scholar]
- Servidio, S., Haynes, C. T., Matthaeus, W. H., et al. 2016, Phys. Rev. Lett., 117, 095101 [NASA ADS] [CrossRef] [Google Scholar]
- Shebalin, J. V., Matthaeus, W. H., & Montgomery, D. 1983, J. Plasma Phys., 29, 525 [Google Scholar]
- Sioulas, N., Isliker, H., & Vlahos, L. 2020, ApJ, 895, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Sorriso-Valvo, L., Marino, R., Carbone, V., et al. 2007, Phys. Rev. Lett., 99, 115001 [CrossRef] [Google Scholar]
- Sorriso-Valvo, L., Perrone, D., Pezzi, O., et al. 2018, J. Plasma Phys., 84, 725840201 [NASA ADS] [CrossRef] [Google Scholar]
- Srivastava, A. K., Zaqarashvili, T. V., Kumar, P., & Khodachenko, M. L. 2010, ApJ, 715, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Andries, J., Goossens, M., et al. 2008, ApJ, 687, L115 [Google Scholar]
- Threlfall, J., Reid, J., & Hood, A. W. 2021, Sol. Phys., 296, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Tooprakai, P., Chuychai, P., Minnie, J., et al. 2007, Geophys. Res. Lett., 34, L17105 [Google Scholar]
- Tooprakai, P., Seripienlert, A., Ruffolo, D., Chuychai, P., & Matthaeus, W. H. 2016, ApJ, 831, 195 [Google Scholar]
- Trotta, D., & Burgess, D. 2019, MNRAS, 482, 1154 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, D., Franci, L., Burgess, D., & Hellinger, P. 2020, ApJ, 894, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, D., Pecora, F., Settino, A., et al. 2022, ApJ, 933, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, D., Pezzi, O., Burgess, D., et al. 2023, MNRAS, 525, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Turkmani, R., Vlahos, L., Galsgaard, K., Cargill, P. J., & Isliker, H. 2005, ApJ, 620, L59 [CrossRef] [Google Scholar]
- Turkmani, R., Cargill, P. J., Galsgaard, K., Vlahos, L., & Isliker, H. 2006, A&A, 449, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valentini, F., Vásconez, C. L., Pezzi, O., et al. 2017, A&A, 599, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vásconez, C. L., Pucci, F., Valentini, F., et al. 2015, ApJ, 815, 7 [Google Scholar]
- Viall, N. M., DeForest, C. E., & Kepko, L. 2021, Front. Astron. Space Sci., 8, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahos, L., Isliker, H., & Lepreti, F. 2004, ApJ, 608, 540 [CrossRef] [Google Scholar]
- Wan, M., Servidio, S., Oughton, S., & Matthaeus, W. H. 2009, Phys. Plasmas, 16, 090703 [NASA ADS] [CrossRef] [Google Scholar]
- Wijsen, N., Aran, A., Scolini, C., et al. 2022, A&A, 659, A187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yordanova, E., Vaivads, A., André, M., Buchert, S., & Vörös, Z. 2008, Phys. Rev. Lett., 100, 205003 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Hunana, P., Mostafavi, P., et al. 2015, J. Phys.: Conf. Ser., 642, 012031 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Nakanotani, M., Zhao, L. L., et al. 2021, ApJ, 913, 127 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Grad-Shafranov equilibria
The Grad–Shafranov equation is an equilibrium-equation of ideal MHD capable of describing several configurations, including the reversed field pinch in fusion devices or the solar prominences. Assuming a static plasma in the absence of visco-resistive forces, the momentum equation (normalized as in Sect. 2) reads as
where j = ∇ × B is the current density and P is the kinetic pressure. Equation A.1 is solved by decomposing the magnetic field via the Euler potentials and assuming a relation between the poloidal and the toroidal fluxes:
The toroidal flux is hence proportional to the stream function ψ (A being constant, for simplicity), which in turn is a poloidal flux.
Here, we focus on the 2.5D configuration. Aψ ≡ Aψ(x, y) is the out-of-plane magnetic vector potential az, with ∇ ≡ (∂x, ∂y). By substituting equation (A.2) in (A.1), one obtains the following PDEs:
The term in the brackets is essentially the Helmholtz equation, which is null in the case of force-free states. The main difference is that the GS equation keeps the parallel component of the magnetic field. Hence, magnetic field lines characterized by helicoidal states are allowed. This new degree of freedom provides a richer variety of solutions.
Equations (A.3–A.4) are solved for a given differentiable stream function ψ to provide the kinetic pressure P. Indeed, these equations correspond to a Poisson equation for P:
where
With the purpose of localizing the magnetic flux in a particular region of the computational domain, we build the flux ψ through the Blackman-Nuttall window. In particular, we initially considered the following one-dimensional axisymmetric profile:
with ψ0 = 0.355768, ψ1 = −0.487396, ψ2 = 0.144232, and ψ3 = −0.012604 being opportune coefficients that control the amplitude and the shear layer width of the flux function, while 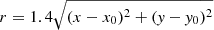 with x0 = y0 = π. Then, we renormalized ψ such that ⟨ψ⟩=1.0, while its amplitude is 0.4. Moreover, A = 1.4. Within these parameters, the resulting magnetic vector potential is the one reported in Fig. 1 (right). The magnetic field associated with such a potential evaluated through equation (A.2) is shown in Fig. A.1. The in-plane magnetic field components have a dipolar structure, while the (toroidal-like) field, Bz, is much more intense. Given the stream function, ψ, equation (A.5) is solved by exploiting the periodic boundary conditions and setting the minimum pressure to the value P0 = 0.5. Finally, by using the adiabatic closure for an ideal gas, we can obtain the density ρ and pressure T.
with x0 = y0 = π. Then, we renormalized ψ such that ⟨ψ⟩=1.0, while its amplitude is 0.4. Moreover, A = 1.4. Within these parameters, the resulting magnetic vector potential is the one reported in Fig. 1 (right). The magnetic field associated with such a potential evaluated through equation (A.2) is shown in Fig. A.1. The in-plane magnetic field components have a dipolar structure, while the (toroidal-like) field, Bz, is much more intense. Given the stream function, ψ, equation (A.5) is solved by exploiting the periodic boundary conditions and setting the minimum pressure to the value P0 = 0.5. Finally, by using the adiabatic closure for an ideal gas, we can obtain the density ρ and pressure T.
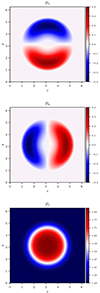 |
Fig. A.1. Contour plots of equilibrium magnetic field. From top to bottom: Bx, By, and Bz. |
The choice of ψ, A, P0 (as well as ρ0 and T0) is rather arbitrary. We selected the above parameters to achieve a configuration qualitatively similar to in situ observations in the solar wind. Different configurations will be considered in a separate work.
All Tables
All Figures
 |
Fig. 1. Overview of initial two-dimensional equilibrium, showing the maps of the kinetic pressure P (top) and the out-of-plane potential vector az (bottom). |
| In the text | |
 |
Fig. 2. Three-dimensional magnetic field lines of equilibrium flux-rope structure. Lines are colored with the magnitude of the magnetic field vorticity; i.e., the current density. |
| In the text | |
 |
Fig. 3. One-dimensional profile of β (red) and density of magnetic helicity hm (blue) along x, evaluated at y = Ly/2. |
| In the text | |
 |
Fig. 4. Time evolution of ⟨j2⟩(t) for different runs in Table 1. Vertical dashed lines indicate the time instant t* at which, for each run, we perform the subsequent analyses on turbulence and particle transport. |
| In the text | |
 |
Fig. 5. Two-dimensional overviews of current density |j| in the plane (x, y, z = Lz/2) perpendicular to flux-rope axis, for the different runs in Table 1 computed at t = t*. |
| In the text | |
 |
Fig. 6. Two-dimensional overviews of current density |j| in the plane (x, y = Ly/2, z) parallel to flux rope axis, for RUN A (top) and RUN D (bottom) computed at t = t*. |
| In the text | |
 |
Fig. 7. Two-dimensional overview of temperature T at vertical position z = Lz/2 for RUN D t = t*. |
| In the text | |
 |
Fig. 8. Magnetic energy spectra for different runs in Table 1 computed at t = t*. Top and bottom plots show the perpendicular and parallel spectra, i.e., Eb(k⊥) and Eb(k∥), respectively. The dashed gray line shows the Kolmogorov prediction, |
| In the text | |
 |
Fig. 9. Local analysis of turbulent properties inside and outside the flux rope for RUN A and RUN D. Top: flatness F(r) of magnetic field increments as a function of separation scale r for RUN A (left) and RUN D (right) and for data sampled inside (red) and outside (blue) the flux rope. Dotted line is the reference Gaussian flatness value. Middle: scaling exponents ζq as function of order q for RUN A (left) and RUN D (right) evaluated inside (red) and outside (blue) the flux rope for the magnetic field. Dotted lines represent the linear scaling, while solid lines indicate the p-model best fit for each data sample. The Hurst exponents h = ζ2/2 are 0.42 (inside) and 0.35 (outside) for RUN A and 0.40 (inside) and 0.42 (outside) for RUN D. Bottom: Politano-Pouquet’s term Y(r) as function of separation scale r, computed inside (red) and outside (blue) the flux rope for RUN A (left) and RUN D (right). The dotted lines indicate the linear scaling. Filled circles correspond to −Y(r) and empty circles to Y(r). |
| In the text | |
 |
Fig. 10. Time evolution of parallel |
| In the text | |
 |
Fig. 11. Particle density in perpendicular plane (x, y) averaged along the z direction for RUN A and at the time t ≃ 1200 tA. Top, center, and bottom plots refer to injecting particles inside and outside the flux rope and randomly in the entire box, respectively. |
| In the text | |
 |
Fig. 12. Average kinetic energy as function of time for RUN A. The inset shows, for the case of uniform injection, the time evolution of the average perpendicular (dot-dashed) and parallel (dashed) energies. For reference, we also report the average kinetic energy with a solid line. |
| In the text | |
 |
Fig. 13. Perpendicular (top) and parallel (bottom) kinetic energy as function of time averaged over the whole particle set (solid line) and for individual particles (shaded lines) for the case of uniform injection. |
| In the text | |
 |
Fig. 14. Energy time-history and position of one of the most accelerated particles in the simulations. (a): total (black), perpendicular (red), and parallel (blue) energy for one of the most accelerated particles in the simulations. (b)–(d): particle position during the shaded times in (a) colored by particle energy. In the background, the magnetic field magnitude is shown in gray scale for the z = Lbox/2 plane. |
| In the text | |
 |
Fig. A.1. Contour plots of equilibrium magnetic field. From top to bottom: Bx, By, and Bz. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



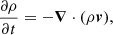
![$$ \begin{aligned} \frac{\partial {\boldsymbol{v}}}{\partial t}&= - \left({\boldsymbol{v}} \cdot {\boldsymbol{\nabla }}\right) {\boldsymbol{v}} + \frac{1}{\rho } \left[\left({\boldsymbol{\nabla }} \times {\boldsymbol{B}}\right) \times {\boldsymbol{B}}\right] - \frac{\beta _0}{2\rho }{\boldsymbol{\nabla }} (\rho T) ,\end{aligned} $$](/articles/aa/full_html/2024/06/aa48700-23/aa48700-23-eq2.gif)
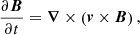
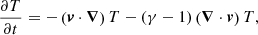
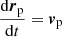
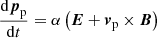
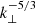
![$$ \begin{aligned} \zeta _q=1-\log _2[p^{hq}+(1-p)^{hq}]. \end{aligned} $$](/articles/aa/full_html/2024/06/aa48700-23/aa48700-23-eq16.gif)
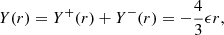
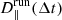
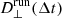
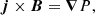
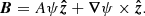
![$$ \begin{aligned}&-\partial _x \psi \left[\partial ^2_{xx}\psi + \partial ^2_{ yy}\psi + A^2 \psi \right]=\partial _x P, \end{aligned} $$](/articles/aa/full_html/2024/06/aa48700-23/aa48700-23-eq30.gif)
![$$ \begin{aligned}&-\partial _{ y} \psi \left[\partial ^2_{xx}\psi + \partial ^2_{ yy}\psi + A^2 \psi \right]=\partial _{ y} P. \end{aligned} $$](/articles/aa/full_html/2024/06/aa48700-23/aa48700-23-eq31.gif)
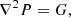
![$$ \begin{aligned} G = \partial _x{\left\{ -\partial _x \psi \left[\partial ^2_{xx}\psi + \partial ^2_{ yy}\psi + A^2 \psi \right]\right\} } + \partial _{ y}{\left\{ -\partial _{ y} \psi \left[\partial ^2_{xx}\psi + \partial ^2_{ yy}\psi + A^2 \psi \right]\right\} }. \end{aligned} $$](/articles/aa/full_html/2024/06/aa48700-23/aa48700-23-eq33.gif)