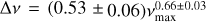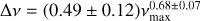EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A174 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A174
Number of page(s) 14
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/202346985
Published online 11 June 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

In recent years, we have seen a rapid development of photometric space telescopes such as the Microvariability and Oscillations of STars (MOST, Walker et al. 2003); Convection, Rotation, and planetary Transits (CoRoT, Auvergne et al. 2009); Kepler (e.g., Gilliland et al. 2010; Koch et al. 2010); and TESS (Ricker et al. 2015), which has allowed us to obtain a wealth of high-resolution data. Studies utilizing these databases can investigate stellar structure and evolution and identify numerous targets that are challenging to detect through ground-based observations. The δ Scuti stars are A-F stars pulsating with pressure modes, typically located in the overlap of the main sequence and pulsating instability strip in the Hertzsprung–Russell (HR) diagram.

There is also a fraction of δ Scuti stars in the pre-main-sequence (Pre-MS) evolutionary stage. The first detection of δ Scuti oscillations in a Pre-MS star was reported by Kurtz & Marang (1995), and analyzing the stellar pulsations of such stars can offer constraints on the physics of protostellar accretion (e.g., Zwintz et al. 2014; Steindl et al. 2021). δ Scuti stars typically have masses in the 1.5–2.5 M⊙ range; thus, they lie on the Kraft break (e.g., Kraft 1967; Royer 2009; Avallone et al. 2022). This represents the transition between slowly rotating low-mass stars with a radiative core and a thick convective envelope and rapidly rotating intermediate-mass stars with a convective core and a major radiative envelope (e.g., Kraft 1967; Royer 2009; Avallone et al. 2022).

Most δ Scuti stars are main-sequence or subgiant stars with no, or a thin, convective envelope. The differences in the structure of stars offer opportunities to investigate various areas of physics such as pulsation, rotation, magnetic fields, and chemical peculiarities (e.g., Murphy 2015; Saio et al. 2015; Thomson-Paressant et al. 2021). Hence, the examination of δ Scuti star is important for testing theoretical models of stellar evolution. These stars manifest numerous pulsation frequencies associated with different modes of pulsation, primarily radial and non-radial modes (e.g., Breger 2000; Uytterhoeven et al. 2011), which are generally excited by the κ mechanism (Aerts et al. 2010). The spectral types of δ Scuti stars usually span from A2 to F2, and their effective temperature falls within the range of 6300 ≤ Teff ≤ 8600 K (Uytterhoeven et al. 2011). These stars exhibit pulsation modes mainly characterized as low-radial-order (n), low-degree (l) pressure (p) modes (e.g., Viskum et al. 1998; Aerts et al. 2010; Lv et al. 2021a, 2022a,b). Investigating binary systems containing δ Scuti stars is also valuable as it provides more accurate stellar parameters. Therefore, such systems are excellent targets for asteroseismic studies, which can help advance our understanding of stellar structure and evolution (e.g., Guo et al. 2019; Murphy et al. 2020; Lv et al. 2021b; Miszuda et al. 2021; Chen et al. 2022).

Bowman et al. (2016) conducted an extensive analysis on the modulation of both amplitude and phase within the frequency spectra of 983 δ Scuti stars. These stars were observed over a span of four years through the Kepler mission. The results revealed that more than 60% of these celestial objects displayed significant fluctuations in both amplitude and phase. The study systematically investigated the root causes of these variations in amplitude and phase, encompassing factors such as unresolved frequencies, whether they were mode frequencies or nonlinear combination frequencies, the presence of three-mode resonances, variations in driving and damping mechanisms, and the intricate exchange of energy among coupled modes.

Since the launch of the first asteroseismic space missions, the power spectra of δ Scuti stars have resisted mode identification for a substantial portion of their frequencies, which is a crucial step in the process of forward modeling. A single star can exhibit the excitation of hundreds of modes, including radial, nonradial, and mixed modes, as well as combination frequencies resulting from nonlinear mode interactions (Aerts et al. 2010), but even the most sophisticated models are incapable of fitting the full number and range of frequencies observed in some cases (e.g., García Hernández et al. 2009; Balona 2023). In particular, in Poretti et al. (2009) a flat power excess made of low-amplitude peaks is shown at low frequencies. Several plausible mechanisms to explain this include a cascade bug in the pre-whitening procedure (Balona 2014), an inconsistency in the analysis due to the non-harmonic nature of the signal (e.g., Pascual-Granado et al. 2015; de Franciscis et al. 2018), mode coupling (e.g., Buchler et al. 1997; Barceló Forteza et al. 2015), and a background signal due to granulation (Kallinger et al. 2010). Furthermore, most δ Scuti stars are characterized as moderate-to-rapid rotators, which causes the rotationally split multiplets of non-radial modes to have uneven separations (e.g., Reese 2022; Kurtz 2022) and the modes to assume complex geometries (e.g., Ballot et al. 2013; Mirouh 2022). This discrepancy between the multi-plet separation and the mode frequency separation complicates efforts to identify specific modes. The lack of a precise identification of pulsation modes within the frequency spectra poses a significant obstacle when attempting to construct accurate aster-oseismology models for these stars. In such cases, asteroseismic indices may offer valuable insights and assistance in the process of mode identification (e.g., Bedding et al. 2020, Hasanzadeh et al. 2021; hereafter H21).

The use of scaling relations based on asteroseismic indices and global stellar properties is a common approach to determining the fundamental parameters of stars (e.g., Brown et al. 1991; Kallinger et al. 2010; Coelho et al. 2015; Rodrigues et al. 2017; Hekker 2020, H21). However, validating the accuracy and reliability of these relations is a crucial step (e.g., Huber et al. 2017, H21). The stellar density and large separation were determined from the characteristics of binaries containing a δ Scuti component by García Hernández et al. (2015, 2017), who found that the relationship between these two parameters deviated slightly from the theoretical expectations obtained from the asymptotic theory of Tassoul (1980). Mirouh et al. (2019) found large separations in models to be about 0.9 times the predictions derived from the asymptotic theory, a phenomenon that was observed in 60 young δ Scuti stars by Bedding et al. (2020) with large separations of 0.85 times their asymptotic value. This is due to the radial orders of the detected modes being too low for the large separation to reach its asymptotic value (García Hernández et al. 2009). Meanwhile, a new relationship between large separation and average density was obtained in (e.g., Mirouh et al. 2019, H21). Bowman & Kurtz (2018) and Barceló Forteza et al. (2018) found a positive correlation between the effective temperature of δ Scuti stars and the frequency with the highest amplitude. According to Bedding et al. (2023), the properties of pulsation spectra for δ Scuti stars display significant variation and do not exhibit a strong correlation with stellar temperature. These findings challenge the usefulness of the νmax relation for δ Scuti , at least for young stars.

In this paper, we present the observations and identification of δ Scuti stars observed by TESS cycle 4 in Sect. 2. Then, we discuss the pulsation properties of these stars in Sect. 3, and the period-luminosity relation of δ Scuti stars is investigated in Sect. 4. Section 5 contains the asteroseismic analysis. Finally, Sect. 6 presents the conclusions.

2 Observations and target identification

The TESS satellite is equipped with four wide-angle cameras, each of which has a 24° × 96° field of view, and each camera consists of four 2K × 2K CCDs (Ricker et al. 2015). The relatively low angular resolution of 21″ per pixel is due to the large field of view. Additionally, each sector of observation is defined as the region of the sky observed over approximately 27.4 days, that is, two consecutive TESS orbits. After a sector is observed, TESS moves the field of view by 27° along the ecliptic to observe the next sector. TESS completes a full hemisphere scan in a single “cycle”. The primary goal of the TESS mission is to detect planetary transits in bright stars across the celestial sphere. Specifically chosen stars undergo high-cadence observations, providing a valuable dataset for exploring previously uncharted astrophysical phenomena within main-sequence A and F stars. These data are particularly valuable for discovering new variability among stars.

We primarily used photometric data processed by the TESS Science Processing Operations Center (SPOC, Jenkins et al. 2016), which is available at the Mikulski Archive for Space Telescopes (MAST)1. The photometric data include Simple Aperture Photometry (SAP) and Pre-Search Data Conditioning (PDC) SAP flux, the latter eliminating long-term trends (Twicken et al. 2010). In order to detect new δ Scuti stars, we initially chose stars in cycle 4 within the typical temperature range of 6300 K ≤ Teff ≤ 9300 K. We subsequently used the widely used, open-source LIGHTKURVE package (Lightkurve Collaboration 2018) to compute a standard Lomb-Scargle periodogram to determine the oscillation frequencies of δ Scuti stars. We chose the frequency with the largest amplitude extracted in the frequency range studied as the main pulsation period and amplitude of the star. For this analysis, frequencies with peaks in the range of 3 ≤ v ≤ 80 day−1 and with amplitude greater than 0.1 mmag were selected (Bowman et al. 2016). The Nyquist frequency of 2 min cadence observations is fN = 360 day−1, which is well above our limit range for the extracted frequencies. Following these criteria, 1056 potential stars were identified. Subsequently, we cross-referenced these stars with the existing δ Scuti star catalog (Zhou 2024), which is a thorough collation of 42 previously published δ Scuti catalogs. To accurately identify the largest amplitude frequencies in the amplitude spectra, and to obtain the corresponding frequency errors. We utilized the FELIX tool (e.g., Charpinet et al. 2010; Zong et al. 2016). The uncertainty in frequency is determined using the method proposed by Montgomery & O’Donoghue (1999), allowing us to estimate the accuracy of our frequency measurements. Finally, we obtained 765 δ Scuti stars, which are listed in Table A.1. The stellar parameters in the table are sourced from Stassun et al. (2019); however, some parameters for certain stars were not provided. Of these stars, 179 have low-resolution spectral parameters from LAMOST2 (Cui et al. 2012), which are listed in Table A.2. We directly utilized the parameters and errors obtained from LAMOST. Figure 1 shows the positions of all 765 δ Scuti stars discovered in TESS cycle-4.

Figure 2 shows the distribution of diverse parameters, including effective temperature, surface gravity, Vmag, luminosity, [Fe/H], mass, radius, and parallax, for both the 765-star and 179-star samples. The mass, radius, effective temperature, and surface gravity values of δ Scuti stars lie within the ranges of 1.4 M⊙ to 2.1 M⊙, 1.2 R⊙ to 3.7 R⊙, 6300 to 9300 K, and 3.3 to 4.5 dex, respectively. Examining the figure, it is evident that the two datasets largely maintain a consistent distribution across eight parameters. Notably, the surface gravity exhibits two distinct peaks in the TIC sample, whereas the LAMOST sample lacks the peak at surface gravity log g = 4.25. It appears that LAMOST performs more effectively with pre-main-sequence, late-main-sequence, and subgiant δ Scuti stars than with early-main-sequence δ Scuti stars. This discrepancy likely arises due to the smaller sample size of LAMOST. The median temperature hovers around 7500 K, with median values of 1.75 for mass and 2 for radius, aligning with prior statistical findings for δ Scuti stars. Vmag remains consistently close to ten, with only a handful of observed targets exceeding 12 mag, owing to the observational limitations of TESS.

thumbnail Fig. 1

Position (Ecliptic latitude and longitude) of 765 δ Scuti stars (blue dots) and 179 δ Scuti stars with low-resolution spectral parameters (red dots) in the celestial sphere.
thumbnail Fig. 2

Effective temperature, Vmag, surface gravity, luminosity, [Fe/H], mass, radius, and parallax distributions are shown for 765 and 179 δ Scuti stars as a blue and a red region, respectively.

3 Pulsation properties of δ Scuti stars observed by TESS

According to the results of Dupret et al. (2005), zero-age-main-sequence (ZAMS) stars located near the blue edge of the classical instability strip may exhibit higher order pulsations in the radial overtone mode compared to stars located at the red edge, leading to higher observed pulsation frequencies. This is caused by the different depths of the He II driving region in the stellar envelope about Teff; if the star is too hot, the ionization region will be located near the surface where the fluid is too tenuous to drive the oscillations, and if the star is too cold, convection will suppress the oscillations.

Figure 3 shows the Teff – log g diagrams for our 765 δ Scuti stars. The blue and red dots correspond to Teff and log g obtained by TIC and LAMOST, respectively. The blue and red lines in the diagram represent the theoretical blue and red edges of the classical instability band, respectively; the solid lines are for p modes of radial order n = 1 and the dashed lines are for radial order n = 6 (Bowman & Kurtz 2018). Most of the δ Scuti stars are located in the instability strip, and the subgroup of stars with LAMOST spectral parameters seems to be more tightly clustered, suggesting that the spectral parameters may provide more accurate estimates of Teff and log g for these δ Scuti stars. The number of stars distributed outside the classical instability strip is likely to be the result of inaccurate parameters or the presence of modes at a higher radial order.

Bowman & Kurtz (2018) analyzed the statistics of the stellar parameters and pulsation modes of δ Scuti stars from Kepler observations, and we performed a similar operation for the first time for δ Scuti stars from TESS observations. The relationship between pulsation frequency and temperature was investigated for both TIC and LAMOST samples. The top row of Fig. 4 shows the distribution of the frequency with the maximum amplitude of 765 δ Scuti stars. The blue region represents the distribution with TIC parameters, while the red region shows the distribution for a subgroup of stars with LAMOST parameters for comparison. No δ Scuti star in our sample show maximum amplitude pulsations at frequencies higher than 60 days−1, which confirms the results of the statistical analysis performed by Bowman & Kurtz (2018). The frequency with the maximum amplitude of δ Scuti stars lies in the range of 5 <ν ≤ 60 day−1 for TESS observations.

The frequency of maximum amplitude plotted against the effective temperature for the two samples of TIC and LAMOST are indicated by blue and red dots in the middle row of Fig. 4, respectively, and the blue and red lines represent statistically significant linear regressions for the two samples. Linear regressions of the frequency of maximum amplitude and Teff using either the TIC or LAMOST values exhibit statistically significant positive correlations, with R = 0.50 and R = 0.42, respectively. It is worth noting that the slope of the LAMOST fit is smaller than that of the TIC fit. The gradient, m, intercept, c, coefficient of correlation, R, and p-value for each data set are listed in Table 1.

During the main-sequence phase, as the stellar radius increases, the pulsation frequency of a star’s modes decreases, but this decrease occurs at a relatively slow rate (Aerts et al. 2010). Therefore, in addition to the effective temperature, the pulsation frequency of a star is also influenced by its surface gravity. Both Teff and log g play important roles in determining the pulsation frequency of a star, indicating that the frequency is dependent on both temperature and the stellar structure, as represented by the surface gravity. Thus, we investigate the relationship between pulsation frequency and Teff by classifying the stars of the TIC sample according to different log g values similarly to Bowman & Kurtz (2018). In comparison to Bowman & Kurtz (2018), we expanded our Pre-MS δ Scuti star sample by cross-referencing our sample with more than ten catalogs, resulting in the identification of 15 Pre-MS δ Scuti stars. The remaining TIC stars are grouped according to log g ≥ 4.0 (ZAMS), 3.5 ≤ log g < 4.0 (MAMS), and log g < 3.5 (terminal-age main sequence; TAMS). Undocumented Pre-MS δ Scuti stars might be confused with MAMS stars due to their similar log g values (Steindl et al. 2021), even if the relative durations of these phases make Pre-MS stars relatively rare. In the bottom panel of Fig. 4, we show Pre-MS, ZAMS, MAMS, and TAMS, which are shown as cyan, green, yellow, and black dots, respectively. Lines of the same color as the sample dots indicate the respective linear regressions. We did not perform the same classification for the 179 δ Scuti stars with LAMOST parameters due to the small number of stars with them. The linear regression results are listed in Table 1. According to our statistical results, the Teff and maximum amplitude pulsation frequency of these four different groups present different fitting results. The R values for ZAMS δ Scuti stars and MAMS δ Scuti stars are 0.47 and 0.36, respectively. Although the values are not significant, the p values are quite small; this statistic is still meaningful, and the relationship between temperature and maximum amplitude pulsation frequency is more significant for MAMS stars than for ZAMS stars. Since there are too few stars in the Pre-MS and TAMS, reliable statistical results cannot be obtained (p = 0.1279 and p = 0.1769), according to the trends reflected in ZAMS and MAMS, the relationship between the temperature and the maximum amplitude pulsation frequency of TAMS stars should be more significant. A follow-up analysis of Pre-MS and TAMS δ Scuti stars will be necessary to obtain accurate results.

thumbnail Fig. 3

Teff – log g diagram for our 765 δ Scuti stars observed by TESS. The blue dots represent the positions of δ Scuti stars using parameters from the TIC, while the red dots correspond to a subgroup of δ Scuti stars with spectroscopic Teff and log g values. The solid blue and red lines indicate the theoretical blue and red edges of the classical instability strip, respectively, for p modes with radial order n = 1, while the dashed blue and red lines represent radial order n = 6 according to Dupret et al. (2005).
thumbnail Fig. 4

Relationship between pulsation frequency and temperature was investigated for both TIC and LAMOST samples. Top row shows distribution of frequency with maximum amplitude (shown as a blue region) for the ensemble of our 765 δ Scuti stars observed by TESS. The red region indicates the distribution for the subgroup of stars with spectro-scopic parameters from LAMOST. The middle row shows the frequency of the maximum amplitude plotted against the effective temperature, with the TIC and LAMOST parameters represented by blue and red dots, respectively. The statistically significant linear regressions are displayed as solid lines. The bottom row shows the same relationship as the middle row, dividing the stars into four groups of TIC stars according to surface gravity with log g ≥ 4.0 representing ZAMS, 3.5 ≤ log g < 4.0 representing the mid-age main sequence (MAMS), and log g < 3.5 representing the terminal age main sequence (TAMS), as well as Pre-MS stars matched to the literature.
Table 1

Statistics of linear regressions of the frequency of maximum amplitude and effective temperature for the δ Scuti stars in this study, using both TIC values and spectroscopic values from LAMOST.

4 Period-luminosity relation for δ Scuti stars

The relations between pulsation periods and the luminosity of pulsating stars, known as period-luminosity (P-L) relations, have been studied extensively and have a rich history dating back to Leavitt & Pickering (1912). When a group of pulsating stars falls within a relatively limited range of Teff, their luminosity becomes highly correlated with their stellar density and, as a result, with the periods of their pressure modes. This phenomenon has been observed and described by scientists (e.g., Eddington 1926; Carroll & Ostlie 2006). To obtain the P-L relations for the two samples, TIC and LAMOST, we performed a series of calculations on the absolute magnitude Mv and some other parameters. The extinction coefficient Av was determined based on the following equation: 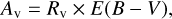(1)

where the coefficient Rv = 3.1 (Fitzpatrick 1999). The equation below was used to calculate Mv: 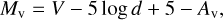(2)

Mv and V refer to the absolute and apparent magnitudes of a star measured in the V band. The distance (d) of the star in parsecs was determined using parallax measurements from Gaia DR3. Additionally, the bolometric absolute magnitude (Mbol) was calculated using the formula Mbol = Mv + BC, where BC is the bolometric correction. The value of BC was obtained by applying polynomial transformation equations developed by Flower (1996) and corrected by Torres (2010). The P-L of different radial pulsation modes are distinct from each other, as noted in the study by Poro et al. (2021). One way to distinguish between different pulsation modes is to calculate their pulsation constants using the formula 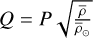, where Q is the pulsation constant expressed in units of days, P is the pulsation period also units of days, 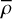is the average density of the star, and 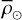is the average density of the Sun, which serves as a normalization factor. The pulsation constant is a measure of how the pulsation period of a star is related to its average density. The above equation can be rewritten as (Breger 1990a): 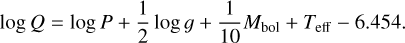(3)

We obtained the Q value of each δ Scuti star and listed it in Table A.1.

The upper and lower rows of Fig. 5 show the P-L relation of TIC and LAMOST, respectively. The P-L relation for high-amplitude δ Scuti stars derived by McNamara (2011) is represented by the black dashed line, while the P-L relation obtained by Ziaali et al. (2019) is shown by the blue dashed line. Additionally, various dashed lines in the figure represent different modes of the P-L relation, as derived by Poro et al. (2021). The color-coding in Fig. 5 represents the different values of the pulsation constant, Q. Typically, the values of the pulsation constant for the fundamental, first, and second overtone radial p modes in δ Scuti stars fall within the range of 0.022 ≤ Q ≤ 0.033 d, as reported by Breger & Bregman (1975). However, it should be noted that there can be significant uncertainties in the determination of pulsation constants, with fractional uncertainties reported by Breger (1990b) as high as 18 percent. This can lead to the misidentifica-tion of a first overtone radial mode as either the fundamental or second overtone radial mode, emphasizing the need for caution when applying this method of mode identification (Bowman & Kurtz 2018). Therefore, determining the accurate pulsation order of each star can be challenging, and additional observations or modeling may be required to confirm the resulting mode identification. The stars with LAMOST parameters are basically all in good agreement with the P-L relation, which confirms that our judgment of this sample of stars is accurate. The availability of LAMOST spectra (and associated Teff, log g) also opens up the possibility of further analytical studies, and therefore our next step will be to analyze the asteroseismic indices of this fraction of stars. The outliers in the bottom right part of Fig. 5 are the stars lying on the red side of the instability strip or colder than the instability strip’s red edge, and they are most likely misidentified γ Dor stars.

Figure 6 shows the HR diagram of the δ Scuti stars. The blue dots indicate the positions of the δ Scuti stars using the TIC parameters, while the red dots represent the subgroup of stars with spectroscopic values of Teff obtained from LAMOST. The evolutionary tracks were computed using MESA v10108 with X = 0.71 and Z = 0.01 (Murphy et al. 2019). The observational instability strip boundaries derived by Murphy et al. (2019) are shown as solid lines. Most of the δ Scuti stars are located within the pulsating instability strip.

thumbnail Fig. 5

P-L relation of TIC and LAMOST samples, respectively. Upper row shows P-L relation of TIC, and the bottom row shows the P-L relation of LAMOST. The black dashed line is the P-L relation for high-amplitude δ Scuti stars derived by McNamara (2011), while the P-L relation obtained by Ziaali et al. (2019) is shown by the blue dashed line. The remaining dashed lines represent different modes of the P-L relation, as derived by Poro et al. (2021). Color-coding represents the different values of the pulsation constant, Q.
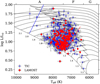thumbnail Fig. 6

HR diagram of δ Scuti stars. The blue dots represent the location of the δ Scuti stars using the TIC parameters, while the red dots represent the subgroup of stars with spectroscopic values of Teff from LAMOST. The observational instability strip boundaries from Murphy et al. (2019) are shown as solid lines. The evolutionary tracks were computed using MESA v10108 with X = 0.71 and Z = 0.01.
thumbnail Fig. 7

Normalized light curve of TIC 17489989 captured by TESS during sectors 51 and 52.

5 Asteroseismic analysis

In order to analyze the TESS cycle-4 short-cadence light curves of 179 δ Scuti stars with LAMOST parameters, the Python LIGHTKURVE package was used to download and analyze TESS data. We eliminated 4σ outlier data points from each star’s light curve. Then, the outcome is smoothed (Savitzky & Golay 1964) and normalized to mean intensity, as shown in Fig. 7, and the asteroseismic power spectrum was derived, as shown in Fig. 8. We only retained frequencies with a signal-to-noise ratio (S/N) of at least four (Breger et al. 1993).

The fundamental radial mode was typically thought to be the frequency with the maximum amplitude, but earlier investigations of δ Scuti stars (e.g., Murphy et al. 2020; Bedding et al. 2020, H21) revealed that, in fact, it is not always the largest peak in the power spectrum. We now describe our combined criteria to identify the fundamental mode. We consider the lowest frequency in the power spectrum with an amplitude greater than 0.2 times the highest peak as the fundamental radial mode (H21). The frequency associated with the highest amplitude in each star’s power spectrum is called v(Amax). We picked TIC 17489989 as an example and used its data to illustrate the analyses. Figure 9 shows the fundamental frequency and v(Amax) of TIC 17489989 in blue and red, respectively. H21 suggested using the frequency of the envelope’s peak νmax rather than ν(Amax) in an S/N frequency spectra. The 2D autocorrelation technique applied to the frequency spectra to obtain νmax is shown in Fig. 10. This method was described in detail by Viani et al. (2019) and has been applied to δ Scuti stars in H21 and Pamos Ortega et al. (2022).

The large frequency separation Δv, that is, the average frequency interval between modes at successive radial orders n and the angular degree l, is a crucial index. In order to calculate Δν, we took into account a window centered on νmax (approximately containing all of the mode peaks) for each S/N frequency spectra. Then, the Δν was determined through the 2D autocorrelation method as shown in Fig.11. We estimated the final value for the large frequency separation by employing an automatic peak finding process (e.g., Huber et al. 2009; Mosser & Appourchaux 2009) for the peaks that are around an empirical value (based on the relationship between the density and Δν). A theoretical relationship between the mean stellar density (ρ) and the large separation Δν of high-order modes (in the asymptotic regime) yields 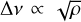. Many works have investigated the empirical relationship between the mean density and for δ Scuti stars. According to Suárez et al. (2014), Δv and mean density could be expressed empirically as Δv ∝ 0.78ρ0.46. García Hernandez et al. (2015, 2017) used accurate parameters of eclipsing binaries to constrain the relation to Δv ∝ 0.82ρ0.49, while Bedding et al. (2020) found a relation, 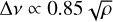, for their sample of young stars. Based on two years of TESS data for 438 δ Scuti stars, H21 modified the relation between the large frequency separation and stellar density as Δv ∝ 0.76ρ0.43. In our analysis, we took into account the large frequency separation of less than 35% divergence from the empirical scaling relation of H21. As a result, 148 targets remain on our final list and are listed in Table A.2.

Some of the targets show regular frequency spacing in the échelle diagram. Figure 12 shows the échelle diagram of TIC 17489989. We fit a Gaussian envelope to the S/N periodogram and took the peak of the Gaussian as the central frequency to search for a pattern around. However, there is no gaussian envelope in this case. To obtain a better Δv, we tried different frequency intervals to search for Δv, and it seems that the ridges appear for frequencies above 30 days−1. Not all the frequencies are present, though. The result of the manual3 search provides a more accurate result than the autocorrelation method, which is a rough approximation based on the asymptotic regime for solar stars. It is, however, a method that can be implemented in an automatic algorithm, so we could cautiously consider the results a rough approximation to the large frequency separation. For the particular case shown in Fig. 12, the star TIC 17489989 shows a Δv of 6.145 day−1, while it was 6.430 days−1 before; so, there is an error of about 0.3 day−1 with the autocorrelation method. We show this example to make it clear that the autocorrelation method can only provide an approximation, but it is acceptable for a statistical sample. The modes with similar angular degrees are positioned close to a vertical ridge in the échelle diagram; although, the significant variations in the large frequency separation give the diagram the appearance of being bent. With the mode spacing in δ Scuti stars not being fully regular as the excited modes have radial orders too low to lie in the asymptotic regime, the large separation varies with frequency (especially for lower radial orders García Hernández et al. 2009).

Figure 13 shows the histogram of the fundamental frequency and large frequency separation for 148 δ Scuti stars. The fundamental frequency and large frequency separation are in the range of 5.01–43.02 days−1 and 2.11–7.33 days−1, respectively. The frequencies are mainly around 10 days−1 and 18 days−1, with very few stars pulsating at high frequency. The distribution of Δv is more even between 2.6 and 6.8 days−1, except for 4.4 days−1. The values of Δv obtained by H21 are mainly concentrated between 6 and 7 days−1. So, there may be no particular pattern to the distribution of Δv values, which might be a selection effect for different samples.

Figure 14 depicts the relation between the large separation and stellar density for δ Scuti stars. A power function Δv = (0.76 ± 0.01)ρ0.44±0.01 is fit to data. As we observed in the figure, the fitting is basically consistent with the results of H21. According to this fit relation, with the known Δv, we can roughly estimate the density of the star. Determining the Δv of the star also aids in identifying the frequency modes for a more detailed modeling.

The scatter plot of ν(Amax) versus νmax is shown in Fig. 15. νmax shows a linear relation, νmax = (0.651 ± 0.033)v(Amax) + (11.622 ± 0.785). The black lines represent the linear fits of those frequencies using emcee (a Markov chain Monte Carlo Ensemble sampler, Foreman-Mackey et al. 2013). As the temporal evolution of the dominant frequency peak is subject to variability (H21), we chose to employ νmax in lieu of the highest amplitude peak for the comparative analysis between Δv and vmax, as well as Teff and vmax. We obtained a power relation, 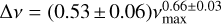, for 148 δ Scuti stars in Fig. 16. Also, Fig. 17 shows the linear correlation Teff = (0.65 ± 0.08)vmax + (1 .270 ± 0.008) obtained through the emcee method for our sample of 179 stars.

According to Hirschi et al. (2008), stars with lower metal-licity are typically hotter, more luminous, and have greater central condensation compared to stars with higher metallicity. This phenomenon is predicted to lead to shorter pulsation periods and higher average densities, as suggested by Dornan & Lovekin (2022). Figure 18 shows a linear relation, v(Amax) = [Fe/H] – (0.098 ± 0.035)/(−0.008 ± 0.001). Based on our results, a decrease in [Fe/H] is related to an increase in pulsation frequencies.

thumbnail Fig. 8

Lomb-Scargle periodogram depicts relationship between amplitude (measured in ppm) and frequency.
thumbnail Fig. 9

For TIC 17489989, the fundamental frequency and ν(Amax) are shown in blue and red, respectively.
thumbnail Fig. 10

S/N frequency spectra for TIC 17489989 is in the upper panel. The vmax is indicated by the red line. Frequency spectra with 2D autocorrelation applied are in the middle panel. Lower panel: Gaussian-smoothed curve (blue line) and the mean collapsed correlation shown against the frequency (see Viani et al. 2019).
thumbnail Fig. 11

2D autocorrelation was used to determine large frequency separation Δv of TIC 17489989. Blue, red, and dashed green lines, respectively, show the theoretical, empirical, and obtained values.
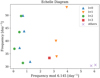thumbnail Fig. 12

Echelle diagram for TIC 17489989 with large frequency separation of approximately 6.145 day−1. Different colored points represent different pulsation modes.
thumbnail Fig. 13

Frequency distribution of fundamental mode (day−1) and large separation (day−1) for 148 δ Scuti stars.
thumbnail Fig. 14

Mean stellar density (ρ) versus Δv (Solar unit) for 148 δ Scuti stars. The fit curve Δv = (0.76 ± 0.01)ρ0.44±0.01 is represented by a black dashed line. The empirical relations Δv = (0.76 ± 0.01)ρ0.43±0.02 (black solid line) were obtained by H21.
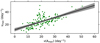thumbnail Fig. 15

Scatter plot of vmax versus v(Amax). vmax showing a linear relation as vmax = (0.651 ± 0.033)v(Amax) + (11.622 ± 0.785).
thumbnail Fig. 16

Scatter plot of Δv versus vmax. The fit curve is represented by black dashed line. The empirical relation (black solid line) was obtained by H21.
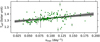thumbnail Fig. 17

Scatter plot of vmax versus Teff. Teff shows a linear relation as Teff = (0.65 ± 0.08)νmax + (1.270 ± 0.008).
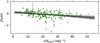thumbnail Fig. 18

Scatter plot of [Fe/H] versus ν(Amax). [Fe/H] shows a linear relation as [Fe/H] = (−0.008 ± 0.001)ν(Amax) + (0.098 ± 0.035).

6 Conclusions

We identified 765 δ Scuti stars using data from the TESS mission, covering Sectors 40–55 with two-minute cadence observations during cycle 4. We compiled two ensembles of δ Scuti stars parameters using TIC and LAMOST, consisting of 765 and 179 stars, respectively, which we used to investigate δ Scuti stars pulsational properties. The frequency distribution of diverse parameters, including effective temperature, surface gravity, Vmag, luminosity, [Fe/H], mass, radius, and parallax, for 765 and 179 δ Scuti stars. The mass, radius, effective temperature, and surface-gravity values of δ Scuti stars lie within the ranges of 1.4 M⊙–2.1 M⊙, 1.2 R⊙–3.7 R⊙, 6300–9300 K, and 3.3– 4.5 dex, respectively, which is consistent with earlier findings on δ Scuti stars (e.g., Daszyńska-Daszkiewicz 2007; Antoci et al. 2019). The Teff – log g diagrams presented in Fig. 3 reveal that the majority of δ Scuti stars detected by TESS observations align with the boundaries of the observational instability strip (Murphy et al. 2019), with the subgroup of stars with LAMOST spectral parameters more closely clustered around the theoretical instability strip. Our sample provides confirmation of the observational instability strip derived from Kepler observations and Gaia parameters by Murphy et al. (2019).

None of the δ Scuti stars observed by TESS exhibit a maximum pulsation frequency exceeding 60 days−1, primarily due to the absence of hot ZAMS stars, as illustrated in Fig. 4. This result is consistent with earlier studies on δ Scuti stars using a subset of Kepler data (e.g., Balona & Dziembowski 2011; Bowman & Kurtz 2018). We investigated the relationship between pulsation frequency and Teff by classifying the stars of the TIC sample. After isolating documented Pre-MS δ Scuti stars, the TIC stars are grouped according to log g ≥ 4.0 (ZAMS), 3.5 ≤ log g < 4.0 (MAMS), and log g < 3.5 (TAMS), as shown in the bottom row of Fig. 4. According to our statistical results, the Teff and maximum amplitude pulsation frequency of Pre-MS δ Scuti stars and these three different log g groups present different fitting results. The fitting results for the ZAMS δ Scuti stars are in general agreement with the conclusions derived from previous theoretical models and statistical studies. ZAMS δ Scuti stars have a higher effective temperature and higher radial order of p modes, leading to frequencies where larger pulsation modes can be observed. The correlation between temperature and the maximum amplitude pulsation frequency is more pronounced among the stars in the MAMS δ Scuti stars compared to the ZAMS δ Scuti stars. Due to the limited number of stars in the Pre-MS and TAMS δ Scuti stars, it is not possible to obtain reliable statistical results. However, based on this trend, it is expected that the TAMS δ Scuti stars exhibit a more correlated relationship between temperature and the highest amplitude pulsation frequency. Further analysis of Pre-MS and TAMS δ Scuti stars is necessary to obtain precise and accurate results.

We employed an empirical relation and a 2D autocorrelation method to determine the asteroseismic indices, such as the large frequency separation for each of the 148 δ Scuti stars and the relationship between these asteroseismic indices. For some of these stars, based on the large frequency separation that has been obtained, it is possible to perform mode identification for the frequencies of these stars. Modeling these most promising stars of our sample, using adapted stellar evolution and oscillation codes that include the effects of rotation, constrains the internal physics of δ Scuti stars and sheds light on the excitation and selection mechanisms, and on the internal distribution of angular momentum. The large number of photometric data the TESS space telescope provides is a valuable resource that can be used for many years.

We employed an empirical relation and a 2D autocorrelation method to determine the asteroseismic indices, such as the large frequency separation for each of the 148 δ Scuti stars and the relationship between these asteroseismic indices. For some of these stars, based on the large frequency separation that has been obtained, it is possible to perform mode identification for the frequencies of these stars. Modeling these most promising stars of our sample, using adapted stellar evolution and oscillation codes that include the effects of rotation, constrains the internal physics of δ Scuti stars and sheds light on the excitation and selection mechanisms, and on the internal distribution of angular momentum. The large number of photometric data the TESS space telescope provides is a valuable resource that can be used for many years.

Acknowledgements

The authors acknowledge Antonio Garcia Hernandez for a preliminary estimation of asteroseismic indices and gratefully thank the referee for the very useful comments. The work is supported by the National Key R&D program of China for the Intergovernmental Scientific and Technological Innovation Cooperation Project under No. 2022YFE0126200. Tian- shan Talent Training Program No. 2023TSYCLJ0053. C.L. would like to acknowledge the funding from the China Scholarship Council scholarship (No 202204910463). A.H. acknowledges support from the Science and Technology Facilities Council (STFC) grant No. ST/X000915/1. J.P.G. acknowledges financial support from project PID2019-107061GB-C63 from the ‘Programas Estatales de Generación de Conocimiento y Fortalecimiento Científico y Tecnológico del Sistema de I+D+i y de I+D+i Orientada a los Retos de la Sociedad’ and from the Severo Ochoa grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033. GMM acknowledges funding support from the Spanish State Research Agency (AEI) project PID2019-107061GB-064. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences.

Appendix A Tables

Table A.1

TIC number, positions, Vmag, effective temperature (Teff), Mass (M/M⊙), Radius (R/R⊙), surface gravity (log g), Luminosity, Parallax(mas), Mv, Period (day), Amplitude (mmag), pulsation constants(Q) for 765 δ Scuti stars. The complete table is available in machine−readable form at the CDS.

Table A.2

Catalogs of 179 δ Scuti stars with LAMOST parameters (Cui et al. 2012) and asteroseismic indices.

References

  1. Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Berlin: Springer) [Google Scholar]
  2. Antoci, V., Cunha, M. S., Bowman, D. M., et al. 2019, MNRAS, 490, 4040 [Google Scholar]
  3. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Avallone, E. A., Tayar, J. N., van Saders, J. L., et al. 2022, ApJ, 930, 7 [NASA ADS] [CrossRef] [Google Scholar]
  5. Ballot, J., Lignières, F., & Reese, D. R. 2013, in Lecture Notes in Physics, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer), Vol. 865, 91 [NASA ADS] [CrossRef] [Google Scholar]
  6. Balona, L. A. 2014, MNRAS, 437, 1476 [NASA ADS] [CrossRef] [Google Scholar]
  7. Balona, L. A. 2023, ArXiv e-prints [arXiv:2310.09805] [Google Scholar]
  8. Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barceló Forteza, S., Michel, E., Roca Cortés, T., & García, R. A. 2015, A&A, 579, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Barceló Forteza, S., Roca Cortés, T., & García, R. A. 2018, A&A, 614, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bedding, T. R., Murphy, S. J., Hey, D. R., et al. 2020, Nature, 581, 147 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bedding, T. R., Murphy, S. J., Crawford, C., et al. 2023, ApJ, 946, L10 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bowman, D. M., & Kurtz, D. W. 2018, MNRAS, 476, 3169 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
  15. Breger, M. 1990a, ASP Conf. Ser., 11, 263 [NASA ADS] [Google Scholar]
  16. Breger, M. 1990b, Delta Scuti Star Newsletter, 2, 13 [NASA ADS] [Google Scholar]
  17. Breger, M. 2000, ASP Conf. Ser., 210, 3 [NASA ADS] [Google Scholar]
  18. Breger, M., & Bregman, J. N. 1975, ApJ, 200, 343 [CrossRef] [Google Scholar]
  19. Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
  20. Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [Google Scholar]
  21. Buchler, J. R., Goupil, M.-J., & Hansen, C. J. 1997, A&A, 321, 159 [NASA ADS] [Google Scholar]
  22. Carroll, B. W., & Ostlie, D. A. 2006, An introduction to modern astrophysics and cosmology (Cambridge: Cambridge University Press) [Google Scholar]
  23. Charpinet, S., Green, E. M., Baglin, A., et al. 2010, A&A, 516, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Chen, X., Ding, X., Cheng, L., et al. 2022, ApJS, 263, 34 [CrossRef] [Google Scholar]
  25. Coelho, H. R., Chaplin, W. J., Basu, S., et al. 2015, MNRAS, 451, 3011 [CrossRef] [Google Scholar]
  26. Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
  27. Daszyńska-Daszkiewicz, J. 2007, Commun. Asteroseismol., 150, 32 [CrossRef] [Google Scholar]
  28. de Franciscis, S., Pascual-Granado, J., Suárez, J. C., García Hernández, A., & Garrido, R. 2018, MNRAS, 481, 4637 [Google Scholar]
  29. Dornan, V., & Lovekin, C. C. 2022, ApJ, 924, 130 [NASA ADS] [CrossRef] [Google Scholar]
  30. Dupret, M. A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Eddington, A. S. 1926, The Scientific Monthly, 11, 297 [NASA ADS] [Google Scholar]
  32. Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
  33. Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
  34. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  35. García Hernández, A., Moya, A., Michel, E., et al. 2009, A&A, 506, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. García Hernández, A., Martín-Ruiz, S., Monteiro, M. J. P. F. G., et al. 2015, ApJ, 811, L29 [Google Scholar]
  37. García Hernández, A., Suárez, J. C., Moya, A., et al. 2017, MNRAS, 471, L140 [CrossRef] [Google Scholar]
  38. Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [Google Scholar]
  39. Guo, Z., Fuller, J., Shporer, A., et al. 2019, ApJ, 885, 46 [Google Scholar]
  40. Hasanzadeh, A., Safari, H., & Ghasemi, H. 2021, MNRAS, 505, 1476 [NASA ADS] [CrossRef] [Google Scholar]
  41. Hekker, S. 2020, Front. Astron. Space Sci., 7, 3 [NASA ADS] [CrossRef] [Google Scholar]
  42. Hirschi, R., Chiappini, C., Meynet, G., Maeder, A., & Ekström, S. 2008, IAU Symp., 250, 217 [NASA ADS] [Google Scholar]
  43. Huber, D., Stello, D., Bedding, T. R., et al. 2009, Commun. Asteroseismol., 160, 74 [Google Scholar]
  44. Huber, D., Zinn, J., Bojsen-Hansen, M., et al. 2017, ApJ, 844, 102 [Google Scholar]
  45. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
  46. Kallinger, T., Mosser, B., Hekker, S., et al. 2010, A&A, 522, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [Google Scholar]
  48. Kraft, R. P. 1967, ApJ, 150, 551 [Google Scholar]
  49. Kurtz, D. 2022, in Annual Conference and General Assembly of the African Astronomical Society, 1 [Google Scholar]
  50. Kurtz, D. W., & Marang, F. 1995, MNRAS, 276, 191 [NASA ADS] [Google Scholar]
  51. Leavitt, H. S., & Pickering, E. C. 1912, Harvard College Observ. Circ., 173, 1 [NASA ADS] [Google Scholar]
  52. Lightkurve Collaboration (Cardoso, J. V. d. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
  53. Lv, C., Esamdin, A., Zeng, X., et al. 2021a, AJ, 162, 48 [NASA ADS] [CrossRef] [Google Scholar]
  54. Lv, C.-L., Esamdin, A., Liu, J.-H., Zeng, X.-Y., & Yang, T.-Z. 2021b, Res. Astron. Astrophys., 21, 224 [CrossRef] [Google Scholar]
  55. Lv, C., Esamdin, A., Pascual-Granado, J., Hernández, A. G., & Hasanzadeh, A. 2022a, AJ, 164, 218 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lv, C., Esamdin, A., Pascual-Granado, J., Yang, T., & Shen, D. 2022b, ApJ, 932, 42 [NASA ADS] [CrossRef] [Google Scholar]
  57. McNamara, D. H. 2011, AJ, 142, 110 [NASA ADS] [CrossRef] [Google Scholar]
  58. Mirouh, G. M. 2022, Front. Astron. Space Sci., 9, 952296 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mirouh, G. M., Angelou, G. C., Reese, D. R., & Costa, G. 2019, MNRAS, 483, L28 [NASA ADS] [CrossRef] [Google Scholar]
  60. Miszuda, A., Szewczuk, W., & Daszyn´ska-Daszkiewicz, J. 2021, MNRAS, 505, 3206 [NASA ADS] [CrossRef] [Google Scholar]
  61. Montgomery, M. H., & O’Donoghue, D. 1999, Delta Scuti Star Newsletter, 13, 28 [NASA ADS] [Google Scholar]
  62. Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Murphy, S. J. 2015, MNRAS, 453, 2569 [Google Scholar]
  64. Murphy, S. J., Hey, D., Van Reeth, T., & Bedding, T. R. 2019, MNRAS, 485, 2380 [NASA ADS] [CrossRef] [Google Scholar]
  65. Murphy, S. J., Saio, H., Takada-Hidai, M., et al. 2020, MNRAS, 498, 4272 [NASA ADS] [CrossRef] [Google Scholar]
  66. Pamos Ortega, D., García Hernández, A., Suárez, J. C., et al. 2022, MNRAS, 513, 374 [NASA ADS] [CrossRef] [Google Scholar]
  67. Pascual-Granado, J., Garrido, R., & Suárez, J. C. 2015, A&A, 581, A89 [NASA ADS] [EDP Sciences] [Google Scholar]
  68. Poretti, E., Michel, E., Garrido, R., et al. 2009, A&A, 506, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Poro, A., Paki, E., Mazhari, G., et al. 2021, PASP, 133, 084201 [NASA ADS] [CrossRef] [Google Scholar]
  70. Reese, D. R. 2022, Front. Astron. Space Sci., 9, 934579 [NASA ADS] [CrossRef] [Google Scholar]
  71. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Teles. Instrum. Syst., 1, 014003 [Google Scholar]
  72. Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
  73. Royer, F. 2009, in The Rotation of Sun and Stars (Berlin: Springer) 765, 207 [NASA ADS] [CrossRef] [Google Scholar]
  74. Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
  75. Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [Google Scholar]
  76. Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
  77. Steindl, T., Zwintz, K., Barnes, T. G., Müllner, M., & Vorobyov, E. I. 2021, A&A, 654, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Suárez, J. C., García Hernández, A., Moya, A., et al. 2014, A&A, 563, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
  80. Thomson-Paressant, K., Neiner, C., Zwintz, K., & Escorza, A. 2021, MNRAS, 500, 1992 [Google Scholar]
  81. Torres, G. 2010, AJ, 140, 1158 [Google Scholar]
  82. Twicken, J. D., Chandrasekaran, H., Jenkins, J. M., et al. 2010, SPIE Conf. Ser., 7740, 77401U [Google Scholar]
  83. Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [CrossRef] [EDP Sciences] [Google Scholar]
  84. Viani, L. S., Basu, S., Corsaro, E., Ball, W. H., & Chaplin, W. J. 2019, ApJ, 879, 33 [NASA ADS] [CrossRef] [Google Scholar]
  85. Viskum, M., Kjeldsen, H., Bedding, T. R., et al. 1998, A&A, 335, 549 [NASA ADS] [Google Scholar]
  86. Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [Google Scholar]
  87. Zhou, A. Y. 2024, New Astron. 105, 102081 [NASA ADS] [CrossRef] [Google Scholar]
  88. Ziaali, E., Bedding, T. R., Murphy, S. J., Van Reeth, T., & Hey, D. R. 2019, MNRAS, 486, 4348 [NASA ADS] [CrossRef] [Google Scholar]
  89. Zong, W., Charpinet, S., & Vauclair, G. 2016, A&A, 594, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Zwintz, K., Fossati, L., Ryabchikova, T., et al. 2014, Science, 345, 550 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Statistics of linear regressions of the frequency of maximum amplitude and effective temperature for the δ Scuti stars in this study, using both TIC values and spectroscopic values from LAMOST.

In the text
Table A.1

TIC number, positions, Vmag, effective temperature (Teff), Mass (M/M⊙), Radius (R/R⊙), surface gravity (log g), Luminosity, Parallax(mas), Mv, Period (day), Amplitude (mmag), pulsation constants(Q) for 765 δ Scuti stars. The complete table is available in machine−readable form at the CDS.

In the text
Table A.2

Catalogs of 179 δ Scuti stars with LAMOST parameters (Cui et al. 2012) and asteroseismic indices.

In the text

All Figures

thumbnail Fig. 1

Position (Ecliptic latitude and longitude) of 765 δ Scuti stars (blue dots) and 179 δ Scuti stars with low-resolution spectral parameters (red dots) in the celestial sphere.
In the text
thumbnail Fig. 2

Effective temperature, Vmag, surface gravity, luminosity, [Fe/H], mass, radius, and parallax distributions are shown for 765 and 179 δ Scuti stars as a blue and a red region, respectively.
In the text
thumbnail Fig. 3

Teff – log g diagram for our 765 δ Scuti stars observed by TESS. The blue dots represent the positions of δ Scuti stars using parameters from the TIC, while the red dots correspond to a subgroup of δ Scuti stars with spectroscopic Teff and log g values. The solid blue and red lines indicate the theoretical blue and red edges of the classical instability strip, respectively, for p modes with radial order n = 1, while the dashed blue and red lines represent radial order n = 6 according to Dupret et al. (2005).
In the text
thumbnail Fig. 4

Relationship between pulsation frequency and temperature was investigated for both TIC and LAMOST samples. Top row shows distribution of frequency with maximum amplitude (shown as a blue region) for the ensemble of our 765 δ Scuti stars observed by TESS. The red region indicates the distribution for the subgroup of stars with spectro-scopic parameters from LAMOST. The middle row shows the frequency of the maximum amplitude plotted against the effective temperature, with the TIC and LAMOST parameters represented by blue and red dots, respectively. The statistically significant linear regressions are displayed as solid lines. The bottom row shows the same relationship as the middle row, dividing the stars into four groups of TIC stars according to surface gravity with log g ≥ 4.0 representing ZAMS, 3.5 ≤ log g < 4.0 representing the mid-age main sequence (MAMS), and log g < 3.5 representing the terminal age main sequence (TAMS), as well as Pre-MS stars matched to the literature.
In the text
thumbnail Fig. 5

P-L relation of TIC and LAMOST samples, respectively. Upper row shows P-L relation of TIC, and the bottom row shows the P-L relation of LAMOST. The black dashed line is the P-L relation for high-amplitude δ Scuti stars derived by McNamara (2011), while the P-L relation obtained by Ziaali et al. (2019) is shown by the blue dashed line. The remaining dashed lines represent different modes of the P-L relation, as derived by Poro et al. (2021). Color-coding represents the different values of the pulsation constant, Q.
In the text
thumbnail Fig. 6

HR diagram of δ Scuti stars. The blue dots represent the location of the δ Scuti stars using the TIC parameters, while the red dots represent the subgroup of stars with spectroscopic values of Teff from LAMOST. The observational instability strip boundaries from Murphy et al. (2019) are shown as solid lines. The evolutionary tracks were computed using MESA v10108 with X = 0.71 and Z = 0.01.
In the text
thumbnail Fig. 7

Normalized light curve of TIC 17489989 captured by TESS during sectors 51 and 52.
In the text
thumbnail Fig. 8

Lomb-Scargle periodogram depicts relationship between amplitude (measured in ppm) and frequency.
In the text
thumbnail Fig. 9

For TIC 17489989, the fundamental frequency and ν(Amax) are shown in blue and red, respectively.
In the text
thumbnail Fig. 10

S/N frequency spectra for TIC 17489989 is in the upper panel. The vmax is indicated by the red line. Frequency spectra with 2D autocorrelation applied are in the middle panel. Lower panel: Gaussian-smoothed curve (blue line) and the mean collapsed correlation shown against the frequency (see Viani et al. 2019).
In the text
thumbnail Fig. 11

2D autocorrelation was used to determine large frequency separation Δv of TIC 17489989. Blue, red, and dashed green lines, respectively, show the theoretical, empirical, and obtained values.
In the text
thumbnail Fig. 12

Echelle diagram for TIC 17489989 with large frequency separation of approximately 6.145 day−1. Different colored points represent different pulsation modes.
In the text
thumbnail Fig. 13

Frequency distribution of fundamental mode (day−1) and large separation (day−1) for 148 δ Scuti stars.
In the text
thumbnail Fig. 14

Mean stellar density (ρ) versus Δv (Solar unit) for 148 δ Scuti stars. The fit curve Δv = (0.76 ± 0.01)ρ0.44±0.01 is represented by a black dashed line. The empirical relations Δv = (0.76 ± 0.01)ρ0.43±0.02 (black solid line) were obtained by H21.
In the text
thumbnail Fig. 15

Scatter plot of vmax versus v(Amax). vmax showing a linear relation as vmax = (0.651 ± 0.033)v(Amax) + (11.622 ± 0.785).
In the text
thumbnail Fig. 16

Scatter plot of Δv versus vmax. The fit curve is represented by black dashed line. The empirical relation (black solid line) was obtained by H21.
In the text
thumbnail Fig. 17

Scatter plot of vmax versus Teff. Teff shows a linear relation as Teff = (0.65 ± 0.08)νmax + (1.270 ± 0.008).
In the text
thumbnail Fig. 18

Scatter plot of [Fe/H] versus ν(Amax). [Fe/H] shows a linear relation as [Fe/H] = (−0.008 ± 0.001)ν(Amax) + (0.098 ± 0.035).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.