EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A42 Full HTML
Open Access
Issue
A&A
Volume 685, May 2024
Article Number A42
Number of page(s) 14
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202347718
Published online 03 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

A black hole binary (BHB) is a system consisting of a stellar-mass black hole (BH) with strong gravity and a nondegenerate secondary star. These systems are often triggered by accretion instability (Lasota 2001), leading to highly variable behavior. BHBs typically exhibit outbursts that can last for weeks to months, during which the flux can vary by up to seven orders of magnitude (e.g., Remillard & McClintock 2006). Throughout an outburst, BHBs commonly transit through distinct spectral states (e.g., Fender et al. 2004; Belloni et al. 2005; Remillard & McClintock 2006). The X-ray spectra in these states are characterized by the relative contributions of two principal components: thermal and nonthermal components. The hard state is typically observed at the beginning and end of an outburst when the source is relatively faint. In this state, the spectra are dominated by a power-law (PL) component emitted from a corona or the base of a jet, generated through inverse-Compton scattering of thermal seed photons from the disk (Markoff et al. 2005). As the outburst progresses towards its peak, the source enters the soft state. In this state, the X-ray spectra are primarily composed of a multi-temperature disk blackbody, characterized by a typical temperature of around ∼1 keV (Shakura & Sunyaev 1973). Moreover, many outbursts also exhibit intermediate states during the transitions between these two states, with the hard-to-soft transitions being brighter than the reverse transitions. Overall, a BHB typically follows a counterclockwise q-shaped trajectory in the hardness-intensity diagram (HID) throughout the course of an outburst (e.g., Homan et al. 2001).

In addition to the disk and corona components, the X-ray spectra of many BHBs exhibit a notable reflection component (Done & Nayakshin 2001). Typically, this reflection component arises when the corona illuminates the accretion disk in the hard and intermediate states (García et al. 2014). The reflection spectra display distinct features, including an iron line at around ∼6–7 keV, which is broadened by the Doppler effect, Compton scattering, and gravitational redshift (Fabian et al. 2000), as well as a Compton hump in the energy range of approximately ∼20–40 keV. However, recent investigations have observed significant reflection components even in soft states (Connors et al. 2020, 2021a; Lazar et al. 2021). The presence of reflection in soft states cannot be adequately explained solely by coronal illumination as the corona component should be considerably weaker during the soft state. Instead, it is likely that the reflection originates from the returning thermal radiation (Cunningham 1976; Riaz et al. 2021), where the disk dominates the emission and its photons are bent back by the strong gravitational pull of the black hole, thereby illuminating the disk surface.

The accretion disk in a BHB exhibits distinct characteristics in different states. In the hard state, the disk is believed to be truncated at a specific radius, gradually extending toward the innermost stable circular orbit (ISCO) as the system transitions to the soft state (e.g., Fender et al. 2004; Remillard & McClintock 2006). Additionally, when the accretion rate exceeds approximately 30% of the Eddington limit, the inner disk deviates from a standard thin disk and expands into a geometrically thick disk due to the dominance of radiation pressure in the inner disk region (Abramowicz et al. 1988; Abramowicz 2005). General relativistic radiative magneto-hydrodynamics (GRRMHD) simulations (Wielgus et al. 2022; Huang et al. 2023) suggest that other features start to become significant in the near-Eddington regime, such as mass-loaded disk outflows, geometric collimation inside a polar funnel, a hot comptonizing region sandwiching the disk, a flatter disk temperature profile, and a reduced radiative efficiency from the inner disk. Such features become more prominent in the super-Eddington regime (typical for example of ultraluminous X-ray sources). Phenomenologically, the near-Eddington transitional regime was already noted in early studies of Galactic BH transients (Kubota & Makishima 2004). Thus, nearby BH transients that approach or exceed the Eddington limit during their outburst can provide important information on the physical evolution of an accretion flow from standard disk to ultraluminous regime. The recent outburst of the Galactic BH 4U 1543−47 is an excellent case study for such a regime.

4U 1543–47 was first discovered in 1971 (Matilsky et al. 1972). It showed outbursts nearly every ten years: in 1971, 1983, 1992, and 2002 (Kitamoto et al. 1984; Buxton & Bailyn 2004). After remaining in quiescence for around 20 years, it underwent a new outburst in 2021, which was first captured by Monitor of All-sky X-ray Image (MAXI; Matsuoka et al. 2009; Negoro et al. 2021a) on June 11, 2021. Its flux has increased quickly since the start of the outburst, and the peak observed flux is up to ∼1.96 × 10−7 erg cm−2 s−1 (∼8.2 Crab) in the 2–10 keV band (Negoro et al. 2021b), much brighter than that of previous outbursts: ∼1.9 Crab (2–6 keV) in 1971 (Matilsky et al. 1972), ∼4 Crab (3.7–7.5 keV) in 1983 (Kitamoto et al. 1984), and ∼3.3 Crab (3.7–7.5 keV) in 2002 (Park et al. 2004; Russell et al. 2020). This outburst is thus the brightest one that MAXI and the Neil Gehrels Swift Observatory (Swift) have ever observed among BHBs (Negoro et al. 2021b; Connors et al. 2021b). By assuming a distance of 7.5 ± 1.0 kpc (Orosz et al. 2002; Park et al. 2004; Jonker & Nelemans 2004), the peak bolometric luminosity is greater than 1039 erg s−1, approaching the Eddington limit (Negoro et al. 2021b) of the BH with mass of 9.4 ± 2.0 M⊙ (Orosz 2003; Park et al. 2004).

The orbital inclination of this source is determined to be 20.7° ± 1.5° (Orosz 2003), while the disk inclination is suggested as ≳30° (Morningstar & Miller 2014; Dong et al. 2020). There is a discrepancy in spin measurements for this source. Shafee et al. (2006) reported a spin of 0.8 ± 0.1 using the continuum-fitting method. Subsequently, Miller et al. (2009) and Morningstar & Miller (2014) utilized the method of continuum and reflection joint fitting, suggesting a low spin of 0.3 ± 0.1 and 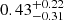0 . 43 − 0.31 + 0.22 $ 0.43_{-0.31}^{+0.22} $, respectively. More recently, Dong et al. (2020) constrained the spin to be 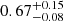0 . 67 − 0.08 + 0.15 $ 0.67_{-0.08}^{+0.15} $ via the reflection fitting.

Some X-ray telescopes, such as the Hard X-ray Modulation Telescope (Insight-HXMT; Zhang et al. 2020), Swift, and the Nuclear Spectroscopic Telescope Array (NuSTAR; Harrison et al. 2013), have monitored the 2021 outburst. Jin et al. (2024) provides an analysis of the long-term evolution of light curves and energy spectra using Insight-HXMT data with some pre-fixed parameters. In this paper we present the spectral results from the quasi-simultaneous Insight-HXMT, NuSTAR, and Swift observations by freeing these parameters, and focus on the accretion geometry at high luminosity. The observational details and data analysis procedures are described in Sect. 2, followed by the presentation of our spectral results in Sect. 3. Finally, in Sect. 4 we discuss our findings.

2. Observations and data reduction

Insight-HXMT observed 4U 1543–47 from June 14, 2021, to September 19, 2021, accumulating a total of 52 observations. Additionally, there are 10 observations conducted by NuSTAR and 12 observations by Swift/XRT during the outburst. For this study we utilized five data sets obtained from quasi-simultaneous observations of Insight-HXMT, NuSTAR, and Swift/XRT, covering the period from June 17 to September 14, 2021. Detailed information regarding these data sets is provided in Table 1. From the light curves of MAXI1 and Insight-HXMT (Fig. 1), we can see that the observations are taken in the outburst peak and decay phase, and cover the typical evolution stages of the complete outburst. The total exposure of Insight-HXMT, NuSTAR, and Swift/XRT are 22 761 ks, 25 599 ks, and 6651 ks, respectively.

thumbnail Fig. 1.

Evolution of count rates and HRs with time. (a) MAXI/GSC 2–20 keV light curve. (b) Insight-HXMT/LE 2–10 keV light curve. (c) MAXI/GSC HR defined as the ratio of (6–20 keV) to (2–6 keV) count rates. (d) Insight-HXMT/LE HR defined as the ratio of (6–10 keV) to (2–6 keV) count rates. Vertical lines indicate five quasi-simultaneous data sets of Insight-HXMT, NuSTAR, and Swift.

Table 1.

Observation information of NuSTAR, Swift/XRT, and Insight-HXMT.

2.1. Insight-HXMT

We performed data reduction using the Insight-HXMT Data Analysis Software (HXMTDAS v2.052) and the latest calibration database files (CALDB v2.06). To select the good time intervals, we applied the following criteria: (1) Earth elevation angle > 10°; (2) pointing offset angle < 0.04°; (3) geomagnetic cutoff rigidity > 8 GeV; (4) at least 300 s away from the crossing of the South Atlantic Anomaly region. The background of the Low Energy (LE), Medium Energy (ME), and High Energy (HE) telescopes are respectively created with the scripts lebkgmap, mebkgmap, and hebkgmap, based on the Insight-HXMT background models (Liao et al. 2020a,b; Guo et al. 2020). The response files of LE, ME, and HE are generated by lerspgen, merspgen, and herspgen, respectively.

Each observation consists of a few individual sub-exposures. To improve the statistical accuracy, we combined the spectra of all sub-exposures from each observation. Following the recommendation of the Insight-HXMT calibration group, the combined spectra were rebinned as follows: (1) LE: channels 0 through 579 and 580 through 1535 respectively with 3 and 5 bins in each group; (2) ME: channels 0 through 1023 with 6 bins in each group; (3) HE: channels 0 through 255 with 16 bins in each group. Additionally, systematic errors of 0.5%, 1%, and 1% were applied to the LE, ME, and HE spectra, respectively.

2.2. NuSTAR

The nupipeline routine of NuSTARDAS v1.9.7 in HEASoft v6.29 with CALDB v20211115 was employed to process the cleaned event files. Due to high brightness, some source counts may be erroneously vetoed by a noise filter in the nupipeline tool, resulting in a lower measured source flux and a discrepancy between the two focal plane modules (FPMA and FPMB)3. To address this issue, following the recommendation provided in the analysis guide, we modified the statusexpr keyword in the nupipeline tool using the expression “STATUS==b0000xxx00xxxx000”. This modification adjusted the behavior of the nufilter tool accordingly. The nuproducts tool was then used to extract the source events by adopting a circular region surrounding the source with a radius of 100″ to optimize the signal-to-noise ratio of the spectra4. The corresponding background extraction region is a nearby source-free circle with a radius of 100″. The spectra were rebinned with 50 counts per bin at least.

2.3. Swift

The Swift/XRT spectra were extracted through the Swift/XRT data products generator (Evans et al. 2009)5 using HEASoft v6.29. The best source position was determined by enabling the centroiding option, using a single-pass cell-detect method and a search radius of 1′. Moreover, a maximum of ten individual observations were allowed to do source detection before using the stacked image. Since the source is very bright, in order to eliminate the pile-up effect to the greatest extent, we only selected the grade 0 events in windowed timing mode, and adjusted the inner radius of the annulus source region (outer radius is 20 pixels) to prevent the count rate from exceeding 150 ct s−1, as recommended by the Swift help desk. The spectra were rebinned with 25 counts per bin at least.

3. Analysis and results

Before conducting a detailed spectral analysis, we initially examine the spectral states of the five data sets using the hardness ratio (HR) and HID. The HRs are calculated as the ratio of the 6–20 keV count rates to the 2–6 keV count rates from MAXI (HR1). Data points with a signal-to-noise ratio below 3σ are excluded. In panel c of Fig. 1, we observe that HR1 rapidly decreases to 0.04–0.05 at the beginning of the outburst. It then gradually increases before displaying a long-term decay. Panel d shows HR2, which is obtained by calculating the ratio of the 6–10 keV count rates to the 2–6 keV count rates from Insight-HXMT. Due to the late start of the observations, the HR has already begun to decline. Combining the intensity and HR, as shown in Fig. 1, we construct the HID using data from MAXI/GSC and Insight-HXMT/LE, as illustrated in Fig. 2. The black arrows in the figures represent the evolutionary direction. From the left panel, it is evident that the system does not follow the typical counterclockwise q-shaped track observed in BHBs. Instead, it transitions to the soft state shortly after the onset of the outburst. Although the subsequent HRs are positively correlated with the count rates, the HRs do not exceed 0.1. The red data points indicate the five data sets used in this study, and they all correspond to a very soft state.

thumbnail Fig. 2.

Hardness-intensity diagrams from MAXI/GSC (left panel) and Insight-HXMT/LE (right panel). The blue dotted line represents the rising phase before the outburst peak, while the black line shows the decay phase. The red dots represent the five data sets used in this paper. If there are no simultaneous MAXI data for some data sets, the MAXI data in approximate date are indicated.

In order to fully understand the spectral behaviors over a broad energy band, we perform joint modeling of the spectra from NuSTAR and Swift/XRT. However, to mitigate the calibration uncertainties between Swift/XRT and NuSTAR for bright sources, we exclude the Swift/XRT data above 4 keV and the NuSTAR data below 4 keV during the fitting process6. The energy bands used for Swift and NuSTAR are 0.5–4 keV and 4–79 keV, respectively. We do not perform a joint fit of Insight-HXMT with NuSTAR/Swift. This is because Insight-HXMT, unlike NuSTAR and Swift, is not a focusing telescope, and different background estimation methods may introduce discrepancies in cross-calibration. Additionally, considering that this source is particularly bright and Crab is not visible for Insight-HXMT in June, there are some uncertainties in the calibration of Insight-HXMT during that month. Therefore, we exclude the first two data sets from Insight-HXMT in the fitting. The adopted energy bands for Insight-HXMT are 2–10 keV for LE and 10–35 keV for ME. Due to the source’s softness and the low signal-to-noise ratio of the HE (35–150 keV) data, the HE data are not utilized. In the subsequent sections, the results from NuSTAR/Swift and Insight-HXMT are presented separately. All spectra are fitted within XSPEC v12.12.0. Abundances are set to WILM Wilms et al. (2000), and cross-sections to VERN (Verner et al. 1996).

3.1. Spectral fitting

Considering that the main emission component of this source is in the soft energy range, the spectral fitting initially uses an absorbed multicolor blackbody model (model 1: Tbabs*diskbb; Makishima et al. 1986). Additionally, a multiplicative constant model (constant) is included to account for the normalization discrepancy between different telescopes. However, this model reveals a significant positive residual in the hard X-ray range. Consequently, a thermal Comptonization component (nthcomp; Zdziarski et al. 1996) is introduced to describe the hard continuum. The seed photon temperature (kTbb) in nthcomp is linked to the inner disk temperature (kTin) of diskbb. Figure 3 shows a soft excess below 1 keV in the Swift spectra, as well as excesses in the 6–7 keV and approximately 10–20 keV bands of the NuSTAR spectra, even though the diskbb parameters of the two telescopes can be different, due to the calibration differences between Swift and NuSTAR.

thumbnail Fig. 3.

Data-to-model ratios of model 2 (tbabs*(diskbb+nthcomp)) for Swift/XRT and NuSTAR/FPMA. The different data sets are shown in different colors (see legend in inset). The plots are grouped to have a S/N ≥ 20 per bin for display clarity.

The presence of positive residuals in the 6–7 keV and 10–20 keV ranges resembles reflection features caused by disk illumination, either from the corona radiation or the returning photons from the disk. Typically, the former scenario occurs in the hard or intermediate state of BHBs, while the latter is commonly observed in the soft state (e.g., Connors et al. 2020, 2021a; Lazar et al. 2021; Wang et al. 2021). Since 4U 1543–47 is currently in the soft state, we include the reflection model with a blackbody as the incident spectrum, specifically relxillNS (García et al. 2022), in the fitting process (model 3: Tbabs*(diskbb+Nthcomp+relxillNS)). The relxillNS model serves as an intermediary representation of the reflection spectrum formed when the returning disk radiation illuminates the accretion disk. Its primary purpose is to describe the reflection phenomenon originating from accretion disks around neutron stars. Unlike a multi-temperature disk blackbody spectrum, the relxillNS model adopts a single-temperature blackbody irradiating spectrum. As a result, its usage demands careful attention to its constraints. Nevertheless, it offers an approximation that proves effective as the lightbending effects have noticeable impact solely in the extremely inner regions of the accretion disk. In addition, we also attempted the reflection model from the Compton component (Tbabs*(diskbb+Nthcomp+relxillCp*nthratio)). nthratio7 is a multiplicative XSPEC model that can correct to first order the unphysical soft excess introduced by relxillcp because of its fixed seed photon temperature of 0.01 keV. However, there are still some noticeable residuals below 1.5 keV and in the 6–7 keV and 10–20 keV energy bands, as depicted in Fig. 4. Therefore, we ultimately choose model 3 to fit the data used in this study. In model 3, kTin of diskbb and the incident blackbody temperature (kTbb) of relxillNS are always linked. However, we also conducted initial fits with Tin untied from kTbb and found that the other parameters were similar to the linking case. The emissivity indices (qin and qout) of relxillNS are linked, and the reflection fraction (Rf) is fixed at −1, indicating that only the blackbody reflected component is considered. The BH spin (a*) is fixed at 0.67 (Dong et al. 2020). It is worth noting that there is a discrepancy in the spin measurements (Shafee et al. 2006; Miller et al. 2009; Morningstar & Miller 2014; Dong et al. 2020), we thus also perform initial fits by allowing a* to vary freely and fixing Rin at the ISCO radius (RISCO). The resulting spin value is 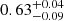0 . 63 − 0.09 + 0.04 $ 0.63_{-0.09}^{+0.04} $, which is consistent with that used in this paper (a* ∼ 0.67; Dong et al. 2020) and the latest result (a* ∼ 0.65) suggested by Yorgancioglu et al. (2023). Additionally, the other parameters remain essentially unchanged. The iron abundance (AFe) and inclination angles (i) of these five data sets are linked, respectively. Similarly, the absorption column density (NH) is also linked across the data sets, while the remaining parameters are free.

thumbnail Fig. 4.

Spectra, model components, and spectral residuals for tbabs*(diskbb+nthcomp+relxillcp*nthratio). Data set 1 of Swift and NuSTAR are taken as representative. The green, red, and gray data points show the Swift, NuSTAR/FPMA, and FPMB data, respectively. The black solid line is the total model, and the orange, purple, and blue solid lines show the diskbb, nthcomp, and relxillcp*nthratio components.

The best-fitting parameters are listed in Table 2 and the persistent spectra are shown in Fig. 5. The reduced χ2 values are ∼1.2, indicating that additional factors not considered in the reflection model may contribute to the broadening of the iron line, such as a re-emission from disk winds (Kallman et al. 2004), the Compton scattering in the disk atmosphere (Steiner et al. 2017), or an unblurred reflection emission. The residuals at ∼2.3 keV may arise from systematic uncertainties in the Si and Au edges8.

thumbnail Fig. 5.

Spectra, model components, and spectral residuals for Swift/XRT (green) and NuSTAR (red and gray) with model 3 (tbabs*(diskbb+nthcomp+relxillNS)). The black solid line is the total model, and the orange, purple, and blue solid lines show the diskbb, nthcomp, and relxillNS components, respectively.

Table 2.

Joint fitting parameters of Swift/XRT and NuSTAR for model 3 (tbabs*(diskbb+nthcomp+relxillNS)).

Following the spectral fitting of Swift and NuSTAR, we used model 3 to fit the last three data sets from Insight-HXMT. We fixed NH at 4.0 × 1021 cm−2 for these data sets due to the absence of low energy data (< 2 keV). The value of Rin was fixed at RISCO. Data sets 3 and 4 contain very few high-energy photons, making it difficult to constrain the normalization of the diskbb component. We note that the normalization values of diskbb for the last three data sets in Table 2 are quite similar. Therefore, we decided to fix the normalization of diskbb in Data sets 3 and 4 at 4000. Moreover, the values of Γ for these three data sets were fixed at 3.4, 3.4, and 2, respectively, based on the quasi-simultaneous observations shown in Table 2. The fitting results for the Insight-HXMT spectra are shown in Fig. 6, indicating a good fit. The corresponding best-fitting parameters are presented in Table 3. The small residuals around 8−10 keV for Data sets 3 and 4 in Fig. 6 may be caused by background since the LE spectra of Insight-HXMT above 8 keV are dominated by the background.

thumbnail Fig. 6.

Spectra (black for LE and red for ME), model components, and spectral residuals for Insight-HXMT with model 3. The black solid line is the total model fitted to the data, and the orange, purple, and blue solid lines show the diskbb, nthcomp, and relxillNS spectral components, respectively.

Table 3.

Joint fitting parameters of Insight-HXMT for model 3.

Since 4U 1543–47 went through a very bright outburst, it is unlikely that its accretion disk remained geometrically thin (Yorgancioglu et al. 2023). Therefore, we also tried fitting the Swift/XRT and NuSTAR spectra with the slim disk model slimbh (Sadowski 2011), designed for high accretion rates. We fixed the BH mass to 9.4 M⊙, the BH spin parameter to 0.67, the α viscosity parameter to 0.01 (Yorgancioglu et al. 2023), and the distance to 7.5 kpc. We selected a spectral hardening parameter fh to −1, which means that the value of fh comes from the TLUSTY9 spectra. The limb darkening switch was disabled (lflag = −1), while the raytracing switch was enabled (rflag = 1), allowing for raytracing calculations to be performed from the photosphere while considering the vertical thickness of the disk. Additionally, we linked the inclination of slimbh to the inclination of relxillNS.

The remaining parameters, namely the total disk luminosity Ldisk (in Eddington units) and the normalization parameter, determine the observed spectral shape and flux of the disk emission. The value of the normalization parameter is the fraction of emitted disk photons that reach infinity rather than self-irradiate the disk. The user notes for slimbh recommended fixing the normalization to 1. However, we find that this choice always leads to smaller intrinsic values of Ldisk compared with the observed luminosity. This is because the model normalization of 1 ignores that a fraction of the intrinsic Ldisk emission is lost to self-irradiation. Instead, we chose to fix Ldisk and left the normalization as a free parameter, under the assumption that the proportion of disk photons returning to the disk remains constant at all energy levels. We used the total luminosity LX obtained from each data set (Table 2) as input for the corresponding Ldisk parameter within the slimbh model. We neglected photon hardening since the relative contribution of hard photons is minimal. We fixed the inclination angle to 30°, in agreement with the values found from the diskbb model fits (Table 2). Then, we estimated the observed and unabsorbed luminosities with the convolution model cflux. We note that the cflux-derived values of the unabsorbed luminosity are ≈1.2 times the input value of Ldisk set in the simulation. Therefore, we divided the fitted values of LX by this correction factor. Finally, we froze the Ldisk parameter for the five data sets at values of 1.4, 0.8, 0.4, 0.33, and 0.30, respectively. The intrinsic luminosity in Data set 1 exceeds the upper parameter limit of slimbh (Eddington limit), hence we excluded this data set from our slimbh analysis. Figure 7 and Table 4 show the detailed fitting results.

thumbnail Fig. 7.

Spectra, model components, and spectral residuals for Swift/XRT (green) and NuSTAR (red and gray) with model 5 (tbabs*(slimbh+nthcomp+relxillNS)). The black solid line is the total model, and the orange, purple, and blue solid lines show the slimbh, nthcomp, and relxillNS components, respectively.

Table 4.

Joint fitting parameters of Swift/XRT and NuSTAR for model 4 (tbabs*(slimbh+nthcomp+relxillNS)).

3.2. Spectral results

By fitting the spectra of NuSTAR/Swift and Insight-HXMT, we find that the complicated spectra of the 2021 outburst can be nicely described by the disk reflections from the returning disk photons and a weak corona. As shown in Tables 2 and 3, the disk temperature Tin gradually decreases from around ∼1.1 keV near the outburst peak (Data set 1) to approximately (0.8 − 0.9) keV at the end of the soft state (Data set 5). This trend is in agreement with the gradual decrease in the accretion rate since the outburst peak. The photon index Γ of the Comptonization component is ≳2, as expected for a soft source. The iron abundances AFe are also found to be relatively consistent across the two tables. However, we also observe that some parameters (e.g., log ξ and log ρ) show discrepancies between the fitting values from different satellites. This is mainly attributed to differences in the cross-calibration between the satellites, as mentioned earlier. Therefore, we do not discuss the specific values of these physical parameters further.

The reflection component accounts for most of the total flux (Tables 2 and 3), which indicates that a large fraction of soft photons return to the disk. This high reflection fraction is also obtained when we substitute slimbh for diskbb (Table 4; see also Sect. 4.1). Moreover, Data Sets 1 and 2 (taken at higher luminosity) have lower values of qin (=qout) than Data Sets 3, 4, and 5.

4. Discussion and conclusion

The 2021 outburst of 4U 1543–47 is the brightest of its five known outbursts, reaching up to ∼8 Crab (Negoro et al. 2021b). In this paper we plot the evolution of the hardness ratio using data from MAXI/GSC and HXMT/LE during the outburst, and we find that 4U 1543–47 rapidly transitioned into a soft state at the beginning of the outburst, which is similar to its outbursts in 1983 (Kitamoto et al. 1984) and 2002 (Park et al. 2004; Russell et al. 2020). Subsequently, we focus on analyzing the spectra of five data sets obtained from quasi-simultaneous observations using Insight-HXMT, NuSTAR, and Swift during the 2021 outburst. Remarkably, although the source is in a soft state, we find a prominent reflection component (more than half of the total flux), a phenomenon rarely reported for black hole systems. Based on these observations, our discussion revolves around the accretion geometry of 4U 1543–47.

4.1. Geometrically thick disk

Although the theory of disk self-irradiation was proposed a long time ago (Cunningham 1976), it was only in 2020 that Connors et al. (2020) presented the first evidence for the existence of returning radiation from the thermal disk radiation, producing the relativistic reflection in the soft state of the black hole XTE J1550–564. Subsequently, in 4U 1630–47 (Connors et al. 2021a) and EXO 1846–031 (Wang et al. 2021), the reflection was also reported during the soft state and effectively modeled using relxillNS. However, the fractional flux (relative to the total flux) of the reflected component in these sources is not high, consistent with the estimated fraction of photons returning to the disk under the assumption of a Shakura & Sunyaev (1973) disk (thin disk). Recently, a high fraction of returning radiation was found in the soft state spectrum of MAXI J1631–479 (Rout et al. 2023), with the flux of ∼1 Crab in the 2−10 keV range (Rout et al. 2021). However, a detailed investigation of this phenomenon has not been conducted yet. To verify whether the high reflection fraction observed in the spectra of 4U 1543–47 could be attributed to disk self-irradiation, we conducted general relativity ray-tracing simulations using SIM5 (Bursa 2017; Pontzen et al. 2013). In our simulations, we set the black hole spin and the outer radius of the disk respectively to 0.67 and 50 Rg (Rg = GM/c2, where M is the BH mass, G is the gravitational constant, and c denotes the speed of light; Dotan & Shaviv 2011; Jiang et al. 2014). Based on the fitting results of relxillNS in Sect. 3, we set the inner radius of the disk at the ISCO. The photons are emitted according to the disk geometry (in the frame of rest of the disk), where the number of photons emitted at each emission angle is proportional to cosΘe, where Θe is the polar emission angle defined with respect to the normal of the disc surface. We initially assumed a razor-thin disk with the coordinate angular velocity as a function of radius R in units of Rg, satisfying ω0 = 1/(R3/2 + a*). We then calculate the fraction of photons that fall into the black hole, return to the disk, or escape to infinity (Fig. 8). The number of photons emitted per unit area per unit time by a blackbody with temperature T is proportional to T3. Assuming a disk temperature T ∝ R−3/4, we sum up the photons returning to the disk at different radii. However, the total fraction was approximately ∼6.0%, much smaller than the result observed (≳50%) in our study.

thumbnail Fig. 8.

Radial profiles of the fraction of disk photons that fall into the black hole, return to the disk, or reach infinity for a razor-thin disk. The spin of the black hole is set to 0.67.

Considering the high accretion rate of 4U 1543–47, the disk is likely to be geometrically thick. Therefore, we perform ray-tracing simulations assuming a “funnel-like” thick disk, where the angle between the disk surface and the equatorial plane is θ. When θ = 0°, it corresponds to the razor-thin disk described above. Moreover, we assume the coordinate angular velocity of the disk surface is ωθ = ω0 × cos3/2θ. We obtain radial profiles of the fraction of disk photons returning to the disk corresponding to different values of θ as shown in Fig. 9. Based on the above discussion, we find that the total fraction of photons returning to the disk is approximately 20.4%, 38.4%, 57.3%, 76.3%, and 91.4% for θ values of 15°, 30°, 45°, 60°, and 75°, respectively, when assuming T ∝ R−3/4. In a possible thick disk scenario where T ∝ R−1/2, the total fraction of photons is also approximately the same for the same α values. Thus, when ≳45°, in the case of a geometrically thick disk, it is expected that the returning radiation will constitute ≳60% of the total flux. This can be used to explain the observational results of 4U 1543–47. Model 4 provides a good fit to the spectra (Table 4 and Fig. 4), further confirming the significant self-irradiation of the disk in the case of a geometrically thick disk. Only about 30−40% of the disk photons are directly emitted to infinity. As shown in Tables 2 and 4, with increasing luminosity, the emissivity index qin (=qout) becomes flatter, which is consistent with a scenario involving a higher accretion rate and thicker accretion disk with a larger angle between the disk surface and the equatorial plane.

thumbnail Fig. 9.

Radial profiles of the fraction of disk photons returning to the disk with different θ for a funnel-shaped disk. The spin of the black hole is set to 0.67.

Furthermore, this funnel-like disk geometry is also consistent with the GRRMHD simulation results in both super-critical and sub-critical states (e.g., Sądowski et al. 2014; Jiang et al. 2014; Wielgus et al. 2022; Huang et al. 2023). Another conclusion drawn from the simulations is that a naturally formed corona with high temperature and low density appears above the black hole in high accretion rate scenarios (Huang et al. 2023). This corona interacts with soft photons through inverse Compton scattering, resulting in a PL component. The high-energy PL tail observed in the spectra of 4U 1543–47 may serve as evidence for the existence of such a corona. In addition, considering the significant fraction (≳50%) of photons returning to the disk, we expect a substantial heating effect on the disk surface, potentially contributing to the formation of radiatively driven outflows.

4.2. Other explanations for the reflection-like residuals in the soft state

Recent investigations on this outburst, such as Draghis et al. (2023), Prabhakar et al. (2023), and Husain et al. (2023) have proposed different physical interpretations. All of these studies used the reflection from the Comptonization component (i.e., relxill or relxilllp) to fit the spectra, and found that either a model invoking a partial covering of the source with ionized absorbing material (zxipcf; Draghis et al. 2023; Husain et al. 2023) or a Gaussian absorption model (gabs; Prabhakar et al. 2023) is required to improve the fit and reduce the spectral residuals. This absorption feature is believed to be associated with the presence of disk winds. However, based on our fitting results and the findings in Prabhakar et al. (2023), we observe that the corona only contributes to a small fraction (less than 8%) of the total flux, suggesting that the illumination from such a weak corona should be correspondingly faint.

We also note that the radiation from the plunging region located inside the ISCO is proposed to explain the reflection-like features of MAXI J1820+070 and MAXI J0637–430 in the soft state (Fabian et al. 2020; Lazar et al. 2021). However, the plunging region was considered to have a negligible contribution to the energy spectrum, due to the small plunging timescale (Page & Thorne 1974). Although the magnetohydrodynamic simulation results show that the plunging region could generate a blackbody emission in the nonzero torque case (Zhu et al. 2012), this effect is prominent only when the BH spin is low, since the ISCO is relatively far from the event horizon. In view of this, the possible emission of the plunging region may be the cause of the spectral features of MAXI J1820+070 and MAXI J0637–430, as their spin is a* ∼ 0.2 (Guan et al. 2021) and a* ≲ 0.25 (Soria et al. 2022), respectively. However, 4U 1543–47, by considering the revised spin value from the continuum fitting (Yorgancioglu et al. 2023) and the spin from the reflection modeling (Dong et al. 2020), has a moderately high spin of ≳0.7, and we thus expect that the emission from the plunging region might be insignificant.

1

The 2–20 keV count rates of MAXI are found in http://134.160.243.88/top/index.html

Acknowledgments

We thank Riley M. T. Connors for useful comments that have improved this paper. This work made use of data from the Insight-HXMT mission, a project funded by China National Space Administration (CNSA) and the Chinese Academy of Sciences (CAS), and the Swift data supplied by the UK Swift Science Data Centre at the University of Leicester. This work is supported by the National Key R&D Program of China (2021YFA0718500). We acknowledge funding support from the National Natural Science Foundation of China (NSFC) under grant Nos. 12122306 and 12073029, the CAS Pioneer Hundred Talent Program Y8291130K2 and the Scientific and technological innovation project of IHEP Y7515570U1. Y.Z. acknowledges support from the China Scholarship Council (CSC), no. 201906100030, and the Dutch Research Council (NWO) Rubicon Fellowship, file no. 019.231EN.021.

References

  1. Abramowicz, M. A. 2005, in Growing Black Holes: Accretion in a Cosmological Context, eds. A. Merloni, S. Nayakshin, & R. A. Sunyaev, 257 [CrossRef] [Google Scholar]
  2. Abramowicz, M. A., Czerny, B., Lasota, J. P., & Szuszkiewicz, E. 1988, ApJ, 332, 646 [Google Scholar]
  3. Belloni, T., Homan, J., Casella, P., et al. 2005, A&A, 440, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bursa, M. 2017, RAGtime 17-19: Workshops on Black Holes and Neutron Stars, 7 [Google Scholar]
  5. Buxton, M. M., & Bailyn, C. D. 2004, ApJ, 615, 880 [NASA ADS] [CrossRef] [Google Scholar]
  6. Connors, R. M. T., García, J. A., Dauser, T., et al. 2020, ApJ, 892, 47 [NASA ADS] [CrossRef] [Google Scholar]
  7. Connors, R. M. T., García, J. A., Tomsick, J., et al. 2021a, ApJ, 909, 146 [NASA ADS] [CrossRef] [Google Scholar]
  8. Connors, R., Steiner, J., Homan, J., et al. 2021b, ATel, 14725, 1 [NASA ADS] [Google Scholar]
  9. Cunningham, C. 1976, ApJ, 208, 534 [NASA ADS] [CrossRef] [Google Scholar]
  10. Done, C., & Nayakshin, S. 2001, MNRAS, 328, 616 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dong, Y., García, J. A., Steiner, J. F., & Gou, L. 2020, MNRAS, 493, 4409 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dotan, C., & Shaviv, N. J. 2011, MNRAS, 413, 1623 [NASA ADS] [CrossRef] [Google Scholar]
  13. Draghis, P. A., Miller, J. M., Zoghbi, A., et al. 2023, ApJ, 946, 19 [NASA ADS] [CrossRef] [Google Scholar]
  14. Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [Google Scholar]
  15. Fabian, A. C., Iwasawa, K., Reynolds, C. S., & Young, A. J. 2000, PASP, 112, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fabian, A. C., Buisson, D. J., Kosec, P., et al. 2020, MNRAS, 493, 5389 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  18. García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [Google Scholar]
  19. García, J. A., Dauser, T., Ludlam, R., et al. 2022, ApJ, 926, 13 [CrossRef] [Google Scholar]
  20. Guan, J., Tao, L., Qu, J. L., et al. 2021, MNRAS, 504, 2168 [NASA ADS] [CrossRef] [Google Scholar]
  21. Guo, C.-C., Liao, J.-Y., Zhang, S., et al. 2020, J. High Energy Astrophys., 27, 44 [NASA ADS] [CrossRef] [Google Scholar]
  22. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
  23. Homan, J., Wijnands, R., van der Klis, M., et al. 2001, ApJS, 132, 377 [NASA ADS] [CrossRef] [Google Scholar]
  24. Huang, J., Jiang, Y.-F., Feng, H., et al. 2023, ApJ, 945, 57 [NASA ADS] [CrossRef] [Google Scholar]
  25. Husain, N., Bhargava, Y., Garg, A., et al. 2023, MNRAS, 524, 5817 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jiang, Y.-F., Stone, J. M., & Davis, S. W. 2014, ApJ, 796, 106 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jin, P., Zhang, G., Zhang, Y., et al. 2024, MNRAS, 530, 929 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jonker, P. G., & Nelemans, G. 2004, MNRAS, 354, 355 [Google Scholar]
  29. Kallman, T. R., Palmeri, P., Bautista, M. A., Mendoza, C., & Krolik, J. H. 2004, ApJS, 155, 675 [Google Scholar]
  30. Kitamoto, S., Miyamoto, S., Tsunemi, H., Makishima, K., & Nakagawa, M. 1984, PASJ, 36, 799 [NASA ADS] [Google Scholar]
  31. Kubota, A., & Makishima, K. 2004, ApJ, 601, 428 [Google Scholar]
  32. Lasota, J.-P. 2001, New Astron. Rev., 45, 449 [Google Scholar]
  33. Lazar, H., Tomsick, J. A., Pike, S. N., et al. 2021, ApJ, 921, 155 [NASA ADS] [CrossRef] [Google Scholar]
  34. Liao, J.-Y., Zhang, S., Lu, X.-F., et al. 2020a, J. High Energy Astrophys., 27, 14 [NASA ADS] [CrossRef] [Google Scholar]
  35. Liao, J.-Y., Zhang, S., Chen, Y., et al. 2020b, J. High Energy Astrophys., 27, 24 [NASA ADS] [CrossRef] [Google Scholar]
  36. Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635 [NASA ADS] [CrossRef] [Google Scholar]
  37. Markoff, S., Nowak, M. A., & Wilms, J. 2005, ApJ, 635, 1203 [NASA ADS] [CrossRef] [Google Scholar]
  38. Matilsky, T. A., Giacconi, R., Gursky, H., Kellogg, E. M., & Tananbaum, H. D. 1972, ApJ, 174, L53 [NASA ADS] [CrossRef] [Google Scholar]
  39. Matsuoka, M., Kawasaki, K., Ueno, S., et al. 2009, PASJ, 61, 999 [Google Scholar]
  40. Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C. 2009, ApJ, 697, 900 [NASA ADS] [CrossRef] [Google Scholar]
  41. Morningstar, W. R., & Miller, J. M. 2014, ApJ, 793, L33 [NASA ADS] [CrossRef] [Google Scholar]
  42. Negoro, H., Nakajima, M., Niwano, M., et al. 2021a, ATel, 14701, 1 [NASA ADS] [Google Scholar]
  43. Negoro, H., Nakajima, M., Kobayashi, K., et al. 2021b, ATel, 14708, 1 [NASA ADS] [Google Scholar]
  44. Orosz, J. A. 2003, Symp. Int. Astron. Union, 212, 365 [NASA ADS] [CrossRef] [Google Scholar]
  45. Orosz, J. A., Polisensky, E. J., Bailyn, C. D., et al. 2002, Am. Astron. Soc. Meet. Abstr., 201, 15.11 [NASA ADS] [Google Scholar]
  46. Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499 [NASA ADS] [CrossRef] [Google Scholar]
  47. Park, S. Q., Miller, J. M., McClintock, J. E., et al. 2004, ApJ, 610, 378 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pontzen, A., Roškar, R., Stinson, G., & Woods, R. 2013, Astrophysics Source Code Library [record ascl:1305.002] [Google Scholar]
  49. Prabhakar, G., Mandal, S., Bhuvana, G. R., & Nandi, A. 2023, MNRAS, 520, 4889 [NASA ADS] [CrossRef] [Google Scholar]
  50. Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
  51. Riaz, S., Szanecki, M., Niedźwiecki, A., Ayzenberg, D., & Bambi, C. 2021, ApJ, 910, 49 [CrossRef] [Google Scholar]
  52. Rout, S. K., Méndez, M., Belloni, T. M., & Vadawale, S. 2021, MNRAS, 505, 1213 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rout, S. K., Vadawale, S., Garćia, J., & Connors, R. 2023, ApJ, 944, 68 [NASA ADS] [CrossRef] [Google Scholar]
  54. Russell, D. M., Casella, P., Kalemci, E., et al. 2020, MNRAS, 495, 182 [NASA ADS] [CrossRef] [Google Scholar]
  55. Sadowski, A. 2011, arXiv e-prints [arXiv:1108.0396] [Google Scholar]
  56. Sądowski, A., Narayan, R., McKinney, J. C., & Tchekhovskoy, A. 2014, MNRAS, 439, 503 [CrossRef] [Google Scholar]
  57. Shafee, R., McClintock, J. E., Narayan, R., et al. 2006, ApJ, 636, L113 [NASA ADS] [CrossRef] [Google Scholar]
  58. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  59. Soria, R., Ma, R., Tao, L., & Zhang, S.-N. 2022, MNRAS, 515, 3105 [NASA ADS] [CrossRef] [Google Scholar]
  60. Steiner, J. F., García, J. A., Eikmann, W., et al. 2017, ApJ, 836, 119 [NASA ADS] [CrossRef] [Google Scholar]
  61. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
  62. Wang, Y., Ji, L., García, J. A., et al. 2021, ApJ, 906, 11 [CrossRef] [Google Scholar]
  63. Wielgus, M., Lančová, D., Straub, O., et al. 2022, MNRAS, 514, 780 [CrossRef] [Google Scholar]
  64. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
  65. Yorgancioglu, E. S., Bu, Q. C., Santangelo, A., et al. 2023, A&A, 677, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
  67. Zhang, S.-N., Li, T., Lu, F., et al. 2020, Sci. China Phys. Mech. Astron., 63, 249502 [NASA ADS] [CrossRef] [Google Scholar]
  68. Zhu, Y., Davis, S. W., Narayan, R., et al. 2012, MNRAS, 424, 2504 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Probability distributions of the parameters from Data Set 3

thumbnail Fig. A.1.

Probability distributions of the parameters for model 3 obtained from the Swift/XRT and NuSTAR Data Set 3 through the Markov chain Monte Carlo algorithm (MCMC).

thumbnail Fig. A.2.

Probability distributions of the parameters for model 3 obtained from the Insight-HXMT Data Set 3 through MCMC.

thumbnail Fig. A.3.

Probability distributions of the parameters for model 4 obtained from the Swift/XRT and NuSTAR Data Set 3 through MCMC.

All Tables

Table 1.

Observation information of NuSTAR, Swift/XRT, and Insight-HXMT.

In the text
Table 2.

Joint fitting parameters of Swift/XRT and NuSTAR for model 3 (tbabs*(diskbb+nthcomp+relxillNS)).

In the text
Table 3.

Joint fitting parameters of Insight-HXMT for model 3.

In the text
Table 4.

Joint fitting parameters of Swift/XRT and NuSTAR for model 4 (tbabs*(slimbh+nthcomp+relxillNS)).

In the text

All Figures

thumbnail Fig. 1.

Evolution of count rates and HRs with time. (a) MAXI/GSC 2–20 keV light curve. (b) Insight-HXMT/LE 2–10 keV light curve. (c) MAXI/GSC HR defined as the ratio of (6–20 keV) to (2–6 keV) count rates. (d) Insight-HXMT/LE HR defined as the ratio of (6–10 keV) to (2–6 keV) count rates. Vertical lines indicate five quasi-simultaneous data sets of Insight-HXMT, NuSTAR, and Swift.
In the text
thumbnail Fig. 2.

Hardness-intensity diagrams from MAXI/GSC (left panel) and Insight-HXMT/LE (right panel). The blue dotted line represents the rising phase before the outburst peak, while the black line shows the decay phase. The red dots represent the five data sets used in this paper. If there are no simultaneous MAXI data for some data sets, the MAXI data in approximate date are indicated.
In the text
thumbnail Fig. 3.

Data-to-model ratios of model 2 (tbabs*(diskbb+nthcomp)) for Swift/XRT and NuSTAR/FPMA. The different data sets are shown in different colors (see legend in inset). The plots are grouped to have a S/N ≥ 20 per bin for display clarity.
In the text
thumbnail Fig. 4.

Spectra, model components, and spectral residuals for tbabs*(diskbb+nthcomp+relxillcp*nthratio). Data set 1 of Swift and NuSTAR are taken as representative. The green, red, and gray data points show the Swift, NuSTAR/FPMA, and FPMB data, respectively. The black solid line is the total model, and the orange, purple, and blue solid lines show the diskbb, nthcomp, and relxillcp*nthratio components.
In the text
thumbnail Fig. 5.

Spectra, model components, and spectral residuals for Swift/XRT (green) and NuSTAR (red and gray) with model 3 (tbabs*(diskbb+nthcomp+relxillNS)). The black solid line is the total model, and the orange, purple, and blue solid lines show the diskbb, nthcomp, and relxillNS components, respectively.
In the text
thumbnail Fig. 6.

Spectra (black for LE and red for ME), model components, and spectral residuals for Insight-HXMT with model 3. The black solid line is the total model fitted to the data, and the orange, purple, and blue solid lines show the diskbb, nthcomp, and relxillNS spectral components, respectively.
In the text
thumbnail Fig. 7.

Spectra, model components, and spectral residuals for Swift/XRT (green) and NuSTAR (red and gray) with model 5 (tbabs*(slimbh+nthcomp+relxillNS)). The black solid line is the total model, and the orange, purple, and blue solid lines show the slimbh, nthcomp, and relxillNS components, respectively.
In the text
thumbnail Fig. 8.

Radial profiles of the fraction of disk photons that fall into the black hole, return to the disk, or reach infinity for a razor-thin disk. The spin of the black hole is set to 0.67.
In the text
thumbnail Fig. 9.

Radial profiles of the fraction of disk photons returning to the disk with different θ for a funnel-shaped disk. The spin of the black hole is set to 0.67.
In the text
thumbnail Fig. A.1.

Probability distributions of the parameters for model 3 obtained from the Swift/XRT and NuSTAR Data Set 3 through the Markov chain Monte Carlo algorithm (MCMC).
In the text
thumbnail Fig. A.2.

Probability distributions of the parameters for model 3 obtained from the Insight-HXMT Data Set 3 through MCMC.
In the text
thumbnail Fig. A.3.

Probability distributions of the parameters for model 4 obtained from the Swift/XRT and NuSTAR Data Set 3 through MCMC.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.