| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A151 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348675 | |
| Published online | 23 April 2024 | |
Long-term dynamics around the Didymos–Dimorphos binary asteroid of boulders ejected after the DART impact
1
IFAC-CNR,
Via Madonna del Piano 10,
50019
Sesto Fiorentino, Italy
2
Dipartimento di Fisica, Università di Padova,
Italy
3
Institute Astronomical Observatory, Faculty of Physics, Adam Mickiewicz University,
Poznań, Poland
e-mail: krzysztof.langner@amu.edu.pl
4
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano,
Milano, Italy
Received:
20
November
2023
Accepted:
5
February
2024
Context. In 2022, the DART mission spacecraft impacted the asteroid Dimorphos, the secondary body of the binary Didymos system, ejecting a large number of dust particles, rocks and boulders. The ESA Hera mission will reach the system in 2026 for post-impact studies and a possible detection of orbiting fragments.
Aims. We aim to investigate the long-term dynamics of the large boulders ejected by DART to test if any of these objects survive in orbit until the arrival of the Hera mission.
Methods. To model the dynamics of the boulders, we used a numerical model that includes the gravity of non-spherical Didymos and Dimorphos, the solar gravity, and the radiation pressure. The SPICE kernels are used to define the correct reference frame for the integrations.
Results. The dynamics of the boulders is highly chaotic, and 1% of the initial boulders survive at least for four years on quasi-stable orbits. These orbits are characterised by wide oscillations in eccentricity in antiphase with those in inclination (including spin flips), a mechanism similar to the Kozai one. This behaviour may protect these bodies from close encounters with both asteroids. We also computed the distribution on the surfaces of the asteroids of sesquinary impacts, which may influence the dust emission (after the initial DART impact) and the surface composition of the asteroids.
Conclusions. The probability of observing boulders by the mission Hera is small but non-negligible, and an almost constant flux of escaping boulders is expected in the coming years since their lifetime after the DART impact covers a large time interval. Most re-impacts on Dimorphos occur in the hemisphere opposite the impact site, preferentially close to the equatorial plane.
Key words: celestial mechanics / minor planets / asteroids: individual: Didymos / minor planets / asteroids: individual: Dimorphos
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
On September 26, 2022, the DART probe impacted Dimorphos, the small moon of the binary 65803 Didymos asteroid system (Daly et al. 2023; Cheng et al. 2023). The event generated a large ejecta plume that was imaged first by the small LICIACube cube-sat (Dotto et al. 2021; Capannolo et al. 2021), released by DART 15 days before the impact during its fly-by. The images revealed a complex plume with a conical structure, crammed with dust, clumps of objects, filaments, and larger boulders (Dotto & al. 2024; Deshapriya et al. 2023). The event and the resulting ejecta were also observed by several space- and ground-based observatories, which allowed the characterisation of the plume evolution and, in particular, the formation of a long tail of debris, pushed by the solar radiation pressure, stretching for thousands of km (Li et al. 2023). Further observations by the Hubble Space Telescope revealed the presence of a large population of dozens of boulders moving in the surroundings of the system (Jewitt et al. 2023). Assuming a geometric albedo of 0.15, these large objects span a range of dimensions between about 4 and ≈7 m in diameter. Jewitt and co-authors estimated sky-plane velocities in a range between 10 cm s−1 to more than 67 cm s−1, without a significant correlation between the size and the velocity of the boulders. Since the escape velocity from the binary system is about 24 cm s−1 , these velocities are consistent with objects that do not re-impact Dimorphos right after the ejection and that can stay within the system for a comparatively long time span on highly perturbed chaotic orbits.
In Rossi et al. (2022), a theoretical analysis of the behaviour of these long survivors was performed highlighting the complex dynamical environment and the possible fate of the ejected large particles (of the order of tens of cm). In this work, we concentrated on a synthetic population of objects similar in size to the observed boulders. By means of a comprehensive model, described in Sect. 2, we explored the long term dynamics of this population with the aim of characterising, also from a statistical point of view, its behaviour with respect to the possible end-states, including re-impact against the two asteroids or escape from the system.
Within the international collaboration for planetary defence, the Hera probe will be launched in October 2024 by the European Space Agency and will reach the Didymos system in late 2026 (Michel et al. 2022). Hera will join the system and perform a detailed in situ analysis of the asteroids to fully characterise the outcomes of the DART impact. The possibility that some of the ejected boulders could survive up to the arrival of Hera poses some caveats both on the safety of the probe and on the best way to possibly observe them. In Sect. 4, some considerations on this subject are presented.
2 Dynamical model
To investigate the long term dynamics of the ejecta fragments, once they left the surface of Dimorphos, we numerically integrated their trajectories. During their evolution, the fragments may have frequent close encounters with either of the components of the binary asteroid, making their orbits highly chaotic. The 15th-order Radau numerical integrator (Everhart 1985), which has a variable step size and is very accurate in modelling close approaches, is very well suited to handling this problem.
The gravitational attraction of both Didymos and Dimorphos is computed taking into account their non-spherical shape. In the model, two computational methods are considered: a less CPU-time-consuming analytical approach based on the MacCullagh formula (Murray & Dermott 2000) and a more cumbersome polyhedral approach (Werner 1994; Werner & Scheeres 1997). In short, the MacCullagh formula approximates the gravitational potential of an irregular body as
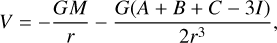 (1)
(1)
where A, B and C are the inertia moments of the body along the principal axes, x, y and z are coordinates measured along those axes, r is the distance from the centre of a body, and
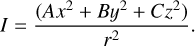 (2)
(2)
For a triaxial ellipsoid, the inertia moments are related to the principal semi-axes a, b, c through the following equations:
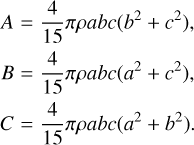
Even if this algorithm is slightly inaccurate close to the body surface, where the polyhedron model would be more precise even if significantly slower, we adopted it because of the strong chaotic nature of the trajectories. The values of a, b and c for both Didymos and Dimorphos are derived from the shape of the objects as observed by DART (Daly et al. 2023) and obtained from the SPICE kernels. We recall that the Spacecraft, Planet, Instrument, C-matrix Events (SPICE) maintained by NASA’s Navigation and Ancillary Information Facility (NAIF) is an observation geometry information system designed to assist scientists in planning and interpreting scientific observations from space-based instruments aboard robotic planetary spacecraft1. As an example, the SPICE typically provide positions and velocities of planets, satellites, comets, asteroids, and spacecraft in several different reference systems.
The numerical integration of the fragments’ orbits is performed in a body-fixed reference frame centred on Dimorphos, rotating with the asteroid’s angular velocity. This reference system is coded within the SPICE kernels as IAU_DIMORPHOS.
Therefore, the apparent forces due to the frame rotation are included in the force equation giving the acceleration
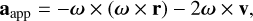 (3)
(3)
where ω is the rotation vector of the reference frame, and r and v are the position and velocity vectors in this rotating frame.
The solar tide force is computed in the model as difference between the Sun gravitational force acting on the fragment and that on Dimorphos. The radial vectors with respect to the Sun are derived from the heliocentric orbit of the binary asteroid, once again as provided by the SPICE kernels in the appropriate integration reference system.
The solar radiation pressure is also included in the trajectory computation with the standard formulation,
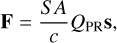 (4)
(4)
where S is the solar radiation flux density at the heliocentric distance of the body, A is the fragment geometrical cross section, and QPR is a dimensionless coefficient determining the amount of radiation that is either reflected or absorbed and re-emitted (Burns et al. 1979). The versor s is directed in the anti-solar direction.
The fragments can be modelled as ellipsoidal rotating particles, therefore posing a time-varying cross-section for the computation of the solar radiation pressure (see Rossi et al. 2022 for details). We note that in the current study, focused on large boulders with a low area-to-mass ratio, the effect of the particle’s shape is not relevant, and therefore spherical particles were considered. The algorithm also allows us to treat collisions between the fragments. These collisions are mostly effective for small objects in the first phases of the plume evolution (see e.g. Fahnestock et al. 2022); therefore, since we are interested in the dynamics of boulders following the first stormy post-collision moments, we assume they are not significantly perturbed by impacts against the smaller fragments and do not consider this effect here. The accurate heliocentric orbit of the Didymos system and the binary orbital dynamics are based on the JPL Ephemeris, as derived from the post-DART impact SPICE kernels.
3 Long-term dynamical behaviour of the boulders
3.1 Initial conditions
In trying to understand the general behaviour of the ejected boulders we have performed a simulation including 10 000 synthetic large objects over an interval of four years after the DART impact, to cover the Hera arrival time-span. The diameters of the simulated objects range from 4 to 10 m and their number, for each size bin in which the size range has been divided, is derived by using a power-law distribution with a slope of q = −3.9. This distribution is derived from the Hubble images taken by Jewitt et al. (2023). The boulders are all started near the location of the DART impact site (Daly et al. 2023, retrieved within the model from the SPICE kernels) and a small delay in their release from the crater is assumed (Raducan et al. 2023), within an interval of time of about 10 min after the impact. The initial velocities with respect to the surface of Dimorphos are encompassed between 6 and 13 cm s−1 with a uniform random distribution. The directions of the velocity vectors are defined by the ejection angle, which is measured from the impact site plane. Such an angle spans the range between 72° and 44° (Li et al. 2023; Dotto & al. 2024; Deshapriya et al. 2023), assuming a linear distribution from the innermost ejecta with the steeper angles to the outermost ones, also including the effects of an oblique impact (Zanotti & Lavagna 2020; Cintala et al. 1999; Anderson et al. 2003); this is based on values estimated from numerical experiments (Raducan et al. 2023). The narrow range of velocities and the large size adopted for the bodies were chosen with the intent of maximising the number of particles potentially surviving for a long time. We note that the number of boulders we simulate is at least two orders of magnitude larger than the expected number. The reason for this choice is to have significant statistics of bodies that are trapped in the gravity field of the binary asteroid for a long time.
 |
Fig. 1 Status of all simulated objects. The time shows the moment when the object left the simulation by re-impacting or escaping. |
3.2 General statistics
The boulders ejected after DART are divided into three groups depending on their final state in the simulation. The first group includes the objects that escape from the system ending in a heliocentric orbit. To determine if an object is outside the Didymos-Dimorphos gravitational influence, we took a simple approach based on the classical definition of a Hill radius:
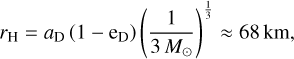 (5)
(5)
where aD is the heliocentric Didymos semi-major axis, eD is its eccentricity, and M⊙ the mass of the Sun. Because of the high eccentricity of Didymos, we found 1rH too restrictive; so, to add extra margin we decided to define the escaping object and object that is at a distance greater than 5rH from the Didymos-Dimorphos barycenter. When a particle reaches that distance, it is considered definitively escaped and removed from the simulation. This is an empirical criterion adopted to define a large enough distance beyond which we can safely claim that the body is not gravitationally tied to the two asteroids. For this reason, even if the Hill’s sphere changes with the heliocentric distance, this does not affect our results in any way. Boulders colliding either with Didymos or Dimorphos belong to group two. Numerically, an object collides with one of the two asteroids if it enters the ellipsoid representing the surface of the asteroid. Finally, group three includes all objects that survive until the end of the simulation, that is, objects that neither escape nor impact the asteroids during the four-year time span of the simulation.
Figure 1 illustrates the boulder’s lifetime versus the initial ejection velocity from Dimorphos’ surface. The red dots show the fragments belonging to group two that re-impact the asteroid after some time, the green dots represent the bodies that escape from the system (group one), while the purple points are the boulders surviving until the end of the simulation (4 years) and therefore belong to group three. According to Fig. 1, most of the low-velocity boulders re-impact Dimorphos on a short timescale, while only a few escape. On the other hand, the higher velocity fragments are more prompt to escape after timescales longer than about 100 days, and a few either impact Dimorphos or, preferentially, Didymos. The long-surviving bodies that accumulate in the rightmost part of the plot do not show a significant dependence of the ejection velocity. The statistics of the final state of the boulders is shown in Table 1. It is worth noticing that the percentages of objects colliding and escaping changes over time; the re-impacts with Dimorphos dominate the early stages of the simulation, while escapes and impacts with Didymos become more frequent later. Most of the particles are removed during the first 100 days, and only 1565 of the original 10 000 remained. At the end of the simulation, after four years, 92 boulders survived, which is slightly less than 1% of the initial objects. In the next section, we describe the evolution in each of the groups of boulders in more detail.
State of the particles in simulation.
3.3 Escaping boulders
The images in Jewitt et al. (2023) show a population of boulders left within the Didymos system after the DART impact. As mentioned before, in our simulation we restricted the initial velocities to a narrow range that is slightly lower than escape velocity from Dimorphos up to slightly greater than escape velocity from Didymos-Dimorphos system. Most of our bodies have velocities between this two limits since we are interested in the long surviving bodies. Therefore, our escaping population might follow a different dynamical path, possibly dominated by close encounters with the two asteroids with respect to the some of the population observed by Hubble, which partly consists of boulders ejected with a higher initial velocity.
If we look at the total number of escaping particles (Fig. 2), we can see the peak in the first 100 days of simulation; then, the number of escape events decreases. The initial peak consists of both objects that initially have a high enough velocity to escape the system and slower ones that achieved the required velocity due to gravitational interaction with asteroids (see Fig. 1). The latter escapes are a product of the dynamical evolution of boulders in the Didymos-Dimorphos system. The number of escape events decreases exponentially as a result of the decrease in the total number of remaining particles. In the simulation, we notice an increase in the number of escapes and in the velocity of escaping particles with a local maximum around 800 days after the Dart impact. This coincides with the moment when Didymos is in its perihelion. The lower Sun-Didymos distance causes stronger solar tides and results in boulders on weakly bounded orbits to escape more likely and with higher relative velocity. We note that this result might suggest that having a dedicated observational campaign will be necessary at the time of the next perihelion passage to check if some escaping boulders could be detected.
3.4 Re-impacting boulders
The investigation of re-impacting boulders on the surface of either Didymos or Dimorphos is relevant to many aspects. They may perform some orbits in the system before colliding, and, therefore, they can be classified as sesquinary. It has been shown that this type of impact may significantly affect the ability of the surface of Phobos to produce low-velocity crater chains (Nayak & Asphaug 2016). In the case of boulders re-impacting the surface of Didymos and Dimorphos, the collision velocity is low, of the order of tens of cm per second. It is possibly too low to produce significant secondary craters on the surface of the bodies. However, the sesquinary impacts can lift dust from the surface of Dimorphos and Didymos; such dust will be subsequently removed by solar radiation pressure. This second-generation dust may explain the extended period of time during which a tail behind Didymos has been observed (see also Moreno et al. 2023; Ferrari et al. 2024). They may also change the surface composition by exposing, after the dust lift, a deeper portion of the surface. These boulders would also increase the overall boulder counting in the densely re-impacted regions, giving an additional contribution to the surface composition alteration. These boulders are in fact produced by the DART impact, which excavated and partly melted material from deeper regions of the asteroid body; when they land on the surface of the asteroids, they bring material with a composition that differs from that of the surroundings. Finally, re-impacts can be relevant for the evolution of the mutual orbit of the binary components (e.g. see Richardson et al. 2022). For this reason, it is important not only to estimate the frequency of this events, but also to find the regions on the surface of both asteroids where most of the primary fragments impact.
A first group of re-impacting particles consists of those that are too slow to escape the gravity of Dimorphos and collide with it after a few hours from the DART impact. They re-impact on Dimorphos with a velocity close to their ejection speed. A second group of bodies leave Dimorphos and orbit Didymos for a while before colliding with either of the two asteroids later in the simulation. As shown in Fig. 3, in the first 40 days most of the boulders impact with Dimorphos, while later on the impacts with Didymos become more likely.
For each of the impacts recorded in the simulation, we calculated the velocity (Fig. 4). The collisions with Dimorphos are generally slower, with a mean velocity equal to 8.9 cm s−1. Most of the slowest impacts occur early, and if we only consider impacts after ten days the mean impact velocity increases to 10.9 cm s−1. The second peak in the histogram of the collision speed on Dimorphos is due to boulders that were injected in a prograde orbit around Didymos and re-impact Dimorphos at a later time, with the earliest one registered 65 days after the beginning of the simulation. This second smaller group of fragments collides with the asteroid with a higher average velocity, which is about 40 cm s−1.
The population of boulders colliding with Didymos has a higher mean velocity of about 26.6 cm s−1 due to the stronger gravity of Didymos. In contrast to Dimorphos, the re-impact velocity is not correlated with the orbit being prograde or retrograde.
The statistical distribution of impacts on the surface of either asteroids is shown in Fig. 5. To define the latitude and longitude we assumed an ellipsoidal shape of both asteroids and used positive rotation axis direction as the North pole (note that both rotations are retrograde with respect to the ecliptic plane or Didymos heliocentric orbital plane). The longitude angle increases in the direction of rotation, and for Dimorphos the prime meridian is directed towards Didymos. On Didymos, the impact locations are uniformly scattered around the equator with a slightly higher probability of impacting on the northern hemisphere. The equatorial preference is related to the initial orbits of most boulders that share an inclination similar to that of Dimorphos, which is close to the equatorial plane of Didymos. A small number of bodies re-impact Didymos at later times, by which point their orbits had had time to evolve in inclination due to the perturbation in the system.
To compute the distribution of re-impacts on the surface of Dimorphos, we assumed that its rotation is tidally locked to its orbital motion. However, it is possible that after DART Dimorphos entered a state of tumbling (e.g. Agrusa et al. 2021; Meyer et al. 2023). However, since most of the re-impacts occur on a very short timescale after the DART collision, our impact map is still roughly reliable even in the case of the switch to tumbling rotation. We note that, even in the case of a principal axis rotation, Dimorphos could still experience a libration with an amplitude of the order of tens of degrees (Agrusa et al. 2021; Meyer et al. 2023) that might slightly alter the simulated distribution on our impact map. The re-impact distribution on Dimorphos significantly differs from that on Didymos, which was expected since most of re-impacting bodies do not come from fragments that have experienced a significant orbital evolution, such as in the case of Didymos. The latitude of the impacts is no longer limited to near equatorial regions, and the distribution of re-impact longitudes becomes non-uniform with a strong preference for positive values. The re-impacts mostly occur on the opposite hemisphere with respect to the DART impact site. To explain this, we use the fact that the initial orientation of the orbit of a boulder is the same as the orientation of Dimorphos orbit. When the collision happens, a boulder is usually near a pericentre of its orbit, so its velocity vector is near perpendicular to their position vector (with regard to Didymos), so it should have similar direction to the Dimorphos velocity vector. The faster object, in this case a boulder, must then hit the slower one from behind (i.e. from the direction opposite to velocity vector of the slower object). Since the boulders are not exactly in their pericentre and their orbital orientation evolves over time, the impact locations are heavily scattered with maximum number of re-impacts around the +90°,0° point.
The distribution of re-impacting bodies may be useful in the analysis of Hera images since some of the observed craters date back to the time of DART impact. These fresh craters may mask some of the older features on the surface of both asteroids and, in the case of crater counting for age determination, they should be excluded from the crater distribution. Therefore, our maps of re-impactors can be a useful tool for interpreting the crater distribution of the asteroid surfaces.
 |
Fig. 2 Objects escaping from Didymos system. The top plot shows the total number of escaping boulders in the simulation (normalised, where 1 is the total number of escapes). In the bottom plot, each point represents a single boulder showing its escape time and velocity relative to the Didymos barycenter at the escape time. |
 |
Fig. 3 Distribution of the re-impact events over time. Bottom panel: total number of re-impact events in the whole simulation time span (logarithmic scale on the y-axis). Top panel: details of period from 10 to 100 days after the DART impact, using a linear scale on the y-axis. The blue line shows the number of re-impacts with Dimorphos, while the orange line represents the re-impacts with Didymos. Both plots are normalised such that 1 is the total number of re-impacts on both asteroids. |
 |
Fig. 4 Velocity of boulders re-impacting with Didymos (top) and Dimorphos (bottom). For Dimorphos, the logarithmic scale is used for better readability. |
 |
Fig. 5 Location of re–impacts on Didymos (top) and on Dimorphos (bottom). Only the re-impacts occurring later than 24 h after DART impact are included. On the bottom, the green dot marks the DART impact location and the (0°,0°) point is the direction towards Didymos, and the north pole (+90° latitude) is in the direction of the rotation axis, while the other one (−90°,0°) is the direction of the Dimorphos orbital motion. Most of the re-impacts are concentrated near the point (90°,0°) that is opposite the direction of orbital motion of Dimorphos and almost opposite the DART impact location. |
 |
Fig. 6 Total number of particles in simulation over time (where 1 is the normalised initial population size). Objects that escaped or re-impacted were removed from the simulation. |
3.5 Quasi-stable orbits
The previous dynamical analyses and simulations of the particle orbits (Rossi et al. 2022) show that stable orbits can exist in the Didymos-Dimorphos system. The stable orbits could be either circumbinary – orbiting both asteroids outside of the orbit of Dimorphos, or circumprimary – orbiting around Didymos inside the orbit of Dimorphos. Those orbits exist only if the solar radiation pressure is weak enough, which means that only larger bodies with a low area-to-mass ratio should remain in the system. The existence of such orbital solutions is not a sufficient condition; there also must be a mechanism placing the boulders released from Dimorphos on this kind of orbit. Therefore, it is necessary to perform simulations where boulders are released from the surface of Dimorphos to test whether some of these bodies are placed in these almost stable orbits.
The large initial population of the boulders in the simulation exponentially decays over time, as shown in Fig. 6. The rate of decay slowly decreases over time, but about 700 days after the DART impact the rate has a temporary increase. This temporary rise occurs when Didymos is near its perihelion around the Sun. After the perihelion, approximately after 1000 days from the beginning of the simulation, the decay rate slows down again. A total of 92 objects survived until the end of the simulation, with six of them on escape trajectories that have not yet reached the limiting distance of 5 Hill radii from Didymos but that are going to escape within the following 30 days. If we exclude these objects and a few others on very distant orbits that are heliocentric rather than circumbinary, 80 objects survive locked in orbit around the binary asteroid, which accounts for about 0.8% of initial number of particles in the simulation.
The histograms of Fig. 7 show the distribution of the osculating orbital elements of the surviving particles at the end of the simulation. The angular elements are measured in the ecliptic J2000 reference frame. It is noteworthy that all the surviving objects are on circumbinary orbits, suggesting that there are no dynamical pathways connecting the boulders from their ejection to an almost stable circumprimary orbit around Didymos lasting at least a few hundred days. Also, there are no particles orbiting Dimorphos in the simulation. The typical orbit of long-term surviving objects has high eccentricity (only 14 of the final orbits have e < 0.7) and is on a retrograde orbit with low inclination. Prograde and inclined orbits are also present, but they are less frequent. All except one of the orbits have the pericentre distance larger than the orbit of Dimorphos around Didymos. Low pericentre distances significantly reduce the survival chances due to the high probability of close encounters with the asteroids. The histograms of the pericentre arguments and nodal longitudes (bottom panels of Fig. 7) show that the ascending nodes concentrate around 120 degrees, while the peri-centres are located close to one of the nodes (i.e. ω close to 0° or 180°).
A more detailed analysis of the distribution of the orbital angles (Fig. 8, top) shows that the boulders with nodes concentrated around 120° are on highly inclined orbits. Almost all bodies (with the exception of two) with inclinations close to 90° have their periapsis argument concentrated around 0°. The evolution of the angular elements (Fig. 8, bottom) shows that this might be a kind of unstable equilibrium point, where the pericentres of highly inclined orbits2 are clustering and angular elements are evolving very slowly. There are also orbits moving away from this equilibrium point, lowering their inclination in the process. The direction of this equilibrium at first glance looks quite arbitrary, but it is located perpendicularly to the Sun-Didymos pericentre line, which has a longitude ~30°. The exact dynamical mechanism of this pericentre clustering requires more detailed analysis.
In Fig. 9, we show the trajectories in the inclination-eccentricity plane and in the inclination-ω plane for all particles during the last two years of the simulation. The different colours on the plots are used to distinguish between different objects. The first plot clearly shows the connection between an increase in eccentricity and inclination, and also that all low-eccentricity orbits are near the ecliptic plane. Both plots shows a behaviour similar to that of orbits affected by the Kozai mechanism, with the Sun as the outer perturbing body. However, the orbital flips observed for many particles in the simulation are quite rapid and occur mostly near the epoch of Didymos perihelion, while in the classical Kozai mechanism the timescale should be longer than a few periods of the perturbing body. This means that the rapid orbital changes observed here are the effect of perturbations near the perihelion of the eccentric Didymos orbit. The other sources of the changes in the inclination are the perturbations from Dimorphos, which may be creating an inner Kozai mechanism (Naoz et al. 2017) that affects orbits regardless of the Sun distance. The coupling of effects by inner and outer perturbing bodies together with other dynamical effects (such as obliquity of the asteroids and radiation pressure) creates a complicated dynamical system, which will be explored theoretically in more detail in future works.
The vast majority of boulders have orbits entirely between the orbit of Dimorphos and the Hill radius of the Didymos system. Only one boulder at the end of the simulation has a peri-centre closer than a Didymos orbit radius, and there are a few boulders with an apocentre more distant than the Hill sphere. The particles with a closer apocentre have relatively strong gravitational bound to Didymos and are usually on a regular elliptical orbit that is processing slowly due to gravitational perturbations. For those objects, the more rapid changes of osculating orbits are present only as the effects of close fly-bys. The second group contains the high-inclination orbits discussed in the previous paragraph undergoing the increase in inclination phenomena. In the final results, we also find some surviving particles ejected on orbits with an apocentre very far (more than two times the Hill radius) from Didymos, where solar tide perturbations are considerably stronger. Those objects are loosely bound with Didymos, but for some reason they did not cover enough distance to reach our escape distance condition. Their trajectory often had a more exotic shape than weakly perturbed Keplerian ellipses and can be considered as being on a heliocentric orbit close to Didymos rather than a perturbed orbit around the asteroid.
Observing different particle trajectories in the simulation, we can propose the following typical scenario for long-surviving particles. First, the boulder is ejected from the surface of Dimorphos by the DART impact. If its velocity is too low, it quickly re-impacts; if it is too large, the boulder escapes the system within few days or weeks. If the boulder lies in the correct velocity range, it remains in the system on its initial orbit with a pericentre close to the DART impact location. This initial orbit can be very chaotic due to possible close encounters with Dimorphos, and sooner or later the particle is either removed (escape or collision) by one of these encounters or sent into an orbit with a more distant apocentre. At those larger distances, solar tides have a greater effect on the orbit and could possibly increase the pericentre distance, allowing the particle to reduce the probability of close fly-bys near Dimorphos. This mechanism could possibly place the boulder on quasi-stable orbits, where some of them can last for hundreds of days. Those quasi-stable orbits are perturbed by the Sun and by asteroids’ gravity, resulting in an increase in eccentricity and inclination or orbital flips from retrograde to prograde and vice versa. This orbital evolution may cause the escape or re-impact of the boulder tens or hundreds of days after it was released from Dimorphos.
 |
Fig. 7 Osculating elements distribution at the end of the simulation. Only elliptic orbits are included. In the last plot showing the distribution of pericentre distance, we excluded five particles with q > 24 for better readability (orange line shows the distance of 1.2 km). |
 |
Fig. 8 Final distribution (top) and evolution during last 365 days of simulation (bottom) of angular osculating elements: longitude of ascending node, argument of periapsis, and inclination (as colour). In the bottom figure, all objects present in the last 365 days are plotted, and those present at the end are marked by a black dot at the end of their track. |
 |
Fig. 9 Trajectories on eccentricity inclination and inclination argument of pericentre planes. The plots include orbits of all objects for the last two years of simulation time span. Different colours are used to distinguish different particles, but due to the large number of objects, the same colour may be used by more than one particle. |
 |
Fig. 10 Mean lifetime of particles in simulation depending on their diameter. The dots are the mean value for all the particles in the size range ±5 cm (about 100 particles per dot), and the solid line is the mean value with moving average for particles in a wider range of sizes ±50 cm. |
3.6 Size dependency
The size of the ejecta is relevant when the solar radiation pressure becomes a significant force, which may significantly perturb gravity. Previous simulations (Yu et al. 2017; Yu & Michel 2018; Rossi et al. 2022) have shown that radiation pressure can quickly destabilise the orbits of small particles around Didymos-Dimorphos and then reduce their lifetime. To test the relevance of the solar radiation pressure for larger bodies we have performed an additional simulation where the size of the particles ranges from 10 cm to 10 m. In randomly creating the particle population, we used a uniform distribution of sizes to equally represent the particles in each size range.
In Fig. 10, we plot the mean particle lifetime in the simulation versus the particle size. Each point is the mean value of the lifetime for all particles encompassed within a size range of +5 cm. The moving average with a range of ±50 cm (solid line in the plot) have a shape similar to a logarithmic function with a rapid initial growth for lower diameters and slower asymptotic growth for larger boulders. In the simulation, the smallest particles have a lifetime of less than 40 days, which rises to about 100 days for particles of a few metres in size. It must be noted that the average may depend on the initial velocities and on the condition for a particle to be considered escaped from the system. For example, particles with low initial velocity that are re-impacting Dimorphos a few hours after the DART impact can decrease the mean value. In addition, in our simulation the particles requires about one month to reach the escape distance of 5rH, increasing the lifetime in this case. However, the analysis of the data shows that these effects ‘democratically’ affect the estimates of the average lifetime.
The number of objects lasting until the end of the simulation (4 Earth years) also shows a dependence on the particle size (see Fig. 11). For particles with diameters around 4 m, the fraction of surviving boulders is almost 0.8% in agreement with our previous computations. For larger boulders, the percentage goes up to 1.2–1.4%, while for smaller boulders it decreases to approximately 0.4%, showing that the solar radiation pressure acts always to destabilise orbits.
 |
Fig. 11 Percentage of boulders that survived in Didymos system until the end of the simulation (4 years after DART impact) depending on size range. |
3.7 Stability of the solutions
To estimate the stability of the long-term orbits described in Sect. 3.5, we performed another set of simulations where we used the orbits of 92 long-surviving boulders to create a large population of clones with slightly altered initial conditions. In the first simulation, we generated 100 clones for each long surviving particle by randomly altering the initial position of the original particle by a factor of 10−4 of the original value in each of the Cartesian coordinates. Therefore, the absolute change was smaller than a few millimetres. These cloned particles are integrated starting at the moment of the DART impact.
The very small change in initial conditions has a significant impact on the resulting particle dynamics and their lifetime. During the first 30 days, more than 3000 clones (i.e. 33% of the total) re-impacted with one of the asteroids. Further on, during the first 100 days, 5322 objects were removed from the simulation due to re-impacting or escaping. This means that the rate of survival in the clone population is only slightly higher than in the original simulation, and still most of the particles are removed. The number of particles surviving until the end of the simulation is 1%, just slightly higher than the global statistics in the original simulation with random initial conditions. The reason for this small difference is that in the simulation with the clones we only include objects with an initial velocity large enough to avoid immediate re-impact against Dimorphos.
To test if a specific set of initial conditions could potentially be more prone to stability, for each of the 92 long-lasting initial boulders we counted the number of clones that survived over a long timescale. For about half (47) of the original 92 quasi-stable boulders, we find that none of their clones survived at least for the same time span of the original cloned boulder. For 25 original bodies, only one clone survived, while for the remaining 67 cases more than one clone lasted until the end of the simulation. In a single case, eight clones (out of 100) of the original body survived, while six clones survived in other two cases. This suggests that the dynamics is strongly chaotic, and a small change (few millimetres as stated above) in the initial position can dramatically alter the lifetime of a particle in the system. In addition, within the assumptions of our model and the explored simulation cases, there is not a specific extended set of initial conditions leading to quasi-stable orbits.
To test whether the particles, after avoiding the initial highly chaotic evolution, can be injected into stable orbits, we performed an additional set of simulations where the clones are created 100 days after the DART impact. For each of the 92 original quasi-stable objects, we generated 100 clones by altering the coordinates of their position vector again by up to 10−4 of its nominal value (corresponding in this case to an absolute change of a few metres). Then we numerically integrated this new population of 9200 clones over a time-span of 4 years (100 days beyond the end of the original integration). Out of this initial population, 3285 particles survived the entire simulation (about 36%), 909 impacted Didymos, 646 re-impacted Dimorphos, and 4360 escaped from the system. A small number of original objects give rise to a line of clones that are quite stable, with most of them surviving until the end of the simulation. Indeed, seven of them have all 100 clones surviving. On the other hand, about half of the original objects have less than 25% of their clones lasting till the end of the simulation, and three have all of their clones removed by escapes and re-impacts.
The higher percentage of survivors (36% vs. 1%) in this second population of clones implies that, after 100 days, the 92 original quasi-stable boulders have reached a zone of the phase space where it is more easy to survive in orbit for a long interval of time. This also points to the possible existence of wide regions in the phase space where quasi-stable orbits can be found, but they are not necessarily accessible by boulders ejected after a collision on the surface of Dimorphos.
4 Discussion
An important question concerning the environment around the Didymos-Dimorphos system is the long-term survival of boulders ejected after the DART impact. If they stay on quasi-stable orbits long enough, they may be observed by the Hera mission, but, at the same time, they would represent a threat for the spacecraft. To answer this question we performed detailed numerical simulations of a large number of bodies in order to see the dynamics of the system. We developed an accurate numerical model able to include all the relevant physics and explore a reasonable range of initial conditions for the ejecta. We also implemented the correct geometry of ejection in the code using the SPICE kernels in order to have the exact orientation of the binary system in the appropriate reference frames.
In general, the dynamics near Didymos-Dimorphos can be viewed as a restricted four-body problem. For particles closer to the asteroid pair, the most relevant forces are the gravity of Didymos and Dimorphos, while for the more distant ones the gravity of the Sun plays an important role. A significant aspect of the combination of all the gravitational perturbations is that they force a relation between the eccentricity and the inclination of the boulders similar to a Kozai state but with a different behaviour. An increase in inclination is connected with an increase in eccentricity (however, not all highly eccentric objects increase their inclination). Paradoxically, this may act as a sort of protection mechanism against instability since the high inclination reduces the probability of a close encounter with Dimorphos when the orbits are eccentric. In addition, these perturbations enable orbital flips leading to polar and prograde orbits.
In our study, we show that a fraction of the ejected boulders can indeed survive and orbit around the binary asteroid for an extended period of time. To estimate the fraction of the initial boulders that are injected in these quasi-stable orbits, we integrated a large number of bodies in order to explore the phase space in more detail and to derive a statistical probability of survival. However, since we do not know the real number of boulders ejected by the impact from observations, we cannot predict even an approximate number of bodies that will orbit the binary at the time of the Hera arrival. The Hubble Space Telescope (HST) observed over 60 large boulders, and several boulders were also observed by the LICIACube. Whereas the boulders observed by HST are mostly on escape trajectories, these observations allow us to assume that a significant number of boulders were ejected, possibly with a low initial velocity. Some of them may end up on the quasi-stable orbits that we outline in our paper. The fraction of surviving objects in our simulation is small, about 1% of the initial sample, but not negligible. Given the strongly chaotic nature of the evolution, it is hard to postulate if the use of more precise initial conditions or of an improved physical model (e.g. including the post-impact binary eccentricity or Dimorphos’s asynchronous rotation state) could lead to more realistic results. In any case, from our statistics, it can be safely inferred that there is a very limited risk of impacts between the arriving Hera spacecraft and a large object trapped within the system.
Since the long term orbits are not stable, there is an almost continuous leak of bodies from the population of boulders moving in the system. The escaping rate grows when Didymos approaches the Sun at pericentre due to the increased solar tide. These boulders might be observed from the ground in particular in 2025 when Didymos passes through the pericentre.
An additional outcome of our modelling is the distribution of re-impacts on the surface of Dimorphos and impacts on that of Didymos that can be classified as sesquinary. Knowledge of their distribution is useful to evaluate the extended emission of dust from the surface of the two bodies that refills the dust tail even at later times with respect to the DART impact. It is also relevant when interpreting the images taken by Hera, since these sesquinary impacts can slightly change the local features by increasing the density of boulders and by affecting the local surface composition in different ways.
Acknowledgments
This work is supported by the Italian Space Agency (ASI) within the Hera agreement (ASI-UNIBO, no. 2022-8-HH.0). The authors wish to thank the anonymous reviewer for the useful and constructive remarks that helped to improve the paper.
References
- Agrusa, H. F., Gkolias, I., Tsiganis, K., et al. 2021, Icarus, 370, 114624 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J. L., Schultz, P. H., & Heineck, J. T. 2003, J. Geophys. Res.: Planets, 108 [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [Google Scholar]
- Capannolo, A., Zanotti, G., Lavagna, M., et al. 2021, Acta Astronautica, 182, 208 [CrossRef] [Google Scholar]
- Cheng, A. F., Agrusa, H. F., Barbee, B. W., et al. 2023, Nature, 616, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Cintala, M. J., Berthoud, L., & Hörz, F. 1999, Meteor. Planet. Sci., 34, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Daly, R. T., Ernst, C. M., Barnouin, O. S., et al. 2023, Nature, 616, 443 [CrossRef] [Google Scholar]
- Deshapriya, J. D. P., Hasselmann, P. H., Gai, I., et al. 2023, Planet. Sci. J., 4, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Dotto, E., Deshapriya, J. D. P., Hasselmann, P. H., et al. 2024, Nature, 627, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Dotto, E., Della Corte, V., Amoroso, M., et al. 2021, Planet. Space Sci., 199, 105185 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1985, Astrophysics and Space Science Library, 115, (Dordrecht: Reidel) 185 [NASA ADS] [CrossRef] [Google Scholar]
- Fahnestock, E. G., Cheng, A. F., Ivanovski, S., et al. 2022, Planet. Sci. J., 3, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, F., Panicucci, P., Merisio, G., et al. 2024, Nat. Commun., submitted [Google Scholar]
- Jewitt, D., Kim, Y., Li, J., & Mutchler, M. 2023, ApJ, 952, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J.-Y., Hirabayashi, M., Farnham, T. L., et al. 2023, Nature, 616, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, A. J., Agrusa, H. F., Richardson, D. C., et al. 2023, Planet. Sci. J., 4, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P., Küppers, M., Bagatin, A. C., et al. 2022, Planet. Sci. J., 3, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Bagatin, A. C., Tancredi, G., et al. 2023, Planet. Sci. J., 4, 138 [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 2000, Solar System Dynamics (Cambridge University Press) [Google Scholar]
- Naoz, S., Li, G., Zanardi, M., de Elía, G. C., & Di Sisto, R. P. 2017, AJ, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nayak, M., & Asphaug, E. 2016, Nat. Commun., 7, 12591 [Google Scholar]
- Raducan, S., Jutzi, M., Cheng, A., et al. 2023, Nat. Astron., in press [Google Scholar]
- Richardson, D. C., Agrusa, H. F., Barbee, B., et al. 2022, Planet. Sci. J., 3, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, A., Marzari, F., Brucato, J. R., et al. 2022, Planet. Sci. J., 3, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, R. A. 1994, Celest. Mech. Dyn. Astron., 59, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, R. A., & Scheeres, D. J. 1997, Celest. Mech. Dyn. Astron., 65, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y., & Michel, P. 2018, Icarus, 312, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y., Michel, P., Schwartz, S. R., Naidu, S. P., & Benner, L. A. M. 2017, Icarus, 282, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Zanotti, G., & Lavagna, M. 2020, in 71st International Astronautical Congress (IAC 2020), 1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Status of all simulated objects. The time shows the moment when the object left the simulation by re-impacting or escaping. |
| In the text | |
 |
Fig. 2 Objects escaping from Didymos system. The top plot shows the total number of escaping boulders in the simulation (normalised, where 1 is the total number of escapes). In the bottom plot, each point represents a single boulder showing its escape time and velocity relative to the Didymos barycenter at the escape time. |
| In the text | |
 |
Fig. 3 Distribution of the re-impact events over time. Bottom panel: total number of re-impact events in the whole simulation time span (logarithmic scale on the y-axis). Top panel: details of period from 10 to 100 days after the DART impact, using a linear scale on the y-axis. The blue line shows the number of re-impacts with Dimorphos, while the orange line represents the re-impacts with Didymos. Both plots are normalised such that 1 is the total number of re-impacts on both asteroids. |
| In the text | |
 |
Fig. 4 Velocity of boulders re-impacting with Didymos (top) and Dimorphos (bottom). For Dimorphos, the logarithmic scale is used for better readability. |
| In the text | |
 |
Fig. 5 Location of re–impacts on Didymos (top) and on Dimorphos (bottom). Only the re-impacts occurring later than 24 h after DART impact are included. On the bottom, the green dot marks the DART impact location and the (0°,0°) point is the direction towards Didymos, and the north pole (+90° latitude) is in the direction of the rotation axis, while the other one (−90°,0°) is the direction of the Dimorphos orbital motion. Most of the re-impacts are concentrated near the point (90°,0°) that is opposite the direction of orbital motion of Dimorphos and almost opposite the DART impact location. |
| In the text | |
 |
Fig. 6 Total number of particles in simulation over time (where 1 is the normalised initial population size). Objects that escaped or re-impacted were removed from the simulation. |
| In the text | |
 |
Fig. 7 Osculating elements distribution at the end of the simulation. Only elliptic orbits are included. In the last plot showing the distribution of pericentre distance, we excluded five particles with q > 24 for better readability (orange line shows the distance of 1.2 km). |
| In the text | |
 |
Fig. 8 Final distribution (top) and evolution during last 365 days of simulation (bottom) of angular osculating elements: longitude of ascending node, argument of periapsis, and inclination (as colour). In the bottom figure, all objects present in the last 365 days are plotted, and those present at the end are marked by a black dot at the end of their track. |
| In the text | |
 |
Fig. 9 Trajectories on eccentricity inclination and inclination argument of pericentre planes. The plots include orbits of all objects for the last two years of simulation time span. Different colours are used to distinguish different particles, but due to the large number of objects, the same colour may be used by more than one particle. |
| In the text | |
 |
Fig. 10 Mean lifetime of particles in simulation depending on their diameter. The dots are the mean value for all the particles in the size range ±5 cm (about 100 particles per dot), and the solid line is the mean value with moving average for particles in a wider range of sizes ±50 cm. |
| In the text | |
 |
Fig. 11 Percentage of boulders that survived in Didymos system until the end of the simulation (4 years after DART impact) depending on size range. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


