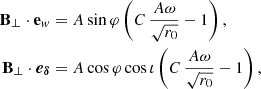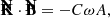| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A194 | |
| Number of page(s) | 19 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348016 | |
| Published online | 24 April 2024 | |
Polarized signatures of orbiting hot spots: Special relativity impact and probe of spacetime curvature
1
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. de Paris, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
e-mail: frederic.vincent@obspm.fr
2
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: maciek.wielgus@gmail.com
3
Research Centre for Computational Physics and Data Processing, Institute of Physics, Silesian University in Opava, Bezručovo nám. 13, 746 01 Opava, Czech Republic
Received:
18
September
2023
Accepted:
9
December
2023
Context. The Galactic Center supermassive black hole is well known to exhibit transient peaks of flux density on a daily basis across the spectrum. Recent infrared and millimeter observations have strengthened the case for the association between these flares and circular orbital motion in the vicinity of the event horizon. The strongly polarized synchrotron radiation associated with these events leads to specific observables called QU loops, that is, looping motion in the Stokes QU plane of linear polarization. These patterns have been observed by the Submillimeter Array, VLTI/GRAVITY, and ALMA.
Aims. We want to deepen the understanding of the QU loops associated with orbiting hot spots. To this end, we computed such loops in Minkowski and Schwarzschild spacetimes in order to determine which aspects of the observed patterns are due to special- or general-relativistic phenomena.
Methods. We considered a parcel of energized plasma in circular motion in Minkowski spacetime and in Keplerian orbit in the Schwarzschild spacetime. We computed, using the GYOTO ray-tracing code, the polarized radiative transfer associated with this orbiting hot spot and derived the evolution of the flux density, astrometry, and Stokes Q and U parameters.
Results. We show that QU loops in Minkowski spacetime at low or moderate inclination i ≲ 45° (where i = 0° is a face-on view) share all the qualitative features of Schwarzschild QU loops. There exist QU loops for all setups considered (including for the face-on view and vertical magnetic field), there may be one or two QU loops per orbital period for a vertical magnetic field configuration, and there are always two QU loops in case of a toroidal magnetic field. The simplicity of Minkowski spacetime is a key asset for allowing us to provide analytical formulas that explain the details of this behavior. Moreover, we analyzed the flux variation of the hot spot and show that it is dictated either by the angular dependence of the radiative transfer coefficients or by relativistic beaming. In the former case, this can lead to extreme flux ratios, even at a moderate inclination. Finally, we highlight the increasing mirror asymmetry of the Schwarzschild QU track with increasing inclination and show that this behavior is a specific Schwarzschild feature caused by light bending.
Conclusions. Although special-relativistic effects have not been extensively discussed in this context, they are a crucial part in generating the observed QU loops. However, general-relativistic light bending leads to a specific observable feature encoded in the asymmetry of the observed loops, and this feature might allow the spacetime curvature to be quantified.
Key words: accretion / accretion disks / black hole physics / gravitation / radiative transfer / relativistic processes
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The emission from the close surroundings of the Galactic supermassive black hole Sagittarius A* (Sgr A*) is variable at all wavelengths with a degree of variability that depends strongly on frequency, from tens of percents in the radio waveband to a factor of more than 100 in X-rays (Genzel et al. 2010). The source exhibits local maxima of variable emission, from radio frequencies to X-rays, called radiation flares. The typical timescale of these events is on the order of tens of minutes (see e.g. Genzel et al. 2010; Morris 2023). The physical nature of these events remains unclear even after 20 years of study since the first detected events (Baganoff et al. 2001; Genzel et al. 2003). Many models have been proposed (we refer to Vincent et al. 2014 for a review). Among them, the class of hot spot models (Broderick & Loeb 2006; Hamaus et al. 2009, and references therein) is of particular interest. The underlying assumption of this model is that Sgr A* flares are caused by the radiation emitted by transient localized (at least initially) compact (few gravitational radii) orbiting (in the disk plane or along the jet funnel) parcels of energized plasma in the inner region of the accretion-ejection flow surrounding the black hole. This model is of particular relevance given the detections of orbital motions consistent with circular trajectories very close to the event horizon associated with infrared and X-ray flares (GRAVITY Collaboration 2018, 2023; Wielgus et al. 2022b). Such hot spots might be the end product of the acceleration of particles in the inner regions of the flow by magnetic reconnection (see e.g. Ripperda et al. 2022; El Mellah et al. 2023). It has recently been shown that hot spots generated by magnetic reconnection may account for photometric and astrometric infrared observations (Aimar et al. 2023a).
The polarization properties of infrared and millimeter flares have been studied since the early 2000s. Eckart et al. (2006) observed swings of the electric vector position angle (EVPA) of up to 40° in 10 min during an infrared flare observed by the NAOS/CONICA adaptive optics instrument, while Trippe et al. (2007) measured a swing reaching 70° within 15 min with the same instrument. Trippe et al. (2007) note that these swings are consistent with a hot spot model with an orbital radius on the order of the innermost stable circular orbit (ISCO) associated with the black hole, which corresponds to a Keplerian period on the order of 30 min for a non-spinning black hole of ∼4 × 106 M⊙. The change of polarization angle has been linked to the variation of the relative orientation between the direction of emission reaching the distant observer and that of the ambient magnetic field as the spot orbits around the black hole. The hot spot model was further discussed in the context of these infrared polarized flare observations by Meyer et al. (2006). Compatible infrared flare observations and similar conclusions were obtained by Nishiyama et al. (2009). At radio frequencies, Marrone et al. (2006) reported a 50° EVPA swing over 2.5 h during a millimeter flare observed by the Submillimeter Array and noticed a roughly periodic evolution of the angle with time. When representing the evolution in the QU plane corresponding to the Stokes Q and U linear polarization parameters, the authors obtained a loop pattern exhibiting two full orbits in the QU plane – the first so-called QU loop reported in the literature. The authors argued that this signature might be associated with a hot spot orbiting at a radius larger than the ISCO of the black hole.
Two different instruments have recently observed QU loops: the Very Large Telescope Interferometer GRAVITY beam combiner and the Atacama Large Millimeter Array (ALMA). Regarding the first instrument, GRAVITY Collaboration (2018; see also GRAVITY Collaboration 2023) observed a series of polarized infrared flares. The QU pattern traced a single loop during the observed astrometric orbital period. The authors showed that this pattern is consistent with a hot spot orbiting at a radius close to the ISCO of a non-spinning black hole. For the second instrument, Wielgus et al. (2022b) observed a QU loop with ALMA at millimeter wavelengths following an X-ray flare reported by Chandra (Wielgus et al. 2022a). The authors showed that the data are consistent with a hot spot orbiting at a radius about two times the ISCO of a non-spinning black hole, with the QU loop period interpreted as the Keplerian period of the hot spot. The hot spot interpretation is not unique though, as the EVPA swings have been interpreted by Yusef-Zadeh et al. (2007) not in terms of an orbiting hot spot but rather within the framework of an ejected expanding blob of plasma. This alternative model has recently been discussed by Michail et al. (2023).
In this article, we investigate the polarized synchrotron radiation emitted by orbiting hot spots. In this context, the orientations of the magnetic field has a crucial impact on the observables. Indeed, the electric vector (the on sky orientation of which is encoded in the QU loop) is oriented along the cross product K × B, where K is the photon’s direction of emission and B is the magnetic field vector, both expressed in the comoving frame of the emitter. There is a growing body of evidence that the magnetic field in the close surroundings of Sgr A* is rather ordered and dynamically important (i.e., the plasma dynamics are sensitive to the magnetic field) and has a dominant poloidal component (i.e., in a plane orthogonal to the equatorial plane of the black hole). The hot spot modeling of infrared data performed by GRAVITY Collaboration (2018, 2020c) favors a strong poloidal field. The QU loop observed by Wielgus et al. (2022b) favors a vertical field, while the persistence of the rotation measure, the sign of the circular polarization, and the magnitude of the linear polarization fraction all favor a structured magnetic field of persistent topology (see also Wielgus et al. 2023). The analysis of Michail et al. (2023) favors a magnetic field orientation aligned with the angular momentum vector of the accretion flow, that is, vertical for an accretion flow centered on the equatorial plane of the black hole. The analysis of the spatially resolved event horizon scale images of Sgr A* obtained by the Event Horizon Telescope (EHT; Event Horizon Telescope Collaboration 2022a,b) further supports the magnetically arrested disk (MAD) accretion flow model interpretation (Event Horizon Telescope Collaboration 2022c) characterized by dynamically important magnetic fields with a strong vertical component near the event horizon (Narayan et al. 2003). Furthermore, ordered magnetic fields in the compact region around Sgr A* were revealed by pre-EHT very long baseline interferometry polarimetric observations (Johnson et al. 2015).
We aim to study the properties of QU loops associated with hot spots around black holes. Such investigations have been the subject of recent intense theoretical efforts (GRAVITY Collaboration 2020c, 2023; Gelles et al. 2021; Narayan et al. 2021; Vos et al. 2022; Najafi-Ziyazi et al. 2023). Through this work, we intend to contribute to this emerging topic by mainly focusing on the impact of special relativity on the observables. We develop a thorough analysis of QU loops in Minkowski spacetime and show that these flat spacetime loops share the main features of their general-relativistic counterparts, demonstrating that QU loops are strongly affected by the relativistic velocities of their emitter and the associated special-relativistic light aberration. We also develop an analytical understanding of the properties of these QU loops. We then compute QU loops in the Schwarzschild spacetime, comparing them to their Minkowski counterparts and to the relevant literature. The main aim of this article is to elucidate which aspects of these observable patterns are due to special-relativistic effects and which are due to general-relativistic effects. This is important for initiating the study of QU loops as a potential probe of strong gravity.
The paper is organized as follows. Section 2 describes our hot spot model. Section 3 introduces in detail the topic of QU loops and all the necessary concepts. Section 4 is the main section of the article and is dedicated to the properties of Minkowski QU loops. Section 5 describes Schwarzschild QU loops. Section 6 compares Schwarzschild and Minkowski loops, while Sect. 7 gives our conclusions and perspectives.
2. Modeling hot spot observables
In this section we present our model of a rotating hot spot around a compact object. We discuss the spacetime geometry, the shape, physical characteristics and emission of the hot spot, and the radiative transfer integration by means of relativistic ray tracing. We consider physically motivated values of the model parameters. (For a more extensive discussion of the impact of the individual parameters on the QU loop patterns, see Vos et al. 2022.)
2.1. Spacetime geometry
The main aim of this article is to discuss the respective influence of special- and general-relativistic effects on the polarized signatures associated with orbiting hot spots. To that end, we perform calculations in Minkowski and Schwarzschild spacetimes. We considered that the spacetime is described in spherical coordinates (t, r, θ, φ). We assumed that the spacetime is static and spherically symmetric, meaning that we do not discuss any impact of the compact object’s spin in this article. The metric line element thus reads
where gμν = ∂μ ⋅ ∂ν are the metric coefficients, which can be expressed as the dot products between the natural basis vectors associated with the spherical coordinates, ∂μ. The two static spacetimes (Minkowski, Schwarzschild) that we consider are thus fully defined by their metric coefficients gtt and grr.
2.1.1. Minkowski spacetime
As a flat manifold, Minkowski spacetime has little a priori relevance for interpreting data originating from the close environment of a supermassive black hole. However, by studying QU loops in this context, we aim at revealing key observable features that can be discussed and interpreted and will enable us to tell which aspects are specific to spacetime curvature and which aspects are already present in a flat spacetime. The Minkowski metric is defined with
2.1.2. Schwarzschild spacetime
The Schwarzschild metric in Schwarzschild coordinates is
where rS = 2M is the location of the Schwarzschild event horizon. The Jebsen-Birkhoff1 theorem (Jebsen 1921; Birkhoff & Langer 1923) ensures that the Schwarzschild geometry uniquely describes the spacetime outside of any spherically symmetric object in vacuum. We note that throughout this article we use a system of units where the gravitational constant G and light speed c have unit values so that the gravitational radius, GM/c2, is simply equal to M.
2.2. Hot spot geometry and physical quantities
We considered two spatial positions P0(x0, y0, z0) and P(x, y, z), where the Cartesian coordinates are related to the spherical ones by means of standard Euclidean formulas. We defined the coordinate distance between P0 and P as the Euclidean distance defined by d2 = (x − x0)2 + (y − y0)2 + (z − z0)2. The center of our hot spot is located at a constant radius r0 in the equatorial plane θ0 = π/2 with a varying azimuthal angle φ0. The hot spot is described by specifying the profiles of the electron number density ne, the temperature of the electrons Te, and the magnitude and direction of the ambient magnetic field B. All of these quantities are measured in the rest frame of the orbiting hot spot, which hereafter we refer to as the “emitter’s frame”. We assumed the following profiles for the physical quantities:
where d2 is the squared coordinate distance (as defined at the beginning of this section) to the center of the hot spot (x0 = r0 cos φ0, y0 = r0 sin φ0, z0 = 0); ne0 and Te0 are the density and temperature at the center of the hot spot; and σr is the Gaussian standard deviation, which is related to the full width at half maximum, that is, the effective diameter Dhs of the hot spot, by Dhs ≈ 2.35 σr; η is the magnetization parameter; and mp is the proton rest mass. We assumed a constant ratio between the particle rest-mass and magnetic energy densities. Furthermore, we assumed that the hot spot is described by a spatial Gaussian profile around its center, while its properties remain constant in time.
The values assumed for the parameters introduced so far are listed in Table 1. We note that the magnetic field maximum magnitude (B0 = 140 G, a consequence of the simple prescription given by the third line of Eq. (4)) is rather high as compared to the typical value that can be derived from the synchrotron cooling time (see e.g. Aimar et al. 2023a), but the precise value of this magnitude, unlike the magnetic field orientation, does not impact the results of this article, as it only scales the absolute value of the flux density. We also note that we fixed the magnetization to η = 1, which corresponds to a strongly magnetized flow, in agreement with hints that Sgr A* is likely a magnetically arrested flow (e.g. GRAVITY Collaboration 2018; Event Horizon Telescope Collaboration 2022c; Wielgus et al. 2022b). The central density and temperature were chosen to ensure a near infrared maximum dereddened flux (corrected from the strong extinction toward the Galactic Center) of ≈10 mJy at low inclination (the inclination angle coincides with the spherical θ angle of the observer; see Fig. 3 for a definition of θ) for a vertical magnetic field. This value corresponds to a rather bright infrared flare (see the percentiles of the Sgr A* dereddened flux distribution provided in Table 1 of GRAVITY Collaboration 2020a) and can be compared first to the dereddened flux density of S2 that reaches ≈16 mJy (GRAVITY Collaboration 2020a) and second to the brightest infrared flare ever observed, which reached ≈60 mJy (Do et al. 2019). We note that other configurations with different magnetic field geometry can lead to much higher fluxes that are not in agreement with observations. Nonetheless, we kept the central density and temperature fixed in order to ease the interpretation of the impact of the magnetic field geometry on the observables.
Parameters of our model.
2.3. Hot spot motion
The hot spot center located at r0 is assumed to follow a circular time-like geodesic, that is, a Keplerian orbit of the spacetime considered. Its four-velocity thus reads
The expressions of ut and Ω depend on the spacetime metric. That of Ω is well known for the Schwarzschild spacetime expressed in Schwarzschild coordinates, ΩSchwarzschild = M1/2 r−3/2 (e.g. Bardeen et al. 1972). Given that this expression coincides with the Newtonian result, we used the same expression in Minkowski, even though there is no reason for the hot spot to follow orbital motion in a flat spacetime (in the absence of a central massive object). Hence, we only considered Minkowski spacetime to determine which features of the observables are specific to a curved spacetime and which features are already present in a flat geometry. With an expression for Ω, it is straightforward to derive the expression of ut by using the normalization of the four-velocity u ⋅ u = −1. We ultimately obtained
2.4. Magnetic field configuration
We have so far only defined the magnitude of the magnetic field through Eq. (4). We proceed in this section to specify its direction. Hence, we needed to define a unit space-like vector normal to the hot spot four-velocity given that the magnetic field vector lies in the rest space of the emitter.
We considered only two different configurations: vertical and toroidal. These two configurations are inspired by two plausible magnetic configurations that could exist around Sgr A*. Either the environment is weakly magnetized and the magnetic field lines follow the motion of the matter swirling toward the black hole, in which case the magnetic field is mostly toroidal (this would correspond to a SANE – standard and normal evolution – situation) or the environment is strongly magnetized and the magnetic field does not follow the motion of the matter, in which case it would have a strong vertical component as in MAD states. Thus, we defined
where the upper bar means that the vector is a unit vector, with the constraints that
The second condition implies that the magnetic field 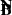 lies in the local rest space of the emitter, that is, the space orthogonal to its four-velocity. We thus defined the magnetic field as measured by the emitter. These conditions immediately led to
lies in the local rest space of the emitter, that is, the space orthogonal to its four-velocity. We thus defined the magnetic field as measured by the emitter. These conditions immediately led to
where Ω is the Keplerian rotation velocity defined in Eq. (6), and we used the orthonormal basis associated to the natural coordinate basis ∂μ
This basis coincides with the locally non-rotating frame (Bardeen et al. 1972) of the Schwarzschild spacetime. We note that although the hot spot’s center r0 orbits in the equatorial plane, the full hot spot is a three-dimensional structure in space and is not restricted to the equatorial plane. This is why the magnetic field is defined for all θ and not only for θ = π/2.
2.5. Radiative transfer
The hot spot is assumed to emit synchrotron radiation, and the emitting electrons are considered to follow a κ distribution, that is, a mix between a thermal core and a power-law tail. This distribution is well adapted to simulate the state of electrons locally accelerated (for instance through magnetic reconnection) that radiate during Sgr A* flares. The κ distribution is thus a more physical assumption, particularly for the infrared emission during a flare, than the thermal spectrum considered by Wielgus et al. (2022b) and Vos et al. (2022). This distribution reads
where γ is the Lorentz factor of the electrons; N is a normalizing coefficient chosen such that the integral of ne(γ) over all γ is equal to the total number density of the hot spot; and θe = kTe/mec2 is the dimensionless electron temperature, with k and me being the Boltzmann constant and electron rest mass. We chose a parameter κ = 4. This translates to an infrared spectral index of α = 0 where νFν ∝ να, which is reasonable for bright flares (Gillessen et al. 2006). We utilized the emission, absorption, and Faraday rotation and conversion coefficients for κ-synchrotron as derived by Marszewski et al. (2021). These coefficients have rather complicated and lengthy expressions that we do not fully repeat here. However, it is useful for the forthcoming discussion to indicate that the emission coefficients for the various Stokes parameters are expressed as
where Xκ = ν[νc(θeκ)2 sin θB]−1, νc is the cyclotron frequency, and θB is the angle between the magnetic field direction and the direction of emission. The proportionality factor in the above expressions depends on κ and on the particular Stokes parameter that is considered. This expression coincides with the so-called high-frequency emission coefficient reported in Eq. (44) of Marszewski et al. (2021), which applies to our typical conditions. The strong directional dependence of this expression, evident in the sin θB term, is crucial for the forthcoming discussion. We note that for κ = 4, the expression behaves as sin2θB, so it cancels in the direction of emission along the magnetic field lines and reaches its maximum in the direction normal to the magnetic field. We also note that the frequency dependence of the emission coefficient follows ν−1. While the Faraday effects are generally negligible for modeling infrared flares, they become important at millimeter wavelengths, for which significant Faraday rotation is most likely associated with the compact emission region, contributing non-trivially to the observed complex linear polarization (Wielgus et al. 2023).
2.6. Polarized ray tracing
We computed the polarized flux emanating from the orbiting hot spot by using the GYOTO code (Vincent et al. 2011; Aimar et al. 2023b). We considered an observer located at a distance D = 8.28 kpc (GRAVITY Collaboration 2021). The compact object’s mass was fixed to M = 4.3 × 106 M⊙ (GRAVITY Collaboration 2020b). The inclination (corresponding to the spherical coordinate θ, as defined in Fig. 3; it is 0° or 180° for a face-on view, and 90° for an edge-on view) is varied in [90 ° ,180 ° ], with 90° corresponding to an edge-on view, and 180° to a face-on view. This range encompasses the best-fit inclination for Sgr A* of ≈160° derived by GRAVITY Collaboration (2018), Wielgus et al. (2022b). Inclinations higher than 90° recover a clockwise on sky motion of the hot spot, consistent with observations.
Null geodesics were traced backward from the observer’s screen toward the hot spot, and the full polarized radiative transfer was solved. We assumed the observer to be located at an azimuthal angle φ = −π/2, defined in Fig. 3. We accounted for the finite velocity of light (the so-called slow-light paradigm). The final product of the computation was a set of maps of the specific Stokes parameters (Iν, Qν, Uν), introduced in Sect. 3.1, for the various orbital phases of the hot spot. We discard Stokes V (circular polarization) in this article, although it was formally computed. Stokes V is generally much lower than the linear polarization component, and it is not observed by GRAVITY. Nonetheless, it may be an interesting additional observable related to QU loops observed at millimeter wavelengths (Yfantis et al. 2024). We always considered a resolution of N × N = 128 × 128 pixels, and a field of view of f = 200 μas. The observing wavelength was set to λobs = 2.2 μm, coinciding with that of the GRAVITY instrument. All parameters discussed in this section are listed in Table 1.
3. Polarization signature of hot spots
Before turning to the detailed properties of QU loops, which are discussed in the context of Minkowski spacetime in the next section, we introduce all relevant material for the following discussions in this section. We define the Stokes Q and U parameters, the electric vector position angle, and intuitively introduce the concept of QU loops associated with orbiting hot spots.
3.1. Stokes Q and U parameters, observed EVPA
We considered a fully linearly polarized wave incident on the observer’s screen. This is a simplification in the sense that synchrotron radiation is mostly linearly polarized but has non-zero circular polarization. Given that in this article we do not discuss circular polarization, we only introduce here the linearly polarized part of the radiation encoded in the Stokes Q and U parameters. We note that our ray-tracing calculations consider the full synchrotron radiative transfer, including a non-zero Stokes V.
The electric field describing the incident wave on the observer’s screen is
where (eα, eδ) are the unit vectors in the plane of the screen of the observer pointing toward the east and north directions respectively (see Fig. 1 for an illustration). The angle χo, called the observed electric vector position angle (EVPA), lies east of north from the north direction, following the International Astronomical Union convention (IAU 1973). The index o is there to remind that this angle is defined in the observer’s frame, hence the name of observed EVPA. We introduce an emission EVPA defined in the emitter’s frame in the next section.
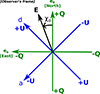 |
Fig. 1. Electric field, observed EVPA, and Stokes Q and U. All quantities are defined in the observer’s frame, as measured by the distant observer. The observed electric field associated with the wave received at the observer’s screen is the black arrow with a position angle east of north corresponding to the observed EVPA. For a fully linearly polarized wave, there is a bijection (up to a sign ambiguity) between providing the electric vector magnitude and direction on screen and the pair of Stokes parameters (Q, U). The electric vector magnitude is given by Eq. (18), while its orientation follows χo = 1/2 atan2(Q, U), see Eq. (17). It is easy to check from the definitions of Eq. (14) that the north-south and east-west directions coincide with positive and negative Stokes Q (and zero Stokes U), respectively, while the diagonals correspond to positive and negative Stokes U (and zero Stokes Q), respectively. |
The linear polarization information is encoded in the observed EVPA, but this angle is not directly observable. In order to only introduce observable quantities, it is useful to introduce the following Stokes parameters
where the various Ei represent the coordinate of the electric vector along the corresponding directions illustrated in Fig. 1. These are observable quantities equal to differences of intensities along specific on sky directions. Equations (13) and (14) immediately led to
where I = E2 is the total intensity, or Stokes I, parameter. Expressing the electric vector on the basis of (ea, ed) associated with the directions (a, d) rotated by 45° with respect to (α, δ) – see Fig. 1 – it is straightforward to obtain
so that the observed EVPA is simply obtained with
and the magnitude of the electric field follows
The EVPA lies in the range
and is defined modulo π, given that it only encodes the oscillation direction of the electric field.
3.2. Emitter’s and observer’s bases, emission EVPA
The natural basis for expressing synchrotron emission in the emitter’s frame is the orthogonal triad made of the following three vectors, all defined in the emitter’s frame: (1) the direction of photon emission K measured by the emitter, (2) the magnetic field vector B⊥ projected orthogonally to K, and (3) the emitter’s frame polarization vector F, which reads
We call these vectors (e1, e2, e3) = (F, −B⊥, K), and we refer to them as the emitter’s polarization basis. They are illustrated by the black vectors in Fig. 2. It is in this emitter’s basis that the polarized synchrotron radiative transfer coefficient are given.
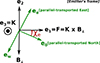 |
Fig. 2. Emitter’s and observer’s polarization bases. All vectors discussed here are expressed in the emitter’s frame. The direction of emission is K, while B⊥ is the ambient magnetic field projected normal to K. The emitter’s frame polarization vector reads F = K × B = K × B⊥. The vectors (e1, e2, e3) = (F, −B⊥, K) form the emitter’s orthogonal basis, naturally adapted for expressing synchrotron radiative transfer. The polarization basis of the observer (eα, eδ), corresponding to unit vectors in the east and north directions, has been parallel transported to the emitter’s frame. The vector ew = −eα is along the west direction such that (ew, eδ, K) forms the observer’s orthogonal triad. The emission EVPA is the angle χe = (eδ, F) evaluated east of north lying between the observer’s and emitter’s bases. It is expressed by Eq. (21). |
However, the observable Stokes parameters are defined in the observer’s polarization basis, (eα, eδ), corresponding to the unit vectors in the east and north directions on the observer’s sky. We thus needed to integrate the polarized radiative transfer equation in this observer-related basis and therefore transformed from the emitter’s basis to the observer’s basis. To do this, we needed to parallel transport the (eα, eδ) basis from the observer to the emitter along the photon’s geodesic. The resulting vectors, parallel transported to the emitter’s frame, are illustrated by the green vectors in Fig. 2. Parallel transport of a polarization vector is simplified in the Kerr metric because of the existence of the Walker-Penrose constant (Walker & Penrose 1970). However, GYOTO simply solves the general parallel transport equation, remaining agnostic about the particular spacetime used. The angle χe between the parallel-transported north direction and the polarization vector F allowed us to rotate between the synchrotron-adapted emitter’s basis and the observer’s basis. We call this angle the emission EVPA, hence the index e in our notation. This wording emphasizes that this angle is expressed in the emitter’s basis and allowed us to make an explicit difference with the observed EVPA, χo, introduced above. There is in general no equality between χe and χo for the simple reason that χe evolves along the geodesic as radiative transfer equations are integrated in the region containing plasma. However, for our setup consisting of a very compact emission region with nearly homogeneous conditions of motion and magnetic field, the emission and observed EVPA are very nearly equal. The distinction that we introduced between χe and χo is thus not important for our results (and we often simply refer to the EVPA without precision), but we consider that it is still important to make the distinction.
The emission EVPA can be easily computed in the emitter’s frame from the projections of the vector B⊥ on the parallel-transported observer’s polarization basis axes:
where ew = −eα is the unit vector in the west direction parallel transported to the emitter. We note that B⊥ is not a unit vector in general, contrary to ew and eδ, but this does not change the result of the atan2 function in Eq. (21). The emission EVPA is a crucial quantity for integrating the polarized radiative transfer. We refer to Aimar et al. (2023b) for details.
3.3. Newtonian QU loops
We considered a hot spot orbiting around a black hole with a toroidal ambient magnetic field observed face-on by an infinitely distant observer, as illustrated in Fig. 3. At this moment in our work, we did not consider any (special or general) relativistic effect (i.e., no lensing, no aberration, no relativistic Doppler, or beaming effects). The radiation is emitted by the hot spot in the vertical direction along the vector K. It is easy to visualize that one complete rotation of the hot spot leads to a complete rotation of the polarization vector F in the plane of the sky, as illustrated in Fig. 3. The bottom-right panel of this figure shows that this leads to a double loop in the QU plane. Hence, at the most basic level, QU loops are a non-relativistic feature and simply a manifestation of an axisymmetric structure of the observed system. For instance, QU loops are obtained in the orbital phase evolution of the flux of light scattered by an exoplanet’s atmosphere illuminated by stellar light (e.g. Chakrabarty & Sengupta 2021).
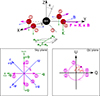 |
Fig. 3. QU loop illustration in a non-relativistic context. Top panel: geometry of the problem. The black hole is represented by the black disk. The hot spot (red disk) orbits in the equatorial XY plane around the black hole (black disk). The Z axis is normal to the equatorial plane. We consider an observer looking face-on at the black hole located toward the negative Z axis. The north direction of the observer’s screen is assumed to lie along the −Y axis. The θ and φ angles of the spherical coordinates are represented. The hot spot rotates in the positive φ direction. The green vector K represents the direction of emission of the photon (we discarded any relativistic effect here), and the blue vector B is the magnetic field, assumed to be toroidal. The polarization vector F = K × B is shown in pink. Successive positions of the hot spot are labeled from 1 to 5. Bottom-left panel: rotation of the polarization vector on the sky plane of the observer with the Stokes directions of Fig. 1 overlaid. Bottom-right panel: associated QU plane and QU loops. The polar coordinates in this plane are |
When considering the same setup as described above but taking a vertical magnetic field instead, our non-relativistic point of view leads to the conclusion that the polarization vector would consistently be zero (K and B being parallel) as the hot spot rotates, leading to no QU loop. As we show in the next section, adding only special relativistic effects (i.e., still no light bending) allows for the recovery of QU loops in all cases, including for a face-on observer with an ambient vertical magnetic field.
4. QU loops in Minkowski spacetime
In this section, we derive an analytical understanding of QU loops in Minkowski spacetime, and in particular, we clarify in what cases the rotating hot spot generates one or two loops in the QU plane. Using Minkowski spacetime is helpful to gaining insight into a simplified framework without accounting for the light bending occurring in a curved spacetime. A non-intuitive conclusion of this section is that all features of QU loops discussed in the literature in the Schwarzschild or Kerr contexts are actually already present in Minkowski. The crucial advantage of the flat geometry is that exact analytical formulas can be derived to explain the QU loops. The next three subsections are devoted to deriving an analytical expression of the evolution of the emission EVPA depending on whether the magnetic field is vertical or toroidal. This analytical model is then compared to numerical simulations, which also constitutes a test of our polarized ray-tracing code.
4.1. Direction of emission and aberration
We consider in this section a hot spot orbiting in Minkowski spacetime. For the time being, we do not specify the magnetic field orientation and only focus on the direction of emission in the emitter’s frame.
The Minkowski four-velocity of the emitter (that is, of the hot spot) defined in Eq. (6), reads
where we replaced the natural basis vectors ∂μ by the orthonormal basis vectors using Eq. (10).
We considered an observer with an inclination of 90 ° ≤i ≤ 180°. We call ι = π − i, which thus lies between 0 and 90°. We emphasize that the observer is located at φ = −π/2, that is, in the YZ plane (see Fig. 3). The four-vector tangent to the photon geodesic at emission reads
where eY = sin φ er + cos φ eφ is the unit vector along the Y axis, illustrated in Fig. 3. The vector k is clearly a null vector of the Minkowski spacetime. In the particular case of an exactly face-on view, we have
such that the spatial component of the four-vector points toward the negative Z axis, that is, toward the face-on observer.
Our final goal is to compute the emission EVPA, so we did not need this null four-vector but rather its space-like projection orthogonal to the four-velocity of the emitter, that is, in the rest-frame of the emitter. This reads
This simple relation is very crucial and contains virtually all the results presented below. Even for a face-on observer, the actual direction of photon emission does not lie along the vertical direction, contrary to what is illustrated in the non-relativistic Fig. 3. It acquires a toroidal component by means of the projection written above, stemming from the toroidal component of u. This is simply the standard special relativistic aberration effect.
We can express
where it is easy to check that ω coincides with the norm of K. That is, ω coincides with the pulsation of the photon as measured by the emitter.
4.2. Vertical magnetic field
In this section, we restrict the discussion to an ambient vertical magnetic field. We wanted to derive an analytic expression of the evolution of the emission EVPA with the orbital phase φ. For simplicity, we considered a point-like hot spot in the equatorial plane, so θ = π/2 in all of this section. The unit vector along the magnetic field direction reads
Our goal was to express the emission EVPA from Eq. (21). We started by writing
where we note that we are working in the flat Minkowski spacetime, so the observer polarization basis is simply conserved along the geodesic. Next, we needed only the expression of the projection of the magnetic field orthogonal to the direction of emission
where 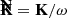 is the unit vector along K.
is the unit vector along K.
At this point, we had expressed all the quantities of interest and could write the emission EVPA expression. The details of the computation are not particularly illuminating, so we provide them in Appendix A. The final expression for the emission EVPA reads
We first checked what happens for an exactly face-on observer, ι = 0. In this case, the expression simplifies considerably to χe(φ) = π/2 − φ. It is clear from this expression that as the hot spot rotates with φ varying on a 2π interval, so does the emission EVPA. The emission EVPA thus covers two times its domain of definition and so does the observed EVPA because the two quantities are nearly equal for our setup (see above). So this leads to a double QU loop being seen by the distant observer.
This is the first non-intuitive conclusion of our analysis. When already in Minkowski, a face-on observer considering a hot spot immersed in a vertical magnetic field will detect a double QU loop signal. We note that the crucial difference between the analysis developed in this section and the non-relativistic analysis of Sect. 3.3 is the aberration affecting the apparent direction of light propagation. The vector K is not purely vertical, as is represented in Fig. 3; it acquires a component in the equatorial plane when projecting orthogonally to the relativistic four-velocity u of the emitter. Figure 4 illustrates this.
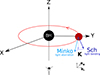 |
Fig. 4. Effect of the spacetime geometry on the emission direction K. A hot spot (red disk) is orbiting around a black hole (black disk). The observer is located face-on toward the negative Z axis. In a Newtonian spacetime, the direction of emission (i.e., the unit vector K along the projection of the null four-vector k normal to the emitter’s four-velocity) is exactly vertical toward the negative Z axis (dashed pale blue arrow). This is the case illustrated in the non-relativistic Fig. 3. Special relativistic light aberration leads to an additional azimuthal component (solid light blue arrow). General relativistic light bending leads to an additional radial component (solid dark blue arrow). We note that the direction of emission in Schwarzschild spacetime is along the sum of the two solid arrows, given that the special relativistic aberration is of course also included in the Schwarzschild geometry. The various vectors are approximately to scale for a Keplerian hot spot at a few gravitational radii. The aberration and light bending effects are not small corrections to an approximately vertical direction; they lead to strong distortions of the apparent emission direction (on the of order tens of percents). |
Next, we discuss a few important properties of Minkowski QU loops in a vertical magnetic field before discussing simulation results.
4.2.1. Emission EVPA symmetry
Our emission EVPA expression has the following property:
where the second equality comes from the fact that the EVPA is defined modulo π. This relation means that the first half of the orbit φ ∈ [0, π] and the second half φ ∈ [π, 2π] have the same EVPA evolution, up to a sign difference. Equivalently, the EVPA orbital evolution is symmetric with respect to φ = π, up to a sign.
4.2.2. QU loop mirror symmetry
EVPA is not the only quantity that shows a symmetry in the orbital evolution of the hot spot. The same goes for the photon’s emitted energy ω. It is indeed obvious from Eq. (26) that
The same also goes for the angle
between the magnetic field and the photon’s direction of emission. Indeed, Appendix A shows that for a vertical magnetic field,
where the φ dependence is made explicit. We thus have
The emitted flux depends only on the photon’s emitted energy and on the direction of emission relative to the magnetic field direction. Indeed, for our circular orbit, all other physical quantities (density, magnetic field magnitude, temperature) are constant. As a consequence, Eqs. (32) and (35) mean that the emitted linearly polarized flux satisfies
Together with Eq. (31) and keeping in mind that for our setup, the emission and observed EVPA are nearly equal, this relation leads to the conclusion that the QU track in the Minkowski spacetime is symmetric with respect to the horizontal axis. Indeed, Fig. 3 shows that the linearly polarized flux and the double of the observed EVPA (compare to Eq. (17)) are the polar coordinates of the QU track. For the rest of this article, we refer to this symmetry with respect to the horizontal Q axis as the QU loop mirror symmetry.
4.2.3. Number of loops
The emission EVPA orbital evolution χe(φ) is dictated by Eq. (30) and is symmetric with respect to φ = π up to a sign. Thus, if the full allowed range of EVPA, [ − π/2, π/2], is covered in the first half of the orbit, then it will be covered again in the second half, leading to two QU loops. This can happen provided that the EVPA visits all possible values in [ − π/2, π/2] during the first orbit, so if its tangent reaches infinity. There will thus be two QU loops provided that
varies between −∞ and +∞ when φ varies between 0 and π. This quantity will reach infinity provided that the denominator
considered as an equation for the variable φ with a given inclination ι, has a root for some value of φ. We note that this is not as trivial an equation as it might seem because ω depends on ι (see Eq. (26)). By examining this function numerically, it is easy to show that it has a root only when
which is the condition for obtaining two loops in a vertical magnetic field in Minkowski spacetime. This is illustrated in the left panel of Fig. 5. The limiting angle ι0 depends on the orbital radius r0, the dependence being illustrated in Fig. 6. We note that the existence of such a limit angle behavior for the existence of one or two loops has already been discussed in the Schwarzschild context by Gelles et al. (2021; see their Fig. 9), but it was without the analytical treatment building on the simplicity of the Minkowski geometry that we provide in this work.
 |
Fig. 5. Denominator of the expression on the rhs of Eqs. (37) (left panel, vertical field) and (44) (right panel, toroidal field). These expressions are strongly dependent on the orbital radius, which is set to r0 = 8M here. The various colors encode various values of ι in [0, 30 ° ] (left panel) or [0, 90 ° ] (right panel). In the vertical case, the denominator has a root only for ι < ι0(r0), and this critical angle verifies ι0 ≈ 20° for r0 = 8M. The condition ι < ι0(r0) leads to two QU loops, while higher inclinations lead to a single QU loop. In the toroidal case, all values of ι lead to the existence of two roots, so there will always be two loops, whatever the inclination. |
 |
Fig. 6. Evolution of the limit inclination angle ι0 (see Eq. (39)). This angle separates double (ι < ι0) and single (ι > ι0) QU loops in Minkowski spacetime for a vertical magnetic field with the hot spot orbital radius r0. This angle converges toward 0 as r0 increases. The profile of i0 with r0 approximately follows an inverse square root ( |
This is the second conclusion of this section: QU loops of the Minkowski spacetime in a vertical magnetic field share the exact same property as already discussed in the Kerr context by several authors (GRAVITY Collaboration 2020c; Gelles et al. 2021; Vos et al. 2022), that is, the existence of either one or two loops depends on the inclination and on the orbital radius. To our knowledge, the relation between this behavior and the special relativistic aberration effect has not been discussed in the literature to date.
4.2.4. Simulated QU loops
Figure 7 illustrates the various results discussed above by showing the results of a polarized ray-tracing calculation in Minkowski spacetime for a hot spot seen under an inclination smaller and bigger than the critical angle ι0 ≈ 20° for r0 = 8M. As predicted, we obtained two QU loops in one case and one QU loop in the other. The EVPA evolution very precisely follows the analytical prediction of Eq. (30) at low inclination, which validates our calculation. At the same time, this comparison represents a non-trivial consistency test of our polarized radiative transfer. We note that this is a clear demonstration of the near equality between the emitted and observed EVPA because the colored dots and the red profile of the EVPA panel in Fig. 7 respectively represent an observed and emitted EVPA. We also find it interesting to note that although the analytical and numerical EVPA profiles remain similar, they are clearly more different at a higher inclination, ι = 30°. This is not due to a limitation of the precision of the numerical integration. Instead, the differences are related to the Roemer effect2 due to the finite velocity of light that is not taken into account in the analytical profile. As a consequence, the numerical data lead the analytical profile in the first of the half orbit (where the hot spot is further away from the observer), while the data lag behind the analytical profile in the second half of the orbit (where the hot spot is closer to the observer). As expected, we observed that the exact same behavior occurs for a toroidal magnetic field. Moreover, the QU track is mirror-symmetric, as predicted above.
 |
Fig. 7. Minkowski QU loops in the vertical magnetic field. The top six panels were computed for ι = 10 ° < ι0, where ι0 is defined in Eq. (39) and defines the highest angle for which there should be two QU loops. The bottom six panels were computed for ι = 10 ° > ι0. The six panels represent the following quantities. Top-left: summed images of the hot spot in normalized intensity. We note that the color coding has been inverted to improve readability (i.e., a darker color means more intense emission). Top-middle: astrometric track on sky. In this panel and the next ones, the color codes (from violet to red) are for time, clockwise motion on sky. Top-right: total flux (colored dots), linearly polarized flux ( |
We find it is interesting to note that the evolution of the observed flux might seem counter-intuitive. Indeed, the source approaches the observer on the left part of the trajectory (east side). But the flux evolution (upper-right panel of Fig. 7) showed that contrary to what relativistic beaming intuition would suggest, the flux is actually at minimum on the approaching side. This is a consequence of the sin θB dependence of the synchrotron radiative transfer coefficients (see Eq. (12)). This angle is close to 0 [π] on the left side of the sky plane (which corresponds to an orbital phase of φ = π), as demonstrated by the analytical profiles in the left panel of Fig. 8. These profiles represent the orbital phase evolution of 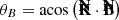 , the expression of which is known analytically from the formulas provided in Appendix A. We note that around ι = ι0 ≈ 20° (for r0 = 8M), the influence of the θB dependence of the emission not only mitigates the relativistic beaming but inverses the tendency by leading to a light curve that peaks on the receding side. We checked that if one averages over sin θB (that is, if one considers an isotropized emission), the usual flux profile, peaking on the approaching side, is recovered. The Doppler effect cannot be responsible for this strong flux depletion at the orbital phase φ = π because the emitted frequency is, at minimum, at the orbital phase φ = π (see the top-left panel of Fig. 14), so the emitted Doppler-shifted flux is actually maximized there (see Eq. (12)). Figure 8 shows that this behavior is specific to the low inclination. Higher inclination progressively leads to the more intuitive situation dominated by relativistic beaming. It is very natural that a vertical magnetic field seen at low inclination leads to θB angles around 0[π], where the sin θB dependence of the radiative transfer coefficient has a strong impact, and that at high inclination, θB varies around π/2, where this dependence is weaker. This is the third conclusion of this section: In the Minkowski spacetime and for a vertical magnetic field, the flux variation is driven by the angular dependence of the synchrotron radiative transfer coefficients at low inclination and by relativistic beaming at high inclination.
, the expression of which is known analytically from the formulas provided in Appendix A. We note that around ι = ι0 ≈ 20° (for r0 = 8M), the influence of the θB dependence of the emission not only mitigates the relativistic beaming but inverses the tendency by leading to a light curve that peaks on the receding side. We checked that if one averages over sin θB (that is, if one considers an isotropized emission), the usual flux profile, peaking on the approaching side, is recovered. The Doppler effect cannot be responsible for this strong flux depletion at the orbital phase φ = π because the emitted frequency is, at minimum, at the orbital phase φ = π (see the top-left panel of Fig. 14), so the emitted Doppler-shifted flux is actually maximized there (see Eq. (12)). Figure 8 shows that this behavior is specific to the low inclination. Higher inclination progressively leads to the more intuitive situation dominated by relativistic beaming. It is very natural that a vertical magnetic field seen at low inclination leads to θB angles around 0[π], where the sin θB dependence of the radiative transfer coefficient has a strong impact, and that at high inclination, θB varies around π/2, where this dependence is weaker. This is the third conclusion of this section: In the Minkowski spacetime and for a vertical magnetic field, the flux variation is driven by the angular dependence of the synchrotron radiative transfer coefficients at low inclination and by relativistic beaming at high inclination.
 |
Fig. 8. Minkowski evolution of the angle θB (angle between magnetic field and emission direction in the emitter’s frame) for r0 = 8M. The various colors encode various inclinations ι between 0° (face-on, dark blue) and 90° (edge-on, light blue), with a 10° step. The synchrotron emission is suppressed at θB = 0[π], so we concluded that the orbital phase φ = π (corresponding to the left part of the image, i.e., toward the east direction) is strongly suppressed around ι = ι0 ≈ 20°. We emphasize that this angle ι0 depends on the orbital radius, and here r0 = 8M. |
The linear polarization of our hot spot is always very high, of order 75%, which is twice as high as the typically observed near infrared values (e.g. GRAVITY Collaboration 2018). This is due to the very simple setup that we consider, with a small isolated emitting body. A more realistic scenario (see e.g. Appendix B of GRAVITY Collaboration 2023), with a more extended or distorted structure, and the addition of the quiescent accretion disk component (e.g. Yfantis et al. 2024), would recover a more realistic level of linear polarization.
4.3. Toroidal magnetic field
The exact same computation that we presented in the last section for a vertical magnetic field can be performed for a toroidal magnetic field. Starting from Eq. (9) and specializing to the Minkowski spacetime in the equatorial plane, we obtained
which is a unit space-like vector normal to u.
We refer the reader to Appendix A for the details of the computation, and we simply give the final result here:
where 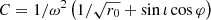 .
.
Similar properties as in the vertical case can be derived in the exact same way as presented in the previous section. In particular, the relation
still holds, and so does the QU loop mirror symmetry, which is due to the symmetry of the expression of the emission angle for a toroidal magnetic field derived in Appendix A,
leading to the same property as in Eq. (35).
The number of QU loops can be studied following the same reasoning as in the previous section. This led us to study the range of variation of the simple expression
and in particular the roots of the denominator
as φ varies in [0, 2π]. Here, there are obviously always two roots at φ = π/2, 3π/2 whatever the inclination (see the illustration in the right panel of Fig. 5), leading to the existence of two QU loops for all inclinations.
Figure 9 shows simulations of Minkowski QU loops in a toroidal magnetic field, and it confirms the existence of a double loop for the same two values of inclinations that lead to either one or two loops in the vertical field case, in perfect agreement with the results above. The numerical profile of the EVPA exactly matches the analytics at low inclination, and it is slightly offset with respect to the analytics at higher inclination because of the Roemer effect, as discussed for the vertical case. We note that contrary to the vertical case, the flux evolution here appears to follow the standard relativistic beaming intuition, with the flux peaking at the approaching side and the flux ratio increasing with the inclination. This is because the θB dependence is very weak at low inclination ι ≲ 45°, as demonstrated by the right panel of Fig. 8. In contrast, at high inclination, the θB dependence becomes very strong and would counteract the beaming effect. This dependence is very natural, as at low inclination, a toroidal magnetic field leads to θB angles much closer to π/2 than to 0[π], while at high inclination, the contrary is true. Compared to the vertical magnetic field case, the dependence is reversed in a toroidal magnetic field.
 |
Fig. 9. Same as Fig. 7 but for a toroidal magnetic field. Two QU loops are present for both inclinations, contrary to the vertical case of Fig. 7, in agreement with our analytical derivation. |
4.4. Impact of the background flow
In this article, we always discard the background accretion flow responsible for the quiescent emission of Sgr A*. As long as the flow is Faraday thin (which is the case in the infrared), adding this contribution would simply lead to translating the QU loops by a quantity (Qbg, Ubg) corresponding to the linear polarization of the background flow. This translation would not alter any of our findings.
5. QU loops in Schwarzschild spacetime
This section presents QU loop computations considering the same setups as illustrated in the previous section but taking into account the spacetime curvature associated with the Schwarzschild geometry. We stress that we considered only the primary image and did not include the secondary or higher-order images formed by the extremely lensed photons executing at least half an orbit around the black hole (e.g., Johnson et al. 2020). These higher-order images do not change the main qualitative features of the QU loops but do have an impact at a finer level, at the low and moderate inclinations that we consider here (see for instance Gelles et al. 2021; Wielgus et al. 2022b). This simplification allowed us to reduce the required imaging resolution.
Figures 10 and 11 show the Schwarzschild QU loops in the case of a vertical and a toroidal magnetic field, respectively. Interestingly, for most cases, there is no pronounced difference between the Schwarzschild QU loops and their Minkowski counterparts computed in the previous section. The main features of the loops are already present in flat spacetime, and while the light bending changes detailed values of the observables, it has little impact on the general picture.
 |
Fig. 10. Same as Fig. 7 but in Schwarzschild spacetime for a vertical magnetic field. It might seem surprising that there is a small kick on the astrometric path toward the southeast. This is due to the dependence of the radiative transfer coefficients on sin θB, where θB is the angle between the direction of the magnetic field and the direction of emission (see Marszewski et al. 2021). The upper-left panel clearly shows a flux depletion toward the southeast due to this effect. At this orbital phase, the direction of emission in the emitter’s frame, K, becomes vertical and parallel to the magnetic field. Due to the combination of special-relativistic aberration and general-relativistic lensing effects, the direction of K varies with the orbital phase. The QU loops of this figure should be compared to that of Fig. 7, as the similarity is striking. |
 |
Fig. 11. Same as Fig. 7 but in Schwarzschild spacetime for a toroidal magnetic field. The QU loops of this figure should be compared to that of Fig. 9, as the similarity is striking. |
Regarding the flux variation, we note that the same behavior was observed for the Schwarzschild-vertical cases as for their Minkowski counterparts. The flux goes through its minimum at the hot spot approaching side due to the θB dependence of the radiative transfer coefficients. We also note that the Schwarzschild-vertical case seen at ι = 10° shows a smaller flux variation than its Minkowski counterpart (factor of approximately two versus a factor of approximately four peak-to-peak ratio). This is because the value of θB is never as close to π in the Schwarzschild case as in the Minkowski case. As a consequence, the flux minimum is higher in the Schwarzschild case. In contrast, for ι = 30°, the value of θB in the Schwarzschild case goes nearly through π, leading to a flux minimum approaching zero, contrary to the Minkowski case that keeps θB further from π. This explains the extreme flux ratio (factor of 50) for the Schwarzschild-vertical case at ι = 30°. The Schwarzschild-toroidal case is also similar to the corresponding Minkowski setup in the sense that the flux variation is dominated by relativistic beaming with the usual flux maximum at the approaching side of the orbit. The flux ratios are similar for Minkowski and for Schwarzschild, showing that the special-relativistic beaming effect is the dominant flux-driving mechanism.
6. Comparing Schwarzschild and Minkowski QU loops
Figure 12 shows a comparison of the QU loops computed in the Schwarzschild and Minkowski spacetimes that were presented in Figs. 7–11 as well as two higher inclination cases, ι = 45 ° ,80°. This figure again shows that flat-space and curved-space QU loops are very similar for most cases. However, there is one important property that we demonstrated in the Minkowski case (see Sect. 4.2.2), the QU loop mirror symmetry, that is lost in Schwarzschild case as inclination increases. This is a direct consequence of light bending. We note that the QU loop fitted to the high-sensitivity ALMA observations appears strongly asymmetric (Wielgus et al. 2022b).
 |
Fig. 12. Comparison of the QU loops computed in Schwarzschild (solid blue) and Minkowski (dashed green) spacetimes. The magnetic field is vertical for the top row and toroidal for the bottom row. The inclination increases from left to right and is specified in the top-right corner of each panel. We note that the various panels have different scalings. |
For purposes of analysis, we considered a hot spot in Schwarzschild spacetime and the wave vector connecting this hot spot to the distant observer. The direction of this wave vector differs from the Minkowski case due to the existence of light bending. We thus wrote
where kS is the Schwarzschild wave vector, kM is the Minkowski wave vector, and δklensing is the shift due to light bending. We note that this equation is not rigorous in the sense that we compare vectors that belong to tangent spaces to different manifolds, but it is still useful to get a sense of the effect of light bending. The situation is illustrated in Fig. 13 for face-on and edge-on inclinations. The lensing shift vector is a radial vector constant with the orbital phase at zero inclination. This means that light bending does not break the QU loop mirror symmetry at zero inclination. Indeed, there are only three quantities that impact the Stokes parameters, namely: the photon’s energy in the emitter’s frame, ω = −k ⋅ u; the cosine of the direction of emission in the emitter’s frame, cos θB = k ⋅ B/ω3; and the EVPA.
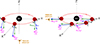 |
Fig. 13. Lensing and asymmetry of Schwarzschild QU loops. The left panel depicts the hot spot seen at zero inclination, and the right one is edge-on. The green arrows show the wave vectors k in Minkowski spacetime that connect the hot spot to the observer. The blue arrows show the corresponding wave vectors for the Schwarzschild case. They differ from Minkowski due to light bending, which adds a shift to the wave vector, depicted in pink. This shift vector is constant with the orbital phase and along the positive radial direction at zero inclination. However, it varies a lot with the orbital phase for the edge-on view, from zero at the closest point to the observer to purely vertical at the furthest point (i.e., “on the other side of the black hole”). The difference in dependence of the shift vector with the orbital phase as a result of inclination has a considerable impact on the Schwarzschild QU loop asymmetry (see text for details). |
These quantities are independent of orbital phase at zero inclination because of the constancy of the lensing shift vector with the orbital phase, illustrated in the left panel of Fig. 13. However, at edge-on inclination, the situation changes completely, and the lensing shift vector becomes very dependent on the orbital phase (see the right panel of Fig. 13). This leads to a strong dependence of the orbital phase on the three quantities discussed above and to the breaking of the QU loop mirror symmetry. This is in perfect agreement with the results of Fig. 12, which shows that the loop mirror symmetry still holds at low inclination and becomes less conserved with increasing inclination.
One point remains to be discussed, and that is why the QU loop mirror symmetry breaks more quickly with increasing inclination for a vertical magnetic field (in this case, the symmetry is already lost at ι ≈ 30°) than for a toroidal field (in this case, the symmetry approximately holds until ι ≈ 80°). This is related to the orbital phase evolution of the three quantities listed above. Figure 14 shows the orbital phase evolution of these quantities at ι = 30° in Minkowski and Schwarzschild and for a vertical or toroidal field. This figure demonstrates that the EVPA and the emission direction are much more asymmetric for a vertical field than for a toroidal field for this moderate inclination. In the toroidal case, the evolution of these quantities, although shifted in phase compared to the Minkowski case, remains rather similar to the flat-spacetime setup. We checked that computing the QU track of a Schwarzschild-vertical setup at ι = 30° leads to a mirror symmetric QU loop, imposing by hand some ad hoc symmetric evolution of the EVPA and of the emission direction.
 |
Fig. 14. Evolution of orbit-varying quantities for Stokes parameters. The inclination is ι = 30°. The various panels show the evolution with the orbital phase φ of the various quantities that impact the Stokes parameters: the EVPA (red), the photon’s emitted energy ω = −k ⋅ u (red, in units of the observed energy), and the sine of the emission angle sin θB (green). The left column was computed in Minkowski spacetime and the right column in Schwarzschild. The top row was computed for a vertical magnetic field and the bottom row for a toroidal field. |
7. Conclusion
This article has two main goals: (i) highlighting the role of special-relativistic aberration in generating the observed QU loops and (ii) identifying an observable feature directly produced by spacetime curvature. Regarding the first goal, we highlighted the crucial importance of special-relativistic effects in generating the observable QU loops associated with the polarized synchrotron flares of Sgr A*. We have shown that most features discussed in the literature so far regarding QU loops (existence of loops, number of loops, dependence with inclination and orbital radius) are already present in the Minkowski spacetime and are thus independent of light bending. The simplicity of Minkowski spacetime is a great asset, as it allows for the develop of a complete understanding of these features. Concerning the second goal, we indicated a specific property that is due to light bending: Minkowski QU loops are always mirror symmetric in the sense that the two half orbits lead to the same QU track. The axis of symmetry corresponds to the horizontal Q axis in our configuration, with the angular momentum of the hot spot projected onto the observer’s screen aligning with the vertical direction. In general, this mirror symmetry is associated with any line of symmetry in the QU plane, be it horizontal or not, following the uncertain orientation of the observed system.
In contrast, and due to light bending, Schwarzschild QU loops are generally not symmetric. Schwarzschild QU loops in a toroidal magnetic field remain approximately (meaning to a better accuracy than current observations could tell) symmetric up to a very high inclination (within ≈10° of edge-on view). Nonetheless, Schwarzschild QU loops in a vertical magnetic field, which is the favored configuration for the likely MAD Sgr A* flow, quickly lose their mirror symmetry with increasing inclination and are already clearly asymmetric at a moderate inclination of about 30°. Thus, the asymmetry of the QU loops might constitute a compelling probe that enables the quantification of the spacetime curvature in the close environment of Sgr A*. Future detailed studies of the QU loops could also constitute a path for confirming the existence of secondary images around black holes, which is another way to characterize curved spacetimes.
We find it is important to keep in mind not only the simplicity of our modeling but also that astrophysical complexity might obscure the spacetime curvature effect on the asymmetry of the observed loop. A non-axisymmetric profile of the physical quantities (density, magnetic field, temperature) along the hot spot orbit might break the QU loop mirror symmetry even in the absence of curvature. Internal physics of the hot spot (e.g., cooling) may have a similar effect by introducing time dependence to the emission coefficient. Non-circular motion, such as an ejection along a jet sheath, might also impact the conclusion. These possible limitations should be addressed in future works.
The famous Birkhoff theorem of general relativity published by Birkhoff in 1923 was first published two years before by the Norwegian physicist Jebsen (see Voje Johansen & Ravndal 2006, for an historical account).
The Roemer effect is related to the difference in light travel time between various ray-traced geodesics. Parts of the emission region located further from the observer lead to an increased light travel time as compared to those located closer. For a face-on view, this effect has little impact given that all points along the circular orbit of the hotspot are located at the same distance from the observer. This is no longer so at a higher inclination.
It is clear from Eq. (25) that K ⋅ B = k ⋅ B.
Acknowledgments
We thank Frank Eisenhauer, Jack Livingston, and Diogo Ribeiro for helpful comments to the draft. This research is supported by the European Research Council advanced grant “M2FINDERS – Mapping Magnetic Fields with INterferometry Down to Event hoRizon Scales” (Grant No. 101018682).
References
- Aimar, N., Dmytriiev, A., Vincent, F. H., et al. 2023a, A&A, 672, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aimar, N., Paumard, T., Vincent, F. H., Gourgoulhon, E., & Perrin, G. 2023b, Class. Quant. Grav., submitted [arXiv:2311.18802] [Google Scholar]
- Baganoff, F. K., Bautz, M. W., Brandt, W. N., et al. 2001, Nature, 413, 45 [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [Google Scholar]
- Birkhoff, G. D., & Langer, R. E. 1923, Relativity and Modern Physics (Cambridge: Harvard University Press) [Google Scholar]
- Broderick, A. E., & Loeb, A. 2006, MNRAS, 367, 905 [Google Scholar]
- Chakrabarty, A., & Sengupta, S. 2021, ApJ, 917, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Witzel, G., Gautam, A. K., et al. 2019, ApJ, 882, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Eckart, A., Schödel, R., Meyer, L., et al. 2006, A&A, 455, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El Mellah, I., Cerutti, B., & Crinquand, B. 2023, A&A, 677, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022a, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022b, ApJ, 930, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022c, ApJ, 930, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Gelles, Z., Himwich, E., Johnson, M. D., & Palumbo, D. C. M. 2021, Phys. Rev. D, 104, 044060 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [Google Scholar]
- Gillessen, S., Eisenhauer, F., Quataert, E., et al. 2006, ApJ, 640, L163 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2020a, A&A, 638, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2020b, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Jiménez-Rosales, A., et al.) 2020c, A&A, 643, A56 [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2021, A&A, 647, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2023, A&A, 677, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamaus, N., Paumard, T., Müller, T., et al. 2009, ApJ, 692, 902 [NASA ADS] [CrossRef] [Google Scholar]
- IAU 1973, Trans. Int. Astron. Union, 15, 165 [CrossRef] [Google Scholar]
- Jebsen, J. T. 1921, Arkiv for Matematik, Astronomi och Fysik, 15, 18 [NASA ADS] [Google Scholar]
- Johnson, M. D., Fish, V. L., Doeleman, S. S., et al. 2015, Science, 350, 1242 [Google Scholar]
- Johnson, M. D., Lupsasca, A., Strominger, A., et al. 2020, Sci. Adv., 6, eaaz1310 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2006, J. Phys. Conf. Ser., 54, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Marszewski, A., Prather, B. S., Joshi, A. V., Pandya, A., & Gammie, C. F. 2021, ApJ, 921, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, L., Eckart, A., Schödel, R., et al. 2006, A&A, 460, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michail, J. M., Yusef-Zadeh, F., Wardle, M., & Kunneriath, D. 2023, MNRAS, 520, 2644 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M. R. 2023, arXiv e-prints [arXiv:2302.02431] [Google Scholar]
- Najafi-Ziyazi, M., Davelaar, J., Mizuno, Y., & Porth, O. 2023, MNRAS, submitted [arXiv:2308.16740] [Google Scholar]
- Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2003, PASJ, 55, L69 [NASA ADS] [Google Scholar]
- Narayan, R., Palumbo, D. C. M., Johnson, M. D., et al. 2021, ApJ, 912, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 702, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Ripperda, B., Liska, M., Chatterjee, K., et al. 2022, ApJ, 924, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Trippe, S., Paumard, T., Ott, T., et al. 2007, MNRAS, 375, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Paumard, T., Gourgoulhon, E., & Perrin, G. 2011, Class. Quant. Grav., 28, 225011 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Paumard, T., Perrin, G., et al. 2014, MNRAS, 441, 3477 [NASA ADS] [CrossRef] [Google Scholar]
- Voje Johansen, N., & Ravndal, F. 2006, Gen. Rel. Grav., 38, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, J., Mościbrodzka, M. A., & Wielgus, M. 2022, A&A, 668, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, M., & Penrose, R. 1970, Commun. Math. Phys., 18, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Wielgus, M., Marchili, N., Martí-Vidal, I., et al. 2022a, ApJ, 930, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Wielgus, M., Moscibrodzka, M., Vos, J., et al. 2022b, A&A, 665, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielgus, M., Issaoun, S., Marti-Vidal, I., et al. 2023, A&A, 682, A97 [Google Scholar]
- Yfantis, A. I., Mościbrodzka, M. A., Wielgus, M., Vos, J. T., & Jimenez-Rosales, A. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348230 [Google Scholar]
- Yusef-Zadeh, F., Wardle, M., Cotton, W. D., Heinke, C. O., & Roberts, D. A. 2007, ApJ, 668, L47 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Analytical expressions in Minkowski spacetime
We reiterate the expressions of the emitter’s four-velocity (Eq. 22)
that of the wave vector (Eq. 23)
that of the photon’s emitted energy (Eq. 26)
that of the projection of k orthogonal to u,
and that of the observer’s basis vectors (Eq. 28)
A.1. Vertical magnetic field
Considering a unit vertical magnetic field
we have
and the projection of  normal to the unit vector
normal to the unit vector 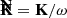 along K reads
along K reads
The projections of this vector along the observer’s basis vectors then read
from which the EVPA expression of Eq. 30 follows.
We also have
where 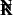 is the unit vector along K. We thus find the result of Eq. 34.
is the unit vector along K. We thus find the result of Eq. 34.
A.2. Toroidal magnetic field
Considering now a toroidal magnetic field
we have
where we introduce
so we get
The projections onto the observer’s basis vectors then read
from which the EVPA expression of Eq. 41 follows. We also have
which is the result of Eq. 43.
All Tables
All Figures
 |
Fig. 1. Electric field, observed EVPA, and Stokes Q and U. All quantities are defined in the observer’s frame, as measured by the distant observer. The observed electric field associated with the wave received at the observer’s screen is the black arrow with a position angle east of north corresponding to the observed EVPA. For a fully linearly polarized wave, there is a bijection (up to a sign ambiguity) between providing the electric vector magnitude and direction on screen and the pair of Stokes parameters (Q, U). The electric vector magnitude is given by Eq. (18), while its orientation follows χo = 1/2 atan2(Q, U), see Eq. (17). It is easy to check from the definitions of Eq. (14) that the north-south and east-west directions coincide with positive and negative Stokes Q (and zero Stokes U), respectively, while the diagonals correspond to positive and negative Stokes U (and zero Stokes Q), respectively. |
| In the text | |
 |
Fig. 2. Emitter’s and observer’s polarization bases. All vectors discussed here are expressed in the emitter’s frame. The direction of emission is K, while B⊥ is the ambient magnetic field projected normal to K. The emitter’s frame polarization vector reads F = K × B = K × B⊥. The vectors (e1, e2, e3) = (F, −B⊥, K) form the emitter’s orthogonal basis, naturally adapted for expressing synchrotron radiative transfer. The polarization basis of the observer (eα, eδ), corresponding to unit vectors in the east and north directions, has been parallel transported to the emitter’s frame. The vector ew = −eα is along the west direction such that (ew, eδ, K) forms the observer’s orthogonal triad. The emission EVPA is the angle χe = (eδ, F) evaluated east of north lying between the observer’s and emitter’s bases. It is expressed by Eq. (21). |
| In the text | |
 |
Fig. 3. QU loop illustration in a non-relativistic context. Top panel: geometry of the problem. The black hole is represented by the black disk. The hot spot (red disk) orbits in the equatorial XY plane around the black hole (black disk). The Z axis is normal to the equatorial plane. We consider an observer looking face-on at the black hole located toward the negative Z axis. The north direction of the observer’s screen is assumed to lie along the −Y axis. The θ and φ angles of the spherical coordinates are represented. The hot spot rotates in the positive φ direction. The green vector K represents the direction of emission of the photon (we discarded any relativistic effect here), and the blue vector B is the magnetic field, assumed to be toroidal. The polarization vector F = K × B is shown in pink. Successive positions of the hot spot are labeled from 1 to 5. Bottom-left panel: rotation of the polarization vector on the sky plane of the observer with the Stokes directions of Fig. 1 overlaid. Bottom-right panel: associated QU plane and QU loops. The polar coordinates in this plane are |
| In the text | |
 |
Fig. 4. Effect of the spacetime geometry on the emission direction K. A hot spot (red disk) is orbiting around a black hole (black disk). The observer is located face-on toward the negative Z axis. In a Newtonian spacetime, the direction of emission (i.e., the unit vector K along the projection of the null four-vector k normal to the emitter’s four-velocity) is exactly vertical toward the negative Z axis (dashed pale blue arrow). This is the case illustrated in the non-relativistic Fig. 3. Special relativistic light aberration leads to an additional azimuthal component (solid light blue arrow). General relativistic light bending leads to an additional radial component (solid dark blue arrow). We note that the direction of emission in Schwarzschild spacetime is along the sum of the two solid arrows, given that the special relativistic aberration is of course also included in the Schwarzschild geometry. The various vectors are approximately to scale for a Keplerian hot spot at a few gravitational radii. The aberration and light bending effects are not small corrections to an approximately vertical direction; they lead to strong distortions of the apparent emission direction (on the of order tens of percents). |
| In the text | |
 |
Fig. 5. Denominator of the expression on the rhs of Eqs. (37) (left panel, vertical field) and (44) (right panel, toroidal field). These expressions are strongly dependent on the orbital radius, which is set to r0 = 8M here. The various colors encode various values of ι in [0, 30 ° ] (left panel) or [0, 90 ° ] (right panel). In the vertical case, the denominator has a root only for ι < ι0(r0), and this critical angle verifies ι0 ≈ 20° for r0 = 8M. The condition ι < ι0(r0) leads to two QU loops, while higher inclinations lead to a single QU loop. In the toroidal case, all values of ι lead to the existence of two roots, so there will always be two loops, whatever the inclination. |
| In the text | |
 |
Fig. 6. Evolution of the limit inclination angle ι0 (see Eq. (39)). This angle separates double (ι < ι0) and single (ι > ι0) QU loops in Minkowski spacetime for a vertical magnetic field with the hot spot orbital radius r0. This angle converges toward 0 as r0 increases. The profile of i0 with r0 approximately follows an inverse square root ( |
| In the text | |
 |
Fig. 7. Minkowski QU loops in the vertical magnetic field. The top six panels were computed for ι = 10 ° < ι0, where ι0 is defined in Eq. (39) and defines the highest angle for which there should be two QU loops. The bottom six panels were computed for ι = 10 ° > ι0. The six panels represent the following quantities. Top-left: summed images of the hot spot in normalized intensity. We note that the color coding has been inverted to improve readability (i.e., a darker color means more intense emission). Top-middle: astrometric track on sky. In this panel and the next ones, the color codes (from violet to red) are for time, clockwise motion on sky. Top-right: total flux (colored dots), linearly polarized flux ( |
| In the text | |
 |
Fig. 8. Minkowski evolution of the angle θB (angle between magnetic field and emission direction in the emitter’s frame) for r0 = 8M. The various colors encode various inclinations ι between 0° (face-on, dark blue) and 90° (edge-on, light blue), with a 10° step. The synchrotron emission is suppressed at θB = 0[π], so we concluded that the orbital phase φ = π (corresponding to the left part of the image, i.e., toward the east direction) is strongly suppressed around ι = ι0 ≈ 20°. We emphasize that this angle ι0 depends on the orbital radius, and here r0 = 8M. |
| In the text | |
 |
Fig. 9. Same as Fig. 7 but for a toroidal magnetic field. Two QU loops are present for both inclinations, contrary to the vertical case of Fig. 7, in agreement with our analytical derivation. |
| In the text | |
 |
Fig. 10. Same as Fig. 7 but in Schwarzschild spacetime for a vertical magnetic field. It might seem surprising that there is a small kick on the astrometric path toward the southeast. This is due to the dependence of the radiative transfer coefficients on sin θB, where θB is the angle between the direction of the magnetic field and the direction of emission (see Marszewski et al. 2021). The upper-left panel clearly shows a flux depletion toward the southeast due to this effect. At this orbital phase, the direction of emission in the emitter’s frame, K, becomes vertical and parallel to the magnetic field. Due to the combination of special-relativistic aberration and general-relativistic lensing effects, the direction of K varies with the orbital phase. The QU loops of this figure should be compared to that of Fig. 7, as the similarity is striking. |
| In the text | |
 |
Fig. 11. Same as Fig. 7 but in Schwarzschild spacetime for a toroidal magnetic field. The QU loops of this figure should be compared to that of Fig. 9, as the similarity is striking. |
| In the text | |
 |
Fig. 12. Comparison of the QU loops computed in Schwarzschild (solid blue) and Minkowski (dashed green) spacetimes. The magnetic field is vertical for the top row and toroidal for the bottom row. The inclination increases from left to right and is specified in the top-right corner of each panel. We note that the various panels have different scalings. |
| In the text | |
 |
Fig. 13. Lensing and asymmetry of Schwarzschild QU loops. The left panel depicts the hot spot seen at zero inclination, and the right one is edge-on. The green arrows show the wave vectors k in Minkowski spacetime that connect the hot spot to the observer. The blue arrows show the corresponding wave vectors for the Schwarzschild case. They differ from Minkowski due to light bending, which adds a shift to the wave vector, depicted in pink. This shift vector is constant with the orbital phase and along the positive radial direction at zero inclination. However, it varies a lot with the orbital phase for the edge-on view, from zero at the closest point to the observer to purely vertical at the furthest point (i.e., “on the other side of the black hole”). The difference in dependence of the shift vector with the orbital phase as a result of inclination has a considerable impact on the Schwarzschild QU loop asymmetry (see text for details). |
| In the text | |
 |
Fig. 14. Evolution of orbit-varying quantities for Stokes parameters. The inclination is ι = 30°. The various panels show the evolution with the orbital phase φ of the various quantities that impact the Stokes parameters: the EVPA (red), the photon’s emitted energy ω = −k ⋅ u (red, in units of the observed energy), and the sine of the emission angle sin θB (green). The left column was computed in Minkowski spacetime and the right column in Schwarzschild. The top row was computed for a vertical magnetic field and the bottom row for a toroidal field. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



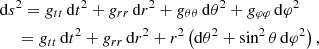
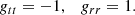
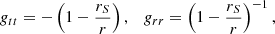
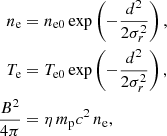
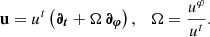
![$$ \begin{aligned}&u^t = \sqrt{\frac{r}{r-M}}, \quad \Omega = M^{1/2} \, r^{-3/2}, \quad \mathrm{[Minkowski]} &u^t = \sqrt{\frac{r}{r-3M}}, \quad \Omega = M^{1/2} \, r^{-3/2}. \quad \mathrm{[Schwarzschild]} \nonumber \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq6.gif)
![$$ \begin{aligned}&\mathbf {\bar{B}} = (0,B^r,B^\theta ,0), \quad \mathrm{[Vertical]} &\mathbf {\bar{B}} = (B^t,0,0,B^\varphi ), \quad \mathrm{[Toroidal]} \nonumber \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq7.gif)
![$$ \begin{aligned}&\mathbf {\bar{B}} = \cos \theta \,\boldsymbol{e_r} - \sin \theta \,\boldsymbol{e_\theta } , \quad \mathrm{[Vertical]} &\mathbf {\bar{B}} = \frac{1}{\sqrt{-\left(g_{tt} + \Omega ^2 g_{\varphi \varphi }\right)}} \left( \sqrt{-\frac{g_{\varphi \varphi }}{g_{tt}}} \, \Omega \, \boldsymbol{\partial _t} + \sqrt{-\frac{g_{tt}}{g_{\varphi \varphi }}} \,\boldsymbol{\partial _\varphi } \right), \! \! \quad \! \! \mathrm{[Toroidal]} \nonumber \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq10.gif)
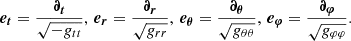
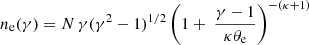
![$$ \begin{aligned} j_\nu \propto \frac{n_\mathrm{e} e^2 \nu _c}{c} X_\kappa ^{-(\kappa -2)/2} \, \sin \theta _B, \left\{ \begin{array}{ll} \propto \sin ^2 \theta _B,&\\ \propto \nu ^{-1},&\end{array} \right. [\text{ for} \kappa =4] \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq13.gif)
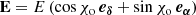
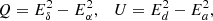
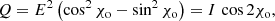
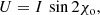

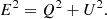
![$$ \begin{aligned} \chi _\mathrm{o} \in [-\pi /2, \pi /2] \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq20.gif)
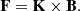
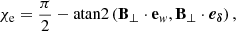
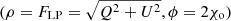
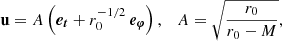
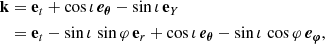
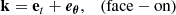
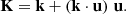
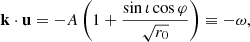
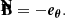
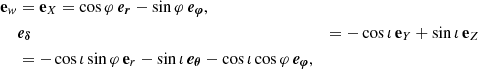
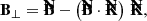
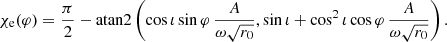
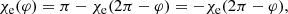
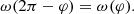
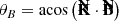
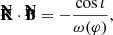
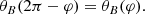
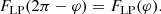
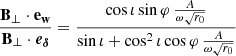
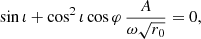
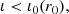
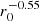
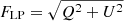
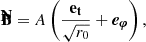
![$$ \begin{aligned} \chi _\mathrm{e} (\varphi ) = \frac{\pi }{2} - \mathrm{atan2} \left(\sin \varphi \left[ C \, \frac{A \omega }{\sqrt{r_0}} - 1 \right], \cos \varphi \cos \iota \left[ C \, \frac{A \omega }{\sqrt{r_0}} - 1 \right]\right), \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq47.gif)
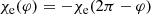
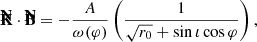
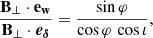
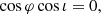
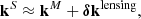
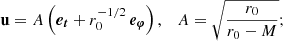
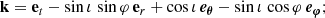
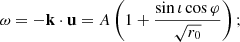
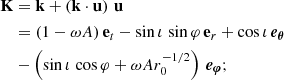
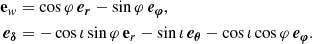
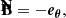
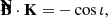
![$$ \begin{aligned} \mathbf B_\perp&= \mathbf {\bar{B}} - \frac{\mathbf{\bar{B} \cdot \mathbf{{K} }}}{{\omega ^2}} \, \mathbf {K} \\ \nonumber&= \frac{\cos \iota }{\omega ^2} \left[\left( 1 - \omega A \right)\mathbf e_t - \sin \iota \, \sin \varphi \,\mathbf e_r + \left(\cos \iota - \frac{\omega ^2}{\cos \iota }\right) \,\boldsymbol{e_\theta } \right. \\ \nonumber&\left. - \left( \sin \iota \, \cos \varphi + \omega A r_0^{-1/2} \right) \,\boldsymbol{e_\varphi } \right]. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq63.gif)
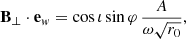
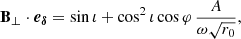
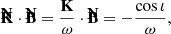
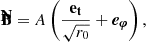
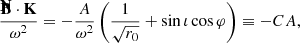
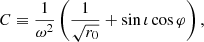
![$$ \begin{aligned} \mathbf B_\perp&= \mathbf {\bar{B}} - \frac{\mathbf{\bar{B}} \cdot \mathbf{{K} }}{\omega ^2} \, \mathbf {K} \\ \nonumber&= A \, \left[\frac{1}{\sqrt{r_0}} + C \left(1 - \omega A \right) \right] \,\mathbf e_t - A C \, \sin \iota \, \sin \varphi \,\mathbf e_r + AC \, \cos \iota \,\boldsymbol{e_\theta } \\ \nonumber& + A \, \left[ 1 - C \left( \sin \iota \, \cos \varphi + \frac{\omega A}{ \sqrt{r_0}} \right) \right]\,\boldsymbol{e_\varphi }. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48016-23/aa48016-23-eq71.gif)