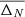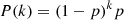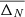| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202347734 | |
| Published online | 28 March 2024 | |
The intermediate neutron capture process
IV. Impact of nuclear model and parameter uncertainties
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles (ULB), CP 226, 1050 Brussels, Belgium
e-mail: sebastien.martinet@ulb.be
Received:
16
August
2023
Accepted:
11
October
2023
Context. The observed surface abundance distributions of carbon-enhanced metal-poor (CEMP) r/s stars suggest that these stars could have been polluted by an intermediate neutron capture process (the so-called i-process) occurring at intermediate neutron densities between the r- and s-processes. Triggered by the ingestion of protons inside a convective He-burning zone, the i-process could be hosted in several sites, a promising one being the early AGB phase of low-mass, low-metallicity stars. The i-process remains affected however by many uncertainties, including those of nuclear origin, since it involves hundreds of nuclei for which reaction rates have not yet been determined experimentally.
Aims. We investigate both the systematic and statistical uncertainties associated with theoretical nuclear reaction rates of relevance during the i-process and explore their impact on the i-process elemental production, and subsequently on the surface enrichment, of a low-mass, low-metallicity star during the early AGB phase.
Methods. We used the TALYS reaction code to estimate both the model and parameter uncertainties affecting the photon strength function and the nuclear level densities, and hence the radiative neutron capture rates. The impact of correlated systematic uncertainties was estimated by considering different nuclear models, as was detailed in Paper II. In contrast, the uncorrelated uncertainties associated with local variation in model parameters were estimated using a variant of the backward-forward Monte Carlo method to constrain the parameter changes to experimentally known cross sections before propagating them consistently to the neutron capture rates. The STAREVOL code (Siess 2006, A&A, 448, 717) was used to determine the impact of nuclear uncertainties on the i-process nucleosynthesis in a 1 M⊙ [Fe/H] = –2.5 model star during the proton ingestion event in the early AGB phase. A large nuclear network of 1160 species coherently coupled to the transport processes was solved to follow the i-process nucleosynthesis.
Results. We find that the uncorrelated parameter uncertainties lead the surface abundance uncertainties of elements with Z ≥ 40 to range between 0.5 and 1.0 dex, with odd-Z elements displaying higher uncertainties. The correlated model uncertainties are of the same order of magnitude, and both model and parameter uncertainties have an important impact on potential observable tracers such as Eu and La. We find around 125 important (n, γ) reactions impacting the surface abundances, including 28 reactions that have a medium to high impact on the surface abundance of elements that are taken as observable tracers of i-process nucleosynthesis in CEMP stars.
Conclusions. Both the correlated model and uncorrelated parameter uncertainties need to be estimated coherently before being propagated to astrophysical observables through multi-zone stellar evolution models. Many reactions are found to affect the i-process predictions and will require improved nuclear models guided by experimental constraints. Priority should be given to the reactions influencing the observable tracers.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: AGB and post-AGB
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Most of the elements heavier than Fe are synthesized by slow (s) and rapid (r) neutron capture processes (e.g., Arnould & Goriely 2020, for a review). These processes are characterized by neutron densities of Nn = 105 − 1010 and Nn > 1024 cm−3, respectively. The s-process develops in asymptotic giant branch stars (AGBs) (e.g., Gallino et al. 1998; Herwig 2005; Cristallo et al. 2011; Karakas & Lattanzio 2014; Goriely & Siess 2018) and in the helium-burning cores of massive stars (e.g., Langer et al. 1989; Prantzos et al. 1990; Choplin et al. 2018). The r-process requires explosive conditions and could arise during the merging of two neutron stars (e.g., Arnould et al. 2007; Goriely et al. 2011a,b; Wanajo et al. 2014; Just et al. 2015), in collapsars, or in magnetorotational supernovae (Winteler et al. 2012; Nishimura et al. 2015; Siegel et al. 2019). It is believed that other secondary neutron capture processes also exist, such as the n-process, with neutron densities of typically 1018 cm−3, that can develop in the helium-burning shells of massive stars during core-collapse supernovae (Blake & Schramm 1976; Thielemann et al. 1979; Meyer et al. 2004; Choplin et al. 2020). The isotopic composition of meteoritic grains may bear the signatures of this process (Meyer et al. 2000; Pignatari et al. 2018).
The so-called intermediate neutron capture process (or i-process, first named by Cowan & Rose 1977) is another secondary neutron capture process that can develop in a variety of astrophysical sites (see Choplin et al. 2021, for a detailed list) and in particular includes low-metallicity, low-mass AGB stars (e.g., Iwamoto et al. 2004; Cristallo et al. 2009; Suda & Fujimoto 2010; Choplin et al. 2021, 2022b; Goriely et al. 2021; Gil-Pons et al. 2022). For the i-process to develop, protons must be mixed in a convective helium-burning zone. This event is often called a proton ingestion event (PIE). In AGB stars, PIEs can develop during the early thermally pulsing (TP) phase. It occurs when the energy of the convective thermal pulse is high enough to overcome the entropy barrier at the bottom of the H-burning shell. The top of the convective pulse encroaches on the H-shell and protons are engulfed in the pulse. They are transported downward by convection (in a timescale of typically 1 h) and burn on the way via 12C(p, γ)13N. After the decay of 13N to 13C (in about 10 min), the 13C(α, n)16O reaction is activated, mostly at the bottom of the convective pulse, where the temperature reaches ∼250 MK. The neutron density goes up to ∼1015 cm−3 and an i-process nucleosynthesis takes place. Quickly after the peak in neutron density, the convective pulse splits (cf. Sect. 3.5 in Choplin et al. 2022b, for a discussion about the split). The upper part eventually merges with the large convective envelope, in which the i-process products are diluted and finally expelled by the stellar wind.
More and more stars are observed showing chemical compositions compatible with i-process nucleosynthesis. This includes so-called carbon-enhanced metal-poor (CEMP) r/s stars (Lugaro et al. 2012; Roederer et al. 2016; Karinkuzhi et al. 2021; Mashonkina et al. 2023; Hansen et al. 2023). Some less metal-poor stars may also bear the signature of an i-process (Mishenina et al. 2015; Karinkuzhi et al. 2023). It has also been suggested that some pre-solar grains could be made of i-process material (Fujiya et al. 2013; Jadhav et al. 2013; Liu et al. 2014).
Despite the occurrence of PIEs in various astrophysical sites, such as the early AGB phase of low-mass, low-metallicity stars (e.g., Choplin et al. 2022b) or rapidly accreting white dwarfs (e.g., Denissenkov et al. 2019), nucleosynthesis predictions are still significantly affected by nuclear uncertainties. These uncertainties were discussed in a few previous works. More specifically, Denissenkov et al. (2018) investigated the uncertainties affecting elements with 35 ≤ Z ≤ 40 using both a one-zone model with constant temperature and density and a 1D multi-zone stellar model whereby nucleosynthesis is calculated in post-processing. They randomly varied 52 relevant (n, γ) reaction rates of unstable species. Because one-zone models led to significantly different results from multi-zone stellar models, they suggest that one-zone models are not reliable for identifying critical reaction rates in convective-reactive regimes such as AGB stars undergoing the i-process. Similarly, McKay et al. (2020) considered the uncertainties for elements with 32 ≤ Z ≤ 48 using one-zone modeling and varying 113 relevant (n, γ) rates of unstable species to predict the impact of (n, γ) reaction rate uncertainties on the abundances of i-process elements in observed metal-poor stars. More recently, Denissenkov et al. (2021) examined the uncertainties for elements with 56 ≤ Z ≤ 74 with both one-zone and multi-zone models. They randomly varied 164 relevant (n, γ) rates of unstable species. In contrast to Denissenkov et al. (2018), they suggested that one-zone simulations are reliable in identifying key reaction rates, provided that the neutron density is similar to the maximum one found in the multi-zone stellar models. Goriely et al. (2021) evaluated the impact of nuclear model uncertainties on the surface abundances of 1D multi-zone AGB models for all elements. Nuclear uncertainties related to the 13C(α, n)16O reaction rate, as well as experimentally unknown β-decay and radiative neutron capture rates were studied. The direct capture contribution, the photon strength functions (PSFs), and the nuclear level densities (NLDs) entering the calculation of (n, γ) rates were shown to be the main source of nuclear uncertainties.
In this paper, we study both nuclear model (or equivalently “systematic”) and nuclear parameter (often referred to as “statistical”) uncertainties affecting the prediction of theoretical radiative neutron capture rates and their impact on the i-process for elements with 14 ≤ Z ≤ 92. We varied the 868 theoretical (n, γ) rates included in our i-process reaction network and considered a low-mass, low-metallicity AGB star model to analyse the impact of nuclear uncertainties on the prediction of elemental and isotopic surface enrichments. Section 2 presents the method of obtaining model and parameter uncertainties, with a special emphasis on the application of the backward-forward Monte Carlo (BFMC) approach to constrain parameter uncertainties on experimental data. In Sect. 3, we study the impact of both the parameter and model uncertainties on the i-process nucleosynthesis in our low-mass, low-metallicity AGB star. In Sect. 4, we present the (n, γ) reactions most impacting the surface abundances of such stars, and we illustrate how the use of a newly constrained rate can significantly reduce the uncertainties. Finally, in Sect. 5 we discuss the results of this work and the potential perspectives of this sensitivity study.
2. Method
As shown in Goriely et al. (2021), the main source of nuclear uncertainties impacting the abundance predictions of the i-process is found in the theoretical determination of (n, γ) rates for neutron-rich nuclei. In contrast to our previous analysis (Goriely et al. 2021) and other works dedicated to this subject (Denissenkov et al. 2018, 2021; McKay et al. 2020), both the model (systematic) and parameter (statistical) uncertainties affecting theoretical (n, γ) rates are studied here. They are both obtained using the TALYS reaction code (Koning et al. 2023). Since most of the atomic masses are known for nuclei produced by the i-process (Wang et al. 2021), the key nuclear ingredients affecting the calculation of the radiative neutron capture are the NLDs and PSFs1. The radiative neutron capture cross section, σn, γ, also formally depends on the neutron-nucleus optical model potential. However, for nuclei produced by the i-process, the cross section remains insensitive to the optical potential due to the prevalence of the strong interaction with respect to the electromagnetic one. Indeed, within the Hauser-Feshbach formalism, σn, γ ∝ TnTγ/(Tn + Tγ)∼Tγ, if the neutron transmission coefficient, Tn, is significantly larger than the electromagnetic one, Tγ, that is, when Tn > > Tγ. For exotic neutron-rich nuclei, the optical potential may affect the cross section, provided the isovector imaginary potential becomes significant, as discussed in Goriely & Delaroche (2007). This is not the case for the i-process nucleosynthesis and the neutron capture cross section can, in a very good approximation, be assumed to remain essentially insensitive to the optical potential. The nuclear uncertainties are consequently directly related to our ability to estimate NLDs and PSFs for the compound systems produced during the i-process. Those are detailed below.
2.1. Nuclear model uncertainties
The model uncertainties were treated in a similar way as in Goriely et al. (2021), by estimating the 868 rates with different combinations of NLD and PSF models. More specifically, we adopted nine different combinations here based on the following (i) NLD models:
-
(1)
Hartree-Fock-Bogolyubov plus combinatorial (HFB+comb) (Goriely et al. 2008);
-
(2)
Constant temperature plus Fermi Gas (Cst-T) (Koning et al. 2008);
-
(3)
Back-Shifted Fermi gas (BSFG) (Koning et al. 2008);
-
(4)
T-dependent HFB plus combinatorial (THFB+comb) (Hilaire et al. 2012);
and (ii) PSF models:
-
(a)
Gogny-HFB plus quasi-particle random phase approximation (D1M+QRPA) (Goriely et al. 2018);
-
(b)
Simple modified Lorentzian (SMLO) (Goriely & Plujko 2019);
-
(c)
Generalized Lorentzian (GLO) (Kopecky & Uhl 1990);
-
(d)
Skyrme-HFB plus QRPA (BSk27+QRPA) (Xu et al. 2021);
-
(e)
Relativistic mean-field + continuum RPA (RMF+cRPA) (Daoutidis & Goriely 2012).
The nine combinations of NLDs (from 1 to 4) and PSFs (from a to e) are defined as the following: set A (1a), set B (2b), set C (2a), set D (1c), set E (1e), set F (1d), set G (3a), set H (4a), and set I (1b).
These combinations all lead to a relatively accurate prediction of the experimental Maxwellian-averaged cross sections (MACS) (Dillmann et al. 2006) for all the 239 nuclei with 20 ≤ Z ≤ 83. To quantify this accuracy, we adopted the root-mean-square (rms) criterion defined by the frms deviation, that is
where Ne is the number of known reaction rates and ⟨σth⟩ and ⟨σexp⟩ are the theoretical and experimentally known MACS, respectively. We find that for the nine adopted combinations, frms deviations range between 1.4 and 1.8. We note, however, that in these TALYS calculations all NLDs are constrained on measured resonance s-wave spacings and a low-lying scheme of excited levels, when available (Capote et al. 2009), but no information on experimental average radiative width is included.
For each of the Ne = 239 nuclei for which data is available, TALYS deviations from the experiment are displayed in Fig. 1, where the error bars give the upper or lower MACS obtained by one of the nine combinations. It should be stressed that the corresponding model uncertainties obtained with the nine combinations of NLDs and PSFs are strongly correlated with the underlying nuclear model.
 |
Fig. 1. Theoretical over experimental (n, γ) MACS for the 239 experimentally known rates at 30 keV. The error bars display the maximum and minimum rates obtained by the nine different combinations of NLD and PSF models (including sets A and B; see text). The full circles correspond to set B and the gray shaded area shows variations within a factor of two. |
For the neutron-rich nuclei relevant to the r-process, for which no experimental information of any kind is available, model uncertainties have been shown to dominate over the parameter uncertainties (see in particular Goriely & Capote 2014, who discuss the extrapolation uncertainties of mass models). However, when dealing with the unstable nuclei close to the valley of β-stability produced by the i-process, parameter uncertainties may be significant. Those are estimated below.
2.2. Nuclear parameter uncertainties
In comparison with model uncertainties, much less effort has been devoted to estimating the parameter uncertainties for a given set of nuclear reaction rates. These are obtained by local variations in the parameters used in a given nuclear model. For this study we considered two different combinations of NLD and PSF models for the TALYS calculation of the neutron capture rates. The first set, A, adopts the HFB+comb NLDs (Goriely et al. 2008) and the D1M+QRPA PSFs for both the dipole electric E1 and magnetic M1 components (Goriely et al. 2018). While set A is based on rather microscopic ingredients, set B considers more phenomenological models, namely Cst-T NLDs (Koning et al. 2008) and SMLO PSFs (Goriely & Plujko 2019). Both sets A and B are sensitive to the parameters adopted in the NLD and PSF models, each of them being dominantly adjusted by two parameters. For the Cst-T NLDs, we allowed for local variations in the temperature, T, and the pairing parameter, E0, leading to a possible energy shift. In the case of the tabulated HFB+comb NLDs, equivalently, two parameters, α and δ, can play a similar role, as detailed in Goriely et al. (2008). For the SMLO and D1M+QRPA PSF models, uncertainties affecting the width and centroid energy of the E1 giant dipole resonance are included by adjusting two related parameters, denoted here as δΓ and δE, respectively. All together, for both sets A and B, local variations in four parameters (two for NLDs and two for PSFs) may consequently affect the reaction rate predictions. However, the range of local variation for each parameter remains to be defined and will be critical to estimating the magnitude of their impact on the predicted reaction rates. For this reason, it is fundamental that such local parameter variations be constrained as much as possible by experimental data where available, before being applied to neutron-rich nuclei for which no data is available. In our case, it is possible to estimate the impact of such parameter uncertainties on calculated rates by propagating them by Monte Carlo (MC) sampling constrained by available experimental rates (Dillmann et al. 2006). The method used here corresponds to the BFMC approach detailed below.
2.2.1. The backward-forward Monte Carlo approach
The BFMC method (see Chadwick et al. 2007; Bauge & Dossantos-Uzarralde 2011; Goriely & Capote 2014) relies on the sampling of the model parameters and the use of a generalized χ2 estimator to quantify the likelihood of each simulation respective to a given set of experimental constraints, here the experimentally known (n, γ) rates (Dillmann et al. 2006). The backward MC is used to select the suitable parameter samples that agree with experimental constraints. In the BFMC method, the χ2 estimator is used to quantify a likelihood function that will weight a given sample of {p1,...,pn} parameters when the Ne associated observables {σ1,...,σNe} are close to the experimental data. In this work, we assumed that experimentally constrained (n, γ) rates are independent. This assumption allowed us to use a χ2 criterion instead of a generalized weighting function, so the weighting function becomes simply 1 when 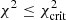 , and 0 otherwise, with
, and 0 otherwise, with 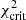 a chosen critical value of the χ2. Then, for the forward MC step, the selected set of the MC parameter sample is applied to the calculation of the unmeasured quantities, here the unknown (n, γ) rates.
a chosen critical value of the χ2. Then, for the forward MC step, the selected set of the MC parameter sample is applied to the calculation of the unmeasured quantities, here the unknown (n, γ) rates.
2.2.2. Assessing TALYS parameter uncertainties
To estimate the uncertainty affecting our four model parameters, we used as χ2 estimator the frms deviation with respect to the 239 experimental (n, γ) MACS at 30 keV from the KADoNiS database (Dillmann et al. 2006). Each of the four parameters, p, affecting the NLDs and PSFs were varied separately and assigned a relative uncertainty, Δp/p, such that an individual change in each parameter leads to a maximum 10% increase in the frms deviation with respect to the 239 experimental nuclear rates in our sample. The diagonal values of a covariance matrix were then assigned the values of Δp corresponding to the 10% increase. This matrix was used to produce a multivariate normal distribution centered on the nominal parameters values. We then generated a distribution of random combinations (here Ncomb = 200 combinations) of these four parameters.
The 10% increase in the frms deviation was chosen to optimize the sampling needed to get significant statistics using the BFMC method, but is not expected to affect the results. Indeed, a value larger than 10% would essentially request more combinations to be calculated to achieve a similar representative sample of runs constrained by the χ2 estimator on experimental data.
2.2.3. Backward Monte Carlo step
We computed the 239 theoretical rates for which experimental data is available for each of the 200 different combinations of parameter values obtained from the multivariate normal distribution described above. The χ2 estimator of the backward MC step is again given by the frms deviation (Eq. (1)) obtained with respect to the 239 experimental (n, γ) rates. The resulting distribution as a function of the frms deviation is displayed in Fig. 2. We find no combination resulting in frms deviations smaller than 1.80 for set A and 1.59 for set B. However, as seen in Fig. 2, many parameter combinations lead to frms deviations larger than 2, typically. Such combinations lead to an unrealistic description of experimental data and should consequently not be considered for the unknown nuclei during the forward MC step. Since the model deviations obtained in Sect. 2.1 all give rise to frms ≤ 2 with respect to experimental data, the parameter ranges in the backward MC procedure were also restricted to variations compatible with an frms ≤ 2. This allows us to select only the combinations of nuclear parameters that are consistent with the experimental data by using the 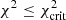 selective criterion with
selective criterion with 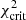 ⇔ frms ≤ 2. The resulting selection of model parameters allows us to estimate the uncorrelated parameter uncertainties for the 239 experimentally known MACS, as illustrated in Fig. 3 for both sets A and B. Some systematic effects can be observed in the parameter uncertainties, especially for set B, for which the MACS is overestimated for closed-shell nuclei around A ∼ 90, 140, and 208, mainly due to the rather approximate treatment of shell effects in the Cst-T NLD formula. These uncertainties are also seen to be of the same order of magnitude as those stemming from model uncertainties shown in Fig. 1. Now that our parameter sample is constrained on experimental data, it can be extended to the non-experimental (n, γ) rates by the forward step of the MC procedure, as explained below.
⇔ frms ≤ 2. The resulting selection of model parameters allows us to estimate the uncorrelated parameter uncertainties for the 239 experimentally known MACS, as illustrated in Fig. 3 for both sets A and B. Some systematic effects can be observed in the parameter uncertainties, especially for set B, for which the MACS is overestimated for closed-shell nuclei around A ∼ 90, 140, and 208, mainly due to the rather approximate treatment of shell effects in the Cst-T NLD formula. These uncertainties are also seen to be of the same order of magnitude as those stemming from model uncertainties shown in Fig. 1. Now that our parameter sample is constrained on experimental data, it can be extended to the non-experimental (n, γ) rates by the forward step of the MC procedure, as explained below.
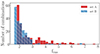 |
Fig. 2. Histogram of the number of parameter combinations for sets A and B as a function of their frms with respect to the experimental MACS. |
 |
Fig. 3. Theoretical over experimental (n, γ) MACS for the 239 (20 ≤ Z ≤ 83) known rates at 30 keV obtained with set A (top) and set B (bottom). The error bars display the uncorrelated parameter uncertainties obtained through the BFMC method using frms≤ 2.0. The gray shaded area guides the eye for a deviation within a factor of two. |
2.2.4. Forward Monte Carlo step
At the end of the backward MC step, we obtain a subset of 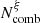 combinations of parameters constrained by experimental MACS (frms ≤ 2). With this subset we can now assess the uncorrelated parameter uncertainties affecting the theoretical (n, γ) rates. We computed the 868 experimentally unknown (n, γ) rates using the subset of parameter combinations (
combinations of parameters constrained by experimental MACS (frms ≤ 2). With this subset we can now assess the uncorrelated parameter uncertainties affecting the theoretical (n, γ) rates. We computed the 868 experimentally unknown (n, γ) rates using the subset of parameter combinations (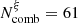 combinations for set A and
combinations for set A and 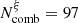 for set B). The resulting parameter uncertainties of the rates are plotted in Fig. 4 (lower panel) by displaying for each reaction the ratio between the maximum and the minimum MACS obtained using set B (we obtain similar results for set A). The 239 experimentally known rates are shown in blue and the theoretical rates in red. Additionally, for comparison, we show in the upper panel of Fig. 4 the maximum-to-minimum rate ratios obtained between the sets A and B with their nominal parametrisation, that is, max[⟨σ⟩A,⟨σ⟩B]/min[⟨σ⟩A,⟨σ⟩B], corresponding to the model uncertainties between sets A and B. Deviations due to both the correlated model and the uncorrelated parameter uncertainties are seen to be of the same order of magnitude and are found to increase with decreasing neutron separation energy, Sn (i.e., for increasingly neutron-rich nuclei). Interestingly, for both types of uncertainties, we still find nuclei with low deviations (typically lower than a factor of 2–3) at low Sn thanks to their relatively well-known scheme of excited states, which reduces the impact of NLDs in these cases.
for set B). The resulting parameter uncertainties of the rates are plotted in Fig. 4 (lower panel) by displaying for each reaction the ratio between the maximum and the minimum MACS obtained using set B (we obtain similar results for set A). The 239 experimentally known rates are shown in blue and the theoretical rates in red. Additionally, for comparison, we show in the upper panel of Fig. 4 the maximum-to-minimum rate ratios obtained between the sets A and B with their nominal parametrisation, that is, max[⟨σ⟩A,⟨σ⟩B]/min[⟨σ⟩A,⟨σ⟩B], corresponding to the model uncertainties between sets A and B. Deviations due to both the correlated model and the uncorrelated parameter uncertainties are seen to be of the same order of magnitude and are found to increase with decreasing neutron separation energy, Sn (i.e., for increasingly neutron-rich nuclei). Interestingly, for both types of uncertainties, we still find nuclei with low deviations (typically lower than a factor of 2–3) at low Sn thanks to their relatively well-known scheme of excited states, which reduces the impact of NLDs in these cases.
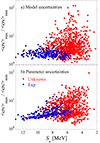 |
Fig. 4. Uncertainties as a function of the neutron separation energy, Sn. (a) Model uncertainties between sets A and B, represented by the ratio of the maximum to minimum (n, γ) rates (max[⟨σ⟩A,⟨σ⟩B]/min[⟨σ⟩A,⟨σ⟩B]). The 239 experimentally known reactions are shown with blue dots and the unknown ones with red dots. (b) Same as the upper panel but for the parameter uncertainties for set B. All rates are estimated at T = 2.5 × 108 K. |
2.3. Parameter correlations
Figure 5 illustrates the correlated model uncertainties against the uncorrelated parameter uncertainties, as extracted from Fig. 4. If both uncertainties were correlated, we would expect each reaction to lie along the 1:1 ratio line depicted in black. Here, we can see a broad dispersion, in which reactions with a high model uncertainty have a low parameter one, and in which, conversely, reactions are described similarly by different nuclear models and show a high parameter uncertainty. This underlines the need to take into account both the correlated model and the uncorrelated parameter uncertainties. It also emphasizes the fact that maximum deviations estimated from model variations are not suited to describing uncorrelated nuclear uncertainties, as is sometimes considered (McKay et al. 2020).
 |
Fig. 5. Correlated model uncertainties represented by the ratio of the maximum to minimum (n, γ) MACS (Fig. 4a) as a function of uncorrelated parameter uncertainties of set B (Fig. 4b). The 239 experimentally known (n, γ) reactions are shown in blue and the 868 theoretical ones in red. All rates are estimated at T = 2.5 × 108 K. |
Figure 6 shows the correlation between the four different parameters used in the selected combinations resulting in frms ≤ 2.0 for both sets A and B. Set A parameters α and δ (E0 and T are the equivalent in set B) are local variations of parameters impacting the NLD, while δE and δΓ impact the PSF. The diagonal shows the marginal distribution of each parameter. As expected from the random multivariate distribution, the parameters are mostly normally distributed around their nominal value. This shows that we consistently explore the parameter space resulting in combinations with frms ≤ 2. For set A, we observe a correlation between (α, δ) and (δE, δΓ), as expected, since the NLD (hence the MACS) increases with increasing α or decreasing δ values and the E1 PSF (and hence the MACS) also increases with increasing δΓ or decreasing δE values. For the same reason, an anti-correlation between δ and δE also appears. For set B, there is also a clear correlation between δE and δΓ. Other correlations are however less pronounced for this set.
 |
Fig. 6. Correlation plots for the four parameters in set A (left) and set B (right) using the total set (Ncomb = 200; black dots) or the selected subset with frms ≤ 2.0 (Ncomb = 61 for set A and Ncomb = 97 for set B; red dots). Each contour corresponds to iso-proportions of the density, with the first contour corresponding to 20% and incrementing by 20%. The diagonal shows the (normalized) marginal distribution of each parameter. |
3. Impact on the i-process nucleosynthesis
To explore the impact of the correlated model and uncorrelated parameter uncertainties, we computed a large set of multi-zone stellar evolution models during the early AGB phase of a low-mass, low-metallicity star using the STAREVOL code (Siess et al. 2000; Siess & Arnould 2008), as described below. In 1D stellar models, the star is divided into spherical zones (or shells) in which the stellar structure equations and nucleosynthesis are solved. The zones can interact with each other through mixing processes such as convection. In our models, during the PIE, the star is divided into ∼3500 zones, of which around 500 are dedicated to the convective thermal pulse where the i-process takes place.
3.1. The proton ingestion episode and the dilution procedure
The 1 M⊙, [Fe/H] = –2.5 AGB model considered here was already extensively discussed in Choplin et al. (2021, 2022a,b), Goriely et al. (2021). We only recall here a few important evolutionary aspects and explain the dilution procedure we devised to save computational time.
During the early TP-AGB phase, protons are engulfed by the convective thermal pulse and burn by the 12C(p, γ)13N reaction while being transported down. After the β+-decay of 13N into 13C in a timescale of 10 min, the 13C(α, n)16O reaction is activated at the bottom of the convective pulse at a temperature of about 250 MK and leads to neutron densities of ∼1015 cm−3. Shortly after the neutron density peak, the convective pulse splits (Choplin et al. 2022b, Sect 3.5 for more details on the split). After the split, the upper part of the convective pulse grows in mass and engulfs additional protons, but the temperature at the bottom of the upper part of the pulse is now too low to activate the 13C(α, n)16O reaction efficiently, so no substantial modification of the abundances of heavy elements is found after the split. However, because H-burning is still operating, species involved in the CNO cycle will keep evolving. The upper part of the pulse eventually merges with the convective envelope, leading to the enrichment of the surface in i-process products (and other C and N isotopes).
The PIE in our reference AGB model was computed for each set of (n, γ) rates. To save computational time, the models were stopped 0.7 yr after the split, before the elements were brought to the surface. Nevertheless, since the i-process nucleosynthesis is restricted to the evolution before the split, the surface abundances can still be estimated accurately thanks to the dilution procedure explained below.
In our reference model, just after the split, we calculated the mean abundance of each element (j) in the upper part of the convective pulse (which did not have time to homogenize yet) as
where M1 and M2 are the mass coordinate boundaries of the upper convective pulse (with M1 very close to the mass coordinate of the split). This material was then diluted into the envelope (which was still disconnected from the pulse at this time), leading to the approximate surface mass fraction
where 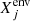 is the (homogeneous) envelope mass fraction of element j. The dilution parameter, fdil, was adjusted on our reference model so as to minimize the difference between the exact final surface abundances, Xsurf, and its estimate, Xdil (all abundances are considered after β- and α-decays). For our AGB model, fdil is equal to 0.9243, which leads to a deviation of |Xsurf − Xdil|/Xsurf < 0.04 for all elements, except for Li (deviation of 0.99), C (deviation of 0.09), and N (deviation of 0.76). All the stellar models considered in this work have almost exactly the same structures and follow the same evolutionary pathway. Hence, this calibration of fdil can be safely used for all of them, as shown by our tests.
is the (homogeneous) envelope mass fraction of element j. The dilution parameter, fdil, was adjusted on our reference model so as to minimize the difference between the exact final surface abundances, Xsurf, and its estimate, Xdil (all abundances are considered after β- and α-decays). For our AGB model, fdil is equal to 0.9243, which leads to a deviation of |Xsurf − Xdil|/Xsurf < 0.04 for all elements, except for Li (deviation of 0.99), C (deviation of 0.09), and N (deviation of 0.76). All the stellar models considered in this work have almost exactly the same structures and follow the same evolutionary pathway. Hence, this calibration of fdil can be safely used for all of them, as shown by our tests.
3.2. Propagating model uncertainties
To propagate the correlated model uncertainties, we used here the same methodology discussed in Goriely et al. (2021), consisting of PIE stellar calculations (as described in Sect. 3.1) for the nine different nuclear models introduced in Sect. 2.1. We note that, in comparison with our previous work (Goriely et al. 2021), alternative combinations of PSFs and NLDs were adopted here but uncertainties associated with the contribution of the direct capture mechanism were not taken into account. Sets A, D, E, F, and I essentially test the impact of PSF models using the same NLDs, while sets A, C, G, and H illustrate the impact of the NLD models using the same PSF. Figure 7 shows the resulting surface abundances [X/Fe] and the corresponding deviations stemming from the correlated model uncertainties for the nine different nuclear models, including sets A and B, for which parameter uncertainties are also explored in more detail in Sect. 3.3. The lower panel shows the difference between the various models and set A. Overall, the correlated nuclear model uncertainties impact the chemical abundances of Z > 40 elements by typically 0.5 − 1 dex, with the exception of Th (Z = 90) and U (Z = 92) for which the effects are stronger. The potential production of Th and U is highly sensitive to the model uncertainties and can lead to orders-of-magnitude differences, but variations in [Th/U] remain constrained to values between −0.84 to −0.61, as discussed in Choplin et al. (2022a). Some nuclear models can lead to quite different surface abundance predictions, especially for important tracers such as Ba (Z = 56), La (Z = 57) and Eu (Z = 63). However, since the model uncertainties are correlated, abundance ratios may be significantly less affected. In particular, the [Ba/Eu] ratio varies from 0.12 to 0.58 and the [Ba/La] ratio from −0.15 to 0.02. Some nuclear models also give rise to systematically different results. In particular, set D, with its relatively slow rates obtained with the low GLO PSFs, tends to overproduce elements between Z = 40 and Z = 75 in comparison to other models.
 |
Fig. 7. Surface [X/Fe] abundance ratios of AGB models for the nine different nuclear models considered. The bottom plot shows the differences between the various models and set A. |
3.3. Propagating parameter uncertainties
To propagate the uncorrelated parameter uncertainties, a large number, N, of sets containing randomly chosen minimum and maximum rates for each of the 868 (n, γ) reactions was produced. These were based on the maximum and minimum rates obtained in Sect. 2.2.4 from the BFMC method. We can choose randomly between these rates due to the uncorrelated nature of these uncertainties. These random sets of rates are then used in stellar evolution models to assess the impact of the parameter uncertainties on the final surface abundances in our 1 M⊙ [Fe/H] = − 2.5 AGB star. Despite the fact that parameter uncertainties are uncorrelated, the resulting surface abundances may remain correlated for a given stellar simulation, since a given rate may influence more than one isotopic abundance.
One of the difficulties with randomly produced sets of rates is ensuring that enough draws have been made to be representative of the full range of possible outcomes. We computed an increasing number of stellar evolution models until the convergence of the upper and lower limits of the surface abundances was reached. More specifically, the convergence is evaluated by the quantity
where NZ is the total number of elements and
where p95 and p5 refer to the 95th and 5th percentiles, respectively, of the [X/Fe] distributions and N refers to the number of AGB i-process simulations considered (up to 50) to estimate these percentiles. We chose to select uncertainties values from the 5th and 95th percentiles to take into account potential numerical artifacts that could lead to spurious abundance over- or under-estimates. Δ50 corresponds to the difference between the percentiles when considering 50 different simulations (hence 50 different sets of randomly chosen rates among their maximum and minimum values).
Figure 8 shows the convergence of the averaged uncertainties, 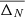 , as a function of the number, N, of simulations. For small values of N, a rapid increase is expected due to the random nature of the draws, leading to large variations in the uncertainties. For simulations of typically more than N = 30, a plateau is found and the global abundance uncertainty does not evolve anymore when compared to the value for N = 50 simulations2. In other words, adding an extra 20 simulations does not give rise to average changes of more than 0.05 dex. Hence, we consider that we have convincingly converged on the total propagation of parameter uncertainties by computing N = 50 stellar simulations with 50 different nuclear sets.
, as a function of the number, N, of simulations. For small values of N, a rapid increase is expected due to the random nature of the draws, leading to large variations in the uncertainties. For simulations of typically more than N = 30, a plateau is found and the global abundance uncertainty does not evolve anymore when compared to the value for N = 50 simulations2. In other words, adding an extra 20 simulations does not give rise to average changes of more than 0.05 dex. Hence, we consider that we have convincingly converged on the total propagation of parameter uncertainties by computing N = 50 stellar simulations with 50 different nuclear sets.
 |
Fig. 8. Evolution of the averaged uncertainties, |
3.3.1. Impact on surface abundances
Figure 9 shows the surface [X/Fe] abundances resulting from the N = 50 simulations computed for the nuclear set A (top panel) and set B (bottom panel). For a given element, each black dot corresponds to the final abundance of one of the 50 simulations. The uncertainties of the i-process abundances are on the order of 0.5 to 1.0 dex on average for all the nuclei with Z ≥ 40. Interestingly, we can discern a clear pattern of higher uncertainties for the odd-Z elements. This comes from the fact that odd-Z elements usually have only one stable isotope, so these isotopes are highly sensitive to the competition between the (n, γ) reaction and the β-decay of the even Z − 1 isotopes. An eye-catching example is the case of Sc (Z = 21), where we can clearly see two groups of abundances separated by almost 1 dex in set A. It clearly underlines the sensitivity to a rate being maximum or minimum and acting directly on the final Sc abundances. We show in Sect. 4.1 that, in the Sc case, this is due to the 45Ca(n, γ) reaction.
 |
Fig. 9. Scatter plot of the surface [X/Fe] abundance ratios of AGB models for the nuclear set A (top) and set B (bottom) with frms ≤ 2.0. The blue (red) line shows the 5th (95th) percentile (Eq. (5)). The bottom subplot in each panel shows Δ50, which is the difference between the 95th and 5th percentile (Eq. (5)) for the N = 50 simulations. |
Since the surface abundances may remain correlated, the uncertainies affecting abundance ratios should be estimated from the maximum and minimum abundance ratios among the 50 different simulations. The range of possible [Ba/Eu] ratios for the nuclear set A (set B) is −0.55 < [Ba/Eu] < 0.85 (−0.46 < [Ba/Eu] < 0.79), that is, an uncertainty of 1.35 dex (1.25 dex). For the [Ba/La] ratio, the ranges become −0.67 < [Ba/La] < 0.31 for set A (an uncertainty of 0.98 dex) and −0.75 < [Ba/La] < 0.63 for set B (an uncertainty of 1.38 dex). The [Th/U] ratio can vary from −1.31 to −0.11 for set A (an uncertainty of 1.20 dex) and from −1.22 to −0.14 for set B (an uncertainty of 1.08 dex). The abundance ratios are significantly more affected by parameter than model uncertainties (see Sect. 3.2). It is consequently of prime importance to decrease the parameter uncertainties, especially on tracer elements, like La, Ba, or Eu.
Sets A and B lead to similar uncertainty patterns, as confirmed in Fig. 10, which compares, for both sets, the surface abundance predictions [X/Fe] and their respective uncertainties. The shaded red and blue zones correspond to set A and set B, respectively, the limits being given by the 5th and 95th percentiles. We can see that the amplitude of the uncertainties from both nuclear sets are comparable for almost all nuclei. A clear difference of more than 1 dex affects the production of Th and U. This highlights the uncertainties still impacting the nuclear physics predictions of sub-actinides and actinides. Otherwise, both nuclear sets lead to fairly close values for the surface abundances.
 |
Fig. 10. Comparison between the surface abundances [X/Fe] and their uncertainties obtained with nuclear sets A and B, for frms ≤ 2.0 case. The red (blue) region shows the extent of the [X/Fe] region between the 5th and 95th percentile for set A (set B). The purple area shows the intersection between the two models. |
3.3.2. Impact of the χ2 threshold value
We additionally explored the impact of the BFMC χ2 criterion, as described in Sect. 2.2.3 (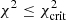 ), by increasing the value of
), by increasing the value of 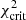 to an upper frms deviation of 2.5 instead of 2.0. To do that, we extended the sets of 4-parameter combinations to a frms ≤ 2.5 (Ncomb = 112 for set A and Ncomb = 161 for set B) to estimate the 868 theoretical MACS. With the corresponding randomly chosen upper and lower limits of these rates in each of the sets A and B, we once again computed 50 stellar evolution models. The extended parameter combinations obviously allow for higher maximum and lower minimum rates, and hence a higher impact on the surface abundances can be expected. Figure 11 compares the surface [X/Fe] abundances and their parameter uncertainties (5th and 95th percentiles) computed with rate combinations restricted to frms ≤ 2.5 and frms ≤ 2.0, both for the nuclear set A. Interestingly, the uncertainties increase mostly for Z ≥ 40 odd-Z elements from ∼1.0 dex for an frms ≤ 2.0 to ∼1.5 dex for frms ≤ 2.5. However, the even-Z elements retain the same uncertainties of about 0.5 dex as for frms≤ 2.0. Similar results are found when adopting set B.
to an upper frms deviation of 2.5 instead of 2.0. To do that, we extended the sets of 4-parameter combinations to a frms ≤ 2.5 (Ncomb = 112 for set A and Ncomb = 161 for set B) to estimate the 868 theoretical MACS. With the corresponding randomly chosen upper and lower limits of these rates in each of the sets A and B, we once again computed 50 stellar evolution models. The extended parameter combinations obviously allow for higher maximum and lower minimum rates, and hence a higher impact on the surface abundances can be expected. Figure 11 compares the surface [X/Fe] abundances and their parameter uncertainties (5th and 95th percentiles) computed with rate combinations restricted to frms ≤ 2.5 and frms ≤ 2.0, both for the nuclear set A. Interestingly, the uncertainties increase mostly for Z ≥ 40 odd-Z elements from ∼1.0 dex for an frms ≤ 2.0 to ∼1.5 dex for frms ≤ 2.5. However, the even-Z elements retain the same uncertainties of about 0.5 dex as for frms≤ 2.0. Similar results are found when adopting set B.
 |
Fig. 11. Comparison between the surface abundances [X/Fe] and their uncertainties obtained with the uncorrelated parameter uncertainties of nuclear set A, with frms≤ 2.0 (blue) and frms≤ 2.5 (red). |
4. Important reactions and their impact
4.1. Determining the most impacting reactions
We explored the potential impact of given reactions on the i-process nucleosynthesis by taking advantage of the method we used to assess the parameters uncertainties. Indeed, the abundance distribution obtained in our stellar simulations for each element can be used to separate random from correlated effects. More specifically, for each nuclei we can sort the abundances from our 50 simulations and obtain the corresponding sorted list of maximum or minimum rate distributions for each of the 868 (n, γ) reactions. If the abundance of a given nucleus is not sensitive to any reaction, the corresponding sorted distribution of rates should be a random distribution of maximum and minimum values. However, if this sorted distribution leads, in the extreme case, to 25 consecutive maxima followed by 25 consecutive minima (a very unlikely random draw), it suggests a correlation between the value of a given reaction rate and the surface abundance of the concerned nucleus. To quantify the likeliness of such a draw, we use the properties of what is in fact here a geometrical distribution. The probability of consecutively drawing the same rate (only maxima or only minima) is defined as
with k the number of consecutive equal rates and p the probability of the trial, here p = 0.5 as we drew randomly between maximum and minimum rates. In the case of 25 consecutive draws, the probability of obtaining such a distribution is then P(25)≃10−8, meaning there is a 1 in 100 million chance of drawing such a distribution, a more than highly unlikely draw for a N = 50 distribution. Using this “random likeliness” criterion, we checked if the sorted abundance value of each nucleus in our network was correlated to their corresponding sorted rate distribution.
Tables A.1 and A.2 present the different elements for which the surface abundance is directly impacted by a given reaction. While Table A.1 lists the reactions, sorted by decreasing values of the surface abundance uncertainty for set A, Table A.2 shows a subset of this table, focusing on the elements that are observable in the atmosphere of CEMP stars and that can be used as tracers of the i-process nucleosynthesis. The adopted selection criterion assumes that at least two consecutive sequences of draws, both with a random likeliness of P ≤ 10−3 (i.e k ≥ 8), are found in the sorted distribution.
Figure 12 illustrates the chart of nuclides, with emphasis on the 868 experimentally unknown (n, γ) reactions relevant to the i-process nucleosynthesis. The reactions are color-coded by their uncorrelated parameter uncertainty (the ratio between maximum and minimum rates) for the nuclear set B, obtained using the BFMC method in Sect. 2.2.4. The nuclei highlighted by square pink-, orange-, or red-colored contours identify elements for which the (n, γ) reaction have a mild, medium, or high impact, x (defined as 0.1 dex ≤ x < 0.5 dex/0.5 dex ≤ x < 1.0 dex/x ≥ 1.0 dex, respectively) on one or multiple isotopic abundances and have a maximum isotopic fraction larger than 15%. Most of the highly uncertain (n, γ) reaction rates are away from the stability zone. However, some of the rates close to the valley of β-stability can also be quite uncertain, leading to a large impact on abundances, especially for targets with an even-Z number. Indeed, these reactions compete with the β-decay to an odd-Z number that usually has only one stable isotope. As a consequence, the rate has a significant influence on whether or not the flux will feed the stable isotope, provided the (n, γ) rate is lower than the β-decay rate, or if the flux will pursue further away from this isobar if the (n, γ) rate is higher.
 |
Fig. 12. Chart of the nuclides highlighting the 868 experimentally unknown (n, γ) reactions relevant to the i-process nucleosynthesis. The reactions are color-coded by their uncorrelated parameter uncertainty (the ratio between maximum and minimum rates) for the nuclear set B. Some of the reaction targets are highlighted by a square contour of a pink, orange, or red color. These correspond to reaction targets, as given in Table A.1 (Sect. 4.1), for which the parameter uncertainties have a mild, medium, or high impact, respectively, on one or multiple isotopic abundances. |
4.2. Impact of reducing the nuclear uncertainties
Now that the most impacting reactions have been determined, it remains to estimate their quantitative effect on the surface abundances. We could estimate the impact of each reaction entering Tables A.1 and A.2 by running two additional simulations with the upper and lower limits of that specific rate only. This procedure is of course costly in terms of computing, so only some illustrative examples are given below. These concern the recently constrained 139Ba(n, γ)140Ba rate directly affecting the s- and i-tracer La, the 153Sm(n, γ)154Sm acting on the production of the r- and i-tracer Eu, and 217Bi(n, γ)218Bi conditioning the production of Th and U.
4.2.1. The 139Ba(n, γ)140Ba reaction
The 139Ba(n, γ)140Ba reaction rate has recently been constrained experimentally by Mücher & Spyrou (priv. comm.). It corresponds to one of the important reactions found in Sect. 4.1 impacting the production of 139La, a relevant observable tracer (see Table A.2). Figure 13 shows the parameter uncertainties for the 139Ba(n, γ) rate for sets A and B3, as well as the new experimental constraint of Mücher & Spyrou (priv. comm.). We can see a clear reduction in the theoretical uncertainties, reaching 85% around the temperature of 250MK at which the i-process nucleosynthesis takes place in AGB stars. The 139La abundance uncertainties obtained for set B amount to 0.77 dex and are unlikely due to the sole variations of the 139Ba(n, γ) rate. Potentially complex combinations of different maximum and minimum rates around La and Ba isotopes will also contribute. To quantify this impact, we ran two stellar simulations, this time only varying the 139Ba(n, γ) rate to evaluate its impact on the 139La production. For this 139Ba(n, γ) analysis, we used the geometric mean between the maximum and minimum rates for all the 867 unknown (n, γ) rates of set B and kept them fixed while running our two simulations with minimum and the maximum values of the 139Ba(n, γ) rate for set B. In doing so, the parameter uncertainty associated with the 139Ba(n, γ) rate is found to affect the 139La production by 0.4 dex out of the 0.77 dex of total uncertainty (obtained when allowing all rates to be changed within their lower and upper limits in set B). The impact on the La production resulting from the reduction of uncertainties thanks to the recent measurement of Mücher & Spyrou can be estimated in the same way. New stellar evolution simulations, still using the geometric mean rates for the 867 theoretical ones and the upper and lower limits of the experimentally constrained rate, now lead to an uncertainty of less than 0.06 dex on the La production compared to the above-mentioned 0.4 dex uncertainty. This test shows how relevant this 139Ba(n, γ)140Ba reaction is for an accurate prediction of the La synthesis by the i-process.
 |
Fig. 13. Theoretical parameter uncertainties vs newly measured 139Ba(n, γ) rate (Mücher & Spyrou, priv. comm.). |
4.2.2. 153Sm(n, γ)154Sm and 217Bi(n, γ)218Bi
We explored two other interesting cases that have yet to be experimentally constrained: 153Sm(n, γ) and 217Bi(n, γ). 153Sm(n, γ) is found to have an impact on the 153Eu surface abundances (see Table A.2), an important observable tracer. The total uncertainty of the 153Eu i-process production by the AGB star amounts to 1.15 dex for set A. We ran two additional stellar simulations, as with the 139Ba method, to quantify the impact of 153Sm(n, γ). The resulting uncertainty for 153Eu stemming directly from the uncertainty of this rate is reduced to 0.69 dex out of the 1.15 dex of the total uncertainty for 153Eu.
The 217Bi(n, γ) is also an interesting reaction, as it seems to impact the production of actinides and more particularly 232Th, 235U, and 238U. In fact, a low 217Bi(n, γ) rate will favor the β-decay to a region where α-decay strongly dominates. This leads to a cycle denying the production of higher Z nuclei and producing elements in the Pb region (cf. Sect. 3 in Choplin et al. 2022a, for more details). In contrast, a 217Bi(n, γ) rate larger than the β-decay rate favors the flux capturing more neutrons, escaping the α-decay dominated region producing higher Z actinides, and especially boosting the production of these few long-lived isotopes in this region of the chart of nuclides. Using the same method as above, we find that the resulting uncertainty coming from the direct uncertainty of this rate is in fact of 0.99 dex for 232Th, 1.01 dex for 235U, and 1.01 dex for 238U. Comparing these values with those given in Table A.1, clearly 217Bi(n, γ) plays a key role in the possible enrichment of Th and U by the i-process, but other combinations of uncertain rates also contribute to the ∼2.5 − 3 dex found in the overall surface abundance uncertainty with set A.
4.2.3. Remaining uncertainties: Combinations of multiple reactions
We have constrained important reactions in Sect. 4.1 and we investigate in this section other reactions or combinations of reactions that can have an important effect on surface abundance uncertainties. For this purpose, we ran another 50 stellar evolution simulations for set A, with the specificity that we froze the reaction rates of all the (n, γ) reactions from Table A.1 (roughly 125 out of 868) to their geometric mean value. All the other reactions were once again randomly distributed among their minimum and maximum rates. In doing so, we expect to see if the reactions listed in Table A.1 can account for most of the uncertainties or if the combinations of all the other remaining reactions still have a significant impact. Figure 14 shows the comparison between the set A and the “frozen” set A described above. With this latter set, the uncertainties are clearly reduced, especially the odd-Z elements. Most of the uncertainties are now below 0.5 dex, meaning an average 0.5 dex reduction in uncertainties for the odd-Z elements. Large uncertainties still remain for the production of Th and U. This truly underlines the sensitivity of their nucleosynthesis to combinations of multiple reactions and not only to a specific one. For the rest of the nuclei above Z = 40, all the other reactions contribute on average to a 0.5 dex uncertainty. Finally, we note that the range of possible [Ba/Eu] ratios for the frozen set A ranges between 0.13 < [Ba/Eu] < 0.68, that is, an uncertainty of 0.55 dex, against 1.35 dex in the standard set A (cf. Sect. 3.3.1). For the [Ba/La] ratio, we obtain −0.15 < [Ba/La] < 0.10, that is, an uncertainty of 0.25 dex, against 0.98 dex in the standard set A.
 |
Fig. 14. Comparison between the surface abundances [X/Fe] and their uncertainties obtained with set A and the “frozen” set A in which all the (n, γ) rates from Table A.1 are fixed at their geometric mean value. |
4.3. Limitations of the method and potential improvements
The method of determining important reactions described in Sect. 4.1 of course has limitations. The two main problems are quantifying the impact of each individual reaction and the completeness of the set of reactions we derive. The method that we use here is double-edged: by exploring the abundance variations with random combinations of maximum and minimum rates, we significantly reduce the number of stellar simulations. Indeed, methods often used in other studies (such as Denissenkov et al. 2018, 2021; McKay et al. 2020) randomly vary individual rates, and hence require thousands of simulations to extract sensitivity results for all possible cases. This is incredibly CPU-consuming for 1D multi-zone stellar models, and hence often implies the use of simpler one-zone models that are not able to capture the complexity of stellar models. By finding first the maximum and minimum rates coming from the statistical uncertainties through the BFMC method, we can in fact perform a complete sensitivity study of a very large number of rates, with a greatly reduced number of stellar simulations (here N = 50). The downside of this method, however, is that by randomly varying rates all together, we cannot estimate the direct impact of a specific rate uncertainty on the final abundances. As discussed in Sect. 4.2, a solution is to compute stellar models with individual rate variations for each reaction to quantify the direct impact of one reaction on the surface abundances. This means 868 reactions times two rates (maximum or minimum) times the number of nuclear models (two here), meaning a tremendous number of stellar simulations. The second downside of our method is the completeness of the set of important reactions derived. Indeed, our method can relatively easily identify the reactions that have a strong impact on one or multiple isotopic abundances (see Sect. 4.1). However, we can only extract reactions from isotopic abundances if those are affected mainly by one given reaction; if many reactions contribute, we cannot disentangle the various contributions. This was illustrated in Sect. 4.2 when quantifying the sensitivity of the 139Ba(n, γ) reaction. While the direct impact of 139Ba(n, γ) on the 139La abundance is of 0.4 dex, the total uncertainty when varying all the 868 unknown (n, γ) rates is of 0.77 dex, and after reducing the uncertainties of the 139Ba(n, γ) rate there is still an uncertainty of roughly 0.4 dex. We find the same result for 153Sm(n, γ) and 217Bi(n, γ). This shows that the contribution from multiple reactions significantly impacts the total uncertainty of an isotopic abundance. One way of unveiling all the multiple reactions that could impact a specific nuclei would be the use of newly developed statistical tools, such as the global sensitivity analysis (see Chatterjee 2021; Bénesse et al. 2022; Bénesse 2022). However, to perform such a statistical analysis, a much larger sample of stellar simulations would be needed. Now that we have showed the stability of the method developed here, we plan to perform such a sensitivity study in a forthcoming work.
5. Conclusions
We investigated both the model (systematic) and parameter (statistical) uncertainties associated with theoretical neutron capture rates relevant for the i-process nucleosynthesis. We computed nine sets of TALYS rates to estimate the correlated model uncertainties and for two of those sets (one based on rather microscopic ingredients, set A, and one that considers more phenomenological models, set B) we applied the BFMC approach to anchor the parameter uncertainties with available experimental data, in other words the known neutron capture rates. In doing so, we obtain for both sets A and B an estimate of the upper and lower limits of the 868 unknown (n, γ) rates involved in our i-process network. Correlated model and uncorrelated parameter uncertainties are globally of the same order of magnitude but can differ quite significantly for the neutron-rich nuclei involved in the i-process.
We determine the impact of these nuclear uncertainties on the surface abundances of a 1 M⊙ [Fe/H] = − 2.5 multi-zone stellar model during its early AGB phase, which is subject to a proton ingestion event followed by an i-process nucleosynthesis with neutron densities of ≈1015 cm−3.
By considering nine different nuclear models with different combinations of NLD and PSF models, we found that the correlated model uncertainties lead to surface abundance uncertainties for Z ≥ 40 elements ranging between 0.5 and 1.0 dex, with the exception of Th and U, for which the uncertainty rises to about 3 dex. Due to the correlated nature of these uncertainties, abundance ratios remain much better constrained.
Similarly, the uncorrelated parameter uncertainties give rise to AGB surface abundance uncertainties for Z ≥ 40 elements also ranging between 0.5 and 1.0 dex, though odd-Z elements display significantly higher uncertainties due to their reduced number of stable isotopes and higher sensitivity to specific rates. Interestingly, the impact of uncorrelated parameter uncertainties obtained with two different nuclear models is found to be rather similar; however, the uncorrelated nature of these nuclear uncertainties has a significant impact on abundance ratios.
Both sources of nuclear uncertainties have an important impact on the predicted abundance of potential observable tracers such as Eu and La. Interestingly, the choice of the BFMC χ2 estimator mainly impacts the abundances of odd-Z elements. We reconfirm that the production of actinides is possible in this i-process site (Choplin et al. 2022a), but remains highly sensitive to both the parameter and model uncertainties. The resulting abundance uncertainties of actinides are in fact much larger than for any other species and underline the need for improved nuclear predictions for the neutron capture rates of Z ≥ 82 nuclei along the i-process path.
We developed a method to estimate surface abundance uncertainties in 1D multi-zone models and extract the impacting reactions affecting one or multiple isotopic abundances. We find roughly 125 (n, γ) reactions, including 25 with a high impact on elemental surface abundance uncertainties. Interestingly, more than 30 (n, γ) reactions have a medium to high impact on the surface abundance of elements that are usually taken as observable tracers of the i-process nucleosynthesis in CEMP stars. One of these reactions, 139Ba(n, γ)140Ba, has been recently experimentally constrained (Mücher & Spyrou, priv. comm.). We find that a 85% reduction in the uncertainties for this rate leads to a reduction of 0.4 dex out of the total 0.77 dex uncertainty of the La production.
Finally, we show that even by greatly reducing the uncertainties of the ∼125 main (n, γ) reactions impacting the AGB surface abundances, there are still uncertainties coming from complex combinations of multiple rate uncertainties. This means that the reductions in rate uncertainties, even for the reactions not listed here, might have a global impact on the surface abundance uncertainties. Moreover, new measurement of neutron captures on neutron-rich nuclei would also help to improve the theoretical nuclear models, in particular the description of NLDs and PSFs. Our analysis of the i-process uncertainty was conducted on a specific stellar model. An interesting perspective would be to apply our method to PIEs in AGB stars of different masses and different metallicities and also to investigate other sites such as RAWD (Denissenkov et al. 2017, 2021). Further developments in using global sensitivity analysis techniques (Bénesse et al. 2022) could also help to identify complete sets of relevant reactions.
Due to its still-complex modelling, the direct contribution to the reaction mechanism is neglected in the present analysis (see Goriely et al. 2021).
Note that the impact of the direct capture mechanism on this specific reaction has been neglected since it is estimated not to exceed 10%, see in particular Fig. 4 of Goriely et al. (2021).
Acknowledgments
S.M. and S.G. have received support from the European Union (ChECTEC-INFRA, project no. 101008324). L.S. and S.G. are senior F.R.S.-FNRS research associates. A.C. is a Postdoctoral Researcher of the Fonds de la Recherche Scientifique – FNRS. Figure 12 is an adaptation from https://github.com/kmiernik/Chart-of-nuclides-drawer.
References
- Arnould, M., & Goriely, S. 2020, Prog. Part. Nucl. Phys., 112, 103766 [NASA ADS] [CrossRef] [Google Scholar]
- Arnould, M., Goriely, S., & Takahashi, K. 2007, Phys. Rep., 450, 97 [Google Scholar]
- Bauge, E., & Dossantos-Uzarralde, P. 2011, J. Korean Phys. Soc., 59, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Bénesse, C. 2022, Ph.D. Thesis, Université Paul Sabatier -Toulouse III, France [Google Scholar]
- Bénesse, C., Gamboa, F., Loubes, J.-M., & Boissin, T. 2022, Mach. Learn., https://doi.org/10.1007/s10994-022-06202-y [Google Scholar]
- Blake, J. B., & Schramm, D. N. 1976, ApJ, 209, 846 [Google Scholar]
- Capote, R., Herman, M., Oblozinsky, P., et al. 2009, Nucl. Data Sheets, 110, 3107 [NASA ADS] [CrossRef] [Google Scholar]
- Chadwick, M., Kawano, T., Talou, P., et al. 2007, Nucl. Data Sheets, 108, 2742 [Google Scholar]
- Chatterjee, S. 2021, J. Am. Stat. Assoc., 116, 2009 [CrossRef] [Google Scholar]
- Choplin, A., Hirschi, R., Meynet, G., et al. 2018, A&A, 618, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choplin, A., Tominaga, N., & Meyer, B. S. 2020, A&A, 639, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choplin, A., Siess, L., & Goriely, S. 2021, A&A, 648, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choplin, A., Goriely, S., & Siess, L. 2022a, A&A, 667, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choplin, A., Siess, L., & Goriely, S. 2022b, A&A, 667, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, J. J., & Rose, W. K. 1977, ApJ, 212, 149 [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2009, PASA, 26, 139 [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Daoutidis, I., & Goriely, S. 2012, Phys. Rev. C, 86, 034328 [CrossRef] [Google Scholar]
- Denissenkov, P. A., Herwig, F., Battino, U., et al. 2017, ApJ, 834, L10 [Google Scholar]
- Denissenkov, P. A., Perdikakis, G., Herwig, F., et al. 2018, J. Phys. G Nucl. Phys., 45, 055203 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Herwig, F., Woodward, P., et al. 2019, MNRAS, 488, 4258 [Google Scholar]
- Denissenkov, P. A., Herwig, F., Perdikakis, G., & Schatz, H. 2021, MNRAS, 503, 3913 [NASA ADS] [CrossRef] [Google Scholar]
- Dillmann, I., Heil, M., Käppeler, F., et al. 2006, AIP Conf. Proc., 819, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiya, W., Hoppe, P., Zinner, E., Pignatari, M., & Herwig, F. 2013, ApJ, 776, L29 [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [Google Scholar]
- Gil-Pons, P., Doherty, C. L., Campbell, S. W., & Gutiérrez, J. 2022, A&A, 668, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goriely, S., & Capote, R. 2014, Phys. Rev. C, 89, 054318 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., & Delaroche, J.-P. 2007, Phys. Lett. B, 653, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., & Plujko, V. 2019, Phys. Rev. C, 99, 014303 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., & Siess, L. 2018, A&A, 609, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goriely, S., Hilaire, S., & Koning, A. J. 2008, Phys. Rev. C, 78, 064307 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., Janka, H. T., & Pearson, J. M. 2011a, A&A, 531, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goriely, S., Bauswein, A., & Janka, H.-T. 2011b, ApJ, 738, L32 [Google Scholar]
- Goriely, S., Hilaire, S., Péru, S., & Sieja, K. 2018, Phys. Rev. C, 98, 014327 [CrossRef] [Google Scholar]
- Goriely, S., Siess, L., & Choplin, A. 2021, A&A, 654, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, T. T., Simon, J. D., Li, T. S., et al. 2023, A&A, 674, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hilaire, S., Girod, M., Goriely, S., & Koning, A. J. 2012, Phys. Rev. C, 86, 064317 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, N., Kajino, T., Mathews, G. J., Fujimoto, M. Y., & Aoki, W. 2004, ApJ, 602, 377 [Google Scholar]
- Jadhav, M., Pignatari, M., Herwig, F., et al. 2013, ApJ, 777, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Just, O., Bauswein, A., Ardevol Pulpillo, R., Goriely, S., & Janka, H.-T. 2015, MNRAS, 448, 541 [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Karinkuzhi, D., Van Eck, S., Goriely, S., et al. 2021, A&A, 645, A61 [EDP Sciences] [Google Scholar]
- Karinkuzhi, D., Van Eck, S., Goriely, S., et al. 2023, A&A, 677, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koning, A. J., Hilaire, S., & Goriely, S. 2008, Nucl. Phys. A, 810, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Koning, A. J., Hilaire, S., & Goriely, S. 2023, Eur. Phys. J. A, 59, 131 [CrossRef] [Google Scholar]
- Kopecky, J., & Uhl, M. 1990, Phys. Rev. C, 41, 1941 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Arcoragi, J.-P., & Arnould, M. 1989, A&A, 210, 187 [Google Scholar]
- Liu, N., Savina, M. R., Davis, A. M., et al. 2014, ApJ, 786, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [Google Scholar]
- Mashonkina, L., Arentsen, A., Aguado, D. S., et al. 2023, MNRAS, 523, 2111 [NASA ADS] [CrossRef] [Google Scholar]
- McKay, J. E., Denissenkov, P. A., Herwig, F., Perdikakis, G., & Schatz, H. 2020, MNRAS, 491, 5179 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, B. S., Clayton, D. D., & The, L.-S. 2000, ApJ, 540, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, B. S., The, L. S., Clayton, D. D., & El Eid, M. F. 2004, in Lunar Planet. Sci. Conf., eds. S. Mackwell, & E. Stansbery, 1908 [Google Scholar]
- Mishenina, T., Pignatari, M., Carraro, G., et al. 2015, MNRAS, 446, 3651 [Google Scholar]
- Nishimura, N., Takiwaki, T., & Thielemann, F.-K. 2015, ApJ, 810, 109 [Google Scholar]
- Pignatari, M., Hoppe, P., Trappitsch, R., et al. 2018, Geochim. Cosmochim. Acta, 221, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Hashimoto, M., & Nomoto, K. 1990, A&A, 234, 211 [NASA ADS] [Google Scholar]
- Roederer, I. U., Karakas, A. I., Pignatari, M., & Herwig, F. 2016, ApJ, 821, 37 [Google Scholar]
- Siegel, D. M., Barnes, J., & Metzger, B. D. 2019, Nature, 569, 241 [Google Scholar]
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., & Arnould, M. 2008, A&A, 489, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Suda, T., & Fujimoto, M. Y. 2010, MNRAS, 405, 177 [NASA ADS] [Google Scholar]
- Thielemann, F.-K., Arnould, M., & Hillebrandt, W. 1979, A&A, 74, 175 [Google Scholar]
- Wanajo, S., Sekiguchi, Y., Nishimura, N., et al. 2014, ApJ, 789, L39 [Google Scholar]
- Wang, M., Huang, W., Kondev, F., Audi, G., & Naimi, S. 2021, Chin. Phys. C, 45, 030003 [CrossRef] [Google Scholar]
- Winteler, C., Käppeli, R., Perego, A., et al. 2012, ApJ, 750, L22 [Google Scholar]
- Xu, Y., Goriely, S., & Khan, E. 2021, Phys. Rev. C, 104, 044301 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tables
The reported quantities are the nucleus properties (columns 1, 2, and 3), the contributing range of the concerned isotope to the total elemental abundance (column 4), the ratio between the maximum and minimum abundances (in log: Δ50) for sets A and B (columns 5 and 6), the reaction directly impacting its abundance (column 7), and the ratio between the maximum and minimum rates of the concerned (n, γ) reaction (columns 8 and 9). Table A.2 is the same as Table A.1 but for isotopes of the main observable heavy elements in CEMP stars, that is, i-process nucleosynthesis tracers.
List of nonexperimental (n, γ) reactions and the impact of their nuclear uncertainty on the surface abundances in our low-mass, low-metallicity AGB star model. See Sect.A for the description of the quantities.
Same as Table A.1 but for isotopes of the main observable heavy elements in CEMP stars, that is, i-process nucleosynthesis tracers.
All Tables
List of nonexperimental (n, γ) reactions and the impact of their nuclear uncertainty on the surface abundances in our low-mass, low-metallicity AGB star model. See Sect.A for the description of the quantities.
Same as Table A.1 but for isotopes of the main observable heavy elements in CEMP stars, that is, i-process nucleosynthesis tracers.
All Figures
 |
Fig. 1. Theoretical over experimental (n, γ) MACS for the 239 experimentally known rates at 30 keV. The error bars display the maximum and minimum rates obtained by the nine different combinations of NLD and PSF models (including sets A and B; see text). The full circles correspond to set B and the gray shaded area shows variations within a factor of two. |
| In the text | |
 |
Fig. 2. Histogram of the number of parameter combinations for sets A and B as a function of their frms with respect to the experimental MACS. |
| In the text | |
 |
Fig. 3. Theoretical over experimental (n, γ) MACS for the 239 (20 ≤ Z ≤ 83) known rates at 30 keV obtained with set A (top) and set B (bottom). The error bars display the uncorrelated parameter uncertainties obtained through the BFMC method using frms≤ 2.0. The gray shaded area guides the eye for a deviation within a factor of two. |
| In the text | |
 |
Fig. 4. Uncertainties as a function of the neutron separation energy, Sn. (a) Model uncertainties between sets A and B, represented by the ratio of the maximum to minimum (n, γ) rates (max[⟨σ⟩A,⟨σ⟩B]/min[⟨σ⟩A,⟨σ⟩B]). The 239 experimentally known reactions are shown with blue dots and the unknown ones with red dots. (b) Same as the upper panel but for the parameter uncertainties for set B. All rates are estimated at T = 2.5 × 108 K. |
| In the text | |
 |
Fig. 5. Correlated model uncertainties represented by the ratio of the maximum to minimum (n, γ) MACS (Fig. 4a) as a function of uncorrelated parameter uncertainties of set B (Fig. 4b). The 239 experimentally known (n, γ) reactions are shown in blue and the 868 theoretical ones in red. All rates are estimated at T = 2.5 × 108 K. |
| In the text | |
 |
Fig. 6. Correlation plots for the four parameters in set A (left) and set B (right) using the total set (Ncomb = 200; black dots) or the selected subset with frms ≤ 2.0 (Ncomb = 61 for set A and Ncomb = 97 for set B; red dots). Each contour corresponds to iso-proportions of the density, with the first contour corresponding to 20% and incrementing by 20%. The diagonal shows the (normalized) marginal distribution of each parameter. |
| In the text | |
 |
Fig. 7. Surface [X/Fe] abundance ratios of AGB models for the nine different nuclear models considered. The bottom plot shows the differences between the various models and set A. |
| In the text | |
 |
Fig. 8. Evolution of the averaged uncertainties, |
| In the text | |
 |
Fig. 9. Scatter plot of the surface [X/Fe] abundance ratios of AGB models for the nuclear set A (top) and set B (bottom) with frms ≤ 2.0. The blue (red) line shows the 5th (95th) percentile (Eq. (5)). The bottom subplot in each panel shows Δ50, which is the difference between the 95th and 5th percentile (Eq. (5)) for the N = 50 simulations. |
| In the text | |
 |
Fig. 10. Comparison between the surface abundances [X/Fe] and their uncertainties obtained with nuclear sets A and B, for frms ≤ 2.0 case. The red (blue) region shows the extent of the [X/Fe] region between the 5th and 95th percentile for set A (set B). The purple area shows the intersection between the two models. |
| In the text | |
 |
Fig. 11. Comparison between the surface abundances [X/Fe] and their uncertainties obtained with the uncorrelated parameter uncertainties of nuclear set A, with frms≤ 2.0 (blue) and frms≤ 2.5 (red). |
| In the text | |
 |
Fig. 12. Chart of the nuclides highlighting the 868 experimentally unknown (n, γ) reactions relevant to the i-process nucleosynthesis. The reactions are color-coded by their uncorrelated parameter uncertainty (the ratio between maximum and minimum rates) for the nuclear set B. Some of the reaction targets are highlighted by a square contour of a pink, orange, or red color. These correspond to reaction targets, as given in Table A.1 (Sect. 4.1), for which the parameter uncertainties have a mild, medium, or high impact, respectively, on one or multiple isotopic abundances. |
| In the text | |
 |
Fig. 13. Theoretical parameter uncertainties vs newly measured 139Ba(n, γ) rate (Mücher & Spyrou, priv. comm.). |
| In the text | |
 |
Fig. 14. Comparison between the surface abundances [X/Fe] and their uncertainties obtained with set A and the “frozen” set A in which all the (n, γ) rates from Table A.1 are fixed at their geometric mean value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} {f_{\mathrm{rms}}}=\exp \left[ {\frac{1}{N_e}\sum ^{N_e}_{i=1}\ln ^2 \left(\frac{\langle \sigma _{\mathrm{th},i}\rangle }{\langle \sigma _{\exp ,i}\rangle }\right)}~\right]^{1/2} \end{aligned} $$](/articles/aa/full_html/2024/04/aa47734-23/aa47734-23-eq1.gif)
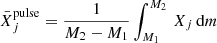
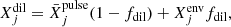
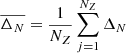
![$$ \begin{aligned} \Delta _N = p_{N}^{95} (\mathrm{[X/Fe]}) - p_{N}^{5} (\mathrm{[X/Fe]}) \end{aligned} $$](/articles/aa/full_html/2024/04/aa47734-23/aa47734-23-eq13.gif)