EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A159 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A159
Number of page(s) 6
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202348549
Published online 15 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

More than 5500 exoplanets have been discovered so far1. This has allowed us to perform statistical studies of their properties that provided valuable insights into their formation and evolution (e.g. Adibekyan 2019; Zhu & Dong 2021; Luque & Pallé 2022). In this respect, a precise, and if possible, accurate determination of the main physical properties of these planets, such as their masses and radii, is critical.

Exoplanetary masses are primarily determined using the radial velocity (RV) method. In some instances, planet-planet interactions can result in transit-timing variations (TTVs), and if these are measured, they can be used to determine the planetary masses (Agol et al. 2005). Interestingly, there is a significant discrepancy between the masses obtained from these two methods for planets with masses up to about that of Neptune (e.g. Mills & Mazeh 2017). Specifically, RV-detected planets appear to be denser than TTV-detected planets of the same radius (Leleu et al. 2023). Although the origins of this discrepancy are not yet fully understood, it is likely influenced by a combination of astrophysical and observational factors (Leleu et al. 2023).

One potential approach for investigating this issue is to consider it from the perspective of the host stars. The composition and density of low-mass planets are connected to the chemical composition of their host stars (Adibekyan et al. 2021). Therefore, a straightforward approach is to compare the abundances of planet-forming elements in the host stars.

We present the results of our spectroscopic analysis of FGK dwarf stars hosting low-mass TTV- and RV-exoplanets. The paper is structured as follows: in Sect. 2, we introduce the sample, and in Sect. 3, we detail the composition of the stars. Our findings are discussed in Sect. 4, and we provide a summary of the work in Sect. 5.

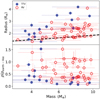thumbnail Fig. 1

Mass-radius (top) and scaled density-radius(bottom) diagrams for the planets in our sample. The blue and red symbols represent planets with TTV and RV mass determinations, respectively. The dashed black curve displays the expected mass-radius relation for an Earth-like composition (32% Fe + 68% MgSiO3, Dorn et al. 2017).

2 The sample

We started our sample selection from the NASA Exoplanet Archive (NEA)2 by selecting planets with masses below 10 M⊕ orbiting FGK-type stars with effective temperatures (Teff) between 5000 and 6500 K. This temperature range allows for the precise determination of stellar atmospheric abundances of relevant elements. We excluded two TTV planets (Kepler-51,c and Kepler-51,d) that have unusually large radii of about 9 R⊕ (Masuda 2014) and were found to be not reliable (Hadden & Lithwick 2017). We selected 62 planets (orbiting 48 stars) with a precision in both mass and radius better than 40%. For 46 of the host stars (hosting 59 planets), we collected high-resolution optical spectra with a signal-to-noise ratio (S/N) of at least 40.

The distribution of 59 planets on the mass-radius diagram is depicted in the top panel of Fig. 1. The masses of 44 of these planets were determined using the RV method, and the masses of the remaining 15 planets were determined through TTV. We note that planetary masses and radii were determined by different authors, which might introduce a factor contributing to uncertainty. The figure confirms previous findings that TTV planets tend to have larger radii for a given mass when compared to planets whose masses are determined via the RV method.

In the bottom panel of Fig. 1, we show the density of the planets (ρ), normalized to that expected for an Earth-like composition (ρEarth-like) (Dorn et al. 2017). This normalization takes into account that planets with different masses may have different densities, even when the composition is the same, due to gravitational compression. The figure suggests systematically lower densities for TTV-detected planets when compared with their RV-detected counterparts.

3 Composition of stars and planet-building blocks

In this section, we outline the method for determining the abundance of stars and the composition of the building blocks for planets.

3.1 Stellar parameters and abundances

As mentioned earlier, we used high-resolution spectra of the 46 planet-hosting stars to homogeneously determine their stellar parameters and eventually, their atmospheric compositions.

We determined the stellar atmospheric parameters (Teff, surface gravity log g, microturbulent velocity Vtur, and metallicity [Fe/H]) of the sample stars following our previous works (e.g. Santos et al. 2013; Sousa 2014). In our local thermodynamic equilibrium (LTE) analysis, we measured the equivalent widths (EW) of iron lines using the code ARES v23 (Sousa et al. 2015) and imposed excitation and ionization equilibrium. We adopted a grid of Kurucz model atmospheres (Kurucz 1993) and the 2014 version of the radiative transfer code MOOG (Sneden 1973). The stars of our sample cover the following range of parameters: 5081 < Teff < 6330 K, −0.47 < [Fe/H] < 0.4 dex, and 4.0 < log g < 4.5 dex (they are all dwarfs).

The stellar abundances of the elements were also derived using the same tools and models as for the stellar parameter determination, and we used the classical curve-of-growth analysis method assuming LTE. Although the EWs of the spectral lines were automatically measured with ARES, for the elements for which only two or three lines were available, we visually inspected the EWs measurements. To derive the chemical abundances of Mg, Si, Ti, and Ni, we closely followed the methods described in our previous works (Adibekyan et al. 2012, 2015). The abundances of the volatile elements O and C were derived following our previous works (Delgado Mena et al. 2010, 2021; Bertran de Lis et al. 2015). Following the discussion in Delgado Mena et al. (2021), we opted to use the 6158 Å line to determine the abundance of O. The EWs of this spectral line were manually measured using the splot task in IRAF.

It is particularly challenging to determine the C and O abundances for stars cooler than about 5200 K, especially when the S/N falls below approximately 200 (Delgado Mena et al. 2010; Bertran de Lis et al. 2015). We were unable to determine the C abundance for 17 of the stars and the O abundance for 21 stars. For these stars, we predicted their C and O abundances using a machine-learning (ML) model, as described in Appendix A.

In Fig. 2, we display the [X/Fe] abundance ratios as a function of metallicity, where X represents C, O, Mg, Si, Ti, and Ni. The stars hosting TTV-mass and RV-mass planets are represented in blue and red, respectively. The two populations visually appear to exhibit a similar distribution of these elements. However, the Anderson-Darling (AD) and Kolmogorov-Smirnov (KS) two-sample tests suggest that the distributions of the [Mg/Fe] and [Si/Fe] abundance ratios do not originate from the same parent distribution (p-values < 0.05). These differences may play a role in the interior structure and composition of low-mass TTV and RV planets, as we discuss in the following sections.

3.2 Composition of the planet-building blocks

Taking the abundances of C, O, Mg, Si, and Fe into account, we estimated the iron-to-silicate mass fraction (ƒiron) and the water-mass fraction (wf) of the protoplanetary disks using the simple stoichiometric model presented in Santos et al. (2015, 2017). While the determination of ƒiron depends solely on the abundances of Mg, Si, and Fe, the determination of wƒ relies on the abundances of all five elements.

In Fig. 3, we show the cumulative distributions of ƒiron and wf for stars hosting TTV-mass and RV-mass planets. Both the two-sample AD and KS tests yield a p-value below 0.02, suggesting that the two samples have distinct distributions of ƒiron. The p-values of the AD and KS tests for wƒ indicate that the distributions might come from the same parent distribution.

thumbnail Fig. 2

Abundance ratios ([X/Fe]) as a function of metallicity for the sample stars. The blue and red symbols represent planets with TTV and RV mass determinations, respectively. The star symbols indicate the abundances predicted using the ML method, and the circles represent the spectroscopic determinations. The gray dots represent stars without planets from the HARPS GTO sample (Adibekyan et al. 2012).
thumbnail Fig. 3

Cumulative distributions of ƒiron and wf for the stars hosting planets with TTV and RV mass determinations.

4 Results

Under the assumption that low-mass (< 10 M⊕) and small (<2 R⊕) planets are composed of metallic cores and mantles, Adibekyan et al. (2021) observed a correlation between the scaled density of these planets and their ƒiron content. In Fig. 4, we show the dependence of the scaled density of planets on their ƒiron and wƒ. The figure does not reveal a clear correlation between these parameters. This lack of a correlation arises because many of the planets in the current sample are larger than 2 R⊕, with non-negligible atmospheres4. In this scenario, the size of the atmospheres, rather than the interior composition, influences the radius, and consequently, the scaled density of the planets.

The size of the atmospheres, among other factors, depends on the proximity of the planets to their stars. In the current sample, all TTV planets have orbital periods longer than 7 days, while 29 out of 44 RV planets have shorter periods. When considering only the long-period planets (see Figs. 5 and 6), we find that primarily the planets with low scaled densities remain. Of these, the TTV planet hosts generally exhibit higher values of ƒiron than the RV planet hosts: Their mean value is 35.3 ± 2.8(±0.75), and 30.6 ± 3.4(±0.9), respectively. The p-values of the AD and KS tests return values lower than 0.001. The TTV planet hosts also seem to have slightly lower values of wƒ (61.1 ± 7.3(±1.9) and 65.7 ± 8.3(±2.1)), although the AD and KS tests indicate that the difference is not statistically significant.

The restriction on orbital period eliminates most RV planets with masses below 5 M⊕ because at relatively wide orbits, only high-mass planets can be detected using the RV method. When applying a lower mass limit cut at 5 M⊕, the two samples display a relatively similar mass distributions. However, the sample sizes decrease to only 6 TTV planets (orbiting 5 stars) and 14 RV planets (orbiting 14 stars). Figure 7 indicates at higher ƒiron (33.1 ± 2.6(±1.1) and 30.9 ± 3.2(±0.9)) and lower wƒ (58.3 ± 5.0(±2.1) and 64.9 ± 8.1(±2.1)) for the TTV planets than for their RV counterparts. Nonetheless, the small sample sizes and large uncertainties make a firm conclusion challenging.

A word of caution should be added here. Figure 8 appears to suggest a relation between ƒiron and S/N, at least for values below about 100. Unfortunately, the spectra of most TTV planet-hosting stars are affected by this6, making it difficult to determine whether the lowest values of ƒiron arise from a low S/N or are caused by the chemically distinct stars that these are TTV planets orbit. In Fig. 9, we show the dependence of the abundance ratios on S/N. The figure shows a slight dependence of [Si/Fe] on S/N. Stars with low S/N spectra also exhibit low ƒiron. To quantify the relation between the abundance ratios and S/N, we computed the Pearson correlation coefficients and their corresponding p-values. The highest correlation coefficient, 0.27, is observed for [Si/Fe], with a p-value of 0.07, indicating that it is not statistically significant. The Si abundances were derived using 14 spectral lines that cover a wide range of wavelengths, making it hard to conclude that a low S/N has a high systematic impact on the abundance determination of this element. In addition, our visiual inspection of the Gaussian fits of the spectral lines of Si did not reveal any indication of incorrect or suspicious measurement.

We also tested whether the stars hosting TTV and RV planets have different kinematic properties or belong to different galactic populations (see Appendix B). In Fig. B.1, we display the distributions of the planet hosts in velocity space. The figure, as well as our tests, revealed no differences in their kinematic properties. For both samples, approximately one out of ten stars belongs to the Galactic thick-disk population, and the rest belong to the thin disk, which is typical for field stars in the solar neighborhood (e.g., Adibekyan et al. 2013).

thumbnail Fig. 4

Scaled density of planets as a function of ƒiron and wƒ.
thumbnail Fig. 5

Same as Fig. 1, but for planets with orbital periods longer than 7 days.
thumbnail Fig. 6

Same as Fig. 4, but for planets with orbital periods longer than 7 days.
thumbnail Fig. 7

Same as Fig. 4, but for planets with orbital periods longer than 7 days and masses higher than 5 M⊕.
thumbnail Fig. 8

Dependence of ƒiron and wf on S/N.
thumbnail Fig. 9

Dependence of the abundance ratios on S/N.

5 Summary

We employed the largest dataset of FGK-type stars hosting planets with massed determined via TTV and RV methods. We determined the host star abundances, and, employing a simple stoichiometric model (Santos et al. 2015, 2017), we estimated the iron-to-silicate mass fraction (ƒiron) and the water-mass fraction (wƒ) of the protoplanetary disks. We then explored the possibility that the discrepant mass/densities in these two populations (e.g. Leleu et al. 2023) might be linked to the composition of the protoplanetary disks in which they formed.

Our tests show indications that TTV planets tend to have higher ƒiron and lower wƒ than RV planets. However, these results should be interpreted with caution due to differences in planetary properties (e.g., orbital periods for a given mass) between the two samples and the relatively small sample sizes. Furthermore, the spectra of stars hosting TTV planets exhibit a significantly lower S/N than their RV counterparts, which could influence the results.

Even when these limitations of the analysis are ignored, it is challenging to interpret the results. In particular, the higher ƒiron and lower wƒ observed in TTV planets would suggest that these planets (without considering the atmospheres) are denser than their RV counterparts on average. This would imply that larger atmospheres are required on TTV planets to account for their lower overall densities. To the best of our knowledge, no previous studies have suggested such a correlation.

It is also possible that the specific composition (e.g., high ƒiron) of the disk might facilitate the formation of compact mul-tiplanet systems (e.g., TTV planets), suggesting that the density could be related to the formation and evolution history of these systems (e.g. Lee & Chiang 2016; Izidoro et al. 2017).

In conclusion, investigating the TTV-RV mass discrepancy through a host star chemical analysis clearly holds promise for future research. However, to make more conclusive determinations, larger sample sizes and higher-quality data are required. In the meantime, we hope that the provided host star abundances can be used by modelers of the exoplanet interior to study the composition of both TTV and RV planets, which may help to shed light on this intriguing problem.

Acknowledgements

This work was supported by Fundação para a Ciência e Tecnologia through national funds and by FEDER through COMPETE2020 -Programa Operacional Competitividade e Internacionalização by these grants: UIDB/04434/2020; UIDP/04434/2020; 2022.06962.PTDC. Funded/Co-funded by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. This research has made use of the NASA Exoplanet Archive operated by the California Institute of Technology under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. In this work we used the Python language and several scientific packages: Numpy (van der Walt et al. 2011), Scipy (virtanen et al. 2020), Pandas (Wes McKinney 2010), and Matplotlib (Hunter 2007).

Appendix A Prediction of C and O abundances with XGBoost

We were unable to determine the spectroscopic abundances of carbon (C) and oxygen (O) for 17 and 21 stars, respectively. For these stars, we empirically estimated the C and O abundances using the machine-learning algorithm called ’XGBRegressor’ (Chen & Guestrin 2016). The estimation of C and O (the target variables) was based on the abundance of iron and the mean abundance of Mg, Si, and Ti (the input feature variables). While using any of these abundances individually or all of them simultaneously provides similar results, taking the mean of the abundances slightly improves the performance of the model predictions.

Our initial sample was based on the HARPS sample Adibekyan et al. (2012). C abundance of 758 stars and O abundance of 610 stars were taken from Delgado Mena et al. (2021), and the iron abundance was taken from Delgado Mena et al. (2017). These samples were divided into training (70%), validation (20%), and testing (10%) datasets. We used the Optuna package for an automatic hyperparameter optimization (Akiba et al. 2019). The mean absolute error for the estimated C and O abundances on the test dataset is 0.06 and 0.07 dex, respectively. We note that this is consistent with the mean uncertainties in the abundance determinations of these elements (0.05 dex for C and 0.07 dex for O).

We also tested the estimated C and O abundances for the current sample of planet-hosting stars, for which we determined the abundances of these elements (see Fig. A.1). The mean difference and standard deviation for C and O are 0.01 ± 0.05 and 0.01 ± 0.08 dex, respectively.

thumbnail Fig. A.1

C and O abundances as a function of metallicity of the sample stars that we spectroscopically determined (leftmost panels), predicted using the model (middle panels), and the difference in the two estimates (rightmost panels).

Appendix B Kinematics of the host stars

We computed the Galactic space velocity (U, V, W) of the planet-hosting stars based on their coordinates, proper motion, parallax, and systemic RV extracted from Gaia DR3, following the formulation developed in Johnson & Soderblom (1987). We considered the solar peculiar motion from Schönrich et al. (2010) to calculate the velocities with respect to the local standard of rest. These velocities were used to estimate the probability that the stars belong to the thin disk, the thick disk, or the halo, based on the kinematic approach presented in Adibekyan et al. (2012)7.

thumbnail Fig. B.1

Toomre diagram for the full sample. The typical uncertainties are below 1 km/s and are hardly visible in the plot. The dotted line shows constant values of the total Galactic velocity Vtot = 100 km/s.

References

  1. Adibekyan, V. 2019, Geosciences, 9, 105 [Google Scholar]
  2. Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 554, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A&A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Adibekyan, V., Dorn, C., Sousa, S. G., et al. 2021, Science, 374, 330 [NASA ADS] [CrossRef] [Google Scholar]
  6. Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [Google Scholar]
  7. Akiba, T., Sano, S., Yanase, T., Ohta, T., & Koyama, M. 2019, arXiv e-prints [arXiv: 1987.18982] [Google Scholar]
  8. Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A&A, 576, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Chen, T., & Guestrin, C. 2016, KDD ’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785 [Google Scholar]
  10. Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2010, ApJ, 725, 2349 [NASA ADS] [CrossRef] [Google Scholar]
  11. Delgado Mena, E., Tsantaki, M., Adibekyan, V. Z., et al. 2017, A&A, 606, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Delgado Mena, E., Adibekyan, V., Santos, N. C., et al. 2021, A&A, 655, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Dorn, C., Venturini, J., Khan, A., et al. 2017, A&A, 597, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Hadden, S., & Lithwick, Y. 2017, AJ, 154, 5 [Google Scholar]
  15. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  16. Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [Google Scholar]
  17. Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [Google Scholar]
  18. Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 18 [Google Scholar]
  19. Lee, E. J., & Chiang, E. 2016, ApJ, 817, 90 [Google Scholar]
  20. Leleu, A., Delisle, J. B., Udry, S., et al. 2023, A&A, 669, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Luque, R., & Pallé, E. 2022, Science, 377, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  22. Masuda, K. 2014, ApJ, 783, 53 [Google Scholar]
  23. Mills, S. M., & Mazeh, T. 2017, ApJ, 839, L8 [Google Scholar]
  24. Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Santos, N. C., Adibekyan, V., Mordasini, C., et al. 2015, A&A, 580, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Santos, N. C., Adibekyan, V., Dorn, C., et al. 2017, A&A, 608, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [Google Scholar]
  28. Sneden, C. A. 1973, PhD thesis, The University of Texas at Austin, USA [Google Scholar]
  29. Sousa, S. G. 2014, in Determination of Atmospheric Parameters of B (Berlin: Springer), 297 [Google Scholar]
  30. Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  32. virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [NASA ADS] [CrossRef] [Google Scholar]
  33. Wes McKinney 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt & J. Millman, 56 [Google Scholar]
  34. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, Proc. Natl. Acad. Sci., 116, 9723 [Google Scholar]
  35. Zhu, W., & Dong, S. 2021, ARA&A, 59, 291 [NASA ADS] [CrossRef] [Google Scholar]
3

The last version of the ARES code (ARES v2) can be downloaded at https://github.com/sousasag/ARES

4

According to Zeng et al. (2019), in an extreme case, if a planet with a mass of 5 M⊕ is composed entirely of water, its radius would be approximately 2 R⊕, which is smaller than the radii of many planets in the current sample.

5

The values in parentheses are standard errors of the mean, calculated as the standard deviation divided by the square root of the sample size.

6

To determine masses with the RV method, a relatively large number of spectra is required, which, when combined, result in a high S/N.

7

We used the GalVel_Pop package available at https://github.com/vadibekyan/GalVel_Pop

All Figures

thumbnail Fig. 1

Mass-radius (top) and scaled density-radius(bottom) diagrams for the planets in our sample. The blue and red symbols represent planets with TTV and RV mass determinations, respectively. The dashed black curve displays the expected mass-radius relation for an Earth-like composition (32% Fe + 68% MgSiO3, Dorn et al. 2017).
In the text
thumbnail Fig. 2

Abundance ratios ([X/Fe]) as a function of metallicity for the sample stars. The blue and red symbols represent planets with TTV and RV mass determinations, respectively. The star symbols indicate the abundances predicted using the ML method, and the circles represent the spectroscopic determinations. The gray dots represent stars without planets from the HARPS GTO sample (Adibekyan et al. 2012).
In the text
thumbnail Fig. 3

Cumulative distributions of ƒiron and wf for the stars hosting planets with TTV and RV mass determinations.
In the text
thumbnail Fig. 4

Scaled density of planets as a function of ƒiron and wƒ.
In the text
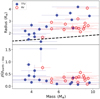thumbnail Fig. 5

Same as Fig. 1, but for planets with orbital periods longer than 7 days.
In the text
thumbnail Fig. 6

Same as Fig. 4, but for planets with orbital periods longer than 7 days.
In the text
thumbnail Fig. 7

Same as Fig. 4, but for planets with orbital periods longer than 7 days and masses higher than 5 M⊕.
In the text
thumbnail Fig. 8

Dependence of ƒiron and wf on S/N.
In the text
thumbnail Fig. 9

Dependence of the abundance ratios on S/N.
In the text
thumbnail Fig. A.1

C and O abundances as a function of metallicity of the sample stars that we spectroscopically determined (leftmost panels), predicted using the model (middle panels), and the difference in the two estimates (rightmost panels).
In the text
thumbnail Fig. B.1

Toomre diagram for the full sample. The typical uncertainties are below 1 km/s and are hardly visible in the plot. The dotted line shows constant values of the total Galactic velocity Vtot = 100 km/s.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.