| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202451704 | |
| Published online | 30 October 2024 | |
SWEET-Cat: A view on the planetary mass-radius relation
1
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762
Porto,
Portugal
2
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre,
4169-007
Porto,
Portugal
3
Instituto de Alta Investigación, Universidad de Tarapacá,
Casilla 7D,
Arica,
Chile
4
Aix Marseille Univ, CNRS, CNES, LAM,
Marseille,
France
5
Instituto de Astrofísica de Canarias,
38200
La Laguna, Tenerife,
Spain
6
School of Physics & Astronomy, University of Birmingham, Edgbaston,
Birmingham
B15 2TT,
UK
7
INAF – Osservatorio Astrofisico di Arcetri,
Largo Enrico Fermi 5,
50125
Firenze,
Italy
★ Corresponding author; sergio.sousa@astro.up.pt
Received:
29
July
2024
Accepted:
16
September
2024
Aims. SWEET-Cat (Stars With ExoplanETs Catalog) was originally introduced in 2013, and since then, the number of confirmed exoplanets has increased significantly. A crucial step for a comprehensive understanding of these new worlds is the precise and homogeneous characterization of their host stars.
Methods. We used a large number of high-resolution spectra to continue the addition of new stellar parameters for planet-hosting stars in SWEET-Cat following the new detection of exoplanets listed both in the Extrasolar Planets Encyclopedia and in the NASA exoplanet archive. We obtained high-resolution spectra for a significant number of these planet-hosting stars, either observed by our team or collected through public archives. For FGK stars, the spectroscopic stellar parameters were derived for the spectra following the same homogeneous process using ARES+MOOG as for the previous SWEET-Cat releases. The stellar properties were combined with the planet properties to study possible correlations that could shed more light on the star-planet connection studies.
Results. We have increased the number of stars with homogeneous parameters by 232 (~25% – from 959 to 1191). We focus on the exoplanets that have had both mass and radius determined to review the mass-radius relation, and we find results consistent with the ones previously reported in the literature. For the massive planets, we also revisit the radius anomaly, confirming a metallicity correlation for the radius anomaly already hinted at in previous results.
Key words: planets and satellites: formation / planets and satellites: fundamental parameters / stars: abundances / stars: fundamental parameters
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Planetary system studies have grown immensely in the last couple of decades following the first detections of exoplanets orbiting solar-type stars (e.g., Mayor & Queloz 1995; Marcy & Butler 1996) and the thousands of exoplanets detected since. More interesting than the fantastic increase in the rate of discoveries is the surprisingly vast diversity of exoplanets present in the Galaxy, unraveled mostly by dedicated search surveys using radial velocity (RV) and transit techniques (e.g. Ehrenreich et al. 2020; Lillo-Box et al. 2020; Armstrong et al. 2020). These discoveries provide crucial constraints for the exhaustive understanding of planet formation and evolution, based initially on our knowledge of the Solar System alone.
Because the main techniques to detect and characterize these exoplanets rely on the observation of their host stars, it is crucial to derive precise, accurate, and homogeneous stellar parameters. The homogeneous determination of such parameters is even more important if we want to perform statistical studies on the different populations of exoplanets that have been discovered in recent years (e.g. Adibekyan et al. 2024; Buchhave et al. 2018; Santos et al. 2017; Goda & Matsuo 2019).
The SWEET-Cat database (“Stars With ExoplanETs Catalog”1) compiles an updated list of all stars known to host planets. First presented in Santos et al. (2013), SWEET-Cat started with a list of only ~700 planet-hosting stars, with about 65% of these having homogeneous spectroscopic parameters derived by our team using a well-defined spectral analysis procedure. The number of planet-hosting stars has grown to more than 4000 stars (hosting approximately 5000 exoplanets in total) over the past decade given the very productive results of many well-known ground- and space-based projects such as HARPS, ESPRESSO, Kepler, and TESS (Mayor et al. 2011; Pepe et al. 2021; Borucki et al. 2010; Ricker et al. 2014, respectively). The high rate of planet-hosting discoveries is hard to follow with the derivation of homogeneous spectroscopic parameters, especially for the many faint stars coming from Kepler transit detections for which it is much more difficult to obtain high-quality spectra. Because of this, in recent years the percentage of planet-hosting stars in SWEET-Cat with homogeneous parameters has decreased to only about 20%.
Here, we present a significant update to SWEET-Cat. This work consists of the addition of 232 new stellar atmospheric parameters for planet hosts, in addition to the 31 recent planet-hosting stars that we also included in SWEET-Cat since its last update in 2021. These came from different planet detection and characterization works to which our team has contributed for the stellar characterization. For all these new planet-hosting stars, we maintain the link to the NASA exoplanet archive database2 (Akeson et al. 2013), as well as the Extrasolar Planets Encyclopedia3 (Schneider et al. 2011) to allow for an easy correlation between stellar and planet properties for the community.
The following sections describe the work done for the update of SWEET-Cat as well as a short review of the mass-radius of exoplanets as an example for the use of SWEET-Cat data. Section 2 describes the spectroscopic data compilation for the catalog. Section 3 recalls how the spectroscopic parameters were homogeneously derived for SWEET-Cat. Section 4 is focused on the planetary mass and radius relations review. In Sec. 5, we revisit the radius anomaly observed for giant massive planets and its observational link with metallicity. In Sec. 6, we conclude with a summary of this work.
2 Spectroscopic data
2.1 Selection of host stars for SWEET-Cat
We used the same procedure as before to add new planet-hosting stars in SWEET-Cat. We started by searching for all confirmed planets in the Extrasolar Planets Encyclopedia and selecting only the ones detected by RV, primary transit, and astrometry methods. We then performed a crossmatch of these with the stars in SWEET-Cat and included the missing hosts, while at the same time we removed some of the stars for which the previous planet detection is controversial at present. The same method was undertaken with the NASA exoplanet archive to add the confirmed host stars missing in the Extrasolar Planets Encyclopedia. We also kept the few confirmed planet hosts that the exoplanet databases do not have in common. The source of the planet’s database was also updated in SWEET-Cat with this information.
2.2 Spectra compilation
The compilation of the spectra follows the same exact procedure as the one described in Sect. 2.2 from Sousa et al. (2021). Here, we briefly summarize the procedure. We used the Spectral Data Product Form of the ESO Archive4 to automatically find and download the data, using the astroquery.eso5 sub-module. This search includes private data from our recent UVES programs for SWEET-Cat (106.20ZM.001, 109.22VY.001, 110.23TD.001, and 111.24HZ.001) as well as high-quality, publicly available data of the host stars with declinations of less than ~+30°.
For each FGK star (with an effective temperature above 4500 K and below 7000 K6 listed in SWEET-Cat, we searched for individual exposures of high-resolution spectra and combined these individual exposures for each instrument (and different configurations, in the case of UVES). The combination of the spectra was done by adding all the individual spectra after the respective RV shift, which was estimated during this process using one of the exposures as a reference spectra.
We also searched spectra in other public archives including data from the SOPHIE7 and HARPS-N8 spectrographs9. We combined these data in the same way as for the ESO spectral data. Here, we would also like to emphasize a specific program (20B.PNP.Hoyer) that was run on SOPHIE to collect planet-hosting spectra from the northern hemisphere.
For this work, we compiled a total of 333 combined spectra for 251 different FGK stars. The typical signal-to-noise (S/N) is around 150–200, and only 18% of these spectra are below an S/N of ~100.
3 Stellar parameters
3.1 Spectroscopic parameters
We carried out the spectroscopic analysis with “ARES+MOOG” for the new spectroscopic data. The spectral analysis relies on the excitation and ionization balance of the iron abundance. The ARES code10 (Sousa et al. 2007, 2015a) automatically measured the equivalent widths of the absorption lines. The radiative transfer code MOOG (version of Nov. 2019; Sneden 1973) was used for the element abundances assuming a local thermodynamic equilibrium (LTE) and using a grid of Kurucz ATLAS9 plane-parallel model atmospheres (Kurucz 1993). We applied this method in our previous spectroscopic studies of planet hosts (e.g., Sousa et al. 2008, 2011, 2015b, 2018, 2021; Mortier et al. 2013; Andreasen et al. 2017). We use the same line list introduced in Sousa et al. (2008), except for the stars with an effective temperature below 5200 K, for which we used the line list provided in Tsantaki et al. (2013).
For a few stars, we were able to collect combined spectra from two or more instruments or configurations. We recall that the results derived from spectra from different instruments are generally very consistent within the errors shown in Sousa et al. (2018). We include only one set of converged parameters per star in SWEET-Cat, following the same reasoning as in our last update (Sousa et al. 2021), which is mostly based on the errors derived in the spectroscopic analysis.
In Fig. 1, we show the comparison between the parameters derived in this work and the values previously listed in SWEET-Cat that were compiled previously from literature values. We derived homogeneous parameters for 232 new stars in SWEET-Cat. For nineteen stars in our starting sample, convergence was not reached, either because the spectra were of bad quality or because the star has a relatively high rotation rate. Both these issues cause difficulties in obtaining good measurements of the lines’ equivalent widths. The general consistency between our values and the literature (mainly gathered from the discovery paper) is similar to previous comparisons: for effective temperature and [Fe/H] (top panels of Fig. 1), the mean differences are 44 ± 133 K and 0.01 ± 0.11 dex, respectively. There are, however, significant differences between the parameters for some host stars, in particular for the hotter stars above ~6500 K. The offset that we see for these hotter stars is mostly related to the increase in rotational velocity at these temperatures, which makes it more difficult to derive spectroscopic parameters with different methodologies. For these fourteen stars for which we derived effective temperatures above 6500 K, all have υ sin i values reported in the literature between 10 and 20 km/s. For several of the stars, we can find a large spread in the effective temperature from different methods. One example can be seen in Raynard et al. (2018), which used three different methods to characterize NGTS-2, for which they derived effective temperatures as high as 6604 ± 134 K, but in the end they adopted a lower value of ![$\[6478_{-89}^{+94} \mathrm{~K}\]$](/articles/aa/full_html/2024/11/aa51704-24/aa51704-24-eq1.png) . Other factors such as the lower quality of spectra data could also contribute to the offset and spread. The bottom line is that caution should be taken when using different estimations from different methods, in particular for these hotter stars.
. Other factors such as the lower quality of spectra data could also contribute to the offset and spread. The bottom line is that caution should be taken when using different estimations from different methods, in particular for these hotter stars.
The metallicity comparison also shows a generally consistent result, with some outliers. Some of these outliers can even be explained by typos in the exoplanet databases11. Moreover, when we compare the difference between the derived metallicity and literature values as a function of the effective temperature (bottom right panel of Fig. 1), there is evidence for a small trend (−6.84e−5 ± 1.07e−5, with a Spearman correlation coefficient of −0.43 and a very low p value of 1.79e−10). The observed difference is generally covered by the provided errors, as we also see in the top right panel of the same figure, but it is a different way of showing the importance of using homogeneous spectral analysis in statistical studies.
In the bottom left panel of Fig. 1, the comparison of the spectroscopic surface gravity is generally consistent with a mean difference of 0.00 ± 0.27 dex, although there are a few outliers with significant differences, and a large spread of values is seen for the dwarf stars. This is similar to our previous results and can be corrected to some degree, as is discussed in Mortier et al. (2014).
We also derived the trigonometric surface gravity, following the same procedure as in Sousa et al. (2021) to obtain more accurate values for all the stars. We matched the new stars with homogeneous parameters listed with the Gaia ID in DR3, using their coordinates and the VizieR catalogs (Gaia Collaboration 2016, 2021). We checked the magnitudes and astrometry data to confirm that we selected the correct star. For each target with Gaia ID, we derived the stellar luminosities directly from the precise data in Gaia DR3, following Eq. (8.6) from the Gaia documentation12 where MG is the absolute Gaia magnitude, Teff is the effective temperature listed in SWEET-Cat, Mbol⊙ = 4.74 (defined by the IAU resolution 2015 B2), and BCG(Teff) is a temperature-dependent bolometric correction provided in the Gaia documentation (Eq. (8.9) and Table 8.3, Andrae et al. 2018). Instead of a simple inversion of the Gaia parallax to provide a distance, we preferred to include the geometric distance and an error directly taken from the maximum of the asymmetric uncertainty measures (16th and 84th percentiles) reported in Bailer-Jones et al. (2021).
To estimate the trigonometric surface gravity, we need the stellar mass. As in previous works, we used the stellar mass calibration in Torres et al. (2010), and for estimates between 0.7 and 1.3 M⊙ we used the recommended Eq. (1) in Santos et al. (2013), which corrects for the offset between the calibrated stellar mass and the ones estimated using isochrones. However, the Torres et al. (2010) calibration requires spectroscopic parameters of the star as inputs, including the surface gravity. Therefore, we performed an iterative process to converge simultaneously on the best estimates of the stellar mass and the trigonometric surface gravity. The procedure only takes a few iterations until it converges and it is described in detail in Sect. 3.4 in Sousa et al. (2021).
 |
Fig. 1 New SWEET-Cat homogeneous parameters (Teff, log g, and [Fe/H]) compared to the literature values previously listed in SWEET-Cat. The bottom right panel shows the difference between [Fe/H] and the derived effective temperature. Here, the dashed black line represents a linear fit. |
Updated statistics for SWEET-Cat.
3.2 SWEET-Cat planet-hosting statistics
Table 1 presents the updated numbers of host stars in SWEET-Cat. The percentage of stars with spectra and homogeneous parameters increases for bright stars listed in SWEET-Cat. With the work presented in this paper, despite the addition of 232 new stars with homogeneous parameters, we continue to have ~86% and ~77% completeness for FGK stars with G < 9 and G < 12, respectively. The completeness represents the number of host stars with homogeneous spectroscopic parameters relative to the total number of stars listed in SWEET-Cat. The continuous increase in new host stars in the catalog keeps the percentage for bright stars almost the same. In Table 1, we can also see that there is still a subset of bright FGK planet-hosting stars (312 stars, about ~25% of the bright FGK stars) for which we had not (yet) obtained good-quality data at the time of the search for this work. These will be the focus of future SWEET-Cat updates.
4 The planetary mass-radius relation
A brief overview of the planetary mass radius relation can be explored with the known exoplanets with both a derived mass and radius. Several works have explored the mass-radius relation of exoplanets (e.g. Bashi et al. 2017; Chen & Kipping 2017; Ulmer-Moll et al. 2019; Otegi et al. 2020; Edmondson et al. 2023). In these works, the mass-radius relation is characterized by fitting into different regimes that correspond to different planet populations. In some cases, there are also suggestions of different correlations with other planetary system properties, which could then be explained by different theoretical arguments. It is out of the scope of this work to discuss theories that could explain the proposed correlations. Instead, our only goal is to give examples and demonstrate how SWEET-Cat can be very useful to update and/or strengthen previously identified observational correlations between different parameters. In particular, we want to explore the planetary mass radius relation dependence with a more homogeneous derivation of the planet equilibrium temperature that could be estimated using SWEET-Cat’s homogeneous effective temperatures derived for their host stars.
We started by crossmatching the updated SWEET-Cat table with the planet properties that one can find in the NASA exoplanet archive as well as the Extrasolar Planets Encyclopedia. This was easily done by following the Python tutorial available on SWEET-Cat’s website13. Here, we collected first the planet properties listed by default in the NASA exoplanet archive14. If for a specific planet no values could be found in the NASA exoplanet archive, then we took the planet’s properties from the Extrasolar Planets Encyclopedia. This allowed us to build a more complete set of planet properties.
The next step was to derive the planet’s equilibrium temperature, which is useful to compare similar planets orbiting different stars with different periods. To derive the equilibrium temperature for each planet, we used Eq. (3.9) from Seager (2010):
![$\[T_{\mathrm{eq}}=T_{\mathrm{eff}, *}\left(\frac{R_*}{a}\right)^{1 / 2}\left[f^{\prime}\left(1-A_B\right)\right]^{1 / 4},\]$](/articles/aa/full_html/2024/11/aa51704-24/aa51704-24-eq2.png) (1)
(1)
using the effective temperature (Teff,*) and stellar radius (R*) listed in SWEET-Cat, and the semi-major axis (a) as the proxy for the average distance of the planet. Moreover, we assumed a bond albedo (AB) of zero in the process for all planets for this estimation15. f′ is the redistribution factor with a value of 1/4, assuming that the stellar radiation is uniformly distributed around the exoplanet.
At this point, we took a subsample of the planets that have relatively precise values for both their mass and radius. We kept only the planets with masses and radii with relative uncertainties below 45% and 15%, respectively. Moreover, we also only considered the planets with a measured velocity semi-amplitude, k. The goal is to make sure that we avoid planet masses determined only by transit time variations (see e.g. Adibekyan et al. 2024, and references therein, for a discussion). Using these constraints, we get a total of 765 exoplanets. Of these, when considering only the planet host with homogeneous spectroscopic parameters listed in SWEET-Cat, the sample is reduced to 426 planets.
Figure 2 presents the mass-radius relation for the two sub-samples of planets, in which the color of the points represents their equilibrium temperature. In both panels, it is evident that the presence of two clear regimes hints at two distinct populations of planets. Both panels of Fig. 2 show the best-fitting lines minimizing a model composed of two linear regimes separated on a common mass or radius point (xc). To find the best fit for this simple bilinear model, we used the lmfit Python package (Newville et al. 2014). In the left panel, the best fit shows a separation of the different populations at xc = 150 ± 29 M⊕ with a slope of m1 = 0.58 ± 0.01 for the low-mass planets, while the slope is zero for the massive planets. An almost equal result was obtained when fitting the points in the right panel of the figure, in which we find the separation between the two population of planets at xc = 159 ± 53 M⊕. The parameters obtained by this two-regime model are reported in Table 2. These values are also close to the ones reported in the work of Bashi et al. (2017), which used a much smaller sample (238 exoplanets) and presented slopes of m1 = 0.55 for the small planets, m2 = 0.01 for the large planets, and a transition point of xc = 124 M⊕.
Other works also present consistent slopes and transition mass between these two populations, although some of these also identify an additional transition at lower masses at around xc2 = 4.37 ± 0.72 M⊕ (e.g. Müller et al. 2024; Otegi et al. 2020; Chen & Kipping 2017). This additional transition of regimes is not clearly seen in our Fig. 2, although there is a hint of this in the lower-mass regime. Looking carefully, one can notice the increase in hotter planets below ~10 M⊕ and below ~2 R⊕, which even seems to follow a different slope when compared with the rest of the surrounding planets in the figure. This might be connected with the known radius gap that is discussed in many different works (e.g. Fulton et al. 2017; Kubyshkina & Fossati 2022). We note, however, that several planets that would fall into these low-mass regimes, such as the ones from the Trappist system (e.g. Gillon et al. 2017), were excluded because the semi-amplitude velocity, k, was not reported in the databases. This comes from our sample selection to try to avoid masses that were not derived by the RV method16. In addition, most of these excluded planets orbit faint host stars and are therefore more difficult to obtain spectroscopic data for, and thus unlikely to have homogeneous parameters in SWEET-Cat. For these reasons, the third population of small planets should be handled with caution, given the generally lower precision of its stellar and planetary properties.
A clearly visible color gradient can be observed for giant planets in Fig. 2, indicating a much stronger positive correlation with the equilibrium temperature rather than with mass. This was already noticed in previous works; for example, in Edmondson et al. (2023), in which the planet radius was fit by a power law both on planet mass and the equilibrium temperature (Eq. (9) of their paper: ![$\[\frac{R}{R_{\oplus}}=C T_{\mathrm{eq}}^{\beta_1}\left(\frac{M}{M_{\oplus}}\right)^{\beta_2}\]$](/articles/aa/full_html/2024/11/aa51704-24/aa51704-24-eq3.png) , where C, β1, and β2 are constants and Teq is the equilibrium temperature of the planet). Edmondson et al. (2023) derived a temperature index of β1 = 0.35 ± 0.02 and a mass index of β2 = 0.00 ± 0.01. Doing a similar fit to our data in Fig. 2 for planets with masses above 150 M⊕, in the left panel, we get a temperature index of β1 = 0.31 ± 0.01 and a mass index of β2 = −0.06 ± 0.01. Doing the same fit but for the planets with homogeneous spectroscopic stellar parameters, with masses above 159 M⊕, we get a temperature index of β1 = 0.40 ± 0.01 and a mass index of β2 = 0.00 ± 0.01. This represents a very substantial difference for the temperature index when comparing both samples. We note that the sampling distributions resulting from this combined fit are close to Gaussian distributions and are quite narrow, as is demonstrated by the adopted parameter errors. We also note a small but noticeable correlation between the parameters, which is more evident between C and β1. The conclusion here is that the correlation with the temperature is stronger when using the smaller sample of planets with the more precise homogeneous spectroscopic parameters, which is relevant for the computation of the equilibrium temperature of the planet.
, where C, β1, and β2 are constants and Teq is the equilibrium temperature of the planet). Edmondson et al. (2023) derived a temperature index of β1 = 0.35 ± 0.02 and a mass index of β2 = 0.00 ± 0.01. Doing a similar fit to our data in Fig. 2 for planets with masses above 150 M⊕, in the left panel, we get a temperature index of β1 = 0.31 ± 0.01 and a mass index of β2 = −0.06 ± 0.01. Doing the same fit but for the planets with homogeneous spectroscopic stellar parameters, with masses above 159 M⊕, we get a temperature index of β1 = 0.40 ± 0.01 and a mass index of β2 = 0.00 ± 0.01. This represents a very substantial difference for the temperature index when comparing both samples. We note that the sampling distributions resulting from this combined fit are close to Gaussian distributions and are quite narrow, as is demonstrated by the adopted parameter errors. We also note a small but noticeable correlation between the parameters, which is more evident between C and β1. The conclusion here is that the correlation with the temperature is stronger when using the smaller sample of planets with the more precise homogeneous spectroscopic parameters, which is relevant for the computation of the equilibrium temperature of the planet.
 |
Fig. 2 Planetary mass-radius relation for planets orbiting stars listed in the SWEET-Cat catalog. The left panel includes all the planets with precise values for the planetary mass and radius, while the right panel includes only the planets hosted by stars with homogeneous stellar parameters. The black box represents the position and its respective uncertainty for the transition between the two regimes in the diagram. |
Planetary mass-radius linear regimes.
 |
Fig. 3 Planet radius, and radius anomaly, dependence on planet temperature and metallicity. Left: planet radius and equilibrium temperature for the 159 massive exoplanets (0.5 MJ < mass < 10 MJ) with homogeneous high precision [Fe/H]. Right: radius anomaly vs. equilibrium temperature for the same planets. The line is the best fit of a power law. |
5 Revisiting the radius anomaly of Jupiter-like planets
The radius dependence on equilibrium temperature for massive planets was previously presented in the work of Laughlin et al. (2011), in which they investigated the radius anomaly observed in giant exoplanets. These planets, despite being expected to follow a mass-radius relationship consistent with a core made of heavy elements and a hydrogen-helium envelope, exhibit anomalously large radii. Potential mechanisms for these inflated radii, including tidal heating, enhanced atmospheric opacities, and heat redistribution, were explored. Understanding which mechanism dominates is crucial for explaining the observed deviations. One of the interesting results presented in the work of Laughlin et al. (2011) was the evidence for a significant correlation between the residual radius anomalies and host star metallicities – a correlation that is generally interpreted as evidence that metal-rich protoplanetary disks lead to planets with larger core masses, and thus with larger radii.
In this section, we quickly revisit the relations presented in Laughlin et al. (2011) using the updated SWEET-Cat data with the only goal being to verify the metallicity correlation on the residual radius anomalies. While in Laughlin et al. (2011) the planets were selected to have masses between 0.1 and 10 Jupiter masses, here we have used our mass transition from the previous section by selecting planets with masses above 159 earth masses (0.5 Jupiter masses). Of these, we only considered the planets hosted by stars with homogeneous stellar parameters and with a good precision below or equal to 0.05 dex in [Fe/H]. This left us with only 158 planets, but with very precise and homogeneous metallicity determinations. The left panel of Fig. 3 shows the dependence of the radius on equilibrium temperature for these massive planets. We also computed the radius anomaly, following the same procedure as in Laughlin et al. (2011) by using its Eq. (3), which provides an acceptable approximation to the Bodenheimer et al. (2003) baseline structural models throughout the mass and temperature ranges in this sample of massive planets:
![$\[\begin{aligned}R_{\mathrm{pl}} / R_{\mathrm{Jup}}= & 1.08417+0.0940857 ~m-0.242831 ~m^2 \\& +0.0947349 ~m^3+0.0387851 ~t+0.00243981 ~m t \\& -0.0244656 ~m^2 t+0.0130659 ~m^3 t+0.0240409~ t^2 \\& -0.0419296 ~m t^2+0.00693348 ~m^2 t^2 \\& +0.00302157 ~m^3 t^2.\end{aligned}\]$](/articles/aa/full_html/2024/11/aa51704-24/aa51704-24-eq4.png) (2)
(2)
The radius anomaly was computed by subtracting the result of this fit to the observed radius values for all the planets. The right panel of Fig. 3 reproduces Fig. 2 of Laughlin et al. (2011) for our sample of massive planets around precisely characterized host stars in SWEET-Cat. In this panel, we also used a power law to fit the distribution points (![$\[\mathcal{R} \propto T_{\mathrm{eq}}^\alpha, \mathcal{R}\]$](/articles/aa/full_html/2024/11/aa51704-24/aa51704-24-eq5.png) being the radius anomaly, and Teq the equilibrium temperature)17 for which we derived α = 1.35 ± 0.51, which is consistent with the value of α = 1.4 ± 0.6 originally presented in their work with only 90 early-detected transiting massive exoplanets.
being the radius anomaly, and Teq the equilibrium temperature)17 for which we derived α = 1.35 ± 0.51, which is consistent with the value of α = 1.4 ± 0.6 originally presented in their work with only 90 early-detected transiting massive exoplanets.
After correcting for the equilibrium temperature trend and plotting the resulting radius anomaly against the host stellar metallicity, Laughlin et al. (2011) reported evidence for a negative correlation in their Fig. 3, but no slope value was presented. Here, we reproduce this correlation using our sample of planets with a precise and homogeneous metallicity in Fig. 4, for which we find a negative slope of m = −0.42 ± 0.04 (we also derived a Spearman correlation coefficient of −0.23 with a low p value of 0.004 for these data points), which confirms the observed trend originally presented.
As a comparison to the use of our homogeneous SWEET-Cat parameters, we performed the same exercise using the parameters that are found directly in the NASA exoplanet archive for the same 158 planets. For these, we directly collected the equilibrium temperature and the stellar metallicity compiled from the literature. For 14 of these exoplanets, the stellar metallicity was not available in the NASA database. For the few other exoplanets that did not had uncertainties for the stellar metallicity, we assumed an error of 0.10 dex. For the few exoplanets with no equilibrium temperature reported in the NASA exoplanet database, we used Eq. (1) with the effective temperature and stellar radius reported in the NASA’s database to estimate the missing values. With these data to hand, the power law fit on the radius anomaly versus equilibrium temperature gave consistent results, with a very similar α = 1.33 ± 0.51, meaning that the changes in equilibrium temperature do not much affect these results. However, when we observe the metallicity dependence on the radius anomaly with the corrected equilibrium temperature trend (Fig. 5), we derived a significant different linear fit, with a stronger negative slope of m = −0.88 ± 0.12, which is also less precise (we also derived a Spearman correlation coefficient of −0.21 with a p value of 0.01 for these data points). Moreover, we derived Spearman correlation coefficient distributions to take into account the errors included for both Figs. 4 and 5. The average correlation coefficient obtained was −0.20 with an average p value of 0.03 for Fig. 4, while for Fig. 5 we obtained a similar correlation of −0.18 but with a significantly higher average p value of 0.07. The higher uncertainty of the fit as well as the higher p values obtained for Fig. 5 are caused by the higher uncertainties of the metallicities available in the literature.
We also performed a simultaneous 3D fit to the radius anomaly with a dependence on both the equilibrium temperature and metallicity. The goal was simply to check if the observed correlations remained consistent with the step-by-step analysis done in Laughlin et al. (2011). Therefore, we used a model to follow the relation ![$\[\mathcal{R}=k T_{\mathrm{eq}}^\alpha+m[\mathrm{Fe} / \mathrm{H}]+b\]$](/articles/aa/full_html/2024/11/aa51704-24/aa51704-24-eq6.png) , for which we derived the following coefficients: k = 2.75e−5 ± 5.46e−5, α = 1.40 ± 0.17, m = −0.23 ± 0.05, and b = −0.18 ± 0.03. We note that there is a significant decrease in the uncertainty of α doing this simultaneous fit. This way we were able to confirm that both trends on equilibrium temperature and metallicity remain present, although the metallicity slope seems to have reduced significantly.
, for which we derived the following coefficients: k = 2.75e−5 ± 5.46e−5, α = 1.40 ± 0.17, m = −0.23 ± 0.05, and b = −0.18 ± 0.03. We note that there is a significant decrease in the uncertainty of α doing this simultaneous fit. This way we were able to confirm that both trends on equilibrium temperature and metallicity remain present, although the metallicity slope seems to have reduced significantly.
All these exercises done on updated exoplanet data confirm that the metallicity trend is present. Using homogeneous data we were able to obtain a more precise correlation, although this depends on the extraction approach used, which can produce different slope values. This metallicity dependence may be connected with the presence of larger and more massive cores for the planets orbiting metal-rich stars, which could compensate for the inflation of their radius. We recall that the baseline models used in Laughlin et al. (2011) come from Bodenheimer et al. (2003), which assumed a near-solar composition. It would be interesting to compare with more updated models, preferably with the metallicity accounted for, but this is out of the scope of this paper.
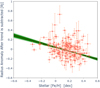 |
Fig. 4 Radius anomaly with corrected equilibrium temperature trend vs. the metallicity of the host star [Fe/H]. |
6 Summary
We present another large update of SWEET-Cat, for which we have derived precise and homogeneous spectroscopic stellar parameters for 232 new planet-hosting stars. To achieve this, we compiled spectra collected from different instruments, by both exploring public archives and making using of our own observation programs at different observatories. The spectroscopic parameters were complemented with additional data as in previous works, including estimation of stellar masses, radius, and trigonometric surface gravities, which are made available at the SWEET-Cat website. For all new planet hosts added in SWEET-Cat, we maintain the cross reference columns for an easy correlation with the planets’s properties listed in the NASA archive exoplanet database as well as the Extrasolar Planets Encyclopedia.
We have conducted a quick review of the planetary mass radius relation of exoplanets using homogeneous spectroscopic data, where we can easily identify the two populations of exoplanets following two different linear relations for low-mass and high-mass planets. The relations derived in this work are consistent with several others derived in different works, including the dependence on equilibrium temperature observed for the massive planets.
We have also revisited the radius anomaly observed for giant planets with the goal of quantifying the metallicity correlation presented as evidence in Laughlin et al. (2011). Using different larger samples of massive exoplanets, we find that the metallicity correlation persists with the same models. However, these studies assume that giant planets are perfectly absorbing (black) bodies, which is unrealistic. Early exoplanet models have demonstrated that the Bond albedo depends on the spectral type of the host stars and the expected composition of planetary atmospheres, considering their temperatures (e.g. Gelino et al. 1999; Sudarsky et al. 2000). Recent research has shown that photochemical hazes, rather than cloud condensates, may serve as the primary aerosols depending on the planets’ temperatures (Steinrueck et al. 2023), thereby altering their expected albedos. Consequently, more comprehensive and recent models should be examined to assess the significance of this metallicity correlation on the radii of these massive planets.
We shall continue to expand SWEET-Cat in the coming years to provide the community with a more complete dataset relevant for statistical studies of exoplanets. There is still a significant number (≳300) of relatively bright planet hosts listed without homogeneous parameters. We shall provide spectroscopic parameters once good-quality spectra are available. Furthermore, we have plans to include additional stellar parameters in SWEET-Cat. These include υ sin i, stellar activity indices, homogeneous element abundances for the stars with the highest-quality spectra, making the spectra available for download on the website, and including more robust determinations of stellar masses, radius, and ages from stellar modeling.
Data availability
A copy of the SWEET-Cat catalog used for this work is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/691/A53.
Acknowledgements
This work was supported by FCT – Fundacção para a Ciência e Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalização by these grants: 2022.06962.PTDC; UIDB/04434/2020; UIDP/04434/2020. S.G.S acknowledges the support from FCT through Investigador FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). E.D.M. further acknowledges the support from FCT through the Stimulus FCT contract 2021.01294.CEECIND. Co-funded by the European Union (ERC, FIERCE, 101052347). BMTBS is supported by an FCT fellowship, grant number 2022.11805.BD. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation. SH acknowledges CNES funding through the grant 837319. AM acknowledges funding from a UKRI Future Leader Fellowship, grant number MR/X033244/1. B.R-A acknowledges funding support from ANID Basal project FB210003.
References
- Adibekyan, V., Sousa, S. G., Delgado Mena, E., et al. 2024, A&A, 683, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akeson, R. L., Chen, X., Ciardi, D., et al. 2013, PASP, 125, 989 [Google Scholar]
- Anderson, D. R., Bouchy, F., Brown, D. J. A., et al. 2018, arXiv e-prints [arXiv:1812.09264] [Google Scholar]
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreasen, D. T., Sousa, S. G., Tsantaki, M., et al. 2017, A&A, 600, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armstrong, D. J., Lopez, T. A., Adibekyan, V., et al. 2020, Nature, 583, 39 [Google Scholar]
- Antoniadis-Karnavas, A., Sousa, S. G., Delgado-Mena, E., et al. 2024, A&A, 690, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bashi, D., Helled, R., Zucker, S., & Mordasini, C. 2017, A&A, 604, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., Laughlin, G., & Lin, D. N. C. 2003, ApJ, 592, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Buchhave, L. A., Bitsch, B., Johansen, A., et al. 2018, ApJ, 856, 37 [Google Scholar]
- Chen, J., & Kipping, D. 2017, ApJ, 834, 17 [Google Scholar]
- Edmondson, K., Norris, J., & Kerins, E. 2023, arXiv e-prints [arXiv:2310.16733] [Google Scholar]
- Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gelino, C. R., Marley, M., Stephens, D., Lunine, J., & Freedman, R. 1999, Phys. Chem. Earth C, 24, 573 [NASA ADS] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Goda, S., & Matsuo, T. 2019, ApJ, 876, 23 [Google Scholar]
- Kubyshkina, D., & Fossati, L. 2022, A&A, 668, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km/sgrid, Kurucz CD-ROM No. 13. (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 13 [Google Scholar]
- Laughlin, G., Crismani, M., & Adams, F. C. 2011, ApJ, 729, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Lillo-Box, J., Figueira, P., Leleu, A., et al. 2020, A&A, 642, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcy, G. W., & Butler, R. P. 1996, ApJ, 464, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, arXiv e-prints [arXiv:1109.2497] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013, A&A, 558, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, S., Baron, J., Helled, R., Bouchy, F., & Parc, L. 2024, A&A, 686, A296 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., & Ingargiola, A. 2014, LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python [Google Scholar]
- Otegi, J. F., Bouchy, F., & Helled, R. 2020, A&A, 634, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raynard, L., Goad, M. R., Gillen, E., et al. 2018, MNRAS, 481, 4960 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 914320 [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Adibekyan, V., Figueira, P., et al. 2017, A&A, 603, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S. 2010, Exoplanet Atmospheres: Physical Processes [Google Scholar]
- Sneden, C. 1973, Ph.D. Thesis, University of Texas, USA [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., et al. 2011, A&A, 526, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015a, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mortier, A., et al. 2015b, A&A, 576, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2018, A&A, 620, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2021, A&A, 656, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinrueck, M. E., Koskinen, T., Lavvas, P., et al. 2023, ApJ, 951, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Sudarsky, D., Burrows, A., & Pinto, P. 2000, ApJ, 538, 885 [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&A Rev., 18, 67 [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ulmer-Moll, S., Santos, N. C., Figueira, P., Brinchmann, J., & Faria, J. P. 2019, A&A, 630, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
For M stars a different spectroscopic analysis is used and is addressed in Antoniadis-Karnavas et al. (2024)
The latest version of ARES can be found on github.com/sousasag/ARES.
As an example, at the time of compilation of these values, for WASP-137 exoplanets.eu listed a metallicity ([Fe/H]) of 0.487 (±0.051), pointing to the work Anderson et al. (2018) where the value listed is 0.08 ± 0.09 dex. The 0.487 value was mistakenly sourced from the line below corresponding to the stellar luminosity.
https://gea.esac.esa.int/archive/documentation/GDR2/ – in particular chapter 8.3.3 authored by Orlagh Creevey and Christophe Ordenovic.
Although we may be expected to have different bond values for different planets, as we observe in planets in our own Solar System, there are only very few measurements available for known exoplanets. Therefore, since our goal is to compare our results with others in the literature, we followed the same assumption made for this and used a zero value for the albedo of all planets in our sample.
All Tables
All Figures
 |
Fig. 1 New SWEET-Cat homogeneous parameters (Teff, log g, and [Fe/H]) compared to the literature values previously listed in SWEET-Cat. The bottom right panel shows the difference between [Fe/H] and the derived effective temperature. Here, the dashed black line represents a linear fit. |
| In the text | |
 |
Fig. 2 Planetary mass-radius relation for planets orbiting stars listed in the SWEET-Cat catalog. The left panel includes all the planets with precise values for the planetary mass and radius, while the right panel includes only the planets hosted by stars with homogeneous stellar parameters. The black box represents the position and its respective uncertainty for the transition between the two regimes in the diagram. |
| In the text | |
 |
Fig. 3 Planet radius, and radius anomaly, dependence on planet temperature and metallicity. Left: planet radius and equilibrium temperature for the 159 massive exoplanets (0.5 MJ < mass < 10 MJ) with homogeneous high precision [Fe/H]. Right: radius anomaly vs. equilibrium temperature for the same planets. The line is the best fit of a power law. |
| In the text | |
 |
Fig. 4 Radius anomaly with corrected equilibrium temperature trend vs. the metallicity of the host star [Fe/H]. |
| In the text | |
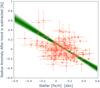 |
Fig. 5 Same as Fig. 4 but using parameters directly listed in the NASA exoplanet archive. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


