EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A252 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A252
Number of page(s) 17
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/202347793
Published online 29 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Eclipsing spectroscopic double-lined (hereafter eSB2) binaries are the prime source of precise and accurate mass measurements of stars, the parameter which, along with the initial composition of the star, determines its evolutionary path and fate. Owing to the fact that their mass determination is largely model independent, eSB2s represent an ideal test bed for the theory of stellar structure and evolution (SSE).

One of the striking outcomes of the SSE model test is mass discrepancy. The term was originally introduced by Herrero et al. (2000) in the context of single stars. The authors reported a discrepancy between stellar masses inferred from the spectroscopic properties of stars and those found from a comparison of the position of the stars in a Hertzsprung–Russell diagram (HRD) with evolutionary tracks. Although the authors concluded that the mass discrepancy is an observational manifestation of shortcomings in SSE models, it is worth noting that the spectroscopic masses are also model dependent, as they are inferred from the spectroscopic estimates of log g and radii of the stars, which are both largely dependent on physics employed in the models of stellar atmospheres and winds.

The conclusions regarding possible imperfections in SSE models are more sound when based on a comparison between model-independent masses inferred from the binary dynamics (dynamical masses hereafter) and those dictated by SSE models (evolutionary masses hereafter). Although earlier works suggest a good agreement between the dynamical and evolutionary masses for stars up to 25 M⊙ (e.g. Burkholder et al. 1997), more recent studies have reported a systematic discrepancy between the two types of mass measurement. Notably, two independent studies of the V380 Cyg system (Guinan et al. 2000; Pavlovski et al. 2009) found a large mass discrepancy for the more evolved primary component. While Guinan et al. (2000) claimed the discrepancy can be resolved with an increased efficiency of the near-core mixing in the form of core overshooting, Pavlovski et al. (2009) focussed on the effect of rotation in SSE models and concluded that it cannot explain the observed mass discrepancy. Moreover, Tkachenko et al. (2014b) re-investigated the V380 Cyg system based on space-based photometric and high-resolution spectroscopic data and found the mass discrepancy for both binary components. The authors concluded that the discrepancy can only be resolved when the combined effect of rotation and core overshooting is included in SSE models.

The need for more efficient near-core mixing has become one of the streamlined theoretical hypotheses to explain the origin of the mass discrepancy in eclipsing binaries. Massey et al. (2012) and Morrell et al. (2014) argued the need for increased efficiency of interior (rotational or core overshoot) mixing in SSE models in order to accommodate a small (around 10%) but systematic discrepancy between dynamical and evolutionary masses in five high-mass eclipsing binaries in the Large Magellanic Cloud (LMC). The same conclusion was presented by Pavlovski et al. (2018) based on the study of four high-mass eclipsing binaries in the Galaxy. Furthermore, Rosu et al. (2020, 2022a,b) invoked a simultaneous measurement of the stellar parameters, rate of the apsidal motion, and k2 internal structure constant in the HD 152248, HD 152219, CPD-41° 7742, and HD 152218 binary systems to demonstrate the lack of efficiency of interior mixing in standard SSE models, in line with the conclusions drawn by Guinan et al. (2000) for the V380 Cyg system.

Claret & Torres (2016, 2017, 2018, 2019) presented a series of papers focusing on the inference of the efficiency of near-core mixing in the form of the convective core overshooting in a sample of some 50 eSB2 systems from Torres et al. (2010) and the catalogue of the Optical Gravitational Microlensing Experiment (OGLE)1. The authors considered two implementations of the core overshooting in Granada (Claret 2004, 2012) and MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019) models, namely, convective penetration (Zahn 1991) and exponential diffusive approximation (Freytag et al. 1996; Herwig 2000). Irrespective of the prescription used, the authors reported a strong dependency of the inferred overshooting parameter on the stellar mass such that there is an almost linear transition from no overshooting to approximately αov (ƒov) = 0.2 (0.02) Hp in the mass range from some 1.2 to 2.0 M⊙. The authors found that the distribution flattens for stars more massive than 2.0 M⊙. Viani & Basu (2020) investigated an asteroseismic sample of stars observed with the Kepler mission in the mass range between 1.1 and 1.5 M⊙. The authors reported a strong positive correlation between the inferred overshooting parameter with the stellar mass.

Costa et al. (2019) revisited the sample of Claret & Torres (2016, 2017, 2018, 2019) using a combination of the Bayesian statistical framework and PARSEC stellar evolution models. The authors confirmed the need for a mild convective core overshooting for stars with masses of M > 1.9 M⊙ and additionally found a large spread in the inferred αov values ranging from some 0.3 to 0.8 Hp. Costa et al. (2019) arrived at the conclusion that while the low boundary of the inferred αov values is likely to be explained by an insufficient amount of core-boundary mixing in standard SSE models, the large spread in the inferred values is likely a manifestation of the natural distribution of initial rotation rates and hence indicates active rotational mixing in these intermediate-mass stars.

Finally, Tkachenko et al. (2020) presented a study of eleven high-mass eSB2 systems for which high-precision stellar quantities were derived in a homogeneous way (Pavlovski et al. 2018, 2023; Tkachenko et al. 2014b; Johnston et al. 2019a). No dependence of the observed mass discrepancy on the stellar mass was reported, but a strong anti-correlation with the surface gravity of the star was found. The same correlation was found to persist when the stellar mass was replaced with the mass of the con-vective core of the star, a finding which the authors interpreted as showing the need for larger convective core masses in standard models of SSE. Remarkably, Johnston (2021) arrived at the same conclusion from the study of a combined large sample of binary components and asteroseismically active single stars. Furthermore, Martinet et al. (2021) investigated a large sample of stars from the literature spanning a mass range from 7 to 25 M⊙ using a large grid of SSE models computed for different values of the overshooting parameter and initial rotation and assuming a moderate and strong angular momentum transport in the models. The authors confirmed the findings of Tkachenko et al. (2020) and Johnston (2021) and reported the need for larger convective cores at higher stellar masses.

An alternative hypothetical explanation of the mass discrepancy came from the nature of binarity itself and the fact that the majority of high-mass stars are expected to be found in binary systems and/or have experienced binary interactions in the past (e.g. Sana et al. 2012, 2014). Mahy et al. (2020) investigated 26 eclipsing binary systems in the LMC and reported a good agreement between their dynamical and spectroscopic masses, whereas the evolutionary masses were found to be systematically overestimated. Upon a closer inspection of the obtained results, the authors found the mass discrepancy to be more pronounced in semi-detached binary configurations, a finding that suggests that binary interactions might be (at least partially) responsible for the observed mass discrepancy.

Despite being known for some three decades and many attempts being made to observationally quantify and pinpoint the most likely theoretical explanation for it, the mass discrepancy persists as a phenomenon, and the only definite statement the stellar astrophysics community can make about it is that the problem exists. The majority of previous studies have focussed on a particular mass regime, and there is a large diversity in the employed data analysis methods and input physics used in SSE models, which makes it non-trivial to account for systematic uncertainties when attempting to quantify and ultimately resolve the mass discrepancy problem. Motivated by the current state of the art, we have initiated a systematic search for intermediate-to high-mass (spectral types OBAF and masses larger than some 1.2 M⊙) eclipsing binaries in TESS (Ricker et al. 2015) space-based photometric data and have organised a complementary ground-based spectroscopic follow-up campaign of the detected candidate eclipsing binaries. Our goal is to build a stellar sample that covers the entire mass range of stars born with the convective core, all the way up to some 30 M⊙, and includes binaries with and without a pulsating component and in different orbital configurations.

Our newly compiled sample is a generalisation of the binary sample presented in Tkachenko et al. (2020), and the aim of its composition is to cover a much larger range of the stellar mass, account for intrinsic variability of stars in binaries, and include systems with different orbital configurations, such as detached versus semi-detached binaries. We ultimately aim at a self-contained and homogeneous detailed analysis of all suitable eSB2 such that the analysis methods remain largely the same, thus minimising systematic uncertainties on the inferred parameters and observational mapping of the mass discrepancy across the HRD. In this paper, we present the sample selection of candidate eclipsing binary systems and provide an overview of the ground-based spectroscopic observations we have obtained so far (Sect. 2). We provide a more detailed look into the spectro-scopic properties of the observed systems with the methods of least-squares deconvolution and spectral disentangling in Sect. 3. Analysis of the TESS photometric data with the aim of providing a photometric classification according to the type of intrinsic variability of the sample stars is presented in Sect. 4. We then proceed with a discussion of the obtained results in the context of the previous studies (Sect. 5) and close the paper with some concluding remarks and a list of future prospects (Sect. 6).

2 Sample selection

Our sample selection is based on the work of IJspeert et al. (2021) that presents a magnitude-limited catalogue of eclipsing binaries observed by the TESS mission. While a detailed description of all the analysis steps is provided in IJspeert et al. (2021), here we provide a brief summary of the steps most relevant to the analysis in this work.

IJspeert et al. (2021) started with a global all-sky selection of OB(A)-type stars from the TESS Input Catalogue (version TICv8 Stassun et al. 2019). The authors limited the selection to TESS magnitudes below 15 and excluded all targets that are resolved in the Gaia DR2 catalogue (Gaia Collaboration 2018) but are recognised as a single object in the 2MASS catalogue. The 2MASS IJ-K)–(J-H) colour–colour plane was employed to select some 205 000 OB(A)-type candidate stars with the exact colour cuts informed by the OB-type star variability samples of Bowman et al. (2019a) and Pedersen et al. (2019) (cf. Fig. 1 in IJspeert et al. 2021). In a next step, the authors excluded white dwarfs and giants from the sample using dedicated Gaia flags and limited themselves to stars for which either TESS-SPOC2 or MIT QLP3 light curves could be retrieved from the MAST database4. This step reduces the stellar sample of unique targets to some 91 000. Ultimately, in a search for eclipsing binaries in the selected sample of OB(A)-type stars with TESS light curves, IJspeert et al. (2021) developed an algorithm for automated detection of eclipses and, if detected, determination of the binary orbital periods. The authors reported 5502 candidate eclipsing binaries of which 2077 were found to be false positives and 3425 were found to be true eclipsing binaries.

Spectroscopic observations

From the above-mentioned sample of 3425 eclipsing binaries, we selected all targets with a V magnitude below 11 and that are accessible from the Roque de los Muchachos Observatory (La Palma, Spain) in the course of the year. A total of 545 systems were proposed for observations with the High-Efficiency and high-Resolution Mercator Echelle Spectrograph (HERMES; Raskin et al. 2011) instrument attached to the 1.2-m Mercator telescope as part of a dedicated large programme. For each of those systems, we requested eight epochs of spectroscopic observations with uniform sampling of the orbital phase. The latter was computed from the orbital period value derived by IJspeert et al. (2021) and a reference date T0 taken to be the date of the first spectroscopic observation. A few systems were followed more extensively to resolve the effect of intrinsic stellar oscillations on spectral line profiles, with the time series ranging from a couple of dozen spectra to almost 200 measurements (e.g. the case of 16 Lac in Table A.1; see Southworth & Bowman 2022).

At the time of writing this work, we had completed spectro-scopic observations with the HERMES instrument for 58 systems from our sample. The criteria of completion are the following: (i) individual epoch observations meet the minimum S/N requirement of 60 per resolution element and (ii) a quasi-uniform orbital phase coverage is achieved to maximise the chances for detecting lines of a companion star in the observed composite spectra. The former requirement guarantees an S/N in excess of 100 in the disentangled spectra of SB2 systems or the combined spectrum for SB1 binaries. Table A.1 gives an overview of the sample of 58 systems, with columns one through seven indicating the star name and a catalogue identifier (Cols. 1–3), orbital period (Col. 4), number of spectra acquired (Ccol. 5), and spectroscopic (Col. 6) and photometric (Col. 7) classifications obtained in this work.

A complementary, albeit smaller, sample of 28 southern hemisphere eclipsing binaries was proposed by us for spectroscopic observations with the Fiber-fed Extended Range Optical Spectrograph (FEROS; Kaufer et al. 1999) instrument attached to the MPG/ESO 2.2-m telescope (under programme 0106.A-0906(A)). Similar to the HERMES-based programme, we requested eight epochs of spectroscopic observations and used exactly the same completion criteria for all the observed systems. The criteria were met for a total of 25 systems, while the remaining three stars received only two epochs of spectroscopic observations. Detailed information is provided in Table A.1 for the 25 systems that we consider completed; the columns of the table are the same as for the HERMES sample.

The HERMES spectra were reduced with version 7.0 of the dedicated HERMES pipeline, while the FEROS spectra were processed with a modification of the CERES pipeline (Brahm et al. 2017) presented in Gebruers et al. (2022). The data reduction steps we used are the standard ones and include bias subtraction, flat fielding, cosmic ray removal, wavelength calibration, barycentric correction, and order merging. Normalisation to the pseudo-continuum was done by selecting knot points and fitting a low-degree polynomial through them. Special care was taken in the regions of broad Balmer lines to ensure the outer line wings were not altered by the normalisation process.

3 Spectroscopic analysis

In this section, we present the results of our preliminary spec-troscopic analysis of 83 systems, that is, 58 in the HERMES sample and 25 in the FEROS sample. We start with spectroscopic classification based on the least-squares deconvolution (LSD) profiles (Sect. 3.1). The classification is validated and, if necessary, refined with the method of spectral disentangling (SPD), which is subsequently used to compute the spectroscopic orbital elements of confirmed binary star systems (Sect. 3.2).

thumbnail Fig. 1

Examples of the LSD profiles computed with the Teff = 11 000 K mask. From top left to bottom right: HD 34382, a single star showing line profile variability; HD 138305, an SB2 binary system; HD 234650, an SB3 triple system; and HD 57158, an SB4 quadruple system. The individual LSD profiles in each panel have been shifted vertically by a constant factor for clarity.

3.1 Least-squares deconvolution

We employed the method of LSD (Donati et al. 1997) as implemented by Tkachenko et al. (2013). The LSD method offers an efficient way to compute a mean profile from an ensemble of spectral lines present in the spectrum. Two fundamental assumptions of the method need to be kept in mind when computing an LSD profile: (i) all spectral lines should have a similar shape, meaning that hydrogen, helium, and metal lines with damping wings need to be excluded from the calculations, and (ii) all spectral lines add up linearly, implying that the depths of spectral blends formed of lines whose absorption coefficients overlap are not accurately reproduced by the method. Within these fundamental assumptions, the stellar spectrum I is represented as a convolution of a line mask M with an a priori unknown average profile Z(υ) such that 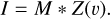I=M*Z(v). $I = M*Z(v){\rm{. }}$(1)

The line mask consists of a set of delta functions that specify wavelength positions and theoretical strengths of spectral lines. This implies that the exact content of a line mask depends on the assumed atmospheric parameters (Teff, log g, ξ, [M/H]) of the star, where the effective temperature has by far the most dominant effect. For the purpose of the analysis in this work and as informed by the spectral classification as OB(A)-type stars in IJspeert et al. (2021), we computed line masks for two values of Teff, 8000 K and 11 000 K, and we used both of them for the calculation of the LSD profiles from every single spectrum of every object in the sample. The two masks are at the same time required and sufficient to account for the variable complexity of the stellar spectrum between these two temperature regimes.

We performed a visual classification of all systems based on the time series of their LSD profiles. Figure 1 shows a time series of the LSD profiles for four objects ranging from a single star to a quadruple system. In the figure, we classify HD 34382 (top left) as a single star exhibiting line profile variations (LPVs). The latter are caused by the intrinsic variability of the star, either due to rotational modulation of inhomogeneities on its surface or stellar pulsations. We found HD 138305 (top right) to be an SB2 system composed of two similar stars. HD 234650 (bottom left) and HD 57158 (bottom right) are higher-order multiple systems, with the former being a spectroscopic triple-lined (SB3) system and the latter being a spectroscopic quadruple-lined (SB4) system.

3.2 Spectral disentangling

The SPD method was originally introduced and formulated by Simon & Sturm (1994). The method allows for a simultaneous, self-consistent inference of the orbital elements for spectroscopic binary and higher-order multiple systems and the disentangled spectra of the components these systems are composed of. The SPD method relies on the principle that the complex spectrum of a binary or multiple-star system is a linear combination of the individual components’ spectra, each shifted due to the Doppler effect in the course of the orbital cycle and diluted by the component’s fractional light contribution.

In the original formulation of Simon & Sturm (1994), the disentangling problem is described by the following matrix equation: 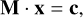M⋅x=c${\bf{M}} \cdot {\bf{x}} = {\bf{c}}$(2)

where the single-column matrices x and c represent a priori unknown disentangled spectra of the components and the time series of the observed spectra, respectively. The rectangular matrix M represents a linear transformation of x to c, has a block structure, and is constructed using individual Doppler shifts for each of the components at each epoch of the observations. Matrix M also contains information on the light dilution factors for each component of the system and each observed spectrum in the time series. In the case of high-resolution spectra and when the number of observed spectra exceeds the number of individual components, the system of linear equations is overde-termined (i.e. number of equations is greater than the number of unknowns). Mathematically, this is an ill-posed problem, and regularisation conditions are required to solve it. Simon & Sturm (1994) employed an algebraic technique known as a singular value decomposition (SVD). Solving the system is typically a computationally demanding problem due to the need to invert matrix M in Eq. (2).

Independently, a Fourier-based formulation of SPD was developed by Hadrava (1995). With the help of the Fourier transform, a large set of equations can be uncoupled into many small sets of equations for each Fourier mode. Such an approach is significantly less computationally demanding than the original formulation. In either formulation, the SPD method can be exploited in two basic modes: (i) spectrum disentangling, where a priori unknown components’ spectra are optimised along with the orbital elements of the system, and (ii) spectrum separation, where RVs or orbital elements are assumed to be known and individual component’s spectra are inferred from the respective fixed orbital solution (e.g. Pavlovski & Hensberge 2010; Serenelli et al. 2021).

The SPD method builds on the following fundamental assumptions: (i) the dominant variability present in the observed composite spectra of a system should be due to the motion of the components around their common centre of mass, and (ii) observationally, the orbital phase coverage should be complete and close to uniform to exploit the full power of the method. In this work, as well as in the future exploitation of our sample (cf. Sect. 6), we are interested in the detection of high-contrast binary SB2 systems (i.e. where one of the binary components is significantly fainter than the other), including those where one of the components is a pulsating star. While the former represents a challenge for the method, the latter is, in principle, a direct violation of one of the method’s fundamental assumptions. Hence, we comment on both of these challenges in more detail to justify the choice of the SPD method for our purpose.

In the method of SPD, the gain in S/N in the final disentangled spectra is proportional to 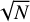N$\sqrt N $, where N is the number of the observed spectra in a time series. The gain is distributed according to the light ratio between the binary components. Previous studies have demonstrated that SPD is a powerful tool to reveal the presence of a faint component (1% to 2% contribution to the total light of the system) in high-contrast systems (e.g. Kolbas et al. 2015; Themeßl et al. 2018; Pavlovski et al. 2022; Johnston et al. 2023).

While time-dependent LPVs, due to the effect of non-radial pulsations, represent an extra source of variability that is not recognised by the SPD method, previous studies of binary systems with pulsating component(s) have demonstrated that the method delivers reliable results provided that (i) the LPV amplitude due to the intrinsic variability of the star is much smaller than due to its binary motion and (ii) the orbital period of the system differs from that of the dominant intrinsic variability of the star (e.g. Uytterhoeven et al. 2005a,b; Ausseloos et al. 2006; Tkachenko et al. 2012). For the case of a radially pulsating star where the RV amplitude of the dominant (radial) pulsation mode is comparable to or exceeds that of the orbital motion, a large set of observed spectra with uniform coverage of the pulsation and orbital cycles is required. Indeed, in such a scenario, a time series of the observed spectra can be binned with respect to the orbital phase of the binary system to average out the effect of oscillations on the line profile of a pulsating component. As a result, spectral line profiles in the orbital phase-binned observed spectra contain a minimum amount of distortion due to stellar pulsations, bringing us to the former case of orbital motion being the dominant source of the apparent line profile variability (e.g. Tkachenko et al. 2014a, 2016).

In this work, we employ the Fourier-based method of SPD as implemented in the FDBINARY software package5 (Ilijic et al. 2004). We used the disentangling method to verify and, if necessary, refine the LSD-based spectroscopic classification, and more importantly, we derived a preliminary set of orbital elements for all systems in our sample. The most common, yet not frequent, case of a refined classification is of an SB1 (LSD-based) to an SB2 (SPD-based) system. This is thanks to the power of the SPD method to detect spectral contributions as faint as a few percent (in the continuum flux units), which may stay unnoticed in the LSD profiles if the most optimal line mask is not chosen for the respective calculations.

The results of our combined LSD- and SPD-based spectro-scopic classification are provided in Table A.1 (sixth column). For all SB1 and SB2 systems, we employed the FDBINARY code to compute their spectroscopic orbital elements, that is, orbital eccentricity e, argument of periastron ω, and semi-amplitudes of the individual components Ki. Owing to the fact that the orbital period value can typically be constrained with a much higher precision from the eclipses in space-based photometric data than from a limited set of ground-based spectroscopic observations, we did not optimise the orbital period value in the SPD method by default. Instead, we improved the period separately using an algorithm described in detail in IJspeert et al. (2024) that searches globally for the best orbital period and then refines it with a granularity of one part in one hundred thousand. The global merit function is a combination of the phase dispersion measure (Stellingwerf 1978) and Lomb-Scargle amplitude (Lomb 1976; Scargle 1982), as well as the number and completeness factor of orbital harmonic frequencies found in the light curve. This period finding algorithm is part of a larger methodological framework for analysing eclipsing binary light curves developed by IJspeert et al. (2024) and implemented in STAR_SHADOW6. Furthermore, we optimised eccentricity only in cases where evidence for a value different from zero was found in the TESS light curve. Ultimately, the SPD solution was computed in three different wavelength regions free of Balmer lines and rich in metal lines: 4375–4490 Å, 4510–4725 Å, and 4900–5230 Å. The orbital elements and their uncertainties are reported in Table B.1 and are the mean and standard deviation of the mean values, respectively. We note that a typical S/N of about 80 or higher was achieved in all spectroscopic epochs for all systems in the studied sample. This is sufficiently high to have a negligible effect on the estimated uncertainties of the obtained orbital elements compared to other contributors to the total error budget. These dominant contributors to the uncertainties are (i) the flux ratio of the binary components, where a lower flux contribution implies larger uncertainties on the K-value of the star and eccentricity of the system; (ii) spectral types of the binary components, where a high density of lines in the spectra of cooler stars leads to more appreciable constraints on the K-values of stars and eccentricity of the orbit; and (iii) spectral line broadening with narrow spectral lines being more constraining on individual spectral shifts in the Fourier space and, as a result, on the eccentricity of the system and K-value of the respective binary component. While we opted for a simple method of uncertainty estimation in this work, our future studies will include a more sophisticated way of estimating uncertainties (e.g. the bootstrap method or jackknife estimator) that will allow us to account for the above-mentioned contributors to the total error budget.

Figure 2 shows example orbital solutions for a selection of four systems from the studied sample. The black lines represent orbital solutions for both binary components as determined with the SPD method. The red and blue filled circles respectively indicate the predicted primary and secondary RVs from the obtained orbital solution and at the epochs of the acquired spectroscopic observations. We note that the method of SPD bypasses the step of RV determination from the observed spectra; hence, the RVs shown in Fig. 2 are inferred quantities and used to illustrate the typical phase coverage we achieved for our systems irrespective of their orbital eccentricity value. Examples of the disentangled spectra for the same four systems are shown in Fig. 3. In the top row of the figure, we show a system with two similar components (V436 Per, light ratio lB/lA = 0.798 ± 0.021; Southworth & Bowman 2022) and a system with an extreme light ratio between the two stars (α CrB, light ratio lB/lA = 0.0180 ± 0.0002, Pavlovski et al., in prep.). In the latter case, spectral lines of the secondary component have a depth of at most 0.5% in the continuum units, owing to their rotational broadening. In the bottom row of the figure, the disentangled spectra are shown for the NY Cep (left) and RX Dra (right) systems. The primary component in the detached eclipsing binary NY Cep is one of the hottest stars in our sample, which is evidenced by the presence of He II lines at 4541 Å and 4687 Å. The SPD method also revealed the spectrum of the secondary component in the RX Dra system (right), which makes it an SB2 system with a γ Dor pulsating component.

thumbnail Fig. 2

Example orbital solutions for SB2 systems with differing numbers of observed spectra and fairly good phase coverage. Black lines depict the orbital solutions, while blue and red dots represent orbital phases of the observed spectra for the primary and secondary components, respectively. V436 Per, α CrB, and NY Cep are highly eccentric binary systems with eccentricities of about 0.37, 0.38, and 0.44, respectively. RX Dra represents the case of a circular-orbit system with the previously undetected secondary component that is revealed by this work.
thumbnail Fig. 3

Examples of the disentangled spectra for the binary systems shown in Fig. 2. In the upper row, V436 Per and α CrB represent systems with an extreme light ratio. In the lower row, binary systems with hot (NY Cep) and cool (RX Dra) components in our sample are shown for comparison.

4 Photometric analysis

Previous efforts have demonstrated the power of combining high-quality TESS light curves with spectroscopic radial velocities for relatively small numbers of high-mass pulsating eclipsing binaries (see e.g. Bowman et al. 2019b; Southworth et al. 2020, 2021; Southworth & Bowman 2022). As discussed in Sect. 2, our large sample of EBs was originally identified as eclipsing systems by IJspeert et al. (2021) using the products of automated light curve extraction tools, such as the MAST SPOC pipeline (Jenkins et al. 2016) and/or the TESS quick-look pipeline (QLP). However, in our current work, we extract a light curve optimised for each pulsating EB using the TESS full-frame images (FFIs), following a similar methodology described in Bowman et al. (2022), which is briefly summarised here for completeness.

TESS pixel cutouts sized 25 × 25 were extracted from the FFIs using ASTROCUT (Brasseur et al. 2019). We used the LIGHTKURVE software package (Lightkurve Collaboration 2018) to select aperture masks optimised to maximise the S/N of the eclipses (and pulsations if present) whilst minimising the contribution from nearby contaminating sources based on cross-checking with the location and fluxes of sources in the Gaia catalogue. The background flux was estimated from the median observed flux per frame after excluding pixels that contain flux from the target or other sources. The background flux was subtracted, and the extracted light curves were normalised by dividing through the median flux. Finally, we performed a principal component analysis (PCA) to remove any remaining instrumental systematics in the light curves (Bowman et al. 2022).

Due to the difference in integration times between different TESS data cycles and the large (i.e. >1 yr) gaps between cycles, we chose to analyse data from each cycle, if available, separately for each star. To classify the dominant variability beyond the eclipses caused by binarity and to ascertain if any additional signal is caused by pulsations or rotational modulation (RotMod) in our sample, we created a multi-frequency co-sinusoid model to remove the orbital harmonics from the extracted TESS light. Our approach is similar to the method used by Bowman et al. (2019b) for the pulsating eclipsing binary system U Gru. After optimising the orbital period and the number of significant orbital harmonic frequencies using a least-squares fit to the light curve, we subtracted the resultant optimised analytical model from the light curve and calculated the residual amplitude spectrum (Kurtz 1985). The dominant variability was identified as being from pulsations or RotMod through visual inspection of the residual amplitude spectrum. We applied this method to all the combined sectors within each TESS cycle to compare our classifications. For all stars, we found that our classification results are consistent across the multiple cycles, if available.

An example figure summarising this methodology is provided in Fig. 4, which contains our FFI-extracted light curve for all available cycle 1 data, the corresponding binary orbit phase-folded light curve, and the original and residual amplitude spectra for TIC 150442264 (HD 46792). In this example, several significant g-mode frequencies can be seen around 1 day−1, as well as a series of harmonics typical of rotational modulation at 0.1 day−1. There are no significant pulsation frequencies above about 2 day−1. We have left the combined binary modelling and pulsational frequency analysis for a future paper, but this approach allowed us to classify the dominant pulsational variability in our targets and to identify promising systems for future asteroseismic modelling, which are listed in Table A.1. In so doing, we dramatically increased the number of pulsating EBs that span spectral types from O through to F and include ß Cep through to γ Dor pulsators.

thumbnail Fig. 4

Example summary figure for TIC 150442264. Top panels: FFI-extracted light curve versus time (left) and phase folded on the orbital period for all available cycle 1 sectors (right). Bottom panels: original and residual amplitude spectra in which vertical red lines denote the location of significant orbital harmonics that comprise the analytic binary model, which is also shown as a red line in the phase-folded light curve panel.

5 Discussion

In this section, we present a summary of the obtained results and discuss them in the context of the previous studies. We recall that our sample selection was done in a blind way based on colour information and available TESS light curves. This approach to the target selection guarantees the presence in our sample of some of the well-studied systems in the literature, allowing us to use those as the methodology validators.

We report the detection of 12 single stars found by us to show either LPVs or no variations at all. We note that two more systems could not be decisively classified by us because their LPVs could be explained by intrisic variability of the star or binary effects equally well. We spectroscopically classified 15 stars as apparent SB1 systems. We note that the SB1 classification is not set in stone and may be revised into an SB2 when or if more spectra become available in the future. The SPD method delivered average disentangled spectra with a gain in S/N of roughly a factor of 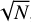N$\sqrt N $with respect to the individual observed composite spectra, where N stands for the number of spectra in a time series. This implies that the detection limit of a hypothetical faint companion star with the SPD method increases with the number of observed spectra in a time series, which may ultimately lead to reclassification of a star from SB1 into SB2. Furthermore, 50 targets were classified by us as SB2 systems. These are the primary candidates for future studies in the context of the observational mapping of the mass discrepancy. Finally, we report the detection of four high-order multiple systems, of which two objects were classified by us as triple (SB3) and two as quadruple (SB4) systems.

We classified 20 eclipsing systems as presumably containing at least one oscillating component. Of these twenty systems, one (u Tau) is a tentative detection where we cannot exclude rotational modulation as a cause of the intrinsic variability of the star, and two systems (V436 Per and HD 84493) are likely to contain a component showing stochastic low-frequency variability (e.g. Bowman et al. 2019a, 2020). Sixteen systems were found to contain either a g- (eight binaries) or p-mode (eight binaries) pulsator, and one system (V350 And) contains a g-/p-mode hybrid pulsator. Finally, the CD-45 4393 system was found by us to show a steadily decreasing eclipse depth across different TESS sectors such that the signal practically disappears in sectors 61 and 62. Such a phenomenon could be a manifestation of the precession of the binary orbit (e.g. due to the presence of a third body in the system), which causes the orbital inclination angle with respect to the observer’s line of sight to change with time.

Below, we discuss systems that have been studied in the literature and, where applicable, compare our photometric and spec-troscopic results with those reported by other research groups. We focus primarily on dedicated studies rather than on large catalogues. Hence, the overview provided in this section is probably not inclusive.

BD+13 1880: Šubjak et al. (2020) reported that the system is composed of a metallic-line Am star and a brown dwarf companion in a 3.6772 ± 0.0001 days orbit. From the analysis of a set of some 50 spectra obtained with multiple high-resolution spec-trographs, the authors reported the RV semi-amplitude K of the host star as 4.64 ± 0.03 km s−1, which is in a good agreement with the value of 5.0 ± 0.1 km s−1 derived in this work from a time series of ten HERMES spectra.

BD+36 3317: Özdarcan et al. (2012) classified the system as an Algol-type binary based on the analysis of ground-based multi-colour photometry and provided evidence of the system being a member of the δ Lyrae cluster. The system was revisited by Kiran et al. (2016) based on photometric observations from the literature and a newly obtained time series of 20 medium-resolution (R = 11 700) spectra. The authors reinforced the conclusion regarding the cluster membership of the system and reported the RV semi-amplitudes of the primary and secondary component to be K1 = 80.8 ± 1.1 and K2 = 124.1 ± 1.3, respectively. Both values are in good agreement with those derived in this work from eight HERMES spectra, namely, K1 = 82.93 ± 0.03 and K2 = 127.3 ± 0.1.

65 UMa B: The star was discovered to be magnetic by Bychkov et al. (2003), while Aurière et al. (2007) measured its longitudinal magnetic field and rotation period as Bl = −166 ± 20 G and 15.830 days, respectively. Joshi et al. (2010) presented a detailed spectroscopic study of the star based on a time series of high-resolution spectra obtained with the 2.56-m Nordic Optical Telescope (NOT). The authors reported on the absence of RV variations in the spectra and on the abundance pattern characteristic of evolved Ap stars. Zasche et al. (2012, see their Fig. 7) reported 65 UMa to be a sextuple system consisting of (i) a close eclipsing pair of nearly identical stars (Aa1+Aa2) orbiting each other with a period of ~1.73 days; (ii) a distant third component (Ab) orbiting the close pair with a period of about 640 days; (iii) a fourth component (65 UMa B), resolved interferometri-cally, whose period is about 118 yr; and (iv) a fifth (65 UMa C) and a sixth (65 UMa D) component with periods of ~14 kyr and ~591 kyr, respectively. Our spectroscopic classification of 65 UMa B as a single star not showing notable RV variability is in full agreement with the literature. The TESS light curve revealed the presence of shallow eclipses that are indicative of an eclipsing binary with a period of about 1.73 days. We concluded that the eclipse signal in the TESS light curve of 65 UMa B is due to a contaminating light from the component A, which has a similar surface brightness.

EL CVn: Maxted et al. (2014) studied the system based on a combined WASP photometry and SES high-resolution (R = 60 000) spectroscopy. The authors found the system to be composed of an A-type primary and a pre-He white dwarf companion residing in a circular orbit, with the RV semi-amplitude of the primary as K1 = 29.0 ± 0.4 km s−1. The latter is in agreement with our determination of K1 = 30.0 ± 1.6 km s−1. Wang et al. (2020) measured the spectral lines of both of the binary components with the far-UV HST/COS spectroscopy and reported the detection of a spectral signature of the pre-He-WD companion in the Mg II 4481 Å optical line in the medium-resolution (R = 31 500) ARCES spectra. The authors reported K1 = 29.0 ± 0.4 km s−1 and K2 = 236.2 ± 1.1 km s−1, which are in good agreement with the determination of the respective parameters in this work.

α CrB: A well-studied object whose orbit was reported for the first time by Jordan (1910), the system was solved spectro-scopically by Ebbighausen (1976), who reported e = 0.404 ± 0.004 and K1 = 35.8 ± 0.2 km s−1. Tomkin & Popper (1986) reported the detection of a secondary component based on newly obtained spectroscopic data with the coudé spectrograph attached to the 2.7-m McDonald Observatory telescope. The authors reported e = 0.371 ± 0.005, K1 = 35.4 ± 0.5 km s−1, and K2 = 99.0 ± 0.5 km s−1, in good agreement with the respective parameters derived in this work from 14 HERMES spectra. Of the more recent studies, Schmitt et al. (2016) provided RV measurements of the fainter secondary component using the method of cross-correlation and combined them with their own and historical RV data of the primary component in order to update the system’s orbital elements and search for evidence of an apsidal motion. The authors reported e = 0.379 ± 0.002, K1 = 36.2 ± 0.1 km s−1, and K2 = 98.0 ± 0.3 km s−1, which are in excellent agreement with the respective orbital elements derived in this work. In addition, Schmitt et al. (2016) found the apsidal motion period to be between 6600 and 10 600 yr, in agreement with the previous findings, and reported on the alignment of the orbit and rotation axes.

V994 Her: The system was discovered to have a quadruple-lined double-eclipsing nature from ground-based multi-colour photometric and high-resolution spectroscopic data by Lee et al. (2008). The authors reported the two eclipsing binaries in the system to have orbital periods of ~2.08 days and ~1.42 days, of which the former is in agreement with the period used in this work and reported by IJspeert et al. (2021). Both binaries were found to have slightly elliptic (e < 0.1) orbits, with reported masses of 2.83 ± 0.20 M⊙, 2.30 ± 0.16 M⊙, 1.87 ± 0.12 M⊙, and 1.86 ± 0.12 M⊙ for the Aa, Ab, Ba, and Bb components, respectively. Zasche & Uhlar (2013) reported V994 Her to be a quintuple system with the two eclipsing binaries orbiting each other with a period of about 6.3 days. These findings were refined in Zasche & Uhlar (2016), where the authors reported an orbital period of ~2.9 days for the two eclipsing pairs and found evidence for apsidal motion with periods of about 116 and 111 yr. The authors also reported updated masses of 3.01 ± 0.06 M⊙, 2.58 ± 0.05 M⊙, 1.84 ± 0.03 M⊙, and 1.93 ± 0.04 M⊙ for the Aa, Ab, Ba, and Bb components, respectively. Ultimately, Zasche et al. (2023) reported the discovery of a third set of eclipses in the TESS space-based and archival ground-based photometric data, which makes the system a triply eclipsing sextuple star system. The authors refined the orbital period of the A(Aa+Ab)–B(Ba+Bb) core system to 1062 ± 2 days and reported on its close to 3:2 mean motion resonance. The eclipsing pair C(Ca+Cb) was reported to have an elliptic orbit with a period of 1.96 days and component masses of 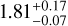1.81−0.07+0.17$1.81_{ - 0.07}^{ + 0.17}$ M⊙ and 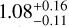1.08−0.11+0.16$1.08_{ - 0.11}^{ + 0.16}$ M⊙, respectively. Our classification of V994 Her as an SB4 system in this work is in agreement with the previous findings.

V1898 Cyg: The system was classified as a spectroscopic double-lined binary by Abt et al. (1972) and as an eclipsing system by Halbedel (1985). A detailed analysis of the system based on the newly obtained spectroscopic and archival photometric data was presented in Dervisoglu et al. (2011). The authors reported K1 and K2 RV semi-amplitudes of 55.2 ± 0.8 km s−1 and 287.6 ± 2.1 km s−1, respectively, which are in good agreement with the findings in this work.

GK Cep: The system was classified as an eclipsing spectroscopic double-lined binary with a period of 0.936171 day and a spectroscopic mass ratio of 0.92 by Bartolini et al. (1965). Furthermore, Pribulla et al. (2009) classified the system as a spectroscopic triple, in agreement with the findings in this work. A detailed study of GK Cep was presented in Zhao et al. (2021), which is based on newly obtained photometric data from the lunar-based ultraviolet telescope and the TESS space-based mission. The authors confirmed the presence of a third body in the system and measured the masses of the close binary components to be 1.93 M⊙ and 2.11 M⊙.

AH Cep: The system was analysed based on a combined photometric and spectroscopic dataset by Bell et al. (1986). The authors reported K1 = 249 ± 8 km s−1 and K2 = 283 ± 8 km s−1 under the assumption of a circular orbit. Holmgren et al. (1990a) and Burkholder et al. (1997) reported K1 = 237 ± 2 km s−1 and K2 = 269 ± 2 km s−1 and K1 = 230.0 ± 3.2 km s−1 and K2 = 277.6 ± 4.4 km s−1, respectively, under the same assumption of e = 0. The latter solution is in agreement with the findings in this work. A recent study by Pavlovski et al. (2018) reported a slightly higher value, K1 = 234.9 ± 1.1 km s−1 while their measure of K2 = 276.9 ± 1.4 km s−1 remains consistent with our determination of the respective parameter.

WW Aur: A detailed analysis of the system Was presented by Southworth et al. (2005). The authors reported K1 = 116.81 ± 0.23 km s−1 and K2 = 126.49 ± 0.28 km s−1 and M1 = 1.964 ± 0.007 M⊙ and M2 = 1.814 ± 0.007 M⊙ for the primary and secondary component, respectively. Our determinations of the RV semi-amplitudes are in agreement for the primary component and slightly lower for the secondary star.

AW Cam: A single-lined binary solution was presented by Mammano et al. (1967) with K1 = 112 ± 5 km s−1 under the assumption of a circular orbit. Frey et al. (2010) provided a simultaneous light- and RV-curve solution estimating K1 to 110 km s−1 . Our estimate of K1 is in agreement with the previous findings, and we establish the double-lined nature of the system in this work.

V453 Cyg: Popper & Hill (1991), Simon & Sturm (1994), and Burkholder et al. (1997) respectively reported spectro-scopic RV semi-amplitudes of K1 = 171 ± 1.5 km s−1 and K2 = 222 ± 2.5 km s−1; K1 = 171.7 ± 2.9 km s−1 and K2 = 223.1 ± 2.9 km s−1; and K1 = 173.2 ± 1.3 km s−1 and K2 = 213.6 ± 3.0 km s−1. Of the more recent studies, Southworth et al. (2004) obtained an eccentricity of e = 0.022 ± 0.002 from the apsidal motion solution and K1 = 173.7 ± 0.8 km s−1and K2 = 224.6 ± 2.0 km s−1 from the RV fitting. Consistent with these findings are the solutions obtained by Pavlovski & Southworth (2009); Pavlovski et al. (2018), where the latter study reported e = 0.022 ± 0.002, K1 = 175.2 ± 0.7 km s−1, and K2 = 220.2 ± 1.6 km s−1. The orbital elements that we determined in this work are in agreement with the previous studies, including the small eccentricity of the system. The star was classified as including a ß Cep variable by Southworth et al. (2020), in line with our own classification in this work.

NY Cep: Holmgren et al. (1990b) presented a detailed spec-troscopic study of the system based on 26 newly obtained high-resolution spectra. Among other things, the authors reported an eccentricity, argument of periastron, and components’ RV semi-amplitudes of e = 0.48 ± 0.02, ω = 58° ± 2, K1 = 112 ± 3 km s−1, and K2 = 158 ± 8 km s−1, respectively. Albrecht et al. (2011) revisited the system based on 46 newly obtained high-resolution spectra with the SOPHIE spectrograph. The authors reported e = 0.443 ± 0.005, ω = 56.3° ± 1, K1 = 113.8 ± 1.2 km s−1, and K2 = 139 ± 4 km s−1 assuming P = 15.27566 days, as derived in Ahn (1992). Our determinations of the eccentricity and argument of periastron of the system as well as the RV semi-amplitudes of both binary components are in good agreement with the findings by Albrecht et al. (2011).

16 Lac (= EN Lac): A detailed spectroscopic analysis of the star as an SB1 system based on some 1200 newly obtained and archival spectra was presented by Lehmann et al. (2001). The authors reported P = 12.096844 days, e = 0.0392 ± 0.0017, ω = 63.7° ± 2.1, and K1 = 23.818 ± 0.033 km s−1. While it has also been known as a single eclipsing system since its discovery by Jerzykiewicz (1980), a grazing secondary eclipse was for the first time detected in the TESS data by Southworth & Bowman (2022). The spectroscopic orbital elements derived by us in this work are in good agreement with those presented by Lehmann et al. (2001). The star has been reported to be a β Cep variable by Jerzykiewicz (1980); Dziembowski & Jerzykiewicz (1996); Lehmann et al. (2001); Aerts et al. (2003); Jerzykiewicz et al. (2015); Southworth & Bowman (2022), in line with our own findings in this work.

V436 Per: Harmanec et al. (1997) presented the first detailed spectroscopic study of the system based on a collection of newly obtained and archival data. Using the SPD method, the authors reported the detection of LPVs and determined the orbital eccentricity, argument of periastron, and RV semi-amplitudes of the components to be e = 0.3882 ± 0.0043, ω = 108.98° ± 0.27, K1 = 98.0± 1.0 km s−1, and K2 = 102.5± 1.2 km s−1, respectively. The system was revisited by Janík et al. (2003) based on a new set of high-resolution spectroscopic observations. The authors did not confirm the previously reported LPVs and presented an updated set of spectroscopic orbital elements: e = 0.3768 ± 0.0014, ω = 109.83° ± 0.10, K1 = 97.4 ± 0.1 km s−1, and K2 = 91.2 ± 0.1 km s−1. A notable finding in the latter study is that the secondary component has a lower RV semi-amplitude, suggesting it is a more massive star in the system. Southworth & Bowman (2022) analysed TESS photometric data of the V346 Per system, reported several local minima in the obtained solution, and emphasised the importance of obtaining an independent (spectroscopic) estimate of the components’ light ratio to resolve the degeneracy they encountered. The spectro-scopic orbital elements of the system that we derived in this work are in agreement with those reported by Harmanec et al. (1997) except that both of the K-values we found are some 0.3% lower. We also note that unlike Janík et al. (2003), we found the primary component to be the more massive one in the system. In addition, we found the star to exhibit stochastic low-frequency photometric variability, in a agreement with the classification by Southworth & Bowman (2022).

RX Dra: We found the system to contain a γ Dor-type pul-sator. This is in agreement with the classification by Southworth & Van Reeth (2022).

V1425 Cyg: A detailed study of the system based on a combined set of spectroscopic and photometric observations was presented by Hill & Khalesseh (1993). The authors reported K1 = 142.3 ± 1.8 km s−1 and K2 = 221.7 ± 2.2 km s−1 under the assumption of a circular orbit. The respective RV semi-amplitudes derived by us in this work are in agreement with the findings by Hill & Khalesseh (1993).

V446 Cep: Our photometric classification of the system as a β Cep pulsator is in agreement with the conclusions by Southworth & Bowman (2022). These authors also reported the star to presumably exhibit tidally induced oscillations.

CM Lac: A study of the system based on a combined set of spectroscopic and photometric observations was presented by Liakos & Niarchos (2012). The authors determined K1 = 119 ± 2 km s−1 and K2 = 156 ± 2 km s−1 under the assumption of a circular orbit. Southworth & Van Reeth (2022) revisited the system based on TESS photometric data and spectroscopic RV measurements from Liakos & Niarchos (2012). The authors reported K1 = 120.0 ± 3.4 km s−1 and K2 = 157.0 ± 3.3 km s−1, in agreement with the previous findings. Our determinations of the RV semi-amplitudes are in good agreement with both of the above-mentioned studies. Southworth & Van Reeth (2022) reported the system to contain a γ Dor pulsator, and we confirm their findings in this work.

V398 Lac: The system was investigated spectroscopically by Çakiılı et al. (2007). The authors reported e = 0.230, K1 = 110.3 ± 3.7 km s−1, and K2 = 128.5 ± 3.8 km s−1 for the eccentricity and RV semi-amplitudes of the components, respectively. A moderate orbital eccentricity of 0.273 and 0.2284 ± 0.0007 was confirmed by Bulut & Demircan (2008) and Wolf et al. (2013), respectively, based on the studies of HIPPARCOS photometry and apsidal motion of the system. While the orbital eccentricity obtained by us is in agreement with the previous studies, the RV semi-amplitudes of both components are lower by some 15% to 20% than those reported by Çakırılı et al. (2007).

V402 Lac: A detailed analysis of the system based on the newly obtained spectroscopic data and TESS space-based photometry was presented by Baroch et al. (2022). The authors determined the eccentricity and RV semi-amplitudes to be e = 0.376 ± 0.003, K1 = 128.5 ± 0.8 km s−1, and K2 = 129.2 ± 0.8 km s−1 from the combined RV and eclipse timing analysis, suggesting the system is composed of two stars with a similar mass. Our findings are similar but not exactly the same as the determinations by Baroch et al. (2022). In particular, we found a slightly lower eccentricity and a K-value for the primary component, the latter being suggestive of a slightly smaller mass ratio of the system.

AE Pic: A spectroscopic orbit of the system was presented by Sahade & Landi Dessy (1950). The authors reported e = 0.1, ω = 39°, and K1 = 119 km s−1. In this work, we classified the star as an SB2 system with a slightly lower eccentricity and RV semi-amplitude of the primary than reported previously. The system was classified as an eclipsing binary containing a pulsator that additionally exhibits signatures of rotational modulation by Barraza et al. (2022). We confirm their findings in this work and classified the star as having a β Cep pulsator with extra signatures of rotational modulation in the light curve.

6 Conclusions

Of the 573 systems proposed for spectroscopic monitoring with the HERMES and FEROS spectrographs, we report phase-resolved spectroscopic observations for 83 of them (cf. Table A.1). We classified 65 systems as either SB1 or SB2, and their respective orbital elements obtained with the SPD method are provided in Table B.1. For two more systems, HD 246047 and CD-47 4364, neither the SPD method nor the LSD-based classification could give a definitive answer as to whether these stars are single and show low-amplitude LPVs or are instead single-lined binaries with low K-values. Furthermore, in total we identified four high-order SB3 or SB4 multiple systems, while we classified the remaining 12 targets as single stars.

The log(Teff)–log(g) Kiel diagram of the above-mentioned 65 SB1 and SB2 systems is shown in Fig. 5. Where possible, the Teff and log g values have been taken from the literature (cf. Sect. 5); otherwise, the respective values have been estimated from the spectral type and luminosity class of the star by interpolating in the tables of Schmidt-Kaler (1982). We also note that Teff and log g of only the hotter and more massive primary components are displayed in Fig. 5. Therefore, the positions of the majority of stars in the Kiel diagram are not precise but rather indicative and used for the purpose of demonstrating the parameter space covered by the sample presented in this work. With a sub-sample comprising slightly over 10% of the total 573 candidate systems that we are currently monitoring spectroscopically, we achieved the coverage of a large range in the effective temperature and mass of the star, that is, Teff ∈ [7000, 30 000] K and M ∈ [1.5, 15] M⊙. Currently, the lower-mass regime with M ≲ 3.5 M⊙ is populated more densely, and the sample consists almost exclusively of stars in the core hydrogen burning phase.

Nevertheless, the present sample allowed us to start looking into the problem of mass discrepancy as a function of stellar mass, surface properties of the star (i.e. Teff, log g, and v sin i), binary configuration (i.e. detached versus semi-detached systems), and intrinsic variability of the star (i.e. pulsating versus non-pulsating components). Indeed, several systems in the sample with AF-type primary components are known Algols, and more of those have light curve characteristics of Algol-type binaries. A mix of well-detached and semi-detached systems in the sample allowed us to assess quantitatively the role of binary interactions in the mass discrepancy problem, as has been suggested by Mahy et al. (2020). Furthermore, diversity of the sample in terms of the effective temperature and mass of the primary component is an asset in the context of the possible connection between the mass discrepancy and amount of the near-core mixing in the form of the convective core overshoot proposed in the literature (e.g. Guinan et al. 2000; Massey et al. 2012; Morrell et al. 2014; Claret & Torres 2016, 2017, 2018, 2019). The fact that the present sample contains binaries with and without pulsating components will allow us to study the role of pulsations in the mass discrepancy problem methodologically (e.g. to what extent the presence of intrinsic variability alters the inference of the absolute stellar dimensions from a light curve) and physics-wise (e.g. to what extent a wave-induced mixing alters interior and atmospheric properties of stars in models that are used to quantify the mass discrepancy). Moreover, the detection of stellar oscillations in at least one of the binary components will enable an independent measurement of the amount of the near-core mixing with asteroseismic methods. A further extension of the sample towards inclusion of more evolved stars will allow us to investigate a possible connection between the mass discrepancy and evolutionary stage of the star, in particular the role of turbulent and radiative pressure terms in the inference of the effective temperature of the star when its surface gravity is accurately known from a photodynamical model of the system (e.g. Tkachenko et al. 2020).

The sub-sample representing slightly over 10% of the total of 573 candidate eclipsing binary systems that we are currently monitoring spectroscopically is one of the largest (if not the largest) eclipsing binary star ensemble being observed in a largely consistent way (i.e. with the same ground-based instruments for spectroscopic data and TESS space-based mission for photometric data sets), and it will be analysed by us with a well-established modelling framework, described in detail in Tkachenko et al. (2020). The high level of consistency in the observational strategy and modelling approach is particularly important for minimising otherwise numerous and hardly traceable systematic uncertainties in the investigation of the mass discrepancy problem. Coupled with a homogeneous and, in the near future, complete coverage of the parameter space, we can conclude that our sample of eclipsing binaries has all the potential to become the foundation to quantify and resolve the mass discrepancy problem in eclipsing binaries.

Finally, we stress an appreciable capability of the SPD method to infer precise and accurate spectroscopic orbital elements and individual components’ spectra from as little as six to eight orbital phase-resolved spectroscopic observations. Indeed, by using an estimate of the orbital period of the system as the only input to the planning of our observational campaign, we have demonstrated that a stable SPD solution can be obtained for the majority of binaries in the sample. This is contrary to the established thinking in the community, namely, that an extensive time series typically comprised of a couple of dozen spectro-scopic observations is required for the SPD method to deliver meaningful results. In particular, by comparing our orbital solutions reported in Table B.1 with those obtained by other research groups based on typically more extended datasets, we found a good agreement for all but a few systems (cf. Sect. 5) in the sample. Moreover, systems like AE Pic or AW Cam, which are known as SB1s in the literature, were discovered by us to be double-lined binaries and thus became ideal candidates for detailed modelling with the goal of inferring absolute dimensions of both binary components. Furthermore, the precision with which we inferred the RV semi-amplitudes of both binary components is often comparable to what is reported in dedicated studies in the literature (e.g. Pavlovski et al. 2018; Schmitt et al. 2016, for the AH Cep and α CrB systems, respectively). This in turn translates into our ability to infer absolute dimensions of stars with precision and accuracy better than 3% when a complementary high-quality ground- or space-based photometric dataset is available (which is the case for all systems in our sample).

The above-mentioned accuracy of 3% in stellar mass is sufficiently high to provide a pertinent calibration of SSE models for scientific exploitation of future space-based missions, such as PLATO (Rauer et al. 2014). Indeed, Chaplin et al. (2014) and Silva Aguirre et al. (2017) demonstrated asteroseismically for solar-like pulsators (i.e. main-sequence Sun-like stars and evolved intermediate-mass stars on the red giant brunch) that ~10% precision in age can be achieved when the mass and radius of the star are measured with the precision of 4% and 2%, respectively. The 10% age accuracy is one of the most fundamental science requirements for the PLATO mission to be able to characterise an Earth-like planet in the habitable zone of a Sun-like star (Rauer et al. 2014). In this work, we demonstrated that our approach to the planning of spectroscopic observations and subsequent analysis of the obtained data precision and accuracy is compliant even with the most stringent requirements of space-based missions such as PLATO.

In the forthcoming papers, we will present detailed analyses of individual systems based on their combined spectroscopic and TESS photometric data. All systems will be studied in the context of the mass discrepancy problem presented in detail in Sect. 1. Also, the forthcoming papers will include updates on our ongoing spectroscopic monitoring of the entire sample of 573 candidate eclipsing binaries in a format similar to that used in the present study.

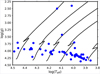thumbnail Fig. 5

Kiel diagram of stars listed in Table B.1. In the case of SB2 systems, parameters of the hotter component are displayed. Solid lines represent MESA evolutionary tracks for the stellar mass values M of (from right to left) 1.5, 3.0, 4.5, 7.0, and 13 M⊙ and a minimum amount of overshoot ƒOV = 0.005 Hp. The tracks are from Johnston et al. (2019b).

Acknowledgements

The research leading to these results has received funding from the KU Leuven Research Council (grant C16/18/005: PARADISE), from the Research Foundation Flanders (FWO) under grant agreement under grant agreements G089422N (NS, AT), V506223N (KP, Scientific stay in Flanders), 11E5620N (SG, PhD Aspirant mandate), 1124321N (LIJ, PhD Aspirant mandate), and 1286521N (DMB, Senior Postdoctoral Fellowship), as well as from the BELgian federal Science Policy Office (BELSPO) through PRODEX grant PLATO. DMB gratefully acknowledges the Engineering and Physical Sciences Research Council (EPSRC) of UK Research and Innovation (UKRI) in the form of a Frontier Research grant under the UK government’s ERC Horizon Europe funding guarantee (grant number [EP/Y031059/1]), and a University Research Fellowship from the Royal Society (grant number: [URF\R1\231631]). Based on observations made with the Mercator Telescope, operated on the island of La Palma by the Flemish Community, at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on observations obtained with the HERMES spectrograph, which is supported by the Research Foundation - Flanders (FWO), Belgium, the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany. Some of the observations used in this work were obtained with the FEROS spectrograph mounted on the 2.2-m MPG/ESO telescope at the ESO La Silla observatory under programme 0106.A-0906(A). The TESS data in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST) at the Space Telescope Science Institute (STScI), which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support to MAST for these data is provided by the NASA Office of Space Science via grant NAG5-7584 and by other grants and contracts. Funding for the TESS mission is provided by the NASA Explorer Program. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France; the SAO/NASA Astrophysics Data System; and the VizieR catalog access tool, CDS, Strasbourg, France.

Appendix A Classification of the sample stars

In this section, we present our spectroscopic and photometric classifications for all stars included in the present sample.

Table A.1

Spectroscopic and photometric classification for stars studied in this work.

Appendix B Spectral disentangling-based orbital solutions

In this section we present SPD-based orbital solutions for all stars that are classified as either SB1 or SB2 systems in Table A.1.

Table B.1

Spectroscopic orbital elements for all SB1 and SB2 systems studied in this work.

References

  1. Abt, H. A., Levy, S. G., & Gandet, T. L. 1972, AJ, 77, 138 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aerts, C., Lehmann, H., Briquet, M., et al. 2003, A&A, 399, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Ahn, Y. S. 1992, Ap&SS, 198, 137 [NASA ADS] [CrossRef] [Google Scholar]
  4. Albrecht, S., Winn, J. N., Carter, J. A., Snellen, I. A. G., & de Mooij, E. J. W. 2011, ApJ, 726, 68 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Ausseloos, M., Aerts, C., Lefever, K., Davis, J., & Harmanec, P. 2006, A&A, 455, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Baroch, D., Giménez, A., Morales, J. C., et al. 2022, A&A, 665, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Barraza, L. F., Gomes, R. L., Messias, Y. S., et al. 2022, ApJ, 924, 117 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bartolini, C., Mammano, A., Mannino, G., & Margoni, R. 1965, Inform. Bull. Variable Stars, 85, 1 [NASA ADS] [Google Scholar]
  10. Bell, S. A., Hilditch, R. W., & Adamson, A. J. 1986, MNRAS, 223, 513 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bowman, D. M., Burssens, S., Pedersen, M. G., et al. 2019a, Nat. Astron., 3, 760 [Google Scholar]
  12. Bowman, D. M., Johnston, C., Tkachenko, A., et al. 2019b, ApJ, 883, L26 [Google Scholar]
  13. Bowman, D. M., Burssens, S., Simón-Díaz, S., et al. 2020, A&A, 640, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bowman, D. M., Vandenbussche, B., Sana, H., et al. 2022, A&A, 658, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Brahm, R., Jordán, A., & Espinoza, N. 2017, PASP, 129, 034002 [Google Scholar]
  16. Brasseur, C. E., Phillip, C., Hargis, J., et al. 2019, in ASP Conf. Ser., 523, Astronomical Data Analysis Software and Systems XXVII, eds. P. J. Teuben, M. W. Pound, B. A. Thomas, & E. M. Warner, 397 [NASA ADS] [Google Scholar]
  17. Bulut, I., & Demircan, O. 2008, New A, 13, 252 [NASA ADS] [CrossRef] [Google Scholar]
  18. Burkholder, V., Massey, P., & Morrell, N. 1997, ApJ, 490, 328 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bychkov, V. D., Bychkova, L. V., & Madej, J. 2003, A&A, 407, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Çakırılı, Ö., Frasca, A., Banoglu, C., Soydugan, F., & Degirmenci, O. 2007, Astron. Nachr., 328, 536 [CrossRef] [Google Scholar]
  21. Chaplin, W. J., Basu, S., Huber, D., et al. 2014, ApJS, 210, 1 [Google Scholar]
  22. Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Claret, A. 2012, A&A, 541, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Claret, A., & Torres, G. 2016, A&A, 592, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Claret, A., & Torres, G. 2017, ApJ, 849, 18 [Google Scholar]
  26. Claret, A., & Torres, G. 2018, ApJ, 859, 100 [Google Scholar]
  27. Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
  28. Costa, G., Girardi, L., Bressan, A., et al. 2019, MNRAS, 485, 4641 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dervisoglu, A., Çakirli, Ö., Ibanoglu, C., & Sipahi, E. 2011, Rev. Mex. Astron. Astrofis., 47, 297 [Google Scholar]
  30. Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [Google Scholar]
  31. Dziembowski, W. A., & Jerzykiewicz, M. 1996, A&A, 306, 436 [NASA ADS] [Google Scholar]
  32. Ebbighausen, E. G. 1976, Publ. Dominion Astrophys. Observatory Victoria, 14, 411 [NASA ADS] [Google Scholar]
  33. Frey, J. R., Angione, R. J., & Sievers, J. R. 2010, Inform. Bull. Variable Stars, 5946, 1 [NASA ADS] [Google Scholar]
  34. Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
  35. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Gebruers, S., Tkachenko, A., Bowman, D. M., et al. 2022, A&A, 665, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Guinan, E. F., Ribas, I., Fitzpatrick, E. L., et al. 2000, ApJ, 544, 409 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
  39. Halbedel, E. M. 1985, Inform. Bull. Variable Stars, 2663, 1 [NASA ADS] [Google Scholar]
  40. Harmanec, P., Hadrava, P., Yang, S., et al. 1997, A&A, 319, 867 [NASA ADS] [Google Scholar]
  41. Herrero, A., Puls, J., & Villamariz, M. R. 2000, A&A, 354, 193 [NASA ADS] [Google Scholar]
  42. Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
  43. Hill, G., & Khalesseh, B. 1993, A&A, 276, 57 [NASA ADS] [Google Scholar]
  44. Holmgren, D. E., Hill, G., & Fisher, W. 1990a, A&A, 236, 409 [NASA ADS] [Google Scholar]
  45. Holmgren, D. E., Hill, G., Fisher, W., & Scarfe, C. D. 1990b, A&A, 231, 89 [NASA ADS] [Google Scholar]
  46. IJspeert, L. W., Tkachenko, A., Johnston, C., et al. 2021, A&A, 652, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. IJspeert, L. W., Tkachenko, A., Johnston, C., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202349079 [Google Scholar]
  48. Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, in ASP Conf. Ser., 318, Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, eds. R. W. Hilditch, H. Hensberge, & K. Pavlovski, 111 [NASA ADS] [Google Scholar]
  49. Janík, J., Harmanec, P., Lehmann, H., et al. 2003, A&A, 408, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
  51. Jerzykiewicz, M. 1980, in Nonradial and Nonlinear Stellar Pulsation, 125, eds. H. A. Hill, & W. A. Dziembowski, 125 [Google Scholar]
  52. Jerzykiewicz, M., Handler, G., Daszynska-Daszkiewicz, J., et al. 2015, MNRAS, 454, 724 [NASA ADS] [CrossRef] [Google Scholar]
  53. Johnston, C. 2021, A&A, 655, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Johnston, C., Pavlovski, K., & Tkachenko, A. 2019a, A&A, 628, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Johnston, C., Tkachenko, A., Aerts, C., et al. 2019b, MNRAS, 482, 1231 [Google Scholar]
  56. Johnston, C., Tkachenko, A., Van Reeth, T., et al. 2023, A&A, 670, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Jordan, F. C. 1910, Publ. Allegheny Observatory Univers. Pittsburgh, 1, 85 [NASA ADS] [Google Scholar]
  58. Joshi, S., Ryabchikova, T., Kochukhov, O., et al. 2010, MNRAS, 401, 1299 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
  60. Kiran, E., Harmanec, P., Degirmenci, Ö. L., et al. 2016, A&A, 587, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Kolbas, V., Pavlovski, K., Southworth, J., et al. 2015, MNRAS, 451, 4150 [NASA ADS] [CrossRef] [Google Scholar]
  62. Kurtz, D. W. 1985, MNRAS, 213, 773 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lee, C. U., Kim, S. L., Lee, J. W., et al. 2008, MNRAS, 389, 1630 [NASA ADS] [CrossRef] [Google Scholar]
  64. Lehmann, H., Harmanec, P., Aerts, C., et al. 2001, A&A, 367, 236 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Liakos, A., & Niarchos, P. 2012, Ap&SS, 340, 281 [NASA ADS] [CrossRef] [Google Scholar]
  66. Lightkurve Collaboration (Cardoso, J. V. d. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
  67. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  68. Mahy, L., Almeida, L. A., Sana, H., et al. 2020, A&A, 634, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Mammano, A., Margoni, R., & Stagni, R. 1967, Mem. Soc. Astron. Italiana, 38, 509 [NASA ADS] [Google Scholar]
  70. Martinet, S., Meynet, G., Ekström, S., et al. 2021, A&A, 648, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Massey, P., Morrell, N. I., Neugent, K. F., et al. 2012, ApJ, 748, 96 [NASA ADS] [CrossRef] [Google Scholar]
  72. Maxted, P. F. L., Bloemen, S., Heber, U., et al. 2014, MNRAS, 437, 1681 [NASA ADS] [CrossRef] [Google Scholar]
  73. Morrell, N. I., Massey, P., Neugent, K. F., Penny, L. R., & Gies, D. R. 2014, ApJ, 789, 139 [NASA ADS] [CrossRef] [Google Scholar]
  74. Özdarcan, O., Sipahi, E., & Dal, H. A. 2012, New A, 17, 483 [CrossRef] [Google Scholar]
  75. Pavlovski, K., & Hensberge, H. 2010, in ASP Conf. Ser., 435, Binaries – Key to Comprehension of the Universe, eds. A. Prša, & M. Zejda, 207 [NASA ADS] [Google Scholar]
  76. Pavlovski, K., & Southworth, J. 2009, MNRAS, 394, 1519 [NASA ADS] [CrossRef] [Google Scholar]
  77. Pavlovski, K., Tamajo, E., Koubský, P., et al. 2009, MNRAS, 400, 791 [NASA ADS] [CrossRef] [Google Scholar]
  78. Pavlovski, K., Southworth, J., & Tamajo, E. 2018, MNRAS, 481, 3129 [NASA ADS] [Google Scholar]
  79. Pavlovski, K., Hummel, C. A., Tkachenko, A., et al. 2022, A&A, 658, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Pavlovski, K., Southworth, J., Tkachenko, A., Van Reeth, T., & Tamajo, E. 2023, A&A, 671, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  82. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  83. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  84. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  85. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  86. Pedersen, M. G., Chowdhury, S., Johnston, C., et al. 2019, ApJ, 872, L9 [Google Scholar]
  87. Popper, D. M., & Hill, G. 1991, AJ, 101, 600 [NASA ADS] [CrossRef] [Google Scholar]
  88. Pribulla, T., Rucinski, S. M., DeBond, H., et al. 2009, AJ, 137, 3646 [NASA ADS] [CrossRef] [Google Scholar]
  89. Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [CrossRef] [EDP Sciences] [Google Scholar]
  90. Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
  91. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
  92. Rosu, S., Noels, A., Dupret, M. A., et al. 2020, A&A, 642, A221 [EDP Sciences] [Google Scholar]
  93. Rosu, S., Rauw, G., Farnir, M., Dupret, M. A., & Noels, A. 2022a, A&A, 660, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Rosu, S., Rauw, G., Nazé, Y., Gosset, E., & Sterken, C. 2022b, A&A, 664, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Sahade, J., & Landi Dessy, J. 1950, ApJ, 111, 191 [NASA ADS] [CrossRef] [Google Scholar]
  96. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  97. Sana, H., Le Bouquin, J. B., Lacour, S., et al. 2014, ApJS, 215, 15 [Google Scholar]
  98. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  99. Schmidt-Kaler, T. 1982, Bull. Inform. Centre Donnees Stellaires, 23, 2 [Google Scholar]
  100. Schmitt, J. H. M. M., Schröder, K. P., Rauw, G., et al. 2016, A&A, 586, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Serenelli, A., Weiss, A., Aerts, C., et al. 2021, A&A Rev., 29, 4 [NASA ADS] [CrossRef] [Google Scholar]
  102. Silva Aguirre, V., Lund, M. N., Antia, H. M., et al. 2017, ApJ, 835, 173 [Google Scholar]
  103. Simon, K. P., & Sturm, E. 1994, A&A, 281, 286 [NASA ADS] [Google Scholar]
  104. Southworth, J., & Bowman, D. M. 2022, MNRAS, 513, 3191 [Google Scholar]
  105. Southworth, J., & Van Reeth, T. 2022, MNRAS, 515, 2755 [NASA ADS] [CrossRef] [Google Scholar]
  106. Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
  107. Southworth, J., Smalley, B., Maxted, P. F. L., Claret, A., & Etzel, P. B. 2005, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
  108. Southworth, J., Bowman, D. M., Tkachenko, A., & Pavlovski, K. 2020, MNRAS, 497, L19 [Google Scholar]
  109. Southworth, J., Bowman, D. M., & Pavlovski, K. 2021, MNRAS, 501, L65 [NASA ADS] [CrossRef] [Google Scholar]
  110. Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
  111. Stellingwerf, R. F. 1978, ApJ, 224, 953 [Google Scholar]
  112. Šubjak, J., Sharma, R., Carmichael, T. W., et al. 2020, AJ, 159, 151 [Google Scholar]
  113. Themeßl, N., Hekker, S., Southworth, J., et al. 2018, MNRAS, 478, 4669 [Google Scholar]
  114. Tkachenko, A., Aerts, C., Pavlovski, K., et al. 2012, MNRAS, 424, L21 [NASA ADS] [Google Scholar]
  115. Tkachenko, A., Van Reeth, T., Tsymbal, V., et al. 2013, A&A, 560, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Tkachenko, A., Aerts, C., Pavlovski, K., et al. 2014a, MNRAS, 442, 616 [Google Scholar]
  117. Tkachenko, A., Degroote, P., Aerts, C., et al. 2014b, MNRAS, 438, 3093 [Google Scholar]
  118. Tkachenko, A., Matthews, J. M., Aerts, C., et al. 2016, MNRAS, 458, 1964 [NASA ADS] [CrossRef] [Google Scholar]
  119. Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Tomkin, J., & Popper, D. M. 1986, AJ, 91, 1428 [NASA ADS] [CrossRef] [Google Scholar]
  121. Torres, G., Andersen, J., & Giménez, A. 2010, A&A Rev., 18, 67 [Google Scholar]
  122. Uytterhoeven, K., Briquet, M., Aerts, C., et al. 2005a, A&A, 432, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Uytterhoeven, K., Harmanec, P., Telting, J. H., & Aerts, C. 2005b, A&A, 440, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Viani, L. S., & Basu, S. 2020, ApJ, 904, 22 [NASA ADS] [CrossRef] [Google Scholar]
  125. Wang, L., Gies, D. R., Lester, K. V., et al. 2020, AJ, 159, 4 [Google Scholar]
  126. Wolf, M., Zasche, P., Kucáková, H., et al. 2013, A&A, 549, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Zahn, J. P. 1991, A&A, 252, 179 [Google Scholar]
  128. Zasche, P., & Uhlar, R. 2013, MNRAS, 429, 3472 [NASA ADS] [CrossRef] [Google Scholar]
  129. Zasche, P., & Uhlar, R. 2016, A&A, 588, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Zasche, P., Uhlár, R., Šlechta, M., et al. 2012, A&A, 542, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Zasche, P., Borkovits, T., Jayaraman, R., et al. 2023, MNRAS, 520, 3127 [NASA ADS] [CrossRef] [Google Scholar]
  132. Zhao, E. G., Qian, S. B., Zhou, X., et al. 2021, MNRAS, 504, 5155 [NASA ADS] [CrossRef] [Google Scholar]
6

STAR_SHADOW will be part of the mentioned publication and published on GitHub.

All Tables

Table A.1

Spectroscopic and photometric classification for stars studied in this work.

In the text
Table B.1

Spectroscopic orbital elements for all SB1 and SB2 systems studied in this work.

In the text

All Figures

thumbnail Fig. 1

Examples of the LSD profiles computed with the Teff = 11 000 K mask. From top left to bottom right: HD 34382, a single star showing line profile variability; HD 138305, an SB2 binary system; HD 234650, an SB3 triple system; and HD 57158, an SB4 quadruple system. The individual LSD profiles in each panel have been shifted vertically by a constant factor for clarity.
In the text
thumbnail Fig. 2

Example orbital solutions for SB2 systems with differing numbers of observed spectra and fairly good phase coverage. Black lines depict the orbital solutions, while blue and red dots represent orbital phases of the observed spectra for the primary and secondary components, respectively. V436 Per, α CrB, and NY Cep are highly eccentric binary systems with eccentricities of about 0.37, 0.38, and 0.44, respectively. RX Dra represents the case of a circular-orbit system with the previously undetected secondary component that is revealed by this work.
In the text
thumbnail Fig. 3

Examples of the disentangled spectra for the binary systems shown in Fig. 2. In the upper row, V436 Per and α CrB represent systems with an extreme light ratio. In the lower row, binary systems with hot (NY Cep) and cool (RX Dra) components in our sample are shown for comparison.
In the text
thumbnail Fig. 4

Example summary figure for TIC 150442264. Top panels: FFI-extracted light curve versus time (left) and phase folded on the orbital period for all available cycle 1 sectors (right). Bottom panels: original and residual amplitude spectra in which vertical red lines denote the location of significant orbital harmonics that comprise the analytic binary model, which is also shown as a red line in the phase-folded light curve panel.
In the text
thumbnail Fig. 5

Kiel diagram of stars listed in Table B.1. In the case of SB2 systems, parameters of the hotter component are displayed. Solid lines represent MESA evolutionary tracks for the stellar mass values M of (from right to left) 1.5, 3.0, 4.5, 7.0, and 13 M⊙ and a minimum amount of overshoot ƒOV = 0.005 Hp. The tracks are from Johnston et al. (2019b).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.