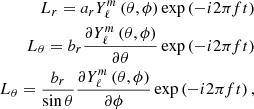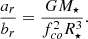| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A167 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202244808 | |
| Published online | 21 February 2023 | |
Tidal perturbations and eclipse mapping in the pulsations in the hierarchical triple system U Gru
1
Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010 6500 GL Nijmegen, The Netherlands
e-mail: cole.johnston@ru.nl
2
Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
3
Department of Physics, Faculty of Science, University of Zagreb, 10 000 Zagreb, Croatia
Received:
23
August
2022
Accepted:
10
October
2022
Context. Unambiguous examples of the influence of tides on self-excited, free stellar pulsations have recently been observationally detected in space-based photometric data.
Aims. We aim to investigate U Gru and contextualise it within the growing class of tidally influenced pulsators. An initial analysis of U Gru revealed frequencies spaced by the orbital frequency that are difficult to explain by currently proposed tidal mechanisms.
Methods. We reinvestigate the TESS photometry for U Gru alongside new UVES spectroscopy. We analyse the UVES spectroscopy with least-squares deconvolution and spectral disentangling techniques, and perform an atmospheric analysis. We remove the binary signature from the light curve using an effective model in order to investigate the pulsation signal in the residuals. We track the amplitudes and phases of the residual pulsations as a function of the orbital period to reveal their tidal influence.
Results. We establish that U Gru is likely a hierarchical triple system. We identify a single p-mode oscillation that exhibits amplitude and phase variation over the binary orbit. We propose a toy model to demonstrate that the series of frequencies separated by the orbital frequency can be reproduced by eclipse mapping. We find no evidence of modulation to the other independent oscillation modes.
Conclusions. We demonstrate that U Gru hosts at least one tidally perturbed pulsation. Additionally, we argue that eclipse mapping of the dominant, tidally perturbed mode can produce the series of frequencies separated by the observed orbital frequency. Our simulations show that the effects of eclipse mapping are mode dependent, and are not expected to produce an observable signature for all pulsation modes in an eclipsing binary.
Key words: asteroseismology / binaries: eclipsing / stars: individual: U Gru / stars: oscillations / binaries: close
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Self-excited, free stellar pulsations give rise to surface flux variations that are observable as brightness variations. The presence of a close binary companion can cause modulations to these brightness variations as seen by the observer. The modulations can be induced by: (1) directly modifying the interior of the pulsating star, giving rise to tidally perturbed pulsations (e.g. Smeyers & Martens 1983; Reyniers & Smeyers 2003); (2) altering the axis about which the pulsations occur (e.g. Handler et al. 2020; Fuller et al. 2020); or (3) through preferentially altering the visibility of the photosphere of the pulsating star along the observer’s line of sight (e.g. eclipse mapping; Gamarova et al. 2003; Reed et al. 2005).
Recently, a new class of tidally tilted pulsators in binary systems was observationally established, wherein the tidal forces are assumed to be strong enough to realign the pulsation axis with the line of apsides connecting the centre of mass of each component (Fuller et al. 2020). As the pulsation axis is no longer aligned with the rotation axis in this scenario, a time-dependent observed amplitude modulation is introduced as the pulsation nodal lines periodically change visibility with orbital phase. This is comparable to the configuration observed in rapidly oscillating Ap stars in which the pulsation axis is inclined with respect to the rotation axis due to the strong magnetic fields of these stars; this is commonly referred to as the oblique pulsator model (Kurtz 1982; Bigot & Dziembowski 2002; Saio & Gautschy 2004). Furthermore, there is a subset of tidally tilted pulsators, called tidally trapped pulsators, in which the tidal deformation of the pulsating star effectively traps the pulsation to a single side of the star due to mode coupling (Fuller et al. 2020). This creates an apparent orbital phase dependence of the pulsation amplitude. When viewed in Fourier space, the amplitude modulation results in pulsation multiplets that have components separated by the orbital frequency.
The phenomenon of tidally tilted pulsations has so far been observed in a handful of stars observed by NASA’s Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015). The cases of HD 74423, CO Cam, and HD 265435 show pulsations that are preferentially trapped to one side of the star (Handler et al. 2020; Kurtz et al. 2020; Jayaraman et al. 2022). However, the example of TIC 63328020, shows non-axisymmetric sectoral modes, which have a tilted pulsation axis and weak trapping (Fuller et al. 2020; Rappaport et al. 2021), while the oscillating eclipsing Algol-type (oEA; Mkrtichian et al. 2003) systems TZ Dra and HL Dra show evidence for a tidally tilted pulsation axis (Shi et al. 2021; Kahraman Aliçavuş et al. 2022).
In addition to these clear examples of tidally tilted pulsators, there are a handful of objects that demonstrate other forms of tidal perturbations to the observed pulsations. Notably, the eclipsing binary RS Cha shows multiple phenomena, including the tidal splitting of intrinsic pulsation modes induced by the tidal bulge acting as the axis of symmetry, and an observed pulsation amplitude decrease due to the presence of eclipses (Balona 2018; Preece et al. 2019; Steindl et al. 2021). Furthermore, there are now several (eclipsing) binaries pulsating in either pressure (p) or gravity (g) mode oscillations that show tidal perturbations or other distortions that modify the observed pulsation amplitude over the orbit (Jerzykiewicz et al. 2020; Southworth et al. 2020, 2021; Lee 2021; Van Reeth et al. 2022). While the sample of tidally perturbed pulsators is increasing, there is no consensus on a proposed underlying mechanism. There is no obvious underlying commonality in orbital configuration, mass range, or previous evolutionary history amongst the known sample of tidally influenced pulsating stars (Handler et al. 2022).
Given the recent increase in the identification of tidal signatures in a diversity of pulsating stars, astronomers are starting to utilise the high precision afforded by space-based telescopes to perform asteroseismology and probe the influence of tides on the stellar interior. However, to be able to exploit tidally influenced modes in asteroseismic analyses, we require the unambiguous identification of the underlying tidal phenomena in question. Therefore, before a tidal asteroseismic analysis, we need to perform a detailed investigation of the combined time-series photometry and spectroscopy of complicated cases, such as that of the oEA system U Gru, which shows signatures of tidal effects as well as eclipse mapping (Reed et al. 2005; Gamarova et al. 2003) in its pulsation modes (Bowman et al. 2019).
U Gru is a bright oEA system with a binary period of 1.8805 d, initially discovered to be an eclipsing binary with an A5 spectral type by Brancewicz & Dworak (1980). Recently, U Gru was observed by TESS in sectors 1 and 28, yielding 54 days of high-precision space-based photometry. Using the initial sector of TESS data, Bowman et al. (2019) report the discovery of several independent p-mode pulsations in addition to a series of significant frequencies split by (multiples of) the orbital frequency. However, there is no clear symmetry in the distribution of the frequencies that are split by the orbital frequency, making its interpretation as a tidal phenomenon challenging given the currently proposed mechanisms (e.g. Balona 2018; Fuller et al. 2020). oEA systems are known to have recently undergone mass transfer, effectively rejuvenating the accretor and placing it closer to the zero-age main-sequence (ZAMS). To further complicate matters, oEA systems are commonly observed to have distant tertiary companions, potentially introducing more complicated tidal forces in the system due to the ever-changing tidal potential (Fuller et al. 2013).
In this paper, we re-visit the TESS photometry of U Gru alongside new UVES spectroscopy in order to identify the mechanisms causing the tidal effects observed in its pulsations. In Sect. 2 we present new spectroscopic observations and atmospheric modelling. In Sect. 3 we discuss the analysis of the existing TESS data. Finally, we discuss the presence and lack of tidal signals and present a toy model to explain our observations in Sect. 4 before concluding in Sect. 5.
2. UVES spectroscopy of U Gru
To characterise the components and the orbit of the system, we obtained high-resolution spectroscopy with the Ultraviolet and Visual Échelle Spectrograph (UVES on UT2 at VLT; Dekker et al. 2000) via a Director’s Discretionary Time proposal (ID: 0104.D-0209; PI: C. Johnston). Our observations utilised the standard DIC-2 blue arm setting, which has both a blue (λ ∼ 300 − 500 nm; λc = 437 nm; R ∼ 80 000) and red (λ ∼ 420 − 1100 nm; λc = 760 nm; R ∼ 110 000) detector equipped on UVES. All observations were taken using a 1″ slit with a 600 s exposure time. We obtained 12 epochs over a three-month period, which are distributed to maximise coverage across the orbital period of the U Gru binary system. The observations are briefly summarised in Table 1.
Barycentric Julian Date, orbital phase, and S/N of UVES observations.
The spectra were extracted, corrected, and calibrated with the standard version of the ESO UVES pipeline (Sacco et al. 2014) and can be obtained directly from the ESO archive1. Further normalisation of the reduced spectra to the local continuum was performed by fitting a third-order polynomial through a set of manually selected continuum points. Barycentric velocity and time corrections were applied to the spectra.
2.1. Least-squares deconvolution
The first step of our spectroscopic analysis involves computing the least-squares deconvolution (LSD; Donati et al. 1997) profiles with a customised version of the LSD algorithm (Tkachenko et al. 2013). An LSD profile is an average line profile that is characterised by a significantly enhanced signal-to-noise ratio (S/N) compared to individual absorption lines in the stellar spectrum. Additionally, the LSD profile captures any type of variability that is common to all spectral lines involved in the calculation. In particular, the LSD method provides an efficient way of detecting line-profile variations due to binarity and/or intrinsic variability of either of the binary components in the form of rotational modulation and/or stellar pulsations (e.g. Tkachenko et al. 2013; Johnston et al. 2021).
To compute the LSD profiles, we used multiple synthetic line lists for an A-type star (Teff = 8000, log g = 4.0 dex, [M/H] = 0), a G-type star (Teff = 6000, log g = 4.0 dex, [M/H] = 0), as well as for a K-type star (Teff = 5000, log g = 4.0 dex, [M/H] = 0). The line lists were constructed from the VALD database (Kupka et al. 2000), covering a wavelength range of 4000−7000 Å, excluding Balmer lines. Although we compute LSD profiles from the spectra obtained with both the blue and red arms of the UVES instrument, below we discuss the results obtained for the blue arm only. We do this to avoid repeating the results given the strong similarities obtained from the red part of the spectrum. Additionally, we do not use the spectrum taken during primary eclipse as the S/N is low and we do not see the signature of the primary. The orbital phase-folded LSD profiles for 11 spectra from the UVES blue arm are shown in Fig. 1. We note that the systemic velocity was not removed from the observations before we calculated the LSD profiles. Two components are clearly visible in the LSD profiles of the blue arm. One component is broadened and shows intrinsic line-profile variability throughout the motion along the orbit. The other component reveals a narrow-lined profile which appears stationary over the orbital period. We identify the broad-lined profile as the rejuvenated A-type primary (i.e. the δ Scuti pulsator), and identify the narrow-lined profile as a potential slowly rotating tertiary component in the system due to its negligible radial velocity (RV) variability. The cool faint secondary component is not firmly detected in either of the two arms of the obtained UVES spectra.
 |
Fig. 1. Least-squares deconvolution profiles of U Gru computed from 11 blue arm UVES spectra. The orbital phase-resolved spectral contribution of the broad-lined primary component is indicated with the dashed line. |
2.2. Spectral disentangling
Spectroscopic observations of multiple star systems are comprised of the composite light of all the N components in the system. The analysis of such a composite spectrum can be done by directly fitting N components to the spectrum with the appropriate RV shifts and light factors, or by separating the components using techniques such as spectral disentangling. The method of spectral disentangling allows one to simultaneously optimise for orbital elements of the system and separate the individual spectra of the stars forming the system (Simon & Sturm 1994; Hadrava 1995). For the purpose of spectral disentangling, we employ the FDBINARY software package (Ilijic et al. 2004), using 11 out of the total 12 acquired blue-arm spectra of U Gru. In particular, we remove the spectrum taken at the time of the eclipse of the more luminous primary component due to the strong variations in the spectral line depths caused by the near total blockage of light from the primary component. We perform the spectral disentangling in the wavelength region between the Hγ and Hβ Balmer profiles spanning 4400−4800 Å.
In the first step, we perform the spectral disentangling in a triple system mode, primarily in an attempt to detect signatures of the faint secondary component. However, similar to the results obtained with the LSD profiles, no trace of the cool secondary component can be found with the spectral disentangling technique. We therefore proceed with the spectral disentangling in a ‘fake binary mode’ where the narrow-lined tertiary component is constrained to have long periods such that it shows little to no RV variability over the three-month time span of our UVES observations. The broad-lined primary component is assumed to be on a circular orbit and is otherwise unconstrained. This is supported by the initial TESS photometry and preliminary binary modelling by Bowman et al. (2019), and both of these assumptions are largely consistent with the scenario arising from the properties of the LSD profiles outlined in Sect. 2.1. From this, we find the RV semi-amplitude of the more luminous primary component to be K1 = 61.5 ± 0.7 km s−1 and find no significant RV variability associated with the tertiary component.
Using the orbital solution and the disentangled spectra of the primary and tertiary components from the ‘fake binary mode’, we shift these disentangled spectra by their individual RVs corresponding to the times of each of the UVES observations and then subtract each shifted disentangled spectrum from the originally observed composite spectra. This way we obtain a time series of 11 residual spectra in which spectral contributions of the primary and tertiary components have been eliminated. In the next step, we explore these residual spectra with the FDBINARY algorithm in a spectroscopic single-lined binary (SB1) mode in an attempt to search for extremely weak signatures of the cool secondary component. This exercise reveals a tentative spectrum of a cool star whose RV semi-amplitude K2 is found to be between 195 and 200 km s−1. Figure 2 shows the disentangled spectra of the primary (blue) and tertiary (black) components of the U Gru system, as well as the tentative disentangled spectrum of the secondary (red) alongside a synthetic spectrum computed for Teff = 5500 K and log g = 3.5 dex (orange) and arbitrarily diluted to the level of 2% (in continuum units) for comparison. We note that the disentangled secondary spectrum has been binned by a factor of two to increase the S/N. Although we do not claim a firm detection of the secondary component, we do identify some similarities between the disentangled secondary spectrum and the synthetic spectrum in Fig. 2.
 |
Fig. 2. Disentangled spectra of the primary (blue) and tertiary (black) components of the U Gru system. A representative synthetic spectrum corresponding to Teff = 5500 K and log g = 3.5 dex and diluted to the level of 2% (in continuum units) is shown for comparison to the secondary component (red). We note that a constant vertical shift has been applied to all the spectra for visibility purposes. |
As a final exercise, we fix K1 and set the initial guess for K2 according to our previous findings, and once again perform spectral disentangling in the SB3 triple-system mode. The inner binary orbit is assumed to be circular and we allow for small RV variability in the narrow-lined tertiary component. We find the RV semi-amplitude of the secondary component to be K2 = 202 ± 3 km s−1 while the disentangled spectra of all three components do not show any significant differences with respect to the solutions described above. We find that the tertiary RV semi-amplitude tends towards 0 km s−1 in this solution. Together with K1, the above value of K2 suggests a mass ratio of q = 0.304 ± 0.005, and ∼2.7 M⊙ and ∼0.8 M⊙ for the mass of the primary and secondary components, respectively, assuming an inclination of i = 90°. All these values are consistent with the system configuration typical for Algols and the mass of the primary is consistent with its late-A spectral type. We note that given the lack of a robust detection of the secondary, we do not attempt a full binary modelling in this work, as any solution would be degenerate without an independent constraint on the mass ratio and semi-major axis of the system.
Figure 3 shows the orbital RV curves for the primary and secondary components of U Gru computed from the corresponding best fit orbital elements. Because the method of spectral disentangling bypasses the step of RV determination and instead solves for the orbital elements directly, the symbols shown in Fig. 3 do not represent the actual RV measurements of the primary, secondary, and tertiary components, respectively. Instead, the symbols represent the RVs computed from the best-fit orbital solution at the times of our UVES observations. We show this to demonstrate the orbital phase coverage achieved with our spectroscopic observations.
 |
Fig. 3. Orbital solution for the primary (blue), secondary (red), and tertiary (black) components of U Gru obtained with the method of spectral disentangling. We note that the symbols do not represent actual RV measurements. Instead, they indicate the distribution of the observed spectra over the orbital cycle of the inner binary system, while the orbital RV curve itself is computed from the best-fit orbital elements. |
2.3. Atmospheric parameters
We employ the Grid Search in Stellar Parameters (GSSP; Tkachenko 2015) software package to infer atmospheric parameter values of the primary and tertiary components from their disentangled spectra. We do not perform a spectral analysis of the faint secondary component owing to the low S/N in its disentangled spectrum. The GSSP package is employed in its ‘unconstrained fitting’ mode, which allows us to analyse the disentangled spectra of stars as if they were single. Although GSSP offers an option to fit the disentangled spectra of binary (or triple system) components simultaneously, whilst also taking into account the wavelength dependence of the components’ light contributions, we do not opt for that particular mode in our analysis. This is mainly because we expect the secondary component to potentially still contaminate the spectrum of the primary component. In turn, the uncertainty in the disentangled spectrum of the primary component propagates into the results obtained for the tertiary component when the two spectra are coupled methodologically.
In our spectral analysis, we explore different combinations of free and fixed atmospheric parameters, of which we consider a total of six for each of the components: effective temperature Teff, surface gravity log g, microturbulent velocity ξ, projected rotational velocity v sin i, metallicity [M/H] (assuming an Asplund et al. (2005) solar composition), and light dilution factor ℓfi. Immediately, we find that although the light dilution factor is well constrained for the tertiary component, no (realistic) optimal value can be obtained for the primary component. Therefore, we start with the atmospheric analysis of the tertiary component and then proceed with the analysis of the primary component where its light dilution factor ℓf1 is fixed according to the relation ℓf1 = 1 − ℓf3. This relation assumes that the secondary component is not present in the system. Instead, in the final stage of our analysis, we re-determine the atmospheric parameters of the primary and tertiary components allowing for variations in the light factors ℓf1 and ℓf3 of a few percent from their optimal values. We do not consider variations larger than a few percent because we do not expect larger contributions to the light factors from the faint secondary component. We account for deviations of the atmospheric parameters of the primary and tertiary components from their optimal values due to variable ℓf1 and ℓf3 in the final reported parameter uncertainties.
Our spectral analysis shows that the most stable spectroscopic solution is achieved when the ξ and [M/H] parameters are fixed to 2 km s−1 and 0.0 dex (solar value), respectively. We note that the metallicity [M/H] in the atmospheric spectroscopic analysis refers to a joint contribution of all elements heavier than helium. Otherwise, we find a statistically significant difference in the metallicity of the two stars. This scenario is not expected in a gravitationally bound binary (or triple) system where all components are formed from the same natal cloud, despite the past history of binary interaction. However, similar to the case with the light factors, we do account for the effects of metallicity and microturbulent velocity in the finally reported uncertainties for Teff, log g, and v sin i. The final atmospheric parameters (and their uncertainties) of the primary (A1V; Pecaut & Mamajek 2013) and tertiary (F3V) components of U Gru are reported in Table 2. Given the surface gravity and mass range of the primary as derived above, the primary is rotating at less than 20% of its critical rate.
Atmospheric parameters of the primary and tertiary components of U Gru.
3. TESS photometry
U Gru was observed by TESS in two sectors separated by roughly two years. During the first sector, U Gru was observed for 27.9 d in two-minute cadence mode, whereas it was observed for 25.2 d at a ten-minute cadence in the full-frame image (FFI) data during sector 28. We find no indication of the tertiary object in either sector of the TESS photometry. Using the two-minute cadence sector 1 data, Bowman et al. (2019) reported 22 significant pulsation frequencies after subtracting a multi-harmonic model to remove the eclipsing binary contribution. However, in this work we remove the strictly periodic eclipsing signal using an interpolated model constructed from the orbital phase-folded light curve. Briefly, we phase fold the original light curve on the orbital period, and then bin the phased light curve. We then construct an interpolated model from the phase-binned data and subtract that model from the original light curve. The phase folded light curves from sectors 1 and 28 are shown in black and grey in the top panel of Fig. 4. The interpolated models are shown in red, and the residuals are shown in the bottom panel. The Lomb-Scargle (LS) periodograms (Lomb 1976; Scargle 1982; Press & Rybicki 1989; Astropy Collaboration 2018) of the interpolation-model-subtracted residuals are shown in the black (sector 1) and grey (sector 28) in Fig. 5. As can be seen, the series of frequencies separated by (multiples of) the orbital frequency are still seen in the residuals from sector 28, suggesting that the underlying phenomenon is stable across the two years separating the data sets. Notably, the amplitudes observed in the periodogram of sector 28 residuals are generally lower than those observed in the sector 1 residuals. This is likely caused by the change in photometric sampling rate (two min to 10 min) between the sectors. There does appear to be an additional amplitude change for the second-highest amplitude frequency. Intrinsic pulsation mode amplitude variability over multiple years is commonly observed in δ Scuti pulsators and is attributed to mode coupling or changes to the internal stellar structure (Bowman et al. 2016).
 |
Fig. 4. Orbitally phase-folded TESS photometry of U Gru. Top: phase-folded light curve of U Gru for sectors 1 (black) and 28 (grey) with the interpolated binary model in red. Grey hatching denotes phases of primary (forward hatching) and secondary (cross hatching) eclipse. Bottom: residuals after subtraction of an interpolation binary model for sectors 1 (black) and 28 (grey). |
We conduct an iterative pre-whitening procedure on the residuals of the sector 1 data using the PYTHIA code2 in order to remove the remaining periodic signals. We identify the signal to be removed at each iteration as the peak with the highest S/N calculated via a 1 d−1 window surrounding the frequency. The signal in question is modelled with a sinusoid, where the optimised parameters are taken as the maximum a posteriori (MAP) non-linear least-squares fit to the light curve. We perform the optimisation using the PYMC3 (Salvatier et al. 2016) and EXOPLANET (Foreman-Mackey et al. 2021a) PYTHON modules. We iterate until we extract all signals with S/N > 4, and then re-calculate the final model with all frequencies as free parameters. We calculate the final S/N with respect to the residual light curve. We find 21 significant frequencies, which are reported in Table 3. The phases are calculated with respect to t0 = 2458325.93900, which is the reference epoch of primary eclipse first reported by Bowman et al. (2019). We report uncertainties on the frequencies, amplitudes, and phases according to Montgomery & O’Donoghue (1999) accounting for the correlated nature of the data according to Schwarzenberg-Czerny (2003). We recover eight fewer frequencies that are split by the orbital frequency than originally reported in Bowman et al. (2019). Five of these modes had a S/N < 4 reported by Bowman et al. (2019), whereas all eight were found to be formally insignificant in our analysis. We find seven additional significant frequencies that Bowman et al. (2019) did not recover in their analysis. The differences in extracted frequencies is likely caused by the different methods used to subtract the binary signal and the different methods for calculating the noise level around a given frequency. We construct and show an Échelle diagram of our extracted frequencies folded over the orbital frequency in Fig. 6, which shows a clear series of frequencies split by (multiples of) the orbital frequency.
Optimised fit parameters, S/N, and frequency phased by the orbital frequency of the significant frequencies identified via iterative pre-whitening.
4. Amplitude and phase tracking
4.1. Tidal effects
In all of the confirmed tidally tilted pulsating stars known to date, the tidal splitting has resulted in a (generally) symmetric multiplet, split by (multiples of) the orbital frequency. However, in the case of U Gru, (Bowman et al. 2019) identified a series of frequencies that did not appear to be centred on a particular oscillation mode, which poses a challenge to the interpretation of this phenomenon as the result of a tidally tilted pulsation axis.
In this work we re-visit the pulsation analysis of U Gru, and track the amplitude and phases of the several frequencies extracted from iterative pre-whitening. We divide the Échelle diagram into distinct sections (e.g. 0−0.1 d−1, 0.1−0.2 d−1, etc.) as shown by the grey dashed lines in Fig. 6, and track the highest amplitude mode for each section of the Échelle diagram; for example f13, f14, f15, f19, and f21. We also consider f20 to be independent and track it. These modes are labelled in Fig. 5 and denoted by orange markers in Fig. 6. To do this, we remove all other significant frequencies from the other sections of the Échelle diagram before dividing the orbital phase-folded light curve into 50 equally sized bins. We fit a sinusoid with a fixed frequency to each bin and record the amplitude and phase following Van Reeth et al. (2022). The tracked amplitudes and phases are shown in Fig. 7, with orbital phase values of 0, 1, and 2 corresponding to primary eclipse, and orbital phase values of 0.5 and 1.5 corresponding to secondary eclipse. In order to compare the modulations for each frequency, we consider the relative amplitude and phase modulations. As such, we divide the tracked amplitude at each phase bin by the average amplitude ⟨A⟩ across all orbital phase-bins considered. Similarly, we subtract the average mode phase ⟨ϕ⟩ for each frequency. Only the highest-amplitude pulsation at f14 = 33.046 d−1 shows amplitude and phase modulation across the orbit, as shown in Fig. 7. Additionally, we note that the remaining frequencies for which we tracked amplitudes and phases show amplitude minima during primary eclipse.
 |
Fig. 5. Top: Lomb-Scargle periodogram of binary-subtracted residuals for sector 1. Bottom: Lomb-Scargle periodogram of binary-subtracted residuals for sector 28. Labelled frequencies denote frequencies that are tracked in Sect. 4.1 and shown in orange in Fig. 6. |
 |
Fig. 6. Échelle diagram of the significant frequencies extracted from the residuals of sector 1 folded over the orbital period. The marker size scales with amplitude. Orange markers denote frequencies labelled in Fig. 5 and tracked in Sect. 4.1. |
 |
Fig. 7. Top: tracked mode amplitude for f14 = 33.046 d−1 as a function of orbital phase. Bottom: tracked relative mode phase for f14 = 33.046 d−1 as a function of orbital phase. Phase values of 0, 1, and 2 correspond to primary eclipse, and phase values of 0.5 and 1.5 correspond to secondary eclipse. |
We find clear evidence that the amplitude and phase of the p mode at f14 = 33.046 d−1 is modulated over the binary orbit. We note that the amplitude modulation displays an apparent minima during secondary eclipse, with maxima occurring at 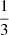 phases of the orbit. The three observed amplitude maxima are difficult to explain with the currently proposed tidal tilting framework, as a tilted mode with degree ℓ should produce maxima of 2ℓ in amplitude across the binary orbit (Fuller et al. 2020). Furthermore, we observe phase modulations with a π/2 rad variation, similar to those observed in distorted modes in roAp stars (e.g. Holdsworth et al. 2016) and the g-mode pulsating binary V456 Cyg (Van Reeth et al. 2022). Finally, we observe a complex behaviour of the amplitude and phase modulation at phases surrounding primary eclipse. Following the oblique pulsator model assumed for the case of tidal trapping, we should observe a symmetric multiplet split by the orbital frequency from the intrinsic pulsation frequency as well as phase variations with values of 0, π, or 2π. This model cannot explain either the full series of frequencies split by (multiples of) the orbital frequency or the observed phased modulations of the dominant p mode in U Gru.
phases of the orbit. The three observed amplitude maxima are difficult to explain with the currently proposed tidal tilting framework, as a tilted mode with degree ℓ should produce maxima of 2ℓ in amplitude across the binary orbit (Fuller et al. 2020). Furthermore, we observe phase modulations with a π/2 rad variation, similar to those observed in distorted modes in roAp stars (e.g. Holdsworth et al. 2016) and the g-mode pulsating binary V456 Cyg (Van Reeth et al. 2022). Finally, we observe a complex behaviour of the amplitude and phase modulation at phases surrounding primary eclipse. Following the oblique pulsator model assumed for the case of tidal trapping, we should observe a symmetric multiplet split by the orbital frequency from the intrinsic pulsation frequency as well as phase variations with values of 0, π, or 2π. This model cannot explain either the full series of frequencies split by (multiples of) the orbital frequency or the observed phased modulations of the dominant p mode in U Gru.
4.2. Eclipse mapping
Photometric observations of distant point-source stars show the total integrated surface brightness of the projected stellar surface at a given time. Stellar pulsations induce brightness variations in time by modifying the surface-brightness distribution according to the geometry of the pulsation modes. In the case of an eclipsing binary, the projected stellar disk is partially (or totally) obscured, resulting in a time-varying amount of the stellar disk that is observed. This produces a time-dependent modification to the partial cancellation of a varying mode over the stellar surface (Aerts et al. 2010). U Gru exhibits total eclipses of the primary, wherein the secondary component obscures nearly the entire visible disk of the pulsating A-type primary. Therefore, there is additional modulation of the observed pulsation amplitude as the disk of the pulsating star is partially obscured during ingress to primary eclipse, is completely obscured during conjunction, and is then partially obscured again during egress from primary eclipse. This process creates a complicated modulation of the observed pulsation amplitude over time as part of the variable surface is preferentially obscured. This phenomenon is sometimes referred to as spatial filtration (Gamarova et al. 2003, 2005; Rodríguez et al. 2004) or eclipse mapping (Reed et al. 2001, 2005). To further complicate this scenario, the pulsation mode of highest amplitude observed in U Gru (f14) shows evidence of being tidally perturbed, adding an additional modulation to the observed pulsation amplitudes and phases.
We constructed a toy model to illustrate the impact that eclipses have on the observed amplitudes and phases of non-tilted and tidally tilted pulsation modes3. The toy model is based on that used by Van Reeth et al. (in prep.), modified to our purposes. A full explanation of the code is given in Appendix A. Briefly, this toy model assumes two spherical stars (with no deformation caused by the equilibrium tide) in a Keplerian orbit. As we are simply trying to illustrate the effect of time-dependent partial cancellation via eclipses and are not attempting to forward model the effect, the use of spherical, non-tidally distorted stars is justified. The stars are inclined with respect to the observer according to the orbit. The pulsating component has its surface perturbed according to spherical harmonics of a given (ℓ, m) combination. We then define a series of points in time, and calculate the total flux as observed considering the pulsation phase as well as the visibility of each star along the line of sight. This simple model allows us to track the observed pulsation phase and amplitude along the orbit as the pulsating star is eclipsed. Furthermore, we allow for the pulsation axis to be inclined such than it can align with the orbital plane to simulate the tidally tilted scenario, but we do not account for mode trapping. This toy model does account for linear limb darkening, but does not account for the light-travel-time effect, which modulates the observed phase of a periodic pulsation because of the physical change in distance travelled by light from the pulsating star. In the case of U Gru, this is a safe assumption as the peak-to-peak phase variation expected for f14 caused by the light-travel-time effect is ∼0.03 rad following Murphy et al. (2014).
We define the orbit and components of our toy model to be qualitatively similar to that of U Gru following an initial analysis with the PHOEBE code (PHOEBE 1; Prša & Zwitter 2005; Prša et al. 2011). This initial analysis uses the TESS light curve and UVES RV solution (see Sect. 2) and was adjusted by hand to match the light-curve morphology and RVs of the primary. As the model was not numerically optimised, we do not consider this a full solution. We set the binary system to have Porb = 1.8805 d, M1 = 2.6 M⊙, R1 = 2.8 R⊙, M2 = 0.8 M⊙, R2 = 2.6 R⊙, and i = 85°. We then simulate several pulsation configurations, each with a different mode geometry (ℓ, m) and obliquity of the pulsation axis with respect to the rotation axis (β). We investigate multiple pulsation geometries in order to demonstrate that the differing pulsation geometries will produce different partial cancellation effects, resulting in different observed pulsation amplitudes and phases. The derived binary light curves, and pulsation amplitude and phase variations for each (ℓ, m, β) configuration are shown in the top, middle, and bottom panels of Fig. 8. The amplitude and phase modulations for the different pulsation configurations clearly demonstrate that the presence of eclipses can add an additional modulation to the pulsation amplitude and phase at orbital phases when the pulsating component is eclipsed. Furthermore, the different models in Fig. 8 demonstrate that the scale, complexity, and sign of the modulation are dependent on the system inclination, the obliquity of the pulsation axis, and the mode geometry (Reed et al. 2005).
 |
Fig. 8. Top: simulated light curves with different pulsation configurations (ℓ, m, β) phase folded over the binary period. The points from the other simulated light curves are poorly visible due to the strong overlap between the models and the size of the markers. Middle: mode amplitude variations for different pulsation configurations as seen by an observer because of changing partial cancellation effects. Bottom: mode phase variations for different pulsation configurations as seen by an observer. |
Any additional periodic amplitude variability in a pulsation mode is captured in the Fourier transform of the time series. To investigate the impact that eclipse mapping has on the pulsation signal as seen in the periodogram, we simulate the light curve for two of the configurations shown in Fig. 8 at the time stamps of the sector 1 TESS data. These simulated light curves are computed considering the full binary and pulsation signal, but have the eclipsing signature removed for clarity. By computing the synthetic light curves at the time stamps of the TESS data, we convolve the observational window function into the resulting periodogram to make our simulations as similar to the observations as possible. The periodograms of the subsequent time series are shown in Fig. 9. As it is a mathematical decomposition of a time series into a sum of sinusoids, the periodogram requires several additional sinusoidal terms to represent any non-sinusoidal variations, such as the amplitude modulations introduced by eclipse mapping. In this case, the signal manifests as multiple additional peaks separated from the intrinsic pulsation frequency by integer multiples of the orbital frequency.
 |
Fig. 9. Left column: simulated light curves of the pulsation mode only. Right column: periodogram of the accompanying light curve. These light curves do not consider the light variations caused by the binary itself. Grey hatching denotes phases of primary (forward hatching) and secondary (cross hatching) eclipse. |
The total number of additional peaks, their amplitudes, and whether or not they are symmetrically distributed about the intrinsic pulsation frequency depends on the mode geometry and orbital configuration. We highlight this by comparing the rows of Fig. 9. The top row considers an (ℓ = 3, m = −2, β = 0°) configuration where the two stars eclipse each other. In the configuration for the middle row, the radius of the secondary has been reduced so that the pulsating star is no longer eclipsed by the secondary, and therefore does not display any eclipse mapping effects. In this comparison, we note that the simulation without eclipses does not display the same series of peaks split by the orbital frequency, whereas the simulation with eclipses does. Furthermore, the bottom row displays a simulation for a different pulsation configuration (ℓ = 2, m = −1, β = 90°) –again with the same orbital configuration as the top row– that results in eclipses. This simulation demonstrates that the resulting signature in the periodogram is dependent on the pulsation geometry being considered, and that the resulting signature may be of insufficient amplitude to be observed in real data with multiple noise components.
4.3. Combined tidal and eclipse mapping effects
Our toy model produces two quantifiable outputs: (1) complex behaviour in the tracked mode amplitude and phase that occurs specifically during eclipse of the pulsating component, and (2) a series of peaks in the periodogram that are separated by the orbital frequency and potentially asymmetrically distributed around the true pulsation frequency. The observed chaotic mode amplitude and phase behaviour during phases of primary eclipse (e.g. Fig. 7) are qualitatively similar to the behaviour predicted by our eclipse mapping model. Given this, we propose that the asymmetrically distributed series of peaks separated by the orbital frequency observed in the residual periodogram of U Gru is also caused by eclipse mapping, similar to the results in Fig. 9. Following this interpretation, we can use the mathematical framework presented by Jayaraman et al. (2022) to investigate the observed amplitude and phase of this mode across the orbit and during primary eclipse. This framework assumes that any frequencies separated from the intrinsic mode by a multiple of the orbital frequency can be used to derive information about the phase and amplitude modulation of the intrinsic pulsation mode. While this methodology was developed to interpret the case of tidally tilted pulsators, it can be generalised for other pulsations that show orbital phase dependence. We simultaneously fit for the amplitude and phase of the mode at f14 = 33.046 d−1, as well as for the amplitudes and phases of those frequencies located at integer multiples of the orbital frequency such as fj = f1 ± nj with n being a real integer. We fit for the 14 frequencies with fmodforb < 0.1 d−1 simultaneously, all of which are taken from Table 3. In addition to the frequency at f14 = 33.046 d−1, we fit 12 sinusoids that are at frequencies below the main frequency, and only one at higher frequencies. While there may be other components to this series of frequencies, they do not have high enough amplitudes to be considered significant in our frequency analysis, and are therefore ignored. Although Handler et al. (2020), Kurtz et al. (2020), Rappaport et al. (2021), and Jayaraman et al. (2022) intentionally set the reference epoch for the pulsations to occur when the fj = n ± 1 frequencies have maximum amplitude, we cannot follow the same procedure as the frequencies we consider are asymmetrically distributed in the case of U Gru. Instead, we retain the same reference epoch as that of superior conjunction reported in Bowman et al. (2019).
The resulting amplitude and phase modulation over the orbit are shown in the middle and bottom panels of Fig. 10. The blue trend represents the fits using sector 1 data. The general phase and amplitude behaviour recovered by this method agree with the behaviour recovered by fitting a sinusoid with f = 33.0456 d−1 to different phase bins carried out in Sect. 4.1 (shown in black in Fig. 10). We also find complex amplitude and phase modulations around primary eclipse in Fig. 10. We further construct a model considering only those frequencies separated from the intrinsic mode by −3 ≤ N ≤ 3 (if significant). This model is shown in orange in the middle and bottom panels of Fig. 10, respectively. When only considering frequencies separated from the intrinsic mode by ±3 times the orbital frequency, we only recover the three amplitude maxima and phase-sign changes, and not the complex behaviour near primary eclipse. This suggests that the remaining asymmetrically distributed frequencies separated by larger integer multiples of the orbital frequency are the result of the complex behaviour at primary eclipse. We argue that this further supports the eclipse mapping origin of the asymmetrically distributed series of frequencies separated by the orbital frequency. We find the same results when using the sector 28 data.
 |
Fig. 10. Top: phase-folded light curve of U Gru for sector 1. Middle: amplitude modulation of f14 = 33.046 d−1 as reconstructed according to the fitting method developed by Jayaraman et al. (2022). The blue considers all 14 significant frequencies split from f14 listed in Table 3. The orange lines only consider those frequencies with f = f14 ± Nforb, where −3 ≤ N ≤ 3, if they were found to be significant in the iterative pre-whitening procedure. Tracked mode amplitudes from Sect. 4 are shown as black crosses. Bottom: same as the middle panel but for the phase modulation. Grey hatching denotes phases of primary (forward hatching) and secondary (cross hatching) eclipse. |
5. Discussion and conclusions
To date there are multiple examples of pulsating stars in binaries that exhibit behaviour consistent with the tidally tilted or trapped pulsator model. In addition to this, there are an increasing number of systems that exhibit pulsational behaviour that cannot be explained by the existing tidally tilted or trapped models. In this work, we increase the diversity of observed behaviours with the case of the bright triple system U Gru.
We used UVES spectroscopy to confirm the Algol-type status of U Gru and further discover that the system consists of an apparently rejuvenated A-type star and cool companion in a tight 1.8805 d orbit with a wide F3V tertiary companion. The atmospheric solution for the primary is consistent with a moderately rotating, early A-type star that has been rejuvenated by recent mass transfer. Unfortunately, due to its low light contribution, we were not able to robustly detect the signature of the cool secondary component. The lack of RV shifts and eclipse timing variations in the TESS data suggests that the orbit of the tertiary is much longer than the two-year time-base covered by the TESS data. To this end, we consider the separation sufficiently large as to not introduce additional tidal forcing from the distant third body.
The first frequency analysis of the TESS light curve by Bowman et al. (2019) revealed a series of significant frequencies separated by the orbital frequency, or integer multiples thereof. In this work, we conducted a follow-up analysis of the TESS light curves for both sectors 1 and 28. We removed the dominant binary signal via an interpolated model and ran an iterative pre-whitening frequency analysis on the residual light curves, recovering the independent pulsations as well as the series of frequencies split by integer multiples of the orbital frequency. Following this approach, we find that the mechanism that produced the series of frequencies separated by multiples of the orbital frequencies is stable over the two-year TESS time base.
The multi-periodic pulsations of U Gru present a challenge for the interpretation that the parameters of this system are the product of a single tidal mechanism. Only one pulsation mode (f14 = 33.046 d−1) shows evidence for amplitude and phase modulation across the binary orbit similar to what is expected in the case of a tidally tilted pulsation axis. However, the odd number of amplitude minima and maxima and phase zero-crossings, combined with the π/2 rad phase variation, are not consistent with predictions from the tidally tilted or trapped pulsator models (Fuller et al. 2020). Nevertheless, it is possible that future developments of this model that include the Coriolis force could produce predictions that more closely match our observations.
Currently, the π/2 rad phase variations we find are most similar to those of V456 Cyg, where small phase and normal amplitude variations were observed in a subset of g modes in a circular, synchronised binary (Van Reeth et al. 2022). Based on their findings, these authors argue that the modes are tidally perturbed and have contributions from non-axisymmetric components. Despite the similarities, it is not clear whether or not the same mechanism that modifies the g modes in V456 Cyg can modify the p modes in U Gru. Alternatively, due to the moderate rotation of the pulsating A-star, we could be observing the effects of rotation modifying and confining p modes to ‘island modes’ (e.g. Ouazzani et al. 2012; Reese et al. 2013, 2017). Moderate-to-rapid stellar rotation can preferentially trap pulsations to specific latitudes and longitudes, depending on the mode geometry and rotation rate (Aerts et al. 2010). As such, moderate rotation that is synchronised with the binary orbit could, in theory, produce an observed amplitude modulation that is commensurate with the orbital period. However, there is no prediction for the observed phase behaviour of such rotationally modified modes. It is also worth noting that while U Gru hosts multiple independent pulsation modes, most do not show any amplitude or phase variation with the orbit. This suggests that the mechanism behind the observed amplitude and phase variation in the dominant pulsation mode is not ubiquitous for all modes. Interestingly, other systems such as RS Cha and HD 265435 also host some pulsations that display amplitude and phase modulation and some others that do not (Steindl et al. 2021; Jayaraman et al. 2022).
The observed series of frequencies that are separated by (multiples of) the orbital frequency cannot be explained by any currently proposed tidal mechanism. Instead, we present a toy model to demonstrate that the observed signals can be explained by eclipse mapping. The results of the toy model demonstrate that eclipse mapping can produce a series of frequencies that are separated by the orbital frequency and that are asymmetrically distributed around the intrinsic pulsation frequency, as is observed in the case of U Gru. This model also demonstrates that the specific resulting signature in the periodogram depends on the mode geometry, such that some mode geometries might not experience any observable effect from eclipse mapping for a given orbital configuration. The mode geometry dependence can explain why some pulsation modes in U Gru are observed to experience eclipse mapping effects, while others do not, despite originating from the same system. This logic can be further extended to other pulsating stars in eclipsing binaries such as RS Cha, TIC 63328020, TZ Dra, HL Dra, V1031 Ori, and VV Ori, where some show complex series of frequencies separated by the orbital frequency and others do not (Steindl et al. 2021; Rappaport et al. 2021; Lee 2021; Southworth et al. 2021; Shi et al. 2021; Kahraman Aliçavuş et al. 2022).
While it has been hypothesised that eclipse mapping can serve as a means of mode identification for pulsations in well-characterised eclipsing binary systems, there are numerous observational considerations to account for (Rodríguez et al. 2004; Reed et al. 2005; Gamarova et al. 2005). Primarily, the amplitude of the eclipse mapping effect depends on the mode geometry and amplitude, as well as the specific details of the binary orbit. To this end, unambiguous mode identification through eclipse mapping would require the observer to be able to identify all of the frequencies distributed about a given pulsation frequency. Given the typical instrumental and astrophysical noise components in astronomical time series, this task is challenging. Furthermore, if any additional tidal phenomena were active that produce frequencies separated from the pulsation frequency by the orbital frequency, a comparison to theoretical predictions would need to account for their contributions as well. Nevertheless, compared to the model-dependent methods of mode identification via amplitude ratios or phase differences from multi-colour photometry (Garrido 2000; Handler 2008), eclipse mapping provides an alternative that does not depend on the underlying detailed stellar model.
The status of U Gru as an oEA star places it in a growing subset of stars with some form of tidally influenced pulsations that have a recent history of mass transfer. Other oEA stars in this category include TZ Dra, HL Dra, V1031 Ori, and V456 Cyg. Future studies that focus on pulsations in oscillating Algol type systems would benefit from searching the signature of tidally tilted pulsation axes or otherwise tidally influenced pulsations in a systematic manner. As we are observing the whole sky with high-precision space-based data, we expect to find more systems with an increasing diversity of tidally related phenomena. Increasing the sample of such pulsators will enable us to investigate the underlying physical mechanisms, as well as to investigate their dependence on stellar properties and potentially their evolutionary history. The multi-colour photometry provided by future missions such as PLATO (Rauer et al. 2014) will be of great benefit in this realm as it will allow for independent constraint of the mode identification, allowing us to further scrutinise the underlying mechanisms behind the increasing diversity of observed tidally related phenomena. Indeed, future work should investigate the relationship between wavelength and the observed effects of eclipse mapping, and the extent of the combined power of eclipse mapping and multi-filter amplitude and phase ratios in mode identification, as these tools often suffer from limitations when individually applied (Daszyńska-Daszkiewicz et al. 2002; Dupret et al. 2003).
Acknowledgments
We thank the anonymous referee for their comments which improved this manuscript. C.J. acknowledges support from the Netherlands Research School of Astronomy (NOVA). The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement N°670519: MAMSIE; CJ, DMB, AT), from the Research Foundation Flanders (FWO) under grant agreement G0A2917N (BlackGEM; CJ), from the KU Leuven Research Council (grant C16/18/005: PARADISE; AT), from the Research Foundation Flanders (FWO) under grant agreements G0H5416N (ERC Runner Up Project; AT), as well as from the BELgian federal Science Policy Office (BELSPO) through PRODEX grant PLATO (AT). T.V.R. and D.M.B. gratefully acknowledge financial support from FWO under grant agreement numbers 12ZB620N and 1286521N, respectively. This work is based on observations collected at the European Southern Observatory under ESO programme 0104.D-0209. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA’s Science Mission Directorate. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. This work has made use of the NUMPY (Harris et al. 2020), MATPLOTLIB (Hunter 2007), PYMC3 (Salvatier et al. 2016), and EXOPLANET (Foreman-Mackey et al. 2021b) python packages.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. I. Barnes, G. Thomas, & F. N. Bash, ASP Conf. Ser., 336, 25 [NASA ADS] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Balona, L. A. 2018, MNRAS, 476, 4840 [NASA ADS] [CrossRef] [Google Scholar]
- Bigot, L., & Dziembowski, W. A. 2002, A&A, 391, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, D. M., Johnston, C., Tkachenko, A., et al. 2019, ApJ, 883, L26 [Google Scholar]
- Brancewicz, H. K., & Dworak, T. Z. 1980, Acta Astron., 30, 501 [NASA ADS] [Google Scholar]
- Daszyńska-Daszkiewicz, J., Dziembowski, W. A., Pamyatnykh, A. A., & Goupil, M. J. 2002, A&A, 392, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 534 [Google Scholar]
- Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [Google Scholar]
- Dupret, M. A., De Ridder, J., De Cat, P., et al. 2003, A&A, 398, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Luger, R., Agol, E., et al. 2021a, Journal of Open Source Software, 6, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Luger, R., Agol, E., et al. 2021b, https://doi.org/10.5281/zenodo.1998447 [Google Scholar]
- Fuller, J., Derekas, A., Borkovits, T., et al. 2013, MNRAS, 429, 2425 [CrossRef] [Google Scholar]
- Fuller, J., Kurtz, D. W., Handler, G., & Rappaport, S. 2020, MNRAS, 498, 5730 [NASA ADS] [CrossRef] [Google Scholar]
- Gamarova, A. Y., Mkrtichian, D. E., Rodriguez, E., Costa, V., & Lopez-Gonzalez, M. J. 2003, in Interplay of Periodic, Cyclic and Stochastic Variability in Selected Areas of the H-R Diagram, ed. C. Sterken, ASP Conf. Ser., 292, 369 [NASA ADS] [Google Scholar]
- Gamarova, A. Y., Mkrtichian, D. E., & Rodríguez, E. 2005, in Tidal Evolution and Oscillations in Binary Stars, eds. A. Claret, A. Giménez, & J. P. Zahn, ASP Conf. Ser., 333, 258 [NASA ADS] [Google Scholar]
- Garrido, R. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 67 [NASA ADS] [Google Scholar]
- Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
- Handler, G. 2008, Commun. Asteroseismol., 157, 106 [NASA ADS] [Google Scholar]
- Handler, G., Kurtz, D. W., Rappaport, S. A., et al. 2020, Nat. Astron., 4, 684 [Google Scholar]
- Handler, G., Jayaraman, R., Kurtz, D. W., Fuller, J., & Rappaport, S. A. 2022, Proc. Polish Astron. Soc., 12, 183 [NASA ADS] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Holdsworth, D. L., Kurtz, D. W., Smalley, B., et al. 2016, MNRAS, 462, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, eds. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 111 [Google Scholar]
- Jayaraman, R., Handler, G., Rappaport, S. A., et al. 2022, ApJ, 928, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Jerzykiewicz, M., Pigulski, A., Handler, G., et al. 2020, MNRAS, 496, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, C., Aimar, N., Abdul-Masih, M., et al. 2021, MNRAS, 503, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Kahraman Aliçavuş, F., Handler, G., Aliçavuş, F., et al. 2022, MNRAS, 510, 1413 [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [Google Scholar]
- Kurtz, D. W. 1982, MNRAS, 200, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Handler, G., Rappaport, S. A., et al. 2020, MNRAS, 494, 5118 [Google Scholar]
- Lee, J. W. 2021, PASJ, 73, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Mkrtichian, D. E., Nazarenko, V., Gamarova, A. Y., et al. 2003, in Interplay of Periodic, Cyclic and Stochastic Variability in Selected Areas of the H-R Diagram, ed. C. Sterken, ASP Conf. Ser., 292, 113 [NASA ADS] [Google Scholar]
- Montgomery, M. H., & O’Donoghue, D. 1999, Delta Scuti Star Newsletter, 13, 28 [NASA ADS] [Google Scholar]
- Murphy, S. J., Bedding, T. R., Shibahashi, H., Kurtz, D. W., & Kjeldsen, H. 2014, MNRAS, 441, 2515 [Google Scholar]
- Ouazzani, R. M., Dupret, M. A., & Reese, D. R. 2012, A&A, 547, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Preece, H. P., Jeffery, C. S., & Tout, C. A. 2019, MNRAS, 489, 3066 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Rybicki, G. B. 1989, ApJ, 338, 277 [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [Google Scholar]
- Prša, A., Matijevic, G., Latkovic, O., Vilardell, F., & Wils, P. 2011, Astrophysics Source Code Library [record ascl:1106.002] [Google Scholar]
- Rappaport, S. A., Kurtz, D. W., Handler, G., et al. 2021, MNRAS, 503, 254 [NASA ADS] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Reed, M., Kawaler, S. D., & Kleinman, S. J. 2001, in 12th European Workshop on White Dwarfs, eds. J. L. Provencal, H. L. Shipman, J. MacDonald, & S. Goodchild, ASP Conf. Ser., 226, 181 [Google Scholar]
- Reed, M. D., Brondel, B. J., & Kawaler, S. D. 2005, ApJ, 634, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Reese, D. R., Prat, V., Barban, C., van ’t Veer-Menneret, C., & MacGregor, K. B. 2013, A&A, 550, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. R., Lignières, F., Ballot, J., et al. 2017, A&A, 601, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reyniers, K., & Smeyers, P. 2003, A&A, 404, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rodríguez, E., García, J. M., Gamarova, A. Y., et al. 2004, MNRAS, 353, 310 [CrossRef] [Google Scholar]
- Sacco, G. G., Morbidelli, L., Franciosini, E., et al. 2014, A&A, 565, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saio, H., & Gautschy, A. 2004, MNRAS, 350, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. 2016, PeerJ Comput. Sci., 2, e55 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Schwarzenberg-Czerny, A. 2003, in Interplay of Periodic, Cyclic and Stochastic Variability in Selected Areas of the H-R Diagram, ed. C. Sterken, ASP Conf. Ser., 292, 383 [NASA ADS] [Google Scholar]
- Shi, X.-D., Qian, S.-B., Li, L.-J., & Liao, W.-P. 2021, MNRAS, 505, 6166 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, K. P., & Sturm, E. 1994, A&A, 281, 286 [NASA ADS] [Google Scholar]
- Smeyers, P., & Martens, L. 1983, A&A, 125, 193 [NASA ADS] [Google Scholar]
- Southworth, J., Bowman, D. M., Tkachenko, A., & Pavlovski, K. 2020, MNRAS, 497, L19 [Google Scholar]
- Southworth, J., Bowman, D. M., & Pavlovski, K. 2021, MNRAS, 501, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Steindl, T., Zwintz, K., & Bowman, D. M. 2021, A&A, 645, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A. 2015, A&A, 581, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Van Reeth, T., Tsymbal, V., et al. 2013, A&A, 560, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Southworth, J., Van Beeck, J., & Bowman, D. M. 2022, A&A, 659, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Pulsating binary model
We construct a binary system consisting of two spherical, non-tidally distorted stars in a Keplerian orbit. The orbit is defined by the masses of the two stars (M1, 2), their orbital period (Porb), the reference epoch of superior conjunction (t0, sc), separation (a), and the inclination of their orbit with respect to the line of sight of the observers (i). In addition to their masses, the stars are characterised by their radii (R1, 2) and the percentage of the total light that they contribute as seen by the observer (ℓ1, 2). Furthermore, we include a third light contribution that has ambiguous origin.
The surface of each star is discretised on a spherical grid with radius r = R⋆, latitude −π ≤ θ ≤ π, and longitude 0 ≤ ϕ ≤ 2π. At any point in time, only a particular range of latitudes and longitudes on the stellar surface are visible, denoted as (θ0, ϕ0)t. The user is allowed to decide if either or both stars are pulsating, and assign a mode identification (ℓ, m) and frequency (fpulse) to the pulsation mode. For this model, only one pulsation per star is allowed. The system, and therefore the surface of each star is inclined according to the binary inclination, changing the visible range of latitudes and longitudes on the stellar surface. The inclined surface ranges are denoted as (θi, ϕi)t. Finally, we allow the surface to be inclined again by some angle β to simulate the case of a tidally tilted pulsation. The final visible surface is then denoted by (θβ, ϕβ)t. We then calculate the perturbation to the surface brightness following the given mode geometry according to:
where 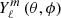 are spherical harmonics, and ar and br are the radial and horizontal amplitudes at the stellar surface, related through the pulsation frequency in the corotating frame fco by:
are spherical harmonics, and ar and br are the radial and horizontal amplitudes at the stellar surface, related through the pulsation frequency in the corotating frame fco by:
For simplicity, we set ar = 1 and calculate br through Eq. A.2.
We initialise a grid of time points, and progress the positions of the stars according to the orbit. At each time point, we check if the surface of either star is being eclipsed, and if so apply a simple boolean mask to the points on the stellar surface that are in eclipse. We calculate the summed fluxes of the stars according to their visible (and potentially pulsating) surfaces and scale them according to their light contributions considering any potential third light. We provide the total summed binary and pulsation flux, as well as the individual fluxes of each component.
All Tables
Optimised fit parameters, S/N, and frequency phased by the orbital frequency of the significant frequencies identified via iterative pre-whitening.
All Figures
 |
Fig. 1. Least-squares deconvolution profiles of U Gru computed from 11 blue arm UVES spectra. The orbital phase-resolved spectral contribution of the broad-lined primary component is indicated with the dashed line. |
| In the text | |
 |
Fig. 2. Disentangled spectra of the primary (blue) and tertiary (black) components of the U Gru system. A representative synthetic spectrum corresponding to Teff = 5500 K and log g = 3.5 dex and diluted to the level of 2% (in continuum units) is shown for comparison to the secondary component (red). We note that a constant vertical shift has been applied to all the spectra for visibility purposes. |
| In the text | |
 |
Fig. 3. Orbital solution for the primary (blue), secondary (red), and tertiary (black) components of U Gru obtained with the method of spectral disentangling. We note that the symbols do not represent actual RV measurements. Instead, they indicate the distribution of the observed spectra over the orbital cycle of the inner binary system, while the orbital RV curve itself is computed from the best-fit orbital elements. |
| In the text | |
 |
Fig. 4. Orbitally phase-folded TESS photometry of U Gru. Top: phase-folded light curve of U Gru for sectors 1 (black) and 28 (grey) with the interpolated binary model in red. Grey hatching denotes phases of primary (forward hatching) and secondary (cross hatching) eclipse. Bottom: residuals after subtraction of an interpolation binary model for sectors 1 (black) and 28 (grey). |
| In the text | |
 |
Fig. 5. Top: Lomb-Scargle periodogram of binary-subtracted residuals for sector 1. Bottom: Lomb-Scargle periodogram of binary-subtracted residuals for sector 28. Labelled frequencies denote frequencies that are tracked in Sect. 4.1 and shown in orange in Fig. 6. |
| In the text | |
 |
Fig. 6. Échelle diagram of the significant frequencies extracted from the residuals of sector 1 folded over the orbital period. The marker size scales with amplitude. Orange markers denote frequencies labelled in Fig. 5 and tracked in Sect. 4.1. |
| In the text | |
 |
Fig. 7. Top: tracked mode amplitude for f14 = 33.046 d−1 as a function of orbital phase. Bottom: tracked relative mode phase for f14 = 33.046 d−1 as a function of orbital phase. Phase values of 0, 1, and 2 correspond to primary eclipse, and phase values of 0.5 and 1.5 correspond to secondary eclipse. |
| In the text | |
 |
Fig. 8. Top: simulated light curves with different pulsation configurations (ℓ, m, β) phase folded over the binary period. The points from the other simulated light curves are poorly visible due to the strong overlap between the models and the size of the markers. Middle: mode amplitude variations for different pulsation configurations as seen by an observer because of changing partial cancellation effects. Bottom: mode phase variations for different pulsation configurations as seen by an observer. |
| In the text | |
 |
Fig. 9. Left column: simulated light curves of the pulsation mode only. Right column: periodogram of the accompanying light curve. These light curves do not consider the light variations caused by the binary itself. Grey hatching denotes phases of primary (forward hatching) and secondary (cross hatching) eclipse. |
| In the text | |
 |
Fig. 10. Top: phase-folded light curve of U Gru for sector 1. Middle: amplitude modulation of f14 = 33.046 d−1 as reconstructed according to the fitting method developed by Jayaraman et al. (2022). The blue considers all 14 significant frequencies split from f14 listed in Table 3. The orange lines only consider those frequencies with f = f14 ± Nforb, where −3 ≤ N ≤ 3, if they were found to be significant in the iterative pre-whitening procedure. Tracked mode amplitudes from Sect. 4 are shown as black crosses. Bottom: same as the middle panel but for the phase modulation. Grey hatching denotes phases of primary (forward hatching) and secondary (cross hatching) eclipse. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.