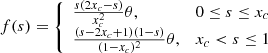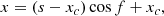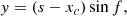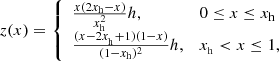| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 14 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202347634 | |
| Published online | 06 March 2024 | |
Modeling the propagation of coronal mass ejections with COCONUT: Implementation of the regularized Biot-Savart law flux rope model
1
School of Astronomy and Space Science and Key Laboratory of Modern Astronomy and Astrophysics, Nanjing University, Nanjing 210023, PR China
e-mail: chenpf@nju.edu.cn
2
Centre for Mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
e-mail: stefaan.poedts@kuleuven.be
3
Institute of Physics, University of Maria Curie-Skłodowska, ul. Radziszewskiego 10, 20-031 Lublin, Poland
4
LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
5
AIM/DAp – CEA Paris-Saclay, Université Paris-Saclay, Université Paris-Cité, Gif-sur-Yvette, France
Received:
2
August
2023
Accepted:
20
November
2023
Context. Coronal mass ejections (CMEs) are rapid eruptions of magnetized plasma that occur on the Sun. They are known to be the main drivers of adverse space weather. The accurate tracking of their evolution in the heliosphere in numerical models is of the utmost importance for space weather forecasting.
Aims. The main objective of this paper is to implement the regularized Biot-Savart law (RBSL) method in a new global corona model, called COCONUT. This approach has the capability to construct the magnetic flux rope with an axis of arbitrary shape.
Methods. We present the implementation process of the RBSL flux rope model in COCONUT, which is superposed onto a realistic solar wind reconstructed from the observed magnetogram around the minimum of solar activity. Based on this, we simulate the propagation of an S-shaped flux rope from the solar surface to a distance of 25 R⊙.
Results. Our simulation successfully reproduces the birth process of a CME originating from a sigmoid in a self-consistent way. The model effectively captures various physical processes and retrieves the prominent features of the CMEs in observations. In addition, the simulation results indicate that the magnetic topology of the CME flux rope at around 20 R⊙ deviates from a coherent structure and manifests as a mix of open and closed field lines with diverse footpoints.
Conclusions. This work demonstrates the potential of the RBSL flux rope model in reproducing CME events that are more consistent with observations. Moreover, our findings strongly suggest that magnetic reconnection during the CME propagation plays a critical role in destroying the coherent characteristics of a CME flux rope.
Key words: magnetohydrodynamics (MHD) / methods: numerical / Sun: corona / Sun: coronal mass ejections (CMEs) / Sun: magnetic fields
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Coronal mass ejections (CMEs) are the most remarkable eruptions observed within the Solar System. These powerful ejections can expel substantial quantities of magnetized plasma from the Sun into interplanetary space, profoundly impacting the heliospheric environment (Chen 2011; Webb & Howard 2012; Schmieder et al. 2015). In general, they serve as the primary drivers of adverse space weather, such as geomagnetic storms and gradual solar energetic particle (SEP) events. These could hinder satellite operations and pose risks to human health (Gosling 1993; Schrijver et al. 2015). Furthermore, the early evolution of CMEs in the solar corona and the subsequent propagation through interplanetary space involve abundant physical processes, such as magnetic reconnection, heating, plasma waves, and particle acceleration (Tsurutani et al. 2023). The significance of these processes extends beyond CMEs and to a wide range of eruptive phenomena observed across various celestial bodies, from (exo)-planet magnetospheres to black holes. Taken as a whole, studies of CMEs not only enable the improvement of forecasting capabilities regarding detrimental space weather events, but also enhance our understanding on the fundamental astrophysical and plasma processes.
Even though CMEs have been observed for several decades, the scientific issues they pose have yet not been addressed in a very satisfactory way, nor are accurate predictions available because observations are limited (Chen 2011). On the one hand, CMEs are generally observed above the solar limb by white-light coronagraphs that occult the low corona (Illing & Hundhausen 1986), indicating that the initial processes of CMEs and their evolution in the early stage are hard to track. On the other hand, the radiation mechanism of the white light means that it is difficult to derive the temperature of CMEs (Vourlidas & Howard 2006). Moreover, the magnetic fields of CMEs cannot be directly measured yet, but this is the basis for predicting the geomagnetic effects of their consequent interplanetary counterparts, especially the orientation and intensity of their southward component that causes interaction with Earth’s magnetosphere. To address these limitations, significant advances have been made in numerical magnetohydrodynamical (MHD) modeling in recent years, such as the models of ENLIL (Odstrcil 2003), the SWMF framework (Tóth et al. 2012), EUHFORIA (Pomoell & Poedts 2018; Poedts et al. 2020), SIP-CESE (Feng et al. 2007; Zhou et al. 2012; Feng 2020), MS-FLUKSS (Singh et al. 2018), AwSoM (van der Holst et al. 2010; Jin et al. 2017), ICARUS (Verbeke et al. 2022; Baratashvili et al. 2022), SUSANOO (Shiota & Kataoka 2016), COIN-TVD (Shen et al. 2014), and MAS (Mikić et al. 2018). These numerical tools play an indispensable role for both space-weather forecasting goals and scientific understandings.
Many observations and theories suggest that magnetic flux ropes play a pivotal role in explaining the generation and subsequent evolution of CMEs. For example, the statistical studies conducted by Ouyang et al. (2017) indicated that about ∼89% of the erupting filaments are supported by flux ropes, meaning that flux ropes already exist prior to eruptions in most CMEs. Besides, Vourlidas et al. (2013) suggested that at least 40% of the CMEs observed by white-light coronagraphs exhibit typical flux rope structures. When CMEs arrive in interplanetary space and are detected by in situ satellites, the magnetic fields they carry often exhibit strong and smooth rotation, which is generally considered the proxy of a helical flux rope (Burlaga et al. 1981). In addition, preexisting flux ropes are often (but not always) indispensable in many models to explain the initiation of CMEs, such as the kink instability (Hood & Priest 1981; Török et al. 2004) and torus instability (Kliem & Török 2006; Aulanier et al. 2010). Therefore, several forecasting models emphasize that the construction of flux ropes is required to initiate CMEs.
The currently extensively used flux rope models for triggering CMEs can mainly be divided into two categories. The first type are sphere-like models without legs. Models representative of this type are the spheromak model (Kataoka et al. 2009; Shiota et al. 2010; Verbeke et al. 2019) and the tear-drop Gibson-Low model (Gibson & Low 1998). The second category are toroidal flux ropes that are anchored on the solar surface, such as the flux rope in 3D (FRi3D; Isavnin 2016), the Titov-Démoulin (TD; Titov & Démoulin 1999), and the Titov-Démoulin-modified models (TDm; Titov et al. 2014), which are thought to be more effective in reproducing flank-encounter events (Maharana et al. 2022).
These flux rope models still deviate considerably from the observed flux ropes, which usually exhibit a sigmoid-shaped, U-shaped, or more irregular morphology (Cheng et al. 2017). It is thus essential to develop a method for constructing a flux rope whose morphology is more accurately aligned with the observations. For this purpose, Titov et al. (2018) proposed an advanced method for constructing a force-free flux rope in the source region, called regularized Biot-Savart law (RBSL) method. This enables the construction of a flux rope with an axis of arbitrary shape that in turn can accurately reproduce CMEs originating from flux ropes with irregular shapes. Based on this method, we successfully reconstructed the magnetic structures of some filaments (Guo et al. 2019, 2021a) and modeled the onset processes of their resulting CMEs in an observational data-driven way (Guo et al. 2021b, 2023b,c). It is therefore expected that the RBSL flux rope model can improve the accuracy of space weather forecasting.
On the other hand, in many heliospheric space-weather forecasting simulations, the CMEs are generally introduced beyond the super-Alfvénic point, typically at around 0.1 AU (Verbeke et al. 2019; Scolini et al. 2019, 2020; Maharana et al. 2022, 2023). The input parameters of CMEs are determined based on coronagraph observations, with the assumption that CMEs evolve self-similarly in the corona up to 0.1 AU. Although this assumption has achieved significant success in contemporary space weather predictions, it is noted that CMEs often undergo rotation and deflection in this region (Shen et al. 2022). For example, Lynch et al. (2009) found that the rotation angle can reach 50° at 3.5 R⊙. Shiota et al. (2010) found that the reconnection between the eruptive flux rope and ambient magnetic field lines can lead to the rotation of the CME flux rope within 5 R⊙. The observational data-constrained simulation performed by Guo et al. (2023a) suggested that magnetic reconnection during the eruption can result in reconstruction of the flux rope axis, manifested as the lateral drifting of filament materials in observations. Heliospheric MHD simulations from the solar surface to 1 AU revealed that the rotation of the flux rope is likely to occur within 15 R⊙ (Regnault et al. 2023). Observations also demonstrated that the magnetic field gradient can result in an orientation change of the flux rope axis (Shen et al. 2011; Gui et al. 2011; Liu et al. 2018) and can thus induce the consequent and otherwise unexpected strong geomagnetic storms. Asvestari et al. (2022) found that the tilt angles between the flux rope axes and their surrounding background fields can affect their rotation angle when they propagate through the heliosphere. Therefore, to input a more realistic CME for the interplanetary simulation, it is essential to track the evolution of the flux rope within 25 R⊙. As demonstrated in some previous studies (Jin et al. 2012, 2017; Zhou & Feng 2017; Török et al. 2018), where the CMEs modeled in the corona module were integrated into the heliosphere simulations, models that couple the corona with interplanetary space might improve the accuracy of space weather predictions.
The main objective of this paper is to implement the RBSL flux rope model into our recently developed three-dimensional (3D) global coronal model, called COolfluid COroNal UnsTructured (COCONUT; Perri et al. 2022), and then simulate its propagation process from the solar surface to a distance of 25 R⊙. In previous work (Linan et al. 2023), we simulated a CME that was initiated from a toroid-shaped TDm flux rope. Built upon this foundation, this work employs the RBSL flux ropes to drive CMEs, enabling us to model eruptions from the flux ropes that are characterized by more realistic shapes, such as a sigmoid. This paper is organized as follows. The modeling description is in Sect. 2, and the results are presented in Sect. 3. They are followed by discussions and a summary in Sects. 4 and 5, respectively.
2. Modeling description
2.1. Infrastructure of the COCONUT solver
In this paper, we use COCONUT, a state-of-the-art MHD solver for global solar coronal modeling that was recently developed by Perri et al. (2022), to model the propagation of CMEs. This code is built upon the Computational Object-Oriented Libraries for Fluid Dynamics (COOLFluiD) platform (Kimpe et al. 2005; Lani et al. 2005, 2013, 2014), which enables the solution of 3D full MHD equations using an implicit scheme. The adoption of the implicit scheme allows disregarding constraints imposed by the Courant-Friedrichs-Lewy (CFL) requirement in explicit solvers, enabling the convergence of steady-state solutions at a significantly faster speed. Moreover, the use of unstructured meshes eliminates the polar singularity, facilitating complete coverage of the solar corona including the solar poles (Brchnelova et al. 2022b). Perri et al. (2023) demonstrated the importance of considering the solar poles even for the ecliptic-plane prediction. Furthermore, the implementation of unstructured meshes in COCONUT makes it well suited for advanced numerical techniques for grid refinement and for the high-order flux-reconstruction method (Vandenhoeck & Lani 2019). These advanced approaches enhance the capabilities and potential of COCONUT in space-weather forecasting applications.
In line with Linan et al. (2023), we employed a polytropic MHD model to simulate the CME propagation in the inner heliosphere. This model incorporates an adiabatic energy equation with a reduced adiabatic index, as previously described by Mikić et al. (1999) and Perri et al. (2022). The governing equations are as follows:
where p is the thermal pressure, E = ρv2/2 + p/(γ − 1)+B2/8π is the total energy density, 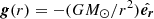 , is the gravitational acceleration, γ = 1.05 is the reduced adiabatic index, ϕ is used to clean the magnetic field divergence, and the other parameters have the usual meanings. Equation (5) is introduced by the hyperbolic divergence cleaning method (Dedner et al. 2002), which is employed to mitigate the divergence of magnetic fields arising during numerical calculations. It is noteworthy that the motivation for using this reduced γ value is based on the fact that the coronal temperature does not change substantially, which mimics quasi-isothermal heating with limited energy injection. As demonstrated in previous works (Mikić et al. 1999; Perri et al. 2022; Kuźma et al. 2023), the polytropic model can successfully drive either the slow or the fast solar wind (but not the bimodal distribution), and reproduce large-scale streamers and the coronal hole distribution in observations, although it is difficult to maintain thermal properties that are consistent with the solar corona, such as plasma β (Regnault et al. 2023). Nevertheless, the evolution of the magnetic topology remains realistic with the full resolution of the MHD equations.
, is the gravitational acceleration, γ = 1.05 is the reduced adiabatic index, ϕ is used to clean the magnetic field divergence, and the other parameters have the usual meanings. Equation (5) is introduced by the hyperbolic divergence cleaning method (Dedner et al. 2002), which is employed to mitigate the divergence of magnetic fields arising during numerical calculations. It is noteworthy that the motivation for using this reduced γ value is based on the fact that the coronal temperature does not change substantially, which mimics quasi-isothermal heating with limited energy injection. As demonstrated in previous works (Mikić et al. 1999; Perri et al. 2022; Kuźma et al. 2023), the polytropic model can successfully drive either the slow or the fast solar wind (but not the bimodal distribution), and reproduce large-scale streamers and the coronal hole distribution in observations, although it is difficult to maintain thermal properties that are consistent with the solar corona, such as plasma β (Regnault et al. 2023). Nevertheless, the evolution of the magnetic topology remains realistic with the full resolution of the MHD equations.
The simulation domain covers the whole global corona, including the two poles, where r spans from the solar surface to 25 R⊙ in radius, θ ranges from −90° to 90° in latitude, and φ ranges from −180° to 180° in longitude. To discretize this domain, we used a six-level subdivision of the geodesic polyhedron, resulting in approximately 1.5 million cells. Further details regarding the effects of unstructured meshes in COCONUT can be found in Brchnelova et al. (2022b). For the boundary conditions, we followed the prescription outlined in Perri et al. (2022). At the inner boundary, the radial component of the magnetic field is determined by the imposed magnetogram, while the other components were extrapolated in a zero-gradient manner. The density and pressure at the inner boundary were set to fixed values of ρ⊙ = 1.67 × 10−16 g cm−3 and p⊙ = 4.15 × 10−2 dyn cm−2, respectively. Additionally, we employed the technique described in Brchnelova et al. (2022a) to reduce the generation of spurious electric fields. The velocity on the surface of the Sun is thus prescribed with a small outflow that aligns with the magnetic field lines. The physical quantities at the outer boundary were extrapolated in a zero-gradient manner. More comprehensive information and numerical tests regarding the boundary prescription can be found in Perri et al. (2022).
Our simulation consisted of two steps. First, we constructed the background solar wind where the coronal plasmas move outward by using the time-independent relaxation module for the steady-state solution of the solar wind developed in Perri et al. (2022). When this background was established, we transitioned to a time-dependent model to simulate the evolution of CMEs. Following the approach presented by Linan et al. (2023), we employed a three-point backward time discretization scheme with a time step of 0.01 in the normalization unit (equivalent to 14.4 s in physical units). The convergence tests indicate that the time resolution primarily affects the magnitude of the plasma profiles only little, while keeping the trend. Hence, we considered it acceptable to adopt this resolution as a benchmark to model CMEs, taking into account the trade-off between the computational speed and solution accuracy. For further insights into the specifics of this numerical scheme and additional testing, we refer to Linan et al. (2023). In the following subsections, we describe the numerical setup process in more detail.
2.2. Quasi-steady solution of the background solar wind
In this subsection, we outline the procedure for modeling the background solar wind. We used the magnetogram of 2019 July 2, observed by the Helioseismic and Magnetic Imager (HMI; Scherrer et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012), which can provide a more realistic solar wind for the CME propagation compared to the dipole. We chose the data near solar minimum because first, this date coincides with a total solar eclipse on Earth, providing unique observations to validate the model. In addition, the solar wind configuration based on this magnetogram has been extensively examined in other COCONUT papers (Perri et al. 2023; Kuźma et al. 2023; Linan et al. 2023). Furthermore, it is comparatively more easy to configure the solar minimum activity, such that the convergence is easier to be obtained compared to the case of solar maximum activity. Following our previously established pretreatment procedure (Perri et al. 2022; Kuźma et al. 2023), the original magnetogram was preprocessed through the projection onto spherical harmonics to smooth the input magnetogram and thereby enhance the numerical stability. The highest reconstruction frequency was lmax = 20.
The initial magnetic fields are provided by the potential field source-surface (PFSS) model, which is computed with a fast finite-volume solver for the Laplace equation in COCONUT (Perri et al. 2022). The initial conditions for density and pressure were set in accordance with Brchnelova et al. (2022a). Subsequently, we initiated a relaxation process using the polytropic MHD equations Eqs. (1)–(5). To assess convergence, we used the global residuals of various physical quantities, which were evaluated using the following formula:
where a is the considered physical quantities in normalization unit, i is the spatial index, and t is the temporal index. Correspondingly, the mean iteration change in physical units can be described as 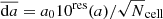 , where a0 denotes the normalization unit (l0 = 6.955 × 1010 cm, ρ0 = 1.67 × 10−16 g cm−3, B0 = 2.2 G, v0 = 4.8 × 107 cm s−1), and Ncell represents the number of cells. After approximately 15 000 iterations, a convergence level of −4.5 in the radial velocity was attained (res(v) = − 4.5), indicating that the average variation of radial velocity during the iteration,
, where a0 denotes the normalization unit (l0 = 6.955 × 1010 cm, ρ0 = 1.67 × 10−16 g cm−3, B0 = 2.2 G, v0 = 4.8 × 107 cm s−1), and Ncell represents the number of cells. After approximately 15 000 iterations, a convergence level of −4.5 in the radial velocity was attained (res(v) = − 4.5), indicating that the average variation of radial velocity during the iteration, 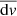 , is close to 1 cm s−1. Moreover, as demonstrated in Linan et al. (2023), the density map of the modeled solar wind exhibits a certain similarity to that derived from the observations with the tomography method (Morgan 2015). Therefore, based on our previous numerical tests (Perri et al. 2022; Kuźma et al. 2023), the obtained solar wind solution can be roughly characterized as a convergence state in our model.
, is close to 1 cm s−1. Moreover, as demonstrated in Linan et al. (2023), the density map of the modeled solar wind exhibits a certain similarity to that derived from the observations with the tomography method (Morgan 2015). Therefore, based on our previous numerical tests (Perri et al. 2022; Kuźma et al. 2023), the obtained solar wind solution can be roughly characterized as a convergence state in our model.
Figure 1 compares the observations and numerical results. Panel a shows white-light images assembled from 128 eclipse pictures (Boe et al. 2020). The finest details of the corona, including equatorial streamers stretching radially on both sides and open streamers extending from the polar regions, are prominently featured. Panel b illustrates the typical fields in our solar wind model, roughly rotated to the viewing angle from Earth on the date of the eclipse. The streamers depicted in our COCONUT model closely match the observations in morphology and placement. The radial velocity profile is shown in panel c, with two large equatorial streamers, in agreement with the distribution of the field lines. Panel d visualizes the 3D structure of the heliospheric current sheet (HCS) using an isosurface of Br = 0. For further details regarding the validation process, we refer to the comprehensive study conducted by Kuźma et al. (2023) and Linan et al. (2023). The agreement between the observed coronal streamers and the magnetic field structures in the simulation indicates that our coronal model is reasonable overall.
 |
Fig. 1. Comparisons between observations and numerical results for the background solar wind. Panel a displays the solar eclipse image of 2 July 2019 (Copyright: 2019 Miloslav Druckmüller, Peter Aniol), corresponding to a minimum of solar activity. Panels b and c correspond to the typical field lines and radial velocity distribution in the meridian plane, respectively. Panel d visualizes the heliospheric current sheet depicted by the isosurface of Br = 0. |
2.3. Implementation of the RBSL flux rope model
When the background solar wind reached a relatively steady state, we proceeded to superpose a flux rope on it to model the eruption and propagation of a CME. In this study, we employed the RBSL method proposed by Titov et al. (2018) to construct the preexisting flux rope. Unlike the TDm model, which was implemented by Linan et al. (2023), they superposed a flux rope fixed to a toroidal shape, while the RBSL method allows for the construction of a flux rope with an arbitrary path for its axis. As a result, it is well suited for simulating CMEs originating from complex morphologies in the source region, such as sigmoids. In the following paragraphs, we detail the implementation process of the RBSL flux rope in COCONUT.
The RBSL flux rope is essentially an electric current channel carrying the axial current I with a parabolic profile. Its magnetic field can be described using the following formulae:
where a(l) represents the minor radius of the flux rope, C represents its axis path, C′ is the mirror path of the axis with respect to the photosphere, l represents the arc length, R(l) is the radius vector, R′ is the tangential unit vector, and r = (x − R(l))/a(l) represents the vector from the source point to the field point. The kernels of the regularized Biot-Savart laws, denoted as KI(r) and KF(r), are described by the piecewise functions that incorporate the internal and external solutions (Titov et al. 2018). The expressions are as follows:
where the kernels in the region r > 1 correspond to the classic Biot-Savart law, and those for 0 ≤ r ≤ 1 correspond to the regularized Biot-Savart law (Titov et al. 2018). This is derived from the force-free condition, assuming a parabolic distribution of electric current density. In this formulation, the relation between the axial flux F and the axial current I satisfies 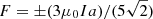 , with the sign determined by the helicity of the flux rope. The positive (negative) sign corresponds to a flux rope with positive (negative) helicity, where the field lines wrap around the axis following the right-hand (left-hand) rule.
, with the sign determined by the helicity of the flux rope. The positive (negative) sign corresponds to a flux rope with positive (negative) helicity, where the field lines wrap around the axis following the right-hand (left-hand) rule.
Equations (7)–(11) outline the fundamental principles for constructing an RBSL flux rope, which is primarily governed by four key parameters: the flux rope path (C), the minor radius (a), the axial flux (F), and the electric current (I). When these parameters are determined, the RBSL flux rope can be uniquely constructed. Hence, the initial step is to define the flux rope path. The main objective of this paper is to implement the RBSL flux rope in COCONUT and model the propagation of its resulting CME. For simplicity, we employed a theoretical curve to govern the morphology of the flux rope axis, rather than using the path directly measured from observations. This means that we did not concentrate on a specific observed event in this work. The insertion of the flux rope leads to two additional poles with strong magnetic fields in the original magnetogram. In future papers, we will reproduce an event observed in reality, in which the construction of the flux rope is highly constrained by the observations and more comparisons with the observations are conducted. Following Török et al. (2010) and Xu et al. (2020), we adopted the following equations to control the path of the flux rope:
where xc controls the intersection of the projected curve and the line connecting two footpoints (defined as the crossing point herein), the angle θ controls the orientation of the tangent vector at the crossing point, xh controls the position of the apex, and h determines the apex height. In particular, because the RBSL method requires a closed path for the current circuit, we added a mirror subphotosphere path to close it. When the path was determined, we set the minor radius a and theaxial flux F, and then the electric current I can be derived from the force-free condition. Subsequently, we obtained the kernels of the RBSL using Eqs. (10) and (11). Finally, the magnetic fields of the flux rope were calculated using Eqs. (7)–(9).
Figure 2 shows the RBSL flux rope constructed with the following parameter values: xc = xh = 0.5, θ = 60°, h = 120 Mm, a = 35 Mm, and F = 3 × 1020 Mx. The flux rope was inserted at the equator with a longitude of 30°, situated within the quiet-Sun region. The selected electric current of the flux rope was about ten times the intensity estimated by Shafranov’s equilibrium equation (Eq. (7) in Titov et al. 2014), meaning that the flux rope was unstable and would undergo a direct eruption upon insertion. We did not change the thermodynamic properties within the flux rope, encompassing the velocity fields, pressure, and density, such that the eruption was fully propelled by the disequilibrium of the magnetic fields.
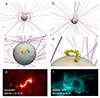 |
Fig. 2. Visualization of the magnetic field lines of the global corona coupled with the RBSL flux rope (yellow tubes) with the background solar wind (pink tubes). Panels a and b illustrate the results viewed from the top and side, respectively. Panels c and d show the zoomed-in views of the red rectangles in panels a and b, respectively. Panels e and f show a typical flux rope in observations that is reflected by the sigmoid viewed on the solar disk and the hot channel at the solar limb. The sigmoid on the solar disk in panel e was observed by the Hinode/XRT. The hot channel above the solar limb in panel f was observed in the SDO/AIA 131 Å band. |
To validate our modeled flux rope, we compared the flux rope proxies in observations, such as sigmoids and hot channels (Zhang et al. 2012; Cheng et al. 2013). Figure 2e presents a sigmoid on the solar disk observed by the Hard X-Ray Telescope (XRT) on board Hinode (Golub et al. 2007). It is immediately clear that the modeled flux rope, when viewed from the top (Fig. 2c), closely resembles the observed sigmoid. Figure 2f displays a hot channel in a side view observed by the SDO/AIA 131 Å band (Cheng et al. 2013). As depicted in Figs. 2d and 2f, the modeled flux rope and the observed hot channel both display a similar arched shape. Therefore, the flexibility of the RBSL flux rope path can effectively reduce the deviations from observed progenitors of CMEs in solar source regions. Even though the path of the flux rope is determined by a theoretical curve in this work, the comparability between the modeled flux rope and observations demonstrates that the RBSL method can reconstruct flux ropes that are consistent with observations.
3. Numerical results
3.1. Global evolution of the CME flux rope
Figure 3 illustrates the propagation of an S-shaped CME flux rope, where the flux rope field lines are traced from the footpoints of the initial flux rope. These illustrations effectively capture the significant changes in the overall morphology of the CME flux rope as it propagates outward. The volume occupied by the CME flux rope expands considerably, which can be attributed to two main factors. First, the magnetic pressure gradient between the flux rope and the surrounding solar atmosphere can drive the flux rope expansion in all directions (Scolini et al. 2019). Second, the magnetic reconnection between the legs of overlying field lines leads to the formation of twisted field lines that wrap around the original flux rope, creating a hierarchical structure with varying twist, magnetic connectivity, and temperature distributions (Guo et al. 2023b). As shown in Fig. 3f, after 8 h, some open field lines with only one line-tied footpoint appear at the periphery of the CME flux rope. In addition, underlying flare loops and highly curved field lines lie above this. These signals strongly indicate the occurrence of magnetic reconnection during the CME propagation. We used an ideal MHD solver in this paper, which means that magnetic reconnection is due to the numerical diffusion.
 |
Fig. 3. Representative magnetic field lines displaying the global evolution of the CME. The yellow and pink tubes represent the magnetic structures of the CME flux rope and the ambient solar wind, respectively. The top row (a–c) illustrates the results viewed from the top of the flux rope, and the bottom row (d–f) presents the side views. Snapshots at different time intervals are displayed in the left (a and d), middle (b and e), and right (c and f) panels, corresponding to 0.4, 3.2, and 8.0 h, respectively. |
Then, we present the velocity and temperature distributions in the equatorial and meridian planes during the CME propagation, as illustrated in Fig. 4. The radial velocity distributions clearly reveal a bow-shock structure that straddles the CME flux rope, which grows in size as it propagates outward. The intermediate area between the CME flux rope and the leading shock corresponds to the sheath region, which is formed due to plasma compression resulting from the propagation of the flux rope (Kilpua et al. 2017; Regnault et al. 2020). Intriguingly, the regions swept by the CME-driven shock do not return to a quasi-steady state prior to the eruption in an elastic manner, and a sustained high-speed flow is induced. This may be attributed to the ongoing outflows resulting from magnetic reconnection processes and the downstream flows after the shock wave. A toroidal region in the temperature slices experiences significant heating and closely envelops the flux rope, which may be due to the dissipation of the strong magnetic fields within the flux rope itself and to the magnetic reconnection that takes place around it. Additionally, the temperature of the flux rope decreases considerably as it propagates outward.
 |
Fig. 4. Radial velocity and temperature distributions in the equatorial and meridian planes. The top (a–f) and bottom two (g–l) panels show the results in the equatorial and meridian planes, respectively. Panels a–c and g–i display the distributions of the radial velocity, and panels d–f and j–l correspond to those of the temperature. The cyan tubes are some typical field lines illustrating the CME flux rope. |
Figure 5 exhibits the quantitative results of the kinetics and thermodynamics evolution of the CME flux rope. Panel a displays the time-distance diagram of the CME flux rope by tracking the highest temperature point along the radial path. Its movement can be linearly fit with an average speed of 379 km s−1, which agrees with the speed range of the observed CMEs (Chen 2011). Panel b displays the evolutions of temperature and density, which are each fit with a power-law function of time. This reveals that as the CME flux rope propagates, both its temperature and density decrease. In addition, the density shows a more rapid decline than the temperature, as inferred from the fitted power exponents. In particular, the CME flux rope temperature within 2 R⊙ is fairly high, reaching up to 10 MK, which is in line with the hot channels observed in the source regions. Afterward, the temperature and density of the CME flux rope both decrease rapidly in one hour and then decrease more gradually. When the CME flux rope reaches a distance of about 20 R⊙, its temperature has decreased to 2 MK, and the density has decreased by three orders of magnitude compared to the initial values. This decrease in the temperature and density of the CME also appeared in the AWSoM simulation (Jin et al. 2013) and the PLUTO simulation (Regnault et al. 2023).
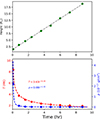 |
Fig. 5. Kinetic and thermodynamic evolution of the CME flux rope. Panel a corresponds to the time-height diagram of the CME flux rope. Panel b presents the temperature (red) and density (blue) evolution of the CME flux rope over time. |
3.2. CME structure and its in situ measurements
Figure 6a exhibits the density distribution overlaid by the high-temperature transparent contours (T > 2 MK) in the meridian plane. It is found that the corona disturbed by the CME is highly hierarchical, including a leading density enhancement, a following high-temperature magnetic ejection, and a hot tail near the Sun. This scenario can be explained by the standard flare model (Carmichael 1964; Sturrock 1966; Hirayama 1974; Kopp & Pneuman 1976) as follows. The eruptive flux rope induces the formation of a current sheet below it, in which magnetic reconnection causes positive feedback to the further rising of the flux rope. The ascending flux rope produces fast-mode MHD waves propagating upward and results in the plasma compression ahead of it, and thus, it forms the bright leading front of the CME (Chen 2009, 2011; Guo et al. 2023b). Therefore, it can be expected that the three distinct regions in Fig. 6a correspond to the CME leading front, the flux rope, and the reconnection area in the standard flare model, respectively. Hereafter, following the approach of analyzing interplanetary CMEs (ICMEs), we plot the in situ plasma profiles measured by a virtual spacecraft at point S4 with a radial distance of 21.5 R⊙ in Fig. 6c (this radial distance serves as the inner boundary of the EUHFORIA simulations). The arrival of the CME from the plasma profiles is clearly visible, and its resulting disturbances of the solar wind can be divided into the following parts. In the leading part (red band in Fig. 6b), the temperature, velocity, density, and plasma β increase strongly. In addition, the magnetic fields fluctuate strongly. This is generally identified as a sheath that forms ahead of a magnetic cloud (Kilpua et al. 2017; Regnault et al. 2020; Linan et al. 2023). The variations in the magnetic field components in our simulation are different from those modeled by the TDm flux rope (Linan et al. 2023), even though the background solar wind is the same. This demonstrates that the initial flux rope might also influence the sheath structure of its resulting CME.
 |
Fig. 6. Magnetic field and thermodynamic structure of the CME. Panel a shows the density and temperature in the meridian plane in 2D. Panel b corresponds to the in situ plasma profile measured by a virtual satellite at around 21.5 R⊙, where the red, green, and blue bands represent the sheath and two subparts of the magnetic cloud (M1 and M2), respectively. Panel c illustrates some typical field lines around the CME, where the yellow, cyan, and red tubes represent the field lines from the original inserting flux rope, newly formed twisted field lines during the CME propagation, and the underlying flare loops, respectively. |
The area in the wake of the sheath exhibits several characteristic features commonly observed in interplanetary magnetic clouds, that is, an enhanced magnetic field strength, a smoothly changing magnetic field orientation, low plasma β, and a decreasing velocity. These signatures are consistent with the main body of the CME, namely, the helical flux rope. Moreover, this can be further divided into two subparts, referred to as M1 (green band in Fig. 6b) and M2 (blue band in Fig. 6b). In M1, the vector magnetic fields exhibit the rotation features: the Bx component rotates from the negative to positive, the By component rotates from the positive to negative, and the Bz component remains almost positive. This orientation reflects the right-handed helix with positive magnetic helicity, which is consistent with that of the initial flux rope. In contrast to M1, the magnetic field orientation of M2 remains almost unchanged throughout. Moreover, the solar wind velocity and temperature in M2 start to increase. We speculate that this secondary acceleration and heating is caused by magnetic reconnection, corresponding to hot reconnection outflows. Similar in situ plasma profiles of CMEs detected near the Sun were also found in previous COCONUT-CME simulations (Linan et al. 2023), the detection of the Parker Solar Probe at around 57.4 R⊙ (Korreck et al. 2020), and the observations derived from the radio occultation measurements with the Akatsuki spacecraft (Ando et al. 2015).
The criteria we employed to distinguish the boundaries between these distinct regions are described as follows: (1) The sheath is principally identified by a prominent bump in the plasma β profile, accompanied by the elevated velocity and density. (2) The magnetic cloud is primarily characterized by the plasma β profile, which exhibits a significantly lower value than that of the background solar wind. (3) The transition point from M1 to M2 is selected as the secondary acceleration and heating, which can serve as an indicator of the newly formed flux rope resulting from magnetic reconnection. Specifically, this secondary increase in velocity and temperature profiles, along with the newly formed twisted field lines due to reconnection, have also been seen in CMEs initiated from TDm flux ropes (Linan et al. 2023). To further illustrate the magnetic structure of the ejection, we plot some typical field lines around the CME in Fig. 6c. Two types of twisted field lines with different connectivity are visible: In the first category, represented by yellow tubes, the flux rope shows a coherent structure and its configuration is analogous to that of the inserted flux rope, implying that it is likely to stem from the eruption of the preexisting flux rope. However, for the second type (cyan tubes), the magnetic connectivity is significantly different from that of the former, which manifests itself as the different footpoints and twist characteristics. This suggests that they could be formed as a result of nonideal processes, such as magnetic reconnection. In addition, we can also recognize the cusp-like highly curved field lines and the flare loops below (as shown in Fig. 6c), which is strong evidence of the occurrence of magnetic reconnection during the CME propagation.
To investigate the temporal evolution of the CME during its propagation, we analyzed the localized plasma profiles at different distances from the Sun. They are depicted in Fig. 7, specifically, at S1 (5 R⊙), S2 (10 R⊙), and S3 (15 R⊙). First, the volume of the CME body is strongly enlarged as it propagates outward (yellow band), which is attributed to its self-expansion and injection of the newly twisted fluxes due to magnetic reconnection. One effect of the CME expansion is the decrease in its magnetic field strength (B). At 15 R⊙, the strength decreases by a factor of ten compared to that at 5 R⊙. Moreover, magnetic reconnection during the propagation can restructure the original flux rope, resulting in a more intricate magnetic structure. In the 3D illustration of the magnetic field lines, this is visible as the twisted field lines with different connectivity and footpoints, as shown in Fig. 6c. In 1D in situ plasma profiles, this is reflected in the formation of a series of subpeaks inside the magnetic cloud. Around 5 R⊙, only one single prominent peak is observed in the B profile. However, as the CME reaches approximately 15 R⊙, its profile evolves into a structure consisting of multiple peaks. The velocity profile increases continuously when propagating, although the slope of the leading front becomes flatter than at earlier stages (Jin et al. 2013).
 |
Fig. 7. In situ plasma profiles measured at different distances from the Sun. Panels a–c present the results measured by S1 (5 R⊙), S2 (10 R⊙), and S3 (15 R⊙) marked in Fig. 6a, respectively. The red and yellow bands represent the sheath and magnetic cloud, respectively. |
4. Discussion
4.1. Complex magnetic topology of the CME flux ropes
It is widely accepted that magnetic flux ropes are commonly present within CMEs and play a crucial role in explaining the CME generation and the observational characteristics of the subsequent interplanetary counterparts (Chen 2011). As a result, the prevailing approach in most existing numerical prediction models is to initiate a CME by inserting an eruptive magnetic flux rope. One of the simple methods that can be used to achieve this is incorporating an analytical (or semi-analytical) flux rope with a coherent structure and simple morphology at the inner boundary of the heliosphere, for instance, around 21.5 R⊙ (Verbeke et al. 2019; Scolini et al. 2019, 2020; Maharana et al. 2022, 2023). However, several issues were ignored in these simulations: (1) It is unclear whether a CME flux rope situated at approximately 20 R⊙ can still be regarded as a coherent structure. (2) It is also unclear whether the physical processes occurring in the corona might lead to a different topological structure of the flux rope compared to that prior to the eruption.
Most observations and numerical simulations indicate that the flux rope would undergo drastic magnetic reconnection during eruption, which will significantly change its magnetic structure (Liu 2020). For example, Wang et al. (2017) demonstrated that a flux rope can be formed due to reconnection in the eruption process and might not exist prior to the eruption. Gou et al. (2023) claimed that magnetic reconnection in the eruption process can completely replace the flux of the original flux rope. Furthermore, the detection of superthermal electrons in interplanetary space indicated that the magnetic cloud might be composed of closed and open field lines (Gosling et al. 1995; Crooker et al. 2004). To explain the complex phenomena in observations, Aulanier & Dudík (2019) proposed a new 3D flare model consisting of three types of magnetic reconnection geometries, that is, the reconnection in the overlying field lines (called aa–rf type), the reconnection between the flux rope and the ambient arcades (ar–rf type), and the reconnection in the flux rope field lines (rr–rf type). Recently, Guo et al. (2023b) performed a data-driven MHD simulation and demonstrated that the magnetic reconnection in the eruption can change the temperature, orientation, and twist number of the flux rope. Therefore, it is expected that magnetic reconnection causes a deviation in the CME flux rope from the coherent structure when it reaches interplanetary space.
To reveal the magnetic topology of the CME flux rope at around 20 R⊙, we examined some representative twisted field lines that were traced from the flux rope footpoints. They are shown in Fig. 8. The magnetic structure of the CME at 20 R⊙ clearly differs from its progenitor in the source region. When the CME flux rope reaches around 20 R⊙, it is composed of a mix of closed and open field lines. The right panels in Fig. 8 illustrate the connectivity of these twisted field lines and characterize them individually. They exhibit notable distinctions in terms of the footpoint placements and orientation. For example, the footpoints of MF1 remain attached to the same locations as the initial flux rope. However, for MF2 and MF3, one of their footpoints migrates toward the polar regions, suggesting the occurrence of large-scale interchange reconnection between the flux rope field lines and the neighboring open field lines extending from the polar regions. Additionally, we also identify an open field line (MF4) with only one footpoint tied to the Sun, which may be formed due to the reconnection between the flux rope field lines and adjacent open streamers.
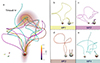 |
Fig. 8. Magnetic structure of the CME flux rope at around 20 R⊙. Panel a shows a collection of typical field lines of the CME flux rope that are enveloped by a high-temperature transparent contour. Panels b–d illustrate the field lines in panel a individually, providing details of their magnetic connectivity and the footpoint placements. |
A secondary peak of the in situ velocity and density profiles inside the magnetic cloud is characterized by the low-β region compared to the background solar wind. Intriguingly, Ando et al. (2015) observed a similar secondary enhancement of the velocity and density profiles at a distance of 12.7 R⊙, which was derived from the radio occultation measurements with the Akatsuki spacecraft (Nakamura et al. 2011). Drawing from the insights of the numerical model performed by Shiota et al. (2005), they suggested that fast flows due to magnetic reconnection cause this secondary velocity and density peak inside the CME. Our simulation results agree very well with their observations. Simulation and observation both indicate that the second enhancement in velocity and density inside the CME might serve as a signature of plasma outflows of magnetic reconnection. Moreover, magnetic reconnection might also contribute to the complexity of the magnetic structure of the CME, as depicted in Figs. 6c and 8.
Accordingly, the magnetic topology of the CME flux rope is considerably complicated and is not a coherent structure. First of all, a CME flux rope may have more than two footpoints that are not always fixed to the initial locations. Additionally, the CME flux rope is not always composed of closed field lines anchored to the solar surface. The interchange reconnection between the CME flux rope and open streamers can form open twisted field lines (Masson et al. 2013). A similar topology has also been found in a data-constrained simulation performed by Lugaz et al. (2011). They found that reconnection with the ambient coronal holes can yield open field lines inside the CME. These open field lines are typically used to explain impulsive SEP bursts (Cane et al. 1986; Masson et al. 2013) and type III radio burst (Krucker et al. 2011; Chen et al. 2018), in which the energetic particles accelerated in the flare are released into interplanetary space along the open field lines. Therefore, our simulation results indicate that the approach to input a CME at 20 R⊙ with an analytical model is not reliable for a space weather prediction. It is likely to lead to a failure in reproducing some ICME events that exhibit complex magnetic field profiles and are associated with impulsive SEP events. Hence, models that couple the solar corona and interplanetary space need to be developed, as was done in some works (Jin et al. 2012, 2017; Zhou & Feng 2017; Török et al. 2018). This approach might provide more self-consistent CME models that could lead to a notable improvement in the prediction accuracy.
4.2. Importance of the solar poles for the global coronal modeling
Another noteworthy point is the importance of solar poles. As illustrated in Fig. 8, the footpoints of some CME flux rope field lines (MF2 and MF3) drift to the poles due to magnetic reconnection. This demonstrates that the streamers extending from the solar poles may interact with a CME even though it is initiated from the equator. However, owing to the singularity problem of the solar poles in the spherical coordinates, the majority of global MHD simulations still fail to contain the solar poles. Perri et al. (2023) investigated the impacts of the input magnetograms and solar poles on the solar wind fields and found that the filling of poles is fairly important even for the forecasts concentrated on the ecliptic plane.
Our simulation indicated that the filling of the solar poles not only influences the background solar wind, but also impacts the structures of CMEs that occur in this medium: The CME flux rope may reconnect with the open field lines extending from the poles. This suggests that the solar poles are indispensable for models aiming to predict global space weather.
5. Summary
We presented the implementation of the RBSL magnetic flux rope in COCONUT and then modeled the self-consistent propagation of an S-shaped flux rope from the solar surface to 25 R⊙ with the numerical model. We analyzed the kinematics, magnetic topology, and in situ plasma properties of the modeled CME. The results demonstrate that the RBSL flux rope can reproduce CMEs that are more in line with observations: this is important for future space weather forecasting. We summarize the main results of our simulation below.
-
We implemented the RBSL flux rope model in COCONUT. COCONUT is an advanced method for constructing the magnetic structure of the CME progenitor that is strongly constrained by observations. This allowed to construct a flux rope with an axis of an arbitrary path. We were able to model a flux rope whose axis path was directly measured from proxies of the observed flux ropes, such as the filaments, sigmoids, and hot channels. The RBSL technique has great potential for future event studies and more accurate space weather predictions.
-
The magnetic structure of the flux rope of a CME at around 20 R⊙ may deviate from a coherent structure. We found that magnetic reconnection can significantly change the magnetic topology of the CME flux rope. For example, the reconnection between the legs of the overlying field lines can inject newly formed twisted field lines encircling the preexisting flux rope, which may lead to a restructuring of the original flux rope. In addition, the interchange reconnection between the flux rope and the open streamers can result in some open twisted field lines. Additionally, the reconnection between the flux rope and ambient sheared arcades can cause the flux rope footpoint to drift. Therefore, the CME flux rope at around 20 R⊙ is a mix of open and closed field lines with footpoints that lie far apart.
-
Solar poles are indispensable in global coronal models that aim to predict CMEs. The CME flux rope and open field lines extending from the polar regions are magnetically reconnected, even though the initial flux rope is launched at the equatorial plane. Due to the advantage of the unstructured mesh grids in COCONUT, the polar singularity can be averted naturally.
Based on the advantage of the RBSL flux rope, the next step of our work could be to model a CME event that was observed in reality. Compared to our previously implemented TDm flux rope model in COCONUT (Linan et al. 2023), whose axis is fixed as a toroidal shape, the RBSL flux rope is more flexible (arbitrary path), leading to a better resemblance to the observations. As demonstrated in our previous observational data-driven MHD simulations constrained in the local Cartesian coordinates (Guo et al. 2021b, 2023b), the onset process of the CME resulting from the RBSL flux rope coincides well with the observations. Following these, we will perform a data-driven simulation with COCONUT to model a truly observed CME in a global domain, which can be used to study the propagation of the global extreme-ultraviolet waves (Chen 2016), the nature of the CME three-part structure (Chen 2011; Song et al. 2022), and the large-scale current sheet (Lin et al. 2005; Cheng et al. 2018). Moreover, to make the simulation results more comparable with observations, we also plan to conduct forward-modeling with the 3D data of the COCONUT simulation in future works, such as the synthesis of the white-light and extreme ultraviolet (EUV) radiation. In addition, the CME at around 21.5 R⊙ obtained from the COCONUT simulations can also be adopted as the input of the EUHFORIA simulations. It is expected that a CME undergoing self-consistent evolution in the corona would yield a higher prediction accuracy compared to the method that launches an analytical CME model with a simple shape at the inner boundary of interplanetary space.
The current version clearly still has several drawbacks that need to be resolved. For example, the plasma β distribution in our simulation is larger than that in observations (Korreck et al. 2020). The higher plasma β compared to the observations could be attributed to the quasi-isothermal approximation in the polytropic model, as mentioned in Regnault et al. (2023). This approximation may lead to the following impacts on our results. First, expanding CMEs push against the higher pressure from the ambient solar wind plasma in a high plasma β environment, which might cause less expansion compared to observations. Second, the Alfvén speed and Lorentz force become lower compared to the sound speed and pressure gradient force in a high plasma β environment, thereby diminishing the effects of magnetic reconnection on CME acceleration. Moreover, the parametric survey conducted by Ni et al. (2012) indicated that plasma β also affects the critical Lundquist number for the plasmoid instability. Consequently, the intricate magnetic topology exhibited in our simulation might be relevant for the modeling setup. Nevertheless, some works have demonstrated that the influence of plasma β may still be limited. For instance, Ni et al. (2012) found that the global evolution and the reconnection rate are very similar in the temperature-stratified atmosphere even when plasma β changes from 0.2 to 50. Additionally, Wang et al. (2021) found that the probability distribution functions of magnetic islands slightly vary for the cases with different plasma β values. Linton & Antiochos (2002) studied the reconnection process of two twisted flux ropes and found that the magnetic energy of the post-reconnection equilibrium state is qualitatively similar in low-β and high-β cases. CME models in a more realistic atmosphere will be developed in our future endeavors. In particular, Brchnelova et al. (2023) recently developed a new method for achieving a more realistic plasma β value in the reconstruction of the solar wind.
We note in passing that the center of the CME flux rope undergoes excessive heating during the initiation process. It reaches up to 10 MK within the first five minutes, followed by a gradual decrease, as illustrated in Fig. 5. This phenomenon may be due to the following two factors. On the one hand, the eruption in our model does not start from an equilibrium flux rope. Even though the force-free condition is automatically fulfilled inside the RBSL flux rope, no external equilibrium condition between the flux rope and the background magnetic fields is achieved, where the intensity of the electric current flowing inside the flux rope exceeds the equilibrium value derived from Shafranov’s equation. The flux rope will therefore immediately rise when the simulation is advanced forward in time, without establishing a thermodynamic coupling with the ambient solar wind. Consequently, additional heating may be induced compared to eruptions originating from stable flux ropes in the realistic corona. On the other hand, the grid resolution is too coarse to accurately resolve the thermodynamic evolution of the CME flux rope in the low corona with strong magnetic fields, thereby contributing to numerical heating. We point out that Jin et al. (2013) found that the two-temperature model (coupling the thermodynamics of electron and proton populations) reproduces the CME temperature far more accurately. To summarize, the thermodynamic evolution of the CME flux rope in the current version remains considerably simplified and departs from that in the realistic corona. For instance, many nonadiabatic terms in the energy equation are omitted in the energy equation of the polytropic model, such as thermal conduction and radiation losses. Moreover, to counterbalance the radiation losses and drive the fast solar wind, the additional physical heating term must also be taken into account. The dissipation of Alfvén waves was demonstrated to be a potential candidate and has been implemented in some global coronal models (van der Holst et al. 2010; Mikić et al. 2018) that can reproduce the EUV and white-light emissions very well, and drive the fast solar wind. A radiation MHD model like this should provide a better overall description for the CME propagation, particularly in terms of the thermodynamic evolution, than the currently employed polytropic model.
In addition to the thermodynamic process, the initial magnetic field model is also an important factor that affects the relaxed solar wind. The simulations performed by COCONUT so far used the PFSS model as the initial magnetic field. However, the coronal magnetic fields deviate from a potential state, which is generally approximated by nonlinear force-free fields (NLFFF; Wiegelmann & Sakurai 2021). Hence, we speculate that adopting the global NLFFF model (Guo et al. 2016; Yeates & Hornig 2016; Koumtzis & Wiegelmann 2023) might speed up convergence. These future updates promise to facilitate more precise and timely space weather forecasting.
Acknowledgments
The SDO data are available courtesy of NASA/SDO and the AIA and HMI science teams. This work is supported by the National Key R&D Program of China (2020YFC2201200, 2022YFF0503004), NSFC (12127901), projects C14/19/089 (C1 project Internal Funds KU Leuven), G.0B58.23N (FWO-Vlaanderen), SIDC Data Exploitation (ESA Prodex-12), and Belspo project B2/191/P1/SWiM. J.H.G. was supported by the China Scholarship Council under file No. 202206190140. The resources and services used in this work were provided by the VSC (Flemish Supercomputer Centre), funded by the Research Foundation - Flanders (FWO) and the Flemish Government.
References
- Ando, H., Shiota, D., Imamura, T., et al. 2015, J. Geophys. Res. (Space Phys.), 120, 5318 [NASA ADS] [CrossRef] [Google Scholar]
- Asvestari, E., Rindlisbacher, T., Pomoell, J., & Kilpua, E. K. J. 2022, ApJ, 926, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., & Dudík, J. 2019, A&A, 621, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aulanier, G., Török, T., Démoulin, P., & DeLuca, E. E. 2010, ApJ, 708, 314 [Google Scholar]
- Baratashvili, T., Verbeke, C., Wijsen, N., & Poedts, S. 2022, A&A, 667, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boe, B., Habbal, S., & Druckmüller, M. 2020, ApJ, 895, 123 [Google Scholar]
- Brchnelova, M., Kuźma, B., Perri, B., Lani, A., & Poedts, S. 2022a, ApJS, 263, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Brchnelova, M., Zhang, F., Leitner, P., et al. 2022b, J. Plasma Phys., 88, 905880205 [NASA ADS] [CrossRef] [Google Scholar]
- Brchnelova, M., Kuźma, B., Zhang, F., Lani, A., & Poedts, S. 2023, A&A, 676, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Cane, H. V., McGuire, R. E., & von Rosenvinge, T. T. 1986, ApJ, 301, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Carmichael, H. 1964, NASA Spec. Pub., 50, 451 [NASA ADS] [Google Scholar]
- Chen, P. F. 2009, ApJ, 698, L112 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F. 2011, Liv. Rev. Sol. Phys., 8, 1 [Google Scholar]
- Chen, P. F. 2016, Geophys. Union Geophys. Monogr. Ser., 216, 381 [NASA ADS] [Google Scholar]
- Chen, B., Yu, S., Battaglia, M., et al. 2018, ApJ, 866, 62 [Google Scholar]
- Cheng, X., Zhang, J., Ding, M. D., Liu, Y., & Poomvises, W. 2013, ApJ, 763, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, X., Guo, Y., & Ding, M. 2017, Sci. China Earth Sci., 60, 1383 [Google Scholar]
- Cheng, X., Li, Y., Wan, L. F., et al. 2018, ApJ, 866, 64 [Google Scholar]
- Crooker, N. U., Forsyth, R., Rees, A., Gosling, J. T., & Kahler, S. W. 2004, J. Geophys. Res. (Space Phys.), 109, A06110 [NASA ADS] [Google Scholar]
- Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
- Feng, X. 2020, Magnetohydrodynamic Modeling of the Solar Corona and Heliosphere (Springer Nature Singapore Pte Ltd) [CrossRef] [Google Scholar]
- Feng, X., Zhou, Y., & Wu, S. T. 2007, ApJ, 655, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. E., & Low, B. C. 1998, ApJ, 493, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, L., DeLuca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T. 1993, J. Geophys. Res., 98, 18937 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Birn, J., & Hesse, M. 1995, Geophys. Res. Lett., 22, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gou, T., Liu, R., Veronig, A. M., et al. 2023, Nat. Astron., 7, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Gui, B., Shen, C., Wang, Y., et al. 2011, Sol. Phys., 271, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Xia, C., Keppens, R., & Valori, G. 2016, ApJ, 828, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Xu, Y., Ding, M. D., et al. 2019, ApJ, 884, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J. H., Ni, Y. W., Qiu, Y., et al. 2021a, ApJ, 917, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Zhong, Z., Ding, M. D., et al. 2021b, ApJ, 919, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J., Qiu, Y., Ni, Y., et al. 2023a, ApJ, 956, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J. H., Ni, Y. W., Zhong, Z., et al. 2023b, ApJS, 266, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Guo, J., Ni, Y., et al. 2023c, ApJ, 958, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, T. 1974, Sol. Phys., 34, 323 [Google Scholar]
- Hood, A. W., & Priest, E. R. 1981, Geophys. Astrophys. Fluid Dyn., 17, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Illing, R. M. E., & Hundhausen, A. J. 1986, J. Geophys. Res., 91, 10951 [Google Scholar]
- Isavnin, A. 2016, ApJ, 833, 267 [Google Scholar]
- Jin, M., Manchester, W. B., van der Holst, B., et al. 2012, ApJ, 745, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, M., Manchester, W. B., van der Holst, B., et al. 2013, ApJ, 773, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, M., Manchester, W. B., van der Holst, B., et al. 2017, ApJ, 834, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, R., Ebisuzaki, T., Kusano, K., et al. 2009, J. Geophys. Res. (Space Phys.), 114, A10102 [NASA ADS] [Google Scholar]
- Kilpua, E., Koskinen, H. E. J., & Pulkkinen, T. I. 2017, Liv. Rev. Sol. Phys., 14, 5 [Google Scholar]
- Kimpe, D., Lani, A., Quintino, T., Poedts, S., & Vandewalle, S. 2005, in Recent Advances in Parallel Virtual Machine and Message Passing Interface, eds. B. Di Martino, D. Kranzlmüller, & J. Dongarra (Berlin, Heidelberg: Springer), 520 [Google Scholar]
- Kliem, B., & Török, T. 2006, Phys. Rev. Lett., 96, 255002 [Google Scholar]
- Kopp, R. A., & Pneuman, G. W. 1976, Sol. Phys., 50, 85 [Google Scholar]
- Korreck, K. E., Szabo, A., Nieves Chinchilla, T., et al. 2020, ApJS, 246, 69 [Google Scholar]
- Koumtzis, A., & Wiegelmann, T. 2023, Sol. Phys., 298, 20 [CrossRef] [Google Scholar]
- Krucker, S., Kontar, E. P., Christe, S., Glesener, L., & Lin, R. P. 2011, ApJ, 742, 82 [Google Scholar]
- Kuźma, B., Brchnelova, M., Perri, B., et al. 2023, ApJ, 942, 31 [CrossRef] [Google Scholar]
- Lani, A., Quintino, T., Kimpe, D., et al. 2005, in Computational Science - ICCS 2005, eds. V. S. Sunderam, G. D. van Albada, P. M. A. Sloot, & J. J. Dongarra, (Berlin, Heidelberg: Springer), 279 [CrossRef] [Google Scholar]
- Lani, A., Villedieu, N., Bensassi, K., et al. 2013, in AIAA 2013–2589, 21th AIAA CFD Conference, San Diego (CA) [Google Scholar]
- Lani, A., Yalim, M. S., & Poedts, S. 2014, Comput. Phys. Commun., 185, 2538 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Ko, Y. K., Sui, L., et al. 2005, ApJ, 622, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Linan, L., Regnault, F., Perri, B., et al. 2023, A&A, 675, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linton, M. G., & Antiochos, S. K. 2002, ApJ, 581, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R. 2020, Res. Astron. Astrophys., 20, 165 [Google Scholar]
- Liu, Y. A., Liu, Y. D., Hu, H., Wang, R., & Zhao, X. 2018, ApJ, 854, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaz, N., Downs, C., Shibata, K., et al. 2011, ApJ, 738, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Antiochos, S. K., Li, Y., Luhmann, J. G., & DeVore, C. R. 2009, ApJ, 697, 1918 [NASA ADS] [CrossRef] [Google Scholar]
- Maharana, A., Isavnin, A., Scolini, C., et al. 2022, Adv. Space Res., 70, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Maharana, A., Scolini, C., Schmieder, B., & Poedts, S. 2023, A&A, 675, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masson, S., Antiochos, S. K., & DeVore, C. R. 2013, ApJ, 771, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mikić, Z., Linker, J. A., Schnack, D. D., Lionello, R., & Tarditi, A. 1999, Phys. Plasmas, 6, 2217 [Google Scholar]
- Mikić, Z., Downs, C., Linker, J. A., et al. 2018, Nat. Astron., 2, 913 [Google Scholar]
- Morgan, H. 2015, ApJS, 219, 23 [CrossRef] [Google Scholar]
- Nakamura, M., Imamura, T., Ishii, N., et al. 2011, Earth Planets Space, 63, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Ni, L., Ziegler, U., Huang, Y.-M., Lin, J., & Mei, Z. 2012, Phys. Plasmas, 19, 072902 [NASA ADS] [CrossRef] [Google Scholar]
- Odstrcil, D. 2003, Adv. Space Res., 32, 497 [CrossRef] [Google Scholar]
- Ouyang, Y., Zhou, Y. H., Chen, P. F., & Fang, C. 2017, ApJ, 835, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, B., Leitner, P., Brchnelova, M., et al. 2022, ApJ, 936, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, B., Kuźma, B., Brchnelova, M., et al. 2023, ApJ, 943, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Poedts, S., Lani, A., Scolini, C., et al. 2020, J. Space Weather Space Clim., 10, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pomoell, J., & Poedts, S. 2018, J. Space Weather Space Clim., 8, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Regnault, F., Janvier, M., Démoulin, P., et al. 2020, J. Geophys. Res. (Space Phys.), 125, e28150 [NASA ADS] [Google Scholar]
- Regnault, F., Strugarek, A., Janvier, M., et al. 2023, A&A, 670, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schmieder, B., Aulanier, G., & Vršnak, B. 2015, Sol. Phys., 290, 3457 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Kauristie, K., Aylward, A. D., et al. 2015, Adv. Space Res., 55, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Scolini, C., Rodriguez, L., Mierla, M., Pomoell, J., & Poedts, S. 2019, A&A, 626, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scolini, C., Chané, E., Temmer, M., et al. 2020, ApJS, 247, 21 [Google Scholar]
- Shen, C., Wang, Y., Gui, B., Ye, P., & Wang, S. 2011, Sol. Phys., 269, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, F., Shen, C., Zhang, J., et al. 2014, J. Geophys. Res. (Space Phys.), 119, 7128 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, F., Shen, C., Xu, M., et al. 2022, Rev. Mod. Plasma Phys., 6, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Shiota, D., & Kataoka, R. 2016, Space Weather, 14, 56 [CrossRef] [Google Scholar]
- Shiota, D., Isobe, H., Chen, P. F., et al. 2005, ApJ, 634, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Shiota, D., Kusano, K., Miyoshi, T., & Shibata, K. 2010, ApJ, 718, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, T., Yalim, M. S., & Pogorelov, N. V. 2018, ApJ, 864, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Song, H., Li, L., & Chen, Y. 2022, ApJ, 933, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sturrock, P. A. 1966, Nature, 211, 695 [Google Scholar]
- Titov, V. S., & Démoulin, P. 1999, A&A, 351, 707 [NASA ADS] [Google Scholar]
- Titov, V. S., Török, T., Mikic, Z., & Linker, J. A. 2014, ApJ, 790, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, V. S., Downs, C., Mikić, Z., et al. 2018, ApJ, 852, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Török, T., Kliem, B., & Titov, V. S. 2004, A&A, 413, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, T., Berger, M. A., & Kliem, B. 2010, A&A, 516, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, T., Downs, C., Linker, J. A., et al. 2018, ApJ, 856, 75 [Google Scholar]
- Tóth, G., van der Holst, B., Sokolov, I. V., et al. 2012, J. Comput. Phys., 231, 870 [Google Scholar]
- Tsurutani, B. T., Zank, G. P., Sterken, V. J., et al. 2023, IEEE Trans. Plasma Sci., 51, 1595 [CrossRef] [Google Scholar]
- Vandenhoeck, R., & Lani, A. 2019, Comput. Phys. Commun., 242, 1 [NASA ADS] [CrossRef] [Google Scholar]
- van der Holst, B., Manchester, W. B. I., Frazin, R. A., et al. 2010, ApJ, 725, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Verbeke, C., Pomoell, J., & Poedts, S. 2019, A&A, 627, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbeke, C., Baratashvili, T., & Poedts, S. 2022, A&A, 662, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vourlidas, A., & Howard, R. A. 2006, ApJ, 642, 1216 [Google Scholar]
- Vourlidas, A., Lynch, B. J., Howard, R. A., & Li, Y. 2013, Sol. Phys., 284, 179 [NASA ADS] [Google Scholar]
- Wang, W., Liu, R., Wang, Y., et al. 2017, Nat. Commun., 8, 1330 [Google Scholar]
- Wang, Y., Cheng, X., Ding, M., & Lu, Q. 2021, ApJ, 923, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, D. F., & Howard, T. A. 2012, Liv. Rev. Sol. Phys., 9, 3 [Google Scholar]
- Wiegelmann, T., & Sakurai, T. 2021, Liv. Rev. Sol. Phys., 18, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Zhu, J., & Guo, Y. 2020, ApJ, 892, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Yeates, A. R., & Hornig, G. 2016, A&A, 594, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J., Cheng, X., & Ding, M.-D. 2012, Nat. Commun., 3, 747 [Google Scholar]
- Zhou, Y., & Feng, X. 2017, J. Geophys. Res. (Space Phys.), 122, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y. F., Feng, X. S., Wu, S. T., et al. 2012, J. Geophys. Res. (Space Phys.), 117, A01102 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1. Comparisons between observations and numerical results for the background solar wind. Panel a displays the solar eclipse image of 2 July 2019 (Copyright: 2019 Miloslav Druckmüller, Peter Aniol), corresponding to a minimum of solar activity. Panels b and c correspond to the typical field lines and radial velocity distribution in the meridian plane, respectively. Panel d visualizes the heliospheric current sheet depicted by the isosurface of Br = 0. |
| In the text | |
 |
Fig. 2. Visualization of the magnetic field lines of the global corona coupled with the RBSL flux rope (yellow tubes) with the background solar wind (pink tubes). Panels a and b illustrate the results viewed from the top and side, respectively. Panels c and d show the zoomed-in views of the red rectangles in panels a and b, respectively. Panels e and f show a typical flux rope in observations that is reflected by the sigmoid viewed on the solar disk and the hot channel at the solar limb. The sigmoid on the solar disk in panel e was observed by the Hinode/XRT. The hot channel above the solar limb in panel f was observed in the SDO/AIA 131 Å band. |
| In the text | |
 |
Fig. 3. Representative magnetic field lines displaying the global evolution of the CME. The yellow and pink tubes represent the magnetic structures of the CME flux rope and the ambient solar wind, respectively. The top row (a–c) illustrates the results viewed from the top of the flux rope, and the bottom row (d–f) presents the side views. Snapshots at different time intervals are displayed in the left (a and d), middle (b and e), and right (c and f) panels, corresponding to 0.4, 3.2, and 8.0 h, respectively. |
| In the text | |
 |
Fig. 4. Radial velocity and temperature distributions in the equatorial and meridian planes. The top (a–f) and bottom two (g–l) panels show the results in the equatorial and meridian planes, respectively. Panels a–c and g–i display the distributions of the radial velocity, and panels d–f and j–l correspond to those of the temperature. The cyan tubes are some typical field lines illustrating the CME flux rope. |
| In the text | |
 |
Fig. 5. Kinetic and thermodynamic evolution of the CME flux rope. Panel a corresponds to the time-height diagram of the CME flux rope. Panel b presents the temperature (red) and density (blue) evolution of the CME flux rope over time. |
| In the text | |
 |
Fig. 6. Magnetic field and thermodynamic structure of the CME. Panel a shows the density and temperature in the meridian plane in 2D. Panel b corresponds to the in situ plasma profile measured by a virtual satellite at around 21.5 R⊙, where the red, green, and blue bands represent the sheath and two subparts of the magnetic cloud (M1 and M2), respectively. Panel c illustrates some typical field lines around the CME, where the yellow, cyan, and red tubes represent the field lines from the original inserting flux rope, newly formed twisted field lines during the CME propagation, and the underlying flare loops, respectively. |
| In the text | |
 |
Fig. 7. In situ plasma profiles measured at different distances from the Sun. Panels a–c present the results measured by S1 (5 R⊙), S2 (10 R⊙), and S3 (15 R⊙) marked in Fig. 6a, respectively. The red and yellow bands represent the sheath and magnetic cloud, respectively. |
| In the text | |
 |
Fig. 8. Magnetic structure of the CME flux rope at around 20 R⊙. Panel a shows a collection of typical field lines of the CME flux rope that are enveloped by a high-temperature transparent contour. Panels b–d illustrate the field lines in panel a individually, providing details of their magnetic connectivity and the footpoint placements. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



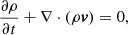
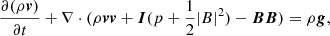
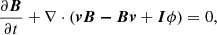
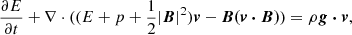
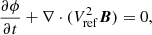
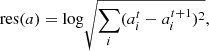
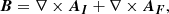
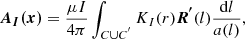
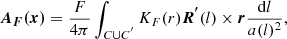
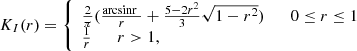
![$$ \begin{aligned} K_{F}(r)= {\left\{ \begin{array}{ll} \frac{2}{\pi r^{2}}(\frac{\arcsin r}{r}-\sqrt{1-r^{2}})+\frac{2}{\pi }\sqrt{1-r^{2}} + \\ \frac{5-2r^{2}}{2\sqrt{6}}[1-\frac{2}{\pi } \arcsin (\frac{1+2r^{2}}{5-2r^{2}})] \qquad 0 \le r \le 1,\\ \frac{1}{r^{3}} \qquad r > 1, \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/03/aa47634-23/aa47634-23-eq14.gif)