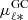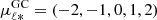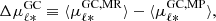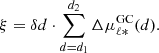| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202347570 | |
| Published online | 06 February 2024 | |
The Blanco DECam Bulge Survey (BDBS)
VIII. Chemo-kinematics in the southern Galactic bulge from 2.3 million red clump stars with Gaia DR3 proper motions
1
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei Mũnchen, Germany
e-mail: tommaso.marchetti.astro@gmail.com
2
Konkoly Observatory, HUN-REN Research Centre for Astronomy and Earth Sciences, Konkoly-Thege Miklós út 15-17, 1121 Budapest, Hungary
3
CSFK, MTA Centre of Excellence, Konkoly Thege Miklós út 15-17., Budapest 1121, Hungary
e-mail: meridith.joyce@csfk.org
4
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
5
Department of Physics and Astronomy, University of California Los Angeles, 430 Portola Plaza, Box 951547 Los Angeles, CA 90095-1547, USA
6
Department of Natural Sciences, University of Michigan-Dearborn, 4901 Evergreen Rd., Dearborn, MI 48128, USA
7
Saint Martins University, 5000 Abbey Way SE, Lacey, WA 98503, USA
8
Shanghai Key Lab for Astrophysics, Shanghai Normal University, 100 Guilin Road, Shanghai 200234, PR China
9
Indiana University Department of Astronomy, SW319, 727 E 3rd Street, Bloomington, IN 47405, USA
Received:
26
July
2023
Accepted:
20
October
2023
Context. The inner Galaxy is a complex environment, and the relative contributions of different formation scenarios to its observed morphology and stellar properties are still debated. The different components are expected to have different spatial, kinematic, and metallicity distributions, and a combination of photometric, spectroscopic, and astrometric large-scale surveys is needed to study the formation and evolution of the Galactic bulge.
Aims. The Blanco DECam Bulge Survey (BDBS) provides near-ultraviolet to near-infrared photometry for approximately 250 million unique stars over more than 200 square degrees of the southern Galactic bulge. By combining BDBS photometry with the latest Gaia astrometry, we aim to characterize the chemodynamics of red clump stars across the BDBS footprint using an unprecedented sample size and sky coverage.
Methods. Our field of view of interest is |ℓ| ≤ 10°, −10° ≤b ≤ −3°. We constructed a sample of approximately 2.3 million red clump giants in the bulge with photometric metallicities, BDBS photometric distances, and proper motions. Photometric metallicities are derived from a (u − i)0 versus [Fe/H] relation; astrometry, including precise proper motions, is from the third data release (DR3) of the ESA satellite Gaia. We studied the kinematics of the red clump stars as a function of sky position and metallicity by investigating proper-motion rotation curves, velocity dispersions, and proper-motion correlations across the southern Galactic bulge.
Results. By binning our sample into eight metallicity bins in the range of −1.5 dex < [Fe/H] < +1 dex, we find that metal-poor red clump stars exhibit lower rotation amplitudes, at ∼29 km s−1 kpc−1. The peak of the angular velocity is ∼39 km s−1 kpc−1 for [Fe/H] ∼ −0.2 dex, exhibiting declining rotation at higher [Fe/H]. The velocity dispersion is higher for metal-poor stars, while metal-rich stars show a steeper gradient with Galactic latitude, with a maximum dispersion at low latitudes along the bulge minor axis. Only metal-rich stars ([Fe/H] ≳ −0.5 dex) show clear signatures of the bar in their kinematics, while the metal-poor population exhibits isotropic motions with an axisymmetric pattern around Galactic longitude ℓ = 0.
Conclusions. This work describes the largest sample of bulge stars with distance, metallicity, and astrometry reported to date, and shows clear kinematic differences with metallicity. The global kinematics over the bulge agrees with earlier studies. However, we see striking changes with increasing metallicity, and, for the first time, kinematic differences for stars with [Fe/H]> − 0.5, suggesting that the bar itself may have kinematics that depends on metallicity.
Key words: Galaxy: kinematics and dynamics / Galaxy: bulge / Galaxy: stellar content
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Observations of the central region of our Galaxy made over the last few decades reveal a highly complex environment, with several distinct and interacting stellar populations coexisting along the same line of sight. Studying the formation, history, and evolution of the Galactic bulge is essential in order to improve our knowledge of the Milky Way, which is a benchmark for understanding the evolution of disk galaxies in the Universe (e.g., Bland-Hawthorn & Gerhard 2016). The reconstruction of its evolutionary history requires precise photometric (e.g., Minniti et al. 2010; Udalski et al. 2015; Rich et al. 2020), spectroscopic (e.g., Rich et al. 2007; Kunder et al. 2012; Freeman et al. 2013; Zoccali et al. 2014; Majewski et al. 2017), and astrometric (e.g., Kuijken & Rich 2002; Clarkson et al. 2008, 2018; Gezari et al. 2022) measurements for statistically large samples of stars covering the whole Galactic bulge. Because of our location in the Milky Way plane, several studies have focused on the removal of the foreground disk population – the presence of which contaminates studies of the Galactic bulge – using a mixture of photometric and astrometric techniques (e.g., Kuijken & Rich 2002; Zoccali et al. 2003; Clarkson et al. 2008, 2011; Valenti et al. 2013; Calamida et al. 2014; Clarkson et al. 2018; Surot et al. 2019a; Queiroz et al. 2021; Marchetti et al. 2022).
While the recent data releases of the European Space Agency satellite Gaia (Gaia Collaboration 2016, 2018, 2021; Gaia Collaboration 2023) provide geometric parallaxes for 1.5 billion stars in the Milky Way, large uncertainties and systematic errors prevent the precise localization of stars beyond a few kiloparsecs from the Sun. Stellar standard candles – whose distance can be derived using photometry – are therefore important tools with which to map the three-dimensional structure of the Galaxy. In particular, red clump (RC) stars have long been used to study and constrain the morphology of the inner parts of the Milky Way (e.g., Stanek et al. 1994, 1997; Rattenbury et al. 2007; McWilliam & Zoccali 2010; Saito et al. 2011; Wegg & Gerhard 2013; Simion et al. 2017; Paterson et al. 2020; Johnson et al. 2022), and they have been critical in uncovering important details about the Galactic bulge’s rotating bar (Binney et al. 1991; Stanek et al. 1994; Wegg & Gerhard 2013) and its X-shaped morphology (Weiland et al. 1994; Nataf et al. 2010; McWilliam & Zoccali 2010; Wegg & Gerhard 2013).
As the nearest example of a spheroidal or bar population, and one that is near enough to resolve individual stars, the Galactic bulge offers the possibility to explore its structure and formation history through analysis of the spatial variation of abundances and kinematics within it, a field of study often called “chemodynamics”. This effort has historically required the correlation of spectroscopically derived metallicities and radial velocities, beginning with Rich (1990) and Minniti et al. (2010), early works that showed a trend of declining velocity dispersion with increasing metallicity. Spectroscopic surveys have grown in size from approximately 10 000 stars in the Bulge Radial Velocity Assay (BRAVA, Rich et al. 2007; Kunder et al. 2012) to tens of thousands of stars with abundances and kinematics in projects such as the Abundances and Radial velocity Galactic Origins Survey (ARGOS, Freeman et al. 2013), the GIRAFFE Inner Bulge Survey (GIBS, Zoccali et al. 2014), and the Apache Point Observatory Galactic Evolution Experiment (APOGEE, Majewski et al. 2017).
However, even sample sizes of 104 or greater can be insufficient when binned by spatial location, kinematics, and abundance. Two revolutionary developments, namely wide field imagers, such as the Dark Energy Camera on the Blanco 4 m telescope (Flaugher et al. 2015) and the Gaia astrometric survey (Gaia Collaboration 2023), have combined to expand sample sizes into the millions. A significant recent breakthrough has been the development of a robust photometric metallicity scale, (u − i)0 versus [Fe/H] for bulge RC giants (Johnson et al. 2020), by correlating photometry with [Fe/H] from GIBS survey spectroscopy (Zoccali et al. 2017). Combining photometric metallicities and distances for the RC with Gaia kinematics potentially unlocks the exploration of chemodynamics for millions of stars, albeit with only [Fe/H] to 0.2 dex precision, and no detailed abundances (e.g., alpha elements). Here, we exploit the large numbers made possible by combining the two datasets, reaching numerical sizes that are of the same order as those of the two planned major bulge surveys, 4MOST and MOONS (Bensby et al. 2019; Gonzalez et al. 2020).
Many investigations have pointed toward a significant break in kinematics at [Fe/H] ∼ −0.5, beginning with Zhao et al. (1994) and continuing with Soto et al. (2007), Zoccali et al. (2008), and Ness et al. (2013b). The break at −0.5 dex is clearly seen when the vertex deviation is derived (this requires the construction of the velocity ellipsoid from radial velocities and longitudinal proper motions, and is thought to be attributable to the location of the metal-rich population being in the bar). Babusiaux et al. (2010) explored Baade’s window and two other fields on the bulge minor axis, combining proper motions from OGLE-II (Sumi et al. 2004) with radial velocities and metallicities from FLAMES/GIRAFFE at the VLT. Babusiaux et al. (2010) identified two distinct populations: one of metal-rich stars, with bar-like kinematics, and another of metal-poor stars consistent with an old spheroid (or thick disk). This supported the co-existence of both a classical and a pseudo-bulge in the central region of our Galaxy (see Kormendy & Kennicutt 2004). Subsequent studies confirmed the different behavior of metal-poor and metal-rich stars in the inner Milky Way (see e.g., Hill et al. 2011; Dékány et al. 2013; Ness et al. 2013a; Rojas-Arriagada et al. 2014, 2017, 2020; Babusiaux 2016; Kunder et al. 2016; Athanassoula et al. 2017; Zoccali et al. 2017, 2018; Clarkson et al. 2018; Arentsen et al. 2020; Du et al. 2020; Simion et al. 2021; Wylie et al. 2021; Rix et al. 2022). Stellar populations with different chemical compositions will also show different kinematics due to the presence of the bar, a process called kinematic fractionation (Debattista et al. 2017). Our investigation lacks radial velocities, but we are able to explore proper motions and proper-motion dispersion versus [Fe/H] over an unprecedented scale, allowing us to study the dependence of kinematics on the metallicity across the spatial extent of the Southern Galactic bulge. Future investigations will benefit from large numbers of stars with spectroscopic abundances and radial velocities, but our work aims to offer some insight into what we can expect from these surveys.
There is good reason to suspect that strong chemodynamic correlations exist in our bulge dataset. Johnson et al. (2022) shows a striking trend in which RC giants of increasing metallicity are more concentrated to the Galactic plane; there is no such trend in the radial direction. This striking vertical abundance gradient, which steepens at [Fe/H] > −0.5, is consistent with a complex bar with properties that depend on metallicity.
The age of the bulge, especially of the metal-rich population, has also been called into question. Early HST-based investigations used proper-motion cleaning to find a compact, old main sequence turnoff (Ortolani et al. 1993; Kuijken & Rich 2002; Clarkson et al. 2008, 2011); these studies have been segregated by metallicity (Renzini et al. 2018). The apparently old age was confirmed over the wider bulge field population (e.g., Zoccali et al. 2003; Valenti et al. 2013; Surot et al. 2019b). While Haywood et al. (2016) proposed that a bulge population with a complex age distribution might fit a more vertical turnoff, the bulge turnoff morphology has been investigated in multiple fields (e.g., Valenti et al. 2013) and does not exhibit the vertical structure required in the study by Haywood et al. (2016).
A more significant case for young populations was put forward by Bensby et al. (2017), who derive spectroscopic ages for microlensed dwarfs in the bulge, finding a large fraction of the suprasolar metallicity stars in the bulge to be < 5 Gyr of age. A new analysis using MIST isochrones by Joyce et al. (2023) suggests the presence of a significantly smaller, but not absent, population of metal-rich stars with ages of ≤8 Gyr, but largely supports a bulge age more tightly clustered around 10–11 Gyr. Though this latter analysis, based on the same sample of microlensed dwarfs presented in Bensby et al. (2017), is in better agreement with HST-based ages, the tension between the microlening-derived ages and the HST- and main sequence turnoff-derived ages is not fully resolved.
If a substantial fraction of the bar is < 10 Gyr old (younger than the thick disk), then one might expect the younger ages to be associated with the formation in the disk and to present a chemodynamic correlation that arises from age as well as metallicity. At present, though a rough mapping between [Fe/H] and age can be constructed from the works of Bensby et al. (2017) and Joyce et al. (2023), we lack age constraints for individual RC stars; nevertheless, our study provides metallicities that can be correlated with kinematics.
We can now build on this legacy to investigate the detailed relationship between stellar metallicity and kinematics by constructing a comprehensive sample of RC stars residing within the Milky Way bulge that combines photometric metallicities and distances for approximately 2.6 million RC stars from Johnson et al. (2022) with the high-quality proper motions from the third data release of Gaia (DR3, Gaia Collaboration 2023; Lindegren et al. 2021b). The present paper is organized as follows. In Sect. 2, we introduce the sample of RC stars with BDBS photometry, distances, and metallicities, and describe the process of assigning Gaia DR3 proper motions and projected velocities that are used in this work. In Sect. 3, we investigate the kinematics of RC stars as a function of metallicity, present our results, and highlight the difference between the motion of the metal-poor and metal-rich components. Finally, in Sect. 4, we discuss our findings and summarize our results.
2. The red clump star sample
In this work, we start with the sample of 2.6 million RC stars extracted from BDBS data in Johnson et al. (2020, 2022), spanning the region in Galactic coordinates (ℓ,b) −10° ≤ℓ≤10°, −10° ≤b ≲ −3° of the southern Galactic bulge1. Thanks to the sensitivity of the near-ultraviolet u band to the metallicity of the RC stars, Johnson et al. (2020, 2022) derived photometric metallicities for the whole sample, with a typical dispersion of 0.2 dex, employing the dust map constructed in Simion et al. (2017) using infrared VVV data. The distance distribution of the RC sample, which was derived using BDBS photometry (Johnson et al. 2020, 2022), is shown in the left panel of Fig. 1. RC distances span a range of [6, 12] kpc, with a median value of 8.83 kpc. The metallicity of the sample, shown in the right panel of Fig. 1, covers a range from −1.5 to 1 dex, with a median value of [Fe/H] ∼ −0.04 dex. The two peaks of the metallicity distribution are at [Fe/H] ∼ −0.15 dex and [Fe/H] ∼ 0.2 dex. More information on the metallicity distribution function and on the spatial distribution of the RC stars is provided in Johnson et al. (2022), including a description of the red clump color and magnitude selection functions (see their Sect. 2).
 |
Fig. 1. Distance (left panel) and metallicity (right panel) distributions of the sample of 2.6 million RC stars, as derived from BDBS photometry in Johnson et al. (2020, 2022). |
We cross-match this dataset to Gaia DR3 data, back-propagating Gaia coordinates to the mean BDBS epoch through Gaia proper motions using a tolerance radius of 1 arcsec (see Marchetti et al. 2022, for further details on the cross-matching procedure). This results in a sample of 2 593 172 RC stars with BDBS photometry (and therefore photometric distances and metallicities), and Gaia DR3 astrometry (parallaxes and proper motions). We further select sources with a value of the Gaia DR3 renormalised unit weight error (RUWE) of less than 1.4 in order to avoid contamination from spurious astrometric solutions (Lindegren et al. 2021b; Belokurov et al. 2020; Penoyre et al. 2020). After this selection cut, we are left with a sample of 2 315 197 RC stars, which is the main focus of this paper. Thanks to the homogeneous Gaia DR3 proper motions and BDBS metallicities over the large BDBS instrumental footprint, this is an ideal dataset with which to study the chemo-kinematics of RC stars across the whole southern Galactic bulge.
While random and systematic uncertainties in Gaia parallaxes are too large to provide reliable distances for individual stars in the Galactic bulge (e.g., Lindegren et al. 2021a), we rely on photometric distances and Gaia DR3 proper motions to investigate the kinematics of the RC sample. We convert Galactic proper motions (μℓ* ≡ μℓ cos b, μb) to Galactocentric velocities along longitude 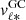 and latitude
and latitude 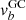 by subtracting the contribution given by the motion of the Sun:
by subtracting the contribution given by the motion of the Sun:
where vi [km s−1] = 4.74 · μi[mas yr−1] · d[kpc] for i = ℓ * , b, and d is the heliocentric distance of the star derived with BDBS photometry (Johnson et al. 2020). We assume a three-dimensional Cartesian velocity of the Sun of [U⊙, V⊙, W⊙]=[12.9, 245.6, 7.78] km s−1 (Reid & Brunthaler 2004; Drimmel & Poggio 2018; GRAVITY Collaboration 2018).
In the left panel of Fig. 2, we show the distribution of the sample of RC stars in Cartesian Galactocentric coordinates (XGC, YGC), where the black cross marks the position of the Galactic Center assuming a distance of 8.122 kpc (GRAVITY Collaboration 2018). The XGC coordinate is aligned to the Sun-Galactic Center direction, and is positive in the direction of the Galactic Center, while the YGC coordinate is positive along the direction of the Sun circular rotation in the disk. As already shown by previous works (e.g., Wegg & Gerhard 2013; Johnson et al. 2022), the over-density at YGC > 0, XGC < 0 is due to the orientation of the near side of the bar, forming an angle of ∼27° with the line of sight at ℓ = 0 (Wegg & Gerhard 2013). If we split our sample in metallicity using the same bins in [Fe/H] adopted by Johnson et al. (2022), Fig. 3 shows that the distribution of the stars is heavily dependent on their chemical composition. Metal-poor stars ([Fe/H] ≲ −0.5 dex) are more centrally distributed around the Galactic Center, while the morphology of more metal-rich stars ([Fe/H] ≳ −0.5 dex) shows the typical asymmetry with Galactic longitude caused by the orientation of the bar.
 |
Fig. 2. Top-down views of the RC stars in Galactocentric Cartesian coordinates. The black cross marks the position of the Galactic Center at (XGC, YGC) = (0, 0). Gray dashed lines correspond to constant values of Galactic longitude (ℓ = −10° , − 5° ,0° ,5° ,10°), and gray dashed arcs correspond to constant heliocentric distances of 6, 7, 8, 9, and 10 kpc. Left: logarithmic density of stars in each bin of position. Middle: galactic longitudinal velocity. The black contour corresponds to the line of nodes |
 |
Fig. 3. Same as in Fig. 2 (left panel), but for the metallicity bins used in Fig. 19 of Johnson et al. (2022). |
3. Chemo-kinematics of the red clump stars
In this section, we inspect the projected kinematics of the RC stars as a function of position and metallicity in the southern Galactic bulge. However, we caution that the spatial distributions presented here are heavily affected by our ∼10%–20% distance uncertainties. As Fig. 8 of Hey et al. (2023) shows, distance uncertainties of this magnitude distort two- and three-dimensional projections, particularly on the near side of the Galactic Center, and can smear out otherwise well-defined features.
In the central and right panel of Fig. 2, we plot the distribution of RC stars color-coded by Galactocentric velocity along Galactic longitude and latitude, respectively (Eqs. (1) and (2)). The clear asymmetry in the velocity field along longitude with respect to YGC is an indication of the presence of the bar, which breaks the axial symmetry of the potential in the inner Galaxy (see also Sanders et al. 2019). The orientation of the 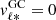 contour line is ∼80° at YGC = 0, which is consistent with results from Sanders et al. (2019). As expected, the mean velocity along latitude is
contour line is ∼80° at YGC = 0, which is consistent with results from Sanders et al. (2019). As expected, the mean velocity along latitude is 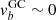 , indicating no clear streaming motion above or below the Galactic plane (e.g., Reid & Brunthaler 2004; Du et al. 2020).
, indicating no clear streaming motion above or below the Galactic plane (e.g., Reid & Brunthaler 2004; Du et al. 2020).
3.1. Proper-motion rotation curves as a function of metallicity
Gaia DR3 proper motions can be further used to construct proper-motion rotation curves as a function of heliocentric distance. Longitudinal Galactic proper motions provide similar results to line-of-sight velocities in the direction of the Galactic bulge (Du et al. 2020). By plotting the median of the Galactic longitudinal velocity (as given by Eq. (1)) as a function of distance d, we can compute the angular velocity ω as the slope of the linear relation (e.g., Du et al. 2020), for different metallicity bins. By binning the stars in metallicity using the same intervals adopted by Johnson et al. (2022), in the upper panel of Fig. 4 we show the resulting ω as a function of [Fe/H] (we report the median metallicity value in each bin) for our sample of RC stars. The uncertainty on ω is computed from the linear fit using the method of least squares, taking into account the uncertainties on the velocity (computed by dividing the velocity dispersion by the square root of the number of stars in each metallicity bin). Metal-poor RC stars rotate slower: ω ∼ 29 km s−1 kpc−1, and then the angular velocity increases significantly at [Fe/H] ∼ −0.5 dex, with a maximum value ω = 39 km s−1 kpc−1 for [Fe/H] ∼ −0.2 dex. The angular velocity starts decreasing again for [Fe/H] ≳ −0.2 dex, reaching a value of ∼35 km s−1 kpc−1 in the most metal-rich bin at [Fe/H] ≳ 0.4 dex. The lower rotation of metal-poor stars is consistent with several studies of the Galactic bulge (e.g., Ness et al. 2013b; Ness & Lang 2016; Zoccali et al. 2017; Clarkson et al. 2018).
 |
Fig. 4. Upper: angular velocity ω as a function of metallicity for the whole sample of RC stars. Uncertainties on the angular velocity are derived by the fitting procedure, while the ones on the x-axis correspond to the 16th and 84th percentiles of the metallicity distribution in each bin. Lower: ages inferred from the age–metallicity relation described in Joyce et al. (2023) are assigned to the metallicity bins shown above, yielding angular velocity as a function of age. The x-axis is inverted (e.g., ages shown in reverse) for better visual alignment with the panel above. |
We can now use the age–metallicity relation presented in Joyce et al. (2023) to roughly estimate the dependence of the angular velocity versus the age of the stars. This is shown in the lower panel of Fig. 4. We do not attempt to compute proper age uncertainties for this analysis, and so no horizontal error bars are given (conservatively, one expects uncertainties of roughly 1.5–2 Gyr; Joyce et al. 2023). As expected by the monotonic behavior of the adopted relation, the shape of the curve reflects the chemical one. The peak of the angular velocity corresponds to a population with an age of ∼11.8 Gyr. The oldest stars in our sample have ages comparable to the age of the Universe, while the metal-rich stars are older than 8 Gyr.
Thanks to the large spatial coverage of our sample in the southern Galactic bulge, and to the availability of homogeneous all-sky Gaia DR3 proper motions, in Fig. 5 we plot the sky distribution in Galactic coordinates of the angular velocity ω for RC stars of all metallicities. We see that ω peaks at ∼40 km s−1 kpc−1 at low latitudes along the bulge minor axis, and decreases to a minimum of ∼25 km s−1 kpc−1 for off-axis fields at higher latitudes. Typical uncertainties from the fitting procedures are ∼3 km s−1 kpc−1, and they do not show any significant dependence on the sky location.
 |
Fig. 5. Angular velocity ω as a function of Galactic coordinates in the southern Galactic bulge region, computed using all the RC stars in our sample. The bins have sizes of 0.5° ×0.5°. |
A comparison between Fig. 5 here and Fig. 16c in Johnson et al. (2022), which shows spatial distribution differences in [Fe/H] between the metal-rich peak and half-power position of the metal-rich tail, indicates that the sky patterns are highly correlated. Both distributions peak along the minor axis close to the plane, and show noticeable enhancements in both values within a region encompassing approximately |ℓ| < 3° and |b| < 6°. This observation provides one of the few clear connections between chemistry and kinematics for bulge formation and evolution, as the regions showing the highest angular velocities are also those for which the broadest high-metallicity tails formed.
Figure 6 incorporates the spatial and chemical dependence of the Galactic longitudinal proper-motion rotation curves by presenting the resulting angular velocity ω as a function of Galactic coordinates for several metallicity bins, which were chosen to match those in Fig. 19 of Johnson et al. (2022). At the lowest metallicities ([Fe/H] ≲ −0.7 dex), there is no evidence for a clear, coherent signal over the survey footprint, with a noisy distribution with values ranging from 20 to 50 km s−1 kpc−1. On the other hand, for [Fe/H] ≳ −0.5 dex, there is a clear continuous pattern over the sky, with a mean value of ω ∼ 40 km s−1 kpc−1. We observe a clear asymmetry with Galactic longitude, showing lower values of ω for positive ℓ. We suspect this to be a projection effect due to the orientation of the bar. We do not observe a strong gradient with Galactic latitude. As also evident from Fig. 4, the angular velocities across the sky decrease to ∼30 km s−1 kpc−1 for [Fe/H] ≳ 0, confirming the slower rotation of the most metal-rich population observed in Fig. 4.
 |
Fig. 6. Angular velocity ω as a function of Galactic coordinates for different metallicities of the RC sample. The metallicity bins are the same as in Fig. 3. |
3.2. Impact of the Galactic bar on the chemo-kinematics of red clump stars
Recent works combining Gaia DR2 and VVV infrared data showed the impact of the Galactic bar on the transverse kinematics of bulge stars (Clarke et al. 2019; Sanders et al. 2019). These authors quantified these aspects by investigating the proper-motion dispersions, dispersion ratio, and correlation between Galactic proper motions as a function of Galactic coordinates across the bulge. They found higher dispersions at low latitudes, a characteristic X-shape structure in the dispersion ratio, and an approximate radial alignment in the proper motions with a clear asymmetry at positive ℓ due to the orientation of the near-side of the bar.
We can now reproduce these transverse kinematic maps using more precise and accurate Gaia DR3 data, adding the further dimension provided by photometric metallicities. We bin the sample in metallicity using the same bins adopted by Johnson et al. (2022) and in Fig. 6, and in Galactic coordinates by adopting bin sizes of 0.5° ×0.5°. In each bin, we then compute the Galactic longitudinal proper-motion dispersion as
and the correlation between the Galactic proper motions as
Figure 7 shows the resulting proper-motion dispersion along Galactic longitude, σμℓ*, as a function of sky positions for the same metallicity bins adopted in Fig. 6. We can see how the metal-poor population is kinematically hotter, σμℓ* ∼ 3 mas yr−1, which corresponds to ∼115 km s−1 at a distance of 8 kpc, while the metal-rich stars show a lower velocity dispersion (e.g., Ness et al. 2013b; Athanassoula et al. 2017; Zoccali et al. 2018). In addition, stars with [Fe/H] ≳ −0.5 dex exhibit a coherent pattern over the sky, reproducing results by Clarke et al. (2019) and Sanders et al. (2019). This is particularly evident at [Fe/H] ∼ 0, where the RC population is kinematically colder at higher latitudes, σμℓ* ∼ 2 mas yr−1 ∼76 km s−1, and the peak is observed on the minor axis towards the center of the Galaxy because of the Galactic potential well (see also Rattenbury et al. 2007). We find that, for metal-rich stars, there is a strong gradient in velocity dispersion with latitude, and on the minor axis at low latitudes the velocity dispersion becomes higher than (or comparable to) that of metal-poor stars (consistent with the findings of Zoccali et al. 2017, in the inner bulge). We also observe an asymmetry with respect to ℓ = 0 for metal-rich stars, with higher values of the dispersion at positive Galactic longitudes. Figure 8 instead shows the velocity dispersion along Galactic latitude, σμb. Once again, we note that metal-poor stars are kinematically hotter, and do not exhibit a clear coherent pattern over the sky.
 |
Fig. 7. Proper-motion dispersion along Galactic longitude as a function of Galactic coordinates in the southern bulge for the metallicity bins considered in this work and in Fig. 19 of Johnson et al. (2022). |
To better illustrate the different kinematics of stars with different chemistry, in the upper panel of Fig. 9 we plot the velocity dispersion along Galactic longitude (left panel) and Galactic latitude (right panel) as a function of metallicity for different slices of Galactic latitude b. In both cases, we clearly see that metal-rich stars are kinematically colder (see also Arentsen et al. 2020). For a given metallicity, stars closer to the Galactic plane show lower values of velocity dispersion (except for the most metal-poor star sample, which also has the largest uncertainties). Finally, we find that the difference in velocity dispersion between the stars at low Galactic latitude and high Galactic latitude increases with metallicity. Following the approach outlined in Sect. 3.1, we can estimate the dependence of the proper-motion dispersions on the ages of the stars, as shown in the lower panel of Fig. 9. Younger stars are kinematically colder, and the highest values of the dispersions (σμℓ* ∼ 3 mas yr−1, σμb ∼ 2.75 mas yr−1) are obtained for stars older than 13 Gyr.
 |
Fig. 9. Upper: proper-motion dispersion along Galactic longitude (left panel) and Galactic latitude (right panel) as a function of metallicity for different values of Galactic latitude. Lower: same as the upper panel, but shown with the age–metallicity substitution from Joyce et al. (2023) described in Sect. 3.1. |
The results shown in Figs. 7–9 closely mirror the metallicity-dependent radial velocity dispersion variations noted by Wylie et al. (2021) in their Fig. 26. Those authors found that stars with [Fe/H] > −0.5 have strongly peaked radial velocity dispersions near ℓ = 0, but only for fields with 3 < |b| < 6. Additionally, Wylie et al. (2021) showed that the difference in radial velocity dispersion between low- and high-latitude fields increases strongly with increasing [Fe/H]. Therefore, we confirm their result that the more metal-poor stars have flatter velocity dispersion profiles as a function of latitude.
In Fig. 10 we plot the dispersion ratio as a function of metallicity and also as a function of sky position, defined as the ratio between the velocity dispersion along longitude and along latitude. Similar to Fig. 6 of Sanders et al. (2019), we find a significantly lower dispersion ratio for sight lines near 0° < ℓ < +5° and b < −6° compared to adjacent fields. This feature appears to be related to the influence of the X-shape structure in the bulge and is only prominent at [Fe/H] > 0.
 |
Fig. 10. Same as Fig. 7, but showing the dispersion ratio, defined as the ratio between the proper-motion dispersion along Galactic longitude and that along Galactic latitude. |
In Fig. 11, we plot the correlation coefficient between Galactic proper motions (Eq. (4)) for the different spatial and metallicity bins. The dipole pattern (which becomes a quadrupole when also given access to the northern Galactic bulge) is a sign of radial alignment towards the Galactic Center, with a stronger amplitude of the correlation at ℓ > 0 due to the orientation of the bar (see Clarke et al. 2019; Sanders et al. 2019). By looking at the different metallicity bins, we see how, similarly to Figs. 6 and 7, the dipole patterns start to become apparent for [Fe/H] ≳ −0.7 dex, with an amplitude of |ρℓb|∼0.1. The maximum amplitude of |ρℓb|∼0.2 is attained for [Fe/H] ≳ 0.1 dex. Interestingly, the asymmetry due to geometric effects at positive Galactic longitudes is most evident for the [Fe/H] = 0.2 bin, but the absence of BDBS fields at ℓ > 3°, b < −8° prevents us from studying this in more detail.
 |
Fig. 11. Correlation between Galactic proper motions as a function of Galactic coordinates in the southern bulge, for the metallicity bins considered in this work, and in Fig. 19 of Johnson et al. (2022). |
3.3. Kinematic fractionation
In the previous sections, we note that the most striking transition features due to the presence of the bar are most evident for [Fe/H] ≳ −0.5 dex. In this section, we therefore split the sample of RC stars into two large metallicity bins, defining metal-poor stars as RC stars with [Fe/H] < −0.5 dex, and metal-rich RC stars as those with [Fe/H] > −0.5 dex. We now make a qualitative comparison between our results and the N-body + smoothed-hydrodynamics star-forming simulations of Debattista et al. (2017) following the approach outlined in Gough-Kelly et al. (2022). We note that the metrics introduced in Gough-Kelly et al. (2022) to investigate kinematic fractionation through proper motions in the bulge are defined not in terms of metallicity but in terms of age, for young (< 7 Gyr) and old (> 9 Gyr) stars, as ages are more natural units than [Fe/H] for their simulations, due to the lack of chemical mixing.
To further investigate the impact of the bar on the kinematics of stars with different metallicities, in Fig. 12 we plot the mean proper motion along longitude 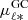 (corrected for the motion of the Sun) as a function of Galactocentric Cartesian coordinates (XGC, YGC) for metal-poor ([Fe/H] < −0.5 dex, top panel) and metal-rich ([Fe/H] > −0.5 dex, middle panel) stars. Confirming the predictions of Gough-Kelly et al. (2022) when inspecting the kinematics of young and old stars in N-body+smoothed particle hydrodynamic simulations (see their Fig. 5), we find that the asymmetry in the velocity field around ±YGC is clearly observed in the metal-rich sample, while metal-poor stars show an axisymmetric rotation field. The nonaxisymmetric pattern observed for more metal-rich stars is a clear signature of the presence of the bar, as shown by the stronger longitudinal variation of the proper motions compared to the metal-poor stars.
(corrected for the motion of the Sun) as a function of Galactocentric Cartesian coordinates (XGC, YGC) for metal-poor ([Fe/H] < −0.5 dex, top panel) and metal-rich ([Fe/H] > −0.5 dex, middle panel) stars. Confirming the predictions of Gough-Kelly et al. (2022) when inspecting the kinematics of young and old stars in N-body+smoothed particle hydrodynamic simulations (see their Fig. 5), we find that the asymmetry in the velocity field around ±YGC is clearly observed in the metal-rich sample, while metal-poor stars show an axisymmetric rotation field. The nonaxisymmetric pattern observed for more metal-rich stars is a clear signature of the presence of the bar, as shown by the stronger longitudinal variation of the proper motions compared to the metal-poor stars.
 |
Fig. 12. Top-down view of the sample of RC stars with [Fe/H] < −0.5 dex (top panel, ∼3 × 105 stars) and [Fe/H] > −0.5 dex (middle panel, ∼2.3 × 106 stars) color-coded according to the proper motion along Galactic longitude corrected by the motion of the Sun, |
To gain further insight into the kinematic differences between metal-rich and metal-poor stars, in the bottom panel of Fig. 12 we plot, in each bin of Galactocentric Cartesian coordinates, the quantity 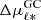 :
:
where 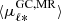 and
and 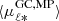 are the mean values of the proper motions along Galactic longitude for metal-rich and metal-poor stars, respectively, in each spatial bin. We observe good qualitative agreement with the simulations from Gough-Kelly et al. (2022): the near positive peak in
are the mean values of the proper motions along Galactic longitude for metal-rich and metal-poor stars, respectively, in each spatial bin. We observe good qualitative agreement with the simulations from Gough-Kelly et al. (2022): the near positive peak in 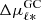 is at (XGC, YGC)∼(−1, 0) kpc with an extended tail towards negative values of Galactic longitude, while the negative peak around (YGC)∼1 kpc extends to positive longitudes. We stress here that this is only a qualitative comparison between the observed and predicted trends, and we defer a more rigorous and careful interpretation of our data in light of realistic models of the Galactic bulge to a future study. The simple adopted definitions of metal-poor and metal-rich stars might result in overlapping age distributions, which might cause the differences in the spatial distribution between our data and the clear dipole pattern shown in Gough-Kelly et al. (2022). Finally, we note that Fig. 12 does not change significantly if we consider vertical slices in ZGC.
is at (XGC, YGC)∼(−1, 0) kpc with an extended tail towards negative values of Galactic longitude, while the negative peak around (YGC)∼1 kpc extends to positive longitudes. We stress here that this is only a qualitative comparison between the observed and predicted trends, and we defer a more rigorous and careful interpretation of our data in light of realistic models of the Galactic bulge to a future study. The simple adopted definitions of metal-poor and metal-rich stars might result in overlapping age distributions, which might cause the differences in the spatial distribution between our data and the clear dipole pattern shown in Gough-Kelly et al. (2022). Finally, we note that Fig. 12 does not change significantly if we consider vertical slices in ZGC.
Following Gough-Kelly et al. (2022), we define the separation amplitude ξ as the integral along the line of sight of the difference in mean proper motion between the metal-rich and metal-poor stars:
To facilitate the comparison with Gough-Kelly et al. (2022), we fix the parameters δd = 0.5 kpc, d1 = 6 kpc, and d2 = 10 kpc, and we bin in distance using a fixed bin size of 0.5 kpc. In the top panel of Fig. 13, we plot the separation amplitude ξ as a function of Galactic coordinates across the BDBS footprint. The observed projected pattern qualitatively matches that inferred from simulations (see the middle panel in Fig. 4 of Gough-Kelly et al. 2022): the separation amplitude ξ is negative for ℓ ≳ 2.5°, and positive for the other lines of sight. The variations of ξ across the Galactic bulge are due to the difference in the intrinsic velocity distributions of the metal-poor and metal-rich populations, tracing different kinematic structures. The presence of negative values of ξ in our data is likely due to the absence of metal-poor stars in the closest distance bins (see Fig. 12) given the longitudinal dependence of the colour cuts implemented in Johnson et al. (2022) to minimize foreground contamination from the stellar disk.
 |
Fig. 13. First panel: separation amplitude ξ. Second panel: error on the separation amplitude. Third panel: mean longitudinal proper-motion difference between metal-rich and metal-poor stars at a distance of ∼8 kpc, δμℓ*. Fourth panel: error on the δμℓ* metric. All the plots are shown as a function of Galactic coordinates, and the angular bins have sizes of 0.5° ×0.5°. |
We compute the error on the separation amplitude, eξ, using Eq. (3) in Gough-Kelly et al. (2022). The second panel of Fig. 13 shows the separation amplitude as a function of Galactic coordinates. The values of eξ are driven by the number of stars in each bin, and we find that the overall distribution loosely traces the underlying one for the metal-rich stars.
To quantify the effect of kinematic fractionation in the southern Galactic bulge, we also define the metric δμℓ* following Gough-Kelly et al. (2022):
where the mean of the proper motions is computed on a large distance bin along the line of sight, from 7 kpc to 9 kpc. In the third panel of Fig. 13, we plot δμℓ* as a function of Galactic coordinates. The large values of δμℓ* result from forbidden velocities in the rotation curves (negative longitudinal proper motions at ℓ > 0, and positive values for ℓ < 0) and are deeply connected to the distribution of radial velocities of stars in the bar (Gough-Kelly et al. 2022). A purely axisymmetric distribution of velocities would not produce forbidden velocities, and therefore their nonzero observed values are a strong signature of the presence of the bar (Gough-Kelly et al. 2022). The observed pattern in the third panel of Fig. 13 again qualitatively matches the results from Gough-Kelly et al. (2022). The uncertainty on δμℓ* shown in the fourth panel of Fig. 13 follows eξ, and is again driven by the underlying number density of [Fe/H] > −0.5 dex RC stars in our sample.
4. Discussion and conclusions
In this work, we combined Gaia DR3 proper motions with BDBS photometric distances and metallicities to investigate the chemo-kinematics of a sample of 2.6 million RC stars in the southern Galactic bulge. Our main results can be summarised as follows:
-
We find that the angular velocity, defined as the slope of the longitudinal proper motion μℓ* curve as a function of distance, is highest at ω ∼ 39 km s−1 kpc−1 for stars with [Fe/H] ∼ −0.25 dex (see Fig. 4). Metal-poor RC stars exhibit the lowest rotation values (ω ∼ 29 km s−1 kpc−1). Surprisingly, the angular velocity is not a monotonic function of metallicity, but decreases for RC stars with [Fe/H] ≳ −0.25 dex, and reaches ω ∼ 35 km s−1 kpc−1 for [Fe/H] ∼ 0.5 dex. When integrated over all metallicities, the angular velocity peaks on the minor axis closer to the plane (Fig. 5). When plotted as a function of both metallicity and sky position (Fig. 6), the angular velocity peaks at low latitudes for stars with [Fe/H] ≳ −0.5 dex, with a clear asymmetry with Galactic longitude, which is possibly due to the orientation of the near side of the bar. Stars with lower metallicities do not exhibit a coherent angular velocity pattern on the sky.
-
Proper-motion dispersions along Galactic longitude and latitude are maximum towards the Galactic Center for stars with [Fe/H] ≳ −0.5 dex because of the Galactic potential well (Figs. 7 and 8, respectively). Metal-poor stars are kinematically hotter, with proper-motion dispersions of ∼3 mas yr−1, while the mean dispersion for metal-rich stars is ∼2 mas yr−1. If we plot the dispersions as a function of metallicity for different latitude bins (Fig. 9), we see that, for a given metallicity bin, RC stars are kinematically hotter closer to the plane. Also, the spread in dispersion between the stars at low latitudes and high latitudes increases with increasing metallicity.
-
The correlation between Galactic proper motions clearly shows a quadrupole pattern corresponding to radial alignment for stars with [Fe/H] ≳ −0.5 dex (Fig. 11). The prominence of the correlation amplitude at ℓ > 0° is a consequence of the orientation of the bar.
-
Based on the striking difference in the sky plots, we split our sample of RC stars into metal-poor ([Fe/H] < −0.5 dex) and metal-rich ([Fe/H] > −0.5 dex) stars. We compare our results to the simulations presented by Gough-Kelly et al. (2022), who analyze the predicted proper motion trends for young and old stars in the Galactic bulge. We observe a nonaxisymmetric pattern around the Galactic center in the proper motions along Galactic longitude only for the metal-rich sample, which is a clear sign of the bar. More generally, we find that the footprint of the bar is clearly present in the metal-rich sample, and is totally absent in the metal-poor one.
Our results clearly demonstrate that RC stars with different metallicities have dramatically different kinematics. In particular, metal-rich stars are kinematically colder, and their orbits show a clear imprint of the Galactic bar. On the other hand, metal-poor RC stars have larger velocity dispersions, and exhibit random motions over the bulge, without showing any radial alignment towards the Galactic Center, or clear asymmetries with Galactic longitude that could be due to the orientation of the bar. At present, we are not able to assess whether the more metal-poor stars trace a weaker bar, or constitute the so-called classical bulge assembled over cosmic time by galaxy mergers. A more detailed comparison with cosmological simulations is needed to assess the contribution of the different formation scenarios to the observed kinematics of the stellar populations in the Galactic bulge, and we defer such an analysis to a future dedicated study.
Our results also help us interpret age–metallicity relations in the Galactic bulge. Though others have proposed a flat age–metallicity relation in the bulge (e.g., Bensby et al. 2017), the present chemodynamical results support the hypothesis that the highest-metallicity star is a member of the bar rather than the bulge. This hypothesis is more broadly consistent with the results of Joyce et al. (2023), who found that, though a handful of the highest–metallicity, micro-lensed subdwarfs identified as belonging to the bulge region may be as young as 2 Gyr, the majority are not. These results, in combination with the kinematic–metallicity correlations presented here suggest that the most metal-rich stars belong to the bar rather than the bulge. Further, based on Fig. 11, the bar orbits become visible for stars with [Fe/H] > −0.2. According to Fig. 4, stars in this metallicity range have ages of less than 12 Gyr, with the youngest stars having ages of around 8.4 Gyr. However, we note that the bar structure itself may be younger than the stars it comprises.
The values of the angular velocity we determine for RC stars are in agreement with findings for RRL stars (Du et al. 2020), but are considerably lower than what was previously found for younger bulge stars (e.g., Sanders et al. 2019; Du et al. 2020). In upcoming years, new Gaia data releases will provide more precise proper motions thanks to the improved observational baseline. In addition, a longer baseline will also improve the accuracy of the astrometric solution, especially in crowded fields, allowing better constraint of proper-motion systematic errors. The Vera C. Rubin Telescope will also monitor the Milky Way bulge, and derive proper motions down to the main sequence turnoff (Gonzalez et al. 2018). In addition, large-scale multifiber spectroscopic facilities such as MOONS (Gonzalez et al. 2020) and 4MOST (de Jong et al. 2012) will measure radial velocities for millions of giants in the bulge, allowing a full three-dimensional kinematic analysis when combined with photometric and spectroscopic metallicities.
An electronic table containing the positions, ugi-band photometry, extinction, distance, and [Fe/H] values for all stars used here is provided in Table 1 of Johnson et al. (2022).
Acknowledgments
T.M. thanks F. Fragkoudi for interesting discussions. M.J. gratefully acknowledges funding of MATISSE: Measuring Ages Through Isochrones, Seismology, and Stellar Evolution, awarded through the European Commission’s Widening Fellowship. This project has received funding from the European Union’s Horizon 2020 research and innovation programme. Data used in this paper comes from the Blanco DECam Survey Collaboration. This project used data obtained with the Dark Energy Camera (DECam), which was constructed by the Dark Energy Survey (DES) collaboration. Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundaçõ Carlos Chagas Filho de Amparo á Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovacão, the Deutsche Forschungsgemeinschaft, and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Enérgeticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Cióncies de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, the Ohio State University, the OzDES Membership Consortium the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. Based on observations at Cerro Tololo Inter-American Observatory (2013A-0529; 2014A-0480; PI: Rich), National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Software used: Numpy (Harris et al. 2020), Matplotlib (Hunter 2007), Scipy (Virtanen et al. 2020), Astropy (Astropy Collaboration 2013, 2018), TOPCAT (Taylor 2005, 2006)
References
- Arentsen, A., Starkenburg, E., Martin, N. F., et al. 2020, MNRAS, 491, L11 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Athanassoula, E., Rodionov, S. A., & Prantzos, N. 2017, MNRAS, 467, L46 [Google Scholar]
- Babusiaux, C. 2016, PASA, 33, e026 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belokurov, V., Penoyre, Z., Oh, S., et al. 2020, MNRAS, 496, 1922 [Google Scholar]
- Bensby, T., Feltzing, S., Gould, A., et al. 2017, A&A, 605, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Bergemann, M., Rybizki, J., et al. 2019, The Messenger, 175, 35 [NASA ADS] [Google Scholar]
- Binney, J., Gerhard, O. E., Stark, A. A., Bally, J., & Uchida, K. I. 1991, MNRAS, 252, 210 [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [Google Scholar]
- Calamida, A., Sahu, K. C., Anderson, J., et al. 2014, ApJ, 790, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, J. P., Wegg, C., Gerhard, O., et al. 2019, MNRAS, 489, 3519 [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W. I., Sahu, K. C., Anderson, J., et al. 2011, ApJ, 735, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W. I., Calamida, A., Sahu, K. C., et al. 2018, ApJ, 858, 46 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, eds. I. S. McLean, S. K. Ramsay, & H. Takami, SPIE Conf. Ser., 8446, 84460T [NASA ADS] [Google Scholar]
- Debattista, V. P., Ness, M., Gonzalez, O. A., et al. 2017, MNRAS, 469, 1587 [Google Scholar]
- Dékány, I., Minniti, D., Catelan, M., et al. 2013, ApJ, 776, L19 [Google Scholar]
- Drimmel, R., & Poggio, E. 2018, Res. Notes Am. Astron. Soc., 2, 210 [Google Scholar]
- Du, H., Mao, S., Athanassoula, E., Shen, J., & Pietrukowicz, P. 2020, MNRAS, 498, 5629 [CrossRef] [Google Scholar]
- Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [Google Scholar]
- Freeman, K., Ness, M., Wylie-de-Boer, E., et al. 2013, MNRAS, 428, 3660 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gezari, S., Bentz, M., De, K., et al. 2022, ArXiv e-prints [arXiv:2202.12311] [Google Scholar]
- Gonzalez, O. A., Clarkson, W., Debattista, V. P., et al. 2018, ArXiv e-prints [arXiv:1812.08670] [Google Scholar]
- Gonzalez, O. A., Mucciarelli, A., Origlia, L., et al. 2020, The Messenger, 180, 18 [NASA ADS] [Google Scholar]
- Gough-Kelly, S., Debattista, V. P., Clarkson, W. I., et al. 2022, MNRAS, 509, 4829 [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Snaith, O., & Calamida, A. 2016, A&A, 593, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hey, D. R., Huber, D., Shappee, B. J., et al. 2023, AJ, 166, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Young, M. D., et al. 2020, MNRAS, 499, 2357 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Simion, I. T., et al. 2022, MNRAS, 515, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Joyce, M., Johnson, C. I., Marchetti, T., et al. 2023, ApJ, 946, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Kennicutt, Robert C. J., 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., & Rich, R. M. 2002, AJ, 124, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Kunder, A., Koch, A., Rich, R. M., et al. 2012, AJ, 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Kunder, A., Rich, R. M., Koch, A., et al. 2016, ApJ, 821, L25 [CrossRef] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021a, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021b, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, ApJ, 154, 94 [CrossRef] [Google Scholar]
- Marchetti, T., Johnson, C. I., Joyce, M., et al. 2022, A&A, 664, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A., & Zoccali, M. 2010, ApJ, 724, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New Astron., 15, 433 [Google Scholar]
- Nataf, D. M., Udalski, A., Gould, A., Fouqué, P., & Stanek, K. Z. 2010, ApJ, 721, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013a, MNRAS, 432, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013b, MNRAS, 430, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., & Lang, D. 2016, AJ, 152, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Bica, E., & Barbuy, B. 1993, ApJ, 408, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Paterson, D., Coleman, B., & Gordon, C. 2020, MNRAS, 499, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Penoyre, Z., Belokurov, V., Wyn Evans, N., Everall, A., & Koposov, S. E. 2020, MNRAS, 495, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Queiroz, A. B. A., Chiappini, C., Perez-Villegas, A., et al. 2021, A&A, 656, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rattenbury, N. J., Mao, S., Debattista, V. P., et al. 2007, MNRAS, 378, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [Google Scholar]
- Renzini, A., Gennaro, M., Zoccali, M., et al. 2018, ApJ, 863, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M. 1990, ApJ, 362, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Reitzel, D. B., Howard, C. D., & Zhao, H. 2007, ApJ, 658, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Johnson, C. I., Young, M., et al. 2020, MNRAS, 499, 2340 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Chandra, V., Andrae, R., et al. 2022, ApJ, 941, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Arriagada, A., Recio-Blanco, A., Hill, V., et al. 2014, A&A, 569, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Arriagada, A., Recio-Blanco, A., de Laverny, P., et al. 2017, A&A, 601, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Arriagada, A., Zasowski, G., Schultheis, M., et al. 2020, MNRAS, 499, 1037 [Google Scholar]
- Saito, R. K., Zoccali, M., McWilliam, A., et al. 2011, AJ, 142, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. L., Smith, L., Evans, N. W., & Lucas, P. 2019, MNRAS, 487, 5188 [CrossRef] [Google Scholar]
- Simion, I. T., Belokurov, V., Irwin, M., et al. 2017, MNRAS, 471, 4323 [NASA ADS] [CrossRef] [Google Scholar]
- Simion, I. T., Shen, J., Koposov, S. E., et al. 2021, MNRAS, 502, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, M., Rich, R. M., & Kuijken, K. 2007, ApJ, 665, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Mateo, M., Udalski, A., et al. 1994, ApJ, 429, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Udalski, A., Szymański, M., et al. 1997, ApJ, 477, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Wu, X., Udalski, A., et al. 2004, MNRAS, 348, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Surot, F., Valenti, E., Hidalgo, S. L., et al. 2019a, A&A, 629, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Surot, F., Valenti, E., Hidalgo, S. L., et al. 2019b, A&A, 623, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, M. B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [Google Scholar]
- Udalski, A., Szymański, M. K., & Szymański, G. 2015, Acta Astron., 65, 1 [NASA ADS] [Google Scholar]
- Valenti, E., Zoccali, M., Renzini, A., et al. 2013, A&A, 559, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
- Weiland, J. L., Arendt, R. G., Berriman, G. B., et al. 1994, ApJ, 425, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Wylie, S. M., Gerhard, O. E., Ness, M. K., et al. 2021, A&A, 653, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, H., Spergel, D. N., & Rich, R. M. 1994, AJ, 108, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Gonzalez, O. A., Vasquez, S., et al. 2014, A&A, 562, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Vasquez, S., Gonzalez, O. A., et al. 2017, A&A, 599, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Valenti, E., & Gonzalez, O. A. 2018, A&A, 618, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Distance (left panel) and metallicity (right panel) distributions of the sample of 2.6 million RC stars, as derived from BDBS photometry in Johnson et al. (2020, 2022). |
| In the text | |
 |
Fig. 2. Top-down views of the RC stars in Galactocentric Cartesian coordinates. The black cross marks the position of the Galactic Center at (XGC, YGC) = (0, 0). Gray dashed lines correspond to constant values of Galactic longitude (ℓ = −10° , − 5° ,0° ,5° ,10°), and gray dashed arcs correspond to constant heliocentric distances of 6, 7, 8, 9, and 10 kpc. Left: logarithmic density of stars in each bin of position. Middle: galactic longitudinal velocity. The black contour corresponds to the line of nodes |
| In the text | |
 |
Fig. 3. Same as in Fig. 2 (left panel), but for the metallicity bins used in Fig. 19 of Johnson et al. (2022). |
| In the text | |
 |
Fig. 4. Upper: angular velocity ω as a function of metallicity for the whole sample of RC stars. Uncertainties on the angular velocity are derived by the fitting procedure, while the ones on the x-axis correspond to the 16th and 84th percentiles of the metallicity distribution in each bin. Lower: ages inferred from the age–metallicity relation described in Joyce et al. (2023) are assigned to the metallicity bins shown above, yielding angular velocity as a function of age. The x-axis is inverted (e.g., ages shown in reverse) for better visual alignment with the panel above. |
| In the text | |
 |
Fig. 5. Angular velocity ω as a function of Galactic coordinates in the southern Galactic bulge region, computed using all the RC stars in our sample. The bins have sizes of 0.5° ×0.5°. |
| In the text | |
 |
Fig. 6. Angular velocity ω as a function of Galactic coordinates for different metallicities of the RC sample. The metallicity bins are the same as in Fig. 3. |
| In the text | |
 |
Fig. 7. Proper-motion dispersion along Galactic longitude as a function of Galactic coordinates in the southern bulge for the metallicity bins considered in this work and in Fig. 19 of Johnson et al. (2022). |
| In the text | |
 |
Fig. 8. Same as Fig. 7, but showing the proper-motion dispersion along Galactic latitude. |
| In the text | |
 |
Fig. 9. Upper: proper-motion dispersion along Galactic longitude (left panel) and Galactic latitude (right panel) as a function of metallicity for different values of Galactic latitude. Lower: same as the upper panel, but shown with the age–metallicity substitution from Joyce et al. (2023) described in Sect. 3.1. |
| In the text | |
 |
Fig. 10. Same as Fig. 7, but showing the dispersion ratio, defined as the ratio between the proper-motion dispersion along Galactic longitude and that along Galactic latitude. |
| In the text | |
 |
Fig. 11. Correlation between Galactic proper motions as a function of Galactic coordinates in the southern bulge, for the metallicity bins considered in this work, and in Fig. 19 of Johnson et al. (2022). |
| In the text | |
 |
Fig. 12. Top-down view of the sample of RC stars with [Fe/H] < −0.5 dex (top panel, ∼3 × 105 stars) and [Fe/H] > −0.5 dex (middle panel, ∼2.3 × 106 stars) color-coded according to the proper motion along Galactic longitude corrected by the motion of the Sun, |
| In the text | |
 |
Fig. 13. First panel: separation amplitude ξ. Second panel: error on the separation amplitude. Third panel: mean longitudinal proper-motion difference between metal-rich and metal-poor stars at a distance of ∼8 kpc, δμℓ*. Fourth panel: error on the δμℓ* metric. All the plots are shown as a function of Galactic coordinates, and the angular bins have sizes of 0.5° ×0.5°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



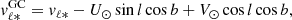
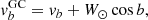
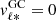
![$$ \begin{aligned} \sigma _{\mu _{\ell *}}(\ell , b, [\mathrm{Fe/H} ]) = \sqrt{\langle \mu _{\ell *}^2\rangle - \langle \mu _{\ell *}\rangle ^2 } , \end{aligned} $$](/articles/aa/full_html/2024/02/aa47570-23/aa47570-23-eq8.gif)
![$$ \begin{aligned} \rho _{\ell , b}(\ell , b, [\mathrm{Fe/H} ]) = \frac{\langle \mu _{\ell *}\mu _b\rangle - \langle \mu _{\ell *}\rangle \langle \mu _b\rangle }{\sqrt{\Bigl (\langle \mu _{\ell *}^2\rangle - \langle \mu _{\ell *}\rangle ^2 \Bigr ) \Bigl (\langle \mu _b^2\rangle - \langle \mu _b\rangle ^2 \Bigr )}} . \end{aligned} $$](/articles/aa/full_html/2024/02/aa47570-23/aa47570-23-eq9.gif)