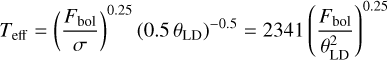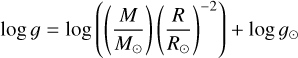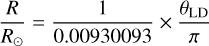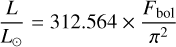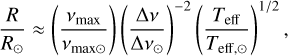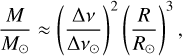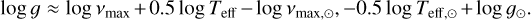| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 23 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202347136 | |
| Published online | 14 February 2024 | |
Gaia FGK benchmark stars: Fundamental Teff and log g of the third version★
1
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS,
B18N, allée Geoffroy Saint-Hilaire,
33615
Pessac,
France
e-mail: caroline.soubiran@u-bordeaux.fr
2
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
Bd de l’Observatoire, CS 34229,
06304
Nice Cedex 4,
France
3
Instituto de Estudios Astrofísicos, Facultad de Ingeniería y Ciencias, Universidad Diego Portales,
Av. Ejército Libertador 441,
Santiago,
Chile
4
Millenium Nucleous ERIS,
Santiago,
Chile
5
GEPI, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Paris Cité,
5 place Jules Janssen,
92190
Meudon,
France
6
Institut de Ciències del Cosmos (ICCUB), Departament de Física Quàntica i Astrofísica, Universitat de Barcelona (UB),
Martí i Franquès, 1,
08028
Barcelona,
Spain
7
Observational Astrophysics, Division of Astronomy and Space Physics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala,
Sweden
8
Instituto de Astrofísica, Pontificia Universidad Católica de Chile,
Av. Vicuña Mackenna 4860,
782-0436
Macul,
Santiago,
Chile
9
School of Physical and Chemical Sciences – Te Kura Matū, University of Canterbury,
Private Bag 4800,
Christchurch
8140,
New Zealand
10
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
Received:
9
June
2023
Accepted:
17
October
2023
Context. Large spectroscopic surveys devoted to the study of the Milky Way, including Gaia, use automated pipelines to determine the atmospheric parameters of millions of stars. The Gaia FGK benchmark stars are reference stars with Teff and log 𝑔 derived through fundamental relations, independently of spectroscopy, to be used as anchors for the parameter scale. The first and second versions of the sample have been extensively used for that purpose, and more generally to help constrain stellar models.
Aims. We provide the third version of the Gaia FGK benchmark stars, an extended set intended to improve the calibration of spectroscopic surveys, and their interconnection.
Methods. We have compiled about 200 candidates that have precise measurements of angular diameters and parallaxes. We determined their bolometric fluxes by fitting their spectral energy distribution. Masses were determined using two sets of stellar evolution models. In a companion paper, we describe the determination of metallicities and detailed abundances.
Results. We provide a new set of 192 Gaia FGK benchmark stars with their fundamental Teff and log 𝑔, and with uncertainties lower than 2% for most stars. Compared to the previous versions, the homogeneity and accuracy of the fundamental parameters are significantly improved thanks to the high quality of the Gaia photometric and astrometric data.
Key words: standards / surveys / stars: atmospheres / stars: fundamental parameters / stars: late-type
The full catalogue is only available at the CDS website/ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/682/A145
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The last decade has been marked by a large observational effort aimed at deciphering the history of our Galaxy based on large samples of stars observed by spectroscopic surveys. This has stimulated the development of efficient methodologies for the massive determination of atmospheric parameters (APs). In particular, the recent Gaia Data Release 3 (Gaia Collaboration 2023c, Gaia DR3) just delivered Teff, log 𝑔, and [Fe/H] for millions of stars (Creevey et al. 2023; Fouesneau et al. 2023). In particular, two datasets were released that mainly include F-, G-, and K-type stars, one for 5.6 million stars with APs based on medium resolution spectra from the Radial Velocity Spectrometer (Recio-Blanco et al. 2023), and the other one for 471 million stars with APs based on low-resolution spectra from the blue and red prisms, parallax, and integrated photometry (Andrae et al. 2023). The methodologies used for the massive determination of atmospheric parameters rely on stellar models that are not perfect and not able to reproduce real spectra exactly, causing some biases that have to be corrected.
The Gaia FGK benchmark stars (GBS) are reference stars to be used for the calibration and the validation of spectro-scopic methods of parametrisation. They are chosen to cover the range of F, G, and K spectral types at different luminosities and metallicities, and to have the necessary observations available to determine their effective temperature and surface gravity independently from spectroscopy, at a precision level of 1–2%. The determination of Teff and log 𝑔 is performed through the fundamental relations implying observable quantities (angular diameters directly measured by interferometry, bolometric fluxes, and parallaxes) and the mass, which is the only parameter that depends on theoretical assumptions.
The first and second versions of the GBS (hereafter V1 and V2, respectively) were presented in a series of papers. Heiter et al. (2015), hereafter Paper I, describe the initial selection of 34 stars, including the Sun, and the determination of their fundamental effective temperatures and surface gravities, resulting in the GBS V1 sample. Blanco-Cuaresma et al. (2014, Paper II) present the library of high-resolution spectra that was assembled and used to determine metallicities (Jofré et al. 2014, Paper III) and elemental abundances of α–capture and iron-peak elements (Jofré et al. 2015, Paper IV). One limitation of the V1 sample was the small number of targets, in particular in the metal-poor regime. Metal-poor stars are usually distant and faint, which makes them difficult to observe in interferometry. In Paper V, Hawkins et al. (2016) proposed a list of ten metal-poor stars to be included in the GBS sample. The GBS V2 sample summarised by Jofré et al. (2018) includes 36 stars, merged from Paper I and Paper V. The change in number from 34 to 36 comes from the addition of five metal-poor stars from Paper V and the removal of some stars from Paper I because their spectroscopic analysis indicated that they could not be recommended as reference stars. However, V2 was an intermediate version where the fundamental properties of the stars were not redetermined owing to the lack of direct and accurate measurements of angular diameters for some stars.
The material provided in these series of papers consists of accurate APs for stars covering an extensive range of spectral types and metallicities, in addition to a library of high-resolution and high signal-to-noise spectra from which line-by-line abundances are also provided. This material can be further exploited in spectroscopic studies. Paper VI of the GBS series (Jofré et al. 2017) does indeed report on a collective work using the GBS to investigate the different sources of uncertainties in elemental abundances in order to improve spectroscopic pipelines.
The ultimate goal of the efforts dealing with GBS is to provide the fundamental Teff and log 𝑔 scales and an external reference for abundances to spectroscopic surveys. Despite their limitation in sample size and parallax precision previous to Gaia data, the GBS have been extensively used in the past years. The Gaia astrophysical parameters’ inference system (Bailer-Jones et al. 2013; Creevey et al. 2023) made use of GBS for the validation of the stellar parameters published in Gaia DR3. The GBS are also a fundamental source of calibration and validation of the Gaia-ESO survey (Gilmore et al. 2022; Randich et al. 2022; Hourihane et al. 2023), of the RAVE survey (Steinmetz et al. 2020b,a), and of the GALAH survey (Buder et al. 2021). The OCCASO project (Casamiquela et al. 2019) has systematically observed two GBS giants, Arcturus and µ Leo, to validate chemical abundances of open clusters. Upcoming large projects such as WEAVE (Jin et al. 2023) are also making use of the GBS.
Calibrations based on GBS can help to make surveys more homogeneous and mutually compatible so that they can be combined into the most comprehensive database of chemical measurements for the study of the Milky Way stellar populations (Jofré et al. 2018). The applications of the GBS, however, can extend far beyond this specific purpose. As for the study presented in Paper VI (see also Blanco-Cuaresma 2019), many spectroscopic studies have benefited from the GBS effort. For example, Adibekyan et al. (2020) used the GBS to assess the performances of the ESPRESSO, PEPSI, and HARPS highresolution spectrographs, while Heiter et al. (2021) used some spectra from Paper II to assess the quality of hundreds of spectral lines and the corresponding atomic and molecular data used for the abundance analyses of FGK-type stars carried out within the Gaia-ESO survey (see also Kondo et al. 2019; Fukue et al. 2021, for lines in the Infrared). Amarsi et al. (2022) and Lind et al. (2022) used the GBS to quantify the differences in abundances derived using state-of-the-art 3D non local thermodynamic equilibrium (LTE) atmosphere models and the standard 1D LTE models.
In addition to spectroscopy, the GBS help to constrain better stellar evolution models. For example, Sahlholdt et al. (2019) determined ages of the GBS as a way to test the reliability of the determination of stellar ages for various stellar populations; Serenelli et al. (2017) used GBS to validate their asteroseismic analysis performed on dwarfs and subgiants. The GBS have also been used as a validation for the PLATO stellar analysis pipeline (Gent et al. 2022). Many of the lessons learnt from the GBS are further discussed in Jofré et al. (2019).
However, we are aware that the current sample of GBS is still imperfect and too small to make a satisfactory interconnection between surveys. This is why an extension of the sample is required. The V1 and V2 GBS samples were also limited by the parallax accuracy needed for a fundamental log 𝑔 determination. This is not an issue anymore thanks to the exquisite astrometric quality of the Gaia data (Gaia Collaboration 2016).
In this Paper VII of the series, we present the extended sample and third version of the GBS (GBS V3) that includes about 200 stars. We took advantage of recent interferometric studies that provided new measurements of angular diameters for large samples of stars (e.g. Ligi et al. 2016; Baines et al. 2018, 2021; van Belle et al. 2021) and for metal-poor stars (e.g. Creevey et al. 2015; Karovicova et al. 2018, 2020). As explained in Sect. 2, we selected new GBS candidates based on quality criteria applied on interferometric measurements. Section 3 describes the compilation of angular diameters and fluxes that are needed to compute the fundamental Teff. Bolometric fluxes (Fbol) were homogeneously computed by the method of spectral energy distribution (SED) fitting based on a large collection of (spectro)photometric data. Section 4 deals with the determination of log 𝑔 with parallaxes from Gaia DR3 (Gaia Collaboration 2023c), or HIPPARCOS (van Leeuwen 2007) for the brightest stars, and with masses inferred from a state-of-the-art methodology and stellar tracks. At each of these different steps, we assess the uncertainties of the stellar parameters. Section 5 provides an overview of the sample properties and shows some comparisons to Teff and log 𝑔 from different catalogues, before our concluding remarks in Sect. 6. All of the compiled and computed parameters of this work are given in the form of a catalogue distributed by the CDS. We note that these parameters still require a last iteration considering [Fe/H] values, which are needed for the estimation of Fbol and masses and have been adopted from the literature for this work, and they are consistent with our fundamental parameters. This is a necessary step to recommend our parameters for reference (Heiter et al. 2015). The accompanying Paper VIII (Casamiquela et al., in prep.) presents homogeneous determinations of [Fe/H] and of detailed abundances of the GBS V3 derived from a spectroscopic analysis. For this purpose a large dataset of high-resolution, high signal-to-noise spectra was collected from public archives and through our own observing programmes. The recommended parameters and abundances of the GBS are appropriately updated at the CDS.
2 Star selection
In order to determine Teff and log 𝑔 through the fundamental relations with a minimum of assumptions and theoretical input, our principal criterion was to choose F, G and K stars with a high-quality measurement of angular diameter. Ideally we want our GBS sample to homogeneously cover the (Teff, log 𝑔,[Fe/H]) space, which implies a special effort to add metal-poor stars. We have therefore searched the literature for GBS candidates fulfilling these criteria.
First, we considered the GBS from V1 and V2 (Heiter et al. 2015; Jofré et al. 2018). The GBS V1 sample has 29 FGK-type stars (including the Sun), four giants with Teff around 4000 K, corresponding to late K and early M spectral types, and one cooler M giant. The V2 sample was built from the V1 one, with the addition of metal-poor stars. For the V3 list we considered all the 39 V1 and V2 stars including several stars with indirect determinations of angular diameters. For all we searched for new direct determinations of angular diameters as well as other data needed to update their fundamental Teff and log 𝑔. We added to this list eight metal-poor stars from Karovicova et al. (2020, 2022a), not part of V1 and V2, and two targets recently observed with the CHARA interferometer (Creevey et al. in prep.). This sample of 49 stars was our initial set.
To further extend the GBS sample, we searched for new candidates observed in interferometry. We used the compilation from the Jean-Marie Mariotti Center (JMMC), the JMMC Measured Stellar Diameters Catalogue (JMDC, Duvert 2016). This catalogue, regularly updated, intends to be as exhaustive as possible in listing all the measurements of stellar apparent diameters made with direct techniques. It is therefore a very appropriate resource to extend the GBS sample. The JMDC is a bibliographical catalogue which implies that some stars have multiple entries, resulting from studies with different instruments, in different bands and with different precisions. Deciding which value of angular diameter is the most appropriate for a given star can be challenging, in particular owing to non-homogeneous uncertainties listed in the JMDC. In addition, there are many stars in the JMDC which are not appropriate for our purpose, such as some classes of variable stars, hot stars, spectroscopic binaries, and fast rotators. In addition, some very uncertain measurements of angular diameters could propagate large uncertainties to Teff and should be discarded. Therefore we made a first selection to reject stars and measurements not relevant for our purpose.
To do so, we followed Salsi et al. (2020) who established accurate surface brightness-colour relations for different spectral types and luminosity classes. They applied three types of rejection criteria on the JMDC data. First they examined the stellar characteristics to reject variable and semi-regular pulsating stars, spectroscopic binaries and other multiple stars, fast rotators and stars with a doubtful luminosity class. Second, they used criteria on the quality of the interferometric measurements that we apply similarly (see Sect. 3.1). The third type of criterion is based on the uncertainty of the K magnitude. We considered their list of 106 carefully selected F5 to K7 dwarfs and giants that we added to the initial set (five stars were already there). However, the study of Salsi et al. (2020) does not take into account the metallicity of the stars since their objective is to infer radii of stars and planets in the context of the PLATO mission which mainly focuses on solar-like stars. For us the metallicity is essential since the GBS should be representative of all the Milky Way stellar populations. We aim to improve the sampling of the GBS in Teff and log 𝑔 but also in [Fe/H] with as many GBS candidates as possible on the metal-poor side. We noticed that the criteria used by Salsi et al. (2020), in particular the photometric one, tend to reject metal-poor stars. The only star with [Fe/H] < −1.0 in Salsi et al. (2020)’s sample is the well-known benchmark star HIP 76976 (HD 140283), part of GBS V1, which has [Fe/H] = −2.36 ± 0.10 in Paper IV.
We then searched for additional stars in the September 2021 version of JMDC available at the CDS which includes 2013 measurements of 1062 stars, a significant increase compared to the February 2020 version used by Salsi et al. (2020). In order to find stars in the appropriate range of atmospheric parameters, we used the PASTEL catalogue (Soubiran et al. 2016) and its recent version which provides mean atmospheric parameters for 14 181 FGK stars (Soubiran et al. 2022). We expect PASTEL to be complete for metal-poor stars brighter than V ~8.25, which is the limiting magnitude of FGK-type stars with an interferomet-ric measurement in JMDC. Among the ~500 stars in common between PASTEL and JMDC, we considered 63 additional stars to include in our sample, because they fill gaps in the AP space, and their interferometric angular diameters fulfil the criteria of Salsi et al. (2020).
The resulting list of selected candidates for GBS V3 includes 201 stars (the Sun is not considered here) They are all members of the HIPPARCOS catalogue (ESA 1997) and only the ten brightest ones are missing in Gaia DR3 (Gaia Collaboration 2016). We keep the Sun in the GBS V3 since it is an obvious benchmark star, although it is not observable in the same conditions as other stars. We do not discuss the Sun in the present paper, keeping its fundamental Teff and log 𝑔 determined in Paper I (we also note that a nominal value for the effective temperature of the Sun was adopted at the XXIXth IAU General Assembly, see Mamajek et al. 2015; Prša et al. 2016).
In the following, metallicities [Fe/H] are needed for the determination of Fbol from SEDs (to initialise the minimisation process, see Sect. 3.4), and for the determination of masses from stellar evolutionary tracks (see Sect. 4.2). We have adopted [Fe/H] from the literature for the 201 stars, mainly from the PASTEL catalogue. For a sake of homogeneity, we have not adopted [Fe/H] from Papers III and V for stars in V1 and V2 because they are corrected from non-local thermodynamic equilibrium (NLTE) effects, while for all the other stars the literature values are assuming LTE. It is the purpose of the forthcoming Paper VIII to provide precise and homogeneous abundances of Fe and other elements. This will imply some iterations to get the recommended Teff and log 𝑔 of our targets.
3 Fundamental effective temperature
The luminosity L, the radius R, and the effective temperature Teff of a given star are linked through the fundamental relation 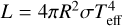 , where σ is the Stefan–Boltzmann constant. The fundamental relation can be expressed in a way that gives Teff as a function of the limb-darkened angular diameter θLD and the bolometric flux Fbol which are measurable quantities:
, where σ is the Stefan–Boltzmann constant. The fundamental relation can be expressed in a way that gives Teff as a function of the limb-darkened angular diameter θLD and the bolometric flux Fbol which are measurable quantities:
where θLD is in milliarcseconds (mas) and Fbol in 10−8 erg s−1 cm−2 or 10−11 W m−2.
In the following subsections we describe our compilation of measured angular diameters and fluxes. The fluxes were used to compute Fbol by means of SED fitting. Subsequently, Eq. (1) was used to obtain Teff for the selected stars.
3.1 Compilation of angular diameters
As explained in Sect. 2, the selection of GBS V3 stars was mainly based on the JMDC which provides one or several values of θLD for each star. In particular, we considered the 106 targets that Salsi et al. (2020) used as calibration stars to define precise surface brightness–colour relations. Salsi et al. (2020) applied interferometric criteria to remove non reliable values of θLD in the JMDC. They rejected measurements with a relative uncertainty on the angular diameter larger than 8%, and those based on observations in the 8–13 micron band or having a bad observation quality and/or a poor spatial frequency coverage in the visibility curve. They also rejected stars with inconsistent redundancies. We adopted their selected values of θLD for the 106 stars. For HIP 112748 and HIP 54539, provided with two values of θLD differing by less than 1%, we adopted the one with the lowest uncertainty.
For the remaining stars, we queried JMDC and the recent literature in order to retrieve the latest values of θLD fulfilling the interferometric criteria applied by Salsi et al. (2020). When provided we inspected the visibility curves to evaluate the reliability of the measurement.
We found recent and precise θLD for ten of the GBS V1 and V2. In particular, for three of the metal-poor benchmark stars new measurements are available, for HD 103095 (HIP 57939) and HD 122563 (HIP 68594) by Karovicova et al. (2020), and for HD 140283 (HIP 76976) by Karovicova et al. (2018). The two components of the binary α Cen were remeasured by Kervella et al. (2017), while four other targets were found in Baines et al. (2018, 2021). Among the six stars which had no direct θLD in Paper I, only one (HIP 48455, µ Leo) was observed in interfer-ometry by Baines et al. (2018). Among the five metal-poor stars from Paper V with indirect values of θLD, one (HIP 92167) was observed by Karovicova et al. (2020). Thus, we are left with nine stars from V1 and V2 that are still without any direct measurement of θLD. We keep them in a separate table for continuity of the samples, but we do not consider them as GBS anymore.
The final version of the GBS V3 includes 192 stars with a direct measurement of θLD. For each we provide the limb darkened angular diameter with its uncertainty and the corresponding reference in Table A.1 and in the catalogue available at the CDS. The sample includes stars with small angular diameters such as HIP 97527 (θLD = 0.231 ± 0.006 mas) and HIP 93427 (θLD = 0.289 ± 0.006 mas), both of which are asteroseismic targets observed with the CHARA/PAVO instrument by Huber et al. (2012). The sample also includes Aldebaran (HIP 21421) and Arcturus (HIP 69673) which have angulardiameters as large as ~20 mas. The median angular diameter of the sample is 1.12 mas.
The relative θLD uncertainties range from 0.1% (HIP 87808) to 7% (HIP 25993) with a median value of 1.1% (see histogram in Fig. 1). Two other stars have relative uncertainties larger than 5%, HIP 7294 and HIP 14838. In absolute values, the largest uncertainties occur for the two giants ψ Phe (HIP 8837) and Arc-turus (HIP 69673), with θLD = 8.0 ± 0.2 mas and θLD = 21.0 ± 0.21 mas, respectively. The two stars do not seem to have been re-observed recently, so that their θLD is still that of Paper I.
We note that, for a small fraction of stars, we had to make a choice between the two or more values of θLD fulfilling the adopted quality criteria. As shown in Fig. 2, several small diameters (typically θLD < 1.5 mas) disagree by more than 10%, but in general the agreement is at the 2σ level. We note three stars with estimations of their angular diameters differing by more than 3σ: HIP 96441, HIP 57939, HIP 108870.
HIP 96441 has three values of θLD reported in the JMDC, that fulfil the interferometric criteria of Salsi et al. (2020): 0.861 ± 0.015 mas in the K band (Boyajian et al. 2012a), 0.753 ± 0.009 mas in the R band (White et al. 2013) and 0.749 ± 0.007 mas in the H band (Ligi et al. 2016). The first determination is not compatible with the two others, but Boyajian et al. (2013) mention a calibration problem and discarded this star. Between the two other values we adopted the most recent one by Ligi et al. (2016).
HIP 57939 (HD 103095) is a well-known metal-poor dwarf studied by several authors. We adopted the latest determination, θLD = 0.593 ± 0.004 mas, by Karovicova et al. (2020) who used the combination of two instruments, VEGA and PAVO on the CHARA interferometer giving a high confidence to their result.
For HIP 108870 we adopted the value θLD = 1.758 ± 0.012 mas by Rains et al. (2020) which significantly differs from that previously reported by Kervella et al. (2004), θLD = 1.89 ± 0.02 mas. Rains et al. (2020) have analysed this discrepancy, considering that they obtained tighter constraints on the angular diameter by better resolving the star, thanks to the configuration now available at the VLTI.
These cases of disagreement also illustrate the inhomo-geneity of uncertainties listed in JMDC, which sometimes only reflect the precision of a fit, or also include systematic effects identified at the calibration level. The dispersion among measurements available for a given star is critical for small angular diameters, typically below ~ 1.5 mas, because it corresponds to discrepancies that can reach 10 to 15%. This illustrates the limitations of measuring interferometric diameters in the sub-mas regime. Some inhomogeneity can also arise from different recipes applied for the limb darkening correction. According to Eq. (1), a variation of 10% in θLD translates into a variation of 5% in Teff. Inversely, a 1% precision on Teff implies angular diameters obtained at the 2% level.
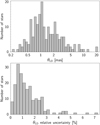 |
Fig. 1 Histogram of θLD (top panel) and its relative uncertainty (bottom panel) for the 192 GBS V3 stars having interferometric measurements. |
 |
Fig. 2 Difference between θLD adopted for this work and other values in JMDC fulfilling the selection criteria by Salsi et al. (2020). |
3.2 Compilation of magnitudes and fluxes
In order to build a SED for each star and measure the corresponding Fbol we compiled fluxes using the VOSA tool1 (Bayo et al. 2008). VOSA allowed us to collect all the photometry available in the Virtual Observatory (VO) for our list of 201 stars (including the nine stars from V1 and V2 with an indirect θLD) and to convert magnitudes into fluxes thanks to an exhaustive description of all the existing filters. We only kept the photometry from the VO catalogues that contain at least fifty of our targets, namely 2MASS (Cutri et al. 2003), AKARI (Yamamura et al. 2010), Gaia DR3 (Gaia Collaboration 2023c), GALEX (Bianchi et al. 2017), Strömgren photometric catalogues (Hauck & Mermilliod 1998; Paunzen 2015), Johnson UBV (Mermilliod 1987), IRAS (Neugebauer et al. 1984), HIPPARCOS (ESA 1997), Tycho-2 (Høg et al. 2000) and WISE (Cutri et al. 2021).
We note that the components of the bright binary star α Cen A and B are not resolved in the 2MASS catalog2, and the magnitudes given for α Cen A contain actually the combined flux of both components. We therefore used J, H, and K magnitudes from Engels et al. (1981), which are given for each component separately, and converted them to flux values using the VOSA tool.
An interesting new feature of the latest VOSA version (July 2022 update) is to provide synthetic photometry based on Gaia DR3 BP/RP spectra analysed with the GaiaXPy tool (De Angeli et al. 2023; Gaia Collaboration 2023b). We therefore collected through VOSA the synthetic photometry from Gaia which is provided in 13 passbands corresponding to the filters of the Hubble Space Telescope, Sloan Digital Sky Survey, PanSTARRS1 and Johnson UBVRI systems. Also from Gaia BP/RP spectra and GaiaXPy, VOSA computes fluxes in the 65 bands of the OAJ/J-PAS and OAJ/J-PLUS surveys. However we noticed that a small fraction of the Gaia synthetic photometry was affected by saturation, causing the corresponding SED to be deformed. We had to remove the Gaia spectrophometry, totally or partially, for about thirty bright stars with G ≃ 4. Finally we added to the compilation the fluxes in the range 320–1080 nm from the Pulkovo spectrophotometric catalogue (Alekseeva et al. 1996), adopting a homogeneous uncertainty of 1% for each value of flux (this value allowed us to give these data an appropriate weighting in our analysis). The Pulkovo catalogue provides 167 or 305 flux values, depending on the star. The details of the number of stars retrieved in each passband or catalogue are provided in Table 1. The number of flux values per star ranges from only 15 for HIP 14135 (α Cet) to 404 for HIP 7294 (χ Cas). The median number of fluxes per star is 101. Fluxes used for the determination of Fbol are available at the CDS.
An illustration of the obtained SEDs is given for two stars in Fig. 4 in Sect. 3.4. HIP 103598 is a K4 giant with a metallicity of −0.36 according to PASTEL, which has a well constrained SED thanks to Gaia and Pulkovo spectrophotometry. HIP 50564 is an F6 turn-off star with a metallicity of +0.10 according to PASTEL, having only broad-band photometric observations. We chose these stars to illustrate both the SED shape variations due to different temperatures, and the more or less good coverage of the SED depending on the availability of spectrophotometric data.
Passbands (VOSA designation) or catalogues with the corresponding number of stars having a valid value of flux (N).
3.3 Extinction
The extinction towards each of the 201 targets was estimated thanks to the recent 3D maps provided by Vergely et al. (2022), based on the inversion of large spectroscopic and photometric catalogues including Gaia DR3. We chose the closest map, covering a volume of 3 kpc × 3 kpc × 800 pc at a resolution of 10 pc, which is particularly well adapted for our sample of nearby stars.
The extinction is low for most of the stars (90% of them have AV < 0.05) which is not surprising owing to the small distances of the GBS V3 from the Sun. Our GBS span distances from 3 pc to 550 pc (deduced from parallaxes, see Sect. 4.1). Five giants have the highest extinction values, between 0.1 and 0.31 mag. As expected, AV is well correlated to the distance, as shown in Fig. 3.
3.4 SED fitting and bolometric fluxes
Although the observed fluxes compiled for the GBS cover a wide range of wavelength, some extrapolation of the SED is needed to integrate the full distribution and measure the total flux from the star received at the Earth, Fbol. To do so we followed the SED fitting method previously used by Creevey et al. (2015) and Ligi et al. (2016), based on the BASEL empirical library of spectra (Lejeune et al. 1997), a highly cited library in the astrophysi-cal community. Our choice for these models is based upon the work in Creevey et al. (2015) where one star was analysed in detail using different approaches and models. A 1% flux difference was found using the BASEL and PHOENIX libraries, with the former being in best agreement with other literature results using different methodologies.
The BASEL library covers the following parameter ranges: 3500 < Teff < 50 000 K, 0.00 < log 𝑔 < 5.00, and −5.0 < [M/H] < +1.0. It extends to 2000 K for a subset of the log 𝑔 and [M/H]. The wavelength range spans 9.1 to 160000 nm on a non-evenly sampled grid of 1221 points, with a mean resolution of 100 nm in the UV and 200 nm in the visible. Beyond 10 000 nm the resolution is 20 000 nm and to avoid issues with numerical integration we interpolate on a log scale before performing the integration. A Levenberg-Marquardt minimisation algorithm finds the optimal template that fits the observed flux points. Fbol is then calculated by integrating the optimal fitted spectrum. Recent improvements of the method include the weighting of the fluxes and the determination of Fbol uncertainties through Monte Carlo simulations.
The parameters of the model are the atmospheric parameters: Teff, log 𝑔, [Fe/H], the extinction, and the scaling factor (stellar radius scaled according to the distance). We used the atmospheric parameters from PASTEL to initialise the minimisation and the extinction from Sect. 3.3. To account for extinction in our method we implemented the IDL routine ccm_unred3 which dereddens theoretical fluxes, and requires colour excess on input. To convert extinction to colour excess we adopted R0 = 3.1. Most of these stars are nearby and as such have little or no extinction. In order to be complete in our analysis, in the catalogue available at the CDS we also provide Fbol for the full sample of stars by assuming zero extinction. Note that for stars with extinction close to 0 mag, the fitted Fbol is not necessarily smaller when assuming AV = 0.0 mag, because AV impacts the shape more than the height of the SED over the full spectral range.
All of the above parameters can be fitted, but in practice due to degeneracies between the parameters, the Teff and the scaling factor are the only free parameters, while log 𝑔, [Fe/H], and the extinction are fixed each time a minimisation is performed. In order to include the impact of the uncertainties of the parameters log 𝑔 and [Fe/H], and of the fluxes, we performed a bootstrapped-based method where we (a) perturbed these parameters by their uncertainty multiplied by a random number drawn from a Gaussian distribution, and (b) perturbed the fluxes by their uncertainties using the same approach. These simulations were done 400 times where 400 was a balance between computing time and having a significant sample size (the results with 200 simulations were equivalent within the uncertainties and the standard deviation of the 400 simulations reproduced the uncertainties of the atmospheric parameters). For the fitted parameters, the result is a distribution of stellar parameters that fit the observational data, and from these fitted parameters we integrated the corresponding semi-empirical flux distribution. We therefore obtained a distribution of Fbol for each star, and from these distributions we calculated the medians and the symmetric 68% confidence intervals, and report half of the latter as the uncertainty.
Two examples of the data and the best-fitted model SED are shown in Fig. 4, left and right panels. The left is an example ofa star with many observational points (in this case HIP 103598), while the right panel shows an example where relatively few data points are available; in this case HIP 50564. The lower panels show the distribution of the fitted Fbol and the individual χ2 values from the 400 Monte Carlo simulations, along with the value of the adopted median and 16 and 84 percentile confidence levels (dashed lines). We defined the uncertainty as the half of the distance between the upper and lower confidence levels.
The distribution of Fbol and relative uncertainties is shown in Fig. 5. The histogram of uncertainties shows a clear peak in the first bin corresponding to uncertainties lower than 0.5%. The relative uncertainties have a median value of 1.4%, and they are lower than 10% except for two stars, namely HIP 8837 (ψ Phe) and HIP 14135 (α Cet). These two M giants combine a low Teff and a lack of spectrophotometric data which make their SED poorly constrained, resulting in a relative uncertainty of about 21% and 18%, respectively. They had uncertain Fbol in Paper I as well. We note that the stars with uncertainties larger than 4% have their SED made of broad-band photometry only, while the majority of stars have spectrophotometry from Gaia and/or Pulkovo, resulting in a very precise Fbol determination.
In this procedure to determine Fbol, we use log 𝑔 and metal-licity from the PASTEL catalogue, a compilation of literature work. We have evaluated the impact of not knowing precisely these parameters. To do so, we made two tests. One test is to adopt a large uncertainty of 0.15 on both log 𝑔 and [Fe/H] inducing a different distribution of the fitted Fbol from the 400 Monte Carlo simulations. The other test is to change the literature values of log 𝑔 and [Fe/H] by an amount of 0.15 dex, in the eight possible configurations, for seven stars selected to cover the parameter space. In this test, the largest effect (<1%) is reached when adding 0.15 dex to [Fe/H] for the hottest stars. Varying log 𝑔 has more of an effect on the coolest stars. When combining the variations of log 𝑔 and [Fe/H] the effect remains at the level of 1% for the coolest and the hottest stars. Interestingly the most metal-poor star chosen for that test, HIP 48152, is less affected by a change of log 𝑔 and [Fe/H]. In the other test, enlarging the log 𝑔 and [Fe/H] uncertainties in the Monte Carlo simulations also has a low impact on the derived value of Fbol. We note four stars with Fbol changed by 1–2%, while 90% of the sample changes by less than 0.5%. We conclude that our procedure weakly depends on the input values of log 𝑔 and [Fe/H]. A change of 1% in Fbol induces a change of 0.2% on Teff. However a more rigorous treatment will be performed through iterations once the spectroscopic analysis of the targets will be performed to derive [Fe/H] homogeneously (Paper VIII, in prep.). This will lead to self-consistent parameters.
In Paper I, the Fbol values of the V1 stars were compiled from the literature and therefore not as homogeneous as here. This is another important improvement of the GBS V3, in addition to the larger number of stars. We still have a good agreement between V1 and V3, with a slight offset of 1.4%, and a typical dispersion of 2.1% (median absolute deviation, MAD).
Our approach is similar to that of Boyajian et al. (2013) and Baines et al. (2018) who collected broadband photometric measurements available in the literature, extended by spectrophotometry when available. They also applied the SED fitting method with reference templates taken from the library of Pickles (1998) which is made of observed spectra, whereas we used a hybrid library of synthetic stellar spectra calibrated from observations (Lejeune et al. 1997). Another difference comes from the Gaia spectrophotometry recently made available, which constrains very well the SED shape in the optical range. We have 66 stars in common with Boyajian et al. (2013) and 24 with Baines et al. (2018). The Fbol comparison is shown in Fig. 6. The agreement with Boyajian et al. (2013) is very good, with differences within 10%. On average our Fbol values are higher than their values by 3.3%, with a typical dispersion of 2.5% (MAD). The offset does not seem correlated with extinction which is lower than 0.03 mag for the stars in common according to our estimations, and that they have not considered given the close distance of the stars. It is likely that the small offset observed between our Fbol determinations and those of Boyajian et al. (2013) is related to their use of magnitudes from photometric catalogues, with a maximum of 17 values per star and fewer than 12 values in most cases, while we have typically ten times more flux values, mostly from Gaia spectrophotometry, providing SEDs of better quality. In addition they did not take photometric uncertainties into account for the fit, while we do. Baines et al. (2018) determine a high extinction for some stars which seems correlated with a larger positive offset. HIP 47431 and HIP 90344 are the most extreme cases with AV = 0.7 mag and AV = 0.54 mag respectively in Baines et al. (2018) while we get AV = 0.02 mag and AV = 0.03 mag from the 3D maps of Vergely et al. (2022), leading to a difference of 50% and 37% on Fbol (HIP 47431 is not shown in Fig. 6). Considering the 24 stars in common, Baines et al. (2018) find Fbol higher than us by 7.6% (median) with a dispersion of 6.6% (MAD).
We also compared our Fbol determinations to those of González Hernández & Bonifacio (2009) who implemented the infrared flux method (IRFM) based on 2MASS magnitudes (see Fig. 6). The 61 stars in common generally agree well with an offset less than 1% and a dispersion of 3.9% (MAD). The extinction is low for the majority of these nearby stars.
Finally, we also made a comparison with the catalogue of empirical bolometric fluxes and angular diameters of 1.6 million Tycho-2 stars built by Stevens et al. (2017) which has 119 stars in common with us. This work is based on the flux-colour relations of Casagrande et al. (2010) with Teff and AV being determined separately in an iterative way. Their Fbol are globally larger than ours by 4.9%, with a dispersion of 7.5% (MAD). Similarly to the tendency observed in the comparison with Baines et al. (2018), the larger differences correspond to stars with the largest values of AV in Stevens et al. (2017) which significantly differ from our lower extinctions. Eight stars do not appear in Fig. 6, given their difference larger than 50%, up to 360% for HIP 112731 and HIP 96837. They are found highly reddened by Stevens et al. (2017) with AV ≥ 0.6 mag, up to more than 2 mag for the two most extreme stars HIP 112731 and HIP 96837. We therefore suspect that some extinctions are overestimated by Stevens et al. (2017) and Baines et al. (2018), leading to overestimated bolometric fluxes.
 |
Fig. 3 Extinction AV deduced from 3D maps of Vergely et al. (2022) as a function of distance, for the 201 targets. |
 |
Fig. 4 Example of fits of the observed (reddened) data to the (reddened) semi-empirical spectra for HIP 103598 (left) and HIP 50564 (right). The bolometric flux is calculated by integrating the un-reddened spectrum. The bottom panels illustrate the distribution of |
 |
Fig. 5 Histogram of Fbol (top panel) and its relative uncertainties (bottom panel). |
 |
Fig. 6 Comparison of Fbol obtained in this work with literature. The colour code relates to the extinction. Several extreme outliers are out of the figure boundaries but they are discussed in the text. |
Median difference (MED) and median absolute deviation (MAD) between direct determinations of Teff from the literature and our values (literature minus this work), for N stars in common.
3.5 Assessment of Teff
We computed the fundamental Teff of each star by applying Eq. (1) with the values of θLD and Fbol obtained as described above. Teff uncertainties were deduced by propagating the θLD and Fbol uncertainties in Eq. (1). We consider here the 192 stars with a direct value of θLD. The resulting uncertainties on Teff span 5 K to 183 K, with a median value of 43 K (see histogram in Fig. 7). Only four giants present a relative uncertainty larger than 3% (absolute uncertainty larger than 150 K): the two M giants HIP 8837 (ψ Phe) and HIP 14135 (α Cet) previously mentioned for their large Fbol uncertainty resulting in Teff uncertainties of ~5%, and the K giants HIP 25993 and HIP 14838 previously mentioned for their large uncertainty on θLD resulting in Teff uncertainties of ~3.5%. These four stars clearly stand as outliers in Fig. 8 which shows how the relative uncertainties on θLD and Fbol propagate on Teff. In order to reach a 1% accuracy on Teff one should restrict the sample to stars with measurements better than 2% in θLD and 4% in Fbol. We have 127 stars fulfilling this condition, while 179 of the 192 stars have Teff uncertainties better than 2%.
In Fig. 9, we compare our values of Teff to other direct determinations from the literature, including those in Paper I. The values of offset (median difference) and dispersion (MAD) are given in Table 2. The dispersion is remarkably low (MAD ≃ 30 K) for the comparison to Paper I and Karovicova et al. (2020, 2022a,b), our determinations being larger by 26 K and 39 K respectively. The agreement is therefore at the 1% level in general. The two outliers in the comparison to Paper I (upper left panel of Fig. 9) are the metal-poor benchmark stars HIP 57939 and HIP 76976 (HD 103095 and HD 140283). Our new Teff values are about 400 K and 250 K higher than in Paper I, where their sub-mas angular diameters were quoted as very uncertain. Both stars have been remeasured by Karovicova et al. (2018, 2020) leading to more precise θLD and higher Teff. Our determination for HD 103095 (Teff = 5235 ± 18 K) is larger by 61 K than that of Karovicova et al. (2020). Since we use their determination of θLD, the difference is only due to Fbol. As noted in Sect. 3.1, the angular diameter of HD 103095 measured by Karovicova et al. (2020) from the combination of two instruments is very reliable. For HD 140283 we find Teff = 5788 ± 45 K, lower by 4 K than their value. Three other stars differ by 2– 3% from Paper I: ψ Phe, 61 Cyg B, and γ Sge. Only γ Sge has a new angular diameter measured by Baines et al. (2021), while for the other ones we used the same θLD as in Paper I, indicating that the difference comes from the new determination of Fbol, which we expect to be more accurate than the previous determination.
Table 2 and Fig. 9 exhibit larger discrepancies in the comparison to Boyajian et al. (2013) with an offset of 59 K and a scatter of 58 K. We note that we have 66 stars in common but 82 measurements since Boyajian et al. (2013) provide a compilation of their own θLD together with other values from the literature (we removed discrepant values quoted by them for HD 146233 and HD 185395). Among the stars that differ by more than 300 K, we have again HD 103095 which is the largest outlier. As explained above, the recent θLD determination by Karovicova et al. (2020) gives a higher Teff which is in better agreement with our value for that star. For HIP 61317 Boyajian et al. (2013) give two values of Teff, only one being in significant disagreement with ours. For HIP 89348 our values of Fbol and θLD (the latter adopted from Ligi et al. 2016) are larger and smaller, respectively, by ~ 10% than those of Boyajian et al. (2013), resulting in a significantly different Teff. Our value of Teff = 6569 ± 69 K seems however more consistent with spectroscopic values listed in the PASTEL catalogue than their lower value of Teff = 6221 ± 39 K.
The comparison to van Belle et al. (2021) gives an offset of 61 K, this time our values being lower, with a dispersion of 77 K. This relies on 17 giants in common. These large differences could partly be due to disagreement in extinction values for some stars. We note four stars (HIP 7607, HIP 111944, HIP 74666, HIP 3031) that van Belle et al. (2021) found significantly reddened (AV from about 0.15 to 0.30 mag) while our AV determinations are below 0.05 mag. This possibly explains the Teff differences from 150 K to 220 K. On the other hand, HIP 22453 has AV = 0.36 mag in van Belle et al. (2021) and AV = 0.08 mag in our work, but the Teff difference is only 31 K.
We note that we use the same determination of angular diameter as in the literature for some of the stars. Hence, the comparison data sets are not completely independent from ours.
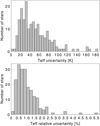 |
Fig. 7 Histogram of Teff absolute (top panel) and relative (bottom panel) uncertainty. The four outliers with Teff uncertainty larger than 150 K (or 3%) are discussed in the text. |
 |
Fig. 8 Propagation of θLD and Fbol relative uncertainties on Teff. |
4 Surface gravity
We determined the surface gravity log 𝑔 with the fundamental relation expressed as:
where M/M⊙ and R/R⊙ are the mass and radius of the star in solar units. For the Sun, we adopt for the surface gravity log 𝑔⊙ = 4.4380 ± 0.0002 dex4 determined in Paper I. The linear radius of each star is deduced from its angular diameter (see Sect. 3.1) and its distance is inferred from its parallax (see below). Masses, which cannot be directly measured, are estimated from evolutionary tracks, using our fundamental Teff, luminosities (from Fbol and parallaxes), radii (from θLD and parallaxes) and metallicities from the literature as input. We consider in this section the full sample of 201 GBS V3, including the nine stars with an indirect θLD.
 |
Fig. 9 Comparison of our fundamental determinations of Teff with other fundamental determinations from the literature in Paper I and Boyajian et al. (2013); Karovicova et al. (2020, 2022a,b); van Belle et al. (2021). |
 |
Fig. 10 Distribution of parallax relative uncertainties versus HIPPARCOS magnitudes for the GBS V3 sample. Parallaxes are mainly from Gaia DR3, but from HIPPARCOS for 8 stars (open squares), and from Akeson et al. (2021) for α Cen A & B (filled squares). |
4.1 Parallaxes, linear radii, and luminosities
The parallax of the stars is needed to convert their angular diameter into linear radius, and their bolometric flux into luminosity. All the targets have a HIPPARCOS parallax, and the majority of them have also an even more precise and accurate Gaia DR3 parallax. Only four stars have a Gaia parallax with an uncertainty larger than 3%, the largest value being 6% for HIP 55219. The ten brightest stars not in Gaia DR3 have a precision of their HIPPARCOS parallax better than 3.5%. For α Cen A & B (HIP 71683 and HIP 71681) we adopt the high precision determination by Akeson et al. (2021) instead of the HIPPARCOS one. Figure 10 shows the distribution of the parallax relative uncertainties as a function of the HIPPARCOS magnitude Hp. The four faintest stars with Hp > 8 mag have an indirect θLD. We applied the zero-point correction derived by Lindegren et al. (2021) to the Gaia parallaxes when applicable, that is for G > 6.
With parallaxes π and θLD we computed linear radii R and their uncertainties, while we used parallaxes and Fbol to compute luminosities L and their uncertainties. Adopting the solar radius and luminosity from the 2015 B3 IAU resolution5 the equations are:
with θLD and π expressed in mas, and Fbol in 10−8 erg s−1 cm−2.
The radii of the GBS V3 span 0.6 to ~140 R⊙ (see Fig. 11). The luminosities span 0.08 to nearly 6000 L⊙ (see Fig. 12).
Solar-like oscillations provide robust constraints to the radius of G and K dwarfs and giants (Chaplin & Miglio 2013), giving us an opportunity to compare our determinations with others obtained in a different way. We estimated seismic radii using the following scaling relation (e.g. Miglio 2012) when the asteroseismic parameters, the so-called large frequency separation ∆v and the frequency of maximum oscillation power vmax, were available:
where we adopt the fundamental Teff determined in Sect. 3 and the solar parameters as in Paper I: ∆v⊙ = 135.229 ± 0.003 µHz, vmax,⊙ = 3160 ± 40 µHz, Teff,⊙ = 5771 ± 1 K. We have compiled ∆v and vmax from the literature and found determinations of both parameters for 37 stars. The comparison is shown in Fig. 13. There is a small systematic offset, the fundamental radii being larger than the seismic ones by 0.7%, with a typical dispersion (MAD) of 3.3%. Several stars show discrepancies larger than 10%, up to 22% for HIP 92984. There is however an ambiguity about the seismic parameters of HIP 92984, measured by Mosser et al. (2009) from CoRoT observations, because Huber et al. (2012) did not detect solar-like oscillations. The other discrepant stars have error bars that still give an agreement at the 3σ level. We also note that Sharma et al. (2016) and Hon et al. (2022) proposed some corrections to the scaling relations to obtain a better agreement for giants. It is however out of the scope of this paper to apply such corrections. We retain from this comparison the general good agreement, with no systematics, between our values and seismic ones, at the level of ~4%.
Figure 14 shows our derived luminosities compared to those available for 36 stars in the Gaia DR3 Golden Sample of Astrophysical parameters for FGKM stars (Gaia Collaboration 2023a). Gaia luminosities were computed from the parallax, the G magnitude and a bolometric correction (Creevey et al. 2023) and are therefore different from our determinations, although not completely independent. The bolometric corrections depend on the atmospheric parameters in DR3 and could contribute to some differences that we find. The three most luminous stars in common are found brighter by Gaia by more than 10%, up to 30% for HIP 70791, known as a horizontal branch star. Only that star shows a discrepancy significantly larger than 3σ. We note six other stars with Gaia luminosities significantly larger than our values, with differences ranging from 5% to 10%. These discrepancies cannot be explained by the extinction that we find negligible for these nine stars. For the other stars, we find luminosities slightly larger than those from Gaia, by 0.35% (median), with a typical dispersion of 0.9% (MAD).
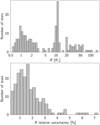 |
Fig. 11 Histogram of linear radii R (top panel) and their relative uncertainty (bottom panel). |
 |
Fig. 12 Histogram of luminosities L (top panel) and their relative uncertainty (bottom panel). |
 |
Fig. 13 Linear radius difference between our determination of R from Eq. (3), and seismic estimations from Eq. (5). |
 |
Fig. 14 Luminosity difference between our determinations L from Fbol and distance, and Gaia DR3 estimations based on G magnitudes and bolometric corrections for 36 stars in common in the Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a). |
4.2 Masses
Masses were computed with the SPInS code (Lebreton & Reese 2020) implemented with the stellar evolutionary tracks from BaSTI (Pietrinferni et al. 2004, 2006), and from STAREVOL (Lagarde et al. 2012, 2017). We implemented the two grids in order to make comparisons owing to the different behaviour of the tracks in some parts of the HR-diagram (HRD), such as the clump. The determination of log 𝑔 is less accurate at clump luminosity (logg ≃ 2.2) because this is a point in the HR diagram where the evolutionary tracks of different masses and [Fe/H] overlap. In the following, we detail the main differences between these two grids that may have an impact on the position on the HRD and thus on the mass determination with SPInS.
For BaSTI, we use stellar tracks coming from the non-canonical grid covering a mass range between 0.5 M⊙ and 10.0 M⊙ and a metallicity range [Fe/H] ∈ [−2.27, +0.40] without α-enhancement. This grid takes into account core convective overshooting during the H-burning phase. The overshoot parameter is set to 0.2 for a stellar mass higher than 1.7 M⊙, no overshooting is considered for a mass lower than 1.1 M⊙, and a linear variation is assumed in-between. The solar mixture comes from Grevesse et al. (1993). We tried the α-enhanced tracks ([α/Fe] = +0.4) for metal-poor stars ([Fe/H]< −0.70 dex) leading to masses higher by 30% on average. However, as explained later, we got a wrong mass for µ Cas, the only metal-poor binary with a reliable dynamical mass. This convinced us to adopt the tracks without α-enhancement for the whole sample.
For STAREVOL, the stellar grid covers a mass range between 0.6 and 6.0 M⊙ and a metallicity range [Fe/H] ∈ [−2.14, +0.51] without α-enhancement, with the exception of [Fe/H] = −2.14 and −1.2 where [α/Fe] = +0.3. Except for convection, additional mixing effects such as rotation-induced mixing are not taken into account. The overshoot parameter is set to 0.05 or 0.10 for stars with masses below or above 2.0 M⊙, respectively; no overshooting is considered for masses lower than 1.1 M⊙. The stellar grid is constructed using the solar mixture coming from Asplund et al. (2009).
The Kroupa initial mass function (Kroupa 2001; Kroupa et al. 2013, IMF) was used as a prior, as well as a truncated uniform star formation rate between 0 and 13.8 Gyr, that is, roughly the age of the Universe. The stellar properties used as an input to SPInS are: (1) our fundamental Teff determinations (Sect. 3); (2) luminosities deduced from Fbol and parallaxes; (3) metallicities from the literature, and (4) radii deduced from θLD and parallaxes. Radii are not independent of Teff and luminosities, but still add a useful constraint to the mass since the correlations are lost in the way we determined the three parameters. The resulting masses and their uncertainties are shown in Fig. 15. Most of the stars have masses < 2 M⊙ but STAREVOL finds more stars in the range 2–2.5 M⊙ than BaSTI. STAREVOL gives a more extended distribution of relative uncertainties with fewer very low values, and five stars within 30–55%.
For the validation of the mass determination, we compared the SPInS results to other determinations. This includes dynamical masses of binary stars, seismic masses, as well as mass determinations based on evolutionary tracks and methods different from those we used.
Dynamical masses are available for four stars, µ Cas, α Cen A & B, and Procyon. We did not consider 61 Cyg A & B since their masses are not well established (Kervella et al. 2022). The comparison to SPInS masses is shown in Fig. 16. The orbit of the binary α Cen has been studied by Akeson et al. (2021) who determined masses of 1.0788 ± 0.0029 M⊙ and 0.9092 ± 0.0025 M⊙ for the A (HIP 71683) and B (HIP 71681) components, respectively. The agreement is at the 0.4% level for the STAREVOL mass and 3.4% for the BaSTI mass, for the component A. Both sets of evolutionary tracks give masses that differ by 5% for the B component, in opposite directions. The dynamical mass of the metal-poor ([Fe/H] = −0.83 dex) visual binary µ Cas (HIP 5336) results from an astrometric study with the Hubble Space Telescope by Bond et al. (2020) who determined a value of 0.7440 + 0.0122 M⊙. BaSTI and STAREVOL underestimate it by 4% and 1.3% respectively. Running SPInS with the α-enhanced BaSTI tracks ([α/Fe] = +0.4) for that star led to an overestimation of its mass by 32%. This convinced us not to adopt the α-enhanced tracks for metal-poor stars. Hence, we have opted to exclusively rely on the BaSTI tracks that do not incorporate any alpha-enrichment. This underscores the importance of presenting mass values obtained from both BaSTI and STAREVOL tracks, since it offers an understanding of the inherent errors linked to relying solely on a single stellar evolution model. The orbit of Procyon (HIP 37279) based on Hubble Space Telescope astrometry (Bond et al. 2015, 2018), yields a dynamical mass of 1.478 ± 0.012 M⊙. The BaSTI mass differs by 0.9% while the STAREVOL mass is lower by 2.6%. There is therefore a satisfactory agreement between the SPInS masses and the dynamical masses for these four stars, whatever the set of evolutionary tracks, considering the few constraints we use with the models, and given the inherent model assumptions of, for example, the chemical enrichment law which constrain the position of the tracks in the HRD.
We estimated seismic masses using the following scaling relation (e.g. Miglio 2012) for the 37 stars having a determination of the asteroseismic parameter ∆v available in the literature (see Sect. 4.1 for the solar values)
where R is the linear radius computed in Sect. 4.1. The resulting comparison is shown in Fig. 17. Although the agreement between SPInS and seismic masses is good in general in the range 1–1.5 M⊙, there is a trend in the sense that SPInS tends to overestimate masses smaller than 1 M⊙ and to underestimate those larger than 1.5 M⊙. This is true for both sets of evolutionary tracks, with more outliers with STAREVOL. However, seismic masses may not necessarily be more accurate than those deduced from evolutionary tracks, given that the range of validity of the scaling relation is not yet clear (e.g. Sharma et al. 2016).
We also compared the two sets of SPInS masses to masses from the literature, based on different evolutionary tracks and methods. Figure 18 shows comparisons to masses from Paper I, Baines et al. (2018) and Boyajian et al. (2013). In Paper I masses were determined by visual interpolation in two grids, the Padova grid (Bertelli et al. 2008, 2009) and the Yonsei-Yale grid (Yi et al. 2003; Demarque et al. 2004), the adopted value being the average of the two. Baines et al. (2018) used a Bayesian method with the PARSEC isochrones developed by da Silva et al. (2006); Bressan et al. (2012). Boyajian et al. (2013) used the Yonsei-Yale isochrones. The resulting comparisons reflect the nature of the stars in common, with a good agreement for dwarfs and a large dispersion for giants. A larger dispersion is expected for giants, in particular at the clump, because of the overlap of the evolutionary tracks of different masses and [Fe/H]. Degeneracies in evolutionary tracks of evolved stars can also lead to different masses for a giant depending on whether it is on the red-giant branch or on the horizontal branch. The sample of Boyajian et al. (2013) is made of dwarfs and exhibits a small dispersion, despite a few outliers with STAREVOL. The sample of Baines et al. (2018) is mostly made of giants and exhibits a large dispersion, while GBS V1 are a mixture of dwarfs and giants.
Figure 19 shows our derived masses compared to those available for 30 stars in the Gaia DR3 Golden Sample of Astrophysical parameters for FGKM stars (Gaia Collaboration 2023a). Gaia masses were derived by comparing Gaia photometric effective temperatures and Gaia luminosities to BaSTI solar metallicity stellar evolution models (Hidalgo et al. 2018; Creevey et al. 2023), and are therefore similar to our determinations. We find an excellent agreement between our two sets of masses and the Gaia ones, except for the three stars in common with the highest masses (≳1.5 M⊙), and one outlier within the STAREVOL set.
From the above comparisons, there is no strong evidence that one set of evolutionary tracks is better than the other one. Therefore, we provide the two masses and their uncertainties in the catalogue available at the CDS.
In this procedure to determine masses we need metallicities as input for SPInS. We have used [Fe/H] values from the literature which are not homogeneous and therefore we have evaluated their impact on the resulting masses. We made two tests similar to those made for Fbol. One test is to adopt a large uncertainty of 0.15 on [Fe/H] for all the stars, much larger than the original ones. The other test is to add or subtract 0.15 dex to the literature values of [Fe/H] for seven stars selected to cover the parameter space. Enlarging the metallicity uncertainty to 0.15 dex affects mainly the clump giants. Based on the BASTI tracks, only five stars in our sample have their mass affected by more than 30%, and only eight stars if we consider the STAREVOL tracks. The most critical stars are not common from one set to the other. This reinforces the interest of considering the masses computed by the two sets of stellar evolution models. Such differences could be explained by different inputs in the computation of the evolutionary tracks (e.g. mass loss, atmosphere models, etc.) which change the position in the HRD. It should be noted that at least 90% of the stars in our sample experience a mass variation less than 10%, while three quarters of the sample remain below 5%, whatever the set of stellar models taken into account. Changing the value of [Fe/H] by ± 0.15 dex for seven stars leads to a similar conclusion: the dwarfs are not affected, whatever their metallicity, while changes occur among giants. However, due to the dependency of log 𝑔 on the logarithm of mass in Eq. (2), in the worst cases where the mass is changed by 30%, the impact on log 𝑔 is limited to 0.11 dex and up to 0.5 dex for the most critical cases.
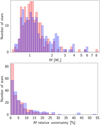 |
Fig. 15 Histogram of masses (top panel) and their relative uncertainty (bottom panel), red for BaSTI, blue for STAREVOL. |
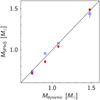 |
Fig. 16 Comparison of masses determined with SPInS (red dots for BaSTI, blue open squares for STAREVOL) to dynamical masses for µ Cas, α Cen B, α Cen A and Procyon, ordered by increasing mass. |
 |
Fig. 17 Comparison between masses from SPInS (red dots for BaSTI, blue open squares for STAREVOL) and seismic masses from Eq. (6). |
 |
Fig. 18 Comparison of masses determined with SPInS (red dots for BaSTI, blue open squares for STAREVOL) to those available in the literature, also based on evolutionary tracks. |
 |
Fig. 19 Comparison between masses from SPInS (red dots for BaSTI, blue open squares for STAREVOL) and masses from the Gaia Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a). |
4.3 Assessment of log 𝑔
We computed the fundamental log 𝑔 of each star by applying Eq. (2) with the values of mass from SPInS, with both evolutionary tracks BaSTI and STAREVOL, and the radius deduced from θLD, with the propagation of their uncertainties. We consider here the 201 stars of the sample. The resulting uncertainties on log 𝑔 span from 0.004 to 0.13 (BaSTI) and 0.23 dex (STAREVOL), with a median value of 0.02 dex. Figure 20 shows the comparison of log 𝑔 determinations, using the mass from SPInS with BaSTI or STAREVOL. The agreement is excellent for dwarfs with log 𝑔 > 4. Below that value, log 𝑔 from STAREVOL is systematically larger by 0.06 dex than log 𝑔 from BaSTI, with an exception around log 𝑔STAREVOL = 2.3.
Following the comparisons made in the previous sections, for radii and masses, we used the seismic data to determine log 𝑔 in another and independent way, through the relation that gives log 𝑔 as a function of the maximum of the power spectrum of oscillation frequencies, vmax, available for 42 stars, and the effective temperature:
The comparison of seismic and fundamental log 𝑔 is shown in Fig. 21. For dwarfs, typically log 𝑔seismic >3.8 dex, the agreement is very good except for one star, HIP 92984. For this star we find log 𝑔 = 4.48 dex with BaSTI and STAREVOL masses, while the seismic log 𝑔 is significantly lower, log 𝑔 = 4.23. We have pointed out the ambiguity about the seismic parameters of that star in the previous section. If this star is excluded, the differences between seismic and fundamental log 𝑔 of dwarfs have a MAD of 0.02 dex. For giant stars, the dispersion is larger (MAD = 0.07 dex), with log 𝑔 based on BaSTI lying slightly below the seismic values (median offset of −0.06 dex), while the log 𝑔 based on STAREVOL tend to lie above (median offset of 0.01 dex). A few outliers, reaching nearly 0.5 dex, correspond to stars with one of the two masses giving a disagreement with the seismic log 𝑔 but not the other one. From that comparison, we cannot say that the agreement is better with BaSTI or with STAREVOL masses.
We also compare our log 𝑔 determinations with those in Paper I and in Karovicova et al. (2020, 2022a,b) in Fig. 22. Offsets are negligible while dispersions (MAD) are 0.04 dex for Paper I, whatever the tracks. The values of log 𝑔 generally agree well within the error bars except for one star, HIP 37826 (Pollux), where the STAREVOL mass gives a discrepant log 𝑔. The dispersions are 0.02 and 0.04 dex, using masses from BaSTI and STAREVOL respectively, for Karovicova et al.’s determinations based on masses obtained with Dartmouth stellar evolution tracks (Dotter et al. 2008). There are two discrepant values with Karovicova et al.’s determinations: HIP 98269 with the BaSTI mass, HIP 70791 with the STAREVOL mass. We can draw similar conclusion as for the comparison to seismic log 𝑔: a better agreement with one or the other set of evolutionary tracks is not obvious. Therefore, since there is no strong argument to adopt masses from BaSTI instead of STAREVOL and vice versa, we compute the average of the two values as the final log 𝑔. This strategy allows us to mitigate some discrepancies among giants while it has no impact for most of the stars which have consistent masses whatever the used tracks.
The final log 𝑔 distribution and uncertainties are shown in Fig. 23. The bottom panel shows separately the uncertainties for dwarfs (log 𝑔 > 3.8) and giants (log 𝑔 ≤ 3.8), highlighting the lower precision obtained for giants. The median uncertainty is 0.02 dex for dwarfs and 0.06 dex for giants. While 90% of the dwarfs have an uncertainty lower than 0.05 dex, 90% of the giants have an uncertainty higher than 0.03 dex.
 |
Fig. 20 Comparison of log 𝑔 determinations, using masses from SPInS with BaSTI or STAREVOL. The area between the two dashed lines indicates an agreement within 0.1 dex. |
 |
Fig. 21 Comparison of our fundamental values of log 𝑔 to those determined from vmax and our fundamental Teff. Red dots for SPInS masses using BaSTI models, blue open squares for STAREVOL models. |
 |
Fig. 22 Comparison of our fundamental values of log 𝑔 to those determined in Paper I and by Karovicova et al. (2020, 2022a,b). Red dots for SPInS masses using BaSTI models, blue open squares for STAREVOL models. |
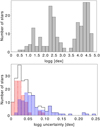 |
Fig. 23 Histogram of log 𝑔 (top panel) and uncertainty (bottom panel). The bottom panel shows the uncertainties for dwarfs (red) and giants (blue). |
5 The new set of Gaia FGK benchmark stars
The fundamental Teff and log 𝑔 determined for the 192 GBS V3 stars with a direct value of θLD are given in Table A.1 while the nine other stars from V1 and V2 with an indirect θLD are provided in Table 3. The metallicity from the literature is provided for convenience, but will be redetermined homogeneously in the coming Paper VIII. The full catalogue with all the other parameters determined in this work is available in VizieR.
The Kiel diagram with fundamental Teff and log 𝑔 is shown in Fig. 24 for the full sample of 192 stars and for a selection of the best stars, with an uncertainty on Teff and log 𝑔 better than 2% and 0.1 dex, respectively. This selection of 165 stars mainly rejects giants with large uncertainties, as discussed in Sect. 4, but still preserves a good distribution across the Kiel diagram.
The metallicity histogram of the GBS V3 is shown in Fig. 25, compared to that of V1 (only considering stars with a direct θLD), highlighting a number of new metal-poor stars. This is however more evident in the interval −1.0 < [Fe/H] < −0.5 than below [Fe/H] = −1.0. There were four stars in GBS V1 with −1.0 < [Fe/H] < −0.5, a number increased to 14 in GBS V3. Four giant stars with [Fe/H] < −1.0 were added, which doubles the V1 number of stars with [Fe/H] < −1.0. The fundamental Teff and log 𝑔 for these eight GBS V3 stars are presented in Table 4 together with the values from Paper I for the four stars in common.
One of the main purposes of the GBS is to calibrate or validate atmospheric parameters from spectroscopy. We therefore checked spectroscopic Teff and log 𝑔 available in different sources, using the subset of 165 most reliable GBS.
Figure 26 compares our fundamental determinations with those available in the PASTEL catalogue, based on high-resolution, high signal-to-noise spectroscopy. Overall, the agreement on Teff is good with a dispersion of MAD = 54 K and a slight offset of 12 K (median), the spectroscopic Teff being larger. Two extreme outliers have differences larger than 400 K. For HIP 86614 we suspect an uncertain angular diameter given its noisy squared visibility curve in Boyajian et al. (2012b) while for HIP 108535 the only spectroscopic Teff in PASTEL is dubious. For that star we note a good agreement with the determination by Prugniel et al. (2011) based on a medium resolution spectrum.
Concerning log 𝑔 we can see three regimes of precision, corresponding to dwarfs, clump giants, and cooler giants, with an increasing dispersion. The dispersion among dwarfs is 0.04 dex (MAD). It rises to 0.1 dex among clump giants (2.0 < log 𝑔 < 3.5) with no offset, while for red giants there is a tendency of spectroscopic log 𝑔 to be larger than the fundamental ones by 0.16 dex (median offset) with a significant dispersion of 0.2 dex (MAD). The GBS can therefore be used to better understand and correct the spectroscopic gravities of evolved stars.
Focusing on the best studied stars we selected in the PASTEL catalogue the stars which are included in at least 15 spectroscopic studies at high-resolution and high signal-to-noise ratio since 1990. The resulting 16 stars are all dwarfs or subgiants, with some of them also in common with Paper I. In general there is a good agreement, within our uncertainties and the standard deviation from the literature values. Three stars, HIP 14954, HIP 57939 and HIP 8159, exhibit a significant difference in Teff, larger than 150 K.
HIP 14954 (94 Cet) has been very much studied, with 41 spectroscopic determinations of Teff, likely because of its exoplanet discovered in 2000 (Queloz et al. 2001). The literature values range from 5916 K to 6424 K with a mean of 6176 K and a standard deviation of 84 K. Our determination is lower, Teff = 5912 ± 59 K, but still in agreement with the coolest spectroscopic determinations. Our fundamental value is in a very good agreement with that of Boyajian et al. (2013), Teff = 5916 ± 98 K, independent from ours since we use the angular diameter from Ligi et al. (2016). It would be important to better understand why spectroscopy gives a higher Teff for that star because it has implications on the parameters of its exoplanet.
HIP 8159 (109 Psc) also hosts an exoplanet and has several recent Teff from high-resolution spectroscopy ranging between 5560 K and 5711 K. The fundamental determinations, from Boyajian et al. (2013) and from us (Teff = 5438 ± 61 K) based on the same θLD, are cooler than the mean spectroscopic value by ~200 K. This discrepancy requires further investigation.
HIP 57939 (HD 103095) has 57 spectroscopic determinations of Teff after 1990, ranging from 4500 K to 5250 K with a mean of 5057 K and a standard deviation of 18 K. Our fundamental determination Teff = 5235 ± 18 K is in agreement with the hottest spectroscopic determinations, for example, by Luck & Heiter (2005).
We also checked atmospheric parameters massively determined by large spectroscopic surveys against our fundamental determinations of the best GBS. We considered APOGEE DR17 (Majewski et al. 2017; Abdurro’uf et al. 2022), the Gaia-ESO survey (Randich et al. 2022; Gilmore et al. 2022) and GALAH DR3 (Buder et al. 2021) in the comparisons shown in Fig. 27. Table 5 gives the median offsets and corresponding MAD for dwarfs and giants separately. Although GALAH and Gaia-ESO have less stars in common than APOGEE, we see the same trends in the three surveys. Their Teff and log 𝑔 for dwarfs are smaller on average than the fundamental ones, and vice-versa for the giants. These trends are worth to be investigated and better understood.
Finally we also assessed the photometric and spectroscopic Teff and log 𝑔 of the Gaia DR3 Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a) with the best GBS, as shown in Fig. 28. Photometric Teff are lower than fundamental ones by 58 K, while the offset of the spectroscopic Teff is negligible (6 K). For log 𝑔 there is an excellent agreement of the photometric values with median offset of −0.03 dex and a dispersion (MAD) of 0.06 dex. Spectroscopic log 𝑔, corrected as suggested by Recio-Blanco et al. (2023), are found smaller than the fundamental values by 0.06 dex, with a dispersion of 0.15 dex. These comparisons are based on 35 and 38 stars in common for the photometric and spectroscopic parameters respectively, mainly dwarfs.
 |
Fig. 24 Kiel diagram with fundamental Teff and log 𝑔. The colour scale is related to metallicities from the literature. The left panel shows the full sample of 192 stars while the right panel shows the stars with uncertainties on Teff and log 𝑔 better than 2% and 0.1 dex respectively. |
Teff and log 𝑔 determined in this work for stars from V1 and V2 with an indirect value of θLD.
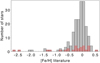 |
Fig. 25 Histogram of [Fe/H] for the 192 fundamental GBS V3 (grey) compared to the V1 version (red). |
Fundamental Teff and log 𝑔 for the eight GBS V3 with [Fe/H] < −1.0 (from the literature), and comparison to the Paper I values, when available.
 |
Fig. 26 Comparison of our fundamental values of Teff (top panel) and log 𝑔 (bottom panel) to spectroscopic ones available in the PASTEL catalogue. |
 |
Fig. 27 Comparison of Teff and log 𝑔 from this work with the spectroscopic ones in surveys: APOGEE DR17 (blue), Gaia-ESO (red), GALAH DR3 (green). |
Median difference (MED) and median absolute deviation (MAD) between our fundamental determinations of Teff and log 𝑔 and the spectroscopic ones from surveys (survey results minus our results), for N stars in common.
 |
Fig. 28 Comparison of Teff and log 𝑔 from this work with the photometric (red dots) and spectroscopic (blue squares) ones from the Gaia DR3 Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a). |
6 Conclusion
Large spectroscopic surveys usually calibrate or validate their determinations of atmospheric parameters using reference stars. Ideally they should adopt a common Teff and log 𝑔 scale in order to minimise systematic differences in abundances provided by different instruments and pipelines. The GBS are intended to provide such an anchor to the fundamental Teff and log 𝑔. GBS can also help one understand any shortcomings in the stellar models.
We have presented determinations of fundamental Teff and log 𝑔, based on the Stefan–Boltzmann law and Newton’s law of gravitation, for the third version of the GBS. Compared to the previous V1 and V2 versions, a significant improvement is the larger number of stars, 192 instead of ~40, resulting from our systematic search of high-quality angular diameters based on interferometric measurements. More accurate log 𝑔 were obtained thanks to the higher precision parallaxes that mostly come from Gaia DR3, while the improved Teff are in part a result of the homogenous photometric data from Gaia DR3, which feed into the Fbol determination. We note that Fbol are now more precise and homogeneous owing to the methodology of SED fitting applied to a combination of photometric and spectrophotometric data including measurements made on BP/RP spectra from Gaia DR3. Better Fbol also result from the adopted extinction values deduced from state-of-the-art 3D maps of the solar neighbourhood. The most difficult part comes from the determination of masses from evolutionary tracks. We have shown that using two different grids can lead to differences of up to more than 50% in masses, giving systematic offsets of about 0.06 dex in log 𝑔 among giants.
At each stage of the compilation and determination of the parameters, we evaluated the uncertainties that we aimed to keep at the 1–2% level. Our results were assessed by comparing them to other determinations of a similar accuracy available in the literature. In general, the comparison with literature data is satisfactory, with differences not exceeding 4%. We can explain most of the outliers. We also determined seismic radii, masses, and surface gravities for comparisons, using scaling relations and seismic parameters available for ~40 stars. They show a good agreement for dwarfs but a trend in masses outside the 1–1.5 M⊙ range. From the different comparisons, we are confident that our uncertainties in Teff are reliable. We reached the expected 1–2% level in Teff. For log 𝑔 only dwarfs have such a level of accuracy. Uncertainties for giants are larger and reflect the difficulty to obtain reliable masses for them from evolutionary tracks.
The Teff and log 𝑔 presented here will be updated. Two steps of our determination process, Fbol and masses, depend on [Fe/H] which we took from the literature. This is the subject of the upcoming paper VIII to determine abundances of the GBS-V3 from a large collection of high-quality spectra. Some iterations will be needed to adjust Teff, log 𝑔, and [Fe/H] in a self-consistent way. In the meantime, we have evaluated the impact of using non-homogeneous metallicities through tests in which we modified the values of [Fe/H] and uncertainties by 0.15 dex in input of the SED fitting and of SPInS. We found that it has a negligible impact on Teff, and also on log 𝑔 for most of the stars, although a few giants have their mass affected by more than 30% inducing a change of log 𝑔 by 0.11 to 0.5 dex.
In order to use the GBS V3 for calibration or validation of atmospheric parameters, we recommend that users select the 165 stars with uncertainties on Teff and log 𝑔 lower than 2% and 0.1 dex, respectively. We have used this subsample to assess Teff and log 𝑔 obtained by high-resolution and high signal-to-noise spectroscopy (PASTEL catalogue), by medium-resolution spectroscopy (APOGEE, GALAH, and Gaia-ESO surveys), and by Gaia photometry and spectroscopy. This has revealed some issues that need to be investigated to improve the future releases.
Due to the lack of metal-poor stars in the solar neighbourhood, the GBS V3 do not yet cover the metallicity range in a uniform way. We still lack angular diameters for stars with [Fe/H] < −1.0, which are important targets in galactic archeology and stellar physics. Interferometric measurements are still limited to stars brighter than V~8, and larger than θLD ≃ 0.2 mas. There are, however, metal-poor candidates that are bright and large enough to fulfil these criteria. They could be observed with powerful interferometers, such as the new SPICA instrument on the CHARA array (Mourard et al. 2022) expected to provide an estimation of the stellar radius of such stars to a 1% precision. It would also be useful to remeasure, either in part or entirely, the GBS with θLD < 1.2 mas, which show a large dispersion of the current measurements, exceeding the quoted uncertainties.
Acknowledgements
C.S., N.L., and L.C. acknowledge financial support from “Programme National de Physique Stellaire” (PNPS) and from the “Programme National Cosmology et Galaxies (PNCG)” of CNRS/INSU, France. C.S., P.J. and L.C. acknowledge financial support from the French-Chilean program of cooperation ECOS C18U02 (ECOS-ANID 180049). We acknowledge support from FONDECYT Regular grant 1231057, 1200703, and Millenium Nucleus ERIS NCN2021_017, Centros ANID Iniciativa Milenio. L.C. acknowledges the grant RYC2021-033762-I funded by MCIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR. U.H. acknowledges support from the Swedish National Space Agency (SNSA/Rymdstyrelsen). D.D.B.S. acknowledges financial support from Becas-ANID scholarship 21220843. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The preparation of this work has made extensive use of Topcat (Taylor 2005), of the Simbad and VizieR databases at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services. This publication makes use of VOSA, developed under the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/through grant PID2020-112949GB-I00. VOSA has been partially updated by using funding from the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement no. 776403 (EXOPLANETS-A). The Stellar Parameters INferred Systematically (SPInS) code is a spin-off of the Asteroseismic Inference on a Massive Scale (AIMS) project, one of the deliverables of the SpaceINN network, funded by the European Community’s Seventh Framework Programme (FP7/2007–2013) under grant agreement no. 312844. SPInS was initially created for the 5th International Young Astronomer School Scientific Exploitation of Gaia Data held in Paris, (26 February–2 March 2018), as a simple tool to estimate stellar ages, as well as other stellar properties.
Appendix A Table with Teff and log ɡ of the GBS V3
Fundamental Teff and log ɡ and their uncertainties determined in this work for the 192 GBS V3, with [Fe/H] from the literature and the θLD adopted measurement.
References
- Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Adibekyan, V., Sousa, S. G., Santos, N. C., et al. 2020, A&A, 642, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akeson, R., Beichman, C., Kervella, P., Fomalont, E., & Benedict, G. F. 2021, AJ, 162, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Alekseeva, G. A., Arkharov, A. A., Galkin, V. D., et al. 1996, Baltic Astron., 5, 603 [NASA ADS] [Google Scholar]
- Amarsi, A. M., Liljegren, S., & Nissen, P. E. 2022, A&A, 668, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrae, R., Fouesneau, M., Sordo, R., et al. 2023, A&A, 674, A27 [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Andrae, R., Arcay, B., et al. 2013, A&A, 559, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baines, E. K., Armstrong, J. T., Schmitt, H. R., et al. 2018, AJ, 155, 30 [Google Scholar]
- Baines, E. K., Thomas Armstrong, J., Clark, J. H., et al. 2021, AJ, 162, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y., Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [Google Scholar]
- Blanco-Cuaresma, S. 2019, MNRAS, 486, 2075 [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Jofré, P., & Heiter, U. 2014, A&A, 566, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, H. E., Gilliland, R. L., Schaefer, G. H., et al. 2015, ApJ, 813, 106 [Google Scholar]
- Bond, H. E., Gilliland, R. L., Schaefer, G. H., et al. 2018, RNAAS, 2, 147 [NASA ADS] [Google Scholar]
- Bond, H. E., Schaefer, G. H., Gilliland, R. L., & VandenBerg, D. A. 2020, ApJ, 904, 112 [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012a, ApJ, 746, 101 [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012b, ApJ, 757, 112 [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casamiquela, L., Blanco-Cuaresma, S., Carrera, R., et al. 2019, MNRAS, 490, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
- Creevey, O. L., Thévenin, F., Berio, P., et al. 2015, A&A, 575, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Creevey, O. L., Sordo, R., Pailler, F., et al. 2023, A&A, 674, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2021, VizieR Online Data Catalog: II/328 [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Angeli, F., Weiler, M., Montegriffo, P., et al. 2023, A&A, 674, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [Google Scholar]
- Duvert, G. 2016, VizieR Online Data Catalog: II/345 [Google Scholar]
- Engels, D., Sherwood, W. A., Wamsteker, W., & Schultz, G. V. 1981, A&AS, 45, 5 [NASA ADS] [Google Scholar]
- ESA 1997, in The Hipparcos and Tycho Catalogues. Astrometric and Photometric Star Catalogues Derived from the ESA HIPPARCOS Space Astrometry Mission (Noordwijk, Netherlands: ESA Publications Division), 1200 [Google Scholar]
- Fouesneau, M., Frémat, Y., Andrae, R., et al. 2023, A&A, 674, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukue, K., Matsunaga, N., Kondo, S., et al. 2021, ApJ, 913, 62 [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Creevey, O. L., et al.) 2023a, A&A, 674, A39 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Montegriffo, P., et al.) 2023b A&A, 674, A33 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023c, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gent, M. R., Bergemann, M., Serenelli, A., et al. 2022, A&A, 658, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Worley, C. C., et al. 2022, A&A, 666, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [Google Scholar]
- Grevesse, N., Noels, A., & Sauval, A. J. 1993, A&A, 271, 587 [NASA ADS] [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawkins, K., Jofré, P., Heiter, U., et al. 2016, A&A, 592, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
- Hidalgo, S. L., Pietrinferni, A., Cassisi, S., et al. 2018, ApJ, 856, 125 [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Hon, M., Kuszlewicz, J. S., Huber, D., Stello, D., & Reyes, C. 2022, AJ, 164, 135 [CrossRef] [Google Scholar]
- Hourihane, A., François, P., Worley, C. C., et al. 2023, A&A, 676, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, D., Ireland, M. J., Bedding, T. R., et al. 2012, ApJ, 760, 32 [Google Scholar]
- Jin, S., Trager, S. C., Dalton, G. B., et al. 2023, MNRAS, in press, [arXiv:2212.03981] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2015, A&A, 582, A81 [Google Scholar]
- Jofré, P., Heiter, U., Worley, C. C., et al. 2017, A&A, 601, A38 [Google Scholar]
- Jofré, P., Heiter, U., Tucci Maia, M., et al. 2018, RNAAS, 2, 152 [Google Scholar]
- Jofré, P., Heiter, U., & Soubiran, C. 2019, ARA&A, 57, 571 [Google Scholar]
- Karovicova, I., White, T. R., Nordlander, T., et al. 2018, MNRAS, 475, L81 [Google Scholar]
- Karovicova, I., White, T. R., Nordlander, T., et al. 2020, A&A, 640, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karovicova, I., White, T. R., Nordlander, T., et al. 2022a, A&A, 658, A47 [CrossRef] [EDP Sciences] [Google Scholar]
- Karovicova, I., White, T. R., Nordlander, T., et al. 2022b, A&A, 658, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Bigot, L., Gallenne, A., & Thévenin, F. 2017, A&A, 597, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Arenou, F., & Thévenin, F. 2022, A&A, 657, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kondo, S., Fukue, K., Matsunaga, N., et al. 2019, ApJ, 875, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in Planets, Stars and Stellar Systems, Galactic Structure and Stellar Populations, eds. T. D. Oswalt, & G. Gilmore, 5, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagarde, N., Robin, A. C., Reylé, C., & Nasello, G. 2017, A&A, 601, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebreton, Y., & Reese, D. R. 2020, A&A, 642, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ligi, R., Creevey, O., Mourard, D., et al. 2016, A&A, 586, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Nordlander, T., Wehrhahn, A., et al. 2022, A&A, 665, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Luck, R. E., & Heiter, U. 2005, AJ, 129, 1063 [Google Scholar]
- Mamajek, E. E., Prsa, A., Torres, G., et al. 2015, arXiv e-prints [arXiv:1510.07674] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J. C. 1987, A&AS, 71, 119 [NASA ADS] [Google Scholar]
- Miglio, A. 2012, in Astrophysics and Space Science Proceedings, Red Giants as Probes of the Structure and Evolution of the Milky Way, 26, 11 [NASA ADS] [Google Scholar]
- Mosser, B., Michel, E., Appourchaux, T., et al. 2009, A&A, 506, 33 [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Berio, P., Pannetier, C., et al. 2022, SPIE Conf. Ser., 12183, 1218308 [NASA ADS] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Paunzen, E. 2015, A&A, 580, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
- Prugniel, P., Vauglin, I., & Koleva, M. 2011, A&A, 531, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Mayor, M., Udry, S., et al. 2001, The Messenger, 105, 1 [NASA ADS] [Google Scholar]
- Rains, A. D., Ireland, M. J., White, T. R., Casagrande, L., & Karovicova, I. 2020, MNRAS, 493, 2377 [Google Scholar]
- Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Palicio, P. A., et al. 2023, A&A, 674, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlholdt, C. L., Feltzing, S., Lindegren, L., & Church, R. P. 2019, MNRAS, 482, 895 [Google Scholar]
- Salsi, A., Nardetto, N., Mourard, D., et al. 2020, A&A, 640, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serenelli, A., Johnson, J., Huber, D., et al. 2017, ApJS, 233, 23 [Google Scholar]
- Sharma, S., Stello, D., Bland-Hawthorn, J., Huber, D., & Bedding, T. R. 2016, ApJ, 822, 15 [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Brouillet, N., & Chemin, L. 2016, A&A, 591, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soubiran, C., Brouillet, N., & Casamiquela, L. 2022, A&A, 663, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020a, AJ, 160, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., Matijevič, G., Enke, H., et al. 2020b, AJ, 160, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, D. J., Stassun, K. G., & Gaudi, B. S. 2017, AJ, 154, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- van Belle, G. T., von Braun, K., Ciardi, D. R., et al. 2021, ApJ, 922, 163 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
- Vergely, J. L., Lallement, R., & Cox, N. L. J. 2022, A&A, 664, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
- Yamamura, I., Makiuti, S., Ikeda, N., et al. 2010, VizieR Online Data Catalog: II/298 [Google Scholar]
- Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, ApJS, 144, 259 [Google Scholar]
This routine is distributed as part of the IDL Astronomy User’s Library at https://github.com/wlandsman/IDLAstro.
All Tables
Passbands (VOSA designation) or catalogues with the corresponding number of stars having a valid value of flux (N).
Median difference (MED) and median absolute deviation (MAD) between direct determinations of Teff from the literature and our values (literature minus this work), for N stars in common.
Teff and log 𝑔 determined in this work for stars from V1 and V2 with an indirect value of θLD.
Fundamental Teff and log 𝑔 for the eight GBS V3 with [Fe/H] < −1.0 (from the literature), and comparison to the Paper I values, when available.
Median difference (MED) and median absolute deviation (MAD) between our fundamental determinations of Teff and log 𝑔 and the spectroscopic ones from surveys (survey results minus our results), for N stars in common.
Fundamental Teff and log ɡ and their uncertainties determined in this work for the 192 GBS V3, with [Fe/H] from the literature and the θLD adopted measurement.
All Figures
 |
Fig. 1 Histogram of θLD (top panel) and its relative uncertainty (bottom panel) for the 192 GBS V3 stars having interferometric measurements. |
| In the text | |
 |
Fig. 2 Difference between θLD adopted for this work and other values in JMDC fulfilling the selection criteria by Salsi et al. (2020). |
| In the text | |
 |
Fig. 3 Extinction AV deduced from 3D maps of Vergely et al. (2022) as a function of distance, for the 201 targets. |
| In the text | |
 |
Fig. 4 Example of fits of the observed (reddened) data to the (reddened) semi-empirical spectra for HIP 103598 (left) and HIP 50564 (right). The bolometric flux is calculated by integrating the un-reddened spectrum. The bottom panels illustrate the distribution of |
| In the text | |
 |
Fig. 5 Histogram of Fbol (top panel) and its relative uncertainties (bottom panel). |
| In the text | |
 |
Fig. 6 Comparison of Fbol obtained in this work with literature. The colour code relates to the extinction. Several extreme outliers are out of the figure boundaries but they are discussed in the text. |
| In the text | |
 |
Fig. 7 Histogram of Teff absolute (top panel) and relative (bottom panel) uncertainty. The four outliers with Teff uncertainty larger than 150 K (or 3%) are discussed in the text. |
| In the text | |
 |
Fig. 8 Propagation of θLD and Fbol relative uncertainties on Teff. |
| In the text | |
 |
Fig. 9 Comparison of our fundamental determinations of Teff with other fundamental determinations from the literature in Paper I and Boyajian et al. (2013); Karovicova et al. (2020, 2022a,b); van Belle et al. (2021). |
| In the text | |
 |
Fig. 10 Distribution of parallax relative uncertainties versus HIPPARCOS magnitudes for the GBS V3 sample. Parallaxes are mainly from Gaia DR3, but from HIPPARCOS for 8 stars (open squares), and from Akeson et al. (2021) for α Cen A & B (filled squares). |
| In the text | |
 |
Fig. 11 Histogram of linear radii R (top panel) and their relative uncertainty (bottom panel). |
| In the text | |
 |
Fig. 12 Histogram of luminosities L (top panel) and their relative uncertainty (bottom panel). |
| In the text | |
 |
Fig. 13 Linear radius difference between our determination of R from Eq. (3), and seismic estimations from Eq. (5). |
| In the text | |
 |
Fig. 14 Luminosity difference between our determinations L from Fbol and distance, and Gaia DR3 estimations based on G magnitudes and bolometric corrections for 36 stars in common in the Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a). |
| In the text | |
 |
Fig. 15 Histogram of masses (top panel) and their relative uncertainty (bottom panel), red for BaSTI, blue for STAREVOL. |
| In the text | |
 |
Fig. 16 Comparison of masses determined with SPInS (red dots for BaSTI, blue open squares for STAREVOL) to dynamical masses for µ Cas, α Cen B, α Cen A and Procyon, ordered by increasing mass. |
| In the text | |
 |
Fig. 17 Comparison between masses from SPInS (red dots for BaSTI, blue open squares for STAREVOL) and seismic masses from Eq. (6). |
| In the text | |
 |
Fig. 18 Comparison of masses determined with SPInS (red dots for BaSTI, blue open squares for STAREVOL) to those available in the literature, also based on evolutionary tracks. |
| In the text | |
 |
Fig. 19 Comparison between masses from SPInS (red dots for BaSTI, blue open squares for STAREVOL) and masses from the Gaia Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a). |
| In the text | |
 |
Fig. 20 Comparison of log 𝑔 determinations, using masses from SPInS with BaSTI or STAREVOL. The area between the two dashed lines indicates an agreement within 0.1 dex. |
| In the text | |
 |
Fig. 21 Comparison of our fundamental values of log 𝑔 to those determined from vmax and our fundamental Teff. Red dots for SPInS masses using BaSTI models, blue open squares for STAREVOL models. |
| In the text | |
 |
Fig. 22 Comparison of our fundamental values of log 𝑔 to those determined in Paper I and by Karovicova et al. (2020, 2022a,b). Red dots for SPInS masses using BaSTI models, blue open squares for STAREVOL models. |
| In the text | |
 |
Fig. 23 Histogram of log 𝑔 (top panel) and uncertainty (bottom panel). The bottom panel shows the uncertainties for dwarfs (red) and giants (blue). |
| In the text | |
 |
Fig. 24 Kiel diagram with fundamental Teff and log 𝑔. The colour scale is related to metallicities from the literature. The left panel shows the full sample of 192 stars while the right panel shows the stars with uncertainties on Teff and log 𝑔 better than 2% and 0.1 dex respectively. |
| In the text | |
 |
Fig. 25 Histogram of [Fe/H] for the 192 fundamental GBS V3 (grey) compared to the V1 version (red). |
| In the text | |
 |
Fig. 26 Comparison of our fundamental values of Teff (top panel) and log 𝑔 (bottom panel) to spectroscopic ones available in the PASTEL catalogue. |
| In the text | |
 |
Fig. 27 Comparison of Teff and log 𝑔 from this work with the spectroscopic ones in surveys: APOGEE DR17 (blue), Gaia-ESO (red), GALAH DR3 (green). |
| In the text | |
 |
Fig. 28 Comparison of Teff and log 𝑔 from this work with the photometric (red dots) and spectroscopic (blue squares) ones from the Gaia DR3 Golden Sample of Astrophysical Parameters (Gaia Collaboration 2023a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.