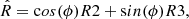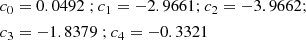EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 681 (January 2024) A&A, 681 (2024) A70 Full HTML
Open Access
Issue
A&A
Volume 681, January 2024
Article Number A70
Number of page(s) 20
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202347133
Published online 02 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Metals have an influence on a number of critical processes in the evolution of the Universe, such as the formation of stars (Girichidis et al. 2020), cooling of the interstellar and the intergalactic medium (Bouché et al. 2007; Smith et al. 2008), stellar evolution (Hurley et al. 2000), production of ionizing photons (Gnedin 2000; Tumlinson & Shull 2000; Ciardi et al. 2003), formation of dust grains (Draine 2003), and so on. As such, the chemical evolution of the interstellar and intergalactic medium provides unique insights into the physical processes governing galaxy formation and evolution. Cosmological simulations, all with various assumptions and prescriptions, are aimed at revealing how the influence of metals on these physical processes results in the measured properties of galaxies, but tight constraints on such models are necessary. Therefore, determining the evolution of gas-phase ionic abundances, namely, the metallicities, on global and resolved scales is crucial in constraining our cosmological models. However, it is first critical to examine the methodology in determining metallicities, especially now as the high-z Universe is being unveiled.

Before the era of the James Webb Space Telescope (JWST), our understanding of the interstellar medium (ISM) at high redshift (z ≳ 3) galaxies was limited to identifying potential local analogs, such as extremely metal-poor galaxies (XMPGs; Izotov et al. 2006, 2021a; Laseter et al. 2022; Thuan et al. 2022), extreme star-forming galaxies (e.g., blueberries, Yang et al. 2017b; blue compact dwarf galaxies, Sargent & Searle 1970; Cairós et al. 2010; green peas, Cardamone et al. 2009; Jaskot & Oey 2013; Henry et al. 2015; Yang et al. 2017a), and damped Lyman-α systems (Wolfe et al. 2005). Several ISM properties such as chemical abundances, ionization states, temperatures, and densities, which can reveal the sources powering the ionization and key evolutionary processes, can be probed by studying the ratio between different rest-frame optical emission lines such as [OII]λλ3727, 3729, [OIII]λλ4959, 5007, and the Hydrogen Balmer series. However, by z ∼ 3, Hα is unobservable from ground-based telescopes, and weaker lines are impractical to observe. Insights from rest-frame optical emission lines primarily originated from photometric techniques (e.g., Shim et al. 2011; González et al. 2012; Labbé et al. 2013; Smit et al. 2014; Rasappu et al. 2016; Roberts-Borsani et al. 2016), but there were difficulties targeting faint sources (e.g., MUV ≈ −17) that are known to exist at these redshifts from Lyman-α surveys (e.g., Cowie & Hu 1998; Finkelstein et al. 2007; Cowie et al. 2011; Matthee et al. 2015; Finkelstein 2016; Bacon et al. 2017; Maseda et al. 2018, 2020; Taylor et al. 2020, 2021; Reddy et al. 2022; Wold et al. 2022). However, these limitations were alleviated when the JWST Early Release Observations (ERO) of SMACS J0723.3 − 7327 demonstrated clear observations of rest-frame optical emission lines (e.g., Carnall et al. 2023), thus ushering in a new era of high-z spectroscopic studies.

One of these JWST observed rest-frame optical emission lines was [OIII]λ4363, which is a collisionally excited emission line originating from higher energy levels (known as an “auroral line”) as compared to the typical nebular lines observed in galaxy spectra. Auroral lines are emitted by different ionic species and at different wavelengths (e.g., OIII]λλ1661, 1666, [OIII]λ4363, [OII]λλ7320, 7330, [SII]λ4069, [NII]λ5755, and [SIII]λ6312) (Castellanos et al. 2002; Maiolino & Mannucci 2019). However, [OIII]λ4363 has become the most sought-after due to its strength compared to other auroral lines and its proximity to rest-frame optical emission lines. When observed, the ratio of [OIII]λ4363 to the stronger, lower energy level lines of [OIII]λλ4959, 5007 can act as an exceptional electron temperature diagnostic. If the electron temperature can be determined, the metallicity can be derived directly from the strengths of common emission lines. This method of determining electron temperatures and metallicities is known as the “direct Te method” (Te) given the direct comparison of energy levels of a single species. The main disadvantage of employing Te is the intrinsic faintness of [OIII]λ4363, which can be 10–100 times fainter than the neighboring oxygen and Balmer lines (Maiolino & Mannucci 2019). As such, observations of [OIII]λ4363 have been restricted predominately to low-z, low-metallicity, individual galaxies or to the stacked spectra of hundreds to thousands of galaxies (e.g., Izotov et al. 2006, 2021a; Hirschauer et al. 2016; Curti et al. 2017; Hsyu et al. 2017; Aver et al. 2022; Laseter et al. 2022), with sparse detections at z ≥ 1 (e.g., Christensen et al. 2012; Maseda et al. 2014; Patrício et al. 2018), thereby limiting our measurements of galaxy metallicities in the high-z Universe.

Metallicity is sensitive to many physical processes driving the baryon cycle in galaxies as it is the result of the complex interplay between gas flows, star formation, and ISM enrichment (Matteucci 2012; Maiolino & Mannucci 2019). A massive effort has been committed to modeling the chemical evolution of galaxies and their surroundings to provide information on the relative importance of such processes. However, such models require tight observational constraints. At z = 0, there is a well-constrained relationship between stellar masses and metallicity known as the mass–metallicity relation (MZR; Tremonti et al. 2004; Kewley & Ellison 2008; Mannucci et al. 2010). Evolution in the MZR has been shown to exist up to z ∼ 3 in that galaxies at higher z have lower metallicity at a given stellar mass. Theoretical works have been tuned to reproduce the MZR at z = 0, along with its evolution (e.g., de Rossi et al. 2007, 2017; Calura et al. 2009; Spitoni et al. 2020; Porter et al. 2022; Zenocratti et al. 2022), although there are differences in the normalization and slope of theoretical MZRs past z ∼ 3, due to limited observations available for making comparisons (Maiolino & Mannucci 2019; Curti et al. 2023b).

Statistical studies of the MZR based on large samples of galaxies do not typically determine metallicities by the direct Te method due to the difficulties in detecting [OIII]λ4363, especially at higher z and in higher metallicity galaxies. Most studies derive metallicities through “strong-line diagnostics”. Strong-line diagnostics typically exploit optical nebular lines (e.g., [OIII]λ5007, [NII]λ6584, [SII]λ6717, Hβ, etc.) that are calibrated against metallicities derived through the direct Te method (e.g., Curti et al. 2017, 2020; Bian et al. 2018; Sanders et al. 2021; Nakajima et al. 2022), with photoionization models (e.g., Pérez-Montero 2014; Dopita et al. 2016), or a hybrid combination of the two (e.g., Pettini & Pagel 2004; Tremonti et al. 2004; Maiolino et al. 2008). However, it has been shown that even for the same galaxy population different calibrations can disagree by up to 0.6 dex (Kewley & Ellison 2008). Curti et al. (2017, 2020) improved calibrations by stacking Sloan Digital Sky Survey (SDSS) galaxies to provide a full empirical calibration for a suite of optical nebular emission lines. However, the properties of the high z universe differ from the local universe, so it is highly uncertain whether locally calibrated strong line diagnostics are appropriate to use in the early Universe.

The pivotal change in this predicament is the observational ability of JWST combined with the near-infrared spectrograph NIRSpec (Böker et al. 2022, 2023; Jakobsen et al. 2022; Ferruit et al. 2022). NIRSpec has opened the capability of obtaining multi-object spectroscopy in the near-IR from space with unmatched sensitivity compared to any current or past facility. JWST/NIRSpec has already observed a number of [OIII]λ4363 emitters (e.g., Schaerer et al. 2022; Taylor et al. 2022; Curti et al. 2023a; Trump et al. 2023; Rhoads et al. 2023), although all these previous works were based on observations from Early Release Observations (ERO) data obtained by targeting galaxies lensed by the cluster SMACS J0723.3−7327 (Repp & Ebeling 2018) and a number of extraction and metallicity prescriptions were employed. Recently, Nakajima et al. (2023) reanalyzed four sources from ERO and four sources from GLASS, along with identifying a new [OIII]λ4363 source from CEERS in the EGS. Sanders et al. (2023) also identified 16 galaxies with [OIII]λ4363 detections from CEERS. In addition, Übler et al. (2023) identified [OIII]λ4363 in a low metallicity AGN at z ∼ 5.55 with the JWST/NIRSpec Integral Field Spectrograph.

However, all of these observations were obtained with relatively shallow spectroscopy. For example, the CEERS observations across six pointings totaled ∼5 h of integration (Finkelstein et al. 2023) and the ERO observations across two pointings totaled ∼5 h of integration (Carnall et al. 2023). Here, we utilize deep spectroscopic data taken from the JWST Advanced Deep Extragalactic Survey (JADES), the deepest spectroscopic observations taken thus far with NIRSpec, to provide a more detailed look at [OIII]λ4363 detections and assess locally derived strong line calibrations up to z ∼ 10. These NIRSpec/JADES observations obtained exposure times of up to 28 h in PRISM/CLEAR (R ∼ 100), along with 7 h in each of the three medium-resolution gratings (R ∼ 1000) and the G395H/F290L high-resolution grating (R ∼ 2700). Overall, our parent sample provides unprecedented new insights into the chemical evolution and ISM properties of galaxies within the first few Gyrs in the history of the Universe.

The structure of this paper is as follows. In Sect. 2, we describe the JADES observations, data reduction, and emission line flux measurements. In Sect. 3, we present our [OIII]λ4363 detections. In Sect. 4, we compare our direct metallicity measurements to strong line calibrations. In Sect. 5, we discuss our findings. Finally, in Sect. 6, we present our conclusions. For this work, we adopt the Planck Collaboration VI (2020) cosmology: H0 = 67.36 km s−1 Mpc−1, Ωm = 0.3153, and Ωλ = 0.6847.

2. Observations, data processing, and data analysis

2.1. Observations

The data presented in this paper were obtained via multi-object spectroscopic observations from JWST/NIRSpec using the micro-shutter assembly (MSA). Observations were carried out in three visits between Oct. 21–25, 2022 (Program ID: 1210; PI: N. Luetzgendorf) in the Great Observatories Origins Deep Survey South (GOODS-S) legacy field as part of JADES. Each visit consisted of 33 613 s integration in the PRISM/CLEAR low-resolution setting and 8403 s integration in each of the G140M/F070LP, G235M/F170LP, G395M/F290LP, and G395H/F290LP filter and grating settings. Across three visits, this totals 28 h of integration in the PRISM, which provides continuous spectral coverage from 0.6 to 5.3 μm at R ∼ 30 − 300, and ∼7 h in each of the medium resolution gratings, which combine to provide R ∼ 700 − 1300 across the full spectral range of NIRSpec, plus 7 hours in the high-resolution grating, which provides R ∼ 2700 from ∼2.8 to 5.1 μm; however, the exact wavelength coverage depends on the target location in the MSA.

Observations within each visit were performed as a three-shutter nod. The central pointing of each visit was dithered (by < 1 arcsec) such that common targets were observed in different shutters and different detector real-estate. Thus, each visit had a unique MSA configuration, although the target allocation (performed with the eMPT1; Bonaventura et al. 2023) was optimized for maximizing target commonality between all three dither positions.

A total of 253 unique targets were observed in the PRISM configuration with the three dithers featuring 145, 155, and 149 targets, respectively. All targets are observed with non-overlapping spectra in the PRISM mode. However, in the medium- and high-resolution gratings, individual spectra are dispersed over a larger number of detector pixels, and thus there is a possibility of spectral overlap. To minimize contamination overlap, we isolate our highest-priority targets by closing the shutters of low-priority targets on the same row (i.e., targets that would cause overlapping spectra) during observations. Thus, for our grating spectra, we observe 198 unique targets (119, 121, and 111 in each dither).

2.2. Data processing

The JWST/NIRSpec observations have been processed by adopting algorithms developed by the ESA NIRSpec Science Operations Team (SOT) and the NIRSpec GTO Team. The details of the data-processing workflow will be presented a the forthcoming NIRSpec GTO collaboration paper. Once we retrieved the level-1a data from the MAST archive, we estimated the count rate per pixel by using the unsaturated groups in the ramp and removing jumps due to cosmic rays identified by estimating the slope of the individual ramps. During this first stage, we also performed the master bias and dark subtraction, corrected snowball artifacts, and flagged saturated pixels.

We then performed the pixel-by-pixel background subtraction by combining the three nod exposures of each pointing. We note that for some targets, we excluded one of the three-shutter nods in the background subtraction stage, as a serendipitous source contaminated the open shutters. We then created two-dimensional (2D) cutouts of each three-shutter slit and performed the flat-field, spectrograph optics, and dispersers corrections. Then we ran the absolute calibration stage and corrected the 2D spectra for the path-losses depending on the relative position of the source within its shutter. We computed and applied the path-losses correction for a point-like source as the size of our targets is smaller or comparable to the spatial angular resolution of the telescope at the redshifted wavelength of the optical nebular lines at z >  7.

We rectified and interpolated the 2D continuum map onto a regular grid for all medium- and high-resolution gratings and an irregular grid for the PRISM/CLEAR to avoid an oversampling of the line spread function at short wavelengths. Finally, the 1D spectra were extracted from the 2D map adopting a box-car aperture as large as the shutter size and centered on the relative position of the target in the shutter. For each target, we combined all 1D spectra and removed bad pixels by adopting a sigma-clipping approach.

2.3. PPXF

Emission-line measurements and continuum modeling are made simultaneously using the penalized pixel fitting algorithm, PPXF (Cappellari 2017, 2023). The algorithm models the continuum as a linear superposition of simple stellar population (SSP) spectra, using non-negative weights and matching the spectral resolution of the observed spectrum. As input, we used the high-resolution (R = 10 000) SSP library combining MIST isochrones (Choi et al. 2016) and the C3K theoretical atmospheres (Conroy et al. 2018). The flux blueward of the Lyman break was manually set to 0. These templates are complemented by a fifth-degree multiplicative Legendre polynomial to take into account systematic differences between the SSPs and the data (e.g., dust, mismatch between the SSP models and high-redshift stellar populations, and residual flux calibration problems). The emission lines are modeled as pixel-integrated Gaussians, again matching the observed spectral resolution. To reduce the number of degrees of freedom, we divided all emission lines into four kinematic groups, constrained to have the same redshift and intrinsic broadening. These are UV lines (blueward of 3000 Å), the Balmer series of hydrogen, non-hydrogen optical lines (blueward of 9000 Å), and NIR lines. The stellar component has the same kinematics as the Balmer lines. Furthermore, we tied together doublets that have fixed ratios and constrained variable-ratio doublets to their physical ranges. In particular, we fit for the following lines of interest: [OII]λλ3726, 3729 , [Ne III]λλ3869, 3967, Hδ, Hγ, [OIII]λ4363, Hβ, [OIII]λλ4959, 5007, Hα, [NII]λ6583, and [SII]λλ6716, 6731.

3. [OIII]λ4363 detections and the Te method

3.1. JADES

We visually inspected the 1D and 2D PRISM/CLEAR and grating spectra for our 253 unique targets and found ten sources with an [OIII]λ4363 detection detected at a S/N ≳ 3. The median S/N in [OIII]λ4363 of our JADES sample is ∼5. We present in Fig. 1 the redshift distribution of our parent sample and identified [OIII]λ4363 emitters. We show in Fig. 2 the [OII]λλ3727, 3729, Hγ and [OIII]λ4363, and Hβ, [OIII]λλ4959, 5007 complexes of our [OIII]λ4363 sources. Object JADES-GS+53.13284−27.80186 has one of the highest S/N [OIII]λ4363 detection in our sample with a S/N = 9.8. However, [OIII]λλ4959, 5007 fell within the detector gap for this object, so instead we used the [OIII]λλ4959, 5007 fluxes from our PRISM observations. We corrected for reddening in our measurements from the available Balmer lines adopting a Calzetti et al. (2000) attenuation curve. We assumed the theoretical ratios of Hα/Hβ = 2.86 and Hβ/Hγ = 2.13 from Case B recombination at T = 1.5 × 104 K. We default to correcting with respect to Hα/Hβ, but we use Hβ/Hγ when Hα is not available.

thumbnail Fig. 1.

Redshift distribution of our parent JADES sample of 198 objects with both PRISM and grating spectra and our ten novel [OIII]λ4363 emitters. No pre-selection was performed on the parent JADES sample as we visually inspected all the objects.

thumbnail Fig. 2.

JWST/NIRSpec R1000 spectra of our 10 novel detections. The best-fit models from PPXF are shown in purple. The lines of interest (located at the vertical dotted lines) shown from left to right are [OII]λλ3727, 3729, Hγ and [OIII]λ4363, and Hβ \AMP [OIII]λλ4959, 5007. [OII]λλ3727, 3729 and Hγ and [OIII]λ4363 share the same y-axis. The top panels show the 2D spectrum for each respective line complex. JADES-GS+53.13284−27.80185 did not have [OIII]λλ4959, 5007 coverage in R1000 due to the detector gap, so we present [OIII]λλ4959, 5007 from our PRISM observations.

We can go on to determine the electron temperatures and oxygen abundances through Te. However, we note it is customary to take oxygen abundances as representative of the total gas-phase metallicity, which has implicit assumptions that all other chemical elements scale proportionally and that individual galaxies are a single HII region comprised of a high-ionization zone traced by O++ and a low-ionization zone traced by O+, which ignores the underlying temperature distribution and ionization structure. A detailed discussion of the nuance of these assumptions is outside the scope of this work (see Stasińska 2002 and Maiolino & Mannucci 2019 for a review), but there is novel work testing the significance of these assumptions (e.g., Cameron et al. 2023a) that we are expanding upon.

Nonetheless, we derived the electron temperature for O++ (t3) by taking flux ratio of the [OIII]λλ4959, 5007 doublet to the [OIII]λ4363 thermal line. We used Pyneb (Luridiana et al. 2015) with O2+ and O+ collision strengths from Aggarwal & Keenan (1999), Palay et al. (2012), Pradhan et al. (2006) and Tayal (2007), respectively. A more problematic step is determining the electron temperature for O+ (t2). Only t3 is derived directly here as we did not have any spectral coverage of [OII] auroral lines at 7320 Å and 7330 Å. In situations where the [OII] auroral lines have not been detected, it is common to interconvert between t3 and t2 using modeled relations. One such t3–t2 relation is presented by Curti et al. (2017; originally presented in Pilyugin et al. 2009), in which they relate directly derived t3 and t2 temperatures to obtain the relation: t2 = 0.264 + t3 × (0.835).

However, t3–t2 relations have not been explored in the high-z Universe. Yates et al. (2020) found local t3–t2 relations have difficulty in matching large samples of local galaxies with Te derived metallicities. Fortunately, there is typically little change in the total derived metallicity when adding O+ to O2+ as O2+ dominates the ionization state of oxygen in galaxies with direct [OIII]λ4363 detections (Izotov et al. 2006; Andrews & Martini 2013; Curti et al. 2017, 2020, 2023a; Laseter et al. 2022). Nonetheless, there is a clear need for future investigation of t3–t2 relations in the high-z Universe.

We determined ionic oxygen abundances using Pyneb with the same collision strengths as before. We assume an electron density of Ne = 300 cm−3 since this is representative of the ISM electron density of z ∼ 2–3 galaxies (Sanders et al. 2016a,b). The choice of electron density does not significantly affect the temperature results. For example, when assuming Ne = 1000 cm−3, there is ∼0.1% change in the derived t3 (Izotov et al. 2006). We determined the total oxygen abundance for each galaxy by taking (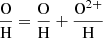). We did not detect any HeII λ4686 in our sample, so we do not apply an ionization correction factor to account for O3+ since HeII has an ionization potential of ≳54.4 eV and O3+ has an ionization potential of ≳55 eV. Even if O3+ is present, a correction would have a nominal change for the total oxygen abundance (Izotov et al. 2006; Berg et al. 2021; Curti et al. 2023a).

To calculate the uncertainties of our measurements, we used a Monte Carlo technique. We evaluate the electron temperature and oxygen abundance 10 000 times using values drawn randomly from normal distributions for the measured fluxes of [OIII]λλλ5007, 4959, 4363, Hβ, Hγ, and [OII]λλ3727, 3729, centered at the measured flux values, and with standard deviations corresponding to the 1σ flux errors from PPXF. Our final reported electron temperatures and metallicities are taken as the median value of the propagated normal distributions with the standard deviation of the distributions being the 1σ error.

In addition to our [OIII]λ4363 emitters, Curti et al. (2023a) measured the chemical abundances of three z ∼ 8 galaxies behind the galaxy cluster SMACS J0723.3−7327 during the initial ERO data release. A number of studies investigated the same objects (e.g., Schaerer et al. 2022; Taylor et al. 2022; Rhoads et al. 2023; Trump et al. 2023). However, Curti et al. (2023a) reprocessed the data through the NIRSPec GTO pipeline. We include these three galaxies (ID: 4590, 6355, and 10612) after reprocessing the initial data from Curti et al. (2023a) with the updated NIRSpec GTO pipeline (Carniani et al., in prep.) and determining oxygen abundances as described above. We find nominal changes in the total metallicities: 0.24 dex for 4590, −0.1 dex for 6355, and 0.04 dex for 10 612. For our combined sample, we report the line fluxes in Table 1 and electron temperatures and metallicities in Table 2.

Table 1.

Measured fluxes and errors of emission lines of interest from PPXF in units of 10−20 erg s−1 cm−2.

Table 2.

Derived galaxy properties of our sample.

Recently, Bunker et al. (2023) provided the first JWST/NIRSpec spectrum of GN-z11 (Oesch et al. 2016) from the JADES collaboration. Bunker et al. (2023) reports a detection of [OIII]λ4363, but there was insufficient wavelength coverage to observe [OIII]λλ4959, 5007, thus we cannot use the Te method. The proceeding analysis and subsequent discussion in Sects. 4 and 5 require a self-consistent metallicity prescription. Therefore, we do not include GN-z11 in our sample, but we highlight the detection of [OIII]λ4363 in the most luminous Lyman break galaxy at z >  10 for context in our discussion in Sect. 5.

3.2. CEERS

3.2.1. Comparison

Recently, Sanders et al. (2023) identified [OIII]λ4363 in 16 galaxies between z ≈ 2.0 − 9.0, measured from JWST/NIRSpec observations obtained as part of the Cosmic Evolution Early Release Science (CEERS) survey program. They further consolidated nine objects with [OIII]λ4363 detections between z ≈ 4 − 9 from the literature using JWST/NIRSpec, along with 21 galaxies between z ≈ 1.4 − 3.7, with detections from ground-based spectroscopy. Sanders et al. (2023) determined metallicities with Te through PyNeb (Luridiana et al. 2015) for their entire sample to construct empirical Te-based metallicity calibrations for strong-line ratios such as R2, O3O2, R3, and R23 in the high-z Universe, which we investigate in Sect. 4. As such, we included the 16 discovered galaxies with [OIII]λ4363 from CEERS in our comparisons. However, Sanders et al. (2023) used O2+ and O+ collision strengths from Storey et al. (2014) and Kisielius et al. (2009), respectively. We re-derived the metallicities for the Sanders et al. (2023) sample, using O2+ and O+ collision strengths from Aggarwal & Keenan (1999), Palay et al. (2012), Pradhan et al. (2006) and Tayal (2007) to remain self-consistent. We investigate the systematics of choosing different O2+ collisional strengths in Appendix A.

One caveat when including the sample from Sanders et al. (2023) is the difference in spectroscopic reduction pipelines employed. Specifically, data were reduced in Sanders et al. (2023) with calwebb detector, STScI’s pipeline, whereas we utilize the GTO pipeline as mentioned in Sect. 2.2. Issues and variations between the pipelines were immediately apparent from the works of Schaerer et al. (2022), Taylor et al. (2022), Rhoads et al. (2023), Trump et al. (2023); and Curti et al. (2023a), with overall conclusions being that analyses and interpretations should avoid absolute flux calibrations and using widely separated line ratios (Trump et al. 2023). Recently, Maseda et al. (2023) provided deeper insight into these discrepancies. However, GTO flux calibrations have improved since these studies, although a full description will be presented in Bunker et al. (in prep.). A full comparison between the current strengths and weaknesses of the pipelines is outside the scope of this work, but for the current comparison between our JADES sample and Sanders et al. (2023), systematics could exacerbate or diminish offsets between metallicity determinations and strong-line ratios.

3.2.2. Metallicity prescription choice

In addition to systematics introduced through data reduction and the choice in collisional strengths, the decision to use a given metallicity prescription will introduce systematics, among other choices (e.g., the t3–t2 relation). We demonstrate these systematics by re-deriving electron temperatures and metallicities for our JADES sample and the Sanders et al. (2023) sample using the Izotov et al. (2006) prescription. We used the atomic data listed in Stasińska (2005) to determine t3 in an iterative manner (Izotov et al. 2006; Eqs. (1) and (2)). We derived t2 using Eq. (14) from Izotov et al. (2006), which was obtained by relating t3 to temperatures of other ions from photoionization models that best fit HII emission line observations (Izotov et al. 2006).

We present in Fig. 3 the systematic offsets between Izotov et al. (2006) and PyNeb derived metallicities for our sample. We find a median offset of Δ12 + log(O/H) of −0.11 dex when using PyNeb instead of Izotov et al. (2006). A critical assessment of the advantages and limitations of Te metallicity prescriptions is outside the scope of this work. However, it is clear that choice does matter, thus demonstrating the need for self-consistency in metallicity studies and comparisons as [OIII]λ4363 samples in the high-z Universe continue to grow. We continue with the analysis using metallicities derived with Pyneb. We include the figures presented in Sect. 4 for the metallicities derived according to Izotov et al. (2006) in Appendix A. Nonetheless, the main results discussed in Sect. 5 remain unchanged regardless of the Te method employed.

thumbnail Fig. 3.

Deviation between metallicites derived by Izotov et al. (2006) and PyNeb. The solid line represents unity, whereas the dashed line represents the median offset between Izotov et al. (2006) and PyNeb.

4. Strong line calibrations

4.1. Comparison to locally derived strong line calibrations

As mentioned in Sect. 1, there are a number of strong-line metallicity diagnostics calibrated against Te derived metallicities (e.g., Pettini & Pagel 2004; Maiolino et al. 2008; Marino et al. 2013; Pilyugin & Grebel 2016; Curti et al. 2017; Bian et al. 2018; Sanders et al. 2021). These calibrations have been applied to large samples of galaxies to determine metallicities when auroral lines are not observed, which allows for larger characteristic studies, such as the MZR (e.g., Tremonti et al. 2004; Mannucci et al. 2010; Pérez-Montero et al. 2013; Lian et al. 2015; Maiolino & Mannucci 2019; Curti et al. 2020; Baker & Maiolino 2023) and the fundamental metallicity relation (FMR; e.g., Mannucci et al. 2010; Lara-López et al. 2010; Brisbin & Harwit 2012; Hunt et al. 2012; Yates et al. 2012; Nakajima & Ouchi 2014; Baker et al. 2023). All calibrations have caveats, however, such as high dependencies on ionization parameter (e.g., Dopita et al. 2006; Pilyugin & Grebel 2016) or an inherent assumption on the N/O–O/H relation (e.g., Dopita et al. 2016; Hayden-Pawson et al. 2022; Schaefer et al. 2020, 2022). Another major uncertainty is the applicability of these strong line calibrations for high-z galaxies. An evolution in the ISM conditions of high-redshift galaxies compared to the local Universe might impact the intrinsic dependence of strong-line ratios on gas-phase metallicity, potentially hampering their use as abundance diagnostics at high redshift, thus biasing the assessment and interpretation of the chemical evolution history of galaxies.

Previously, using the same parent data set as the current work, Cameron et al. (2023c) found z ∼ 5.5 − 9.5 galaxy emission line ratios are generally consistent with galaxies with extremely high ionization parameters (log(U)= − 1.5) and are traced by the extreme ends of z ∼ 0 ionization-excitation diagrams of R23–O3O2 and R23–Ne3O2. In addition, Cameron et al. (2023c) found more than an order of magnitude of scatter in line ratios such as [OII]λλ3727, 3729/Hβ and [OIII]λ5007/[OII]λλ3727, 3729, while simultaneously not observing any [NII]λ6583, indicating significant diversity in metallicity and ionization within the ISM conditions of the sample. To complicate the landscape, recent JADES/NIRSpec observations of the GN-z11, which is also an [OIII]λ4363 emitter, revealed rarely seen NIV]λ1486 and NIII]λ1748 lines that may imply an unusually high N/O abundance (Bunker et al. 2023; Cameron et al. 2023b; Senchyna et al. 2023).

Here, we utilize the Te derived abundances and emission line ratios delivered by the ‘Deep’ spectroscopic tier of JADES to provide a more detailed look at strong line calibrations in the high-z Universe. We include the aforementioned ERO objects from Curti et al. (2023a) and the CEERS objects from Sanders et al. (2023) derived in a self-consistent manner for a complete JADES+ERO+CEERS data set. We investigate some of the most widely adopted strong-line metallicity diagnostics, and also explore a novel diagnostic labeled R̂ and based on a different projection in the [OII]/Hβ − [OIII]/Hβ diagram, as discussed in Sect. 4.8 and Appendix B:

A common strong-line calibration, especially at high-z, is N2 = [NII]λ6583/Hα. We exclude this diagnostic from this study, however, because we find no convincing evidence for [NII]λ6583, analogous to Cameron et al. (2023c).

In Figs. 4–7, we present the strong-line ratios of our sample and the Sanders et al. (2023) sample plotted against metallicity and an array of locally-derived strong-line calibrations. Specifically, we include Maiolino et al. (2008), Curti et al. (2017, 2020), Bian et al. (2018), and Nakajima et al. (2022). In brief, Curti et al. (2017, 2020) provided calibrations based on Te metallicity measurements derived from SDSS stacked spectra and direct [OIII]λ4363 detections. Here, we consider a slightly revisited version of these calibrations, based on the full galaxy sample adopted to derive the R̂ diagnostic (see Appendix B); in particular, in comparison with the original Curti et al. (2017) curves, the polynomial fits are now better constrained (and not anymore extrapolated) in the low-metallicity regime down to 12 + log(O/H)∼7. Maiolino et al. (2008) combined a sample of Te derived low-metallicity galaxies from Nagao et al. (2006) with predictions from photoionization models in the high-metallicity regime. Bian et al. (2018) 2 constructed calibrations from a sample of local [OIII]λ4363 emitters selected to match the location of z ∼ 2 star-forming sources in the [NII]–BPT diagram (Kewley et al. 2013). Finally, Nakajima et al. (2022) extended the Curti et al. (2017, 2020) SDSS stacks to the extremely metal-poor regime by including XMPGs identified from the EMPRESS survey (Kojima et al. 2020). Nakajima et al. (2022) further subdivided their calibrations characterized by high and low EW(Hβ); namely: EW(Hβ)> 200 Å and < 100 Å, respectively. Overall, the metallicity range for these calibrations differs, but we extrapolated each calibration over 6.9 ≤ 12 + log(O/H ≤ 9.0). We indicate the calibrated ranges as reported in the original papers as solid lines, whereas the extrapolations in Figs. 4–7 are displayed as as dotted lines. We stress that extrapolating calibrations past their defined range can lead to nonphysical behaviors; however, we are extrapolating to examine the limitations of the calibrations.

thumbnail Fig. 4.

Relationship between Te metallicity and R2 for our JADES sample compared with strong-line calibrations from Maiolino et al. (2008), Curti et al. (2017), Curti et al. (2020), and the “all”, “large equivalent width (EW)”, and “small EW” calibrations from Nakajima et al. (2022). Bian et al. (2018) does not include a calibration for R2, but we include their calibrations for O3O2, R3, and R23 in Figs. 5–7. Solid lines indicate calibrated ranges whereas dotted lines indicate the extrapolation of the calibration over the metallicity range 6.9 ≤ 12 + log(O/H)≤9.0. The six subplots demonstrate the difference between Te derived metallicities and calibration-derived metallicities for our individual galaxies. The vertical lines represent galaxies in our sample, where the respective strong-line calibration cannot compute a metallicity for the measured line ratios.

thumbnail Fig. 5.

Identical to Fig. 4, except the relationship is between Te metallicity and O3O2.

thumbnail Fig. 6.

Identical to Fig. 4, except the relationship is between Te metallicity and R3.

thumbnail Fig. 7.

Identical to Fig. 4, except for the relationship between Te metallicity and R23.

We determine the significance of deviation (in units of σ) for our JADES+ERO+CEERS sample to the predictions of each of the strong-line calibrations presented in Figs. 4–7. We determine the total deviation of our sample from the calibrations through a Monte Carlo technique. We evaluate the difference between our data points and the calibration values 10 000 times using values drawn randomly from normal distributions for the measured line ratios, metallicities, and calibrations. We include the line uncertainties, metallicity uncertainties, and the intrinsic dispersion of the calibrations (σcal) as the standard deviation for the respective distributions3; thus we are computing a deviation in a 2D space, considering both quantities (i.e., the respective strong-line calibration and metallicity). We present in Table 3 the total deviation between our sample and the respective calibrations.

Table 3.

Significance of deviation (in units of σ) for the expected line ratios from each strong-line calibration to our JADES sample presented in Figs. 4–7.

However, the sensitivity to metallicity varies over metallicity space for each strong-line diagnostic. For example, R23 has a weak dependence on metallicity at the turnaround point between 8.0 ≲ 12 + log(O/H)≲8.5, but a stronger dependence at lower metallicity (12  +  log(O/H)≲7.65). A primary concern for studies investigating the MZR is its slope, which is dependent upon how well the metallicities of galaxies, especially at the lower-mass end (lower metallicity), are determined. We, therefore, investigated how well each calibration does in predicting the Te derived oxygen abundances for each galaxy in our sample (computing a deviation in 1D space). We determined the offset between derived oxygen abundances by performing the same MC technique as above and then taking 12 + log(O/H)Te − 12 + log(O/H)cal. We present at the bottom of Figs. 4–7 the offset to each respective calibration for our individual galaxies. The vertical lines represent galaxies in our sample where the respective strong-line calibration cannot compute a metallicity for the measured line ratios.

4.2. R2

There is approximately an order of magnitude in scatter in the R2 ratio from Fig. 4, suggesting there is notable diversity in the ISM conditions of our sample since R2 is highly dependent on the ionization parameter and hardness of the ionizing spectrum. In comparison, we find a median R2 value of −0.38 with a standard deviation of 0.41; whereas Cameron et al. (2023c), using the same parent sample of this work but with selection criteria of 5.5 ≤ zspec ≤ 9.5 and S/N of Hβ ≥ 5, found a median R2 value of −0.28 with a standard deviation of 0.38. We find the high-EW R2 calibration from Nakajima et al. (2022) has the smallest significance of deviation to our sample with a 1.09σ deviation, although there are metallicity offsets over ∼ − 0.5 dex and 11 of our objects cannot be accounted for.

R2 is rarely used in isolation but is often employed to break the degeneracies of other calibrations. However, for the high-z Universe, we clearly see there is significant scatter, thus suggesting the use of R2 as a degeneracy breaker in the high-z Universe is problematic. We performed a Spearman correlation test on our JADES sample and found ρs = 0.58 with a p-value of 0.001, thus demonstrating a monotonic relationship with a low probability of an uncorrelated system reproducing the distribution. However, we see similar R2 values across ∼1 dex in metallicity. This insensitivity of R2 ratios to metallicity is possibly due to the ionization parameter–metallicity relation at these epochs, i.e., the ionization parameter–metallicity relation is not constant or has other dependencies (e.g., Reddy et al. 2023). Overall, our sample demonstrates R2 is a poor metallicity diagnostic in the high-z Universe, but the diversity in R2 values of our sample warrants a deeper investigation that is currently beyond the scope of this paper.

4.3. O3O2

O3O2 also acts as a degeneracy breaker for other strong-line calibrations (Maiolino & Mannucci 2019), as it primarily traces the ionization parameter, with the metallicity dependence being secondary due to the ionization parameter–metallicity relation. We found a median O3O2 value of 1.08 with a standard deviation of 0.36, while Cameron et al. (2023c) found a median O3O2 value of 1.03 with a standard deviation of 0.36. Almost our entire sample exhibits high O3O2 values with the smallest deviation calibrations (0.96σ) from Bian et al. (2018) and the high-EW O3O2 calibration from Nakajima et al. (2023) still failing to account for 22 of our galaxies and producing metallicity offsets ∼0.6 dex.

We find a Spearman correlation of ρs = −0.44, with a p-value of 0.02, thus demonstrating a correlation (albeit a weak one). However, we find similar O3O2 values across ∼1 dex in metallicity similar to R2. Therefore, although our sample is small, this finding suggests that O3O2 is neither a good O/H diagnostic nor an appropriate degeneracy breaker for other strong-line diagnostics in the high-z Universe. A more detailed picture of O3O2 was presented by Cameron et al. (2023c), in which they compared O3O2 against R23 (their Fig. 5), which ultimately compares tracers of ionization parameter and total excitation, respectively. Cameron et al. (2023c) found the JADES sample to exhibit much higher O3O2 values at a given R23 value compared to z ∼ 2 MOSDEF galaxies, which already traced the extremes of SDSS z ∼ 0 populations. Cameron et al. (2023c) concluded that galaxies across the sample exhibit very high ionization parameters. This high ionization is reflected in Fig. 5 and Table 3, as the majority of calibrations fail to return a 12 + log(O/H) value at the O3O2 ratios we measured. An explanation for this high ionization would be simple if our sample had lower O/H values since that would suggest the ionization–metallicity relation is constant. However, ionization is generally higher at a fixed metallicity in our sample, thus suggesting a physically driven change. Nonetheless, a full characterization will be explored in forthcoming work.

4.4. R3

In contrast to R2 and O3O2, we see little scatter in our sample for R3. We find a median R3 value of 0.81 with a standard deviation of 0.12. Cameron et al. (2023c) also found a median R3 value of 0.74 with a standard deviation of 0.86. We find that the calibration from Bian et al. (2018) has the smallest significance of deviation for our sample with a 0.50σ deviation, although four of our galaxies cannot be predicted by the calibration, the metallicity offsets are up to ∼ − 0.6 dex, and we are ultimately comparing against the extrapolation. Nonetheless, the R3 calibration from Bian et al. (2018) best traces our sample out of the local calibrations.

We find a Spearman correlation of ρs = 0.62 with a p-value of 0.0004, thus demonstrating there is still a strong relationship between R3 and metallicity. However, R3 has a characteristic turnover locally, which requires identifying which of the two branches applies. Interestingly, we see an apparent flattening of our sample across the double-valued R3 sequence. R3 is similar to R2 in that it is highly degenerate with the ionization parameter, the hardness of the ionizing spectrum, and the relation between metallicity and ionization parameter (Kewley & Ellison 2008; Maiolino & Mannucci 2019). As such, the flattening of our objects across the double-valued sequence, in addition to the large scatter in R2 and O3O2, suggests significant ionization across ∼1 dex in metallicity in our sample. Without probing higher metallicities it is difficult to conclude whether the characteristic turnover is present in the high-z Universe. If R3 is confirmed to have a minimal turnover then R3 as a metallicity diagnostic is not viable in the high-z Universe. Overall, forthcoming work will investigate whether R3 turns over and the origins of the excess R3 values.

4.5. R23

R23 is the most widely used strong-line calibration in determining metallicity because, unlike R2 and R3, R23 is an indication of the total excitation of a galaxy as it combines the different ionization states of oxygen. There is still a high dependence on the ionization parameter, however, along with a double branching that requires employing other strong-line diagnostics, such as R2 or O3O2, to break the degeneracy. R23 has already been employed in the high-z Universe (e.g., Nakajima et al. 2023); however, we find a moderate deviation from our sample for the R23 calibrations. Specifically, we find the calibration from Bian et al. (2018) to have the smallest significance of deviation to our sample (0.58σ), although as can be seen in Fig. 7, the majority of our points do not fall within the calibrated range of Bian et al. (2018), 24 of our galaxies cannot be reproduced and metallicity offsets up to ∼0.5 dex exist. From Fig. 7, however, we see visually the large EW sample from Nakajima et al. (2022) best traces the upper envelope of our objects for a calibrated range, although metallicity offsets range between ∼ − 0.5 and 0.5 dex. We find a median R23 value of 0.97 and a standard deviation of 0.13. Cameron et al. (2023c) also found a median R23 value of 0.90 with a standard deviation of 0.10. Overall, the R23 ratios of our JADES sample suggest significant excitation across ∼1 dex in metallicity than what is typically seen in local galaxies.

It is clear that a self-consistent calibration of R23 is needed for the high-z Universe, but it is difficult to conclude whether R23 is appropriate for the high-z Universe. We find a Spearman correlation of ρs = 0.68 with a p-value of 4.4 × 10−5, which indicates there is a strong correlation of R23 with metallicity. However, similar to our R3 ratios, we cannot determine whether R23 turns over or not. We cannot probe past the low-z turnover point (8.0 ≲ 12 + log(O/H)≲8.5) with our limited sample, but visually and with the Spearmen Rank correlation/p-value, the metallicity dependency of R23 is possibly inadequate for a high-z metallicity indicator, especially if this trend continues past the low-z turnover point. A stacking procedure, similar to Curti et al. (2017, 2020), is necessary to probe past the low-z turnover point.

4.6. Comparison to high-z calibration

In addition to a high-z [OIII]λ4363 sample, Sanders et al. (2023) provided the first high-z strong-line calibrations. Accordingly, we compared their calibrations for R2, O3O2, R3, and R23 to our sample, as shown in Figs. 4–7. We determined the significance of deviation as described in Sect. 4.1 for each calibration from Sanders et al. (2023). We find our sample to be 1.24σ, 1.17σ, 0.77σ, 0.81σ away for R2, O3O2, R3, and R23, respectively. The R3 and R23 calibrations from Sanders et al. (2023) visually trace the upper envelope of our sample where other local calibrations have failed to reproduce our measured line ratios. However, at 12 + log(O/H)≲8.0 the extrapolation of the calibration from Bian et al. (2018) predicts higher R3 ratios at a given metallicity than Sanders et al. (2023), thus leading to the higher deviation reported for the Sanders et al. (2023) calibration. For R2 and O3O2, the deviations reported for the Sanders et al. (2023) calibration are due to the significant scatter in our sample.

We note here (and demonstrate in Appendix A) that there would be a systematic offset introduced when comparing a calibration and a sample with different metallicity prescriptions (e.g., Pyneb and Izotov et al. 2006), thus emphasizing the importance of self-consistency until systematics between Te prescriptions are better constrained. Nonetheless, the high-z calibration from Sanders et al. (2023) visually traces our sample well in the strong lines investigated in the current work, but (as discussed in Sect. 5) larger [OIII]λ4363 samples are clearly needed for future high-z Universe strong-line calibrations.

4.7. Photoionization models

A common alternative to determining metallicities through the Te method or strong-line calibrations is the use of photoionization models due to the range of properties that can be explored (e.g., Tremonti et al. 2004; Pérez-Montero 2014; Dopita et al. 2016; Vale Asari et al. 2016). However, this approach is currently limited as it is difficult to capture the complexity of HII regions and a number of assumptions are employed (e.g., plane-parallel atmospheres, the ionizing spectrum, and dust depletion; Maiolino & Mannucci 2019). This area has improved with certain frameworks that introduce Bayesian approaches where multiple emission lines are used to identify the best corresponding model returned from a grid (e.g., PyNeb, Luridiana et al. 2015; CLOUDY, Ferland et al. 2013, etc.), while minimizing the assumptions. One such code is HII-CHI-Mistry from Pérez-Montero (2014).

Pérez-Montero (2014) used the synthesis spectral code CLOUDY v13.03 (Ferland et al. 2013) using POPSTAR (Mollá et al. 2009) stellar evolutionary models assuming an instantaneous burst with an age of 1 Myr with an initial mass function from Chabrier (2003). They ranged the ionization parameter between −1.50 ≤ log(U)≤ − 4.00 in steps of 0.25 dex, the oxygen abundance between 7.1 ≤ 12 + log(O/H)≤9.1 in steps of 0.1 dex, and considered variations in the N/O ratio between 0.0 ≤ N/O ≤ −2.0 in steps of 0.125 dex, thus totaling 3927 models. It would be excessive to compare all the models, so we compared against the full metallicity range for N/O values of −2.0, −1.0, and 0.0, and log(U) values of −1.5, −2.5, and −3.5.

In addition to the work of Pérez-Montero (2014), Hirschmann et al. (2023) provided metallicity calibrations specifically designed for galaxies at z >  4 using the IllustrisTNG50 and IllustrisTNG100 simulation suite (Pillepich et al. 2018, 2019). Hirschmann et al. (2023) combined their simulated galaxies with emission line models including HII regions, AGNs, PAGBs, and shocks, which together constitute the total nebular emission.

We present in Fig. 8 our JADES sample, the grid models returned from Pérez-Montero (2014), and the high-zHirschmann et al. (2023) calibrations. Our JADES sample is best traced by the log(U)= − 1.5 models from Pérez-Montero (2014), although our most metal-poor galaxies require a higher ionization parameter, while our least metal-poor galaxies fall close to log(U)= − 2.5 models. The nitrogen-oxygen ratio (N/O) models are indistinguishable from one another, as the values converge for our sample range. As such, it is still unclear whether we are dealing with extremely nitrogen-poor systems. Nitrogen enrichment could be moderate yet exist in higher ionization states that we are unable to probe with [NII]. As mentioned, Cameron et al. (2023c) found no detections of nitrogen even with 7-h deep G395M/F290LP spectra, suggesting future difficulties in examining N/O abundance ratios in metal-poor galaxies. However, GN-z11 revealed rarely seen NIV]λ1486 and NIII]λ1748 lines (Bunker et al. 2023), with subsequent explanations implying unusually high N and O abundances (Cameron et al. 2023b; Senchyna et al. 2023). The N/O ratio trends at high-z are outside the scope of the current work, but our JADES sample demonstrates the importance of constraining N/O trends in the high-z Universe and how nitrogen is handled in photoionization models.

thumbnail Fig. 8.

R3 versus 12 + log(O/H) and R23 vs. 12 + log(O/H) with calibrations from Hirschmann et al. (2023; black, dot-dashed) and photoionization models from Pérez-Montero (2014). We investigate N/O values of −2.0 (purple), −1.0 (green), and 0.0 (red), and log(U) values of −1.5 (dashed), −2.5 (solid), and −3.5 (dotted). Symbols are the same as in Fig. 4.

We find the Hirschmann et al. (2023) calibrations for R3 and R23 match our sample at lower metallicities (12 + log(O/H)≲7.6), whereby the locally calibrated diagnostics from Figs. 6 and 7 failed in this regard, thus demonstrating the inclusion of the various ionization sources from Hirschmann et al. (2023) is robust. However, the calibrations from Hirschmann et al. (2023) slightly overestimate the excitation ratios at intermediate metallicities (7.9 ≲ 12 + log(O/H)≲8.3), which may either suggest an adjustment of the model parameters or could be due to the low-number statistics of observed galaxies in this metallicity regime since the simulations fully sample the galaxy population down to 108 M⊙. Overall, the R3 and R23 theoretical calibrations from Hirschmann et al. (2023) trace our sample well, though intermediate redshifts require further investigation, and we cannot comment on the model’s success past the turnover point until larger high-z samples are created where spectral stacking can be completed.

4.8. A new projection in the R2–R3–O/H space

The set of calibrations presented by Sanders et al. (2023; in particular those related to the R3 and R23 diagnostics) are starting to provide a more accurate representation of the distribution of galaxies with direct metallicities in the high-z Universe. Nonetheless, the calibration curves are still poorly sampled at both the low- and high-metallicity end, with the majority of galaxies with Te measurements distributed within the 7.6 <  12 + log(O/H)< 8.2 abundance range, close to the plateau of the calibrations. Moreover, given the relatively high-excitation properties of these sources (which boosts R3 and R23 at a fixed O/H), the slope of the calibration curves appears to flatten further compared to most of the low-z calibrations, the plateau is, hence, wider, and the dynamic range in which these line ratios are sensitive to a variation in metallicity is reduced: this means that, for instance, at a value of R3 = 0.8 (above which more than 50% of the currently available calibration sample resides) the “gap” between the low- and high-metallicity solutions of the calibration is ∼0.6 dex.

Here, we attempt to provide a novel calibration based on a similar sample as described in Nakajima et al. (2022), but that, however, involves a different projection in the space defined by log([OII]λ3727, 29/Hβ), log([OIII]λ5007/Hβ), and metallicity. More specifically, such a new diagnostic, which we label as R̂, is defined as R̂ = 0.47 R2 + 0.88 R3. As described in greater detail in Appendix B, such a linear combination corresponds to a rotation of 61.82 degrees around the O/H-axis in the R2–R3–O/H space. This projection minimizes the scatter of our calibration sample in R̂ at fixed metallicity over the full O/H range spanned by the galaxy calibration sample. We fit a fourth-order polynomial to the R̂ versus O/H relation as shown in Fig. 9, with the best-fit coefficients that are provided in Appendix B. Compared to R23, this diagnostic has a wider dynamic range in its low-metallicity branch, spanning an interval of values between −0.2 and 0.8 between 7.0 <  12 + log(O/H)< 8.0, and shows a narrower turnover and plateau region.

thumbnail Fig. 9.

JWST sample with auroral lines measurements analyzed in this work is compared against the R̂ diagnostic presented in Sect. 4.8. Symbols are the same as in Fig. 4. The shaded region shows the intrinsic dispersion of the calibration. The high-z sample with Te metallicities is predicted by the R̂ calibration with a median absolute offset of 0.13 dex and a standard deviation of 0.19 dex.

We compare our observed JWST sample with the R̂ diagnostic in Fig. 9. We find a reasonably good agreement between R̂-predicted and observed metallicities for the high-z sample, with no systematic offset above or below the calibration curve: the points scatter around the best-fit relation with a median offset in R̂ of 0.002 dex at fixed O/H, a median absolute deviation of 0.13 dex, a dispersion of 0.19 dex, and a significance of 1.00σ4 given an intrinsic dispersion of the calibration of 0.058 dex.

5. Discussion

5.1. Strong-line diagnostics

From Figs. 4–7 and Table 3, we see clear discrepancies between locally-derived strong-line calibrations and our JADES sample. We find that a single calibration cannot simultaneously account for all galaxies across all diagnostics.

The largest discrepancies between local calibrations and our JADES sample are for the R2 and O3O2 diagnostics, which is most likely caused by R2 and O3O2 being insensitive to metallicity at these redshifts, namely, R2 and O3O2 are not appropriate metallicity indicators or degeneracy breakers for the high-z Universe. Recently, Reddy et al. (2023) concluded that electron gas density potentially has a larger responsibility than metallicity in modulating the ionization parameter in these early epochs. We are potentially observing this result in Figs. 4 and 5 where we have consistently high ionization ratios over our metallicity space, but further investigation is needed.

For our sample, R3 and R23 still indicate a dependency on metallicity at these high redshifts. Spearman correlations of ρs = 0.62 and 0.68 with p-values of 0.0004 and 4.4 × 10−5, respectively, further corroborate this finding. However, we do observe flattening of our sample compared with local R3 and R23 calibrations, possibly suggesting future difficulty when applying these diagnostics in the high-z Universe, especially at moderate metallicities. This flattening is potentially a result of an evolution in the ionization parameter-metallicity relation that has a higher dependency on electron densities (Reddy et al. 2023), however, a much more detailed analysis on a larger sample size of high-z [OIII]λ4363 emitters and stacked spectra of several hundreds of galaxies to probe to higher metallicities (12 + log(O/H)≳8.0 − 8.5) is required to examine the physical origins and establish whether there is a turnover for R3 and R23.

Overall, any local calibration for R2, O3O2, R3, and R23 clearly fails to simultaneously match our sample: there is a clear need for a self-consistent revision of the calibrations in the high-z Universe using JWST and we caution against the use of locally derived calibrations being applied to high-z Universe. We postpone deriving new R2, O3O2, R3, and R23 calibrations for the high-z Universe as our sample is limited and it is best to remain self-consistent until systematics between spectroscopic reduction pipelines are better characterized. As such, it is essential to continue constructing samples of [OIII]λ4363 in the high-z Universe with JWST.

While [OIII]λ4363 sample sizes increase and calibrations improve, the R̂ projection presented in this paper and the high-z calibrations from Sanders et al. (2023) provide the best match to high-z [OIII]λ4363 derived metallicities.

5.2. EW0(Hβ) Discrepancies

Rest-frame EWs(Hβ) can range between 10 and 600 Å for [OIII]λ4363 emitters (e.g., Maiolino & Mannucci 2019; Izotov et al. 2021b; Laseter et al. 2022; Nakajima et al. 2022). As such, when Nakajima et al. (2022) were developing their calibrations they investigated whether the accuracy of strong-line diagnostics could be improved if one includes rest-frame EWs(Hβ) as an additional parameter. This investigation lead Nakajima et al. (2022) to separate calibrations over the rest-frame EWs(Hβ) range of 20 Å ≲ EW0( Hβ) ≲ 300 Å, as we have shown in Figs. 4–7. Therefore, their high EW fit (EW0(Hβ)≥200 Å) is based on the most extreme EW0(Hβ) objects in their calibration sample. It is thus warranted to determine the rest-frame EWs of Hβ for our JADES galaxies and examine their strength.

To determine EW0(Hβ) for our JADES objects we interpolated the best-fit continuum to our PRISM data from PPXF over a 60 Å bin around the Hβ line center in our R1000 data, divided the measured flux of Hβ from the R1000 fits by the interpolated best-fit continuum and then divided by (1 + z). We include EW0(Hβ) Å for our objects in Table 2.

Although our JADES sample demonstrates excitation ratios higher than any local R3 and R23 calibration (excluding the extrapolation of Bian et al. 2018), the high EW0 calibration (EW0(Hβ)> 200 Å) from Nakajima et al. (2022) lies closest to the upper envelope of our sample. However, we find the median EW0(Hβ) for our JADES sample to be ∼170 Å, with the minimum being ∼70 Å and the max being ∼550 Å. Interestingly, we find the median EW0(Hβ) becomes ∼120 Å when excluding galaxies in our sample below z = 4.0. As such, there is an apparent decrease in the rest-frame EWs(Hβ) of high-z [OIII]λ4363 emitters, compared to local metal-poor objects with [OIII]λ4363 detections, even though we find higher ionization and excitation ratios for our sample.

An increase in the luminosity of [OIII]λ4363 in the high-z Universe could account for the EW0(Hβ) disparity in that galaxies in earlier epochs have intrinsically brighter [OIII]λ4363 at a fixed EW0(Hβ). However, it is difficult to characterize whether there is a physically driven increase in the luminosity of [OIII]λ4363 for our sample due to limited z >  1 [OIII]λ4363 samples, lack of flux calibrations for most studies, and undetermined mass completion limits. Nonetheless, a line luminosity increase is expected due to the FMR. At lower metallicities and/or masses, we expect an increase in the SFR, and thus luminosity.

However, it is debatable whether the FMR evolves with redshift (Mannucci et al. 2010; Curti et al. 2023b), although most studies out to z ∼ 2 agree with the local FMR originally characterized by Mannucci et al. (2010) (Cresci et al. 2012; Nakajima et al. 2012; Yabe et al. 2012, 2014, 2015; Belli et al. 2013; Stott et al. 2013; Henry et al. 2013a,b; Maier et al. 2014, 2015; Nakajima & Ouchi 2014; Song et al. 2014; Stott et al. 2014; Salim et al. 2015; Kacprzak et al. 2016; Wuyts et al. 2016; Calabrò et al. 2017; Hirschauer et al. 2018; Sanders et al. 2018). However, Curti et al. (2023b), using the same parent data set as the current work, demonstrated galaxies sit preferentially below local FMR predictions with increasing redshift (z ≳ 6), such that these galaxies are significantly less enriched at a given SFR and stellar mass.

In general, [OIII]λ4363 would be more luminous with an increase in sSFR and/or a decrease in metallicity. However, we would expect an increase in sSFR to be associated with higher rest-frame EWs(Hβ) relative to local counterparts, but for our JADES objects, we find rest-frame EWs(Hβ) lower than local galaxies that have reduced ionization/excitation ratios at similar metallicities compared to our sample. Therefore, we expect the [OIII]λ4363 luminosity of our JADES sample to be driven by lower metallicities, thus reflecting a number of possible processes such as pristine gas accretion (Mannucci et al. 2010) and efficient metal removal from stellar winds that are expected to increase with a top-heavy IMF (Palla et al. 2020). However, as mentioned, Cameron et al. (2023c) found our parent sample exhibits excitation ratios resembling extreme star-formation galaxies, such as blueberries (Yang et al. 2017b) and blue compact dwarf galaxies (Sargent & Searle 1970; Cairós et al. 2010) that are known to have high sSFRs (10−7 yr−1 ≲ sSFR ≲ 10−8 yr−1). In addition, Curti et al. (2023b) found our parent sample occupies the same region of the MZR as these extreme star-forming galaxies.

Overall, the picture is opaque. It is peculiar that we are simultaneously observing galaxies with lower rest-frame EWs(Hβ) and higher excitation values relative to local analogs that have high sSFRs. In addition, a number of possible processes, such as an evolving FMR, variations in metal-cooling due to elemental production timescales (e.g., oxygen being enriched rapidly due to the production from core-collapse supernovae, compared to similar cooling curves from nitrogen and carbon that are enriched by massive stars and type Ia supernovae), or more extreme, poorly understood thermal and density structure variations in the emitting nebulae (Cameron et al. 2023a; Reddy et al. 2023), could all affect the luminosity of [OIII]λ4363, metallicity determinations, and ionization and excitation values.

6. Summary and conclusions

We have identified ten [OIII]λ4363 detections discovered from ultra-deep JWST/NIRSpec MSA spectroscopy from the JADES DEEP survey, which is only a small fraction of the final JADES spectroscopic dataset. We applied the Te method to determine gas-phase oxygen abundances to examine how well local strong-line calibrations match a robust high-z [OIII]λ4363 sample. Our main findings are summarized as follows:

  • 1.

    The local strong-line calibrations investigated fail to reproduce our Te derived metallicities at our measured line-ratios as seen in Figs. 4–7. Specific calibrations have smaller deviations for various diagnostics while completely failing for lower metallicity galaxies, thus demonstrating the necessity for a systematic re-calibration of R2, O3O2, R3, and R23 strong-line diagnostics in the high-z Universe. We caution against employing locally derived calibrations in the high-z Universe.

  • 2.

    There is weak correlation between R2 and O3O2 with metallicity. If larger samples with higher metallicity galaxies support this finding then R2 and O3O2 would be inadequate diagnostics for deriving metallicities or breaking degeneracies in the high-z Universe. There is also an order of magnitude scatter at fixed metallicity in our sample for R2 and O3O2 diagnostics, further demonstrating ISM diversity that is potentially diminishing the dependency of R2 and O3O2 with metallicity. R3 and R23 are correlated with metallicity, but elevated, comparable line ratios across ∼1 dex in metallicity demonstrate a flattening of the strong lines with metallicity. If this trend continues past the turnover point between 8.0 ≲ 12 + log(O/H)≲8.5 then R3 and R23 would be problematic to use in the high-z Universe as metallicity would be indistinguishable without a substantial degeneracy breaker.

  • 3.

    The new R̂ projection (R̂ = 0.47 R2 + 0.88 R3) and high-z calibrations (R3 and R23) from Sanders et al. (2023) provide the best match to our sample overall. However, larger high-z [OIII]λ4363 sample sizes are needed that extend to higher metallicities past the plateaus of the calibrations.

  • 4.

    The rest-frame Hβ EWs of our JADES sample are moderate with the median being ∼170 Å. However, excluding galaxies lower than z = 4 in our JADES sample yields a median of ∼120 Å, which contrasts local galaxies with rest-frame EWs(Hβ) ∼300 Å used to derive local calibrations that still fall beneath the ionization/excitation ratios of our sample. In addition, our elevated excitation values, along with the findings of Cameron et al. (2023c) and Curti et al. (2023b), demonstrates our sample closely matches extreme star-formation galaxies, such as blueberries (Yang et al. 2017b) and blue compact dwarf galaxies (Sargent & Searle 1970; Cairós et al. 2010) that are known to have some of the highest sSFRs (10−7 yr−1 ≲ sSFR ≲ 10−8 yr−1). The combination of these findings does not present a clear description of [OIII]λ4363 production in the high-z Universe, thus requiring a much deeper examination of the possible processes.

2

Bian et al. (2018) did not include a strong-line calibration for R2.

3

Bian et al. (2018) did not provide an estimate of the intrinsic dispersion for their calibrations. Following the procedure from Curti et al. (2023a), we assume σcal = 0.15.

4

The dispersion of the R̂ calibration is lower than all local calibrations. A lower intrinsic dispersion can increase the significance of deviation since the calibration varies less compared to a calibration with higher dispersion that is able to “roam” closer to more distant points when performing a Monte Carlo procedure.

Acknowledgments

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. 2137424. E.C.L. acknowledges the support of an STFC Webb Fellowship (ST/W001438/1). S.C. acknowledges support by the European Union’s HE ERC Starting Grant No. 101040227 – WINGS. A.J.C. acknowledges funding from the “FirstGalaxies” Advanced Grant from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 789056). R.M. and W.B. acknowledge support from the Science and Technology Facilities Council (STFC) and by the ERC through Advanced Grant 695671 “QUENCH”. R.M. also acknowledges funding from a research professorship from the Royal Society. A.J.B., A.J.C., J.C., I.E.B.W., A.S., and G.C.J. acknowledge funding from the “FirstGalaxies” Advanced Grant from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 789056). S.A. and B.R.P. acknowledge support from the research project PID2021-127718NB-I00 of the Spanish Ministry of Science and Innovation/State Agency of Research (MICIN/AEI). JWST/NIRCam contract to the University of Arizona NAS5-02015. D.J.E. is supported as a Simons Investigator and by JWST/NIRCam contract to the University of Arizona, NAS5-02015. Funding for this research was provided by the Johns Hopkins University, Institute for Data Intensive Engineering and Science (IDIES). R.S. acknowledges support from an STFC Ernest Rutherford Fellowship (ST/S004831/1). B.E.R. acknowledges support from the NIRCam Science Team contract to the University of Arizona, NAS5-02015. The authors acknowledge the use of the lux supercomputer at UC Santa Cruz, funded by NSF MRI grant AST 1828315. The research of CCW is supported by NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. This research is supported in part by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. B.R.P. acknowledges support from the research project PID2021-127718NB-I00 of the Spanish Ministry of Science and Innovation/State Agency of Research (MICIN/AEI). J.S. acknowledges support by the Science and Technology Facilities Council (STFC), ERC Advanced Grant 695671 “QUENCH”.

References

  1. Aggarwal, K. M., & Keenan, F. P. 1999, ApJS, 123, 311 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aver, E., Berg, D. A., Hirschauer, A. S., et al. 2022, MNRAS, 510, 373 [Google Scholar]
  4. Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Baker, W. M., & Maiolino, R. 2023, MNRAS, 521, 4173 [CrossRef] [Google Scholar]
  6. Baker, W. M., Maiolino, R., Belfiore, F., et al. 2023, MNRAS, 519, 1149 [Google Scholar]
  7. Belli, S., Jones, T., Ellis, R. S., & Richard, J. 2013, ApJ, 772, 141 [NASA ADS] [CrossRef] [Google Scholar]
  8. Berg, D. A., Skillman, E. D., Marble, A. R., et al. 2012, ApJ, 754, 98 [NASA ADS] [CrossRef] [Google Scholar]
  9. Berg, D. A., Chisholm, J., Erb, D. K., et al. 2021, ApJ, 922, 170 [CrossRef] [Google Scholar]
  10. Bian, F., Kewley, L. J., & Dopita, M. A. 2018, ApJ, 859, 175 [CrossRef] [Google Scholar]
  11. Böker, T., Arribas, S., Lützgendorf, N., et al. 2022, A&A, 661, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Böker, T., Beck, T. L., Birkmann, S. M., et al. 2023, PASP, 135, 038001 [CrossRef] [Google Scholar]
  13. Bonaventura, N., Jakobsen, P., Ferruit, P., Arribas, S., & Giardino, G. 2023, A&A, 672, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bouché, N., Lehnert, M. D., Aguirre, A., Péroux, C., & Bergeron, J. 2007, MNRAS, 378, 525 [CrossRef] [Google Scholar]
  15. Brisbin, D., & Harwit, M. 2012, ApJ, 750, 142 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cairós, L. M., Caon, N., Zurita, C., et al. 2010, A&A, 520, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Calabrò, A., Amorín, R., Fontana, A., et al. 2017, A&A, 601, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Calura, F., Pipino, A., Chiappini, C., Matteucci, F., & Maiolino, R. 2009, A&A, 504, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cameron, A. J., Katz, H., & Rey, M. P. 2023a, MNRAS, 522, L89 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cameron, A. J., Katz, H., Rey, M. P., & Saxena, A. 2023b, MNRAS, 523, 3516 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cameron, A. J., Saxena, A., Bunker, A. J., et al. 2023c, A&A, 677, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
  25. Cappellari, M. 2023, MNRAS, 526, 3273 [NASA ADS] [CrossRef] [Google Scholar]
  26. Cardamone, C., Schawinski, K., Sarzi, M., et al. 2009, MNRAS, 399, 1191 [NASA ADS] [CrossRef] [Google Scholar]
  27. Carnall, A. C., Begley, R., McLeod, D. J., et al. 2023, MNRAS, 518, L45 [Google Scholar]
  28. Castellanos, M., Díaz, A. I., & Terlevich, E. 2002, MNRAS, 329, 315 [CrossRef] [Google Scholar]
  29. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  30. Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
  31. Christensen, L., Laursen, P., Richard, J., et al. 2012, MNRAS, 427, 1973 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ciardi, B., Ferrara, A., & White, S. D. M. 2003, MNRAS, 344, L7 [NASA ADS] [CrossRef] [Google Scholar]
  33. Conroy, C., Villaume, A., van Dokkum, P. G., & Lind, K. 2018, ApJ, 854, 139 [Google Scholar]
  34. Cowie, L. L., & Hu, E. M. 1998, AJ, 115, 1319 [Google Scholar]
  35. Cowie, L. L., Barger, A. J., & Hu, E. M. 2011, ApJ, 738, 136 [NASA ADS] [CrossRef] [Google Scholar]
  36. Cresci, G., Mannucci, F., Sommariva, V., et al. 2012, MNRAS, 421, 262 [NASA ADS] [Google Scholar]
  37. Curti, M., Cresci, G., Mannucci, F., et al. 2017, MNRAS, 465, 1384 [Google Scholar]
  38. Curti, M., Mannucci, F., Cresci, G., & Maiolino, R. 2020, MNRAS, 491, 944 [Google Scholar]
  39. Curti, M., D’Eugenio, F., Carniani, S., et al. 2023a, MNRAS, 518, 425 [Google Scholar]
  40. Curti, M., Maiolino, R., Curtis-Lake, E., et al. 2023b, A&A, submitted [arXiv:2304.08516] [Google Scholar]
  41. de Rossi, M. E., Tissera, P. B., & Scannapieco, C. 2007, MNRAS, 374, 323 [NASA ADS] [CrossRef] [Google Scholar]
  42. de Rossi, M. E., Bower, R. G., Font, A. S., Schaye, J., & Theuns, T. 2017, MNRAS, 472, 3354 [NASA ADS] [CrossRef] [Google Scholar]
  43. Dopita, M. A., Fischera, J., Sutherland, R. S., et al. 2006, ApJ, 647, 244 [NASA ADS] [CrossRef] [Google Scholar]
  44. Dopita, M. A., Kewley, L. J., Sutherland, R. S., & Nicholls, D. C. 2016, Ap&SS, 361, 61 [NASA ADS] [CrossRef] [Google Scholar]
  45. Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
  47. Ferruit, P., Jakobsen, P., Giardino, G., et al. 2022, A&A, 661, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Finkelstein, S. L. 2016, PASA, 33, e037 [Google Scholar]
  49. Finkelstein, S. L., Rhoads, J. E., Malhotra, S., Pirzkal, N., & Wang, J. 2007, ApJ, 660, 1023 [NASA ADS] [CrossRef] [Google Scholar]
  50. Finkelstein, S. L., Bagley, M. B., Ferguson, H. C., et al. 2023, ApJ, 946, L13 [NASA ADS] [CrossRef] [Google Scholar]
  51. Girichidis, P., Offner, S. S. R., Kritsuk, A. G., et al. 2020, Space. Sci. Rev., 216, 68 [NASA ADS] [CrossRef] [Google Scholar]
  52. Gnedin, N. Y. 2000, ApJ, 535, 530 [NASA ADS] [CrossRef] [Google Scholar]
  53. González, V., Bouwens, R. J., Labbé, I., et al. 2012, ApJ, 755, 148 [CrossRef] [Google Scholar]
  54. Hayden-Pawson, C., Curti, M., Maiolino, R., et al. 2022, MNRAS, 512, 2867 [NASA ADS] [CrossRef] [Google Scholar]
  55. Henry, A., Martin, C. L., Finlator, K., & Dressler, A. 2013a, ApJ, 769, 148 [NASA ADS] [CrossRef] [Google Scholar]
  56. Henry, A., Scarlata, C., Domínguez, A., et al. 2013b, ApJ, 776, L27 [NASA ADS] [CrossRef] [Google Scholar]
  57. Henry, A., Scarlata, C., Martin, C. L., & Erb, D. 2015, ApJ, 809, 19 [Google Scholar]
  58. Hirschauer, A. S., Salzer, J. J., Skillman, E. D., et al. 2016, ApJ, 822, 108 [NASA ADS] [CrossRef] [Google Scholar]
  59. Hirschauer, A. S., Salzer, J. J., Janowiecki, S., & Wegner, G. A. 2018, AJ, 155, 82 [NASA ADS] [CrossRef] [Google Scholar]
  60. Hirschmann, M., Charlot, S., & Somerville, R. S. 2023, MNRAS, 526, 3504 [NASA ADS] [CrossRef] [Google Scholar]
  61. Hsyu, T., Cooke, R. J., Prochaska, J. X., & Bolte, M. 2017, ApJ, 845, L22 [NASA ADS] [CrossRef] [Google Scholar]
  62. Hunt, L., Magrini, L., Galli, D., et al. 2012, MNRAS, 427, 906 [NASA ADS] [CrossRef] [Google Scholar]
  63. Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [Google Scholar]
  64. Izotov, Y. I., Stasińska, G., Meynet, G., Guseva, N. G., & Thuan, T. X. 2006, A&A, 448, 955 [CrossRef] [EDP Sciences] [Google Scholar]
  65. Izotov, Y. I., Guseva, N. G., Fricke, K. J., & Henkel, C. 2019, A&A, 623, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Izotov, Y. I., Guseva, N. G., Fricke, K. J., et al. 2021a, A&A, 646, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Izotov, Y. I., Thuan, T. X., & Guseva, N. G. 2021b, MNRAS, 504, 3996 [NASA ADS] [CrossRef] [Google Scholar]
  68. Jakobsen, P., Ferruit, P., Alves de Oliveira, C., et al. 2022, A&A, 661, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Jaskot, A. E., & Oey, M. S. 2013, ApJ, 766, 91 [Google Scholar]
  70. Kacprzak, G. G., van de Voort, F., Glazebrook, K., et al. 2016, ApJ, 826, L11 [CrossRef] [Google Scholar]
  71. Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
  72. Kewley, L. J., Dopita, M. A., Leitherer, C., et al. 2013, ApJ, 774, 100 [NASA ADS] [CrossRef] [Google Scholar]
  73. Kisielius, R., Storey, P. J., Ferland, G. J., & Keenan, F. P. 2009, MNRAS, 397, 903 [NASA ADS] [CrossRef] [Google Scholar]
  74. Kojima, T., Ouchi, M., Rauch, M., et al. 2020, ApJ, 898, 142 [NASA ADS] [CrossRef] [Google Scholar]
  75. Labbé, I., Oesch, P. A., Bouwens, R. J., et al. 2013, ApJ, 777, L19 [CrossRef] [Google Scholar]
  76. Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010, A&A, 521, L53 [CrossRef] [EDP Sciences] [Google Scholar]
  77. Laseter, I. H., Barger, A. J., Cowie, L. L., & Taylor, A. J. 2022, ApJ, 935, 150 [NASA ADS] [CrossRef] [Google Scholar]
  78. Lian, J. H., Li, J. R., Yan, W., & Kong, X. 2015, MNRAS, 446, 1449 [NASA ADS] [CrossRef] [Google Scholar]
  79. Luridiana, V., Morisset, C., & Shaw, R. A. 2015, A&A, 573, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Maier, C., Lilly, S. J., Ziegler, B. L., et al. 2014, ApJ, 792, 3 [NASA ADS] [CrossRef] [Google Scholar]
  81. Maier, C., Ziegler, B. L., Lilly, S. J., et al. 2015, A&A, 577, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
  83. Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
  85. Marino, R. A., Rosales-Ortega, F. F., Sánchez, S. F., et al. 2013, A&A, 559, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Maseda, M. V., van der Wel, A., Rix, H.-W., et al. 2014, ApJ, 791, 17 [CrossRef] [Google Scholar]
  87. Maseda, M. V., Bacon, R., Franx, M., et al. 2018, ApJ, 865, L1 [Google Scholar]
  88. Maseda, M. V., Bacon, R., Lam, D., et al. 2020, MNRAS, 493, 5120 [Google Scholar]
  89. Maseda, M. V., Lewis, Z., Matthee, J., et al. 2023, ApJ, 956, 11 [NASA ADS] [CrossRef] [Google Scholar]
  90. Matteucci, F. 2012, Chemical Evolution of Galaxies (Berlin: Springer-Verlag) [Google Scholar]
  91. Matthee, J., Sobral, D., Santos, S., et al. 2015, MNRAS, 451, 400 [Google Scholar]
  92. Mollá, M., García-Vargas, M. L., & Bressan, A. 2009, MNRAS, 398, 451 [CrossRef] [Google Scholar]
  93. Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Nakajima, K., & Ouchi, M. 2014, MNRAS, 442, 900 [Google Scholar]
  95. Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2012, ApJ, 745, 12 [NASA ADS] [CrossRef] [Google Scholar]
  96. Nakajima, K., Ouchi, M., Xu, Y., et al. 2022, ApJS, 262, 3 [CrossRef] [Google Scholar]
  97. Nakajima, K., Ouchi, M., Isobe, Y., et al. 2023, ApJS, 269, 33 [NASA ADS] [CrossRef] [Google Scholar]
  98. Oesch, P. A., Brammer, G., van Dokkum, P. G., et al. 2016, ApJ, 819, 129 [NASA ADS] [CrossRef] [Google Scholar]
  99. Palay, E., Nahar, S. N., Pradhan, A. K., & Eissner, W. 2012, MNRAS, 423, L35 [NASA ADS] [CrossRef] [Google Scholar]
  100. Palla, M., Calura, F., Matteucci, F., et al. 2020, MNRAS, 494, 2355 [NASA ADS] [CrossRef] [Google Scholar]
  101. Patrício, V., Christensen, L., Rhodin, H., Cañameras, R., & Lara-López, M. A. 2018, MNRAS, 481, 3520 [CrossRef] [Google Scholar]
  102. Pérez-Montero, E. 2014, MNRAS, 441, 2663 [CrossRef] [Google Scholar]
  103. Pérez-Montero, E., Contini, T., Lamareille, F., et al. 2013, A&A, 549, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
  105. Pillepich, A., Nelson, D., Hernquist, L., et al. 2018, MNRAS, 475, 648 [Google Scholar]
  106. Pillepich, A., Nelson, D., Springel, V., et al. 2019, MNRAS, 490, 3196 [Google Scholar]
  107. Pilyugin, L. S., & Grebel, E. K. 2016, MNRAS, 457, 3678 [NASA ADS] [CrossRef] [Google Scholar]
  108. Pilyugin, L. S., Mattsson, L., Vílchez, J. M., & Cedrés, B. 2009, MNRAS, 398, 485 [NASA ADS] [CrossRef] [Google Scholar]
  109. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Porter, L. E., Orr, M. E., Burkhart, B., et al. 2022, MNRAS, 515, 3555 [NASA ADS] [CrossRef] [Google Scholar]
  111. Pradhan, A. K., Montenegro, M., Nahar, S. N., & Eissner, W. 2006, MNRAS, 366, L6 [NASA ADS] [CrossRef] [Google Scholar]
  112. Pustilnik, S. A., Kniazev, A. Y., Perepelitsyna, Y. A., & Egorova, E. S. 2020, MNRAS, 493, 830 [NASA ADS] [CrossRef] [Google Scholar]
  113. Pustilnik, S. A., Egorova, E. S., Kniazev, A. Y., et al. 2021, MNRAS, 507, 944 [NASA ADS] [CrossRef] [Google Scholar]
  114. Rasappu, N., Smit, R., Labbé, I., et al. 2016, MNRAS, 461, 3886 [NASA ADS] [CrossRef] [Google Scholar]
  115. Reddy, N. A., Topping, M. W., Shapley, A. E., et al. 2022, ApJ, 926, 31 [NASA ADS] [CrossRef] [Google Scholar]
  116. Reddy, N. A., Topping, M. W., Sanders, R. L., Shapley, A. E., & Brammer, G. 2023, ApJ, 952, 167 [CrossRef] [Google Scholar]
  117. Repp, A., & Ebeling, H. 2018, MNRAS, 479, 844 [NASA ADS] [Google Scholar]
  118. Rhoads, J. E., Wold, I. G. B., Harish, S., et al. 2023, ApJ, 942, L14 [NASA ADS] [CrossRef] [Google Scholar]
  119. Roberts-Borsani, G. W., Bouwens, R. J., Oesch, P. A., et al. 2016, ApJ, 823, 143 [NASA ADS] [CrossRef] [Google Scholar]
  120. Salim, S., Lee, J. C., Davé, R., & Dickinson, M. 2015, ApJ, 808, 25 [NASA ADS] [CrossRef] [Google Scholar]
  121. Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016a, ApJ, 825, L23 [NASA ADS] [CrossRef] [Google Scholar]
  122. Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016b, ApJ, 816, 23 [Google Scholar]
  123. Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2018, ApJ, 858, 99 [NASA ADS] [CrossRef] [Google Scholar]
  124. Sanders, R. L., Shapley, A. E., Jones, T., et al. 2021, ApJ, 914, 19 [CrossRef] [Google Scholar]
  125. Sanders, R. L., Shapley, A. E., Topping, M. W., Reddy, N. A., & Brammer, G. B. 2023, ApJ, submitted [arXiv:2303.08149] [Google Scholar]
  126. Sargent, W. L. W., & Searle, L. 1970, ApJ, 162, L155 [NASA ADS] [CrossRef] [Google Scholar]
  127. Schaefer, A. L., Tremonti, C., Belfiore, F., et al. 2020, ApJ, 890, L3 [NASA ADS] [CrossRef] [Google Scholar]
  128. Schaefer, A. L., Tremonti, C., Kauffmann, G., et al. 2022, ApJ, 930, 160 [NASA ADS] [CrossRef] [Google Scholar]
  129. Schaerer, D., Marques-Chaves, R., Barrufet, L., et al. 2022, A&A, 665, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Senchyna, P., Plat, A., Stark, D. P., & Rudie, G. C. 2023, AAS J., submitted [arXiv:2303.04179] [Google Scholar]
  131. Shim, H., Chary, R.-R., Dickinson, M., et al. 2011, ApJ, 738, 69 [NASA ADS] [CrossRef] [Google Scholar]
  132. Smit, R., Bouwens, R. J., Labbé, I., et al. 2014, ApJ, 784, 58 [NASA ADS] [CrossRef] [Google Scholar]
  133. Smith, B., Sigurdsson, S., & Abel, T. 2008, MNRAS, 385, 1443 [NASA ADS] [CrossRef] [Google Scholar]
  134. Song, M., Finkelstein, S. L., Gebhardt, K., et al. 2014, ApJ, 791, 3 [Google Scholar]
  135. Spitoni, E., Calura, F., Mignoli, M., et al. 2020, A&A, 642, A113 [EDP Sciences] [Google Scholar]
  136. Stasińska, G. 2002, Rev. Mex. Astron. Astrofis. Conf. Ser., 12, 62 [Google Scholar]
  137. Stasińska, G. 2005, A&A, 434, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Storey, P. J., Sochi, T., & Badnell, N. R. 2014, MNRAS, 441, 3028 [CrossRef] [Google Scholar]
  139. Stott, J. P., Sobral, D., Bower, R., et al. 2013, MNRAS, 436, 1130 [CrossRef] [Google Scholar]
  140. Stott, J. P., Sobral, D., Swinbank, A. M., et al. 2014, MNRAS, 443, 2695 [NASA ADS] [CrossRef] [Google Scholar]
  141. Tayal, S. S. 2007, ApJS, 171, 331 [CrossRef] [Google Scholar]
  142. Taylor, A. J., Barger, A. J., Cowie, L. L., Hu, E. M., & Songaila, A. 2020, ApJ, 895, 132 [NASA ADS] [CrossRef] [Google Scholar]
  143. Taylor, A. J., Cowie, L. L., Barger, A. J., Hu, E. M., & Songaila, A. 2021, ApJ, 914, 79 [CrossRef] [Google Scholar]
  144. Taylor, A. J., Barger, A. J., & Cowie, L. L. 2022, ApJ, 939, L3 [NASA ADS] [CrossRef] [Google Scholar]
  145. Thuan, T. X., Guseva, N. G., & Izotov, Y. I. 2022, MNRAS, 516, L81 [NASA ADS] [CrossRef] [Google Scholar]
  146. Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
  147. Trump, J. R., Haro, P. A., Simons, R. C., et al. 2023, ApJ, 945, 35 [NASA ADS] [CrossRef] [Google Scholar]
  148. Tumlinson, J., & Shull, J. M. 2000, ApJ, 528, L65 [NASA ADS] [CrossRef] [Google Scholar]
  149. Übler, H., Maiolino, R., Curtis-Lake, E., et al. 2023, A&A, 677, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  150. Vale Asari, N., Stasińska, G., Morisset, C., & Cid Fernandes, R. 2016, MNRAS, 460, 1739 [NASA ADS] [CrossRef] [Google Scholar]
  151. Wold, I. G. B., Malhotra, S., Rhoads, J., et al. 2022, ApJ, 927, 36 [NASA ADS] [CrossRef] [Google Scholar]
  152. Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [Google Scholar]
  153. Wuyts, E., Wisnioski, E., Fossati, M., et al. 2016, ApJ, 827, 74 [NASA ADS] [CrossRef] [Google Scholar]
  154. Yabe, K., Ohta, K., Iwamuro, F., et al. 2012, PASJ, 64, 60 [NASA ADS] [Google Scholar]
  155. Yabe, K., Ohta, K., Iwamuro, F., et al. 2014, MNRAS, 437, 3647 [NASA ADS] [CrossRef] [Google Scholar]
  156. Yabe, K., Ohta, K., Akiyama, M., et al. 2015, PASJ, 67, 102 [NASA ADS] [CrossRef] [Google Scholar]
  157. Yang, H., Malhotra, S., Gronke, M., et al. 2017a, ApJ, 844, 171 [NASA ADS] [CrossRef] [Google Scholar]
  158. Yang, H., Malhotra, S., Rhoads, J. E., & Wang, J. 2017b, ApJ, 847, 38 [NASA ADS] [CrossRef] [Google Scholar]
  159. Yates, R. M., Kauffmann, G., & Guo, Q. 2012, MNRAS, 422, 215 [NASA ADS] [CrossRef] [Google Scholar]
  160. Yates, R. M., Schady, P., Chen, T. W., Schweyer, T., & Wiseman, P. 2020, A&A, 634, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  161. Zenocratti, L. J., De Rossi, M. E., Theuns, T., & Lara-López, M. A. 2022, MNRAS, 512, 6164 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Metallicity prescriptions and collisional strengths

In Section 3.2.2, we examined systematic offsets introduced when changing metallicity prescriptions between PyNeb and the empirical relations from Izotov et al. (2006). We demonstrated there is a −0.11 dex offset between PyNeb and Izotov et al. (2006) for our sample. The median error of PyNeb derived abundances for our sample is 0.12 dex, so the systematics introduced when choosing a metallicity prescription are comparable to the associated error with our measurements. We demonstrate these systematics further in Figures A.1 and A.2 by deriving metallicities for our sample using the Izotov et al. (2006) prescription and comparing against strong-line calibrations as we did in Figures 4-7. We clearly see our sample more closely matches R3 and R23 local calibrations when using Izotov et al. (2006). However, more recent local calibrations, such as Curti et al. (2017, 2020) and Nakajima et al. (2023), along with the high-z calibrations from Sanders et al. (2023), employed PyNeb for their Te determinations and therefore their calibrations. As such, if we were to determine the respective PyNeb calibrations using Izotov et al. (2006) instead then the main findings of the paper remain. It is clear that choosing a metallicity prescription matters and, thus, future studies combining multiple samples should consistently re-derive metallicities for each respective sample to remain self-consistent.

thumbnail Fig. A.1.

Our sample with derived abundances using Izotov et al. (2006) compared against local calibrations for R2 and O3O2, respectively.

In addition to metallicity prescription choice, the atomic data used, such as the options provided in PyNeb or the CLOUDY configurations used in Izotov et al. (2006), can introduce systematic offsets. For example, we use the O2+ collision strengths from Aggarwal & Keenan (1999) and Palay et al. (2012) when determining our metallicities, but Sanders et al. (2023) used O2+ collision strengths from Storey et al. (2014) (the default of PyNeb) when deriving their metallicities; hence, why we re-derived metallicities from Sanders et al. (2023) for our sample. Similarly to Fig. 3, we present in Fig. A.3 the systematic offsets in metallicity for our sample introduced when choosing to use O2+ collision strengths between Storey et al. (2014) and Aggarwal & Keenan (1999) & Palay et al. (2012) internal to PyNeb. We find a median metallicity offset of 0.02 dex, but there are offsets between ∼ − 0.1 and 0.1 dex in our sample. It is clear the systematic offsets between metallicity prescriptions are overall larger, but the offsets introduced when choosing collisional strengths can be non-negligible.

Overall, it is clear that choosing a metallicity prescription and (to a lesser extent) the collisional strengths, matters. The systematics introduced with choice will affect future studies investigating the MZR and FMR, especially as we begin establishing these principal scaling relations in the high-z Universe (e.g., Curti et al. 2023b). The slope and normalization of these scaling relations are essential in constraining galaxy chemical evolution models and interpreting the driving mechanisms behind their respective existence, shape, and evolution, thus self-consistency is key before the systematics and their effects are more closely examined.

thumbnail Fig. A.2.

Same as Figure A.1, except for R3 and R23.

thumbnail Fig. A.3.

Deviation between metallicites derived by PyNeb using O2+ collision strengths from Aggarwal & Keenan (1999) and Palay et al. (2012) as well as Storey et al. (2014). The solid line represents unity, whereas the dashed line represents the median offset between Aggarwal & Keenan (1999) and Palay et al. (2012) as well as Storey et al. (2014).

Appendix B: Calibration of the new 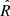diagnostic

In Section 4.8, we provide the calibration to a new metallicity diagnostic based on a combination of log([OIII]λ5007/Hβ) and log([OII]λ3727, 29/Hβ), which differs from the standard R23 and we test it against galaxies with direct metallicities at high-z (z >  2) from ERO, CEERS, and JADES. Here, we provide a more detailed description of the calibration sample and rationale.

The sample combines the stacked spectra of SDSS galaxies in bins of log([OIII]λ5007/Hβ) vs log([OII]λ3727, 29/Hβ) at high metallicity (12+log(O/H)≳8.2) from Curti et al. (2017) with individual galaxies at intermediate and low metallicities compiled from the literature. In particular, the latter include 364 low-metallicity SDSS and blue compact dwarf galaxies from Izotov et al. (2006), 41 galaxies from Berg et al. (2012), 18 galaxies from Izotov et al. (2019), 5 galaxies from Pustilnik et al. (2020, 2021), and 95 galaxies from Nakajima et al. (2022) (and Nakajima, private communication), for a total of 465 low-metallicity objects with Te-based oxygen abundances.

In the top-left panel of Figure B.1, we plot the distribution of this sample in the log([OIII]λ5007/Hβ) versus log([OII]λ3727, 29/Hβ) diagram; each data point is color-coded by its metallicity derived with the Te method, with squared symbols representing stacked spectra from Curti et al. (2017) and circles marking individual galaxies from the literature. The distribution of points in the diagram reflects the well-known sequence in metallicity and ionization parameter observed in large local surveys like SDSS; however, several among the most extremely metal-poor galaxies deviate from the sequence in its upper-left branch, while preferentially occupying a region of significantly lower R3, at fixed R2. This makes it difficult to find a parameterization in such a 2D space that correctly predicts the metallicity over the entire range spanned by the sample.

Therefore, we searched for a re-projection of the axis that facilitates the metallicity prediction over the whole abundance scale. Ideally, such projection should incorporate the different dependencies between line ratios, ionization parameter, and metallicity seen in many metal-poor galaxies of the sample, whose ISM properties more closely resemble those of high redshift objects also observed with JWST/NIRSpec Cameron et al. (2023c). The projection is shown in the top-right panel of Figure B.1. More specifically, we search for a linear combination of R2 and R3 in the form:

(B.1)

which is equivalent to a rotation of the R2-R3 plane around the O/H axis. We then fit a fourth-order polynomial to the resulting ratio versus the metallicity, in the form of R = ∑ncnxn where x = 12+log(O/H) − 8.69, and identify the angle ϕ that allows the scatter to be minimized in metallicity from the best-fit relation. This procedure leads to a best-fit ϕ = 61.82deg, which translates into =0.47R2 + 0.88R3, that is, the best possible projection of the R2 vs R3 diagram that predicts the metallicity, given the calibration sample. The best-fit coefficients for the new calibration are reported below, and the RMS of the fit is 0.058 dex. The new calibration, with its best fit, is shown in the bottom panel of Figure B.1.

thumbnail Fig. B.1.

Determination of calibration. Top-left: Distribution of our combined sample of stacked spectra (solid squares, from Curti et al. 2017) and individual galaxies (solid circles, compiled from literature as described in the text of Appendix B) in the R2 vs R3 diagram. Each point is color-coded by the Te-derived metallicity. Top-right: Rotation by 61.82 degrees of the R2-R3 plane around the O/H axis. Such a projection minimizes the scatter in metallicity at fixed = 0.47 R2 + 0.88 R3. Bottom panel : Best-fit polynomial relation (black curve) defining the calibration for the diagnostic is shown together with the full calibration sample.

All Tables

Table 1.

Measured fluxes and errors of emission lines of interest from PPXF in units of 10−20 erg s−1 cm−2.

In the text
Table 2.

Derived galaxy properties of our sample.

In the text
Table 3.

Significance of deviation (in units of σ) for the expected line ratios from each strong-line calibration to our JADES sample presented in Figs. 4–7.

In the text

All Figures

thumbnail Fig. 1.

Redshift distribution of our parent JADES sample of 198 objects with both PRISM and grating spectra and our ten novel [OIII]λ4363 emitters. No pre-selection was performed on the parent JADES sample as we visually inspected all the objects.
In the text
thumbnail Fig. 2.

JWST/NIRSpec R1000 spectra of our 10 novel detections. The best-fit models from PPXF are shown in purple. The lines of interest (located at the vertical dotted lines) shown from left to right are [OII]λλ3727, 3729, Hγ and [OIII]λ4363, and Hβ \AMP [OIII]λλ4959, 5007. [OII]λλ3727, 3729 and Hγ and [OIII]λ4363 share the same y-axis. The top panels show the 2D spectrum for each respective line complex. JADES-GS+53.13284−27.80185 did not have [OIII]λλ4959, 5007 coverage in R1000 due to the detector gap, so we present [OIII]λλ4959, 5007 from our PRISM observations.
In the text
thumbnail Fig. 3.

Deviation between metallicites derived by Izotov et al. (2006) and PyNeb. The solid line represents unity, whereas the dashed line represents the median offset between Izotov et al. (2006) and PyNeb.
In the text
thumbnail Fig. 4.

Relationship between Te metallicity and R2 for our JADES sample compared with strong-line calibrations from Maiolino et al. (2008), Curti et al. (2017), Curti et al. (2020), and the “all”, “large equivalent width (EW)”, and “small EW” calibrations from Nakajima et al. (2022). Bian et al. (2018) does not include a calibration for R2, but we include their calibrations for O3O2, R3, and R23 in Figs. 5–7. Solid lines indicate calibrated ranges whereas dotted lines indicate the extrapolation of the calibration over the metallicity range 6.9 ≤ 12 + log(O/H)≤9.0. The six subplots demonstrate the difference between Te derived metallicities and calibration-derived metallicities for our individual galaxies. The vertical lines represent galaxies in our sample, where the respective strong-line calibration cannot compute a metallicity for the measured line ratios.
In the text
thumbnail Fig. 5.

Identical to Fig. 4, except the relationship is between Te metallicity and O3O2.
In the text
thumbnail Fig. 6.

Identical to Fig. 4, except the relationship is between Te metallicity and R3.
In the text
thumbnail Fig. 7.

Identical to Fig. 4, except for the relationship between Te metallicity and R23.
In the text
thumbnail Fig. 8.

R3 versus 12 + log(O/H) and R23 vs. 12 + log(O/H) with calibrations from Hirschmann et al. (2023; black, dot-dashed) and photoionization models from Pérez-Montero (2014). We investigate N/O values of −2.0 (purple), −1.0 (green), and 0.0 (red), and log(U) values of −1.5 (dashed), −2.5 (solid), and −3.5 (dotted). Symbols are the same as in Fig. 4.
In the text
thumbnail Fig. 9.

JWST sample with auroral lines measurements analyzed in this work is compared against the R̂ diagnostic presented in Sect. 4.8. Symbols are the same as in Fig. 4. The shaded region shows the intrinsic dispersion of the calibration. The high-z sample with Te metallicities is predicted by the R̂ calibration with a median absolute offset of 0.13 dex and a standard deviation of 0.19 dex.
In the text
thumbnail Fig. A.1.

Our sample with derived abundances using Izotov et al. (2006) compared against local calibrations for R2 and O3O2, respectively.
In the text
thumbnail Fig. A.2.

Same as Figure A.1, except for R3 and R23.
In the text
thumbnail Fig. A.3.

Deviation between metallicites derived by PyNeb using O2+ collision strengths from Aggarwal & Keenan (1999) and Palay et al. (2012) as well as Storey et al. (2014). The solid line represents unity, whereas the dashed line represents the median offset between Aggarwal & Keenan (1999) and Palay et al. (2012) as well as Storey et al. (2014).
In the text
thumbnail Fig. B.1.

Determination of calibration. Top-left: Distribution of our combined sample of stacked spectra (solid squares, from Curti et al. 2017) and individual galaxies (solid circles, compiled from literature as described in the text of Appendix B) in the R2 vs R3 diagram. Each point is color-coded by the Te-derived metallicity. Top-right: Rotation by 61.82 degrees of the R2-R3 plane around the O/H axis. Such a projection minimizes the scatter in metallicity at fixed = 0.47 R2 + 0.88 R3. Bottom panel : Best-fit polynomial relation (black curve) defining the calibration for the diagnostic is shown together with the full calibration sample.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.