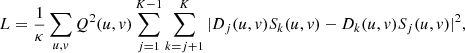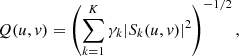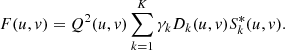EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 681 (January 2024) A&A, 681 (2024) A58 Full HTML
Issue
A&A
Volume 681, January 2024
Solar Orbiter First Results (Nominal Mission Phase)
Article Number A58
Number of page(s) 7
Section 9. The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346019
Published online 11 January 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The Polarimetric and Helioseismic Imager (PHI or SO/PHI; Solanki et al. 2020) is one of the ten instruments on board the Solar Orbiter mission (Müller et al. 2020). The spacecraft was launched in 2020 to perform both in situ and remote sensing observations of the Sun and the inner heliosphere. The goal of SO/PHI is to map the magnetic field and the line-of-sight velocities of the plasma in the solar photosphere from observations of the spectrum of the full Stokes vector of the Fe I line at 617.3 nm. SO/PHI has two telescopes: the High Resolution Telescope (HRT; Gandorfer et al. 2018) and the Full-Disk Telescope (FDT). The former offers a 0.28° × 0.28° field of view (FoV) with an angular sampling of 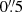0 . ″ 5 $ 0{{\overset{\prime\prime}{.}}}5 $ per pixel. The latter provides a larger 2° circular FoV at the expense of a decreased angular sampling of 3 . 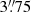″ 75 $ 3{{\overset{\prime\prime}{.}}}75 $.

The instrument undergoes large variations in temperature due to the elongated orbit of the Solar Orbiter spacecraft, which approaches the Sun as close as 0.28 au at the perihelion. The two telescopes make use of phase diversity (PD) and refocusing capabilities to compensate for both thermo-mechanic deformations within the telescopes and (primarily) thermo-optic effects in the Heat Rejecting Entrance Windows (HREWs; see Kahil et al. 2023). Phase diversity is employed to obtain the wavefront error caused by the optical system and to restore the polarized images taken by the instrument. The refocusing mechanism allows the focal plane of the instrument to be adjusted. Both PD and focusing run images are acquired periodically in order to calibrate the telescopes.

The standard PD technique is based on the acquisition of a pair of images, one close to the focus of the instrument and another defocused by a known amount. When combined with a simplified model of the telescope, it allows for wavefront sensing and reconstruction of the solar scene. The method was devised by Gonsalves & Chidlaw (1979) and was later adapted by Löfdahl & Scharmer (1994) to deal effectively with extended (solar) images. Its use in solar astronomy has been consolidated over the past decades with outstanding results (e.g., Bonet et al. 2004). The PD technique can be employed alone (Martínez Pillet et al. 2011) or together with multiframe blind deconvolution (MFBD; Löfdahl et al. 1998; Criscuoli et al. 2005), or it can be combined with the multiobject multiframe blind deconvolution (MOMFBD) method (Van Noort et al. 2005). The combinations of PD with MFBD and MOMFBD are very powerful, as they allow for the correction of both temporally varying seeing-induced wavefront errors and static aberrations – through the PD channel (van Noort & Rouppe van der Voort 2008; Henriques 2012; Löfdahl et al. 2021).

Typically, in the PD process, the two images are recorded simultaneously to avoid the emergence of differential aberrations caused by atmospheric turbulence (“seeing”) or by vibrations of the instrument (“jitter”), as well as to prevent the evolution of the solar scene from corrupting the reconstruction. A simultaneous approach is not possible in SO/PHI because it is equipped with a single camera1. Instead, the nominal PD program follows a sequential strategy: a focused image is recorded and then a 0.5 λ peak-to-valley (PV) defocus is applied to take the second image. In the HRT, an Image Stabilization System (ISS; Volkmer et al. 2012) minimizes contamination from jitter, and only the net image shifts caused by the refocusing mechanism have to be taken into account. In the case of the FDT, jitter is governed by the platform vibrations and is dealt with by realigning the two images, which is relatively straightforward, given that the solar limb is always visible. The impact of solar evolution cannot be avoided, but it is expected to be negligible, provided that the two images are acquired within a few seconds of difference (Bailén et al. 2022a). Experimental validations of this approach with real data observed by SO/PHI have been carried out recently (Kahil et al. 2022, 2023).

Images acquired during focus calibrations of the instrument can also be used for PD purposes provided that: (1) they are recorded close enough in time, and (2) the relative defocus among them is comparable to the one employed in the nominal PD mode. The availability of a series of images defocused by different amounts can be particularly valuable, as the combination of multiple phase diversities can overcome wavefront retrieval and object restoration limitations arising from high noise levels in the observations. A generalization of the algorithm of Löfdahl & Scharmer (1994) to accommodate an arbitrary number of PD images in a single merit function (Paxman et al. 1992) has been presented by Bailén et al. (2022b). The authors confirmed through different numerical experiments that the addition of multiple PD images improves both the wavefront retrieval and the scene restoration because more information is available to build the merit function and to restore the object. The approach followed by Bailén et al. (2022b) can be regarded as a particular case of the MFBD algorithm of Löfdahl (2002) and of the MOMFBD technique. An application of PD with more than two images with the MOMFBD code developed by Van Noort et al. (2005) can be found in Löfdahl & Scharmer (2012).

In this work, we assess the wavefront distortion caused by the HRT telescope from a series of images taken during the commissioning phase of the SO/PHI instrument that are part of the focusing runs (hereafter referred to as “through-focus” images). We evaluate the inferred wavefront error and the restoration of the scene as a function of the number of phase diversities. Our analysis is based on the algorithm presented by Bailén et al. (2022b). In Sect. 2 we describe the data we have employed and the conditions under which they were recorded. In Sect. 3 we present the technique that has been followed to determine the wavefront error and restore the original scene. In Sect. 4 we show the results obtained for two focusing series of the HRT with different defocus steps. Finally, we summarize our main conclusions in Sect. 5.

2. Observations

We have taken advantage of the series of through-focus images acquired during in-flight calibrations of the SO/PHI instrument to both retrieve its wavefront distortion and restore the solar scene. Through-focus images were obtained by means of a dedicated refocusing mechanism for each telescope (Solanki et al. 2020)2. As a first step, 50 through-focus images were recorded with a “coarse” step. The best focus was then inferred by identifying the image with the highest contrast and a second “fine” scan of another 20 through-focus images was performed to improve the focusing. Figure 1 shows the contrast of the images along the coarse (top panel) and fine (bottom panel) through-focus series for the HRT telescope, as well as a parabolic fitting of the data. We observed that the fine scan allows for a more accurate search of the best focus of the instrument around the position of the highest contrast inferred for the coarse scan. Table 1 displays the corresponding PV fine and coarse defocus steps of their refocusing mechanism and the parameters needed to model the telescope for PD3.

thumbnail Fig. 1.

Contrast of the through-focus images as a function of the PV defocus with respect to the best-focused image (blue solid dots) and parabolic interpolation of the data around the best-focus position (orange solid line). The top and bottom panels correspond to the coarse and fine through-focus series, respectively.

Table 1.

Parameters employed for the PD analysis of the HRT data.

Although refocusing calibrations are performed regularly, data are not generally available on the ground, as the focus is determined automatically onboard, and the acquired images are generally discarded. However, telemetry rates were sufficiently high to download the full uncompressed series of through-focus images during the near-Earth commissioning phase of the instrument, starting in February 2020 and finishing in June 2020. The downside of choosing this dataset is that the long distance of the spacecraft from the Sun during those dates complicates the analysis of the data and the interpretation of the results, as the observed granulation by the instrument presents a very small contrast (HRT) or is even unresolved (FDT).

The data used in this work comes from the refocusing scans that were recorded on April 17, 2020, at a distance of 0.82 au away from the Sun for the HRT. The instrument was set to accumulate 20 images per position through the coarse series, while it acquired only one image per position through the fine series. This means that the S/N of the observations is about four times larger for the coarse series than for the fine through-focus data. The retrieved wavefront degradation was inferred over a small quiet-sun region of the FoV of the telescope. The selected region of interest was divided into 5 × 5 subfields. The average wavefront was applied to restore the original scene observed during the focus calibration. Data from the FDT was excluded from the analysis because the spatial information contained in the images is very limited for PD purposes at such a large distance from the Sun.

Through-focus data enables the use of several images with different defocuses for PD, contrary to the nominal PD program of SO/PHI. The range of useful phase diversities is only limited by the position of the best-focused image, by the restricted number of available positions, and by the maximum time gap allowed between the PD images. For the HRT, the focus was inferred to be located at the 16th position of the fine refocusing scan. The best-focused image for the coarse scan was found at the 29th position. This means that the maximum available defocus is 0.453 λ for the fine series of HRT and 8.260 λ for the coarse series. In the latter, the defocus difference among the images employed for PD was kept below ±0.6 λ in order to ensure that the maximum gap time between them is 30–40 s. This way we could prevent the observed solar scene from being too different between any pair of images (Bailén et al. 2022a).

3. Method

All images have been flat-fielded, dark corrected, and aligned with pixel accuracy by means of a cross-correlation technique. These images feed the algorithm of Bailén et al. (2022b), which attempts to minimize the merit function presented by Paxman et al. (1992):

L = 1 κ ∑ u , v Q 2 ( u , v ) ∑ j = 1 K − 1 ∑ k = j + 1 K | D j ( u , v ) S k ( u , v ) − D k ( u , v ) S j ( u , v ) | 2 , $$ \begin{aligned} L=\frac{1}{\kappa }\sum _{u,v}Q^2(u,v)\sum _{j=1}^{K-1}\sum _{k=j+1}^{K}|D_j(u,v)S_k(u,v)-D_k(u,v)S_j(u,v)|^2, \end{aligned} $$(1)

where K is the number of PD images – two in the classic PD approach –, (u, v) are the coordinates of the images in frequency domain, Dj refers to the Fourier transform of the jth image, Sj represents the optical transfer function (OTF) corresponding to the jth PD, κ ≡ K(K − 1)/2, and Q is given by by Eq. (4) of Bailén et al. (2022b),

Q ( u , v ) = ( ∑ k = 1 K γ k | S k ( u , v ) | 2 ) − 1 / 2 , $$ \begin{aligned} Q(u,v)=\left(\sum _{k=1}^{K}\gamma _k|S_k(u,v)|^2\right)^{-1/2}, \end{aligned} $$(2)

where γk is a regularization factor that equalizes the noise contribution of each image and is typically close to unity.

We note that the normalization factor, κ, is simply the number of possible combinations of pairs of images with different phases that are summed in Eq. (1). This factor does not appear in Paxman et al. (1992). We introduced it here to allow for the comparison of merit functions obtained when varying K. The normalization factor chosen here is possibly subject to debate, as Eq. (14) of Paxman et al. (1992), from which Eq. (1) is derived, includes only K terms. The best way of comparing the results retrieved with different numbers of PD images is therefore an open question that should be investigated further.

The merit function can be parameterized by a set of Zernike coefficients, usually ordered following Noll (1976)4. An iterative algorithm adjusts the coefficients to minimize the merit function by inverting a set of equations through the singular value decomposition (SVD) method. Once the wavefront error is retrieved, the scene is restored in the Fourier domain using Eq. (19) of Paxman et al. (1992):

F ( u , v ) = Q 2 ( u , v ) ∑ k = 1 K γ k D k ( u , v ) S k ∗ ( u , v ) . $$ \begin{aligned} F(u,v)=Q^2(u,v)\sum _{k=1}^{K}\gamma _k D_k(u,v)S_k^*(u,v). \end{aligned} $$(3)

The first Zernike term can be omitted from the fitting since it only introduces an offset of the wavefront error that is irrelevant to computing the OTF. The next two terms (vertical and horizontal tip/ tilt) represent a shift on the point spread function (PSF).

A good alignment of the PSFs is important to obtaining accurate results. Differential shifts can be corrected by cross-correlating the images with subpixel accuracy (e.g., Guizar-Sicairos et al. 2008), but this is not recommended, as it can induce errors when inferring coma-like aberrations, which also displace the PSF. Therefore, we estimated the individual tip/tilt terms for each defocused image jointly with the remaining Zernike aberrations in a way similar to the one described by Löfdahl & Scharmer (1994) for K = 2.

4. Results

4.1. Fine through-focus series

We inferred the wavefront degradation caused by the HRT by employing different combinations of fine through-focus images. For each set, one of the images is focused, while the others are defocused. The range of the defocused images goes from −0.45 λ to +0.12 λ to cover the whole range of available positions. The upper half of Table 2 displays the amounts of defocus that correspond to each choice of K for the fine through-focus series. We note that K = 2 represents the “classic” PD case, that is, where only a focused-defocused pair of images is employed. The amount of defocus corresponding to K = 2 was chosen as being the closest to the one employed during the nominal PD calibrations of the instrument (0.5 λ).

Table 2.

Values of the phase diversities and results obtained for each choice of K.

We also note that in our sign convention, negative defocuses refer to shifts of the image beyond the detector’s plane, while positive values are related to displacements induced in the opposite direction. Only one positive defocus was chosen in this case due to the very limited amount of defocus that can be achieved in that direction (Sect. 2).

We set the number of fitted Zernike polynomials, J, to 21. This choice was made for the following reasons: (1) a larger value of J does not produce significant changes in the retrieved wavefront; (2) higher-order coefficients show small amplitudes that fluctuate around zero; and (3) the stability – and hence the accuracy – of the method is reduced when too many coefficients are fitted (Hirzberger et al. 2011). The latter translates into larger fluctuations of the highest-order terms and in more pronounced differences of the retrieved coefficients for different choices of K.

By trial and error, we manually adjusted the cutoff value for SVD. We applied a value of 0.02, expressed as a fraction of the maximum singular value, as we observed it provides a faster convergence – smaller number of iterations – than what was obtained with other cutoff choices.

Figure 2 shows the Zernike coefficients retrieved for the different combinations of employed through-focus images. We observe that terms tend to converge toward a particular value as K is increased. In fact, the retrieved wavefront error is almost identical for K = 4 and K = 5, with only some small differences, observed mostly in Z15 and Z18. This behavior is in very good agreement with the one found for synthetic data by Bailén et al. (2022b). The relatively large deviation of the wavefront retrieved for K = 2 when compared to other choices of K is possibly influenced to a large extent by the impact of noise on the method performance. Increasing the number of phase diversities reduces the influence of noise and facilitates the convergence of the algorithm toward the “optimal” wavefront, up to a certain level.

thumbnail Fig. 2.

High Resolution Telescope Zernike coefficients (in wavelength units) retrieved from the fine through-focus series data for K = 2 (black dashed-dotted line), K = 3 (red dashed line), K = 4 (blue dotted line), and K = 5 (green dashed line).

Figure 3 shows a central 180″ × 180″ region of the original (top panel) and restored scenes (middle and bottom panels) – to be compared with the full 1000″ × 1000″ FoV of the HRT. The bottom panel displays the restoration corresponding to K = 5. The scene shown in the middle panel was reconstructed using the same five images but assuming a perfect (flat) wavefront. In the two cases, the previously inferred tip/tilt terms were corrected during the restoring process. The contrasts are labeled in the upper-right corner of the images in the figure. The contrast increases from 4.5% for the original image up to 10% for the PD-restored scene. These values should be compared with the 7.4% contrast obtained when a flat wavefront is employed.

thumbnail Fig. 3.

Focused image of the fine scan series. Top: central part of the HRT recorded image corresponding to the best-focused fine focusing scan. Middle: reconstructed scene with an unaberrated wavefront. Bottom: restored scene for K = 5. Contrasts are displayed in the top-right corner of the images.

The last four columns of Table 2 display for each choice of K the rms value of the retrieved wavefronts, the quiet-sun contrasts, the rms difference between the reconstructed scene with respect to the one obtained for K = 5, and the value of the optimized merit function (Eq. (1)). We observe that the amplitude of the wavefront is in the range λ/10.6 − λ/10.9, while the quiet-sun contrasts increases from 9.6% for K = 2 to 10% for K = 5, and the restored images seem to converge toward the one obtained for K = 5. This is consistent with the behavior of the merit function, which decreases when K increases, and thus indicates that the found solution is possibly approaching the optimal one.

4.2. Coarse through-focus series

Images recorded during the coarse focusing of the instrument can be employed for PD purposes, too. They present several advantages over the fine scans: (1) the range of available defocuses is larger, (2) symmetric choices of the PD with respect to the focused image are now allowed, and (3) the S/N is about four times larger than for the fine through-focus data. The defocuses chosen for each value of K are displayed in Table 2. We note that the defocus for K = 2 is again the closest one to the value employed during nominal PD observations. For K > 2, we employed symmetric defocuses since they are expected to produce better wavefront sensing (Bailén et al. 2022b). We restricted the range of defocuses to ±0.590 λ in order to keep the gap time among the images below 40 s, as this has been demonstrated to be a safe limit for sequential PD observations of evolving solar scenes (Bailén et al. 2022a).

Figure 4 shows the Zernike coefficients for the three values of K, as well as the ones displayed in Fig. 2 corresponding to K = 5 for comparison. Again, the Zernike coefficients are very similar when K > 2, with small differences only in a few terms (e.g., Z10, Z15, Z18, Z19). Most Zernike terms above Z4 are quite similar to the ones retrieved for the fine through-focus series, as we would expect if the wavefront fittings for the coarse and fine series were close to the optimal one. The defocus term (Z4) is about five times higher than that of the fine through-focus data, in good agreement with the worst accuracy of the coarse through-focus scan. The positive sign of Z4 is also consistent with what is expected from the parabolic fitting of the contrast displayed in the top panel of Fig. 1.

thumbnail Fig. 4.

High Resolution Telescope Zernike coefficients (in wavelength units) retrieved from the coarse through-focus series for K = 2 (black dashed-dotted line), K = 3 (red dashed line), K = 4 (blue dotted line), and K = 5 (green dashed line). The coefficients from the fine through-focus series for K = 5 are also displayed for comparison (gray dotted line).

The wavefront error, the contrast of the restored scenes, their differences compared to the one obtained for K, and the value of the normalized merit function can be found in Table 2. The wavefront degradation is larger than that of the fine through-focus series, in the range λ/9.1 − λ/9.5, as the Z4 contribution is much more important. Excluding Z4, the wavefront error for K = 5 is around ∼λ/10.5 and in good agreement with the results found for the fine through-focus scan. We also note that the slightly larger wavefront error retrieved for K = 3 (λ/9.2) with respect to K = 5 (λ/9.4) comes mostly from the outlier found in Z18.

The contrasts are about 1% larger than the ones found for the fine through-focus images, even for K = 2 (∼11%). The contrast improvement is consistent with the higher S/N of the coarse data, as lower noise levels are expected to translate into more accurate restorations of the scene and higher contrasts (Bailén et al. 2022a). The contrast is reduced 0.3 percentage points from K = 2 to K = 3, but the merit function and the differences between restorations decrease with K, as in Sect. 4.1. Hence, we again think that the restorations found for K = 3, and especially for K = 5, are probably more reliable. Figure 5 shows the reconstruction of the coarse series corresponding to K = 5, to be compared with the bottom panel of Fig. 3, obtained for the fine series.

thumbnail Fig. 5.

Restored scene for the coarse series corresponding to K = 5.

We also observe that the values of the merit function found for the coarse through-focus data are smaller than the ones retrieved for the same choice of K in the fine through-focus. Differences between the coarse and fine series can be partly ascribed to a possibly better wavefront retrieval in this case due to both the use of symmetric defocuses and the smaller noise level of these images.

5. Summary and conclusions

We inferred the wavefront error of the HRT telescope of the SO/PHI instrument from several, K ≥ 2, through-focus images taken during the commissioning phase of the instrument. We used a generalized version of the classic PD method (Bailén et al. 2022b) to both sense the wavefront error and restore the scene from the series of through-focus images.

We employed data recorded in the fine (∼0.03 λ defocus step) and coarse (∼0.3 λ defocus step) focusing calibrations of the instrument carried out during its commissioning. For the fine through-focus images, defocuses were chosen asymmetrically and closer to the true focus of the instrument. Meanwhile, the coarse scan allowed for the use of symmetrically defocused images around the best-focused one with a higher S/N level. In the two cases, most of the inferred Zernike coefficients converge as the number of phase diversities increase. The retrieved wavefronts of the fine and coarse series also agree very well for K > 2, except for the defocus term, which is several times larger for the latter, as expected. The wavefront error rms is λ/10 − λ/11 for the fine through-focus images and approximately λ/9 for the coarse series.

The contrast of the reconstructed object is about 10% and 11% for the fine and coarse series, respectively. We attribute the larger contrasts obtained for the coarse through-focus images mostly to their lower noise level, which is expected to produce better restorations of the object. These values of the contrast should be compared to that of the original (non-restored) focused image (4.5%) and to the one retrieved when restoring with an unaberrated wavefront (7.4%). Contrasts increase with K in the fine series but stay constant or even decrease from K = 2 to K = 3 in the coarse series. However, both the value of the merit function and the differences between restorations are lower when increasing K.

Our results are in agreement with the ones obtained from the numerical experiments carried out in Bailén et al. (2022b), where the convergence of Zernike terms implies a better wavefront sensing and differences between the restored and the true scene are minimized when increasing K. This also supports the idea that the wavefront error is better inferred and reconstructions are closer to the unaberrated and noiseless scene when we increase K.

In light of these results, we believe that the use of (at least) three accumulated images in the nominal PD mode of the instrument could improve both the wavefront error sensing and the object restoration with only a marginally increased cost. This should be especially true for images acquired at a distance closer to the Sun, for which solar granulation will be better resolved, thus increasing the amount of information needed for the algorithm to construct the merit function and possibly allowing the FDT to benefit from this method, too. Notably, these results have motivated the SO/PHI Science Team to modify the nominal PD mode to include five differently defocused images in the regular calibrations of the instrument.

1

Observing the pair of focused-defocused images in the same detector is also possible, but at the expense of decreasing the FoV (Löfdahl et al. 1998; Hirzberger et al. 2011).

2

Significant changes on the plate scale are not expected when refocusing since the cameras are placed in telecentric space.

3

Hereafter, defocuses are expressed as PV wavelength units, in agreement with the convention followed in the literature.

4

In fact, the quantity that can be parameterized is the phase of the wavefront over the pupil. The OTFs are directly related to this phase.

Acknowledgments

Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. We are grateful to the ESA SOC and MOC teams for their support. The German contribution to SO/PHI is funded by the BMWi through DLR and by MPG central funds. The Spanish contribution is funded by FEDER/AEI/MCIU (ESP-2016-77548-C5-1-R and RTI2018-096886-C5), Grant PID2021-125325OB-C51 funded by MCIN/AEI/ 10.13039/501100011033 and by “ERDF A way of making Europe”, by the “European Union”, a “Center of Excellence Severo Ochoa” award to IAA-CSIC (CEX2021-001131-S), and a Ramón y Cajal fellowship awarded to DOS. The French contribution is funded by CNES.

References

  1. Bailén, F. J., Orozco Suárez, D., Blanco Rodríguez, J., & del Toro Iniesta, J. C. 2022a, ApJS, 263, 7 [CrossRef] [Google Scholar]
  2. Bailén, F. J., Orozco Suárez, D., Blanco Rodríguez, J., & del Toro Iniesta, J. C. 2022b, ApJS, 263, 43 [CrossRef] [Google Scholar]
  3. Bonet, J. A., Márquez, I., Muller, R., et al. 2004, A&A, 423, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Born, M., & Wolf, E. 1999, Principles of Optics (Cambridge: Cambridge University Press), 986 [Google Scholar]
  5. Collados, M. 1999, Third Advances in Solar Physics Euroconference: Magnetic Fields and Oscillations, 184, 3 [NASA ADS] [Google Scholar]
  6. Criscuoli, S., del Moro, D., Bonet, J. A., et al. 2005, Sol. Phys., 228, 177 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dean, B. H., & Bowers, C. W. 2003, J. Opt. Soc. Am. A, 20, 1490 [NASA ADS] [CrossRef] [Google Scholar]
  8. del Toro Iniesta, J. C. 2003, Introduction to Spectropolarimetry (Cambridge: Cambridge University Press), 244 [Google Scholar]
  9. Gandorfer, A., Grauf, B., Staub, J., et al. 2018, Proc. SPIE, 10698, 106984N [NASA ADS] [Google Scholar]
  10. Gonsalves, R. A., & Chidlaw, R. 1979, Proc. SPIE, 207, 32 [NASA ADS] [CrossRef] [Google Scholar]
  11. Guizar-Sicairos, M., Thurman, S. T., & Fienup, J. R. 2008, Opt. Lett., 33, 156 [NASA ADS] [CrossRef] [Google Scholar]
  12. Henriques, V. M. J. 2012, A&A, 548, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Hirzberger, J., Feller, A., Riethmüller, T. L., et al. 2011, A&A, 529, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Kahil, F., Gandorfer, A., Hirzberger, J., et al. 2022, Proc. SPIE, 12180, 121803F [NASA ADS] [Google Scholar]
  15. Kahil, F., Gandorfer, A., Hirzberger, J., et al. 2023, A&A, 675, A61 (SO Nominal Mission Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Lee, D. J., Roggemann, M. C., & Welsh, B. M. 1999, J. Opt. Soc. Am. A, 16, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  17. Löfdahl, M. G. 2002, Proc. SPIE, 4792, 146 [CrossRef] [Google Scholar]
  18. Löfdahl, M. G., & Scharmer, G. B. 1994, A&AS, 107, 243 [NASA ADS] [Google Scholar]
  19. Löfdahl, M. G., & Scharmer, G. B. 2012, A&A, 537, A80 [Google Scholar]
  20. Löfdahl, M. G., Berger, T., Shine, R. S., et al. 1998, ApJ, 495, 965 [CrossRef] [Google Scholar]
  21. Löfdahl, M. G., Hillberg, T., de la Cruz Rodríguez, J., et al. 2021, A&A, 653, A68 [Google Scholar]
  22. Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [Google Scholar]
  23. Meynadier, L., Michau, V., Velluet, M.-T., et al. 1999, Appl. Opt., 38, 4967 [NASA ADS] [CrossRef] [Google Scholar]
  24. Mugnier, L. M., Blanc, A., Idier, J., et al. 2006, Adv. Imag. Electr. Phys., 141, 1 [CrossRef] [Google Scholar]
  25. Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Noll, R. J. 1976, J. Opt. Soc. Am. (1917-1983), 66, 207 [Google Scholar]
  27. Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992, J. Opt. Soc. Am. A, 9, 1072 [CrossRef] [Google Scholar]
  28. Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
  29. Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Van Noort, M., Rouppe Van Der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
  31. van Noort, M. J., & Rouppe van der Voort, L. H. M. 2008, A&A, 489, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Vargas Dominguez, S. 2009, PhD Thesis, Instituto de Astrofisica de Canarias, Spain [Google Scholar]
  33. Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
  34. Volkmer, R., Bosch, J., Feger, B., et al. 2012, Proc. SPIE, 8442, 84424P [NASA ADS] [CrossRef] [Google Scholar]
  35. Zhang, P., Yang, C., Xu, Z., et al. 2017, Sci. Rep., 7, 15361P [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Parameters employed for the PD analysis of the HRT data.

In the text
Table 2.

Values of the phase diversities and results obtained for each choice of K.

In the text

All Figures

thumbnail Fig. 1.

Contrast of the through-focus images as a function of the PV defocus with respect to the best-focused image (blue solid dots) and parabolic interpolation of the data around the best-focus position (orange solid line). The top and bottom panels correspond to the coarse and fine through-focus series, respectively.
In the text
thumbnail Fig. 2.

High Resolution Telescope Zernike coefficients (in wavelength units) retrieved from the fine through-focus series data for K = 2 (black dashed-dotted line), K = 3 (red dashed line), K = 4 (blue dotted line), and K = 5 (green dashed line).
In the text
thumbnail Fig. 3.

Focused image of the fine scan series. Top: central part of the HRT recorded image corresponding to the best-focused fine focusing scan. Middle: reconstructed scene with an unaberrated wavefront. Bottom: restored scene for K = 5. Contrasts are displayed in the top-right corner of the images.
In the text
thumbnail Fig. 4.

High Resolution Telescope Zernike coefficients (in wavelength units) retrieved from the coarse through-focus series for K = 2 (black dashed-dotted line), K = 3 (red dashed line), K = 4 (blue dotted line), and K = 5 (green dashed line). The coefficients from the fine through-focus series for K = 5 are also displayed for comparison (gray dotted line).
In the text
thumbnail Fig. 5.

Restored scene for the coarse series corresponding to K = 5.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.