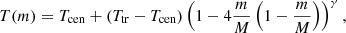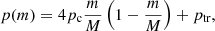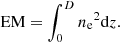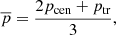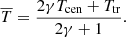| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 23 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202345970 | |
| Published online | 12 December 2023 | |
Two-horn quiescent prominence observed in Hα and Mg II h&k lines with THEMIS and IRIS⋆
1
ETH-Zurich, Hönggerberg campus, HIT building, Zürich, Switzerland
2
PMOD/WRC, Dorfstrasse 33, 7260 Davos Dorf, Switzerland
e-mail: krzysztof.barczynski@pmodwrc.ch
3
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris-Diderot, 5 place Jules Janssen, 92190 Meudon, France
4
SUPA School of Physics and Astronomy, The University of Glasgow, Glasgow G12 8QQ, UK
5
KU-Leuven, 3001 Leuven, Belgium
6
THEMIS, INSU, CNRS, UPS 3718 IAC, Via Lactea, 38200 La Laguna, Tenerife, Spain
7
University of Wrocław, Centre of Scientific Excellence – Solar and Stellar Activity, Kopernika 11, 51-622 Wrocław, Poland
Received:
22
January
2023
Accepted:
22
August
2023
Context. Prominences are large magnetic structures in the corona filled by cool plasma with fast evolving fine structure.
Aims. We aim to better understand the plasma conditions in the fine structure of a quiescent prominence including two transient horns observed at the bottom of the cavity using the high resolution Interface Region Imaging Spectrograph (IRIS) and the MulTi-Raies (MTR) spectrograph of the Télescope Heliographique pour l’Etude du Magnétisme et des Instabilités Solaires (THEMIS) in the Canary Islands.
Methods. We analysed the spectra obtained in Hα by THEMIS and Mg II by IRIS and compare them with a grid of 23 940 1D radiative transfer models which include a prominence-to-corona transition region (PCTR). The full observed profiles of Mg II in each pixel are fitted completely by synthesised profiles with ×RMS (Cross RMS; an improved version of the rolling root mean square (rRMS) method). When the RMS is below a certain threshold value, we recover the plasma conditions from the parameters of the model best fitting the observed line profile. This criterion is met in two regions (the horns and edge of the prominence) where the line profiles can generally be described as single peaked.
Results. The 1D models suggest that two different kinds of model atmospheres correspond to these two regions. The region at the edge is found to be fitted mainly with isothermal and isobaric models, while the other area (the horns) is seen to be fitted with models with a PCTR that have optical thicknesses of less than 5. In the prominence edge, the theoretical relationship between the integrated intensities in Hα and Mg II is verified and corresponds to low emission measure values. In these regions the electron density is around 1010 cm−3, while it is one order of magnitude less in the horn regions around 109 cm−3.
Conclusions. In the horns, we find some profiles are best fitted with models with high mean temperatures. This suggests that the hot PCTR found in the horns could be interpreted as prominence plasma in condensation phase at the bottom of the coronal cavity.
Key words: Sun: filaments / prominences / Sun: magnetic fields
Movies associated to Figs. 2, 7, A.1–A.3 are available at https://www.aanda.org.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Prominences are intriguing and enigmatic structures with a fine balance of forces (e.g., gravity and magnetic tension), which exhibit evolving magnetic topology. Solar prominences are cool dense structures suspended in the solar corona, at heights typically ranging from a few thousand kilometres up to hundreds of thousands of kilometres. Typical temperatures of the central regions of prominences are between 6000 and 8500 K. Outside of this region, the temperature and pressure rapidly increase up to coronal values of around 1 MK and 0.05 dyn cm−2 (Aschwanden 2004). The region where this rapid temperature and pressure change occurs is called the prominence-to-corona transition region (PCTR). The plasma density in the central coolest parts is about two orders of magnitude larger than that in the corona, and thus the presence of magnetic field is necessary for the support and stability of a prominence. Nevertheless, it is surprising that this relatively cool material reaches coronal heights. The driving forces behind their stability, evolution, and fine structure remain open questions in the field (Schmieder et al. 2014).
Once formed, prominences come in a wide variety of morphologies. They display large varieties of dynamics, which are understood to be driven by their formation, and internal and global evolution (Labrosse et al. 2010; Mackay et al. 2010). Their appearance is strongly influenced by projection effects (Schmieder et al. 2017; Gunár et al. 2018).
Prominences may appear at the limb surrounded by a cavity when their corresponding filaments have their axis lying along the east-west direction (Gibson 2018). Gibson (2015) observed well contrasted cavities in AIA 171 Å and 211 Å. A cavity is a tunnel-like plasma depletion with a coronal temperature and a central hotter core. The cavity reflects the fact that prominences have a flux rope topology with dips in the magnetic field lines (Aulanier & Schmieder 2002).
Horns connect the cool and dense prominence core to the hot and tenuous corona, representing a field-aligned prominence-corona transition region where large amplitude oscillations may appear (Luna et al. 2012; Wang et al. 2016). Horns are located at the base of coronal cavities and have different plasma characteristics to that of the prominence body (Schmit & Gibson 2013; Schmit et al. 2013). These authors proposed that horns are formed by cooling and condensating plasma. This is supported by magnetohydrodynamic (MHD) simulations (Luna et al. 2012; Schmit et al. 2013; Xia et al. 2014). On the contrary, Wang et al. (2016) described the horns as the sites of heating and diluted plasma. From the MHD simulations of Fan & Liu (2019), horns are described as the sites of high current concentrations among quasi-separatrices and hyperbolic flux tube. Prominence ‘horns’ are threaded by twisted field lines containing shallow dips, where the prominence condensations have evaporated to coronal temperatures (Fan & Liu 2019). In horns, it is predicted that magnetic field lines are weakly twisted favouring high-speed flows and very transient condensation (Guo et al. 2022).
The modelling of solar prominences in order to obtain their diagnostics is a topic of current scientific research. As of now, the use of 1D NLTE modelling is the most computationally efficient due to the exponentially increasing parameter space of current 2D multithread models (Gunár et al. 2022; Peat 2023). Jejčič et al. (2022) based their fitting on five parameters with isobaric and isothermal models – the integrated intensity of Hα, Mg II h, Mg II k, their FWHM, and the k/h ratio. These observations were also presented in Ruan et al. (2018, 2019), but a smaller number of combined profiles were analysed. Using a similar method of fitting observations with 1D isobaric model results, Vial et al. (2019) and Zhang et al. (2019) discussed the physical parameters pixel by pixel at the base of an eruptive prominence from IRIS spectra.
A step forward compared to this multi-parameter fitting method is the fitting of the full observed Mg II h&k profiles. These profiles are fitted using 1D radiative transfer models. These models can use one of two types of atmospheric model: an isothermal and isobaric atmosphere, or an atmosphere with a PCTR. This method of fitting has the benefit of fitting the intensity in each wavelength point of the observed and synthesised profiles. Additionally, this consequently recovers the integrated intensities and FWHM of the profiles. This is a useful step to determine the physical parameters of fine structure in prominences which exhibit mainly non-reversed profiles. Heinzel et al. (2015) showed that single-peak profiles could correspond to a fine structure with a relatively high gas pressure in models with PCTR. This is contrary to isobaric models, which fit single-peaked profiles with only low gas pressures (Heinzel et al. 2014).
From this perspective, Peat et al. (2021) developed the rRMS method to match the output of the 1D NLTE radiative transfer code, PROM (Gouttebroze et al. 1993; Heinzel et al. 1994; Levens & Labrosse 2019), directly to that of observation. In this aforementioned paper, full Mg II h&k profiles were fitted from a grid consisting of 1007 pre-generated models. For every raster, each of the synthesised line profiles – produced from the 1007 models – is ‘rolled’ through some wavelength window with the RMS at each pixel position being measured. The model that produces the lowest RMS value is selected as the best fit for that pixel. Additionally, a Dopplershift can be recovered from this method as a consequence of the rolling. Peat et al. (2021) demonstrated that the Dopplershift map obtained from rRMS was consistent with the Dopplershifts derived from the quantile method (Kerr et al. 2015). This method has since been improved with a vectorised cross-correlation and now produces conservative errors associated with each of the fits (Peat et al., in prep.).
In this paper we present a highly dynamic, twin-horned quiescent prominence, observed with high resolution spectrographs in Hα and Mg II (Table 1). Section 2 describes the observations and calibration; Sect. 3 covers the morphology of the prominence; Sect. 4 details the characteristics of the observed profiles (Hα and Mg II); Sect. 5 presents the theoretical grid of models; Sect. 6 provides the theoretical parameters that are deduced from the comparison of theory and observations; and, finally, Sect. 7 summarises the results.
Observed line or band characteristics.
2. Observation and data preparation
2.1. Observation
In this work, we used simultaneous observations obtained by the Interface Region Imaging Spectrograph (IRIS; De Pontieu et al. 2014), the Télescope Heliographique pour l’Etude du Magnétisme et des Instabilités Solaires (THEMIS; Mein & Rayrole 1985), the X-Ray Telescope (XRT; Golub et al. 2007) onboard Hinode (Kosugi et al. 2007), and the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) onboard the Solar Dynamics Observatory (SDO; Pesnell et al. 2012). We focused on prominences at the west solar limb and analysed their properties based on imaging and spectroscopic observations.
On 26 September 2019, images from the Global Oscillation Network Group (GONG; Harvey et al. 1996), of the National Solar Observatory (NSO) show the presence of a long polar filament channel in the southern hemisphere along the S40 parallel. This channel displayed a few bushes of dark filamentary material, which can be seen in Fig. 1. The Meudon spectroheliograph of the Observatoire de Paris observed this prominence in Ca II H&K on 28 September. Later, a second prominence was seen in Hα by GONG on 1 October. These prominences were the targets of THEMIS and IRIS on 28 September 2019 and 1 October 2019, respectively. In Table 1, we summarise the characteristics of the spectral lines and instrument filters used for these IRIS, THEMIS, and AIA observations.
 |
Fig. 1. Filaments and prominences in survey images from Meudon spectroheliograms in Ca II and from GONG in Hα. The prominence on September 28 corresponds to filament F1. |
2.2. IRIS
IRIS can provide observations in two far-ultraviolet (FUV) channels (FUV1: 1332–1358 Å, and FUV2: 1389–1407 Å) and a single near-ultraviolet (NUV) channel (NUV: 2783–2834 Å). These channels include strong chromospheric (Mg II, C II) and transition region (Si IV) lines. The observation program of 28 September 2019 focused only on the Mg II lines. We used the raster data to provide statistics of the Mg II (intensity, Doppler velocity, and FWHM). The IRIS Slit Jaw Imager (SJI) provides the context of the position and surroundings of the slit with the 2796 Å filter, which has a bandpass of 4 Å.
We focused on the simultaneous Mg II rasters and SJI 2796 Å observations of the prominence obtained on 28 September 2019 between 11:09 UTC and 14:56 UTC. There is only SJI 2796 Å from slit-jaw data for this observation.
The observation comprised of thirteen very large, coarse, 64-step rasters taken over a duration of approximately four hours. The spatial step of the rasters is 2″. It took 16 s to perform one single slit observation and 17 min to perform a full raster scan including the time of reading the device. Meanwhile, the cadence of the SJI is 16 s. Thus, we have one SJI image for each slit position. The SJIs allow us to study the fast transverse dynamics of the prominence material, which we cannot do with the spectra. The details of the IRIS observations are summarised in Table 2. The data were downloaded from the Lockheed Martin Solar and Astrophysics Laboratory (LMSAL) IRIS database1. We used IRIS level-2 data corrected for the dark current, flat field, and geometric distortion (De Pontieu et al. 2014).
Characteristics of the IRIS observations.
The IRIS data are given in Data Number units (DN). The conversion to a flux in physical units was provided using IDL SolarSoft (SSW; Freeland & Handy 1998) procedure iris_getwindata2 with keywords /calib and /perang. The obtained intensity is presented in erg s−1 sr−1 cm−2 Å−1.
2.3. THEMIS
To study the Hα prominence, we used the observations provided by THEMIS on the island of Tenerife in the Canary Islands. The observations have the following characteristics: a lateral spatial resolution of 0.5″ (1 pixel size = 0.234/0.250″), a spectral resolution of 11/12 mÅ per pixel with a bandpass of 6.3 Å centred around 6563 Å. The field of view (FOV) is 100″ × 128″. The exposure time is 100 ms, taking around one minute to complete a full raster; however, here, with the accumulation of data during 1 s, the cadence is around 2.5 min.
Two prominences were well observed with IRIS during this campaign; the first of which was observed on the 28 September 2019 located on the south western solar limb at S44 between 11:15 and 15:19 UTC (sequences 64–121); and the second on the 1 October 2019 also located on the south western solar limb at S20 between 08:09–09:54 and 10:09–14:48 UTC (sequences 125–131).
The second prominence is used as a case study to test the method of cross-correlation of the Mg II profiles by Peat et al. (in prep.).
In this study we focused on the prominence observed on the 28 September 2019. This prominence is at high latitude and corresponds to a very weak filament containing only a few dark features according to observations a few days before in the Meudon spectroheliograms in Hα (Fig. 1).
2.4. SDO
To investigate the temporal evolution of the prominence at different temperatures corresponding to the chromosphere, transition region and the solar corona, we used the imaging data obtained by AIA in the 304 Å (0.1 MK), 171 Å (0.6 MK) and 193 Å (1.2 MK) channels. The data presents the full solar disc with a spatial scale of 0.6″/pixel (resolution 1.2″/pixel) at a cadence of 12 s. The pre-processed SDO data were downloaded via JSOC.
3. Morphology
3.1. Cavity
We followed the evolution of the prominence using the SJI 2796 Å movie (SJI2796.mp4), and the AIA online movies in three different wavelength channels, 171 Å (AIA171.mp4), 193 Å (AIA193.mp4), and 304 Å (AIA304.mp4), after a co-alignement of the images. Snapshots of the movies are presented in Fig. 2 and in Figs. A.1–A.3. The SJI 2796 Å movie in particular shows the tremendous dynamics of the fine structures in the prominence. These fine structures are very transient. In all the wavelengths, two horns appear at the top of the prominence between 11:19 UTC and 12:29 UTC. They are no longer visible by 13:15 UTC. The lifetime of these horns is around 90 min – this is consistent with a past study by Schmit & Gibson (2013). They correspond to the bottom of the cavity detectable in X-ray seen by XRT (Fig. 3).
 |
Fig. 2. Overview of prominence in IRIS SJI images in Mg II during the three hours of observations, including snapshots of the online movie (SJI2796.mp4). The vertical dashed lines indicate the field of view of the rasters. The two horns of the prominence are well visible in the top panels; white arrows point to the location of the horns. |
 |
Fig. 3. Hinode/XRT image clearing showing the cavity around 620″, −800″ (half ellipse indicated by a white arrow). |
3.2. IRIS raster
We reconstructed 13 images from the rasters and computed Dopplershifts and the FWHM assuming that the line profiles are of a Gaussian shape (Figs. 4 and 5). The horns are visible until 12:53 UTC in the SJI 2796 Å movie. In the raster data, at the beginning of the sequence one horn is blue shifted and the other is redshifted – suggesting a possible rotational motion. This indicates the presence of a cylindrical flux rope in the cavity visible from its section in the disc plan. Large areas in the prominences are blueshifted and redshifted. This coherence in large areas has already been noted for other prominences (Schmieder et al. 2010). We produced histograms of Dopplershifts and FWHM. The recovered velocities are mostly around ±20 km s−1 (Fig. 6). The FWHM values are in the range of 0.2 − 0.4 Å. Few points have a FWHM outside of this range; they are located between the two horns at the bottom of the flux rope.
 |
Fig. 4. Evolution of the Mg II k integrated intensity maps from 11:26 UT to 13:46 UT (rasters 1–8). Each map corresponds to a raster of the prominence obtained in the field of view (127 arcsec × 175 arcsec) indicated in Fig. 2 by two vertical dashed lines. The time needed to raster the prominence is indicated at the top of the image (around 16.5 min). The maps are reconstructed by using the 64 Mg II k slit spectra of the raster scan and integrating the intensity in a wavelength range of ±2 Å around the Mg II peak intensity. Two horns are visible at the top of the prominence in the first five maps; white arrows point to the horn’s location. |
 |
Fig. 5. Evolution of the Mg II k Doppler shift velocity maps from 11:26 UTC to 13:46 UTC (rasters 1–8). Each map corresponds to a raster of the prominence obtained in the field of view (127 arcsec × 175 arcsec) indicated in Fig. 2 by two vertical dashed lines. The Dopplershift velocities are obtained by Gaussian fitting of the profiles. |
 |
Fig. 6. Histograms of Doppler velocities for the prominence in Hα and in Mg II k for the whole Mg II prominence using two methods for the computation of Dopplershifts: the Gaussian fit or the quantile method. |
3.3. Coalignment of IRIS and THEMIS
We co-aligned the Mg II raster data with that of the SJI 2796 Å data. THEMIS Hα observations were co-aligned approximately co-temporally with AIA 304 Å, allowing us to finally co-align THEMIS with the IRIS Mg II SJI. We used AIA 304 Å to obtain larger context view than provided by IRIS and THEMIS. It was necessary because header information in THEMIS data does not contain pointing information.
To define the limb of the solar disc in IRIS raster data, we computed the total photospheric emission at 2800 Å in a 2 Å large passband and provide a map of such computed total intensity. Based on this map, we define a region out of disc and out of prominence [x, y]=[600 : 640, −810 : −840] arcsec in raster map obtained between 11:26 and 11:43 UT, hereafter named the background region. We defined that the solar limb at the location where the photospheric intensity is three times larger than the intensity of the background region. A so defined solar limb is presented in Figs. 5 and 7a–c.
 |
Fig. 7. Prominence intensity (a), Dopplershift (b), and FWHM (c) images (top panels): reconstructed from the 64 Mg II k spectra of raster 5 obtained by IRIS between 12:36 UT and 12:53 UT; Prominence intensity (d), Dopplershift (e), and FWHM (f) images (bottom panels): reconstructed from the Hα spectra obtained by THEMIS around 12:48 UT in two minutes. In panel d the vertical dashed cyan line corresponds to the slit position 42 in the IRIS raster 5 shown above. The horizontal small blue lines indicate the pixels, B, where the profiles have been analysed (Table 4). The pixels A are not visible in Hα image. A movie is available online. |
In the second step, we define the solar limb and the edge of the solar prominence in Hα. We compute the total photospheric emission at 6564.38 Å in a 0.6 Å large passband and provide a map of such computed integrated intensity. Based on this map, we define a region out of disc and out of prominence ([x, y]=[600 : 640, −810 : −840] arcsec in raster map, hereafter named the THEMIS background region). We define the solar limb as having an intensity two times larger than the mean intensity of the THEMIS background region. A visual inspection of the photospheric intensity was used to create the definition for the limb used in this paper. However, another method, such as the inflection point method, could be used. Our definition of the limb is consistent with that found by the inflection point method. The prominence is defined as the region outside of the limb, and additionally the mean intensity between 6561.85 Å and 6564.07 Å is larger than three times the standard deviation of the THEMIS background region.
We verified that our method to define the limb gives identical results to the infletion point method within an error of 1–2 pixels for Mg II maps. The THEMIS observations are obtained with a slit scanning the prominence. Hence, we estimate an error bar of a few pixels is in the error bar of the definition of the limb. The limb is corrugated due to the technical process and seeing; therefore, it is impossible to have a better level of accuracy with the intensity inflection point method than with our threshold method (see Appendix D).
Figure 7 shows the comparison of the prominence in both lines (Mg II and Hα). The horns are observed in Mg II, but they are not seen in Hα as the material in the horns is too thin to be visible. In Hα, the prominence consists of three columns overlaid by arches. The Dopplershifts in Hα are a factor of two lower (Fig. 6) than in Mg II. This is due to the difference of spatial resolution of the two instruments. Moreover, the structures observed in Mg II are different from that observed in Hα – due to their difference in optical depth. Hα is generally optically thin in prominences, and therefore the radiation we see is integrated along the line of sight. Mg II h&k, on the other hand, is typically optically thick, only allowing us to see the front-most material. The FWHM pattern of the prominence in both lines is comparable.
4. Characteristics of Hα and Mg II profiles
4.1. Hα profiles
We used the THEMIS observations obtained at 12:48 UTC composed by a scan of 512 by 100 pixels. The scan is performed in the y direction with a step size of 1″; x is the length of the slit oriented approximately east to west. The length of the slit is 128″ and corresponds to 512 pixels obtained by oversampling the data by a factor of four. From this, 100 Hα spectra are observed. We calibrated these profiles in wavelength by using the telluric lines and by comparing the intensity of the Hα line profile references obtained on the disc. These reference profiles are taken along circles parallel to the limb at μ = 0.95, 0.98, 0.99 with the David profiles as a reference, taking into account the μ value (David 1961; Fig. B.1). This allows us to compute a proportional factor to multiply the DN number of the observations to retrieve the Hα profile intensities in erg cm−2 sr−1 s−1 Hz−1 (see Appendix B). Some example Hα profiles are presented in Fig. C.3. We reconstruct the THEMIS scan using the integrated intensity and rotate it to north-south to better compare to the IRIS images (Fig. 7).
4.2. Mg II h&k profiles
Each IRIS raster consists of 64 slit spectra of Mg II h&k obtained with a spatial step of 2″ covering 128″. As an example of this IRIS spectra, Fig. 8 presents 17 of the 64 slit spectra of raster 5. These presented slit spectra cross the prominence horns. After processing the data we obtain radiometrically calibrated Mg II profiles. In the spectra of 12:48:07 UTC in Fig. 8 – corresponding to position 42 of the slit – a handful of the 1D spectra are presented in Appendix C. We were able to match a few IRIS pixels with their corresponding Hα pixels. Figure C.2 shows the Mg II k line profiles corresponding to the Hα profiles of Fig. C.3.
 |
Fig. 8. Examples of 17 Mg II k slit spectra in the scan of raster 5 covering the prominence. The top left image is a slit jaw image, the vertical dashed-dotted lines indicate the FOV of the raster, and the thin dashed line the position of the slit S42 at 12:48 UTC used to draw the profiles in Appendix C. In Figs. C.1 and C.2 and in the bottom spectra, a series of green and blue lines indicate the position of these profiles along the slit for positions A1–12 and B1–16, respectively. |
5. Theoretical grid of models
To understand the thermodynamic properties of the prominence, we use the 1D NLTE radiative transfer code, PROM (Gouttebroze et al. 1993; Heinzel et al. 1994). Here, we used the version of PROM presented in Levens & Labrosse (2019), which builds on the version from Labrosse & Gouttebroze (2004), which introduced the PCTR.
We used a grid of 23 940 models that produce Mg II h&k and H I spectra (Peat et al., prep.). The models comprise both isothermal and isobaric atmospheres and atmospheres with a prominence-to-corona transition region (PCTR). This large grid of models allows us to explore a larger domain of parameters than in previous studies (Peat et al. 2021; Barczynski et al. 2021). The parameters of these models can be seen in Table 3. Tcen and pcen are the central temperature and pressure, respectively; Ttr and ptr are the temperature and pressure at the edge of the PCTR, respectively; slab width is the width of the slab; M is the column mass; H is the height above the solar surface; vT is the microturbulent velocity; vrad is the outwards radial velocity of the slab; and γ is a dimensionless number that dictates the extent of the PCTR. A γ value of zero indicates the model is isothermal and isobaric. For isothermal and isobaric models, Ttr ≡ Tcen, and ptr ≡ pcen.
Model parameters.
The version of PROM includes a PCTR that is formulated as a function of column mass as in Anzer & Heinzel (1999):
where pc = pcen − ptr and γ ≥ 2. These equations are not used for the isobaric and isothermal atmospheres, when γ = 0 it is simply a placeholder indicating that the model is isobaric and isothermal. The PCTR pressure profile is derived from magnetohydrostatic equilibrium, whereas the temperature profile is empirical. Additionally, the Ca II atom from Gouttebroze et al. (1997) was used as the foundation on which Levens & Labrosse (2019) built the Mg II ion. The prominence is illuminated on both sides by the solar disc; this incident radiation is taken from disc centre IRIS observations on 29 September 2013 (Levens & Labrosse 2019). All the details of the used code PROM are presented in Levens & Labrosse (2019).
A parametric study of the variation of the parameters in the space defined by Table 3 is suitable but outside the scope of this study. Such a study is planned for Peat et al. (prep.).
5.1. Theoretical relationship between Hα and Mg II intensities
The new grid of 23 940 models expand on and include the original 1007 models from Peat et al. (2021). These models allow us to compute the relationship between the integrated Mg II intensities (E(Mg II)) and the integrated Hα intensities (E(Hα)) and segregate the models according to mean temperature and thickness. Figure 9 (left panel) shows this relationship between the computed values of E(Mg IIk) and E(Hα) for a microturbulent velocity of 5 km s−1. The relationship between E(Mg IIk) and the emission measure (EM) is presented in the top right panel, and the relationship between E(Hα) and EM is presented in the bottom right panel. EM is defined by
 |
Fig. 9. Theoretical correlations between emission measure and integrated intensity. Left: relationship between the integrated intensity of Mg II k and the integrated intensity of Hα derived from the theoretical models computed with a micro-turbulence equal to 5 km s−1 and for different values of temperature and slab thickness. Top right: integrated Mg II k intensity versus EM. Bottom right: integrated Hα intensity versus EM. The horizontal (vertical) lines limit the range of Mg II k (Hα) intensities. Integrated intensities are in erg s−1 cm−2 sr−1 and EM are in cm−5. The small slab thickness models (stars) are new models. They fit quite well in the box of the observations. |
For comparison with the observations, we selected pixels belonging to the fine structure of the prominence.
5.2. Comparing observations and synthetic profiles
Peat et al. (in prep.) worked to improve the rRMS method presented in Peat et al. (2021). The ‘rolling’ aspect of the algorithm was replaced with a cross-correlation to predetermine the ‘roll’. This increased the computation speed by a factor of ten. Due to the removal of the rolling aspect, the procedure was renamed cross-RMS (×RMS) to account for the new cross-correlation. We obtain a relatively good match between observed and synthesised profiles for all the rasters.
As an example, in raster 5, good matches are found for 45% of the pixels with an RMS value less than 15 000, 22.5% of which are fitted with models with a PCTR of a higher mean temperature. However, it is difficult to find a 1D model that fits the Mg II profiles in the main core of the prominence due to its complex profiles, as shown in Fig. 10. This is why we concentrated our study of the parameters on the horns and edge of the prominence.
 |
Fig. 10. Classification of the Mg II k line profiles in raster 5 (panels a and b), map of the intensity ratio of the Mg II k/h in raster 5 (panel c). The coordinates of the maps are given in pixels to identify the selected points of Tables 4 and 5 along x = 42 px. The location x = 42 px is marked with an arrow. |
5.3. Horn and edge profile characteristics
As mentioned previously, we worked on a select few IRIS Mg II h&k profiles along slit 42 in raster 5, which corresponds to a time of 12:48:07 UT. Slit 42 crosses the column edge and one of the horns of the prominence. The selection of the Mg II h&k profiles is based on three criteria: the peak intensity should be not lower than 5 × 104 erg sr−1 s−1 Å−1 cm−2; the Mg II h&k profile should have a main single peak; the fitted model profile must not exceed a main temperature of 30 000 K.
In Table 4 we present our selection. The A profiles are located in the horn (between 249 and 309 y-pixel positions). The B profiles are in the column or edge of the column of the prominence (between 326 and 397 y-pixel positions). Figure 11 shows two profiles: one (A2) in the horn, which is well fitted by one synthetic profile and the RMS value is low; and another (B11) in the prominence body which is not well fitted, with a large RMS value. This shows how the model chosen by the code is very sensitive to the shape of the profile. The RMS values are around 4000–20 000 for the horn and much larger than this in the main body of the prominence and even at the edge of the prominence (pixels B1–16). We observe that the peak intensity of the horn profiles is much lower than the prominence by a factor of two.
 |
Fig. 11. Example of fitted theoretical profiles. The left shows an image of the prominence with an orange cross indicating the location of the profile Top: A2, A profile in the horn well-fitted with one theoretical model. Bottom: B11, Example of a profile in the prominence where the algorithm has attempted to fit a complex model to the complex structure found in this location. However, the RMS value is unsatisfactory. |
Characteristics of Mg II k and h line profiles of IRIS raster 5 (slit 42 at 12:48:07 UT) and simultaneous Hα line profiles obtained with the THEMIS.
All the pixels (A1–12 and B1–16) of the selection did not completely match with our three criteria. For example, for two pixels (A1, B15) the mean temperature of the models exceeds 30 000 K.
For half the pixels in our selection the RMS value exceeds 15 000 but we keep them because it is nearly impossible to fit these profiles with a single Gaussian (see pixel B11 in Fig. 11).
For the A profiles, no Hα emission was identified in the THEMIS observations. The Hα prominence is limited to areas where the prominence is geometrically thick enough. This has been previously found in earlier studies (Heinzel et al. 2001; Barczynski et al. 2021). A large area extending out of the Hα prominence contour is detected in the Mg II h&k lines, this corresponds to the horns. The characteristics of the horns were analysed using only the Mg II h&k line profiles (Sect. 6.2). Finally, our selection for comparison of Hα and Mg II h&k is reduced to the fine structure seen in Hα where Mg II h&k profiles exhibit mostly single peak (B profiles). These pixels correspond relatively to thin single threads.
5.4. Results of non-LTE modelling
When discussing temperatures and pressures here, we are strictly speaking of the mean temperature and pressure – defined by (Peat 2023),
and
For PCTR models, it should be noted that this is a mean temperature, that is parts of the prominence atmosphere exist at lower and higher temperatures. The results found for each point after choosing the best models for fitting Mg II profiles are presented in Table 5. The values of τ(k) are very small between points 1 and 5 when the profiles are fitted with models with PCTR and high temperatures. On the other hand, the values of τ(k) may reach 40–500 when the profiles are fitted with isobaric models. There are significant variations of solutions for adjacent pixels due to the mode of IRIS observations with a large x step (2″). We find relatively high values of τ(k) for pixels fitted with isobaric models in comparison to the prominence tornado, which used the rRMS technique (Peat et al. 2021) where the highest value of τ(k) are around 60.
Plasma parameters of the selected prominence and horn pixels in raster 5 and slit at 12:48:07 UT (slit 42 counting from 0) from non-LTE radiative transfer models.
6. Physical parameters
6.1. Emission measure from Hα and Mg II
The observed integrated intensities of the Mg II k line and Hα can be compared with the general trend obtained with the theoretical models (Fig. 9). As we explain in Sect. 5.4, the A profiles have no counterpart in Hα; they are located in the horns. The B profiles, however, do have counterparts in Hα and are located at the edge of the prominence. In this study, we did not consider the main columns of the prominence visible in Hα and Mg II because the fitting of the profiles is nearly impossible for profiles with many peaks instead of one single peak. A multithread model would be necessary to have a good fitting, but this is very computationally expensive. Table 5 presents pixels with a mix of good and ‘bad’ fits in Mg II h&k profiles. However, the selected B points still have a reasonable RMS (only twice the threshold) that we consider acceptable (Fig. 11 point B11).
Figure 9 shows models with smaller Mg II integrated intensities compared with graphs of the previous study of Barczynski et al. (2021). In that figure we draw the limits of the integrated intensity values for the B pixels using the Mg II k and Hα measurements from Table 4. The models with small thread diameters of 0−1000 km and temperature range (6000 K–20 000K) are found to be consistent with our observational bounds. The emission measure values found from the right hand panels are in the range of 7 × 1027 < EM < 1.5 × 1029 cm−5 corresponding to E(Mg II k) and 4 × 1027 < EM < 8 × 1028 cm−5 for E(Hα).
This corresponds to a relatively large range of electron densities between 5 × 109 and 5 × 1010 cm−3. This uncertainty is rather large.
6.2. Plasma parameters from fitting Mg II profiles
In Tables 5 and 6 we present the relevant outputs of the modelling for the selected pixels in the horns (A) and at the edge of the prominence (B) where the prominence is visible in Hα. We note that the threshold of the ×RMS method is reached in both cases for some pixels; in zone A, seven (out of twelve) have a fitting with a RMS lower than 15 000, and in zone B nearly all have a RMS larger than 15 000. This means that it is difficult to fit the observed profiles in B, mainly because they have two peaks and a self reversal as in Fig. 11 (B11). Therefore, the values of the parameters of pixels B are only given as an estimation or a trend value. The FWHM (k) reaches 0.3 Å in many pixels of zone B contrary to pixels where the FWHM (k) is between 0.11 and 0.25 Å with single peak profiles. This suggests that the line-of-sight crosses several fine structures.
Complementary plasma parameters of the fits in the selected pixels in the prominence and horns (raster 5, slit 42 at 12:48 UT) from non-LTE radiative transfer models: central temperature, central gas pressure, mean temperature, mean gas pressure, mean electron density, mean NH, γ.
We note that more isobaric, isothermal models are found to fit Mg II profiles in zone B (six out of ten). The mean temperature is between 6000 and 8000 K. The optical thickness of the Mg II k line can be large (540 for B11). The corresponding optical thickness for Hα is around one, which is consistent with the observations, and the prominence is visible in Hα in zone B. Mg II lines are optically thicker, and along the LOS only a part of the prominence is observed. The electron density in zone A is around 2 × 109 cm−3 with a few points of 1.3 − 2 × 1010 cm−3, while for zone B it is around 2 × 1010 cm−3 and a few values of 5 × 109 cm−3.
The conclusions obtained from the outputs of the modelling should be taken with caution. For example, the incident radiation used in our non-LTE calculations may not accurately represent the true incident radiation on the observed prominence. This may have an effect on the results as discussed by Gunár et al. (2022). There are also other uncertainties associated with IRIS radiometric calibration and degradation of the detector over time. The radiometric calibration is determined using spectral radiance measurements from the International Ultraviolet Explorer (IUE; Boggess et al. 1978) – the radiances of which are quoted as having an uncertainty of 10–15% (Tian et al. 2014).
6.3. Comparison with previous studies
Our EM values are in a first approximation similar to those found by other authors (Gouttebroze et al. 1993; Heinzel et al. 1994; Jejčič et al. 2018). However, we note that our range of EM values is narrower.
Using the fitting profile method (Tables 5 and 6), in zone B we find values of electron density (∼1010 cm−3) typical of prominences when the prominence is also visible in Hα using the classical method based on the emission measure, as presented in the previous paragraph or in other studies (Ruan et al. 2019; Jejčič et al. 2022). In zone A, we see a similar behaviour of the physical parameters found in the top of a tornado prominence with lower electron density except in a few points with value exceeding 2 × 1010 cm−3 (Barczynski et al. 2021). However, it is found for narrower threads.
Our method of fitting full profiles succeeds to reach such single threads which have very specific physical characteristics. These profiles correspond to thin threads with PCTRs that have an optical thickness in Hα too low to be detectable and may be too hot to be visible in Hα.
There are still a few pixels (A10, A11, A12) showing a higher electron density, higher pressure (0.1 dyne cm−2), and a higher temperature in the horn. When the temperature is over 15 000 K, Peat et al. (2021) concluded that the inclusion of a PCTR can dramatically influence the value of the ionisation degree (n(H II)/n(H I); Tandberg-Hanssen 1995) and electron density. Past studies (such as Vial 1998; Zhang et al. 2019) have shown that the ionisation degree generally does not rise above ten. However, such studies do not exceed temperatures of 15 000 K, where the ionisation degree is seen to exponentially rise (Peat et al. 2021). This was likely due to the isothermal and isobaric nature of the models used, and that Mg II is said to ionise to Mg III in the 15 000 K–30 000 K range (see Fig. 7 in Heinzel et al. 2014). This kind of behaviour was found in the tornado and interpreted as plasma in the condensation phase (Barczynski et al. 2021).
7. Discussion and conclusion
During a coordinated campaign between THEMIS and IRIS, we observed a very active quiescent prominence on 28 September 2019 with small transient threads. Two horns at the top of the prominence were well visible for one hour. We focused our study on the horn and the edge of the prominence. Using 23 940 NLTE 1D radiative transfer models we were able to fit the Mg II profiles in these thin structures, which mostly present one-peak Mg II profiles. We derived a few physical parameters such as electron density, mean temperature, and optical thickness. The observed Hα profiles from the coordinated campaign allowed us to compare the theoretical relationship between the integrated intensities of Mg II and Hα and the emission measure (EM). Due to our selection of non-reversed Mg II profiles, our Hα and Mg II profile analysis is restricted to the edge of the prominence. These observations behave in a similar manner to the relationship shown in Fig. 9, but there is a large uncertainty in the determination of the parameters. In the future, we would like to analyse full prominence observations with 2D Mg II modelling.
By performing pixel-by-pixel analyses on selected Mg II h&k and Hα profiles in the edge of the prominence, and on selected Mg II h&k profiles in the horns, we were able to derive the physical parameters of the plasma reliably. Overall, these two regions show similar ranges of values for the different parameters, but we note some trends – namely that more models with a PCTR are selected in the horns, whereas more isothermal and isobaric models fit the profiles in the edge region. We found that the electron density in the horns is slightly less than in the prominence column edge. However, we also find a few pixels with relatively large electron density reaching nearly 2 × 1010 cm−3. This has already been observed in tornado-like prominences and interpreted as plasma condensation (Barczynski et al. 2021; Jenkins & Keppens 2022). It was demonstrated that electron density could be high in fine structures at the prominence edges if narrow threads (of the order of 750 km) were considered (Wiik et al. 1992).
We suggest that horns could be due to the LOS emission of the PCTR of prominence in dipped field lines, as proposed by Xia et al. (2014). The density depletion in the cavity, visible in EUV and X-ray, is probably not due to a heating process of the plasma as suggested by Fan & Liu (2019). Instead, it may be attributed to the formation of plasma condensation or perhaps some drainage of material towards the chromosphere. The horn lifetime – around 30 m to 1 h – corresponds to the cooling time of coronal plasma and is therefore good support for this argument (Schmieder et al. 1996). The fine structures are very transient and could correspond to condensation in a weak twisted flux rope (Guo et al. 2022). Before drawing a conclusion regarding the formation of the horns, we would require the full temporal evolution of the spectra.
Solar Orbiter remote-sensing instruments (EUI, SPICE) should be able to observe the horns of a prominence. In the future, the Chinese ASO-S satellite and onboard Lyman alpha telescope will be able to image these horns (Zhao et al. 2022). 2D radiative transfer code models should be able to provide a definitive answer on the formation of these horns in prominences (Labrosse & Rodger 2016; Gunár et al. 2022). Additionally, they may also be able to supply the amplitude and height of the heating influence, the topology of the fine structures, the density, and the temperature (Jerčić et al. 2022).
Movies
Movie 1 associated with Fig. 2 (SJI2796) Access here
Movie 2 associated with Fig. 7 (iris_raster) Access here
Movie 3 associated with Fig. A.1 (AIA304) Access here
Movie 4 associated with Fig. A.2 (AIA171) Access here
Movie 5 associated with Fig. A.3 (AIA193) Access here
Acknowledgments
We thank the THEMIS team which assisted us in acquisition of the data during the coordinated THEMIS-IRIS campaign in September and October 2019. IRIS is a NASA small explorer mission developed and operated by LMSAL with mission operations executed at NASA Ames Research Center and major contributions to downlink communications funded by ESA and the Norwegian Space Centre. AIA data courtesy of NASA/SDO and the AIA, EVE, and HMI science teams. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and UKSA as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), UKSA (U.K.), NASA, ESA, and NSC (Norway). The Global Oscillation Network Group (GONG) is a community-based program to conduct a detailed study of solar internal structure and dynamics using helioseismology. In order to exploit this new technique, GONG has developed a six-station network of extremely sensitive, and stable velocity imagers located around the Earth to obtain nearly continuous observations of the Sun’s “five-minute” oscillations, or pulsations. This study benefited from financial support from the Programme National Soleil Terre (PNST) of the CNRS/INSU, as well as from the Programme des Investissements d’Avenir (PIA) supervised by the ANR. Support from STFC grants ST/S505390/1 (AWP) and ST/T000422/1 (NL) is gratefully acknowledged. Also thank you to Kathy Reeves for providing information on XRT data. This research used version 3.7.1 of Matplotlib (Hunter 2007), version 1.24.3 of NumPy (Harris et al. 2020), version 1.10.1 of SciPy (Virtanen et al. 2020), version 4.1.5 of the SunPy open source software package (SunPy Community 2020), and version 5.2.2 of Astropy (http://www.astropy.org) a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018)
References
- Anzer, U., & Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] [Google Scholar]
- Aschwanden, M. J. 2004, Physics of the Solar Corona: an Introduction, Springer-Praxis Books in Geophysical Sciences (New York: Springer) [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Aulanier, G., & Schmieder, B. 2002, A&A, 386, 1106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barczynski, K., Schmieder, B., Peat, A. W., et al. 2021, A&A, 653, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boggess, A., Carr, F. A., Evans, D. C., et al. 1978, Nature, 275, 372 [NASA ADS] [CrossRef] [Google Scholar]
- David, K.-H. 1961, Veroeffentlichungen der Universitaets-Sternwarte zu Goettingen, 7, 367 [NASA ADS] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [Google Scholar]
- Fan, Y., & Liu, T. 2019, Front. Astron. Space Sci., 6, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [Google Scholar]
- Gibson, S. 2015, in Solar Prominences, eds. J. C. Vial, & O. Engvold, Astrophys. Space Sci. Lib., 415, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. E. 2018, Liv. Rev. Sol. Phys., 15, 7 [Google Scholar]
- Golub, L., DeLuca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gouttebroze, P., Heinzel, P., & Vial, J. C. 1993, A&AS, 99, 513 [NASA ADS] [Google Scholar]
- Gouttebroze, P., Vial, J. C., & Heinzel, P. 1997, Sol. Phys., 172, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Dudík, J., Aulanier, G., Schmieder, B., & Heinzel, P. 2018, ApJ, 867, 115 [Google Scholar]
- Gunár, S., Heinzel, P., Koza, J., & Schwartz, P. 2022, ApJ, 934, 133 [CrossRef] [Google Scholar]
- Guo, J. H., Ni, Y. W., Zhou, Y. H., et al. 2022, A&A, 667, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. W., Hill, F., Hubbard, R. P., et al. 1996, Science, 272, 1284 [Google Scholar]
- Heinzel, P., Gouttebroze, P., & Vial, J. C. 1994, A&A, 292, 656 [NASA ADS] [Google Scholar]
- Heinzel, P., Schmieder, B., & Tziotziou, K. 2001, ApJ, 561, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Vial, J.-C., & Anzer, U. 2014, A&A, 564, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Schmieder, B., Mein, N., & Gunár, S. 2015, ApJ, 800, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comp. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jejčič, S., Schwartz, P., Heinzel, P., Zapiór, M., & Gunár, S. 2018, A&A, 618, A88 [Google Scholar]
- Jejčič, S., Heinzel, P., Schmieder, B., et al. 2022, ApJ, 932, 3 [CrossRef] [Google Scholar]
- Jenkins, J. M., & Keppens, R. 2022, Nat. Astron., 6, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Jerčić, V., Keppens, R., & Zhou, Y. 2022, A&A, 658, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerr, G. S., Simões, P. J. A., Qiu, J., & Fletcher, L. 2015, A&A, 582, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [Google Scholar]
- Labrosse, N., & Gouttebroze, P. 2004, ApJ, 617, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., & Rodger, A. S. 2016, A&A, 587, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Levens, P. J., & Labrosse, N. 2019, A&A, 625, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luna, M., Karpen, J. T., & DeVore, C. R. 2012, ApJ, 746, 30 [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [Google Scholar]
- Mein, P., & Rayrole, J. 1985, Vistas Astron., 28, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, C. E., Minnaert, M. G. J., & Houtgast, J. 1966, The Solar Spectrum 2935 A to 8770 A (Washington: USGPO) [Google Scholar]
- Peat, A. W. 2023, PhD Thesis, University of Glasgow, UK [Google Scholar]
- Peat, A. W., Labrosse, N., Schmieder, B., & Barczynski, K. 2021, A&A, 653, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Ruan, G., Schmieder, B., Mein, P., et al. 2018, ApJ, 865, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Ruan, G., Jejčič, S., Schmieder, B., et al. 2019, ApJ, 886, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Heinzel, P., Wiik, J. E., Lemen, J., & Hiei, E. 1996, Adv. Space. Res., 17, 111 [CrossRef] [Google Scholar]
- Schmieder, B., Chandra, R., Berlicki, A., & Mein, P. 2010, A&A, 514, A68 [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Tian, H., Kucera, T., et al. 2014, A&A, 569, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Mein, P., Mein, N., et al. 2017, A&A, 597, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmit, D. J., & Gibson, S. 2013, ApJ, 770, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Schmit, D. J., Gibson, S., Luna, M., Karpen, J., & Innes, D. 2013, ApJ, 779, 156 [NASA ADS] [CrossRef] [Google Scholar]
- SunPy Community (Barnes, W. T., et al.) 2020, ApJ, 890, 68 [Google Scholar]
- Tandberg-Hanssen, E. 1995, The Nature of Solar Prominences (Dordrecht: Kluwer Academic Publishers), 199 [CrossRef] [Google Scholar]
- Tian, H., De Pontieu, B., DeLuca, E., et al. 2014, IRIS Technical Note 24: Stellar Calibration [Google Scholar]
- Vial, J. C. 1998, ASP Conf. Ser., 150, 175 [NASA ADS] [Google Scholar]
- Vial, J. C., Zhang, P., & Buchlin, É. 2019, A&A, 624, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wang, B., Chen, Y., Fu, J., et al. 2016, ApJ, 827, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wiik, J. E., Heinzel, P., & Schmieder, B. 1992, A&A, 260, 419 [NASA ADS] [Google Scholar]
- Xia, C., Keppens, R., Antolin, P., & Porth, O. 2014, ApJ, 792, L38 [Google Scholar]
- Zhang, P., Buchlin, É., & Vial, J. C. 2019, A&A, 624, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J., Zhang, P., Gibson, S. E., et al. 2022, A&A, 665, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Prominence evolution
Figures A.1, A.2, and A.3 are snapshots of the AIA 304 Å, AIA 171Å, and AIA 193 Å movies. They show the evolution of the prominence with the two horns at the top. The contour of the prominence with horns obtained from the AIA 304 Å map at 12:29 UT is overlaid in the AIA 171 Å and, AIA 193 Å maps (panels c) to clearly identify the horns, which are also well observed in the panels (b).
 |
Fig. A.1. AIA 304 images; snapshots of the online movie (AIA304.mp4). The white line marks the raster position. The contour of the AIA 304 Å is overlaid in panel (c) to show the horns at the top of the prominence. |
 |
Fig. A.2. AIA 171 images; snapshots of the online movie (AIA171.mp4). The white line marks the raster position. The contour of the AIA 304 Å is overlaid in panel (c) to show the horns at the top of the prominence. The cavity is marked with a white dotted line. |
 |
Fig. A.3. AIA 193 images; snapshots of the online movie (AIA193.mp4). The white line marks the raster position. The contour of the AIA 304 Å is overlaid in panel (c) to show the horns at the top of the prominence. The cavity is marked with a white dotted line. |
Appendix B: Calibration
The Multi Thermal Raie mode (MTR) of THEMIS observes in a large wavelength domain (6Å), which allows us to almost reach the continuum in the environment of the Hα line (Figure B.1). This permits us to calibrate the wavelength domain, to correct the scattering light, and to have relatively precise measurements of the FWHM. This is not the case with other instruments such as the SST, which observes with filters (±1.5 Å) or with the MSDP (±0.7 Å).
 |
Fig. B.1. Mean Hα line profile obtained on disc at μ = 0.99 along a circular slit used to fit with the David profile for the intensity calibration. The vertical red lines indicate the position of the telluric lines for the wavelength calibration. |
To calibrate the Hα line in wavelength, we used two telluric lines of H2O located in the spectrum on the right (line A, 6560.555Å) and left (line B, 6564.206Å) sides of Hα. We chose the ROI located at the solar disc. For each telluric line, we defined a band that covers the whole line, and we fitted a Gaussian function with a slope and an offset (Moore et al. 1966).
The Hα intensity was calibrated by fitting the profiles observed at different μ values on the disc with the David profile, taking into account the limb darkening and the position on the disc. The value of the continuum intensity close to the Hα line at the disc centre is 4.077 ×10−5 erg cm−2 s−1 sr−1 Hz−1.
Appendix C: Co-temporal and co-spatial Hα and Mg II line profiles
Figures C.1, C.2, and C.3 present the series of profiles corresponding to pixels enumerated in Table 5. Hα profiles are co-temporal and co-spatial of IRIS profiles in the B series. There are no Hα profiles corresponding to the A IRIS series because there are no counts.
 |
Fig. C.2. IRIS,:Mg II k along slit 42 in raster 5 in the area at the edge of the prominence column (pixels B Table 5). |
 |
Fig. C.3. Hα profiles in the prominence observed with THEMIS, corresponding to the B pixels in Table 5. |
Appendix D: The solar limb detection
The photospheric limb can be detected using several methods. The photospheric limb is significantly sharper than the coronal one. In our work, we defined the limb using the pre-defined intensity threshold value.
Another method is, for example, to define the inflexion point, which consists of defining a limb as the extremum of the first derivative of the intensity in the function of position along the line perpendicular to the limb. We checked the inflexion method to define the limb of Mg II continuum and H-α continuum. In Fig. D.1, we show the intensity profile crossing the limb and the first derivative plot in the position function along the such profile. The strongest extremum (highlighted by a red line) defines a limb position.
 |
Fig. D.1. Inflexion method to define limb. The intensity profile along straight line perpendicular to the limb in Mg II continuum (panel a) and the intensity-position derivative in the function of position (panel b) along the same profile line. The limb is defined as the strongest derivative extremum and highlighted by a red line (panel a and b). The intensity profile parallel to the limb in H-α continuum (panel c) and the intensity-position derivative in the function of position (panel d). The limb is defined as the strongest derivative extremum and highlighted by a red line (panel c and d). |
After considering the possible errors using our threshold method compared with the inflexion method, we decided to keep our maps. The errors for Mg II reach one or two pixels. For Hα, due to the corrugated limb (result of the slit scanning the FOV and of the seeing conditions), other methods than our threshold method would not lead to more accurate results. Our method takes into account 2D mapping and a threshold that is more valuable for the data that we have.
All Tables
Characteristics of Mg II k and h line profiles of IRIS raster 5 (slit 42 at 12:48:07 UT) and simultaneous Hα line profiles obtained with the THEMIS.
Plasma parameters of the selected prominence and horn pixels in raster 5 and slit at 12:48:07 UT (slit 42 counting from 0) from non-LTE radiative transfer models.
Complementary plasma parameters of the fits in the selected pixels in the prominence and horns (raster 5, slit 42 at 12:48 UT) from non-LTE radiative transfer models: central temperature, central gas pressure, mean temperature, mean gas pressure, mean electron density, mean NH, γ.
All Figures
 |
Fig. 1. Filaments and prominences in survey images from Meudon spectroheliograms in Ca II and from GONG in Hα. The prominence on September 28 corresponds to filament F1. |
| In the text | |
 |
Fig. 2. Overview of prominence in IRIS SJI images in Mg II during the three hours of observations, including snapshots of the online movie (SJI2796.mp4). The vertical dashed lines indicate the field of view of the rasters. The two horns of the prominence are well visible in the top panels; white arrows point to the location of the horns. |
| In the text | |
 |
Fig. 3. Hinode/XRT image clearing showing the cavity around 620″, −800″ (half ellipse indicated by a white arrow). |
| In the text | |
 |
Fig. 4. Evolution of the Mg II k integrated intensity maps from 11:26 UT to 13:46 UT (rasters 1–8). Each map corresponds to a raster of the prominence obtained in the field of view (127 arcsec × 175 arcsec) indicated in Fig. 2 by two vertical dashed lines. The time needed to raster the prominence is indicated at the top of the image (around 16.5 min). The maps are reconstructed by using the 64 Mg II k slit spectra of the raster scan and integrating the intensity in a wavelength range of ±2 Å around the Mg II peak intensity. Two horns are visible at the top of the prominence in the first five maps; white arrows point to the horn’s location. |
| In the text | |
 |
Fig. 5. Evolution of the Mg II k Doppler shift velocity maps from 11:26 UTC to 13:46 UTC (rasters 1–8). Each map corresponds to a raster of the prominence obtained in the field of view (127 arcsec × 175 arcsec) indicated in Fig. 2 by two vertical dashed lines. The Dopplershift velocities are obtained by Gaussian fitting of the profiles. |
| In the text | |
 |
Fig. 6. Histograms of Doppler velocities for the prominence in Hα and in Mg II k for the whole Mg II prominence using two methods for the computation of Dopplershifts: the Gaussian fit or the quantile method. |
| In the text | |
 |
Fig. 7. Prominence intensity (a), Dopplershift (b), and FWHM (c) images (top panels): reconstructed from the 64 Mg II k spectra of raster 5 obtained by IRIS between 12:36 UT and 12:53 UT; Prominence intensity (d), Dopplershift (e), and FWHM (f) images (bottom panels): reconstructed from the Hα spectra obtained by THEMIS around 12:48 UT in two minutes. In panel d the vertical dashed cyan line corresponds to the slit position 42 in the IRIS raster 5 shown above. The horizontal small blue lines indicate the pixels, B, where the profiles have been analysed (Table 4). The pixels A are not visible in Hα image. A movie is available online. |
| In the text | |
 |
Fig. 8. Examples of 17 Mg II k slit spectra in the scan of raster 5 covering the prominence. The top left image is a slit jaw image, the vertical dashed-dotted lines indicate the FOV of the raster, and the thin dashed line the position of the slit S42 at 12:48 UTC used to draw the profiles in Appendix C. In Figs. C.1 and C.2 and in the bottom spectra, a series of green and blue lines indicate the position of these profiles along the slit for positions A1–12 and B1–16, respectively. |
| In the text | |
 |
Fig. 9. Theoretical correlations between emission measure and integrated intensity. Left: relationship between the integrated intensity of Mg II k and the integrated intensity of Hα derived from the theoretical models computed with a micro-turbulence equal to 5 km s−1 and for different values of temperature and slab thickness. Top right: integrated Mg II k intensity versus EM. Bottom right: integrated Hα intensity versus EM. The horizontal (vertical) lines limit the range of Mg II k (Hα) intensities. Integrated intensities are in erg s−1 cm−2 sr−1 and EM are in cm−5. The small slab thickness models (stars) are new models. They fit quite well in the box of the observations. |
| In the text | |
 |
Fig. 10. Classification of the Mg II k line profiles in raster 5 (panels a and b), map of the intensity ratio of the Mg II k/h in raster 5 (panel c). The coordinates of the maps are given in pixels to identify the selected points of Tables 4 and 5 along x = 42 px. The location x = 42 px is marked with an arrow. |
| In the text | |
 |
Fig. 11. Example of fitted theoretical profiles. The left shows an image of the prominence with an orange cross indicating the location of the profile Top: A2, A profile in the horn well-fitted with one theoretical model. Bottom: B11, Example of a profile in the prominence where the algorithm has attempted to fit a complex model to the complex structure found in this location. However, the RMS value is unsatisfactory. |
| In the text | |
 |
Fig. A.1. AIA 304 images; snapshots of the online movie (AIA304.mp4). The white line marks the raster position. The contour of the AIA 304 Å is overlaid in panel (c) to show the horns at the top of the prominence. |
| In the text | |
 |
Fig. A.2. AIA 171 images; snapshots of the online movie (AIA171.mp4). The white line marks the raster position. The contour of the AIA 304 Å is overlaid in panel (c) to show the horns at the top of the prominence. The cavity is marked with a white dotted line. |
| In the text | |
 |
Fig. A.3. AIA 193 images; snapshots of the online movie (AIA193.mp4). The white line marks the raster position. The contour of the AIA 304 Å is overlaid in panel (c) to show the horns at the top of the prominence. The cavity is marked with a white dotted line. |
| In the text | |
 |
Fig. B.1. Mean Hα line profile obtained on disc at μ = 0.99 along a circular slit used to fit with the David profile for the intensity calibration. The vertical red lines indicate the position of the telluric lines for the wavelength calibration. |
| In the text | |
 |
Fig. C.1. IRIS: Mg II k along slit 42 in raster 5 in the area of the horns (pixels A in Table 5). |
| In the text | |
 |
Fig. C.2. IRIS,:Mg II k along slit 42 in raster 5 in the area at the edge of the prominence column (pixels B Table 5). |
| In the text | |
 |
Fig. C.3. Hα profiles in the prominence observed with THEMIS, corresponding to the B pixels in Table 5. |
| In the text | |
 |
Fig. D.1. Inflexion method to define limb. The intensity profile along straight line perpendicular to the limb in Mg II continuum (panel a) and the intensity-position derivative in the function of position (panel b) along the same profile line. The limb is defined as the strongest derivative extremum and highlighted by a red line (panel a and b). The intensity profile parallel to the limb in H-α continuum (panel c) and the intensity-position derivative in the function of position (panel d). The limb is defined as the strongest derivative extremum and highlighted by a red line (panel c and d). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.