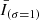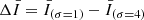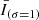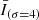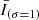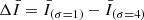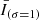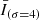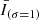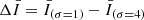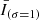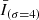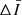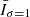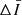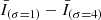EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A9 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A9
Number of page(s) 9
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346944
Published online 30 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

One of the most challenging problems in solar physics is how the solar corona is heated up to a temperature of millions of degrees, which is far above that of the photosphere. Although, it is widely accepted that the magnetic field plays a major role in the energetics of the bright corona.

The bright coronal loops are the building blocks of the solar corona. Therefore, the heating mechanisms for the coronal loops are important to understand how the corona is heated. Based on the temperature regime, the loops observed in the extreme-ultraviolet (EUV) are classified as warm loops and hot loops (Reale 2014), which confine plasma at temperatures around 1–1.5 MK and around or above 2 MK, respectively. The model developed by van Ballegooijen et al. (2017) indicates that the Alfvén wave turbulence launched from the photosphere can produce enough heat to maintain a peak temperature of about 2.5 MK of the coronal loops. Also, a large number of transverse waves are deduced from the observed Alfvénic motion of the coronal features (McIntosh et al. 2011), spicules (De Pontieu et al. 2007), and network jets (Tian et al. 2014; Shen 2021), as well as the falling solar prominence knots (Bi et al. 2020).

Energy releases from small-scale magnetic reconnections are another promising mechanism to heat the corona (Klimchuk 2006). It has been accepted that the small-scale events of magnetic reconnections (Testa et al. 2013; Gupta et al. 2018; Priest et al. 2018; Asgari-Targhi et al. 2019; Chitta et al. 2020) are responsible for the heating of the hot loops or hot plasma in the corona (Klimchuk 2006; Schmelz et al. 2015; Ishikawa et al. 2017; Yang et al. 2018; Zhang et al. 2023). It seems more controversial how the warm loops are heated. Some warm loops might be globally cooling from the hot loops (Winebarger & Warren 2005; Viall & Klimchuk 2011; Li et al. 2015), but many long-lived warm loops would be much less visible in the hot EUV channels. Although Alfvén waves originating in the photosphere may provide sufficient energy for heating the warm loops (van Ballegooijen et al. 2017), observations supporting the magnetic reconnection-type heating in the warm loops were also presented, such as the transient brightnesses found around the footpoints of the warm loops (Régnier et al. 2014; Subramanian et al. 2018), short-lived warm loops that impulsively appeared and faded out after a few minutes and never achieved million-degree temperatures (Winebarger et al. 2013), and the reconnection outflow-like plasma (referred to as a nanojet) within the warm loops composed of misaligned strands (Antolin et al. 2021).

A nanoflare refers to an impulsive energy release in the coronal-braided magnetic field (Parker 1988), which is considered the most promising mechanism for the generation of hot plasma in active regions by small-scale reconnection. According to the nanoflare scenario, when the strands reconnect, they exchange segments and footpoints (Berger & Asgari-Targhi 2009; Klimchuk 2015). However, the morphological evolutions of sub-arcsecond strands linked to nanoflares are still challenging to identify, probably due to the existing performance limits of coronal observations and the scarcity of coronal observations with a spatial resolution less than 1″, such as the High-resolution Coronal Imager (Hi-C; Kobayashi et al. 2014) and Extreme Ultraviolet Imager (EUI).

It has been reported that two braiding structures (Cirtain et al. 2013) were detected in the images taken by the Hi-C, which observed a bandpass dominated by the Fe XII 193 Å line with a pixel size of ∼0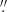 . ″ $ {{\overset{\prime\prime}{.}}} $1 (∼75 Km on the Sun) in a period of a few minutes. Using non-linear force-free field (NLFFF) extrapolation, Thalmann et al. (2014) have found that the braided structure observed by Hi-C was a low-lying twisted flux rope above a penumbral filament region. However, limited to a brief period of observation, Hi-C is unable to confirm whether these tangled loops are associated with energy release in the solar corona. Most recently, using new observations with high spatial resolution (a pixel size of 125–135 km on the Sun) from EUI on board Solar Orbiter, Chitta et al. (2022) reported the untangling of small-scale coronal braids, giving rise to coronal loops that run more parallel with each other. By contrast, the uninterrupted observations taken by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO) have a larger pixel size of ∼0 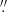. ″ $ {{\overset{\prime\prime}{.}}} $6 and then hardly recognize the braiding substructures as resolved in the Hi-C and EUI images.

Recently, various machine learning (ML) models have been applied to create artificial solar images to further extend the performance of the current solar observations (Kim et al. 2019; Szenicer et al. 2019; Bai et al. 2021; Hong et al. 2021; Dos Santos et al. 2021; Pineci et al. 2021; Yu et al. 2021). In particular, Díaz Baso & Asensio Ramos (2018) adopted a deep neural network approach to deconvolve and supper-resolve Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) images and found that the synthetic HMI images contained information not present in the original data, which supported the idea that a certain deep convolutional neural network could be applied to solar image enhancement. Super resolution (SR) is a classic problem in computer vision, which is to recover a high-resolution image from a low-resolution image. Because there are multiple solutions for any given low-resolution pixel, SR is generally an ill-posed inverse problem. Its solution pipeline is suggested to be equivalent to a deep convolutional neural network (Dong et al. 2016), and then a proper architecture of a convolutional neural network could be applied to directly learn an end-to-end mapping between low- and high-resolution images.

The rest of the paper is structured as follows. Section 2 introduces the details of the algorithm for upscaling the AIA 193 Å images. Here, the images are upscaled by the ML-based mapping from AIA to Hi-C 193 Å images, as well as by the method of deconvolution and upscaling interpolation. Section 3 presents three events not covered by Hi-C observations, in which the reconnection-like rearrangements of the braiding strands are observed in the upscaled 193 Å images and the transient hot emissions are detected on the AIA 94 Å images. Discussions and a brief summary are presented in Sects. 4 and 5.

2. Method

We used two methods to upscale the AIA 193 Å images to the pixel size of 0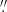 . ″ $ {{\overset{\prime\prime}{.}}} $15. Firstly, the AIA images were deconvolved with the point spread function (PSF1; Boerner et al. 2012) via the Richardson-Lucy algorithm, and then the resulting PSF-matched images were upsampled using bicubic interpolation. We refer to them as PFS-bicubic-upscaled images. Secondly, the ML-upscaled AIA 193 Å images were generated using a SR network mapping the AIA 193 Å images to Hi-C images.

To generate the ML-upscaled AIA 193 Å images, we applied the WiDe activation Super-Resolution networks (WDSR; Yu et al. 2018; Fan et al. 2018), a kind of ML network for single image SR, to upsample the AIA 193 Å images by a factor of 4. As shown in Fig. 1, the network mainly consists of 16 residual blocks (He et al. 2016). Each basic block is made up of three convolutional layers and starts with the feature maps being extended to 384 with 1 × 1 kernel. The channel number expansion before the rectified linear unit (ReLu) pooling layer, referred to as wide activation (Yu et al. 2018), allows more information to pass from shallow layers to deeper ones. A global residual connection was applied to relieve the redundant features potentially generated by the deep network architectures (Ledig et al. 2017). A pixel-shuffling layer (Shi et al. 2016) was utilized at the end of the network to upsample the final feature maps into the SR output. Weight normalization layers (Salimans & Kingma 2016) were used to ease the training difficulty of deep networks. The total number of trainable parameters for the network modelling amounts to 1.2 × 106.

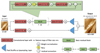thumbnail Fig. 1.

Architecture of the WDSR convolutional neural network for upsampling factor ×4. All of the feature maps in each convolutional layer have the size H × W, which is the same as that of the input images. For upscaling factor ×S (×4), the number of channels used as the input for the Pixel-Shuffle layer is exactly S2 (16).

Five pairs of AIA and Hi-C images were used to train the ML-upscaled model. The observed time difference between each pair of images is less than 3 s. Using these images we built the training set and validation set as follows. Firstly, the Hi-C images with a pixel size of 0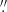 . ″ $ {{\overset{\prime\prime}{.}}} $1 were downsampled via bilinear interpolation to a pixel size of 0 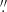. ″ $ {{\overset{\prime\prime}{.}}} $15, which is a quarter of the pixel size of the AIA images. Secondly, we aligned the Hi-C to AIA images via cross-correlation. Finally, two small patches (indicated by the lower and upper blank regions in Fig. 2d) in these images were extracted as the validation and testing sets. The training set is made up of all frames of the data with the validation and test sets being removed. That is, to prevent the model from training the known state of those regions shortly before or after that frame, it is necessary to ensure that the regions in the validation and testing set are not taken for training from any frame.

thumbnail Fig. 2.

Training, testing, and validation sets for ML. Panels a–b: comparison of close-ups of the unprocessed AIA, PSF-bicubic-upscaled AIA, Ml-upscaled AIA, and Hi-C images. The images in panels a and b are taken from the testing set and validation set, respectively. Panel c: slice plots exhibiting intensities along the line indicated in panel b. Panel d: Hi-C image with its full field of view (FOV), in which the lower and upper blanked regions are taken as the validation set and testing set, respectively, and all of the left region is used as the training set. Panels e–f: time history of the value of MAE (e) and SSIM (f) between the model outputs and the Hi-C images in each dataset.

The frame patches for training have a size of 48 × 48 pixels, which were randomly extracted both spatially and temporally from the training set and were randomly rotated in multiples of 90 degrees. The number of patches used in one single training epoch amounts to 100 and the number of epochs used for training is 105. We set an initial learning rate of 1.2 × 10−5, which decreased by 90% every 2000 epochs, and we used the loss function of the mean absolute error (MAE) function for optimizing the network. The code and trained model are based on Pytorch and available at GitHub2.

For training, validation, and testing sets, the quantities of MAE between the ML-upscaled and Hi-C images (ground truth) are seen to be flattened out finally after about 5 × 104 training epochs are performed (Fig. 2e). This indicates that the model has not been overfitted. To further evaluate how well our model enhances the AIA 193 Å images, we used the structural similarity index measure (SSIM; Wang et al. 2004; Aydin et al. 2008) to measure the similarity between the ML-upscaled and Hi-C images. A greater value of SSIM reflects a smaller difference between them. As expected, the value of SSIM in each set increased initially during training and was then close to an asymptotic state (Fig. 2f). Figures 2a and b compare the unprocessed AIA, PSF-bicubic-upscaled AIA, Ml-upscaled AIA, and Hi-C images in the testing and validation sets. On the Hi-C image, an apparent single AIA loop in the validation set appears to have three separate strands, which were identified by Cirtain et al. (2013) as a set of braiding loops. The split strands were clearly visible in the ML-upscaled AIA images, as well as slightly in the PSF-bicubic-upscaled AIA images (Fig. 2b). Figure 2c shows the slice plots across the loop in the various images, with three peaks evident in the slice plots taken from the ML-upscaled and Hi-C image. In the testing set, again, a bifurcation of an AIA loop could be seen on both ML-upscaled AIA and Hi-C images (as indicated by the arrows in Fig. 2a). Thus, while both the PSF-bicubic and ML upscaling methods are capable of improving the AIA 193 Å images in a reasonable manner, the ML upscaling method appears to perform better in both the validation and testing sets.

3. Results

To investigate the nanoflare candidates, this work focusses on the braiding strands recognized in the upscaled AIA 193 Å images. We investigated the AIA 193 Å observation of a sample of non-flare active regions (Schmelz et al. 2015), all of which were not covered by the Hi-C observation. We present three events as follows.

3.1. Overview of the recognizable braiding strands and their evolutions

In Event 1, a bifurcated loop was observed in the raw AIA 193 Å images (Fig. 3a). Subsequently, the loop seemingly departed into two separate ones. Both the PFS-bicubic-upscaled and ML-upscaled images show more detail of the evolution of the loop. In these upscaled images (Figs. 3b and c), the AIA loop appears to be a pair of strands braiding with each other at the beginning of Event 1. The disappearance of the thinner strand (indicated by the magenta dotted line at 05:04:56 UT) was followed by the appearance of a newly formed strand (indicated by the magenta dotted line at 05:09:20 UT), which was parallel with the thicker one that seems to be nearly unchanged (indicated by the cyan dotted lines).

thumbnail Fig. 3.

Evolution of the braiding strands on 5 January 2012 (Event 1). Panel a: SDO/AIA 193 Å images. Panels b–c: bicubic-upscaled versions of the PSF-matched AIA 193 Å images and ML-upscaled versions of the AIA 193 Å images, on which the various coloured dotted lines indicate the various recognizable strands. Panels d–e: images of I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and Δ I ¯ = I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \Delta \bar{I}=\bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $, where the I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=4)} $ are the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 smoothed with a Gaussian kernel of 1 and 4 min, respectively. These images were taken at the peak time of the hot emission indicated by the brown box in panel d, which is also plotted in the other panels. The boxes in panel d outline the locations of all hot emissions that were identified from 05:00:08 UT to 05:10:08 UT. Panel f: vertical component (Br) of the photospheric vector data from SDO/HMI. All images have the same FOV. The evolution of the braiding strands is shown in a movie (anim3.mpeg) available online.

Figures 4 and 5 show two other examples (Events 2 and 3) exhibiting similar evolutions of substructures from braiding to being parallel with each other. They were observed in both the PFS-bicubic-upscaled and the ML-upscaled AIA 193 Å images but were hardly seen in the raw AIA images.

thumbnail Fig. 4.

Evolution of the braiding strands on 22 June 2010 (Event 2). Panel a: SDO/AIA 193 Å images. Panels b–c: bicubic-upscaled versions of the PSF-matched AIA 193 Å images and ML-upscaled versions of the AIA 193 Å images, on which the various coloured dotted lines indicate the various recognizable strands. Panels d–e: images of I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and Δ I ¯ = I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \Delta \bar{I}=\bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $, where the I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=4)} $ are the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 smoothed with a Gaussian kernel of 1 and 4 min, respectively. These images were taken at the peak time of the hot emission indicated by the brown box in panel d, which is only one hot emission identified from 00:35:08 UT to 00:45:08 UT. The brown box is also plotted in the other panels. Panel f: vertical component (Br) of the photospheric vector data from SDO/HMI. All images have the same FOV. The evolution of the braiding strands is shown in a movie (anim4.mpeg) available online.

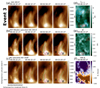thumbnail Fig. 5.

Evolution of the braiding strands on 30 August 2011 (Event 3). Panel a: SDO/AIA 193 Å images. Panels b–c: bicubic-upscaled versions of the PSF-matched AIA 193 Å images and ML-upscaled versions of the AIA 193 Å images, on which the various coloured dotted lines indicate the various recognizable strands. Panels d–e: images of I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and Δ I ¯ = I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \Delta \bar{I}=\bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $, where the I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=4)} $ are the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 smoothed with a Gaussian kernel of 1 and 4 min, respectively. The boxes in panel d outline the locations of all hot emissions that were identified from 09:44:08 UT to 09:54:08 UT, and the three brown boxes marking the hot emissions A, B, and C are also plotted in the other panels. These images in panels d and e were taken at the peak time of the hot emission A. Panel f: vertical component (Br) of the photospheric vector data from SDO/HMI. All images have the same FOV. The evolution of the braiding strands is shown in a movie (anim5.mpeg) available online.

3.2. Transient brightenings at the footpoints of the braiding structures

We used an empirical approach to isolate the hot plasma component (produced by Fe XVIII emission) present in the AIA 94 Å images for coronal diagnostics of impulsive heating. A reasonable estimate of Fe XVIII emission is I(94 Å) − I(211 Å)/120 − I(171 Å))/450 (Del Zanna 2013). The process eliminates the warm plasma component from the emission observed in the 94 Å images, which is around 1 MK. The peak formation temperature of Fe XVIII is at 7.1 MK (Warren et al. 2012), but Fe XVIII emission from plasma at 3 MK may detected due to the large fraction of plasma present at this temperature (Del Zanna 2013). This information shows that the hot emissions are typically believed to have a temperature of at least 3 MK. 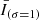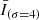To improve its signal-to-noise ratio, the light curve of the Fe XVIII intensity from each AIA pixel was smoothed in time, and the resulting I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma =1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma =4)} $ indicate the data smoothed with a Gaussian kernel of 1 and 4 min. We applied the high-pass filter of the Fe XVIII intensity, corresponding to 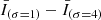I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma =1)}- \bar{I}_{(\sigma =4)} $, to extract the short hot emissions since the durations of the fluctuations in the 94 Å channel in response to the nanoflare-scale heat pulses last for minutes (Reale et al. 2011; Tajfirouze et al. 2016b). A pixel-wise emission enhancement was identified when 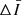Δ I ¯ $ \Delta \bar{I} $ was greater than 1.5 times the standard deviation of 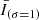I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma =1)} $ for at least one minute. The decision to use a threshold of 1.5 standard deviations was made because picking a standard deviation with a smaller multiple would likely pick up some trivial disturbances. When such three or more adjacent pixel-wise emission enhancements were detected at the same time, we define them as a transient hot emission.

The hot emissions were found in all events studied here. As shown in Figs. 3d, 4d, and 5d, the brown boxes outline the concerned hot emissions, which seem to be associated with the evolutions of the braiding structures. Specifically, a hot emission took place at one of the footpoints of the braiding stands in Events 1 and 2 (Figs. 3 and 4), respectively; three hot emissions, in turn, occurred in the south-east, south-west, and north-west endpoints of the evolving strands in Event 3 (Fig. 5 and its accompanying animation).

Figure 6a presents each light curve of the Fe XVIII intensity from each hot emission. The light-grey areas show that the fluctuations in Fe XVIII intensity last for 1.2–2.2 min. Each peak time indicated by the vertical line corresponds to the moment when 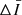Δ I ¯ $ \Delta \bar{I} $ reached its maximum. The comparisons of the peak times and evolutions of the braiding strands (Figs. 3–5, and their accompanying animations) reveal that the hot emissions always reached their peaks before the braiding strands evolved into two parallel ones. Such hot plasma provides evidence supporting the idea that the energy was released from the magnetic reconnection (Klimchuk 2006; Schmelz et al. 2015) during the morphological changes of the braiding strands.

thumbnail Fig. 6.

Evolutions of the identified hot emissions. Panel a: light curves of the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 from the hot emissions outlined by the brown boxes in Figs. 3–5. In each panel, the light-grey area indicates the time period in which the value of Δ I ¯ $ \Delta \bar{I} $ is higher than 1.5 times the standard deviation of I ¯ σ = 1 $ \bar{I}_{\sigma =1} $. Panels b–c: evolutions of EM at 5–10 MK and thermal energy E from the locations of the hot emissions, in which the grey-shaded area denotes the standard deviation of 200 Monte Carlo simulations by adding random AIA instrument noise into the EM inversion. In each panel, the dots with thin lines indicate the raw data; the blue and orange curves indicate the data smoothed with a Gaussian kernel of 1 and 4 min, respectively. The vertical line indicates the peak time of Δ I ¯ $ \Delta \bar{I} $, which amounts to I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $.

Since the plasma along a given line of sight may have a range of temperatures rather than being isothermal, it is common to describe the coronal temperature distribution by reconstruction of differential emission measures (DEMs). For this study, we applied a fast, simple, robust algorithm (Plowman & Caspi 2020) to inverse the DEM from AIA images in the six optically thin wavelengths, including 94 Å, 131 Å, 171 Å, 193 Å, 211 Å, and 335 Å. The temperature points in the inversion were selected to range from 105.5 to 107.0 K. The choice of the maximum temperature of 10 MK ensured that the hot emission would not be overestimated since the emission above 10 MK is not as well constrained by the six AIA channels. The DEM analysis demonstrates that the hot plasma include a significant high-temperature component (T > 5 MK), as shown in Fig. 6b, which presents the evolutions of the emission measure (EM) at 5–10 MK from each hot emission.

Since the coronal plasma is multi-thermal, we estimated the thermal energy as Eq. (12) in Aschwanden et al. (2015), where the volume of the transient emission was estimated as V = A3/2, where A refers to the area of each brightening, and a unity filling factor was assumed. In Fig. 6c, the time evolution of the thermal energy of each hot emission shows that Epeak ranges from 3.0 × 1025 to 1.5 × 1026 erg and ΔEpeak ranges from 1.5 × 1024 − 5.5 × 1024 erg. For this work, the values of E and ΔE were also estimated from the amount of energy smoothed with a Gaussian kernel of 1 minute (blue curves in Fig. 6c) and its difference with respect to that smoothed with a Gaussian kernel of 4 min (orange curves in Fig. 6c). This amount of change in the thermal energy ΔEpeak corresponds to the level of the most common nanoflare energy suggested by Parker (1988).

The hot emissions were often found to be rooted in the unipolar region according to simultaneous measurements of the radial component Br of the photospheric magnetic field from SDO/HMI, such as in Events 1 and 2 (Figs. 3f and 4f). This excludes the possibility that the magnetic reconnections between opposite-polarity magnetic flux on the photosphere produce the hot plasma at the endpoints of the loops (Samanta et al. 2019) unless there is minority-polarity invisible in the HMI magnetogram (Wang et al. 2019). When compared to Events 1 and 2, which were centred at (−190″, 280″) and (370″, 385″) from Sun centre, respectively, Event 3 (Fig. 5f) was centred at (−660″, −440″), and it was then observed farther from the disk centre. Determining the magnetic polarities in Event 3 from the HMI is therefore challenging due to near-limb projection effects.

3.3. Coronal magnetic extrapolation

The braiding strands may mark the bundles of coronal magnetic flux winding around each other (Berger & Asgari-Targhi 2009). This is supported by the comparisons of the braiding structures and the NLFFF coronal magnetic fields, which were constructed by the optimization method (Wheatland et al. 2000) with the required boundary conditions being provided by HMI vector data. The modelled field shows good alignment to the coronal loops in Events 1 and 2, suggesting that force-free extrapolation could be considered as a consistent model of the corona in these events (De Rosa et al. 2009). Similar to the appearance of the braiding strands, the modelled field aligning well with the AIA loop consists of two bundles of modelled field lines twisting with each other (Fig. 7). Again, possibly due to magnetogram degradation by near-limb projection effects, the NLFFF field even failed to match the majority of coronal loops in Event 3.

thumbnail Fig. 7.

Modelled magnetic field lines matching the loops. Left column: ML-upscaled versions of AIA 193 Å images taken in Events 1 (top) and 2 (bottom), in which the magenta and cyan lines outline the two loop stands. The misalignment angle θ between the two lines amounts to 55° and 29° in Events 1 and 2, respectively. Right column: deposited upon the ML-upscaled AIA images, the field lines were traced from the NLFFF field. In Events 1 (top) and 2 (bottom), the NLFFF field was extrapolated based on the set of HMI vector data taken at 05:00:00 UT on 5 January 2012 and 00:36:00 UT on 22 June 2010, respectively.

The crossing manners of the strands imply that a localized tangential discontinuity (Parker 1987) of the magnetic field may exist at the crossing site of the braiding strands. The magnetic-free energy carried in the localized current sheet would convert into heat and kinetic energy when magnetic reconnection occurs there. The amount of free energy is of the order of 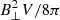B ⊥ 2 V / 8 π $ B^{2}_{\bot}V/8\pi $, where B⊥ is of the order of Bsin(θ). For this work, B was estimated as the magnetic field strength of the NLFFF lines, which amounts to ∼60 G and ∼105 G in Event 1 and 2, respectively. The discontinuity in the field direction θ is assumed to be of the order of the misalignment angle θ between the two braiding strands, which is about 55° and 29° in Event 1 and 2, respectively. Moreover, we assume that characteristic length ΔL is of the order of 1″, corresponding to the characteristic width of the strands detected in the upscaled AIA 193 Å images (see Appendix A), and then the volume V ≈ (ΔL)3. The number estimated above the magnetic-free energy associated with a discontinuity is of the order of 3.7 × 1025 erg and 3.9 × 1025 erg for Event 1 and Event 2, respectively. Therefore, the amount of magnetic-free energy could account for the thermal energy of the order of 1024 erg released by a nanoflare.

4. Discussions

The investigation of the widths of the detectable loop structures (see Appendix A) shows that the widths of strands recognized in both the PSF-bicubic-upscaled and ML-upscaled AIA 193 Å images range from 0 . ″ $ {{\overset{\prime\prime}{.}}} $7 to 1 . ″ $ {{\overset{\prime\prime}{.}}} $3 (Fig. A.2), corresponding to a physical size ranging from about 500 km to 1000 km, and that each pair of strands is resolved in an AIA loop with a characteristic width of 2″–3″ (Aschwanden & Peter 2017). The uncertainty as to the width of the upscaled structures amounts to ± 0 . 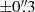″ 3 $ {\pm} 0{{\overset{\prime\prime}{.}}}3 $ and is roughly determined by the results from various networks trained with slightly different training sets. Therefore, the upscaled AIA 193 Å images have a performance to resolve the strands with widths less than 1 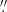. ″ $ {{\overset{\prime\prime}{.}}} $2, which could hardly be resolved on the raw AIA images with a spatial resolution of 1 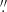. ″ $ {{\overset{\prime\prime}{.}}} $2. According to Brooks et al. (2013), the lowest and mean Gaussian widths of loops observed in Hi-C were about 90 km and 270 km, or 0 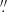. ″ $ {{\overset{\prime\prime}{.}}} $12 and 0 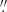. ″ $ {{\overset{\prime\prime}{.}}} $37, respectively. By contrast, strands in the upscaled AIA 193 Å images always have widths no less than a pixel size of 0 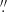. ″ $ {{\overset{\prime\prime}{.}}} $6 of AIA images. This is mostly because no more information can be extracted from the AIA images and then the minimum width of the strands detected on the ML-upscaled images is close to the pixel size of AIA images.

From our observations, we infer the schematic picture of Fig. 8 for two flux tubes braiding in various patterns and their subsequent evolutions are due to magnetic reconnection. In the upscaled AIA 193 Å image, we could recognize some pairs of strands with their footpoints separated randomly (e.g. Fig. 8b,c), instead of a pair of strands braiding coherently in a well-combed pattern (Fig. 8a), which is difficult to observe due to the limit of the resolution and the effect of cross-field diffusion electrons in tangled magnetic fields (Galloway et al. 2006; Berger & Asgari-Targhi 2009). Figure 8b shows two identical tubes braiding with each other and the magnetic reconnection between them would result in a total exchange of their footpoints. The picture could explain the morphological evolution exhibited in Events 2 and 3 (Figs. 4 and 5), in which the two braiding strands evolved to be two parallel ones. Figure 8c shows the evolutions of two braiding flux tubes with a nonequal axial flux. As the two nonidentical flux tubes collide with each other, the reconnection halts once all of the flux of the smaller tube has reconnected, and a final state is that only the outer shell of the larger flux tube is reconnected and the rest are unreconnected (Linton 2006). Moreover, when the two nonidentical flux tubes braid with two crossings (Fig. 8c), magnetic reconnection between them would occur twice and then produce two thoroughly separated tubes. Consistently, we can see in Event 1 (Fig. 3) that the unequal width strands braided with two apparent crossings and that subsequently, the thinner one became parallel with the other one nearly unchanged. Accordingly, the morphological evolutions of the two braiding strands presented here are consistent with the schematic pictures of two braiding bundles of magnetic flux driven to reconnect with each other.

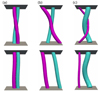thumbnail Fig. 8.

Picture of evolutions of two flux tubes with various braid patterns. Top row: flux tubes braiding with various patterns. Bottom row: their final states after occurrences of magnetic reconnection at their crossings. Panel a: two coherent flux tubes braid with each other in a well-combed pattern. Panels b,c: two flux tubes braid with their legs separating from each other randomly. The two flux tubes in panels a and b initially had an identical flux, while the two tubes in panels c have a nonidentical flux and cyan-coloured tubes have more axial flux than that coloured magenta. The pairs of flux tubes in panels a,b initially braid with one crossing and the two tubes in panel c braid with two crossings.

Pontin et al. (2017) claim that the existence of crossed loop strands does not always imply magnetic discontinuities and subsequent magnetic reconnection. Here, further evidence for the occurrence of magnetic reconnection between the braiding strands is provided by the transient hot emission around the footpoints of the loop strands. The impulsive brightenings at the footpoints of the loops were also noted to happen at lower temperatures between 1 and 2 MK (Régnier et al. 2014; Subramanian et al. 2018). By contrast, transient emissions with higher temperatures were detected in the events reported here. According to the EM analysis, the hot emissions contain a temperature component greater than 5 MK. This value can be easily obtained using reconnection models (Schmelz et al. 2015) but are difficult to get using wave models (van Ballegooijen et al. 2017).

The footpoints of the loops could have been heated by the energetic electrons produced by magnetic reconnections high in the corona, even though hot plasma components were undetectable at the locations of reconnection sites (e.g. Zhang & Ni 2019). This is due to the fact that there were low densities higher in the corona and that, as predicted by a simulation conducted by Polito et al. (2018), the energtic electrons then deposited raw kinetic energy in the corona until they reached the low corona with an increasing density. Given that loops are isothermal along their coronal parts, heat pulses at their footpoints might cause the loop to heat up and become denser as a result of thermal conduction and chromospheric evaporation. However, the measurable increase in the 94 Å emission was also absent throughout the entirety of the loops reported here. This could be as a result of smaller 94 Å variations in the loops’ lower-density sections than at their footpoints (Tajfirouze et al. 2016a). To explore the locations and temperatures of hot plasma created in response to the braided magnetic field forming the coronal loops and to evaluate the implications provided from this study, more simulation model findings would be helpful.

5. Summary

In this article, the evolutions of the strands braiding with each other in the apparent single AIA loops are presented. The main results are summarized as follows:

  1. We performed two validations to confirm that the substructures recorded in the AIA pictures could be seen after the images were appropriately enhanced and upscaled. The width of the strands that make up what appear to be single AIA loops ranges from 0 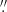. ″ $ {{\overset{\prime\prime}{.}}} $7 to 1 . ″ $ {{\overset{\prime\prime}{.}}} $3.

  2. The braided substructured loops were discovered to closely match the twisted NLFFF field lines in some events that were observed near the disk centre and then the photospheric magnetic data were properly recorded. The magnetic-free energy in the modelled field is sufficient to match the thermal energy required for a nanoflare.

  3. The braided strands developed into pairs of almost parallel ones together with the hot emission that was present at their footpoints, supporting the occurrence of magnetic reconnection in the coronal loops shown in the AIA images.

A comparison of the raw AIA, ML-upscaled AIA, and Hi-C images (Figs. 2 and A.1) reveals that the ML algorithm only detected a portion of the features at a scale smaller than ∼1 . ″ $ {{\overset{\prime\prime}{.}}} $2 that can be seen by Hi-C. As a result, it would appear that the evolutions of the braided structures pertaining to nanoflares are predicted to be discovered more frequently in the higher-resolution observations, such as EUI on board Solar Orbiter.

Movies

Movie 1 associated with Fig. 3 (anim3) Access here

Movie 2 associated with Fig. 4 (anim4) Access here

Movie 3 associated with Fig. 5 (anim5) Access here

1

The PSF for AIA is available in SolarSoft (http://www.lmsal.com/solarsoft/).

Acknowledgments

The authors are grateful to the anonymous referee for detailed comments and useful suggestions that improved this manuscript. We acknowledge the High resolution Coronal Imager instrument team for making the flight data publicly available. MSFC/NASA led the mission and partners include the Smithsonian Astrophysical Observatory in Cambridge, Mass.; Lockheed Martin’s Solar Astrophysical Laboratory in Palo Alto, Calif.; the University of Central Lancashire in Lancashire, England; and the Lebedev Physical Institute of the Russian Academy of Sciences in Moscow. The NASA/SDO data used here are courtesy of the AIA and HMI science teams. This work is supported by the National Key Research and Development Program of China (2019YFA0405000), and the Natural Science Foundation of China under grants 12273106, 12073077, 12163004, U2031140, 12073072, 11933009, 12273108, 12203097, 12003068, 11873088, 12173084, and 11973088, the CAS “Light of West China” Program, and the Strategic Priority Research Program of Chinese Academy of Sciences, Grant No. XDB 41000000.

References

  1. Antolin, P., Pagano, P., Testa, P., Petralia, A., & Reale, F. 2021, Nat. Astron., 5, 54 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aschwanden, M. J., & Peter, H. 2017, ApJ, 840, 4 [CrossRef] [Google Scholar]
  3. Aschwanden, M. J., Boerner, P., Ryan, D., et al. 2015, ApJ, 802, 53 [Google Scholar]
  4. Asgari-Targhi, M., van Ballegooijen, A. A., & Davey, A. R. 2019, ApJ, 881, 107 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aydin, T. O., Mantiuk, R., Myszkowski, K., & Seidel, H.-P. 2008, ACM Trans. Graphics, 27, 69 [Google Scholar]
  6. Bai, X., Liu, H., Deng, Y., et al. 2021, A&A, 652, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Berger, M. A., & Asgari-Targhi, M. 2009, ApJ, 705, 347 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bi, Y., Yang, B., Li, T., Dong, Y., & Ji, K. 2020, ApJ, 891, L40 [NASA ADS] [CrossRef] [Google Scholar]
  9. Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [Google Scholar]
  10. Brooks, D. H., Warren, H. P., Ugarte-Urra, I., & Winebarger, A. R. 2013, ApJ, 772, L19 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chitta, L. P., Peter, H., Priest, E. R., & Solanki, S. K. 2020, A&A, 644, A130 [EDP Sciences] [Google Scholar]
  12. Chitta, L. P., Peter, H., Parenti, S., et al. 2022, A&A, 667, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cirtain, J. W., Golub, L., Winebarger, A. R., et al. 2013, Nature, 493, 501 [NASA ADS] [CrossRef] [Google Scholar]
  14. De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007, Science, 318, 1574 [Google Scholar]
  15. De Rosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [NASA ADS] [CrossRef] [Google Scholar]
  16. Del Zanna, G. 2013, A&A, 558, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Díaz Baso, C. J., & Asensio Ramos, A. 2018, A&A, 614, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dong, C., Loy, C. C., He, K., & Tang, X. 2016, IEEE Trans. Pattern Anal. Mach. Intell., 38, 295 [CrossRef] [Google Scholar]
  19. Dos Santos, L. F. G., Bose, S., Salvatelli, V., et al. 2021, A&A, 648, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Fan, Y., Yu, J., & Huang, T. S. 2018, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2621 [Google Scholar]
  21. Galloway, R. K., Helander, P., & MacKinnon, A. L. 2006, ApJ, 646, 615 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gupta, G. R., Sarkar, A., & Tripathi, D. 2018, ApJ, 857, 137 [NASA ADS] [CrossRef] [Google Scholar]
  23. He, K., Zhang, X., Ren, S., & Sun, J. 2016, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Los Alamitos, CA, USA: IEEE Computer Society), 770 [Google Scholar]
  24. Hong, J., Liu, H., Bi, Y., et al. 2021, ApJ, 915, 96 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ishikawa, S.-N., Glesener, L., Krucker, S., et al. 2017, Nat. Astron., 1, 771 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kim, T., Park, E., Lee, H., et al. 2019, Nat. Astron., 3, 397 [Google Scholar]
  27. Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [Google Scholar]
  28. Klimchuk, J. A. 2015, Philos. Trans. Roy. Soc. London Ser. A, 373, 20140256 [NASA ADS] [Google Scholar]
  29. Kobayashi, K., Cirtain, J., Winebarger, A. R., et al. 2014, Sol. Phys., 289, 4393 [Google Scholar]
  30. Ledig, C., Theis, L., Huszár, F., et al. 2017, in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 105 [CrossRef] [Google Scholar]
  31. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  32. Li, L. P., Peter, H., Chen, F., & Zhang, J. 2015, A&A, 583, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Linton, M. G. 2006, J. Geophys. Res. (Space Phys.), 111, A12S09 [Google Scholar]
  34. McIntosh, S. W., de Pontieu, B., Carlsson, M., et al. 2011, Nature, 475, 477 [Google Scholar]
  35. Parker, E. N. 1987, ApJ, 318, 876 [NASA ADS] [CrossRef] [Google Scholar]
  36. Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
  37. Pineci, A., Sadowski, P., Gaidos, E., & Sun, X. 2021, ApJ, 910, L25 [NASA ADS] [CrossRef] [Google Scholar]
  38. Plowman, J., & Caspi, A. 2020, ApJ, 905, 17 [NASA ADS] [CrossRef] [Google Scholar]
  39. Pontin, D. I., Janvier, M., Tiwari, S. K., et al. 2017, ApJ, 837, 108 [NASA ADS] [CrossRef] [Google Scholar]
  40. Polito, V., Testa, P., Allred, J., et al. 2018, ApJ, 856, 178 [NASA ADS] [CrossRef] [Google Scholar]
  41. Priest, E. R., Chitta, L. P., & Syntelis, P. 2018, ApJ, 862, L24 [Google Scholar]
  42. Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
  43. Reale, F., Guarrasi, M., Testa, P., et al. 2011, ApJ, 736, L16 [NASA ADS] [CrossRef] [Google Scholar]
  44. Régnier, S., Alexander, C. E., Walsh, R. W., et al. 2014, ApJ, 784, 134 [CrossRef] [Google Scholar]
  45. Salimans, T., & Kingma, D. P. 2016, in Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS’16 (Red Hook, NY, USA: Curran Associates Inc.), 901 [Google Scholar]
  46. Samanta, T., Tian, H., Yurchyshyn, V., et al. 2019, Science, 366, 890 [NASA ADS] [CrossRef] [Google Scholar]
  47. Schmelz, J. T., Asgari-Targhi, M., Christian, G. M., Dhaliwal, R. S., & Pathak, S. 2015, ApJ, 806, 232 [CrossRef] [Google Scholar]
  48. Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
  49. Shen, Y. 2021, Proc. Roy. Soc. London Ser. A, 477, 217 [NASA ADS] [Google Scholar]
  50. Shi, W., Caballero, J., Huszár, F., et al. 2016, arXiv e-prints [arXiv:1609.05158] [Google Scholar]
  51. Subramanian, S., Kashyap, V. L., Tripathi, D., Madjarska, M. S., & Doyle, J. G. 2018, A&A, 615, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Szenicer, A., Fouhey, D. F., Munoz-Jaramillo, A., et al. 2019, Sci. Adv., 5, eaaw6548 [NASA ADS] [CrossRef] [Google Scholar]
  53. Tajfirouze, E., Reale, F., Petralia, A., & Testa, P. 2016a, ApJ, 816, 12 [Google Scholar]
  54. Tajfirouze, E., Reale, F., Peres, G., & Testa, P. 2016b, ApJ, 817, L11 [CrossRef] [Google Scholar]
  55. Testa, P., De Pontieu, B., Martínez-Sykora, J., et al. 2013, ApJ, 770, L1 [NASA ADS] [CrossRef] [Google Scholar]
  56. Thalmann, J. K., Tiwari, S. K., & Wiegelmann, T. 2014, ApJ, 780, 102 [Google Scholar]
  57. Tian, H., DeLuca, E. E., Cranmer, S. R., et al. 2014, Science, 346, 1255711 [Google Scholar]
  58. van Ballegooijen, A. A., Asgari-Targhi, M., & Voss, A. 2017, ApJ, 849, 46 [Google Scholar]
  59. Viall, N. M., & Klimchuk, J. A. 2011, ApJ, 738, 24 [Google Scholar]
  60. Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. 2004, IEEE Trans. Image Process., 13, 600 [Google Scholar]
  61. Wang, Y. M., Ugarte-Urra, I., & Reep, J. W. 2019, ApJ, 885, 34 [Google Scholar]
  62. Warren, H. P., Winebarger, A. R., & Brooks, D. H. 2012, ApJ, 759, 141 [NASA ADS] [CrossRef] [Google Scholar]
  63. Wheatland, M. S., Sturrock, P. A., & Roumeliotis, G. 2000, ApJ, 540, 1150 [Google Scholar]
  64. Winebarger, A. R., & Warren, H. P. 2005, ApJ, 626, 543 [NASA ADS] [CrossRef] [Google Scholar]
  65. Winebarger, A. R., Walsh, R. W., Moore, R., et al. 2013, ApJ, 771, 21 [NASA ADS] [CrossRef] [Google Scholar]
  66. Yang, K. E., Longcope, D. W., Ding, M. D., & Guo, Y. 2018, Nat. Commun., 9, 692 [NASA ADS] [CrossRef] [Google Scholar]
  67. Yu, J., Fan, Y., Yang, J., et al. 2018, arXiv e-prints [arXiv:1808.08718] [Google Scholar]
  68. Yu, X., Xu, L., & Yan, Y. 2021, Sol. Phys., 296, 56 [NASA ADS] [CrossRef] [Google Scholar]
  69. Zhang, Q. M., & Ni, L. 2019, ApJ, 870, 113 [Google Scholar]
  70. Zhang, J., Hou, Y., Fang, Y., et al. 2023, ApJ, 942, L2 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Estimation of the width of a loop

We estimated the width of loops on various images as follows. Firstly, we extracted a straight stripe along a segment of the loop axis with a width of 11 pixels. Secondly, we obtained the average intensity across the axis of the stripe, which was fitted to a Gaussian function with a linear term, expressed as 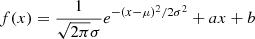f ( x ) = 1 2 π σ e − ( x − μ ) 2 / 2 σ 2 + a x + b $ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-(x-\mu)^{2}/2\sigma^{2}}+ax+b $ where σ, μ, a, and b are fitting parameters. Thus, we defined a full width at half maximum (FWHM) of 2.355σ as the width of a loop. In the validation set, as shown in Fig. A.1, a single AIA loop with a width of 1″.8 appears to be two separated strands with the widths of 0″.6 and 0″.4 in the simultaneous Hi-C image. Similarly, the ML-upscaled AIA 193 Å images resolved the two strands, but slightly wider, with the width of 0″.6 and 0″.8, respectively. The strands with the width of 0″.8 were also recognizable in the PSF-bicubic-upscaled AIA 193 Å images. In each event reported here, the widths of the resolved strands range from 0″.7 to 1″.3, which compose the apparent single AIA loops, with widths ranging from 1″.8 to 2″.6 (Fig. A.2).

thumbnail Fig. A.1.

Estimated widths of the loops in the various images taken from testing and validation sets. Panel a: Comparison of close-ups of the AIA, PSF-bicubic-upscaled, ML-upscaled, and Hi-C images taken in the validation set. Panel b: Comparison of more detailed close-ups of these images. The plots above and below each panel in b show the distribution of the corresponding average intensity across the axis of the strip as indicated by the magenta and blue-dashed line, respectively. In each plot, the curve refers to the fitted Gaussian function with the linear term; the distance between the vertical line corresponds to the FWHM for the fitted function. In a, each pair of parallel lines were deposited to cover the FWHM area for the corresponding fitting function as plotted in b.

thumbnail Fig. A.2.

Estimated widths of the loops in the various images taken from each event. Panel a: Close-ups of the AIA 193 Å images. Panel b: More detailed close-ups of the AIA 193 Å images. Panels c-d: PSF-bicubic-upscaled and the ML-upscaled AIA 193 Å images with the same FOV as b, covering the braiding strands. In each panel, the distance of the parallel lines coloured the same is considered as the width of the corresponding loop or strand.

All Figures

thumbnail Fig. 1.

Architecture of the WDSR convolutional neural network for upsampling factor ×4. All of the feature maps in each convolutional layer have the size H × W, which is the same as that of the input images. For upscaling factor ×S (×4), the number of channels used as the input for the Pixel-Shuffle layer is exactly S2 (16).
In the text
thumbnail Fig. 2.

Training, testing, and validation sets for ML. Panels a–b: comparison of close-ups of the unprocessed AIA, PSF-bicubic-upscaled AIA, Ml-upscaled AIA, and Hi-C images. The images in panels a and b are taken from the testing set and validation set, respectively. Panel c: slice plots exhibiting intensities along the line indicated in panel b. Panel d: Hi-C image with its full field of view (FOV), in which the lower and upper blanked regions are taken as the validation set and testing set, respectively, and all of the left region is used as the training set. Panels e–f: time history of the value of MAE (e) and SSIM (f) between the model outputs and the Hi-C images in each dataset.
In the text
thumbnail Fig. 3.

Evolution of the braiding strands on 5 January 2012 (Event 1). Panel a: SDO/AIA 193 Å images. Panels b–c: bicubic-upscaled versions of the PSF-matched AIA 193 Å images and ML-upscaled versions of the AIA 193 Å images, on which the various coloured dotted lines indicate the various recognizable strands. Panels d–e: images of I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and Δ I ¯ = I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \Delta \bar{I}=\bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $, where the I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=4)} $ are the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 smoothed with a Gaussian kernel of 1 and 4 min, respectively. These images were taken at the peak time of the hot emission indicated by the brown box in panel d, which is also plotted in the other panels. The boxes in panel d outline the locations of all hot emissions that were identified from 05:00:08 UT to 05:10:08 UT. Panel f: vertical component (Br) of the photospheric vector data from SDO/HMI. All images have the same FOV. The evolution of the braiding strands is shown in a movie (anim3.mpeg) available online.
In the text
thumbnail Fig. 4.

Evolution of the braiding strands on 22 June 2010 (Event 2). Panel a: SDO/AIA 193 Å images. Panels b–c: bicubic-upscaled versions of the PSF-matched AIA 193 Å images and ML-upscaled versions of the AIA 193 Å images, on which the various coloured dotted lines indicate the various recognizable strands. Panels d–e: images of I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and Δ I ¯ = I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \Delta \bar{I}=\bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $, where the I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=4)} $ are the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 smoothed with a Gaussian kernel of 1 and 4 min, respectively. These images were taken at the peak time of the hot emission indicated by the brown box in panel d, which is only one hot emission identified from 00:35:08 UT to 00:45:08 UT. The brown box is also plotted in the other panels. Panel f: vertical component (Br) of the photospheric vector data from SDO/HMI. All images have the same FOV. The evolution of the braiding strands is shown in a movie (anim4.mpeg) available online.
In the text
thumbnail Fig. 5.

Evolution of the braiding strands on 30 August 2011 (Event 3). Panel a: SDO/AIA 193 Å images. Panels b–c: bicubic-upscaled versions of the PSF-matched AIA 193 Å images and ML-upscaled versions of the AIA 193 Å images, on which the various coloured dotted lines indicate the various recognizable strands. Panels d–e: images of I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and Δ I ¯ = I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \Delta \bar{I}=\bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $, where the I ¯ ( σ = 1 ) $ \bar{I}_{(\sigma=1)} $ and I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=4)} $ are the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 smoothed with a Gaussian kernel of 1 and 4 min, respectively. The boxes in panel d outline the locations of all hot emissions that were identified from 09:44:08 UT to 09:54:08 UT, and the three brown boxes marking the hot emissions A, B, and C are also plotted in the other panels. These images in panels d and e were taken at the peak time of the hot emission A. Panel f: vertical component (Br) of the photospheric vector data from SDO/HMI. All images have the same FOV. The evolution of the braiding strands is shown in a movie (anim5.mpeg) available online.
In the text
thumbnail Fig. 6.

Evolutions of the identified hot emissions. Panel a: light curves of the Fe XVIII intensity of I(94 Å) − I(211 Å)/120 − I(171 Å))/450 from the hot emissions outlined by the brown boxes in Figs. 3–5. In each panel, the light-grey area indicates the time period in which the value of Δ I ¯ $ \Delta \bar{I} $ is higher than 1.5 times the standard deviation of I ¯ σ = 1 $ \bar{I}_{\sigma =1} $. Panels b–c: evolutions of EM at 5–10 MK and thermal energy E from the locations of the hot emissions, in which the grey-shaded area denotes the standard deviation of 200 Monte Carlo simulations by adding random AIA instrument noise into the EM inversion. In each panel, the dots with thin lines indicate the raw data; the blue and orange curves indicate the data smoothed with a Gaussian kernel of 1 and 4 min, respectively. The vertical line indicates the peak time of Δ I ¯ $ \Delta \bar{I} $, which amounts to I ¯ ( σ = 1 ) − I ¯ ( σ = 4 ) $ \bar{I}_{(\sigma=1)}-\bar{I}_{(\sigma=4)} $.
In the text
thumbnail Fig. 7.

Modelled magnetic field lines matching the loops. Left column: ML-upscaled versions of AIA 193 Å images taken in Events 1 (top) and 2 (bottom), in which the magenta and cyan lines outline the two loop stands. The misalignment angle θ between the two lines amounts to 55° and 29° in Events 1 and 2, respectively. Right column: deposited upon the ML-upscaled AIA images, the field lines were traced from the NLFFF field. In Events 1 (top) and 2 (bottom), the NLFFF field was extrapolated based on the set of HMI vector data taken at 05:00:00 UT on 5 January 2012 and 00:36:00 UT on 22 June 2010, respectively.
In the text
thumbnail Fig. 8.

Picture of evolutions of two flux tubes with various braid patterns. Top row: flux tubes braiding with various patterns. Bottom row: their final states after occurrences of magnetic reconnection at their crossings. Panel a: two coherent flux tubes braid with each other in a well-combed pattern. Panels b,c: two flux tubes braid with their legs separating from each other randomly. The two flux tubes in panels a and b initially had an identical flux, while the two tubes in panels c have a nonidentical flux and cyan-coloured tubes have more axial flux than that coloured magenta. The pairs of flux tubes in panels a,b initially braid with one crossing and the two tubes in panel c braid with two crossings.
In the text
thumbnail Fig. A.1.

Estimated widths of the loops in the various images taken from testing and validation sets. Panel a: Comparison of close-ups of the AIA, PSF-bicubic-upscaled, ML-upscaled, and Hi-C images taken in the validation set. Panel b: Comparison of more detailed close-ups of these images. The plots above and below each panel in b show the distribution of the corresponding average intensity across the axis of the strip as indicated by the magenta and blue-dashed line, respectively. In each plot, the curve refers to the fitted Gaussian function with the linear term; the distance between the vertical line corresponds to the FWHM for the fitted function. In a, each pair of parallel lines were deposited to cover the FWHM area for the corresponding fitting function as plotted in b.
In the text
thumbnail Fig. A.2.

Estimated widths of the loops in the various images taken from each event. Panel a: Close-ups of the AIA 193 Å images. Panel b: More detailed close-ups of the AIA 193 Å images. Panels c-d: PSF-bicubic-upscaled and the ML-upscaled AIA 193 Å images with the same FOV as b, covering the braiding strands. In each panel, the distance of the parallel lines coloured the same is considered as the width of the corresponding loop or strand.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.