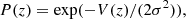| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202345868 | |
| Published online | 30 November 2023 | |
Exploring the correlation between dark matter, intracluster light, and globular cluster distribution in SMACS0723
1
Instituto de Física de Cantabria (CSIC-UC), Avda. Los Castros s/n, 39005 Santander, Spain
e-mail: jdiego@ifca.unican.es
2
Department of Astronomy, University of California, 501 Campbell Hall #3411, Berkeley, CA 94720, USA
3
Department of Astronomy/Steward Observatory, University of Arizona, 933 N Cherry Ave., Tucson, AZ 85721, USA
4
Physics Department, Ben-Gurion University of the Negev, PO Box 653, Be’er-Sheva 8410501, Israel
5
Department of Physics, University of the Basque Country UPV/EHU, 48080 Bilbao, Spain
6
DIPC, Basque Country UPV/EHU, 48080 San Sebastian, Spain
7
Ikerbasque, Basque Foundation for Science, 48011 Bilbao, Spain
8
Centre for Extragalactic Astronomy, Durham University, South Road, Durham DH1 3LE, UK
9
Institute for Computational Cosmology, Durham University, South Road, Durham DH1 3LE, UK
10
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
11
Astrophysics Research Centre, University of KwaZulu-Natal, Westville Campus, Durban 4041, South Africa
12
School of Mathematics, Statistics & Computer Science, University of KwaZulu-Natal, Westville Campus, Durban 4041, South Africa
13
Astronomy Program, Department of Physics and Astronomy, SNUARC, Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Republic of Korea
14
Department of Astronomy & Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
15
Instituto de Astrofísica de Canarias, c/ Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
16
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
Received:
9
January
2023
Accepted:
14
September
2023
We present a free-form model of SMACS0723, the first cluster observed with JWST. This model does not make any strong assumptions on the distribution of mass (mostly made up of dark matter) in the cluster and we use it to study the possible correlation between dark matter with the intracluster light and distribution of globular clusters (GCs). To explore the uncertainty in mass modeling, we derived three lens models based on spectroscopically confirmed systems and new candidate systems with redshifts predicted by the lens model derived from the spectroscopic systems. We find that beyond the radius of influence for the brightest cluster galaxy (BCG), the total mass does not trace the intracluster light (ICL), implying the need for a dark component (dark matter). Two loop-like structures observed in the intracluster light do not have any obvious correspondence with the total mass (of mostly dark matter) distribution. The radial profiles of the ICL and the distribution of GCs are similar to each other, but they are steeper than the profile of the lens model. More specifically, we find that the total mass is shallower by 1 dex in log scale than both ICL and GC profiles. This is in excellent agreement with current N-body simulations of cold dark matter.
Key words: gravitational lensing: strong / galaxies: clusters: individual: SMACS0723 / galaxies: clusters: intracluster medium / dark matter
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Following its launch on December 25, 2021, the first color image from James Webb Space Telescope (JWST) was presented to the world on July 11, 2022. The image showed a view of the distant infrared universe with a level of detail and depth never seen before at these wavelengths. This image was centered on a massive galaxy cluster at z = 0.39, SMACS J0723.3-7327 (or SMACS0723 hereafter), acting as a powerful gravitational lens. This natural lens magnifies the galaxies in the background. Some of these background galaxies appear repeated several times in the JWST image, since photons from those galaxies take different paths, which are later refocused by the gravitational lens into the JWST telescope.
In anticipation of these first JWST data, a lens model based on Hubble Space Telescope (HST) data and a listing of the first few sets of multiple images and some spectroscopic redshifts for them were posted on the arXiv by Golubchik et al. (2022) on the same date (July 11). The JWST data became itself public on July 13, 2022 and just a day after the data release, two papers presenting new candidates to multiply lensed galaxies and new lens models were submitted simultaneously to arXiv (Mahler et al. 2023; Pascale et al. 2022)1. A day after these two papers appeared on arXiv, a third one was submitted presenting an additional lens model and new lensed system candidates (Caminha et al. 2022). Other papers focusing on the high-redshift galaxies lensed by SMACS0723 and their properties quickly followed (Ferreira et al. 2022; Cheng et al. 2022; Laporte et al. 2022; Adams et al. 2023; Carnall et al. 2023). This frenzy over the new data reflects the excitement and anticipation of the community for the new JWST data. JWST is revolutionizing the field of astronomy in a similar fashion as its predecessor, HST, at the end of the 20th and beginning of the 21st centuries.
The first image of JWST reveals approximately two dozen lensed system candidates, six of which have spectroscopic redshift estimations from MUSE and JWST data (Golubchik et al. 2022; Sharon et al. 2023; Pascale et al. 2022; Mahler et al. 2023; Caminha et al. 2022)2. One of the surprises in the new data is the presence of hundreds of point-like sources near the large member galaxies in the cluster, which are possibly stripped galactic nuclei or compact globular clusters (Lee et al. 2022; Faisst et al. 2022). Some of the lensed galaxies also show small unresolved structures that could be compact star-forming regions, globular clusters (GCs), groups of stars, or even individual stars in cases of extreme magnification (Mowla et al. 2022). These can prove very valuable in upcoming works searching for flux anomalies between pairs of counterimages (Pooley et al. 2012; Chan et al. 2020). The unresolved nature of these substructures, together with the large magnification of some of them can be used to study models of dark matter (DM) that predict anomalous flux ratios between these pairs of images. An additional surprise in the new data is the unusual distribution of the intracluster light (ICL, hereafter), already noted in Pascale et al. (2022) and Mahler et al. (2023) and studied in more detail in Montes & Trujillo (2022). The ICL is formed by stars not bound to any galaxy of the cluster, but to the gravitational potential of the cluster as a whole (see Montes 2022, for a review). ICL is observed to be older near the center of the clusters (Montes & Trujillo 2018), suggesting an earlier accretion of the central ICL region. The ICL is particularly interesting in the context of DM. Similarly to DM particles, the stars responsible for the ICL (as well as the GCs and galactic core remnants) can be considered as non-interacting particles that respond only to gravity. Hence, we would expect a tight correlation between the distribution of ICL and DM (Montes & Trujillo 2019; Alonso Asensio et al. 2020). In the case of SMACS0723, the ICL departs from the expected smooth distribution predicted for DM from N-body simulations (Alonso Asensio et al. 2020) and shows two loop-like structures at ≈200 kpc from the central BCG, one to the east and one to the west of the cluster core. These loop-like structures may be the result of a relatively recent merger, but given the expected connection between the stars in the ICL and the DM, it is interesting to consider whether similar structures can be found in the distribution of DM from the lens model.
Previous lens models rely on some parameterization of the mass distribution, usually by placing ellipsoids at the positions of galaxies, and/or large elliptical halos near the center of the cluster to account for the contribution from DM, or by assuming it follows the cluster galaxy distribution. Hence, they are less than ideal with respect to studying the possible correlation between the DM and ICL distributions. In this paper, we present an additional lens model based on a free-form technique that makes no assumptions about the underlying distribution of DM. A comparison between the DM and ICL (or GC) distributions can then be done without being subject to assumptions made about the distribution of DM.
The paper is organized as follows. In Sect. 2, we discuss the lensing constraints used to derive the lens model. Section 3 gives a brief introduction to the free-form algorithm used to derive the lens model, making no assumptions about the distribution of DM. In Sect. 4, we present the driver model, or model-1, which is derived using only lensed systems with known (spectroscopic) redshifts. Section 5 uses the driver model to make predictions for the redshifts of the candidate lensed systems without spectroscopic redshifts. These redshifts are an interesting alternative to (and some times are more precise than) the more common photometric redshifts. In Sect. 6, we use the lens model predicted redshifts and present two additional models (model-2 and model-3), which use all the additional systems with constrained redshifts and, in the case of model-3, also increases the spatial resolution of the DM component. Model-2 and model-3 are useful for exploring the uncertainty in the lens model due to (i) the lens system definition (spectroscopic sample versus the full sample) and (ii) the spatial resolution in the lens model. In Sect. 7, we study the correlation between the ICL, GC distribution, and DM. We discuss our results and present our conclusions in Sect. 8. We adopt a standard flat cosmological model with Ωm = 0.3 and h = 0.7. At the redshift of the lens (z = 0.39), and for this cosmology, one arcsecond corresponds to 5.29 kpc.
2. Lensing constraints
The lensing constraints used in this work were compiled from the three most recent works discussed previously (Pascale et al. 2022; Mahler et al. 2023; Caminha et al. 2022). The positions and IDs of these systems are presented in Table A.1. When possible, we maintain the original ID of earlier works. Candidates 6.3 and 16.3 in Pascale et al. (2022) are updated with the nearby candidates 7.3 and 11.3, respectively, from Mahler et al. (2023). For convenience, Table A.1 also includes the IDs used in earlier works. Among the systems in this table, six of them have spectroscopic redshifts. All systems are marked in Fig. 1 with their corresponding ID. The six systems with spectroscopic redshifts are marked with white labels, while the systems without spectroscopic redshift are shown in yellow. For the uncertainty in the position of the arcs, we adopted an error of 0.1″ for all arcs.
 |
Fig. 1. Central ≈1 arcmin region of SMACS0723 with systems of lensed galaxies. This image was obtained by combining different filters from JWST. Systems in white have spectroscopic redshifts and are the ones used to build the driver model or model-1. Systems in yellow do not have spectroscopic redshifts but are used in combination with the spectroscopic systems to build lens model-2 and model-3. We note the hundreds of unresolved sources surrounding the BCG, which are mostly GCs and galactic core remnants. Unless otherwise noted, all figures in this paper are in the same orientation as this one. The two critical points, CP5 and CP7, are shown in the bottom-left portion of the plot. |
In addition to the classic lensing constraints, we add the position of critical curves that can be determined from the radial arc in system 5 (at z = 1.425) and the merging pair of images in system 7 (at z = 5.17). The positions of these critical points are added at the end of Table A.1 and labeled CP5 and CP7, respectively. Each critical point contributes with two constraints as detailed in Diego et al. (2022). Since at a critical point the magnification diverges, this can be easily incorporated by applying a rotation to the data by the angle determined by the elongation of the arc. After this rotation, we can simply impose the rule that the inverse of the tangential magnification equals zero (or, similarly, 1 = κ − γ). The second constraint is simply γ2 = 0, which is satisfied when the rotation is applied. The error associated to these critical points in our reconstructions is 0.1″, similar to the error adopted for the arc positions. This error is based on the accuracy at which these critical points can be selected. This accuracy is good for these two points due to the existence of symmetrical features at a fraction of an arcsecond from the critical points. The critical points have a relatively small impact in our lens model since a model derived without these critical points produces critical curves that already pass very close to the two critical points.
3. WSLAP+
To optimize the lens model, we used the code WSLAP+ (Diego et al. 2005, 2007, 2016; Sendra et al. 2014). A lens model derived using WSLAP+ is considered a hybrid type of model as it combines a free-form decomposition of the lens plane for the smooth large-scale component with a small-scale contribution from the member galaxies. Details can be found in references above. Here, we give a brief description of the method.
We start with the classic definition of the lens equation:
where θ is the observed position of the multiple images, α is the deflection angle, Σ(θ) is the unknown total surface mass-density of the cluster at the position θ, and β is the unknown position of the background source. The optimization of the WSLAP+ solution takes advantage of the fact that the lens equation can be expressed as a linear function of the total surface mass-density, Σ. WSLAP+ parameterizes Σ as a linear superposition of functions, which translates into α(θ, Σ) being also linear in Σ.
In WSLAP+, the total surface mass-density, Σ, is described by the combination of two components: (i) a smooth component (usually parameterized as superposition of Gaussians) corresponding to the free-form part of the model or large scale cluster potential and (ii) a compact component that accounts for the mass associated with the individual galaxies in the cluster.
For the smooth component, we used Gaussian functions defined over a grid of points. A Gaussian function is simple and enables fast computation of the deflection field, but also provides a good compromise between the desired compactness and smoothness of the basis function. The grid configuration can be defined as regular (all grid points have the same size) or irregular (grid points near the center are in general smaller). Adopting a regular grid is similar to a flat prior in the mass distribution, while an irregular grid can be interpreted as a model with a prior on the mass distribution with a higher mass density assigned to smaller cells. Since one of the goals of this paper is to study the possible correlation between the DM distribution and the ICL, we adopted a regular grid, since this makes minimal assumptions about the mass distribution.
For the compact component, we directly adopted the light distribution in the JWST band F277W around the brightest member elliptical galaxies in the cluster. This filter offers a good compromise between resolution and sensitivity, especially for red galaxies, such as ellipticals. For each galaxy, we assign a mass proportional to its surface brightness. We define an aperture around each galaxy that typically extends up to 2–3 times their half light radius. Diffraction spikes from bright stars are avoided by these apertures. Some of the ICL enters this aperture but this has negligible impact on our results since the member galaxies contribute to the total mass at the percent level. Member galaxies contribute to the total mass model with only free parameter, which accounts for the re-normalization factor multiplying the fiducial mass. This parameter is later re-adjusted as part of the optimization process. The number of parameters connected with the compact component depends on the number of adopted layers. Each layer contains a number of member galaxies. The minimum number of layers is 1, corresponding to the case where all galaxies are placed in the same layer, that is, they are all assumed to have the same mass-to-light ratio. In this case, the single layer is proportional to the light distribution of all member galaxies, and is assigned a fiducial mass for the entire mass of the member galaxies. For each layer, there is one extra parameter that accounts for the renormalization constant multiplying the map of the mass distribution that is optimized by WSLAP+. For the particular case of SMACS0723, we used four layers. The first layer contains the main BCG, the second layer contains a large elliptical galaxy ≈9″ west of the main BCG. The third layer contains two large elliptical galaxies near the Beret galaxy discussed in Mahler et al. (2023). Finally, the fourth layer contains all remaining member galaxies. Member galaxies were selected from the standard red sequence, while also making sure that spectroscopic members identified in Mahler et al. (2023) were included in this set. Only the brightest galaxies are selected for the compact component. In total, the number of member galaxies that define the compact component is 40.
As shown by Diego et al. (2005, 2007), the strong and weak lensing problem can be expressed as a system of linear equations that can be represented in a compact form,
where the measured strong lensing observables (and weak lensing if available) are contained in the array Θ of dimension NΘ = 2Nsl (plus 2Nwl if weak lensing data are available), the unknown total surface mass-density and source positions are in the array X of dimension:
and the matrix Γ is known (for a given grid configuration and fiducial galaxy deflection field) and has a dimension of NΘ × NX. Then, Nsl is the number of strong lensing observables (each one contributing with two constraints, x, and y), Nc is the number of grid points (or cells) that we use to divide the field of view, Nl is the number of layers (Nl = 4 in our case as mentioned above), and Ns is the number of background sources being strongly lensed (each source representing two unknowns in X, βx, and βy). In general, the number of variables (mass in grid points, re-scaling factors for the compact component and source positions) is larger than the number of constraints. The solutions are normally poorly constrained in the outskirts of the cluster, where the number of constraints is poor or simply non-existent. The grid points that are better constrained are those in the central region of the cluster, or around the positions where constraints exist. Although the matrix in the system of equations in Eq. (2) generally has more columns than rows, the optimization is done over a quadratic function of this system with a well-determined minimum.
The solution, X, of the system of equations in Eq. (2) is found after minimizing a quadratic function of X (derived from Eq. (2), as described in Diego et al. 2005). The minimization of the quadratic function is done with the constraint that the solution, X, has to be positive. Since the vector X contains the grid masses, the renormalization factors for the galaxy deflection field and the background source positions (and all these quantities) are always positive (the zero of the source positions is defined in the bottom-left corner of the field of view). Imposing X > 0 helps constrain the space toward meaningful solutions and to regularise the solution, as it avoids unwanted large negative and positive contiguous fluctuations. One of the limitations of this procedure is that the matrix Γ is fixed during the entire optimization process. This means that the redshifts of all systems are fixed and, thus, it is not possible to explore the uncertainty due to imprecise redshift measurements. To explore this uncertainty, multiple optimizations needs to be carried out, each one with a different realization of the redshifts. For this work, we simply present one realization per model, corresponding to the redshifts that are predicted by model-1. In an earlier work, we found that uncertainties due to the choice of grid dominate over uncertainties from redshifts (when using photometric redshift errors), so we focus here on the uncertainty due to the particular choice of the grid, but noting that additional uncertainty is expected from the systems lacking spectroscopic redshift measurements. A detailed discussion of the quadratic algorithm can be found in Diego et al. (2005). For a discussion of its convergence and performance (based on simulated data), we refer to Sendra et al. (2014). In that work, we also discuss how the overfitting problem can be avoided when adding the compact component in our description of the mass distribution. The mass associated to the galaxies in the lens model act as an anchor for the global mass distribution. Without the small-scale mass component, the algorithm continues to optimize the solution by adding more mass in the lens plane, thereby leading to the so-called point-source solution (see, e.g., Ponente & Diego 2011). This point-source solution is usually unphysical, with large fluctuations in the lens plane and often requires regularization. Regularization is not needed when the compact component is added as part of the model, as described in Sendra et al. (2014). For our particular case, we find that the solution reaches a quasi-stable state when the number of iterations ranges between ≈5000 and ≈100 000. When the number of iterations is larger than 100 000, the solutions increase the mass around the edges of the field of view. This is a known artifact of free-form reconstruction methods that results on spurious rings of DM around the central region constrained by lensed galaxies (see Ponente & Diego 2011, for a more in depth discussion of this effect). We fixed the number of iterations to 50 000, well within the stability region of the solutions – but far from the overfitting regime.
The anchoring effect due to the addition of the member galaxies in the lens model is effective provided the number of grid points is in a given range. A very small number of grid points (Nc < 50) results in nonphysical solutions with negligible mass assigned to the compact component and large mass fluctuations, typically in the edge of the field of view. On the other hand, when the number of grid points is too large (Nc > 1500), this also results in large mass fluctuations concentrated in the central region. The case of a large number of grid points can be partially mitigated by the addition of a regularization process (see for instance Cha & Jee 2022). In our case, we avoid these two extreme regimes by choosing a number of grid points which is typically between two to five times the number of available constraints, where solutions exhibit a stable behaviour. The larger number of variables than constraints is not an issue in the minimization process since the quantity that is being minimized is built from the square of the system of linear equations in Eq. (2). By construction, the quadratic function has the same dimension as the number of constraints (see Diego et al. 2005, for specific details on the quadratic function undergoing minimization).
As discussed in Diego et al. (2022), critical points can also be added as extra constraints. We identify two such constraints in systems 5 (at z = 1.425) and system 7 (at z = 5.1727) with spectroscopic redshifts and we include them in our set of lensing constraints. The addition of these two points act as anchors for the lens model, enforcing the critical curve to pass through the desired point at the given redshift.
4. Driver lens model
Using the constraints listed in Table A.1, we first derived the driver model (or model-1). This model is only based on systems with spectroscopic redshifts. For the case of SMACS0723 and, at the time of writing, six systems were known to have spectroscopic redshifts3. These are marked in bold in Table A.1. For the grid, we used a regular distribution of 20 × 20 = 400 grid points. Given the relatively small number of lensing constraints, a significantly larger number of grid points results in nonphysical solutions with large mass fluctuations. Based on the five lensed systems with spectroscopic redshift, the driver model can be used to predict the redshift of the other system candidates in Table A.1. We describe this process in the next section.
5. Redshifts predicted by the lens model
Using the driver model, we derived redshifts for all systems listed in Table A.1. The probability of a system to be at redshift z is computed as:
where V(z) is the variance between the arc positions of a given system projected on the source plane at redshift z. The projection is done with the deflection field of the driver model (computed at redshift z = 3) which is re-scaled to the desired redshift. The dispersion, σ, in the expression above is fixed to three pixels (or ≈0.18″). This is the typical dispersion found in the source plane for the spectroscopic systems and, hence, serves as a reasonable choice for well-constrained systems, resulting in relatively narrow distributions for the redshift and with the uncertainty in the error prediction consistent with the observed error (see, e.g., Diego et al. 2023 for a more in-depth analysis of the errors expected with this technique and for WSLAP+). Systems that are well reproduced by the driver model result in a small variance V(z) near the optimal redshift, which, in turn, results in maximum values of P(z) close to 1. Systems that are poorly reproduced by the driver model have larger values of V(z), thus reducing the maximum value of P(z). The probability in Eq. (4) is not normalized, so its integrated value is not equal to 1. Hence, although we refer to it as probability, it is not in the purest sense of its definition. A low maximum probability for P(z) does not necessarily mean that the system is a bad candidate. This can simply be the result of the driver model not being well constrained in that part of the lens system. Systems at high redshift tend to have broader probabilities, since for a source redshift of z > 2, the deflection field varies slowly with redshift.
The derived probabilities P(z) can be divided in two groups. In the first group, we find systems with well-defined and relatively narrow probabilities. The probabilities for these systems are shown in Fig. 2. Among these we find the systems with spectroscopic redshifts that were used to derive the driver model. Naturally, the maximum of P(z) for these systems falls very close to the spectroscopic value. System 4 had its spectroscopic redshift estimated recently in Noirot et al. (2023) where they find z = 2.211. As shown in Fig. 2, the P(z) for this system contains the correct redshift within the 95% confidence interval.
 |
Fig. 2. Redshifts predicted by the driver model for the case of well-constrained systems. |
In a different group, we find systems for which the redshift is not so well constrained. The probabilities for these systems is shown in Fig. 3. Two systems (14 and 26) have no constrain on their redshift (z > 13). The bad performance of these systems can be easily understood since they correspond to cases of galaxy-galaxy lensing, where the member galaxy acting as a lens is not optimized individually (these galaxies are part of layer 4, as discussed in Sect. 3).
 |
Fig. 3. Redshifts predicted by the driver model for the case of poorly constrained systems. The probability of system 8, shown as a dashed line at z ≈ 8, has been multiplied by a factor of 100. |
System 8 has a very low probability of P(z). This probability is shown as a dashed line in Fig. 3 and the probability has been multiplied by a factor 100 to make it visible in the figure. The low probability of system 8 can be interpreted as being a bad system or being in a region with poor constraints in the driver model. This is the case on the western part of the cluster, where system 8 lies, since only one system has a spectroscopic redshift in this region of the lens. Since we cannot rule out the possibility that the low probability of system 8 is due to the poor performance in this portion of the lens plane of the driver lens model, we include this system in the set of constraints used in the next section. The main results discussed in Sect. 7 are not affected by this choice, since the mass profiles are very similar, whether this system is included or not.
Redshifts predicted by gravitational lenses are an interesting alternative to photometric redshifts, specially for high-redshift candidates for which the photometry may be poor or nonexistent in more than one band (such as in the case of dropouts). A similar technique has been used in the past in other lenses with positive results and was recently applied in Diego et al. (2023) to predict the redshift of the new systems identified in the JWST data of El Gordo cluster.
6. Full-sample lens models
Taking advantage of the redshifts predicted by the lens model discussed in the previous section, we expand the number of constraints and update the lens model. As discussed above, the redshift for systems 14 and 26 cannot be constrained by the lens model so we exclude these two systems from our list of constraints. The remaining number of systems totals 25 and the number of constraints exceeds 150 (x and y positions of each arc plus the two critical point positions, each contributing also with two constraints). Using these constraints, we derived two models. One is model-2, which was derived with the full set of constraints (excluding systems 14 and 26) and a regular grid of 20 × 20 = 400 points. We increased the number of grid points to 25 × 25 = 625 in another model, which we refer to as model-3. Increasing the number of grid points even further can result in unstable solutions. For instance, with a grid of 30 × 30 = 900 points, we obtained a solution that places too much mass in the edges of the field of view and introduces relatively large mass fluctuations across the entire field, so we did not consider solutions with more than 625 grid points.
The three models perform reasonably well in terms of reproducing the position of the lensed images, with typical offsets of ∼1″. These offsets are usually larger than those derived from parametric models (Remolina González et al. 2018), although this does not necessarily mean that models with larger offsets are worse (in terms of reproducing the true underlying mass). All models make necessarily some wrong assumptions, so a model which perfectly reproduces the arc positions must do so at the expense of a solution that cannot be correct in order to correct for the initial wrong assumptions. The more we insist on reaching a perfect solution, the more biased the answer will be. This was tested in the context of WSLAP+ with mock data in Ponente & Diego (2011)4, where it was shown that artifacts, such as rings of DM, appear when solutions that perfectly reproduce the arc positions are insisted upon.
The critical curves for model-2 and model-3 are shown in Fig. 4 as green and blue curves respectively. For convenience, we include again in this figure the critical curve for the driver model (or model-1) in red. All three curves are again computed at the redshift of system 7 (z = 5.1727). The three models produce consistent results in the eastern part of the lens, which is the portion of the cluster where the number density of spectroscopic redshifts is the highest. In contrast, the critical curves in the west differ significantly from one another, indicating that the western part of the cluster is more poorly constrained. The addition of new spectroscopic systems in this part of the lens will reduce the uncertainty in the lens model.
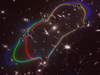 |
Fig. 4. Critical curves of alternative lens models. All critical curves are computed at the redshift of system 7 (z = 5.1727). The red curve corresponds to the driver model derived with the six spectroscopic systems and a grid of 20 × 20 points. The green curve uses the same grid configuration but is derived from the 25 systems with constrained redshifts. The blue curve uses the same 25 systems but it is based on a higher resolution grid of 25 × 25 points. |
In terms of mass, we can compare with previous published results based on parametric models. Both Mahler et al. (2023) and Caminha et al. (2022) quote the total projected mass within a cylinder of radius 128 kpc centered in the BCG. This radius corresponds approximately to the Einstein radius for a source at z > 2, and it is the radius within which the lens model can be properly constrained with strong lensing data. They found masses of 8.26 ± 0.04 × 1013 M⊙ and 8.7 ± 0.2 × 1013 M⊙, respectively, and within the aforementioned 128 kpc radius. For our three lens models, we find 7.28 × 1013 M⊙, 7.31 × 1013 M⊙, and 7.15 × 1013 M⊙ for model-1, model-2, and model-3, respectively, and within the same radius. This is approximately 10% less than in the parametric models.
7. Correlation between DM, ICL, and GCD
For all the three models discussed in the previous sections, we find that their critical curves are consistent among them, with the largest differences concentrating in the west portion of the cluster. Hence, the lens model is relatively well constrained for different choices of lensed systems and grid configurations. In this section, we pay special attention to the distribution of light in the ICL, and the distribution of GCs. We are interested in the possible correlation between the ICL, the GC, and the DM distributions. Figure 5 shows how the ICL presents two loop-like structures to the east and west of the cluster. At ≈200 kpc from the central BCG and towards west, a cavity-like structure can be appreciated in the ICL (giant west loop in Montes & Trujillo 2022). Although it is not as clear, a similar cavity can be also observed towards the east at approximately the same distance from the central BCG. This is a surprising feature in the ICL, where we would expect to find more uniform distributions. Recent merger activity can result in trails of stars being stripped away from their host galaxy by tidal forces. These tails are however much smaller than the observed loops in the ICL of SMACS0723 and connect with the host galaxy. In the case of the loops of SMACS0723, we cannot establish any correspondence between the loops and a member galaxy. On the other hand, as noted by Mahler et al. (2023), the offset between the radial velocity of the central BCG and the mean redshift of the cluster suggests a recent past merger (a relaxed cluster would have no offset), offering a possible explanation for the odd distribution of the ICL.
 |
Fig. 5. Projected total mass versus ICL. The contours represent the smooth component of the lens model obtained with the 25 constrained systems. The yellow contour is obtained with a regular grid of 20 × 20 cells while the blue contour is obtained with a higher resolution grid of 25 × 25 cells. The image is a masked version of the F277W band, where the ICL light can be better appreciated. The contours correspond to values of the convergence, κ, computed at a fiducial source redshift of zs = 3. Space between contours correspond to δκ = 0.1, with values starting at κ = 0.5. The last contour is for κ = 1.15. The white straight line marks the direction over which we constructed the 1D scan of the light profile and DM models. |
Whatever the cause for the morphology of the ICL, it is interesting to compare its two-dimensional distribution with the distribution of mass from our lens models. Since approximately 85% of the projected mass of the cluster is expected to be DM, if the DM and the ICL are related, we should expect a correlation between the two. In Fig. 5, we show (as yellow contours) the distribution of smooth mass (mostly DM) from our model-2, while in blue we show the contours for the distribution of the smooth component of mass from our model-3 (model-1 is not shown but it is very similar to model-2). The smooth mass component is obtained after subtracting the mass associated to the galaxies from the total mass. In general we find good correspondence between the distribution of the ICL and the two mass models.
A more quantitative comparison is shown in Fig. 6, where we compute the average of the ICL or the DM along a straight line. This line is shown in Fig. 5 and it intersects the ICL from west to east, passing through the central BCG in the middle. The average is computed at each position as the mean over a box of size 0.18″ × 0.18″ and centered in the line. The black curve in Fig. 6 corresponds to the light distribution. The colored lines are for the driver model or model-1 (red), model-2 (green), and model-3 (blue). The curves for the DM models have been re-scaled by an arbitrary number to match the black curve.
 |
Fig. 6. 1D scan of the light distribution versus DM. The x-axis is the distance to the BCG. The solid black line shows the mean of the light emission in the F277W band along the straight line shown in Fig. 5. The mean is computed over a box of 10 × 10 pixels at each position. The colored lines are the corresponding mean of the DM component for the three lens models discussed in this work. The red color is for the driver model, the green line is for model-2, or low-resolution (20 × 20 grid points) with 25 systems, and the blue model is for the high-resolution (25 × 25 grid points) model-3 with 25 systems. The DM profiles are re-scaled by arbitrary units to visually match the profile of the light emission. See Fig. 8 for a direct comparison of the profiles without the re-scaling. |
In the eastern part of the cluster, we find good correspondence between all three models and the ICL. This is not true in the west part of the cluster, where the cavity that clearly seen in the ICL at ≈ − 200 kpc in Fig. 6 is not observed in any of the DM models.
In addition to the ICL, another possible tracer of the potential are GCs, whose distribution could be correlated with the distribution of DM, since as the stars in the ICL and GCs respond to gravitational forces. The superior sensitivity and spatial resolution of JWST allows us to detect these clusters in unprecedented detail. Preliminary results based on JWST data in SMACS0723 are presented in Lee et al. (2022), Faisst et al. (2022). It is interesting to compare our results with those from earlier works. Figure 7 compares the observed ICL in the F356W filter with the distribution of DM (yellow contour) and the distribution of GCs (blue contours) from Lee et al. (2022). To compute the blue contours we have smoothed the distribution of GCs with a Gaussian of FWHM = 1.5″. To first order, there is a good spatial correspondence between the DM, ICL and GC distribution, with all three components centered in the same point (BCG) and having similar alignments in the east-west direction. As in the case of the ICL, the distribution of GCs appears to show a similar deficit in number density at the position of the cavity on the west side of the cluster. This cavity has no correspondence in the distribution of DM.
 |
Fig. 7. Comparison of the DM and GC distribution (number density). The image corresponds to the F356W JWST filter. Yellow contours are the smooth component of the DM distribution (model-2), while the blue contours are for a Gaussian filtered version (FWHM = 1.5″) of the distribution of GCs from Lee et al. (2022). |
In terms of radial profiles, we show a comparison of our lens model with the ICL profiles from Montes & Trujillo (2022) and the GC profile from Lee et al. (2022) in Fig. 8. For the GCs, we re-scaled the surface number density (expressed as number per kpc2) by a factor 2 × 109 in order for the resulting profile to overlap with the ICL profile. For comparison we plot a power law R−1.3 as a dashed line. This power law reproduces well the profile of the ICL and the GC number density.
 |
Fig. 8. Comparison of the total mass profile from the three lens models (solid lines) with the ICL profile from Montes & Trujillo (2022; shaded orange and blue regions for the east and west sectors, respectively) and the GC number profile from Lee et al. (2022; blue dots). For the latter, we re-scaled the number density by an arbitrary number of 2 × 109 in order to overlap with the ICL profile. The black dashed line is a power law that scales with distance as R−1.3. The red dashed line is a power law that scales as R−0.3. The dotted lines are the density profiles from Mahler et al. (2023), while the blue solid line is the lens model from Pascale et al. (2022). These models are derived with similar lensing constraints but using different algorithms. The light-blue shaded region displays the range of models (minimum and maximum profiles) we obtained when we varied the initial condition of the optimization process. |
The mass profiles from the three lens models are shown as a solid lines. Within the inner 20 kpc region, the total mass and the ICL have similar profiles. This is expected in our lens model since the compact component of the lens model takes directly the light distribution of member galaxies, including the central BCG. Since near the center of the BCG, the bulk of the mass is expected to come from stars (or the baryonic component in general); by comparing our lens model with the ICL profile from Montes & Trujillo (2022), we find that either (i), there is ≈10 times more DM than stellar mass within the central 20 kpc or (ii) the stellar mass from the ICL is underestimated by some factor.
Beyond ≈20 kpc, the total mass profile is clearly shallower than the profile of the ICL and the number density of GCs. This departure is interesting and needs to be studied in other clusters with more constraints. Increasing the number of lensing constraints will allow for the spatial resolution of the lens model to be improved.
These conclusions are robust independently of the modeling technique used to derive the mass model. In Fig. 8, we show the comparison between our free-form lens models and models derived in previous work (Pascale et al. 2022; Mahler et al. 2023) that rely on different techniques. The profiles agree well in the range constrained by strong lensing (≈30–250 kpc), confirming our findings.
8. Discussion and conclusions
The new data from JWST reveal a wealth of new candidate lensed galaxies. Future observations of these candidates will secure their redshifts, which can then be compared with the geometric redshift estimate based on our driver model. If spectroscopic confirmation validates the method of estimating distances through geometric redshifts, future observations by the JWST can take advantage of a similar technique, where a handful of spectroscopic lensed galaxies may suffice to calibrate a lens model for distance estimation. Recent work has shown how photometric redshifts can predict erroneous redshifts for the case of dropout galaxies in the JWST bands (Harikane et al. 2023; Naidu et al. 2022; Zavala et al. 2023). An independent estimation of the distance to these galaxies can help reduce the uncertainty in the estimation of the redshift and identify those galaxies that have large photometric redshifts (z > 10); however, they have been predicted by the lens model to be at much lower redshift.
Lens models such as the one presented in this work are also needed to interpret sources near caustics. In the case of SMACS0723, Pascale et al. (2022) discuss a small pair of knots in the middle of the merging pair of images of system 5 (see their Fig. 2). Since the lens model has a resolution comparable to the separation between the knots in the pair, the magnification in these knots is better estimated by interpolating the magnification. Based on symmetry arguments, the critical curve must pass between these two points, so they are equidistant to it (d ≈ 0.08″). Since the magnification near a fold caustic scales as μ = A/d (Schneider et al. 1992), we can estimate A from our lens model. We find A ≈ 58″, which results in μ ≈ 725 for each of the images in the pair. This estimate matches the value quoted in Pascale et al. (2022) of μ ≈ 750 very well.
The greater sensitivity of JWST to the ICL offers new opportunities to study the correlation between the DM and ICL. In addition, the improved spatial resolution in the infrared bands allows for the detection of small clumps of old stellar populations in the cluster stripped from their hosts galaxies. The first image of JWST on this cluster reveals hundreds of unresolved clumps that have been interpreted as GCs (Lee et al. 2022; Faisst et al. 2022); however, they could also be the surviving remnants (after a close encounter with a larger galaxy in the cluster, such as the BCG) of compact galactic cores. Both the stars in the ICL and in GCs are expected to interact with the rest of the matter in the cluster mostly through gravitational forces, thus behaving similarly to DM.
In this work we use a free-form modeling technique which makes minimal assumptions about the distribution of DM and we find that, in general, the DM traces the ICL and GC distribution well. However, we also find that the small loop-like structures (and associated cavities) to the east and west of the central region of SMACS0723 have no obvious correspondence in the DM distribution. At distances from the center comparable to the Einstein radius (∼100 kpc, and hence well constrained by the available data), we find that the DM profile is significantly shallower than the ICL and GC distributions. This is also found in simulation of galaxy clusters. In Alonso Asensio et al. (2020), the authors analyzed the EAGLE simulations and found that the ICL profile is steeper than the total mass profile. In particular, they found that the ratio between the ICL and total mass profiles is a power law with a slope of −1. Interestingly, in the range between ≈20 kpc and ≈200 kpc we find a similar ratio between the total mass and ICL (and GC) profiles, with the ICL and GC profiles falling to ∼R−1.3, while the total mass falls to ∼R−0.3 (see Fig. 8). Similar conclusions are found in Pillepich et al. (2018) where, based on the IllustrisTNG simulations, the 3D profile of the ICL in massive clusters is found to fall faster (by approximately 1 dex from their Fig. 6 at around 100 kpc distance) than the canonical NFW profile commonly used to describe DM profiles. Earlier work based on the EAGLE simulations shows a similar trend (Schaller et al. 2015). Hence, our results on SMACS0723 are in agreement with the ones derived from N-body simulations.
We observe differences in the range ≈20–200 kpc between the ICL (and GC) profiles and the total mass (mostly dominated by DM in this distance range). We speculate that this may be related to the different formation times of the cluster DM halo and ICL. Since DM is more loosely bounded to their host halos (as it mostly resides on the outskirts of the galaxies, with the central region being more baryon-dominated), it can be stripped more easily during the first encounters with the cluster, and hence retaining the initial (relatively large) angular momentum. The baryonic component (stars in our case) is more concentrated around the center of the satellite galaxies and can survive more encounters with the cluster, and without being stripped away. In each encounter, the satellite galaxy looses angular momentum due to dynamical friction and can get closer to the BCG (Contini et al. 2018; Chun et al. 2023). Stars that are stripped at a later time lose part of their bulk kinetic energy this way and when they stripped from their hosts, they can remain at shorter radii, resulting in profiles that are steeper (more concentrated) than the DM profiles. Globular clusters and galactic core remnants are subject also to dynamical friction, hence, they are expected to orbit closer to the BCG, resulting in more concentrated profiles. N-body simulations also show how the radial distribution of subhalos is steeper than the distribution of DM (Gao et al. 2004).
The presence of cavities in the distribution of the ICL but not detected in the total mass distribution is another interesting difference. The formation of cavities in the ICL, but not in the DM distribution, could be due to the different distribution of stars and DM inside the satellite galaxies before they enter the galaxy cluster and the stripping mechanism starts to take place. The DM, forming an extended halo around the satellite galaxy, is easily tidally stripped from its host galaxy as it enters the cluster and starts orbiting around the BCG. The better ability of the baryonic matter to cool down more efficiently and form more concentrated structures, such as disks or bulges, facilitates the survival of the bulge (or disk) as they orbit the minimum of the potential. During a close encounter with the BCG, parts of the bulge or disc of a satellite galaxy can be tidally stripped, creating the loop-like structures and associated cavities. The tidal stripping of satellite galaxies has been claimed as responsible for filamentary structures seen in the ICL of the nearby Virgo cluster (Mihos et al. 2005). Structures that resemble the loop-cavity system are also observed in nearby galaxies that had recent encounters with satellite galaxies (Martínez-Delgado et al. 2023). In the simulations, faint structures in the ICL that resemble the loop-cavity structures can be appreciated in Figs. 3 and 4 in Pillepich et al. (2018).
Perhaps one of the most interesting findings is the connection between the ICL and GC distribution, given both have a similar profile. This connection could be easily explained if the ICL were found to correspond to the outer envelopes of the alleged GCs. In this case, the GCs should be re-interpreted as the surviving galactic cores of the infalling satellite galaxies.
More examples similar to the one studied in this work are needed in order to extract a firmer conclusion regarding the connection between the ICL, GCs, and DM distributions. In particular, the addition of new constraints (with confirmed spectroscopic redshift) will allow us to increase the resolution of the lens model, revealing perhaps finer details in the distribution of DM that could not be unveiled with the current set of constraints. For the particular case of SMACS0723, the number of lensing constraints around the west cavity is very small (with about four lensed galaxies in this region). Future analyses based on JWST data, especially of low redshift clusters for which both ICL and GCs are more easily detected, and including abundant lensing constraints (such as the Hubble Frontier Fields Clusters) will enable us to draw more precise conclusions on the correlation between the ICL, GCs, and DM distributions.
As this paper was being finished, a new spectroscopic redshift for system 4 (z = 2.211) is provided in Noirot et al. (2023).
As noted earlier, a new spectroscopic redshift was recently made available for system 4 in Noirot et al. (2023) at the time of finishing this paper. This new redshift (z = 2.211) was not used in our analysis where we adopted our geometric redshift estimate (z = 2). The difference in redshift is small and is not expected to have any significant impact in our results.
Acknowledgments
J.M.D. acknowledges the support of project PGC2018-101814-B-100 (MCIU/AEI/MINECO/FEDER, UE) Ministerio de Ciencia, Investigación y Universidades. This project was funded by the Agencia Estatal de Investigación, Unidad de Excelencia María de Maeztu, ref. MDM-2017-0765. M.P. was funded through the NSF Graduate Research Fellowship grant No. DGE 1752814. A.Z. acknowledges support by Grant No. 2020750 from the United States-Israel Binational Science Foundation (BSF) and Grant No. 2109066 from the United States National Science Foundation (NSF), and by the Ministry of Science & Technology, Israel. G.M. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No MARACHAS-DLV-896778. M.J. is supported by the United Kingdom Research and Innovation (UKRI) Future Leaders Fellowship “Using Cosmic Beasts to uncover the Nature of Dark Matter” (grant number MR/S017216/1). M.G.L. was supported by the National Research Foundation grant funded by the Korean Government (NRF-2019R1A2C2084019). M.M. acknowledges the Project PCI2021-122072-2B, financed by MICIN/AEI/10.13039/501100011033, and the European Union “NextGenerationEU”/RTRP.
References
- Adams, N. J., Conselice, C. J., Ferreira, L., et al. 2023, MNRAS, 518, 4755 [Google Scholar]
- Alonso Asensio, I., Dalla Vecchia, C., Bahé, Y. M., Barnes, D. J., & Kay, S. T. 2020, MNRAS, 494, 1859 [CrossRef] [Google Scholar]
- Caminha, G. B., Suyu, S. H., Mercurio, A., et al. 2022, A&A, 666, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carnall, A. C., Begley, R., McLeod, D. J., et al. 2023, MNRAS, 518, L45 [Google Scholar]
- Cha, S., & Jee, M. J. 2022, ApJ, 931, 127 [CrossRef] [Google Scholar]
- Chan, J. H. H., Schive, H.-Y., Wong, S.-K., Chiueh, T., & Broadhurst, T. 2020, Phys. Rev. Lett., 125, 111102 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, C., Yan, H., Huang, J.-S., et al. 2022, ApJ, 936, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Chun, K., Shin, J., Smith, R., Ko, J., & Yoo, J. 2023, ApJ, 943, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, E., Yi, S. K., & Kang, X. 2018, MNRAS, 479, 932 [NASA ADS] [Google Scholar]
- Diego, J. M., Protopapas, P., Sandvik, H. B., & Tegmark, M. 2005, MNRAS, 360, 477 [Google Scholar]
- Diego, J. M., Tegmark, M., Protopapas, P., & Sandvik, H. B. 2007, MNRAS, 375, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J. M., Broadhurst, T., Chen, C., et al. 2016, MNRAS, 456, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J. M., Pascale, M., Kavanagh, B. J., et al. 2022, A&A, 665, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diego, J. M., Meena, A. K., Adams, N. J., et al. 2023, A&A, 672, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faisst, A. L., Chary, R. R., Brammer, G., & Toft, S. 2022, ApJ, 941, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, L., Adams, N., Conselice, C. J., et al. 2022, ApJ, 938, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, L., White, S. D. M., Jenkins, A., Stoehr, F., & Springel, V. 2004, MNRAS, 355, 819 [Google Scholar]
- Golubchik, M., Furtak, L. J., Meena, A. K., & Zitrin, A. 2022, ApJ, 938, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Ouchi, M., Oguri, M., et al. 2023, ApJS, 265, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, N., Zitrin, A., Dole, H., et al. 2022, A&A, 667, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. G., Bae, J. H., & Jang, I. S. 2022, ApJ, 940, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Mahler, G., Jauzac, M., Richard, J., et al. 2023, ApJ, 945, 49 [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Roca-Fàbrega, S., Miró-Carretero, J., et al. 2023, A&A, 669, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [Google Scholar]
- Montes, M. 2022, Nat. Astron., 6, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, M., & Trujillo, I. 2018, MNRAS, 474, 917 [Google Scholar]
- Montes, M., & Trujillo, I. 2019, MNRAS, 482, 2838 [Google Scholar]
- Montes, M., & Trujillo, I. 2022, ApJ, 940, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Mowla, L., Iyer, K. G., Desprez, G., et al. 2022, ApJ, 937, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Oesch, P. A., Setton, D. J., et al. 2022, ApJL, submitted [arXiv:2208.02794] [Google Scholar]
- Noirot, G., Desprez, G., Asada, Y., et al. 2023, MNRAS, 525, 1867 [NASA ADS] [CrossRef] [Google Scholar]
- Pascale, M., Frye, B. L., Diego, J., et al. 2022, ApJ, 938, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018, MNRAS, 475, 648 [Google Scholar]
- Ponente, P. P., & Diego, J. M. 2011, A&A, 535, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pooley, D., Rappaport, S., Blackburne, J. A., Schechter, P. L., & Wambsganss, J. 2012, ApJ, 744, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Remolina González, J. D., Sharon, K., & Mahler, G. 2018, ApJ, 863, 60 [CrossRef] [Google Scholar]
- Schaller, M., Frenk, C. S., Bower, R. G., et al. 2015, MNRAS, 452, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Berlin Heidelberg, New York: Springer-Verlag), 112 [Google Scholar]
- Sendra, I., Diego, J. M., Broadhurst, T., & Lazkoz, R. 2014, MNRAS, 437, 2642 [NASA ADS] [CrossRef] [Google Scholar]
- Sharon, K., Chen, M. C., Mahler, G., Coe, D., & RELICS: Reionization Lensing Cluster Survey 2023, ApJS, 264, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, J. A., Buat, V., Casey, C. M., et al. 2023, ApJ, 943, L9 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Arc positions and redshifts
This appendix presents all arc system candidates used in this work. The table is a compilation of systems presented in Mahler et al. (2023), Pascale et al. (2022), Caminha et al. (2022). The last two rows are the positions of the two critical points used as extra constraints.
The IDs of the systems are shown in column 1. Columns 2 and 3 give the RA and DEC positions in degrees. Column 4 lists the spectroscopic redshifts when available. Spectroscopic redshifts are marked in bold face. Column 5 lists the redshifts predicted by the driver model. In this case, errors correspond to the 68% interval of the PDF. For all systems, only the first arc is given with its redshift. Colums 6-8 give the original ID in Pascale et al. (2022), Caminha et al. (2022), and Mahler et al. (2022), respectively.
‡While finishing this paper, Noirot et al. (2023) published spectroscopic redshifts of some galaxies in the field of SMACS0723 including a redshift for our system 4, for which they found zspec = 2.211; this result is in good agreement (2σ) with our geometric redshift estimate (zgeo = 2 ± 0.1). No other redshifts have been published for the remaining arcs without spectroscopic redshifts.
Arc positions and redshifts.
All Tables
All Figures
 |
Fig. 1. Central ≈1 arcmin region of SMACS0723 with systems of lensed galaxies. This image was obtained by combining different filters from JWST. Systems in white have spectroscopic redshifts and are the ones used to build the driver model or model-1. Systems in yellow do not have spectroscopic redshifts but are used in combination with the spectroscopic systems to build lens model-2 and model-3. We note the hundreds of unresolved sources surrounding the BCG, which are mostly GCs and galactic core remnants. Unless otherwise noted, all figures in this paper are in the same orientation as this one. The two critical points, CP5 and CP7, are shown in the bottom-left portion of the plot. |
| In the text | |
 |
Fig. 2. Redshifts predicted by the driver model for the case of well-constrained systems. |
| In the text | |
 |
Fig. 3. Redshifts predicted by the driver model for the case of poorly constrained systems. The probability of system 8, shown as a dashed line at z ≈ 8, has been multiplied by a factor of 100. |
| In the text | |
 |
Fig. 4. Critical curves of alternative lens models. All critical curves are computed at the redshift of system 7 (z = 5.1727). The red curve corresponds to the driver model derived with the six spectroscopic systems and a grid of 20 × 20 points. The green curve uses the same grid configuration but is derived from the 25 systems with constrained redshifts. The blue curve uses the same 25 systems but it is based on a higher resolution grid of 25 × 25 points. |
| In the text | |
 |
Fig. 5. Projected total mass versus ICL. The contours represent the smooth component of the lens model obtained with the 25 constrained systems. The yellow contour is obtained with a regular grid of 20 × 20 cells while the blue contour is obtained with a higher resolution grid of 25 × 25 cells. The image is a masked version of the F277W band, where the ICL light can be better appreciated. The contours correspond to values of the convergence, κ, computed at a fiducial source redshift of zs = 3. Space between contours correspond to δκ = 0.1, with values starting at κ = 0.5. The last contour is for κ = 1.15. The white straight line marks the direction over which we constructed the 1D scan of the light profile and DM models. |
| In the text | |
 |
Fig. 6. 1D scan of the light distribution versus DM. The x-axis is the distance to the BCG. The solid black line shows the mean of the light emission in the F277W band along the straight line shown in Fig. 5. The mean is computed over a box of 10 × 10 pixels at each position. The colored lines are the corresponding mean of the DM component for the three lens models discussed in this work. The red color is for the driver model, the green line is for model-2, or low-resolution (20 × 20 grid points) with 25 systems, and the blue model is for the high-resolution (25 × 25 grid points) model-3 with 25 systems. The DM profiles are re-scaled by arbitrary units to visually match the profile of the light emission. See Fig. 8 for a direct comparison of the profiles without the re-scaling. |
| In the text | |
 |
Fig. 7. Comparison of the DM and GC distribution (number density). The image corresponds to the F356W JWST filter. Yellow contours are the smooth component of the DM distribution (model-2), while the blue contours are for a Gaussian filtered version (FWHM = 1.5″) of the distribution of GCs from Lee et al. (2022). |
| In the text | |
 |
Fig. 8. Comparison of the total mass profile from the three lens models (solid lines) with the ICL profile from Montes & Trujillo (2022; shaded orange and blue regions for the east and west sectors, respectively) and the GC number profile from Lee et al. (2022; blue dots). For the latter, we re-scaled the number density by an arbitrary number of 2 × 109 in order to overlap with the ICL profile. The black dashed line is a power law that scales with distance as R−1.3. The red dashed line is a power law that scales as R−0.3. The dotted lines are the density profiles from Mahler et al. (2023), while the blue solid line is the lens model from Pascale et al. (2022). These models are derived with similar lensing constraints but using different algorithms. The light-blue shaded region displays the range of models (minimum and maximum profiles) we obtained when we varied the initial condition of the optimization process. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.