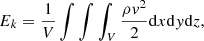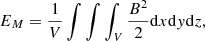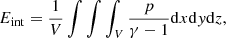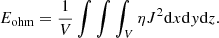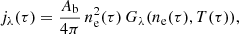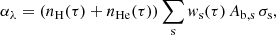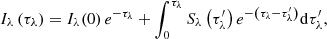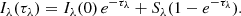| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 12 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202347038 | |
| Published online | 13 October 2023 | |
3D coupled tearing-thermal evolution in solar current sheets⋆
Centre for mathematical Plasma-Astrophysics, Celestijnenlaan 200B, 3001 Leuven, Belgium
e-mail: samrat.sen@iac.es; samratseniitmadras@gmail.com
Received:
29
May
2023
Accepted:
16
August
2023
Context. The tearing instability plays a major role in the disruption of current sheets, whereas thermal modes can be responsible for condensation phenomena (forming prominences and coronal rain) in the solar atmosphere. However, how current sheets made unstable by combined tearing and thermal instability evolve within the solar atmosphere has received limited attention to date.
Aims. We numerically explore a combined tearing and thermal instability that causes the break up of an idealized current sheet in the solar atmosphere. The thermal component leads to the formation of localized, cool condensations within an otherwise 3D reconnecting magnetic topology.
Methods. We constructed a 3D resistive magnetohydrodynamic simulation of a force-free current sheet under solar atmospheric conditions that incorporates the non-adiabatic influence of background heating, optically thin radiative energy loss, and magnetic-field-aligned thermal conduction with the open source code MPI-AMRVAC. Multiple levels of adaptive mesh refinement reveal the self-consistent development of finer-scale condensation structures within the evolving system.
Results. The instability in the current sheet is triggered by magnetic field perturbations concentrated around the current sheet plane, and subsequent tearing modes develop. This in turn drives thermal runaway associated with the thermal instability of the system. We find subsequent, localized cool plasma condensations that form under the prevailing low plasma-β conditions, and demonstrate that the density and temperature of these condensed structures are similar to more quiescent coronal condensations. Synthetic counterparts at extreme ultraviolet (EUV) and optical wavelengths show the formation of plasmoids (in EUV) and coronal condensations similar to prominences and coronal rain blobs in the vicinity of the reconnecting sheet.
Conclusions. Our simulations imply that 3D reconnection in solar current sheets may well present an almost unavoidable multi-thermal aspect that forms during their coupled tearing-thermal evolution.
Key words: instabilities / magnetohydrodynamics (MHD) / Sun: corona / Sun: filaments / prominences
Movies are available at https://www.aanda.org.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Magnetic reconnection is a fundamental process understood to play a critical role throughout the solar atmosphere. The change in magnetic field topology during reconnection leads to the conversion of magnetic energy into thermal and kinetic energies (Biskamp 2000), frequently leading to fast energy release of solar flares (Giovanelli 1939, 1947, 1948; Priest & Forbes 2000; Hesse & Cassak 2020) and coronal mass ejections (Gosling et al. 1995; Schmidt & Cargill 2003; Karpen et al. 2012) out into the heliosphere.
It was suggested by Furth et al. (1963) that reconnection in an incompressible plasma may be triggered due to small perturbations in a current layer, correspondingly breaking up the current sheet in the form of the tearing instability. Linear analysis by Loureiro et al. (2007) suggests that the tearing instability in a single current sheet may lead to the formation of a chain of plasmoids (secondary magnetic islands). This was later verified in 2D numerical simulations by Huang & Bhattacharjee (2013) and Huang et al. (2013). Extensions to 2D double-current layer models were seen to give rise to the development and layer-layer interactions of tearing modes with smaller-scale plasmoid formation (Zhang & Ma 2011; Keppens et al. 2013; Akramov & Baty 2017; Paul & Vaidya 2021, and references therein).
None of these previous studies considers the nonadiabatic effects of background heating, radiative energy loss, and thermal conduction, which are essential components of the solar atmosphere. It is well established that the solar corona is in a delicate overall thermal balance. If this balance resulting from optically thin radiative loss and background heating in combination with thermal conduction is perturbed, an increment of the thermal energy loss cooling down the plasma may lead to an enhancement of the plasma density. This in turn radiates more energy (radiative loss in an optically thin medium is proportional to the square of plasma density), and the material becomes cooler still. A catastrophic runaway process hence ensues, leading to a rapid rise in the density and a drop in temperature that is in essence the thermal instability. A detailed linear analysis of the thermal instability is presented by Parker (1953) and Field (1965), who derived the criteria governing the onset of a catastrophic radiative loss in an infinite homogeneous medium. The linear magnetohydrodynamic (MHD) analysis was extended to a 1D slab configuration (van der Linden & Goossens 1991b; van der Linden et al. 1992) and cylindrical geometry (van der Linden & Goossens 1991a; Soler et al. 2011) under solar coronal conditions. Linear and follow-up nonlinear theory of thermal instability is a powerful tool to explain various fascinating features of the solar atmosphere. For example, the possible formation of a prominence in a current sheet is discussed by Smith & Priest (1977) and the dynamic thermal balance in a coronal arcade is studied in Priest & Smith (1979). The post-flare loop formation in a line-tied current sheet configuration with radiative energy loss was simulated in a 2D MHD setup by Forbes & Malherbe (1991).
More recently, multidimensional simulations related to prominence formation emerged in a variety of magnetic topologies. Xia et al. (2012) reported the ab initio formation of a solar prominence in a 2.5D MHD simulation in a bipolar magnetic arcade due to chromospheric evaporation and thermal instability. This was revisited in a quadrupolar arcade setup in which reconnection was induced by the condensing prominence by Keppens & Xia (2014). That prominences can also form by feeding chromospheric matter within plasmoids during a flux rope eruption is developed by Zhao & Keppens (2022). 3D models of prominence formation that establish the needed plasma cycle between chromosphere and corona are shown in Xia & Keppens (2016). More recently, prominence formation due to levitation-condensation (Kaneko & Yokoyama 2015); Jenkins:2021 was demonstrated, in which a 3D realization is needed to allow magnetic Rayleigh-Taylor instability (Jenkins & Keppens 2022). The effect of thermal instability has also been explored in relation to the formation and dynamics of coronal rain in magnetic arcades in 2.5D geometry (Fang et al. 2013, 2015), in a weak magnetic bipole in 3D geometry (Xia et al. 2017), in a more self-consistent 3D radiative-MHD setup in Kohutova et al. (2020), and for randomly heated arcades by Li et al. (2022) in a 2.5D geometry.
These works also triggered a renewed interest in more idealized studies of linear thermal instability and its nonlinear evolution, and in how the various linear MHD waves and instabilities may interact. Numerical analysis in the linear and nonlinear domains due to the interaction of the slow MHD and entropy (thermal) modes was carried out in recent studies by Claes & Keppens (2019) and Claes et al. (2020), while the effect of different radiative loss functions on the onset and far nonlinear behavior of thermal modes was analyzed by Hermans & Keppens (2021). However, the influence of thermal instability on the tearing mode of solar current sheets has not gained much attention to date. Linear analysis by Ledentsov (2021a,b,c) shows that the instability growth rate in a pre-flare current sheet is modified if the nonadiabatic effects of radiative energy loss, resistivity, and thermal conductivities are included. Sen & Keppens (2022; SK22 hereafter) extended this into the nonlinear domain and incorporated background heating and optically thin radiative loss into a series of 2D resistive MHD simulations. This study finds that the instability growth rate of tearing modes in a solar current sheet increases by an order of magnitude when these nonadiabatic effects are incorporated, such that we can meaningfully speak of coupled tearing-thermal evolutions. The 2D current sheet produced a chain of plasmoid-trapped condensations with cool material, which are thermodynamically similar to prominence (or coronal rain) in the solar atmosphere.
In this work, we extend our study to a 3D geometry and explore the tearing-thermal evolutionary process of an idealized current sheet model in the solar atmosphere that is essentially nonadiabatic (with background heating, optically thin radiative loss, and thermal conduction). Due to the mutual reinforcement of these instabilities, we demonstrate the combined effect of the complex evolution of the current layer, which disintegrates into finer structures with the subsequent development of flux ropes, along with the formation of cool plasma condensations in the vicinity of this evolving current sheet. These localized cool and plasma-condensed regions share similarities with the prominence and coronal rain structures observed in the solar atmosphere. Our findings here augment the growing theoretical basis for the combined effect of a current sheet fragmentation and the formation of cool, condensed plasma due to a coupled tearing-thermal instability. This multimode evolution of the system occurring in association with or during reconnection in a current sheet is an important aspect in understanding the dynamics and multi-thermal processes in the solar atmosphere.
The paper is organized as follows. In Sect. 2, we describe the numerical model with an initial configuration with a precise magnetic and thermodynamic structure, and detail algorithmic aspects and boundary conditions. In Sect. 3, we discuss the main results of the study, and the relevance of the model in the solar atmosphere. Section 4 addresses the significance and novelty of the work for a typical coronal atmosphere and the scope for further development, and points out how this work will be useful for future studies.
2. Numerical setup
We constructed a resistive MHD simulation using MPI-parallelised Adaptive Mesh Refinement Versatile Advection Code or MPI-AMRVAC1 (Keppens et al. 2012, 2021, 2023; Porth et al. 2014; Xia et al. 2018) in 3D Cartesian geometry. The spatial domain of the simulation box spans from −10 to 10 (in dimensionless units) in the x − y − z directions. We activated the adaptive mesh refinement (AMR) up to level three, which gives a maximum resolution of 5123. If the box size is set in units of 10 Mm, this achieves the smallest cell size of 390 km in each direction. Automated refinement and derefinement is triggered based on the errors estimated by the instantaneous density (gradient) at each time step.
To explore the influence of thermal instability on the tearing mode in a current sheet, the following normalized MHD equations are solved numerically:
We used magnetic units where the magnetic permeability is unity. Here, I is the unit tensor, and ρ, T, B, v, and η represent mass density, temperature, the magnetic field vector, the velocity vector, and resistivity, respectively. A uniform resistivity, η = 0.001 (or 1.2 × 1014 cm2 s−1 in physical units), was taken throughout the entire simulation domain. We adopted the Spitzer-type thermal conductivity, κ|| = 10−6T5/2 erg cm−1 s−1 K−1, which is purely aligned along the magnetic field. The total pressure, ptot, is the sum of the plasma and the magnetic pressure, given by
where p is the gas pressure linked with the thermodynamic quantities through the ideal gas law. The total energy density is
where γ = 5/3 is the ratio of specific heats for a monoatomic gas (fully ionized hydrogen plasma). We set up a current sheet configuration using the magnetic field components
where B0 = 1 (corresponding to 2 G in physical units) is the magnetic field strength, which is comparable with observations in the solar corona, where the field strength at the height of the 1.05–1.35 solar radius are reported between 1–4 G (Lin et al. 2004; Kumari et al. 2019; Yang et al. 2020). The unit plasma density, temperature, and length scales are set as 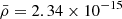 g cm−3,
g cm−3, 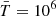 K, and
K, and 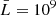 cm, which are relevant for the solar corona. The initial width of the current sheet is set to ls = 0.5 (5 Mm in physical units), which is comparable with the observed flare current sheet thickness (Li et al. 2018); savage:2010. The magnetic field configuration given by Eqs. (9)–(11) represents a force-free field, and the polarity reversal of the magnetic field occurs around the z = 0 plane, where the current sheet is. In line with a fully force-balanced equilibrium of the system, we used isothermal and isobaric conditions as the initial setup of the model.
cm, which are relevant for the solar corona. The initial width of the current sheet is set to ls = 0.5 (5 Mm in physical units), which is comparable with the observed flare current sheet thickness (Li et al. 2018); savage:2010. The magnetic field configuration given by Eqs. (9)–(11) represents a force-free field, and the polarity reversal of the magnetic field occurs around the z = 0 plane, where the current sheet is. In line with a fully force-balanced equilibrium of the system, we used isothermal and isobaric conditions as the initial setup of the model.
The third term at the right-hand side (RHS) of Eq. (3) represents the radiative cooling in the optically thin corona, where Λ(T) is the cooling function developed by Colgan & Abdallah (2008) and extended to lower temperatures following Dalgarno & McCray (1972). The precise temperature dependence of Λ(T) was shown in Fig. 1 of our previous 2D simulation (SK22). To maintain the initial thermal balance between optically thin radiative loss and background heating, Hbgr, of the system, we prescribed a uniform, time-independent value,
The motivation for using the above form was that the radiative cooling term at the initial state exactly compensates for the background heating term, and the heating-cooling (mis)balance in the system occurs after a long-term evolution triggered by the external perturbations (which is the magnetic field in this study). This heating model is similar to our earlier study in SK22, although uniform in space. However, the role of different heating models based on the power-law behavior of the magnetic field strength, and the density at the thermal runaway, and condensation processes, has been reported by Brughmans et al. (2022), which finds that the different heating models can change the evolution and morphology of the condensations. How the different heating rates change the thermal balance of our model could therefore be interesting to study in future. With a homogeneous density, ρ0 = 0.2 (4.68 × 10−16 g cm−3 in physical units), and isothermal atmosphere, T0 = 0.5 (0.5 MK in physical units), as the initial condition, we have an initially uniform plasma-β = 0.2, less than unity, as appropriate for the solar corona. We used the initial temperature, T0 = 0.5 MK, which is in the temperature regime in which the cooling function we used in this study has a very sharp gradient, and the heating-cooling misbalance may be dominated due to perturbation from the equilibrium temperature. However, we also notice that the system achieves the thermal runaway state, and cool, condensed materials form for another equilibrium temperature regime, T0 = 1 MK, which is shown in Appendix A. It is to be noted from the last term in the RHS of Eq. (3) that there is no role for thermal conduction at the initial time as the system starts off isothermal. The system is therefore initially in thermal equilibrium, but the finite value of resistivity will drive the ideal force-balanced state away from its initial state, albeit only on the (slow) resistive timescale. This setup is liable to both linear resistive tearing modes, for which finite resistivity is key, and has all the thermodynamic ingredients to allow for thermal instability. The equilibrium system is perturbed to trigger tearing modes, which can further trigger the thermal modes, and thus they reinforce each other in a coupled tearing-thermal fashion. We use parametrically controlled, monopole-free magnetic field perturbations mainly confined in the vicinity of the z = 0 plane (where the initial current sheet is present) and exponentially decaying for |z|> 0,
Here, the parameter 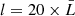 matches the geometric sizes of the simulation domain in the x and y directions, respectively, the perturbation amplitudes ψ01 = ψ02 = 0.1 ensure a variation of 10% in the magnetic field strength B0, and we obtain the multimode distribution of the perturbations using n1 = 4 and n2 = 2. The magnetic field distribution (Eqs. (9)–(11)) and the perturbations (Eqs. (13) and (14)) ensure the solenoidal condition, ∇ ⋅ B = ∇ ⋅ δB = 0.
matches the geometric sizes of the simulation domain in the x and y directions, respectively, the perturbation amplitudes ψ01 = ψ02 = 0.1 ensure a variation of 10% in the magnetic field strength B0, and we obtain the multimode distribution of the perturbations using n1 = 4 and n2 = 2. The magnetic field distribution (Eqs. (9)–(11)) and the perturbations (Eqs. (13) and (14)) ensure the solenoidal condition, ∇ ⋅ B = ∇ ⋅ δB = 0.
After the initial setup, the system was allowed to evolve as governed by the Eqs. (1)–(6). The equations were solved numerically using a three-step Runge-Kutta time integration with a second-order slope-limited reconstruction method (Ruuth 2006) with the ‘Vanleer’ flux limiter (van Leer 1974), and a Total Variation Diminishing Lax-Friedrichs (TVDLF) flux scheme. We followed the evolution of the system for up to 214.7 min and saved the data at a cadence of 85.87 s, which gave 151 snapshots. We used periodic boundary conditions in the x, y directions and an open boundary condition in the z direction. The wall clock time for the entire simulation run was ≈90 h, using eight nodes with 288 processors in total with a GNU-Fortran (version 6.4.0) compiler and open MPI 2.1.2.
There are some important differences in the initial conditions of this model with respect to SK22. (i) This is a force-free magnetic field configuration, and therefore an isobaric and isothermal medium ensures a fully force-balanced equilibrium, whereas the magnetic field configuration in SK22 was not force-free, and therefore we used a nonuniform density profile (though the initial temperature was also uniform) in such a way that it maintained the force-balance equilibrium. (ii) The magnetic field strength near the current sheet in SK22 is ≪1, which sets the plasma-β ≫ 1 near the current sheet. Our current model, on the other hand, initially has a uniform and low plasma-β = 0.2 throughout the entire simulation domain. (iii) The direction of imposed magnetic field perturbations for SK22 were both parallel and perpendicular to the current sheet, but in the current work we set the perturbation as only parallel and concentrated around the current sheet plane. Besides the difference in affordable numerical resolution, SK22 has a maximum resolution of 20482, whereas the current setup has a maximum resolution of 5123). The system studied here is intrinsically 3D and is hence more relevant for actual current sheet conditions.
3. Results and discussion
3.1. Global evolution
The spatial distribution of the current density squared, J2, as well as representative corresponding field line evolutions, are shown in Fig. 1. The equilibrium configuration of the current sheet (at t = 0) is formed due to the fact that the magnetic field shears across z = 0, as given by Eqs. (9) and (11). The initial current distribution is mostly oriented in the x − y plane and concentrated around z = 0, with its main contribution from Jx = −dBy/dz and Jy = dBx/dz (while Jz is purely from the perturbed field). Due to the magnetic field perturbations, given by Eqs. (13) and (14), which are (mainly) confined near the z = 0 plane and extend along the x − y directions, linear resistive tearing modes start to develop, leading to the disintegration of the current sheet. The inhomogeneities of J2 in the current sheet plane due to the multimode perturbation (n1 = 4, n2 = 2) appear at the initial stage of the evolution, as shown in Fig. 1a. Magnetic reconnections lead to pronounced magnetic topology changes, modifying the current sheet as shown in Fig. 1b. We see the perturbed field lines near z = 0 (see Fig. 1c) turn into extended flux rope-like structures while the system evolves (see Fig. 1d), yet the planar (x-oriented) field lines away from the current sheet plane remain unperturbed. The signature of flux ropes in the current density distribution in Fig. 1b can be clearly noticed. In a 2D setup, these would be the familiar magnetic islands or plasmoids, due to the development of tearing modes in the current sheet. We notice the self-consistent development of Bz due to the perturbed fields around the current sheet plane, as shown in Fig. 2a (note that the initial Bz was set to zero, with no magnetic field perturbation along z). Figure 2b represents the plasma pressure distribution at the x − z plane (at y = 0), while the variation along the vertical dashed green line is shown in Fig. 2c, which shows the expected linear eigenmode structure of the tearing mode, seen as the kinks in the pressure distribution around z = 0. This implies the development of the tearing modes at the initial stage of the current sheet evolution. The nonlinearly developing tearing evolution creates density perturbations in the surroundings of the current sheet, and the radiative cooling (in combination with thermal conduction) becomes dominant over the constant background heating in localized regions of the domain. This triggers the cooling of those regions, which in turn condenses the regions even more, and hence a runaway process starts whereby the tearing and thermal modes reinforce each other, which causes the spontaneous growth of density and temperature inhomogeneities in the surroundings of the current sheet. Note that our box is periodic along x and y, so field-aligned thermal conduction does not play a big role in the heating-cooling misbalance of the system (in the sense that it can not lead to heat fluxes down into lower-lying chromospheric regions: we have no stratification here). It just tries to homogenize the temperature along field lines, in competition with local resistive heating.
 |
Fig. 1. Isosurface (five isosurface values are taken from instantaneous minimum to maximum) plots of the current density squared J2, which represent the 3D structure of the evolving current sheet. Panel (a) represents the perturbations appearing in the current sheet plane due to the multimode (n1 = 4, n2 = 2) magnetic field perturbations in Eqs. (13)–(14), and (b) represents a time when the current sheet disintegrated due to the tearing-thermal coupled evolution of the system. Panels (c) and (d) represent the magnetic field corresponding to panels (a) and (b), respectively. Distances along the x, y, and z axes are scaled in units of 104 km, where we see the field lines perturbed at 14.3 min around the current sheet plane only, which evolves to sizeable flux rope structures at 207.5 min. An animation of the figures is available online. |
The temporal variations in the instantaneous maximum plasma density and minimum temperature are shown in Fig. 3a. The peak density increases from the initial uniform 4.68 × 10−16 g cm−3 at t = 0 to 7.11 × 10−14 g cm−3 at t = 214.7 min. A sharp rise in the peak density starts from ≈150 min. The instantaneous minimum temperature starts at 0.5 MK (the initial uniform equilibrium temperature) and drops sharply at the same time as the density peak has the sharp rise (t ≈ 150 min), reaching as low as 10, 148 K at t = 214.7 min. This signals the formation of cool plasma condensations in the system at ≈150 min, or more than two and a half hours following the initial tearing onset. The variation in the instantaneous maximal velocities (vx, vy and vz) in Fig. 3b demonstrates that a dynamical instability of the system occurs at the condensation onset time (≈150 min). Here, the velocities are scaled in terms of the Alfvén velocity, va = 261 km s−1, which is calculated based on the initial equilibrium density and the magnetic field strength of the system. We notice from Fig. 4 that the Bz field evolves up to ≈0.4 G along the x − z plane (at y = 0) at t = 207.5 min, which is around an order of magnitude higher than the Bz(x, z) field at t = 14.3 min shown in Fig. 2a. The kinks appear in the bottom panel of Fig. 4 in the Bz field around z = 0 plane (at y = 0) along x = ±2 Mm shows the evolution of the tearing mode around the current sheet plane. The evolution of the density and temperature distributions along three orthogonal planes at x = 0, y = 0, and z = 0, and its 3D visualization, are shown in Fig. 5. Density and temperature inhomogeneities that are aware of the initial multimode (n1 = 4, n2 = 2) magnetic field perturbation appear in and around the current sheet plane, as shown at t = 14.3 min in Figs. 5a and d, respectively. Due to tearing-associated thermal instability, localized condensed structures can be clearly seen in the x = 0, y = 0, and z = 0 plane at t = 207.5 min (see Fig. 5b). The 3D visualization of the density distribution is shown in Fig. 5c, where we see the condensed structures are formed around the current sheet plane. These condensed structures correspond to the cooler (∼104 K) regions compared to the background medium (see Figs. 5e and f). Their order 100 density and temperature contrasts are similar to coronal rain or prominence features. Note that they happen near the evolving current sheet, which is heated up to several million degrees due to effective Ohmic heating. The periodic boundary treatments that we use in this study are acceptable for the entire evolution, since the plasmoid sizes do not reach the lateral domain size of the simulation box. The condensations from thermal instability develop locally and are not expected to be influenced by the type of boundary used laterally. Histograms of the mass and temperature distributions in the entire domain at t = 207.5 min are shown in Fig. 6, where we see in Fig. 6a that 98.8% of the cells within the simulation box contain mass within the range of 4.84 × 104–1.43 × 105 kg (the total number of cells in the simulation box used here is the effective resolution 5123), while the number of cells with mass ≳1.43 × 105 kg is very low (≈1.2%). The mass range with the most number of cells is in accord with the mass determined by the initial equilibrium density of the medium (since the density remains almost unperturbed away from the current sheet plane). Similarly, most cells contain the temperature value in the range of ≈0.32 − 0.63 MK, namely 75.1% of the total cells in the box, as shown in Fig. 6b. The initial equilibrium temperature of the system, 0.5 MK, lies within this range. The fraction of cell numbers with temperature ≲105 K and ≳1 MK is low, and they are 2.1% and 1.2%, respectively. This implies that the cool, condensed structures, as well as the hot regions with ≳MK temperatures (which appear around the current sheet plane due to reconnection-induced heating), are very localized in the medium. So that the thermodynamics of the cool, condensed structures can be appreciated, we show slices of plasma pressure and different velocity components in Fig. 7. We notice that the velocities that develop in the different cutting planes in Figs. 7d–f are associated with pressure-gradient-driven flows (see Figs. 7a–c), also called siphon flows. They are directed from higher to lower pressure regions and demonstrate sub-Afvénic speeds (Alfvénic Mach number reaches up to ≈0.075). Due to plasma accumulation, as evident from the velocity maps, the cool condensation sites develop in these same regions, as shown in Fig. 5. When the thermal runaway sets in after a long-term evolutionary process, the velocities are dominated by pressure gradient flows. In this stage, initial condensation seeds merge along each other to form larger condensation sites and drag along the magnetic field lines, which entangle and form flux ropes. The heating-cooling (mis)balance in different planes is shown in Fig. 8. We use a uniform (and constant in time) background heating of 6.244 × 10−53 erg g2 cm−3 s−1, which is equal to the radiative loss (no field-aligned thermal conduction at the initial state due to the isothermal condition) at the initial equilibrium state of the system. But this balance breaks down due to tearing-influenced thermal changes around the current sheet, and the radiative loss in some regions near the current sheet plane dominates over the heating. These regions correspond to the cool condensed structures shown in Fig. 5. The regions away from the current sheet plane maintain the heating-cooling balance as the initial perturbation was concentrated around the current sheet plane, and therefore those regions maintain the initial equilibrium density and temperature of the system. The energetic evolution of the system is shown in Fig. 9. As expected (despite the open boundaries along z), this shows that the mean total energy density (ET), which is a sum of mean kinetic (Ek), magnetic (EM), and internal (Eint) energy densities (see Eq. (8)) given by
 |
Fig. 2. Growth of the tearing mode around the current sheet plane. We show data at t = 14.3 min, where (a) represents the evolution of the Bz component (perpendicular to the current sheet, Bz was initially zero, with no magnetic field perturbation along the z direction), (b) plasma pressure in the x − z plane (at y = 0), and (c) the variation in the plasma pressure along the vertical dashed green line in figure (b). |
 |
Fig. 3. Temporal variation in the (a) instantaneous maximal plasma density (blue line), and minimum temperatures (red line), and (b) instantaneous absolute peak velocities. The sharp rise in the density, and drop in the minimum temperature over two orders of magnitude at ≈150 min, signals the runaway thermal instability causing local condensations, when the absolute peak velocities, vx, vy, and vz, also rise sharply. Here, the velocities are scaled in terms of the Alfvén velocity, va ≈ 261 km s−1. |
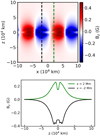 |
Fig. 4. Signature of tearing modes around the fragmented current sheet plane at t = 207.5 min. The top panel represents the variation in Bz along x − z at the y = 0 plane. The bottom panel shows the variation in Bz along the dashed vertical lines in the top panel at x = ±2 Mm. |
 |
Fig. 5. Spatial distribution of density (top panel) and temperature (bottom) in the 3D domain, where the distances along the x, y, and z directions are in units of 104 km. Density (a and b) and temperature (d and e) distribution along three orthogonal slices along the x = 0, y = 0, and z = 0 planes for two different times, t = 14.3 and 207.5 min, are shown. (c) and (f) represent isosurface views (five isosurfaces ranging from minimum to maximum values) of density and temperature, respectively. Panels (a) and (d) are the early phase of the evolution, where the density and temperature inhomogeneities appear around the current sheet plane due to the multimode magnetic field perturbation. Panels (b) and (c) illustrate where high-density structures appear, cospatial with cool (∼104 K) regions in (e) and (f). An animation is available online. |
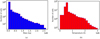 |
Fig. 6. Histograms for (a) mass, and (b) temperature distribution for t = 207.5 min. The cells containing the minimum and maximum masses are 4.8 × 104 and 2.7 × 106 kg, respectively, and the temperature minima and maxima for the cells are 5000 K and 3.1 MK, repectively. The number of bins for (a) and (b) is 20, with bin sizes 1.38 × 105 kg and 0.15 MK, respectively. |
 |
Fig. 7. Distribution of plasma pressure (top panels) and velocity (bottom panels) at t = 207.5 min in different planes, where the velocities are scaled in units of Alfvén velocity, va ≈ 261 km s−1. (a) at z = 0. (b) at y = 0. (c) at x = 0. (d) at z = 0. (e) at y = 0. (f) at x = 0. |
 |
Fig. 8. Distribution of radiative cooling (RC) losses for optically thin coronal conditions at t = 207.5 min in different planes. (a) at z = 0. (b) at y = 0. (c) at x = 0. |
 |
Fig. 9. Time series of mean kinetic (Ek), magnetic (EM), internal (Eint), total (ET) energy density, and ohmic heating rate (Eohm), normalised with respect to their maximum values, which are 1.89 × 10−3, 1.61 × 10−1, 7.40 × 10−2, 2.13 × 10−1 erg cm−3, and 2.23 × 10−9 erg cm−3 s−1, respectively. |
respectively (where V is the total volume of the simulation box) is nearly conserved in time. The resistivity and thermal conduction effects do not cause any deviation from the total energy conservation, and only the heating-cooling misbalance may lead to net energy losses (or gains). Due to the resistive MHD evolution of the system, the energy exchange between magnetic and internal energies show an anti-correlation nature while the system evolves. This energy exchange occurs due to the mean Ohmic dissipation, which is quantified as
We notice that the mean magnetic energy density decreases up to ≈150 min due to the release of magnetic energy through reconnection. Thereafter, when the thermal runaway process happens in the system in a coupled tearing-thermal fashion, the field lines start to entangle with each other and form flux ropes. This generates magnetic stress and leads to the enhancement of the magnetic energy density; however, the open boundaries in the z-direction, which are sufficiently far away from the central current sheet plane, allow the magnetic energy flux to flow through the boundaries. The current density (spatially) distributes rapidly due to the implemented perturbation, and therefore we see a sharp drop in volume-averaged J2 initially. The temporal evolution of the mean kinetic energy density shows that the instability dynamic of the system has a (nearly) quasi-equilibrium nature up to ≈150 min (the onset time of the condensations) and then rises sharply due to a tearing-thermal coupled unstable evolution.
3.2. Synthetic observation
The SDO is a near-Earth orbiting satellite suite capable of routinely observing the Sun, from its photosphere to the corona. The AIA on board captures images of the solar atmosphere with a temporal cadence of ∼12 s at a spatial resolution of ∼0.6″ per pixel across a range of UV and EUV wavelengths, the latter mainly associated with the different ionization states of iron, namely Fe XII–XXIV. Emission from such highly ionized iron corresponds to coronal temperatures in the broad range of a few hundred kK to around 20 MK. The emission coefficient for such coronal plasma is given by
where Ab is the abundance of the emitting species, ne is the ambient electron number density, and Gλ is the contribution function for a specific wavelength, indicated to be additionally dependent on ne as well as the temperature, T. In the absence of a modelled ne, it is instead approximated using LTE Saha-Boltzman. This contribution function is precomputed for each of the AIA passbands using the CHIANTI atomic package for a range of electron number densities and temperatures between 106–1012 cm−3, and 104–108 K, respectively (Landi & Reale 2013; Verner et al. 1996). τ here denotes the local optical depth, computed within each voxel that a given LOS intersects as the product of the local absorption coefficient, αλ, and the length of the ray within that voxel. The atmosphere of the Sun is optically thin at the wavelengths corresponding to the emission by these Fe lines. As such, the standard approach to synthesizing simulations so as to resemble the appearance of structures as seen by SDO/AIA is to employ Eq. (19) in a local manner and apply an arbitrary LOS integration according to the position of an observer. For structures that are majority-comprised of material at coronal temperatures, such as coronal loops, this is deemed a sufficient approach (Van Doorsselaere et al. 2016; Gibson et al. 2016).
Cool condensations within the solar corona appear dim in EUV contrast (cf. Carlyle et al. 2014), and indeed the value of Gλ for the AIA passbands that we consider is many orders of magnitude lower at condensation temperatures than for coronal temperatures. However, the strong contrast is due not only to small Gλ but also the direct absorption and removal of background EUV photons from the light beam Kucera et al. (1998). This is due to a number of the wavelengths observed by SDO/AIA lying below the head of the hydrogen Lyman continuum at 912 Å, and so H, He, and He I (with characteristic temperatures < 10 kK) are photo-ionized by this EUV emission up to the ionization continuum of He II at 227 Å (Williams et al. 2013). EUV photons are hence progressively removed from the LOS if such cool material is encountered. The absorption coefficient as a consequence of this EUV photo-ionization can be approximated in LTE by
where s refers to the photo-ionized element and Ab, s and σs are the assumed abundance and cross section of the ionization of element s, measured observationally and experimentally/theoretically, respectively. The summation weights, ws(τ), are the ratios of the number densities as wH = 1 − nH I/nH, wHe = 1 − (nH I − nHe II)/nHe, and wH I = nH II/nHe. To obtain an approximation of these weights, and in accordance with our previous assumptions of LTE, we iteratively solved for each of the considered population densities using the Saha equation and associated partition functions. We consider convergence under the LTE assumption to be achieved once the absolute relative difference of ne between iterations drops below an arbitrary value of 10−4 (a method developed by Zhou et al. 2019). One must necessarily consider this photo-ionization to correctly approximate the appearance of cold plasma condensations, if present, when synthesizing simulations of the solar atmosphere (Jenkins & Keppens 2022).
Both the emission and absorption quantities as defined above are purely local properties. The total emergent intensity, Iλ(τλ), along a given LOS through these local voxels is then given by the integral form of the transport equation
where the combined influence of jλ and αλ is taken into account in the source function Sλ = jλ/αλ, τλ now represents the total optical thickness along the chosen LOS, and Iλ(0) is the intensity of any background illumination when the emergent intensity is calculated along the specific LOS with the zero optical thickness region (Rybicki & Lightman 1986). The nonstandard inclusion of the absorption coefficient requires every local voxel, with its respective optical depth, 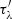 , to have access to a globally integrated and LOS-specific optical depth, τλ. Such a requirement is not compatible with the block-based architecture of MPI-AMRVAC and is hence completed in post-processing using a combination of yt-project, numpy, scipy, and matplotlib in Python. The implementation here represents an update of that previously presented in Jenkins & Keppens (2022).
, to have access to a globally integrated and LOS-specific optical depth, τλ. Such a requirement is not compatible with the block-based architecture of MPI-AMRVAC and is hence completed in post-processing using a combination of yt-project, numpy, scipy, and matplotlib in Python. The implementation here represents an update of that previously presented in Jenkins & Keppens (2022).
Ground-based observatories do not have access to EUV wavelengths as recorded by SDO/AIA and instead commonly observe, among others, the strong hydrogen n = 3 → n = 2 (Hα) line at 6563 Å. This line is known to straddle the optically thick – thin divide under solar atmospheric conditions, and a complete handling of the plasma-light interaction of such photons through the simulation domain would require NLTE modelling outside the scope of this study (but we point an interested reader to the recent work of Jenkins et al. 2023, for comparison). Instead, Heinzel et al. (2015) reported an approximate approach to relating local pressure and temperature conditions to Hα opacity (αλ) according to their series of 1.5D radiative transfer models. A key property of these models considers the source function of Eq. (21) to remain constant along a given LOS and enables the following simplification,
The resulting emergent (specific) intensity of the Hα line is therefore found through a LOS integration of the approximate αλ according to the tables of Heinzel et al. (2015), wherein the authors also provide a coarse height-dependent estimation to the constant value of Sλ.
To convert the physical variables (plasma density and temperature) into spectroscopic observables (namely specific intensity), we generated synthetic maps of the simulation output using forward modeling. Measuring LOS-integrated specific intensity depends on the (theoretical) viewing position of the observer, and thus, due to the spatial distribution of the substructures due to the condensations, the synthetic maps show differences for different LOS views. Figure 10 shows the synthetic maps of the reoriented spatial domain (we now show the current sheet vertically) capturing the internal structures as being viewed sideways, representative for the solar limb. We do so for three different EUV passband filters of AIA, 171, 193, and 304 Å using the contribution functions of their specific spectral lines, which each highlight material at ≈0.8 MK, 1.5 MK, and 80 kK, respectively, for a LOS integration in our y direction at t = 207.5 min. An animation of the synthetic maps for different LOS directions around the z axis is available online. Due to the absorption features of the condensed plasma regions, the strongest absorption corresponds to the LOS direction in the y direction, as the condensations are aligned with it (see Fig. 5). The cool, condensed plasma appears darker in AIA 171, 193, and 304 Å passband filters due to photo-ionization of H, He, and He I, as previously outlined. For the remaining optical Hα line, we obtain a positive intensity in the absence of any background illumination, as would be the case for, among others, prominences and jets positioned at or above the limb. The island-like structures near z = 0 in the EUV maps in Fig. 10 represent plasmoids, which are the manifestation of the extended flux ropes in the y direction, as shown in Fig. 1d. The central current sheet is hotter than the surroundings, and therefore we see the widened area of the bright band in AIA 171 and 193 filters. The small dark features that appear in the EUV maps are due to absorption from the dense materials, as those are located in the y direction. These cool materials with a temperature ∼104 K appear bright in the Hα map. The synthetic observations for other LOS directions (shown in the animation) demonstrate a wide range of cool, dense structures distributed in the x and y directions.
 |
Fig. 10. Specific intensity counterparts to the simulation, where we account for emission and absorption. Synthetic maps for the broadband 171, 193, 304 Å SDO/AIA filters, and a narrowband Hydrogen-Hα filter, for a LOS view in the y direction at t = 207.5 min, are shown from the left to right panels, respectively. An animation of this figure for a rotating LOS view around the z (from 0 to 360°) axis is available online. This shows the limb view on a current sheet that shows thermal-tearing evolutions. |
The resolution of the presented simulation is 390 km2 per pixel. In all cases, the spatial resolutions of our synthesized images have been modified to match those of an equivalent observatory. For the EUV pass bands, this is set to the instrumental resolution of the AIA filters (≈430 km2 per pixel) and leads to a minor smearing of the finer structures inside the finest condensations. This blurring is stronger for the Hα line, where the resolution is set to 1″ = 725.27 km so as to match the GONG ground-based instruments Harvey et al. (2011). It will be useful to increase our model resolution for comparisons against the state-of-the-art observations anticipated from Solar Orbiter’s High Resolution Imager campaigns (Rochus et al. 2020).
4. Summary and conclusions
The study of the combined tearing-thermal instability of an idealized 3D current sheet configuration as addressed in this work is to understand the theoretical basis of the multimode evolution of a current sheet, which is an important aspect of understanding the dynamics and multi-thermal behavior of the solar atmosphere. In contrast to our earlier 2D simulations of a non-force-free current sheet (SK22), in which thermal runaway was happening simultaneously with chaotic tearing and condensations were trapped and gathered within coalescing plasmoid structures, the current setup shows a clear tearing evolution at first, leading to 3D topological changes in the magnetic field, and later on shows runaway condensations near the central current sheet. There are some important differences between the initial setup of the current model and the one used in SK22, as explained in Sect. 2, most notably perhaps the plasma beta regime, which is uniformly low in the current 3D simulation. Here, the condensation onset time in the current model is much later than in SK22 because the initial setup and adopted perturbations do not directly modify the heat-loss balance and a purely tearing evolution starts at first. In a long-term 3D simulation of a macroscopic current sheet, we find that cool plasma condensations are produced in the vicinity of the current sheet due to tearing-influenced thermal instability. Our findings are based on a 3D resistive MHD simulation with nonadiabatic effects of radiative cooling (for an optically thin medium), background heating, and magnetic field-aligned thermal conduction, which are relevant for the solar corona. We find that the plasma density of the condensations can go up to ∼10−14 g cm−3, which is two orders of magnitude more than the initial background density (4.6 × 10−16 g cm−3), and the temperature of the condensations can drop down to ∼104 K, which is an order of magnitude less than the initial equilibrium temperature (0.5 MK) of the medium. These local, in situ forming cool, condensed structures hence show similar thermodynamic contrasts with their surroundings, just like coronal rain or prominences observed in the solar atmosphere. This is highlighted by synthetic views, which account for important absorption effects within the synthesis of the EUV channels of SDO/AIA. However, our model ignores the effect of the stratified solar atmosphere due to solar gravity. The condensation timescales in this idealized current sheet model is ≈150 min, which is larger than the timescales (≈30 min) in the earlier study for a post-flare coronal rain model by Ruan et al. (2021), in which they use a stratified atmosphere and reveal the multi-thermal aspects of a post-flare loop underneath the current sheet and reconnection sites. Our study, by contrast, demonstrates the development of multi-thermal plasma (10 kK–MK) in and around the current sheet and reconnection sites. Earlier models of coronal rain in arcades also show a clear tendency to develop strong shearing motions (Li et al. 2022; Zhou et al. 2021; Fang et al. 2015), and velocity shear can alter the tearing mode growth, which we plan to explore by incorporating velocity shear flows into the model. Future efforts should exploit a more realistic 3D model by using the initial magnetic field configuration from an extrapolated magnetic field for an active region vector magnetogram. Nevertheless, the current study sheds new light on the instability of solar current sheets due to the combined effect of tearing and thermal modes, and unifies multi-thermal processes in current sheets with the formation mechanism of cool condensations, such as prominences and coronal rain in the solar atmosphere, which are important aspects in understanding the broader solar coronal heating.
Movies
Movie 1 associated with Fig. 1 (fig1a) Access here
Movie 2 associated with Fig. 1 (fig1b) Access here
Movie 3 associated with Fig. 5 (fig5a) Access here
Movie 4 associated with Fig. 5 (fig5b) Access here
Movie 5 associated with Fig. 10 (fig10) Access here
Open source at: http://amrvac.org/
Acknowledgments
Data visualization and analysis were performed using https://visit-dav.github.io/visit-website/index.html and https://yt-project.org/. SS and RK acknowledge support by the C1 project TRACESpace funded by KU Leuven. JMJ and RK acknowledge the support by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (grant agreement no. 833251 PROMINENT ERC-ADG 2018) and a FWO project, G0B4521N. The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation Flanders (FWO) and the Flemish Government – department EWI. RK acknowledges the International Space Science Institute (ISSI) in Bern, ISSI international team project #545.
References
- Akramov, T., & Baty, H. 2017, Phys. Plasmas, 24, 082116 [CrossRef] [Google Scholar]
- Biskamp, D. 2000, Magnetic Reconnection in Plasmas, 3 (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Brughmans, N., Jenkins, J. M., & Keppens, R. 2022, A&A, 668, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlyle, J., Williams, D. R., van Driel-Gesztelyi, L., et al. 2014, ApJ, 782, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Claes, N., & Keppens, R. 2019, A&A, 624, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claes, N., Keppens, R., & Xia, C. 2020, A&A, 636, A112 [EDP Sciences] [Google Scholar]
- Colgan, J., Abdallah, J. J., Sherrill, M. E., et al. 2008, ApJ, 689, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A., & McCray, R. A. 1972, ARA&A, 10, 375 [Google Scholar]
- Fang, X., Xia, C., & Keppens, R. 2013, ApJ, 771, L29 [Google Scholar]
- Fang, X., Xia, C., Keppens, R., & Van Doorsselaere, T. 2015, ApJ, 807, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B. 1965, ApJ, 142, 531 [Google Scholar]
- Forbes, T. G., & Malherbe, J. M. 1991, Sol. Phys., 135, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Furth, H. P., Killeen, J., & Rosenbluth, M. N. 1963, Phys. Fluids, 6, 459 [Google Scholar]
- Gibson, S., Kucera, T., White, S., et al. 2016, Front. Astron. Space Sci., 3, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R. G. 1939, ApJ, 89, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R. G. 1947, MNRAS, 107, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R. G. 1948, MNRAS, 108, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., McComas, D. J., Phillips, J. L., et al. 1995, Geophys. Rev. Lett., 22, 1753 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. W., Bolding, J., Clark, R., et al. 2011, in AAS/Solar Physics Division Abstracts #42, 17.45 [Google Scholar]
- Heinzel, P., Gunár, S., & Anzer, U. 2015, A&A, 579, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hermans, J., & Keppens, R. 2021, A&A, 655, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hesse, M., & Cassak, P. A. 2020, J. Geophys. Res. (Space Phys.), 125, e25935 [NASA ADS] [Google Scholar]
- Huang, Y.-M., & Bhattacharjee, A. 2013, Phys. Plasmas, 20, 055702 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y.-M., Bhattacharjee, A., & Forbes, T. G. 2013, Phys. Plasmas, 20, 082131 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., & Keppens, R. 2021, A&A, 646, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. M., & Keppens, R. 2022, Nat. Astron., 6, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Osborne, C. M. J., & Keppens, R. 2023, A&A, 670, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaneko, T., & Yokoyama, T. 2015, ApJ, 806, 115 [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & DeVore, C. R. 2012, ApJ, 760, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Xia, C. 2014, ApJ, 789, 22 [Google Scholar]
- Keppens, R., Meliani, Z., van Marle, A. J., et al. 2012, J. Comput. Phys., 231, 718 [Google Scholar]
- Keppens, R., Porth, O., Galsgaard, K., et al. 2013, Phys. Plasmas, 20, 092109 [CrossRef] [Google Scholar]
- Keppens, R., Teunissen, J., Xia, C., & Porth, O. 2021, Comput. Math. Appl., 81, 316 [Google Scholar]
- Keppens, R., Popescu Braileanu, B., Zhou, Y., et al. 2023, A&A, 673, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kohutova, P., Antolin, P., Popovas, A., Szydlarski, M., & Hansteen, V. H. 2020, A&A, 639, A20 [EDP Sciences] [Google Scholar]
- Kucera, T. A., Andretta, V., & Poland, A. I. 1998, Sol. Phys., 183, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kumari, A., Ramesh, R., Kathiravan, C., Wang, T. J., & Gopalswamy, N. 2019, ApJ, 881, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Reale, F. 2013, ApJ, 772, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Ledentsov, L. 2021a, Sol. Phys., 296, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ledentsov, L. 2021b, Sol. Phys., 296, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Ledentsov, L. 2021c, Sol. Phys., 296, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Xue, J. C., Ding, M. D., et al. 2018, ApJ, 853, L15 [Google Scholar]
- Li, X., Keppens, R., & Zhou, Y. 2022, ApJ, 926, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., Kuhn, J. R., & Coulter, R. 2004, ApJ, 613, L177 [Google Scholar]
- Loureiro, N. F., Schekochihin, A. A., & Cowley, S. C. 2007, Phys. Plasmas, 14, 100703 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1953, ApJ, 117, 431 [Google Scholar]
- Paul, A., & Vaidya, B. 2021, Phys. Plasmas, 28, 082903 [CrossRef] [Google Scholar]
- Porth, O., Xia, C., Hendrix, T., Moschou, S. P., & Keppens, R. 2014, ApJS, 214, 4 [Google Scholar]
- Priest, E., & Forbes, T. 2000, Magnetic Reconnection (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Priest, E. R., & Smith, E. A. 1979, Sol. Phys., 64, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruan, W., Zhou, Y., & Keppens, R. 2021, ApJ, 920, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Ruuth, S. J. 2006, Math. Comput., 75, 183 [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Savage, S. L., McKenzie, D. E., Reeves, K. K., Forbes, T. G., & Longcope, D. W. 2010, ApJ, 722, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, J. M., & Cargill, P. J. 2003, J. Geophys. Res. Space Phys., 108, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, S., & Keppens, R. 2022, A&A, 666, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, E. A., & Priest, E. R. 1977, Sol. Phys., 53, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Ballester, J. L., & Goossens, M. 2011, ApJ, 731, 39 [NASA ADS] [CrossRef] [Google Scholar]
- van der Linden, R. A. M., & Goossens, M. 1991a, Sol. Phys., 131, 79 [NASA ADS] [CrossRef] [Google Scholar]
- van der Linden, R. A. M., & Goossens, M. 1991b, Sol. Phys., 134, 247 [NASA ADS] [CrossRef] [Google Scholar]
- van der Linden, R. A. M., Goossens, M., & Hood, A. W. 1992, Sol. Phys., 140, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Antolin, P., Yuan, D., Reznikova, V., & Magyar, N. 2016, Front. Astron. Space Sci., 3, 4 [Google Scholar]
- van Leer, B. 1974, J. Comput. Phys., 14, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
- Williams, D. R., Baker, D., & van Driel-Gesztelyi, L. 2013, ApJ, 764, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, C., & Keppens, R. 2016, ApJ, 823, 22 [Google Scholar]
- Xia, C., Chen, P. F., & Keppens, R. 2012, ApJ, 748, L26 [Google Scholar]
- Xia, C., Keppens, R., & Fang, X. 2017, A&A, 603, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xia, C., Teunissen, J., El Mellah, I., Chané, E., & Keppens, R. 2018, ApJS, 234, 30 [Google Scholar]
- Yang, Z., Tian, H., Tomczyk, S., et al. 2020, Sci. China E: Technol. Sci., 63, 2357 [CrossRef] [Google Scholar]
- Zhang, C. L., & Ma, Z. W. 2011, Phys. Plasmas, 18 [Google Scholar]
- Zhao, X., & Keppens, R. 2022, ApJ, 928, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Z., Cheng, X., Zhang, J., et al. 2019, ApJ, 877, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y.-H., Ruan, W.-Z., Xia, C., & Keppens, R. 2021, A&A, 648, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Evolution of the system with T0 = 1 MK temperature
To investigate whether condensation occurs in the experiment with a different equilibrium temperature, we ran the simulation with T0 = 1 MK, keeping all other parameters the same. In this case, we used a lower resolution with an AMR level of up to two, which gives the maximum resolution of 2563 in the x, y, and z directions. Figure A.1a shows that the instantaneous peak density increases by more than an order of magnitude at ≈300 min, and the minimal temperature drops down to ∼10 kK (which is two orders of magnitude less than the initial temperature) at the same point in time, whereas the maximum temperature rises from 1 MK to ≈5 MK. From Figures A.1b and A.1c, we notice that the cool (∼104 K) and condensed (∼10−15 g cm−3) structures are spatially colocated, which demonstrates that the condensation occuring in our experiment is a common phenomena in different temperature ranges and not specific to a particular temperature regime.
 |
Fig. A.1. (a) represents the temporal evolution of the instantaneous peak density (red curve), and the maximum and minimum temperatures (dashed blue and solid blue, respectively). (b) and (c) represent the density and temperature distribution between x, y ∈ [ − 10, 0], and z ∈ [0, 10] at t = 372 min, respectively, where x, y, and z are in units of 104 km. |
All Figures
 |
Fig. 1. Isosurface (five isosurface values are taken from instantaneous minimum to maximum) plots of the current density squared J2, which represent the 3D structure of the evolving current sheet. Panel (a) represents the perturbations appearing in the current sheet plane due to the multimode (n1 = 4, n2 = 2) magnetic field perturbations in Eqs. (13)–(14), and (b) represents a time when the current sheet disintegrated due to the tearing-thermal coupled evolution of the system. Panels (c) and (d) represent the magnetic field corresponding to panels (a) and (b), respectively. Distances along the x, y, and z axes are scaled in units of 104 km, where we see the field lines perturbed at 14.3 min around the current sheet plane only, which evolves to sizeable flux rope structures at 207.5 min. An animation of the figures is available online. |
| In the text | |
 |
Fig. 2. Growth of the tearing mode around the current sheet plane. We show data at t = 14.3 min, where (a) represents the evolution of the Bz component (perpendicular to the current sheet, Bz was initially zero, with no magnetic field perturbation along the z direction), (b) plasma pressure in the x − z plane (at y = 0), and (c) the variation in the plasma pressure along the vertical dashed green line in figure (b). |
| In the text | |
 |
Fig. 3. Temporal variation in the (a) instantaneous maximal plasma density (blue line), and minimum temperatures (red line), and (b) instantaneous absolute peak velocities. The sharp rise in the density, and drop in the minimum temperature over two orders of magnitude at ≈150 min, signals the runaway thermal instability causing local condensations, when the absolute peak velocities, vx, vy, and vz, also rise sharply. Here, the velocities are scaled in terms of the Alfvén velocity, va ≈ 261 km s−1. |
| In the text | |
 |
Fig. 4. Signature of tearing modes around the fragmented current sheet plane at t = 207.5 min. The top panel represents the variation in Bz along x − z at the y = 0 plane. The bottom panel shows the variation in Bz along the dashed vertical lines in the top panel at x = ±2 Mm. |
| In the text | |
 |
Fig. 5. Spatial distribution of density (top panel) and temperature (bottom) in the 3D domain, where the distances along the x, y, and z directions are in units of 104 km. Density (a and b) and temperature (d and e) distribution along three orthogonal slices along the x = 0, y = 0, and z = 0 planes for two different times, t = 14.3 and 207.5 min, are shown. (c) and (f) represent isosurface views (five isosurfaces ranging from minimum to maximum values) of density and temperature, respectively. Panels (a) and (d) are the early phase of the evolution, where the density and temperature inhomogeneities appear around the current sheet plane due to the multimode magnetic field perturbation. Panels (b) and (c) illustrate where high-density structures appear, cospatial with cool (∼104 K) regions in (e) and (f). An animation is available online. |
| In the text | |
 |
Fig. 6. Histograms for (a) mass, and (b) temperature distribution for t = 207.5 min. The cells containing the minimum and maximum masses are 4.8 × 104 and 2.7 × 106 kg, respectively, and the temperature minima and maxima for the cells are 5000 K and 3.1 MK, repectively. The number of bins for (a) and (b) is 20, with bin sizes 1.38 × 105 kg and 0.15 MK, respectively. |
| In the text | |
 |
Fig. 7. Distribution of plasma pressure (top panels) and velocity (bottom panels) at t = 207.5 min in different planes, where the velocities are scaled in units of Alfvén velocity, va ≈ 261 km s−1. (a) at z = 0. (b) at y = 0. (c) at x = 0. (d) at z = 0. (e) at y = 0. (f) at x = 0. |
| In the text | |
 |
Fig. 8. Distribution of radiative cooling (RC) losses for optically thin coronal conditions at t = 207.5 min in different planes. (a) at z = 0. (b) at y = 0. (c) at x = 0. |
| In the text | |
 |
Fig. 9. Time series of mean kinetic (Ek), magnetic (EM), internal (Eint), total (ET) energy density, and ohmic heating rate (Eohm), normalised with respect to their maximum values, which are 1.89 × 10−3, 1.61 × 10−1, 7.40 × 10−2, 2.13 × 10−1 erg cm−3, and 2.23 × 10−9 erg cm−3 s−1, respectively. |
| In the text | |
 |
Fig. 10. Specific intensity counterparts to the simulation, where we account for emission and absorption. Synthetic maps for the broadband 171, 193, 304 Å SDO/AIA filters, and a narrowband Hydrogen-Hα filter, for a LOS view in the y direction at t = 207.5 min, are shown from the left to right panels, respectively. An animation of this figure for a rotating LOS view around the z (from 0 to 360°) axis is available online. This shows the limb view on a current sheet that shows thermal-tearing evolutions. |
| In the text | |
 |
Fig. A.1. (a) represents the temporal evolution of the instantaneous peak density (red curve), and the maximum and minimum temperatures (dashed blue and solid blue, respectively). (b) and (c) represent the density and temperature distribution between x, y ∈ [ − 10, 0], and z ∈ [0, 10] at t = 372 min, respectively, where x, y, and z are in units of 104 km. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



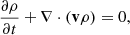
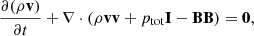
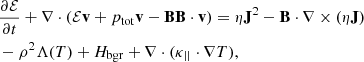
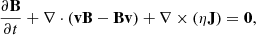
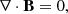
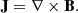
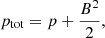
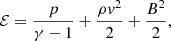
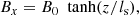
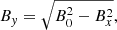
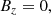
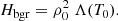
![$$ \begin{aligned}&\delta B_x = -\frac{2\pi }{l}\bigg [\psi _{01}\ \text{ cos}\bigg (\frac{2\pi n_1 x}{l}\bigg )\ \text{ sin}\bigg (\frac{2\pi n_1 y}{l}\bigg )\nonumber \\&\qquad + \psi _{02}\ \text{ cos}\bigg (\frac{2\pi n_2 x}{l}\bigg )\ \text{ sin}\bigg (\frac{2\pi n_2 y}{l}\bigg )\bigg ]\ \text{ Exp}(-z^2/l_{\rm s}),\end{aligned} $$](/articles/aa/full_html/2023/10/aa47038-23/aa47038-23-eq16.gif)
![$$ \begin{aligned}&\delta B_y = +\frac{2\pi }{l}\bigg [\psi _{01}\ \text{ sin}\bigg (\frac{2\pi n_1 x}{l}\bigg )\ \text{ cos}\bigg (\frac{2\pi n_1 y}{l}\bigg )\nonumber \\&\qquad + \psi _{02}\ \text{ sin}\bigg (\frac{2\pi n_2 x}{l}\bigg )\ \text{ cos}\bigg (\frac{2\pi n_2 y}{l}\bigg )\bigg ]\ \text{ Exp}(-z^2/l_{\rm s}). \end{aligned} $$](/articles/aa/full_html/2023/10/aa47038-23/aa47038-23-eq17.gif)