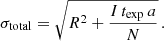EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 678 (October 2023) A&A, 678 (2023) A188 Full HTML
Issue
A&A
Volume 678, October 2023
Solar Orbiter First Results (Nominal Mission Phase)
Article Number A188
Number of page(s) 10
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202345892
Published online 20 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open access funding provided by Max Planck Society.

1. Introduction

In studying the coronal heating problem, three main regions are acknowledged to have been observed within the corona. These are active regions (ARs), coronal holes (CHs), and the quiet Sun (QS). Active regions are the brightest and most dynamic portions of the corona, often associated with underlying strong magnetic field patches including sunspots, that consist of coronal loops, as observed in the extreme ultraviolet (EUV) and X-rays. In contrast, CHs are the darkest portions in the solar corona in EUV and are attributed to open magnetic fields that connect the solar surface to the heliosphere. Physically beyond ARs and CHs, is the QS region. As the QS makes up the largest proportion of the solar surface, understanding the processes at work within this portion of the corona is crucial to understanding coronal heating.

Based on observations, a variety of small-scale dynamic features, such as nanoflares, coronal bright points, and jets, are all considered to be of high importance to balance the overall energy losses from the QS corona (e.g., Aschwanden et al. 2000; Hosseini Rad et al. 2021; Shen 2021; Chitta et al. 2021a). More recently, based on high spatial resolution and high-cadence EUV observations from the Extreme Ultraviolet Imager (EUI; Rochus et al. 2020) on board the Solar Orbiter (Müller et al. 2020), Berghmans et al. (2021) observed compact isolated coronal brightenings termed campfires. A main characteristic of all these nanoflare-type heating events, including campfires, is that they are all clearly distinguishable from the local background coronal emission. Whether these observable discrete heating events are sufficient to explain the energy losses from the QS corona is still an open question (Aschwanden et al. 2000; Chitta et al. 2021a). While much focus has been placed on these more distinguishable elements or events in the past, there remains much to be learned from the quieter portions of plasma that are devoid of these obvious localized transient brightenings. In particular, we are referring to the areas of seemingly stable and featureless EUV emission in the QS that we call the diffuse corona.

Diffuse emission associated with ARs has been studied in the past. Viall & Klimchuk (2011) looked at the diffuse portions of AR emission (i.e., areas not associated with any distinguishable loops or loop footpoints) and determined that these regions encompass a majority of the emitting portion of ARs; are only marginally less bright (10–35%) compared to AR loops; and are dynamically heated, as opposed to being energized by some steady process. Whether or not a similar significance and heating mechanism can be attributed to the diffuse corona in the QS remains to be seen.

In most studies, however, this diffuse emission is only considered a background. Usually, no particular consideration is given to it, apart from the urge to correct for (i.e., subtract) it when looking at features resolved in space and time embedded in this background.

In this work we analyze the evolution of the diffuse quiescent corona observed with the high spatial and temporal resolution allowed by the EUI instrument. We compare the diffuse emission and its fluctuations to those seen in the more dynamic features within the observational field of view (FOV). We find that not only is the diffuse corona an enduring contributor of seemingly stable and unstructured emission, but that it also is more widespread and is therefore considered to be an important factor in the overall energy balance of the solar corona.

2. Observations

On March 26, 2021, Solar Orbiter (Müller et al. 2020) was located at a distance of 0.72 AU from the Sun on the far side with respect to Earth. The EUV High Resolution Imager (HRIEUV) on the Extreme Ultraviolet Imager was pointed toward the limb at a latitude of about 30°, and recorded images with very high cadence of 2 s (1.65 s exposure) between 23:32:20 UT and 23:57:18 UT (25 min)1.

The HRIEUV has a plate scale of 0.492″ pixel−1, which amounts to roughly 260 km pixel−1 on the Sun (as seen from Solar Orbiter) for this data set. The pass-band of HRIEUV is centered at 17.4 nm, and its response peaks at temperatures of about 1 MK due to the presence of spectral lines of Fe IX (at 17.11 nm) and Fe X (at 17.45 nm and 17.72 nm). Before conducting our analysis, we aligned the level 2 (L2) data to remove the jitter in the image sequence as described in Chitta et al. (2022).

The region observed by EUI is a QS region outside coronal holes. While the target area was not visible from Earth-based telescopes, the Full Sun Imager (FSI) of EUI acquired images in the 304 Å and the 174 Å channels. These show a north polar coronal hole at latitudes well above 60° north, while the field of view of HRIEUV is below 55° north (i.e., located far from the coronal hole).

3. Results

We focus on the on-disk portion of these observations that also covered the limb and regions off the disk. An overview of the observational FOV, including the primary areas of interest for this study, is shown in Fig. 1. Panel a depicts the full FOV of HRIEUV, and panel b shows a zoomed-in image of the on-disk portion of the observation that is of interest for this study. For both panels, the intensity shown was averaged over the entire 25 min observing time of this EUI sequence, and then was normalized by the minimum and maximum intensities within the zoomed-in FOV shown in panel b. Thus, the image color scale in the full FOV and the zoomed-in FOV in Fig. 1 are different. With the above normalization for panel b it is limited between 0 and 1 and for panel a, which contains pixels with both greater and weaker intensities, it ranges from −0.7 to 1.1.

thumbnail Fig. 1.

Observation summary. Panel a: full FOV covered in the 17.4 nm band of HRIEUV. The red box outlines the zoomed-in FOV shown in panel b. Both panels show the time-averaged normalized intensity (to the minimum and maximum in the area in panel b). Panel b: location of the cut (vertical black line) used in the time–distance plot displayed in Fig. 2 and the intensity–distance plot shown in Fig. 3. The cyan box (i) and the orange box (ii) outline the diffuse region and the bright point used in Fig. 4. The green box (iii) outlines the loop-like features shown in Fig. B.1 (see Sect. 3.1).

3.1. Diffuse region, loop-like features, and coronal bright points

We find several distinct regions in the corona at ∼1 MK. There are dark patches (with normalized intensities of 0.25 or less), bright patches associated with loop-like structures and coronal bright points containing intensities at or near the saturation limit of the detector, and, finally, what we refer to as “diffuse” regions.

These diffuse regions are areas that seem to lack structure in both time and space. They are hazy portions seen throughout the FOV with time-averaged normalized intensities mostly in the range 0.25–0.6. An example patch of diffuse corona is outlined by the cyan box (panel i) in Fig. 1b. The diffuse corona appears to cover a significant area when compared to the brighter regions in the FOV. However, the diffuse corona lacks any of the obvious structuring that is associated with the well-studied structures of the quiet solar corona, such as coronal bright points that are composed of ∼10 Mm long loops (see, e.g., the review article on coronal bright points by Madjarska 2019).

Our analysis aims to compare these differing regions in both a qualitative and quantitative manner to determine the extent of this apparent discrepancy in terms of spatial structuring. For this we investigated a cut through the FOV that runs through these different features (black line in Fig. 1b): diffuse regions, loop-like features, and a coronal bright point. While many bright features are saturated in the exposure, in particular at the limb, this bright point is not. The intensity along this cut as a function of time is presented in a time–distance plot (see Fig. 2). It is evident from this plot that the bright point stretching from y = 106 Mm to 117 Mm shows intensity structuring in both space and time. The same also applies to the clear loop-like features situated around y = 65 Mm to 100 Mm. The bright point and the loop-like features appear to be continually evolving on spatial scales of roughly a few Mm and timescales on the order of a few minutes, although the loop-like features are less variable than the bright point.

thumbnail Fig. 2.

Temporal evolution of cut through the diffuse region and coronal bright point. This time–distance plot shows the intensity in HRIEUV from along the cut (1 pixel in x) outlined by the black vertical line in Fig. 1b as it evolves over the entire 25 min observing time. The intensity is scaled linearly from 915 DN s−1 (black) to 2500 DN s−1 (white). Above the panel the location in the y direction of three types of regions are labeled. The two arrows indicate transient brightenings in the diffuse region (see Sects. 3.1 and 4.2).

The bright point is a typical small coronal bright point in appearance and size. It consists of a number of short coronal loops with the core region (Fig. 4ii) having a size of just over 5 Mm (cf. Madjarska 2019). Such compact small-loop-type bright points are found in abundance in the QS and have been used, for example to determine the coronal rotation (Brajša et al. 2001, 2002), even though the spatial resolution of the older data was inadequate to sufficiently resolve the internal structure of the bright points. The region with loop-like features does not show clearly distinguishable loops, but (in the time-averaged image) elongated features reminiscent of loops (Fig. B.1iii). Because we concentrate in this study on the diffuse regions, we do not follow this up (see Appendix B for a further discussion of the loop-like features).

In contrast to these more dynamic features, the diffuse regions seen in Fig. 2 are invariable. The time–distance plot reveals the overall temporal stability of the diffuse corona. The emission is diffuse in the y-direction in a range of 15–65 Mm, with two seemingly distinct regions of differing intensity levels: a brighter portion between 15–42 Mm and a darker portion from 42–65 Mm. For both portions there is a hazy quality that remains stable throughout the 25 min observing time on spatial scales comparable to that of a supergranule. The brighter and darker sections both show no obvious jumps in intensity across their width. There is a small brightening at about y = 48 Mm occurring periodically over intervals of time limited to a few minutes (highlighted by arrows in Fig. 2). This could be categorized as an HRIEUV campfire (see Berghmans et al. 2021). However, the brightening is only a few pixels in width and makes up only a small fraction of the overall emission in that region.

We note that the data shown in the space–time plot in Fig. 2 have a time cadence of only 2 s and a spatial sampling of 260 km on the Sun. This implies that transient small-scale features should be visible if they are present (down to those temporal and spatial scales).

3.2. Spatial and temporal variability

We now inspect the time–distance plot for a closer look at the difference between the coronal bright points and the diffuse regions. To this end, the intensity along the cut from Fig. 1b was averaged over each subsequent 30 s interval, which are displayed as line plots of time-averaged intensity versus distance, several of which are shown stacked in Fig. 3. Essentially, these stacked plots are horizontal cuts through Fig. 2 for a given time span.

thumbnail Fig. 3.

Spatial variability along a cut through a diffuse region, loop-like features, and a coronal bright point at four different times. This intensity–distance plot shows the intensity along the cut outlined by the black vertical line in Fig. 1b for several intervals of time during the observation. For each 30 s interval (15 time-consecutive images), the intensity at each pixel along the cut is averaged over that time period and plotted as a function of distance. Four of these light curves are shown as a stack: the bottom curve is the intensity–distance 30 s average (starting at 30 s) ending at 1 min, the curve directly above it is the 30 s average ending at 10 min, and so on. The black vertical bars with each curve show the maximum error for that curve (see Appendix A). Above the panel the location in the y direction of the three types of regions are labeled (see Sects. 3.2 and 4.1).

Across these diffuse regions (i.e., y = 15 − 65 Mm), spatial changes in the intensity are gradual. As we discuss below, the small fluctuations seen in addition to this gradual variation are at the level of the calculated maximum error. The shape of the curve is also similar for each plot, although there are 5–10 min of separation between them. This implies that the diffuse corona behaves in a spatially coherent fashion over its entire extent corresponding to the scale of a supergranule of about 20 Mm.

The peak intensity in the brighter diffuse area (at y ≈ 35 Mm) is only slightly less than, or even equal to the peak intensity seen in the bright point and loop-like features (in particular before t = 15 min). Conversely, the morphology of the loop-like features and coronal bright point changes markedly over time, and the intensity fluctuations within these features at each point in time varies significantly (i.e., well-above the maximum error). This further differentiates the characteristics of the diffuse regions from those of the bright points and loop-like features.

To quantitatively characterize the temporal stability of the diffuse corona, its relative intensity fluctuations provide clearer insight (Fig. 4). Here we compared the absolute and relative intensity variations of the diffuse corona (box i in Fig. 1b) to that within the coronal bright point (box ii). The absolute fluctuations are derived by simply spatially averaging the intensity within each of the sub-fields a to d for each snapshot. The relative fluctuations were then calculated by subtracting the overall time-averaged intensity within each sub-field from its spatially averaged intensity and then dividing this difference by the time-averaged intensity. Figures 4i and ii show which sub-fields of the observation are sampled, either from a diffuse region (a, b) or from a bright point (c, d).

thumbnail Fig. 4.

Intensity fluctuations in diffuse and bright point regions. The two left panels show the zoomed-in FOV covering the diffuse region (panel i) and bright point (panel ii) outlined by the cyan and orange boxes in Fig. 1b, respectively. Each image is the same time-averaged and normalized figure as shown in Fig. 1b, except the intensity range shown is further limited to the minimum and maximum for each zoomed-in FOV. Within the regions of interest, four smaller sub-fields a to d are outlined. Each of these boxes has the same area. The spatially averaged relative (left y-axis) and absolute (right y-axis) intensities for the respective sub-fields are plotted as a function of time on the right in panels a–d. The vertical bars shown in each of these panels represent the maximum error for each time series (see Appendix A).

The relative fluctuations in the sub-fields of the diffuse region (a, b) remain within a few percentage points (less than ±5%) over the entire 25 min (Figs. 4a, b). In contrast, in the sub-fields of the coronal bright point (c, d), the intensity changes by over 10% on shorter timescales of about 5 min and can sway by up to almost 40% over the entire 25 min (Figs. 4c, d).

To judge the significance of these fluctuations, we have to compare the observed variability to the measurement errors. In Appendix A we discuss how we calculate the maximum estimated error. As a very rough estimate of this, for our current data set in regions that are moderately bright, the typical error of the intensity is on the order of 3%.

In general, the sub-fields of the bright point show trends that rise well above the level of the maximum estimated error, both on shorter and longer timescales. In contrast, in the diffuse regions the variability we see would essentially be consistent with measurement errors. There might be some dynamics within the diffuse regions with amplitudes just above the noise that persist for more than a few time steps, but these fluctuations are still smaller than the overall level of fluctuations over the observing period (of 25 min). While the fluctuations shown here are only for two subsections of each feature, the behavior is similar when more subsections are analyzed.

This relative temporal stability of the diffuse corona and the larger variability seen in the coronal bright point are further demonstrated using the respective snapshots, at three instances, without time-averaging (see Fig. 5). It is clear from these images that the diffuse region is not only temporally stable compared to the bright point, but it also lacks any distinguishable spatial structuring.

thumbnail Fig. 5.

Snapshots of diffuse region and bright point without time-averaging. The snapshots at three times as indicated by the time stamps are shown in the three columns. The top row shows the diffuse region (marked i) and the bottom row the bright point (marked ii). Images are commonly scaled to the same minimum and maximum values of intensity. Boxes a–d have the same meaning as in Fig. 4. See Sects. 3.2 and 4.1.

This time series analysis emphasizes that the diffuse corona, often considered as mere background, contributes a significant amount of the coronal emission in the QS (for a quantitative estimate of this contribution, see Sect. 4.1).

4. Discussion

We note the general pervasiveness of the diffuse corona seen at temperatures of 1 MK with HRIEUV. These regions remain featureless in both time and space, and yet are relatively bright compared to the more dynamic features within the FOV. This naturally leads to questions about the significance of these regions in terms of their contribution to the emission of the 1 MK corona and about the possible heating mechanisms operating in such regions. Similarly, questions arise regarding the reasoning behind the lack of noticeable structuring and how this is related to the overall energy balance within the solar atmosphere.

4.1. Contribution of diffuse regions to radiative losses

The intensity observed in the diffuse regions is relatively strong, even when compared with bright points. This is illustrated in Figs. 4a–d where we show the relative and absolute average intensity values [DN] within sub-fields of the diffuse and bright point regions. We see that, over the entire observing period, the time-averaged diffuse intensity (i.e., radiative flux per area) is about 80% that of the bright point (i.e., on the same order of magnitude). In addition, in Fig. 3, the peak intensities along the cut from the brighter diffuse portion (around y = 35 Mm) are very similar to those from the bright point (around y = 110 Mm) and are also about equal to those from the loop-like features sampled between y = 65 Mm and 100 Mm. All of this points to the conclusion that the emission coming from the diffuse regions is non-negligible and should be an important consideration in any coronal heating model, in particular when considering that the diffuse corona can cover a large fraction of the QS.

We further investigate the significance of diffuse emission by conducting a rough estimate of the total emission contribution from the diffuse areas compared to the bright points within the FOV. For this we classify the regions in the FOV in Fig. 1b into areas covered by coronal bright points and diffuse regions by a simple by-eye estimate. These regions are marked and labeled in Fig. 6. Some of the bright points host a few pixels that are saturated on the detector. Hence our estimate for the bright point emission will be a lower limit only. However, this effect should be well below a factor of two and thus our calculation should be just fine for the order-of-magnitude estimate we aim for here.

thumbnail Fig. 6.

Grouping of diffuse coronal regions and bright points in QS. The intensity image is the same as Fig. 1b. The diffuse coronal regions (dc1 to dc4) are outlined in blue; the bright points (bp1 to bp6) are highlighted in yellow (see Sect. 4.1).

Based on the integration of the emission from the respective diffuse and bright point areas, we find that the seemingly quiet diffuse areas provide almost 2.7 times more emission than the more dynamic features. Thus overall, the diffuse emission would dominate the QS radiative losses at around 1 MK, while discernible bright features would contribute a minor fraction, maybe half at best. This is not surprising since these diffuse regions defined by-eye also have almost three times more area than the bright points (see Fig. 6).

4.2. Diffuse quiet-Sun corona and small loops

The magnetic field is space-filling and is the driver behind the energetics of the corona. The work of Dowdy et al. (1986) described the solar magnetic scene as comprised of both (locally) open field lines expanding into funnels with height and small-scale closed loops that connect back to the surface. Based on studies of magnetic field extrapolations, these loops are expected to be rooted not only in the network regions at the edges of supergranules, but also in the internetwork within a few Mm of the network boundaries (Schrijver & Title 2003; Wiegelmann et al. 2010).

Quiet Sun observations reveal the presence of very short loops clearly distinguishable in EUV observations, only a few Mm long. They probably come at high coronal temperatures (Peter et al. 2013; Barczynski et al. 2017) as well as at lower transition region temperatures (Hansteen et al. 2014). These short loops have lifetimes of only a few minutes. More recent observations also reveal the dynamic nature and substructure of such small EUV loops including propagating features (Mandal et al. 2021) and small jets associated with them (Chitta et al. 2021b). Transition region loops crossing a super-granular cell in the QS (i.e., with a length of ca. 20 Mm), have also been reported (e.g., Fig. 1 in Teriaca et al. 2004). However, all these types of loops are discrete units and are far from space-filling.

Even so, the presence of loops in the QS would mean that we should expect the presence of small-scale coronal loops (a few Mm in length) in our observation even within the so-called diffuse areas. As discussed above, these smaller loops are expected to be dynamic, showing brightness fluctuations on timescales on the order of minutes (see also Reale 2010). Similar lifetimes of (magnetic) loops of a few minutes are also found based on magnetic field extrapolations from time series of high-resolution QS magnetograms (Wiegelmann et al. 2010). As a case in point, our observations do show such brightness fluctuations in the coronal bright points, which are indeed on shorter timescales compared to the 25 min of observed stability for our diffuse areas.

If the diffuse areas were composed of such smaller loops, then we would expect loop-like brightenings at some point during our analysis unless a different loop emission behavior is at play. We do see that there are a limited number of small-scale brightenings occurring within some diffuse portions of Fig. 2 (see white arrows) that last for a few minutes at a time and are only a few pixels in length (i.e., ∼500 km in y-distance). These brightenings, however, are not ubiquitous, as would be expected for the typical picture of low-lying loops crisscrossing everywhere in the FOV. In addition, these small intensity enhancements barely rise above the level of the local diffuse region (or background). When compared to the intensity level local to the area of the brightening in the minutes before and after its enhancement, the brightening only rises to a level of 5% above this background.

The coherent spatial intensity variations on supergranular scales in these diffuse regions indicate that all the constituting smaller loops, if present, must evolve in unison, which is unlikely. Based on this, we think that the small coronal loops reported above may not be the source of emission from the diffuse regions. In that case we should occasionally see a transient brightening caused by one of the transient megameter-scale loops that have been reported before, but we do not see them.

4.3. Diffuse quiet-Sun corona and jets

Chromospheric spicules (de Pontieu et al. 2007) and transition region network jets (Tian et al. 2014) are other common small-scale jet features whose imprint should be seen everywhere on the QS. Spicules are chromospheric jets and are categorized as two types (de Pontieu et al. 2007). Type I spicules are longer-lived, and are seen to both rise and fall at the limb, remaining at chromospheric temperatures throughout their lifetime. Type II spicules are more transitory and often appear to shoot up before disappearing from chromospheric imaging channels, sometimes then appearing in the hotter channel imaging transition region (TR) plasma (Pereira et al. 2014), which can also include the return flows when cooling back down from hotter temperatures (Bose et al. 2021). Spicules have typical speeds ranging from tens of km s−1 (type I) to 100 km s−1 (type II), lifetimes of several minutes, and characteristic lengths ranging from a few hundred to several thousand km (e.g., Tsiropoula et al. 2012, and references therein).

While spicular material is easiest to detect at the cooler temperatures found in the chromosphere and TR (T ≤ 105 K), recent investigations show that there are exceptions to this where spicule signatures can be observed as corrugations in the EUV emission. For example, signatures have been found that the on-disk counterparts of spicules, namely dynamic fibrils, show EUV emission (Mandal et al. 2023). This might indicate higher temperatures of more than 105 K, although this is not yet conclusive (Henriques et al. 2016; Martínez-Sykora et al. 2018; Samanta et al. 2019). Similarly, coronal counterparts of network jets remain elusive (Kayshap et al. 2018; Gorman et al. 2022).

Small coronal jets are, in general, a common phenomenon in QS regions. In particular, recent EUI observations have shown an abundance of small-scale jets (e.g., Chitta et al. 2021b; Mandal et al. 2022). Small jets and their substructures (e.g., plasmoids) have recently also been observed in radio emission (e.g., Shimojo et al. 2017; Rodger et al. 2019). Still, the question remains whether highly dynamic small-scale features such as these jets or spicules can provide an explanation for the diffuse corona.

At 2 s cadence and about 500 km resolution, the observation from HRIEUV that we analyze in this study could certainly pick up any spicules or network jets that showed counterparts in the EUV. However, we do not detect any such signatures in the far-reaching diffuse areas. This either means that these jets only very rarely reach coronal temperatures or at least that they do not get heated to 1 MK in the magnetic regime that is responsible for the diffuse emission. Another possibility could be that those small-scale jets that do reach coronal temperatures might lose their identity and structuring as their energy gets dissipated.

4.4. Diffuse quiet-Sun corona and small-scale heating events

The simple presence of a diffuse, seemingly featureless structure has implications for the heating mechanism that has to sustain the hot corona. The energization has to be either continuous or be concentrated in a very large number of small-scale heating events so that this does not leave an imprint at the resolution of our observations. Hence, we explore the applicability of several proposed heating mechanisms for the diffuse corona. Clearly, we cannot relate our findings to all possible heating scenarios; instead, we picked those we considered most relevant for our study. We refer to recent reviews that discuss the heating problem in general (e.g., Klimchuk 2006), with respect to 3D models (e.g., Peter 2015), in terms of waves (e.g., Van Doorsselaere et al. 2020), or in light of field-line braiding (e.g., Pontin & Hornig 2020).

One heating scenario involves a power-law distribution of the number of brightening events with energy characterized by a slope of −2, at least for the smaller flare-like events with less than 1026 ergs (Hudson 1991). This requires there to be an increasingly larger number of distinct events on ever-smaller spatial and energy scales. These events would be so small that they are not yet resolvable by Sun-observing instruments (Parnell & Jupp 2000; Chitta et al. 2021a). To date, however, results are mixed regarding whether or not the energy distribution for impulsive heating events has the necessary slope to account for coronal heating (e.g., Berghmans et al. 1998; Krucker & Benz 1998; Aschwanden et al. 2000; Parnell & Jupp 2000; Pauluhn & Solanki 2007; Aschwanden & Shimizu 2013). It has also been pointed out that even if the power index is greater than 2, this is not necessarily sufficient to heat the QS (Berghmans 2002). Joulin et al. (2016) argue that regardless of the actual energy distribution slope, it is inherently unlikely to be able to detect high-frequency small-scale brightenings against the background coronal emission. The authors state that their study combined with the works of others before them shows that heating cannot be guaranteed to be observed as broken up into discrete events.

Perhaps such unresolved, impulsive brightenings are what is the cause behind the diffuse corona. If there were a sufficiently high number of small-scale events resulting in the diffuse emission that we see, they would still have to be driven in a spatially coherent fashion to create a diffuse region of about 10 to 20 Mm in size (i.e., the size of a supergranule). Considering the significant structuring found at the base below the corona, in the chromosphere, it is not very plausible that the diffuse corona is driven by small-scale events.

Should small-scale events drive and heat the diffuse coronal patches, we would also expect larger events in these regions. This is based on the finding that even on the smallest scales resolved to date, power-law-like distributions prevail (Berghmans et al. 2021). However, with two exceptions of events barely resolved by HRIEUV (arrows in Fig. 2), we do not see any distinguishable transient brightenings in the diffuse regions (above the noise level). A more rigorous statistical analysis is required to draw a final conclusion, but at this point we consider it unlikely that individual events distributed through a power law could create a diffuse corona, as we observe here.

It is possible to speculate that some form of magnetohydrodynamic (MHD) turbulence might lead to energy dissipation far below the scales resolvable by current observations, thus creating a quasi-continuous heating in these regions. This would raise the question of why this should be operating in the diffuse regions, while other areas show much higher contrast in the coronal QS features. As this discussion would go far beyond the scope of this observational study, we refrain here from any further speculation.

4.5. Diffuse quiet-Sun corona and wave heating

If the energization of the hot diffuse QS corona has to be quasi-continuous, then wave heating could also be an option. In the first theoretical attempts to explain the hot outer atmosphere, heating through waves had already been suggested, at that time through the dissipation of sound waves (Biermann 1946; Schwarzschild 1948). On average, an energy flux of about 100 W m−2 is required to balance the energy losses of the corona in the QS (e.g., Withbroe & Noyes 1977), and in general upward-propagating magneto-acoustic waves have the potential to heat the plasma in magnetically closed structures (see, e.g., review by Arregui 2015). Such waves have been observed (e.g., Tomczyk et al. 2007), and they carry an energy flux sufficient to heat the QS corona (e.g., McIntosh et al. 2011).

Assuming that the upward-propagating waves are generated by p-mode leakage (e.g., de Moortel 2009), we might expect quite a homogeneous distribution of the energy flux into the upper atmosphere. In the photosphere we can expect a spatial structure on the scale of granulation; however, the rapid expansion of the magnetic field with height guiding the wave flux might quickly even out spatial inhomogeneities. However, a detailed investigation of the expansion of the underlying magnetic field in the diffuse coronal regions would be required before drawing any final conclusions on this.

In the time series of small sub-fields, some indications for three-minute oscillations might be found. A by-eye inspection of Figs. 4a–d suggests the presence of fluctuations on a timescale of a few minutes in the diffuse corona (panels a, b) and the bright point (c, d). If such fluctuations were present, that would indeed support the leakage of wave power from the photosphere into the higher atmospheric regions seen in the diffuse corona. Just as with the expansion of the magnetic field, a detailed analysis of a possible presence of three-minute oscillations in the diffuse regions will have to be conducted in the future.

5. Conclusions

We analyzed the diffuse quiescent corona observed by HRIEUV on board Solar Orbiter. Here we find large patches of diffuse corona lacking resolvable physical structuring on scales below those of a supergranule (i.e., about 20 Mm). Even so, the coronal emission from these diffuse regions is of comparable brightness to the more dynamic features, such as loop-like features or coronal bright points. The spatial variability in the diffuse corona is below about 5%. The diffuse corona remains temporally stable throughout the observing period (i.e., for at least 25 min).

This diffuse regime is rather commonplace within the coronal makeup, contributing a large proportion of the emission seen at 1 MK, yet its underlying nature is still unclear. We consider it unlikely to be connected to features such as spicules or small loops. A power-law-like distribution of discrete heating events seems inconsistent with our observations. We speculate that small-scale processes like MHD turbulence or upward-propagating waves might be energizing the diffuse regions, but at this point we cannot offer a conclusive explanation for the nature of the diffuse regions.

The lower atmosphere in the QS shows a high degree of temporal and spatial complexity. This is illustrated, for example, by the cartoon suggested by Wedemeyer-Böhm et al. (2009) in their Fig. 16. The diffuse region we investigated in this study might well be related to the mixture of structures in the inter-network, above and below the canopy domain. This would also fit into the interpretation of Milanović et al. (2023) of a diffuse region between network patches of the same polarity on opposite sides of a super-granular cell.

A more extensive investigation of this diffuse component of the QS corona, using increasingly diverse data sets would help to better estimate how common this component is, including observations of plasma at other temperatures. The brightness distribution in the diffuse patches, the lifetimes and size distributions of such diffuse patches, and whether wave patterns (of whatever nature) are commonly seen in them also need further consideration. Just as important will be studies combining EUV data with magnetic field measurements provided by the SO/PHI instrument Solanki et al. (2020), for example. Finally, there is also a clear need for studies of possible heating mechanisms leading to such diffuse parts of the corona.

1

Data release 4.0 2021-12. DOI: https://doi.org/10.24414/s5da-7e78

Acknowledgments

We would like to thank the anonymous referee for helpful comments on this paper. This work was supported by the International Max-Planck Research School (IMPRS) for Solar System Science at the University of Göttingen. L.P.C. gratefully acknowledges funding by the European Union (ERC, ORIGIN, 101039844). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. Solar Orbiter is a mission of international cooperation between ESA and NASA, operated by ESA. The EUI instrument was built by CSL, IAS, MPS, MSSL/UCL, PMOD/WRC, ROB, LCF/IO with funding from the Belgian Federal Science Policy Office (BELSPO/PRODEX PEA 4000134088, 4000112292, 4000117262, and 4000134474); the Centre National d’Etudes Spatiales (CNES); the UK Space Agency (UKSA); the Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft- und Raumfahrt (DLR); and the Swiss Space Office (SSO).

References

  1. Arregui, I. 2015, Philos. Trans. R. Soc. London Ser. A, 373, 20140261 [Google Scholar]
  2. Aschwanden, M. J., & Shimizu, T. 2013, ApJ, 776, 132 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aschwanden, M. J., Tarbell, T. D., Nightingale, R. W., et al. 2000, ApJ, 535, 1047 [Google Scholar]
  4. Barczynski, K., Peter, H., & Savage, S. L. 2017, A&A, 599, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Berghmans, D. 2002, in Solar Variability: From Core to Outer Frontiers, ed. A. Wilson, ESA Spec. Publ., 2, 501 [NASA ADS] [Google Scholar]
  6. Berghmans, D., Clette, F., & Moses, D. 1998, A&A, 336, 1039 [NASA ADS] [Google Scholar]
  7. Berghmans, D., Auchère, F., Long, D. M., et al. 2021, A&A, 656, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Biermann, L. 1946, Naturwissenschaften, 33, 118 [Google Scholar]
  9. Bose, S., Rouppe van der Voort, L., Joshi, J., et al. 2021, A&A, 654, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Brajša, R., Wöhl, H., Vršnak, B., et al. 2001, A&A, 374, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Brajša, R., Wöhl, H., Vršnak, B., et al. 2002, A&A, 392, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Chitta, L. P., Peter, H., & Young, P. R. 2021a, A&A, 647, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Chitta, L. P., Solanki, S. K., Peter, H., et al. 2021b, A&A, 656, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Chitta, L. P., Peter, H., Parenti, S., et al. 2022, A&A, 667, A166 (SO Nominal Mission Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. de Moortel, I. 2009, Space Sci. Rev., 149, 65 [NASA ADS] [CrossRef] [Google Scholar]
  16. de Pontieu, B., McIntosh, S., Hansteen, V. H., et al. 2007, PASJ, 59, S655 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dowdy, J. F., Jr., Rabin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gorman, J., Chitta, L. P., & Peter, H. 2022, A&A, 660, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Hansteen, V., De Pontieu, B., Carlsson, M., et al. 2014, Science, 346, 1255757 [Google Scholar]
  20. Henriques, V. M. J., Kuridze, D., Mathioudakis, M., & Keenan, F. P. 2016, ApJ, 820, 124 [Google Scholar]
  21. Hosseini Rad, S., Alipour, N., & Safari, H. 2021, ApJ, 906, 59 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hudson, H. S. 1991, Sol. Phys., 133, 357 [Google Scholar]
  23. Joulin, V., Buchlin, E., Solomon, J., & Guennou, C. 2016, A&A, 591, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Kayshap, P., Murawski, K., Srivastava, A. K., & Dwivedi, B. N. 2018, A&A, 616, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [Google Scholar]
  26. Krucker, S., & Benz, A. O. 1998, ApJ, 501, L213 [Google Scholar]
  27. Madjarska, M. S. 2019, Liv. Rev. Sol. Phys., 16, 2 [Google Scholar]
  28. Mandal, S., Peter, H., Chitta, L. P., et al. 2021, A&A, 656, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Mandal, S., Chitta, L. P., Peter, H., et al. 2022, A&A, 664, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Mandal, S., Peter, H., Chitta, L. P., et al. 2023, A&A, 670, L3 (SO Nominal Mission Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Martínez-Sykora, J., De Pontieu, B., De Moortel, I., Hansteen, V. H., & Carlsson, M. 2018, ApJ, 860, 116 [Google Scholar]
  32. McIntosh, S. W., de Pontieu, B., Carlsson, M., et al. 2011, Nature, 475, 477 [Google Scholar]
  33. Milanović, N., Chitta, L. P., & Peter, H. 2023, A&A, 673, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
  35. Parnell, C. E., & Jupp, P. E. 2000, ApJ, 529, 554 [Google Scholar]
  36. Pauluhn, A., & Solanki, S. K. 2007, A&A, 462, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Pereira, T. M. D., De Pontieu, B., Carlsson, M., et al. 2014, ApJ, 792, L15 [Google Scholar]
  38. Peter, H. 2015, Philos. Trans. R. Soc. London Ser. A, 373, 20150055 [NASA ADS] [Google Scholar]
  39. Peter, H., Bingert, S., Klimchuk, J. A., et al. 2013, A&A, 556, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Pontin, D. I., & Hornig, G. 2020, Liv. Rev. Sol. Phys., 17, 5 [NASA ADS] [CrossRef] [Google Scholar]
  41. Reale, F. 2010, Liv. Rev. Sol. Phys., 7, 5 [Google Scholar]
  42. Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Rodger, A. S., Labrosse, N., Wedemeyer, S., et al. 2019, ApJ, 875, 163 [Google Scholar]
  44. Samanta, T., Tian, H., Yurchyshyn, V., et al. 2019, Science, 366, 890 [NASA ADS] [CrossRef] [Google Scholar]
  45. Schrijver, C. J., & Title, A. M. 2003, ApJ, 597, L165 [NASA ADS] [CrossRef] [Google Scholar]
  46. Schwarzschild, M. 1948, ApJ, 107, 1 [Google Scholar]
  47. Shen, Y. 2021, Proc. R. Soc. London Ser. A, 477, 217 [NASA ADS] [Google Scholar]
  48. Shimojo, M., Hudson, H. S., White, S. M., Bastian, T. S., & Iwai, K. 2017, ApJ, 841, L5 [Google Scholar]
  49. Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Teriaca, L., Banerjee, D., Falchi, A., Doyle, J. G., & Madjarska, M. S. 2004, A&A, 427, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Tian, H., DeLuca, E. E., Cranmer, S. R., et al. 2014, Science, 346, 1255711 [Google Scholar]
  52. Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [Google Scholar]
  53. Tsiropoula, G., Tziotziou, K., Kontogiannis, I., et al. 2012, Space Sci. Rev., 169, 181 [Google Scholar]
  54. Van Doorsselaere, T., Srivastava, A. K., Antolin, P., et al. 2020, Space Sci. Rev., 216, 140 [Google Scholar]
  55. Viall, N. M., & Klimchuk, J. A. 2011, ApJ, 738, 24 [Google Scholar]
  56. Wedemeyer-Böhm, S., Lagg, A., & Nordlund, Å. 2009, Space Sci. Rev., 144, 317 [Google Scholar]
  57. Wiegelmann, T., Solanki, S. K., Borrero, J. M., et al. 2010, ApJ, 723, L185 [NASA ADS] [CrossRef] [Google Scholar]
  58. Withbroe, G. L., & Noyes, R. W. 1977, ARA&A, 15, 363 [Google Scholar]

Appendix A: Preliminary error estimates

To better quantify and compare the intensity fluctuations, we calculated the total error, σtotal, associated with the observed emission in the following manner. First, we converted the observed spatially averaged intensities, I, from DN s−1 to DN by multiplying them by exposure time, texp, and then converted this to photon count by considering the current high gain estimate, a, for the HRIEUV channel. Next, we used this to calculate the photon noise, σph, by taking the square root of the total number of photons. This photon noise was then divided by the square root of the number of pixel values, N, averaged over to obtain the initial average intensity. After converting the photon noise back into DN with the conversion factor, a, the square of this amount was summed with the square of the read-out noise, R, and then the square root of this sum gave the final σtotal. A final reduced equation for this is

σ total = R 2 + I t exp a N . $$ \begin{aligned} \sigma _{\rm {total}} = \sqrt{R^2+\frac{I\,t_{\rm {exp}}\,a}{N}} \, .\end{aligned} $$(A.1)

Here σtotal is in DN, R =  2 DN, I is in DN s−1, texp is in s, and a =  6.85 DN photon−1. For a typical bright point with an average intensity of 3450 DN, we find a maximum error of 27 DN. For the diffuse regions, a typical average intensity of 2765 DN has a maximum error of 23 DN. Due to the current early stage of the Solar Orbiter mission, the error estimation calculation is not yet fully clarified. So, we expect that any reasonable calculated errors should be comparable to the root mean square (RMS) fluctuations, as these are expected as an upper limit. For this observation, the maximum errors estimated in the manner detailed above are comparable to the high-frequency (1 min) RMS fluctuations, which are typically of a few percent. Thus, we consider our error estimation to be reasonable.

Appendix B: Region of loop-like features

In the main text we concentrated on the properties of the diffuse region and compared them to the coronal bright point. Here we concentrate on an area with loop-like features (green box iii in Fig. 1). This region shows a spatio-temporal structuring of a higher degree than the diffuse region, but much less variability than the bright point (see Fig. 2). In this Appendix we briefly compare the properties of this region with loop-like features to the diffuse region and the bright point.

The time averaged intensity map of this region shows distinct structures, even though it is not simple to attribute a particular nature to these features. The left panel of Fig. B.1 shows a zoomed-in view of this area. In contrast to the diffuse region (Fig. 4i) it shows clear elongated structures. For simplicity we call these structures loop-like features.

thumbnail Fig. B.1.

Intensity fluctuations in the region with loop-like features. The layout of this figure corresponds to Fig. 4. The left panel shows a zoomed-in image of the green box in Fig. 1b (region iii). Within this region a smaller sub-field e is outlined. This has the same area as the sub-fields in Fig. 4 i and ii. The spatially averaged relative (left y-axis) and absolute (right y-axis) intensity for sub-field e is plotted as a function of time in the right panel. The vertical bar represents the maximum error for the time series (see Appendix B).

The fluctuations seen in this region are comparable to or larger than in the diffuse region, but much less pronounced than in the bright point. This is evident when comparing the time variability near the center of the loop-like features (Fig. B.1e) to the corresponding variability seen in the other regions (Fig. 4a-d).

The individual snapshots in this region of loop-like features are noisy, but still show distinct structures. For example, the first snapshot in Fig. B.2 shows some short-lived individual compact brightenings and the last snapshot some elongated structures (at low contrast) from the bottom left to the top right. This presence of spatial structures is markedly different from the snapshots of the diffuse region (top row of Fig. 5). The levels of the count rates are comparable in the diffuse region and the loop-like features, hence noise cannot explain the absence of structures in the diffuse region.

thumbnail Fig. B.2.

Snapshots of region with loop-like features without time averaging. This figure corresponds to Fig. 5. The snapshots are shown at three times, as indicated by the time stamps. Images are commonly scaled to the same minimum and maximum values of intensity. Box e has the same meaning as in Fig. B.1 (see Appendix B).

From this discussion we conclude that the region with loop-like features (box iii in Fig. 1) hosts small-scale distinct features that cannot be identified in the diffuse region, even though the count rates are comparable. We can speculate if this region with loop-like features is in a transition phase from diffuse to more active, like the bright point, or vice versa. To draw solid conclusions on this a more comprehensive study of loop-like features would be required, in particular including data on the magnetic field configuration in the photosphere below.

All Figures

thumbnail Fig. 1.

Observation summary. Panel a: full FOV covered in the 17.4 nm band of HRIEUV. The red box outlines the zoomed-in FOV shown in panel b. Both panels show the time-averaged normalized intensity (to the minimum and maximum in the area in panel b). Panel b: location of the cut (vertical black line) used in the time–distance plot displayed in Fig. 2 and the intensity–distance plot shown in Fig. 3. The cyan box (i) and the orange box (ii) outline the diffuse region and the bright point used in Fig. 4. The green box (iii) outlines the loop-like features shown in Fig. B.1 (see Sect. 3.1).
In the text
thumbnail Fig. 2.

Temporal evolution of cut through the diffuse region and coronal bright point. This time–distance plot shows the intensity in HRIEUV from along the cut (1 pixel in x) outlined by the black vertical line in Fig. 1b as it evolves over the entire 25 min observing time. The intensity is scaled linearly from 915 DN s−1 (black) to 2500 DN s−1 (white). Above the panel the location in the y direction of three types of regions are labeled. The two arrows indicate transient brightenings in the diffuse region (see Sects. 3.1 and 4.2).
In the text
thumbnail Fig. 3.

Spatial variability along a cut through a diffuse region, loop-like features, and a coronal bright point at four different times. This intensity–distance plot shows the intensity along the cut outlined by the black vertical line in Fig. 1b for several intervals of time during the observation. For each 30 s interval (15 time-consecutive images), the intensity at each pixel along the cut is averaged over that time period and plotted as a function of distance. Four of these light curves are shown as a stack: the bottom curve is the intensity–distance 30 s average (starting at 30 s) ending at 1 min, the curve directly above it is the 30 s average ending at 10 min, and so on. The black vertical bars with each curve show the maximum error for that curve (see Appendix A). Above the panel the location in the y direction of the three types of regions are labeled (see Sects. 3.2 and 4.1).
In the text
thumbnail Fig. 4.

Intensity fluctuations in diffuse and bright point regions. The two left panels show the zoomed-in FOV covering the diffuse region (panel i) and bright point (panel ii) outlined by the cyan and orange boxes in Fig. 1b, respectively. Each image is the same time-averaged and normalized figure as shown in Fig. 1b, except the intensity range shown is further limited to the minimum and maximum for each zoomed-in FOV. Within the regions of interest, four smaller sub-fields a to d are outlined. Each of these boxes has the same area. The spatially averaged relative (left y-axis) and absolute (right y-axis) intensities for the respective sub-fields are plotted as a function of time on the right in panels a–d. The vertical bars shown in each of these panels represent the maximum error for each time series (see Appendix A).
In the text
thumbnail Fig. 5.

Snapshots of diffuse region and bright point without time-averaging. The snapshots at three times as indicated by the time stamps are shown in the three columns. The top row shows the diffuse region (marked i) and the bottom row the bright point (marked ii). Images are commonly scaled to the same minimum and maximum values of intensity. Boxes a–d have the same meaning as in Fig. 4. See Sects. 3.2 and 4.1.
In the text
thumbnail Fig. 6.

Grouping of diffuse coronal regions and bright points in QS. The intensity image is the same as Fig. 1b. The diffuse coronal regions (dc1 to dc4) are outlined in blue; the bright points (bp1 to bp6) are highlighted in yellow (see Sect. 4.1).
In the text
thumbnail Fig. B.1.

Intensity fluctuations in the region with loop-like features. The layout of this figure corresponds to Fig. 4. The left panel shows a zoomed-in image of the green box in Fig. 1b (region iii). Within this region a smaller sub-field e is outlined. This has the same area as the sub-fields in Fig. 4 i and ii. The spatially averaged relative (left y-axis) and absolute (right y-axis) intensity for sub-field e is plotted as a function of time in the right panel. The vertical bar represents the maximum error for the time series (see Appendix B).
In the text
thumbnail Fig. B.2.

Snapshots of region with loop-like features without time averaging. This figure corresponds to Fig. 5. The snapshots are shown at three times, as indicated by the time stamps. Images are commonly scaled to the same minimum and maximum values of intensity. Box e has the same meaning as in Fig. B.1 (see Appendix B).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.