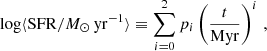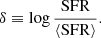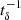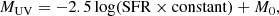EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) L4 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number L4
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202347384
Published online 31 August 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Understanding the physics regulating the evolution of star formation in galaxies is one of the most fundamental problems in present-day cosmology and astrophysics. The star formation rate (SFR) seems to depend on a deceptively simple and universal function of the gas mass (Schmidt 1959; Kennicutt 1998; Krumholz et al. 2012) despite the variety of non-linear processes, the huge dynamical range (103 − 1011 M⊙), and the diverse environment (from single molecular clouds to very massive galaxies) that are involved and probed. In addition, in the relatively low-redshift Universe (z ≲ 4), remarkably accurate predictions for the galaxy mass build-up can be obtained from minimal quasi-equilibrium models, where the star formation history (SFH) is a consequence of a so-called bathtub balance between cosmic accretion and feedback from stars and quasi-stellar objects (QSO) (Bouché et al. 2010; Dekel & Mandelker 2014). These models can explain fundamental observables such as the mass–metallicity relation (Maiolino & Mannucci 2019) or the dust content (Dayal et al. 2014), and are able to predict the ultraviolet luminosity functions (UV LF) up to z ∼ 6 (Tacchella et al. 2018).

However, as we consider progressively higher-redshift galaxies, the timescale of the feedback processes (e.g., energy input from massive stars and supernovae) becomes comparable to or longer than the dynamical time of the system (Faucher-Giguère 2018), and their regulatory effect on the SFR is thus delayed and decreased. As a consequence, SFR variations develop a stochastic character (Orr et al. 2019). Stated differently, the quasi-equilibrium assumption should eventually break down at sufficiently high z. Early galaxies are then expected to be bursty and burstiness strongly affects the determination of their properties (Furlanetto & Mirocha 2022). Already at z ∼ 5 − 8, the burstiness/suppression of SFR of galaxies, that is, whether they are above/below the Schmidt (1959)–Kennicutt (1998) relation, is key to explaining (Ferrara et al. 2019; Pallottini et al. 2019) the deviation from the [CII]–SFR relation observed in local (z = 0) galaxies (De Looze et al. 2014; Herrera-Camus et al. 2018). The natural expectation is that this stochastic variability has an even stronger impact on the super-early galaxies seen by the James Webb Space Telescope (JWST).

A stochastic SFR might affect the observable fraction of high-z galaxies as they flicker in and out of the current magnitude-limited surveys (Sun et al. 2023). Moreover, it seems that more abrupt variations than the relatively gentle ones induced by supernova explosions are needed (Gelli et al. 2023; Dome et al. 2023) to explain the detection of the rapid quenching that is observed in some early systems (Looser et al. 2023).

Perhaps more importantly, stochastic variability is one possible mechanism that has been invoked to explain the over-abundance of z ≳ 10 galaxies that has been probed via the UV luminosity function inferred from the public JWST early-release science programs (Roberts-Borsani et al. 2022; Finkelstein & Bagley 2022; Naidu et al. 2022; Adams et al. 2023; Atek et al. 2023; Donnan et al. 2023; Harikane et al. 2023), and the results from the cosmic evolution early release science survey (CEERS, Finkelstein et al. 2022) and grism lens-amplified survey from space (GLASS, Castellano et al. 2022; Treu et al. 2022; Santini et al. 2023).

Pre-JWST models cannot predict the observed flatness and limited evolution of the bright end of the LF. Thus, multiple cosmological and astrophysical scenarios have been proposed to explain this conundrum.

On the one hand, there are rather extreme frameworks that for instance (a) require ΛCDM modifications invoking a different primordial power spectrum (Liu & Bromm 2022; Padmanabhan & Loeb 2023), or (b) suggest a feedback-free boosted star formation (Dekel et al. 2023; Qin et al. 2023). On the other hand, more mundane options boost the UV luminosity function via (c) the temporary removal of dust (Ferrara et al. 2023) as a consequence of radiation-driven outflows (Ziparo et al. 2023) promoted by a high specific SFR and small galactic sizes (Fiore et al. 2023) or (d) a stochastic variability of the SFR (Mason et al. 2023; Shen et al. 2023; Mirocha & Furlanetto 2023; Muñoz et al. 2023).

The latter scenario can be formulated as follows. Time-variance in the dark matter (DM) halo assembly history induces a stochastic variation in the gas mass that can accrete on a galaxy, thus causing a flickering of the SFR (Mason et al. 2023). This flickering shifts low-mass galaxies to brighter-than-expected UV luminosities, in principle compensating for the overabundance seen at z ≳ 10 by the JWST if the distribution of the UV variability has a standard deviation (s.d.) of σUV ≳ 2 (Shen et al. 2023). However, this interpretation tends to differ from the high stellar masses derived from spectral energy density (SED) fitting of JWST observations (Santini et al. 2023). However, because the SED determination of M⋆ is degenerate with dust attenuation (Markov et al. 2023), the bursty scenario might still be viable provided low-mass galaxies are substantially reddened (Mirocha & Furlanetto 2023).

In principle, the stochastic UV boost does not depend on the physical mechanism driving it (Shen et al. 2023). In fact, UV variability can be induced by the DM halo assembly history (Mason et al. 2023) or an imbalance in the feedback regulation of SFR (Mirocha & Furlanetto 2023), and to some extent, it includes the effect of variation caused by a reduced dust attenuation (Ferrara et al. 2023). In this Letter, we clarify the amplitude of the SFR variability by using the SERRA simulations (Pallottini et al. 2022).

2. Method

SERRA is a suite of cosmological zoom-in simulations that follows the evolution of z ≳ 6 galaxies (Pallottini et al. 2022). DM, gas, and stars are evolved with a customized version of the adaptive mesh refinement code RAMSES (Teyssier 2002). KROME (Grassi et al. 2014) was used to generate a procedural numerical solver (see Branca & Pallottini 2023) to follow the non-equilibrium chemistry of H, H+, H−, He, He+, He++, H2, H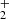, and electrons (Bovino et al. 2016; Pallottini et al. 2017a).

The metallicity (Z) is tracked as the sum of heavy elements, assuming solar abundance ratios of different metal species (Asplund et al. 2009). We assumed that dust follows metals by adopting a constant dust-to-metal ratio 𝒟 = 𝒟⊙(Z/Z⊙), where 𝒟⊙/Z⊙ ≃ 0.3 for the MW (Hirashita & Ferrara 2002) and a MW-like grain size distribution (Weingartner & Draine 2001). An initial Z = 10−3 Z⊙ metallicity floor was adopted, as expected from a pre-enrichment scenario (Wise et al. 2012; Pallottini et al. 2014).

Radiation was tracked on the fly using the moment-based radiative transfer code RAMSES-RT (Rosdahl et al. 2013), which is coupled to the chemical evolution of the gas (Pallottini et al. 2019; Decataldo et al. 2019). The energy bins cover part of the Habing band (one bin, 6.0 < hν < 11.2), the Lyman-Werner band (one bin, 11.2 < hν < 13.6) to account for H2 photoevaporation, and the ionisation of H up to the first ionisation level of He (three bins, 13.6 < hν < 24.59).

We used a Schmidt (1959)–Kennicutt (1998) like relation to convert H2 into stars, which act as a source for mechanical energy, photons, and reprocessed elements, depending on the metallicity Z⋆ and the age t⋆ of the stellar population (Bertelli et al. 1994). Feedback included supernovae, winds from massive stars, and an approximate treatment of the radiation pressure. Note that we did not adopt the standard radiation pressure prescription of RAMSES-RT (Rosdahl & Teyssier 2015) because the feedback modelling was ported from simulations that did not include radiative transfer (see Pallottini et al. 2019, for details). Depending on the type, the energy input could be both thermal and kinetic, and we accounted for the dissipation of energy in molecular clouds for supernova (SN) blast waves (Pallottini et al. 2017b).

Simulations were initialised at z = 100 from cosmological initial conditions generated with MUSIC (Hahn & Abel 2011) by adopting a PlanckΛCDM model with vacuum, matter, and baryon densities in units of the critical density ΩΛ = 0.692, Ωm = 0.308, and Ωb = 0.0481, the Hubble constant H0 = 67.8 km s−1 Mpc−1, the spectral index n = 0.967, and σ8 = 0.826 (Planck Collaboration XVI 2014). Each simulation zoomed in on a target DM halo (Mh ∼ 1012 M⊙ at z = 6) and its environment (∼(2 Mpc h−1)3, that is, about 23 times the Lagrangian volume of the target halo), reaching a gas mass and spatial resolution of Δmg ≃ 1.2 × 104 M⊙ and Δl ≃ 21 pc at z = 7.7 in the densest regions. This is the typical mass and size of Galactic molecular clouds.

3. Analysis

We used the z = 7.7 sample of SERRA galaxies with M⋆ > 106.5 M⊙, that is, those containing ≳100 star particles, for a total of 245 objects. The maximum stellar mass of the sample was about 5 × 1010 M⊙. In the original paper of Pallottini et al. (2022), 202 galaxies were presented. We added 43 new simulated objects that shared the same physical modelling, but were obtained for different seeds for the perturbations of the initial cosmological conditions Within two virial radii, all galaxies in the sample have a contamination of ≲0.1% of low-resolution particles outside the zoomed-in region.

3.1. Star formation: Stochastic variability

High-z galaxies are observed to have an increasing SFH (e.g., Topping et al. 2022) that is predicted to be exponential in our simulations (i.e., Pallottini et al. 2017a, in particular, see Fig. 2). Thus, for each galaxy, we reconstructed the SFH with a 2 Myr time resolution and defined its average trend by adopting a polynomial fit in log space,

(1)

where the order was limited to the scond order to avoid removing oscillatory terms that might be present in the SFR (see Sect. 3.2 for the a posteriori motivation). Alternative methods that can be used to determine the variability also implied informed choices, for example the maximum order selected for a principal component analysis (Chaves-Montero & Hearin 2021) and the number and width of time windows for an averaged SFR for non-parametric fits (Leja et al. 2019). We considered the SFH of a galaxy starting from the time t0 when the stellar mass was higher than 106.5 M⊙. Using ⟨SFR⟩ from Eq. (1), we defined the stochastic time variability (or flickering) of the star formation as the residual of the fit,

(2)

Figure 1 shows an example of the procedure for two representative galaxies with high (log M⋆/M⊙ ≃ 10.2) and low (log M⋆/M⊙ ≃ 8.5) mass. As expected for high-redshift systems (see e.g., Fig. 3 in Pallottini et al. 2022), the SFR of the SERRA galaxies increases with time. The most massive galaxy has a higher SFR, with peaks up to 200 M⊙ yr−1, and a longer SFH, typically starting at z ∼ 20 and lasting for about 500 Myr. The lower-mass galaxy barely reaches 10 M⊙ yr−1, and it forms stars only for a short time-span (∼150 Myr). In both cases, the average trend is well captured by the fitting procedure, as can be appreciated by eye and as is highlighted by the low p-value of the two Kolmogorov–Smirnov (KS) tests performed on SFR and ⟨SFR⟩.

thumbnail Fig. 1.

Example of SFH fitting and variability definitions for high-mass (log M⋆/M⊙ ≃ 10.2, left panel) and low-mass galaxies (log M⋆/M⊙ ≃ 8.5, right panel) in the SERRA simulation at z = 7.7. For each galaxy, we plot the star formation (SFR) in the upper panel as a function of cosmic time (t) and its fit (⟨SFR⟩, Eq. (1)) as a continuous and dashed line, respectively. We report the SFR starting from the time when the galaxy has a stellar mass higher than 106.5 M⊙, the SFR is averaged in temporal bins of 2 Myr, and on the upper axis, we plot the redshift (z). In the lower left panel, we plot the variation (δ, Eq. (2)) as a function of time, add a constant line for no variation (δ = 0) to guide the eye, and report the p-value from the Kolmogorov–Smirnov test (pKS) for the fit. In the lower right inset, we show the PDF of the variation, along with its Gaussian fit and standard deviation (σδ).

For both galaxies, the probability distribution function (PDF) of δ is a zero-mean Gaussian. This is partly expected considering the goodness of the fit (p-value ≪ 1) and because the flickering is defined as a residual (Eq. (2)). However, the amplitude of the s.d. is similar for the two galaxies, σδ ≃ 0.29 (0.19) for the low-mass (high-mass) galaxy. In both cases, the maximum amplitude of the flickering is |δ|max ∼ 0.7 − 0.8. However, extreme fluctuations like this are rare and short-lived. The high-mass galaxy, for instance, exhibits a ≃4.7 σδ peak (probability ≃2 × 10−4%) at t ≃ 600 Myr that only lasts for ∼10 Myr. Furthermore, due to the Gaussian nature of the fluctuations, the duty cycle associated with episodes of mini-quenching (Dome et al. 2023) with an amplitude νσδ can be written as fduty(νσδ) = erf(ν), where erf is the error function.

The same fitting procedure can be applied to the full sample of 245 galaxies. After confirming that the fit gives a satisfactorily low p-value (≤0.05) for all objects, we collected δ(t)−M⋆(t) pairs in each 2 Myr time bin. Treating each pair independently from the SFH of the original galaxy, we investigated the dependence of the flickering on the stellar mass. Note that adopting a first order for the fit (Eq. (1)) yields a poorer KS performance, but qualitatively the same results as presented in Sect. 3.2.

The result of the analysis is reported in Fig. 2, where we show the PDF in the δ − M⋆ plane. The most striking feature is the flat trend of the standard deviation of the flickering, that is, σδ ≃ 0.24, almost independently of M⋆. Interestingly, the scatter of the z < 6 galaxy main sequence (Popesso et al. 2023) is also constant across the mass range 108.5 − 11.5 M⊙, but with a smaller s.d. of 0.09. Higher deviations (|δ|max ≃ 0.75 ≃ 3.1σδ) can occur in 7.5 ≲ log(M⋆/M⊙)≲8.5 objects. However, these extreme values are not statistically relevant (probability ≃0.2%), and they do not affect the value of σδ.

thumbnail Fig. 2.

Distribution of the SFR variation (δ) as a function of stellar mass (M⋆). The colour bar indicates the PDF in the δ − M⋆ plane. The dashed and solid lines report the mean and variance of δ as a function of M⋆. The average standard deviation is indicated as an inset. Horizontal and vertical insets are the 1D PDFs, normalised to give the probability in each bin.

Similarly to Furlanetto & Mirocha (2022), we find that flickering is common in all galaxies, up to the massive galaxies hosted by DM halos Mh ≃ 1.2 × 1012 M⊙. However, while these authors find that δ(M⋆) slightly decreases with mass because in their case, modulation is solely induced by the delay in the feedback regulation of the SFR, the SFR varibility in SERRA can additionally be caused by cosmic accretion and/or merging events (for an analysis, see Kohandel et al. 2020) which play an important role in massive galaxies. We return to this point in Sect. 3.2.

Finally, the δ-PDF is symmetric, which might suggest that intense phases of SFR activity (high δ) are followed by quiescent phases (low δ): As a galaxy enters a starburst regime, the enhanced mechanical, radiative, and turbulent feedback energy injection can temporarily quench or reduce the SFR (Looser et al. 2023; Gelli et al. 2023). Gas cooling is likely to play a major role in re-enabling a stable SFR after burst. This study is left to future work (Gelli et al., in prep.).

3.2. SFR variability: Periodicity analysis

To investigate the presence of periodicity in δ(t), we adopted the Lomb (1976)–Scargle (1998) periodogram (see VanderPlas 2018 for a practical guide). Instead of a Fourier power spectrum analysis, we used a periodogram estimate because it yields a cleaner peak recognition and a more convenient way to define the peak significance via the false-alarm probability, that is, w = 1 − false alarm.

For illustration, we show in Fig. 3 the periodogram analysis for the same two galaxies as in Fig. 1. Note that we extracted all the peaks above a selected noise threshold; the results were mostly unchanged when the noise threshold was varied within reasonable limits.

thumbnail Fig. 3.

Example of a periodicity analysis of the SFR variability for the same high-mass (upper panel) and low-mass galaxies (lower) as presented in Fig. 1. For each galaxy, we plot the Lomb (1976)–Scargle (1998) periodogram of the variability (P(tδ)) as a function of the frequency (). Each peak recovered above the selected noise threshold (dotted line) is marked in the plot with a dashed line, and its characteristic time (tδ) and significance (w) are given. As a reference, we plot in the inset the evolution of δ vs. cosmic time (t) shifted by t0, that is, the time at which the stellar mass becomes > 106.5 M⊙.

For the log M⋆/M⊙ ≃ 10.2 galaxy, the periodogram identifies a prominent (significance w ≃ 100%) peak with a characteristic timescale tδ ≃ 91.2 Myr. This periodicity is visible by eye in the SFH of the galaxy and corresponds to a modulation consistent with cosmological accretion/merging timescales of massive (Mh ∼ 1011 M⊙) DM halos at z ≃ 6 − 10 (Furlanetto et al. 2017, Fig. 1). Furthermore, a less significant (w ≃ 3.4%) peak is found at tδ ≃ 45.6 Myr, corresponding to the time at which all massive stars (8 ≲ m⋆/M⊙ ≲ 40) have exploded as SNs. Finally, a tδ ≃ 30.4 Myr feature is also present. Although it might also be associated with SN feedback, the peak has a very low significance (w ≃ 0.0%), and we reject it as spurious.

For the log M⋆/M⊙ ≃ 8.5 galaxy, the periodogram shows a solid (w ≃ 85.3%) peak with an SN-compatible timescale (tδ ≃ 50.0 Myr). A second peak is present in the periodogram of this galaxy at tδ ≃ 7.9 Myr. This timescale is consistent with radiative feedback from massive stars. UV radiation might efficiently and quickly affect a low-mass dust-poor galaxy by photo-dissociating H2, thus temporarily halting the star formation (for an extreme example, see the Alyssum effect in Pallottini et al. 2022). In practice, however, the significance of the peak is almost null, and therefore, we cannot firmly confirm our hypothesis in this case. Higher-order fits (Eq. (1)) tend to suppress longer timescale modulations present in the SFH, for instance the significant tδ ≃ 50.0 Myr (tδ ≃ 91.2 Myr) for the log M⋆/M⊙ ≃ 8.5 (log M⋆/M⊙ ≃ 10.2) galaxy.

To complete our study, we performed the periodogram analysis on all our galaxies. Based on the value of their stellar mass at z = 7.7, we divided the galaxies into four sub-samples with increasing M⋆, that is, 6.5 < log(M⋆/M⊙) < 8, 8 < log(M⋆/M⊙) < 8.5, 8.5 < log(M⋆/M⊙) < 9.5, and log(M⋆/M⊙) > 9.5, which contain 35, 89, 100, and 11 galaxies, respectively. For each galaxy, we collected all the tδ peaks found above the noise threshold (usually, about four peaks per galaxy were found), and computed the PDF of the timescales of the sub-sample by weighing each tδ with its significance w. The results are shown in Fig. 4.

thumbnail Fig. 4.

Distributions of characteristic timescales (tδ) of the periodicity of the flickering δ. Each line is a PDF that is computed by weighting for the peak significance (w) for a sub-sample of galaxies falling in a different mass by z = 7.7. For increasing mass bins, the sub-samples contain 35, 89, 100, and 11 galaxies (typically, about four peaks per galaxy are found). The PDF was computed via a kernel density estimator, adopting the rule of thumb of Silverman (1986) for the size of the bandwidth.

The low-mass sub-sample (6.5 < log(M⋆/M⊙) < 8) shows a clear maximum at tδ ∼ 9 Myr and has a long tail that extends to ≳100 Myr. For intermediate-mass systems, the maximum of the PDF shifts at 48 and 55 Myr for the 8 < log(M⋆/M⊙) < 8.5 and 8.5 < log(M⋆/M⊙) < 9.5 sub-samples, respectively; both distributions retain their high-tδ tails, which become more pronounced. For the most massive galaxies (log(M⋆/M⊙) > 9.5), the maximum remains at about the same timescales, but the tail has grown so much stronger that the PDF is almost flat between the maximum at tδ ∼ 53 Myr and up to tδ ∼ 100 Myr.

Physically, this can be interpreted as follows. The SFR of galaxies in the early stages of growth (M⋆/M⊙ ≤ 108 M⊙) is modulated by radiative feedback effects (i.e., H2 photo-dissociation). As they grow more massive (M⋆ ∼ 109 M⊙), the timescale for the SFR stochasticity is dominated by SNs; for galaxies at the high-mass end (M⋆/M⊙ ≳ 5 × 109), SNs co-regulate the flickering along with cosmological accretion/merging, which is equally important, but acts on longer timescales.

3.3. Flickering: Implications for the UV luminosity

Shen et al. (2023) noted that σUV can be decomposed into contributions from variations produced by accretion history, delay in the feedback regulation of the star formation, and dust attenuation. However, in our analysis, we showed that the first two contributions are both encapsulated in δ, that is, the flickering in SERRA galaxies is mostly induced by feedback regulation, and DM assembly history plays a role at the high-mass end.

To discuss the effect of the flickering on the bright end of the luminosity function, it is sufficient to assume that the UV luminosity is sensitive to the instantaneous SFR,

(3)

where the constant accounts for the efficiency of photo-production depending on the stellar population (e.g., Madau & Dickinson 2014, for a review), and M0 is a normalisation constant. As noted in Furlanetto & Mirocha (2022), the UV luminosity is sensitive to the SFR in the last ∼20 Myr, which means that if the timescale for the stochastic variation is shorter, the induced UV variation should be reduced. As shown in Sect. 3.2, M⋆ ≳ 108 M⊙ galaxies indeed have tδ ≳ 50 Myr (Fig. 4). We note that assuming an instantaneous photon production (Eq. (3)) maximises the UV variation. While in principle the photo-production depends on Z⋆, SERRA galaxies quickly reach almost solar values (Gelli et al. 2020). For MUV the induced variation is therefore negligible.

Thus, considering the instantaneous UV production (Eq. (3)) and the fact that all SFR variations are encapsulated in δ (Eq. (2)), a standard deviation in the SFR of σδ ≃ 0.24 would induce an analogous s.d. in the UV magnitude of σUV ≃ 0.61. This variation is too small to explain the over-abundance of luminous galaxies seen by the JWST at z ≳ 10. As shown by Mason et al. (2023; see also Shen et al. 2023; Muñoz et al. 2023), a σUV ≃ 1.5 (≃2), that is, ≃3× higher than what we find here, is required to reconcile the models with data. Alternatively, this requirement could be directly cast in terms of σδ and compared with the results in Mirocha & Furlanetto (2023), who implied that ±1 dex scatter in the SFR is needed, that is, approximately four times the value found here.

4. Discussion

Our results show that the over-abundance of super-early luminous JWST galaxies cannot be easily explained by SFR stochasticity. It is therefore necessary to explore different scenarios.

Among the various possibilities, it has been suggested (Ferrara et al. 2023) that radiation-driven outflows, which are expected to be very common in these luminous compact objects (Fiore et al. 2023; Ziparo et al. 2023), effectively clear the dust and make the galaxies more luminous. Unfortunately, this effect is currently only coarsely modelled in SERRA and other similar simulations.

Alternatively, modifications to the ΛCDM cosmology have also been considered (Boylan-Kolchin 2023; Gong et al. 2023; Haslbauer et al. 2022; Parashari & Laha 2023). Although interesting, a more thorough exploration of the implications of a different matter power spectrum on the properties and abundance of low-mass galaxies (M⋆ ≲ 107 M⊙), which do not differ from JWST data at the moment (McCaffrey et al. 2023), is necessary to draw firm conclusions. Particular care should be taken in solving the JWST over-abundance problem by modifying the ΛCDM power spectrum because this change can induce strong tensions at lower z (Gouttenoire et al. 2023; Sabti et al. 2023).

Finally, the feedback-free starburst scenario (e.g., Dekel et al. 2023) remains an intriguing if extreme alternative. However, the implications of this scenario (globular cluster formation, merging of intermediate-mass black holes, and consequences for the reionization history) are yet to be explored.

5. Summary

We have analysed stochastic time variations δ(t) of the SFR in high-z galaxies by using the growth histories of 245 z = 7.7 galaxies with stellar mass 5 × 106 ≲ M⋆/M⊙ ≲ 5 × 1010 from the SERRA simulation suite (Pallottini et al. 2022). After fitting the average star formation history, ⟨SFR⟩, for each galaxy, the variation was quantified as δ(t) ≡ log[SFR/⟨SFR⟩]. The main results are listed below.

The variation δ(t) is independent of M⋆ and is distributed as a zero-mean Gaussian with a standard deviation σδ ≃ 0.24.

δ(t) is periodic on timescales that increase with M⋆: tδ ∼ (9, 50, 100) Myr for M⋆ ∼ (0.1, 1, 5)×109 M⊙, respectively. These modulations for low, intermediate, and high stellar mass are induced by (i) photoevaporation of molecular hydrogen, (ii) SN explosions, and (iii) cosmic accretion. Feedback (either radiative and/or mechanical) regulation is important in the whole mass range, and cosmic accretion becomes the dominant variability source for ≃5 × 109 M⊙ galaxies.

SFR variations induce analogous UV magnitude variations with a standard deviation σUV ≃ 0.61. Thisamplitude falls short by about three times (Shen et al. 2023) or about four times (Mirocha & Furlanetto 2023) to explain the over-abundance of luminous z ≳ 10 galaxies seen by the JWST. This over-abundance is instead more readily explained by models in which radiation-driven outflows efficiently clear the dust from these super-early systems (e.g., Ferrara et al. 2023).

Acknowledgments

A.F. acknowledges support from the ERC Advanced Grant INTERSTELLAR H2020/740120 (PI: Ferrara). Any dissemination of results must indicate that it reflects only the author’s view and that the Commission is not responsible for any use that may be made of the information it contains. Partial support (AF) from the Carl Friedrich von Siemens-Forschungspreis der Alexander von Humboldt-Stiftung Research Award is kindly acknowledged. We acknowledge the CINECA award under the ISCRA initiative, for the availability of high performance computing resources and support from the Class B project SERRA HP10BPUZ8F (PI: Pallottini). We gratefully acknowledge computational resources of the Center for High Performance Computing (CHPC) at SNS. A.P. would like to thank R. Poggiani for a discussion on the Lomb–Scargle periodogram of a few years ago. We acknowledge usage of the Python programming language (Van Rossum & de Boer 1991; Van Rossum & Drake 2009), Astropy (Astropy Collaboration 2013), Cython (Behnel et al. 2011), Matplotlib (Hunter 2007), Numba (Lam et al. 2015), NumPy (van der Walt et al. 2011), PYNBODY (Pontzen et al. 2013), and SciPy (Virtanen et al. 2020).

References

  1. Adams, N. J., Conselice, C. J., Ferreira, L., et al. 2023, MNRAS, 518, 4755 [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Atek, H., Shuntov, M., Furtak, L. J., et al. 2023, MNRAS, 519, 1201 [Google Scholar]
  5. Behnel, S., Bradshaw, R., Citro, C., et al. 2011, Comput. Sci. Eng., 13, 31 [Google Scholar]
  6. Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
  7. Bouché, N., Dekel, A., Genzel, R., et al. 2010, ApJ, 718, 1001 [Google Scholar]
  8. Bovino, S., Grassi, T., Capelo, P. R., Schleicher, D. R. G., & Banerjee, R. 2016, A&A, 590, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Boylan-Kolchin, M. 2023, Nat. Astron., 7, 731 [NASA ADS] [CrossRef] [Google Scholar]
  10. Branca, L., & Pallottini, A. 2023, MNRAS, 518, 5718 [Google Scholar]
  11. Castellano, M., Fontana, A., Treu, T., et al. 2022, ApJ, 938, L15 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chaves-Montero, J., & Hearin, A. 2021, MNRAS, 506, 2373 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dayal, P., Ferrara, A., Dunlop, J. S., & Pacucci, F. 2014, MNRAS, 445, 2545 [CrossRef] [Google Scholar]
  14. Decataldo, D., Pallottini, A., Ferrara, A., Vallini, L., & Gallerani, S. 2019, MNRAS, 487, 3377 [Google Scholar]
  15. Dekel, A., & Mandelker, N. 2014, MNRAS, 444, 2071 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dekel, A., Sarkar, K. C., Birnboim, Y., Mandelker, N., & Li, Z. 2023, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]
  17. De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dome, T., Tacchella, S., Fialkov, A., et al. 2023, MNRAS, submitted [arXiv:2305.07066] [Google Scholar]
  19. Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023, MNRAS, 518, 6011 [Google Scholar]
  20. Faucher-Giguère, C.-A. 2018, MNRAS, 473, 3717 [Google Scholar]
  21. Ferrara, A., Vallini, L., Pallottini, A., et al. 2019, MNRAS, 489, 1 [Google Scholar]
  22. Ferrara, A., Pallottini, A., & Dayal, P. 2023, MNRAS, 522, 3986 [NASA ADS] [CrossRef] [Google Scholar]
  23. Finkelstein, S. L., & Bagley, M. B. 2022, ApJ, 938, 25 [NASA ADS] [CrossRef] [Google Scholar]
  24. Finkelstein, S. L., Bagley, M. B., Haro, P. A., et al. 2022, ApJ, 940, L55 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fiore, F., Ferrara, A., Bischetti, M., Feruglio, C., & Travascio, A. 2023, ApJ, 943, L27 [NASA ADS] [CrossRef] [Google Scholar]
  26. Furlanetto, S. R., & Mirocha, J. 2022, MNRAS, 511, 3895 [NASA ADS] [CrossRef] [Google Scholar]
  27. Furlanetto, S. R., Mirocha, J., Mebane, R. H., & Sun, G. 2017, MNRAS, 472, 1576 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gelli, V., Salvadori, S., Ferrara, A., Pallottini, A., & Carniani, S. 2023, ApJ, submitted [arXiv:2303.13574] [Google Scholar]
  29. Gelli, V., Salvadori, S., Pallottini, A., & Ferrara, A. 2020, MNRAS, 498, 4134 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gong, Y., Yue, B., Cao, Y., & Chen, X. 2023, ApJ, 947, 28 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gouttenoire, Y., Trifinopoulos, S., Valogiannis, G., & Vanvlasselaer, M. 2023, ArXiv e-prints [arXiv:2307.01457] [Google Scholar]
  32. Grassi, T., Bovino, S., Schleicher, D. R. G., et al. 2014, MNRAS, 439, 2386 [Google Scholar]
  33. Hahn, O., & Abel, T. 2011, MNRAS, 415, 2101 [Google Scholar]
  34. Harikane, Y., Ouchi, M., Oguri, M., et al. 2023, ApJS, 265, 5 [NASA ADS] [CrossRef] [Google Scholar]
  35. Haslbauer, M., Kroupa, P., Zonoozi, A. H., & Haghi, H. 2022, ApJ, 939, L31 [NASA ADS] [CrossRef] [Google Scholar]
  36. Herrera-Camus, R., Sturm, E., Graciá-Carpio, J., et al. 2018, ApJ, 861, 95 [Google Scholar]
  37. Hirashita, H., & Ferrara, A. 2002, MNRAS, 337, 921 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  39. Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
  40. Kohandel, M., Pallottini, A., Ferrara, A., et al. 2020, MNRAS, 499, 1250 [Google Scholar]
  41. Krumholz, M. R., Dekel, A., & McKee, C. F. 2012, ApJ, 745, 69 [Google Scholar]
  42. Lam, S. K., Pitrou, A., & Seibert, S. 2015, in Proc. Second Workshop on the LLVM Compiler Infrastructure in HPC, 1 [Google Scholar]
  43. Leja, J., Carnall, A. C., Johnson, B. D., Conroy, C., & Speagle, J. S. 2019, ApJ, 876, 3 [Google Scholar]
  44. Liu, B., & Bromm, V. 2022, ApJ, 937, L30 [NASA ADS] [CrossRef] [Google Scholar]
  45. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  46. Looser, T. J., D’Eugenio, F., Maiolino, R., et al. 2023, ArXiv e-prints [arXiv:2302.14155] [Google Scholar]
  47. Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
  48. Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
  49. Markov, V., Gallerani, S., Pallottini, A., et al. 2023, ArXiv e-prints [arXiv:2304.11178] [Google Scholar]
  50. Mason, C. A., Trenti, M., & Treu, T. 2023, MNRAS, 521, 497 [NASA ADS] [CrossRef] [Google Scholar]
  51. McCaffrey, J., Hardin, S., Wise, J., & Regan, J. 2023, Open J. Astrophys., submitted [arXiv:2304.13755] [Google Scholar]
  52. Mirocha, J., & Furlanetto, S. R. 2023, MNRAS, 519, 843 [Google Scholar]
  53. Muñoz, J. B., Mirocha, J., Furlanetto, S., & Sabti, N. 2023, MNRAS, 526, L47 [CrossRef] [Google Scholar]
  54. Naidu, R. P., Oesch, P. A., van Dokkum, P., et al. 2022, ApJ, 940, L14 [NASA ADS] [CrossRef] [Google Scholar]
  55. Orr, M. E., Hayward, C. C., & Hopkins, P. F. 2019, MNRAS, 486, 4724 [NASA ADS] [CrossRef] [Google Scholar]
  56. Padmanabhan, H., & Loeb, A. 2023, ApJ, 953, L4 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pallottini, A., Ferrara, A., Gallerani, S., Salvadori, S., & D’Odorico, V. 2014, MNRAS, 440, 2498 [NASA ADS] [CrossRef] [Google Scholar]
  58. Pallottini, A., Ferrara, A., Bovino, S., et al. 2017a, MNRAS, 471, 4128 [NASA ADS] [CrossRef] [Google Scholar]
  59. Pallottini, A., Ferrara, A., Gallerani, S., et al. 2017b, MNRAS, 465, 2540 [CrossRef] [Google Scholar]
  60. Pallottini, A., Ferrara, A., Decataldo, D., et al. 2019, MNRAS, 487, 1689 [Google Scholar]
  61. Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
  62. Parashari, P., & Laha, R. 2023, MNRAS, in press https://doi.org/10.1093/mnrasl/slad107 [Google Scholar]
  63. Planck Collaboration XVI 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Pontzen, A., Roškar, R., Stinson, G. S., & Woods, R. 2013, Astrophysics Source Code Library [record ascl:1305.002] [Google Scholar]
  65. Popesso, P., Concas, A., Cresci, G., et al. 2023, MNRAS, 519, 1526 [Google Scholar]
  66. Qin, Y., Balu, S., & Wyithe, J. S. B. 2023, MNRAS, in press https://doi.org/10.1093/mnras/stad2448 [Google Scholar]
  67. Roberts-Borsani, G., Morishita, T., Treu, T., et al. 2022, ApJ, 938, L13 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rosdahl, J., & Teyssier, R. 2015, MNRAS, 449, 4380 [Google Scholar]
  69. Rosdahl, J., Blaizot, J., Aubert, D., Stranex, T., & Teyssier, R. 2013, MNRAS, 436, 2188 [Google Scholar]
  70. Sabti, N., Muñoz, J. B., & Kamionkowski, M. 2023, ArXiv e-prints [arXiv:2305.07049] [Google Scholar]
  71. Santini, P., Fontana, A., Castellano, M., et al. 2023, ApJ, 942, L27 [NASA ADS] [CrossRef] [Google Scholar]
  72. Scargle, J. D. 1998, ApJ, 504, 405 [Google Scholar]
  73. Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
  74. Shen, X., Vogelsberger, M., Boylan-Kolchin, M., Tacchella, S., & Kannan, R. 2023, MNRAS, in press, https://doi.org/10.1093/mnras/stad2508 [Google Scholar]
  75. Silverman, B. W. 1986, Density Estimation for Statistics and Data Analysis (London: Chapman and Hall) [Google Scholar]
  76. Sun, G., Faucher-Giguère, C.-A., Hayward, C. C., & Shen, X. 2023, MNRAS, submitted [arXiv:2305.02713] [Google Scholar]
  77. Tacchella, S., Bose, S., Conroy, C., Eisenstein, D. J., & Johnson, B. D. 2018, ApJ, 868, 92 [NASA ADS] [CrossRef] [Google Scholar]
  78. Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
  79. Topping, M. W., Stark, D. P., Endsley, R., et al. 2022, MNRAS, 516, 975 [NASA ADS] [CrossRef] [Google Scholar]
  80. Treu, T., Roberts-Borsani, G., Bradac, M., et al. 2022, ApJ, 935, 110 [NASA ADS] [CrossRef] [Google Scholar]
  81. VanderPlas, J. T. 2018, ApJS, 236, 16 [Google Scholar]
  82. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  83. Van Rossum, G., & de Boer, J. 1991, CWI Quart., 4, 283 [Google Scholar]
  84. Van Rossum, G., & Drake, F. L. 2009, Python 3 Reference Manual (Scotts Valley: CreateSpace) [Google Scholar]
  85. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  86. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 563, 842 [NASA ADS] [CrossRef] [Google Scholar]
  87. Wise, J. H., Turk, M. J., Norman, M. L., & Abel, T. 2012, ApJ, 745, 50 [NASA ADS] [CrossRef] [Google Scholar]
  88. Ziparo, F., Ferrara, A., Sommovigo, L., & Kohandel, M. 2023, MNRAS, 520, 2445 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Example of SFH fitting and variability definitions for high-mass (log M⋆/M⊙ ≃ 10.2, left panel) and low-mass galaxies (log M⋆/M⊙ ≃ 8.5, right panel) in the SERRA simulation at z = 7.7. For each galaxy, we plot the star formation (SFR) in the upper panel as a function of cosmic time (t) and its fit (⟨SFR⟩, Eq. (1)) as a continuous and dashed line, respectively. We report the SFR starting from the time when the galaxy has a stellar mass higher than 106.5 M⊙, the SFR is averaged in temporal bins of 2 Myr, and on the upper axis, we plot the redshift (z). In the lower left panel, we plot the variation (δ, Eq. (2)) as a function of time, add a constant line for no variation (δ = 0) to guide the eye, and report the p-value from the Kolmogorov–Smirnov test (pKS) for the fit. In the lower right inset, we show the PDF of the variation, along with its Gaussian fit and standard deviation (σδ).
In the text
thumbnail Fig. 2.

Distribution of the SFR variation (δ) as a function of stellar mass (M⋆). The colour bar indicates the PDF in the δ − M⋆ plane. The dashed and solid lines report the mean and variance of δ as a function of M⋆. The average standard deviation is indicated as an inset. Horizontal and vertical insets are the 1D PDFs, normalised to give the probability in each bin.
In the text
thumbnail Fig. 3.

Example of a periodicity analysis of the SFR variability for the same high-mass (upper panel) and low-mass galaxies (lower) as presented in Fig. 1. For each galaxy, we plot the Lomb (1976)–Scargle (1998) periodogram of the variability (P(tδ)) as a function of the frequency (). Each peak recovered above the selected noise threshold (dotted line) is marked in the plot with a dashed line, and its characteristic time (tδ) and significance (w) are given. As a reference, we plot in the inset the evolution of δ vs. cosmic time (t) shifted by t0, that is, the time at which the stellar mass becomes > 106.5 M⊙.
In the text
thumbnail Fig. 4.

Distributions of characteristic timescales (tδ) of the periodicity of the flickering δ. Each line is a PDF that is computed by weighting for the peak significance (w) for a sub-sample of galaxies falling in a different mass by z = 7.7. For increasing mass bins, the sub-samples contain 35, 89, 100, and 11 galaxies (typically, about four peaks per galaxy are found). The PDF was computed via a kernel density estimator, adopting the rule of thumb of Silverman (1986) for the size of the bandwidth.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.