| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A172 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346937 | |
| Published online | 22 September 2023 | |
Dust giant: Extended and clumpy star-formation in a massive dusty galaxy at z = 1.38
1
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700 AV
Groningen, The Netherlands
e-mail: vasily.kokorev.astro@gmail.com
2
Cosmic Dawn Center (DAWN),
Jagtvej 128,
2200
Copenhagen N, Denmark
3
DTU-Space, Technical University of Denmark,
Elektrovej 327,
2800 Kgs.
Lyngby, Denmark
4
Université Paris-Saclay, Université Paris-Cité, CEA, CNRS, AIM,
91191,
Gif-sur-Yvette, France
5
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching bei Munchen, Germany
6
Max-Planck-Institut fur Extraterrestrische Physik (MPE),
Giessenbachstr. 1,
85748
Garching, Germany
7
International Space Science Institute (ISSI),
Hallerstrasse 6,
3012
Bern, Switzerland
8
Astronomy Centre, Department of Physics and Astronomy, University of Sussex,
Brighton
BN1 9QH, UK
9
Department of Astronomy, University of Massachusetts,
Amherst, MA
01003, USA
Received:
18
May
2023
Accepted:
13
July
2023
We present NOEMA CO (2–1) line and ALMA 870 µm continuum observations of a main-sequence galaxy at z = 1.38. The galaxy was initially deemed a “gas giant” based on the gas mass derived from sub-mm continuum (log(Mgas/M⊙) = 11.20 ± 0.20), however, the gas mass derived from CO (2−1) luminosity brings the gas mass value down to a level that is consistent with typical values for star-forming galaxies at that redshift (log(Mgas/M⊙) = 10.84 ± 0.03). Meanwhile, the dust-to-stellar mass ratio remains elevated above the scaling relations by a factor of 5. In this work, we explore the potential physical picture and consider an underestimated stellar mass and optically thick dust as possible explanations. Based on the updated gas-to-stellar mass ratio, we can rule out the former; while the latter may indeed contribute to the overestimation of the dust mass, it is not sufficient enough to explain the observed physical picture overall. Instead, other plausible explanations include enhanced HI reservoirs, an unusually high metallicity, or the presence of an optically dark, dusty contaminant. Using the ALMA data at 870 µm coupled with HST/ACS imaging, we find an extended morphology in dust continuum and clumpy star-formation in rest-frame UV in this galaxy. In addition, a tentative ~10 kpc dusty arm is found to be bridging the galaxy center and a clump in F814W image. The galaxy shows levels of dust obscuration similar to the so-called HST-dark galaxies at higher redshifts, thus falling into the optically faint and dark JWST color-color selection at z > 2. It is therefore possible that our object may stand as a low-z analog of the HST-dark populations. This galaxy serves as a caveat to the gas masses based on the continuum alone, with a larger sample required to unveil the full picture.
Key words: galaxies: evolution / galaxies: ISM
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The interaction between the interstellar medium (ISM), which consists mostly of gas and dust, and the radiation fields produced by stellar activity is thought to be the main mechanism driving galaxy evolution. Within the contemporary picture of galaxy formation and evolution, the star formation rate (SFR), molecular gas masses (Mgas), dust mass (Mdust), gas-to-stellar-mass ratio (ƒgas ≡ Mgas/M*) and dust-to-stellar-mass ratio (ƒdust ≡ Mdust/M*) play a critical role in enabling us to interpret the mode and onset of star formation (Magdis et al. 2012; Tan et al. 2014; Santini et al. 2014), as well as the assembly of stellar mass, the final quenching of galaxies, and their structure and dynamics (Magdis et al. 2021; Whitaker et al. 2021). In particular, the amount of gas with respect to ongoing star formation (star formation efficiency, SFE ≡ SFR/Mgas) and the depletion timescale (τdepl ≡ 1/SFE) allow us to clearly distinguish the star-formation modes between main-sequence (MS) and starburst (SB) galaxies (e.g., see Daddi et al. 2007; Noeske et al. 2007; Elbaz et al. 2010; Sargent et al. 2014; Whitaker et al. 2014). However, it is still unclear whether it is enhanced SFE, galaxy mergers, or increased molecular gas reservoirs that are behind the manifestation of galaxies in the SB regime. To this end, the evolution of ƒdust and ƒgas across the cosmic time has been extensively studied and constrained both observationally (see Magdis et al. 2012; Santini et al. 2014; Sargent et al. 2014; Genzel et al. 2015; Tacconi et al. 2018; Liu et al. 2019; Donevski et al. 2020; Magnelli et al. 2020; Kokorev et al. 2021), as well as theoretically (e.g., Tan et al. 2014; Lagos et al. 2015; Lacey et al. 2016). The important takeaway point of these studies is that both ƒdust and ƒgas increase slowly from z = 0 to their peak at z ~ 2–3, mirroring the evolution of star formation rate density (SFRD; Madau & Dickinson 2014).
The other key parameter in studying the evolution of galaxies is the metallicity (Z). Metals are introduced into the ISM by either stellar winds and/or via the injection by supernovae (Dwek & Scalo 1980; Kobayashi et al. 2020). In this context, the gas-to-dust-mass ratio (δGDR) connects the amount of metals locked in the gas phase with the metals present as dust, thus acting as a powerful tool in elucidating the evolutionary stage of a galaxy. Observations of both atomic (HI) and molecular hydrogen (H2) have revealed that δGDR decreases as a function of metallicity, at least for the local galaxies, (e.g., see Rémy-Ruyer et al. 2014); however, the exact evolutionary scenarios are still uncertain.
One critical aspect of understanding both the metallicity and modes of star formation is related to the way we derive Mgas. The most common techniques involve utilising the carbon monoxide (CO) or neutral carbon [CI] line luminosities (Papadopoulos et al. 2004; Bolatto et al. 2013; Carilli & Walter 2013; Valentino et al. 2018) or the dust continuum (e.g., Magdis et al. 2012; Scoville et al. 2016). In relation to the dust method, in particular, the steadily growing number of galaxy populations with well-sampled IR properties has produced a series of unexpected results. One such discovery is an unusually large ƒdust (e.g., Tan et al. 2014; Kokorev et al. 2021), in excess of what would be possible to produce involving return fractions from evolved stellar populations (Béthermin et al. 2015; Michałowski 2015; Dayal et al. 2022). Far IR (FIR) galaxy spectral energy distributions (SEDs) are generally modeled under the assumption of optically thin FIR emission. However, in cases where FIR dust emission is truly optically thick (e.g., the case of Arp220; Scoville et al. 2017b), using an approximation for optically thin dust results in colder dust temperatures (Tdust) and, therefore, overestimated Mdust and Mgas values (Hodge et al. 2016; Simpson et al. 2017; Scoville et al. 2017b; Cortzen et al. 2020; Jin et al. 2022). Alternatively, some use a constant mass-weighted temperature instead (Tdust ~ 25 K), as suggested by Scoville et al. (2014). Recent results by Harrington et al. (2021) have revealed that there is little difference between mass and luminosity weighted temperatures at least at 1 mm, suggesting that 25 K might be insufficient. Given there is an adequate mid-to-far-IR coverage, it is possible to model galaxies with a more complex, optically thick assumption. However discriminating between the optically thick and thin solutions, when the data are limited, is often not possible due to degeneracies involved in the fitting. As such, to robustly determine the Mgas, dust continuum alone is often insufficient, and independent proxies are thus required to break these degeneracies.
In our homogeneous analysis of the “super-deblended” catalog (Kokorev et al. 2021) in the COSMOS field (Laigle et al. 2016; Jin et al. 2018), we have recovered scaling relations for FIR properties from thousands of galaxies. Among those we have identified some outliers which appear to have significantly elevated ƒdust and ƒgas values, compared to the typical scaling relations at z < 3 and log10(M*/M⊙) ~ 10.7. Alternative gas mass tracers are thus necessary to confirm the extreme nature of these objects. In this paper we report observations of the CO (2−1) transition line with Northern Extended Millimeter Array (NOEMA), for one such gas giant candidate, presented in Kokorev et al. (2021). Throughout this work we assume a flat ΛCDM cosmology with Ωm,0 = 0.3, ΩΛ,0 = 0.7, and H0 = 70 km s−1 Mpc−1, as well as a Chabrier (2003) initial mass function (IMF) within 0.1–100 M⊙.
2 Selection, data, and reduction
2.1 Gas giants
The sample of gas giants was initially identified as a number of extreme outliers from the average ƒdust and ƒgas evolutionary trends. They typically exhibit log(ƒgas) > 0.5, namely, their gas mass reservoir takes ~75% of total baryonic matter budget. The individual best-fit STARDUST (Kokorev et al. 2021) SEDs of these objects have been examined along with the cut-out images in order to rule out either bad or insufficient optical photometry, resulting in an incorrect M* estimate, poor coverage of the FIR peak, or blending issues that could result in erroneously high Mgas estimates. These sources are in stark contrast when compared to the expected evolutionary tracks, with the “gas giant sample” being elevated by at least a factor of 3× in both ƒdust and ƒgas compared to median empirical trends, and appearing as ~5σ outliers to the parent sample. When contrasted with simulations, the results are even more puzzling, with ƒdust displaying a deviation of a factor 5× and a staggering factor of 10× in ƒgas, when parameterized to the same SFR/SFRMS, M*, and z. The possible explanations for the very high Mdust (and, subsequently, the Mgas estimates) could be optically thick FIR emission, poorly deblended FIR photometry, or simply a significantly different gas-to-dust ratio (δGDR). All three of these hypotheses have been thoroughly tested via simulations and alternative SED fitting techniques, failing, however, to demote a significant fraction of these gas giants. We refer to Kokorev et al. (2021) for a more detailed description of the sample.
In an attempt to explain the unusually elevated ƒdust and ƒgas values, we selected a robust subsample of gas giant candidates to follow up on. These fulfill the following criteria: (1) Secure FIR coverage with ≥3 continuum detections above a 3σ level, and at least a single rest-frame λ > 150 µm detection for a reasonable Mdust and Mgas estimates (see e.g., Berta et al. 2016; Kokorev et al. 2021), (2) the galaxy needs to be isolated to facilitate a secure M* estimate and minimize the possibility of blending in the FIR. From this subsample, we selected a single object as the focus of a pilot study into this potential population. We computed the metallicity for our object by using the M* and SFR relation from Mannucci et al. (2010); after converting it to the PP04 scaling (Kewley & Ellison 2008), this gives as a value of 12+log(O/H) = 8.67 ± 0.15. We double checked that result by using the metallicity relation from Zahid et al. (2014) for z ~ 1.5 galaxies and obtained a similar value of 12+log(O/H) = 8.68 ± 0.14. To calculate the gas-to-dust ratio, we used the δGDR-metallicity relation from Magdis et al. (2012) and derived δGDR = 95, which then leads to Mgas = δGDR × Mdust = 1011.49±0.20 M⊙. Our galaxy exhibits what can be considered “typical” values as MS galaxies at log(M*/M⊙) ~ 10.9. Also, there does not appear to be a strong starburst with SFR/SFRMS ~ 2.5, making the picture even more unique and puzzling.
2.2 NOEMA observations
To confirm or rule out the high Mgas, we used IRAM NOEMA to conduct observations of the CO (2−1) line transition a COSMOS galaxy ID: 10100707 (Jin et al. 2018), with a photometric redshift of zphot = 1.35 from the COSMOS2015 catalog (Laigle et al. 2016). The NOEMA observations took place in April 2022, for a total of 8.6 h, using the 12D configuration (Program W21CO, PIs: V. Kokorev, C. Gómez-Guijarro). In our galaxy the CO(J = 2−1) line (νrest = 230.5 GHz) is redshifted to vobs = 98 GHz at zphot = 1.35. The pointing was centered at the coordinates included in the “super-deblended” parent catalog (Jin et al. 2018). While the D configuration has a generally lower angular resolution (~3–6″), our original proposal was focused on the line detection and thus was the most optimal balance between S/N and requested time. The source was observed with three tracks, reaching rms sensitivities of 0.13 mJy per 500 km s−1.
The separate tracks were calibrated and recombined into a single uυ table, using the GILDAS software package CLIC. No continuum was detected in the map generated by collapsing uυ data of all channels, thus we derived an upper limit on the underlying 98 GHz (3 mm) continuum. This further assists in deriving robust FIR properties from SED fitting. To produce the final 1D spectrum for the CO(2−1) line, we used the CRAB.TOOLKIT.PDBI1, which is a wrapper around the MAPPING module in GILDAS. Finally, we fit a point source model in the uυ space at the position of peak flux in order to measure the flux density of the line. The line profile presented in Fig. 1 appears to be double peaked. Due to this, in addition to the single Gaussian peak fit, we also modeled the line profile with two normal distributions. We find the double Gaussian to be marginally better (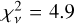 ), compared to a single profile fit (
), compared to a single profile fit (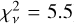 ). In our subsequent analysis, we adopted the results from the double Gaussian fit. We display our best-fit double profile fit on top of the 1D spectrum in Fig. 1.
). In our subsequent analysis, we adopted the results from the double Gaussian fit. We display our best-fit double profile fit on top of the 1D spectrum in Fig. 1.
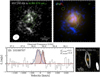 |
Fig. 1 Gas giant candidate from our original NOEMA proposal. The galaxy was confirmed at zspec = 1.38. Top Left: 5″.0 HST F814W cutout of our source with ALMA 870 µm 2, 3, 5, and 8σ levels shown in green. In the bottom left we show the size of the ALMA beam. Top right: RGB composite with blue: HST/F814W, green: UVISTA/H, and red: UVISTA/KS. Bottom left: extracted spectrum of the CO (2−1) line for our galaxy – ID 10100707. The double Gaussian fit to the spectrum is shown in blue and red, while the sum of the two is represented by a dashed black line. Shaded maroon region shows the channels used to extract the line flux. Bottom right: 20″.0 RGB cutout of our source. We additionally show the 2, 3, and 5σ contours of the CO(2−1) line. The solid white ellipse displays the NOEMA beam size. |
2.3 ALMA data
The galaxy has been observed with ALMA band 7 at 341 GHz (870 µm) as a part of the program 2015.1.00137.S (PI: N. Scoville). The data for our galaxy were taken in March 2016. Following the method in Jin et al. (2019, 2022), we reduced and calibrated the raw data using CASA pipeline. The calibrated data were exported into uvfits format to generate uυ tables of the IRAM GILDAS, after which we perform further analysis in the uυ space (visibility). The continuum map of the galaxy was imaged by combining uυ visibilities of all spectral windows using uv_aveгage and clean procedures in GILDAS/Mapping. The clean continuum image has an rms of 114.3 µJy and a peak flux of 1.096 mJy. The synthesized beam is 0.65″ × 0.54″ with a position angle of −65°.
As the contours show in Fig. 1, the ALMA 870 µm image is clearly resolved, as evidenced by the larger size than the synthesized beam. Therefore, we further fit the dust continuum with an elliptical Gaussian model in uυ space using GILDAS uv_fit, which gives a total flux of 1.81 ± 0.26 mJy and a size of (0.65 ± 0.11)″ × (0.32 ± 0.10)″ (PA= −90°). The total flux is higher than the peak flux density, indicating that the source is spatially resolved.
We find that the total ALMA 870 µm flux is a factor of 2.3 lower compared to the deblended SCUBA2 850 µm flux (S850 = 4.16 ± 1.24 mJy). In order to capture the total ALMA flux, we also adopted an aperture of 2″.5 × 2″.0 with the same PA as the Gaussian model, which results in a maximum flux of 2.05 ± 0.31 mJy, still lower than the SCUBA2 flux by a factor of ~2. This flux discrepancy could be caused by ALMA over-resolving the galaxy, however flux variations of the calibrator can produce a similar effect. We examined the flux calibrator (J1008+0621) in ALMA calibrator archive and found its flux adopted in Cycle 3 is abnormally higher than that in both Cycle 2 and Cycle 4 and thereafter. It is very likely that adopted flux was overestimated for the calibrator, which thus underestimates the continuum of the target. Therefore, we assume that the calibrator flux should instead be an average between 2015 and 2017 (Cycle 2–Cycle 4). This in return boosts the ALMA 870 µm continuum by a factor of 1.27 to 2.6 ± 0.6 mJy, which is now consistent with the SCUBA2 measurement within one standard deviation. We adopt this ALMA 870 µm flux for the following analysis.
 |
Fig. 2 Best-fit SED and cutouts for our source. Left: multi-component template STARDUST spectrum (grey line and shaded areas), the observed photometry (red squares), including the upper limits (red arrows) are also displayed. Radio measurements from VLA at 1.4 (Schinnerer et al. 2010) and 3 GHz (Smolčić et al. 2017) are overlaid in blue. The SED is separated into three components – stellar emission (blue), AGN emission (green), dust (red). Right: optical-NIR-FIR cutouts of our galaxy, ranging from 5″.0 in the optical-MIR range to 50″.0 in FIR. |
3 Results
We present the resultant 1D spectrum in the bottom panel of Fig. 1, along with the RGB image which was created by combining the HST/ACS F814W, UltraVista DR2 (UVISTA; McCracken et al. 2012) H and Ks filters. For our object we compute the integrated CO (2−1) line flux by taking the product of the average flux density in the appropriate channels, maximizing the S/N and the velocity in these channels (e.g., see Daddi et al. 2015). Generally, the line flux estimates are performed by modeling the emission with a Gaussian profile, however, we compared our non-parametric approach to the Gaussian fit and find results to be consistent.
While it quickly becomes uncertain for high ionization states of CO, the conversion factor between CO J=2→1 and CO J = 1→0 is small and very well constrained, it is also applicable for normal BzK galaxies on the MS, and presumably even more extreme objects which we describe in this work (Daddi et al. 2015). We therefore convert the 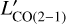 to
to 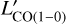 by assuming a standard CO SLED with the conversion factor
by assuming a standard CO SLED with the conversion factor 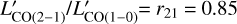 (Bothwell et al. 2013).
(Bothwell et al. 2013).
3.1 Revised gas mass
The best-fit SED, along with the cutouts for the galaxy are shown in Fig. 2. This galaxy lies on the main sequence of star formation, as parametrized in Schreiber et al. (2015) with SFR/SFRMS<5. Therefore, to convert the final value of 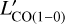 to
to 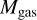 we assume αCO = 4.0 (Bolatto et al. 2013). In Table 1 we present the final results from our CO J=2→1 observations, alongside other optical and FIR properties computed with STARDUST in our previous work.
we assume αCO = 4.0 (Bolatto et al. 2013). In Table 1 we present the final results from our CO J=2→1 observations, alongside other optical and FIR properties computed with STARDUST in our previous work.
This gas giant was initially identified due to its elevated ƒdust rather than ƒgas, with the former being robustly computed from the Herschel Space Observatory (Herschel) and SCUBA2 detections, which securely cover the Rayleigh-Jeans (RJ) tail (>250 µm, rest-frame). Using the additional constraint on the upper limit derived from the underlying 3 mm continuum, and the secure zspec, we re-fit our object to ensure that the previously derived properties are robust. We find that all FIR parameters remain unchanged from the ones presented in Kokorev et al. (2021), apart from the Mdust which has fallen by 0.3 dex, from log(Mdust/M⊙) = 9.54 ± 0.10 to log(Mdust/M⊙) = 9.25 ± 0.21. As such we also update the previous estimate of the sub-mm continuum derived Mgas from log(Mgas/M⊙) = 11.49 ± 0.20 to log(Mgas/M⊙) = 11.20 ± 0.20. The results from the revised SED fitting are, however, still insufficient to bring our galaxy on the ƒdust and ƒgas evolutionary tracks.
In a stark contrast to the updated Mgas, which we computed from re-fitting the FIR data, the CO derived mass is found to be lower by 0.4 dex. We display the updated physical parameters with respect to the ƒgas vs cosmic age and distance to the main sequence (SFR/SFRMS) versus the τ relations of our source in Fig. 3, additionally contrasting it to the updated SED fitting predictions of the Mgas. The new CO-based Mgas value has resulted in a decrease of both ƒgas and τ, thus placing our object within the range of values expected from observational results (Scoville et al. 2017a; Tacconi et al. 2018; Liu et al. 2019; Magnelli et al. 2020; Kokorev et al. 2021), as well as the simulations (Laigle et al. 2019). As a result our new observations now can rule out this object as a gas giant, along with the plausible physical scenarios discussed in Kokorev et al. (2021).
The elevated ƒdust still remains in disagreement with the existing literature trends, and now, in light of our CO(2−1) observations, creates even more tension with the updated Mgas estimate. For example, as displayed in Fig. 4, the re-computed δGDR is a factor of ~2.5× lower compared to our previous prediction. We will discuss the potential reasons for this newfound tension in the next section.
Description of the source.
 |
Fig. 3 Evolution of ISM properties. Left: evolution of ƒgas as a function of z/cosmic age. Values of Mgas derived from Mdust, and CO J = 2→1 are shown as red and blue diamonds, respectively. Downward arrows denote upper limits. Solid colored lines correspond to empirical evolutionary trends derived in Scoville et al. (2017a), Tacconi et al. (2018), Liu et al. (2019), Magnelli et al. (2020). The dashed purple line shows the fit to the COSMOS Super Deblended catalog data, as described in Kokorev et al. (2021), with shaded purple region denoting the 16th and 84th percentile confidence intervals. Both the data and the derived relations have been re-scaled to ∆MS = 1 and M* = 5 × 1010 M⊙. White diamonds show median positions of the Horizon AGN star-forming galaxies at that redshift (Laigle et al. 2019), normalised in the same way as our data. Right: change in the distance to the main-sequence as a function of depletion time (τ). Labels and lines are the same as on the first panel. |
3.2 Morphology
Even though it is still in agreement within the uncertainty, the value of the deblended SCUBA2 850 µm flux (S850 = 4.16 ± 1.24 mJy) is a factor of 1.6 higher, as compared to the total ALMA 870 µm flux (2.6 ± 0.6 mJy). However, we argue that the high SCUBA2 flux is not due to blending, because this galaxy is the only source visible in ALMA primary beam (20″.0). The SCUBA2 beam is 15″.0, and, thus, it is not contaminated by a dusty neighbor. The SCUBA2 photometry itself is measured appropriately using the Ks prior position, with the uncertainty calibrated using Monte Carlo simulations (Jin et al. 2018). As we have already discussed in Sect. 2, the reasonable explanations behind the flux discrepancy are either due to ALMA over-resolving the galaxy, uncertain flux calibration, or (more likely) a combination of the two. In detail, the ALMA max recovery scale of this pointing is only 4.7″, the emission from larger scale would be largely lost. This resolved nature is again confirmed by the extended morphology as present in both NIR and ALMA images. The flux loss in ALMA also hints that the dust emission is potentially more extended out to >1″. 2 (~10 kpc), which is consistent with the sizes reported in Valentino et al. (2020) for a sample at 〈z〉 = 1.2. Given the linear scaling of Mdust with flux in the RJ tail, we find that ALMA continuum may end up resolving out ~40% of the total Mdust reservoir.
In Fig. 1, we show the ALMA 870 µm together the RGB composite consisting of the F814W, UVISTA-H, and UVISTA-Ks bands. We find that while our galaxy is not fully detected in F814W it appears to display a clumpy morphology. The emission in F814W appears to trace the UV-bright clumps with the rest of the galaxy being dust obscured. In this scenario, the H and K band emissions could just trace the central region of the galaxy, with the stellar distribution potentially extending beyond that. Such an extended morphology would align with a possible over-resolved dust emission by ALMA and an underestimate of the stellar mass. A similar target has been recently reported in the JADES GTO data release (#1180 PI: D.Eisenstein, #1210 PI: N. Luetzgendorf; Eisenstein et al. 2023), where the authors report a detection of a grand design spiral at z ~ 2. The JADES spiral is marginally detected in HST/ACS F814W and F850LP filters, while being brought into full view with NIRCam, extending beyond 5″. 0, consistent with the galaxy presented in our paper.
In order to estimate the optical size of the galaxy, we fit the UVISTA/Ks band image with IMFIT (Erwin 2015), using a Sérsic (1963) profile. In addition, we verified our result by computing the band reff from the mass-size relation presented in van der Wel et al. (2014). Both methods return a consistent result of reff = 0″.6 ± 0″.1. We also compute the ALMA size by converting the elliptical axes measured by GILDAS into reff = 0″.23 ± 0″ 06. At z = 1.38, we get a final size of 5.1 ± 0.8 kpc in KS band, and 1.9 ± 0.4 kpc in ALMA. However, while the peak of the ALMA emission coincides with the apparent center of the galaxy, we also report the tentative (2σ level) and large (~ 10 kpc) dust arm. This dusty structure appears to be connected to the secondary clump seen in the south part of the F814W image, likely belonging to the same galaxy. It is likely that the dusty arm is associated with the smaller peak in the CO (2−1) profile, however, subsequent high-resolution observations would be required to verify this.
 |
Fig. 4 Gas-to-dust ratio and CO emission. Left: gas-to-dust ratio as a function of metallicity for the galactic CO to molecular gas conversion from Rémy-Ruyer et al. (2014, RR14). The dashed line represents the reference scaling of the δGDR with metallicity and the dotted and dash-dotted lines represent the best power-law and best broken power-law fits to the data presented in RR14. The dashed blue line with the shaded envelope show the δGDR – metallicity relation from Magdis et al. (2012) which we used to derive the original Mgas. The δGDR measurement from CO and dust continuum is shown as a red diamond. Right: CO(2−1) line luminosity to Mdust ratio and δGDR as a function of Mdust. For the δGDR, we assume αCO = 4.0 for all galaxies. We also show the sample of MS (blue) and SB (purple) galaxies from Valentino et al. (2020). The BzK galaxies from Daddi et al. (2015) are shown as black squares. Our galaxy is shown as a red diamond. A typical uncertainty on the data is shown in the bottom left corner. |
3.3 Dynamical mass
Using the fact that the CO J = 2→ 1 line is detected in multiple channels, we also compute the dynamical mass (Mdyn) for our object. To do that we consider both the UVISTA/Ks and ALMA sizes measured in the previous section. We use the M(r < reff) relation from from Daddi et al. (2010) and estimate an inclination angle for our galaxy to be i = (60 ± 4)° from the axis ratio measured on the ALMA 870 µm image. This is also consistent with the statistical average of (57 ± 21)° (Coogan et al. 2018). The total Mdyn is then given as the mass contained within the full diameter of the galaxy −2 × M(r < reff). We assume the contribution of dark matter to be ~10%, as there is evidence that dark matter fraction at this redshift is negligible within the reff (Daddi et al. 2010; Wuyts et al. 2016; Genzel et al. 2017).
We find dynamical masses of log10(Mdyn/M⊙) = 11.32 ± 0.10 and log10 (Mdyn/M⊙) = 10.87 ± 0.10, using the optical and ALMA reff, respectively. Given our previous discussion, it is very likely that the galaxy is over-resolved at 870 µm, and thus its size and Mdyn would be underestimated, which is in line with Mdyn,ALMA being lower than the value of M*. We therefore based our Mdyn on the Ks size of the galaxy. While it is rare for the sub-mm size to extend as far as the star-forming stellar disk, probed by the Ks band (e.g., see Puglisi et al. 2021; Gómez-Guijarro et al. 2022), this Mdyn estimate can serve as a robust upper limit. The Mdyn are listed in Table 1 without the dark matter correction.
4 Discussion
4.1 Stellar mass underestimate
One of the potential reasons behind the gas giant population discussed in Kokorev et al. (2021) is an underestimate in M*. In return leading to erroneously larger dust- or gas-to-stellar mass ratios. The optical-NIR data that was used to derive the M* relies mostly on the ground-based observations. This can result in potential flux losses, as a result of seeing limited point spread function (PSF). The Laigle et al. (2016) catalog used in our work utilizes apertures to measure flux density, and might not adequately model the flux losses due to the wings of the PSF (e.g., see Weaver et al. 2022). The morphology of our object is also quite extended in rest-frame UV traced by the F814W filter, while the stellar mass is primarily derived from more centrally concentrated in H and K bands. It is therefore possible that some stellar mass in our galaxy extends beyond the central region.
Despite the fact that when using the CO derived Mgas to compute Mgas/M*, our galaxy is in line with the literature predictions for a MS galaxy at that redshift (Scoville et al. 2017a; Tacconi et al. 2018; Liu et al. 2019; Magnelli et al. 2020; Kokorev et al. 2021), as well as an extrapolation of Horizon AGN simulations results to higher-z (Laigle et al. 2019). Therefore, we have little reason to believe that an underestimation of M* would be responsible for the elevated Mdust/M*.
4.2 Optically thick dust
Another mechanism that could be responsible for the elevated Mdust/M* found in our galaxy could be the presence of optically thick FIR emission. Indeed in Kokorev et al. (2021) we report that ID: 10100707 can be fit with a generalized form of the modified blackbody (MBB) function (e.g., see Casey et al. 2012). In that case, we find the effective wavelength (λeff) at which the optical depth τ becomes unity, to be λeff ~ 600 µm, deep in the RJ tail. In this case, the intrinsic SED is shifted blueward, reducing the derived Mdust by a factor of a few. The unusually high dust-to-stellar mass ratio and δGDR when using the CO derived Mgas can therefore be the result of the optical depth effects. As we reported in Kokorev et al. (2021), however, adopting an optically thick dust emission model reduces the Mdust by 0.25 dex, compared to the 0.4 dex correction required, which is insufficient to bring our galaxy back up to the expected dust-to-stellar mass ratio relation. We show this in Fig. 3.
4.3 Dust and metallicity
In Fig. 4, we examine the location of our source on the δGDR vs. Z relation. We also overplot the δGDR-Z relation from Magdis et al. (2012), which was originally used to compute the original Mgas as well as the relations from Rémy-Ruyer et al. (2014). Our findings indicate that ID: 10100707 displays a δGDR that is 2.5 times lower than what is expected from the scaling relations for star-forming galaxies, given the metallicity we have estimated (~Z⊙). For our galaxy to follow the scaling relations with its δGDR, it would require a super-solar metallicity of >3 × Z⊙. Although it is possible that our object is simply very metal-rich, the confirmation would require more direct metallicity indicators.
Conversely, an increasing number of theoretical studies highlight the significance of grain growth in dust production within the ISM, particularly for metal-rich galaxies (e.g., Asano et al. 2013; Rémy-Ruyer et al. 2014; Hirashita et al. 2015; Zhukovska et al. 2016; De Vis et al. 2019). Depending on the star-formation history within the galaxy, grain growth can become the dominant mechanism of dust production once a certain metallicity threshold is reached. As a result, metals are depleted from the ISM as the Mdust increases significantly (also see Donevski et al. 2023). Therefore, it is possible that our galaxy indeed has solar metallicity, and the observed δGDR may be a result of rapid metal-to-dust conversion via grain growth.
4.4 Dust to gas conversion
From our discussion and analysis, we predicted that the systematic shifts induced on M* and Mdust are inapplicable or insufficient to explain the derived δGDR. Generally, the metallicity is not the only driver of the observed scatter in the δGDR values, and other phenomena in galaxies can lead to a large variation of this parameter. These would include the morphological type, stellar mass and SFR, however, each of them having an effect on the observed δGDR (Rémy-Ruyer et al. 2014).
It is understood that in the process of deriving the Mgas via the Mdust method, what is actually being computed is the total mass of hydrogen HI+H2 (e.g., see Magdis et al. 2012). It is therefore possible that our galaxy has elevated HI reservoirs (not traceable by CO) that could cause the observed discrepancy. By combining our dust and CO based Mgas measurements we compute the HI to stellar mass ratio MHI/M* ~ 1, which is roughly two times greater than expected at that redshift (Heintz et al. 2022). Using the 21-cm line emission, however, Chowdhury et al. (2020, Chowdhury et al. 2021) found that at z ~ 1 some galaxies can indeed reach MHI/M* similar to (or even in excess of) our findings. A large HI reservoir is therefore a plausible explanation for the lower δGDR.
The observed disparity between the δGDR – Z relation for our object could also be caused by the presence of the CO-dark molecular gas. In low-metallicity environments, the lack of dust shielding of gas clouds leads to dissociation of molecular gas. What remains, as a result, is a small amount of self-shielding H2 (Madden et al. 2020). In this case, the H2 reservoirs that cannot be traced by CO (e.g., Papadopoulos et al. 2002; Röllig et al. 2006; Wolfire et al. 2010; Glover & Clark 2012; Madden et al. 2020) will require another method of tracing optically thick gas not normally probed by CO. In this case, hydrodynamical simulations (e.g., see Smith et al. 2014; Offner et al. 2014; Franeck et al. 2018; Seifried et al. 2020) have shown that neutral [CI] and ionized [CII] carbon have the ability to trace molecular hydrogen in optically thick and warm environments. While the dust in our object was found to be both warm, compared to MS galaxies at the same redshift (e.g., Schreiber et al. 2015, 2018), and optically thick out to ~600 µm, our metallicity estimates from M, and SFR (Mannucci et al. 2010; Zahid et al. 2014) strongly suggest that our galaxy must be close to a solar metallicity. It is therefore unlikely that our CO (2−1) study fails to quantify the full H2 reservoir, however, further [CI] observations would be necessary to verify the CO – derived Mgas. Moreover, while optically thick HI has been suggested as a potential source of CO-dark gas, there is currently no convincing evidence to support its significant contribution to the dark neutral gas (Murray et al. 2018).
Based on the CO Mgas estimate, the galaxy can no longer be classified as a gas giant, yet the Mdust/M* ratio remains high. We find that the Mgas/M* ratio is marginally consistent with expected values, while the dust reservoir and δGDR are abnormal compared to galaxies of similar mass and redshift. Therefore, it would be more accurate to refer to ID: 10100707 as a dust giant.
Finally, in the right panel of Fig. 4 we examine the position of our galaxy on the 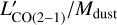 and δGDR versus Mdust diagram. We find that our galaxy is not an outlier compared to either the MS and SB sources from Valentino et al. (2020), as well as the BzK population discussed in Daddi et al. (2015). However, we find that our dust giant displays
and δGDR versus Mdust diagram. We find that our galaxy is not an outlier compared to either the MS and SB sources from Valentino et al. (2020), as well as the BzK population discussed in Daddi et al. (2015). However, we find that our dust giant displays 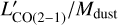 ratio consistent with those of SB objects, despite it lying on the main-sequence. In fact the object most closely associated with ID: 10100707 is an extreme starburst (SFR/SFRMS ~ 9) of similar Mdust and M* presented in Puglisi et al. (2021).
ratio consistent with those of SB objects, despite it lying on the main-sequence. In fact the object most closely associated with ID: 10100707 is an extreme starburst (SFR/SFRMS ~ 9) of similar Mdust and M* presented in Puglisi et al. (2021).
4.5 Dynamical mass budget
Using the Mdyn computed in the previous section we would like to understand whether the derived submm continuum and CO Mgas are compatible with the total mass budget. Assuming a dark matter fraction of 10% and using the KS galaxy size, we obtained the log10(Mbar/M⊙) = 11.25 ± 0.10. While the KS galaxy size is most likely larger than the CO (2−1) emitting region (e.g., see Puglisi et al. 2021; Gómez-Guijarro et al. 2022), we believe it represents an adequate upper limit on the total bary-onic mass of our galaxy, as opposed to the over-resolved ALMA 870 µm emission. Subtracting the M* and Mdust leaves us with the allowed log10(Mgas/M*) ≤ 10.97 ± 0.15, which lies within 1σ from our sub-mm and CO Mgas estimates. In this case, taking into account the measured 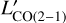 this would require an αCO = 4.3 ± 0.5, a value typical of MS galaxies, which aligns with our SFR/SFRMS characterization. Due to the large uncertainty on the Mdyn it is not, however, possible to ascertain which one of Mgas estimates is most likely to be correct.
this would require an αCO = 4.3 ± 0.5, a value typical of MS galaxies, which aligns with our SFR/SFRMS characterization. Due to the large uncertainty on the Mdyn it is not, however, possible to ascertain which one of Mgas estimates is most likely to be correct.
4.6 Optically dark dusty contaminant
Finally, a presence of the optically dark companion, contaminating the FIR-mm emission, could potentially explain the elevated dust content. The existence of these dust-obscured, optically faint, star-forming galaxies has been demonstrated by a large number of detections with Spitzer Space Telescope (Spitzer) and Herschel (see Huang et al. 2011; Caputi et al. 2012; Alcalde Pampliega et al. 2019), as well as in the sub-mm regime (Talia et al. 2021; Wang et al. 2021), specifically by Atacama Large Millimeter/submillimeter Array (ALMA; Simpson et al. 2014; Franco et al. 2018; Yamaguchi et al. 2019; Wang et al. 2019; Williams et al. 2019; Umehata et al. 2020; Caputi et al. 2021; Fudamoto et al. 2021; Manning et al. 2022; Gómez-Guijarro et al. 2022; Kokorev et al. 2022; Xiao et al. 2023). It is possible that the additional Mdust component is coming from the an optically dark companion, where the dust is too warm to be detected with SCUBA2/ALMA. To explore this possibility, we fit our IR (λrest > 40 µm) photometry with two optically thin MBB functions, for warm and cold dust. We assume that the contaminant has to be at the same redshift as our galaxy and fix the temperature ranges such that the warm SED cannot exceed the ALMA rms flux. Our analysis finds this scenario to be physically possible, with the warm and cold dust components being fit at ~35 and ~20 K, respectively. If we subtract the Mdust contribution of the warm dust, we find that the Mdust of the dust giant is reduced to log10(Mdust/M⊙) ~ 8.9, which would bring it in line with the Mdust/M* trend expected at this redshift.
A potentially similar case was presented in Kokorev et al. (2023), where a spatially resolved analysis with James Webb Space Telescope (JWST) NIRCam reveals a highly dust-obscured disk (Av ~ 5) at z = 2.58. Previously only seen as a sub-mm galaxy (SMG) in Laporte et al. (2017) and Muñoz Arancibia et al. (2018), this HST-dark source has only been possible to detect with deep JWST observations in the NIR. If such an object does indeed boost the sub-mm flux density, it would have to be a warm FIR/ALMA only source, with Tdust larger than 35 K. Further deep observations with JWST would be necessary to confirm whether the extreme δGDR seen in our galaxy is in fact a result of such a dusty contaminant.
4.7 Low-z analog of HST-dark galaxies
We find that this galaxy displays a similar amount of dust obscuration (AV ~ 1.81) and it is on the main sequence, with comparable M, and Mdust values to those of the optically faint sources at higher-z that were recently presented in the literature (e.g., Franco et al. 2018; Wang et al. 2019; Kokorev et al. 2022, 2023; Nelson et al. 2023; Barrufet et al. 2023; Gómez-Guijarro et al. 2023). To investigate this possibility, we applied the JWST color-color classification presented in Nelson et al. (2023), which uses the F115W-F444W and F150W-F444W colors to identify candidate objects. We integrated our best-fit Stardust template through the JWST filters and obtained the synthetic flux densities. In Fig. 5, we display the location of our galaxy, along with the Nelson et al. (2023) objects and the HST-dark galaxy reported in Kokorev et al. (2023), on the color-color diagram. Furthermore, we trace the position of ID: 10100707 on the diagram if it were located at the same redshift as the Kokorev et al. (2023) object or at z = 4. Our analysis suggests that while our object would not qualify as an HST-dark galaxy at z = 1.38, it would meet the criteria for such classification at z > 2.
Following a similar analysis presented in Kokorev et al. (2023), we would like to test how likely is it to detect analogs of this object at high z. We use the detection limits of major JWST surveys, including UNCOVER (PIs: I. Labbe, R. Bezanson; Bezanson et al. 2022) and CEERS (PI: S. Finkelstein; Bagley et al. 2023a) as well as COSMOS-Web (PIs: J. Kartaltepe, C. Casey; Casey et al. 2023). We also included the 5σ limit of the deepest public NIRCam observations taken at the moment of writing, from NGDEEP (PI: S. Finkelstein; Bagley et al. 2023b). We find that at z ~ 4 a similarly dusty galaxy would become an F200W dropout with NGDEEP – like depths (~31 AB mag), and is JWST-dark in all other major surveys. Dusty 2 µm dropouts with elevated Mdust could be misidentified as z > 15 galaxies, as discussed in Naidu et al. (2022); Zavala et al. (2023); Donnan et al. (2023) and most recently in Arrabal Haro et al. (2023). We thus highlight that the identification of dust-obscured main-sequence galaxies at and beyond the epoch of reionization remains a challenging task for JWST, indicating that such these galaxies will likely end up being missed.
 |
Fig. 5 Color diagnostic. JWST color-color diagram for selecting HST-dark objects presented in Nelson et al. (2023). Black points show the positions of the Nelson et al. (2023) sources. The maroon star denotes the highly dust obscured AV ~ 5 galaxy from Kokorev et al. (2023). Blue squares denote the location of our object, as well as how it would appear at z = 2.58 and z = 4. |
5 Conclusions
In this paper, we describe NOEMA CO (2−1) line observations and analysis in a galaxy originally selected for its elevated Mgas/Mgas The object constitutes a pilot study of the gas giant population presented in Kokorev et al. (2021). With our new observations we have been able to spectroscopically confirm the redshift of our galaxy, as well as to use the line luminosity to derive the Mgas. Additionally we updated the initial estimate of Mdust and dust-based Mgas with the addition of the 3 mm continuum upper limit from our NOEMA observations. With the re-computed CO based Mgas, however, we found that our initial gas giant selection no longer applies. The updated mass estimates, differ by −0.4 dex from the ones computed from Mdust, and position our galaxy along the expected evolutionary trends of Mgas/M*. At the same time, we found that the Mdust remains elevated, both with respect to the M, and now Mgas, leading to unusually low δGDR judging from the fundamental metallicity relations for a MS galaxy at this redshift and M*. Given the above it is more appropriate to refer to this galaxy as a “dust giant” instead.
Using the additional ALMA data at 870 µm, we found that the dust in our galaxy is likely to be extended, which is also supported by the fact that ALMA recovers a lower flux compared to the SCUBA2 data. Coupled with the double peaked CO (2–1) line this hints that gas in our galaxy is present both in the central region, as well as the spiral arms. In addition, we note the presence of the blue clumps visible in the F814W image (rest-frame UV).
We find that even though modeling our galaxy with optically thick dust emission reduces the dust mass, it is still not sufficient to bring it in line with the scaling relations. Instead, the discrepancy in the physical picture could potentially be explained by enhanced HI reservoirs, an unusually high metallicity, or the presence of an optically dark, dusty contaminant. What is clear is that it is important to be cautious when drawing conclusions about the physical picture based solely on Mgas derived from dust continuum measurements, given the significant difference between expected and measured values. Problems with the continuum derived Mgas are becoming very apparent due to the extreme optically thick dust, as found in Jin et al. (2022).
Our object also displays a similar amount of dust obscuration compared to the so-called HST-dark galaxies that exist at a higher z. Using the JWST based color-color selection for such galaxy types, we find that if our galaxy would exist at z > 2, it would be meet the criteria of such a color selection. In our work we aim to highlight that the identification of dust-obscured MS galaxies at and beyond the epoch of reionization remains a challenging task for JWST, and the most dusty galaxies will end up being missed.
While the source analyzed and discussed in our work will not be imaged as a part of COSMOS-Web JWST survey (Casey et al. 2023), we expect that a few tens of galaxies that belong to the “gas giant” or plausible “dust giant” populations will still be covered. Future observations with JWST/NIRCam and MIRI instruments as a part of COSMOS-Web, as well as deep multiband sub-mm ALMA or NOEMA data, would therefore be key in improving our understanding of the true nature of objects with elevated dust-to-stellar mass ratios.
Acknowledgements
We are grateful to the anonymous referee for their valuable feedback. We thank Pratika Dayal for her suggestions which helped improve this manuscript. We would like to thank Orsolya Feher for her help with NOEMA data reduction process. This work is based on observations carried out under project number W21CO with the IRAM NOEMA Interferometer [30-meter telescope]. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). S.J. is supported by the European Union’s Horizon Europe research and innovation program under the Marie Skłodowska-Curie grant agreement No. 101060888. The Cosmic Dawn Center is funded by the Danish National Research Foundation under grant No. 140. G.E.M. acknowledges the Villum Fonden research grant 13160 “Gas to stars, stars to dust: tracing star formation across cosmic time”, grant 37440, “The Hidden Cosmos”, and the Cosmic Dawn Center of Excellence funded by the Danish National Research Foundation under the grant No. 140. M.T. acknowledges support from the NWO grant 016.VIDI.189.162 (“ODIN”).
References
- Alcalde Pampliega, B., Pérez-González, P. G., Barro, G., et al. 2019, ApJ, 876, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023, Nature, https://doi.org/10.1038/s41586-023-06521-7 [Google Scholar]
- Asano, R. S., Takeuchi, T. T., Hirashita, H., & Nozawa, T. 2013, MNRAS, 432, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Bagley, M. B., Finkelstein, S. L., Koekemoer, A. M., et al. 2023a, ApJ, 946, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Bagley, M. B., Pirzkal, N., Finkelstein, S. L., et al. 2023b, AAS, submitted [arXiv:2302.05466] [Google Scholar]
- Barrufet, L., Oesch, P. A., Weibel, A., et al. 2023, MNRAS, 522, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Lutz, D., Genzel, R., Förster-Schreiber, N. M., & Tacconi, L. J. 2016, A & A, 587, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A & A, 573, A113 [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, R., Labbe, I., Whitaker, K. E., et al. 2022, ApJ, submitted [arXiv:2212.04026] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA & A, 51, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
- Caputi, K. I., Dunlop, J. S., McLure, R. J., et al. 2012, ApJ, 750, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K. I., Caminha, G. B., Fujimoto, S., et al. 2021, ApJ, 908, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA & A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Berta, S., Béthermin, M., et al. 2012, ApJ, 761, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Kartaltepe, J. S., Drakos, N. E., et al. 2023, ApJ, 954, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chowdhury, A., Kanekar, N., Chengalur, J. N., Sethi, S., & Dwarakanath, K. S. 2020, Nature, 586, 369 [Google Scholar]
- Chowdhury, A., Kanekar, N., Das, B., Dwarakanath, K. S., & Sethi, S. 2021, ApJ, 913, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Coogan, R. T., Daddi, E., Sargent, M. T., et al. 2018, MNRAS, 479, 703 [NASA ADS] [Google Scholar]
- Cortzen, I., Magdis, G. E., Valentino, F., et al. 2020, A & A, 634, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A & A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dayal, P., Ferrara, A., Sommovigo, L., et al. 2022, MNRAS, 512, 989 [NASA ADS] [CrossRef] [Google Scholar]
- De Vis, P., Jones, A., Viaene, S., et al. 2019, A & A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donevski, D., Lapi, A., Małek, K., et al. 2020, A & A, 644, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donevski, D., Damjanov, I., Nanni, A., et al. 2023, A & A, in press, https://doi.org/10.1051/0004-6361/202346066 [Google Scholar]
- Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023, MNRAS, 518, 6011 [Google Scholar]
- Dwek, E., & Scalo, J. M. 1980, ApJ, 239, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Willott, C., Alberts, S., et al. 2023, ApJS, submitted [arXiv:2306.02465] [Google Scholar]
- Elbaz, D., Hwang, H. S., Magnelli, B., et al. 2010, A & A, 518, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erwin, P. 2015, ApJ, 799, 226 [Google Scholar]
- Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A & A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franeck, A., Walch, S., Seifried, D., et al. 2018, MNRAS, 481, 4277 [NASA ADS] [CrossRef] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Schouws, S., et al. 2021, Nature, 597, 489 [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [Google Scholar]
- Genzel, R., Förster Schreiber, N. M., Übler, H., et al. 2017, Nature, 543, 397 [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 9 [NASA ADS] [Google Scholar]
- Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022, A & A, 658, A43 [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez-Guijarro, C., Magnelli, B., Elbaz, D., et al. 2023, A & A, 677, A34 [CrossRef] [EDP Sciences] [Google Scholar]
- Harrington, K. C., Weiss, A., Yun, M. S., et al. 2021, ApJ, 908, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, K. E., Oesch, P. A., Aravena, M., et al. 2022, ApJ, 934, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., Nozawa, T., Villaume, A., & Srinivasan, S. 2015, MNRAS, 454, 1620 [NASA ADS] [CrossRef] [Google Scholar]
- Hodge, J. A., Swinbank, A. M., Simpson, J. M., et al. 2016, ApJ, 833, 103 [Google Scholar]
- Huang, J. S., Zheng, X. Z., Rigopoulou, D., et al. 2011, ApJ, 742, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., Daddi, E., Liu, D., et al. 2018, ApJ, 864, 56 [Google Scholar]
- Jin, S., Daddi, E., Magdis, G. E., et al. 2019, ApJ, 887, 144 [Google Scholar]
- Jin, S., Daddi, E., Magdis, G. E., et al. 2022, A & A, 665, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020, ApJ, 900, 179 [Google Scholar]
- Kokorev, V. I., Magdis, G. E., Davidzon, I., et al. 2021, ApJ, 921, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Kokorev, V., Brammer, G., Fujimoto, S., et al. 2022, ApJS, 263, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kokorev, V., Jin, S., Magdis, G. E., et al. 2023, ApJ, 945, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [Google Scholar]
- Lagos, C. D. P., Crain, R. A., Schaye, J., et al. 2015, MNRAS, 452, 3815 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
- Laigle, C., Davidzon, I., Ilbert, O., et al. 2019, MNRAS, 486, 5104 [Google Scholar]
- Laporte, N., Bauer, F. E., Troncoso-Iribarren, P., et al. 2017, A & A, 604, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, D., Schinnerer, E., Groves, B., et al. 2019, ApJ, 887, 235 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA & A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Cormier, D., Hony, S., et al. 2020, A & A, 643, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Gobat, R., Valentino, F., et al. 2021, A & A, 647, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Boogaard, L., Decarli, R., et al. 2020, ApJ, 892, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Manning, S. M., Casey, C. M., Zavala, J. A., et al. 2022, ApJ, 925, 23 [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A & A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, M. J. 2015, A & A, 577, A80 [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz Arancibia, A. M., González-López, J., Ibar, E., et al. 2018, A & A, 620, A125 [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, C. E., Peek, J. E. G., Lee, M.-Y., & Stanimirovic, S. 2018, ApJ, 862, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Oesch, P. A., Setton, D. J., et al. 2022, ApJL, submitted [arXiv: 2208.02794] [Google Scholar]
- Nelson, E. J., Suess, K. A., Bezanson, R., et al. 2023, ApJ, 948, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Offner, S. S. R., Bisbas, T. G., Bell, T. A., & Viti, S. 2014, MNRAS, 440, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Thi, W. F., & Viti, S. 2002, ApJ, 579, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Thi, W. F., & Viti, S. 2004, MNRAS, 351, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Puglisi, A., Daddi, E., Valentino, F., et al. 2021, MNRAS, 508, 5217 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A & A, 563, A31 [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A & A, 451, 917 [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A & A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A & A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A & A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Sheth, K., et al. 2014, ApJ, 783, 84 [CrossRef] [Google Scholar]
- Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [Google Scholar]
- Scoville, N., Lee, N., Vanden Bout, P., et al. 2017a, ApJ, 837, 150 [Google Scholar]
- Scoville, N., Murchikova, L., Walter, F., et al. 2017b, ApJ, 836, 66 [Google Scholar]
- Seifried, D., Haid, S., Walch, S., Borchert, E. M. A., & Bisbas, T. G. 2020, MNRAS, 492, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1963, BAAA, 6, 41 [Google Scholar]
- Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
- Simpson, J. M., Smail, I., Wang, W.-H., et al. 2017, ApJ, 844, L10 [Google Scholar]
- Smith, R. J., Glover, S. C. O., Clark, P. C., Klessen, R. S., & Springel, V. 2014, MNRAS, 441, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Smolcic, V., Delvecchio, I., Zamorani, G., et al. 2017, A & A, 602, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tacconi, L. J., Genzel, R., Saintonge, A., et al. 2018, ApJ, 853, 179 [Google Scholar]
- Talia, M., Cimatti, A., Giulietti, M., et al. 2021, ApJ, 909, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, Q., Daddi, E., Magdis, G., et al. 2014, A & A, 569, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umehata, H., Smail, I., Swinbank, A. M., et al. 2020, A & A, 640, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2018, ApJ, 869, 27 [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2020, ApJ, 890, 24 [Google Scholar]
- van der Wel, A., Chang, Y.-Y., Bell, E. F., et al. 2014, ApJ, 792, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Schreiber, C., Elbaz, D., et al. 2019, Nature, 572, 211 [Google Scholar]
- Wang, L., Gao, F., Best, P. N., et al. 2021, A & A, 648, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weaver, J. R., Kauffmann, O. B., Ilbert, O., et al. 2022, ApJS, 258, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Narayanan, D., Williams, C. C., et al. 2021, ApJ, 922, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, C. C., Labbe, I., Spilker, J., et al. 2019, ApJ, 884, 154 [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Wisnioski, E., et al. 2016, ApJ, 831, 149 [Google Scholar]
- Xiao, M. Y., Elbaz, D., Gómez-Guijarro, C., et al. 2023, A & A, 672, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yamaguchi, Y., Kohno, K., Hatsukade, B., et al. 2019, ApJ, 878, 73 [Google Scholar]
- Zahid, H. J., Kashino, D., Silverman, J. D., et al. 2014, ApJ, 792, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, J. A., Buat, V., Casey, C. M., et al. 2023, ApJ, 943, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Dobbs, C., Jenkins, E. B., & Klessen, R. S. 2016, ApJ, 831, 147 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Gas giant candidate from our original NOEMA proposal. The galaxy was confirmed at zspec = 1.38. Top Left: 5″.0 HST F814W cutout of our source with ALMA 870 µm 2, 3, 5, and 8σ levels shown in green. In the bottom left we show the size of the ALMA beam. Top right: RGB composite with blue: HST/F814W, green: UVISTA/H, and red: UVISTA/KS. Bottom left: extracted spectrum of the CO (2−1) line for our galaxy – ID 10100707. The double Gaussian fit to the spectrum is shown in blue and red, while the sum of the two is represented by a dashed black line. Shaded maroon region shows the channels used to extract the line flux. Bottom right: 20″.0 RGB cutout of our source. We additionally show the 2, 3, and 5σ contours of the CO(2−1) line. The solid white ellipse displays the NOEMA beam size. |
| In the text | |
 |
Fig. 2 Best-fit SED and cutouts for our source. Left: multi-component template STARDUST spectrum (grey line and shaded areas), the observed photometry (red squares), including the upper limits (red arrows) are also displayed. Radio measurements from VLA at 1.4 (Schinnerer et al. 2010) and 3 GHz (Smolčić et al. 2017) are overlaid in blue. The SED is separated into three components – stellar emission (blue), AGN emission (green), dust (red). Right: optical-NIR-FIR cutouts of our galaxy, ranging from 5″.0 in the optical-MIR range to 50″.0 in FIR. |
| In the text | |
 |
Fig. 3 Evolution of ISM properties. Left: evolution of ƒgas as a function of z/cosmic age. Values of Mgas derived from Mdust, and CO J = 2→1 are shown as red and blue diamonds, respectively. Downward arrows denote upper limits. Solid colored lines correspond to empirical evolutionary trends derived in Scoville et al. (2017a), Tacconi et al. (2018), Liu et al. (2019), Magnelli et al. (2020). The dashed purple line shows the fit to the COSMOS Super Deblended catalog data, as described in Kokorev et al. (2021), with shaded purple region denoting the 16th and 84th percentile confidence intervals. Both the data and the derived relations have been re-scaled to ∆MS = 1 and M* = 5 × 1010 M⊙. White diamonds show median positions of the Horizon AGN star-forming galaxies at that redshift (Laigle et al. 2019), normalised in the same way as our data. Right: change in the distance to the main-sequence as a function of depletion time (τ). Labels and lines are the same as on the first panel. |
| In the text | |
 |
Fig. 4 Gas-to-dust ratio and CO emission. Left: gas-to-dust ratio as a function of metallicity for the galactic CO to molecular gas conversion from Rémy-Ruyer et al. (2014, RR14). The dashed line represents the reference scaling of the δGDR with metallicity and the dotted and dash-dotted lines represent the best power-law and best broken power-law fits to the data presented in RR14. The dashed blue line with the shaded envelope show the δGDR – metallicity relation from Magdis et al. (2012) which we used to derive the original Mgas. The δGDR measurement from CO and dust continuum is shown as a red diamond. Right: CO(2−1) line luminosity to Mdust ratio and δGDR as a function of Mdust. For the δGDR, we assume αCO = 4.0 for all galaxies. We also show the sample of MS (blue) and SB (purple) galaxies from Valentino et al. (2020). The BzK galaxies from Daddi et al. (2015) are shown as black squares. Our galaxy is shown as a red diamond. A typical uncertainty on the data is shown in the bottom left corner. |
| In the text | |
 |
Fig. 5 Color diagnostic. JWST color-color diagram for selecting HST-dark objects presented in Nelson et al. (2023). Black points show the positions of the Nelson et al. (2023) sources. The maroon star denotes the highly dust obscured AV ~ 5 galaxy from Kokorev et al. (2023). Blue squares denote the location of our object, as well as how it would appear at z = 2.58 and z = 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


