| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | L13 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202345925 | |
| Published online | 18 May 2023 | |
Letter to the Editor
Molecular gas content and high excitation of a massive main-sequence galaxy at z = 3
1
Cosmic Dawn Center (DAWN), Copenhagen, Denmark
2
Niels Bohr Institute, University of Copenhagen, Jagtvej 128, 2200 Copenhagen N, Denmark
e-mail: xmg125@alumni.ku.dk
3
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
4
DTU-Space, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
5
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
6
Max-Planck-Institut für extraterrestrische Physik (MPE), Giessenbachstrasse 1, 85748 Garching, Germany
7
Astrophysics, Department of Physics, University of Oxford, Keble Road, Oxford OX1 3RH, UK
8
School of Sciences, European University Cyprus, Diogenes Street, Engomi, 1516 Nicosia, Cyprus
9
CEA, IRFU, DAp, AIM, Université Paris-Saclay, Université de Paris, CNRS, 91191 Gif-sur-Yvette, France
Received:
17
January
2023
Accepted:
17
April
2023
We present new CO (J = 5 − 4 and 7 − 6) and [C I] (3P2−3P1 and 3P1−3P0) emission line observations of the star-forming galaxy D49 at the massive end of the main sequence at z = 3. We incorporate previous CO (J = 3 − 2) and optical-to-millimetre continuum observations to fit its spectral energy distribution. Our results hint at high-J CO luminosities exceeding the expected location on the empirical correlations with the infrared luminosity. [CI] emission fully consistent with the literature trends is found. We do not retrieve any signatures of a bright active galactic nucleus that could boost the J = 5 − 4, 7 − 6 lines in either the infrared or X-ray bands, but warm photon-dominated regions, shocks, or turbulence could in principle do so. We suggest that mechanical heating could be a favourable mechanism able to enhance the gas emission at fixed infrared luminosity in D49 and other main-sequence star-forming galaxies at high redshift, but further investigation is necessary to confirm this explanation. We derive molecular gas masses from dust, CO, and [C I] that all agree within the uncertainties. Given its high star formation rate ∼500 M⊙ yr−1 and stellar mass > 1011.5 M⊙, the short depletion timescale of < 0.3 Gyr might indicate that D49 is experiencing its last growth spurt and will soon transit to quiescence.
Key words: galaxies: high-redshift / galaxies: evolution / galaxies: individual: D49 / galaxies: ISM / galaxies: star formation / submillimeter: ISM
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Star formation plays an essential role in the evolution of galaxies. It is the driver of their stellar mass (M⋆) growth; it leads to the chemical enrichment of the interstellar and circumgalactic media (ISM, CGM) via supernova explosions and stellar wind ejections; and its cessation determines the death of galaxies and their final transition to quiescence. It is now well established that the ensemble of galaxies in the Universe forms stars at a pace that, in terms of cosmic star formation rate (SFR) density, peaks around z ∼ 2 − 3, the period of maximum activity dubbed ‘cosmic noon’ (Madau & Dickinson 2014). Interestingly, most star-forming galaxies seem to follow tight correlations between M⋆ and SFR, which is known as the main sequence of star formation (Daddi et al. 2007; Elbaz et al. 2007; Noeske et al. 2007), and between the surface densities of gas mass (Σgas) and SFR (ΣSFR), the Schmidt–Kennicutt relation (Kennicutt 1998b). Only a small percentage of galaxies undergoing intense star formation activity (dubbed “starbursts”) seem to fall out of the correlations (Daddi et al. 2010; Genzel et al. 2010; Rodighiero et al. 2011, 2014; Tacconi et al. 2020). Accurate estimates of the amount and properties of the molecular hydrogen reservoirs (H2), the primary fuel for the formation of new stars, therefore become the key to understanding how galaxies evolve across cosmic time.
The lack of dipole moment and the warm temperatures (∼500 K) necessary to excite the first rotational transition make H2 difficult to be directly detected in galaxies. Thus, alternative proxies are used to trace the bulk of their cold molecular gas and measure its mass (Mgas). Carbon monoxide (CO), the second most abundant molecule after H2, is a traditional choice. However, its first rotational transition CO(J = 1 − 0) (νrest = 115.27 GHz; hereafter CO (1 − 0) ) is difficult to observe for galaxies at the peak of star formation activity at cosmic noon (z ∼ 2 − 3). Moreover, the conversion from the CO luminosity to Mgas depends on the physical conditions of local ISM (Carilli & Walter 2013). Optically thin dust emission has emerged as a reliable and observationally inexpensive alternative. The Mgas can be estimated by multiplying dust masses (Mdust) from the modelling of the far-infrared spectral energy distribution (SED) by a metallicity-dependent gas-to-dust ratio (Magdis et al. 2011, 2012; Berta et al. 2016). In alternative, Mgas can be derived directly from single sub-millimetre band observations calibrated against CO (Scoville et al. 2014, 2016; Liu et al. 2019a,b; Kaasinen et al. 2019). In the past, the [C I](3P1−3P0) and [C I](3P2−3P1) transitions of neutral atomic carbon (νrest = 492.16 GHz and 809.34 GHz, respectively; hereafter [CI] (1 − 0) and [CI] (2 − 1)) were brought forward to serve as potentially robust tracers of Mgas, and were even better than the traditional CO under certain circumstances (e.g. Papadopoulos & Greve 2004; Papadopoulos et al. 2004; Madden et al. 2020; Dunne et al. 2022). Being optically thin even in the most extreme star-forming environment (Harrington et al. 2021), [C I] line fluxes can be converted to Mgas with an assumption of the gas excitation and an abundance (Papadopoulos et al. 2004). Furthermore, the combination of several CO and [CI] transitions can constrain the properties and plausible gas heating mechanisms in galaxies (e.g. Bothwell et al. 2017; Harrington et al. 2021; Liu et al. 2021; Papadopoulos et al. 2022). However, due to their intrinsic brightness, observations and modelling of typical galaxies on the main sequence of star formation at cosmic noon have been explored to a much lesser extent compared to their starbursting counterparts (Valentino et al. 2020; Brisbin et al. 2019; Bourne et al. 2019; Boogaard et al. 2020; Henríquez-Brocal et al. 2022).
Here we present a comprehensive study of the massive star-forming galaxy D49 located at the high-mass end of the main sequence at z = 2.84 (Magdis et al. 2017). This object is spectroscopically confirmed via Lyman-α (Steidel et al. 2003; Shapley et al. 2003) and CO (3 − 2) (Magdis et al. 2017). Moreover, its SED is finely sampled from the optical to the millimetre regime. This makes D49 a perfect test-bed for the calibration of different gas tracers and the exploration of the molecular gas properties on the main sequence, possibly during the last epoch of assembly before quenching.
In this Letter we present new measurements of the CO (5 − 4), CO (7 − 6), [CI] (2 − 1), and [CI] (1 − 0) emission lines and their underlying dust continuum using the NOrthern Extended Millimetre Array (NOEMA). When estimating gas masses, we assume Mgas ≈ MH2 to be consistent with the Magdis et al. (2017) values. We adopt throughout Ωm = 0.3, ΩΛ = 0.7, H0 = 71 km s−1 Mpc−1, and a Chabrier (2003) IMF.
2. Observations
D49 is a massive and infrared-bright galaxy, originally identified from the optically selected (U, G, R) sample of Lyman-break galaxies (LBGs) in the Extended Groth Strip field (EGS) at z ∼ 3 in Steidel et al. (2003). We observed D49 with NOEMA (W18DT, PI: I. Cortzen). The antennas were pointed at (RA, Dec) = (14 h:17 m:29 s.234, 52°:34′:34″.450). The galaxy redshift z = 2.846 is known from previous detections of the CO(3-2) line (Magdis et al. 2017) and from optical spectroscopy described in Steidel et al. (2003). Therefore, the expected frequencies of CO (7 − 6), + [CI] (2 − 1), and CO (5 − 4), + [CI] (1 − 0) are 209.74+210.43 GHz and 149.84 GHz+127.97 GHz, respectively, falling in Bands 3 and 2. We observed D49 in each band for 2.5 h in D configuration on March 28 and April 13, 2019. The data were calibrated by the standard pipeline contained in the GILDAS package1. In the images cleaned with default recipes with MAPPING (Högbom 1974), the final beam sizes are 1.93″ × 1.48″ (PA = 62°) and 3.19″ × 2.50″ (PA = 63°) at Band3/1.3 mm and Band 2/2 mm, respectively. The spectra were extracted with circular Gaussian profiles centred at the location of the CO (3 − 2) emission and with a fixed full width at half maximum (FWHM) of 0.6″(=4.8 kpc at z = 2.84) to be consistent with the results in Magdis et al. (2017). The extraction was performed in the u − v space with the task UV_FIT. The continuum emission was extracted in a similar way after averaging the line-free spectral windows. Given the spatial resolution, we did not resolve the source. This is further confirmed by the consistent continuum flux densities extracted by fitting the emission with a circular Gaussian, a point source profile, and by reading the brightest pixel in the cleaned image.
3. Results
3.1. CO and [CI] emission lines
In the extracted spectra shown in Fig. 1, we fit Gaussian profiles for lines and a power-law dust continuum to the observed data. We fixed the redshift and line widths of the three clearly detected lines (CO (5 − 4) at 14σ, CO (7 − 6) at 16σ, and [CI] (2 − 1) at 8σ), assuming that the molecules and atoms producing them belong to the same regions of the unresolved galaxy. The best-fit results are listed in Table 1. The best-fit redshift and line FWHM are (2.8469 ± 0.0001) and (590 ± 25) km s−1, which are similar to those in Magdis et al. (2017). We then derived L′ line luminosities as in Solomon & Vanden Bout (2005):
 |
Fig. 1. Spectra of (a) CO (7 − 6) + [CI] (2 − 1), (b) CO (5 − 4), and (c) [CI] (1 − 0) emission of D49. The binned step width is ∼90 km s−1 in panels (a) and (c) and ∼40 km s−1 in panel (b). The red curves indicate the fitted Gaussian profiles combined with a power-law dust continuum, the latter shown by a dashed line. The blue and green shaded areas in panel (c) indicate the 1σv and ±3σv velocity width used to set the upper limit on [CI] (1 − 0). |
Best-fit results of CO and [CI] lines of D49, obtained by fixing the redshift and FWHM for CO (5 − 4), CO (7 − 6), and [CI] (2 − 1).
Here SlineΔv is the integrated line flux in Jy km s−1, DL is the luminosity distance in Mpc, and νobs is the observed frequency of the emission line in GHz. We also fit the spectra without fixing line width and redshift and the results are fully consistent within the uncertainties.
We did not detect any significant [CI] (1 − 0) emission line (Fig. 1). We thus set an upper limit following Eq. (7) in Bothwell et al. (2013),
where rmschannel is the root mean square per channel estimated locally around the expected location of the line, σv is the line width that we impose to be identical to that of all the other lines (FWHM ≈ 2.355 × σv), and dv is the channel velocity width. We computed a conservative upper limit within ±3σv (Fig. 1), corresponding to the 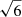 factor in Eq. (2).
factor in Eq. (2).
3.2. Spectral energy distribution modelling
We modelled the full SED of D49 with the novel algorithm Stardust2 (Kokorev et al. 2021). Stardust can simultaneously, but independently fit linear combinations of stellar active galactic nuclei (AGN), and dust templates without explicitly imposing an energy balance between the absorbed UV–optical radiation and the IR emission. The latter is often assumed in SED modelling (e.g., CIGALE, Burgarella et al. 2005; Noll et al. 2009; Boquien et al. 2019; MAGPHYS da Cunha et al. 2008; Battisti et al. 2019). This approach assumes that the stellar and dust emissions are spatially coincident, meaning that the UV absorption and the subsequent re-emission at IR wavelengths occur in the same environment (da Cunha et al. 2008). However, resolved observations of distant galaxies at z ∼ 2 have revealed offsets between the dust and stellar spatial distributions, challenging the energy balance assumption (Chen et al. 2017; Calistro Rivera et al. 2018; Cochrane et al. 2021). We thus relinquish this assumption in our models. For each component, we used the standard libraries released with Stardust: stellar population synthesis models in common with eazy from Brammer et al. (2008), AGN templates in Mullaney et al. (2011), and dust emission from Draine & Li (2007) and Draine et al. (2014). The modelled photometric data, including the new dust continuum emission measurements presented in this work, are listed in Table A.1 and the best-fit SED is shown in Fig. 2. We list the best-fit properties returned by Stardust in Table 2. Even including the AGN templates, the best fit does not favour a meaningful solution with a strong AGN. Its possible contribution to the total IR budget is fAGN = LIR, AGN/LIR, total = 0.01 ± 0.33, with S/N ≪ 3 on LIR, AGN). In other words, the emission can be fully accounted for with stellar and dust templates. We find that the infrared luminosity LIR(8 − 1000 μm) and dust mass Mdust are consistent with those in Magdis et al. (2017), while Stardust returns 0.3 dex larger M⋆. We convert LIR into SFR as LIR [L⊙] = 1010 × SFR [M⊙ yr−1] (Kennicutt 1998a for a Chabrier 2003 IMF). Assuming that D49 follows the fundamental metallicity relation (FMR, Mannucci et al. 2010), we derive a gas-to-dust ratio of δGDR(12 + log(O/H) = 8.71 ∼ Z⊙)≈83 following Magdis et al. (2017).
 |
Fig. 2. Spectral energy distribution of D49. The red open squares and downward arrow indicate the fitted photometry and upper limits. The black line shows the Stardust best-fit SED, while the contribution from stars and dust are respectively shown as a blue and red filled region. The grey region presents the predicted contribution from radio continuum, based on the radio-FIR model described in Delvecchio et al. (2021). |
Stardust fitting result.
4. Discussion
4.1. CO and [CI] emission compared with that of other galaxies
In Fig. 3, we show the location of D49 in the LIR − (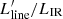 ) planes. As a comparison, we plot the local and high-redshift samples in Valentino et al. (2020, 2021) and galaxies from the ALMA Spectroscopic Survey in the Hubble Ultra Deep Field (ASPECS, Boogaard et al. 2020). We recomputed the best-fit linear correlations between line luminosities and LIR in the logarithmic space using linmix3 (Kelly 2007). The best-fit parameters and intrinsic scatters (σ ≲ 0.3 dex) are reported in Fig. 3 and are consistent with previous works (Greve et al. 2014; Liu et al. 2015; Daddi et al. 2015; Yang et al. 2017; Valentino et al. 2020). D49 displays some of the highest
) planes. As a comparison, we plot the local and high-redshift samples in Valentino et al. (2020, 2021) and galaxies from the ALMA Spectroscopic Survey in the Hubble Ultra Deep Field (ASPECS, Boogaard et al. 2020). We recomputed the best-fit linear correlations between line luminosities and LIR in the logarithmic space using linmix3 (Kelly 2007). The best-fit parameters and intrinsic scatters (σ ≲ 0.3 dex) are reported in Fig. 3 and are consistent with previous works (Greve et al. 2014; Liu et al. 2015; Daddi et al. 2015; Yang et al. 2017; Valentino et al. 2020). D49 displays some of the highest 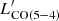 and
and 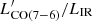 ratios in our literature compilation, falling in the 93rd and 96th percentiles of the distributions. The measured
ratios in our literature compilation, falling in the 93rd and 96th percentiles of the distributions. The measured 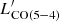 /LIR and
/LIR and 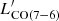 /LIR ratios are 1.9× (1.3σ) and 3.3× (2.4σ) higher than the medians of the ensemble of local and distant galaxies. These differences further increase when comparing D49 with IR and sub-millimetre selected high-redshift galaxies only (2.1× and 3.7× times higher at 1.7σ and 2.0σ for Jup = 5 and 7, respectively). The significance is slightly reduced owing to the smaller number statistics increasing the scatter. Interestingly, the ratios are more consistent with those from the blind ASPECS survey (Boogaard et al. 2020). However, we note that 25% (62.5%) of the ASPECS sources with CO (5 − 4) (CO (7 − 6)) detections in Fig. 3 are X-ray detected sources and candidate AGN – which might boost the molecular gas excitation. Our target is also consistent with the literature sample and general trends in the LIR − ([C I]/LIR) luminosity planes.
/LIR ratios are 1.9× (1.3σ) and 3.3× (2.4σ) higher than the medians of the ensemble of local and distant galaxies. These differences further increase when comparing D49 with IR and sub-millimetre selected high-redshift galaxies only (2.1× and 3.7× times higher at 1.7σ and 2.0σ for Jup = 5 and 7, respectively). The significance is slightly reduced owing to the smaller number statistics increasing the scatter. Interestingly, the ratios are more consistent with those from the blind ASPECS survey (Boogaard et al. 2020). However, we note that 25% (62.5%) of the ASPECS sources with CO (5 − 4) (CO (7 − 6)) detections in Fig. 3 are X-ray detected sources and candidate AGN – which might boost the molecular gas excitation. Our target is also consistent with the literature sample and general trends in the LIR − ([C I]/LIR) luminosity planes.
 |
Fig. 3.
|
4.2. Potential gas heating mechanisms
In the literature samples mentioned above, we highlighted Q2343-BX610 and Q1700-MD94 (hereafter BX610 and MD94), two massive star-forming main-sequence galaxies at z ∼ 2 (Brisbin et al. 2019; Henríquez-Brocal et al. 2022). These two galaxies have similar line and continuum coverage to D49, despite being at slightly lower redshifts. We also note NGC 6240, a widely studied local galaxy (e.g., Komossa et al. 2003; Rieke et al. 1985; Vignati et al. 1999). The reason is clear from Fig. 3: all these galaxies occupy similar loci in the 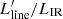 vs. LIR relations. For D49, we estimate
vs. LIR relations. For D49, we estimate 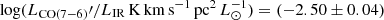 , while this value is ∼ − 2.32 for NGC 6240 (Meijerink et al. 2013), and ∼ − 2.69 for BX610 (Brisbin et al. 2019). For MD94, we derive its LIR [L⊙] from the SFR = 271 M⊙ yr−1 (Tacconi et al. 2013) with the same conversion adopted above. Also in this case we find
, while this value is ∼ − 2.32 for NGC 6240 (Meijerink et al. 2013), and ∼ − 2.69 for BX610 (Brisbin et al. 2019). For MD94, we derive its LIR [L⊙] from the SFR = 271 M⊙ yr−1 (Tacconi et al. 2013) with the same conversion adopted above. Also in this case we find 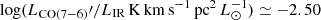 consistent with that of D49. All these galaxies exhibit a CO (7 − 6) emission brighter than what is expected from their LIR. Inverting the argument, following Eq. (1) in Lu et al. (2015), the SFR of D49 derived by LCO(7 − 6) [L⊙] would be ∼3500 M⊙ yr−1, which is ∼6× larger than what we derive from the SED fitting (SFR ∼ 600 M⊙ yr−1). Figure 4 presents the CO spectral line energy distributions of these four galaxies, normalised by
consistent with that of D49. All these galaxies exhibit a CO (7 − 6) emission brighter than what is expected from their LIR. Inverting the argument, following Eq. (1) in Lu et al. (2015), the SFR of D49 derived by LCO(7 − 6) [L⊙] would be ∼3500 M⊙ yr−1, which is ∼6× larger than what we derive from the SED fitting (SFR ∼ 600 M⊙ yr−1). Figure 4 presents the CO spectral line energy distributions of these four galaxies, normalised by  . Despite the undersampling at low-J for D49, its spectral line energy distribution (SLED) shows a similar trend to those of NGC 6240 and BX610 at J > 3, while looking more excited than MD94.
. Despite the undersampling at low-J for D49, its spectral line energy distribution (SLED) shows a similar trend to those of NGC 6240 and BX610 at J > 3, while looking more excited than MD94.
 |
Fig. 4. CO spectral line energy distributions of D49, compared to BX610, NGC 6240, and MD94, normalised by their own |
Brisbin et al. (2019) showed how a single photon-dominated region (PDR) model is not sufficient to explain the line ratios in BX610. At least one additional warm PDR component should be introduced, considering this heating source only. However, since the CO emission is brighter than expected from LIR, and thus from SFR-driven heating mechanisms, one would either conclude that either CO (7 − 6) is not a good SFR tracer (Brisbin et al. 2019) or that other possibilities not affecting LIR should be considered.
Brisbin et al. (2019) proposed slow shocks as alternative contributors to the CO excitation in BX610. These were brought forward also in the case of NGC 6240 (Meijerink et al. 2013; Lu et al. 2014). However, while shocks in NGC 6240 are driven by the collision of two galaxies, their origin in BX610 and other high-redshift galaxies on and above the main sequence remains unknown. Turbulence could also contribute to the heating of the ISM in strongly star-forming galaxies (Harrington et al. 2021). High-redshift galaxies are more gas rich than local objects and the ISM densities and temperatures increase at least up to z ∼ 1.5 (Liu et al. 2021), which naturally leads to more turbulent ISM and shocks originating from higher Mach numbers.
X-ray dominated regions (XDRs, Wolfire et al. 2022) could also contribute to the enhancement of high-J CO transitions. This might be the case for MD94, for which Erb et al. (2006) determined the existence of an AGN from spectra. In addition, signatures of low-luminosity AGN have been found in NGC 6240 and BX610 (Rosenberg et al. 2015; Bolatto et al. 2015). Interestingly, the CO excitation in MD94 does not seem as high as for the remaining three galaxies, at least up to CO (7 − 6) (Fig. 4). The absence of X-ray emission (Magdis et al. 2017) and strong mid-IR excess in our target D49 makes the AGN solution less favourable.
At this stage, the relatively small number of transitions observed for D49 and other high-redshift objects does not allow us to strongly constrain the contribution of different heating mechanisms. For reference only, large velocity gradient (LVG) modelling with a minimal set of free parameters (gas densities nH, kinetic temperatures Tkin, and [CI]/CO ratios; Liu et al. 2021) returns log(nH/cm−3) = 3.7 ± 0.2, but not meaningful constraints on the remaining variables. It is even less likely that a complex model with more parameters can be constrained by the current data. A simple PDR model (pdrtpy, Pound & Wolfire 2023) would favour ∼1 dex higher densities, inconsistent with the LVG result, and would suffer from a series of limitations that are well documented in the literature (Papadopoulos & Greve 2004; Papadopoulos et al. 2022; Harrington et al. 2021; Liu et al. 2021). Slow C-shocks in high-density environments (v ∼ 10 km s−1, nH ∼ 104 cm−3) would be able to reproduce some of the CO line ratios observed in D49 ( <
<  and
and 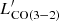 ; Table A1 in Flower & Forêts 2010).
; Table A1 in Flower & Forêts 2010).
4.3. Benchmarking gas tracers in a main-sequence galaxy
D49 offers the opportunity to estimate Mgas from several different tracers and cross-check their calibrations. We summarise the results of our multi-variate approach in Table A.2.
First, we re-derived Mgas from CO (3 − 2) applying an excitation correction factor of r31 = 0.5 ± 0.15 and a CO conversion factor of αCO = 3.5 consistent with Magdis et al. (2017). We then turned to dust-based estimates and derived Mgas from the full SED modelling with Stardust or single-band extrapolations from the Rayleigh-Jeans tail (Scoville et al. 2016). We allowed for metallicity-dependent gas-to-dust ratios δGDR(Z) at fixed solar metallicity or for implementing the FMR (Sect. 3.2). Finally, we took advantage of the availability of both [C I] transitions. As local thermodynamic equilibrium (LTE) is not necessarily fulfilled in galaxies (Papadopoulos et al. 2022), we derived hydrogen mass under non-LTE assumption as
where A10 = 10−7.10 s−1 is the Einstein A coefficient (Papadopoulos & Greve 2004; Bothwell et al. 2017). We adopt the neutral carbon abundance for main-sequence galaxies at z ∼ 1.2 in Valentino et al. (2018) log X[CI]=(−4.7 ± 0.1). According to our measurements, we find a [CI] (2 − 1)/[CI] (1 − 0) line ratio of ℛ = S[CI](2 − 1)Δv/S[CI](1 − 0)Δv > 2.25, where SΔv are the velocity integrated fluxes in Jy km s−1. We then derived the kinetic temperature of [CI] as Tkin = αTdust adopting α = 1.2 for main-sequence galaxies (Papadopoulos et al. 2022) and dust temperature Tdust = 41 K (Magdis et al. 2017). Thus, Tkin ∼ 49 K. For a typical gas density of n ≈ 104 cm−3, we expect excitation corrections Q10 ≈ 0.45 and Q21 ≈ 0.3 (Figs. 4 and 5 in Papadopoulos et al. 2022). We note that the helium contribution is not included in Eq. (3). We thus include an additional factor of 1.36 to account for the latter, thus resulting in a final estimate of log(Mgas/M⊙) < 11.22 from [CI] (1 − 0). By replacing all the [CI] (1 − 0)-related terms with those for [CI] (2 − 1), we obtain a consistent Mgas upper limit, set by the uncertainty on [CI] (1 − 0). As a cross-check, we applied the recent calibration by Dunne et al. (2022). The authors found that [CI] (1 − 0) is the preferred tracer for galaxies with log(LIR/L⊙) > 11 with the mean conversion factor αCI = (17.0 ± 0.3 M⊙) [K km s−1 pc2]−1, based on a sample of 407 metal-rich galaxies ranging from local to z ≈ 6. Given our upper limit on } $](/articles/aa/full_html/2023/05/aa45925-23/aa45925-23-eq24.gif) , we derive
, we derive } < 10^{11.16}\,M_\odot $](/articles/aa/full_html/2023/05/aa45925-23/aa45925-23-eq25.gif) , consistent with our estimates. As noted in Dunne et al. (2022), caution should be exerted when deriving Mgas from [CI] (2 − 1) given the uncertain excitation conditions.
, consistent with our estimates. As noted in Dunne et al. (2022), caution should be exerted when deriving Mgas from [CI] (2 − 1) given the uncertain excitation conditions.
All the Mgas estimates for D49 are consistent within the uncertainties and a factor of three or less, the highest being that from CO (3 − 2). However, given the high CO excitation, a higher r31 value for D49 could be expected. Among the examples detailed in the previous section, r31 = 1.1 ± 0.2 is found for NGC 6240, 0.9 ± 0.2 for BX610, and 1.2 ± 0.2 for MD94. By adopting the average of these values ⟨r31⟩ = 1.1 ± 0.1 (consistent with thermalisation up to J = 3), we find log(Mgas/M⊙) = 11.14 ± 0.08, more in line with the rest of the values in Table A.2.
4.4. Massive galaxy at the last stage of its evolution
Even considering a conservative upper limit of Mgas < 1011.22 M⊙, we estimate a gas depletion timescale of τdep = Mgas/SFR < 0.29 Gyr. For reference, for their main-sequence sample at z = 3.2, Schinnerer et al. (2016) found an average 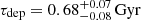 . The high SFE of D49 is typical of starburst galaxies, but its location is on the main sequence (the distance from the parametrisation of Sargent et al. 2014 is ΔMS = SFR/SFRMS = 0.9). Therefore, if the gas reservoirs are not replenished, D49 will exhaust its gas mass in a relatively short time, and will possibly transit to quiescence. This would be consistent with the fact that D49 is a very massive object in the bending part of the main sequence (Schreiber et al. 2015). We might thus be witnessing the ending growth spurt of this massive galaxy.
. The high SFE of D49 is typical of starburst galaxies, but its location is on the main sequence (the distance from the parametrisation of Sargent et al. 2014 is ΔMS = SFR/SFRMS = 0.9). Therefore, if the gas reservoirs are not replenished, D49 will exhaust its gas mass in a relatively short time, and will possibly transit to quiescence. This would be consistent with the fact that D49 is a very massive object in the bending part of the main sequence (Schreiber et al. 2015). We might thus be witnessing the ending growth spurt of this massive galaxy.
5. Conclusions
We presented robust (≳10σ) NOEMA measurements of CO (5 − 4), CO (7 − 6), [CI] (2 − 1), and a conservative upper limit on the [CI] (1 − 0) emission from the massive main-sequence galaxy D49 at z = 2.846. These add to previously available CO (3 − 2) measurements from the literature. Armed with these five lines and exquisite optical to millimetre photometry, we find the following:
-
We measure a higher CO (7 − 6)-to-IR ratio than the average at low and high redshifts. With such a ratio, the SFR predicted by CO (7 − 6) according to empirical LIR − LCO(7 − 6) relations would be approximately six times larger than that derived from its infrared luminosity. Either CO (7 − 6) is not a good tracer of SFR in D49 or mechanisms enhancing the high-J CO emission, but not affecting LIR, should be considered.
-
By comparing D49 with selected IR-bright galaxies in the local universe (NGC 6240) or objects on the main sequence at z ∼ 2 (BX610, MD94) displaying similar line ratios and CO (7 − 6) enhancements, we consider shocks or mechanical heating in general as a possible cause of the excess CO (7 − 6) emission. The physical drivers of mechanical heating are unknown for D49, but, as noted in the past, the high gas densities and temperatures are conditions naturally favouring turbulence, of which high CO excitation could be a reflection.
-
We benchmark gas mass estimates from CO, [C I], and dust under several assumptions in D49, finding them overall consistent within a factor of < 3×.
-
Given its high SFR ∼ 600 M⊙ yr−1, the ensuing gas depletion time of D49 is < 0.3 Gyr, indicating that it might possibly transition to quiescence shortly if no replenishment is ensured.
Future observations mapping more CO lines would help us to determine the SLED at much higher accuracy, also anchoring to low-J transitions. Direct observations of H2 lines (as a shock tracer) in the mid-IR with JWST would allow us to constrain the conversion factor and understand what contributes to the mechanical heating in D49.
Acknowledgments
The authors warmly thank the anonymous referee for the insightful comments that improved the presentation of our work and Isabella Cortzen for her contribution to the data reduction. The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under grant No. 140. SJ is supported by the European Union’s Horizon Europe research and innovation program under the Marie Skłodowska-Curie grant agreement No. 101060888.
References
- Battisti, A. J., da Cunha, E., Grasha, K., et al. 2019, ApJ, 882, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Lutz, D., Genzel, R., Förster-Schreiber, N. M., & Tacconi, L. J. 2016, A&A, 587, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Warren, S. R., Leroy, A. K., et al. 2015, ApJ, 809, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
- Bothwell, M. S., Aguirre, J. E., Aravena, M., et al. 2017, MNRAS, 466, 2825 [Google Scholar]
- Bourne, N., Dunlop, J. S., Simpson, J. M., et al. 2019, MNRAS, 482, 3135 [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [Google Scholar]
- Brisbin, D., Aravena, M., Daddi, E., et al. 2019, A&A, 628, A104 [EDP Sciences] [Google Scholar]
- Burgarella, D., Buat, V., & Iglesias-Páramo, J. 2005, MNRAS, 360, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Calistro Rivera, G., Hodge, J. A., Smail, I., et al. 2018, ApJ, 863, 56 [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chen, C.-C., Hodge, J. A., Smail, I., et al. 2017, ApJ, 846, 108 [Google Scholar]
- Cochrane, R. K., Best, P. N., Smail, I., et al. 2021, MNRAS, 503, 2622 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Daddi, E., Sargent, M. T., et al. 2021, A&A, 647, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [Google Scholar]
- Dunne, L., Maddox, S. J., Papadopoulos, P. P., Ivison, R. J., & Gomez, H. L. 2022, MNRAS, 517, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 647, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Forêts, Pineau Des. G. 2010, MNRAS, 406, 1745 [NASA ADS] [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, T. R., Leonidaki, I., Xilouris, E. M., et al. 2014, ApJ, 794, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, K. C., Weiss, A., Yun, M. S., et al. 2021, ApJ, 908, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Henríquez-Brocal, K., Herrera-Camus, R., Tacconi, L., et al. 2022, A&A, 657, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Högbom, J. A. 1974, A&AS, 15, 417 [Google Scholar]
- Kaasinen, M., Scoville, N., Walter, F., et al. 2019, ApJ, 880, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C. 2007, ApJ, 665, 1489 [Google Scholar]
- Kennicutt, R. C., Jr 1998a, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998b, ApJ, 498, 541 [Google Scholar]
- Kokorev, V. I., Magdis, G. E., Davidzon, I., et al. 2021, ApJ, 921, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Burwitz, V., Hasinger, G., et al. 2003, ApJ, 582, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Gao, Y., Isaak, K., et al. 2015, ApJ, 810, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Lang, P., Magnelli, B., et al. 2019a, ApJS, 244, 40 [Google Scholar]
- Liu, D., Schinnerer, E., Groves, B., et al. 2019b, ApJ, 887, 235 [Google Scholar]
- Liu, D., Daddi, E., Schinnerer, E., et al. 2021, ApJ, 909, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, N., Zhao, Y., Xu, C. K., et al. 2014, ApJ, 787, L23 [Google Scholar]
- Lu, N., Zhao, Y., Xu, C. K., et al. 2015, ApJ, 802, L11 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Madden, S. C., Cormier, D., Hony, S., et al. 2020, A&A, 643, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E., Daddi, E., Elbaz, D., et al. 2011, ApJ, 740, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Rigopoulou, D., Daddi, E., et al. 2017, A&A, 603, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Meijerink, R., Kristensen, L. E., Weiß, A., et al. 2013, ApJ, 762, L16 [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadopoulos, P. P., & Greve, T. R. 2004, ApJ, 615, L29 [Google Scholar]
- Papadopoulos, P. P., Thi, W. F., & Viti, S. 2004, MNRAS, 351, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P., Dunne, L., & Maddox, S. 2022, MNRAS, 510, 725 [Google Scholar]
- Pound, M. W., & Wolfire, M. G. 2023, AJ, 165, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Cutri, R. M., Black, J. H., et al. 1985, ApJ, 290, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Rigopoulou, D., Huang, J. S., Papovich, C., et al. 2006, ApJ, 648, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [Google Scholar]
- Rodighiero, G., Renzini, A., Daddi, E., et al. 2014, MNRAS, 443, 19 [Google Scholar]
- Rosenberg, M. J. F., van der Werf, P. P., Aalto, S., et al. 2015, ApJ, 801, 72 [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Groves, B., Sargent, M. T., et al. 2016, ApJ, 833, 112 [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Sheth, K., et al. 2014, ApJ, 783, 84 [CrossRef] [Google Scholar]
- Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [Google Scholar]
- Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728 [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2018, ApJ, 869, 27 [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2020, ApJ, 890, 24 [Google Scholar]
- Valentino, F., Daddi, E., Puglisi, A., et al. 2021, A&A, 654, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vignati, P., Molendi, S., Matt, G., et al. 1999, A&A, 349, L57 [NASA ADS] [Google Scholar]
- Wolfire, M. G., Vallini, L., & Chevance, M. 2022, ARA&A, 60, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C., Omont, A., Beelen, A., et al. 2017, A&A, 608, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Data of D49
In Tables A.1 and A.2 we list the photometric data we used in SED fitting and the Mgas estimates described in Section 4.3.
Optical to millimetre photometry of D49.
Hydrogen mass estimations by different methods.
All Tables
Best-fit results of CO and [CI] lines of D49, obtained by fixing the redshift and FWHM for CO (5 − 4), CO (7 − 6), and [CI] (2 − 1).
All Figures
 |
Fig. 1. Spectra of (a) CO (7 − 6) + [CI] (2 − 1), (b) CO (5 − 4), and (c) [CI] (1 − 0) emission of D49. The binned step width is ∼90 km s−1 in panels (a) and (c) and ∼40 km s−1 in panel (b). The red curves indicate the fitted Gaussian profiles combined with a power-law dust continuum, the latter shown by a dashed line. The blue and green shaded areas in panel (c) indicate the 1σv and ±3σv velocity width used to set the upper limit on [CI] (1 − 0). |
| In the text | |
 |
Fig. 2. Spectral energy distribution of D49. The red open squares and downward arrow indicate the fitted photometry and upper limits. The black line shows the Stardust best-fit SED, while the contribution from stars and dust are respectively shown as a blue and red filled region. The grey region presents the predicted contribution from radio continuum, based on the radio-FIR model described in Delvecchio et al. (2021). |
| In the text | |
 |
Fig. 3.
|
| In the text | |
 |
Fig. 4. CO spectral line energy distributions of D49, compared to BX610, NGC 6240, and MD94, normalised by their own |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} L\prime _{\rm line}\,\mathrm{[K\,km\,s^{-1}\,pc^2]} = 3.25 \times 10^7 S_{\rm line}\Delta { v} \, \nu _{\rm obs}^{-2} D_{\rm L}^2(1+z)^{-3}. \end{aligned} $$](/articles/aa/full_html/2023/05/aa45925-23/aa45925-23-eq1.gif)
}\Delta v < 3\times \mathrm{rms}_{\rm channel} \times \sqrt{6\sigma _v \mathrm{d}v}, \end{aligned} $$](/articles/aa/full_html/2023/05/aa45925-23/aa45925-23-eq2.gif)
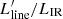
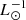
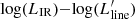
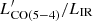
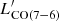
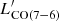
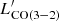
![$$ \begin{aligned} M_{\rm H_2} = 1375.8 D_{\rm L}^2 (1+z)^{-1} \left(\frac{X[\mathrm{CI}]}{10^{-5}}\right)^{-1}\left(\frac{A_{10}}{10^{-7}\,\mathrm{s^{-1}}}\right)^{-1} \nonumber \\ \times Q_{10}^{-1}S_{\rm [CI](1{-}0)}\Delta v, \end{aligned} $$](/articles/aa/full_html/2023/05/aa45925-23/aa45925-23-eq23.gif)