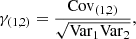| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A178 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202346309 | |
| Published online | 22 September 2023 | |
Intermittent properties of the quasi-periodic oscillations of MAXI J1820+070 revealed by Insight-HXMT
1
College of Science, China Three Gorges University, Yichang 443002, PR China
e-mail: zhangpeng@ctgu.edu.cn
2
Center for Astronomy and Space Sciences, China Three Gorges University, Yichang 443002, PR China
3
College of Astronomy and Space Sciences, University of the Chinese Academy of Sciences, Beijing 100049, PR China
e-mail: rsoria@nao.cas.cn
4
INAF-Osservatorio Astrofisico di Torino, Strada Osservatorio 20, 10025 Pino Torinese, Italy
5
Sydney Institute for Astronomy, School of Physics A28, The University of Sydney, Sydney, NSW 2006, Australia
6
Key Laboratory of Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, 19B Yuquan Road, Beijing 100049, PR China
e-mail: szhang@ihep.ac.cn
7
School of Physics and Astronomy, Sun Yat-Sen University, Zhuhai 519082, PR China
8
Institut für Astronomie und Astrophysik, Kepler Center for Astro and Particle Physics, Eberhard Karls, Universität, Sand 1, 72076 Tübingen, Germany
9
University of Chinese Academy of Sciences, Chinese Academy of Sciences, Beijing 100049, PR China
10
CAS Key Laboratory for Research in Galaxies and Cosmology, Department of Astronomy, University of Science and Technology of China, Hefei 230026, PR China
11
School of Astronomy and Space Science, University of Science and Technology of China, Hefei 230026, PR China
12
Key Laboratory of Dark Matter and Space Astronomy, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210008, PR China
13
School of Sciences, Hangzhou Dianzi University, Hangzhou 310018, PR China
Received:
3
March
2023
Accepted:
11
July
2023
We investigate the dynamical properties of low-frequency quasi-periodic oscillations (QPOs) observed from the black hole X-ray binary MAXI J1820+070 during the early part of its 2018 outburst, when the system was in a bright hard state. To do this, we used a series of observations from the Hard X-ray Modulation Telescope Insight-HXMT and applied a wavelet decomposition (weighted wavelet Z-transforms) to the X-ray light curve. We find that the QPO phenomenon is intermittent within each individual observation, with some subintervals in which the oscillation is strongly detected (high root-mean-square amplitude) and others in which it is weak or absent. The average lifetime of individual QPO segments is about 5 oscillation cycles, with a 3σ tail of up to about 20 cycles. There is no substantial difference between the energy spectra during intervals with strong and weak or absent QPOs. Alternatively, we suggest that the changes in oscillation amplitude can be caused by changes in the jet speed. We discuss a possible reason for the intermittent QPO strength within the precessing-jet model previously proposed for MAXI J1820+070: we suggest that the changes in oscillation amplitude are caused by changes in the jet speed. We argue that a misaligned precessing-jet scenario is also consistent with other recent observational findings that suggest that the oscillation of the Compton reflection component is in phase with the QPOs.
Key words: X-rays: binaries / X-rays: individuals: MAXI J1820+070
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Stellar mass black holes (BHs) in low-mass X-ray binaries accrete matter from their companion via Roche-lobe overflow and undergo occasional outbursts. The outburst evolution reflects the change in the balance between the thermal emission from the disk and the nonthermal emission from either a corona or a jet. During outbursts, these systems go through a series of spectral states, which are the low-hard state (LHS), the hard-intermediate state (HIMS), the soft-intermediate state (SIMS) and the high-soft state (HSS; Homan & Belloni 2005; Belloni 2010; Belloni & Motta 2016).
An important observational property of stellar mass BH X-ray binaries, potentially a probe of the inflow structure just outside the horizon, are quasi-periodic oscillations (QPOs; Remillard & McClintock 2006). QPOs are distinct peaks in the power density spectra of their X-ray light curves. QPOs are usually classified primarily into high-frequency (∼10–103 Hz) and low-frequency (∼10−2–10 Hz) oscillations. The latter are further divided into subtypes (types A, B, and C; Casella et al. 2004) based on their coherence and on the strength of different frequencies (Wijnands et al. 1999; Homan et al. 2001; Remillard et al. 2002). The coherence is expressed by the quality factor Q = ν/Δν, where ν is the centroid frequency and Δν is the full width at half maximum near the centroid frequency. The most common QPO subtype (also the one with the highest Q factor) is type C. It usually has a frequency in the range of a few mHz to 10 Hz, but has sometimes been detected at up to 30 Hz (Revnivtsev et al. 2000). Explanations for the origin of type C QPOs are still controversial. Alternative models include inner-disk instabilities and Lense-Thirring (LT) precession of either the jet or the inner hot flow or corona (Stella et al. 1999; Ingram et al. 2009; Ingram & Done 2011).
The Galactic X-ray transient MAXI J1820+070 is a particularly suitable target for the study of type C QPOs. It is a dynamically confirmed Galactic BH (Torres et al. 2019), discovered by the Monitor of All-sky X-ray Image (MAXI) on 2018 March 11 (Kawamuro et al. 2018). The position of the transient is consistent with that of ASASSN-18ey, an optical transient discovered 5 days earlier (Denisenko 2018). Gaia also detected an optical counterpart at the J2000 position of RA = 18h20m21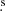 94, Dec = +07°11
94, Dec = +07°11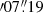 , with an apparent brightness g ≈ 17.41 mag. Its distance was estimated as
, with an apparent brightness g ≈ 17.41 mag. Its distance was estimated as 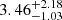 kpc from the Gaia Data Release 2 data (Gandhi et al. 2019). Atri et al. (2020) provided a consistent and more precise distance measurement of (2.96 ± 0.33) kpc using the parallax obtained from radio interferometry. The mass of the BH in MAXI J1820+070 was originally estimated as ≈6–8 M⊙ (Torres et al. 2019) from optical spectroscopic studies and was later revised to ≈8–9 M⊙ (Torres et al. 2020) based on the distance and inferred jet orientation angle of 63° ±3° of Atri et al. (2020). The mass donor is a low-mass star with M2 ≈ (0.6 ± 0.1) M⊙ (Torres et al. 2020).
kpc from the Gaia Data Release 2 data (Gandhi et al. 2019). Atri et al. (2020) provided a consistent and more precise distance measurement of (2.96 ± 0.33) kpc using the parallax obtained from radio interferometry. The mass of the BH in MAXI J1820+070 was originally estimated as ≈6–8 M⊙ (Torres et al. 2019) from optical spectroscopic studies and was later revised to ≈8–9 M⊙ (Torres et al. 2020) based on the distance and inferred jet orientation angle of 63° ±3° of Atri et al. (2020). The mass donor is a low-mass star with M2 ≈ (0.6 ± 0.1) M⊙ (Torres et al. 2020).
MAXI J1820+070 remained in a hard state throughout the initial outburst phase (2018 March–June; Shidatsu et al. 2018, 2019). As expected in the hard state, a large number of type C QPOs were detected (Uttley et al. 2018; Bright et al. 2018). Detailed X-ray timing studies during this hard state outburst have been presented in several recent works (e.g., Paice et al. 2019, 2021; Dziełak et al. 2021; Axelsson & Veledina 2021; De Marco et al. 2021; Mao et al. 2022; Thomas et al. 2022; Prabhakar et al. 2022; Zhou et al. 2022; Gao et al. 2023; Kawamura et al. 2023).
We focus on the timing information from the X-ray satellite Insight-Hard X-ray Modulation Telescope (Insight-HXMT). With Insight-HXMT, QPOs were detected at energies as high as 250 keV during the LHS. A precessing-jet scenario was proposed as a possible explanation (Ma et al. 2021). Here, we revisit the Insight-HXMT observations during the LHS and apply a wavelet decomposition to the light curves to determine the dynamic properties of the QPOs. We describe the observations and data analysis in Sect. 2, present the main results in Sect. 3, and discuss possible interpretations in Sect. 4.
2. Observations and data analysis
Insight-HXMT (Zhang et al. 2014, 2020) was launched on 2017 June 15 and is the first Chinese X-ray astronomical satellite. It carries three X-ray instruments: the High Energy (HE; Liu et al. 2020), Medium Energy (ME; Chen et al. 2020), and Low Energy (LE; Cao et al. 2020) X-ray Telescopes. All three work in a collimated way and are equipped with blind detectors. The HE is made of 18 cylindrical NaI(TI)/CsI(Na) phoswich detectors and covers the 20.0–250.0 keV band, with a total detection area of 5100 cm2. The ME consists of 1728 Si-PIN detectors, sensitive in the 5.0–30.0 keV band, with a total detection area of 952 cm2. The LE operates with swept charged devices in the 1.3–15.0 keV band and has a total detection area of 384 cm2.
MAXI J1820+070 was monitored by Insight-HXMT 146 times for a total exposure time of 2.56 Ms (Fig. 1). Sixty observations for a total exposure of 1.56 Ms were taken during the LHS (2018 March 14–July 6). We reduced the LHS data following the standard procedure in the Insight-HXMT data analysis software HXMTDAS, version v2.021. The good-time intervals were selected with the following criteria: elevation angle > 10°, geomagnetic cutoff rigidity > 8 GeV, pointing offset angle < 0.04°, and > 600 s away from the South Atlantic Anomaly (SAA). The background model was produced with standard python scripts (hebkgmap, mebkgmap, and lebkgmap) and subtracted in both timing and spectral analyses.
 |
Fig. 1. Insight-HXMT/HE light curve of MAXI J1820+070 in the 30–150 keV band during the 2018 LHS outburst. Calendar dates in the month – day format are reported on the top horizontal axis. The dotted red line marks the time of ObsID P01146610150 that was chosen for the dynamic QPO study in this work. |
Traditional tools for time-variability studies include the analysis of the power spectral density (PSD), the short-time Fourier transform (STFT) of the light curve, and the Lomb-Scargle periodogram (LSP; Lomb 1976; Scargle 1982; Zechmeister & Kürster 2009). PSDs and LSPs are best suited for the search of strictly periodic signals, but they are not designed for the analysis of signals with a time-varying frequency. STFTs can handle variable frequencies, but are heavily dependent on the choice of window function as they often have significant side effects if chosen poorly (Zhao et al. 2021). Instead, weighted wavelet Z-transforms (WWZ2; Foster 1996; Torrence & Compo 1998) produce a robust map in the frequency–time domain, and are the best available tool for variability studies of QPOs in both strength and frequency. Examples of the use of WWZ analysis to investigate the transient nature of QPOs in various astrophysical systems are, for example, Bravo et al. (2014), Ait Benkhali et al. (2020), and Urquhart et al. (2022).
For our study of MAXI J1820+070, we used a version of WWZ modified with a Morlet parent function (Foster 1996). We produced three sets of 2D WWZ color maps (power spectrum versus elapsed time) for the LE (2–8 keV), ME (8–30 keV) and HE (30–150 keV) bands. By performing the WWZ analysis on the three bands independently and then comparing and correlating the results, we can more confidently identify real structures (present in all three bands) as opposed to possible artifacts.
We also extracted energy spectra over the same time intervals using the HXMTDAS tools hespecgen, mespecgen, and lespecgen. We used the task grppha within FTOOLS (Blackburn 1995) to rebin the spectral data to a minimum of 30 counts per bin, so that we could later fit the spectra with the χ2 statistics. For our spectral analysis (Sect. 3.2), we used XSPEC (v. 12.9.0n, Arnaud 1996). We fit the LE, ME, and HE spectra simultaneously. A systematic error of 1% was added to account for the calibration uncertainties, and we also allowed for a free normalization constant between the three instruments.
3. Results
3.1. Timing results
As a starting point of our time-resolved WWZ analysis, we used the observation-averaged QPO frequencies determined by Ma et al. (2021) as central frequencies for each observation. This is possible because the frequencies do not vary substantially within each observation. Instead, the strength of the QPO is strongly variable within each observation: Each interval of QPO detection is short, and for most of the exposure time, the oscillation is weak or undetected. Here, we chose ObsID P011466101502 (exposure time:3172 s, on 2018 April 8, Fig. 1) to illustrate this general behavior (Fig. 2).
 |
Fig. 2. 2D plot on the left: Dynamic WWZ power in time-frequency space during ObsID P011466101502. The red contours represent regions (in time-frequency space) of QPO activity with a significance > 3σ. the units of WWZ power are (root-mean-square/mean)2 Hz−1. The line plot on the right side of all panels shows the corresponding time-averaged WWZ power spectrum over the whole observation in each band. The dashed red line indicates the peak power at a QPO frequency of 0.082 Hz, and the dashed blue lines correspond to ±20% around peak frequency. Top panel: For the HE data in the 30–250 keV band. Middle panel: For the ME data in the 5–30 keV band. Bottom panel: For the LE data in the 1.3–15.0 keV band. |
We determined the significance of intra-observation QPO structures by comparing their power with the distribution of power values within 20% of the central QPO frequency. We selected all QPO intervals with a significance higher than 3σ (red contours in the left panels of Fig. 2) by calculating the average and standard deviation within the region. We applied this procedure separately for the three detectors. Then, we determined the duration of each significant QPO interval, expressed in units of the average QPO period measured over that segment. The lifetime depends on the threshold we chose for the definition of QPO significance. If we were to choose a much lower significance, not only will the lifetime of each QPO segment increase, but neighboring segments may connect into a single interval. However, the main qualitative finding of our analysis, which is the presence of stronger and weaker intervals of QPO behavior, remains valid. For simplicity, we sometimes refer to observation subintervals in which a QPO is or is not detected at the 3 − σ level as QPO and non-QPO intervals.
The QPO frequencies increase with time during the LHS outburst phase (Ma et al. 2021). However, we found that the dimensionless lifetime of each QPO segment remains approximately constant. The average lifetime is 6.4 cycles in the LE band, 6.6 in the ME band, and 6.8 cycles in the HE band, and the standard deviations are 4.0, 4.4, and 4.6, respectively. Calculated over the full energy band, the average lifetime is (6.7 ± 4.4) cycles. When we fit the lifetime distributions with Gaussians (Fig. 3), the mode is (4.82 ± 0.24) cycles in the HE data, (4.89 ± 0.22) cycles in the ME data, (4.88 ± 0.26) cycles in the LE data, and (4.85 ± 0.21) over the full energy band. The standard deviations (1 σ) are 4.51, 4.03, 3.98, and 4.31 cycles, respectively. There is a slight excess of apparently long QPO segments (lifetimes of ≈15–20 cycles) over the best-fitting Gaussian distributions (Fig. 3). Events like this likely correspond to adjacent shorter QPO intervals that are connected in our WWZ analysis. Furthermore, we calculated the QPO lifetime distributions at different QPO frequencies (0–0.2 Hz, 0.2–0.4 Hz, and 0.4–0.63 Hz), shown as blue, red and green histograms in Fig. 3. The three distributions are not significantly different. We conclude that the average lifetime of QPO events in the LHS of MAXI J1820+070 is about five cycles, with a standard deviation of the lifetime distribution of about four cycles, regardless of the energy band and QPO frequency. Finally, we used the FTOOLS (Blackburn 1995) task powspec to calculate the power spectral density of all observations, and the root-mean-square (rms) value of the QPOs (fit with Lorentz functions). We used the WWZ maps to distinguish exposure time intervals with and without a QPO. We obtain an average rms ≈11.3% for the intervals of QPO detection and an rms < 9.6% for the intervals in which no significant oscillations are detected.
 |
Fig. 3. QPO lifetime distribution over all the 2018 March–June Insight-HXMT observations in units of cycles. The left panel shows the LE energy band, the middle panel shows the ME, and the right panel shows the HE. In all panels, the blue histogram is the lifetime distribution of QPOs with frequencies < 0.2 Hz. The red histogram is the distribution for QPOs with frequencies of 0.2–0.4 Hz. The green histogram shows QPO frequencies of 0.4–0.63 Hz. The black histogram is the lifetime distribution for all QPOs of any frequency. The total lifetime distribution in each panel has been fitted with a Gaussian (solid black curve), and the dashed black lines mark the Gaussian mean lifetime and the value of 1σ above the mean. |
To ensure that the QPO segments found in our WWZ analysis are real physical events and not just statistical artifacts, we correlated the three WWZ maps in the LE, ME and HE bands for each observation. The Pearson correlation coefficient γ(1, 2) between a band 1 and a band 2 is
where Var1 and Var2 are the variances of the WWZ powers in the two bands, and Cov(1, 2) is their covariance.
For each observation, we calculated the correlation coefficient over a frequency range of ±20% of the average QPO frequency in that observation. For the specific observation P011466101502 illustrated here as an example, the frequency range for the correlation coefficient is 0.064–0.096 Hz (around the average QPO frequency of 0.082 Hz). We obtain γLE, HE = 0.84 and γME, HE = 0.90. This suggests that the QPO structures independently seen in the three bands at the same time (Fig. 2) are indeed real. In total, there are 60 Insight-HXMT observations for which we were able to conduct a QPO correlation analysis between the three bands. The average LE-ME correlation coefficient over all those observations is γLE, HE = 0.83, with a standard deviation of their distribution σLE, HE = 0.06. For the ME-HE bands, the average correlation γME, HE = 0.90, with a standard deviation σME, HE = 0.05. We also examined the observation epochs with relatively low Pearson correlation coefficients and found that their QPO signals were weak and the noise was too strong, which lowered the significance of the Pearson correlation coefficient. We removed from our estimate the 11 observations with the lowest QPO signals (significance ≤ 3σ) and re-calculated the band-to-band correlations over the remaining 49 observations with a stronger QPO detection. This gives γLE, HE = 0.90 with a standard deviation of their distribution σLE, HE = 0.04 and γME, HE = 0.94 with a standard deviation of their distribution σLE, HE = 0.03, respectively.
In order to verify that the measured correlations are not an artifact of the wavelet analysis, we performed the following test. We assumed the same stationary power spectrum for all three bands. We used Fourier transforms to generate 1000 simulated light curves for each band. We also generated independent backgrounds and added 5% counting noise for each light curve. Then, we applied a wavelet analysis to the simulated light curves and selected the same frequency range to calculate the correlation coefficients. We obtained correlation coefficients consistent with 0: for LE–HE, an average simulated γLE, HE = 0.015 with a dispersion σLE, HE = 0.076, and for ME–HE, an average simulated γME, HE = 0.022 with a dispersion σME, HE = 0.081. We conclude that the correlation between QPO intervals across nonoverlapping energy bands found in our observational data is a real physical property and not an artifact of WWZ analysis.
3.2. Spectral results
For each observation, we built three sets of spectra (LE, ME, and HE) of the QPO and non-QPO intervals (defined again from the WWZ maps). We then fit them simultaneously for the three instruments over the 2–150 keV energy band (2–10 keV for LE, 10–30 keV for ME, and 30–150 keV for HE), with standard models suitable for BH X-ray binaries. As an example, we illustrate here the results from ObsID P011466101502, chosen again because of its high signal-to-noise ratio. The spectral modeling results from the other observations are qualitatively similar.
As a first trial, we used an absorbed disk-blackbody plus Comptonization plus Fe line model, const × TBabs × (diskbb + gaussian + cutoffpl), where the constant factor accounts for the systematic uncertainty in the normalization of the three instruments. The neutral absorption component tbabs (Wilms et al. 2000) was fixed at NH = 1.5 × 1021 cm−2 (Uttley et al. 2018; You et al. 2021). This model does not give an acceptable fit, with a reduced 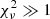 (bottom panel of Fig. 4). The systematic residuals clearly suggest the presence of a reflection component with a characteristic bump around 30–60 keV.
(bottom panel of Fig. 4). The systematic residuals clearly suggest the presence of a reflection component with a characteristic bump around 30–60 keV.
 |
Fig. 4. Insight-HXMT spectrum from 2018 April 8 (ObsID P011466101502). Top panel: Spectrum fit with the model TBabs × constant × TBabs × (diskbb + gaussian + relxill). The black datapoints show observation intervals in which QPOs are detected, and red datapoints show non-QPO intervals. Middle panel: Residuals for the same spectral model. Bottom panel: Residuals when the same spectrum is fit with the simpler model constant × TBabs × (diskbb + gaussian + cutoffpl), i.e., without disk reflection. |
To account for the apparent reflection, we replaced the phenomenological power-law component with the more physical relxill3 model (Dauser et al. 2014; García et al. 2014) version 1.2.0 (Dauser et al. 2016). Relxill computes the combined direct and reflected spectrum of an incident primary continuum (a power law with exponential high-energy cutoff) reflecting off an accretion disk. In our fits, we left the incident power-law photon index Γ and cutoff energy Ecut as free parameters, as well as the Fe abundance AFe, the maximum ionization ξ of the disk, and the reflection fraction Rf. We fixed the power-law index of the disk emissivity profile at q = 3 for both the inner and outer disk regions to reduce the number of free parameters. We also fixed the viewing angle at i = 63°, based on the estimate of You et al. (2021). In any case, the choice of viewing angle has only a small effect on the shape of the reflected spectrum. We also fixed the spin of BH at a = 0.13 based on the estimate of Guan et al. (2021). We froze the inner disk radius parameter Rin at the innermost stable circular orbit (default in relxill). We also tested the possibility of leaving it as a free parameter, but we realized that it would tend to the lowest possible value during the fitting process. The outer disk radius parameter Rout was fixed at a high value outside the X-ray emitting region. Finally, we included a Gaussian line to model the Fe–K line emission around 6.4 keV, and a diskbb component to model the direct thermal emission from the disk. In summary, our final XSPEC model was const × tbabs × (diskbb + gaussian + relxill). The best-fitting parameter values (Table 1) were obtained with a Markov chain Monte Carlo algorithm. The model provides a good fit (Table 1 and the top two panels of Fig. 4), with reduced χ2 ≤ 1.0.
Best-fitting spectral parameters derived from our modeling of Obs.
We stress that we did not try to give a physical interpretation of the inflow structure or derive the system parameters of MAXI J1820+070 from our spectral modeling here. Our only motivation for this modeling is to test whether there is a significant spectral difference between subintervals with and without a QPO. Thus, we only aimed at obtaining a phenomenologically good fit over the Insight-HXMT energy range. For a more physical modeling of the spectral components, it is necessary to also use spectral data in the softer X-ray band, for instance, from XMM-Newton, Swift, or NICER. This detailed analysis was carried out elsewhere (e.g., Shidatsu et al. 2019; Bharali et al. 2019; Kajava et al. 2019; Chakraborty et al. 2020; Paice et al. 2021; Dziełak et al. 2021; De Marco et al. 2021; Axelsson & Veledina 2021; Prabhakar et al. 2022; Kawamura et al. 2022, 2023). For example, we are aware that the inner radius of the geometrically thin accretion disk in the 2018 LHS, even near peak luminosity, was a few times larger than the innermost stable circular orbit RISCO (Bharali et al. 2019; Shidatsu et al. 2019; De Marco et al. 2021; Kawamura et al. 2023). RISCO itself was estimated to be ≈70 km (Shidatsu et al. 2019; Fabian et al. 2020, using the system parameters of Atri et al. 2020). We are also aware that more than one Comptonization region (e.g., a two-temperature corona, or a corona plus jet) may be required to fit the broadband X-ray spectrum (e.g., Chakraborty et al. 2020; Dziełak et al. 2021; Paice et al. 2021).
Keeping in mind the previous caveats, our spectral results from an individual observation show that there is no substantial spectral difference between the times with and without a QPO. The only slight changes are in the photon index Γ, which is slightly steeper during QPO intervals (Table 1), and (as a consequence of this) in the 30–150 keV flux (f30 − 150 = (2.7 ± 0.1)×10−8 erg cm−2 s−1 in QPO intervals, and f30 − 150 = (2.9 ± 0.1)×10−8 erg cm−2 s−1 in non-QPO intervals). There is no difference (within the 90% confidence limit) in the normalization of the reflection component, in the reflection fraction, and in the broadband luminosity. However, the error range of the best-fitting values for an individual observation are too large to detect subtle effects. To achieve this, more work over the whole Insight-HXMT dataset is currently in preparation.
4. Discussion and conclusions
We applied a WWZ analysis to the Insight-HXMT light curve of MAXI J1820+070 in the LHS during the 2018 March–June outburst to study the stability of flux oscillations in time–frequency space. We found that type C QPOs in this system are an intermittent rather than a persistent phenomenon. We showed that the average duration of each oscillatory interval is about 5 QPO cycles, with a 3σ upper limit of about 20 cycles.
Short-duration (intra-observation) QPO intervals were found in other Galactic BH X-ray binaries: in Cyg X-1 during a failed outburst (Lachowicz & Czerny 2005), and in XTE J1550−564 in a very high state (Su et al. 2015). In another Galactic BH in the very high state, GRS 1915+105, van den Eijnden et al. (2016) identified periods of high-amplitude coherent oscillations separated by time intervals in which the QPO loses phase coherence. This behavior is probably analogous to the intermittent QPO behavior highlighted here. An ultraluminous X-ray source in M 51 (possibly a neutron star) exhibits intermittent oscillations with characteristic periods of ∼500–700 s and a lifetime of a few cycles (Urquhart et al. 2022). Intermittent QPOs with timescales of a few hours have been seen in narrow-line Seyfert I galaxies such as RE J1034+396 (Middleton et al. 2011), 1H 0707−495 (Pan et al. 2016; Zhang et al. 2018), and Mrk 766 (Zhang et al. 2017). The sources mentioned above were in different accretion states (e.g., near-Eddington for narrow-line Seyfert I galaxies, and super-Eddington for the ultraluminous source in M 51), and their oscillations are likely to have a different physical origin. We simply mention these other examples to stress that the intermittency characteristics of QPOs at different scales, and what distinguishes periods with and without a coherent oscillation, are still poorly known.
In the case of the intermittent QPOs of MAXI J1820+070 studied here, their frequency and the outburst state in which they were found leads to their classification as type C low-frequency QPOs. The X-ray photons in the oscillating component come from the Comptonizing region (Chakrabarti & Manickam 2000), either directly or via disk reflection, but the physical origin of the oscillation is still unclear (Ingram & Motta 2019). One model (Ingram et al. 2009) attributes them to the LT precession (Lense & Thirring 1918) of the inner geometrically thick hot flow (corona or advective flow). This precession causes periodic modulations of the projected area and a maximum optical depth of the hot emission region with respect to our line of sight. It also modulates the flux of disk photons (seed thermal component) irradiating the Comptonizing region. The rigid precession model provides a physical explanation for intermittent QPOs, which are predicted to occur with a coherence Q of approximately a few when the alignment timescale tal is only a few times the precession timescale tpr. In this framework, the most important factors that determine the ratio tal/tpr(≈Q) are the outer radius of the geometrically thick part of the disk (the precessing region) and the BH spin (Motta et al. 2018). For a given spin parameter, larger radii of the thick precessing region correspond to a lower ratio of tal/tpr and therefore, to more intermittent shorter-lived QPOs, down to the point where QPOs can no longer be produced (tal/tpr < 2). This also implies a minimum QPO frequency (maximum precessing radius) for any given spin. In particular, only slowly spinning BHs can produce type C QPOs with frequencies ≲0.1 Hz (Motta et al. 2018, their Fig. 8), as we observed in MAXI J1820+070. This is consistent with the slow spin proposed for MAXI J1820+070 from the continuum-fitting method (Guan et al. 2021). Alternatively, the precessing region might be temporarily blocked from our view by intervening disk material. However, the latter scenario is not consistent with our spectral results (Sect. 3.2), which show no change in the energy spectrum between QPO and non-QPO epochs.
Several other low-frequency QPO models are based on disco-seismic oscillations (e.g., corrugation modes, inertial-acoustic modes, and inertial-gravity modes). These are standing ways inside the disk, trapped between two characteristic radii, which give rise to characteristic resonant frequencies (e.g., Wagoner 1999; Kato 2001; Tsang & Butsky 2013; Ingram & Motta 2019). The advantage of these models is that they include mechanisms for excitation and damping of the various oscillatory modes (e.g., Li et al. 2003; Zhang & Lai 2006; Tsang & Lai 2009; Fu & Lai 2009). A comparison of the observed QPO lifetimes with the predicted excitation and damping timescales is beyond the scope of this work. Similarly, we will leave to further work any discussion of excitation and damping in other well-known QPO models, such as those based on propagating oscillatory shocks near a centrifugal boundary layer (Chakrabarti et al. 2008; Debnath et al. 2010), on the accretion-ejection instability in disks threaded by a strong poloidal magnetic field (Tagger & Pellat 1999; Rodriguez et al. 2002; Tagger 2007; Varnière et al. 2012), or on disk oscillations and jet wobbling in response to instabilities near a magnetic recollimation zone (Ferreira et al. 2022).
Based on the Insight-HXMT detection of low-frequency QPOs in MAXI J1820+070 at energies as high as ∼200–250 keV and on the large soft lag (increasing with photon energy), Ma et al. (2021) argued that the QPOs in the LHS of this system are caused by LT precession of a compact jet. Furthermore, based on the evolution of the reflection fraction, You et al. (2021) suggested that the Comptonizing region in MAXI J1820+070 is a standing shock at the base of the jet, rather than a static hot region above the disk. Thus, we need to examine whether the jet-precession scenario is consistent with the intermittent QPO properties seen in the WWZ maps. We already noted that the main difference between the two regimes is a reduced rms amplitude of the oscillation. In the precessing-jet model (Ma et al. 2021), the observed fractional rms amplitude of the low-frequency QPOs is a function of jet speed (via Doppler beaming of the X-ray photons): Lower jet speeds lead to fainter QPOs. Therefore, we speculate that the discontinuity of the QPO signal may be caused by changes in the jet velocity on timescales of a few tens to a few hundred seconds. For example, the average fractional rms of ≈11.3% measured for QPO intervals (Sect. 3.1) corresponds to a jet speed of ≈0.52c (Extended Data Fig. 8 in Ma et al. 2021). For the non-QPO intervals, the observed rms upper limit corresponds to a 3σ upper limit of ≈0.47c.
The characteristic timescale of the jet speed variability (∼5–20 QPO cycles) may in turn be determined by mass loading, hence by variations of the accretion rate, or other inflow properties such as inner-disk or boundary layer oscillations. A discussion of this disk-jet coupling is beyond the scope of this preliminary work. As an empirical comparison, the jet speed in the best-studied Galactic microquasar, SS 433, was observed to vary between ≈0.21c and ≈0.32c, correlated with the collimation angle (Blundell & Bowler 2005; Blundell et al. 2007; Jeffrey et al. 2016).
Recently, Gao et al. (2023) carried out a timing study of type C QPOs in the 2018 March–June outburst of MAXI J1820+070, also based on Insight-HXMT data. Their method is somewhat complementary to our analysis: They selected subintervals with strong QPOs and extracted phase-resolved spectra around the peaks and the troughs of the oscillation. Their main finding is that QPOs are dominated by an oscillation of the reflection fraction for photons with energies ≲30 keV, and by an oscillation of the direct Comptonized component above those energies. We examined whether our proposed scenario of variable speed in a precessing jet is consistent with these results. At first sight (as argued by Gao et al. 2023), a precessing jet alone seems to be unable to create an oscillating reflection fraction because the solid angle of the disk seen by Comptonized photons does not change during the jet precession. However, a misaligned jet will always illuminate one side of the disk more strongly. During the precession cycle, Doppler boosting in the disk will increase the observed reflection component when the jet illuminates the approaching side of the rotating disk, and decrease the reflection component when it illuminates the receding side (Ingram et al. 2017). Thus, we conclude that an LT precession (at constant jet speed) is perfectly consistent with the observed X-ray properties of the oscillation during QPO subintervals. A change in jet speed is consistent with the observed strengthening and weakening (or disappearance) of the QPO over characteristic timescales of tens to hundreds of seconds, as highlighted in this study.
Acknowledgments
This work is supported by the National Key R&D Program of China (2021YFA0718500) and the National Natural Science Foundation of China under grants 12203029, U1838201, U1838202, U1938101, 12073029, 11733009, 12233002 and U2031205. This work made use of data from the Insight-HXMT mission, a project funded by China National Space Administration (CNSA) and the Chinese Academy of Sciences (CAS). We thank Sandip Chakrabarti for discussions on QPO models.
References
- Ait Benkhali, F., Hofmann, W., Rieger, F. M., & Chakraborty, N. 2020, A&A, 634, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Atri, P., Miller-Jones, J. C. A., Bahramian, A., et al. 2020, MNRAS, 493, L81 [CrossRef] [Google Scholar]
- Axelsson, M., & Veledina, A. 2021, MNRAS, 507, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. M. 2010, in Lecture Notes in Physics (Springer Verlag: Springer Verlag), 794, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. M., & Motta, S. E. 2016, in Astrophysics of Black Holes: From Fundamental Aspects to Latest Developments, ed. C. Bambi, Astrophys. Space Sci. Libr., 440, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Bharali, P., Chauhan, J., & Boruah, K. 2019, MNRAS, 487, 5946 [Google Scholar]
- Blackburn, J. K. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 367 [Google Scholar]
- Blundell, K. M., & Bowler, M. G. 2005, ApJ, 622, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Bowler, M. G., & Schmidtobreick, L. 2007, A&A, 474, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bravo, J. P., Roque, S., Estrela, R., Leão, I. C., & De Medeiros, J. R. 2014, A&A, 568, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bright, J., Fender, R., & Motta, S. 2018, ATel., 11420, 1 [NASA ADS] [Google Scholar]
- Cao, X., Jiang, W., Meng, B., et al. 2020, Sci. Chin. Phys. Mech. Astron., 63, 249504 [NASA ADS] [CrossRef] [Google Scholar]
- Casella, P., Belloni, T., Homan, J., & Stella, L. 2004, A&A, 426, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chakrabarti, S. K., & Manickam, S. G. 2000, ApJ, 531, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., Debnath, D., Nandi, A., & Pal, P. S. 2008, A&A, 489, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chakraborty, S., Navale, N., Ratheesh, A., & Bhattacharyya, S. 2020, MNRAS, 498, 5873 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Cui, W., Li, W., et al. 2020, Sci. Chin. Phys. Mech. Astron., 63, 249505 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Garcia, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [Google Scholar]
- Dauser, T., García, J., & Wilms, J. 2016, Astron. Nachr., 337, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Debnath, D., Chakrabarti, S. K., & Nandi, A. 2010, A&A, 520, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Marco, B., Zdziarski, A. A., Ponti, G., et al. 2021, A&A, 654, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denisenko, D. 2018, ATel., 11400, 1 [NASA ADS] [Google Scholar]
- Dziełak, M. A., De Marco, B., & Zdziarski, A. A. 2021, MNRAS, 506, 2020 [Google Scholar]
- Fabian, A. C., Buisson, D. J., Kosec, P., et al. 2020, MNRAS, 493, 5389 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., Marcel, G., Petrucci, P. O., et al. 2022, A&A, 660, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foster, G. 1996, AJ, 112, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, W., & Lai, D. 2009, ApJ, 690, 1386 [NASA ADS] [CrossRef] [Google Scholar]
- Gandhi, P., Rao, A., Johnson, M. A. C., Paice, J. A., & Maccarone, T. J. 2019, MNRAS, 485, 2642 [Google Scholar]
- Gao, C., Yan, Z., & Yu, W. 2023, MNRAS, 518, 526 [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [Google Scholar]
- Guan, J., Tao, L., Qu, J. L., et al. 2021, MNRAS, 504, 2168 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., & Belloni, T. 2005, Ap&SS, 300, 107 [Google Scholar]
- Homan, J., Wijnands, R., van der Klis, M., et al. 2001, ApJS, 132, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., & Done, C. 2011, MNRAS, 415, 2323 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A. R., & Motta, S. E. 2019, New A Rv., 85, 101524 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., Done, C., & Fragile, P. C. 2009, MNRAS, 397, L101 [Google Scholar]
- Ingram, A., van der Klis, M., Middleton, M., Altamirano, D., & Uttley, P. 2017, MNRAS, 464, 2979 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffrey, R. M., Blundell, K. M., Trushkin, S. A., & Mioduszewski, A. J. 2016, MNRAS, 461, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Kajava, J. J. E., Motta, S. E., Sanna, A., et al. 2019, MNRAS, 488, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S. 2001, PASJ, 53, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, T., Axelsson, M., Done, C., & Takahashi, T. 2022, MNRAS, 511, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, T., Done, C., Axelsson, M., & Takahashi, T. 2023, MNRAS, 519, 4434 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamuro, T., Negoro, H., Yoneyama, T., et al. 2018, ATel., 11399, 1 [NASA ADS] [Google Scholar]
- Kubota, A., Tanaka, Y., Makishima, K., et al. 1998, PASJ, 50, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Lachowicz, P., & Czerny, B. 2005, MNRAS, 361, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Lense, J., & Thirring, H. 1918, Phys. Z., 19, 156 [Google Scholar]
- Li, L.-X., Goodman, J., & Narayan, R. 2003, ApJ, 593, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Zhang, Y., Li, X., et al. 2020, Sci. Chin. Phys. Mech. Astron., 63, 249503 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Ma, X., Tao, L., Zhang, S.-N., et al. 2021, Nat. Astron., 5, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, D. M., Yu, W. F., Zhang, J. J., et al. 2022, Res. Astron. Astrophys., 22, 045009 [CrossRef] [Google Scholar]
- Middleton, M., Uttley, P., & Done, C. 2011, MNRAS, 417, 250 [CrossRef] [Google Scholar]
- Motta, S. E., Franchini, A., Lodato, G., & Mastroserio, G. 2018, MNRAS, 473, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Paice, J. A., Gandhi, P., Shahbaz, T., et al. 2019, MNRAS, 490, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Paice, J. A., Gandhi, P., Shahbaz, T., et al. 2021, MNRAS, 505, 3452 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, H.-W., Yuan, W., Yao, S., et al. 2016, ApJ, 819, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Prabhakar, G., Mandal, S., Athulya, M. P., & Nandi, A. 2022, MNRAS, 514, 6102 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
- Remillard, R. A., Muno, M. P., McClintock, J. E., & Orosz, J. A. 2002, ApJ, 580, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M. G., Trudolyubov, S. P., & Borozdin, K. N. 2000, MNRAS, 312, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Varnière, P., Tagger, M., & Durouchoux, P. 2002, A&A, 387, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Shidatsu, M., Nakahira, S., Yamada, S., et al. 2018, ApJ, 868, 54 [CrossRef] [Google Scholar]
- Shidatsu, M., Nakahira, S., Murata, K. L., et al. 2019, ApJ, 874, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., Vietri, M., & Morsink, S. M. 1999, ApJ, 524, L63 [CrossRef] [Google Scholar]
- Su, Y.-H., Chou, Y., Hu, C.-P., & Yang, T.-C. 2015, ApJ, 815, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Tagger, M. 2007, Rev. Mex. Astron. Astrofis. Conf. Ser., 27, 26 [NASA ADS] [Google Scholar]
- Tagger, M., & Pellat, R. 1999, A&A, 349, 1003 [NASA ADS] [Google Scholar]
- Thomas, J. K., Buckley, D. A. H., Charles, P. A., et al. 2022, MNRAS, 513, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
- Torres, M. A. P., Casares, J., Jiménez-Ibarra, F., et al. 2019, ApJ, 882, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, M. A. P., Casares, J., Jiménez-Ibarra, F., et al. 2020, ApJ, 893, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, D., & Butsky, I. 2013, MNRAS, 435, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, D., & Lai, D. 2009, MNRAS, 393, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, R. T., Soria, R., Di Stefano, R., et al. 2022, MNRAS, 511, 4528 [CrossRef] [Google Scholar]
- Uttley, P., Gendreau, K., Markwardt, C., et al. 2018, ATel., 11423, 1 [NASA ADS] [Google Scholar]
- van den Eijnden, J., Ingram, A., & Uttley, P. 2016, MNRAS, 458, 3655 [Google Scholar]
- Varnière, P., Tagger, M., & Rodriguez, J. 2012, A&A, 545, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagoner, R. V. 1999, Phys. Rep., 311, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Homan, J., & van der Klis, M. 1999, ApJ, 526, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- You, B., Tuo, Y., Li, C., et al. 2021, Nat. Commun., 12, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, H., & Lai, D. 2006, MNRAS, 368, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., Zhang, P.-F., Yan, J.-Z., Fan, Y.-Z., & Liu, Q.-Z. 2017, ApJ, 849, 9 [CrossRef] [Google Scholar]
- Zhang, P.-F., Zhang, P., Liao, N.-H., et al. 2018, ApJ, 853, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Lu, F. J., Zhang, S. N., Li, T. P., et al. 2014, in Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, eds. T. Takahashi, J. W. A. den Herder, & M. Bautz, SPIE Conf. Ser., 9144, 914421 [NASA ADS] [Google Scholar]
- Zhang, S.-N., Li, T., Lu, F., et al. 2020, Sci. Chin. Phys. Mech. Astron., 63, 249502 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, A., Subramani, K., & Smaragdis, P. 2021, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 736 [Google Scholar]
- Zhou, D.-K., Zhang, S.-N., Song, L.-M., et al. 2022, MNRAS, 515, 1914 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Insight-HXMT/HE light curve of MAXI J1820+070 in the 30–150 keV band during the 2018 LHS outburst. Calendar dates in the month – day format are reported on the top horizontal axis. The dotted red line marks the time of ObsID P01146610150 that was chosen for the dynamic QPO study in this work. |
| In the text | |
 |
Fig. 2. 2D plot on the left: Dynamic WWZ power in time-frequency space during ObsID P011466101502. The red contours represent regions (in time-frequency space) of QPO activity with a significance > 3σ. the units of WWZ power are (root-mean-square/mean)2 Hz−1. The line plot on the right side of all panels shows the corresponding time-averaged WWZ power spectrum over the whole observation in each band. The dashed red line indicates the peak power at a QPO frequency of 0.082 Hz, and the dashed blue lines correspond to ±20% around peak frequency. Top panel: For the HE data in the 30–250 keV band. Middle panel: For the ME data in the 5–30 keV band. Bottom panel: For the LE data in the 1.3–15.0 keV band. |
| In the text | |
 |
Fig. 3. QPO lifetime distribution over all the 2018 March–June Insight-HXMT observations in units of cycles. The left panel shows the LE energy band, the middle panel shows the ME, and the right panel shows the HE. In all panels, the blue histogram is the lifetime distribution of QPOs with frequencies < 0.2 Hz. The red histogram is the distribution for QPOs with frequencies of 0.2–0.4 Hz. The green histogram shows QPO frequencies of 0.4–0.63 Hz. The black histogram is the lifetime distribution for all QPOs of any frequency. The total lifetime distribution in each panel has been fitted with a Gaussian (solid black curve), and the dashed black lines mark the Gaussian mean lifetime and the value of 1σ above the mean. |
| In the text | |
 |
Fig. 4. Insight-HXMT spectrum from 2018 April 8 (ObsID P011466101502). Top panel: Spectrum fit with the model TBabs × constant × TBabs × (diskbb + gaussian + relxill). The black datapoints show observation intervals in which QPOs are detected, and red datapoints show non-QPO intervals. Middle panel: Residuals for the same spectral model. Bottom panel: Residuals when the same spectrum is fit with the simpler model constant × TBabs × (diskbb + gaussian + cutoffpl), i.e., without disk reflection. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.