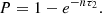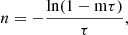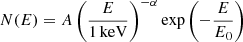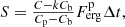| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202346128 | |
| Published online | 29 August 2023 | |
Letter to the Editor
The peak flux of GRB 221009A measured with GRBAlpha
1
Department of Theoretical Physics and Astrophysics, Faculty of Science, Masaryk University, Kotlářská 267/2, Brno 611 37, Czech Republic
e-mail: ripa.jakub@gmail.com
2
Department of Physics, Graduate School of Advanced Science and Engineering, Hiroshima University, Higashi-Hiroshima, Japan
3
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Budapest, Hungary
4
Eötvös Loránd University, Egyetem tér 1-3, Budapest, Hungary
5
Wigner Research Centre for Physics, Konkoly-Thege Miklós út 29-33, Budapest, Hungary
6
Spacemanic Ltd, Jablonec 110, 900 86 Jablonec, Slovakia
7
Needronix Ltd, Ilkovičová 3, 812 19 Bratislava, Slovakia
8
EDIS vvd., 04001 Košice, Slovakia
9
Faculty of Aeronautics, Technical University of Košice, Košice, Slovakia
10
Department of Radio Electronics, Faculty of Electrical Engineering and Communication, Brno University of Technology, Brno, Czech Republic
11
Tokyo University of Science, Noda, Chiba, Japan
12
Department of Physics, Nagoya University, Nagoya, Aichi, Japan
13
Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, Kanagawa, Japan
14
Institute of Earth Physics and Space Science (EPSS), Csatkai E. u. 6-8., 9400 Sopron, Hungary
15
Department of Physics and Astronomy, Universiteit Gent, 9000 Ghent, Belgium
16
School of Science, Kyoto University, Kyoto, Japan
17
Department of Physics, Rikkyo University, Tokyo, Japan
18
Department of Theoretical Physics, Institute of Physics, Budapest University of Technology and Economics, Műegyetem rkp. 3, 1111 Budapest, Hungary
19
MTA-BME Quantum Dynamics and Correlations Research Group, Budapest University of Technology and Economics, Műegyetem rkp. 3, 1111 Budapest, Hungary
20
Department of Earth and Space Science, Osaka University, Toyonaka, Osaka, Japan
21
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica, Via A. Corti 12, 20133 Milano, Italy
Received:
12
February
2023
Accepted:
14
March
2023
Context. On 2022 October 9 the brightest gamma-ray burst (GRB) ever observed lit up the high-energy sky. It was detected by a multitude of instruments, attracting the close attention of the GRB community, and saturated many detectors.
Aims. GRBAlpha, a nano-satellite with a form factor of a 1U CubeSat, detected this extraordinarily bright long-duration GRB, GRB 221009A, without saturation but affected by pile-up. We present light curves of the prompt emission in 13 energy bands, from 80 keV to 950 keV, and performed a spectral analysis to calculate the peak flux and peak isotropic-equivalent luminosity.
Methods. Since the satellite’s attitude information is not available for the time of this GRB, more than 200 incident directions were probed in order to find the median luminosity and its systematic uncertainty.
Results. We find that the peak flux in the 80 − 800 keV range (observer frame) was Fphp = 1300−200+1200 ph cm−2 s−1, or Fergp = 5.7−0.7+3.7 × 10−4 erg cm−2 s−1, and the fluence in the same energy range of the first GRB episode, which lasted 300 s and was observable by GRBAlpha, was S = 2.2−0.3+1.4 × 10−2 erg cm−2, or Sbol = 4.9−0.5+0.8 × 10−2 erg cm−2 for the extrapolated range of 0.9 − 8690 keV. We infer the isotropic-equivalent released energy of the first GRB episode to be Eisobol = 2.8−0.5+0.8 × 1054 erg in the 1 − 10 000 keV band (rest frame at z = 0.15). The peak isotropic-equivalent luminosity in the 92 − 920 keV range (rest frame) was Lisop = 3.7−0.5+2.5 × 1052 erg s−1, and the bolometric peak isotropic-equivalent luminosity was Lisop,bol = 8.4−1.5+2.5 × 1052 erg s−1 (4 s scale) in the 1 − 10 000 keV range (rest frame). The peak emitted energy is Ep∗ = Ep(1+z) = 1120 ± 470 keV. Our measurement of Lisop,bol is consistent with the Yonetoku relation. It is possible that, due to the spectral evolution of this GRB and the orientation of GRBAlpha at the peak time, the true values of peak flux, fluence, Liso, and Eiso are even higher.
Key words: gamma-ray burst: individual: GRB 221009A
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
On 2022 October 9 at 13:16:59.988 UT, the Fermi Gamma-ray Burst Monitor (GBM) detected the exceptionally bright long gamma-ray burst (GRB) GRB 221009A (Veres et al. 2022; Lesage et al. 2022, 2023). The burst was also observed by the Fermi Large Area Telescope (LAT) up to the energy of 100 GeV (Pillera et al. 2022). Potentially remarkable detections of over 5000 very high-energy photons with energies up to 18 TeV were reported by the Large High Altitude Air Shower Observatory (LHAASO; Huang et al. 2022), and a possible 251 TeV photon was reported by Carpet-2 (Dzhappuev et al. 2022), triggering the interest of the broader physics community.
The burst was localised by the Neil Gehrels Swift Observatory’s Burst Alert Telescope (Dichiara et al. 2022) and followed up by the Very Large Telescope (VLT) X-shooter instrument (de Ugarte Postigo et al. 2022; Malesani et al. 2023), which determined that it occurred at a redshift of 0.151 and belongs to very near long GRBs (Oates 2023). It was also detected by a multitude of other instruments: AGILE/GRID (Piano et al. 2022), AGILE/MCAL (Ursi et al. 2022), BepiColombo/MGNS (Kozyrev et al. 2022), Insight-HXMT and SATech-01/GECAM-C (HEBS; An et al. 2023), INTEGRAL/SPI-ACS (Gotz et al. 2022), Konus-WIND & SRG/ART-XC (Frederiks et al. 2023), MAXI and NICER (Williams et al. 2023), Solar Orbiter/STIX (Xiao et al. 2022), STPSat-6/SIRI-2 (Mitchell et al. 2022), and XMM-Newton (Tiengo et al. 2023).
This brightest ever recorded GRB (Burns et al. 2023; O’Connor et al. 2023) saturated many of the GRB detectors in orbit, hampering the efforts to determine its peak luminosity. In this Letter, we present the peak flux and peak isotropic-equivalent luminosity of this extraordinary transient as measured by the GRBAlpha nano-satellite.
2. GRBAlpha
GRBAlpha (Pál et al. 2020) is a 1U CubeSat carrying a GRB detector as a technology demonstration for an envisioned future CubeSat constellation (Werner et al. 2018; Mészáros et al. 2022). It was launched on 2021 March 22 into a Sun-synchronous polar orbit at an altitude of ∼550 km and thus became the smallest astrophysical space observatory. About a third of the polar orbit is affected by high particle background, and the duty cycle of the detector is around 67%. GRBAlpha’s detector consists of a 75 × 75 × 5 mm3 CsI(Tl) scintillator read out by an array of Silicon PhotoMultipliers (SiPMs), called multi-pixel photon counters (MPPCs), by Hamamatsu. The SiPM detectors are protected from proton damage by a 2.5 mm thick lead (PbSb3 alloy) shield, and their degradation is being monitored. The on-board data acquisition software stack is being continuously upgraded to increase the duty cycle and data downlink rate. The ground segment is also supported by the radio amateur community, and it takes advantage of the Satellite Networked Open Ground Station (SatNOGS)1.
Following a commissioning phase, GRBAlpha started collecting data, monitoring the particle and photon background environment on a low-Earth polar orbit, and detecting transients (see Řípa et al. 2022a). When the satellite operates continuously, on average it detects a transient every 5–6 days2. GRBAlpha detected GRB 221009A (Řípa et al. 2022b) when traversing the northern polar regions, and during the peak brightness of the burst its detectors were not saturated; however, the measurement was influenced by pile-up.
The pile-up effect occurs due to the chance coincidence of the arrival and interaction of two or more gamma-ray photons in the detector’s scintillator within the detector’s inherent resolving time. In that case, two or more events are registered as one event, and the energies of the events within the same resolving time window are added (Knoll 2000).
3. Data analysis
GRBAlpha observed a peak count rate of 22 000 cnt s−1 in the ∼80 − 950 keV energy band at 13:20:51.5 UTC on 2022 October 9. The duration of the GRB was > 250 s (Řípa et al. 2022b). During the detection, the satellite was flying above the northern polar region with elevated background levels. The end part of the GRB was recorded while passing the outer Van Allen radiation belt; therefore, we can only report the lower limit on the duration and cannot determine the T90 duration of the GRB. The GRBAlpha data for this event are composed of binned light curves with 4 s temporal resolution recorded in 16 energy bands. However, the three lowest-energy bands are below the set on-board low-energy threshold limited by the noise peak of the MPPCs, making only 13 energy bands suitable for spectral analysis. The recorded raw count-rate curves in multiple energy bands are presented in Fig. 1. We note that the energy calibration was performed by using radionuclides in the laboratory and by observing activation lines in orbit.
 |
Fig. 1. Raw light curve of GRB 221009A as observed by GRBAlpha in multiple energy bands with 4 s cadence. The bottom-rightmost panel shows the light curve in the whole sensitivity range. Times tb, ts, and tp mark the beginning of the used background interval, the source spectral data, and the peak time, respectively. About 30 s after the peak at tp, the GRB shows a second strong peak. Time tr marks the approximate moment when the satellite entered the outer Van Allen radiation belt, which resulted in the final part of the GRB prompt emission being flooded by the particle background. The sharp increase just after tr is due to this background. |
We performed spectral analysis to determine the peak flux of the GRB and its isotropic-equivalent peak luminosity. The mass model of GRBAlpha used for generating detector response matrices employed in the spectral analysis is displayed in Fig. 2. It contains: the detector made of a 75 × 75 × 5 mm3 CsI(Tl) scintillator in a 1.5 mm thick Al casing; a 2.5 mm thick PbSb3 radiation shield; a standard 1U CubeSat Al platform with four stacks of empty printed circuit boards (PCBs; glass epoxy FR4) and two LiFePO4 batteries.
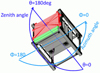 |
Fig. 2. Mass model of GRBAlpha used for generating detector response matrices, with zenith and azimuth angles marked. The CsI(Tl) detector in its aluminium casing is shown in red and the PbSb3 radiation shield in green. The aluminium CubeSat platform, with four stacks of PCBs and two LiFePO4 batteries, is shown in grey. |
A full Monte Carlo simulation based on the GEometry ANd Tracking (Geant4) toolkit3 (Allison & Amako 2016) was carried out to simulate incident photons with a flat energy distribution in the 5 − 1000 keV band, covering the entire satellite structure. The deposited energy as a function of input photon energy was calculated by scanning more than 200 incident Θ (zenith) and Φ (azimuth) angles. The effective area versus incident photon energy for a few zenith angles, Θ, and a constant azimuth angle Φ = 270° is shown in Fig. 3. The drop over 900 keV is an artefact because we simulated photon energies only up to 1000 keV and the photo-absorption peak (with broadening of the energy resolution) of such high-energy photons is not accounted for in this response. Therefore, in the spectral analysis, we conservatively only used data up to ∼810 keV.
 |
Fig. 3. Total response efficiency (effective area) vs. incident photon energy for a few zenith angles, Θ, and a constant azimuth angle, Φ = 270°. |
To check for pile-up, we plotted the fraction of the detected counts in each spectral band versus the total counts over the whole energy range for GRB 221009A (see Fig. 4). The figure shows that above ∼10 000 cnt bin−1 = 2500 cnt s−1 the fraction of counts in the lower-energy bands decreases while the fraction of counts in the higher-energy bands increases, which may indicate the presence of pile-up. We note that below ∼10 000 cnt bin−1 the decrease in the rates at high energies as a function of total counts in each bin is due to very low count numbers, and the diagonal lines correspond to 1, 2, 3… cnt bin−1. At the peak of this transient, GRBAlpha measured a count rate of m = 22 000 cnt s−1 in the full band. The shaping parameter of the analogue electronics is τ1 ≈ 10 μs. During the signal digitisation, the pulse processing is done within the resolution time of τ2 = 15 μs. We can calculate the probability that a pile-up appears as (Knoll 2000)
 |
Fig. 4. Fraction of the detected counts in each spectral band vs the total counts over the whole energy range for GRB 221009A and for the background as it passed the north polar region. The counts were detected in 4 s time bins. The figure shows that above ∼10 000 cnt bin = 2500 cnt s−1 the fraction of counts in low-energy bands decreases while the fraction of counts in high-energy bands increases, which can indicate a pile-up effect. |
Here n is the true event rate, which can be calculated from the detected count rate, m, as
where for m = 22 000 cnt s−1 we obtain n = 26 700 event s−1. For the observed peak count rate we obtain a pile-up probability of ∼33%, whereas the probability drops to ∼3.7% for a count rate of m = 2500 cnt s−1. Therefore, the observed spectrum at the peak time is affected by pile-up, and in the following spectral analysis we avoid fitting the peak spectrum (which results in a flatter power-law fit) and instead fit the GRB spectrum before the peak time, when the pile-up is negligible.
The spectral fitting was performed by the X-ray spectral fitting package XSPEC4 (Arnaud 1996). The source spectrum was fitted from time ts = 13 : 20 : 33.5 UTC to ts + 4 s, and the background spectrum was taken from time tb = 13 : 17 : 33.5 UTC to tb + 4 s. By applying this background, we obtained a background-subtracted spectrum without any substantial bump or dip around 500 keV, where the GRBAlpha background shows a bump. The average background rate in the whole sensitivity range in this part of the orbit is 340 cnt s−1, and the rate in the chosen 4 s background bin is 345 cnt s−1. We set a systematic error of 2% to be added when evaluating χ2. The peak time in the measured light curve in the whole sensitivity range of ∼80 − 950 keV was measured to be from tp = 13 : 20 : 49.5 UTC to tp + 4 s. Figure 5 displays the detected count spectra at the time bins ts, tb, and tp. At an approximate time tr = ∼ 13 : 24 : 42.0 UTC, the GRBAlpha nano-satellite entered the outer Van Allen radiation belt, and the signal from the GRB became flooded by particle background. These times are marked in Fig. 1.
 |
Fig. 5. Detected count spectra of GRB 221009A and the background spectrum. The count spectrum of the GRB at time ts minus the background spectrum at time tb is shown in black. The background spectrum at time tb is shown in red. The count spectrum of the GRB at the peak time tp = 13 : 20 : 49.5 UT on 2022 October 9, minus the background spectrum at time tb, is shown in green and it reveals a spectral hardening at the highest energies present around the GRB peak. |
GRBAlpha does not have an active attitude control system, and the attitude knowledge was not being recorded at the time of GRB 221009A. The background variation had a periodicity of ∼47 s when the satellite was near the north pole. From the communication with the satellite on the same day, we observed in the radio waterfall a periodicity of ∼23 s in the received radio power. The Ultra High Frequency (UHF) antenna on GRBAlpha is a half-wave dipole, and thus a periodicity in the waterfall corresponds to half of the rotation or precession period of the satellite. Hence, the satellite completed more than one revolution during the duration of the GRB. We therefore performed the spectral analysis for many detector response matrices simulated for various Θ and Φ incident angles. We fitted the measured spectra each time in order to obtain the best-fit χ2 map and to obtain the most likely direction of the GRB with respect to the satellite’s coordinate system.
We performed the spectral fitting with the power-law model, a power law with an exponential cutoff model (CPL), and with the Band function. The lowest reduced χ2 was obtained for the CPL model, as described in the following section. The reduced χ2 maps show a similar trend; therefore, in the next section, we report results obtained with the CPL model only.
After we determined the most likely incidence angle of the GRB with respect to the detector, we calculated the flux and the isotropic-equivalent luminosity of the GRB using the best-fit spectral model. Scaling up the flux and the luminosity obtained from the spectral fit at time ts allowed us to determine the flux and the luminosity at the peak time, tp. The scaling factor is approximately the ratio of the total detected counts at the time bin tp over the total detected counts at the time bin ts. The results are described in detail in the following section.
4. Results
The best fit for the source spectrum at the time bin ts and after subtraction of the background at the time bin tb was obtained for the on-axis direction Θ = 180° and Φ = 0° by the CPL model:
(see Fig. 6). The fit was performed in the range 76 − 809 keV, giving χ2/D.o.F. = 13.4/8 = 1.68. The best-fit parameters are: the photon index α = 0.7 ± 0.1; the roll-off energy 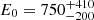 keV; and the normalisation
keV; and the normalisation 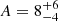 ph keV−1 cm−2 s−1 at 1 keV. The relatively large uncertainty of the normalisation is due to its correlation with the photon index alpha and the roll-off energy. The 68% confidence interval (CI) parameter uncertainties were calculated by XSPEC from the fit covariance matrix. The peak energy is Ep = E0(2 − α) = 980 ± 410 keV.
ph keV−1 cm−2 s−1 at 1 keV. The relatively large uncertainty of the normalisation is due to its correlation with the photon index alpha and the roll-off energy. The 68% confidence interval (CI) parameter uncertainties were calculated by XSPEC from the fit covariance matrix. The peak energy is Ep = E0(2 − α) = 980 ± 410 keV.
 |
Fig. 6. Spectrum of the GRB 221009A best fit by the CPL model fitted from ts = 13 : 20 : 33.5 UTC on 2022 October 9 to ts + 4 s in the range 76 − 809 keV for Θ = 180° and Φ = 0°. |
The flux in the energy range of 80 − 800 keV in the observer frame for the best-fit model for the same time interval ts and the same Θ and Φ angles was derived to be 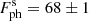 ph cm−2 s−1, or
ph cm−2 s−1, or 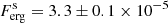 erg cm−2 s−1 (68% CI). For the isotropic-equivalent luminosity in the energy range 92 − 920 keV in the rest frame for the redshift z = 0.151 (de Ugarte Postigo et al. 2022; Malesani et al. 2023), the cosmological parameter ΩΛ = 0.685, a flat universe, and a Hubble constant of H0 = 67.4 km s−1 Mpc−1 (Planck Collaboration VI 2020), we obtain
erg cm−2 s−1 (68% CI). For the isotropic-equivalent luminosity in the energy range 92 − 920 keV in the rest frame for the redshift z = 0.151 (de Ugarte Postigo et al. 2022; Malesani et al. 2023), the cosmological parameter ΩΛ = 0.685, a flat universe, and a Hubble constant of H0 = 67.4 km s−1 Mpc−1 (Planck Collaboration VI 2020), we obtain 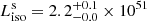 erg s−1 (68% CI). The uncertainties in flux and luminosity were derived from the Markov chain Monte Carlo method (Hastings 1970) with following parameters: a proposal Gaussian fit; the covariance matrix used in the proposal distribution re-scaled by a factor of 0.125; a chain length of 50 000; the first 1000 steps discarded prior to storing the chain; and a Goodman-Weare chain type with 16 walkers.
erg s−1 (68% CI). The uncertainties in flux and luminosity were derived from the Markov chain Monte Carlo method (Hastings 1970) with following parameters: a proposal Gaussian fit; the covariance matrix used in the proposal distribution re-scaled by a factor of 0.125; a chain length of 50 000; the first 1000 steps discarded prior to storing the chain; and a Goodman-Weare chain type with 16 walkers.
The approximate scaling factor f = (Cp − Cb)/(Cs − Cb) – the ratio between the total detected counts Cp at the peak time bin tp minus mean background counts Cb = 1360 cnt bin = 340 cnt s−1 and the total detected counts Cs at the time bin ts minus the mean background counts – gives f = (87 950 − 1360)/(8689 − 1360) = 11.8. We scaled the flux and the luminosity obtained from the spectral fit at time ts by this factor and by the pile-up correction factor of 1.21 in order to determine the flux and the luminosity at the peak time, tp. By applying this scaling to the flux and the isotropic-equivalent luminosity derived above for the time bin ts, we obtain for the peak flux 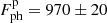 ph cm−2 s−1, or
ph cm−2 s−1, or 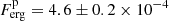 erg cm−2 s−1, and for the peak luminosity
erg cm−2 s−1, and for the peak luminosity 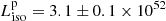 erg s−1.
erg s−1.
We have so far not considered the systematic uncertainty due to the uncertain attitude of the satellite (detector). Although we derived the most likely orientation of the satellite with respect to the GRB from the best-fit χ2 map, the difference in reduced χ2 near the on-axis direction (Θ = 180°) and near the backside direction (Θ = 0°) is relatively low, implying that the on-axis direction is not guaranteed. Therefore, we also calculated the flux and the luminosity using a more conservative approach.
We took the distribution of fluxes and luminosities obtained by fitting the spectra by the CPL model at the same time bin ts with the same background time bin, tb, as described above, and used 192 different Θ and Φ directions, which isotropically sample the sphere around the satellite following the Hierarchical Equal Area isoLatitude Pixelization (HEALPix)5 tessellation (Górski et al. 2005). The best-fit χ2 was obtained for each direction. The reduced 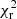 map is shown in Fig. 7. We removed six cases that have reduced
map is shown in Fig. 7. We removed six cases that have reduced 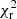 > 4 because these we consider as not acceptable fits. They correspond to the direction towards the MPPCs’ lead shield. The resulting distribution contains 186 fluxes (luminosities). The median flux in the 80 − 800 keV range (observer frame) and the isotropic-equivalent luminosity in the 92 − 920 keV range (rest frame) at the same time bin ts are:
> 4 because these we consider as not acceptable fits. They correspond to the direction towards the MPPCs’ lead shield. The resulting distribution contains 186 fluxes (luminosities). The median flux in the 80 − 800 keV range (observer frame) and the isotropic-equivalent luminosity in the 92 − 920 keV range (rest frame) at the same time bin ts are: 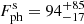 ph cm−2 s−1, or
ph cm−2 s−1, or 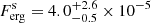 erg cm−2 s−1; and
erg cm−2 s−1; and 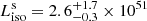 erg s−1.
erg s−1.
 |
Fig. 7. Reduced χ2 map of the best fits with the CPL model for different angles of Θ (vertical) and Φ (horizontal) in degrees. |
By applying the scaling factor f = (Cp − Cb)/(Cs − Cb) = 11.8 and a pile-up correction factor of 1.21, we obtain for the peak flux 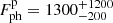 ph cm−2s−1, or
ph cm−2s−1, or 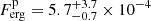 erg cm−2 s−1, and for the isotropic-equivalent peak luminosity
erg cm−2 s−1, and for the isotropic-equivalent peak luminosity 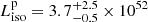 erg s−1. When we repeated this analysis for the fluxes integrated over a larger extrapolated energy range of 0.9 − 8690 keV, we obtain a peak flux
erg s−1. When we repeated this analysis for the fluxes integrated over a larger extrapolated energy range of 0.9 − 8690 keV, we obtain a peak flux 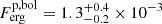 erg cm−2s−1 and a bolometric isotropic-equivalent peak luminosity
erg cm−2s−1 and a bolometric isotropic-equivalent peak luminosity 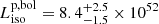 erg s−1 (4 s scale) in the 1 − 10 000 keV range (rest frame). Results for the on-axis direction and those obtained by varying different incident directions are summarised in Table 1.
erg s−1 (4 s scale) in the 1 − 10 000 keV range (rest frame). Results for the on-axis direction and those obtained by varying different incident directions are summarised in Table 1.
Summary of obtained fluxes and luminosities for the on-axis direction (Θ = 180°, Φ = 0°), the median values obtained by varying different incident angles, and the values for the edge-on direction (Θ = 90°, Φ = 101°).
Knowing the peak flux, 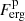 , we can calculate the approximate fluence, S, of the GRB as
, we can calculate the approximate fluence, S, of the GRB as
where C is the total number of detected counts during the GRB, Cp is the number of detected counts at the peak time bin (tp) of duration Δt = 4 s, Cb is the mean counts per bin, and k is the number of bins over which we calculate the fluence. We obtain the fluence 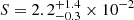 erg cm−2 in the 80 − 800 keV range of the first GRB episode, which lasted 300 s and was observable by GRBAlpha from time 13:19:29.5 to 13:24:29.5 UTC on 2022 October 9. In the same way, but using the wider extrapolated energy range 0.9 − 8690 keV, we obtain the fluence
erg cm−2 in the 80 − 800 keV range of the first GRB episode, which lasted 300 s and was observable by GRBAlpha from time 13:19:29.5 to 13:24:29.5 UTC on 2022 October 9. In the same way, but using the wider extrapolated energy range 0.9 − 8690 keV, we obtain the fluence 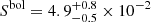 erg cm−2 and the isotropic-equivalent released energy
erg cm−2 and the isotropic-equivalent released energy 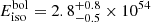 erg in the 1 − 10 000 keV range (rest frame).
erg in the 1 − 10 000 keV range (rest frame).
5. Discussion
The highest peak flux and fluence of all GRBs recorded with CGRO/BATSE (Paciesas et al. 1999) and Fermi/GBM (von Kienlin et al. 2020) are 496 ph cm−2 s−1 (50−300 keV) and 8.1 × 10−4 erg cm−2 (50−300 keV) for GRB 130427A. The measured peak flux and fluence of GRB 221009A are 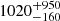 ph cm−2 s−1 and
ph cm−2 s−1 and 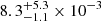 erg cm−2 in the 50−300 keV band. The duration of GRB 221009A is longer than 100 s, compared to the 10−20 s for GRB 130427A, resulting in a relatively large fluence ratio. This indicates that GRB 221009A is indeed exceptionally bright. While the size of the CsI scintillator on GRBAlpha is not small (∼55 cm2 face-on), the low-energy threshold of the detector is relatively high at around 80 keV due to the radiation damage of the SiPM detectors. This allowed GRBAlpha to avoid saturation of the count rate in the digital processing, in turn allowing us to trace the light curve. We note that the brightest gamma-ray flux from a celestial object was observed during the giant flare from the magnetar SGR 1806-20 in 2004; its peak flux was around 10–20 erg s−1 in the 20–10 000 keV band (Mazets et al. 2005; Terasawa et al. 2005), which is 4–5 orders of magnitude higher than that of GRB 221009A.
erg cm−2 in the 50−300 keV band. The duration of GRB 221009A is longer than 100 s, compared to the 10−20 s for GRB 130427A, resulting in a relatively large fluence ratio. This indicates that GRB 221009A is indeed exceptionally bright. While the size of the CsI scintillator on GRBAlpha is not small (∼55 cm2 face-on), the low-energy threshold of the detector is relatively high at around 80 keV due to the radiation damage of the SiPM detectors. This allowed GRBAlpha to avoid saturation of the count rate in the digital processing, in turn allowing us to trace the light curve. We note that the brightest gamma-ray flux from a celestial object was observed during the giant flare from the magnetar SGR 1806-20 in 2004; its peak flux was around 10–20 erg s−1 in the 20–10 000 keV band (Mazets et al. 2005; Terasawa et al. 2005), which is 4–5 orders of magnitude higher than that of GRB 221009A.
This exceptionally bright GRB has one of the highest isotropic-equivalent peak luminosities ever reported (Burns et al. 2023). Gamma-ray bursts with higher peak luminosities have been observed in the past, but at significantly larger redshifts (see e.g., Yonetoku et al. 2010). In their Fig. 3, Yonetoku et al. 2010 provide the correlation between the rest-frame spectral peak energy and 1-s peak luminosity of short and long GRBs. Our measurements of 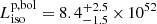 erg s−1 and
erg s−1 and 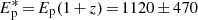 keV are consistent with this relation within the systematic errors.
keV are consistent with this relation within the systematic errors.
In Fig. 1 one can see that at low energies, mainly at 80 − 120 keV, the background shows a wavy pattern. This is most likely due to the periodic motion of GRBAlpha that exposes a different cross-section of its detector to the cosmic X-ray background and the secondary gamma-rays induced by cosmic rays in the Earth’s atmosphere (Galgóczi et al. 2021). On the same day that we detected this GRB, we also observed a periodicity in the received radio power in the waterfalls while downloading data from the satellite; this indicates that the satellite completed more then one revolution during the duration of the GRB. Therefore, a change in the satellite’s attitude between times ts and tp can result in a systematic error of the reported peak luminosity and total emitted energy. As shown in Table 1, the luminosity derived for the edge-on direction is 3.5 times higher than the median value. We cannot exclude that the detector on board GRBAlpha was oriented edge-on towards the GRB at the time of the peak, and therefore, we cannot exclude that the obtained median peak flux and luminosity are underestimated.
The time-resolved spectral analysis of GRB 221009A by Konus-WIND (Frederiks et al. 2023) reveals a spectral evolution during the burst with a higher photon index, α, and the peak energy, Ep, around the peak time reaching Ep ≈ 3 MeV. Hence, our method based on scaling the flux from the spectrum at time ts to peak time tp may underestimate the resultant peak flux and fluence. It is possible that the true peak flux and fluence are higher.
The highest-energy bands around 800 − 950 keV, as shown in Fig. 1, have an increased number of counts during the GRB peak compared to lower-energy bands around 700 − 800 keV. This is also evident in the raw count spectrum at the peak time, tp, presented in Fig. 5. This could be due to an instrumental effect because of the high incident photon rate.
6. Conclusions
Our conclusions can be summarised as follows:
-
GRBAlpha, a low-cost nano-satellite in a low-Earth orbit, detected the exceptionally bright long gamma-ray burst GRB 221009A without saturation, but affected by pile-up, providing light curves of the prompt emission in 13 energy bands from 80 keV to 950 keV.
-
The peak flux in the 80 − 800 keV range (observer frame) is measured to be
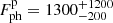 ph cm−2 s−1, or
ph cm−2 s−1, or 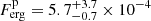 erg cm−2 s−1, and for the wider extrapolated energy range of 0.9 − 8, 690 keV we obtain
erg cm−2 s−1, and for the wider extrapolated energy range of 0.9 − 8, 690 keV we obtain 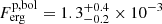 erg cm−2 s−1.
erg cm−2 s−1. -
The peak isotropic-equivalent luminosity in the 92 − 920 keV range (rest frame) was
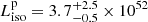 erg s−1, and the bolometric peak isotropic-equivalent luminosity in the 1 − 10 000 keV range (rest frame) was
erg s−1, and the bolometric peak isotropic-equivalent luminosity in the 1 − 10 000 keV range (rest frame) was 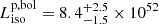 erg s−1 (4 s scale). Our measurement of
erg s−1 (4 s scale). Our measurement of 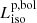 is consistent with the Yonetoku relation between the rest-frame spectral peak energy and the peak luminosity of GRBs.
is consistent with the Yonetoku relation between the rest-frame spectral peak energy and the peak luminosity of GRBs. -
The fluence in the 80 − 800 keV range of the first GRB episode, which lasted 300 s and was observable by GRBAlpha from 13:19:29.5 to 13:24:29.5 UTC on 2022 October 9, was measured to be
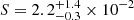 erg cm−2 and
erg cm−2 and 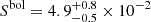 erg cm−2 for the extrapolated range of 0.9 − 8690 keV. We infer from this extrapolated fluence that the isotropic-equivalent released energy of the first GRB episode was
erg cm−2 for the extrapolated range of 0.9 − 8690 keV. We infer from this extrapolated fluence that the isotropic-equivalent released energy of the first GRB episode was 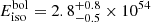 erg in the 1 − 10 000 keV band (rest frame).
erg in the 1 − 10 000 keV band (rest frame). -
It is possible that, due to the spectral evolution during the peaks of this GRB, as reported by Konus-WIND (Frederiks et al. 2023), the true peak flux, fluence, Liso, and Eiso may be higher than our obtained values. We cannot exclude that the GRBAlpha’s detector was oriented near edge-on with respect to the GRB 221009A at the peak time, which would also mean that the true values may be higher than our estimations.
The list of all GRBAlpha-detected transients is available at https://monoceros.physics.muni.cz/hea/GRBAlpha/
Acknowledgments
We are thankful to Peter Veres and Stephen Lesage for discussions regarding the detection of this GRB by Fermi/GBM and other instruments and to Tomáš Plšek for discussions about MCMC and XSPEC. We are also thankful to Nozomu Kogiso, Maumu Yoneyama, Mizuki Moritaki, Tatsuya Kano and James W. Cutler for providing their SatNOGS stations for collecting GRBAlpha’s telemetry. We acknowledge support by the KEP-7/2018 and KEP2/2020 grants of the Hungarian Academy of Sciences and SA-40/2021 of the Eötvös Loránd Research Network for satellite components and payload developments and the grant IF-7/2020 for providing the financial support for ground infrastructure. This research has been supported by the European Union’s Horizon 2020 programme under the AHEAD2020 project (grant agreement n. 871158) and by the MUNI Award for Science and Humanities funded by the Grant Agency of Masaryk University. G.D. is supported by the Ghent University Special Research Funds (BOF) project BOF/STA/202009/040 and the Fonds Wetenschappelijk Onderzoek (FWO) iBOF project BOF20/IBF/124. This work was supported by the Internal Grant Agency of Brno University of Technology, project no. FEKT-S-20-6526. This research has been also supported by JSPS and HAS under Japan-Hungary Research Cooperative Program, JSPS KAKENHI Grant Number 17H06362, 19H01908, and 21KK0051. We are grateful to the Ministry of Education, Science, Research and Sport of the Slovak Republic for the support of the GRBAlpha mission.
References
- Allison, J., Amako, K., et al. 2016, Nucl. Instrum. Methods Phys. Res. Sect. A, 835, 186 [CrossRef] [Google Scholar]
- An, Z.-H., Antier, S., Bi, X.-Z., et al. 2023, Natl. Sci. Rev., submitted [arXiv:2303.01203] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Burns, E., Svinkin, D., Fenimore, E., et al. 2023, ApJ, 946, L31 [NASA ADS] [CrossRef] [Google Scholar]
- de Ugarte Postigo, A., Izzo, L., Pugliese, G., et al. 2022, General Coordinates Network, 32648, 1 [NASA ADS] [Google Scholar]
- Dichiara, S., Gropp, J. D., Kennea, J. A., et al. 2022, ATel, 15650, 1 [NASA ADS] [Google Scholar]
- Dzhappuev, D. D., Afashokov, Y. Z., Dzaparova, I. M., et al. 2022, ATel, 15669, 1 [NASA ADS] [Google Scholar]
- Frederiks, D., Svinkin, D., Lysenko, A. L., et al. 2023, ApJ, 949, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Galgóczi, G., Řípa, J., Campana, R., et al. 2021, J. Astron. Telesc. Instrum. Syst., 7, 028004P [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Gotz, D., Mereghetti, S., Savchenko, V., et al. 2022, General Coordinates Network, 32660, 1 [NASA ADS] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Huang, Y., Hu, S., Chen, S., et al. 2022, General Coordinates Network, 32677, 1 [NASA ADS] [Google Scholar]
- Knoll, G. F. 2000, Radiation Detection and Measurement (New York: Wiley) [Google Scholar]
- Kozyrev, A. S., Golovin, D. V., Litvak, M. L., et al. 2022, General Coordinates Network, 32805, 1 [NASA ADS] [Google Scholar]
- Lesage, S., Veres, P., Roberts, O. J., et al. 2022, General Coordinates Network, 32642, 1 [NASA ADS] [Google Scholar]
- Lesage, S., Veres, P., Briggs, M. S., et al. 2023, ApJ, 952, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Malesani, D. B., Levan, A. J., Izzo, L., et al. 2023, A&A, submitted [arXiv:2302.07891] [Google Scholar]
- Mazets, E. P., Cline, T. L., Aptekar, R. L., et al. 2005, ArXiv e-prints [arXiv:astro-ph/0502541] [Google Scholar]
- Mészáros, L., Pál, A., Werner, N., et al. 2022, in SPIE Conf. Ser., eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, 12181, 121811L [Google Scholar]
- Mitchell, L. J., Phlips, B. F., & Johnson, W. N. 2022, General Coordinates Network, 32746, 1 [NASA ADS] [Google Scholar]
- Oates, S. 2023, Universe, 9, 113 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connor, B., Troja, E., Ryan, G., et al. 2023, Sci. Adv., 9, eadi1405 [CrossRef] [Google Scholar]
- Paciesas, W. S., Meegan, C. A., Pendleton, G. N., et al. 1999, ApJS, 122, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Ohno, M., Mészáros, L., et al. 2020, in Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 11444, 114444V [Google Scholar]
- Piano, G., Verrecchia, F., Bulgarelli, A., et al. 2022, General Coordinates Network, 32657, 1 [NASA ADS] [Google Scholar]
- Pillera, R., Bissaldi, E., Omodei, N., La Mura, G., & Longo, F. 2022, ATel, 15656, 1 [NASA ADS] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terasawa, T., Tanaka, Y. T., Takei, Y., et al. 2005, Nature, 434, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Tiengo, A., Pintore, F., Vaia, B., et al. 2023, ApJ, 946, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Ursi, A., Panebianco, G., Pittori, C., et al. 2022, General Coordinates Network, 32650, 1 [NASA ADS] [Google Scholar]
- Veres, P., Burns, E., Bissaldi, E., et al. 2022, General Coordinates Network, 32636, 1 [NASA ADS] [Google Scholar]
- von Kienlin, A., Meegan, C. A., Paciesas, W. S., et al. 2020, ApJ, 893, 46 [Google Scholar]
- Řípa, J., Pál, A., Ohno, M., et al. 2022a, in Space Telescopes and Instrumentation 2022: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 12181, 121811K [Google Scholar]
- Řípa, J., Pal, A., Werner, N., et al. 2022b, General Coordinates Network, 32685, 1 [Google Scholar]
- Werner, N., Řípa, J., Pál, A., et al. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 10699, 106992P [NASA ADS] [Google Scholar]
- Williams, M. A., Kennea, J. A., Dichiara, S., et al. 2023, ApJ, 946, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, H., Krucker, S., & Daniel, R. 2022, General Coordinates Network, 32661, 1 [NASA ADS] [Google Scholar]
- Yonetoku, D., Murakami, T., Tsutsui, R., et al. 2010, PASJ, 62, 1495 [NASA ADS] [Google Scholar]
All Tables
Summary of obtained fluxes and luminosities for the on-axis direction (Θ = 180°, Φ = 0°), the median values obtained by varying different incident angles, and the values for the edge-on direction (Θ = 90°, Φ = 101°).
All Figures
 |
Fig. 1. Raw light curve of GRB 221009A as observed by GRBAlpha in multiple energy bands with 4 s cadence. The bottom-rightmost panel shows the light curve in the whole sensitivity range. Times tb, ts, and tp mark the beginning of the used background interval, the source spectral data, and the peak time, respectively. About 30 s after the peak at tp, the GRB shows a second strong peak. Time tr marks the approximate moment when the satellite entered the outer Van Allen radiation belt, which resulted in the final part of the GRB prompt emission being flooded by the particle background. The sharp increase just after tr is due to this background. |
| In the text | |
 |
Fig. 2. Mass model of GRBAlpha used for generating detector response matrices, with zenith and azimuth angles marked. The CsI(Tl) detector in its aluminium casing is shown in red and the PbSb3 radiation shield in green. The aluminium CubeSat platform, with four stacks of PCBs and two LiFePO4 batteries, is shown in grey. |
| In the text | |
 |
Fig. 3. Total response efficiency (effective area) vs. incident photon energy for a few zenith angles, Θ, and a constant azimuth angle, Φ = 270°. |
| In the text | |
 |
Fig. 4. Fraction of the detected counts in each spectral band vs the total counts over the whole energy range for GRB 221009A and for the background as it passed the north polar region. The counts were detected in 4 s time bins. The figure shows that above ∼10 000 cnt bin = 2500 cnt s−1 the fraction of counts in low-energy bands decreases while the fraction of counts in high-energy bands increases, which can indicate a pile-up effect. |
| In the text | |
 |
Fig. 5. Detected count spectra of GRB 221009A and the background spectrum. The count spectrum of the GRB at time ts minus the background spectrum at time tb is shown in black. The background spectrum at time tb is shown in red. The count spectrum of the GRB at the peak time tp = 13 : 20 : 49.5 UT on 2022 October 9, minus the background spectrum at time tb, is shown in green and it reveals a spectral hardening at the highest energies present around the GRB peak. |
| In the text | |
 |
Fig. 6. Spectrum of the GRB 221009A best fit by the CPL model fitted from ts = 13 : 20 : 33.5 UTC on 2022 October 9 to ts + 4 s in the range 76 − 809 keV for Θ = 180° and Φ = 0°. |
| In the text | |
 |
Fig. 7. Reduced χ2 map of the best fits with the CPL model for different angles of Θ (vertical) and Φ (horizontal) in degrees. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.