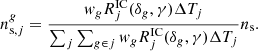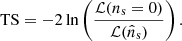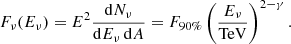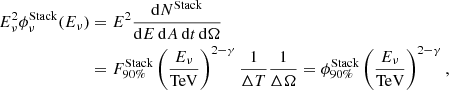| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244815 | |
| Published online | 06 April 2023 | |
Neutrino search from γ-ray bursts during the prompt and X-ray afterglow phases using 10 years of IceCube public data
1
Département de physique nucléaire et corpusculaire, Université de Genève, 24 Quai Ernest-Ansermet, 1211 Genève, Switzerland
e-mail: francescolucarelli@hotmail.it
2
Gran Sasso Science Institute (GSSI), Via F. Crispi 7, 67100 L’Aquila, Italy
e-mail: gor.oganesyan@gssi.it
3
INFN–Laboratori Nazionali del Gran Sasso, via Giovanni Acitelli 22, 67100 L’Aquila, Italy
Received:
26
August
2022
Accepted:
14
February
2023
Neutrino emission from γ-ray bursts (GRBs) has been sought for a long time, and stringent limits on the most accredited GRB emission models have been obtained from IceCube. Multiwavelength GRB observations of the last decades have improved our knowledge of the GRB emission parameters, such as the Lorentz factor and the luminosity, which can vary from one GRB to another by several orders of magnitude. Empirical correlations among such parameters have been identified during the prompt phase, with direct implications on GRB models. In this work, we use the PSLab open-access code, developed for IceCube data analyses, to search for individual neutrino emission from the prompt and afterglow phases of selected GRBs, and for stacking emission from the ensemble of such GRBs. For the afterglow phase, we focus on GRBs with X-ray flares and plateaus in particular. While past stacking searches assumed the same GRB fluence at Earth, we present a stacking scheme based on physically motivated GRB weights. Moreover, we conceive a new methodology for the prompt phase that uses the empirical correlations to infer the GRB luminosity and Lorentz factor, when redshift measurements are not available. We do not observe any significant neutrino excess. Hence, we set constraints on the GRB neutrino fluxes and on relevant GRB parameters, including the magnetic field in the jet. Notably, the baryon loading is found to be less than ten for typical GRB jets.
Key words: astroparticle physics / neutrinos / gamma rays: general / radiation mechanisms: general
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the Universe, γ-ray bursts (GRBs) are among the brightest electromagnetic transient events. They consist of second- or minute-scale bursts in the soft gamma-ray band, known as the prompt phase, followed by a broadband afterglow emission in the radio, optical, and X-rays, lasting a few hours to several days. The observed photon spectra of the prompt GRB emission are typically fit by two power laws:
In the double power-law model, the break energy of the spectrum coincides with the peak energy Eγ,peak of the 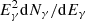 spectrum. Typical spectral indices are α ≃ 0 − 1 and β ≃ 2 − 3.
spectrum. Typical spectral indices are α ≃ 0 − 1 and β ≃ 2 − 3.
The very fact that the best fit to GRB spectra is a power-law function above Eγ,peak supports the idea that the GRB spectra are produced by nonthermal phenomena. Nonetheless, twenty years of detailed investigation of the spectra of GRBs did not result in the clear identification of the dominant radiative processes responsible for the prompt emission production. Therefore, a clear understanding of the nature of the GRB jet composition and dissipation processes therein is lacking. However, it is well established, that shocks or reconnection regions produce nonthermal populations of protons and electrons (for a review, see Zhang 2018).
Given the nonthermal nature of GRB spectra and their cosmic rate, GRBs are candidate accelerators of ultra-high energy cosmic rays (UHECRs) and are considered promising sources of high-energy neutrinos, as initially proposed in Waxman & Bahcall (1997). As a matter of fact, GRBs can provide the sufficient power to justify the spectrum of UHECRs above 1017 eV, as they are the brightest explosions in the Universe with a rate on the order of approximately one per day, as observed by the Burst And Transient Source Experiment (BATSE). Such explosions can release energies as high as ∼1054 erg over time intervals of a few seconds (short GRBs or sGRBs) and around 100 s up to about 1000 s (long GRBs or lGRBs).
The bimodal distribution of the BATSE GRBs hints at two subclasses (Kouveliotou et al. 1993), which might be generated by two different progenitors, possibly binary mergers for the sGRBs (Eichler et al. 1989) and collapsars for lGRBs (Woosley & Bloom 2006). This separation-progenitor dichotomy might not be absolute (see Bromberg et al. 2012), as the recent detection of a lGRB in coincidence with an identified kilonova light curve proves (Rastinejad et al. 2022), followed by evidence of the Fermi Large Area Telescope (Fermi-LAT) observation (Mei et al. 2022). Recent reviews on GRBs and on models of electromagnetic and neutrino emission can be found for instance in Pitik et al. (2021) and Kimura (2022).
The first X-ray afterglow emission was observed by the Beppo-SAX satellite in 1997 (Costa et al. 1997). Before the launch of The Neil Gehrels Swift Observatory (Swift, hereafter) in 2004, the observational data could be accommodated for with an external shock model, in which the afterglow emission was induced by the interactions of the forward and reverse shock of the GRB ejecta with the circum-burst medium (Meszaros & Rees 1997). Nevertheless, the early Swift era revealed that a more complex scenario must be considered to explain the unexpected features in the X-ray light curve, such as flares and plateaus.
X-ray flares are rapid rises and falls of the intensity of the X-ray emission observed in nearly 50% of the GRBs detected by Swift (Gehrels et al. 2009). They occur tens to hundreds of seconds after the prompt trigger, and last 10 s to 103 s. X-ray flares cannot be produced by external shocks, and they show similarities with the prompt emission (Margutti et al. 2010), which might indicate a common origin powered by a late, long-lasting activity of the central engine (Chincarini et al. 2007). In this regard, an internal-shock model is proposed at the origin of X-ray flares, in which the production is due to internal dissipation mechanisms (Fan & Wei 2005). Given the similarities with the prompt phase and the longer duration, such X-ray flares can lead to a more efficient production of high-energy neutrinos than during the prompt emission, provided that the internal dissipation mechanisms involve a population of nonthermal protons (Murase & Nagataki 2006; Kimura et al. 2017; Kimura 2022). The high-energy neutrino production is, however, suppressed if the jet is highly magnetized.
Plateaus are a shallow decay phase of the X-ray emission with time, ∝t−a, with a typical temporal slope1a < 0.7. Plateaus usually occur 102 s to 104 s after the prompt trigger, and they are observed in roughly 60% of the Swift GRBs (Gehrels et al. 2009). The plateau can be followed by a normal (slope 1 ≲ a ≲ 2) or a steep (slope 3 ≲ a ≲ 10) decay phase in the light curve, with no spectral changes across the break. If followed by a normal decay phase, the plateau can be interpreted within the external shock model (Zhang et al. 2006). In this case, the flattening of the X-ray light curve can be attributed to a continuous energy injection supplied by a late-time activity of the central engine (Dai & Lu 1998) or to a structured jet (Oganesyan et al. 2020; Beniamini et al. 2020). The plateau followed by a steep decay phase cannot originate from external shocks (Troja et al. 2007). In this regard, many authors believe that the plateau phase is induced by internal dissipation mechanisms powered by a magnetar wind, and that the subsequent steep decay phase is associated with the abrupt collapse of the magnetar to a black hole (Lyons et al. 2010).
Neutrino telescopes have conducted many GRB searches. Prominently, IceCube has previously performed searches for spatial and temporal correlation of astrophysical neutrinos and GRBs, finding no significant association. The first exclusion was provided in Abbasi et al. (2012), in a search for neutrino emission in time windows up to ±1 d from GRBs observed from April 2008 to May 2010. In 2015, the analysis of the prompt phase of 506 GRBs in the Northern Sky from April 2008 to May 2012 yielded constraints on parameters of the single-zone fireball model, and estimated the contribution of GRB neutrinos to ∼1% of the diffuse astrophysical flux (Aartsen et al. 2015). The analysis was extended in 2017 to include three more years of IceCube data up to May 2015, and prompt GRBs observed in the whole sky (Aartsen et al. 2017a). An overall catalog of 1172 prompt GRBs was selected for this analysis. More recently, searches for generic extended time windows up to 14 d after the prompt phase and for targeted precursors have been presented in Abbasi et al. (2022). These searches, which covered more than 2000 GRBs observed from May 2011 to October 2018, place upper limits on the afterglow emission and on the contribution of GRB neutrinos to the diffuse flux, and constrain precursor GRB models. While all the aforementioned analyses adopted an IceCube sample optimized for muon selection, more suitable for point-like source searches (see Sect. 4), in Aartsen et al. (2016a) IceCube extended the search to include all-flavor high-energy neutrinos detected in three years, from May 2010 to May 2013. A total of 807 GRBs over the entire sky were analyzed.
Despite many in-depth investigations of GRB neutrinos, the emission from X-ray plateaus and/or flare afterglows has been constrained by the IceCube collaboration only as a generic afterglow emission. In the work described in this paper, we analyze the publicly available IceCube point-source data (Abbasi et al. 2021a), searching for temporal and spatial coincidence of high-energy neutrinos with the prompt phase and with the plateaus and flares of the X-ray afterglow phase to constrain a model inspired from Murase (2007), Zhang & Kumar (2013), Kumar & Zhang (2015), Kimura (2022), Guarini et al. (2022). We describe this model for clarity in Sect. 3. Along with a search from individual GRBs (referred to as “single-source search” in the following), we also perform a search for a cumulative neutrino emission (“stacking search”).
With respect to other IceCube stacking searches, our stacking method adopts physically motivated weights for the contribution of each GRB to the overall emission, thus avoiding the assumption of an equal fluence at Earth. For instance, Aartsen et al. (2017a) provides upper limits on the cumulative neutrino flux from GRBs and constraints on the parameter space of the fireball model, with the underlying assumption that the parameters determining the neutrino emission (e.g., the bulk Lorentz factor Γ and luminosity) have the same values for all GRBs. Nonetheless, it is nowadays well established that such parameters can span orders of magnitude for different GRBs. In this paper, motivated by the progress of the last decade in the understanding of the GRB phenomena, and given the increased GRB observations, we exploit the luminosity–Lorentz factor correlation (Ghirlanda et al. 2012; Lü et al. 2012) and the luminosity–peak energy correlation (Yonetoku et al. 2004) observed during the prompt phase to determine these parameters on a per-GRB case (see also Sect. 3.1). This approach improves the physical reliability of the results presented in this work compared to past searches.
The paper is structured as follows. In Sect. 2, we introduce the GRB catalogs analyzed by this work. Then, we discuss the model and we derive the stacking weights for the different GRB catalogs in Sect. 3. We describe the IceCube neutrino sample in Sect. 4. We provide details about the statistical method adopted for the single-source and the stacking searches in Sect. 5. We report the results in Sect. 6, and we discuss the related limits and physical implications in Sect. 7. Final remarks are then summarized in Sect. 8.
2. Definition of the GRB catalogs
This work analyzes three GRB catalogs. Two catalogs are based on the X-ray afterglow emission, and include GRBs with X-ray plateaus or X-ray flares, hence referred to as “plateau catalog” and “flare catalog”, respectively. A third catalog is based on the prompt phase of selected GRBs, and thus referred to as “prompt catalog”. We additionally require that the selected GRBs occur during the IceCube uptime provided with the data release (Abbasi et al. 2021a). Furthermore, the GRBs with declination δ above 80° in absolute value are excluded, as the technique used to estimate the background of IceCube neutrino events (see Sect. 5) is not efficient around the equatorial poles.
The plateau catalog comprises 260 GRBs detected by Swift/XRT, whose X-ray light curve, reconstructed by the automatic analysis of the Swift/XRT products (Evans et al. 2009), presents a power-law attenuation in time ∝t−a, with index a < 0.7. This is the shallowest expected temporal attenuation from synchrotron radiation of external shock (Zhang et al. 2006). The flare catalog collects 200 GRBs detected by Swift/XRT, for which the online light curve analysis identifies X-ray flaring activity in the afterglow emission. A total of 85 GRBs have both X-ray plateaus and X-ray flares. They are in common to both catalogs and analyzed considering the corresponding time intervals. Examples of light curves with an X-ray plateau and an X-ray flare are provided in Fig. 1. The uncertainty on the sky localization of the GRBs that compose these two X-ray-based catalogs benefits from the very good accuracy that characterizes Swift/XRT, and that is generally smaller than the typical angular uncertainty of the IceCube track-like events (see Sect. 4).
 |
Fig. 1. Examples of a prompt emission light curve (a) observed by Fermi/GBM, a flare (b) and a plateau (c) of the X-ray afterglow observed by Swift/XRT. |
The 1751 GRBs of the prompt catalog are selected from GRBweb (Coppin 2022), an IceCube project that collects some relevant GRB parameters observed by different telescopes (Swift/XRT Lien et al. 2016, Fermi/GBM Hurley et al. 2013; von Kienlin et al. 2020, and others Ajello et al. 2019) into a single, online database. In general, Fermi/GBM is characterized by a poor angular resolution, that can be as high as ∼10° and that can exceed the typical resolutions of the track-like neutrino events. In these cases, the GRB is treated as an extended source and its spatial size is taken into account in the analysis method (see Sect. 5 for more details). Nearly 90% of the prompt catalog is composed of lGRBs.
The plateau and flare catalogs are analyzed both with the single-source and the stacking searches, described in Sect. 5, while the prompt catalog is only analyzed with the stacking search. The latter choice is motivated by the fact that IceCube has already performed extensive investigations of GRB neutrinos from the prompt phase (Abbasi et al. 2012, 2022; Aartsen et al. 2015, 2016a, 2017a). While our single-source search does not add anything to those searches, we think that a significant difference stems in using the weights defined in Sect. 3 for the stacking search. For each catalog, the stacking search is also performed on the subsamples of GRBs with measured redshift, that will be referred to as “subcatalogs”. Despite their smaller size, these subcatalogs allow us to reduce the number of assumptions on the GRBs, thus producing less strong, but more reliable results. Table 1 provides the number of GRBs in each (sub)catalog and in each hemisphere. It also anticipates the stacking weights (derived in Sect. 3), defined in terms of the prompt and X-ray isotropic equivalent fluence (Siso and 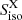 ) and luminosity (Liso and
) and luminosity (Liso and 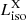 ), as well as the peak energy Eγ,peak and the redshift z. Finally, it provides information about the parameters constrained in each catalog, namely the baryon loading factor ξp, the bulk Lorentz factor Γ, the variability timescale of the prompt phase δtobs, or the magnetic field B (see also Sect. 3).
), as well as the peak energy Eγ,peak and the redshift z. Finally, it provides information about the parameters constrained in each catalog, namely the baryon loading factor ξp, the bulk Lorentz factor Γ, the variability timescale of the prompt phase δtobs, or the magnetic field B (see also Sect. 3).
Description of the GRB catalogs (all-GRB inclusive) and subcatalogs (GRBs with measured redshift) analyzed by this work.
The catalogs are separated into the Northern (δ ≥ −5°) and Southern (δ < −5°) Hemisphere due to the different sensitivity of IceCube in these two regions of the sky. This is due to the different nature of the background, mostly downgoing muons in the Southern Hemisphere, and atmospheric neutrinos in the Northern Hemisphere.
3. The model
Protons accelerated to high energies can undergo photo-pion production with ambient photons:
The branching ratios (BR) of the two channels are shown at the resonant energy for the production of an on-shell Δ+ baryon. Nonetheless, out of resonance the two channels are about equally probable, with BR ∼ 1/2 in each. While π0’s decay into photon pairs, the decay chain of π+’s leads to a copious production of high-energy GRB neutrinos, as also illustrated in Fig. 2:
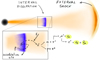 |
Fig. 2. Illustration of the photo-pion processes that lead to the production of high-energy neutrinos inside the dissipation region of GRB jets. |
In these photo-pion interactions, each neutrino carries on average 25% of the parent pion energy. The expected ratio of each neutrino+antineutrino flavor at the source is (νe : νμ : ντ)S = (1 : 2 : 0). Nevertheless, flavor oscillations of TeV–PeV neutrinos over cosmological baselines alter the proportions, and one expects on average the same flux of all flavors at Earth, (νe : νμ : ντ)E = (1 : 1 : 1). Given the chain of reactions above, the emitted neutrino fluence is linked to the proton spectrum 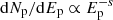 , which depends on the GRB spectral shape.
, which depends on the GRB spectral shape.
The proton contribution to the GRB emission is typically expressed in terms of the baryon loading factor 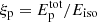 , defined as the ratio of the total energy in nonthermal protons
, defined as the ratio of the total energy in nonthermal protons 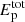 to the isotropic-equivalent bolometric energy released in photons during the prompt phase Eiso. Typically, ξp ≳ 20 is required for the GRBs to be the sources of the observed UHECR flux (for a review, see Kimura 2022, and references therein). Eiso is defined through the observed GRB fluence during the prompt phase Siso and the luminosity distance dL at a given redshift z:
to the isotropic-equivalent bolometric energy released in photons during the prompt phase Eiso. Typically, ξp ≳ 20 is required for the GRBs to be the sources of the observed UHECR flux (for a review, see Kimura 2022, and references therein). Eiso is defined through the observed GRB fluence during the prompt phase Siso and the luminosity distance dL at a given redshift z:
In turn, the GRB fluence Siso is given by the product of the observed GRB flux Fiso (in units erg s−1 cm−2), and the total observation time of the prompt phase T100 as defined in GRBweb (Coppin 2022).
In terms of the GRB parameters, the proton spectrum can then be written as (Kimura 2022)
where fp is the fraction of energy in protons that produce neutrinos via the photo-meson interactions. It is calculated in Eq. (10) of Zhang & Kumar (2013) for an injection proton spectrum 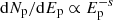 with s = 2 (that we assume through all this work), and for a range of neutrino energy from 0 to ∞. In first approximation, fp ∼ 1/ln(Ep, max/Ep, min), where Ep, min and Ep, max are respectively the minimum and maximum energy of the nonthermal proton spectrum.
with s = 2 (that we assume through all this work), and for a range of neutrino energy from 0 to ∞. In first approximation, fp ∼ 1/ln(Ep, max/Ep, min), where Ep, min and Ep, max are respectively the minimum and maximum energy of the nonthermal proton spectrum.
On average, one expects to observe the same flux ϕν of all neutrino flavors at Earth. In the following, we focus on muon neutrinos and antineutrinos, that constitute the large majority of the events of the IceCube data analyzed by this work (see Sect. 4). The muon neutrino+antineutrino fluence 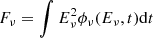 , at the neutrino energy Eν, can be linked to the proton spectrum, and ultimately, using Eq. (6), to the observable GRB parameters (Kimura 2022):
, at the neutrino energy Eν, can be linked to the proton spectrum, and ultimately, using Eq. (6), to the observable GRB parameters (Kimura 2022):
The parameters of this equation are described below in this paragraph. The factor 1/8 accounts for the fraction of the pion energy carried by each neutrino (∼1/4) and the branching ratio of nonresonant pγ interactions into the π+ channel (∼1/2, as stated above). 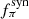 and
and 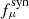 , called pion and muon synchrotron suppression factors, are included in Eq. (7) to account for a possible suppression of the high-energy neutrino component due to synchrotron emission of pions and muons that cool down before decaying. The suppression factors are defined as follows:
, called pion and muon synchrotron suppression factors, are included in Eq. (7) to account for a possible suppression of the high-energy neutrino component due to synchrotron emission of pions and muons that cool down before decaying. The suppression factors are defined as follows:
where i indicates the particle type, pion or muon. The typical timescale for synchrotron cooling of a particle with energy Ei in a magnetic field B is 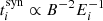 . If this is shorter than the decay timescale
. If this is shorter than the decay timescale 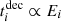 , the suppression factors are
, the suppression factors are 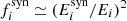 , and the neutrino flux can be suppressed at high energy. Normally, this occurs above an energy threshold
, and the neutrino flux can be suppressed at high energy. Normally, this occurs above an energy threshold 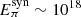 eV for pions and
eV for pions and 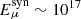 eV for muons, assuming typical GRB parameters (Kimura 2022). Below these thresholds, the suppression factors are negligible,
eV for muons, assuming typical GRB parameters (Kimura 2022). Below these thresholds, the suppression factors are negligible, 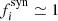 . Finally, the factor fpγ in Eq. (7) is the fraction of protons that participate in the photo-pion production. The functional dependency of fpγ on the GRB parameters provides an important part of the physical weights of the stacking search, and will be discussed in detail for each (sub)catalog in the following of this section. It is worth noticing that numerical computations of the expected neutrino signals provide factor of ∼3 − 5 more flux in high energy neutrinos (e.g. see Hümmer et al. 2012; He et al. 2012), thus the analytical approximation we use to constrain the amount of nonthermal protons in the GRB jets is conservative.
. Finally, the factor fpγ in Eq. (7) is the fraction of protons that participate in the photo-pion production. The functional dependency of fpγ on the GRB parameters provides an important part of the physical weights of the stacking search, and will be discussed in detail for each (sub)catalog in the following of this section. It is worth noticing that numerical computations of the expected neutrino signals provide factor of ∼3 − 5 more flux in high energy neutrinos (e.g. see Hümmer et al. 2012; He et al. 2012), thus the analytical approximation we use to constrain the amount of nonthermal protons in the GRB jets is conservative.
The expected GRB neutrino flux is a double broken power law, with a low-energy and a high-energy break point, 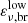 and
and 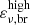 respectively (Waxman & Bahcall 1997; Kumar & Zhang 2015):
respectively (Waxman & Bahcall 1997; Kumar & Zhang 2015):
The low-energy neutrino flux break 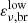 can be calculated from the break of the proton energy, assuming a typical neutrino-to-proton energy ratio of 5%. This proton break (see for instance Eq. (29) in Kimura 2022) is due to the photo-pion threshold. Hence, the neutrino low-energy break is:
can be calculated from the break of the proton energy, assuming a typical neutrino-to-proton energy ratio of 5%. This proton break (see for instance Eq. (29) in Kimura 2022) is due to the photo-pion threshold. Hence, the neutrino low-energy break is:
Given that IceCube is mostly sensitive in the energy range from few TeV to few PeV, it is very likely to observe GRB neutrinos in the region around 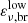 . The high-energy break
. The high-energy break 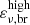 is associated to the pion transition from a decay-dominated to a synchrotron-cooling-dominated regime, where the neutrino production is suppressed. Assuming a neutrino-to-pion energy ratio of 25%, the high-energy break can be estimated as
is associated to the pion transition from a decay-dominated to a synchrotron-cooling-dominated regime, where the neutrino production is suppressed. Assuming a neutrino-to-pion energy ratio of 25%, the high-energy break can be estimated as 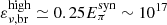 eV. Neutrinos above the high-energy break are unlikely to be observed by IceCube, and therefore they are not considered in this analysis. The neutrino spectral index γ in each power-law region is correlated with the proton spectral index s and the photon spectral indices α and β. Below the low-energy break (
eV. Neutrinos above the high-energy break are unlikely to be observed by IceCube, and therefore they are not considered in this analysis. The neutrino spectral index γ in each power-law region is correlated with the proton spectral index s and the photon spectral indices α and β. Below the low-energy break (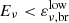 ), neutrinos are produced by the interactions of protons with the high-energy part of the photon spectrum (spectral index β). In this energy region, the neutrino spectrum scales as
), neutrinos are produced by the interactions of protons with the high-energy part of the photon spectrum (spectral index β). In this energy region, the neutrino spectrum scales as 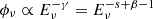 . Above the low-energy break, (
. Above the low-energy break, (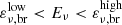 ), protons can interact with the low-energy photons with spectrum with spectral index α, producing a neutrino spectrum
), protons can interact with the low-energy photons with spectrum with spectral index α, producing a neutrino spectrum 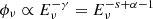 . Above the high-energy break (
. Above the high-energy break (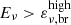 ), the neutrino production is suppressed by synchrotron cooling, and the spectrum is softened by the synchrotron suppression factors,
), the neutrino production is suppressed by synchrotron cooling, and the spectrum is softened by the synchrotron suppression factors, 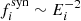 . The high-energy part of the neutrino spectrum is thus
. The high-energy part of the neutrino spectrum is thus 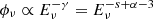 . Assuming a proton spectral index s = 2 and typical photon parameters α ≃ 1 and β ≃ 2, the corresponding neutrino spectral indices are γ = 1 (
. Assuming a proton spectral index s = 2 and typical photon parameters α ≃ 1 and β ≃ 2, the corresponding neutrino spectral indices are γ = 1 (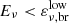 ), γ = 2 (
), γ = 2 (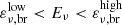 ), and γ = 4 (
), and γ = 4 (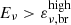 ), respectively.
), respectively.
3.1. Empirical correlations for the prompt emission of GRBs
The stacking weights, that are derived in Sects. 3.2 and 3.3, depend on GRB parameters, such as the isotropic-equivalent bolometric luminosity Liso and the bulk Lorentz factor Γ. For GRBs with measured redshift, it is trivial to calculate the bolometric luminosity as 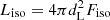 from the observed GRB flux Fiso and luminosity distance dL. However, the majority of GRBs do not have measured redshifts. While the past IceCube analyses (e.g. Aartsen et al. 2017a; Abbasi et al. 2022) adopted the same benchmark values of the relevant parameters for all GRBs, here we propose a novel approach, that exploits empirical correlations observed in lGRBs to estimate the needed quantities for the prompt phase, as first used in Albert et al. (2020) to estimate the GRB bulk Lorentz factor. Such an approach benefits from the improvements of the last decade in the understanding of the GRB mechanisms, and it is motivated by the wide sample of GRB observations currently available.
from the observed GRB flux Fiso and luminosity distance dL. However, the majority of GRBs do not have measured redshifts. While the past IceCube analyses (e.g. Aartsen et al. 2017a; Abbasi et al. 2022) adopted the same benchmark values of the relevant parameters for all GRBs, here we propose a novel approach, that exploits empirical correlations observed in lGRBs to estimate the needed quantities for the prompt phase, as first used in Albert et al. (2020) to estimate the GRB bulk Lorentz factor. Such an approach benefits from the improvements of the last decade in the understanding of the GRB mechanisms, and it is motivated by the wide sample of GRB observations currently available.
Two solid correlations have been found between the GRB luminosity and bulk Lorentz factor (Ghirlanda et al. 2012; Lü et al. 2012), and between the GRB luminosity and the photon energy peak in the rest frame (Yonetoku et al. 2004), Eγ,peak,300,rest = (1+z)Eγ,peak,300, where Eγ,peak,300 = Eγ,peak/300 keV. In Fig. 3 we plot and fit the Γ2 − Eγ,peak,300,rest and the Liso,52 − Eγ,peak,300,rest data from the most updated samples in the literature, Ghirlanda et al. (2018) and Yonetoku et al. (2010) respectively, where2Γ2 = Γ/102 and Liso, 52 = Liso/1052 erg s−1. Although the original Yonetoku relation in Yonetoku et al. (2004) involves the peak luminosity, here we use the (time-averaged) isotropic luminosity, that is more appropriate given that the analysis described in the following of this paper is based on time-averaged GRB properties and on a search for neutrinos from the prompt phase as a whole. For both relationships, the data suggest a linear log-log dependence. In the first case, assuming homogeneous circum-burst medium around the lGRB progenitors (since Γ is mainly derived from the peak of the afterglow emission), the best-fit parameters are:
 |
Fig. 3. Correlation plots of the bulk Lorentz factor Γ2 = Γ/102 (a) and luminosity Liso, 52 = Liso/1052 erg s−1 (b) with the photon energy peak in the rest frame Eγ,peak,300,rest for the prompt emission, useful for the catalog of the GRB prompts. The best exponential fit is shown as a dashed line, with the 3σ error bands represented by the blue, shaded regions. GRB data are taken from Ghirlanda et al. (2018), (a) and Yonetoku et al. (2010), (b). |
For the second relationship, the best fit returns:
These relationships are used to estimate the luminosity and Lorentz factor of prompt GRBs for which the redshift is not measured (see below). To derive the Γ, Ghirlanda et al. (2018) assumed constant efficiency of the prompt emission, that is 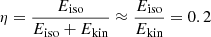 , where Ekin is the total kinetic energy of the jet. The baryon-loading factor in the prompt emission is ξp = ϵp/η, where ϵp is the fraction of total kinetic energy in nonthermal protons. The relevance of these parameters, namely the peak energy, the luminosity, and the bulk Lorentz factor, to determine the neutrino fluence from individual GRBs was first proposed for GRBs of the BATSE catalog in the AMANDA era (Guetta et al. 2004).
, where Ekin is the total kinetic energy of the jet. The baryon-loading factor in the prompt emission is ξp = ϵp/η, where ϵp is the fraction of total kinetic energy in nonthermal protons. The relevance of these parameters, namely the peak energy, the luminosity, and the bulk Lorentz factor, to determine the neutrino fluence from individual GRBs was first proposed for GRBs of the BATSE catalog in the AMANDA era (Guetta et al. 2004).
In principle, the bulk Lorentz factor can also be inferred by using the Γ2 − Liso, 52 relation (fit in Fig. 4) together with the Liso, 52 − Eγ, peak, 300, rest relation in Eq. (12). While leading to the same weighting dependencies derived in Sects. 3.2 and 3.3, this approach is more convoluted, and here we prefer to fit and use the direct relation in Eq. (11).
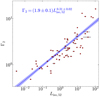 |
Fig. 4. Correlation plot of the bulk Lorentz factor Γ2 = Γ/100 with the isotropic luminosity Liso, 52 = Liso/(1052 erg s−1) for the prompt emission. The best exponential fit is shown as a dashed line, with the 3σ error bands represented by the blue, shaded regions. GRB data are taken from Ghirlanda et al. (2018). |
3.2. Stacking weights for γ = 2 (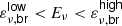 )
)
In this subsection, we derive the weights for the prompt and X-ray (sub)catalogs in the energy range 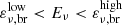 , where the expected neutrino spectral index is γ = 2. To do so, we estimate the factor fpγ in terms of relevant GRB parameters mentioned above and the size of the emission region R:
, where the expected neutrino spectral index is γ = 2. To do so, we estimate the factor fpγ in terms of relevant GRB parameters mentioned above and the size of the emission region R:
where 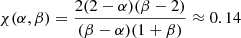 assuming typical α = 1 and β = 2.3.
assuming typical α = 1 and β = 2.3.
In the analysis of the prompt subcatalog, consisting of GRBs with measured redshift, the size of the emission region R can be inferred from the observed time variability δtobs of the prompt phase (Piran 2004):
Replacing Eq. (14) in Eq. (13), one finds for the prompt emission
where δtobs, 0 = δtobs/1 s. Combining Eq. (15) with Eq. (7), and neglecting the synchrotron suppression factors, the expected neutrino fluence is estimated as
The value of ln(Ep, max/Ep, min) is estimated from simulations. Therefore, the stacking weights for the analysis of the prompt subcatalog are:
For this subcatalog, we place constraints on ξp vs. Γ assuming benchmark values of the time variability δtobs.
For the analysis of the prompt catalog, where the redshift is not measured for all GRBs and the luminosity and Lorentz factor can be unavailable, we use the correlations in Eqs. (11) and (12) to replace the dependence of Fν from Γ2 and Liso, 52 in Eq. (16) with the observable Eγ, peak. We obtain the following expected neutrino fluence:
Therefore, the stacking weights for the analysis of the full prompt catalog (that includes GRBs with no measured redshift) are defined as
In this case, we constrain ϵp vs δtobs for fixed values of redshift z. We have chosen the fiducial value of η of 0.20 according to the common value inferred from the X-ray and the GeV afterglow modeling of lGRBs (Nava et al. 2014; Beniamini et al. 2016).
When considering the plateau and flare subcatalogs, the relationship in Eq. (14), used to remove the dependence of fpγ from the size R of the emission region during the prompt phase, cannot be used, as the variability timescale for the X-ray flares and plateaus is not defined. In this case, the parameter R cannot be removed from the equations, and the expected neutrino fluence for the X-ray flares and plateaus is
Here, 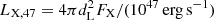 is the X-ray luminosity normalized to 1047 erg s−1, FX and
is the X-ray luminosity normalized to 1047 erg s−1, FX and 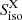 are the observed X-ray flux and fluence respectively, and Eγ, peak, 1 = Eγ, peak/1 keV is the energy peak normalized at 1 keV. For the plateau and flare subcatalogs, comprising GRBs with measured redshift, the stacking weights are defined as
are the observed X-ray flux and fluence respectively, and Eγ, peak, 1 = Eγ, peak/1 keV is the energy peak normalized at 1 keV. For the plateau and flare subcatalogs, comprising GRBs with measured redshift, the stacking weights are defined as
In this case, the analysis is used to place constraints on ξp vs Γ for benchmark values of R14.
For the full plateau and flare catalogs, comprising GRBs with and without measured redshift, the basic weight is used:
In this case, no constraints are placed, as too many parameters in Eq. (20) cannot be estimated in a robust way.
3.3. Stacking weights for γ = 1 (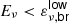 )
)
In this subsection, we derive the weights for the prompt and X-ray (sub)catalogs in the energy range 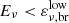 , where the expected neutrino spectral index is γ = 1. The neutrino fluence at 1 TeV can be parametrized as
, where the expected neutrino spectral index is γ = 1. The neutrino fluence at 1 TeV can be parametrized as
For the analysis of the prompt subcatalog, the relationship (14) is adopted to reduce the dependence of Fν in Eq. (23) from R:
and the following weights for the GRB prompt emission of GRBs with measured redshifts are defined:
Constraints are then placed on ξp vs. Γ for benchmark values of the variability timescale δtobs.
When considering the full prompt catalog, the luminosity Liso, 52 and Lorentz factor Γ2 can be replaced with Eγ, peak, using the relationships in Eqs. (11) and (12):
Therefore, the weights for the analysis of the prompt catalog are
As for the case with γ = 2, in this case we constrain ϵp vs. δtobs considering benchmark values of the redshift z.
For the analysis of the flare and plateau subcatalogs, we go back to Eq. (23), and we replace the prompt parameters with the corresponding X-ray parameters. We define the following weights:
Constraints are set on ξp vs. Γ for some values of R14.
For the flare and plateau catalogs, the basic weight is used:
Similarly to the case with γ = 2, no constraints are placed from these two catalogs.
So far we have been ignoring the suppresion of the high energy neutrinos by the synchrotron losses of muons and pions (see Eq. (8)). Let us introduce another parameter, ϵB which is the fraction of the kinetic energy of the jet in the magnetic field energy, that is
where B is the strength of the magnetic field in the comoving frame of the emitting region of a GRB. In the Fig. 5 we show the neutrino suppression factors by the synchrotron losses of pions and muons for the neutrino energies of 1 TeV, 10 TeV, and 100 TeV. One can notice that the magnetic field of > 104 G is enough to suppress the high energy neutrinos in the IceCube energy range. To estimate ϵB which corresponds to a value of B ∼ 104 G for a typical long GRB, we use the relation (30) together with Eqs. (11), (12), and (14):
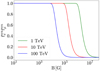 |
Fig. 5. Neutrino suppression factor by the synchrotron losses of muons and pions as the function of the comoving strength of the magnetic field in the emission region of a GRB. Green, red, and blue lines correspond to the energies of neutrinos equal to 1 TeV, 10 TeV, and 100 TeV. |
This means that the synchrotron losses can be safely ignored for ϵB < 0.01.
4. The IceCube open-access neutrino data
The IceCube Neutrino Observatory (Aartsen et al. 2017b) is a km3 sized telescope located at the South Pole and designed to detect high-energy (E > 100 GeV) astrophysical neutrinos. Since 2011, the detector has consisted of 86 strings embedded in the Antarctic ice at a depth of 1.5−2.5 km, but the data taking period already started in 2006 in partial detector configurations. The strings are equipped with a total of 5160 digital optical modules, each hosting a 10-inch photomultiplier tube. IceCube detects Cherenkov light from neutrino-induced muon tracks and cascades from neutral and charged current neutrino interactions of tau and electron neutrinos.
The analysis presented in this paper uses the data collected by IceCube in 10 years of operation, from April 6, 2008 to July 8, 2018, and publicly released as described in Abbasi et al. (2021a). The data are grouped into five independent sets that reflect the different detector configurations with 40, 59, and 79 strings (from 2008 to 2010), and the different event selections adopted in the full 86-string configuration for the years 2011 and 2012−2018. Details about the filtering and selection to final level of analyses of the five data sets can be found in Table 1 of Aartsen et al. (2020a).
These data are selected for point-source searches, and thus optimized for muon track-like events, that provide the best angular resolution. The sample spans a neutrino energy range between about a hundred GeV to above PeV energies, with median angular resolution below 0.4° above 10 TeV. The roughly 1.1 million events collected in 10 years are mostly dominated by muons from atmospheric neutrino interactions in the Northern Hemisphere (declination δ ≥ −5°), and by high-energy atmospheric muons beyond several TeV or large bundles of low-energy muons in the Southern Hemisphere (δ < −5°).
5. Analysis method
For all the searches of this work, we use an unbinned maximum likelihood method similar to the one used for previous point-source IceCube searches (e.g. Braun et al. 2008, 2010; Aartsen et al. 2016b, 2020a,b; The IceCube Collaboration 2018; Abbasi et al. 2021b,c). Such a method is implemented in a public code, known as PSLab, that has recently been released to the community by the IceCube collaboration. This method is used to search for astrophysical neutrino correlations with individual GRBs (single-source search) and with each (sub)catalog as a whole (stacking search). In the two searches, the tested background hypothesis is the absence of astrophysical neutrinos correlated with individual GRBs for the single-source search, or with the ensemble of GRBs in each (sub)catalog for the stacking search.
5.1. Single-source search
For a GRB g at direction Ωg = (αg, δg), with right ascension αg and declination δg, observed at the instant tg and lasting Δtg, the unbinned likelihood of the single-source search reads as follows:
As the 10-yr IceCube data consist of five independent sets, that differ for the detector configuration and event selection criteria, the index j denotes the IceCube data set (from 1 to 5) that contains the time range of the analyzed phase of GRB g. The index i runs over the events collected in the IceCube data set j, for a total of Nj events. ns is the amount of signal-like events observed from the tested GRB g, and it is the only free likelihood parameter. 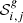 and
and 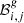 are the single-source signal and background probability density functions (PDFs) respectively, that depend on the GRB parameters (Ωg, tg, Δtg) and on the localization error σGRB, g, as well as on the assumed spectral index γ of the astrophysical neutrino flux, on the energy proxy Ei, on the reconstructed direction Ωi = (αi, δi), and on the estimated angular uncertainty σi of the ith event.
are the single-source signal and background probability density functions (PDFs) respectively, that depend on the GRB parameters (Ωg, tg, Δtg) and on the localization error σGRB, g, as well as on the assumed spectral index γ of the astrophysical neutrino flux, on the energy proxy Ei, on the reconstructed direction Ωi = (αi, δi), and on the estimated angular uncertainty σi of the ith event.
The signal and background PDFs can be decomposed into the product of a spatial, an energy, and a time PDF. The signal spatial PDF, also called Point-Spread Function (PSF), is modeled as a symmetric bivariate Gaussian distribution, centered at the GRB location and with a variance given by the quadratic sum of the neutrino angular uncertainty and the GRB localization error: 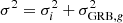 . For large standard deviations, σ > 10°, the PSF extends over a nonnegligible fraction of the sky, and following the prescription adopted in one of the previous IceCube searches (Aartsen et al. 2017a), the PSF is replaced by the first-order nonelliptical component of the Kent distribution (Kent 1982):
. For large standard deviations, σ > 10°, the PSF extends over a nonnegligible fraction of the sky, and following the prescription adopted in one of the previous IceCube searches (Aartsen et al. 2017a), the PSF is replaced by the first-order nonelliptical component of the Kent distribution (Kent 1982):
Here, 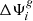 is the angular distance between the reconstructed direction of the event i and the location of the GRB g, and κ = 1/σ2 is called concentration parameter. The Kent distribution is the extension of the bivariate Gaussian distribution onto a spherical support, and the two distributions do not differ significantly for large values of the concentration parameter. The signal energy PDF is modeled as a power law with fixed spectral index, E−γ, as also adopted in both past IceCube searches from GRBs (Aartsen et al. 2017a; Abbasi et al. 2022). The analysis is performed by independently assuming γ = 1 or γ = 2, that correspond to the expected shape of the neutrino spectrum below the low-energy and the high-energy break, respectively (Kimura 2022). The signal time PDF is constant during the period of the tested GRB, [tg, tg + Δtg], and null otherwise. For the analysis of the prompt phase, Δtg is taken as the full prompt duration T100, while for the X-ray afterglow it is derived from the automatic analysis of the Swift/XRT products (Evans et al. 2009).
is the angular distance between the reconstructed direction of the event i and the location of the GRB g, and κ = 1/σ2 is called concentration parameter. The Kent distribution is the extension of the bivariate Gaussian distribution onto a spherical support, and the two distributions do not differ significantly for large values of the concentration parameter. The signal energy PDF is modeled as a power law with fixed spectral index, E−γ, as also adopted in both past IceCube searches from GRBs (Aartsen et al. 2017a; Abbasi et al. 2022). The analysis is performed by independently assuming γ = 1 or γ = 2, that correspond to the expected shape of the neutrino spectrum below the low-energy and the high-energy break, respectively (Kimura 2022). The signal time PDF is constant during the period of the tested GRB, [tg, tg + Δtg], and null otherwise. For the analysis of the prompt phase, Δtg is taken as the full prompt duration T100, while for the X-ray afterglow it is derived from the automatic analysis of the Swift/XRT products (Evans et al. 2009).
As the large majority of the IceCube events are of atmospheric origin, the background spatial PDF is determined through a data-driven method, also referred to as “scramble method”, where the time of the events is randomized within the uptime of the detector, and the right ascension is corrected accordingly, assuming fixed local coordinates (i.e., azimuth and zenith). Due to the peculiar position of the IceCube experiment at the geographical South Pole, the spatial background PDF depends only on the declination, and it is independent of the particular right ascension of the GRBs. Furthermore, since the directional reconstruction efficiency is slightly enhanced if the track events are aligned with the strings of the IceCube detector, an azimuth-dependent correction is included in the background spatial PDF, as described in Abbasi et al. (2021b). The background energy PDF is also estimated from scrambled data, and it depends on the event declination and energy proxy. The background time PDF is uniform within the time boundaries of each IceCube data set. We neglect the seasonal variations of the atmospheric neutrino and muon background, which is on the order of ∼4% for neutrino events (Heix et al. 2020) and ∼8% for downgoing muons (Tilav et al. 2019).
5.2. Stacking search
The stacking likelihood is based on the same PDFs and parameters as described for the single-source search. It is obtained by extending the single-source likelihood in Eq. (32) to include all the five IceCube data sets, and by replacing the signal PDF with the sum of single-source signal PDFs (for simplicity, the dependence on the neutrino and GRB parameters is omitted):
The sum runs across all GRBs g occurring in the livetime of the data set j. 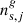 is the expected amount of signal-like events in the data set j originating from GRB g, and it is related to the “cumulative” signal-like neutrino events ns through the following equation:
is the expected amount of signal-like events in the data set j originating from GRB g, and it is related to the “cumulative” signal-like neutrino events ns through the following equation:
Here, 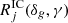 is the detector acceptance for a neutrino flux ∝E−γ related to the data set j at declination δg, and ΔTj = ∑g ∈ jΔtg is the overall time extension of all GRBs in the data set j. wg is the theoretical weight on the relative contribution of GRB g to the overall neutrino flux, and it is computed as described in Sect. 3. By definition,
is the detector acceptance for a neutrino flux ∝E−γ related to the data set j at declination δg, and ΔTj = ∑g ∈ jΔtg is the overall time extension of all GRBs in the data set j. wg is the theoretical weight on the relative contribution of GRB g to the overall neutrino flux, and it is computed as described in Sect. 3. By definition, 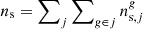 , that is in the stacking search ns is the amount of signal-like neutrinos from all the stacked GRBs and across the entire analysis period.
, that is in the stacking search ns is the amount of signal-like neutrinos from all the stacked GRBs and across the entire analysis period.
5.3. Test statistics and p value
In both the single-source and the stacking searches, the likelihood is maximized with respect to its parameter. The maximum-likelihood parameter is denoted with a hat, 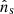 . By setting ns = 0, the likelihood describes the background-only hypothesis, and it is thus referred to as background likelihood. The log-likelihood ratio is then used to define the test statistics (TS) of the analysis:
. By setting ns = 0, the likelihood describes the background-only hypothesis, and it is thus referred to as background likelihood. The log-likelihood ratio is then used to define the test statistics (TS) of the analysis:
To avoid loss of generality, in the above definition, the likelihood ℒ is written with no label and it is intended to be the single-source likelihood 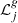 (Eq. (32)) or the stacking likelihood ℒstack (Eq. (34)), depending on the analysis. To quantify the significance of an observed TS, the analyses are repeated for background pseudo-experiments generated with the scramble method, each returning a “background-like” TS. The pretrial p value of an analysis is then estimated as the fraction of background pseudo-experiments that produce a TS value larger than the one observed in the data. When needed, the pretrial p value is eventually corrected for the so-called “look-elsewhere effect” into a post-trial p value that takes into account the number of searches performed. The detail of such a correction are provided in the appropriate Sect. 6. In the following, we refer to cases in which TS = 0 as “under-fluctuations”, and cases in which TS > 0 as “over-fluctuations”.
(Eq. (32)) or the stacking likelihood ℒstack (Eq. (34)), depending on the analysis. To quantify the significance of an observed TS, the analyses are repeated for background pseudo-experiments generated with the scramble method, each returning a “background-like” TS. The pretrial p value of an analysis is then estimated as the fraction of background pseudo-experiments that produce a TS value larger than the one observed in the data. When needed, the pretrial p value is eventually corrected for the so-called “look-elsewhere effect” into a post-trial p value that takes into account the number of searches performed. The detail of such a correction are provided in the appropriate Sect. 6. In the following, we refer to cases in which TS = 0 as “under-fluctuations”, and cases in which TS > 0 as “over-fluctuations”.
The major difference of the analysis described in this paper and the previous IceCube analyses of GRB neutrinos (Aartsen et al. 2017a; Abbasi et al. 2022) lies in the stacking method. In the stacking analysis in Aartsen et al. (2017a), the TS is calculated by summing the TS of the individual GRBs from the single-source search. However, the TS distribution is generally declination-dependent, and it might differ for GRBs at different declinations. In Abbasi et al. (2022), the stacking method coincides with the one adopted for this work, but the individual GRB contributions in Eq. (35) are only calculated based on the detector acceptance, implicitly assuming an equal GRB fluence at Earth. As a matter of fact, both analyses prefer GRBs that are located in strategic declination bands for IceCube, regardless of the intrinsic properties of the GRBs. In this work, we have proposed a weighted stacking method that, based on physical motivations, estimates the GRB contribution to the expected neutrino fluence by also incorporating relevant GRB observational properties expressed by the weights.
6. Results
The results of the single-source search from the plateau catalog are summarized in Table 2. The search returns GRB 140518A as the most significant GRB, and one signal-like neutrino event identified in temporal coincidence with the X-ray plateau. With a reconstructed muon energy of 3.3 TeV and a directional angular uncertainty of 1.6°, this event lies 3.3° from the location of the source. The corresponding pretrial p value of GRB 140518A is ploc = 1.1 × 10−3 (3.1σ) for a spectral index γ = 1, and ploc = 1.6 × 10−3 (3.0σ) for γ = 2. The post-trial p value is calculated by repeating the analysis on many background pseudo-experiments with the corresponding spectral index, and counting the fraction of pseudo-experiments that produces a smaller p value than the one observed in the data. This translates into a post-trial p value of 69% for both spectral indices, thus not significant.
Results of the single-source analysis of GRBs with X-ray plateau afterglow.
All the GRBs of the X-ray flare catalog are under-fluctuations, except for GRB 120213A when γ = 2 is considered, as reported in Table 3. In this case, the data contain one neutrino event in temporal coincidence with the X-ray flare. However, the reconstructed muon energy for this event is only 562 GeV, and the reconstructed track direction is displaced with respect to the source location by 5.8°, with an angular uncertainty of 2.9°. This results in a loose association of such neutrino with GRB 120213A, thus explaining the likelihood preference to fit only a fractional event, 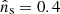 . The pretrial p value of this GRB is ploc = 2.9 × 10−2 (1.9σ), corresponding to a post-trial p value of 77%.
. The pretrial p value of this GRB is ploc = 2.9 × 10−2 (1.9σ), corresponding to a post-trial p value of 77%.
Results of the single-source analysis of GRBs with flare afterglow in X-rays, assuming a spectral index γ = 2.
The number of under-fluctuating GRBs (∼96% for the plateau catalog and ∼99.5% for the flare catalog) is much larger than the number of over-fluctuating, and for the flare catalog only one over-fluctuating GRB is identified. This is due to the short duration of the time window in which neutrinos are searched, that reduce the expected amount of events for a fixed event rate. This is particularly true for flares, whose associated search time window ranges between few tens to few hundreds of seconds. In the flare catalog, the expected average under-fluctuation rate under the background hypothesis is ≳99%. However, the very low event rate expected for the flare catalog search makes this analysis almost background-free, suggesting that even the smaller amount of signal can be spotted in the data, potentially carrying a high (pretrial) significance. This can be easily understood by looking at the background and signal TS distributions of one example GRB from the flare catalog, notably the over-fluctuating GRB 120213A, shown in Fig. 6. These distributions are obtained by running the single-source analysis at the location of GRB 120213A for many background and signal pseudo-experiments: the former are produced with the scramble method described in Sect. 5.1, and the latter by additionally injecting signal-like neutrino events simulated with the PSLab code (The IceCube Collaboration 2022).
 |
Fig. 6. (a) Example of TS distributions for the background (injected ns = 0, with 100 000 generated pseudo-experiments) and various signal hypotheses (injected ns > 1, with 10 000 pseudo-experiments each) at the location of GRB 120213A, for the single-source search of the flare catalog and assuming spectral index γ = 2. The signal distributions are very different from the background distribution already for ns = 1, suggesting that few signal events can lead to a high pretrial significance. (b) Background TS distribution, the same as in (a), but with different binning and axis ranges. The bin at TS = 0 corresponds to under-fluctuations: for this GRB, about 96% of the background pseudo-experiments result in under-fluctuations. |
All the results of the single-source analyses are compatible with the background hypothesis. As such, 90% confidence-level (CL) upper limits on the neutrino fluence from individual non-underfluctuating sources are placed. The upper-limit neutrino fluence for the single-source searches is defined as follows:
The factor F90%, corresponding to the normalization of the upper-limit fluence at the benchmark value of 1 TeV, is reported in the last column of Tables 2 and 3 for the related sources.
The results of the stacking searches are summarized in Table 4. These searches produce underfluctuations in all the (sub)catalogs, except for the analysis of the prompt catalog in the Northern Hemisphere with spectral index γ = 2, with no requirements on the measured redshift. In this case, the stacking likelihood fits 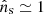 event, resulting in a pretrial p value of ploc = 3.5 × 10−2 and a post-trial p value of 13%. The post-trial correction of the stacking search is due to performing several searches of this kind, on different hemispheres, on different catalogs, with different spectral indices (γ = 1 and γ = 2), and with different requirements on the measured GRB redshift.
event, resulting in a pretrial p value of ploc = 3.5 × 10−2 and a post-trial p value of 13%. The post-trial correction of the stacking search is due to performing several searches of this kind, on different hemispheres, on different catalogs, with different spectral indices (γ = 1 and γ = 2), and with different requirements on the measured GRB redshift.
Results of the stacking analysis of the three GRB catalogs (prompt, plateau, flare) in each hemisphere, with and without requirements on the GRB redshift.
As no significant astrophysical correlation is observed by the stacking searches, these analyses are used to place 90% CL upper limits on the cumulative neutrino flux from each (sub)catalog. The upper-limit neutrino flux for the stacking searches is defined as follows:
where ΔT ≃ 10 yr is the full livetime of the data used for the analysis, and ΔΩ ≃ 2π is the solid angle of each hemisphere. 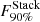 and
and 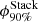 are the normalizations at 1 TeV on the 90% CL upper limit of the neutrino stacking fluence and the neutrino stacking flux, respectively. The 90% CL upper-limit flux normalization for each (sub)catalog is reported in Table 4. For a better visualization, such upper limits are also displayed in Fig. 7, assuming the same neutrino spectrum
are the normalizations at 1 TeV on the 90% CL upper limit of the neutrino stacking fluence and the neutrino stacking flux, respectively. The 90% CL upper-limit flux normalization for each (sub)catalog is reported in Table 4. For a better visualization, such upper limits are also displayed in Fig. 7, assuming the same neutrino spectrum 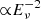 for all the GRBs. This figure additionally shows the energy-dependent stacking sensitivity of this analysis, and a comparison of the estimated IceCube-Gen2 sensitivity for the prompt (sub) catalog, assuming an
for all the GRBs. This figure additionally shows the energy-dependent stacking sensitivity of this analysis, and a comparison of the estimated IceCube-Gen2 sensitivity for the prompt (sub) catalog, assuming an 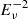 neutrino spectrum. The IceCube-Gen2 (Clark 2021) sensitivity is calculated by considering a 10 times larger detector volume, and by scaling the current effective area (and hence the sensitivity) by a factor 102/3, close to the designed factor ∼5 (Aartsen et al. 2014). The flux in Eq. (38) follows a similar definition as for the IceCube search in Abbasi et al. (2022), but it differs from the previous IceCube search in Aartsen et al. (2017a).
neutrino spectrum. The IceCube-Gen2 (Clark 2021) sensitivity is calculated by considering a 10 times larger detector volume, and by scaling the current effective area (and hence the sensitivity) by a factor 102/3, close to the designed factor ∼5 (Aartsen et al. 2014). The flux in Eq. (38) follows a similar definition as for the IceCube search in Abbasi et al. (2022), but it differs from the previous IceCube search in Aartsen et al. (2017a).
 |
Fig. 7. Differential sensitivity (solid lines) and 90% CL upper limits (dashed lines) for the stacking analysis of the plateau (red), flare (yellow), and prompt (green) catalog, assuming γ = 2. Curves are shown for the Northern (left) and Southern (right) Hemisphere, and for catalogs comprising all the GRBs (first row) or the subcatalogs of GRBs with measured redshift (second row). As a comparison, the shaded green region shows the 10-yr differential sensitivity calculated for IceCube-Gen2 (Clark 2021) as explained in the text. |
7. Discussion
The upper limits derived in Sect. 6 from the nonobservation of significant events in the various stacking searches are used to constrain relevant quantities of the model discussed in Sect. 3. Our assumption for the prompt emission is based on the empirical correlations between the GRB luminosities and the peak energies, and between the GRB bulk Lorentz factors and the peak energies, as detailed in Yonetoku et al. (2010) and Ghirlanda et al. (2012), respectively. Unlike previous GRB analyses performed by IceCube, that assumed all GRBs to have the same bulk Lorentz factor, fluence, or luminosity, we take into account the large range of values for these parameters (e.g. the luminosity spans five orders of magnitude). We assume the aforementioned correlations to estimate realistic values for these parameters of each GRB.
We obtain constraints on the baryon loading factor ξp of the prompt emission as a function of the timescale variability δtobs and bulk Lorentz factor Γ. Such constraints are shown in Figs. 8 (assuming a neutrino spectral index γ = 2) and 9 (assuming a neutrino spectral index γ = 1), for the two hemispheres and considering measured redshifts or benchmark values (when not measured), as well as some values of the variability timescale δtobs. Our analysis generally limits the baryon loading factor to ξ ≲ 10, unless extreme GRB values are considered (e.g. Γ > 500, δtobs ∼ 1 s, z ∼ 10). This seems to disfavor a baryonic origin of the GRB prompt, as also indicated by the absence of significant astrophysical neutrino results. Furthermore, if the synchrotron cooling suppression factors in Eq. (8) are not neglected, we can use Eq. (7) to similarly constrain ϵp as a function of the magnetic equipartition parameter ϵB, assuming typical values of δtobs = 0.1 s, η = 0.20 and z = 1. This is shown in Fig. 10, and indicates that for neutrino energies ≲100 TeV (where most of the IceCube events are observed), a large magnetic field B ≳ 104 G (ϵB > 0.01, see Eq. (31)) must be considered to accommodate the observations reported in this work. In other words, considering a single-zone model and considering protons and not heavier nuclei, the neutrino limits on the prompt emission phase imply that the fraction of total kinetic energy in nonthermal protons is less than 10% or that the magnetization is so high that GRB associated neutrinos should be found in the lower energies (sub-TeV range). The latter might hint at the fact that GRB jets are mostly magnetic-dominated, as already proposed by some authors (Usov 1992; Thompson 1994; Lyutikov & Blandford 2003; Ghisellini et al. 2020).
 |
Fig. 8. 90% CL upper limits for the baryon equipartition parameter ϵp and the baryon loading parameter ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the prompt catalog (upper plots) and subcatalogs of GRBs with available redshift (bottom plots), assuming a neutrino spectral index γ = 2. Excluded values are shown as shaded regions for different hypotheses of the redshift z (top plots) and of the timescale variability δtobs (bottom plots). |
 |
Fig. 9. 90% CL upper limits for the baryon equipartition parameter ϵp and the baryon loading parameter ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the prompt catalog (upper plots) and subcatalog of GRBs with available redshift (bottom plots), assuming a neutrino spectral index γ = 1. Excluded values are shown as shaded regions for different hypothesis of the redshift z (upper plots) and of the timescale variability δtobs (bottom plots). |
 |
Fig. 10. 90% CL upper limits for the baryon equipartition parameter ϵp in the Northern (left) and Southern (right) Sky as a function of the magnetic equipartition ϵB. These constraints are obtained with the stacking analysis of the prompt catalog, assuming a neutrino spectral index γ = 2. Excluded values are shown as shaded regions for different values of the neutrino energy Eν. Typical values of the timescale variability δtobs = 0.1 s and redshift z = 1 are used to compute these limits. To derive ϵB, we assumed a typical observed spectrum of lGRB with the peak energy of 300 keV (see Eq. (31)). It is worth notice that the asymptotic value of ϵp in the low-magnetic field regime in the Southern Sky is consistent with the limits computed in Fig. 8 in the same hemisphere, assuming the same parameters. |
We additionally constrain the baryon loading factor of the plateau and flare subcatalogs (with available redshift) as a function of the Lorentz factor Γ, for some values of the normalized radius of the GRB emission site R14. In this case, we cannot use the empirical correlations observed for the prompt phase and mentioned above, but we exploit all the available observations of the X-ray afterglows, namely the observed luminosity, fluence, and redshift. The constraints of our analyses are shown in Figs. 11 (assuming a neutrino spectral index γ = 2) and 12 (assuming a neutrino spectral index γ = 1). It should be noticed that in the case of X-ray afterglows, the variability range of the bulk Lorentz factor is typically lower (10 < Γ < 102) than for prompt (102 < Γ < 103), (Kimura 2022). The constraints on the X-ray afterglows are looser than those on the prompt phase, and the analysis does not exclude a possible baryonic origin of the plateau and flare emission.
 |
Fig. 11. 90% CL upper limits for the baryon loading factor ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the plateau (upper plots) and flare (bottom plots) subcatalogs of GRBs with available redshift, assuming γ = 2. Excluded values are shown as shaded regions for different hypotheses on the normalized radius of the GRB emission site. |
 |
Fig. 12. 90% CL upper limits for the baryon loading factor ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the plateau (upper plots) and flare (bottom plots) subcatalogs of GRBs with available redshift, assuming γ = 1. Excluded values are shown as shaded regions for different hypotheses on the normalized radius of the GRB emission site R14 (see Sect. 3). |
The nonobservation of an astrophysical neutrino signal from GRB prompt and afterglow phases is compatible with previous IceCube results, and with the estimated upper limits of GRB neutrinos to the diffuse flux of ≲1% (Aartsen et al. 2017a; Abbasi et al. 2022).
8. Conclusions
In this paper, we analyzed the 10-year IceCube data publicly available (Abbasi et al. 2021a). We used the PSLab code (The IceCube Collaboration 2022), recently released by the IceCube collaboration, to perform an unbinned maximum-likelihood search for spatial and temporal coincidence of astrophysical neutrinos from individual GRBs with X-ray flare and X-ray plateau afterglows. We also performed a stacking search for a cumulative neutrino excess from a flare, a plateau, and a prompt catalog. Unlike previous IceCube stacking searches, that assumed the same fluence at Earth for all GRBs, in our analysis we proposed a stacking scheme based on physically motivated GRB weights and observational properties. Furthermore, while past searches adopted the same benchmark values of relevant parameters for all the GRBs, we fit and used empirical relationships to estimate the GRB luminosities and Lorentz factors in the analysis of the prompt catalog when the redshift is not available. Since such parameters can vary across several orders of magnitude, our novel approach improves the physical reliability of the results.
We did not find any statistically significant neutrino correlations in our searches, consistently with previous IceCube results (Aartsen et al. 2017a; Abbasi et al. 2022). The nonobservation of neutrinos is therefore used to place upper limits on the individual and stacking flux, and to constrain general parameters of fundamental interest, such as the baryon loading, the Lorentz factor, and the magnetic field of the jet in a general single-zone fireball model. The results of the stacking analysis for the prompt phase suggest a typical baryon loading factor ξp ≲ 10, thus excluding the hypothesis of a baryonic origin of the jets and supporting the scenario of a magnetic-dominated ejecta. In this scenario, GeV neutrinos might be expected as a consequence of the highly efficient synchrotron cooling of pions and muons, and potentially detectable by IceCube DeepCore and KM3NeT/ORCA (Zegarelli et al. 2022). The constraints of the afterglow phase are less tight, but it is worth mentioning that this is the first analysis that specifically targets GRB X-ray plateaus and flares.
Acknowledgments
We thank the IceCube Collaboration which offered the optimal environment for the analysis code development and for its many applications and for having released the 10-year data sample. This work also made use of data supplied by the UK Swift Science Data Centre at the University of Leicester. We are thankful to Christopher Wiebusch for his detailed comments to the paper, and to the Publication Committee of IceCube for having discussed it. G.O. thanks Annalisa Celotti and Dafne Guetta for fruitful discussions. The work was financed by the Swiss National Foundation grant n. 200020_178918 and by the University of Geneva. G.O. and M.B. acknowledge financial support from the AHEAD2020 project (grant agreement n. 871158). B.B. and M.B. acknowledge financial support from MUR (PRIN 2017325 grant 20179ZF5KS).
References
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2014, ArXiv e-prints [arXiv:1412.5106] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2015, ApJ, 805, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. 2016a, ApJ, 824, 115 [CrossRef] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. 2016b, JCAP, 2016, 037 [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2017a, ApJ, 843, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M., Ackermann, M., Adams, J., et al. 2017b, J. Instrum., 12, P03012 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2020a, Phys. Rev. Lett., 124, 051103 [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2020b, ApJ, 892, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2012, Nature, 484, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Ackermann, M., Adams, J., et al. 2021a, ArXiv e-prints [arXiv:2101.09836] [Google Scholar]
- Abbasi, R., Ackermann, M., Adams, J., et al. 2021b, ApJ, 920, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Ackermann, M., Adams, J., et al. 2021c, ApJ, 911, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Ackermann, M., Adams, J., et al. 2022, Ap, 939, J116 [NASA ADS] [Google Scholar]
- Ajello, M., Arimoto, M., Axelsson, M., et al. 2019, ApJ, 878, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, A., André, M., Anghinolfi, M., et al. 2020, MNRAS, 500, 5614 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Nava, L., & Piran, T. 2016, MNRAS, 461, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Duque, R., Daigne, F., & Mochkovitch, R. 2020, MNRAS, 492, 2847 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, J., Dumm, J., De Palma, F., et al. 2008, Astropart. Phys., 29, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, J., Baker, M., Dumm, J., et al. 2010, Astropart. Phys., 33, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2012, ApJ, 749, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Chincarini, G., Moretti, A., Romano, P., et al. 2007, ApJ, 671, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, B. A. 2021, J. Instrum., 16, C10007 [NASA ADS] [CrossRef] [Google Scholar]
- Coppin, P. 2022, GRBweb, https://icecube.wisc.edu/ grbweb_public [Google Scholar]
- Costa, E., Frontera, F., Heise, J., et al. 1997, Nature, 387, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 1998, A&A, 333, L87 [NASA ADS] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [Google Scholar]
- Fan, Y. Z., & Wei, D. M. 2005, MNRAS, 364, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Ramirez-Ruiz, E., & Fox, D. B. 2009, ARA&A, 47, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Nava, L., Ghisellini, G., et al. 2012, MNRAS, 420, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Nappo, F., Ghisellini, G., et al. 2018, A&A, 609, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Oganesyan, G., et al. 2020, A&A, 636, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarini, E., Tamborra, I., Bégué, D., Pitik, T., & Greiner, J. 2022, JCAP, 2022, 034 [CrossRef] [Google Scholar]
- Guetta, D., Hooper, D., Alvarez-Muniz, J., Halzen, F., & Reuveni, E. 2004, Astropart. Phys., 20, 429 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-N., Liu, R.-Y., Wang, X.-Y., et al. 2012, ApJ, 752, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Heix, P., Tilav, S., Wiebusch, C., & Zöcklein, M. 2020, 36th International Cosmic Ray Conference (ICRC 2019), 465 [Google Scholar]
- Hümmer, S., Baerwald, P., & Winter, W. 2012, Phys. Rev. Lett., 108, 231101 [CrossRef] [Google Scholar]
- Hurley, K., Pal’shin, V. D., Aptekar, R. L., et al. 2013, ApJS, 207, 39 [Google Scholar]
- Kent, J. T. 1982, J. R. Stat. Soc. Ser. B (Methodol.), 44, 71 [Google Scholar]
- Kimura, S. S. 2022, ArXiv e-prints [arXiv:2202.06480] [Google Scholar]
- Kimura, S. S., Murase, K., Mészáros, P., & Kiuchi, K. 2017, ApJ, 848, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Zhang, B. 2015, Phys. Rep., 561, 1 [Google Scholar]
- Lien, A., Sakamoto, T., Barthelmy, S. D., et al. 2016, ApJ, 829, 7 [Google Scholar]
- Lü, J., Zou, Y. C., Lei, W. H., et al. 2012, ApJ, 751, 49 [CrossRef] [Google Scholar]
- Lyons, N., O’Brien, P. T., Zhang, B., et al. 2010, MNRAS, 402, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., & Blandford, R. 2003, ArXiv e-prints [arXiv:astro-ph/0312347] [Google Scholar]
- Margutti, R., Guidorzi, C., Chincarini, G., et al. 2010, MNRAS, 406, 2149 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, A., Banerjee, B., Oganesyan, G., et al. 2022, Nature, 612, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Meszaros, P., & Rees, M. J. 1997, ApJ, 476, 232 [CrossRef] [Google Scholar]
- Murase, K. 2007, Phys. Rev. D, 76, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., & Nagataki, S. 2006, Phys. Rev. Lett., 97, 051101 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Vianello, G., Omodei, N., et al. 2014, MNRAS, 443, 3578 [NASA ADS] [CrossRef] [Google Scholar]
- Oganesyan, G., Ascenzi, S., Branchesi, M., et al. 2020, ApJ, 893, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Pitik, T., Tamborra, I., & Petropoulou, M. 2021, JCAP, 2021, 034 [Google Scholar]
- Rastinejad, J. C., Gompertz, B. P., Levan, A. J., et al. 2022, Nature, 612, 223 [NASA ADS] [CrossRef] [Google Scholar]
- The IceCube Collaboration 2018, Science, 361, 147 [NASA ADS] [CrossRef] [Google Scholar]
- The IceCube Collaboration 2022, PSLab Code, https://github.com/icecube/PSLab_PS_analysis [Google Scholar]
- Thompson, C. 1994, MNRAS, 270, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Tilav, S., Gaisser, T. K., Soldin, D., & Desiati, P. 2019, ArXiv e-prints [arXiv:1909.01406] [Google Scholar]
- Troja, E., Cusumano, G., O’Brien, P. T., et al. 2007, ApJ, 665, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Usov, V. V. 1992, Nature, 357, 472 [NASA ADS] [CrossRef] [Google Scholar]
- von Kienlin, A., Meegan, C. A., Paciesas, W. S., et al. 2020, ApJ, 893, 46 [Google Scholar]
- Waxman, E., & Bahcall, J. N. 1997, Phys. Rev. Lett., 78, 2292 [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [Google Scholar]
- Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [Google Scholar]
- Yonetoku, D., Murakami, T., Tsutsui, R., et al. 2010, PASJ, 62, 1495 [NASA ADS] [Google Scholar]
- Zegarelli, A., Celli, S., Capone, A., et al. 2022, Phys. Rev. D, 105, 083023 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2018, The Physics of Gamma-Ray Bursts (Cambridge: Cambridge University Press) [Google Scholar]
- Zhang, B., & Kumar, P. 2013, Phys. Rev. Lett., 110, 121101 [Google Scholar]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [Google Scholar]
All Tables
Description of the GRB catalogs (all-GRB inclusive) and subcatalogs (GRBs with measured redshift) analyzed by this work.
Results of the single-source analysis of GRBs with flare afterglow in X-rays, assuming a spectral index γ = 2.
Results of the stacking analysis of the three GRB catalogs (prompt, plateau, flare) in each hemisphere, with and without requirements on the GRB redshift.
All Figures
 |
Fig. 1. Examples of a prompt emission light curve (a) observed by Fermi/GBM, a flare (b) and a plateau (c) of the X-ray afterglow observed by Swift/XRT. |
| In the text | |
 |
Fig. 2. Illustration of the photo-pion processes that lead to the production of high-energy neutrinos inside the dissipation region of GRB jets. |
| In the text | |
 |
Fig. 3. Correlation plots of the bulk Lorentz factor Γ2 = Γ/102 (a) and luminosity Liso, 52 = Liso/1052 erg s−1 (b) with the photon energy peak in the rest frame Eγ,peak,300,rest for the prompt emission, useful for the catalog of the GRB prompts. The best exponential fit is shown as a dashed line, with the 3σ error bands represented by the blue, shaded regions. GRB data are taken from Ghirlanda et al. (2018), (a) and Yonetoku et al. (2010), (b). |
| In the text | |
 |
Fig. 4. Correlation plot of the bulk Lorentz factor Γ2 = Γ/100 with the isotropic luminosity Liso, 52 = Liso/(1052 erg s−1) for the prompt emission. The best exponential fit is shown as a dashed line, with the 3σ error bands represented by the blue, shaded regions. GRB data are taken from Ghirlanda et al. (2018). |
| In the text | |
 |
Fig. 5. Neutrino suppression factor by the synchrotron losses of muons and pions as the function of the comoving strength of the magnetic field in the emission region of a GRB. Green, red, and blue lines correspond to the energies of neutrinos equal to 1 TeV, 10 TeV, and 100 TeV. |
| In the text | |
 |
Fig. 6. (a) Example of TS distributions for the background (injected ns = 0, with 100 000 generated pseudo-experiments) and various signal hypotheses (injected ns > 1, with 10 000 pseudo-experiments each) at the location of GRB 120213A, for the single-source search of the flare catalog and assuming spectral index γ = 2. The signal distributions are very different from the background distribution already for ns = 1, suggesting that few signal events can lead to a high pretrial significance. (b) Background TS distribution, the same as in (a), but with different binning and axis ranges. The bin at TS = 0 corresponds to under-fluctuations: for this GRB, about 96% of the background pseudo-experiments result in under-fluctuations. |
| In the text | |
 |
Fig. 7. Differential sensitivity (solid lines) and 90% CL upper limits (dashed lines) for the stacking analysis of the plateau (red), flare (yellow), and prompt (green) catalog, assuming γ = 2. Curves are shown for the Northern (left) and Southern (right) Hemisphere, and for catalogs comprising all the GRBs (first row) or the subcatalogs of GRBs with measured redshift (second row). As a comparison, the shaded green region shows the 10-yr differential sensitivity calculated for IceCube-Gen2 (Clark 2021) as explained in the text. |
| In the text | |
 |
Fig. 8. 90% CL upper limits for the baryon equipartition parameter ϵp and the baryon loading parameter ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the prompt catalog (upper plots) and subcatalogs of GRBs with available redshift (bottom plots), assuming a neutrino spectral index γ = 2. Excluded values are shown as shaded regions for different hypotheses of the redshift z (top plots) and of the timescale variability δtobs (bottom plots). |
| In the text | |
 |
Fig. 9. 90% CL upper limits for the baryon equipartition parameter ϵp and the baryon loading parameter ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the prompt catalog (upper plots) and subcatalog of GRBs with available redshift (bottom plots), assuming a neutrino spectral index γ = 1. Excluded values are shown as shaded regions for different hypothesis of the redshift z (upper plots) and of the timescale variability δtobs (bottom plots). |
| In the text | |
 |
Fig. 10. 90% CL upper limits for the baryon equipartition parameter ϵp in the Northern (left) and Southern (right) Sky as a function of the magnetic equipartition ϵB. These constraints are obtained with the stacking analysis of the prompt catalog, assuming a neutrino spectral index γ = 2. Excluded values are shown as shaded regions for different values of the neutrino energy Eν. Typical values of the timescale variability δtobs = 0.1 s and redshift z = 1 are used to compute these limits. To derive ϵB, we assumed a typical observed spectrum of lGRB with the peak energy of 300 keV (see Eq. (31)). It is worth notice that the asymptotic value of ϵp in the low-magnetic field regime in the Southern Sky is consistent with the limits computed in Fig. 8 in the same hemisphere, assuming the same parameters. |
| In the text | |
 |
Fig. 11. 90% CL upper limits for the baryon loading factor ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the plateau (upper plots) and flare (bottom plots) subcatalogs of GRBs with available redshift, assuming γ = 2. Excluded values are shown as shaded regions for different hypotheses on the normalized radius of the GRB emission site. |
| In the text | |
 |
Fig. 12. 90% CL upper limits for the baryon loading factor ξp in the Northern (left) and Southern (right) Sky. These constraints are obtained with the stacking analysis of the plateau (upper plots) and flare (bottom plots) subcatalogs of GRBs with available redshift, assuming γ = 1. Excluded values are shown as shaded regions for different hypotheses on the normalized radius of the GRB emission site R14 (see Sect. 3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



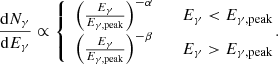
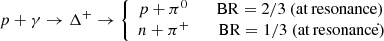
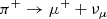
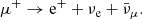
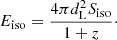
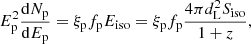
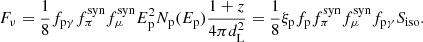
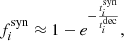
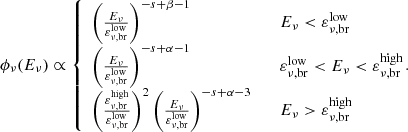
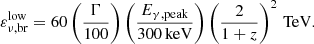
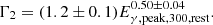
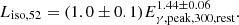
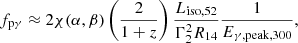
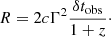
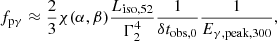
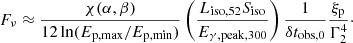
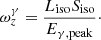
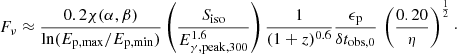
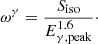
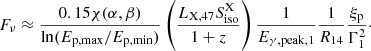
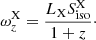
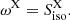
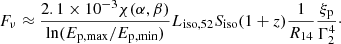
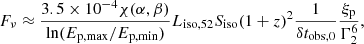
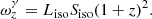
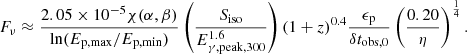
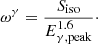
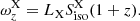
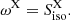
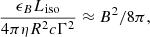
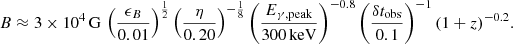
![$$ \begin{aligned} \begin{aligned} \mathcal{L} ^g_j(n_{\rm s})=\prod _{i=1}^{N_j}&\left[\frac{n_{\rm s}}{N_j} \mathcal{S} _{i,j}^g(E_i, {\boldsymbol{\Omega }}_i, \sigma _{i}|{\boldsymbol{\Omega }}_g, t_{g}, \Delta t_{g}, \sigma _{\mathrm{GRB} , g}, \gamma )\right.\\&\left.+\frac{N_j-n_{\rm s}}{N_j}\mathcal{B} ^g_{i,j}(\delta _i, E_i)\right]. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/04/aa44815-22/aa44815-22-eq85.gif)
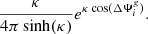
![$$ \begin{aligned} \mathcal{L} _{\rm stack}(n_{\rm s})=\prod _{j=1}^{5}\prod _{i=1}^{N_j}\left[\sum _{g\in j}\left(\frac{n_{\mathrm{s},j}^g\mathcal{S} ^g_{i,j}}{N_j}+\frac{N_j-n_{\mathrm{s},j}^g}{N_j}\mathcal{B} _{i,j}^g\right)\right]. \end{aligned} $$](/articles/aa/full_html/2023/04/aa44815-22/aa44815-22-eq91.gif)