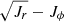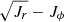EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A90 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A90
Number of page(s) 21
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202244233
Published online 11 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Thanks to a long dynamical timescale, a stellar halo serves as a fossil record, revealing the galactic assembly history (Helmi et al. 1999; Bullock & Johnston 2005; Abadi et al. 2006). Stars stripped off from different dwarf galaxies can be identified as streams or moving groups in the halo (Ibata et al. 1994, 2001; Belokurov et al. 2007), which are visible on top of the in situ stellar halo formed via either dissipative collapse (Eggen et al. 1962; Sandage & Fouts 1987) or heating a pre-existing stellar disc (Zolotov et al. 2009; Purcell et al. 2010). Stars from accreted massive satellites result in large-scale stellar substructures in the halo, which are not spatially coherent at z = 0, and are thus expected to preserve their common origin imprinted into their chemical and kinematical properties (Bullock & Johnston 2005; Abadi et al. 2006; Stewart et al. 2008; De Lucia & Helmi 2008; Cooper et al. 2010; Font et al. 2011; Brook et al. 2012; Pillepich et al. 2015; Rodriguez-Gomez et al. 2016; Deason et al. 2016).

Although merger stellar remnants disperse across a large volume in the halo, it is believed that even after a long time they can still be identified in purely kinematic, phase-space coordinates or in integrals of motion (e.g., energy-angular momentum, Lz − E). For instance, Helmi & White (1999) showed that there is a strong correlation between different velocity components of merger debris, making it possible to associate certain kinematic groups with particular mergers (see, also, e.g., Villalobos & Helmi 2009; Koppelman et al. 2019). Broadly speaking, a number of models suggest that individual merger remnants can be identified as coherent structures in the total energy-angular momentum components space (Lz − E, see, e.g. Johnston et al. 1996; Re Fiorentin et al. 2005, 2015; Kepley et al. 2007; Helmi & de Zeeuw 2000; Choi et al. 2007; Morrison et al. 2009; Gómez et al. 2010; Gómez & Helmi 2010). These results are based on the assumption that energy and angular momentum are both approximately conserved over the galaxy life-time and thus the merger debris stars follow trajectories of their progenitor systems (see Sect. 3.3 in Helmi 2020, for the caveats). However, simulations with evolving galactic potentials suggest that the merger remnants can be smeared significantly in the Lz − E coordinates due to dynamical friction, mass growth and halo shape evolution, and this finding is valid for the baryonic components (Knebe et al. 2005; Amorisco 2017; Jean-Baptiste et al. 2017; Tissera et al. 2018; Grand et al. 2019; Panithanpaisal et al. 2021; Vasiliev et al. 2021; Amarante et al. 2022) and for dark matter (Knebe et al. 2005). Moreover, the finite size of accreting dwarf galaxies and their own self-gravity will also affect the coherence of their merger debris (Sanders & Binney 2013). Recently, Pagnini et al. (2023) showed that the globular clusters of accreted dwarf galaxies barely trace their stellar debris progenitor in the kinematic space. It is also worth mentioning that chaotic mixing may affect the tidal streams’ density on a rather short timescale, making it hard to isolate the debris, especially in a small volume of space (Vogelsberger et al. 2008; Price-Whelan et al. 2016). However, Maffione et al. (2015, 2018) showed that diffusion due to chaotic mixing in the neighbourhood of the Sun does not efficiently erase phase space signatures of past accretion events.

Nowadays, the Milky Way (MW) is the best laboratory for studying the assembly history of a massive galaxy via the identification of merger debris, since the number of stars with 6D phase-space information has been boosted drastically by data from the Gaia (ESA) satellite (Gaia Collaboration 2016, 2018b). These data complemented by the information from spectroscopic surveys make it possible to identify the merger remnants and disentangle them from the in situ disc and halo populations not only in kinematic space but also in the chemical abundances (Mackereth et al. 2019; Horta et al. 2020; Naidu et al. 2020; Zhao & Chen 2021; Matsuno et al. 2021; Simpson et al. 2021).

Prior to the Gaia mission, Nissen & Schuster (2010) and Schuster et al. (2012) were the first to identify the presence of two distinct halo populations at a metallicity lower than that of the Galactic disc in the solar neighbourhood (see, also, Chiba & Beers 2000, 2001; Brook et al. 2003). More recently, using Gaia data, Belokurov et al. (2018) discovered stellar debris in the inner halo deposited in a major accretion event by a satellite between 8 and 11 Gyr ago (Gaia-Sausage, see also; Myeong et al. 2018; Deason et al. 2018). The Gaia-Sausage populations is the most distinct in the (VR, Vϕ) space at −2 < [Fe/H] <  − 1 where it corresponds to the non-rotating component with large radial orbital excursion. The second Gaia data release revealed a double colour–magnitude sequence (Gaia Collaboration 2018a) observed for the stars with high transverse velocities which was used to more closely constrain the last significant merger in MW history (Haywood et al. 2018; Helmi et al. 2018, Gaia-Enceladus) which, similar to Nissen & Schuster (2010), can be identified as a distinct low-[Fe/H] sequence in [α/Fe]–[Fe/H] plane.

A number of recent works provide the estimates of the stellar mass of accreted Gaia-Sausage-Enceladus (GSE) satellite to be in the range of 2 × 108 − 5 × 109 M⊙ (Fernández-Alvar et al. 2018; Vincenzo et al. 2019; Fattahi et al. 2019; Mackereth et al. 2019; Feuillet et al. 2020). Theory suggests that such massive accretion events significantly perturb the pre-existing disc populations (Quinn et al. 1993; Velazquez & White 1999; Gómez et al. 2016, 2017; Grand et al. 2016). In the MW the impact of the GSE merger is associated with the heating of the in situ populations (“Splash” in Belokurov et al. 2020, or “Plume” as it was introduced in Di Matteo et al. 2019). The stellar kinematic fossil record shows the imprint left by this accretion event, which heated the (metal-rich) thick disc which is now found in the Galactic halo leaving little room for the existence of in situ stellar halo component (Di Matteo et al. 2019, but see recent findings by Belokurov & Kravtsov 2022).

Analysis of the MW halo stars orbits suggest that GSE arrived in the Galaxy on a highly retrograde orbit (Helmi et al. 2018; Naidu et al. 2021); however, recently Vasiliev et al. (2022) highlighted the importance of radialization of the stellar orbits due to angular momentum exchange between the host and massive satellite, thus making it difficult to constrain the actual orbit of the GSE. This result also suggests that the individual merger debris could lead to the appearance of a number of different phase-space (or energy-angular momentum) features (see, e.g. Helmi & de Zeeuw 2000; Choi et al. 2007; Morrison et al. 2009; Gómez et al. 2010, 2013; Jean-Baptiste et al. 2017; Grand et al. 2019; Naidu et al. 2021) because the satellite stars lost at different pericentre passages can escape their progenitor with different mean energies or angular momenta (see also the case of leading/trailing tidal debris analysis in cosmological context in Simpson et al. 2019). Gómez et al. (2013) showed that the fraction of the halo substructures that can be resolved using the integrals of motions and purely kinematic space varies from 31% to 82% while the rest of accreted mass is smoothly distributed in the phase space.

Since the revolutionary discovery of the GSE merger, the existence of several other merger remnants are being discussed in the literature, for example Sequoia (Myeong et al. 2019), Thamnos (Koppelman et al. 2019), Arjuna structure (Naidu et al. 2020) and others (see, Helmi 2020; Malhan et al. 2022, for review). All the above-mentioned discoveries reveal a number of mergers remnants with similar (within the uncertainties) chemical abundances and substantial overlap in the phase-space and Lz − E coordinates, thus making it difficult to uncover the actual MW assembly history (Buder et al. 2022; Feuillet et al. 2021; Horta et al. 2023). However, some hints on how to understand the complexity of the observational data can be taken from the simulations. A nearly complete MW assembly history has been predicted by using the E-MOSAICS simulations, where artificial neural networks have been used to link the phase-space parameters of the globular clusters in cosmological simulations with those measured in the MW (Kruijssen et al. 2019, 2020).

Thanks to the advances in subgrid physics implementation and increased spatial and mass resolution, modern cosmological hydrodynamic simulations make possible to study various galaxy-scale properties of accreted and in situ stellar populations (see, e.g. Schaye et al. 2015; Wetzel et al. 2016; Sawala et al. 2016; Pillepich et al. 2018; see also the recent review by Vogelsberger et al. (2020). Using the EAGLE suite of simulations, Mackereth et al. (2019) studied the chemical composition of accreted satellites and the orbital eccentricity of their stellar remnants, suggesting that the low-α MW halo populations is associated with the debris of massive 108.5 − 109 M⊙ satellites, which is quite unusual for the MW-type galaxies in EAGLE. Auriga cosmological simulations of the MW-type galaxies (Grand et al. 2017) show that a small number of relatively massive destroyed dwarf galaxies dominate the mass of stellar haloes where 90% percent of the mass in the inner 20 kpc is contributed by only three massive progenitors (Fattahi et al. 2020; Monachesi et al. 2019); however, the fraction of accreted stars is well below 1% in the galactic center (see also Fragkoudi et al. 2020). Fattahi et al. (2019) find that around one-third of the simulated galaxies have a significant population of stars which resemble the Gaia-Sausage structure at low-[Fe/H]. Grand et al. (2020) found evidence that the Splash-like component is produced from a gas-rich merger that dynamically heats stars from the MW proto-disc onto halo-like orbits (see, also, Belokurov et al. 2020).

Although, the mounting growth of evidence is in favour of a large number of building blocks of the MW stellar halo, their disentangling from each other and from the in situ stars remains uncertain. Therefore, the aim of the paper is to investigate the structure of ancient mergers debris in a set of HESTIA1 cosmological simulations of the Local Group (LG). In particular, we analyse a set of six galaxies from three high-resolution HESTIA simulations (Libeskind et al. 2020). These simulations were tailored to reproduce the LG galaxies populations, which resemble both realistic M31/MW galaxies in terms of their halo mass, stellar disc mass, morphology separation, relative velocity, rotation curves, bulge-disc morphology, satellite galaxy stellar mass function, satellite radial distribution, and the presence of a Magellanic cloud like objects (Libeskind et al. 2020), thus making the HESTIA simulations the best tool for studying the assembly history relevant for the M31/MW galaxies.

In a series of works based on a new set of the HESTIA high-resolution cosmological simulations of the LG galaxies we investigate the impact of the ancient mergers on the in situ stellar populations (Khoperskov et al. 2023a, hereafter Paper I) and the chemical abundance patterns as a function of stellar ages and kinematics of both accreted and in situ stellar populations (Khoperskov et al. 2023b, hereafter Paper III). In this paper, we investigate the present-day phase-space structure and evolution over time of the mergers debris in six M31/MW analogues from the high-resolution hydrodynamical HESTIA simulations. The paper is structured as follows. The HESTIA simulations are briefly described in Sect. 2, where we also provide the merger histories and morphology of the stellar debris. In Sect. 3 we present stellar debris of the mergers in the integrals of motions. In Sect. 4 we present the Gaia-Sausage-like features in the HESTIA galaxies. Section 5 describes the action space and orbital properties of the mergers debris. In Sect. 6 we discuss the dual nature of the kinematically defined stellar haloes. Finally, in Sect. 7 we summarize our main results.

2. Model

2.1. HESTIA simulations

In this work we analyse the three highest resolution HESTIA simulations of the LG. Each simulation is tailored to reproduce a number of the LG properties (Libeskind et al. 2020), including the massive disc galaxies resembling the MW and Andromeda analogues with the population of smaller satellites at z = 0.

The HESTIA simulations are performed by using the AREPO code (Springel 2005; Pakmor et al. 2016), where gravitational forces are computed using a hybrid TreePM technique (Springel 2005). The HESTIA simulations use the galaxy formation model from Grand et al. (2017), which is based on the Illustris model (Vogelsberger et al. 2013), and implements the most important physical processes relevant for the formation and evolution of galaxies. HESTIA simulations assume a cosmology consistent with the best fit values (Planck Collaboration XVI 2014): σ8 = 0.83 and H0 = 100 h km s−1 Mpc−1 where h = 0.677. We adopt ΩΛ = 0.682 throughout and ΩM = 0.270 and Ωb = 0.048. Haloes and subhaloes are identified at each redshift by using the publicly available AHF2 halo finder (Knollmann & Knebe 2009). For more details we refer the reader to the HESTIA simulations introductory paper (Libeskind et al. 2020) and Paper I.

In the rest of the paper, the term ‘in situ’ refers to the stars formed in the most massive M31/MW galaxy progenitor, while ‘accreted’ refers to stars formed in other galaxies and then accreted onto the most massive one (see, e.g. Fattahi et al. 2020; Agertz et al. 2021).

2.2. Orbital parameters and actions calculation

For each simulation snapshot we define a coordinate system (x, y, z) centred on the 10% of the most bound in situ star particles and aligned with their principal axes, such that the disc plane of the host galaxy is aligned with the x − y plane. We use galactocentric cylindrical coordinates with velocities Vϕ, Vr, and Vz, corresponding to the tangential, radial, and vertical directions. We also use the integrals of motion, focusing on angular momentum in the z direction Lz, the total orbital energy per unit mass E, and the axisymmetric actions Jr, Jϕ, and Jz.

To characterize the stellar orbital parameters (eccentricity, apocentre Rmax, and maximum vertical excursion from the disc mid-plane Zmax), we integrated the orbits of star particles in a smooth potential rather than tracing them across different simulation snapshots. This allowed us to obtain their instantaneous values for each snapshot independently, which is not possible from the direct output data. To calculate the orbital parameters, we first used AGAMA (Vasiliev 2019) to compute a smooth version of the gravitational potential. In order to avoid the perturbation of orbits from massive satellites, we interpolated the galaxy potential using the host galaxy particles. The potential due to dark matter and halo gas is represented by a symmetric expansion in spherical harmonics up to l = 4, and the potential of the stars and the gaseous disc is approximated by an azimuthal harmonic expansion up to m = 4. We next integrated the orbits of star particles in this potential for 20 Gyr. This long timescale was chosen to account for halo particles with small orbital frequencies. The orbits were integrated using an eighth-order Runge-Kutta DOP853 integrator with an adaptive time step from AGAMA (Vasiliev 2019).

Once the approximation for the gravitational potential is computed, we use the positions and velocities of star particles to calculate three actions Jr, Jϕ (same as angular momentum Lz), and Jz. The three actions are evaluated approximately using the Stäckel fudge method (Binney 2012) from AGAMA, which, thus delivers only axisymmetric actions. However, Trick et al. (2021) demonstrated that axisymmetrically estimated actions is a powerful diagnostic tool even for the analysis of stellar orbits in a disc of a barred galaxy. Therefore, we suggest that for the purpose of the comparison of accreted and in situ halo stellar populations, the adopted approximation is reasonable (see, also Wu et al. 2022).

3. Merger remnants in the energy-angular momentum space

3.1. Morphology of the merger debris

Before analysing the merger debris in various phase-space and energy-momentum coordinates, we take a look at the morphology of the merger remnants at the time of the accretion and at redshift zero. In Fig. 1 we show the X − Z stellar density maps (in situ stellar disc is placed in the X − Y plane) of five of the most significant mergers (M1–M5; see Fig. 4 in Paper I for the mass-time of accretion) for each M31/MW galaxy at the time of accretion (i.e. when the satellite can no longer be identified as a bound structure). In each panel, we mark the lookback time of accretion, stellar mass at the time of accretion log10(M*) and the stellar mass ratio μ* relative to the main M31/MW progenitor. In Fig. 1 the earlier mergers are shown at the top. There is a diverse morphology of the merger structures; in particular, we can see several examples of tidal tails and shell-like structures, a few quasi-circular streams or loops, but most of the mergers are seen as smooth quasi-spherical stellar density distribution with a prominent density peak (the core of a dwarf galaxy). We note that earlier mergers tend to be smoother at the time of accretion, while more recent ones exhibit streams, tails and in general a more complex morphology. This morphological diversity of the remnants is likely because the galaxies that merged at early epochs simply do not have enough time to evolve into internally complex objects. In addition, to be accreted earlier, they should appear relatively close to the main progenitor with a peculiar velocity that is much lower than the escape velocity. The galaxies that merged later have more time to grow and, thus they can have a more complex and long-term orbital evolution around the host galaxy (M31 or MW).

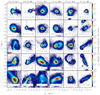thumbnail Fig. 1.

Morphology of individual mergers at the time of accretion for the five most significant events, for each M31/MW analogues in HESTIA. The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given at the bottom of each panel. The colour bar represents stellar density, in units of M*/kpc2. The merger debris show diverse morphologies, likely caused by the different trajectories of accreting systems and internal mass/kinematics distributions.

At redshift zero most of the merger debris look flattened towards the galactic plane of the host galaxy, and appear as smooth stellar ellipsoids (see Fig. 2). Only a few debris are not featureless, which is typical behaviour for unrelaxed remnants from relatively recent mergers. Another interesting behaviour is that more ancient mergers tend to be more compact, while more recent debris extend farther away from the center of the host galaxy (Pfeffer et al. 2020). This picture can be understood if the earlier mergers happened when the main progenitor was less massive, and the gravitational potential well was relatively shallow. Later on the mass of the galaxy increases together with gravitational forces, which squeeze the merger debris over time. Obviously, this effect should lead to the change in the total energy of the debris and its transformation in the energy-angular momentum space.

thumbnail Fig. 2.

Same as Fig. 1, but merger debris are shown at z = 0 instead of at the time of accretion. At this time they appear well phased-mixed with some structure found for the most recent events and the earlier mergers seem to be more compact compared to the later ones.

In the following sections we analyse the structure of the most significant merger debris in the HESTIA galaxies in different phase-space, integrals of motions and action space used to uncover the composition of the stellar halo of the MW.

3.2. Evolution of the Lz − E distribution

We demonstrated that since the merger time, the morphology of the merger debris changes drastically, where coherent tidal structures and streams are completely phase-mixed (see Figs. 1 and 2). We recall that in the case of axisymmetric and time-independent gravitational potential, a given merger debris is expected to remain clustered in the Lz − E coordinates if the dynamical friction is not taken into account (Jean-Baptiste et al. 2017). However, we already showed that the main M31/MW progenitors acquire a substantial amount of their mass since the very first mergers (see Fig. 4 in Paper I), suggesting that, at least, the energy of the stellar merger remnants can be changed and can thus affect the initial phase-space configuration.

In order to study the impact of the galaxy mass growth on the merger debris in Fig. 3 we show the Lz − E distribution for five of the most significant mergers. Each panel shows the distribution at the time of the merger (upper distributions, blue contours), and at z = 0 (bottom distributions, red contours). The vertical displacement in Fig. 3, or the energy change, is explained by the mass growth of the host. At early times a dwarf galaxy is accreted into a low-mass M31/MW progenitor and, thus has higher energy in a shallow potential. Later on, the mass of the host galaxy increases (due to accretion of other systems and gas) and the total energy of the debris decreases. Thus, the mass growth of the main progenitor plays an essential role in the evolution of the total energy of any merger remnant. Another effect contributing to the change in the total energy is dynamical friction which is, however, most important at the early phases of the merger when the dwarf galaxies are still massive and dense enough (Errani & Peñarrubia 2020).

thumbnail Fig. 3.

Energy-angular momentum relation for the stellar remnants. Five most significant mergers (M1–M5; see Fig. 4 in Paper I) are shown at the time of accretion (blue contours) and with at z = 0 (red contours). The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given in the bottom left corner of each panel. Since the total host mass increases over time, the initial Lz − E distributions have lower energies (upper half in each panel), while at z = 0 clumps at higher |E|. The density maps are transparent to distinguish the overlap for some of the most recent mergers. Both the energy and angular momentum of accreted systems are not conserved after the time of accretion, as often assumed in the literature. This energy change is caused by the mass growth of the host galaxy and the angular momentum transformations are due to the non-axisymmetric time-dependent potential of the galaxy with a certain contribution from the population of satellites orbiting the host.

Another interesting feature seen in Fig. 3 is that the mergers debris do not conserve their initial (at the time of accretion) angular momentum Lz distribution. The evolution of the angular momentum distribution can be understood because the galaxies are non-axisymmetric, and the potential is constantly perturbed by orbiting satellites. In this context it is worth mentioning the work by Dillamore et al. (2022) where by using the ARTEMIS set of 45 high-resolution cosmological simulations, the authors found a transformation of the merger debris caused by subsequent accretion of dwarf galaxies. Although most of the mergers show a little net rotation, we can see that the tails of the distribution may change the direction of rotation (see e.g. M3 mergers in 09–18 M31/MW, M2 and M3 in 17–11 M31 and M4 in 37–11 MW). More generally, most of the different debris contribute to slowly co-rotating or non-rotating stellar components near Lz ≈ 0 where they overlap with each other. This overlap suggests that different merger remnants cannot be disentangled from each other, at least not by using their distribution in the Lz − E plane at z = 0.

3.3. Individual mergers and in situ stars in Lz − E

Next, we provide the structure of the Lz − E space of the stellar haloes in the M31/MW HESTIA galaxies, including in situ, all the accreted populations and some individual merger debris at z = 0. In Fig. 4 (top) we show the Lz − E plane for all the stars > 1 kpc away from the galactic plane at z = 0. The in situ stars (formed inside the main progenitor) are shown in the second row, and the third row corresponds to all accreted populations. Overall, the Lz − E distributions look quite similar for all the M31/MW galaxies, which suggests that slightly different accretion and mass growth histories (see Fig. 4 in Paper I) result in rather similar halo compositions. Using a simple spatial cut, we find the mass of accreted stellar components in the range of 34 − 61% of the total stellar mass > 1 kpc from the galactic plane. Therefore, about a half of the stellar mass is made of the in situ stars (1.3 − 8 × 109 M⊙).

thumbnail Fig. 4.

Energy-angular momentum space. Top three rows: Energy-angular momentum relation for all stars (first row), in situ stars (main progenitor, second row), and accreted stars (third row) at z = 0. To focus on the stellar halo, only stars with |z|> 1 kpc (away from the disc mid-plane) were selected. The corresponding stellar mass is shown in the bottom right of each panel. Bottom five rows: Lz − E relation for the five most significant mergers at z = 0 (M1,...,M5; see Fig. 4 in Paper I). The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given in the bottom left corner of each panel with individual mergers debris. All colour bars represent stellar density, in units of M⊙. The in situ stars, being kicked out from the plane, show some net rotation with some overdensities and features similar to those of the accreted stars. The latter contain a number of overdensities, which are the relics of the different merger events. Some individual merger remnants are represented by a number of features and overdensities.

Interestingly, the Lz − E distributions of the accreted stars look very similar to the distributions of all stars, making an impression that accreted stellar populations visually hide within the in situ halo, which, as we already showed in Paper I (see, also Gómez et al. 2017), is composed of the disc stars heated up by the mergers. Compared to the in situ stars, the accreted populations span over the larger range of Lz dominating in the counter-rotating tail (Lz < 0) of the distribution. Nevertheless, the averaged kinematics of the accreted stars shows slightly co-rotating or non-rotating behaviour, similar to that observed in the MW. A single exception here is the MW galaxy from the 09–18 simulation where a very prominent counter-rotating debris appears (M5) as the result of a rather recent (3.7 Gyr ago) and massive (stellar mass 109.5 M⊙) accretion event.

Another feature is that the accreted stars show a number of small-scale clumps or elongated overdensities (see, also, Helmi & de Zeeuw 2000; Choi et al. 2007; Morrison et al. 2009; Gómez et al. 2010; Re Fiorentin et al. 2015; Amarante et al. 2022) while the distributions of the in situ stars seem to be almost featureless (except for the very high energies), suggesting that the individual mergers do not produce coherent substructures made of in situ stars (but see Jean-Baptiste et al. 2017, regarding the substructures made of in situ stars). The individual merger remnants distributions (rows 4 to 8 rows in Fig. 3) show that not every particular feature in the Lz − E plane corresponds to any particular merger debris. Almost all the merger remnants (with no exceptions) contribute to a non-rotating region (Lz  ≈  0) and, at the same time, depict a number of different overdensities. Of course, more prominent features are made of the debris from the most recent mergers; however, even the very early mergers (from 9 − 10 Gyr ago) show some distinct substructures. In some cases, the individual merger debris depict a sequence of small-scale overdensities or group of clumps along the energy axis while being stretched along the angular momentum.

To discuss in more detail the overlap between the merger debris in Fig. 5 we show the Lz − E plane colour-coded by a number of merger debris that can be found in a given range of parameters. The top row corresponds to all the merger debris we have identified, while the bottom row shows the maps based on the five most significant M1–M5 mergers. The general trend is that most of the mergers contribute to the parameters of the stellar halo with no prominent rotation, where the GSE merger remnant is found in the MW (see, e.g. Belokurov et al. 2018, 2020; Helmi et al. 2018; Naidu et al. 2020), while the edges of the Lz − E distribution show the presence of a fewer number of merger debris. Roughly the same picture is observed for the most significant mergers (see bottom of Fig. 5).

thumbnail Fig. 5.

Overlap of debris from different mergers in the Lz − E plane. Each pixel is coloured by the number of merger events contributing to that region, as given in the colour bar. Top row: Debris from all mergers for each HESTIA galaxy, as indicated above each panel. The largest overlap of mergers are shown in maroon. Bottom row: Same as top row, but limited to the five most significant mergers. These maps suggest that the most crowded region of the Lz − E space corresponds to the non-rotating region, which is where the Gaia-Enceladus merger was identified (Helmi et al. 2018). The number of merger remnants decreases in the regions of substantial rotation.

3.4. Dissecting individual debris in Lz − E by age and origin

Although it is expected that merger debris should be clustered in integrals of motion space (e.g., Lz − E), we have shown that in the HESTIA galaxies, a given merger debris occupies a wide range of parameter space and consists of several prominent overdensities. Next we focus on the variations in parameters across the merger debris in Lz − E coordinates. In Fig. 6 for each galaxy in our sample, for simplicity we show two individual merger debris in Lz − E coordinates (first and second rows). The next two columns (third and fourth) show the distribution of the mean distance relative to the centre of a dwarf galaxy before the merger that results in a given stellar remnant. In other words, these columns show how far from the centre the stars were inside the dwarf galaxy before it merged into the host galaxy. The last two columns in Fig. 6 show the mean stellar age distribution of the individual mergers in Lz − E coordinates.

thumbnail Fig. 6.

Energy-angular momentum relation for each of the two most significant mergers at z = 0 per galaxy in our sample. The two left columns show the density distributions of each of the two mergers, the two middle columns are colour-coded by the mean distance (R0) of stars inside the dwarf galaxies before they accreted, and the two right columns show the mean stellar age. This figure demonstrates that even a single merger event could result in a number of overdensities in the E − Lz space. More recent events tend to show more substructures; however, even the merger remnants from 9 − 10 Gyr ago are not featureless at z = 0. The R0-gradient suggests how the internal structure of dwarf galaxies is being mapped into the Lz − E space once the system is accreted.

Figure 6 highlights that even a single merger can result in several prominent groups of stars isolated from each other in Lz − E space. In most cases, these groups can be found along the smooth density distribution stretched along the total energy. The next two columns show that stars in different Lz − E parts arrive from different distances inside the dwarf galaxy prior to the merger. In particular, the smallest total energy stars at z = 0 were captured from the outer parts of dwarf galaxies. The outer parts of the dwarf galaxies being less bound are captured earlier and do not penetrate much to the centre of the host, thus building the (relative) outer parts of the stellar halo. The central parts of the dwarf appear to sink towards the centre of the host galaxy due to dynamical friction where they have the lowest total energy. As a result, these populations dominate in the low-E regions of the Lz − E space.

The mean age maps in Fig. 6 (rightmost columns) do not imply a unique picture. However, in most cases, we can see the age gradient as a function of the total energy. In particular, relatively older stars from the outer parts of dwarf galaxies tend to occupy the upper parts of the Lz − E distribution, while the mean age decreases towards the lower values of the total energy. Coupling this information with the previous result, can explain the observed trends. Before the merger, stars formed earlier in the ‘upside-down’ regime occupy the outer parts of dwarfs galaxies; therefore, when the galaxy is being accreted, these older stars are stripped first and appear at higher energies inside the host. At the same time, the cores of dwarf galaxies could have a more extended star formation history and, thus be younger or, at least, have a larger fraction of younger stars. Therefore, being dragged towards the central parts of the hosts, the stars from the cores of the dwarf galaxies populate lower energy levels where the mean age of stellar debris is relatively smaller. The strength of the age gradient in the Lz − E space is rather low, especially for the very early mergers (see, e.g. the MW galaxy in the 17–11 simulation). However, typical age uncertainties for oldest MW stars may not allow to capture the age gradient of the merger debris, but some parameters of stellar populations can change very quickly with the stellar age, for example chemical abundances (see the metallicity analysis in Paper III), and, can thus be detected in the observational data.

To explore a bit more the age variations of the merger debris in Fig. 7, we show the mean stellar age as a function of the galactocentric distance (top) and the overall age distributions (bottom) for the individual merger debris. First, we confirm the results seen in the previous figure where the inner parts of the mergers debris tend to be younger (see also Monachesi et al. 2019). There are a number of exceptions, probably depending on the details of a particular merger evolution. However, the age gradient tends to be larger for the most recent mergers. Once we consider the overall age distribution (or the star formation history, see bottom of Fig. 7), we note a substantial increase in the star formation rate just before the merger. Some merger remnants show a few peaks, possibly related to the pericentric passages (see, e.g. Di Cintio et al. 2021). This suggests that, in most cases, the age of the youngest stellar populations can be used as a proxy for the merger time; however, for better estimates the stars from the inner galaxy should be considered (see also Monachesi et al. 2019; Dillamore et al. 2022).

thumbnail Fig. 7.

Age structure of the accreted halo components. Top: Mean age of stars accreted from the five most significant mergers as a function of galactocentric distance (Rgal) at z = 0. Bottom: Corresponding age distributions, colour-coded as above. The strongest burst of star formation is typically for the youngest stars in a given merger, thus corresponding to the time of accretion. Age estimates for accreted stars can therefore be used to time each merging event.

If the relations we observe in the HESTIA galaxies are relevant to the MW, this may affect some of the conclusions regarding the merger history of the MW. In particular, the mean age of the GSE progenitor can be overestimated because its measurements are based on the stars in the solar suburb (see, e.g. Gallart et al. 2019; Feuillet et al. 2021; Montalbán et al. 2021; Borre et al. 2022); however, the youngest stars of the GSE will likely appear in the innermost galaxy, which is still poorly covered by the existing spectroscopic surveys and the stellar age information is even more limited in that regions. Therefore, once we extend the analysis of the MW stellar halo towards its innermost regions, we may constrain even better the age distribution (and thus the merger time) of the GSE and possibly even infer the star formation history of its progenitor.

4. Gaia-Sausage-like features in HESTIA galaxies

We already mentioned in the Introduction that the last significant merger (GSE) in the MW was initially discovered as a horizontally aligned structure in the VR − Vϕ coordinates with zero net rotation (Vϕ ≈ 0) for low-[Fe/H] stars (Gaia-Sausage, Belokurov et al. 2018). Therefore, it is worth testing how much the HESTIA simulations are able to reproduce this particular feature in a pure kinematic space. In Fig. 8 we show the density distribution in the (VR, Vϕ)-plane for stars located in the radial range of (1 − 3)Rd (where Rd is the disc scale length) and > 1 kpc from the galactic mid-plane. In the figure we also separate in situ (second row) and accreted stellar populations (third row). In the adopted region the accreted halo constitutes from 34 to 81% of the mass, while the rest is represented by the heated in situ stars. First, we find that in the M31/MW HESTIA galaxies in situ stars are represented by a single blob whose tail however spans to Vϕ ≤ 0 km s−1 (or even below in the case of the M31 galaxy in the 09–18 simulation). The in situ stars distribution is almost featureless and shows a behaviour typical for thick-disc stars, however, with some asymmetry in the 09–18 M31 and 17–11 M31 galaxies caused by the very recent mergers (see Fig. 4 in Paper I).

thumbnail Fig. 8.

Kinematic structure of the stellar haloes. Top three rows: Stellar density distributions in the VR − Vϕ plane at redshift zero for stars in the range (1 − 3)Rd (where Rd is the disc scale-length from Libeskind et al. 2020) and |z|> 1 kpc including all stars (first row), only in situ stars (second row), and only accreted populations (third row). The mass fractions of the in situ and accreted populations are shown at the bottom of the second and third rows, respectively. Bottom five rows: As above, but for the five most significant mergers at z = 0 (M1–M5; see Fig. 4 in Paper I). The merger accretion lookback time (Gyr), the total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given at the bottom of each panel. The colour bar represents a normalized density relative to the maximum value. All M31/MW HESTIA galaxies demonstrate the presence of Gaia-Sausage-like features, which exhibit different individual shapes and radial velocity ranges.

The accreted stars distributions in the VR − Vϕ plane is much more interesting. In particular, we note the presence of multiple distinct kinematic components with a certain level of similarity between the galaxies. The morphology here can be described as a blob on top of the horizontally aligned structure(s). The blobs for accreted stars have a wider range of radial velocity range compared to the in situ populations and lower median azimuthal velocities (except for 37–11 MW where the ⟨Vϕ⟩ are essentially the same). This demonstrates a smooth transition from fast-rotating in situ stars to slower accreted stars.

The most striking features in the accreted density distribution are the horizontally aligned structure(s). The third row in Fig. 8 shows a diverse morphology of slowly rotating components, which can be described as horizontal features with zero net rotation (17–11 M31, 17–11 MW, 37–11 MW; similar to the Gaia-Sausage) and negative net rotation (37–11 MW); and positively (09–18 M31) and negatively (09–18 MW, 37–11 MW) bent moustache-like features. We note that in the 37–11 MW galaxy we can directly identify two prominent features below the high-Vϕ blob that correspond to different accretion events, while in other galaxies the separation between different mergers is not evident.

In order to decompose the density distribution of the accreted stars in Fig. 8 (rows 4–8), we show the VR − Vϕ structure of five of the most significant mergers (M1–M5) separately. Most of the individual merger remnants can be seen as high-velocity dispersion ovals that have different but mostly positive (or prograde relative to the host component) bulk rotation. Gaia-Sausage-like horizontally aligned features are rare in a given galaxy, and they tend to correspond to the most recent mergers (09–18 M31/MW, 37–11 M31). In the 17–11 MW galaxy accreted stars show a Gaia-Sausage-like feature, but the corresponding merger is very recent (1–2 Gyr ago) with the relative mass smaller than M1–M5 mergers.

The MW galaxy from the 37–11 simulation is an exceptional case because at least four merger remnants (M1–M4) are seen as flattened structures in the VR − Vϕ plane, with different bulk values Vϕ. In this galaxy the relative mass of the mergers decreases with time, and thus each subsequent merger introduces less perturbation to the structure of the previous one. More likely, the mergers are to be accreted with some angular momentum and settle in the galaxy with a certain bulk Vϕ. Later on, the following mergers perturb the galaxy by heating up all the previous debris, thus leading to an increase in the velocity dispersion, also in the azimuthal direction. Therefore, the transformation from the horizontally aligned structures in the VR − Vϕ space can be caused by the subsequent mergers.

So far, we have presented only the most significant mergers; therefore, the VR − Vϕ space for accreted stars decomposition is not complete, and the variety of kinematic structures is not fully explored. In order to show a diversity of the accreted populations in the VR − Vϕ space, in Fig. 9 we show two different merger debris in each HESTIA galaxy which result in the structures that are the most similar to the Gaia-Sausage. Although we have a very large sample of mergers (> 60 for all the galaxies) we can see that only a single merger remnant from the MW in the 37–11 (see bottom right) simulation matches precisely the Gaia-Sausage kinematics.

thumbnail Fig. 9.

Examples of the Gaia-Sausage-like features in the (VR, Vϕ) plane for all M31/MW HESTIA galaxies. Each panel corresponds to different merger remnants in the range |z|> 1 kpc and (1 − 3)Rd where Rd is the disc scale-length from Libeskind et al. (2020). The merger accretion lookback time (Gyr), the total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor in the time of the merger are given at the bottom of each panel.

In order to understand the radial structure of accreted populations and the merger debris in Fig. 10, we show the stellar density map in (R, vϕ) plane for all the stars, in situ, accreted and individual merger remnants for stars > 1 kpc away from the disc plane. The figure reveals a number of radially extended nearly horizontal overdensities, which at large distances from the centre occupy rather narrow Vϕ ranges, and the azimuthal velocity dispersion (magenta contours) remains roughly constant along the radius. Some of the debris show a fine structure with some clumps or diagonal overdensities. We note an important difference between these accreted structures and the diagonal (R, vϕ)-ridges, discovered by the Gaia (Antoja et al. 2018). In HESTIA galaxies, accreted components have nearly constant Vϕ, while centre (R, vϕ)-ridges typically have nearly constant energy or angular momentum (Ramos et al. 2018). Figure 10 also suggests that the galactic centre is a very crowded region because different mergers debris contribute there. However, the outer disc seems to be a promising region for the analysis of accreted components. Taking into account similarities between some individual merger remnants in Fig. 8 and the Gaia-Sausage structure, we could expect that in the MW, the accreted populations should be seen as radially extended structures with certain values of the azimuthal velocity depending on the orbital parameters of the merger (see, e.g. recent works by Naidu et al. 2020; Amarante et al. 2022).

thumbnail Fig. 10.

Radial structure of the azimuthal velocity distribution. Different stellar populations are shown: all stars (first row), in situ (second) and accreted populations (third row) taken > 1 kpc away from the galactic plane. All other rows below (fourth to eighth) correspond to the most significant merger remnants. The merger accretion lookback time (Gyr), the total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given at the bottom of each panel. Magenta lines in the individual merger debris distribution show the dispersion level along the radius. The in situ stars rotate faster around the galactic centre and show the presence of diagonal ridges similar to those discovered in the MW (Antoja et al. 2018), which are likely to be the manifestation of spiral arms (Khoperskov & Gerhard 2022) and/or bar resonances (Fragkoudi et al. 2019). The accreted stars depict a number of radially extended structures with no net rotation and multiple co-rotating and counter-rotating components and small-scale overdensities. The important feature of the individual merger debris is that the azimuthal velocity dispersion remains nearly constant along the galactocentric distance, except for the innermost parts of the galaxies.

5. Action space (Jr, Jz, Jϕ) and orbital analysis

In this section we analyse the orbital composition and axisymmetric actions of the stellar component of the HESTIA galaxies. For all star particles, we reconstructed their orbital eccentricity by integrating their orbits in the fixed galactic potential at z = 0 using the AGAMA code (Vasiliev 2019) which was also used to compute the actions (Jr, Jz, Jϕ; see Sect. 2.2).

5.1. Action space for in situ, accreted stars, and satellite galaxies

In the previous section we demonstrate that the accreted stellar populations have a complex structure in Lz − E, VR − Vϕ, (R, vϕ). In these kinematic coordinates, the mergers debris overlap with each other and with the in situ stars heated up by merging events. In this section, we focus our analysis on the orbital actions, which are conserved under adiabatic changes of the gravitational potential of a galaxy (Binney & Tremaine 2008) and, thus, the merger debris should be clustered in the action space. Although we already demonstrated that the last assumption is not exactly applicable for the HESTIA galaxies, it is still worth testing what we can learn about the mergers debris structure in the action space.

This section only analyses the M31 galaxy in the 09–18 M31 simulation; however, we tested that the results are similar to other M31/MW HESTIA galaxies. For reference, in Fig. 11 (top row) we show the X − Z density distribution for the in situ stars and all accreted stars at z = 0 together with a population of surviving satellites (different colours correspond to different dwarf galaxies). Since we focus on the stellar halo, we remove from our sample in situ and accreted stars located close to the galactic mid-plane (|z|< 1 kpc) where the disc stars dominate and the impact of spiral arms and bar is more important in shaping the orbital action space (Trick et al. 2017, 2021).

thumbnail Fig. 11.

Action space analysis. Top: X–Z projection of in situ stars (left), all accreted stars (middle), and surviving satellites (right) in 09–18 M31 galaxy at z = 0. The density maps and the action space analysis are based on the stars (accreted and in situ) > 1 kpc from the galactic plane. Different survived satellites are shown in different colours. Second row: Jz − Jr plane for in situ (left), the fraction of accreted stellar mass (centre), and surviving satellites (right). Third row: (Jr − Jz)/Jtot − Jϕ/Jtot plane for in situ (left), faction of accreted stellar mass (centre), and survived satellites (right). Bottom row: plane for in situ (left), faction of accreted stellar mass (center), and survived satellites (right). While in situ and accreted stars do not show any prominent features in the action space, the dwarf satellites, as expected, are seen as coherent structures. Accreted stars have on average larger radial and vertical actions, but still substantially overlap with the in situ populations at smaller values.

In the second row of Fig. 11 we show the mass distribution for the in situ stars (left), which are mostly confined near (Jr, Jz) = (0, 0) with a rather small tail of the distribution. Instead of showing the (Jr, Jz) distribution for accreted stars, which do not demonstrate any prominent overdensities, we present the fraction of accreted stars in these coordinates. We see that accreted stars span over a larger area compared to the in situ stars, and only the accreted stars can be found at (Jr, Jz) > 1000 kpc km s−1. In contrast to the smooth halo component, represented by the in situ and the mergers debris, despite some overlap, surviving satellites demonstrate a clear clustering in the (Jr, Jz) space (rightmost column in Fig. 11). We notice the clustering of the satellites in other action spaces ((Jr − Jz)/Jtot − Jϕ/Jtot and 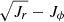); however, this analysis does not deliver much information since the satellites are the distinct objects in galactic halo (top right of Fig. 11).

Similar to (Jr, Jz), we also do not detect any prominent substructures of the merger debris in the (Jr − Jz)/Jtot − Jϕ/Jtot or 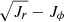coordinates; however, the fractional distribution of accretes stars allows us to use the action space to disentangle between accreted and in situ stars that substantially overlap in Lz − E and other phase-space coordinates (see Sects. 3 and 4). This is better seen in the 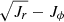coordinates where stars above 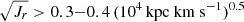certainly represent accreted populations. Nevertheless, we suggest that the application of advanced clustering algorithms in the action space taking into account the chemical abundances of stars will make it possible to differentiate better the merger remnants.

5.2. Individual merger debris in the action space

In order to test how different mergers are mapped in the action spaces, in Fig. 12 we show the stellar mass distribution for five of the most significant mergers (M1–M5) from the M31 galaxy (09–18 simulation) in XZ, (Jr, Jz), (Jr − Jz)/Jtot − Jϕ/Jtot and 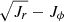coordinates. There is not much diversity in the morphology of the merger remnants at z = 0 however, different mergers show a certain level of differentiation in (Jr, Jz) space. One can notice that the M5 merger is elongated in the galactic plane having possibly larger radial (in cylindrical coordinates) motions. This is clearly seen in (Jr, Jz) where the density distribution is stretched along the Jr compared to the Jz. A more spherical remnant M3 has nearly equal distribution in both Jr and Jz actions. Finally, the M1 merger seems to be puffed up perpendicular to the plane and, as a result, its (Jr, Jz) distribution is more elongated in Jz compared to Jr. Since all the merger remnants slowly co-rotate with the galactic disc in (Jr − Jz)/Jtot − Jϕ/Jtot, all M1–M5 mergers mainly contribute to the right corner with complete overlap. A similarity in the net rotation is also evident from the 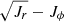plane where, except for the tails of the distributions, all the mergers occupy essentially the same region and are practically indistinguishable from each other. We note that the unmixed tidal tails of the merger debris can be captured in the action space, for example the M3 and M4 mergers, where some features outside the bulk of the distribution can be seen.

thumbnail Fig. 12.

Action space for five of the most significant merger remnants in the 09–18 M31 galaxy. From top to bottom: X-Z density maps, Jz − Jr space, (Jr − Jz)/Jtot − Jϕ/Jtot plane, and plane. Similar to Fig. 11 (for the entire accreted population), the individual merger debris completely fill the (Jr − Jz)/Jtot − Jϕ/Jtot plane; nevertheless, different remnants peak at slightly different regions of the diagram depending on the orbital parameters. The interesting feature, seen in the second row, is that the merger remnants show a different ratio of Jz to Jr. Some substructures, however, can be seen at the very large radial and vertical actions, which correspond to the outer parts of the debris where the dynamical time is longer and, thus phase mixing is not yet completed for the most recent mergers at z = 0.

To summarize, the action space analysis of the HESTIA galaxies does not allow us to isolate accreted stars from the in situ in (Jr, Jz), (Jr − Jz)/Jtot − Jϕ/Jtot and 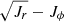coordinates. However, some action ranges can be used to capture the accreted stellar populations. Different mergers debris show some systematic differences in the above-mentioned coordinates, despite the substantial overlap with each other. Since the dwarf galaxies are isolated substructures in the action space, the overlap between accreted populations suggests that the gravitational potential of the HESTIA galaxies grows non-adiabatically and/or dynamical friction significantly affects the trajectories of stars in the merger debris. Nevertheless, we suggest that some information from the actions still can be used to identify the merger debris.

We already noted some differences in the behaviour of the merger debris in (Jr, Jz) space, where the ratio between vertical-to-radial actions correlates with the shape of the merger debris in the halo, which likely depends on the orbit of the infall and the internal structure of merging galaxies. For instance, for a disc-like component, one could expect that the distribution of stars is stretched along Jr, while a sphere should have a ratio similar to that of the Jr, Jz actions. Therefore, we can introduce the angle between radial and vertical actions characterizing the shape of the debris Θ = atan(Jz/Jr). At the same time, stars from different debris could have different eccentricities in the galactic plane, also depending on the merger parameters. In Fig. 13 we combine these two parameters and present the distribution of all stars (top row), in situ (second row), and all accreted stars (third row) together with five individual merger debris with a higher stellar mass ratio relative to the main progenitor at the time of accretion (M1–M5). In order to separate the prograde from the retrograde stars, we multiply the eccentricity by the sign of the angular momentum. The figure shows the density distribution of stars located in the galactocentric range of (1 − 2)Rd. Figure 13 reveals many substructures where the in situ stars tend to have lower Θ and rather low eccentricities (mainly < 0.5), which is a typical behaviour of a regularly rotating disc-like component. Meanwhile, the accreted component shows a diverse morphology with some isolated clumps or overdensities with nearly constant or slightly varying eccentricity. The most important feature here is that in many cases we can see very different features typical for different merger debris, which, especially in combination with some other parameters or chemical abundances, can be used to clean the samples of accreted stellar populations.

thumbnail Fig. 13.

Density distribution in the Θ = arctan(Jz/Jr)-eccentricity plane for all stars (first row), in situ stars (second row), and all accreted populations (third row). All other rows below (fourth to eighth) correspond to the most significant merger remnants. The eccentricity values are multiplied by the sign of the angular momentum; thus, the counter-rotating stars have negative values of eccentricity and can be found to the right of the vertical magenta lines. To sharpen the structures, only the stars located in the (1 − 2)Rd radial range, where Rd is the disc scale-length from Libeskind et al. (2020), are presented here. The figure shows how the anisotropy of actions correlates with the orbital eccentricity for different populations. The in situ stars distribution shows the presence of vertically cold (low Θ angles) low-eccentricity stars representing a disc component; at higher eccentricities, Θ remains roughly the same. The accreted stars distribution is even more interesting, where there are many substructures, and the overall distribution is different from the in situ stars; moreover, different merger debris, in many cases, show different behaviour. The individual merger debris (fourth to eighth) do not represent the entire complexity of the arctan(Jz/Jr)-eccentricity space, which is more complex in the third row where all the merger debris are taken into account.

5.3. Merger remnants: Combining orbital parameters and actions

A number of recent studies suggest that highly eccentric orbits characterize the stars in the accreted MW halo population (> 0.85) (see, e.g. Deason et al. 2018; Helmi et al. 2018; Belokurov et al. 2020). This result is supported by the analysis of the EAGLE simulations, which shows that dwarf galaxies with mass in the range 108.5 − 109 M⊙ accreted around z ≈ 1.5 would result in similar orbital parameters of the merger debris (Mackereth et al. 2019). In Fig. 13 we can see that the debris have a broad range of eccentricities, where the mean value could be different for different mergers. Since the EAGLE simulations include all types of galaxies with a small fraction of the MW-type objects (Mackereth et al. 2018), it is worth investigating the eccentricity distribution of accreted stars in the HESTIA simulations, which were tailored to the LG galaxies.

In Fig. 14 (left), we show the mean eccentricity of stars accreted from different satellite galaxies as a function of the accretion time and redshift. In the figure, we present all the mergers in all the M31/MW HESTIA galaxies colour-coded by the stellar mass of the merger. Similar to Mackereth et al. (2019) we find that more recent mergers have higher masses and result in the highly eccentric orbits of stars in the debris. It is worth noticing that the mean eccentricity values are indeed higher than ≈0.6. The left panel gives a somewhat misleading impression, suggesting that the merger debris result only in high-eccentricity stars. This becomes evident once we consider the distribution of eccentricities for all the stars in the mergers debris. In the right panel of Fig. 14 we present the distribution of the eccentricity for the individual mergers debris (grey) where the sign of the eccentricity is negative for stars with the negative angular momentum. We find that overall (red lines) about 10 − 30% of accreted stars have eccentricities below 0.5. This result shows that the accreted stars do not necessarily have high eccentricities, and more recent events are more likely to produce populations with a disc-like kinematics.

thumbnail Fig. 14.

Orbital structure of accreted populations. Left: Mean eccentricity of merger remnants stars as a function of accretion time for all the mergers in the M31/MW HESTIA galaxies. The different symbols correspond to different simulations and galaxies and they are colour-coded by the stellar mass at the time of the merger. Right: Stellar-mass weighted distributions of the eccentricities for individual merger remnants (grey) and the mean distribution (red) at z = 0. Here, the eccentricity is multiplied by the sign of the angular momentum. Although the stars in the merger debris show a wide range of eccentricities, the mean eccentricity of the debris tends to decrease with time, whereas more recently accreted debris have slightly lower eccentricity. This evidently correlates with the stellar mass of the accreted system, which tends to be higher for the galaxies that accreted earlier, and thus evolved longer.

6. Dual nature of kinematically-defined stellar halo: In situ versus accreted populations

In this section we discuss the relations between in situ and accreted components of the stellar haloes in the HESTIA galaxies. In particular, we focus our analysis on the kinematically defined stellar haloes, which is done following a number of similar studies (see, e.g. Nissen & Schuster 2010; Helmi et al. 2018; Koppelman et al. 2019), by using a Toomre diagram. In Fig. 15 we show the Toomre diagram for all stars (top row), in situ stars only (second row), and all stars from the merger remnants (third row) at z = 0. To enhance the structure of the distributions in Fig. 15 we only consider stars located in (1 − 3) Rd, which is roughly accessible for the MW large-scale surveys. In all the galaxies in our sample, the distributions on top show the presence of two distinct components, where one is centred near the LSR (Vϕ ≈ 200 km s−1, disc). In contrast, the others tend to show slow prograde to retrograde rotation with a higher peculiar velocity. The latter one is mainly made of stars from disrupted dwarf galaxies – mergers, presented in the third row. The properties and formation paths of the in situ stellar halo components are discussed in Paper I.

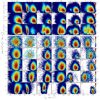thumbnail Fig. 15.

Toomre diagram for all stars in (1 − 3)Rd (Rd is the disc scale-length) and |z|> 2 kpc (first row), in situ stars (second row), and all accreted populations (third row). The mass fraction of in situ and accreted populations are shown at the bottom in the second and third rows, respectively. The five rows below the gap correspond to the Toomre diagram for five of the most significant mergers at z = 0 (M1–M5; see Fig. 4 in Paper I). The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given in the bottom left corner of each panel. The colour bar is in M* scale. The white circle corresponds to the thick disc selection: Vcirc180(km s−1)/240(km s−1), where Vcirc is the circular velocity value at 2Rd for each galaxy; 180 km s−1 corresponds to the selection made for the MW; and 240 km s−1 is the MW circular velocity. We suggest that the disc-like regions in the Toomre diagram are populated by the accreted stars. A single debris spans over a large volume, and, in some cases, the bulk of the accreted stars have (thick) disc-like kinematics.

To define the stellar halo in the Toomre diagrams we introduce a threshold separating stars with a halo-like kinematics from stars with a disc-like kinematics. We estimate the LSR velocity value VLSR for each disc galaxy as the mean circular velocity value in the (1 − 3) Rd radial range. For the kinematically defined stellar halo we require a peculiar velocity component 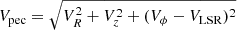to be larger than 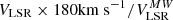, where 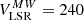km s−1 and 180 km s−1 are the values adopted in the MW to separate the disc from the halo (see, e.g. Di Matteo et al. 2019). The boundary between the halo and disc kinematics is shown by the white lines in all the panels of Fig. 15. Similar to a number of phase-space coordinates presented above, in Fig. 15 the individual mergers debris (fifth to eighth rows) have a diverse morphology, but interestingly most of them show a significant contribution to the region usually associated with the disc inside the white circle. We recall that we present only the structure of the most significant mergers while some others are missing, but their total contribution can be inferred from the third row. The structure of the Toomre diagrams in Fig. 15 shows that in a given radial range (1 − 3)Rd many accreted stars (≈17 − 40%) contribute to the kinematically selected disc and, in contrast, the in situ populations (20 − 50%) can be identified as the stellar halo. We suppose that these numbers are relevant for the MW. In that case, more work should be done in searching for the merger debris in the disc-like region of the Toomre diagram, also because in some cases, the individual merger debris is only deposited to this region (e.g., M3 in the MW 09–18, M2 in the M31 17–11, M5 in the 17–11 MW and so on).

Figure 15 nicely illustrates the dual nature of the kinematically defined stellar halo, where it is made of both accreted and in situ stellar populations, demonstrating the complexity of the stellar halo and how its components overlap and affect each other. We already showed that in most of the HESTIA galaxies, there are only a few massive mergers in each galaxy (see Fig. 4 in Paper I). At the same time, it is believed that the GSE merger is the biggest accretion event over the lifetime of the MW (Belokurov et al. 2018; Helmi et al. 2018). Therefore, we can test how much the most massive merger contributes to the accreted component of the kinematically defined stellar halo. In Fig. 16 (top) we show the fraction of the most massive merger (Mmmm) among all accreted stars as a function of the most massive merger mass. The figure shows that 20 − 70% of the accreted mass in the M31/MW-type disc galaxies comes from a single merger with a median value of about 40% and the fraction of a single merger is larger for more massive accretion events. We note that the correlation does not depend on the definition of the accreted component (either total or kinematically defined halo).

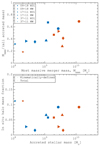thumbnail Fig. 16.

Relations between stellar haloes masses and masses of accreted systems. Top: mass of the most massive merger (Mmmm) relative to the accreted mass vs mass of the most massive merger. Bottom: In situ halo mass fraction versus the total accreted stellar mass. Different symbols show different M31/MW HESTIA galaxies. Shown are the kinematically defined components using Toomre diagrams (in blue), while the total mass without any kinematics selections (in red). Depending on the definition, the single most massive merger contributes from 20% to 70% of the total accreted mass (see also, Cooper et al. 2010; Monachesi et al. 2019). At the same, the in situ mass fraction correlates well with the total accreted mass.

Finally, in the bottom panel of Fig. 16 we show how the fraction of the in situ kinematically defined stellar halo depends on the total accreted stellar mass. With a single exception, the MW in the 37–11 simulation, we find a positive correlation, which is somewhat counter-intuitive because, in this case, the fraction of accreted halo components is lower for more massive ex situ haloes. Therefore, more accreted material results in a more heavily perturbed disc, which deposits more stars to the kinematically defined halo. Since these relations are based on the constrained simulations of the LG, they can be used to estimate the total accreted mass once the in situ halo is constrained, for example by using chemical abundances.

7. Summary

In this work we analysed six M31/MW analogues in the HESTIA suite of cosmological hydrodynamics zoom-in simulations. All the galaxies experienced between one and four significant mergers with stellar mass ratios between 0.2 and 1 (relative to the host), where all the significant mergers (with a single exception) happened between 7 and 11 Gyr ago. We studied the merger debris using integrals of motions (total energy and angular momentum), phase-space coordinates, orbital parameters, and actions. Focusing our analysis on the most significant merger debris, with the larger stellar mass fraction relative to the host galaxy at the time of accretion, we arrived at the following conclusions:

  • Different stellar merger debris show a diverse morphology at the time of accretion, varying from streams and shell-like structures to smooth nearly spherical distributions (see Fig. 1). At redshift zero, the vast majority of stellar merger debris have similar and almost featureless density distributions, flattened towards the disc plane. Some exceptions were found for the most recent mergers, which show some unmixed substructures (see Fig. 2). More ancient merger debris are more compact compared to more recent accretion events, likely due to the mass growth of the galaxy over time, deepening the potential well.

  • The self-consistent cosmological HESTIA simulations suggest the Lz − E distributions of individual merger debris evolve in time due to the host’s mass growth and its non-axisymmetric gravitational potential (see Fig. 4). Therefore, we demonstrate that neither energy nor angular momentum of the merger remnants are conserved after the merger has concluded. In some cases, we observe a substantial change in the direction of the angular momentum and noticeable changes in the energy distribution of the stellar debris.

  • We showed that merger remnants from a single event are not clustered in the integrals of motion space, but cover a large area in these coordinates. At the same time, however, the Lz − E distributions are not featureless as a single merger remnant often contributes to a few overdensities (see Fig. 4).

  • By dissecting the Lz − E distributions by age and the location inside dwarf galaxies before the mergers, we found that inside the host galaxy, the accreted stars with lowest total energy are typically older and were acquired from the outer parts of the dwarf galaxies (see Fig. 7). This variation in parameters is translated into a prominent radial positive age gradient for individual merger debris. However, the mean age of the debris is largely biased towards the time of accretion because most of the mergers are accompanied by an enhancement of star formation. Moreover, the most significant bursts of star formation inside the merger debris correspond to the merger time. This result also suggests that in the MW the merger time estimation can be done by using the age distribution of the stellar debris, but that the accreted stars from the innermost disc should be taken into account.

  • The merger remnants show a diverse appearance in phase-space coordinates with some examples similar to the ones discovered in the Gaia data. In particular, the HESTIA simulations reproduce the Gaia-Sausage-like features in the (VR, Vϕ) plane with prominent non-rotating or weakly counter-rotating components (see Fig. 8). Moreover, in some cases we can see the presence of more that one Gaia-Sausage-like feature (see Fig. 9). We also demonstrate that the local (VR, Vϕ) Gaia-Sausage-like features are the parts of large-scale radially extended components traceable across the entire disc (see Fig. 10).

  • Apart from the dwarf galaxy population, the merger debris do not show any isolated structures in the action space being distributed over a large area, as well as overlapping with each other and in situ stars (see Figs. 11 and 12). However, we suggest that accreted stars can more likely be identified with the cut 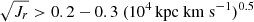. We also propose that some merger debris can be disentangled from each other in the (Jz/Jr – orbital eccentricity) space. Nevertheless, we showed that the actions, once combined with the orbital parameters (e.g. eccentricity), demonstrate different behaviour for different merger debris, thus making it possible to disentangle accretion events (see Fig. 13).

  • The accreted stars in HESTIA have a broad distribution of eccentricities, peaking at ≈0.6 − 0.9. The mean eccentricity of the accreted stars correlates with the mass of the accreted dwarf galaxy and the time of accretion. In particular, more massive mergers and more recent ones result in lower eccentricity of stars at z = 0.

  • Finally, we showed that identifying stellar haloes in the Toomre diagram selects both accreted and in situ stars, which in total represent 45 − 65% of the stellar mass of the galaxy (excluding dwarf galaxies). The accreted component of such kinematically defined stellar haloes is mainly made of a single merger (≈40 − 50%). The in situ mass fraction also correlates with the total accreted mass (see Fig. 16).

The structure of accreted stellar populations in the MW provides valuable insights into its assembly history. Accreted stars typically exhibit distinct kinematic and chemical properties compared to the stars that formed in situ. These accreted populations often display more random and retrograde orbits, indicating their external origin. In the HESTIA galaxies, we showed how the accreted stars contribute to the growth of stellar halos and analysed kinematic signatures of past mergers events. Our study demonstrates how the structure of accreted stellar populations helps unravel the dynamical processes and interactions that have shaped the MW galaxy over cosmic time.

Acknowledgments

We thank the anonymous referee for their valuable comments. S.K. acknowledges the HESTIA collaboration for providing access to the simulations. F.A.G. acknowledges support from ANID FONDECYT Regular 1211370 and from the ANID BASAL project FB210003. F.A.G. acknowledges funding from the Max Planck Society through a Partner Group grant. A.K. is supported by the Ministerio de Ciencia e Innovación (MICINN) under research grant PID2021-122603NB-C21 and further thanks Smashing Pumpkins for Siamese dreams. J.S. acknowledges support from the French Agence Nationale de la Recherche for the LOCALIZATION project under grant agreements ANR-21-CE31-0019. Y.H. has been partially supported by the Israel Science Foundation grant ISF 1358/18. E.T. acknowledges support by ETAg grant PRG1006 and by EU through the ERDF CoE TK133. Software: IPython (Perez & Granger 2007), Astropy (Astropy Collaboration 2013, 2018), NumPy (van der Walt et al. 2011), SciPy (Virtanen et al. 2020), AGAMA (Vasiliev 2019), Matplotlib (Hunter 2007), Pandas (McKinney 2010), TOPCAT (Taylor 2005).

References

  1. Abadi, M. G., Navarro, J. F., & Steinmetz, M. 2006, MNRAS, 365, 747 [Google Scholar]
  2. Agertz, O., Renaud, F., Feltzing, S., et al. 2021, MNRAS, 503, 5826 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amarante, J. A. S., Debattista, V. P., Beraldo e Silva, L., Laporte, C. F. P., & Deg, N. 2022, ApJ, 937, 12 [NASA ADS] [CrossRef] [Google Scholar]
  4. Amorisco, N. C. 2017, MNRAS, 464, 2882 [Google Scholar]
  5. Antoja, T., Helmi, A., Romero-Gómez, M., et al. 2018, Nature, 561, 360 [Google Scholar]
  6. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  8. Belokurov, V., & Kravtsov, A. 2022, MNRAS, 514, 689 [NASA ADS] [CrossRef] [Google Scholar]
  9. Belokurov, V., Evans, N. W., Irwin, M. J., et al. 2007, ApJ, 658, 337 [Google Scholar]
  10. Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
  11. Belokurov, V., Sanders, J. L., Fattahi, A., et al. 2020, MNRAS, 494, 3880 [Google Scholar]
  12. Binney, J. 2012, MNRAS, 426, 1324 [Google Scholar]
  13. Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition, 2nd edn, eds. J. Binney, & S. Tremaine (Princeton, USA: Princeton University Press) [CrossRef] [Google Scholar]
  14. Borre, C. C., Aguirre Børsen-Koch, V., Helmi, A., et al. 2022, MNRAS, 514, 2527 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brook, C. B., Kawata, D., Gibson, B. K., & Flynn, C. 2003, ApJ, 585, L125 [NASA ADS] [CrossRef] [Google Scholar]
  16. Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [Google Scholar]
  17. Buder, S., Lind, K., Ness, M. K., et al. 2022, MNRAS, 510, 2407 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [Google Scholar]
  19. Chiba, M., & Beers, T. C. 2000, AJ, 119, 2843 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chiba, M., & Beers, T. C. 2001, ApJ, 549, 325 [NASA ADS] [CrossRef] [Google Scholar]
  21. Choi, J.-H., Weinberg, M. D., & Katz, N. 2007, MNRAS, 381, 987 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cooper, A. P., Cole, S., Frenk, C. S., et al. 2010, MNRAS, 406, 744 [Google Scholar]
  23. Deason, A. J., Mao, Y.-Y., & Wechsler, R. H. 2016, ApJ, 821, 5 [NASA ADS] [CrossRef] [Google Scholar]
  24. Deason, A. J., Belokurov, V., Koposov, S. E., & Lancaster, L. 2018, ApJ, 862, L1 [Google Scholar]
  25. De Lucia, G., & Helmi, A. 2008, MNRAS, 391, 14 [NASA ADS] [CrossRef] [Google Scholar]
  26. Di Cintio, A., Mostoghiu, R., Knebe, A., & Navarro, J. F. 2021, MNRAS, 506, 531 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dillamore, A. M., Belokurov, V., Font, A. S., & McCarthy, I. G. 2022, MNRAS, 513, 1867 [NASA ADS] [CrossRef] [Google Scholar]
  28. Di Matteo, P., Haywood, M., Lehnert, M. D., et al. 2019, A&A, 632, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
  30. Errani, R., & Peñarrubia, J. 2020, MNRAS, 491, 4591 [Google Scholar]
  31. Fattahi, A., Belokurov, V., Deason, A. J., et al. 2019, MNRAS, 484, 4471 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fattahi, A., Deason, A. J., Frenk, C. S., et al. 2020, MNRAS, 497, 4459 [NASA ADS] [CrossRef] [Google Scholar]
  33. Fernández-Alvar, E., Carigi, L., Schuster, W. J., et al. 2018, ApJ, 852, 50 [CrossRef] [Google Scholar]
  34. Feuillet, D. K., Feltzing, S., Sahlholdt, C. L., & Casagrande, L. 2020, MNRAS, 497, 109 [Google Scholar]
  35. Feuillet, D. K., Sahlholdt, C. L., Feltzing, S., & Casagrande, L. 2021, MNRAS, 508, 1489 [NASA ADS] [CrossRef] [Google Scholar]
  36. Font, A. S., McCarthy, I. G., Crain, R. A., et al. 2011, MNRAS, 416, 2802 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fragkoudi, F., Katz, D., Trick, W., et al. 2019, MNRAS, 488, 3324 [NASA ADS] [Google Scholar]
  38. Fragkoudi, F., Grand, R. J. J., Pakmor, R., et al. 2020, MNRAS, 494, 5936 [Google Scholar]
  39. Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Gaia Collaboration (Babusiaux, C., et al.) 2018a, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gaia Collaboration (Brown, A. G. A., et al.) 2018b, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Gallart, C., Bernard, E. J., Brook, C. B., et al. 2019, Nat. Astron., 3, 932 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gómez, F. A., & Helmi, A. 2010, MNRAS, 401, 2285 [Google Scholar]
  44. Gómez, F. A., Helmi, A., Brown, A. G. A., & Li, Y.-S. 2010, MNRAS, 408, 935 [Google Scholar]
  45. Gómez, F. A., Helmi, A., Cooper, A. P., et al. 2013, MNRAS, 436, 3602 [CrossRef] [Google Scholar]
  46. Gómez, F. A., White, S. D. M., Marinacci, F., et al. 2016, MNRAS, 456, 2779 [Google Scholar]
  47. Gómez, F. A., Grand, R. J. J., Monachesi, A., et al. 2017, MNRAS, 472, 3722 [CrossRef] [Google Scholar]
  48. Grand, R. J. J., Springel, V., Gómez, F. A., et al. 2016, MNRAS, 459, 199 [Google Scholar]
  49. Grand, R. J. J., Gómez, F. A., Marinacci, F., et al. 2017, MNRAS, 467, 179 [NASA ADS] [Google Scholar]
  50. Grand, R. J. J., Deason, A. J., White, S. D. M., et al. 2019, MNRAS, 487, L72 [Google Scholar]
  51. Grand, R. J. J., Kawata, D., Belokurov, V., et al. 2020, MNRAS, 497, 1603 [NASA ADS] [CrossRef] [Google Scholar]
  52. Haywood, M., Di Matteo, P., Lehnert, M. D., et al. 2018, ApJ, 863, 113 [Google Scholar]
  53. Helmi, A. 2020, ARA&A, 58, 205 [Google Scholar]
  54. Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [Google Scholar]
  55. Helmi, A., & White, S. D. M. 1999, MNRAS, 307, 495 [CrossRef] [Google Scholar]
  56. Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [Google Scholar]
  57. Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
  58. Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2020, MNRAS, 493, 3363 [NASA ADS] [CrossRef] [Google Scholar]
  59. Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2023, MNRAS, 520, 5671 [NASA ADS] [CrossRef] [Google Scholar]
  60. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  61. Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [Google Scholar]
  62. Ibata, R., Irwin, M., Lewis, G., Ferguson, A. M. N., & Tanvir, N. 2001, Nature, 412, 49 [Google Scholar]
  63. Jean-Baptiste, I., Di Matteo, P., Haywood, M., et al. 2017, A&A, 604, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Johnston, K. V., Hernquist, L., & Bolte, M. 1996, ApJ, 465, 278 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kepley, A. A., Morrison, H. L., Helmi, A., et al. 2007, AJ, 134, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  66. Khoperskov, S., & Gerhard, O. 2022, A&A, 663, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Khoperskov, S., Minchev, I., Libeskind, N., et al. 2023a, A&A, 677, A89 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Khoperskov, S., Minchev, I., Libeskind, N., et al. 2023b, A&A, 677, A91 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Knebe, A., Gill, S. P. D., Kawata, D., & Gibson, B. K. 2005, MNRAS, 357, L35 [NASA ADS] [CrossRef] [Google Scholar]
  70. Knollmann, S. R., & Knebe, A. 2009, ApJS, 182, 608 [Google Scholar]
  71. Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019, A&A, 631, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Kruijssen, J. M. D., Pfeffer, J. L., Reina-Campos, M., Crain, R. A., & Bastian, N. 2019, MNRAS, 486, 3180 [Google Scholar]
  73. Kruijssen, J. M. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [NASA ADS] [CrossRef] [Google Scholar]
  74. Libeskind, N. I., Carlesi, E., Grand, R. J. J., et al. 2020, MNRAS, 498, 2968 [NASA ADS] [CrossRef] [Google Scholar]
  75. Mackereth, J. T., Crain, R. A., Schiavon, R. P., et al. 2018, MNRAS, 477, 5072 [NASA ADS] [CrossRef] [Google Scholar]
  76. Mackereth, J. T., Schiavon, R. P., Pfeffer, J., et al. 2019, MNRAS, 482, 3426 [Google Scholar]
  77. Maffione, N. P., Gómez, F. A., Cincotta, P. M., et al. 2015, MNRAS, 453, 2830 [Google Scholar]
  78. Maffione, N. P., Gómez, F. A., Cincotta, P. M., et al. 2018, MNRAS, 478, 4052 [NASA ADS] [CrossRef] [Google Scholar]
  79. Malhan, K., Ibata, R. A., Sharma, S., et al. 2022, ApJ, 926, 107 [NASA ADS] [CrossRef] [Google Scholar]
  80. Matsuno, T., Hirai, Y., Tarumi, Y., et al. 2021, A&A, 650, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 56 [Google Scholar]
  82. Monachesi, A., Gómez, F. A., Grand, R. J. J., et al. 2019, MNRAS, 485, 2589 [NASA ADS] [CrossRef] [Google Scholar]
  83. Montalbán, J., Mackereth, J. T., Miglio, A., et al. 2021, Nat. Astron., 5, 640 [Google Scholar]
  84. Morrison, H. L., Helmi, A., Sun, J., et al. 2009, ApJ, 694, 130 [CrossRef] [Google Scholar]
  85. Myeong, G. C., Evans, N. W., Belokurov, V., Sanders, J. L., & Koposov, S. E. 2018, ApJ, 863, L28 [NASA ADS] [CrossRef] [Google Scholar]
  86. Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
  87. Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
  88. Naidu, R. P., Conroy, C., Bonaca, A., et al. 2021, ApJ, 923, 92 [NASA ADS] [CrossRef] [Google Scholar]
  89. Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Pagnini, G., Di Matteo, P., Khoperskov, S., et al. 2023, A&A, 673, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Pakmor, R., Springel, V., Bauer, A., et al. 2016, MNRAS, 455, 1134 [Google Scholar]
  92. Panithanpaisal, N., Sanderson, R. E., Wetzel, A., et al. 2021, ApJ, 920, 10 [NASA ADS] [CrossRef] [Google Scholar]
  93. Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
  94. Pfeffer, J. L., Trujillo-Gomez, S., Kruijssen, J. M. D., et al. 2020, MNRAS, 499, 4863 [CrossRef] [Google Scholar]
  95. Pillepich, A., Madau, P., & Mayer, L. 2015, ApJ, 799, 184 [Google Scholar]
  96. Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
  97. Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Price-Whelan, A. M., Johnston, K. V., Valluri, M., et al. 2016, MNRAS, 455, 1079 [NASA ADS] [CrossRef] [Google Scholar]
  99. Purcell, C. W., Bullock, J. S., & Kazantzidis, S. 2010, MNRAS, 404, 1711 [NASA ADS] [Google Scholar]
  100. Quinn, P. J., Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [Google Scholar]
  101. Ramos, P., Antoja, T., & Figueras, F. 2018, A&A, 619, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Re Fiorentin, P., Helmi, A., Lattanzi, M. G., & Spagna, A. 2005, A&A, 439, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Re Fiorentin, P., Lattanzi, M. G., Spagna, A., & Curir, A. 2015, AJ, 150, 128 [NASA ADS] [CrossRef] [Google Scholar]
  104. Rodriguez-Gomez, V., Pillepich, A., Sales, L. V., et al. 2016, MNRAS, 458, 2371 [Google Scholar]
  105. Sandage, A., & Fouts, G. 1987, AJ, 93, 74 [NASA ADS] [CrossRef] [Google Scholar]
  106. Sanders, J. L., & Binney, J. 2013, MNRAS, 433, 1813 [NASA ADS] [CrossRef] [Google Scholar]
  107. Sawala, T., Frenk, C. S., Fattahi, A., et al. 2016, MNRAS, 457, 1931 [Google Scholar]
  108. Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
  109. Schuster, W. J., Moreno, E., Nissen, P. E., & Pichardo, B. 2012, A&A, 538, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Simpson, C. M., Gargiulo, I., Gómez, F. A., et al. 2019, MNRAS, 490, L32 [NASA ADS] [CrossRef] [Google Scholar]
  111. Simpson, J. D., Martell, S. L., Buder, S., et al. 2021, MNRAS, 507, 43 [NASA ADS] [CrossRef] [Google Scholar]
  112. Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
  113. Stewart, K. R., Bullock, J. S., Wechsler, R. H., Maller, A. H., & Zentner, A. R. 2008, ApJ, 683, 597 [NASA ADS] [CrossRef] [Google Scholar]
  114. Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
  115. Tissera, P. B., Machado, R. E. G., Carollo, D., et al. 2018, MNRAS, 473, 1656 [NASA ADS] [CrossRef] [Google Scholar]
  116. Trick, W. H., Bovy, J., D’Onghia, E., & Rix, H.-W. 2017, ApJ, 839, 61 [NASA ADS] [CrossRef] [Google Scholar]
  117. Trick, W. H., Fragkoudi, F., Hunt, J. A. S., Mackereth, J. T., & White, S. D. M. 2021, MNRAS, 500, 2645 [Google Scholar]
  118. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  119. Vasiliev, E. 2019, MNRAS, 482, 1525 [Google Scholar]
  120. Vasiliev, E., Belokurov, V., & Erkal, D. 2021, MNRAS, 501, 2279 [NASA ADS] [CrossRef] [Google Scholar]
  121. Vasiliev, E., Belokurov, V., & Evans, N. W. 2022, ApJ, 926, 203 [NASA ADS] [CrossRef] [Google Scholar]
  122. Velazquez, H., & White, S. D. M. 1999, MNRAS, 304, 254 [NASA ADS] [CrossRef] [Google Scholar]
  123. Villalobos, Á., & Helmi, A. 2009, MNRAS, 399, 166 [NASA ADS] [CrossRef] [Google Scholar]
  124. Vincenzo, F., Spitoni, E., Calura, F., et al. 2019, MNRAS, 487, L47 [NASA ADS] [CrossRef] [Google Scholar]
  125. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  126. Vogelsberger, M., White, S. D. M., Helmi, A., & Springel, V. 2008, MNRAS, 385, 236 [NASA ADS] [CrossRef] [Google Scholar]
  127. Vogelsberger, M., Genel, S., Sijacki, D., et al. 2013, MNRAS, 436, 3031 [Google Scholar]
  128. Vogelsberger, M., Marinacci, F., Torrey, P., & Puchwein, E. 2020, Nat. Rev. Phys., 2, 42 [Google Scholar]
  129. Wetzel, A. R., Hopkins, P. F., Kim, J.-H., et al. 2016, ApJ, 827, L23 [NASA ADS] [CrossRef] [Google Scholar]
  130. Wu, Y., Valluri, M., Panithanpaisal, N., et al. 2022, MNRAS, 509, 5882 [Google Scholar]
  131. Zhao, G., & Chen, Y. 2021, Sci. Chin. Phys. Mech. Astron., 64, 239562 [NASA ADS] [CrossRef] [Google Scholar]
  132. Zolotov, A., Willman, B., Brooks, A. M., et al. 2009, ApJ, 702, 1058 [Google Scholar]

All Figures

thumbnail Fig. 1.

Morphology of individual mergers at the time of accretion for the five most significant events, for each M31/MW analogues in HESTIA. The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given at the bottom of each panel. The colour bar represents stellar density, in units of M*/kpc2. The merger debris show diverse morphologies, likely caused by the different trajectories of accreting systems and internal mass/kinematics distributions.
In the text
thumbnail Fig. 2.

Same as Fig. 1, but merger debris are shown at z = 0 instead of at the time of accretion. At this time they appear well phased-mixed with some structure found for the most recent events and the earlier mergers seem to be more compact compared to the later ones.
In the text
thumbnail Fig. 3.

Energy-angular momentum relation for the stellar remnants. Five most significant mergers (M1–M5; see Fig. 4 in Paper I) are shown at the time of accretion (blue contours) and with at z = 0 (red contours). The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given in the bottom left corner of each panel. Since the total host mass increases over time, the initial Lz − E distributions have lower energies (upper half in each panel), while at z = 0 clumps at higher |E|. The density maps are transparent to distinguish the overlap for some of the most recent mergers. Both the energy and angular momentum of accreted systems are not conserved after the time of accretion, as often assumed in the literature. This energy change is caused by the mass growth of the host galaxy and the angular momentum transformations are due to the non-axisymmetric time-dependent potential of the galaxy with a certain contribution from the population of satellites orbiting the host.
In the text
thumbnail Fig. 4.

Energy-angular momentum space. Top three rows: Energy-angular momentum relation for all stars (first row), in situ stars (main progenitor, second row), and accreted stars (third row) at z = 0. To focus on the stellar halo, only stars with |z|> 1 kpc (away from the disc mid-plane) were selected. The corresponding stellar mass is shown in the bottom right of each panel. Bottom five rows: Lz − E relation for the five most significant mergers at z = 0 (M1,...,M5; see Fig. 4 in Paper I). The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given in the bottom left corner of each panel with individual mergers debris. All colour bars represent stellar density, in units of M⊙. The in situ stars, being kicked out from the plane, show some net rotation with some overdensities and features similar to those of the accreted stars. The latter contain a number of overdensities, which are the relics of the different merger events. Some individual merger remnants are represented by a number of features and overdensities.
In the text
thumbnail Fig. 5.

Overlap of debris from different mergers in the Lz − E plane. Each pixel is coloured by the number of merger events contributing to that region, as given in the colour bar. Top row: Debris from all mergers for each HESTIA galaxy, as indicated above each panel. The largest overlap of mergers are shown in maroon. Bottom row: Same as top row, but limited to the five most significant mergers. These maps suggest that the most crowded region of the Lz − E space corresponds to the non-rotating region, which is where the Gaia-Enceladus merger was identified (Helmi et al. 2018). The number of merger remnants decreases in the regions of substantial rotation.
In the text
thumbnail Fig. 6.

Energy-angular momentum relation for each of the two most significant mergers at z = 0 per galaxy in our sample. The two left columns show the density distributions of each of the two mergers, the two middle columns are colour-coded by the mean distance (R0) of stars inside the dwarf galaxies before they accreted, and the two right columns show the mean stellar age. This figure demonstrates that even a single merger event could result in a number of overdensities in the E − Lz space. More recent events tend to show more substructures; however, even the merger remnants from 9 − 10 Gyr ago are not featureless at z = 0. The R0-gradient suggests how the internal structure of dwarf galaxies is being mapped into the Lz − E space once the system is accreted.
In the text
thumbnail Fig. 7.

Age structure of the accreted halo components. Top: Mean age of stars accreted from the five most significant mergers as a function of galactocentric distance (Rgal) at z = 0. Bottom: Corresponding age distributions, colour-coded as above. The strongest burst of star formation is typically for the youngest stars in a given merger, thus corresponding to the time of accretion. Age estimates for accreted stars can therefore be used to time each merging event.
In the text
thumbnail Fig. 8.

Kinematic structure of the stellar haloes. Top three rows: Stellar density distributions in the VR − Vϕ plane at redshift zero for stars in the range (1 − 3)Rd (where Rd is the disc scale-length from Libeskind et al. 2020) and |z|> 1 kpc including all stars (first row), only in situ stars (second row), and only accreted populations (third row). The mass fractions of the in situ and accreted populations are shown at the bottom of the second and third rows, respectively. Bottom five rows: As above, but for the five most significant mergers at z = 0 (M1–M5; see Fig. 4 in Paper I). The merger accretion lookback time (Gyr), the total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given at the bottom of each panel. The colour bar represents a normalized density relative to the maximum value. All M31/MW HESTIA galaxies demonstrate the presence of Gaia-Sausage-like features, which exhibit different individual shapes and radial velocity ranges.
In the text
thumbnail Fig. 9.

Examples of the Gaia-Sausage-like features in the (VR, Vϕ) plane for all M31/MW HESTIA galaxies. Each panel corresponds to different merger remnants in the range |z|> 1 kpc and (1 − 3)Rd where Rd is the disc scale-length from Libeskind et al. (2020). The merger accretion lookback time (Gyr), the total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor in the time of the merger are given at the bottom of each panel.
In the text
thumbnail Fig. 10.

Radial structure of the azimuthal velocity distribution. Different stellar populations are shown: all stars (first row), in situ (second) and accreted populations (third row) taken > 1 kpc away from the galactic plane. All other rows below (fourth to eighth) correspond to the most significant merger remnants. The merger accretion lookback time (Gyr), the total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given at the bottom of each panel. Magenta lines in the individual merger debris distribution show the dispersion level along the radius. The in situ stars rotate faster around the galactic centre and show the presence of diagonal ridges similar to those discovered in the MW (Antoja et al. 2018), which are likely to be the manifestation of spiral arms (Khoperskov & Gerhard 2022) and/or bar resonances (Fragkoudi et al. 2019). The accreted stars depict a number of radially extended structures with no net rotation and multiple co-rotating and counter-rotating components and small-scale overdensities. The important feature of the individual merger debris is that the azimuthal velocity dispersion remains nearly constant along the galactocentric distance, except for the innermost parts of the galaxies.
In the text
thumbnail Fig. 11.

Action space analysis. Top: X–Z projection of in situ stars (left), all accreted stars (middle), and surviving satellites (right) in 09–18 M31 galaxy at z = 0. The density maps and the action space analysis are based on the stars (accreted and in situ) > 1 kpc from the galactic plane. Different survived satellites are shown in different colours. Second row: Jz − Jr plane for in situ (left), the fraction of accreted stellar mass (centre), and surviving satellites (right). Third row: (Jr − Jz)/Jtot − Jϕ/Jtot plane for in situ (left), faction of accreted stellar mass (centre), and survived satellites (right). Bottom row: plane for in situ (left), faction of accreted stellar mass (center), and survived satellites (right). While in situ and accreted stars do not show any prominent features in the action space, the dwarf satellites, as expected, are seen as coherent structures. Accreted stars have on average larger radial and vertical actions, but still substantially overlap with the in situ populations at smaller values.
In the text
thumbnail Fig. 12.

Action space for five of the most significant merger remnants in the 09–18 M31 galaxy. From top to bottom: X-Z density maps, Jz − Jr space, (Jr − Jz)/Jtot − Jϕ/Jtot plane, and plane. Similar to Fig. 11 (for the entire accreted population), the individual merger debris completely fill the (Jr − Jz)/Jtot − Jϕ/Jtot plane; nevertheless, different remnants peak at slightly different regions of the diagram depending on the orbital parameters. The interesting feature, seen in the second row, is that the merger remnants show a different ratio of Jz to Jr. Some substructures, however, can be seen at the very large radial and vertical actions, which correspond to the outer parts of the debris where the dynamical time is longer and, thus phase mixing is not yet completed for the most recent mergers at z = 0.
In the text
thumbnail Fig. 13.

Density distribution in the Θ = arctan(Jz/Jr)-eccentricity plane for all stars (first row), in situ stars (second row), and all accreted populations (third row). All other rows below (fourth to eighth) correspond to the most significant merger remnants. The eccentricity values are multiplied by the sign of the angular momentum; thus, the counter-rotating stars have negative values of eccentricity and can be found to the right of the vertical magenta lines. To sharpen the structures, only the stars located in the (1 − 2)Rd radial range, where Rd is the disc scale-length from Libeskind et al. (2020), are presented here. The figure shows how the anisotropy of actions correlates with the orbital eccentricity for different populations. The in situ stars distribution shows the presence of vertically cold (low Θ angles) low-eccentricity stars representing a disc component; at higher eccentricities, Θ remains roughly the same. The accreted stars distribution is even more interesting, where there are many substructures, and the overall distribution is different from the in situ stars; moreover, different merger debris, in many cases, show different behaviour. The individual merger debris (fourth to eighth) do not represent the entire complexity of the arctan(Jz/Jr)-eccentricity space, which is more complex in the third row where all the merger debris are taken into account.
In the text
thumbnail Fig. 14.

Orbital structure of accreted populations. Left: Mean eccentricity of merger remnants stars as a function of accretion time for all the mergers in the M31/MW HESTIA galaxies. The different symbols correspond to different simulations and galaxies and they are colour-coded by the stellar mass at the time of the merger. Right: Stellar-mass weighted distributions of the eccentricities for individual merger remnants (grey) and the mean distribution (red) at z = 0. Here, the eccentricity is multiplied by the sign of the angular momentum. Although the stars in the merger debris show a wide range of eccentricities, the mean eccentricity of the debris tends to decrease with time, whereas more recently accreted debris have slightly lower eccentricity. This evidently correlates with the stellar mass of the accreted system, which tends to be higher for the galaxies that accreted earlier, and thus evolved longer.
In the text
thumbnail Fig. 15.

Toomre diagram for all stars in (1 − 3)Rd (Rd is the disc scale-length) and |z|> 2 kpc (first row), in situ stars (second row), and all accreted populations (third row). The mass fraction of in situ and accreted populations are shown at the bottom in the second and third rows, respectively. The five rows below the gap correspond to the Toomre diagram for five of the most significant mergers at z = 0 (M1–M5; see Fig. 4 in Paper I). The merger accretion lookback time (Gyr), total stellar mass of the merger debris at the time of the merger (log10(M*/M⊙)), and the stellar mass ratio (μ*) relative to the main M31/MW progenitor at the time of the merger are given in the bottom left corner of each panel. The colour bar is in M* scale. The white circle corresponds to the thick disc selection: Vcirc180(km s−1)/240(km s−1), where Vcirc is the circular velocity value at 2Rd for each galaxy; 180 km s−1 corresponds to the selection made for the MW; and 240 km s−1 is the MW circular velocity. We suggest that the disc-like regions in the Toomre diagram are populated by the accreted stars. A single debris spans over a large volume, and, in some cases, the bulk of the accreted stars have (thick) disc-like kinematics.
In the text
thumbnail Fig. 16.

Relations between stellar haloes masses and masses of accreted systems. Top: mass of the most massive merger (Mmmm) relative to the accreted mass vs mass of the most massive merger. Bottom: In situ halo mass fraction versus the total accreted stellar mass. Different symbols show different M31/MW HESTIA galaxies. Shown are the kinematically defined components using Toomre diagrams (in blue), while the total mass without any kinematics selections (in red). Depending on the definition, the single most massive merger contributes from 20% to 70% of the total accreted mass (see also, Cooper et al. 2010; Monachesi et al. 2019). At the same, the in situ mass fraction correlates well with the total accreted mass.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.