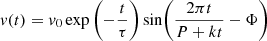EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 676 (August 2023) A&A, 676 (2023) A32 Full HTML
Open Access
Issue
A&A
Volume 676, August 2023
Article Number A32
Number of page(s) 9
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346671
Published online 01 August 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Coronal structures act as wave guides for a variety of magnetohydrodynamic (MHD) oscillation modes (Nakariakov & Verwichte 2005; Nakariakov & Kolotkov 2020). There is extensive observational evidence that transverse oscillations are ubiquitous in the solar corona in both closed coronal loops and open coronal structures (Tomczyk et al. 2007; McIntosh et al. 2011; Anfinogentov et al. 2015). The transverse oscillations that are commonly observed in coronal loops are identified as standing kink modes (Aschwanden et al. 1999; Nakariakov et al. 1999). Coronal oscillations carry magnetic energy that is deposited through the oscillation damping and dissipation. The commonly proposed physical mechanisms that cause the oscillation damping and dissipation include resonant absorption (Hollweg & Yang 1988; Goossens et al. 2002), phase mixing (Heyvaerts & Priest 1983), and the Kelvin-Helmholtz instability (Terradas et al. 2008; Antolin et al. 2014). These mechanisms have mostly been analysed using simplified models of coronal loops as straight magnetic flux-tubes that are clearly distinct from the surroundings. There are several advantages to this approach: It is straightforward to isolate individual effects and processes linked to wave evolution and to have full control over the parameters of the modelled loop. These models also allow for the very high spatial resolution, that is necessary for modelling of certain physical processes such as resonant absorption (Van Doorsselaere et al. 2004). These models, however, also require making several assumptions about the shape, density structure, and morphology of coronal loops that might be too idealised.

The solar corona is a dynamic environment with complex density structuring, and the coronal magnetic field changes and evolves continuously. Models of static and idealised coronal loops therefore neglect this evolution. In order to account for realistic magnetic field configurations and density structuring in the solar corona, a more self-consistent approach to modelling the evolution of coronal structures is necessary. This can be achieved by taking advantage of realistic convection-zone-to-corona models (e.g., Carlsson et al. 2016; Cheung et al. 2019; Kohutova & Popovas 2021; Breu et al. 2022). The evolution of the corona in these models is self-consistently driven by the dynamics of the lower solar atmosphere. This type of simulation therefore reflects the dynamic and continuously evolving nature of the solar corona.

One common feature of these simulations is the lack of clearly identifiable coronal loops with well-defined boundaries. In realistic solar simulations, the actual 3D structure of coronal features with increased emissivity in the optically thin coronal emission lines is much more complex, even though it appears as thin, well-defined loops in forward-modelled emission as a result of line-of-sight effects. This structure of the corona is referred to as coronal veil, and has been described using the self-consistent MURaM simulation spanning from the convection zone into the corona (Malanushenko et al. 2022). Different codes capable of producing self-consistent convection-zone-to-corona models, including MURaM (Rempel 2016) and Bifrost (Gudiksen et al. 2011), seem to reproduce the coronal veil structure of the solar corona. The question remains how well the simulated corona that forms in these models represents the real solar corona. On one hand, the coronal veil model can explain certain properties of the coronal loops seen in extreme-ultraviolet (EUV) observations, such as loop cross-sections that appear to be constant with height (Aschwanden & Nightingale 2005), which are difficult to explain otherwise. We note that alternative explanations include a specific density and temperature distribution across the magnetic field (Peter & Bingert 2012) and magnetic twist (Li et al. 2020). This would also question the applicability of coronal loop oscillation models because most rely on the assumption that coronal loops are well represented by idealised magnetic cylinders. On the other hand, the existence and omnipresence of transverse MHD waves such as kink waves directly indicates the existence of structures acting as waveguides that lead to a collective behaviour in the coronal volume. Moreover, the occurrence of coronal rain showers (Şahin & Antolin 2022) and long-period intensity pulsations (Froment et al. 2015) that are ubiquitous over active regions indicates the existence of coronal entities (which we refer to as loops or loop bundles) with a similar thermodynamic behaviour.

Most models for wave dissipation rely on a modelling of coronal loops as straight magnetic flux-tubes. The mechanism of resonant absorption depends on the conversion of a global kink mode into local azimuthal Alfvén modes in an inhomogeneous layer, with an Alfvén speed gradient at the boundary of a cylindrical coronal loop (Goossens et al. 2002; Pascoe et al. 2010; Howson et al. 2019). Similarly, the development of Kelvin-Helmholtz instability vortices at the boundary of a transversely oscillating loop has mostly been studied using models of cylindrical loops (e.g., Antolin et al. 2014; Karampelas et al. 2017; Howson et al. 2017, 2019) in which a distinct density or magnetic interface separates them from the background plasma.

The main shortcoming of these models is that the observational evidence for the proposed damping and dissipation mechanisms is largely inconclusive. Signatures reminiscent of resonant absorption have been observed in oscillating prominence threads (Antolin et al. 2015; Okamoto et al. 2015) and in transversely oscillating spicules (Antolin et al. 2018). To the best of our knowledge, these are the only observational evidence of these mechanisms to date. Models for the damping of coronal oscillations would therefore benefit from being extended into more realistic setups. Numerical studies using setups that do not correspond to magnetic cylinders have been performed for oscillations in the chromosphere (Khomenko & Cally 2012; Leenaarts & Carlsson 2015) and in the corona (Matsumoto 2018), most works, however, lack the self-consistent treatment of the lower solar atmosphere driving the corona.

In this work, we therefore focus on analysing coronal oscillations in a more advanced numerical setup. We exploit the potential of convection-zone-to-corona simulations with the radiation-MHD code Bifrost for coronal studies. We have previously shown that coronal oscillations are abundant in self-consistent convection-zone-to-corona simulations and that the detected oscillation modes and regimes match those seen in solar observations (Kohutova & Popovas 2021). Here we analyse the evolution of an oscillating bundle of magnetic loops that forms in the simulation and focus on the oscillation damping. Despite the complex evolution of the bundle, and the variable length the individual magnetic field lines contained in the bundle are found to exhibit a collective evolution during extended periods of time, including collective oscillations triggered by impulsive events and subsequent oscillation damping.

The manuscript is structured as follows. Section 2 describes the numerical model. Section 3 describes the methods we used for the analysis of the evolution of a bundle of magnetic loops and of the corresponding oscillatory behaviour seen in the simulation. In Sect. 4 we focus on the damping of the oscillating loops and on the physical mechanism that causes the damping. In Sect. 5 we discuss the results and implications for the coronal loop models. We summarise our conclusions in Sect. 6.

2. Numerical model

We analysed the evolution, oscillatory behaviour and damping of a bundle of magnetic loops in the numerical simulation of a magnetically enhanced network spanning from the upper convection zone to the corona using the radiation-MHD code Bifrost (Gudiksen et al. 2011). This simulation corresponds to the extended run of the public Bifrost simulation of the enhanced network (Carlsson et al. 2016). The simulation subset with 2000 s duration analysed in this work covers the time range from t = 100 s to t = 2100 s of the extended run of the enhanced network simulation run from the last snapshot of the public simulation and has the same physical setup.

Bifrost is a 3D radiation-MHD code that solves the resistive MHD equations and includes radiative transfer with scattering in the photosphere and low chromosphere, and parametrised radiative losses and heating in the upper chromosphere, transition region and corona. The effects of field-aligned thermal conduction and the non-equilibrium ionisation of hydrogen in the equation of state are included in the simulation.

The physical size of the simulation grid is 24 × 24 × 16.8 Mm and the grid resolution is 504 × 504 × 96. The grid spans from 2.4 Mm below the photosphere to 14.4 Mm in the corona. The photosphere is located at z = 0 surface and corresponds to the (approximate) height, where the optical depth τ500 is equal to unity. The grid spacing is 48 km and uniform in the x and y direction, while in the z direction, it varies from 19 km to 98 km in order to resolve steep density and temperature gradients in the lower solar atmosphere.

The simulation domain uses periodic boundaries in the x and y directions and open boundaries in the z direction. The top boundary uses characteristic boundaries that transmit disturbances with minimum reflection (Gudiksen et al. 2011). At the bottom boundary the flows are let through and the magnetic field is passively advected without introducing any additional magnetic field into the domain. The average horizontal pressure is driven towards a constant value with a characteristic timescale of 100 s, creating a pressure node at the bottom boundary. This leads to acoustic wave reflection resembling the refraction of waves in the deeper solar atmosphere, resulting in global radial box oscillations with a period of 450 s, which are a simulation counterpart of solar p-modes (Stein & Nordlund 2001; Carlsson et al. 2016).

The photospheric magnetic field is concentrated in two patches of opposite polarity and has an average unsigned value of about 50 G (Fig. 1). The dipolar structure of the magnetic field creates several magnetic loops in the simulated corona. The convective motions in the lower solar atmosphere lead to magnetic field braiding. The Ohmic and viscous heating associated with the braiding together maintain high temperatures in the chromosphere and corona. An artificial heating term is employed for plasma with temperatures below 2500 K, in order to prevent the temperature from dropping too low in regions that are rapidly expanding. Only a few isolated regions in the simulation domain are affected by this, and the heating in the vast majority of the domain is self-consistent. The processes contributing to the heating include small-scale reconnection events which heat the plasma through a combination of direct Ohmic dissipation and by inducing shear flows that are then converted into heat by viscous dissipation as well as dissipating oscillations. In order to ensure numerical stability, the code employs a diffusive operator; this consists of a small global diffusion term as well as of a directionally dependent hyper diffusion component that enhances the diffusion locally. Further details of the numerical setup can be found in Carlsson et al. (2016) and Kohutova et al. (2020).

thumbnail Fig. 1.

Simulation setup. Left: bundle of magnetic loops and the photospheric magnetic field at t = 880 s. Top right: cut across the density structure at x = 13 Mm intersecting the apex of the magnetic bundle. Bottom right: cut across the temperature structure at x = 13 Mm. The white points mark the positions at which the individual loops in the bundle intersect the cuts. An animation of this figure is available online.

3. Evolution of a magnetic loop bundle

The corona in the simulation is filled with closed magnetic loops that can extend up to heights of 10 − 14 Mm. The density structure of the simulated corona is complex, and there are several structures with enhanced densities compared to the surroundings. Most of the overdense structures are filled by chromospheric evaporation in response to heating (Kohutova et al. 2020). A cut across the simulation domain shows a lack of loops with clearly defined cross sections in the density or temperature structure (Fig. 1).

The magnetic field configuration in the simulation domain is driven by the dynamics of the lower solar atmosphere and the footpoints of coronal structures are shuffled and dragged around by the convective motions. The magnetic loops in the corona therefore evolve continuously and undergo complex motions that include sideways displacement, oscillatory and torsional motion, and vertical expansion or contraction.

We focused on the evolution of a bundle of magnetic loops located in the centre of the simulation domain shown in Fig. 1. It reached a height of around 10 Mm. In order to obtain the evolution of this bundle in three dimensions, it is necessary to trace the evolution of the corresponding magnetic field lines in the bundle through both time and space, because the magnetic field in the simulated corona evolves. To do this, we used the field-tracing method described in Leenaarts & Carlsson (2015) and Kohutova & Popovas (2021).

A magnetic field line is defined as a curve in a 3D space r(s) that is parametrised by the arc length along the curve s, for which dr/ds = B/|B|. It is therefore a representation of the magnetic connectivity of the coronal plasma. We traced the evolution of magnetic field lines by inserting seed points into the simulation domain at the apex of the magnetic bundle. The seed points were then passively advected forward and backward in time using the velocity at the seed point position. The magnetic field was then traced through the instantaneous seed point position in order to determine the spatial coordinates of the traced field line at every time step. The accuracy of this method is given by the size of the time step between two successive simulation snapshots (i.e. 1 second in this case). We find that the method works well for a step size of 10 s, and there are no major differences in the field-line evolution for step sizes of 1 s and 10 s. We therefore used a time-step size of 10 s to trace the field line evolution in the following analysis. We note that this approach requires that the evolution is smooth and that no large-amplitude velocity variations occur on timescales shorter than the size of the time-step. Similarly, in the instances when magnetic reconnection occurs, this approach fails, and the tracing leads to a jump in the field-line evolution. This is not the case in the coronal part of the magnetic bundle during the analysed time-period, however. In two instances rapid transverse displacement occurred close to the foootpoints of the traced loops at t = 830 s and t = 1100 s. This was caused either by an external perturbation or by a change in the magnetic connectivity in the lower solar atmosphere. These displacements did not lead to discontinuities in the evolution of the physical quantities in the coronal part of the analysed loops.

The magnetic bundle is shown in different projections in Fig. 2. The evolution of the bundle evolution is shown in the online animation. The individual magnetic loops display a high degree of collective behaviour, and the magnetic bundle behaves as a coherent structure during most of the duration of the simulation. The footpoints of the magnetic bundle are not static, and the bundle continuously changes and evolves. The lengths of the individual loops in the magnetic bundle change significantly over the duration of the simulation, sometimes on a timescale of minutes.

thumbnail Fig. 2.

projected view of the magnetic bundle in the xz-plane (left), yz-plane (centre), and xy-plane (right) at t = 880 s. An animation of this figure is available online.

4. Oscillations and damping

The full spatial coordinates of the magnetic loops in the bundle at any point in time enable us to obtain the evolution of the physical quantities along the loops, including both scalar and vector quantities. To aid the oscillation analysis, we decomposed the velocity vector into three velocity components relative to the direction of the magnetic field, vT, vN, and vR. The longitudinal velocity vT = v ⋅ T corresponds to the velocity component aligned with the tangent vector of the magnetic field line given by T = B/|B|. The normal velocity vN = v ⋅ N corresponds to the velocity component along the normal vector of the field line given by 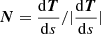N = d T d s / | d T d s | $ \boldsymbol{N} = \frac{\mathrm{d}\boldsymbol{T}}{\mathrm{d}s} / |\frac{\mathrm{d}\boldsymbol{T}}{\mathrm{d}s}| $. In the case of a closed magnetic loop, vN represents the motion in the plane of the loop and perpendicular to the loop tangent. Finally the third velocity component aligned with the binormal vector is given by vR = v ⋅ R where R = T × N. In the case of a closed magnetic loop, vR corresponds to transverse motion perpendicular to the plane of the loop and to the loop tangent. The unit vectors T, N, and R together form an orthogonal coordinate system known as the Frenet frame of reference. This coordinate system is well-suited to analysing oscillations in complex 3D magnetic field geometries (e.g., Carlsson & Bogdan 2006; Felipe 2012; Leenaarts & Carlsson 2015; González-Morales et al. 2019; Kohutova & Popovas 2021).

The collective behaviour of the loop bundle is apparent from Fig. 3, which shows the evolution of the height of the individual magnetic loops in the bundle at x = 13 Mm. The evolution shows two clear instances of oscillatory behaviour, starting at t = 400 s and t = 1100 s and lasting about 400 s in both cases, as shown by the blue regions in Figs. 3 and 4. The oscillations are damped and occur in a plane perpendicular to the bundle axis. The evolution in the animations of Figs. 1 and 2 clearly show that these oscillations correspond to a transverse standing mode of the bundle. The point of maximum oscillation displacement and hence maximum oscillation velocity amplitude lies close to the apex of the bundle. The bundle footpoints act as nodes of the standing oscillation. The oscillations are triggered by impulsive events in the corona that are associated with a peak in the Joule heating and subsequent large-scale displacement of the analysed bundle.

thumbnail Fig. 3.

Eolution of the height of the individual loops in the bundle at x = 13 Mm as a function of time. The blue regions indicate the two instances of damped oscillatory motion in the vertical direction.

We analysed the evolution of the vR and vN components by averaging the velocity components over the oscillating loops in the bundle at the loop apex, which we define as the point halfway between the two footpoints of the loop (Fig. 4). The oscillations are most clearly detectable in the vN component. In both cases, the oscillations follow large-scale perturbations of the magnetic bundle.

thumbnail Fig. 4.

Bundle evolution time series. Top: evolution of the longitudinal (green), normal (orange) and binormal velocity component (blue) at the apex of the bundle. Middle: evolution of the Joule volumetric heating rate (dashed red), the viscous volumetric heating rate (dotted red) and the temperature (black) at the apex of the bundle. Bottom: evolution of the average length (blue) and the Alfvén speed at the apex of the loops in the bundle. The blue regions indicate the time range of the two oscillations.

To remove the large-scale trends in the vN evolution corresponding to a bulk motion of the bundle, the oscillation time-series were detrended by subtracting a best-fit second-degree polynomial. The time-series were then fitted with the function

v ( t ) = v 0 exp ( − t τ ) sin ( 2 π t P + k t − Φ ) $$ \begin{aligned} v(t) = v_0 \exp {\biggl (-\frac{t}{\tau }\biggr )}\sin \biggl (\frac{2 \pi t}{P+kt} - \Phi \biggr ) \end{aligned} $$(1)

which includes both the oscillation damping and linear change in the oscillation period (Fig. 5). Here v0 corresponds to the velocity amplitude, τ is the decay time, P is the oscillation period, k is a parameter controlling the linear change in period and Φ is the phase. We find that the initial velocity amplitudes are 10 km s−1 and 16 km s−1. They are damped with decay times of 176 s and 198 s, respectively, which means that roughly 3 oscillation periods are detectable before the oscillation decays. The periods for the first and second oscillation are 177 s and 191 s, respectively. The oscillation periods in both cases decrease during the oscillation by approximately 15 s for oscillation 1 and 100 s for oscillation 2. The Joule and viscous volumetric heating rates shown in Fig. 5 are also averaged over the oscillating loops at the apex bundle. During the oscillations, the heating rates at the apex of the bundle are variable, but they increase overall during the later stages of both oscillations. Similarly, the average temperature at the bundle apex increases by around 0.5 MK over the duration of the oscillation in both cases. Finally, we show the evolution of the absolute value of the x-component of the vorticity ωx in the y − z plane at x = 13 Mm, averaged over the area surrounding the bundle apex. The ωx-component was chosen because the axis of the loop at the apex is roughly aligned with the x-axis, and the oscillatory motion mostly occurs in the plane perpendicular to the loop axis. During the first oscillation, the vorticity in the surroundings of the oscillating bundle increases to reach the maximum value around 170 s after the oscillation onset, followed by a gradual decrease to the pre-oscillation values. In the latter case, the vorticity in the vicinity of the bundle apex decreases during the entire oscillation duration. For the second oscillation, we also calculated the evolution of the ωz vorticity component at the right footpoint at a height of 3 Mm because this undergoes strong transverse displacement. A similar vorticity peak as at the apex position of the first oscillation can be seen in the evolution here.

thumbnail Fig. 5.

Oscillation time series. Top: evolution of the detrended normal velocity component at the bundle apex averaged over the oscillating field lines in the bundle. The best-fit is shown in red. Middle: evolution of the Joule (dashed line) and viscous volumetric heating rate (dotted line) at the bundle apex. Bottom: temperature (black), the x-component of the vorticity averaged in the vicinity of the bundle apex (solid blue line) and the z-component of the vorticity averaged in the vicinity of the right bundle footpoint (dotted blue line). The time intervals correspond to the time ranges highlighted in blue in Figs. 3 and 4.

To further understand the evolution of the vorticity close to the oscillating bundle, we show the velocity field given by vyey + vzez in the y − z plane at x = 13 Mm, which is nearly perpendicular to the bundle axis and in the plane of the bundle oscillations (Fig. 6). We calculated the velocity field before the onset of the oscillation, during the oscillation and at the end of the oscillation. The shear flows are abundant in the vicinity of the bundle. This is visible as counter-directional strong magnitude flows in the vz component of the velocity. We find that the velocity shear is strongest before and during the oscillation. Associated with this is the development of several vortices that are visible in the velocity streamlines in the close proximity of the oscillating structures. The velocity shear in this region weakens, and the vortices mostly disappear after the oscillations decay. The vortices visible in the velocity streamlines are always located in the regions with strong velocity shear, suggesting that they develop because of the Kelvin-Helmholtz instability. The size of the vortices is of the order of few megameters, which matches the transverse length scale in the Alfvén speed variation (Fig. 7), as predicted by the straight flux-tube models (Antolin & Van Doorsselaere 2019). The Kelvin Helmholtz instability in magnetised plasmas is inhibited by the magnetic tension, but in this case, the direction of the magnetic field is perpendicular to the flow velocity vector as a result of the oscillatory motion. The vortices can therefore develop without distorting the magnetic field, which would lead to stabilising magnetic tension (Hillier et al. 2019; Barbulescu et al. 2019). We note that both vortices and shear flows contribute to the increased values of ωx in the analysed region.

thumbnail Fig. 6.

Development of Kelvin-Helmholtz vortices near the oscillating loops. Top: vz velocity component and the corresponding velocity field streamlines in cuts parallel to the y − z plane at x = 13 Mm shown before the oscillation onset (left), during the oscillation (middle), and at the end of the oscillation (right). Bottom: same as above, but for oscillation 2. The red crosses correspond to the positions at which the individual loops in the bundle intersect the cut. The locations of the enhanced shear in the vz velocity component correspond to strong counter-directional flows. In both cases, several vortices develop in the vicinity of oscillating structures.

thumbnail Fig. 7.

Development of Kelvin-Helmholtz vortices and the Alfvén speed variation. Top: Alfvén speed and the corresponding velocity field streamlines in cuts parallel to the y − z plane at x = 13 Mm shown before the oscillation onset (left), during the oscillation (middle), and at the end of the oscillation (right). Bottom: same as above, but for oscillation 2. The red crosses correspond to the positions at which the individual loops in the bundle intersect the cut.

5. Discussion

5.1. Oscillation parameters

The displacement and velocity amplitudes in the two instances of bundle oscillations agree with the values that are typically observed in active region coronal loops (e.g., White & Verwichte 2012), although this also depends on the type and magnitude of the perturbation that causes the excitation of the oscillation. The detected oscillation periods are also within the range that is commonly seen in the observations (Nechaeva et al. 2019). We note that the oscillation periods decrease during the oscillation in both cases. This can be explained by changing physical properties in the magnetic loop bundle, such as the changing loop length or the distribution of the plasma along the loop. This evolution is expected in a dynamic environment like this because the length of the oscillating loops as well as the values of Alfvén speed can change on timescales comparable to the duration of the oscillation. The expected values of the oscillation periods estimated from P ∼ 2L/vA using the values for the average length and the Alfvén speed at the apex of the oscillating bundle loops at the beginning of each oscillation are 205 s and 175 s for oscillations 1 and 2, respectively. This roughly agrees with the detected initial periods. The change in the loop properties during the oscillation duration will affect the oscillation periods, however. Changes in the oscillation period over the duration of the oscillation due to changes in properties of the oscillating loop have both been seen in observations and were reproduced by numerical modelling (Kohutova & Verwichte 2017; Verwichte & Kohutova 2017; Su et al. 2018). This shift in oscillation properties has a diagnostic potential using coronal seismology methods. A more detailed test of coronal seismology methods in convection-zone-to-corona simulations involving synthetic observables will be addressed in a follow-up study. The oscillation damping times are comparable to oscillation periods in both cases and in agree with the observations of damped transverse oscillations, which are typically observed to decay within three to four oscillation periods (Goddard et al. 2017). We did not analyse the detailed profile of the oscillation damping, that is, whether the damping profile is better represented by an exponential profile, a Gaussian profile or a transition from Gaussian to an exponential profile, as described in Hood et al. (2013) and Pascoe et al. (2016). This model is based on the assumption of a monolithic cylindrical coronal loop with a non-homogeneous boundary layer at the loop interface, which is not representative of coronal structures in the self-consistent convection-zone-to-corona simulations.

5.2. Collective behaviour

The bundle of magnetic loops in the simulation does not oscillate in isolation. It is in fact difficult to isolate the oscillating structures from a static, background plasma because there is a high degree of collective behaviour among the structures in the simulated corona. The evolution of the individual magnetic loops in the bundle is not identical, but averaging the physical quantities at the bundle apex gives us the overall evolution of the bundle. This implies that care should be taken when modelling individual coronal loops as isolated structures. As the coronal loop evolution is coupled to the environment, the arcade model described by Hindman & Jain (2021) is more representative of the evolution of the coronal structures in our simulation. The observations also suggest that the oscillations of individual coronal loops are often coupled to the oscillation of nearby magnetic structures and rarely occur in isolation (Verwichte et al. 2004, 2009; Jain et al. 2015).

Regardless of the geometry, oscillating large-scale structures create shear flows that lead to Kelvin-Helmholtz instability and the subsequent development of vortices if the instability is not inhibited by the magnetic tension. The shear created by large-scale translational motions also contributes to the development of Kelvin-Helmholtz instability, provided the direction of the motion is perpendicular to the coronal magnetic field (Hillier et al. 2019; Barbulescu et al. 2019). The development of vortices in our simulation may therefore be a result of a complex interplay of oscillatory and translational motions of coronal structures. The traditional models of Kelvin-Helmholtz-unstable loops (e.g., Terradas et al. 2008; Antolin et al. 2014; Karampelas et al. 2017) assuming well-defined oscillating cylindrical loops embedded in a static plasma are too idealised, however, as there are no loops with clearly defined cross sections in our simulation. Because of a lack of clear loop boundaries, the vortices are instead developed at the locations of maximum velocity shear.

5.3. Oscillation damping and dissipation

We stress the importance of the oscillation damping time τ as this corresponds to the rate at which the wave energy is either converted into another wave mode or is dissipated. Empirical scaling of the damping time with the loop oscillation period is commonly cited as an indirect evidence that resonant absorption is the primary mechanism that causes loop oscillation damping (see e.g., the review by Nakariakov & Kolotkov 2020). It has been argued, however, that the use of these scaling laws for distinguishing between different damping mechanisms is questionable bacause of the inherent dependence of the damping time on the loop parameters (Arregui et al. 2008). We note that traditionally used scaling laws for resonant absorption assume a high density contrast between the loop and the surrounding plasma (Ofman & Aschwanden 2002), which is not the case in our simulation, as shown in Fig. 1. The oscillation damping times are further expected to depend on the magnetic Reynolds number given by Rm = UL/η, where U is the typical velocity scale, L is the typical length scale, and η is the magnetic diffusivity. Rm varies in the simulation as Bifrost uses η(r, t) which is spatially and temporally dependent; Rm in the simulation is several orders of magnitude smaller than the estimated values in the solar corona, however.

We note that the traditional models for oscillation damping due to resonant absorption rely on an inhomogeneous layer at the boundary of a thin cylindrical loop with an Alfvén speed gradient (Ruderman & Roberts 2002). This is not a valid approximation for the loops in our simulation, event though Alfvén speed gradients are abundant in the simulated corona. We see no clear evidence of mode conversion in the oscillating bundle (i.e. conversion to clearly identifiable spatially localised azimuthal oscillations); instead, the evolution of the physical quantities at the apex of the loop bundle suggests that the wave energy is dissipated into heat through the development of shear flows, leading to an increase in the viscous and resistive dissipation during the oscillation (in MHD models, the resistive and viscous dissipation terms are a parametrisation of processes operating on kinetic scales). Velocity shear leads to the development of Kelvin-Helmholtz vortices, which are detectable in the velocity field in the plane perpendicular to the bundle cross section. The increase in the ωx component in the vicinity of the bundle apex during the first oscillation decay suggests that the shear due to the oscillatory motion drives the development of vortices, which then dissipate, leading to subsequent ωx decrease effectively explaining oscillation damping and dissipation. However, the absence of such a clear vorticity peak at the loop apex during the second oscillation decay suggests that the picture in this case is not as clear, and multiple processes can contribute to the oscillation damping. The evolution of loop oscillations might be further affected by the motion of the loop footpoints, because they are not static. We note that the wave dissipation is only one of several possible mechanisms contributing to the large temperature increase seen at the apex of the oscillating loops.

The onset of Kelvin-Helmholtz instability in models of transversely oscillating loops is linked to the development of turbulence that leads to the formation of small scales which allows for fast dissipation of the wave energy (Hillier et al. 2020). For a loop to be considered truly turbulent it is necessary to demonstrate a non-linear cascade of energy to small scales, however. We cannot draw any conclusions about the presence of turbulent behaviour or a lack thereof in our simulation because of the limits posed by spatial resolution as well as by the magnetic diffusivity and viscosity. We also note that low Reynolds numbers in self-consistent MHD simulations artificially restrict the cascade to small scales (Howson et al. 2017).

Kelvin-Helmholtz vortices developed during oscillation damping have also been proposed to cause coronal oscillations to appear decayless in certain emission lines (Antolin et al. 2016). In that model, however, the KHI vortices were formed at much smaller spatial scales due to the sharp density (and Alfvén speed) contrast at the loop boundary, which is not the case for the loop bundle analysed in this work.

5.4. Implication for coronal loop models

We find that oscillation parameters and evolution observed in coronal loops are reproduced by self-consistent simulations that include complex magnetic field geometry and density structuring and that do not contain well-defined coronal loops. This approach provides insight into the evolution of the oscillating loop bundle in three dimensions, including the detailed evolution of the magnetic field, into the degree of collective oscillation of the surrounding plasma, and into the physical mechanisms associated with the oscillation damping and dissipation. This type of dynamics cannot be captured by idealised straight flux tube models. This might have widespread implications for the accuracy of the coronal seismology methods, which are mostly based on cylinder approximations for coronal loops. Even recent numerical studies of the evolution of initially homogeneous coronal loops in response to transverse motions suggest that the highly idealised picture of coronal loops as monolithic plasma cylinders is unlikely to be realistic in the first place (Antolin & Van Doorsselaere 2019). The question remains how realistic our current self-consistent simulations really are when detailed characteristics of the solar corona are to be reproduced. However, despite the complex collective behaviour in these self-consistent simulations, some results from simple coronal loop models are reproduced, namely the generation of the Kelvin-Helmholtz vortices by the transverse motions. The simple coronal loop models provide much value for understanding the fundamental physical processes at play. Caution should be taken when drawing conclusions from observations, however, whether the assumptions made in the models are still applicable in the analysed scenario. The combination of simple and self-consistent models is necessary for a detailed understanding of the oscillatory behaviour in the corona.

Finally, we note that the length of loops we can simulate in this type of setup is limited by the size of the simulation domain. The maximum length of magnetic loops in the simulation used in this work was 20–30 Mm. This affects the parameter space that is accessible by these models because several oscillation parameters scale with loop length. Larger domains are therefore needed for a more accurate one-to-one comparison of the oscillation parameters with the observations.

6. Conclusions

For the first time, we analysed the damping of coronal oscillations using a self-consistent 3D radiation-MHD model of the solar atmosphere spanning from the convection zone into the corona, the associated oscillation dissipation and heating, and finally, the physical processes that cause the damping and dissipation. The simulated corona that formed in this model does not depend on any prior assumptions about the shape of the coronal loops. Using magnetic field tracing, we analysed the evolution of a bundle of magnetic loops in the centre of the simulation domain. The magnetic bundle shows dynamic evolution and a high degree of collective behaviour of the individual loops in the bundle. We find that the bundle of magnetic loops shows damped transverse oscillations in response to perturbations in two separate instances with oscillation periods of 177 s and 191 s, velocity amplitudes of 10 km s−1 and 16 km s−1, and damping times of 176 s and 198 s, respectively. The oscillation parameters and evolution observed are in line with the values typically seen in observations of coronal loop oscillations. The oscillation periods decrease in both instances during the oscillations. We find that transverse coronal oscillations lead to the development of velocity shear in the simulated corona, resulting in the formation of vortices with sizes around one megameter seen in the velocity field caused by the Kelvin-Helmholtz instability. This contributes to the damping and dissipation of the transverse oscillations into heat. If the structure of the corona in the self-consistent models is indeed realistic, our models of monolithic and static coronal loops with constant lengths might need to be reevaluated in favour of more realistic models that account for loop properties that change with time and that relax the assumption of highly idealised wave guides.

Movies

Movie 1 associated with Fig. 1 Access here

Movie 2 associated with Fig. 2 Access here

Acknowledgments

P.K. acknowledges funding from the Research Council of Norway, project no. 324523. This research was also supported by the Research Council of Norway through its Centres of Excellence scheme, project no. 262622 and through grants of computing time from the Programme for Supercomputing. P.A. acknowledges funding from his STFC Ernest Rutherford Fellowship (No. ST/R004285/2).

References

  1. Anfinogentov, S. A., Nakariakov, V. M., & Nisticò, G. 2015, A&A, 583, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Antolin, P., & Van Doorsselaere, T. 2019, Front. Phys., 7, 85 [Google Scholar]
  3. Antolin, P., Yokoyama, T., & Van Doorsselaere, T. 2014, ApJ, 787, L22 [Google Scholar]
  4. Antolin, P., Okamoto, T. J., De Pontieu, B., et al. 2015, ApJ, 809, 72 [Google Scholar]
  5. Antolin, P., De Moortel, I., Van Doorsselaere, T., & Yokoyama, T. 2016, ApJ, 830, L22 [Google Scholar]
  6. Antolin, P., Schmit, D., Pereira, T. M. D., De Pontieu, B., & De Moortel, I. 2018, ApJ, 856, 44 [Google Scholar]
  7. Arregui, I., Ballester, J. L., & Goossens, M. 2008, ApJ, 676, L77 [NASA ADS] [CrossRef] [Google Scholar]
  8. Aschwanden, M. J., & Nightingale, R. W. 2005, ApJ, 633, 499 [Google Scholar]
  9. Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [Google Scholar]
  10. Barbulescu, M., Ruderman, M. S., Van Doorsselaere, T., & Erdélyi, R. 2019, ApJ, 870, 108 [Google Scholar]
  11. Breu, C., Peter, H., Cameron, R., et al. 2022, A&A, 658, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Carlsson, M., & Bogdan, T. J. 2006, Philos. Trans. Royal Soc. A, 364, 395 [NASA ADS] [CrossRef] [Google Scholar]
  13. Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Cheung, M. C. M., Rempel, M., Chintzoglou, G., et al. 2019, Nat. Astron., 3, 160 [NASA ADS] [CrossRef] [Google Scholar]
  15. Felipe, T. 2012, ApJ, 758, 96 [Google Scholar]
  16. Froment, C., Auchère, F., Bocchialini, K., et al. 2015, ApJ, 807, 158 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goddard, C. R., Pascoe, D. J., Anfinogentov, S., & Nakariakov, V. M. 2017, A&A, 605, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. González-Morales, P. A., Khomenko, E., & Cally, P. S. 2019, ApJ, 870, 94 [Google Scholar]
  19. Goossens, M., Andries, J., & Aschwanden, M. J. 2002, A&A, 394, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
  22. Hillier, A., Barker, A., Arregui, I., & Latter, H. 2019, MNRAS, 482, 1143 [Google Scholar]
  23. Hillier, A., Van Doorsselaere, T., & Karampelas, K. 2020, ApJ, 897, L13 [Google Scholar]
  24. Hindman, B. W., & Jain, R. 2021, ApJ, 921, 29 [CrossRef] [Google Scholar]
  25. Hollweg, J. V., & Yang, G. 1988, J. Geophys. Res., 93, 5423 [Google Scholar]
  26. Hood, A. W., Ruderman, M., Pascoe, D. J., et al. 2013, A&A, 551, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Howson, T. A., De Moortel, I., & Antolin, P. 2017, A&A, 602, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Howson, T. A., De Moortel, I., Antolin, P., Van Doorsselaere, T., & Wright, A. N. 2019, A&A, 631, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Jain, R., Maurya, R. A., & Hindman, B. W. 2015, ApJ, 804, L19 [NASA ADS] [CrossRef] [Google Scholar]
  30. Karampelas, K., Van Doorsselaere, T., & Antolin, P. 2017, A&A, 604, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Khomenko, E., & Cally, P. S. 2012, ApJ, 746, 68 [Google Scholar]
  32. Kohutova, P., & Popovas, A. 2021, A&A, 647, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Kohutova, P., & Verwichte, E. 2017, A&A, 606, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Kohutova, P., Antolin, P., Popovas, A., Szydlarski, M., & Hansteen, V. H. 2020, A&A, 639, A20 [EDP Sciences] [Google Scholar]
  35. Leenaarts, J., & Carlsson, M., & Rouppe Van Der Voort, L. 2015, ApJ, 802, 136 [NASA ADS] [CrossRef] [Google Scholar]
  36. Li, D., Yuan, D., Goossens, M., et al. 2020, A&A, 639, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Malanushenko, A., Cheung, M. C. M., DeForest, C. E., Klimchuk, J. A., & Rempel, M. 2022, ApJ, 927, 1 [NASA ADS] [CrossRef] [Google Scholar]
  38. Matsumoto, T. 2018, MNRAS, 476, 3328 [NASA ADS] [CrossRef] [Google Scholar]
  39. McIntosh, S. W., De Pontieu, B., Carlsson, M., et al. 2011, Nature, 475, 477 [NASA ADS] [CrossRef] [Google Scholar]
  40. Nakariakov, V. M., & Kolotkov, D. Y. 2020, ARA&A, 58, 441 [Google Scholar]
  41. Nakariakov, V. M., & Verwichte, E. 2005, Liv. Rev. Sol. Phys., 2, 3 [Google Scholar]
  42. Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [Google Scholar]
  43. Nechaeva, A., Zimovets, I. V., Nakariakov, V. M., & Goddard, C. R. 2019, ApJS, 241, 31 [NASA ADS] [CrossRef] [Google Scholar]
  44. Ofman, L., & Aschwanden, M. J. 2002, ApJ, 576, L153 [Google Scholar]
  45. Okamoto, T. J., Antolin, P., De Pontieu, B., et al. 2015, ApJ, 809, 71 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pascoe, D. J., Wright, A. N., & De Moortel, I. 2010, ApJ, 711, 990 [Google Scholar]
  47. Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016, A&A, 585, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Peter, H., & Bingert, S. 2012, A&A, 548, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Rempel, M. 2016, ApJ, 834, 10 [NASA ADS] [CrossRef] [Google Scholar]
  50. Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [Google Scholar]
  51. Şahin, S., & Antolin, P. 2022, ApJ, 931, L27 [CrossRef] [Google Scholar]
  52. Stein, R. F., & Nordlund, Å. 2001, ApJ, 546, 585 [Google Scholar]
  53. Su, W., Guo, Y., Erdélyi, R., et al. 2018, Sci. Rep., 8, 4471 [NASA ADS] [CrossRef] [Google Scholar]
  54. Terradas, J., Andries, J., Goossens, M., et al. 2008, ApJ, 687, L115 [Google Scholar]
  55. Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [Google Scholar]
  56. Van Doorsselaere, T., Andries, J., Poedts, S., & Goossens, M. 2004, ApJ, 606, 1223 [Google Scholar]
  57. Verwichte, E., & Kohutova, P. 2017, A&A, 601, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [Google Scholar]
  59. Verwichte, E., Aschwanden, M. J., Van Doorsselaere, T., Foullon, C., & Nakariakov, V. M. 2009, ApJ, 698, 397 [NASA ADS] [CrossRef] [Google Scholar]
  60. White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1.

Simulation setup. Left: bundle of magnetic loops and the photospheric magnetic field at t = 880 s. Top right: cut across the density structure at x = 13 Mm intersecting the apex of the magnetic bundle. Bottom right: cut across the temperature structure at x = 13 Mm. The white points mark the positions at which the individual loops in the bundle intersect the cuts. An animation of this figure is available online.
In the text
thumbnail Fig. 2.

projected view of the magnetic bundle in the xz-plane (left), yz-plane (centre), and xy-plane (right) at t = 880 s. An animation of this figure is available online.
In the text
thumbnail Fig. 3.

Eolution of the height of the individual loops in the bundle at x = 13 Mm as a function of time. The blue regions indicate the two instances of damped oscillatory motion in the vertical direction.
In the text
thumbnail Fig. 4.

Bundle evolution time series. Top: evolution of the longitudinal (green), normal (orange) and binormal velocity component (blue) at the apex of the bundle. Middle: evolution of the Joule volumetric heating rate (dashed red), the viscous volumetric heating rate (dotted red) and the temperature (black) at the apex of the bundle. Bottom: evolution of the average length (blue) and the Alfvén speed at the apex of the loops in the bundle. The blue regions indicate the time range of the two oscillations.
In the text
thumbnail Fig. 5.

Oscillation time series. Top: evolution of the detrended normal velocity component at the bundle apex averaged over the oscillating field lines in the bundle. The best-fit is shown in red. Middle: evolution of the Joule (dashed line) and viscous volumetric heating rate (dotted line) at the bundle apex. Bottom: temperature (black), the x-component of the vorticity averaged in the vicinity of the bundle apex (solid blue line) and the z-component of the vorticity averaged in the vicinity of the right bundle footpoint (dotted blue line). The time intervals correspond to the time ranges highlighted in blue in Figs. 3 and 4.
In the text
thumbnail Fig. 6.

Development of Kelvin-Helmholtz vortices near the oscillating loops. Top: vz velocity component and the corresponding velocity field streamlines in cuts parallel to the y − z plane at x = 13 Mm shown before the oscillation onset (left), during the oscillation (middle), and at the end of the oscillation (right). Bottom: same as above, but for oscillation 2. The red crosses correspond to the positions at which the individual loops in the bundle intersect the cut. The locations of the enhanced shear in the vz velocity component correspond to strong counter-directional flows. In both cases, several vortices develop in the vicinity of oscillating structures.
In the text
thumbnail Fig. 7.

Development of Kelvin-Helmholtz vortices and the Alfvén speed variation. Top: Alfvén speed and the corresponding velocity field streamlines in cuts parallel to the y − z plane at x = 13 Mm shown before the oscillation onset (left), during the oscillation (middle), and at the end of the oscillation (right). Bottom: same as above, but for oscillation 2. The red crosses correspond to the positions at which the individual loops in the bundle intersect the cut.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.